Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailoring defects and nanocrystal transformation for optimal heating power in bimagnetic CoyFe1−yO@CoxFe3−xO4 particles†
George
Antonaropoulos
 ab,
Marianna
Vasilakaki
ab,
Marianna
Vasilakaki
 c,
Kalliopi N.
Trohidou
c,
Kalliopi N.
Trohidou
 c,
Vincenzo
Iannotti
c,
Vincenzo
Iannotti
 d,
Giovanni
Ausanio
d,
Milinda
Abeykoon
d,
Giovanni
Ausanio
d,
Milinda
Abeykoon
 e,
Emil S.
Bozin
e,
Emil S.
Bozin
 f and
Alexandros
Lappas
f and
Alexandros
Lappas
 *a
*a
aInstitute of Electronic Structure and Laser, Foundation for Research and Technology – Hellas, Vassilika Vouton, 71110 Heraklion, Greece. E-mail: lappas@iesl.forth.gr
bDepartment of Chemistry, University of Crete, Voutes, 71003 Heraklion, Greece
cInstitute of Nanoscience and Nanotechnology, National Center for Scientific Research Demokritos, 15310 Athens, Greece
dCNR-SPIN and Department of Physics “E. Pancini”, University of Naples Federico II, Piazzale V. Tecchio 80, 80125 Naples, Italy
ePhoton Sciences Division, National Synchrotron Light Source II, Brookhaven National Laboratory, Upton, New York 11973, USA
fCondensed Matter Physics and Materials Science Division, Brookhaven National Laboratory, Upton, New York 11973, USA
First published on 30th November 2021
Abstract
The effects of cobalt incorporation in spherical heterostructured iron oxide nanocrystals (NCs) of sub-critical size have been explored by colloidal chemistry methods. Synchrotron X-ray total scattering methods suggest that cobalt (Co) substitution in rock salt iron oxide NCs tends to remedy their vacant iron sites, offering a higher degree of resistance to oxidative conversion. Self-passivation still creates a spinel-like shell, but with a higher volume fraction of the rock salt Co-containing phase in the core. The higher divalent metal stoichiometry in the rock salt phase, with increasing Co content, results in a population of unoccupied tetrahedral metal sites in the spinel part, likely through oxidative shell creation, involving an ordered defect-clustering mechanism, directly correlated to core stabilization. To shed light on the effects of Co-substitution and atomic-scale defects (vacant sites), Monte Carlo simulations suggest that the designed NCs, with desirable, enhanced magnetic properties (cf. exchange bias and coercivity), are developed with magnetocrystalline anisotropy which increases due to a relatively low content of Co ions in the lattice. The growth of optimally performing candidates combines also a strongly exchange-coupled system, secured through a high volumetric ratio rock salt phase, interfaced by a not so defective spinel shell. In view of these requirements, specific absorption rate (SAR) calculations demonstrate that the rock salt core sufficiently protected from oxidation and the heterostructure preserved over time, play a key role in magnetically mediated heating efficacies, for potential use of such NCs in magnetic hyperthermia applications.
Introduction
Magnetic nanoparticles (MNPs), a sub-class of nanoscale crystals (nanocrystals: NCs)1 that consist of open-shell transition metal elements, have been the subject of considerable research endeavor in recent years. Their advantages stem from their capability to respond to electromagnetic stimuli (e.g. a magnetic field), thus enabling a broad spectrum of applications ranging from catalysis,2 photonics,3 and data storage,4 to water treatment,5 energy storage6 and printing technologies.7 Moreover, from the standpoint of the present work, MNPs offer highly exploitable capabilities in the rapidly developing field of nanobiotechnology.8 The latter, amongst others, includes medical diagnostics with contrast agents, for magnetic resonance imaging (MRI) technologies and therapeutic strategies with heat emission carriers, for magnetic hyperthermia treatments, both taking advantage of facile bottom-up pathways for controlling and boosting the nanoparticles’ magnetic performance.9 In this endeavor, biocompatibility and low toxicity are necessary, but understanding how structural and morphological characteristics can be utilized as materials’ design parameters still requires insights into improving MNPs’ performance. More specifically, magnetic heating under the influence of alternating (AC) magnetic fields depends on Néel-Brown relaxations, which evolve with the magnetic anisotropy constant (K) and saturation magnetization (Ms),10 thus offering a pathway for hyperthermia efficiency optimization. Changing the NCs’ geometrical parameters, such as size11 and shape,12 offer another avenue to tune the associated relaxation times. While bottom-up, colloidal chemistry approaches are exploited with the purpose to imprint the aforementioned materials’ design characteristics in favor of hyperthermia, top-down fabrication methods offer alternative exploitable morphologies. The derived MNPs may entail either a multi-layered structure called synthetic antiferromagnet (SAF), or involve a single magnetic layer having a magnetic vortex configuration.13 Interestingly, such artificial MNPs mimic the superparamagnetic ones prepared by chemical synthesis, but with advantages when dispersion and actuation in biological media are required. Furthermore, the bottom-up growth of topologically distinct phases, such as in a core@shell-like geometry,14 involving contrasting magnetic-ordering states between the core and the shell [e.g. antiferromagnetic (AFM), ferromagnetic (FM) and/or ferrimagnetic (FiM)], has proven to be particularly effective in introducing exchange anisotropies. Such systems take advantage of the technologically exploitable exchange-bias effect,15,16 with a concomitant enhancement of the NCs’ hyperthermia response.12 Last but not least, the chemical composition also plays a key role in changing the MNPs’ magnetocrystalline anisotropy,17 thus allowing for further regulation of the Néel-Brown relaxation behaviour. In this respect, chemical substitution strategies have been evaluated, in an effort to tune the magnetic response of iron oxide NCs.18,19Compositional control of NCs
With the purpose to either provide new or enhance existing properties (cf. mechanical, electrical, optical, biological, magnetic, etc.), changing the chemical composition by introducing structurally compatible ions, has become a widely used method for the modification of the crystal lattice of a number of materials. Such an adjustment is being achieved through the incorporation of usually a small amount of atoms or ions, which would not normally be present in the matrix of the parent material crystal lattice. The ion being incorporated, can be either introduced in an interstitial crystallographic site or, most usually in the case of NCs, it can substitute another ion from the matrix.20 A special case of crystal lattice chemical alteration is doping, where ions of the matrix are replaced with ions of the same21 or different number of valence electrons,22 aiming mainly at the modification of their electronic structure related physical properties.23 The effects of such chemical substitutions become particularly noticeable on the nanoscale and great progress has been achieved in recent years, concerned with the control of chemical composition in nanocrystalline materials. Epitaxial growth of doped NCs gave great results in the past, allowing for significant technological development in novel materials, such as quantum dots.24 On the other hand, the fabrication of doped colloidal NCs offers additional advantages, as for example, the opportunity to control the photoluminescence of colloidal semiconductor NCs, raising at the same time technological challenges.25 Thus, over the last 15 years, research efforts have focused on ionic substitution in nanocrystals by means of colloidal chemistry principles. In this effort, two main pathways can be identified, substitution through ion diffusion or by mixing the appropriate precursors. In the first pathway, pre-formed colloidal NCs are being further subjected to an additional synthetic step, which includes a colloidal solution, containing the dopant/additive ions. For bulk materials, this demands elevated temperatures, as the procedure is governed by diffusion effects. The same procedure, for nanocrystalline derivatives on the other hand, can take place at moderate temperatures, typically lower than the temperatures routinely used in high-temperature colloidal syntheses. On the nanoscale, given the increased surface to volume ratio, the predominant effect is the absorption of the added ion at the highly active surface of the nanocrystal. Such procedures are known as ion-exchange methods, as the “additive” replaces an anion or cation accordingly, in the host crystal lattice. Their success is determined by the accurate control of four distinct processes: surface adsorption of the new ion, incorporation in the crystal lattice of the parent phase, lattice diffusion, and lattice ejection.26 The recent years have seen a surge of interest in using this method to form otherwise hard to obtain nanocrystal morphologies, with fine-tuned properties.27 The second pathway, requires mixing of all the ingredients necessary for the fabrication of the final product at the initial stage of the chemical reaction. Precursors which contain the necessary ions for the synthesis (e.g. metal–organic compounds), surfactant molecules and an appropriate solvent are typical ingredients for a colloidal nanoparticle synthesis. This assumes that both the ions of the host material and the substitutes are chemically compatible and capable of forming precursors, which react under the specified experimental conditions in a similar and predictable way. Choosing one over the other approach for the growth of core@shell iron oxide NCs is further discussed in the subsequent Experimental section.Advantages of chemical substitution in MNPs
The challenges for optimal nanomaterials’ composition occasionally come along with questions of how efficiently MNPs generate heat under AC magnetic field excitation. As magnetic hyperthermia is considered an innovative approach in synergistic therapeutic avenues for cancer treatment,28,29 materials’ design pathways to improve the hyperthermic properties are needed. One common strategy is to attempt to increase the magnetic anisotropy. At the same time, size is a critical factor for MNPs, especially for biomedical applications, where minimal amounts of relatively small yet magnetically active particles should be used to avoid possible cytotoxicity. Thus, designed MNPs ideally would rest in the superparamagnetic regime (i.e. at critical sizes, d < 20–30 nm),9,30 without compromising much of their magnetic power. Many promising strategies have been explored in this direction, including, modification of morphological features (size-shape tuned; d ∼ 20–40 nm),31 growth of shells (for interfacial interactions; d ∼ 15 nm)12,32 and alteration of the chemical composition (e.g. Zn-substituted ferrites; d ∼ 15 nm).33 The efficiency of the first two strategies, together with favourable nano-structural effects due to emerging Fe-site vacancies, mediating the composition, have been recently discussed for FexO@Fe3−δO4 bimagnetic NCs (d < 25 nm).34 The beneficial influence of defective structures with subcritical nanocrystal sizes (d ∼ 8–10 nm) has also been demonstrated with doped ferrites. In such cases, partial substitution of Fe by transition metals in the nanostructure optimizes the effective magnetic anisotropy of iron oxide nanocrystals (IONCs).19 While this pathway maintains the desired morphology/size, it also provides improved heating generation (cf. specific absorption rate, SAR), at least up to a certain level of substitution (e.g. at x ∼ 0.6, in CoxFe3−xO4).35,36Keeping in mind these findings, the present work aims to shed light on how atomic scale defect control can be manipulated by chemical substitution in suitably shaped core@shell IONCs in the sub-critical size range. For this purpose, synchrotron X-ray total scattering was utilized to probe their structure evolution at different Co-substitution levels. The findings were complemented by atomistic Monte Carlo simulations, which together with bulk magnetic measurements, offered a means to rationalize how tuning the population of crystal lattice vacancies may tailor heating power generation for hyperthermia applications.
Experimental
Synthesis of core@shell CoyFe1−yO@CoxFe3−xO4 IONCs
Here we follow a synthetic route designed to produce uniformly sized, core@shell CoyFe1−yO@CoxFe3−xO4 colloidal NCs, which were slightly modified from a previously demonstrated procedure that produced pure FexO@Fe3O4 particles.34,37–39 Importantly, this allows for the direct comparison of the magnetic behaviour and structural characteristics among these series. The chosen protocol offered nanocrystal samples in the size range of 14–18 nm that is below the nominal critical size for IONCs to present superparamagnetic behavior and enhance magnetic losses, adequate for energy conversion into heat.28 The protocol enables easy tuning of size and shape (spherical or cubic), while preserving a well-defined core@shell structure and good control of the composition; the cobalt content (x,y) of the samples made here varies from 12% to 35%. As mentioned earlier, the substitution of an ion in the host material could be realized through ion exchange. However, there is a drawback, associated with this technique when implemented in Wüstite@Spinel-ferrite core@shell-type NCs.40 Thermal treatment of the pre-formed NCs could compromise the highly sensitive core@shell structure, causing the undesired oxidation of the core.41 Even mild heating of the NCs in a colloidal solution containing the ions involved in the ionic exchange procedure can provide the chemical potential for the initiation of diffusion effects, in both the rock-salt and spinel crystal structures, which leads to the oxidation of the rock-salt phase (core) and the particle conversion to the spinel type.42Here, we suggest ways to improve the magnetic response and especially the magnetically induced heating performance of the MNPs, which is associated with the existence of an interface, between an AFM phase in the core and a FiM phase in the shell, while other types of magnetic anisotropy are also operational (cf. magneto-crystalline and surface anisotropy, etc.). Thus, we considered to grow the substituted MNPs either (i) by mixing the desired amounts of two distinct metal–organic precursors, one containing iron and one containing cobalt, at the initial stages of the reaction, a strategy which ensures the preservation of both magnetic phases or (ii) by utilizing a single metal–organic precursor, containing both iron and cobalt in a predetermined ratio. Both approaches produced well-shaped CoyFe1−yO@CoxFe3−xO4 NCs, with adjustable Co/Fe levels. The method of mixing different precursors, exclusively containing one metal ion, is slightly more practical, since it allows for a wider Co-content range, just by varying the precursor proportion during the synthesis, whereas the other approach is more favorable when precise control of the Co-content of the nanoparticles is needed.
Materials
All reagents were used as received without further purification. Oleic acid (technical grade, 90%), octadecene (technical grade, 90%), hexane (ACS reagent, ≥99%), absolute ethanol (≥98%) and sodium oleate powder (82%) were purchased from Sigma Aldrich. Iron(III) chloride (FeCl3·6H2O, ACS/Ph Eur reagent, ≥99%) and cobalt(II) chloride (CoCl2·6H2O, ACS reagent, 98%) were purchased from Merck. Deionized water was used when needed. Fe(III) oleate, Co(II) oleate and mixed Fe(III)/Co(II) oleate precursors were synthesized in the laboratory, as described in the following protocols.Synthesis protocols
Colloidal syntheses were carried out in 100 mL round bottom three-neck flasks connected via reflux condensers to a standard Schlenk line setup. Immersion temperature probes and digitally controlled heating mantles ensured accurate temperature control of the colloidal mixture. Ar gas has been used as a protective atmosphere. Previous studies have shown that FexO NCs formed under such synthetic conditions become oxidized to Fe3O4 and/or γ-Fe2O3 after removing the Ar-gas protection and exposing them to ambient air.43 Alternatively, a 5% H2/Ar gas mixture can also be used as a protective atmosphere in order to take advantage of the reductive action of H2, to further protect the sensitive rock-salt from being oxidized to the spinel forms. Since Co and Fe are introduced simultaneously into the colloidal mixture, it is assumed that based on the shell formation mechanism, Co is equally distributed in the whole nanoparticle volume, namely in both the core and the shell phases.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8–1
8–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 with respect to the metal-oleate precursor, is adequate to promote the formation of cubic NPs.39 Under the described experimental conditions, slightly larger nano-cubes, with edge diameters ranging from 18 to 20 nm can be realized in this way. The mixing of two separate oleate precursors or the use of a mixed Fe/Co oleate precursor seems to make the fine tuning of the sodium oleate/metal oleate ratio more difficult for the fabrication of well-formed cubic NPs, compared to pure iron oxide NPs. At the end of the synthesis, the colloidal mixture, containing the nanocrystals (NCs), was left to cool down at room temperature. The NCs were precipitated upon ethanol addition. They were then separated by centrifugation at 6000 rpm for 5 min, redispersed in hexane and centrifuged once more after adding ethanol in a 1
5 with respect to the metal-oleate precursor, is adequate to promote the formation of cubic NPs.39 Under the described experimental conditions, slightly larger nano-cubes, with edge diameters ranging from 18 to 20 nm can be realized in this way. The mixing of two separate oleate precursors or the use of a mixed Fe/Co oleate precursor seems to make the fine tuning of the sodium oleate/metal oleate ratio more difficult for the fabrication of well-formed cubic NPs, compared to pure iron oxide NPs. At the end of the synthesis, the colloidal mixture, containing the nanocrystals (NCs), was left to cool down at room temperature. The NCs were precipitated upon ethanol addition. They were then separated by centrifugation at 6000 rpm for 5 min, redispersed in hexane and centrifuged once more after adding ethanol in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with respect to the hexane. A short stay in a sonication bath may be needed after the centrifugation for the complete re-dispersion of the particles. Excessive sonication though may affect the quality of the dispersion, since this removes the surfactants from the particle surface. The whole process was repeated two additional times at a centrifugation speed of 1000 rpm. Although the size distribution is tuned during the synthesis, a well-chosen post-synthetic purification protocol is essential for an effective size-selective separation of the MNPs.46
1 ratio with respect to the hexane. A short stay in a sonication bath may be needed after the centrifugation for the complete re-dispersion of the particles. Excessive sonication though may affect the quality of the dispersion, since this removes the surfactants from the particle surface. The whole process was repeated two additional times at a centrifugation speed of 1000 rpm. Although the size distribution is tuned during the synthesis, a well-chosen post-synthetic purification protocol is essential for an effective size-selective separation of the MNPs.46
Characterization techniques
Morphological characterization
Structural characterization
The atomic PDF gives information about the number of atoms in a spherical shell of unit thickness at a distance r from a reference atom49 and is defined as
| G(r) = 4πr[ρ(r) – ρ0] | (1) |
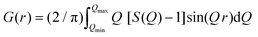 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) is the magnitude of the momentum transfer for elastic scattering, and S(Q) is the properly corrected and normalized total scattering function measured from Qmin to Qmax (0.25 ≤ Q ≤ 25 Å−1). The PDF data, collected over a sufficiently wide Q-range, thus carry structural information over a broad range of length scales, in contrast to traditionally used (bulk) probes, such as EXAFS and NMR, whose sensitivity is limited to the nearest-neighbor interactions. The experimental PDF, G(r), can subsequently be modelled by calculating the following quantity directly from a presumed structural model:
θ/λ) is the magnitude of the momentum transfer for elastic scattering, and S(Q) is the properly corrected and normalized total scattering function measured from Qmin to Qmax (0.25 ≤ Q ≤ 25 Å−1). The PDF data, collected over a sufficiently wide Q-range, thus carry structural information over a broad range of length scales, in contrast to traditionally used (bulk) probes, such as EXAFS and NMR, whose sensitivity is limited to the nearest-neighbor interactions. The experimental PDF, G(r), can subsequently be modelled by calculating the following quantity directly from a presumed structural model: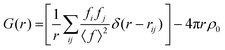 | (3) |
Magnetic characterization
The magnetic behaviour of the nanoparticle samples was evaluated using a vibrating sample magnetometer (VSM, Oxford instruments, Maglab 9 T), operating at a vibration frequency of 55 Hz. The measurements of the temperature-dependent magnetization, M(T), were carried out at 50 Oe at a fixed temperature rate of 1 K min−1 after either zero-field cooling (ZFC) or field cooling (FC) in 50 Oe from 5–300 K. Hysteresis loops, M(H), were obtained at room temperature and 5 K by sweeping the applied field from +50 kOe to −50 kOe and back to +50 kOe after cooling the sample from 300 K to 5 K under ZFC or an applied field 0 < Hcool ≤ 50 kOe (FC) for selected samples. In the FC procedure, once the measurement temperature was reached, the field was increased from Hcool to H = 50 kOe and the measurement of the loop was pursued. The M(H) data were recorded under a magnetic field sweep with an optimised rate of 30 Oe s−1 in order to minimize the propagation of a possible synchronization error of the measuring electronics, present in the case of sweeping rates greater than 200 Oe s−1. Special precautions were taken to maintain the structural integrity of the samples and more specifically to avoid possible spontaneous oxidation of the rock-salt core to spinel. The specimens for magnetic characterization were prepared by absorbing colloidal MNP dispersions on pre-weighed cotton wool pieces and letting the hexane to evaporate, until a pure nano-powder weight of ∼10 mg was obtained. They were subsequently placed in suitable size gel capsules, and then sealed under an Ar atmosphere (in a glovebox) in airtight vials. The vials were then opened just before the magnetic measurements to avoid unnecessary exposure to ambient air. This ensured that the magnetic behavior of the samples corresponds to that of the specimens probed by the synchrotron X-ray studies, as similar actions were undertaken at the NSLS-II facility.Monte Carlo simulations
To aid the interpretation of the experimental results for the MNPs, we have developed a microscopic core/shell model, where the interface (IF) of the two regions was explicitly included. The calculations were carried out with the Monte Carlo (MC) technique and the implementation of the Metropolis algorithm.53 Spherical MNPs were considered, with a diameter d, expressed in units of lattice spacing of a simple cubic lattice (cf. magnetite cell, a = 8.39 Å). The simulated MNPs consist of an AFM core and a FiM shell.54 For this purpose, we studied three model systems, with different structural features, to simulate the magnetic behaviour of a pure core@shell particle (“pure” corresponds to FexO@Fe3−δO4 MNPs, identified as sample S15 in reference34), and two Co-substituted core@shell MNPs involving a lower Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe proportion (“model #1”) and another one with a higher Co
Fe proportion (“model #1”) and another one with a higher Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe content (“model #2”). The radius of these three modelled MNPs remains the same, while other structural characteristics (e.g. core/shell volume ratio, vacant sites etc.) differ according to the degree of Co-substitution at the Fe-sites. Such a parameterization was motivated by the trends derived from the experimental xPDF data and the subsequent structural analysis. The exact morphological and structural characteristics of the simulated model MNPs are schematically illustrated in Fig. 1, and are as follows:
Fe content (“model #2”). The radius of these three modelled MNPs remains the same, while other structural characteristics (e.g. core/shell volume ratio, vacant sites etc.) differ according to the degree of Co-substitution at the Fe-sites. Such a parameterization was motivated by the trends derived from the experimental xPDF data and the subsequent structural analysis. The exact morphological and structural characteristics of the simulated model MNPs are schematically illustrated in Fig. 1, and are as follows:
“pure”, spherical MNPs of an average radius R = 9.1 and a shell thickness of 4 lattice spacings, assume 20% core and 80% shell, as fractions of the whole particle volume, entailing an AFM core and a FiM shell. The MNPs are assumed to have 25% vacant metal-ion crystallographic sites (with no cobalt content), randomly dispersed in both the core and shell phases.
The introduction of Co in the crystal structure at different levels, assumes two CoyFe1−yO@CoxFe3−xO4 MNPs of the same average radius, namely:
“model #1”, the MNPs have a radius of R = 9.1, shell thickness of 3.3 lattice spacings, resulting in 25% core and 75% shell volume, with a Co substitution level of 10% in both phases, meaning that now 10% of the provided Fe-sites in the core are occupied by Co and 10% of Fe-sites in shell are also occupied by Co. The model adopts 40% vacant metal-ion sites, randomly distributed over the core phase only, including the core interface (see eqn (4)).
“model #2”, the MNPs have a radius of R = 9.1, shell thickness of 1.9 lattice spacings, thus resulting in 50% core and 50% shell volume, with a Co substitution level of 35% in both phases, following the same concept as in model #1. This model adopts 40% vacant metal-ion sites, randomly distributed over the shell phase only, including the shell interface and surface.
The spins in the MNPs were assumed to interact with the nearest neighbor Heisenberg exchange interaction and at each crystal site they experience a uniaxial anisotropy. Under an external magnetic field, the energy of the system is calculated as:34,53,54
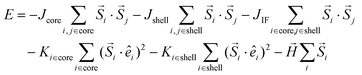 | (4) |
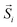 is the atomic spin at site i and êi is the unit vector in the direction of the easy-axis at site i. We consider the magnitude of the atomic spins in the two AFM sublattices to be equal to 1 and in the two FiM sublattices of the shell to be equal to 1 and 1.5, respectively. The first term in eqn (4) gives the exchange interaction between the spins in the AFM core and the second term gives the exchange interaction between the spins in the FiM shell. To take into account the difference of the magnetic transition temperatures [TN(core) < TC(shell)], we consider the exchange coupling constant of the core as Jcore = −0.1 JFM and that of the shell as Jshell = −1.5 JFM, where JFM is a reference value and it is considered to be the exchange coupling constant of a pure ferromagnet (FM), JFM = 1. The third term gives the exchange interaction at the interface between the core and the shell. The interface includes the last layer of the AFM core and the first layer of the FiM shell. The exchange coupling constant of the interface JIF is taken, JIF = −0.3 JFM. The fourth term gives the anisotropy energy of the AFM core, KC. If the site i lies in the outer layer of the AFM core Ki-core = KIF = 5 JFM (due to strong lattice mismatch) and Ki-core = KC = 0.5 JFM elsewhere. The fifth term gives the anisotropy energy of the FiM shell, which is taken as Kshell = 0.1 JFM and at the shell IF KIF = 5 JFM. If the site i lies in the outer layer (i.e., the surface) of the shell then the anisotropy is taken as Ki-shell = KS = 1.0 JFM, which is assumed to be random (rather than uniaxial). The last term in eqn (4) is the Zeeman energy. The relative values of Jshell and KS were calculated starting from the bulk values and then taking into account the size of the experimentally studied MNPs and the corresponding surface effects, in line with earlier atomistic simulations.34,53,55 Moreover, in the three models depicted Fig. 1, the structural defects (vacancies) were also taken into account as described by Lappas et al.,34 while in models #1 and #2, the Co ions were randomly distributed, assuming randomly oriented anisotropy axes, with K = 5 JFM (10 times larger than the Kcore), since the magnetocrystalline site anisotropy of Co ions is ten times larger than that of Fe ions.56
is the atomic spin at site i and êi is the unit vector in the direction of the easy-axis at site i. We consider the magnitude of the atomic spins in the two AFM sublattices to be equal to 1 and in the two FiM sublattices of the shell to be equal to 1 and 1.5, respectively. The first term in eqn (4) gives the exchange interaction between the spins in the AFM core and the second term gives the exchange interaction between the spins in the FiM shell. To take into account the difference of the magnetic transition temperatures [TN(core) < TC(shell)], we consider the exchange coupling constant of the core as Jcore = −0.1 JFM and that of the shell as Jshell = −1.5 JFM, where JFM is a reference value and it is considered to be the exchange coupling constant of a pure ferromagnet (FM), JFM = 1. The third term gives the exchange interaction at the interface between the core and the shell. The interface includes the last layer of the AFM core and the first layer of the FiM shell. The exchange coupling constant of the interface JIF is taken, JIF = −0.3 JFM. The fourth term gives the anisotropy energy of the AFM core, KC. If the site i lies in the outer layer of the AFM core Ki-core = KIF = 5 JFM (due to strong lattice mismatch) and Ki-core = KC = 0.5 JFM elsewhere. The fifth term gives the anisotropy energy of the FiM shell, which is taken as Kshell = 0.1 JFM and at the shell IF KIF = 5 JFM. If the site i lies in the outer layer (i.e., the surface) of the shell then the anisotropy is taken as Ki-shell = KS = 1.0 JFM, which is assumed to be random (rather than uniaxial). The last term in eqn (4) is the Zeeman energy. The relative values of Jshell and KS were calculated starting from the bulk values and then taking into account the size of the experimentally studied MNPs and the corresponding surface effects, in line with earlier atomistic simulations.34,53,55 Moreover, in the three models depicted Fig. 1, the structural defects (vacancies) were also taken into account as described by Lappas et al.,34 while in models #1 and #2, the Co ions were randomly distributed, assuming randomly oriented anisotropy axes, with K = 5 JFM (10 times larger than the Kcore), since the magnetocrystalline site anisotropy of Co ions is ten times larger than that of Fe ions.56
On these grounds, the hysteresis loops M(H) were calculated upon a field-cooling procedure, starting at a temperature T = 3.0 JFM/kB and down to Tf = 0.01 JFM/kB, at a constant rate under a static magnetic field Hcool, directed along the z axis. The exchange bias field was estimated by the hysteresis loop shift along the field axis HEB = −(Hright + Hleft)/2 and the coercive field was defined as Hc = (Hright − Hleft)/2, where Hright and Hleft are the points where the loop intersects the field axis. The fields H, Hc, and HEB are given in dimensionless units of JFM/gμB, the temperature T in units JFM/kB and the anisotropy constants K in units JFM. In this work, 104 MC steps per spin (MCSS) were used at each field step for the hysteresis loops and the results were averaged over 60 different samples.
Results and discussion
Cobalt-substituted spinel ferrites
In the spinel (M3+)8[M3+,M2+]16O32 (M = transition metal) structural type [where round brackets represent tetrahedral (Td) and the square brackets octahedral (Oh) coordination by oxygen crystallographic sites], typically, Co2+ (ref. 57) tends to replace Fe3+/Fe2+ resting at the Oh sites58 although some distribution at the tetrahedral spinel sites (cf. Td) cannot be excluded (Fig. 2). In such ferrospinels, the ratio of Co2+ → Fe3+/Co2+ → Fe2+ also affects the degree of inversion,18 but based on the characterization tools at our disposal (i.e. synchrotron X-ray PDF is not able to distinguish the different metal species in this case) we cannot conclude on such effects. As the substituting ion is introduced in the mixture of reactants simultaneously with the other precursors, at the early stages of the reaction, we are of the opinion that Co2+ ions are distributed over the whole volume of each particle, in both the core and shell, in proportion to their relative volume fraction. This behavior would be in line with earlier findings for the partial oxidative conversion of the initially grown wüstite to create the spinel shell.18,42,59–61 High resolution single-particle elemental mapping of the MNPs would be required to confirm this proposition.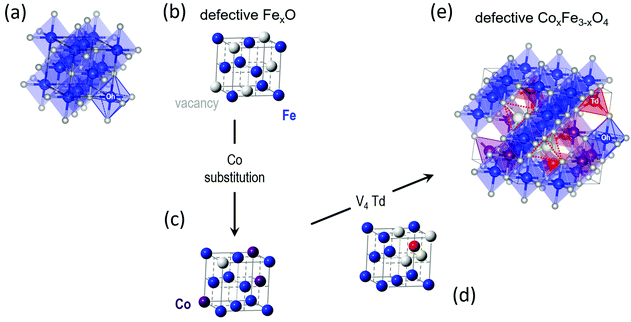 | ||
| Fig. 2 Crystal structure of (a) stoichiometric rock salt wüstite (FeO), with octahedrally (Oh) coordinated by oxygen (small white spheres) ferrous Fe2+ sites (blue spheres). The same structure, simplified not to show oxygen and coordination polyhedra, where (b) is a defective FexO structure, showing Fe and vacant (V) metal-ion sites only (large grey spheres), and (c) is a Co-(purple spheres)-substituted derivative, depicting a less-defected rock-salt structure. (d) A plausible ordered-defect rock-salt structure, with Fe2+ Oh sites, and interstitial ferric (Fe3+) tetrahedral sites (Td; red spheres) surrounded by four vacant (V) iron positions for charge balance. (e) Coalescence of V4-Td defect clusters59 upon further oxidation, may offer a likely pathway towards the nucleation of a defective (Td, vacant sites – depicted by dotted red line trigonal pyramids), Co-substituted ferrospinel structure. | ||
Structural insights from microscopy
Structural insights from synchrotron X-ray PDF
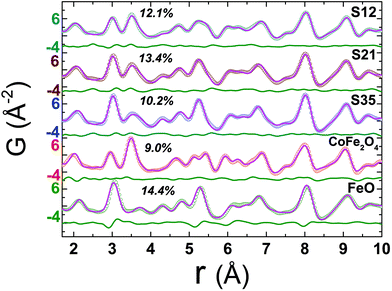
The need for both qualitative and semi-quantitative, phase-specific structural information from large ensembles of particles that could reveal Angstrom-long localized lattice and bonding distortions in the unit cells, motivated us to acquire the synchrotron X-ray total scattering data, for all nanoparticle specimens and compare them to the bulk reference materials (Fig. 4). These, combined with the PDF method, offer insights that move beyond the findings of techniques that focus on single nanoscale particles (e.g. HRTEM).40 Our effort here is concerned with (i) confirming the coexistence of two distinct crystallographic phases (i.e. rock salt and spinel) in a core@shell structure, (ii) estimating their average relative volume fractions, (iii) unveiling possible deviations of the local structure from the cubic symmetry and (iv) uncovering likely temperature-mediated effects; thus, we recorded the PDFs for all the materials between 10 < T < 300 K. Our analysis addressed mainly the low-r region in the atomic PDFs (r = 1–10 Å), as the field of view was limited due to the moderate Q space resolution of the experimental setup used.Local structure – rock salt phase modifications
Bulk CoFe2O4 was measured as a reference material. However, due to the similar electron count for Fe and Co, there is lack of sensitivity in X-ray PDF (xPDF) to differentiate between the two. For this reason, without loss of relevant information to which the method is sensitive to we have utilized models approximated by the magnetite Fe3O4 composition. The technique though is able to identify the differences between tetrahedral (Td) and octahedral (Oh) crystallographic sites, based on their quite different chemical environments. Thus, an iron-only spinel offers an adequate approximation for the description of our systems. This is confirmed by the observation that the atomic PDF in the low-r region for the bulk reference sample (CoFe2O4) is described equally well with the cubic cobalt ferrite spinel, as well as with the cubic magnetite models (Fig. S5, in ESI†). As the valence state differences are indistinguishable too, a possible site inversion could not be verified and the degree of inversion also could not be determined with this technique. Therefore, we performed the structure refinements based on the simplified, normal spinel, cubic configuration of magnetite, (Fe3+)8[Fe3+,Fe2+]16O32.62 Especially in the case of our model, this could be simply expressed as (M)8[M]16O32, where M stands for the transition metal cation (Fe or Co), the round brackets represent tetrahedral (Td) and the square brackets octahedral [Oh] coordination by oxygen crystallographic sites, assuming no M2+/M3+ inversion between Td and Oh sites. This model was then utilized to fit the xPDF data for nanoparticles of variable Co-concentrations, with a reasonably good quality of the fit (Rw) in the low-r region, at room temperature. However, the introduction of an additional crystallographic phase of rock-salt type cubic cell (FexO)63 is essential (vide infra) for obtaining adequate fit quality (Fig. 5).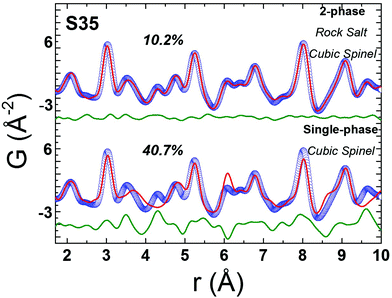 | ||
Fig. 5 Representative xPDF fits of data at T = 300 K over the low-r PDF region (1 nm) for nanocrystal sample S35, assuming a single-phase cubic spinel model (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Rw = 40.7%) at the bottom and a 2-phase rock-salt/cubic spinel model (Fm m, Rw = 40.7%) at the bottom and a 2-phase rock-salt/cubic spinel model (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m/Fd m/Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Rw = 10.2%) at the top, indicating clearly a structure consisting of two crystallographic phases for nanocrystals (S35). Similar results verify the core@shell structure for the rest of NCs studied (ESI, Fig. S6†). m, Rw = 10.2%) at the top, indicating clearly a structure consisting of two crystallographic phases for nanocrystals (S35). Similar results verify the core@shell structure for the rest of NCs studied (ESI, Fig. S6†). | ||
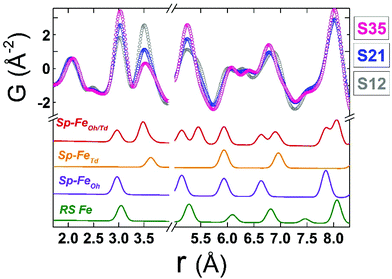
The resulting simplified 2-phase rock-salt@spinel cubic model describes well all the nanoparticle samples, unlike our previous work,34 where this model systematically failed to describe the peak at r ∼ 3 Å (PDF data of FexO@Fe3−δO4 or the fully oxidized Fe3−δO4 NCs), which implied a deviation of the nanoparticle local structure from the ideal cubic lattice configuration, that was better described with a distorted, tetragonal spinel model.34 In the samples studied here, there is no evidence for a local structure symmetry lowering from cubic to tetragonal. Another significant difference in these samples arises from their tendency to preserve the core@shell structure, as shown in the fit results, from the increased volume fraction of the rock-salt phase (see ESI, Table S3†). Interestingly, the higher the Co-content, the larger the volume fraction of the rock-salt phase. More specifically, as evidenced from the raw data, the nanoparticle PDF peak centered at r ∼ 3 Å shows a systematic shift to higher interatomic distances (of the same extent for all samples), compared to the bulk spinel reference (Fig. 6 and 7). At the same time, there is a clear evolution in peak intensity as the Co content rises (Fig. 7). It is helpful though to refer to the PDF peak identification, based on the expected positions of metal (Fe) interatomic distances in a 2-phase rock-salt@spinel system, as shown in Fig. 7 in the form of calculated partial PDFs. The peak at r ∼ 3 Å may correspond to the closest distance between the metal atoms at the Oh sites in the spinel structure (Fig. 2 and 7) Nevertheless, the experimentally observed shift to higher-r can be attributed to the strong presence of the rock-salt phase in all samples, since the nearest distance of a pair of M–M in the rock-salt is just above 3 Å (see Fig. 7, green line). That is why we were able to account for it when fitting the G(r) data by introducing an additional phase of rock-salt type in the model. Along these lines, the observable increase in peak intensity can also be explained by the growth of the rock-salt volume in the MNPs, occurring during the increase of the Co content, as demonstrated by the PDF fit results (ESI, Table S3†).
 | ||
| Fig. 6 Representative low-r raw data collected at T = 300 K for reference materials FeO (green circles), CoFe2O4 (red circles) and the FeO@CoFe2O4 nanocrystal sample S35 (blue line). The normalization is realized by dividing the x-PDF patterns with the intensity of the peak centered at ∼2.0 Å (first peak, attributed to nearest-neighbour Fe–O pairs). The various contributions of the two different crystallographic phases, represented here by the bulk reference samples, account for slight peak shifts and, in some cases, variations of peak intensities of the experimental PDFs in the NCs. For clarity, only data for nanocrystal sample S35 are shown here, whereas data for the remaining NCs (S12, S21) are compared in Fig. 7. | ||
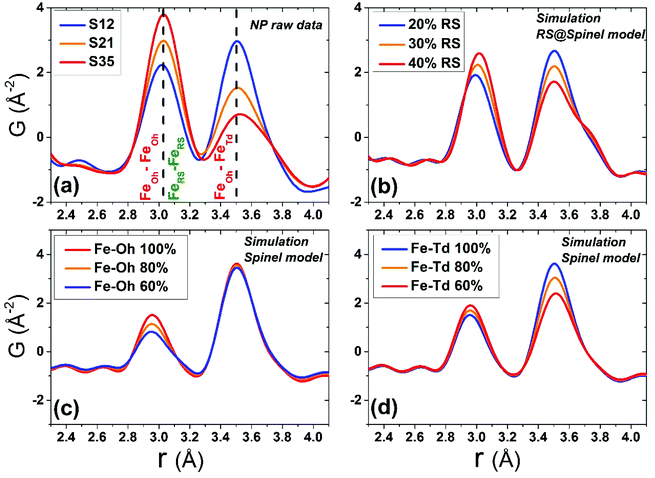
Although all fits were of reasonably good quality, significant conclusions were made from model-independent assessment of the raw PDF data and related simulations, compared to the PDF data obtained for the FexO@Fe3−δO4 nanoparticle system reported before.34 In the latter, the IONCs displayed variable shifts of the PDF peaks at r ∼ 3 Å (attributed to FeOh–FeOh and FeOh–FeTd interatomic distances, see Fig. 2 and 7, purple and red lines), even when no rock-salt phase was present, implying deviations from the ideal cubic local structure, stabilized by variable levels of Fe-site vacancies present in the spinel phase.34 In the Co-substituted samples, though, the peak shift towards higher r-values is accompanied by a dramatic increase of the peak intensity, clearly originating from rock-salt phase contribution, as corroborated by our PDF simulations (Fig. 8a and b). More specifically, the simulation shown in Fig. 8b implies that in a two-phase model, if a rock salt contribution is enhanced (no other changes made in the model) it causes the 3 Å peak intensity to grow and the 3.5 Å intensity to drop. Notably, the higher the Co-content in the nanoparticle samples, the higher the peak associated with the rock-salt phase, as presented in Fig. 8a. This is in line with the findings from data fittings over the low-r region (1 nm) of the PDFs. Thus, it seems that chemical substitution of Fe for M (M = Mn, Co, Ni), has two effects: it does not only partially eliminate the local distortions observed in pure iron oxide specimens,64 but also helps the preservation of the rock-salt core, at least in this type of Co-substituted core@shell systems. This could be rationalized by a less defective structure of the rock-salt cobalt-based oxide (CoO) core, while the CoxFe3−xO4 shell supports a higher resistance to oxygen diffusion.61
The behavior may imply that upon creation, the Co-mediated spinel shell acts as an effective barrier, impeding further core oxidation, commonly observed in heterostructured FeO@Fe3O4 nanoparticles.40 Indeed, earlier studies found that 12.5 nm, Co-substituted FeO presents limited surface oxidation, with a rock-salt@spinel structure, where the core is preserved 120 days after being exposed to air,61 while even smaller, 9.5 nm, MNPs appear not to change with aging, as indicated by their rather unchanged magnetic behaviour, 120 days after exposure to ambient conditions.65 The observation suggests that samples richer in Co exhibit a better-preserved core, possibly arising from the enhanced stability of the Co2+ ions against oxidation to Co3+ rather than that of Fe2+ counterparts, hence paving the way for synthesizing core@shell nanostructures that are highly oxidation-resistant over time. The observed intensity increase of the PDF peak in question, also complies with a higher metal ion occupancy in the rock-salt phase, due to its less defective structure (Fig. 2).
Local structure – defect mediated changes
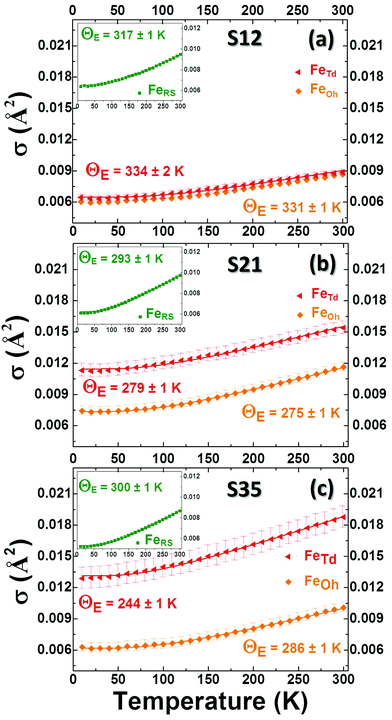
When the contribution of the rock-salt phase is enhanced, as described above, an inevitable lowering of the peak maximum at r ∼ 3.5 Å is to be expected, changing the 3.0/3.5 Å relative peak intensity ratio, favoring the 3 Å peak. This phenomenon is observed in the PDF data, but it is additionally intensified, implying possible sub-stoichiometry effects, which further lower the intensity of the 3.5 Å peak. The peak at r ∼ 3.5 Å corresponds to the closest distance between MOh and MTd in the spinel lattice, (Fig. 2) while a weaker contribution attributed to MTd–MTd pairs, at slightly higher interatomic distances (r), affects this peak as well (Fig. 7), as M ions could be either Fe or Co in the spinel structure in our nanoparticle samples. This complexity makes it challenging to investigate whether the peak intensity suppression is caused by atomic site defects (i.e. vacant crystallographic sites) either in MOh sites alone, or MTd sites alone, or both. To further explore whether the dramatic changes in the relative PDF peak intensities are indeed driven by the presence of vacancies at M sites, and to evaluate whether these vacancies have any site-specific preference, simulated xPDF patterns were obtained based on the normal cubic spinel configuration, while the population of either M-vacancies at the Oh sites or M-vacancies at the Td sites was varied (Fig. 8c and d). The simulations show that the higher the level of MOh vacancies in the spinel structure, the less intense the 3 Å peak, whereas the 3.5 Å peak is rather unaffected (Fig. 8c). Additionally, when MTd sites become vacant, this decreases dramatically the peak intensity at 3.5 Å and somewhat increases the intensity of the 3 Å peak (Fig. 8d). Combining the above-described trends, we conclude that given a significant percentage of rock-salt volume fraction, M sub-stoichiometry at the Td sites is the dominant effect, although some extent of vacancies on Oh sites cannot be excluded.To independently verify this proposal, we further extracted the atomic displacement parameters (ADPs) as a function of temperature (T = 10–300 K), based on the 2-phase model fits of the PDF data mentioned earlier. ADPs reflect atomic thermal motion and possible static disorder of atoms in the structure.66 Isotropic T-dependent ADPs (characterised by Uiso Å−2) for M sites in the two phases considered are plotted in Fig. 9. All the ADPs in sample S12 (Fig. 9(a)) show similar values that are typical of nanostructured systems,67,68 displaying a smooth upward trend with increased temperature. When going to Co-richer samples (S21 – Fig. 9(b), S35 – Fig. 9(c)) the ADPs for the Oh metal atoms in the spinel phase and those for the metal atoms in the rock-salt phase, remain approximately the same, as depicted by interpolating the ADP curves to T = 0 K and T = 300 K. On the other hand, the ADPs for the Td metal atoms in the spinel grow with the Co-content (cf. %Co increases on going from Fig. 9(a) to Fig. 9(c)), indicating possibly higher static disorder in the MTd sublattice. The absence of MTd ions from their predicted crystallographic sites, as suggested from the previous analysis based on simulations, makes the corresponding MTd–MTd pair bonds more compressible, thus allowing for broader atomic thermal motion. In fact, the ADPTd curve, observably pushes away from the ADPOh curve on going from S12 to S21 and S35 (Fig. 9). This apparent “splitting” becomes more significant as the Co content increases, implying significantly different static disorder associated with more dramatically perturbed chemical environment of the Td coordinated metal ions as compared to the Oh sites. This trend is further corroborated by the extracted Einstein temperature, ΘE, obtained from fitting the T-evolution of the ADPs with the correlated Einstein-model (Fig. 9):69
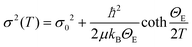 | (5) |
In this description, assuming Fe–Fe atom pairs only, ΘE become significantly smaller for Td ions, when the Co-content increases, thus suggesting lattice softening. At the same time a significant increase of σ0 for Td sites indicates a notable increase of static disorder in the MTd sub-lattice (ESI, Table S3†). A similar trend could be recognized for the rock-salt ADPs, which however show slightly lower values upon the Co-level increase, implying the subtle stabilization of the rock-salt phase against the spinel one. Minimal variations in the crystallographic site preference of Co ions (Td or Oh) from sample to sample cannot be excluded as well. Overall, the significant changes in ADPs, ΘE and σ0 for Td sites confirm that disorder in the Td spinel sites, mediated by Co incorporation in the lattice, is the predominant effect.
A plausible explanation of the above-mentioned effects may arise from an earlier proposed pathway for rock-salt self-passivation, through clusters of defect-units that coalesce in order to nucleate ferrospinel phases.42,59,60 Based on this mechanism, highly defective rock-salt structures would have a large population of vacant M2+ sites in the rock-salt lattice, which would give rise to a significant amount of interstitial M3+ ions for charge balancing reasons (Fig. 2d). Such interstitial ions are coordinated by ordered vacant sites (V) in such a manner (cf. V4-Td defect clusters),59 which resembles the MTd sites in spinels (Fig. 2e). Thus, during the rock-salt to spinel oxidative conversion, these interstitials may have the tendency to become M-ions occupying Td atomic sites in the spinel structure. In a less-defective rock-salt system, such as that obtained by Co-substitutions (Fig. 2c), there is less need for such charge balancing, thus resulting in fewer interstitial ions. It seems that the lower population of these interstitials in the Co-mediated rock salt phase has as a consequence, a lower population of MTd ions in its oxidized form (spinel) that reflects in more abundant Td vacant sites.
In summary, the PDF analysis was able to evaluate the crystal structure of the rock salt core and the spinel shell and quantify their average relative volumetric ratio (see ESI, Table S3†) for each particle batch. The analysis suggests that the incorporation of Co ions in the FexO phase, cures the commonly suffering from defects structure by effectively increasing the occupancy of metal ion sites in the rock salt phase. This seems to give the core a higher degree of resistance against oxidative conversion to a spinel shell. Thus particles with a higher Co content have also higher volume fractions of the rock salt phase in the core (ESI, Table S3†). The xPDF results indicate that a higher M2+ stoichiometry in the rock salt part by Co-substitutions, results in increased levels of unoccupied Td sites in the spinel, likely through oxidative shell creation involving an ordered defect clustering mechanism, while Oh sites may retain a typical moderate sub-stoichiometry, as implied by the comparable across the samples ADPs (Fig. 9).
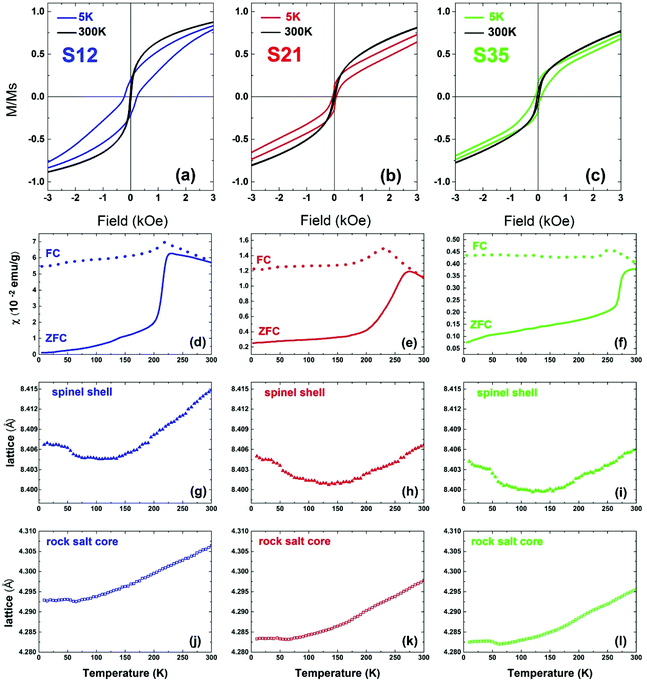
Magnetic behavior
In view of the variation of Co% content among the nanoparticle samples, the consequent structural evolution of the core@shell structure and the deviation from a perfect, fully stoichiometric crystallographic ordering (vide supra), we measured and evaluated their magnetic properties. Our main interest was to investigate whether and at what extent the identified structural characteristics affect the magnetization of the particles, the exchange interactions and the magnetocrystalline anisotropy, as depicted in measurable quantities, such as χ (magnetic susceptibility), MS (saturation magnetization), HEB (exchange bias field) and HC (coercive field). The dc magnetic susceptibility χ(T) curves (Fig. 10d–f), measured based on zero-field cooled (ZFC) and field cooled (FC) protocols,70 show a broad maximum, indicative of the characteristic temperature, TB, separating the superparamagnetic from the blocked state, as a result of the competition between the thermal energy and the magnetocrystalline anisotropy on the nanoscale, and is commonly expressed to be proportional to the particle volume and magnetic anisotropy.71 Here, for similar particle volumes, TB seems to be governed by the Co content and is increasing in a nearly linear way (Fig. S7, ESI†), probably due to increased magnetocrystalline anisotropy caused by the incorporation of Co in the lattice. Additionally the ZFC part of the χ(T) curves presents a sudden drop in all samples (Fig. 10d–f), which resembles the paramagnetic to antiferromagnetic (AFM) transition, marked by the characteristic Néel temperature, TN. The latter, progressively shifts from a low-temperature transition, as in wüstite (cf. FeO, TN = 198 K) towards room temperature, with Co-level increase (cf. CoO, TN = 291 K).72 It is peculiar though to think whether the subtle anomaly at 125–150 K in the low-Co% sample S12, with an increased volume fraction of the spinel shell, could be linked to a Verwey-like transition (TV), usually observed in bulk magnetite,73 as well as in its nanostructured counterparts.74,75 Actually, similar Verwey-like transitions at various characteristic temperatures for Mn-, Zn-, and Co-substituted spinel ferrites have been reported.76In view of assessing the coupling of lattice to magnetic transitions, the temperature variation of the refined lattice parameters from xPDF is considered. For the spinel phase, they show a systematic evolution with increasing temperature for all samples (Fig. 10g–i). Namely, an initial drop at ∼50 K until they reach a minimum between 120 K and 150 K and then a constant expansion with further T increase. It is worth noting that the more intense, step-like drop of the lattice parameter for sample S35 at 50 K coincides with a subtle anomaly shown in the ZFC χ(T) around the same temperature. It is however unclear if these barely visible anomalies in the magnetization curves are indeed related to delicate magnetoelastic effects, as the resolution of our magnetometer could not permit identifying such systematics across all samples studied. However, the lattice parameters of the rock salt core present also a similar anomaly, in the same T-range as that corresponding to the spinel phase. As the two crystallographic phases are mechanically coupled, magnetostriction (cf. compressive strain) may operate through their common inorganic interface to mediate the cross-coupling between the distinct structures.
Additionally, hysteresis loops were recorded under field-cooling conditions to further support the development of a macroscopic, exchange bias field (HEB) caused by interfacial exchange interactions. To further investigate the processes leading to HEB, M(H) loops under gradually increasing cooling fields have been recorded for selected NP samples. Fig. 11(a) shows the evolution of HEB with increasing cooling fields for samples S12 and S21, compared to an earlier studied 15 nm core@shell spherical FeO@Fe3O4 sample (identified as S15 in reference34). A quite peculiar observation results from their comparison. In S12 HEB values are much higher than those of S15, as expected from the better-preserved AFM core and the subsequently larger interface between the AFM and FiM phases, further assisted by the possible magnetic inhomogeneities stemming from higher magnetocrystalline anisotropy due to Co substitution. There is however, an important diminution of HEB for sample S21, which presents even weaker exchange-bias than the non-Co-containing iron oxide sample. Furthermore, while all samples present a weak discontinuous step like variation of magnetization near zero field (Fig. 10a–c), only sample S12, compared to S21, shows two switching field distributions, marked by different maxima in dM/dH ZFC and FC protocols (ESI, Fig. S9†), suggesting an inhomogeneous magnetic behavior possibly arising from coexisting magnetic components of contrasting Hcs. Summarizing, magnetization characteristics, such as χ, MS, and TB appear to present the expected, Co-mediated behaviour for such particles, which is mainly related to the spinel phase.18,35,77 On the other hand, the morphological and structural study of S12 and S21 (HRTEM and xPDF) suggests that both samples have a rather narrow size distribution, similar average sizes and core to shell volume ratios (Fig. 3,Table S3 in ESI†), which merely would not give rise to such inhomogeneities in magnetism and the differences in the HEBs.
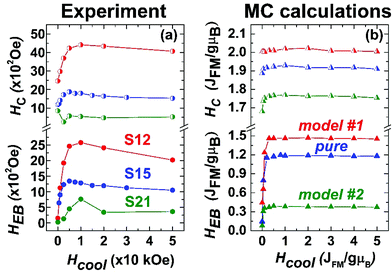 | ||
| Fig. 11 (a) Experimentally determined exchange bias (HEB, full circles) and coercive fields (HC, half-full circles) and (b) Monte Carlo calculations of HEB (full triangles) and HC (half-full triangles) for the three heterostructured nanocrystal models (Fig. 1). | ||
One can however argue that the outcomes are a likely consequence of the clustering of MNPs that perturbs the intrinsic magnetic properties due to dipolar interactions. We are of the opinion that such an effect may be negligible, because (i) even when the “concentration” of MNPs is the largest (e.g. S35: take into account the mass of cotton wool and nanoparticle powder used, 10.3 vs. 14.6 mg), the estimated volume of the nanoparticle powder is approximately 2% of the volume of cotton wool, inferring a large average distance of the embedded in the cotton wool NCs and (ii) the emerging anisotropy contribution due to Co and vacancies (vide infra: Monte Carlo simulations) plays the dominant role in the magnetic behaviour of the MNPs and masks the interparticle interactions even in the lower anisotropy case. Thus, a cause for the observed differences must be sought in view of the lattice compositional variations imposed by Co-substitutions and the different distribution of defects (in terms of Fe-vacancies) in the nanoparticle volume.
Monte Carlo modeling of MNPs
The corresponding amount and type of spin in each region of the three simulated MNPs (“pure”, model #1, and model #2; Fig. 1) are given in Table S1 in the ESI.†HEB is directly related to the applied Hcool, as a result of uncompensated spins frozen at the core–shell interface. There is a sharp increase in the HEB, when starting from zero-field and gradually applying larger Hcool (Fig. 11). This is attributed to the competition between the Zeeman energy and the other magnetic interactions within the system. As the Hcool increases, the magnetic coupling between the field and the magnetic moments (Zeeman energy) increases, tending to orient them along the field direction. For high enough fields, such coupling competes with the other magnetic interactions within the system overcoming the exchange coupling at the interface, which leads to a peak and then a gradual decrease of the HEB when the Zeeman energy dominates. This decrease is mainly determined by the intrinsic magnetic anisotropy of the system and by its microstructure.53,78 Differences between the observed and the MC calculated results are attributed to the fact that the model takes into account only the essential characteristics of the particle microstructure. HC on the other hand, although similarly affected by Zeeman energy, is much less dependent on the Hcool because it is governed largely by the magnetocrystalline anisotropy in both magnetic phases, thus allowing for relatively high values even at HCool = 0. Experimental and MC calculated results shown in Fig. 11 are in line with the described mechanisms. For an in-depth understanding of the mechanisms that dominate these measurable quantities, one has to look more closely into the details of crystal lattice configuration of the simulated models (Fig. 1, section S1 in the ESI†).
Apart from the competition of the spins at the core–shell (AFM-FiM) interface, some spins in the AFM phase (closed to-, but not necessarily at the interface) can contribute to the exchange bias. Such spins are pinned to a certain direction after the field cooling, and are coupled to the FiM layer.79 The origin of these pinned moments is not yet quite clear, but they are believed to be related with some kind of disorder, such as point defects.80 In fact, weak HEBs have been measured in the past for highly defective (due to crystallographic vacancies), single phase sub-critical size (d ∼ 10 nm) FiM NCs.34 In order to give an estimate of these effects in the MC calculation (Fig. 11b), the contribution of defects accounted for in these models was also examined (Fig. 1,Table S1 in the ESI†). So, upon Co-substitution:
model #1, represents particles with a significant amount of defects in their AFM core and core-IF, acting as pinning centres. The shell, with no defects at all, adopts a perfect FiM ordering. Additionally, the shell's large volume fraction in relation to the total particle volume means that the pinned moments around the defects should exhibit a strong coupling with the easily magnetized FiM phase, resulting in a large exchange bias. The inhomogeneous reversal of spins found in such exchange-bias systems leads to an increased HC as well,81 illustrated also in Fig. 11b for model #1.
“pure” model, offers a somewhat lower exchange bias and coercive fields. Although this model has a similar AFM volume (20% core compared to 25% core in model #1), the significantly smaller population of defects in the core and the core-IF results in less pinning centres and consequently exchange interactions, lowering the HEB and HC. A more defective FiM shell should also negatively affect its ability to couple with pinned spins near the AFM/FiM interface.
model #2, presents the lowest calculated HEB. In this case, there are no defects at all in the AFM core, which could play the role of pinning centres. The increased volume fraction of the core (50%) results in a relatively thin and highly defective FiM shell, which along with a high Co percentage (Co substitution decreases the magnetization of spinel: Fig. 10d–f, Table S4 in ESI†) is unable to strongly interact with the uncompensated spins at the AFM/FiM interface. Thus, such a small HEB, as shown in Fig. 11b, is the outcome. Normally, an increased Co-level in a given Fe/Co spinel system would increase its coercivity, due to the increased magnetocrystalline anisotropy, mediated by Co. This is not the case in model #2 because of the discussed morphological characteristics (smaller volume of the spinel-FiM phase, which has a rather negligible contribution in HC) and the very weak exchange coupling interactions.
To shed light on the effects of Co-substitution and defects (vacant sites), on HEB and HC, we further investigated several variations of model #1 and model #2, looking into how the core or shell separately may be affected (S1, Fig. S1 and Fig. S2 in ESI†). A particle with a perfectly ordered, non-defective core would exhibit the poorest magnetic response. However, this extreme case is rather impossible to obtain in a lab-based chemical synthesis protocol. Realistically, the rock salt core plays mainly a role in the exchange interactions to the extent that it creates a well-defined AFM/FiM interface, so, it is crucial that it can be sufficiently protected from oxidation and preserved over time. On the other hand, the spinel shell seems to be strongly, negatively impacted by a large population of defects, because these perturb the FiM ordering, and thus the shell's ability to interact with uncompensated or pinned spins in the core, near the interface. We find that raising the Co-concentration has a favourable effect on the properties of interest (Fig. S2, ESI†), including counter-balancing the detrimental defect-induced effects.
Therefore, designing plausible optimized core@shell MNPs, where sizeable HEB and HC are combined, while high magnetization values are maintained, would require devising NCs, bearing key characteristics, namely: (i) grown in the size range close to 15 nm, (ii) have a moderate Co substitution level (∼10%), (iii) involve a well-preserved core, accounting for a low-fraction (∼20–30%) of the entire particle volume, with defects typical of a sub-stoichiometric rock-salt phase, and (iv) a spinel shell that is as less defective as possible, preferably resembling the ideal spinel structure. It is not surprising that S12, which presents a desired magnetic behavior (Fig. 10d and 11a), has such characteristics, making this sample a nearly optimal candidate for applications.
Calculation of the specific absorption rate (SAR)
The measured magnetic properties and the associated lattice-driven effects, discussed in the previous sections, aimed to set the stage for assessing the MNPs’ application potential as smart heating mediators. The possibility for exploiting magnetic heating, generated by ferrite particles exposed to AC magnetic fields, offers an innovative modality in biomedical applications. To this extent magnetic hyperthermia treatment of tumours, has been extensively studied in recent years.82 Ferrite particles have been widely considered for such applications, as their heating power shows a marked dependency on the particle size and high sensitivity in size-distribution met in real samples.11 In that respect, the largest among them (d ∼ 25 nm), display enhanced magnetically-induced heating performances, especially when structural defects occurring during synthesis are eliminated.30 However, under particular circumstances, during the oxidative transformation of FexO@Fe3O4 core–shell nanocubes (d ∼ 23 nm), atomic scale defects, such as Fe2+ deficient sites, may positively influence hyperthermic properties.83 Along this direction, raising the population of Fe-vacancies, in small size Fe3O4 nanospheres (d ∼ 8 nm), seems to offer an alternative exploitable pathway for magnetic hyperthermia.34 The differences in the observed heating responses are generally related to critical particle sizes84 and magnetic anisotropy terms.85 Thus, optimizing the latter for particle sizes, tailored within the biological compatible limits, set by toxicity and patient discomfort,86 is particularly important. In this endeavor, heat generation capabilities can be assisted further by tuning the MNPs’ morphology,55 including topologically arranged coupled core and shell phases,12 and increased cation deficiency or even control composition.The detailed characterization of the CoyFe1−yO@CoxFe3−xO4 IONCs, involving properties such as HEB and HC, pertaining to exchange and magnetocrystalline anisotropies, was aimed at exploring possible complementary pathways for enhancing the heating performance of exchange coupled AFM/FiM phases. For this purpose, we calculated the SAR values for the studied MNPs, according to the linear response theory for the Néel-Brown relaxation model.10 (S2, ESI†) The calculations were performed for different AC field amplitudes, H0, at a frequency of f = 500 kHz. The SAR performance for MNPs with various structural characteristics is compiled in Fig. 12. The calculations compare Co-substituted (12%–35%) mixed-metal oxides, developed for this work, and two contrasting iron oxide particles, with no Co-incorporation, reported earlier. The latter are either similar to the Co-derivatives’ size, with a FexO@Fe3O4 core@shell (S15; d ∼ 15 nm) structure, or of a sub-critical size, involving single-phase (S8; d ∼ 8 nm), highly defective ferrospinel NCs.34
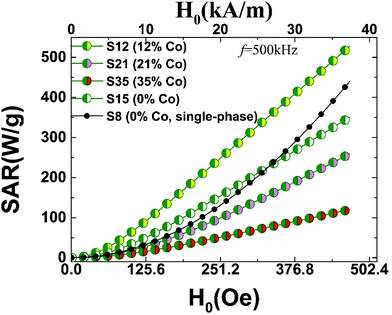 | ||
| Fig. 12 Specific absorption rate (SAR) calculated on the grounds of susceptibility losses (AC field amplitude, H0 and f = 500 kHz) for Co-substituted heterostructured nanocrystals (15 nm), which are compared with 8 nm (S8) and 15 nm (S15) Fe-containing only34 nanocrystals; SAR values are derived in view of the linear response theory of a modified Néel-Brown relaxation Monte Carlo model. | ||
Since SAR shows a marked dependency on particle size, the size distribution in real samples is crucial when comparisons are drawn. For example, experiments on cobalt ferrite MNPs (8–25 nm) find SAR values ranging from 40–50 W g−1 in small sizes (8 nm) and depending on the conditions (H0, f), raise up to about 600–800 W g−1 at intermediate sizes (13–15 nm).87 To place the present work in the context of related experiments, we would like to note that our calculated magnetic fluid heating power of 300–400 W g−1 (Fig. 12) for the present core@shell nanoparticles, are for example, within the window of measured SAR values, obtained from polydisperse iron-oxide (cf. maghemite and cobalt ferrite) nanoparticles,11 with characteristic diameters between 12–17 nm (i.e. similar to our MNPs), studied also under related conditions (H0 = 24.8 kA m−1 and f = 700 kHz).
The calculated SAR values follow a smooth monotonic increase (Fig. 12), resembling the experimentally measured upward trends reported previously.84 The higher anisotropy volume of MNPs with a core@shell topology results in a deviation from the quadratic field dependence of the SAR,87 displayed only by the smaller particle (S8). On one hand, increasing the anisotropy of ferrite MNPs, consisting of a single magnetic phase (S8) by introducing a large amount of defects and thus spin-pining centers, makes such particles to perform comparably to the FexO@Fe3O4 system (S15) carrying higher exchange anisotropy (cf. S8–S15,Fig. 12). However, when the magnetocrystalline anisotropy is raised by introducing Co ions in the lattice, in addition to an already strongly exchange-coupled system, the resulting SAR performance is assisted further (cf. S12, Fig. 12), thus supporting our aforementioned hypothesis for a nearly optimally designed candidate (S12). Worth noting though, that the simple coexistence of Co ions and AFM/FiM interfaces does not warrant enhanced SARs. Our calculations indicate that high magnetocrystalline anisotropies, usually expressed by large HCs, and high exchange anisotropies, supported by sizeable HEBs, are prerequisites for optimal SAR values. In fact, the evolution of the calculated SARs (cf. S12 > S15 > S21; Fig. 12) follows the trend obeyed by the related magnetic quantities (Fig. 11) that are mediated by compositional changes (i.e. Co-content and vacancies). Further Co-content increase generates an even weaker SAR performance (S35), due to the Co-mediated nanocrystal transformations and the consequent HEB and HC weakening, already discussed.
Conclusions
The effects of cobalt incorporation in spherical core@shell CoyFe1−yO@CoxFe3−xO4 NCs (d ∼ 15 nm) have been studied on an atomistic level. We find that the sub-stoichiometric rock salt-like wüstite (FeyO) tends to heal its vacant Fe sites upon Co substitution, helping its stabilization. The trend becomes more prominent at elevated Co levels that appear to impede the mechanism for the oxidative conversion of rock salt to spinel. Self-passivation of the initially formed rock salt NCs is still possible, creating a spinel-like shell, which yields core@shell nanostructures with relatively high volumetric ratios of the core phase that grows with the Co content. The xPDF analysis indicate that a higher divalent metal (M2+) stoichiometry in the rock salt part by Co-substitutions, results in increased levels of unoccupied tetrahedral (Td) sites in the spinel, likely through oxidative shell creation involving an ordered defect-clustering mechanism. The population of Td site atomic-scale defects of the shell is directly correlated to the core stabilization and increases when Co abundance increases. On the other hand, the extent of octahedral (Oh) vacant sites seems to follow the more conventional behavior met in ferrospinel nanostructured systems.Concerning the magnetic properties, the core-to-shell volumetric ratio is shown to have an immediate effect on the buried interface dimensions, thus affecting the exchange coupling interactions, reflecting a sizeable exchange-bias field (HEB). The latter shows a strong correlation with the cooling field strength and depends on the ability of the available uncompensated spins at the AFM-FiM interfaces. On the other hand, the coexistence of Co sites and atomic-scale defects in the crystal structure, in the form of Fe- and/or Co-ion Td vacancies (predominantly in the spinel phase), significantly affects the magnetocrystalline anisotropy and magnetic ordering. We find that raising Co-concentration has favorable effect on the properties of interest, including changes in the magnetization values and coercive fields (HC). In fact, the enhanced HC and HEB seem to be prerequisites for hyperthermic effects entailing high specific absorption rates (SAR).
Combining experiments with Monte Carlo simulations, we are able to suggest that designed heterostructured NCs of about 15 nm total diameter (cf. below the critical size, d < 20–30 nm), synthesized by controlled colloidal chemistry protocols, with a Co content level of about 10%, which leads to a volumetric fraction of the core to about 20–30% (over the whole particle volume), should result in optimal heating power. To achieve such a performance, the nanoarchitecture is dressed with the advantageous protection of the spinel shell, in contrast to not that well-performing, in terms of SAR, non-Co-containing iron oxide NCs. The suggested Co substitution level allows for a certain amount of desirable defects in the rock salt core, but would not create excessive vacancies in the Td sites in the spinel, which would perturb its otherwise beneficial FiM ordering and the shell's ability to interact with uncompensated spins near the buried interface. Fine tuning of such quantities, could result in MNPs with remarkable magnetically mediated heating power for possible hyperthermia applications.
Author contributions
Investigation: GAnt – synthesis/XRD/TEM/EDS; investigation: EB, MA, GAnt – PDF; investigation: VI and GAus – magnetic measurements; formal analysis; GAnt – experiment; formal analysis: MV and KNT – theory; writing – original draft: GAnt; writing – review and editing: GAnt, EB, AL; supervision: AL; project administration: AL; conceptualisation: AL.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research used the beamline 28-ID-2 of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) User Facility operated by Brookhaven National Laboratory (BNL). Work in the Condensed Matter Physics and Materials Science Division at BNL was supported by the DOE Office of Basic Energy Sciences. Both activities were supported by the DOE Office of Science under Contract No. DE-SC0012704. KNT and MV acknowledge the support received by the European Union's Horizon 2020 Research and Innovation Programme: FET Proactive under grant agreement No. 731976 MAGnetic nanoparticle based liquid ENergy materials for Thermoelectric device Applications (MAGENTA) www.magenta-h2020.eu.Notes and references
- M. Casavola, R. Buonsanti, G. Caputo and P. D. Cozzoli, Eur. J. Inorg. Chem., 2008, 2008, 837–854 CrossRef.
- A.-H. Lu, W. Schmidt, N. Matoussevitch, H. Bönnemann, B. Spliethoff, B. Tesche, E. Bill, W. Kiefer and F. Schüth, Angew. Chem., Int. Ed., 2004, 43, 4303–4306 CrossRef CAS PubMed.
- L. He, M. Wang, J. Ge and Y. Yin, Acc. Chem. Res., 2012, 45, 1431–1440 CrossRef CAS PubMed.
- N. A. Frey and S. Sun, Inorganic Nanoparticles: Synthesis, Applications, and Perspectives, CRC Press, 2011 Search PubMed.
- D. W. Elliott and W. Zhang, Environ. Sci. Technol., 2001, 35, 4922–4926 CrossRef CAS PubMed.
- P. Tartaj, M. P. Morales, T. Gonzalez-Carreño, S. Veintemillas-Verdaguer and C. J. Serna, Adv. Mater., 2011, 23, 5243–5249 CrossRef CAS PubMed.
- D. V. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2010, 110, 389–458 CrossRef CAS PubMed.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- G. C. Papaefthymiou, Nano Today, 2009, 4, 438–447 CrossRef CAS.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- J.-P. Fortin, C. Wilhelm, J. Servais, C. Ménager, J.-C. Bacri and F. Gazeau, J. Am. Chem. Soc., 2007, 129, 2628–2635 CrossRef CAS PubMed.
- S. Noh, W. Na, J. Jang, J.-H. Lee, E. J. Lee, S. H. Moon, Y. Lim, J.-S. Shin and J. Cheon, Nano Lett., 2012, 12, 3716–3721 CrossRef CAS PubMed.
- S. Leulmi, H. Joisten, T. Dietsch, C. Iss, M. Morcrette, S. Auffret, P. Sabon and B. Dieny, Appl. Phys. Lett., 2013, 103, 132412 CrossRef.
- R. Ghosh Chaudhuri and S. Paria, Chem. Rev., 2012, 112, 2373–2433 CrossRef CAS PubMed.
- J. Nogués and I. K. Schuller, J. Magn. Magn. Mater., 1999, 192, 203–232 CrossRef.
- M.-H. Phan, J. Alonso, H. Khurshid, P. Lampen-Kelley, S. Chandra, K. Stojak Repa, Z. Nemati, R. Das, Ó. Iglesias and H. Srikanth, Nanomaterials, 2016, 6, 221 CrossRef PubMed.
- A. H. Habib, C. L. Ondeck, P. Chaudhary, M. R. Bockstaller and M. E. McHenry, J. Appl. Phys., 2008, 103, 07A307 CrossRef.
- W. Baaziz, B. P. Pichon, Y. Liu, J.-M. Grenèche, C. Ulhaq-Bouillet, E. Terrier, N. Bergeard, V. Halté, C. Boeglin, F. Choueikani, M. Toumi, T. Mhiri and S. Begin-Colin, Chem. Mater., 2014, 26, 5063–5073 CrossRef CAS.
- A. Pardo, B. Pelaz, J. Gallo, M. Bañobre-López, W. J. Parak, S. Barbosa, P. del Pino and P. Taboada, Chem. Mater., 2020, 32, 2220–2231 CrossRef CAS.
- R. Kant, D. Sharma, A. Bansal and R. Singh, Mater. Technol., 2021, 36, 513–520 CrossRef CAS.
- K. Pradeev raj, K. Sadaiyandi, A. Kennedy, S. Sagadevan, Z. Z. Chowdhury, M. R. B. Johan, F. A. Aziz, R. F. Rafique, R. Thamiz Selvi and R. Rathina bala, Nanoscale Res. Lett., 2018, 13, 229 CrossRef CAS PubMed.
- B. Cojocaru, D. Avram, V. Kessler, V. Parvulescu, G. Seisenbaeva and C. Tiseanu, Sci. Rep., 2017, 7, 9598 CrossRef PubMed.
- P. Bhattacharya and S. Neogi, Rev. Chem. Eng., 2019, 35, 861–876 CrossRef CAS.
- P. R. Kratzert, J. Puls, M. Rabe and F. Henneberger, Appl. Phys. Lett., 2001, 79, 2814–2816 CrossRef CAS.
- R. Beaulac, P. I. Archer, S. T. Ochsenbein and D. R. Gamelin, Adv. Funct. Mater., 2008, 18, 3873–3891 CrossRef CAS.
- D. Chen, R. Viswanatha, G. L. Ong, R. Xie, M. Balasubramaninan and X. Peng, J. Am. Chem. Soc., 2009, 131, 9333–9339 CrossRef CAS PubMed.
- S. Gupta, S. V. Kershaw and A. L. Rogach, Adv. Mater., 2013, 25, 6923–6944 CrossRef CAS PubMed.
- X. Liu, Y. Zhang, Y. Wang, W. Zhu, G. Li, X. Ma, Y. Zhang, S. Chen, S. Tiwari, K. Shi, S. Zhang, H. M. Fan, Y. X. Zhao and X.-J. Liang, Theranostics, 2020, 10, 3793–3815 CrossRef CAS PubMed.
- A. Rajan and N. K. Sahu, J. Nanopart. Res., 2020, 22, 319 CrossRef CAS.
- R. Chen, M. G. Christiansen, A. Sourakov, A. Mohr, Y. Matsumoto, S. Okada, A. Jasanoff and P. Anikeeva, Nano Lett., 2016, 16, 1345–1351 CrossRef CAS PubMed.
- S. Tong, C. A. Quinto, L. Zhang, P. Mohindra and G. Bao, ACS Nano, 2017, 11, 6808–6816 CrossRef CAS PubMed.
- J.-H. Lee, J. Jang, J. Choi, S. H. Moon, S. Noh, J. Kim, J.-G. Kim, I.-S. Kim, K. I. Park and J. Cheon, Nat. Nanotechnol., 2011, 6, 418–422 CrossRef CAS PubMed.
- D. Yoo, H. Jeong, S.-H. Noh, J.-H. Lee and J. Cheon, Angew. Chem., Int. Ed., 2013, 52, 13047–13051 CrossRef CAS PubMed.
- A. Lappas, G. Antonaropoulos, K. Brintakis, M. Vasilakaki, K. N. Trohidou, V. Iannotti, G. Ausanio, A. Kostopoulou, M. Abeykoon, I. K. Robinson and E. S. Bozin, Phys. Rev. X, 2019, 9, 041044 CAS.
- S. Anjum, R. Tufail, K. Rashid, R. Zia and S. Riaz, J. Magn. Magn. Mater., 2017, 432, 198–207 CrossRef CAS.
- E. Fantechi, C. Innocenti, M. Albino, E. Lottini and C. Sangregorio, J. Magn. Magn. Mater., 2015, 380, 365–371 CrossRef CAS.
- J. Park, K. An, Y. Hwang, J.-G. Park, H.-J. Noh, J.-Y. Kim, J.-H. Park, N.-M. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895 CrossRef CAS PubMed.
- H. Khurshid, W. Li, S. Chandra, M.-H. Phan, G. C. Hadjipanayis, P. Mukherjee and H. Srikanth, Nanoscale, 2013, 5, 7942 RSC.
- M. I. Bodnarchuk, M. V. Kovalenko, H. Groiss, R. Resel, M. Reissner, G. Hesser, R. T. Lechner, W. Steiner, F. Schäffler and W. Heiss, Small, 2009, 5, 2247–2252 CrossRef CAS PubMed.
- R. U. Ichikawa, A. G. Roca, A. López-Ortega, M. Estrader, I. Peral, X. Turrillas and J. Nogués, Small, 2018, 14, 1800804 CrossRef PubMed.
- A. Lak, M. Kraken, F. Ludwig, A. Kornowski, D. Eberbeck, S. Sievers, F. J. Litterst, H. Weller and M. Schilling, Nanoscale, 2013, 5, 12286–12295 RSC.
- E. Wetterskog, C.-W. Tai, J. Grins, L. Bergström and G. Salazar-Alvarez, ACS Nano, 2013, 7, 7132–7144 CrossRef CAS PubMed.
- C.-J. Chen, R.-K. Chiang, H.-Y. Lai and C.-R. Lin, J. Phys. Chem. C, 2010, 114, 4258–4263 CrossRef CAS.
- D. W. Kavich, J. H. Dickerson, S. V. Mahajan, S. A. Hasan and J.-H. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174414 CrossRef.
- J. Lohr, M. Vasquez Mansilla, M. V. Gerbaldo, M. S. Moreno, D. Tobia, G. F. Goya, E. L. Winkler, R. D. Zysler and E. Lima Jr., J. Nanopart. Res., 2021, 23, 140 CrossRef CAS.
- B. Kowalczyk, I. Lagzi and B. A. Grzybowski, Curr. Opin. Colloid Interface Sci., 2011, 16, 135–148 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- Underneath the Bragg Peaks Structural Analysis of Complex Materials, ed., T. Egami and S. J. L. Billinge, Pergamon, 2012, vol. 16, pp. ii Search PubMed.
- S. J. L. Billinge and M. G. Kanatzidis, Chem. Commun., 2004, 749–760 RSC.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248 CrossRef.
- P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- M. Vasilakaki and K. N. Trohidou, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 144402 CrossRef.
- M. Vasilakaki, K. N. Trohidou and J. Nogués, Sci. Rep., 2015, 5, srep09609 Search PubMed.
- M. Vasilakaki, C. Binns and K. N. Trohidou, Nanoscale, 2015, 7, 7753–7762 RSC.
- B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, John Wiley & Sons, Inc., 2nd edn, 2009 Search PubMed.
- M. Fantauzzi, F. Secci, M. Sanna Angotzi, C. Passiu, C. Cannas and A. Rossi, RSC Adv., 2019, 9, 19171–19179 RSC.
- A. Lak, S. Disch and P. Bender, Adv. Sci., 2021, 8, 2002682 CrossRef CAS PubMed.
- C. R. A. Catlow and B. E. F. Fender, J. Phys. C: Solid State Phys., 1975, 8, 3267–3279 CrossRef CAS.
- R. M. Hazen and R. Jeanloz, Rev. Geophys., 1984, 22, 37–46 CrossRef CAS.
- C.-J. Chen, R.-K. Chiang, S. Kamali and S.-L. Wang, Nanoscale, 2015, 7, 14332–14343 RSC.
- W. H. Bragg, London, Edinburgh Dublin Philos. Mag. J. Sci., 1915, 30, 305–315 CrossRef CAS.
- R. W. G. WyckofF and E. D. Crittenden, Z. Kristallogr. – Cryst. Mater., 1926, 63, 144–147 CrossRef.
- F. L. Deepak, M. Bañobre-López, E. Carbó-Argibay, M. F. Cerqueira, Y. Piñeiro-Redondo, J. Rivas, C. M. Thompson, S. Kamali, C. Rodríguez-Abreu, K. Kovnir and Y. V. Kolen'ko, J. Phys. Chem. C, 2015, 119, 11947–11957 CrossRef CAS.
- E. Lottini, A. López-Ortega, G. Bertoni, S. Turner, M. Meledina, G. Van Tendeloo, C. de Julián Fernández and C. Sangregorio, Chem. Mater., 2016, 28, 4214–4222 CrossRef CAS.
- K. N. Trueblood, H.-B. Bürgi, H. Burzlaff, J. D. Dunitz, C. M. Gramaccioli, H. H. Schulz, U. Shmueli and S. C. Abrahams, Acta Crystallogr., Sect. A: Found. Crystallogr., 1996, 52, 770–781 CrossRef.
- H. Rijckaert, J. De Roo, M. Van Zele, S. Banerjee, H. Huhtinen, P. Paturi, J. Bennewitz, S. Billinge, M. Bäcker, K. De Buysser and I. Van Driessche, Materials, 2018, 11, 1066 CrossRef PubMed.
- S. Banerjee, C.-H. Liu, J. D. Lee, A. Kovyakh, V. Grasmik, O. Prymak, C. Koenigsmann, H. Liu, L. Wang, A. M. M. Abeykoon, S. S. Wong, M. Epple, C. B. Murray and S. J. L. Billinge, J. Phys. Chem. C, 2018, 122, 29498–29506 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- D. S. Schmool and H. Kachkachi, Solid State Physics, ed. R. E. Camley and R. L. Stamps, Academic Press, 2016, vol. 67, pp. 1–101 Search PubMed.
- S. Bedanta and W. Kleemann, J. Phys. D: Appl. Phys., 2008, 42, 013001 CrossRef.
- P. A. Cox, Transition Metal Oxides: An Introduction to Their Electronic Structure and Properties, Clarendon Press, 1992, p. 134 Search PubMed.
- E. J. W. Verwey and J. H. de Boer, Recl. Trav. Chim. Pays-Bas, 1936, 55, 531–540 CrossRef CAS.
- M. Bohra, K. E. Prasad, R. Bollina, S. C. Sahoo and N. Kumar, J. Magn. Magn. Mater., 2016, 418, 137–142 CrossRef CAS.
- A. Mitra, J. Mohapatra, S. S. Meena, C. V. Tomy and M. Aslam, J. Phys. Chem. C, 2014, 118, 19356–19362 CrossRef CAS.
- K. L. López Maldonado, L. Vazquez Zubiate, P. de la Presa, J. A. Matutes Aquino and J. T. Elizalde Galindo, J. Appl. Phys., 2014, 115, 17C705 CrossRef.
- L. Hu, C. de Montferrand, Y. Lalatonne, L. Motte and A. Brioude, J. Phys. Chem. C, 2012, 116, 4349–4355 CrossRef CAS.
- L. Del Bianco, D. Fiorani, A. M. Testa, E. Bonetti and L. Signorini, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 052401 CrossRef.
- M. Y. Khan, C.-B. Wu and W. Kuch, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094427 CrossRef.
- A. P. Malozemoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 3679–3682 CrossRef PubMed.
- M. D. Stiles and R. D. McMichael, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 064405 CrossRef.
- C. H. Li, P. Hodgins and G. P. Peterson, J. Appl. Phys., 2011, 110, 054303 CrossRef.
- A. Lak, M. Cassani, B. T. Mai, N. Winckelmans, D. Cabrera, E. Sadrollahi, S. Marras, H. Remmer, S. Fiorito, L. Cremades-Jimeno, F. J. Litterst, F. Ludwig, L. Manna, F. J. Teran, S. Bals and T. Pellegrino, Nano Lett., 2018, 18, 6856–6866 CrossRef CAS PubMed.
- G. Vallejo-Fernandez, O. Whear, A. G. Roca, S. Hussain, J. Timmis, V. Patel and K. O'Grady, J. Phys. D: Appl. Phys., 2013, 46, 312001 CrossRef.
- R. Hergt, S. Dutz and M. Zeisberger, Nanotechnology, 2010, 21, 015706 CrossRef PubMed.
- M. S. Carrião and A. F. Bakuzis, Nanoscale, 2016, 8, 8363–8377 RSC.
- T. E. Torres, E. Lima, M. P. Calatayud, B. Sanz, A. Ibarra, R. Fernández-Pacheco, A. Mayoral, C. Marquina, M. R. Ibarra and G. F. Goya, Sci. Rep., 2019, 9, 3992 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr05172e |
| This journal is © The Royal Society of Chemistry 2022 |