Open Access Article
Open Access ArticleSynthetically tuneable biomimetic artificial photosynthetic reaction centres that closely resemble the natural system in purple bacteria†
Sai-Ho
Lee
a,
Iain M.
Blake
a,
Allan G.
Larsen
a,
James A.
McDonald
a,
Kei
Ohkubo
b,
Shunichi
Fukuzumi
*cd,
Jeffrey R.
Reimers
*aef and
Maxwell J.
Crossley
*a
aSchool of Chemistry F11, The University of Sydney, 2006, NSW, Australia. E-mail: maxwell.crossley@sydney.edu.au
bDepartment of Material and Life Science, Graduate School of Engineering, Osaka University, Suita, Osaka 565-0871, Japan. E-mail: fukuzumi@chem.eng.osaka-u.ac.jp
cDepartment of Chemistry and Nano Science, Ewha Womans University, Seoul 120-750, Korea
dFaculty of Science and Engineering, Meijo University, Nagoya, Aichi 468-0073, Japan
eInternational Centre for Quantum and Molecular Structure, Shanghai University, 200444, Shanghai, China. E-mail: reimers@shu.edu.cn
fSchool of Mathematical and Physical Sciences, The University of Technology Sydney, 2007, NSW, Australia. E-mail: jeffrey.reimers@uts.edu.au
First published on 16th June 2016
Abstract
Porphyrin-based photosynthetic reaction centre (PRC) mimics, ZnPQ-Q2HP-C60 and MP2Q-Q2HP-C60 (M = Zn or 2H), designed to have a similar special-pair electron donor and similar charge-separation distances, redox processes and photochemical reaction rates to those in the natural PRC from purple bacteria, have been synthesised and extensive photochemical studies performed. Mechanisms of electron-transfer reactions are fully investigated using femtosecond and nanosecond transient absorption spectroscopy. In benzonitrile, all models show picosecond-timescale charge-separations and the final singlet charge-separations with the microsecond-timescale. The established lifetimes are long compared to other processes in organic solar cells or other organic light harvesting systems. These rigid, synthetically flexible molecules provide the closest mimics to the natural PRC so far synthesised and present a future direction for the design of light harvesters with controllable absorption, redox, and kinetics properties.
1. Introduction
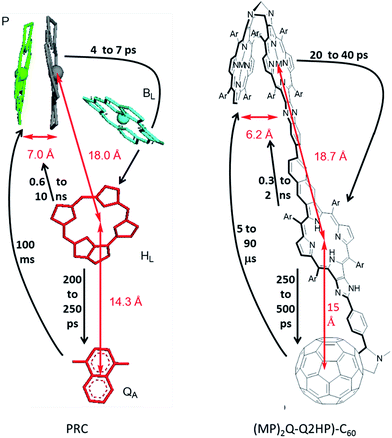
Long-lived photochemical charge separation provides means of harvesting solar energy for subsequent use in e.g., photovoltaic or photosynthetic devices,1–5 and many different types of systems have been investigated in the last two years.6–32 Other possible applications include as photosensitizers for cancer treatment,33–40 modulators of DNA,41 neuron controllers,42,43 biosensors,44,45 logic switches,46 and injecting charges into nanomaterials.47 A long-standing objective has been the mimicking of biological photosynthetic reaction centres (PRCs)48,49 in order to design efficient charge-separation units.50–57 In the PRC from purple bacteria, the solar to electrical energy conversion process starts with a multistep photoinduced electron transfer sequence between a special-pair bacteriochlorophyll dimer (P) and ubiquinone (QB), and the mechanism has been thoroughly studied over the past few decades48,49 (for recent mini-reviews see e.g.ref. 58–62). Knowledge about the photoinduced-electron transfer mechanism has led to the development of numerous artificial photosynthetic systems that show the possibility for photovoltaic and photonic applications.57,63–65 Indeed, the natural systems are often taken as model devices to be mimicked in artificial solar-energy generation and solar-photochemical processes.1,57,66–71The purple bacteria Rhodopseudomonas sphaeroides72,73 and Rhodopseudomonas viridis74,75 are known to have a high degree of similarity in the structures of their PRCs. Similar arrangements are also found in the more complex photosystems I and II of the cyanobacterium Synechococcus elongatus,76,77 implying that at least some features of the arrangement of the porphinoid pigments are generally useful in biological photosynthesis. Organic solar-energy capture systems usually mimic these natural systems in a variety of ways, including aspects of exciton transfer, primary charge separation, and secondary charge separation. Here we explore what happens when artificial systems are designed to mimic in considerable detail the chemical, structural and kinetics properties of natural photosystems48,49 (for recent mini-reviews see e.g.ref. 58–62), choosing the known structure of PRCs from purple bacteria, as illustrated in Fig. 1. The mimics have improved properties for use in device applications, however, instead of bacteriochlorophylls and quinones, we use the related compounds, porphyrins and fullerenes, as these are chemically much more stable. Also we use rigid linkers to control structure rather than an external protein environment, maintaining structural integrity to affect similar degrees of charge separation in each step but done in a more easily controllable way. An interesting functional similarity is that porphyrin–fullerene molecules have been shown to support long-lived (1 ms at room temperature) spin-polarized long-distance charge-separated states,78 somewhat akin to natural PRCs.79–82 Such species are also particularly relevant in modern device contexts55,83 but could lead to photochemical damage and so chemical means to control them in artificial systems are required.
In search of biomimetic charge-separating units, previously we designed and investigated the photophysical properties of the tris- and tetrakis-porphyrin arrays, ZnPQ-Q2HPQ-QAuP+ and ZnPQ-Q2HPQ-Q2HPQ-QAuP+,84–87 that to some degree also resemble the arrangement of the natural PRCs. Indeed, these compounds contain the quinoxaline Tröger's base linkage that establishes the C2 symmetry in the ‘special pair’ (see Fig. 1), and the biquinoxalinyl linkage provides a very similar charge-separation distance to that between the ‘special pair’ and the primary electron acceptor. Both arrays show multistep positive charge shift from the gold(III) porphyrin to the zinc(II) porphyrin at the other end of the array after photoexcitation, and the final charge-shift states, namely ZnPQ˙+-Q2HPQ-QAuP and ZnPQ˙+-Q2HPQ-Q2HPQ-QAuP, are long-lived in benzonitrile. Besides, the addition of the chloride ligand has been shown to control the gradient of energy and charge-shift processes,86,87 and is able to afford the long-lived final charge-shift state in a non-polar solvent (e.g., toluene), which is close to the dielectric constant of the natural PRC. This showed the importance of controlling the redox gradient in achieving long-lived charge-separation, a critical feature in any organic artificial photovoltaic device.
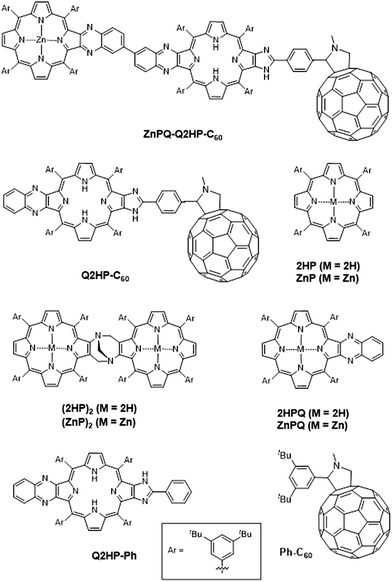
However, these model compounds were also found to have several deficiencies, including: (i) the quinoxaline Tröger's base linkage separates the ‘special pair’ porphyrins too far apart for an efficient cation radical delocalization, and (ii) the system lacks an electron acceptor to mimic the quinones and iron–sulfur complexes of the natural systems. Here we introduce the modified photosynthetic mimics (MP)2Q-Q2HP-C60 (where M = Zn or 2H) shown in Fig. 1 to remove these differences. The inclusion of a ‘special pair’ is not essential in an artificial device and most compounds in current use are more like our previous designs. However, in biology the function of the special pair is readily controlled by protein mutation effects,88 and the inclusion of a similar feature in artificial compounds can be subsequently explored using established synthetic strategies to allow similar control in an artificial environment.
In (MP)2Q-Q2HP-C60, the ‘special pair’ porphyrins “(MP)2” are connected directly through a Tröger's base bridge on the porphyrin β-pyrrolic position without the use of the quinoxalinyl groups that linked the chromophores in ZnPQ-Q2HPQ-QAuP+ and in ZnPQ-Q2HPQ-Q2HPQ-QAuP+.84–87 The (MP)2 unit is closely modelled by the Tröger's base linked porphyrin dimer (ZnP)2, and for this molecule an X-ray crystal structure confirms the pseudo C2 symmetry of the porphyrin dimer that mimics the “special-pair” of natural PRCs.89,90 Significantly, the intra-dimer porphyrin-centre to porphyrin-centre distance is reduced from 16.8 Å84,85 for the quinoxalinyl-bridged mimics to 6.2 Å for this Tröger's base dimer, close to the inter-chromophore separation of 7.0 Å75 found within the special pair in the natural PRC. Also, the new compound (MP)2Q-Q2HP-C60 includes additional functionality through the bonding of the fullerene electron acceptor so as to permit secondary charge-separation processes to occur. This group mimics the electron acceptor function of the quinones in the natural system. Numerous studies showed that the use of fullerene as an electron acceptor significantly reduced the reorganization energy for electron transfer due to its symmetrical shape, large size, and delocalized π-electron system,91–93 a change from the natural system likely to bring benefit in device applications.
As Fig. 1 shows, the critical aspects of these biomimetic compounds is that they separate charges over similar distances to the natural system, keep them separated for similar times, are readily controllable, and could show similar effects such as long-lived charge-separated triplet-state production.78 However, the mechanisms driving exciton transport, charge separation, and charge combination are quite different. In the natural system, through-space interactions mediated dynamically by intervening matter are critical.48,49,58–62,94 Such effects are difficult to control in artificial systems and so are replaced with through-bond coupling mechanisms in rigid molecules,78,84,95–103 and a critical design criteria is therefore to establish similar couplings using this device-robust mechanism. A great advantage of the chemical routes presented to biomimetic solar-energy harvesting is that it can readily be modified to make broadband or narrowband absorbers, for example, for use in solar cells or phototherapy, respectively,40,96,98,104 for upconversion units with unprecedented efficiency,105–107 and as tailor-made components for determining mechanism and improving solar cell functions.108
We report the details of the synthesis of the new photosynthetic mimic (MP)2Q-Q2HP-C60, along with model systems ZnPQ-Q2HP-C60, Q2HP-C60, Q2HP-Ph, (ZnP)2, (2HP)2, ZnPQ, 2HPQ, ZnP and 2HP (Chart 1). The electrochemical and photophysical properties of these systems are also presented in detail, and its performance is compared to that of natural PRCs.
2. Experimental section
2.1 General
Ultraviolet-visible spectra were recorded on a Cary 5E UV-Vis spectrophotometer in stated solvents. Steady-state fluorescence spectra were recorded on a Varian Cary Eclipse fluorescence spectrophotometer in deacidified benzonitrile. 1H NMR spectra were recorded on a Bruker AVANCE300 (300 MHz) spectrometer or Bruker DPX400 (400 MHz) spectrometer. Samples were dissolved in deacidified CDCl3. MALDI-TOF mass spectrometry was recorded on a Waters (Micromass) TOF SPEC 2E mass spectrometer. Infrared spectra were recorded on a Shimadzu Model 8400 FT-IR as solutions in deacidified CHCl3.2.2 Electrochemical measurements
The cyclic voltammetry measurements were performed on a CHI 900B electrochemical analyser in deaerated PhCN containing 0.10 M n-Bu4NPF6 as supporting electrolyte at 298 K. A gold working electrode was polished with BAS polishing alumina suspension and rinsed with acetone before use. A platinum wire was used as a counter electrode and a silver wire was used as a reference electrode. All experiments were followed by the addition of ferrocene with the ferrocene/ferrocenium couple used as an internal reference.2.3 Spectroelectrochemical measurements
UV-Vis spectroelectrochemical measurements were performed with a thin-layer quartz spectroelectrochemical cell and a platinum gauze working electrode. Potentials were applied and monitored using a CHI 900B electrochemical analyser. UV-Vis spectra were recorded on a Cary 4E UV-Vis spectrophotometer.2.4 Spectral measurements and fitting
Femtosecond transient absorption spectroscopy experiments were conducted at Osaka University, Japan, using an ultrafast source: Integra-C (Quantronix Corp.), an optical parametric amplifier: TOPAS (Light Conversion Ltd.) and a commercially available optical detection system: Helios provided by Ultrafast Systems LLC. The source for the pump and probe pulses were derived from the fundamental output of Integra-C (780 nm, 2 mJ per pulse and fwhm = 130 fs) at a repetition rate of 1 kHz. As much as 75% of the fundamental output of the laser was introduced into TOPAS which has optical frequency mixers, resulting in a tuneable range from 285 to 1660 nm, while the rest of the output was used for white light generation. Prior to generating the probe continuum, a variable neutral density filter was inserted into the path in order to generate a stable continuum, the laser pulse was then fed to a delay line that provides an experimental time window of 3.2 ns with a maximum step resolution of 7 fs. A wavelength between 350 and 450 nm of the TOPAS output, which are the fourth harmonic of the signal or idler pulses, was chosen as the pump beam. As this TOPAS output consists of not only the desirable wavelength but also unnecessary wavelengths, the latter were deviated using a wedge prism with wedge angle of 18°. The desirable beam was irradiated at the sample cell with a spot size of 1 mm diameter where it was merged with the white probe pulse in a close angle (<10°). The probe beam after passing through the 2 mm sample cell was focused on a fibre optic cable that was connected to a CCD spectrograph for recording the time-resolved spectra (410–800 nm). Typically, 2500 excitation pulses were averaged for 5 s to obtain the transient spectrum at a set delay time. Kinetic traces at appropriate wavelengths were assembled from the time-resolved spectral data. All measurements were conducted at room temperature (RT), 298 K, using porphyrin concentrations of 1.0 × 10−6 M (fs transient spectra and fluorescence spectra).Spectral components were obtained from the time-dependent spectra by fitting the observed data to kinetics schemes involving the unexcited ground-state reactant R and up to six transient or final photochemical products named in rough order of production P1 up to P6. Different rate constants are then ascribed to observed unimolecular reactions amongst these species. The time sequence of observed transient absorption spectra ΔA(ν, t) was then fitted to reveal the transient spectrum of each component ΔAi(ν) and the set of rate constants k for each of the included reactions. These rate constants are reported as the isolated-process lifetimes τ = 1/k. The transient absorption ΔA is the difference in sample absorption caused by the excitation pulse at t = 0. The fitting procedure involved first smoothing and interpolating the raw experimental data using Gaussian convolution. Prior to fitting, the data was assembled on a linear frequency scale and a logarithmic time scale so as to properly weight the different spectral and temporal regions. The fit was optimized to minimize the residual between the observed and fitted spectra using over-determined linear least-squares analysis to fit the spectral components, combined with Newton–Raphson optimization of the rate constants in an external loop.
A shortcoming of the fitting procedure is that typically there is insufficient data available to determine the properties of low-yield processes and pathways. For example, the absorption of light will excite a mixture of initial products arising from individual absorptions on each chromophore, each of which will react independently. The signal to noise ratio of the observed data, however, typically supports only the identification of the resultant state mix rather than each chemical component of the mix. As a result, the extracted spectra of P1 and subsequent species each reflect differently weighted sums of individual molecular component spectra.
Nanosecond laser flash photolysis experiments were performed at Osaka University, Japan. Porphyrins in deaerated benzonitrile solutions (3.0 × 10−6 M) were excited by a Panther OPO pumped by a Nd:YAG laser (Continuum, SLII-10, 4–6 ns fwhm) at λ = 355 nm with a power of 16 mJ per pulse. The photochemical reactions were monitored by continuous exposure to a Xe-lamp (150 W) as a probe light and a photomultiplier tube (Hamamatsu 2949) as a detector. For transient absorption spectra in the near-IR region (800–1200 nm), monitoring light from a pulsed Xe-lamp was detected with a Ge-avalanche photodiode (Hamamatsu Photonics, B2834). All experiments were performed at 298 K.
2.5 Synthesis
The synthesis109 and characterization of: zinc(II) 12/13-nitro{(formylphenyl)imidazo}porphyrin 2, 12/13-nitro{(fullerene-N-methylpyrrolidinylphenyl)imidazo}porphyrin 3, {6′-(3,4-diaminobenzene)quinoxalino}{(fullerene-N-methylpyrrolidinylphenyl)imidazo}porphyrin 5, (12/13-nitroquinoxalino)(fullereneimidazo)quinoxalino}bisporphyrin 7, (Tröger's base-quinoxalino){(fullereneimidazo)quinoxalino}trisporphyrin (2HP)2Q-Q2HP-C60, and (di-zinc(II) Tröger's base-quinoxalino){(fullereneimidazo)quinoxalino}trisporphyrin (ZnP)2Q-Q2HP-C60 is described in detail in ESI Section S1.†3. Results and discussion
3.1 Synthesis
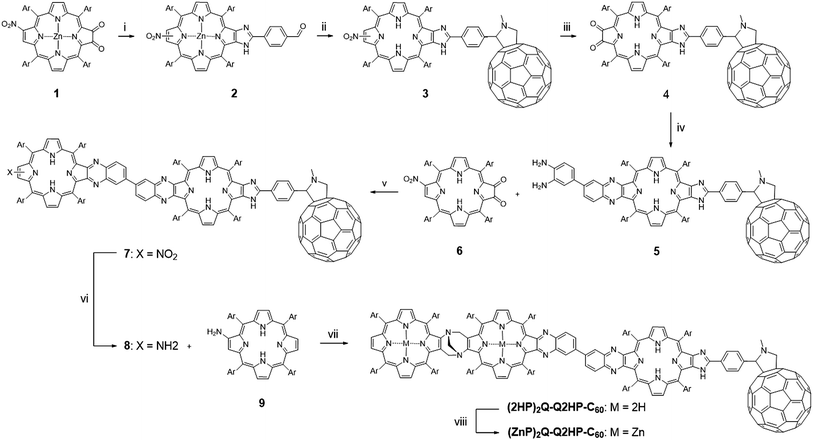
The synthesis of (MP)2Q-Q2HP-C60 is outlined in Scheme 1. The precursor zinc(II) nitroporphyrin-2,3-dione 1 was prepared according to the method published elsewhere.109 Following the imidazole-forming condensation method developed earlier,110 zinc(II) nitroporphyrin-dione 1 was reacted with an excess of terephthalaldehyde (5 eq.) in the presence of ammonium acetate in refluxing CHCl3 and gave zinc(II) formyl-imidazoporphyrin 2 in 90% yield. Remarkably, zinc(II) chelation is a crucial step in this particular reaction as using free-base formyl-imidazoporphyrin 6 gave only 40% yield under the same conditions. The aldehyde functionality provides a convenient means to attach a fullerene by cycloaddition of the azomethine ylide formed upon condensation of N-methylglycine with 2 to give 3.111,112 This reaction exhibits an opposite effect in term of metal chelation as the imidazole-forming condensation reaction (step i), where this reaction afforded a higher yield of fullerene appended nitroporphyrin using free-base porphyrin as a precursor (75% for free base porphyrin vs. 37% for zinc(II) porphyrin) under the same conditions. Zinc(II) formyl-imidazoporphyrin 2 was thereafter demetallated by stirring in a mixture of hydrochloric acid and CH2Cl2 before promoting the azomethine–fullerene reaction. Conversion of the nitro into the amino using tin(II) chloride reduction, followed by photooxidation afforded the fullerene appended porphyrin-dione 4 in 54% yield for the two steps. Condensation of 4 with 3,3′-diaminobenzidine (1 eq.) gave the diaminobenzidine-quinoxalinyl porphyrin 5.84,85,113 To minimize the formation of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct, a solution of 4 was added slowly over 1 h to a dilute solution of 3,3′-diaminobenzidine. Condensation of 5 with 6 afforded the fullerene-appended bisporphyrin 7 in 56% yield. Finally reduction of the nitro group followed by the acid-catalysed condensation of the resultant aminoporphyrin 9 (∼2 eq.) and an excess of formaldehyde,84,85,113,114 with heating at 70 °C under nitrogen for four days gave (2HP)2Q-Q2HP-C60 which was purified by size exclusion chromatography. (ZnP)2Q-Q2HP-C60 was simply prepared by stirring (2HP)2Q-Q2HP-C60 with zinc acetate in CH3OH and CH2Cl2 mixture. Interestingly, zinc metallation occurred preferentially at the ‘special pair’ porphyrin rings that have porphyrin and ‘chlorin-like’ quinoxalinoporphyrin aromatic delocalisation pathways and hence more acidic inner protons rather than at the less acidic ‘bacteriochlorin-like’ quinoxalino-imidazolo-porphyrin that has the appended fullerene. The difference in rate of metallation of chlorin-like and bacteriochlorin-like rings was recognised and exploited in earlier work on the synthesis of extended porphyrins.115
1 adduct, a solution of 4 was added slowly over 1 h to a dilute solution of 3,3′-diaminobenzidine. Condensation of 5 with 6 afforded the fullerene-appended bisporphyrin 7 in 56% yield. Finally reduction of the nitro group followed by the acid-catalysed condensation of the resultant aminoporphyrin 9 (∼2 eq.) and an excess of formaldehyde,84,85,113,114 with heating at 70 °C under nitrogen for four days gave (2HP)2Q-Q2HP-C60 which was purified by size exclusion chromatography. (ZnP)2Q-Q2HP-C60 was simply prepared by stirring (2HP)2Q-Q2HP-C60 with zinc acetate in CH3OH and CH2Cl2 mixture. Interestingly, zinc metallation occurred preferentially at the ‘special pair’ porphyrin rings that have porphyrin and ‘chlorin-like’ quinoxalinoporphyrin aromatic delocalisation pathways and hence more acidic inner protons rather than at the less acidic ‘bacteriochlorin-like’ quinoxalino-imidazolo-porphyrin that has the appended fullerene. The difference in rate of metallation of chlorin-like and bacteriochlorin-like rings was recognised and exploited in earlier work on the synthesis of extended porphyrins.115
3.2 Steady-state absorption and emission spectroscopy
To identify the products formed at each stage of the photochemical reactions, detailed information concerning the assignment of the absorption spectra of the photoexcited molecule is required. Spectra for the dyad, triad and tetrad molecules studied, plus analogous spectra for each molecular fragment of these compound systems, are presented in ESI Section S2 Fig. S1–S5.† This absorption data is therein interpreted by comparison with emission spectra.53,85,97,116–129Table 1 lists the key results required for the analyses of the photochemical experiments, including the origin band energies of the lowest transition observed in both absorption and emission, the Stoles shift between them, and the estimated origin energy E0–0, while detailed assignment information is discussed in the text. Besides these critical quantitative results, the spectra also provide qualitative insight into the chemical interactions present within the compounds. All chromophores interact with each other only weakly so that the absorption spectra of dyad, triad, and tetrad species are simply the sum of those of the isolated chromophores. However, bands do shift considerably, indicating, e.g., the presence of significant π conjugation likely to contribute significantly to the observed charge separation and recombination mechanisms.78,99| Molecule | Chromophore | Abs.a (cm−1) | Emiss.b (cm−1) | Stokes shiftc (cm−1) | E 0–0 (eV) |
|---|---|---|---|---|---|
| a The wavenumber of the origin Qx band obtained from absorption spectrum. b The wavenumber of the origin Qx band obtained from emission spectrum. c Difference between the absorption and emission spectra of the origin Qx band. d The energy of the lowest excited-state calculated as the average energy of origin Qx bands in the absorption and the emission spectra. e Estimated based on the Stokes shift of ZnPQ. f Estimated based on the stokes shift of ZnPQ and (ZnP)2. g Estimated based on the stokes shift of 2HPQ. | |||||
| ZnP | ZnP | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
200 | 2.05 |
| ZnPQ | ZnPQ | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
450 | 1.97 |
| 2HP | 2HP | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
100 | 1.90 |
| 2HPQ | 2HPQ | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
100 | 1.90 |
| (ZnP)2 | (ZnP)2 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 820 |
600 | 2.00 |
| (2HP)2 | (2HP)2 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
550 | 1.81 |
| Q2HP-C60 | 2HPQ | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
100 | 1.89 |
| ZnPQ-Q2HP-C60 | ZnPQ | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650e 650e |
450e | 1.97 |
| 2HPQ | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
100 | 1.89 | |
| (ZnP)2Q-Q2HP-C60 | (ZnP)2Q | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 ± 100 650 ± 100 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700f ± 175 700f ± 175 |
[450–600]f | 1.95 ± 0.02 |
| 2HPQ | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
100 | 1.89 | |
| (2HP)2Q-Q2HP-C60 | (2HP)2Q | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 ± 150 640 ± 150 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
300 ± 150 | 1.80 ± 0.01 |
| 2HPQ | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 220 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120g 120g |
100g | 1.88 | |
Alternatively, emission spectra can show significant differences when comparing that from dyads, triads, or tetrads to that from their molecular components, indicative of the photochemical processes that take place. By assigning emission to a particular chromophore, the nature of the lowest energy states are determined (using Kasha's rule),119 Stokes shifts determined, and components of the much more complex absorption spectra assigned. Asymmetry between absorption and emission indicates that symmetric Troger's base dimers (ZnP)2 and (2HP)2 adsorb with excitation localized on their individual porphyrins but emit through an exciton-delocalized state. However, in extended Troger's base compounds containing (ZnP)2Q units, the asymmetry prevents delocalization.
The arguments made make extensive use of the expected symmetry between absorption and emission coming from the same chromophore, and the difference between Franck–Condon allowed vibrational progressions and vibronic intensification arising from the Herzberg–Teller principle.124 A critical feature discussed in ESI† is that the for a Franck–Condon progression the intensity ratio of the origin and side bands in traditional spectra gets distorted by a factor of [(ΔE − hν)/ΔE]6 ∼ (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/15
000/15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500)6 = 0.54, where ΔE is the origin energy and hν the vibrational sideband spacing. This and vibronic effects can dramatically reduce perceived asymmetry, and understanding them proved critical to the recent assignment of the Q-band spectrum of chlorophyll-a, a feature critical to photosynthesis understanding that defied mankind for over 50 years.130,131
500)6 = 0.54, where ΔE is the origin energy and hν the vibrational sideband spacing. This and vibronic effects can dramatically reduce perceived asymmetry, and understanding them proved critical to the recent assignment of the Q-band spectrum of chlorophyll-a, a feature critical to photosynthesis understanding that defied mankind for over 50 years.130,131
3.3 Electrochemistry
Cyclic voltammetry was carried out in 0.1 M n-Bu4NPF6 solution in benzonitrile and redox potentials of investigated compounds are summarized in Table 2. Cyclic voltammograms of Q2HP-C60, ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60 are shown in ESI Section S3 Fig. S6,† while those for model systems ZnP, (ZnP)2, 2HP, (2HP)2, Q2HP-Ph and Ph-C60 are given in Fig. S7.† From the observed redox potentials given in Table 2, the free-energy changes associated with all the possible charge-separation and charge-recombination processes for Q2HP-C60, ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60 can be estimated and are given in Table 3.| Molecule | E°/mV (vs. Fc+/Fc) in PhCN | ||||
|---|---|---|---|---|---|
| P2+/P˙+ | P˙+/P | C60/C60˙− | C60˙−/C602− | P/P˙− | |
a The standard potentials were determined as 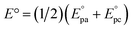 by cyclic voltammetry in deaerated PhCN using n-Bu4NPF6 (0.1 M) as supporting electrolyte.
b Two distinct first oxidation potentials of free-base porphyrin were observed (ESI Fig. S2).
c The first oxidation potential of C60-appended 2HPQ is shown in parentheses.
d Peak potential at a scan rate 100 mV s−1 for irreversible reaction.
e The first reduction potential of the free-base porphyrin dimer (2HP)2 is shown in parentheses. by cyclic voltammetry in deaerated PhCN using n-Bu4NPF6 (0.1 M) as supporting electrolyte.
b Two distinct first oxidation potentials of free-base porphyrin were observed (ESI Fig. S2).
c The first oxidation potential of C60-appended 2HPQ is shown in parentheses.
d Peak potential at a scan rate 100 mV s−1 for irreversible reaction.
e The first reduction potential of the free-base porphyrin dimer (2HP)2 is shown in parentheses.
|
|||||
| ZnP | 693 | 306 | — | — | −1849 |
| 2HP | 886 | 506 | — | — | −1671 |
| Ph-C60 | — | — | −1023 | −1449 | — |
| (ZnP)2 | 585 | 213 | — | — | — |
| (2HP)2 | — | 363/454b | — | — | −1755 |
| Q2HP-Ph | — | 503 | — | — | −1648 |
| Q2HP-C60 | — | 500 | −1048 | −1458 | −1655 |
| ZnPQ-Q2HP-C60 | — | 328 (522)c | −1053 | −1450 | ∼−1560 |
| (ZnP)2Q-Q2HP-C60 | — | 228 (533)c | −1042 | −1463 | −1560 |
| (2HP)2Q-Q2HP-C60 | — | 371d (502)c | −1038 | −1456 | ∼−1660 (−1785)e |
| Reaction | Seq. | EN | CS1 | CR1 | CS2 | CR2 |
|---|---|---|---|---|---|---|
| a ΔGCR1 = E0(anion red.) − E0(cation ox.) + e/4πε0εsR is for charge-recombination from the primary charge-separated state where R is the charge-separation distance determined from DFT; ΔGCS1 = −ΔGCR1 − ΔE0–0 is the driving force for primary charge-separation where ΔE0–0 is the energy of the lowest excited-state calculated as the average of the energy of the (0–0) band in the absorption and the emission spectra and listed in Table 1; ΔGCS2 = E0(new group ox.) − E0(old group ox.) + (e/4πε0εs)(1/Rold − 1/Rnew) is the driving force for secondary charge-separation where Rold is the distance from the counter ion to the originally charged group and Rnew is the distance from the counter ion to the newly charged group; ΔGCR2 = ΔGCR1 − ΔGCS2 is the driving force for the charge-recombination from the fully charge-separated state; and EN is the excitation energy transfer obtained as the difference of the ΔE0–0 values of the excited states. The parameters used are: ε0 = 25.2 for PhCN, R(Pdimer–C60) = 32.5 Å, R(PC60-appended–C60) = 15 Å, R(Pdimer–PC60-appended) = 19.5 Å and R(ZnPQ–C60) = 31 Å (for ZnPQ-QH2P-C60). b ±0.02 eV. c ±0.01 eV. | ||||||
| Q2HP*-C60 → Q2HP˙+-C60˙− | — | −0.38 | −1.51 | — | — | |
| ZnPQ*-Q2HP-C60 → ZnPQ-Q2HP*-C60 → ZnPQ-Q2HP˙+-C60˙− → ZnPQ˙+-Q2HP-C60˙− | a | −0.08 | −0.35 | −1.54 | −0.17 | −1.36 |
| ZnPQ*-Q2HP-C60 → ZnPQ-Q2HP*-C60 → ZnPQ˙+-Q2HP˙−-C60 → ZnPQ˙+-Q2HP-C60˙− | b | −0.08 | −0.03 | −1.86 | −0.49 | −1.36 |
| ZnPQ*-Q2HP-C60 → ZnPQ˙+-Q2HP˙−-C60 → ZnPQ˙+-Q2HP-C60˙− | c | — | −0.11 | −1.86 | −0.49 | −1.36 |
| (ZnP)2Q*-Q2HP-C60 → (ZnP)2Q-Q2HP*-C60 → (ZnP)2Q-Q2HP˙+-C60˙− → (ZnP)2Q˙+-Q2HP-C60˙− | a | −0.06b | −0.35b | −1.54 | −0.28 | −1.25 |
| (ZnP)2Q*-Q2HP-C60 → (ZnP)2Q-Q2HP*-C60 → (ZnP)2Q˙+-Q2HP˙−-C60 → (ZnP)2Q˙+-Q2HP-C60˙− | b | −0.06b | −0.14b | −1.75 | −0.51 | −1.24 |
| (ZnP)2Q*-Q2HP-C60 → (ZnP)2Q˙+-Q2HP˙−-C60 → (ZnP)2Q˙+-Q2HP-C60˙− | c | — | −0.20b | −1.75 | −0.51 | −1.24 |
| (2HP)2Q-Q2HP*-C60 → (2HP)2Q*-Q2HP-C60 → (2HP)2Q˙+-Q2HP˙−-C60 → (2HP)2Q˙+-Q2HP-C60˙− | a | −0.08c | 0.20c | −2.00 | −0.61 | −1.39 |
| (2HP)2Q-Q2HP*-C60 → (2HP)2Q-Q2HP˙+-C60˙− → (2HP)2Q˙+-Q2HP-C60˙− | b | — | −0.38 | −1.50 | −0.11 | −1.39 |
| (2HP)2Q-Q2HP*-C60 → (2HP)2Q˙+-Q2HP˙−-C60 → (2HP)2Q˙+-Q2HP-C60˙− | c | — | 0.12 | −2.00 | −0.61 | −1.39 |
As expected, the attachment of a phenyl group to an imidazole on the β-pyrrolic position and the introduction of the quinoxalinyl group extents the conjugation and significantly affects the unoccupied orbitals (Table 2). The P/P˙− reduction hence becomes easier by ca. 23 mV, comparing 2HP with Q2HP-Ph. The C60/C60˙− reduction is harder by ca. 28 mV in Q2HP-C60 compared to that of Ph-C60. Such effects are also observed on ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60. More significantly, the Tröger's base porphyrin dimers (ZnP)2 and (2HP)2 are easier to oxidize by 90 and 140 mV, respectively. A split of 90 mV is observed for the first oxidation of the porphyrins for (2HP)2. This suggests that one of the porphyrin macrocycles is oxidized in advance and yields H2P˙+–H2P, while the oxidation of the second porphyrin macrocycle occurs subsequently to give H2P˙+–H2P˙+. This potential difference of 90 mV is due the Coulomb repulsion between the two positive charges. A similar result is also observed for (ZnP)2 in which the redox signal is broadened and the splitting cannot be resolved.
These estimates include screened coulombic interactions between the zwitterionic regions of the excited-states, expressed in terms of the distance R between the centres of positive and negative charge obtained from the calculated dipole moments at DFT-optimized molecular structures. The energies of the lowest excited-state (E0–0) are determined from the average energy of origin Qx bands in the absorption and emission spectra (Table 1).
3.4 Transient absorption spectroscopy
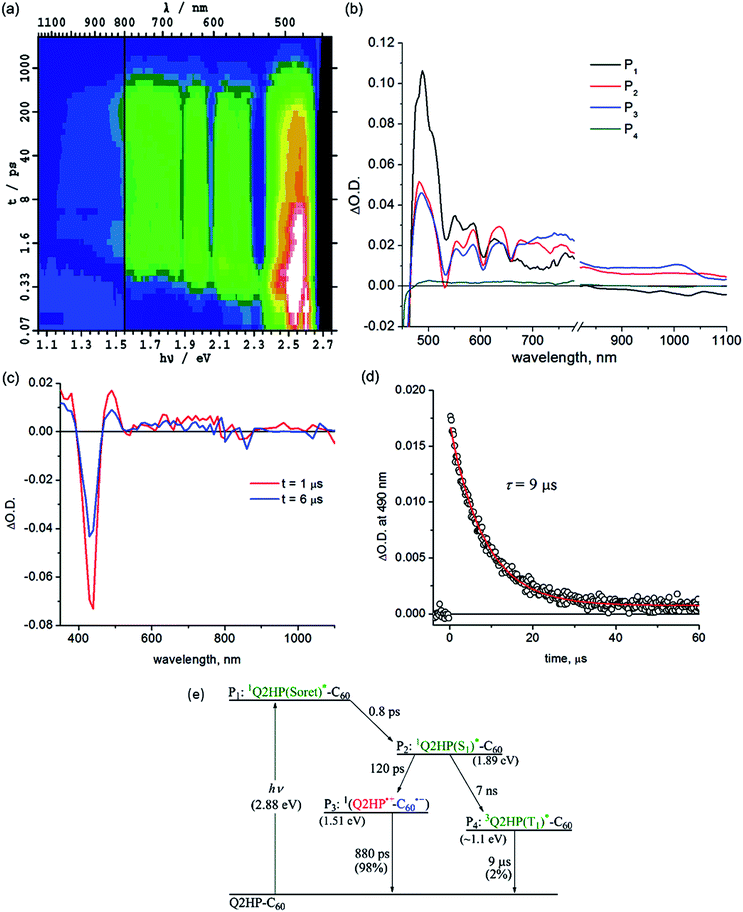
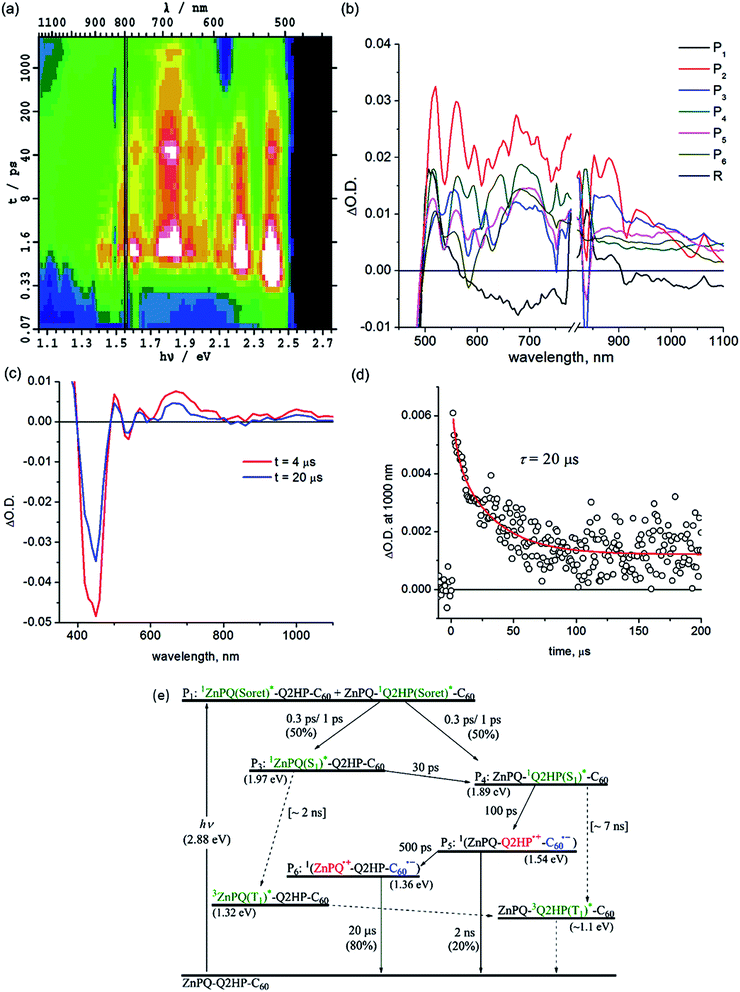
Femtosecond and nanosecond laser flash photolysis experiments were used to characterize the electron-transfer processes in Q2HP-C60, ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60. The resulting spectra ΔA(ν, t) display the combined absorption of the active photochemical species with positive sign at time t after excitation minus the spectrum of the ground-state molecule. The femtosecond spectra are fitted to give spectral components ΔAi(ν) and rate constants k = 1/τ. Full details of the observed spectra, the fitted spectra, and the deduced component concentrations as a function of time are provided in Section S4 Fig. S8–S11 of the ESI.†Subsequent to the formation of the 1P(S1)*, an electron-transfer process occurs with τ3 = 120 ps forming the charge-separated species Q2HP˙+-C60˙− (P4). The visible region (450–780 nm) of the observed component spectrum (ESI Fig. S5b†) is consistent with the spectrum of 2HPQ˙+ reported earlier.86 The observed spectrum of this component in the 950–1050 nm region also matches that expected for C60˙−,53,126,132,133 unambiguously identifying the product state as Q2HP˙+-C60˙−. The charge-separated state of Q2HP-C60 recombines on a timescale of τ4 = 880 ps leaving behind a final component with an estimated quantum yield of about 2%.
Fig. 2c shows results from nanosecond transient absorption spectroscopy. A long-lived component with a similar spectrum to the final component observed in the femtosecond experiments is observed. This species is identified as 32HPQ(T1)*, most likely produced from 1P(S1)* through intersystem crossing (ISC) with the time constant determined from its yield to be 7 ns. This rate is slightly faster than the observed fluorescence decay rate of 2HP, 14 ns, and slower than the lower bound found for free-base porphyrin-fullerene dyad without the fusion of quinoxaline, 4 ns.78,134 While the energy of 32HPQ(T1)* has not been measured, comparison of the energies of 3ZnPQ(T1)* (1.32 eV)135 and 3ZnP(T1)* (1.53 eV)53 suggests a value near 1.1 eV which is clearly much lower than that of the charge-separated state (1.51 eV). Hence the triplet state could also have been produced by charge-recombination and the observed data do not exclude this possibility. As ISC alone can account for the observed triplet yield, this process appears unlikely to have occurred, however. The nanosecond data indicates that 32HPQ(T1)* decays by phosphorescence with a time constant of 9 μs.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. The transient absorption spectrum of component P3 shows dips at 525 and 626 nm indicating the formation of 1ZnPQ(S1)*; similarly, the dips for component P4 at 580, 608 and 655 nm arise from 12HPQ(S1)*. The equal yield of these products could arise from their similar absorption coefficients at the excitation wavelength (430 nm), but in addition exciton coupling between the 1P(Soret)* states of each chromophore would most likely occur on a timescale much faster than τ1 and/or τ2, redistributing the energy.
50. The transient absorption spectrum of component P3 shows dips at 525 and 626 nm indicating the formation of 1ZnPQ(S1)*; similarly, the dips for component P4 at 580, 608 and 655 nm arise from 12HPQ(S1)*. The equal yield of these products could arise from their similar absorption coefficients at the excitation wavelength (430 nm), but in addition exciton coupling between the 1P(Soret)* states of each chromophore would most likely occur on a timescale much faster than τ1 and/or τ2, redistributing the energy.
Intramolecular singlet–singlet energy transfer from 1ZnPQ(S1)* to the energetically lower lying 12HPQ(S1)* state takes place with a time constant of 30 ps, eliminating the ZnPQ bleach whilst intensifying the 2HPQ bleach from the transient absorption spectra. After this energy transfer, an electron is injected into the fullerene unit through process CS1a (Table 3) to form the primary charge-separated state ZnPQ-Q2HP˙+-C60˙−, component P5, with a time constant of 100 ps. Two other possible charge-separation reactions, namely CS1b and CS1c (see Table 3), could also have occurred. However, the yields of these processes are too low to facilitate the identification of the resulting spectral components. Charge recombination from ZnPQ-Q2HP˙+-C60˙− was difficult to quantify as the spectra are only measured for up to 3000 ps and the process is of low yield. This charge-recombination lifetime is much slower than that observed for Q2HP-C60, 880 ps from Fig. 2e, despite primary charge-separation occurring at a similar rate, 100 ps compared to 120 ps.
The final component P6 observed in the femtosecond transient absorption spectra has a visible spectrum matching that for ZnPQ˙+ reported earlier,86,135 while the C60˙− signal in the near-infrared region remains. Hence this component results from the secondary charge-separation process CS2a forming the final charge-separated state ZnPQ˙+-Q2HP-C60˙−. The lifetime of this species is out of the measurable range of this femtosecond-timescale pulsed experiment.
Nanosecond transient absorption spectra taken at 4 and 20 μs are shown in Fig. 3c. These spectra retain all the spectral features of the final component P6 determined from the femtosecond measurements, ZnPQ˙+-Q2HP-C60˙−. From the transient decay profiles also shown in this figure, the lifetime of ZnPQ˙+-Q2HP-C60˙− is determined to be 20 μs; this species is seen to decay to the ground state rather than to a locally excited triplet state. No long-lived triplet charge-separated species or 3ZnP(T1)* is observed as the energy of 32HPQ(T1)* (∼1.1 eV) lies below that of 3(ZnPQ˙+-Q2HP-C60˙−) (1.54 eV) and 3ZnPQ(T1)* (1.32 eV),135 so that only long-lived 32HPQ(T1)* is expected. Based on the known intersystem crossing rates for Q2HP-C60 and ZnP-Ph (2 ns), a net yield of less than 2% is expected for ZnPQ-32HPQ(T1)*-C60 with a lifetime near 9 μs. The observed data in Fig. 3 does not facilitate the identification of such a component as the major product decays over the same period.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
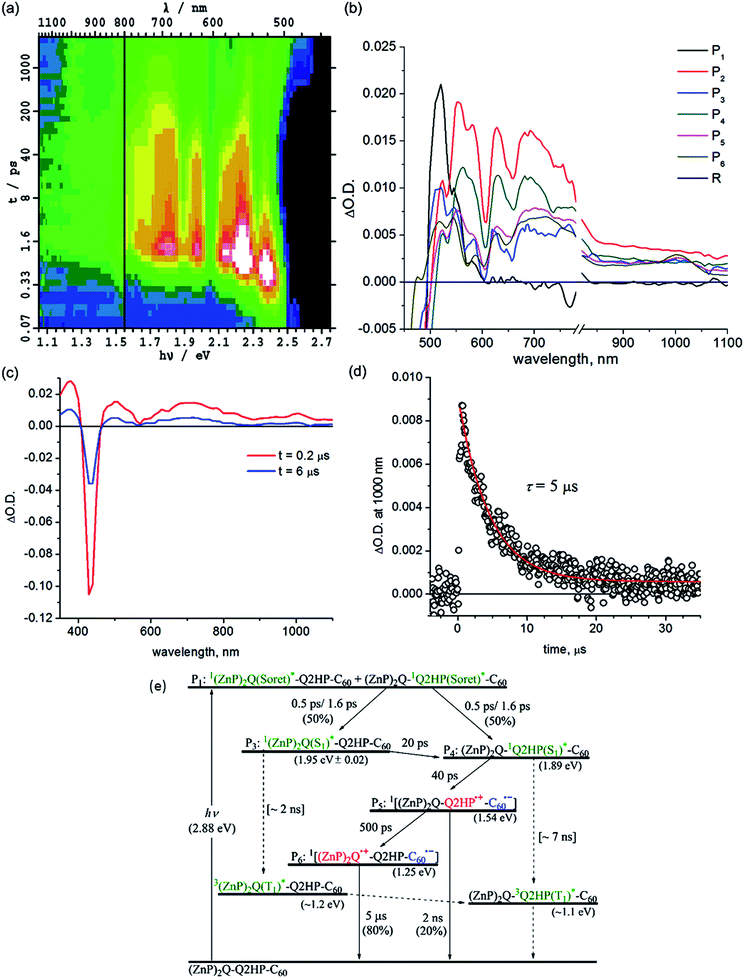
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This result indicates that there was significant exciton transfer between the excited Soret states of each porphyrin before internal conversion was complete.
1. This result indicates that there was significant exciton transfer between the excited Soret states of each porphyrin before internal conversion was complete.
The contribution of 1(ZnP)2Q(S1)* to the transient spectra diminishes 20 ps after internal conversion is complete, leaving behind only the contribution of 12HPQ(S1)*. This indicates intramolecular singlet–singlet energy transfer from zinc to free-base porphyrin. Subsequent to this energy transfer, primary charge-transfer CS1a occurs after 40 ps, generating component P5, (ZnP)2Q-Q2HP˙+-C60˙−. An alternate process CS1b, involving hole transfer from Q2HP to (ZnP)2Q is also thermodynamically possible (Table 3), but the component spectrum provides no indication of (ZnP)2Q˙+-Q2HP˙−-C60 formation. Secondary charge-separation CS2a then occurs to form the final charge-separated species (ZnP)2Q˙+-Q2HP-C60˙− with at least 80% yield after 500 ps, in competition with weak primary charge recombination that occurs on a timescale of at least 2 ns.
The final charge-separated state is also observed in the nanosecond transient absorption spectra shown in Fig. 4c. From the decay curves at 700 and 1000 nm, the lifetime of (ZnP)2Q˙+-Q2HP-C60˙− is determined to be 5 μs. While the energies of both 32HPQ(T1)* and 3(ZnP)2Q(T1)* are expected to be less than that for (ZnP)2Q˙+-Q2HP-C60˙−, no evidence for charge recombination to triplet states is obtained. The yield of these triplet states following ISC from the corresponding singlets is estimated to be 1%, and, as their estimated lifetime is ca. 9 μs, these components are not detectable in the observed transient absorption spectra.
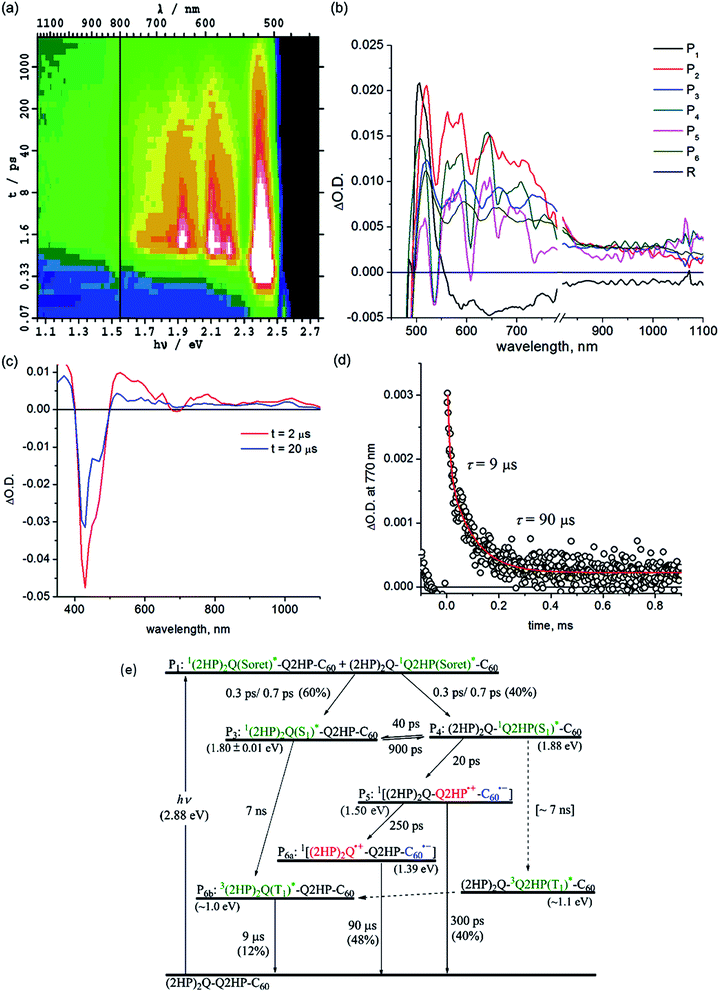
Other processes with yields too small to be observed in (ZnP)2Q-Q2HP-C60 also become manifest for (2HP)2Q-Q2HP-C60 such as phosphorescence, requiring more component spectra and more rate constants to be extracted from the data to complete the chemical model. Attempts to extract all of this information were unsuccessful as the fitting procedure proved to be underdetermined. In particular, somewhat similar spectra of long-lived components, P6a (2HP)2Q˙+-Q2HP-C60˙− and P6b3(2HP)2Q(T1)*, could not be differentiated and so a combined spectrum is reported as component P6. With this restriction, determination of unique rate constants becomes possible in principle, but five rate constants are required to describe the same temporal region while only three were required for (ZnP)2Q-Q2HP-C60; as a result, a range of viable solutions could be obtained for each parameter.
To aid the spectral fitting process, a ratio of 22 for the forward and reverse rate constants for the exciton transfer from P31(2HP)2Q(S1)* to P412HPQ(S1)* was determined from the observed free-energy difference of 0.08 eV; however, the free energy different is uncertain to at least ±0.01 eV, allowing this ratio to vary from 15 to 33, and good fits to the spectral data could be obtained using any ratio in this range. The extracted rate constants are thus only accurate to at most a factor of two.
The yields of component P3, 1(2HP)2Q(S1)*, and component P4, 12HPQ(S1)*, are fitted to be 60 and 40%, respectively, close to the ratio of the extinction coefficients of each chromophore. Primary and secondary charge-separation initiated by 12HPQ(S1)* are deduced to occur in 20 and 250 ps, respectively, both processes being faster than those observed for ZnPQ-Q2HP-C60 (100 and 500 ps) and (ZnP)2Q-Q2HP-C60 (40 and 500 ps).
However, the activated exciton transfer between 1(2HP)2Q(S1)* and 12HPQ(S1)*, with forward and reverse reaction times of 900 and 40 ps, respectively, ensures that 1(2HP)2Q(S1)* remains present for a long time. The fitted component concentrations reported in Fig. S11† reveal that the proportion of 1(2HP)2Q(S1)* is 12% after 2 ns, indicating the significance of this metastable trapped species.
Component P5 is identified as (2HP)2Q-Q2HP˙+-C60˙−, the product of primary charge-separation process CS1b, through assignment of the visible and NIR spectra to 2HPQ˙+ and C60˙−, respectively. Component P6a is identified as (2HP)2Q˙+-Q2HP-C60˙−, generated via the secondary charge-separation process CS2b, based on the observed transient absorption spectrum of (2HP)2˙+ produced electrochemically, that is shown in ESI Fig. S13b,† combined with the continuity of the NIR absorption of C60˙−. In contrast to the observed spectra for the other molecules considered, the observed signal strength decreases significantly in the nanosecond regime, indicating that primary charge-recombination CR1b competes with secondary charge-separation. The fitted lifetime for this process is 300 ps, shorter than the value of 880 ps deduced for Q2HP-C60 and much shorter that the value of >2 ns deduced for ZnPQ-Q2HP-C60 and (ZnP)2Q-Q2HP-C60.
The lifetime of the final charge-separated state is determined to be 90 μs by nanosecond laser flash photolysis (Fig. 5c). Notably, the time decay profiles at 770 nm (Fig. 5d) show biexponential character with a fast decay component of 9 μs (20%) and a slow component of 90 μs (80%). The time profiles at 1000 nm (ESI Fig. S12†), however, show only single exponential decay with a lifetime of 90 μs. As the 1000 nm transient absorption is attributed to C60˙−, it is clear that the slow component corresponds to the charge-recombination of the final charge-separated state (2HP)2Q˙+-Q2HP-C60˙−. The fast decay component is only observed in the visible region and clearly comes from the porphyrin macrocycle. This process is hence associated with phosphorescence from the lowest-energy triplet state, 3(2HP)2Q(T1)*. It is possible that this species is produced by charge-recombination of (2HP)2Q˙+-Q2HP-C60˙−, either directly or via3Q2HP(T1)*. In Fig. 5e, however, this process is not included, only production via ISC from in particular 1(2HP)2Q(S1)*. This process is expected to be important as 1(2HP)2Q(S1)* is a long-lived trap in the photochemical process, and indeed the fitted lifetime of 1(2HP)2Q(S1)* is 7 ns, in good agreement with expectations based on the observed value of 7 ns for Q2HP-C60 (Fig. 2e).
3.5 Extraction of solvent reorganization energies and electronic couplings from the observed lifetimes
The observed rate constants of the deduced components of all the compounds studied by transient absorption spectroscopy are summarized in Table 4. With the free-energy changes listed in Table 3, the coupling parameters V and solvent reorganization energies λo are determined (Table 4) using the semiclassical rate equation:136| Molecule | Process | τ | λ o (eV) | V (cm−1) |
|---|---|---|---|---|
| a The instrument-limited rise time of the initial excited-state. b Internal conversion from the excited Soret-states of the porphyrin 1P(Soret)* to the lowest-energy Q-state of the porphyrin 1P(S1)*. c The intramolecular singlet–singlet energy-transfer from the energetically higher lying 1P(S1)* to the lower lying 1P(S1)*. d The available charge-separation process options are defined in Table 3, CS1a and/or CS1betc., may in principle be observed. e Phosphorescence lifetime. | ||||
| Q2HP-C60 | 1P(Soret)a | 0.22 ps | — | — |
| 1ICb | 0.8 ps | — | — | |
| ISC | 7 ns | — | — | |
| CS1 | 120 ps | 0.69 | 19 | |
| CR1 | 880 ps | 0.69 | 19 | |
| 3P*e | 9 μs | — | — | |
| ZnPQ-Q2HP-C60 | 1P(Soret)a | 0.24 | — | — |
| 1ICb | 0.3, 1.0 ps | — | — | |
| ENc | 30 ps | — | — | |
| CS1ad | 100 ps | 0.64 | 20 | |
| CR1ad | 2 ns | 0.64 | 20 | |
| CS2ad | 500 ps | [0.65–0.85] | 31–84 | |
| CR2 | 20 μs | [0.6–0.8] | 0.041–0.102 | |
| (ZnP)2Q-Q2HP-C60 | 1P(Soret)a | 0.3 ps | — | — |
| 1ICb | 0.5, 1.6 ps | — | — | |
| ENc | 20 ps | — | — | |
| CS1ad | 40 ps | 0.60 | 25 | |
| CR1ad | 2 ns | 0.60 | 25 | |
| CS2ad | 500 ps | [0.6–0.8] | 12–30 | |
| CR2 | 5 μs | [0.55–0.75] | 0.070–0.163 | |
| (2HP)2Q-Q2HP-C60 | 1P(Soret)a | 0.24 ps | — | — |
| 1ICb | 0.3, 0.7 ps | — | — | |
| ISC | 7 ns | — | — | |
| CS1bd | 20 ps | 0.64 | 40 | |
| CR1bd | 300 ps | 0.64 | 40 | |
| CS2bd | 250 ps | [0.65–0.85] | 70–190 | |
| CR2 | 90 μs | [0.6–0.8] | 0.021–0.055 | |
The Franck–Condon factors associated with changes in the intramolecular modes required for this procedure are evaluated from DFT frequency calculations of the vibrational modes of the molecular fragments in their various states of ionization; the vibrational parameters deduced by this procedure are given in full in ESI Table S1.†
The coupling V and solvent reorganization energy λo for Q2HP-C60 are extracted using the rates for charge-separation and charge-recombination, using the common assumption that the coupling and reorganization energy for both processes are the same. While calculated reorganization energies for these processes typically are very similar, coupling strengths can vary by an order of magnitude and so this analysis is actually quite approximate.78 The coupling V and solvent reorganization energies λo are determined to be 19 cm−1 and 0.69 eV, respectively. A reorganization energy of 0.64 eV and a coupling of 20 cm−1 are obtained for the primary charge-separation process of ZnPQ-Q2HP-C60. For secondary charge-recombination (CR2), using 0.6 eV < λo < 0.8 eV, the values deduced for V range from 0.041 to 0.102 cm−1 for recombination on the singlet manifold. Similarly, the reorganization energies λo and couplings V of the primary charge-separation process for (ZnP)2Q-Q2HP-C60 are determined to be 0.60 eV and 25 cm−1, and for (2HP)2Q-Q2HP-C60 are 0.64 eV and 40 cm−1. For CR2, the couplings V are deduced to be 0.07–0.163 cm−1 and 0.021–0.055 cm−1 for (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60, respectively. The non-planar Qx–Qx linkage reduces the conjugation and therefore weakens the couplings. Chemical substitutions on the molecules to artificially control the non-planarity of these groups can therefore be used as an easy way of controlling photochemical properties.
4. Conclusions
The photoinduced electron-transfer reactions of photosynthetic reaction centre (PRC) models, Q2HP-C60, ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60, were synthesised and studied using the femtosecond and nanosecond transient absorption spectroscopy and the lifetimes of the photochemical reaction, the solvent reorganization energies and couplings were extracted (Table 4). All molecules show picosecond-timescale charge-separations, ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60 restrained singlet charge-separations to the microsecond-timescale, whereas this process occurs on the picosecond-timescale for Q2HP-C60. The long-lived component is maintained on the singlet manifold and the quantum yield for its production is high. ZnPQ-Q2HP-C60, (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60 increase the distance between the final charge-separated ion pair while the internal biquinoxalinyl linkage reduces the coupling, affording the longer-lived species on the singlet manifold in these molecules. Also, all charge-recombination is observed to occur to the ground state rather than to the energetically accessible local triplet states.The PRC model molecules (ZnP)2Q-Q2HP-C60 and (2HP)2Q-Q2HP-C60 incorporating porphyrin arrays and fullerene connected by Tröger's base, biquinoxalinyl and imidazole linkers were designed to have similar inter-chromophoric distances to those in the natural PRC. The centre-to-centre distance of 6.2 Å in the Tröger's base porphyrin dimer is close to that of 7.0 Å for the special pair in the natural PRC, see Fig. 1, suggesting that control over the system can be achieved by introducing small chemical modifications,78,84,95–103 just the way in which mutagenesis controls the natural PRC.88,137 Also, the distances for electron-transfer reactions are 18.7 and 15.0 Å for these models that is very close to that of 18.0 and 14.3 Å found in the natural system, so the electron-transport properties are quite similar.
While the processes driving charge separation and recombination are quite different in the natural and artificial systems, the resulting process lifetimes (Fig. 1) are comparable. In the natural system, charge separation to the first state stable for times longer than its production time is to species P+HL−, that takes 4–7 ps to appear,62 secondary charge separation then occurs62 in 200–250 ps ahead of primary charge recombination (0.6 to 10 ns),62 and then secondary charge recombination takes 100 ms.94 The corresponding times for the biomimetic compounds are 20–40 ps, 250–500 ps, 0.3–2 ns, and 5–90 μs, respectively. All are within an order of magnitude of the natural system except for the secondary charge recombination times, which are 3–4 orders of magnitude shorter. This discrepancy is not necessarily of concern, however, as processes that take and utilize separated charges typically occur on the scale of a few μs and so the model compounds are stable enough, more so than most alternatives that have been considered. Related compounds show secondary charge separation lasting for over 1 ms at room temperature,78 so synthetic methods are available to meet specific requirements.
Acknowledgements
This work was supported by Discovery Research Grants (DP0773847 and DP12010259) to M.J.C. and J.R.R. from the Australian Research Council. This work was partially supported by a Grant-in-Aid (No. 16H02268 to S.F. and 21750146 to K.O.) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. S.H.L. expresses his special thanks for The Global COE (centre of excellence) program “Global Education and Research Centre for Bio-Environmental Chemistry” of Osaka University for his stay in Japan. We thank National Computing Infrastructure (NCI) and the Australian Centre for Advanced Computing and Communications (AC3) for the provision of computer resources.Notes and references
- S. Fukuzumi, K. Ohkubo and T. Suenobu, Acc. Chem. Res., 2014, 47, 1455 CrossRef CAS PubMed.
- G. Li, R. Zhu and Y. Yang, Nat. Photonics, 2012, 6, 153 CrossRef CAS.
- H. Imahori, T. Umeyama and S. Ito, Acc. Chem. Res., 2009, 42, 1809 CrossRef CAS PubMed.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890 CrossRef CAS PubMed.
- M. J. Llansola-Portoles, R. E. Palacios, D. Gust, T. A. Moore and A. L. Moore, in From Molecules to Materials: Pathways to Artificial Photosynthesis, 2015, p. 71 Search PubMed.
- S. Zhou, M. Yamamoto, G. A. D. Briggs, H. Imahori and K. Porfyrakis, J. Am. Chem. Soc., 2016, 138, 1313 CrossRef CAS PubMed.
- T. Miura, R. Tao, S. Shibata, T. Umeyama, T. Tachikawa, H. Imahori and Y. Kobori, J. Am. Chem. Soc., 2016, 138, 5879 CrossRef CAS PubMed.
- G. J. Huang, M. A. Harris, M. D. Krzyaniak, E. A. Margulies, S. M. Dyar, R. J. Lindquist, Y. Wu, V. V. Roznyatovskiy, Y. L. Wu, R. M. Young and M. R. Wasielewski, J. Phys. Chem. B, 2016, 120, 756 CrossRef CAS PubMed.
- M. Rudolf, S. V. Kirner and D. M. Guldi, Chem. Soc. Rev., 2016, 45, 612 RSC.
- T. Higashino, T. Yamada, M. Yamamoto, A. Furube, N. V. Tkachenko, T. Miura, Y. Kobori, R. Jono, K. Yamashita and H. Imahori, Angew. Chem., Int. Ed., 2016, 55, 629 CrossRef CAS PubMed.
- L. Martín-Gomis, G. Rotas, K. Ohkubo, F. Fernández-Lázaro, S. Fukuzumi, N. Tagmatarchis and A. Sastre-Santos, Nanoscale, 2015, 7, 7437 RSC.
- S. Fukuzumi, in Chemical Science of π-Electron Systems, ed. T. Akasada, A. Osuka, S. Fukuzumi, H. Kandori and Y. Aso, Springer, Japan, 2015, p. 529 Search PubMed.
- R. C. Huber, A. S. Ferreira, R. Thompson, D. Kilbride, N. S. Knutson, L. S. Devi, D. B. Toso, J. R. Challa, Z. H. Zhou, Y. Rubin, B. J. Schwartz and S. H. Tolbert, Science, 2015, 348, 1340 CrossRef CAS PubMed.
- T. Kamimura, K. Ohkubo, Y. Kawashima, S. Ozako, K. I. Sakaguchi, S. Fukuzumi and F. Tani, J. Phys. Chem. C, 2015, 119, 25634 CAS.
- A. Arrigo, A. Santoro, F. Puntoriero, P. P. Lainé and S. Campagna, Coord. Chem. Rev., 2015, 304–305, 109 CrossRef CAS.
- M. Vizuete, M. J. Gómez-Escalonilla, M. Barrejón, J. L. G. Fierro, M. Zhang, M. Yudasaka, S. Iijima, P. Atienzar, H. García and F. Langa, Phys. Chem. Chem. Phys., 2016, 18, 1828 RSC.
- C. Stangel, C. Schubert, S. Kuhri, G. Rotas, J. T. Margraf, E. Regulska, T. Clark, T. Torres, N. Tagmatarchis, A. G. Coutsolelos and D. M. Guldi, Nanoscale, 2015, 7, 2597 RSC.
- S. V. Kirner, C. Henkel, D. M. Guldi, J. D. Megiatto Jr and D. I. Schuster, Chem. Sci., 2015, 6, 7293 RSC.
- S. V. Kirner, D. M. Guldi, J. D. Megiatto Jr and D. I. Schuster, Nanoscale, 2015, 7, 1145 RSC.
- M. Rudolf, O. Trukhina, J. Perles, L. Feng, T. Akasaka, T. Torres and D. M. Guldi, Chem. Sci., 2015, 6, 4141 RSC.
- S. V. Kirner, D. Arteaga, C. Henkel, J. T. Margraf, N. Alegret, K. Ohkubo, B. Insuasty, A. Ortiz, N. Martín, L. Echegoyen, S. Fukuzumi, T. Clark and D. M. Guldi, Chem. Sci., 2015, 6, 5994 RSC.
- L. Moreira, J. Calbo, R. M. Krick Calderon, J. Santos, B. M. Illescas, J. Aragó, J. F. Nierengarten, D. M. Guldi, E. Ortí and N. Martín, Chem. Sci., 2015, 6, 4426 RSC.
- O. Trukhina, M. Rudolf, G. Bottari, T. Akasaka, L. Echegoyen, T. Torres and D. M. Guldi, J. Am. Chem. Soc., 2015, 137, 12914 CrossRef CAS PubMed.
- D. Gust, Faraday Discuss., 2015, 185, 9 RSC.
- J. Arero, G. Kodis, R. A. Schmitz, D. D. Mendez-Hernandez, T. A. Moore, A. L. Moore and D. Gust, J. Porphyrins Phthalocyanines, 2015, 19, 934 CrossRef CAS.
- N. L. Bill, M. Ishida, Y. Kawashima, K. Ohkubo, Y. M. Sung, V. M. Lynch, J. M. Lim, D. Kim, J. L. Sessler and S. Fukuzumi, Chem. Sci., 2014, 5, 3888 RSC.
- V. M. Blas-Ferrando, J. Ortiz, K. Ohkubo, S. Fukuzumi, F. Fernández-Lázaro and Á. Sastre-Santos, Chem. Sci., 2014, 5, 4785 RSC.
- M. Supur, Y. Kawashima, Y. X. Ma, K. Ohkubo, C. F. Chen and S. Fukuzumi, Chem. Commun., 2014, 50, 15796 RSC.
- T. Zhang and W. Lin, Chem. Soc. Rev., 2014, 43, 5982 RSC.
- S. Pillai, J. Ravensbergen, A. Antoniuk-Pablant, B. D. Sherman, R. Van Grondelle, R. N. Frese, T. A. Moore, D. Gust, A. L. Moore and J. T. M. Kennis, Phys. Chem. Chem. Phys., 2013, 15, 4775 RSC.
- V. Garg, G. Kodis, P. A. Liddell, Y. Terazono, T. A. Moore, A. L. Moore and D. Gust, J. Phys. Chem. B, 2013, 117, 11299 CrossRef CAS PubMed.
- M. Maiuri, J. J. Snellenburg, I. H. M. Van Stokkum, S. Pillai, K. Wongcarter, D. Gust, T. A. Moore, A. L. Moore, R. Van Grondelle, G. Cerullo and D. Polli, J. Phys. Chem. B, 2013, 117, 14183 CrossRef CAS PubMed.
- C. Zhou, Q. Liu, W. Xu, C. Wang and X. Fang, Chem. Commun., 2011, 47, 2982 RSC.
- M. G. Alvarez, C. Prucca, M. E. Milanesio, E. N. Durantini and V. Rivarola, Int. J. Biochem. Cell Biol., 2006, 38, 2092 CrossRef CAS PubMed.
- X. F. Zhang and W. Guo, J. Photochem. Photobiol., A, 2011, 225, 117 CrossRef CAS.
- F. F. Sperandio, S. K. Sharma, M. Wang, S. Jeon, Y. Y. Huang, T. Dai, S. Nayka, S. C. O. M. de Sousa, L. Y. Chiang and M. R. Hamblin, Nanomed.: Nanotechnol., Biol. Med., 2013, 9, 570 CrossRef CAS PubMed.
- Y. Chen, D. Zhao and Y. Liu, Chem. Commun., 2015, 51, 12266 RSC.
- J. Shi, L. Wang, J. Gao, Y. Liu, J. Zhang, R. Ma, R. Liu and Z. Zhang, Biomaterials, 2014, 35, 5771 CrossRef CAS PubMed.
- Y. Y. Huang, S. K. Sharma, R. Yin, T. Agrawal, L. Y. Chiang and M. R. Hamblin, J. Biomed. Nanotechnol., 2014, 10, 1918 CrossRef CAS PubMed.
- S. A. Dingsdag, B. C. M. Yap, N. Hunter and M. J. Crossley, Org. Biomol. Chem., 2015, 13, 98 CAS.
- A. P. N. Singh, M. A. Harris, R. M. Young, S. A. Miller, M. R. Wasielewski and F. D. Lewis, Faraday Discuss., 2015, 185, 105 RSC.
- Y. Takano, T. Numata, K. Fujishima, K. Miyake, K. Nakao, W. D. Grove, R. Inoue, M. Kengaku, S. Sakaki, Y. Mori, T. Murakami and H. Imahori, Chem. Sci., 2016, 7, 3331 RSC.
- J. G. Rohan, Y. R. Citron, A. C. Durrell, L. E. Cheruzel, H. B. Gray, R. H. Grubbs, M. Humayun, K. L. Engisch, V. Pikov and R. H. Chow, ACS Chem. Neurosci., 2013, 4, 585 CrossRef CAS PubMed.
- H. Takakura, R. Kojima, M. Kamiya, E. Kobayashi, T. Komatsu, T. Ueno, T. Terai, K. Hanaoka, T. Nagano and Y. Urano, J. Am. Chem. Soc., 2015, 137, 4010 CrossRef CAS PubMed.
- C. Schubert, M. Wielopolski, L.-H. Mewes, G. d. M. Rojas, C. van der Pol, K. C. Moss, M. R. Bryce, J. E. Moser, T. Clark and D. M. Guldi, Chem.–Eur. J., 2013, 19, 7575 CrossRef CAS PubMed.
- G. Copley, T. A. Moore, A. L. Moore and D. Gust, Adv. Mater., 2013, 25, 456 CrossRef CAS PubMed.
- L. Wibmer, L. M. O. Lourenço, A. Roth, G. Katsukis, M. G. P. M. S. Neves, J. A. S. Cavaleiro, J. P. C. Tomé, T. Torres and D. M. Guldi, Nanoscale, 2015, 7, 5674 RSC.
- R. E. Blankenship, Molecular mechanisms of photosynthesis, Blackwell Science, Oxford, 2002 Search PubMed.
- W. W. Parson and A. Warshel, in The Purple Prototropic Bacteria, Springer, Dordrecht, 2009, p. 355 Search PubMed.
- J. M. Warman, M. P. d. Haas, M. N. Paddon-Row, E. Cotsaris, N. S. Hush, H. Oevering and J. W. Verhoeven, Nature, 1986, 320, 615 CrossRef CAS.
- M. R. Wasielewski, D. G. Johnson, W. A. Svec, K. M. Kersey and D. W. Minsek, J. Am. Chem. Soc., 1988, 110, 7219 CrossRef CAS.
- M. R. Wasielewski, Chem. Rev., 1992, 92, 435 CrossRef CAS.
- C. Luo, D. M. Guldi, H. Imahori, K. Tamaki and Y. Sakata, J. Am. Chem. Soc., 2000, 122, 6535 CrossRef CAS.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2001, 34, 40 CrossRef CAS PubMed.
- Z. E. X. Dance, Q. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. B, 2006, 110, 25163 CrossRef CAS PubMed.
- S. Fukuzumi, Phys. Chem. Chem. Phys., 2008, 10, 2283 RSC.
- B. D. Sherman, M. D. Vaughn, J. J. Bergkamp, D. Gust, A. L. Moore and T. A. Moore, Photosynth. Res., 2014, 120, 59 CrossRef CAS PubMed.
- M. Malferrari, A. Mezzetti, F. Francia and G. Venturoli, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 328 CrossRef CAS PubMed.
- A. G. Yakovlev and V. A. Shuvalov, J. Theor. Biol., 2014, 343, 92 CrossRef CAS PubMed.
- K. Gibasiewicz, M. Pajzderska, A. Dobek, J. Karolczak, G. Burdzinski, K. Brettel and M. R. Jones, Phys. Chem. Chem. Phys., 2013, 15, 16321 RSC.
- K. Gibasiewicz, M. Pajzderska, A. Dobek, K. Brettel and M. R. Jones, J. Phys. Chem. B, 2013, 117, 11112 CrossRef CAS PubMed.
- K. Gibasiewicz, R. Białek, M. Pajzderska, J. Karolczak, G. Burdziński, M. R. Jones and K. Brettel, Photosynth. Res., 2016, 1 Search PubMed.
- A. C. Benniston, Phys. Chem. Chem. Phys., 2007, 9, 5739 RSC.
- K. Ohkubo and S. Fukuzumi, Bull. Chem. Soc. Jpn., 2009, 82, 303 CrossRef CAS.
- Y. Pellegrin and F. Odobel, Coord. Chem. Rev., 2011, 255, 2578 CrossRef CAS.
- S. Kirner, M. Sekita and D. M. Guldi, Adv. Mater., 2014, 26, 1482 CrossRef CAS PubMed.
- M. E. El-Khouly, S. Fukuzumi and F. D'Souza, ChemPhysChem, 2014, 15, 30 CrossRef CAS PubMed.
- Z.-Y. Gu, J. Park, A. Raiff, Z. Wei and H.-C. Zhou, ChemCatChem, 2014, 6, 67 CrossRef CAS.
- M. K. Panda, K. Ladomenou and A. G. Coutsolelos, Coord. Chem. Rev., 2012, 256, 2601 CrossRef CAS.
- S. Yang, Z. Wu, X. Wan and J. Yan, Progr. Chem., 2011, 23, 1123 CAS.
- R. Tange, K. Inai, T. Sagawa and S. Yoshikawa, J. Mater. Res., 2011, 26, 306 CrossRef CAS.
- C. H. Chang, D. Tiede, J. Tang, U. Smith, J. Norris and M. Schiffer, FEBS Lett., 1986, 205, 82 CrossRef CAS PubMed.
- J. P. Allen, G. Feher, T. O. Yeates, H. Komiya and D. C. Rees, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 5730 CrossRef CAS.
- J. Deisenhofer and H. Michel, Science, 1989, 245, 1463 CAS.
- S. G. Boxer, R. A. Goldstein, D. J. Lockhart, T. R. Middendorf and L. Takiff, J. Phys. Chem., 1989, 93, 8280 CrossRef CAS.
- P. Jordan, P. Fromme, H. T. Witt, O. Klukas, W. Saenger and N. Krauss, Nature, 2001, 411, 909 CrossRef CAS PubMed.
- A. Zouni, H.-T. Witt, J. Kern, P. Fromme, N. Krauss, W. Saenger and P. Orth, Nature, 2001, 409, 739 CrossRef CAS PubMed.
- S.-H. Lee, A. G. Larsen, K. Ohkubo, Z.-L. Cai, J. R. Reimers, S. Fukuzumi and M. J. Crossley, Chem. Sci., 2012, 3, 257 RSC.
- L. P. Dutton, J. S. Leigh and M. Seibert, Biochem. Biophys. Res. Commun., 1972, 46, 406 CrossRef PubMed.
- M. C. Thurnauer, J. J. Katz and J. R. Norris, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3270 CrossRef CAS.
- A. J. Hoff, Q. Rev. Biophys., 1984, 17, 153 CrossRef CAS PubMed.
- M. Volk, A. Ogrodnik and M. E. Michel-Beyerle, in Anoxygenic photosynthetic bacteria, ed. R. E. Blankenship, M. T. Madigan and C. E. Bauer, Kluwer, Dordrecht, 1995, p. 595 Search PubMed.
- A. Rao, P. C. Y. Chow, S. Gélinas, C. W. Schlenker, C. Z. Li, H. L. Yip, A. K. Y. Jen, D. S. Ginger and R. H. Friend, Nature, 2013, 500, 435 CrossRef CAS PubMed.
- M. J. Crossley, P. J. Sintic, R. Walton and J. R. Reimers, Org. Biomol. Chem., 2003, 1, 2777 CAS.
- M. J. Crossley, P. J. Sintic, J. A. Hutchison and K. P. Ghiggino, Org. Biomol. Chem., 2005, 3, 852 CAS.
- J. A. Hutchison, P. J. Sintic, M. J. Crossley, T. Nagamura and K. P. Ghiggino, Phys. Chem. Chem. Phys., 2009, 11, 3478 RSC.
- J. A. Hutchison, P. J. Sintic, P. R. Brotherhood, C. Scholes, I. M. Blake, K. P. Ghiggino and M. J. Crossley, J. Phys. Chem. C, 2009, 113, 11796 CAS.
- J. R. Reimers and N. S. Hush, J. Am. Chem. Soc., 2004, 126, 4132 CrossRef CAS PubMed.
- M. J. Crossley, L. G. Mackay and A. C. Try, J. Chem. Soc., Chem. Commun., 1995, 1925 RSC.
- P. R. Brotherhood, R. A. S. Wu, P. Turner and M. J. Crossley, Chem. Commun., 2007, 225 RSC.
- D. M. Guldi, Chem. Commun., 2000, 321 RSC.
- H. Imahori, Bull. Chem. Soc. Jpn., 2007, 80, 621 CrossRef CAS.
- D. M. Guldi, B. M. Illescas, C. M. Atienza, M. Wielopolski and N. Martin, Chem. Soc. Rev., 2009, 38, 1587 RSC.
- G. Feher, J. P. Allen, M. Y. Okamura and D. C. Rees, Nature, 1989, 339, 111 CrossRef CAS.
- M. J. Crossley, A. C. Try and R. Walton, Tetrahedron Lett., 1996, 37, 6807 CrossRef CAS , submitted.
- J. R. Reimers, L. E. Hall, M. J. Crossley and N. S. Hush, J. Phys. Chem. A, 1999, 103, 4385 CrossRef CAS.
- P. J. Sintic, W. E, Z. Ou, J. Shao, J. A. McDonald, Z.-L. Cai, K. M. Kadish, M. J. Crossley and J. R. Reimers, Phys. Chem. Chem. Phys., 2008, 10, 268 RSC . This article was unfortunately duplicated later in 10(4), p. 515–527, their note 10 P7328.
- W. E, K. M. Kadish, P. J. Sintic, T. Khoury, L. J. Govenlock, Z. Ou, J. Shao, K. Ohkubo, J. R. Reimers, S. Fukuzumi and M. J. Crossley, J. Phys. Chem. A, 2008, 112, 556 CrossRef CAS PubMed.
- D. Curiel, K. Ohkubo, J. R. Reimers, S. Fukuzumi and M. J. Crossley, Phys. Chem. Chem. Phys., 2007, 9, 5260 RSC.
- K. Sendt, L. A. Johnston, W. A. Hough, M. J. Crossley, N. S. Hush and J. R. Reimers, J. Am. Chem. Soc., 2002, 124, 9299 CrossRef CAS PubMed.
- M. J. Crossley and P. L. Burn, J. Chem. Soc., Chem. Commun, 1991, 1569 RSC.
- J. R. Reimers, T. X. Lü, M. J. Crossley and N. S. Hush, Chem. Phys. Lett., 1996, 256, 353 CrossRef CAS.
- T. X. Lü, J. R. Reimers, M. J. Crossley and N. S. Hush, J. Phys. Chem., 1994, 98, 11878 CrossRef.
- T. Khoury and M. J. Crossley, New J. Chem., 2009, 33, 1076 RSC.
- A. Nattestad, Y. Y. Cheng, R. W. MacQueen, T. F. Schulze, F. W. Thompson, A. J. Mozer, B. Fueckel, T. Khoury, M. J. Crossley, K. Lips, G. G. Wallace and T. W. Schmidt, J. Phys. Chem. Lett., 2013, 4, 2073 CrossRef CAS PubMed.
- T. F. Schulze, J. Czolk, Y. Y. Cheng, B. Fuckel, R. W. MacQueen, T. Khoury, M. J. Crossley, B. Stannowski, K. Lips, U. Lemmer, A. Colsmann and T. W. Schmidt, J. Phys. Chem. C, 2012, 116, 22794 CAS.
- Y. Y. Cheng, B. Fueckel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795 CrossRef CAS.
- P. C. Dastoor, C. R. McNeill, H. Frohne, C. J. Foster, B. Dean, C. J. Fell, W. J. Belcher, W. M. Campbell, D. L. Officer, I. M. Blake, P. Thordarson, M. J. Crossley, N. S. Hush and J. R. Reimers, J. Phys. Chem. C, 2007, 111, 15415 CAS.
- M. J. Crossley, C. S. Sheehan, T. Khoury, J. R. Reimers and P. J. Sintic, New J. Chem., 2008, 32, 340 RSC.
- M. J. Crossley and J. A. McDonald, J. Chem. Soc., Perkin Trans. 1, 1999, 2429 RSC.
- M. Maggini, G. Scorrano and M. Prato, J. Am. Chem. Soc., 1993, 115, 9798 CrossRef CAS.
- T. Drovetskaya, C. A. Reed and P. Boyd, Tetrahedron Lett., 1995, 36, 7971 CrossRef CAS.
- M. J. Crossley, A. C. Try and R. Walton, Tetrahedron Lett., 1996, 37, 6807 CrossRef CAS.
- M. J. Crossley, T. W. Hambley, L. G. Mackay, A. C. Try and R. Walton, J. Chem. Soc., Chem. Commun., 1995, 1077 RSC.
- M. J. Crossley, L. J. Govenlock and J. K. Prashar, J. Chem. Soc., Chem. Commun., 1995, 2379 RSC.
- Z. Ou, W. E, J. Shao, P. L. Burn, C. S. Sheehan, R. Walton, K. M. Kadish and M. J. Crossley, J. Porphyrins Phthalocyanines, 2005, 9, 142 CrossRef CAS.
- K. M. Kadish, W. E, P. J. Sintic, Z. Ou, J. Shao, K. Ohkubo, S. Fukuzumi, L. J. Govenlock, J. A. McDonald, A. C. Try, Z.-L. Cai, J. R. Reimers and M. J. Crossley, J. Phys. Chem. B, 2007, 111, 8762 CrossRef CAS PubMed.
- M. J. Crossley and L. A. Johnston, Chem. Commun, 2002, 1122 RSC.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 9th edn, 2010 Search PubMed.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138 CrossRef CAS.
- R. L. Fulton and M. Gouterman, J. Chem. Phys., 1961, 35, 1059 CrossRef CAS.
- R. L. Fulton and M. Gouterman, J. Chem. Phys., 1964, 41, 2280 CrossRef CAS.
- M. Gouterman, J. Chem. Phys., 1965, 42, 351 CrossRef CAS.
- G. Fischer, Vibronic Coupling, Academic Press, London, 1984 Search PubMed.
- E. K. L. Yeow, P. J. Sintic, N. M. Cabral, J. N. H. Reek, M. J. Crossley and K. P. Ghiggino, Phys. Chem. Chem. Phys., 2000, 2, 4281 RSC.
- H. Imahori, K. Tamaki, D. M. Guldi, C. Luo, M. Fujitsuka, O. Ito, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 2607 CrossRef CAS PubMed.
- K. Tamaki, H. Imahori, Y. Sakata, Y. Nishimura and I. Yamazaki, Chem. Commun., 1999, 625 RSC.
- S. I. Yang, R. K. Lammi, J. Seth, J. A. Riggs, T. Arai, D. Kim, D. F. Bocian, D. Holten and J. S. Lindsey, J. Phys. Chem. B, 1998, 102, 9426 CrossRef CAS.
- K. Kilsa, J. Kajanus, J. Martensson and B. Albinsson, J. Phys. Chem. B, 1999, 103, 7329 CrossRef.
- J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg and E. Krausz, Sci. Rep., 2013, 3, 2761 Search PubMed.
- M. Rätsep, Z.-L. Cai, J. R. Reimers and A. Freiberg, J. Chem. Phys., 2011, 134, 024506 CrossRef PubMed.
- D. M. Guldi, Chem. Soc. Rev., 2002, 31, 22 RSC.
- D. M. Guldi, Phys. Chem. Chem. Phys., 2007, 9, 1400 RSC.
- Y. Kashiwagi, K. Ohkubo, J. A. McDonald, I. M. Blake, M. J. Crossley, Y. Araki, O. Ito, H. Imahori and S. Fukuzumi, Org. Lett., 2003, 5, 2719 CrossRef CAS PubMed.
- K. Ohkubo, P. J. Sintic, N. V. Tkachenko, H. Lemmetyinen, W. E, Z. Ou, J. Shao, K. M. Kadish, M. J. Crossley and S. Fukuzumi, Chem. Phys., 2006, 326, 3 CrossRef CAS.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218 CrossRef CAS.
- J. R. Reimers, J. M. Hughes and N. S. Hush, Biochemistry, 2000, 39, 16185 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Electrochemistry, fitting of data measured by femtosecond laser flash photolysis, vibrational parameters deduced for the molecular fragments from B3LYP vibrational frequency analysis, and vibrational parameters used in the determination of Franck–Condon factors for charge-transfer processes. See DOI: 10.1039/c6sc01076h |
| This journal is © The Royal Society of Chemistry 2016 |