Conductance of metal superatom-based molecular wires influenced by nanoscale effects

Abstract

High-conductance molecular wires are critical for advancing molecular-scale electronics, yet their performance typically diminishes exponentially with length. Here, we reveal an unconventional phenomenon where nanoscale molecular wires constructed from metal superatoms demonstrate enhanced conductance as their length increases. Through first-principles calculations, we find that quasi-one-dimensional assemblies of W@Cu₁₂ superatoms, below 2.5 nanometers in length, exhibit a gradual conductance decay. Importantly, when organized into bundle-like configurations, their conductance transitions to an increasing trend, with the decay factor shifting from 1.25 nm⁻¹ to −0.95 nm⁻¹. This reverse phenomenon can be attributed to the energy alignment of the dominant electron transport orbitals with the Fermi level of the electrode–scattering region–electrode systems, effectively lowering the tunneling barrier. Our results demonstrate that negative decay factors in molecular-scale devices are not intrinsic but can be engineered through structural design. This study provides a theoretical foundation for optimizing molecular circuitry through structural control and highlights the potential of metal superatoms in next-generation electronic transport applications.

---

Rui-Qin Zhang

Prof. Ruiqin Zhang is a Chair Professor in the Department of Physics at the City University of Hong Kong. His research encompasses the energetics, kinetics, and novel properties of low-dimensional functional materials, using computational and experimental approaches. He has published numerous papers on nanoscale systems, contributing significantly to nanoscience. His recent work focuses on interactions of nanomaterials with chemical, biological, and medical systems, aiming to advance nanostructured materials for practical applications in energy and healthcare. Recognized as an Outstanding Reviewer for Nanoscale Horizons in 2021, he is honored to contribute to its 10th anniversary collection.

New concepts

This study demonstrates that the structural engineering of superatomic molecular wires can reverse the inherent length-dependent conductance decay in electronic systems. This phenomenon occurs because the extended three-dimensional coupling in bundled superatomic molecular wires brings the electron-transport-dominant orbitals closer to the Fermi level of the electrode–scattering region–electrode system, thereby effectively reducing the tunneling barrier. Our work establishes that this behavior is contingent upon structural design, thereby advancing new pathways for engineering non-classical transport through structural dimensionality. These findings highlight for the first time the potential of superatoms in electronic transport, emphasizing that unconventional conductance trends can be achieved through the rational assembly of superatomic building blocks.

Introduction

The development of electronics is trending towards the molecular scale, requiring the understanding of material structures at the atomic level.^1–4 One of the important research topics is to discover molecular wires (MWs) that facilitate efficient electron transport over long distances.^5–7 However, some studies have shown that the electron transport mechanism for nanoscale MWs shorter than ∼2.5 nanometers (nm) is attributed to tunnelling,^5,8–10 and the conductance G₀ decays exponentially by molecular length L according to equation G₀ = A × exp(−βL), where A is the prefactor and β is the decay factor.^11,12 In this context, the search for small values of β in molecular-scale electronics had been continuing for decades,^11,13–15 until, in 2018, a theoretical study reported fuse-assembled quasi-1D porphyrin-based MWs possessing vanishing or even a negative β value.¹⁶ Subsequently, in 2020, a report based on a scanning tunnelling microscope based-break junction (STM-BJ) technique indicated that cumulene wires display increasing conductance with increasing length.¹⁷ Moreover, the reports based on comparative analysis methods reveal that this abnormal electrical transport phenomenon occurs in assemblies where the units are strongly coupled.^16,17 Thus, the quest for molecular-scale devices exhibiting increasing conductance with increasing length can begin with the search for units assembled by strong coupling interactions.

Superatoms are molecular systems composed of multiple atoms whose orbitals exhibit angular momentum symmetry similar to that of electrons arranged in shells within atoms.^18–22 As fundamental building blocks at the atomic level, they enable the bottom-up assembly of a wide range of functional systems, thereby facilitating the exploration of unique and uncommon physical phenomena.^23–31 For instance, the asymmetric monolayer assembled via C₆₀ superatoms endows anisotropic phonon modes and conductance, forming a topological structure that distinguishes them from traditional two-dimensional materials.^32,33 Endohedral metallofullerene superatoms can achieve bottom-up customized assemblies through spin-polarized magnetic coupling,³⁴ such as superatom-based chiral assemblies.³⁵ It is noteworthy that recent studies have reported that W@Cu₁₂ superatoms can be directly assembled into oligomers and crystals through highly conjugated superatomic molecular orbitals (SAMOs),³⁶ which may directly benefit electrical transport.^11,16,37 In addition, considering that the metal systems generally exhibit better conductance than many organic molecules,^5,38 it can be inferred that highly conjugated superatomic molecular wires (SMWs) assembled from W@Cu₁₂ metal superatoms have the potential to exhibit enhanced conductance with increasing length through rational structural control.

In this work, we conducted research studies on the electrical transport properties of quasi-1D assemblies using superatoms as building blocks. Specifically, we selected structurally stable W@Cu₁₂ with a closed-shell electronic configuration as a unit and performed this study using the non-equilibrium Green's function (NEGF) formalism within density functional theory (DFT). The results show that the decay factor of quasi-1D SMWs is smaller than that of many organic molecular junctions, and that quasi-1D bundle-like SMWs exhibit enhanced conductance with increasing length within 2.5 nm. Projected density of states (PDOS) analysis reveals that the enhancement of conductance with increasing length can be attributed to the gradual convergence of SMWs’ electron-transport-dominant orbitals toward the Fermi level of the electrode–scattering region–electrode system. Therefore, this work establishes superatoms as a novel platform for functional device design and provides fundamental insights into the rational structural control to regulate electronic transport properties and even explore anomalous quantum-mechanism-dominated transport phenomena.

Results and discussion

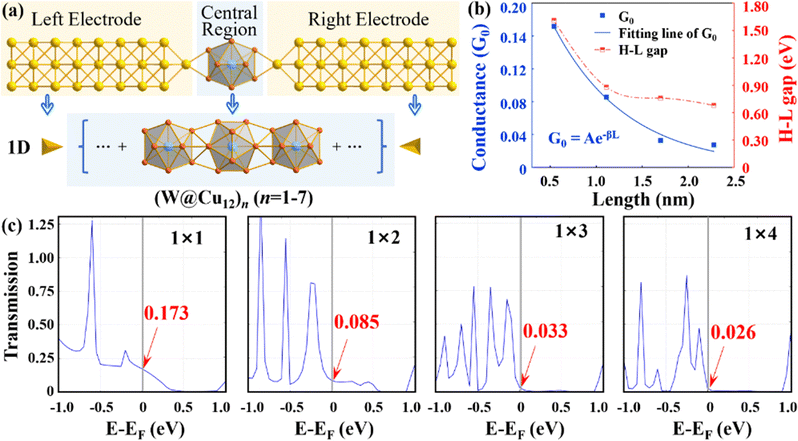
To calculate the conductance of quasi-1D W@Cu₁₂ SMWs, the two-probe devices use Au semi-infinite electrodes laterally connected to the contacts, with one Au atom on the Au(111) surface connected to the scattering region per device.³⁹ The two axially protruding Cu atoms bond directly to the Au electrodes, ensuring a quasi-1D electron transport configuration, as shown in Fig. 1(a). Computational models are provided in Section S2 (ESI†). Among them, the I_h-symmetric W@Cu₁₂ superatom is constructed by embedding a W atom at the center of a three-dimensional cage formed by 12 Cu atoms. The stable configuration of the SMWs is achieved through a 90° counter-rotation of adjacent W@Cu₁₂ about the perpendicular assembly axis,⁴⁰ as shown in Fig. 1(a). First-principles calculations show that the conductance values of 1 × 1, 1 × 2, 1 × 3, 1 × 4, 1 × 5, 1 × 6 and 1 × 7 quasi-1D W@Cu₁₂ SMWs are 0.172, 0.085, 0.033, 0.027, 0.054, 0.048 and 0.027 G₀, respectively, as visually detailed in Fig. S2(a) of the ESI.† The conductance does not follow a consistently decreasing trend with increasing length. This observation could be attributed to unique quantum properties inherent in these small-scale nano-devices. This aspect, while not the focus of the current study, is worthy of further investigation in future research. For the assemblies ranging from 1 × 1 to 1 × 4, a length-dependent conductance trend is observed and can be fitted using the equation G₀ = A × exp(−βL), where the sign of β indicates the trend of conductance change with length. The decrease in conductance with the length is fitted in Fig. 1(b) and the decay factor is determined by 1.25 nm⁻¹, while the decay factor ranges from 2 to 6 nm⁻¹ for conjugated molecules,^8,41–43 and from 6 to 12 nm⁻¹ for nonconjugated molecules.^44–46 Such a low decay constant facilitates quasi-1D W@Cu₁₂ SMWs to become a promising candidate for interconnection in molecular-scale circuitry. Note that slight deviations exist between the fitted β values and experimental observations (see Section S4 in the ESI† for details). However, given that the error sources primarily affect the absolute magnitude of β values rather than their relative trend with length variation, the conductance trend obtained through DFT-NEGF calculations remains reliable. This demonstrates that theoretical study provides valuable guidance for exploring anomalous electron transport properties in superatom-based devices.

Fig. 1 Models and electrical transport properties of quasi-1D W@Cu₁₂ SMWs. (a) Two-probe structures are used in the electrical transport calculations. The positions of Au electrodes are indicated by yellow triangles. (b) Conductance and HOMO–LUMO gap of quasi-1D W@Cu₁₂ SMWs with different lengths. H and L indicate HOMO and LUMO, respectively. (c) Average transmission spectra for quasi-1D W@Cu₁₂ SMWs with different lengths. The corresponding Fermi level is indicated by the gray line, and the transmission function at the Fermi level is marked by the red label.

To explore the possibility of conductance increase with length, it is imperative to first understand why the conductance of quasi-1D W@Cu₁₂ SMWs diminishes slightly as their length increases within 2.5 nm. Here, the HOMO–LUMO gap was analyzed, which influences the conductance.^47,48 As shown in Fig. 1(b), the HOMO–LUMO gap exhibits dramatic narrowing with increasing length, leading to a slow reduction in the conductance. In addition, the transmissions represent the probability that an electron with a given energy will transmit through a system between the electrodes. As shown in Fig. 1(c), the transmission function at the Fermi level for W@Cu₁₂, 2W@Cu₁₂, 3W@Cu₁₂ and 4W@Cu₁₂ SMWs is 0.173, 0.085, 0.033 and 0.026, respectively. The relationship between the transmission coefficient and conductance is given by⁴⁹

where e is the electron charge, h is Planck's constant and E_F is the Fermi level. The transmission function decreases slowly as the length of 1D W@Cu₁₂ increases, which agrees with the conductance trend. The discoveries here present promising prospects for achieving conductance regulation.

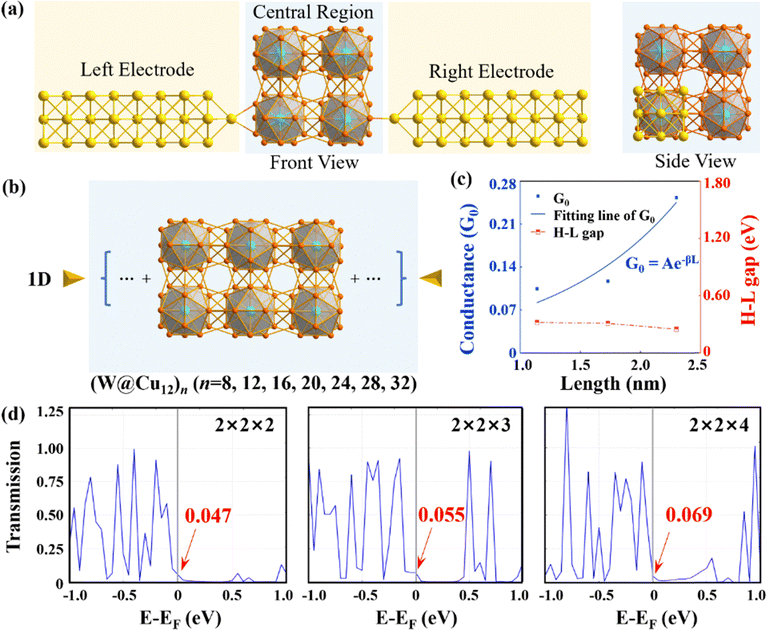
Considering the factors affecting the molecular orbitals and subsequently the gap, we directly choose the approach of increasing the radius in the perpendicular 1D direction, that is, forming bundle-like structures. The reason for this choice is that increasing the units in the perpendicular 1D direction can introduce strong coupling effects in a new dimension,³⁶ which is generally recognized as potentially having a significant impact on the electronic structure.^50,51 Here, it should be noted that when the length of the 1 × 1 structure is fixed, expanding it into a bundle-like configuration would lead to its transformation into a monolayer arrangement, which is therefore not considered in the present work. Thus, the 2 × 2 × 2 W@Cu₁₂ octamer is regarded as an initial system, and the length is increased layer by layer until it is increased to a 2 × 2 × 8 32-polymer. The bundle-like SMWs consist of quasi-1D SMWs assembled via the aforementioned counter-rotation paradigm, as shown in Fig. 2(a) and (b). This assembly mechanism aligns with that of the stable face-centered cubic (fcc) W@Cu₁₂ crystal.³⁶

Fig. 2 Models and electrical transport properties of quasi-1D bundle-like W@Cu₁₂ SMWs. (a) and (b) Two-probe structures are used in the electron transport calculations. The positions of Au electrodes are indicated by yellow triangles. (c) Conductance and HOMO–LUMO gap of quasi-1D bundle-like W@Cu₁₂ SMWs with different lengths. H and L indicate HOMO and LUMO, respectively. (d) Average transmission spectra for quasi-1D bundle-like W@Cu₁₂ SMWs with different lengths. The corresponding Fermi level is indicated by the gray line, and the transmission function at the Fermi level is marked by the red label.

To reliably calculate the conductance of quasi-1D bundle-like W@Cu₁₂ SMWs and effectively compare the results with different radii, the same two-electrode configuration as quasi-1D W@Cu₁₂ SMWs was adopted (Fig. 2(a) and (b)). Computational models are provided in Section S5 of the ESI.† The results show that the conductance for 2 × 2 × 2, 2 × 2 × 3, 2 × 2 × 4, 2 × 2 × 5, 2 × 2 × 6, 2 × 2 × 7 and 2 × 2 × 8 W@Cu₁₂ SMWs is 0.105, 0.117, 0.253, 0.235, 0.134, 0.077 and 0.050 G₀, respectively. These results are visually detailed in Fig. S2(b) of the ESI.† For bundle-like assemblies, the conductance initially increases with the length, peaking at the configuration 2 × 2 × 4 (corresponding to the third data point in Fig. S2(b), ESI†). This initial increase in conductance is consistent with the well-established behaviour of nano-devices shorter than 2.5 nm, where electron tunnelling is the predominant mechanism of conductance.^5,9,10,48 As the length exceeds 2.5 nm, the conductance begins to decrease, which can be attributed to a reduced probability of electron tunnelling across the increased distance. This phenomenon is observed specifically in these bundle-like structures. From Fig. 2(c), the conductance increases with the length shorter than 2.5 nm, and the decay constant is determined to be −0.95 nm⁻¹. Especially, the conductance of 2 × 2 × 4 SMWs even surpasses that of the individual W@Cu₁₂ monomer. Additionally, the calculated transmission functions at the Fermi level for 2 × 2 × 2, 2 × 2 × 3 SMWs show trends aligned with conductance variability (Fig. 2(d)), further corroborating the reliability of the conductance trend. The negative attenuation of quasi-1D bundle-like W@Cu₁₂ SMWs renders them candidates for the construction of molecular electronic devices.

It is noteworthy that as the size of quasi-1D bundle-like W@Cu₁₂ SMWs increases from 2 × 2 × 2 to 2 × 2 × 4, their HOMO–LUMO gaps decrease from 0.32 eV to 0.25 eV, showing a downward trend of 10⁻¹ eV. This small variation is insufficient to directly explain the enhancement of the conductance with increasing length. To gain deeper insights into the uncommon transport properties emerging upon radius expansion, the PDOS analysis was performed to investigate the positioning of frontier molecular orbitals within the central scattering region of electrode–scattering region–electrode systems. As shown in Fig. 3(a), for quasi-1D W@Cu₁₂ SMWs, increased length induces an upward energy shift of the occupied frontier orbital, while the unoccupied frontier orbital remains relatively stable. Although the occupied orbital moves closer to the Fermi level with wire elongation, this shift fails to compensate for conductivity reduction, as is evidenced by scattering state analysis showing progressively attenuated wavefunction amplitudes across all 10 transmission channels in 1 × 1 to 1 × 4 devices, shown in Fig. 4(a). Due to the near identity of incoming states between left and right electrodes, only the left electrode's states are listed here (all scattering states are listed in Section S7 of the ESI†). This indicates electron tunneling is primarily mediated through unoccupied frontier orbitals, with conductivity decrease attributed to SMW elongation impeding wavefunction propagation. Conversely, Fig. 3(b) reveals bundle-like W@Cu₁₂ SMWs exhibiting simultaneous leftward energy shifts of both occupied and unoccupied frontier orbitals upon length increase, causing the occupied orbital to retreat from the Fermi level while the unoccupied orbital approaches it, consequently enhancing conductivity. Similarly, this suggests that conductance in bundle-like SMWs remains dominated by unoccupied frontier orbitals. The anomalous conductance enhancement is directly demonstrated in Fig. 4(b) by intensifying wavefunction amplitudes in dominant transmission channels with length, contrasting sharply with quasi-1D systems. Therefore, the geometry-modulated anomalous transport mechanism stems from energy convergence of the electron-tunneling-dominant unoccupied frontier orbitals toward the Fermi level of the electrode–scattering region–electrode system.

Fig. 3 Projected density of states (PDOS) of SMWs. (a) PDOS of quasi-1D W@Cu₁₂ SMWs. (b) PDOS of quasi-1D bundle-like W@Cu₁₂ SMWs. The gray dashed line represents the Fermi level. The arrows indicate the tendency of the HOMO and the LUMO to shift in energy as the length of the SMWs increases.

Fig. 4 Real-space scattering states at E_F. (a) Scattering states of quasi-1D SMWs. (b) Scattering states of bundle-like SMWs. L, C, and R represent the left electrode, the central scattering region, and the right electrode, respectively.

This study theoretically elucidates the electronic transport properties of W@Cu₁₂ SMWs, with experimental verification expected to advance systematically based on existing technologies. At the synthesis level, W@Cu₁₂ may adopt the established laser vaporization synthesis and photoelectron spectroscopy characterization successfully implemented for W@Au₁₂ superatoms.⁵² For assembly engineering, picometer-precision probe manipulation techniques show promise for precise organization.⁵³ Regarding electrical transport characterization, the already maturely applied STM-BJ technique in Ag systems has led to the accumulation of substantial empirical knowledge,⁵ establishing a technical foundation for W@Cu₁₂ system characterization. Collectively, experimental approaches provide a comprehensive technological pathway for both the fabrication and performance validation of W@Cu₁₂ SMWs. Certainly, given the complexity of practical experiments, the experimental strategy outlined above will still encounter challenges with specific issues, requiring further long-term and systematic work.

Conclusions

In summary, by using typical superatom W@Cu₁₂ as building blocks to construct the highly conjugated quasi-1D SMWs, we investigated the electron transport properties of quasi-1D and quasi-1D bundle-like SMWs within 2.5 nm. First-principles calculations reveal that the decay factor of quasi-1D W@Cu₁₂ SMWs is determined to be 1.25 nm⁻¹, which is smaller than that of many organic MWs. More importantly, the conductance of quasi-1D bundle-like W@Cu₁₂ SMWs is enhanced with increasing length. Besides, the 2 × 2 × 4 quasi-1D bundle-like W@Cu₁₂ SMWs even exhibit higher conductance than that of a single W@Cu₁₂ monomer. This trend of increasing conductance with SMW length can be attributed to structural modulation that brings the energy of electron-transport-dominant orbitals of the quasi-1D bundle-like W@Cu₁₂ SMWs closer to that of the electrode–scattering region–electrode systems, thereby reducing the tunnelling barriers. Therefore, this study contributes to the regulation of molecular-scale circuit performance and promotes the application of superatom-based electronic devices.

Author contributions

Zhigang Wang and Rui-Qin Zhang supervised the work. Famin Yu performed the theoretical simulations. Famin Yu, Wei Feng, Baiqiang Liu, Rui-Qin Zhang and Zhigang Wang discussed the results. Famin Yu, Rui-Qin Zhang and Zhigang Wang wrote the manuscript.

Data availability

The data supporting this article have been included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (under grant numbers 11974136), the Research Grant Council of Hong Kong SAR (11317122) and the Natural Science Foundation of Changchun Normal University (005003038). We gratefully acknowledge HZWTECH for providing computation facilities. Z. W. also acknowledges the High-Performance Computing Center of Jilin University and National Supercomputing Center in Shanghai.

Notes and references

1. J. Liu, X. Zhao, J. Zheng, X. Huang, Y. Tang, F. Wang, R. Li, J. Pi, C. Huang, L. Wang, Y. Yang, J. Shi, B.-W. Mao, Z.-Q. Tian, M. R. Bryce and W. Hong, Chemistry, 2019, 5, 390–401.
2. H. N. Khan, D. A. Hounshell and E. R. H. Fuchs, Nat. Electron., 2018, 1, 14–21.
3. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440.
4. C. Joachim, J. K. Gimzewski and A. Aviram, Nature, 2000, 408, 541–548.
5. A. Feng, S. Hou, J. Yan, Q. Wu, Y. Tang, Y. Yang, J. Shi, Z.-Y. Xiao, C. J. Lambert, N. Zheng and W. Hong, J. Am. Chem. Soc., 2022, 144, 15680–15688.
6. A. Vilan, D. Aswal and D. Cahen, Chem. Rev., 2017, 117, 4248–4286.
7. Z. Tan, D. Zhang, H.-R. Tian, Q. Wu, S. Hou, J. Pi, H. Sadeghi, Z. Tang, Y. Yang, J. Liu, Y.-Z. Tan, Z.-B. Chen, J. Shi, Z. Xiao, C. Lambert, S.-Y. Xie and W. Hong, Nat. Commun., 2019, 10, 1748.
8. S. Ho Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486.
9. W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60–63.
10. T. Hines, I. Diez-Perez, J. Hihath, H. Liu, Z.-S. Wang, J. Zhao, G. Zhou, K. Müllen and N. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664.
11. E. Leary, B. Limburg, A. Alanazy, S. Sangtarash, I. Grace, K. Swada, L. J. Esdaile, M. Noori, M. T. González, G. Rubio-Bollinger, H. Sadeghi, A. Hodgson, N. Agraït, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883.
12. S. Sangtarash, A. Vezzoli, H. Sadeghi, N. Ferri, H. M. O’Brien, I. Grace, L. Bouffier, S. J. Higgins, R. J. Nichols and C. J. Lambert, Nanoscale, 2018, 10, 3060–3067.
13. H. Sadeghi, S. Sangtarash and C. Lambert, Nano Lett., 2017, 17, 4611–4618.
14. G. Sedghi, K. Sawada, L. J. Esdaile, M. Hoffmann, H. L. Anderson, D. Bethell, W. Haiss, S. J. Higgins and R. J. Nichols, J. Am. Chem. Soc., 2008, 130, 8582–8583.
15. F.-R. F. Fan, J. Yang, L. Cai, D. W. Price, Jr., S. M. Dirk, D. V. Kosynkin, Y. Yao, A. M. Rawlett, J. M. Tour and A. J. Bard, J. Am. Chem. Soc., 2002, 124, 5550–5560.
16. N. Algethami, H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2018, 18, 4482–4486.
17. Y. Zang, T. Fu, Q. Zou, F. Ng, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2020, 20, 8415–8419.
18. S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664–1667.
19. D. E. Bergeron, A. W. Castleman, T. Morisato and S. N. Khanna, Science, 2004, 304, 84–87.
20. X. Roy, C.-H. Lee, C. Crowther Andrew, L. Schenck Christine, T. Besara, A. Lalancette Roger, T. Siegrist, W. Stephens Peter, E. Brus Louis, P. Kim, L. Steigerwald Michael and C. Nuckolls, Science, 2013, 341, 157–160.
21. Y. Gao, W. Jiang, L. Chen, J. Wang and Z. Wang, J. Mater. Chem. C, 2017, 5, 803–806.
22. H. Hirai, T. Nakashima, S. Takano, Y. Shichibu, K. Konishi, T. Kawai and T. Tsukuda, J. Mater. Chem. C, 2023, 11, 3095–3100.
23. P. Jena, J. Phys. Chem. Lett., 2013, 4, 1432–1442.
24. A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263.
25. D. Bista, A. P. Aydt, K. J. Anderton, D. W. Paley, T. A. Betley, A. C. Reber, V. Chauhan, A. K. Bartholomew, X. Roy and S. N. Khanna, J. Am. Chem. Soc., 2022, 144, 5172–5179.
26. E. A. Doud, A. Voevodin, T. J. Hochuli, A. M. Champsaur, C. Nuckolls and X. Roy, Nat. Rev. Mater., 2020, 5, 371–387.
27. A. K. Bartholomew, E. Meirzadeh, I. B. Stone, C. S. Koay, C. Nuckolls, M. L. Steigerwald, A. C. Crowther and X. Roy, J. Am. Chem. Soc., 2022, 144, 1119–1124.
28. J. J. Yang, J. C. Russell, S. S. Tao, M. Lessio, F. F. Wang, A. C. Hartnett, S. R. Peurifoy, E. A. Doud, E. S. O'Brien, N. Gadjieva, D. R. Reichman, X. Y. Zhu, A. C. Crowther, S. J. L. Billinge, X. Roy, M. L. Steigerwald and C. Nuckolls, Nat. Chem., 2021, 13, 607–613.
29. S. Takano and T. Tsukuda, J. Am. Chem. Soc., 2021, 143, 1683–1698.
30. A. Turkiewicz, D. W. Paley, T. Besara, G. Elbaz, A. Pinkard, T. Siegrist and X. Roy, J. Am. Chem. Soc., 2014, 136, 15873–15876.
31. M.-H. Du, H. Shi and S. B. Zhang, J. Mater. Chem. C, 2019, 7, 14342–14349.
32. L. Hou, X. Cui, B. Guan, S. Wang, R. Li, Y. Liu, D. Zhu and J. Zheng, Nature, 2022, 606, 507–510.
33. E. Meirzadeh, A. M. Evans, M. Rezaee, M. Milich, C. J. Dionne, T. P. Darlington, S. T. Bao, A. K. Bartholomew, T. Handa, D. J. Rizzo, R. A. Wiscons, M. Reza, A. Zangiabadi, N. Fardian-Melamed, A. C. Crowther, P. J. Schuck, D. N. Basov, X. Zhu, A. Giri, P. E. Hopkins, P. Kim, M. L. Steigerwald, J. Yang, C. Nuckolls and X. Roy, Nature, 2023, 613, 71–76.
34. F. Yu, Z. Liu, J. Li, W. Huang, X. Yang and Z. Wang, Chin. Phys. B, 2022, 31, 128107.
35. F. Yu, R. Li, X. Yang, Y. Shi and Z. Wang, Aggregate, 2024, 5, e539.
36. F. Yu, X. Yang, R. Li, R. Liu, C. Wan, Y. Dai and Z. Wang, Acta Mater., 2024, 275, 120047.
37. T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943–969.
38. G. Schön and U. Simon, Colloid Polym. Sci., 1995, 273, 101–117.
39. M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419.
40. F. Yu, Y. Zhu, Y. Gao, R. Wang, W. Huang, Y. Gao and Z. Wang, Nano Res., 2022, 15, 8665–8672.
41. B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223.
42. Z. L. Cheng, R. Skouta, H. Vazquez, J. R. Widawsky, S. Schneebeli, W. Chen, M. S. Hybertsen, R. Breslow and L. Venkataraman, Nat. Nanotechnol., 2011, 6, 353–357.
43. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907.
44. B. Capozzi, E. J. Dell, T. C. Berkelbach, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2014, 136, 10486–10492.
45. P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240.
46. W. Hong, H. Li, S.-X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431.
47. B. Q. Xu, X. L. Li, X. Y. Xiao, H. Sakaguchi and N. J. Tao, Nano Lett., 2005, 5, 1491–1495.
48. Y. X. Zhou, F. Jiang, H. Chen, R. Note, H. Mizuseki and Y. Kawazoe, J. Chem. Phys., 2008, 128, 044704.
49. D. S. Fisher and P. A. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6851–6854.
50. J. T. Arantes and A. Fazzio, Nanotechnology, 2007, 18, 295706.
51. H. J. Xiang, J. Yang, J. G. Hou and Q. Zhu, Appl. Phys. Lett., 2006, 89, 223111.
52. X. Li, B. Kiran, J. Li, H. J. Zhai and L. S. Wang, Angew. Chem., Int. Ed., 2002, 41, 4786–4789.
53. S. Gwo, H.-Y. Chen, M.-H. Lin, L. Sun and X. Li, Chem. Soc. Rev., 2016, 45, 5672–5716.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00180c

---