Open Access Article
Open Access ArticleExploring the local solvation structure of redox molecules in a mixed solvent for increasing the Seebeck coefficient of thermocells†
Hirotaka
Inoue
a,
Hongyao
Zhou
 *a,
Hideo
Ando
*a,
Hideo
Ando
 b,
Sakuya
Nakagawa
b and
Teppei
Yamada
b,
Sakuya
Nakagawa
b and
Teppei
Yamada
 *a
*a
aDepartment of Chemistry, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, 113-0033, Japan. E-mail: teppei@chem.s.u-tokyo.ac.jp; hozhou@chem.s.u-tokyo.ac.jp
bFaculty of Science, Yamagata University, 1-4-12 Kojirakawa-machi, Yamagata, 990-8560, Japan
First published on 27th November 2023
Abstract
A thermocell is an emerging alternative to thermoelectric devices and exhibits a high Seebeck coefficient (Se) due to the large change of solvation entropy associated with redox reactions. Here, the Se of p-chloranil radicals/dianions (CA˙−/2−) in acetonitrile was drastically increased from −1.3 to −2.6 mV K−1 by the addition of ethanol, and the increment surpassed the estimation of the classical Born model with continuum solvent media. UV-vis spectroscopy and electrochemical measurements at various mixing ratios of acetonitrile to ethanol revealed that the strong hydrogen bonding between ethanol and oxygen atoms of CA2− forms a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent–ion pair, while the ethanol molecules binding to CA2− dissociate upon its oxidation to CA˙−. The local solvation structures of CA2− are in good agreement with density functional theory. This order–disorder transition of the local solvation structure around the CA˙−/2− ions produces a large entropy change and results in a large Se value. The tailored solvation structure of redox ions by hydrogen bonding is a versatile method applicable to a variety of redox pairs and solvents, contributing to the development of electrolyte engineering for thermocells.
1 solvent–ion pair, while the ethanol molecules binding to CA2− dissociate upon its oxidation to CA˙−. The local solvation structures of CA2− are in good agreement with density functional theory. This order–disorder transition of the local solvation structure around the CA˙−/2− ions produces a large entropy change and results in a large Se value. The tailored solvation structure of redox ions by hydrogen bonding is a versatile method applicable to a variety of redox pairs and solvents, contributing to the development of electrolyte engineering for thermocells.
Introduction
The recovery of low-grade waste heat, especially in the temperature range below 100 °C, is an important task for realizing an energy-sustainable society.1 A thermocell is an electrochemical system constructed from a pair of identical electrodes and a liquid electrolyte containing a redox pair. A thermoelectric voltage (ΔV) is generated when a temperature gradient (ΔT) is applied between the two electrodes.2 Thermocells have gained increasing attention recently, thanks to the inherently higher Seebeck coefficient (Se, voltage per unit temperature difference), greater scalability, and lower materials cost compared to solid thermoelectric materials. Thermocells have various applications from self-powered liquid-cooling systems3,4 to wearable devices converting body heat into electricity.5–13The improvement of Se is always desirable, especially for the utilization of a small temperature difference. Increasing the Se value of thermocells is a major challenge in improving the output power and thermal efficiency. The Se value is proportional to the entropy change induced by the redox reaction (ΔSrc) and can be expressed with the number of electrons mediating the redox reaction (n) and Faraday constant (F):
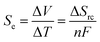 | (1) |
The value of ΔSrc is induced by the reorganization entropy of the solvation structure around the redox species in the charge-transfer process.2,14 Weaver and Hupp evaluated the ΔSrc of transition metal complexes in various solvents.14 Based on the experimental results and the Born model, the authors found that the ΔSrc values increase with a larger charge density of the redox pair and smaller acceptor numbers of the solvents. Their theory agreed well with the general observations that a ferri/ferrocyanide redox pair (Fe(CN)63−/4−)15,16—with its extremely large charge density—shows a large ΔSrc value (−135 J K−1 mol−1) and a large Se value (−1.4 mV K−1).17
For improving the ΔSrc values, solvent mixing to decrease the acceptor numbers of the electrolyte was studied previously.18,19 Pringle and coworkers showed that an addition of 50 vol% dimethyl sulfoxide (DMSO) in an ionic liquid increased the Se value of the cobalt(II/III) tris(bipyridyl) redox pair from +1.64 to +1.97 mV K−1.19 In contrast, mixing of DMSO in water decreased the Se of Fe(CN)63−/4−, because of the weakened interaction between water and Fe(CN)63−/4−.18 The two opposite effects of mixing DMSO in the ionic liquid or in water indicate that the influence of solvent mixing on the Se value is unpredictable solely by the simple addition rule of the physical properties of the bulk solvents based on the Born model of solvation.
Recently, molecular dynamics (MD) simulation provided detailed information on the local solvation structures of redox-active ions.20,21 Sun and coworkers improved the Se of an aqueous ferrous/ferric (Fe2+/Fe3+) thermocell in a hydrogel by mixing acetone,21 and Yang and coworkers investigated the microscopic solvation structure around Fe2+/Fe3+ ions.20 The authors revealed that the insertion of one acetone molecule into the solvation shell of Fe2+ results in its structural distortion. The authors claimed that the order–disorder transition of the solvation structure upon the redox reaction of Fe3+ to Fe2+ increases the ΔSrc and the Se. Furthermore, the hydration structure of the Fe2+/3+ redox pair can be tailored by changing pH and counter anions to increase the ΔSrc and Se.22,23 Tailored local solvation around the redox molecules or ions is the key to increasing the Se; however, in a water–organic mixed solvent, the strong hydrogen bonding between the solvent water molecules themselves in the organic media often limits the designability of the solvation structure.
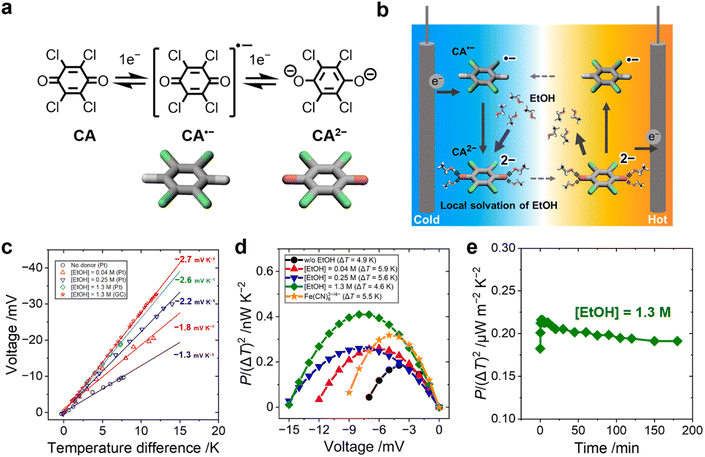
In this work, we focused on designing the local solvation structure of an organic redox molecule in an organic–organic solvent mixture. We used a p-chloranil radical anion and dianion (CA˙−/CA2−, Fig. 1a) as the redox pair, and ethanol (EtOH) as the modifier of their local solvation structure in acetonitrile media. Previously, a positive shift of the electrochemical potential of chloranil was observed when methanol was added in an acetonitrile electrolyte.24 In this study, acetonitrile was selected as the solvent medium because of its high dielectric constant, and ethanol was selected as the additive because of its higher boiling point compared to methanol. CA2− creates an ordered solvation structure with EtOH via hydrogen bonding between the negatively charged oxygen atoms of CA2− and the hydroxy group of EtOH (Fig. 1b). When CA2− is oxidized to CA˙−, the solvation structure of EtOH is broken because of the decreasing charge density of the CA˙− species. UV-vis spectroscopy and density functional theory (DFT) calculations confirmed that the hydroxy group of EtOH is strongly attracted to the electronegative oxygen atoms of CA2−. In addition, electrochemical measurements showed that EtOH and CA2− form a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent–ion pair in the acetonitrile media. The order–disorder transition of the EtOH–CA2− pair increased the ΔSrc by −160 J K−1 mol−1 and resulted in the highest Se of −2.6 mV K−1 in the organic–organic mixed solvent system. Our results give a new concept of tailoring the local solvation structure around organic redox molecules, which is potentially applicable to many other combinations of benzoquinone derivatives and hydrogen bonding donors.
1 solvent–ion pair in the acetonitrile media. The order–disorder transition of the EtOH–CA2− pair increased the ΔSrc by −160 J K−1 mol−1 and resulted in the highest Se of −2.6 mV K−1 in the organic–organic mixed solvent system. Our results give a new concept of tailoring the local solvation structure around organic redox molecules, which is potentially applicable to many other combinations of benzoquinone derivatives and hydrogen bonding donors.
Results and discussion
Thermoelectric conversion by the CA˙−/CA2− redox pair in EtOH–acetonitrile mixed solvent
CA undergoes two-step one-electron redox reactions in an organic electrolyte, as shown in Fig. 1a. The Se value of CA˙−/2− (0.5 mM) in the acetonitrile electrolyte was evaluated with an H-shape glass cell (Fig. S1a and S2b, ESI†). Fig. 1c shows a linear increase of ΔV with increasing ΔT between the two platinum electrodes. The addition of EtOH increased the Se from −1.3 to −2.6 mV K−1 ([EtOH] = 1.3 M) when measured with a Pt electrode. A similar Se value (−2.7 mV K−1) was observed when glassy carbon (GC) was used as the electrode.The normalized power output, P/(ΔT)2, of the CA˙−/2− cell was measured with various concentrations of EtOH (Fig. 1d). The result was compared with that of an aqueous electrolyte containing the same concentration of Fe(CN)63−/4− (0.5 mM each).25,26 The Se value of Fe(CN)63−/4− was −1.6 mV K−1 (Fig. S3, ESI†) and agreed with the literature value.27 The P/(ΔT)2 of the organic CA˙−/2− thermocell surpassed the value of the aqueous Fe(CN)63−/4− thermocell when 1.3 M EtOH was added to acetonitrile electrolyte because of the increased Se value (see Fig. S4, ESI,† for the I–V curve). One drawback of the organic CA˙−/2− thermocell is, however, a much lower solubility of CA˙−/2− in acetonitrile compared to the solubility of Fe(CN)63−/4− in water. The output power of the CA˙−/2− thermocell could be improved by using quinone derivatives as the redox molecule with a high solubility in organic electrolytes.
Continuous power generation of the CA˙−/2− thermocell with EtOH (1.3 M) was confirmed at a constant voltage load (Fig. 1e). Stable power output for more than three hours was observed without any precipitation. Previously, an addition of 20 wt% methanol (MeOH) in water was reported to increase the Se of the Fe(CN)63−/4− thermocell to −2.9 mV K−1.28 The low solubility of Fe(CN)63−/4− in MeOH caused precipitation,18 which increased the Se values by the concentration gradient of Fe(CN)63−/4− between the hot and cold electrodes,29–31 while this precipitation can prevent the diffusion of the redox species and deteriorate the output power over time.32,33 In this study, no precipitation is caused by the mixing of EtOH, clearly discerning the influence of precipitation and the solvation effect.
Local solvation structure of the CA2− dianion
We investigated the solvation structure of CA species by UV-vis spectroscopy of neutral CA, CA˙−, and CA2− in acetonitrile electrolyte. We also studied the EtOH solvation structure in the acetonitrile continuum medium and its spectral effects using DFT and time-dependent extension (TD-DFT),34 respectively, along with the B3LYP functional35–37 and (aug-)cc-pVDZ basis set.38,39 (The details of the DFT-based exhaustive search for EtOH configurations and the TD-DFT calculations are summarized in the ESI†). The calculated (λcalc) and observed (λobs) UV-vis spectra of the CA species in solvent acetonitrile without EtOH are shown in Fig. S9 and S5 (ESI†), respectively. The absorption peaks of the CA species (Table 1) agree well with literature values.24,40| λ calc (nm) | λ obs (nm) | Peak assignment | |
|---|---|---|---|
| a The λcalc values correspond to the calculated excitation energies in stick spectra (see the ESI for further details, including the molecular orbitals in Fig. S7 and S8). | |||
| CA˙− | 219 | 214 | 2B3u ← 2B2g (π*(au) ← π(b1g)) |
| 274 | 321 | 2B3u ← 2B2g (π*(b3u) ← π*(b2g), π*(au) ← π(b1g)) | |
| 406 | 420 | 2Au ← 2B2g (π*(au) ← π*(b2g)) | |
| 428 | 448 | 2B3u ← 2B2g (π*(b2g) ← π(b3u)) | |
| CA2− | 219, 222 | 223 | 1B1u ← 1Ag (π*(au) ← π(b1g), Rydberg(b3u) ← π*(b2g)) |
| 253 | 258 | 1B1u ← 1Ag (π*(b3u) ← π*(b2g)) | |
| 381 | 359 | 1B2u ← 1Ag (π*(au) ← π*(b2g)) | |
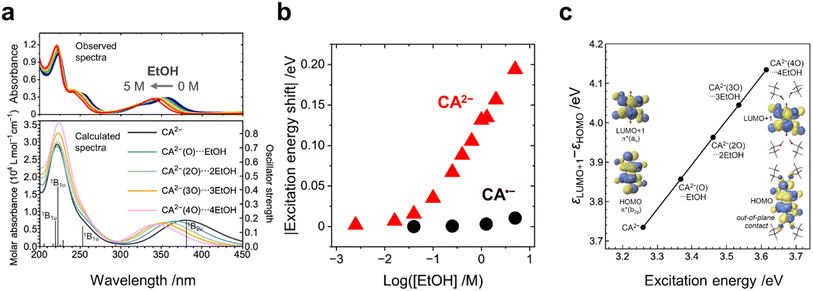
The UV-vis spectra of the CA species with the addition of EtOH were measured to investigate the effect of EtOH on the electronic states of the CA species. The addition of EtOH caused negligibly small red shifts (by 2 nm at maximum) in the absorption peaks of CA (at 288 nm) and CA˙− (at 448 nm) (Fig. S6a and b, ESI†). In contrast, a significantly large blue shift (by 30 nm at maximum) was observed in the absorption peak of CA2− at 359 nm with increasing concentration of EtOH (Fig. 2a (top), Fig. 2b, and S6c, ESI†). The TD-DFT calculations show a similar blue shift (Fig. 2a, bottom) and indicate that the absorption peak at 359 nm (381 nm in theory) is assignable to the electron excitation from a π*(b2g) orbital to a π*(au) orbital. The π*(b2g) one is the highest occupied molecular orbital (HOMO), and the π*(au) one is the second lowest unoccupied molecular orbital (LUMO+1) (Fig. 2c). Solvent exchange from acetonitrile to EtOH within the polarizable continuum model (PCM) framework resulted in no peak shift of CA2− (Fig. S9b, ESI†). The change in the dielectric constant of the solvent causes a minimum effect on the electronic structures of the CA species, which highlights the importance of the hydrogen bonding around CA2−.
The calculated molecular geometry of the EtOH–CA2− solvent–ion pair shows that, because of a balance between the hydrogen bonding and the steric jamming among the EtOH molecules, four EtOH molecules are expected to bind with one CA2− ion at maximum (Fig. 2c; the detailed explanation presented in the ESI†). The energy gap between π*(b2g) and π*(au) (i.e., the HOMO–LUMO+1 gap), as well as the corresponding excitation energy, increases with increasing number of EtOH molecules binding with CA2− (Fig. 2c). The electropositive proton of the hydroxy group of EtOH approaches the two electronegative oxygen atoms of CA2−, particularly their out-of-plane 2p-type lobes of the π*(b2g) orbital (Fig. 2c), thereby decreasing the π*(b2g) energy level, increasing the HOMO–LUMO+1 gap and causing the blue shift.
Entropy and enthalpy changes upon the association of EtOH with CA2−
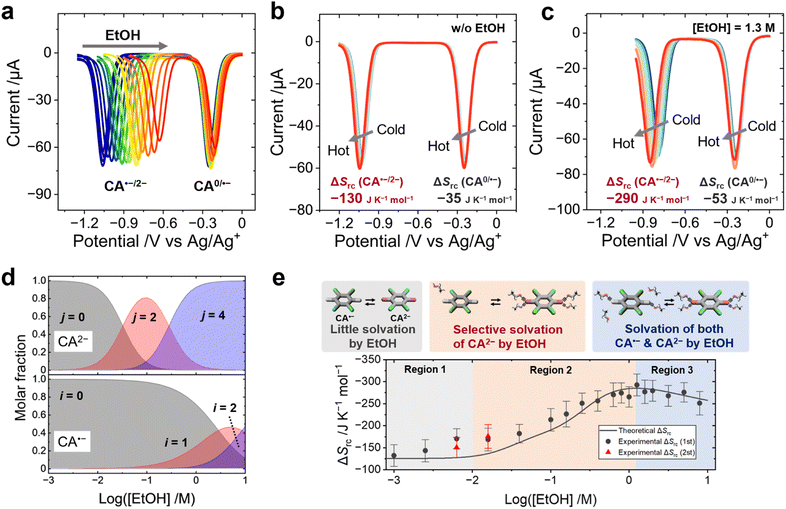
The entropy (ΔSas) and enthalpy (ΔHas) changes produced upon the association of EtOH with the CA˙−/2− redox pair were estimated from the shift of the equilibrium potentials (E1/2) with increasing EtOH concentrations and temperatures. Previously, hydrogen bonding between benzoquinone dianions and hydrogen-donating additives—such as alcohols24,41–45 and amides46—was reported to shift the E1/2 toward positive potential. In this study, square wave voltammetry (SWV) of CA was performed to evaluate the influence of EtOH on the E1/2 of each CA species (CA0/˙−/2−). One peak at −0.25 V was assigned to the redox equilibrium of the CA0/˙− pair (EI1/2) and the other peak at −1.1 V was assigned to the redox equilibrium of CA˙−/2− (EII1/2) (Fig. 3a). The addition of EtOH drastically shifted the EII1/2 to a positive potential, which results from the reduced HOMO level caused by the coordination of EtOH to CA2−.The temperature dependence of E1/2 corresponds to the ΔSrc according to eqn (1), and changes in ΔSrc caused by the addition of EtOH can be ascribed to the effect of ΔSas. The SWV measurement at various temperatures shows that the addition of EtOH drastically enhances the negative shift of EII1/2 with increasing temperature, indicating that the coordination of EtOH to CA2− increases the ΔSrc (Fig. 3b and c). The increment of EI1/2 and EII1/2versus the EtOH concentration was fitted by using theoretical models based on the Nernst equation, and the binding constant, ΔHas and ΔSas of EtOH to CA˙−/2− were obtained from the fitting parameters (Fig. S18–S20, ESI,† the derivation of the theoretical models is shown in the ESI†).
The maximum coordination number of EtOH molecules to one CA2− dianion was set to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 based on the calculated molecular geometry (Fig. 2c). To reduce the number of fitting parameters, only even numbers of EtOH molecules (2 or 4) were allowed to associate with one CA2− in this fitting, which is a reasonable approximation, considering the symmetric structure of CA2−. The fitting results of ΔHas and ΔSas are summarized in Table 2, and the selective association of EtOH to CA2− can be attributed to the larger ΔHas with CA2− than with CA˙−. The average number of EtOH molecules associated with one CA˙− or CA2− anion at each EtOH concentration was calculated from the binding constants, and the result shows that two EtOH molecules associate with one CA2− ion at 0.1 M EtOH, and four EtOH molecules above 1 M EtOH on average, which is larger than the association number of EtOH to CA˙− (Fig. 3d). This result is consistent with the DFT calculation—EtOH more strongly binds with CA2− than with CA˙− (Fig. S15 and S16, ESI†).
1 based on the calculated molecular geometry (Fig. 2c). To reduce the number of fitting parameters, only even numbers of EtOH molecules (2 or 4) were allowed to associate with one CA2− in this fitting, which is a reasonable approximation, considering the symmetric structure of CA2−. The fitting results of ΔHas and ΔSas are summarized in Table 2, and the selective association of EtOH to CA2− can be attributed to the larger ΔHas with CA2− than with CA˙−. The average number of EtOH molecules associated with one CA˙− or CA2− anion at each EtOH concentration was calculated from the binding constants, and the result shows that two EtOH molecules associate with one CA2− ion at 0.1 M EtOH, and four EtOH molecules above 1 M EtOH on average, which is larger than the association number of EtOH to CA˙− (Fig. 3d). This result is consistent with the DFT calculation—EtOH more strongly binds with CA2− than with CA˙− (Fig. S15 and S16, ESI†).
| Number of EtOH | ΔHas (kJ mol−1) | ΔSas (J K−1 mol−1) | |
|---|---|---|---|
| CA˙− | i = 1 | −9.1 ± 0.2 | −39 ± 1 |
| i = 2 | −12 ± 0 | −66 ± 0 | |
| CA2− | j = 2 | −34 ± 1 | −59 ± 3 |
| j = 4 | −77 ± 0 | −180 ± 1 |
The ΔSrc of the CA˙−/2− redox pair at various EtOH concentrations was evaluated by temperature-variable SWV measurement (Fig. S21, Table S2, ESI†) and plotted together with the theoretical curve (Fig. 3e; the derivation is shown in the ESI†). Fig. 3e can be divided into three regions: Region 1 shows only a minimum increase of ΔSrc, because of little or no association of EtOH with CA2− or CA˙− ions; Region 2 shows the maximum increase of ΔSrc, because the number of EtOH binding with CA2− significantly increases and forms a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent–ion pair at maximum, while the association number with CA˙− remains low; Region 3 shows decreasing ΔSrc values, mainly because the number of EtOH binding with CA˙− increases at such a high EtOH concentration (Fig. S22, ESI†). The above discussions point out that, in the mixed solvent system, the Born model—regarding the solvent as a continuum medium—fails to explain the molecular-level interaction between the redox ions and the solvent molecules. Rather, the molecular dynamics and the intermolecular forces at the microscopic level play a critical role in determining ΔSrc. The slight deviation of the experimental values of ΔSrc from the simulation curve is likely due to the gradual vaporization of EtOH from the electrolyte during the SWV measurement at high temperature (details are discussed in the ESI†).
1 solvent–ion pair at maximum, while the association number with CA˙− remains low; Region 3 shows decreasing ΔSrc values, mainly because the number of EtOH binding with CA˙− increases at such a high EtOH concentration (Fig. S22, ESI†). The above discussions point out that, in the mixed solvent system, the Born model—regarding the solvent as a continuum medium—fails to explain the molecular-level interaction between the redox ions and the solvent molecules. Rather, the molecular dynamics and the intermolecular forces at the microscopic level play a critical role in determining ΔSrc. The slight deviation of the experimental values of ΔSrc from the simulation curve is likely due to the gradual vaporization of EtOH from the electrolyte during the SWV measurement at high temperature (details are discussed in the ESI†).
Supramolecular thermocells developed previously by us exemplify that the molecular-level host–guest interaction can boost the Se value.30,47–49 Briefly, cyclodextrins (CDs) encapsulate the redox-active triiodide anion at the cold electrode and release the guest triiodide at the hot electrode. This host–guest interaction is driven by the hydrophobic interaction, and the increment of Se values induced by the addition of CDs is linearly proportional to the entropy change induced by the host–guest encapsulation.2
The CA-based thermocell developed here was inspired by the selective host–guest interaction used in a supramolecular thermocell system. The formation of the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 EtOH–CA2− pair produces a ΔSas of −180 J K−1 mol−1, surpassing the largest entropy change obtainable from the host–guest encapsulation between the CD and triiodide (−150 J K−1 mol−1). The order–disorder transition of the solvent–ion pair was found to be a more effective strategy for enhancing the ΔSrc and Se.
1 EtOH–CA2− pair produces a ΔSas of −180 J K−1 mol−1, surpassing the largest entropy change obtainable from the host–guest encapsulation between the CD and triiodide (−150 J K−1 mol−1). The order–disorder transition of the solvent–ion pair was found to be a more effective strategy for enhancing the ΔSrc and Se.
The charge-transfer kinetics of CA2−
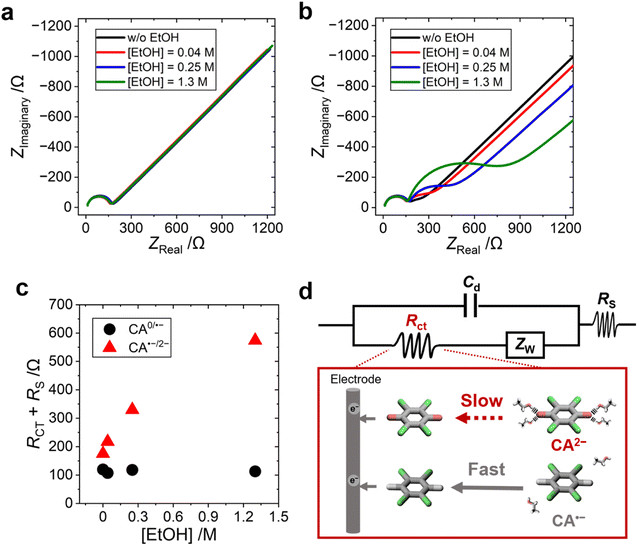
The influence of EtOH on the electron-transfer kinetics of CA0/˙− and CA˙−/2− redox pairs was studied by electrochemical impedance spectroscopy (EIS) performed at different potentials (−0.277 or −1.085 V vs. Ag/Ag+ for studying the charge-transfer process of CA0/˙− or CA˙−/2−, respectively). One semi-circle was observed in the Nyquist plot of the CA0/˙− redox pair (Fig. 4a), while two semi-circles were observed in that of the CA˙−/2− redox pair (Fig. 4b). One of the semi-circles observed in the higher-frequency region was attributed to the solution resistance (Rs) and the formation of the electric double layer (Cd), and the other semi-circle observed in the lower-frequency region was attributed to the charge transfer resistance (Rct). The two semicircles are merged in the redox process between CA0 and CA˙− (Fig. 4a) because of the extremely fast electron-transfer kinetics of the organic radical anion (see Fig. S23, ESI,† for the detailed discussion). The addition of EtOH increased the Rct of the CA˙−/2− redox pair, while that of the CA0/˙− redox pair showed no change (Fig. 4c).The equivalent circuit diagram and the molecular pictures of the charge-transfer process of the CA˙−/2− redox pair on the electrode surface are shown in Fig. 4d. The EtOH molecules around CA2− form a strong hydrogen bonding, and the dissociation of EtOH molecules is the rate-determining step in the electron-transfer process from CA2− to the electrode. In contrast, the CA˙− radical anion and neutral CA0 species form weak or no hydrogen bonding with EtOH solvent molecules, and the electron-transfer process is unhindered between CA0 and CA˙−. A similar result was previously reported that the reorganization of solvent water molecules influences the kinetics of the Fe(CN)63−/4− redox reaction.50 The increasing Rct of the CA˙−/2− redox pair with increasing concentration of EtOH further supported our hypothesis that the large ΔSrc is caused by the tight hydrogen bonding between the solvent EtOH and CA2− dianion.
Conclusions
The new concept of forming a selective hydrogen bonding between a protic solvent and an organic redox molecule was presented here. The Se value of CA˙−/2− in acetonitrile electrolyte was enhanced from −1.3 to −2.6 mV K−1 by mixing 1.3 M EtOH. The Se value of −2.6 mV K−1 is the highest value among other thermocells based on all-organic electrolytes without introducing the precipitation of the redox species. The organized local solvation structure of EtOH molecules around CA2− was observed from the blue shift in the UV-vis spectra and confirmed by DFT calculations. SWV and EIS measurements supported our concept that the order–disorder transition of the EtOH-binding local solvation structure can significantly increase the entropy change of the redox reaction from CA2− to CA˙−. Our concept of using hydrogen bonding to maximize the entropy change of redox reactions is applicable to many other benzoquinone derivatives, organic solvents, and hydrogen-bonding donor solvents and provides a versatile way of improving the performance of thermocells. Organic thermocells are potentially advantageous in terms of the inherently high boiling point and low thermal conductivity and hold great promise to overperform conventional aqueous thermocells. In addition, our method of exploiting the entropy change of organic redox molecules can give a deeper understanding on the thermodynamics of organic redox-flow batteries. The concept of order–disorder transition of organized local solvation structures can be applied to various electrochemical systems using organic redox molecules.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
H. I., H. Z., and T. Y. formulated the original concept; H. I. performed all the experiments; S. N and H. A. performed the theoretical calculations. H. I. analyzed and visualized all the experimental data. H. I. wrote the original draft, and H. Z., H. A., and T. Y. reviewed and edited the manuscript. All authors agree with the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI grant numbers: 21H00017 (Hydrogenomics), 20H02714, 21H05870, 20K21176, 21J21893, JST CREST grant number: JPMJCR22O5, The Murata Science Foundation, The Asahi Glass Foundation, Tanikawa Fund Promotion of Thermal Technology, Yamada Science Foundation, The Iwatani Naoji Foundation, and The Canon Foundation. We would like to show our appreciation to Mr Takashi Kobayashi for his experimental support in square wave voltammetry measurements.Notes and references
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- H. Zhou, H. Inoue, M. Ujita and T. Yamada, Angew. Chem., Int. Ed., 2023, 62, e202213449 CrossRef CAS.
- Y. Ikeda, Y. Cho and Y. Murakami, Sustainable Energy Fuels, 2021, 5, 5967–5974 RSC.
- A. H. Kazim, A. S. Booeshaghi, S. T. Stephens and B. A. Cola, Sustainable Energy Fuels, 2017, 1, 1381–1389 RSC.
- Y. Liu, S. Zhang, Y. Zhou, M. A. Buckingham, L. Aldous, P. C. Sherrell, G. G. Wallace, G. Ryder, S. Faisal, D. L. Officer, S. Beirne and J. Chen, Adv. Energy Mater., 2020, 10, 2002539 CrossRef CAS.
- C. Bai, Z. Wang, S. Yang, X. Cui, X. Li, Y. Yin, M. Zhang, T. Wang, S. Sang and W. Zhang, ACS Appl. Mater. Interfaces, 2021, 13, 37316–37322 CrossRef CAS.
- T. Ding, Y. Zhou, X. Q. Wang, C. Zhang, T. Li, Y. Cheng, W. Lu, J. He and G. W. Ho, Adv. Energy Mater., 2021, 11, 2102219 CrossRef CAS.
- Y. Zhou, Y. Liu, M. A. Buckingham, S. Zhang, L. Aldous, S. Beirne, G. Wallace and J. Chen, Electrochem. Commun., 2021, 124, 106938 CrossRef CAS.
- J. Zhang, C. Bai, Z. Wang, X. Liu, X. Li and X. Cui, Micromachines, 2023, 14, mi14010155 Search PubMed.
- X. Li, J. Li, T. Wang, S. A. Khan, Z. Yuan, Y. Yin and H. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 48743–48751 CrossRef CAS.
- C. Tian, C. Bai, T. Wang, Z. Yan, Z. Zhang, K. Zhuo and H. Zhang, Nano Energy, 2023, 106, 108077 CrossRef CAS.
- L. Liu, D. Zhang, P. Bai, Y. Mao, Q. Li, J. Guo, Y. Fang and R. Ma, Adv. Mater., 2023, 35, 2300696 CrossRef CAS.
- C. Xu, Y. Sun, J. Zhang, W. Xu and H. Tian, Adv. Energy Mater., 2022, 12, 2201542 CrossRef CAS.
- J. T. Hupp and M. J. Weaver, Inorg. Chem., 1984, 23, 47907 Search PubMed.
- M. A. Trosheva, M. A. Buckingham and L. Aldous, Chem. Sci., 2022, 13, 4984–4998 RSC.
- N. F. Antariksa, T. Yamada and N. Kimizuka, Sci. Rep., 2021, 11, 11929 CrossRef CAS.
- R. Hu, B. A. Cola, N. Haram, J. N. Barisci, S. Lee, S. Stoughton, G. Wallace, C. Too, M. Thomas, A. Gestos, M. E. Dela Cruz, J. P. Ferraris, A. A. Zakhidov and R. H. Baughman, Nano Lett., 2010, 10, 838–846 CrossRef CAS.
- A. Taheri, D. R. MacFarlane, C. Pozo-Gonzalo and J. M. Pringle, Aust. J. Chem., 2019, 72, 709–716 CrossRef CAS.
- M. A. Lazar, D. Al-Masri, D. R. Macfarlane and J. M. Pringle, Phys. Chem. Chem. Phys., 2016, 18, 1404–1410 RSC.
- Y. Chen, Q. Huang, T. H. Liu, X. Qian and R. Yang, EcoMat, 2023, 5, e12385 CrossRef.
- Y. Liu, Q. Zhang, G. O. Odunmbaku, Y. He, Y. Zheng, S. Chen, Y. Zhou, J. Li, M. Li and K. Sun, J. Mater. Chem. A, 2022, 10, 19690–19698 RSC.
- M. A. Buckingham, F. Marken and L. Aldous, Sustainable Energy Fuels, 2018, 2, 2717–2726 RSC.
- K. Kim, S. Hwang and H. Lee, Electrochim. Acta, 2020, 335, 135651 CrossRef CAS.
- B. Uno, N. Okumura, M. Goto and K. Kano, J. Org. Chem., 2000, 65, 1448–1455 CrossRef CAS.
- J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Nat. Commun., 2018, 9, 5146 CrossRef PubMed.
- M. A. Buckingham, S. Hammoud, H. Li, C. J. Beale, J. T. Sengel and L. Aldous, Sustainable Energy Fuels, 2020, 4, 3388–3399 RSC.
- L. Zhang, T. Kim, N. Li, T. J. Kang, J. Chen, J. M. Pringle, M. Zhang, A. H. Kazim, S. Fang, C. Haines, D. Al-Masri, B. A. Cola, J. M. Razal, J. Di, S. Beirne, D. R. MacFarlane, A. Gonzalez-Martin, S. Mathew, Y. H. Kim, G. Wallace and R. H. Baughman, Adv. Mater., 2017, 29, 1605652 CrossRef.
- T. Kim, J. S. Lee, G. Lee, H. Yoon, J. Yoon, T. J. Kang and Y. H. Kim, Nano Energy, 2017, 31, 160–167 CrossRef CAS.
- H. Wang, X. Zhuang, W. Xie, H. Jin, R. Liu, B. Yu, J. Duan, L. Huang and J. Zhou, Cell Rep. Phys. Sci., 2022, 3, 100737 CrossRef CAS.
- H. Inoue, Y. Liang, T. Yamada and N. Kimizuka, Chem. Commun., 2020, 56, 7013–7016 RSC.
- B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Zhuang, H. Wang, B. Qi, M. Xu, Z. L. Wang and J. Zhou, Science, 2020, 370, 342–346 CrossRef CAS.
- L. Jiang, K. Kirihara, V. Nandal, K. Seki, M. Mukaida, S. Horike and Q. Wei, ACS Appl. Mater. Interfaces, 2022, 14, 22921–22928 CrossRef CAS PubMed.
- L. Jiang, S. Horike, M. Mukaida, K. Kirihara, K. Seki and Q. Wei, Global Chall., 2023, 7, 2200207 CrossRef.
- M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Time-Dependent Density Functional Theory, Springer-Verlag, Berlin: Heidelberg, Germany, 2006 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- B. Uno, N. Okumura and K. Seto, J. Phys. Chem. A, 2000, 104, 3064–3072 CrossRef CAS.
- N. Gupta and H. Linschitz, J. Am. Chem. Soc., 1997, 119, 6384–6391 CrossRef CAS.
- M. Gómez, F. J. González and I. González, J. Electrochem. Soc., 2003, 150, E527 CrossRef.
- M. Gómez, F. J. González and I. González, Electroanalysis, 2003, 15, 635–645 CrossRef.
- M. Quan, D. Sanchez, M. F. Wasylkiw and D. K. Smith, J. Am. Chem. Soc., 2007, 129, 12847–12856 CrossRef CAS PubMed.
- M. E. Tessensohn and R. D. Webster, Electrochem. Commun., 2016, 62, 38–43 CrossRef CAS.
- M. Gómez, C. Z. Gómez-Castro, I. I. Padilla-Martínez, F. J. Martínez-Martínez and F. J. González, J. Electroanal. Chem., 2004, 567, 269–276 CrossRef.
- H. Zhou, T. Yamada and N. Kimizuka, J. Am. Chem. Soc., 2016, 138, 10502–10507 CrossRef CAS.
- Y. Liang, T. Yamada, H. Zhou and N. Kimizuka, Chem. Sci., 2019, 10, 773–780 RSC.
- Y. Liang, J. Ka-Ho Hui, M. A. Morikawa, H. Inoue, T. Yamada and N. Kimizuka, ACS Appl. Energy Mater., 2021, 4, 5326–5331 CrossRef CAS.
- B. Huang, S. Muy, S. Feng, Y. Katayama, Y. C. Lu, G. Chen and Y. Shao-Horn, Phys. Chem. Chem. Phys., 2018, 20, 15680–15686 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04955h |
| This journal is © The Royal Society of Chemistry 2024 |