Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Backscattering silicon spectrometer (BASIS): sixteen years in advanced materials characterization
Naresh C.
Osti
 *,
Niina
Jalarvo
*,
Niina
Jalarvo
 * and
Eugene
Mamontov
* and
Eugene
Mamontov
 *
*
Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA. E-mail: ostinc@ornl.gov; jalarvonh@ornl.gov; mamontove@ornl.gov
First published on 7th August 2024
Abstract
Quasielastic neutron scattering (QENS) is an experimental technique that can measure parameters of mobility, such as diffusion jump rate and jump length, as well as localized relaxations of chemical species (molecules, ions, and segments) at atomic and nanometer length scales. Due to the high penetrative power of neutrons and their sensitivity to neutron scattering cross-section of chemical species, QENS can effectively probe mobility inside most bulk materials. This review focuses on QENS experiments performed using a neutron backscattering silicon spectrometer (BASIS) to explore the dynamics in various materials and understand their structure–property relationship. BASIS is a time-of-flight near-backscattering inverted geometry spectrometer with very high energy resolution (approximately 0.0035 meV of full width at half maximum), allowing measurements of dynamics on nano to picosecond timescales. The science areas studied with BASIS are diverse, with a focus on soft matter topics, including traditional biological and polymer science experiments, as well as measurements of fluids ranging from simple hydrocarbons and aqueous solutions to relatively complex room-temperature ionic liquids and deep-eutectic solvents, either in the bulk state or confined. Additionally, hydrogen confined in various materials is routinely measured on BASIS. Other topics successfully investigated at BASIS include quantum fluids, spin glasses, and magnetism. BASIS has been in the user program since 2007 at the Spallation Neutron Source of the Oak Ridge National Laboratory, an Office of Science User Facility supported by the U.S. Department of Energy. Over the past sixteen years, BASIS has contributed to various scientific disciplines, exploring the structure and dynamics of many chemical species and their fabrication for practical applications. A comprehensive review of BASIS contributions and capabilities would be an asset to the materials science community, providing insights into employing the neutron backscattering technique for advanced materials characterization.
Wider impactA material's macroscopic-level performance (function) is critically defined by its atomic- and nanoscopic scale structure and dynamics. Among numerous spectroscopic techniques, inelastic (in particular, quasielastic) neutron scattering has the distinction of being a true structure-dynamics probe, as suggested by its measured quantity, the dynamic structure factor as a function of the momentum and energy transfer. The dynamic structure factor is a double Fourier transformation of the van Hove correlation function that represents the correlation of the scattering particles at different distances and times, that is, the sample's microscopic structure and dynamics. As a simultaneous structure-dynamics probe, inelastic/quasielastic neutron scattering is coupled, uniquely among experimental techniques, with simulation methods such as molecular dynamics that compute the space-time trajectories of atoms and molecules in materials. Notwithstanding many unique properties of neutrons as a materials probe, neutron scattering remains an intensity-limited technique. Thus, neutron spectrometers at neutron sources must be custom-designed and built to achieve the best possible utilization of the limited intensity, usually tailored to a specific neutron scattering technique. This is especially true for high-energy-resolution neutron spectrometers. Large investments into a new neutron spectrometer will eventually bear fruits in the form of decades-long service to research communities to address versatile problems in materials science and beyond. BASIS, a high energy-resolution backscattering neutron spectrometer at the Spallation Neutron Source of the Oak Ridge National Laboratory, has been pioneering in its class instrument that enabled new approaches to the structure-dynamics materials studies using quasielastic neutron scattering. After 16 years in the official user program and several hundred publications, the time might be ripe to review and categorize the scientific problems targeted by BASIS, to describe the new approaches developed to tackle these problems as was necessitated by the novel features of this spectrometer, and to think over the future directions in neutron backscattering spectroscopy for studies of materials based on the experience with BASIS. The current comprehensive review is intended to provide insights into utilizing neutron backscattering for advanced materials characterization. |
1. Introduction
The macroscopic properties of a material, whether man-made or natural, in a solid or liquid state, are largely defined by its atomic-level and nanoscopic structure and dynamics. To progress from empirical to rational design of new materials, analysis of the existing materials’ structure and dynamics is needed to gain understanding and eventually develop predictive capabilities for the bottom-up materials design. The requirements for probing the discrete structure of a condensed matter system include appreciable interaction of the probe with the atoms in the system so that scattering resulting in an exchange of the momentum between the sample and the probe could occur, and the probe's wavelength comparable to the interatomic or inter- and intramolecular spacings so that the momentum transfer is easily measurable. X-ray scattering is an excellent structural probe that satisfies all the above requirements. However, X-rays with a wavelength on the Angstrom length scale have energies on the keVs and tens of keV scale, while the atomic- and molecular level dynamics in condensed matter range from meV to tens or hundreds of meV for vibrations and from μeV to tens or hundreds of μeV for diffusive and relaxational excitations. On the other hand, neutrons produced by “thermal” or “cold” sources not only have wavelengths comparable to typical intra- and intermolecular spacings, similar to X-rays, but also possess relatively low energies, in the meV to hundreds of meV range, comparable with inter- and intramolecular vibrational energies. Typical energies of neutrons available at spectrometers at neutron scattering facilities make it easy to measure not only the momentum but also the energy transfer between the sample and the probe, especially for vibrational excitations. Even diffusive and relaxational dynamics in the μeV range can be relatively easily probed by resolving ∼10−3–10−2 changes in the energy of the ∼meV neutrons in QENS experiments. On the other hand, state-of-the-art inelastic X-ray scattering resolving ∼10−6 changes in the energy of the ∼keV photons can, at best, measure ∼meV dynamics. Neutrons are also efficiently scattered in a condensed manner, although in a manner very different from X-rays, as will be discussed below.QENS and neutron backscattering spectroscopy terms are often used interchangeably, but they are not synonymous. The former refers to a powerful experimental technique that measures the stochastic dynamics in materials of diffusive or relaxational origin on the atomic and nanometer length scale, as defined by the momentum transfer of the neutrons scattered by the sample. Stochastic atomic, ionic, or molecular motions on this length scale are detected on a characteristic time scale of picoseconds to nanoseconds, depending on their character (localized vs. long-range) and the sample temperature. To resolve such motions on the longer end of the time range, a neutron spectrometer needs to have an energy resolution on the μeV scale, much finer than a typical energy resolution of a neutron spectrometer for inelastic neutron scattering (INS). This is achieved using crystal analyzers of the energy of neutrons scattered by the sample that are positioned in backscattering or near-backscattering Bragg reflection conditions, hence the term neutron backscattering spectroscopy. It should be noted that “backscattering” or “near-backscattering” refers to the angle not between an incident and subsequently scattered by the sample neutron but between the neutron scattered by the sample in any direction and subsequently Bragg-reflected by crystal analyzers toward the detectors. The energy spread of the reflected neutrons is minimal when the neutrons are Bragg-reflected perpendicular or almost perpendicular to the crystal analyzers, hence the utility of backscattering geometry for high energy-resolution measurements. This is because, to the first approximation, the energy resolution of a time-of-flight (TOF) crystal analyzer spectrometer, such as BASIS, can be written as:
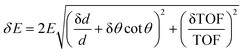 | (1) |
Here δd/d is the spread of the analyzer lattice constant, and θ is the Bragg angle. The second term in the first bracket is minimized when θ approaches 90° (“backscattering”) thus leading to the best possible energy resolution. Modern backscattering neutron spectrometers maintain backscattering or near-backscattering sample to analyzer to detector geometry for all the scattering angles, that is, all measured momentum transfers. This greatly improves counting statistics yet imposes restrictions on access to the sample position, as will be evident when the current technique limitations are discussed below. Neutron backscattering spectroscopy at dedicated neutron backscattering spectrometers is used for QENS measurements predominantly, but not exclusively, as sometimes this spectroscopy can be used to resolve non-stochastic dynamics, such as, e.g., quantum tunneling, provided that the associated scattering signal is not positioned too far away from the spectrometer's elastic line (at zero energy transfer). This is because, for various practical reasons, the energy transfer range accessible at neutron backscattering spectrometers tends to be very limited compared to general-purpose neutron spectrometers. Compared to the latter, neutron backscattering spectrometers gain in energy resolution while losing severely in the accessible energy transfer range.
Currently, operational reactor-based neutron backscattering spectrometers have an energy resolution of ca. 1 μeV and a maximum energy transfer of 30–35 μeV,1–3 whereas the near-backscattering spectrometers built on pulsed neutron sources historically had an energy resolution of ca. 17–25 μeV and a maximum energy transfer of several hundred μeV.4–6 A near-backscattering spectrometer for the newly constructed spallation neutron source (SNS)7 in Oak Ridge National Laboratory (ORNL), USA, eventually named BASIS (an acronym for Backscattering Silicon Spectrometer), was the first attempt to bridge the gap between ca. 1 μeV- and ca. 20 μeV-resolution neutron spectrometers.
A few decades of productive operation may be anticipated from a successful neutron spectrometer at a major scattering facility. Even though the lifespan of such a spectrometer does not quite match the typical human working lifespan, the spectrometer goes through many similar stages, from inception, building, and commissioning to entering routine operation, maturation, undergoing improvements, productive life, and eventual retirement. The age of 16 may mark the dawn of productive life for a human, but for a neutron spectrometer, this is a point from which hindsight may be warranted, as the spectrometer may be nearing or might have passed the middle of its working life. BASIS officially entered the user program in December 2007 after seeing the first SNS neutrons on April 28, 2006, and going through commissioning. Conceptualized around 1998/1999 by Ken Herwig,8 BASIS was the first among the backscattering or near-backscattering neutron spectrometers worldwide to combine the high energy resolution afforded by the nearly perfect (not mosaic) silicon analyzer crystals with the large accessible range of energy transfers provided by polychromatic neutron pulses at a spallation source.9 The combination of high energy resolution at the elastic line and the large accessible range of energy transfers at BASIS enabled simultaneous measurements of dynamics associated with the same species on different time scales. Most importantly, this includes the “fast dynamics” (spatially localized and traditionally, though not always correctly, described as rotational motion) and a slower motion associated with long-range translational diffusion. The data fitting ansatz had to be developed in the early days of BASIS operation to rationalize multi-component QENS data measured from relatively viscous liquids.10–12 The same ansatz was later derived and applied independently for multi-component QENS data from water measured at a time-of-flight spectrometer with a coarser energy resolution and a wider range of energy transfers.13 The multi-component QENS signal fitting from the localized and long-range translational dynamics has become common not only for liquids but also for solids measured at BASIS and will be featured in many examples discussed below. While a combination of high energy resolution and large energy transfers was a distinctive qualitative feature of BASIS from the beginning of its operation, the high scientific productivity achieved by BASIS was largely due to the high, by the standards of neutron backscattering spectroscopy, incident neutron flux and counting statistics. When the SNS power was about 0.5 MW, the incident neutron flux of 1.3 × 107 n cm−2 s−1 was measured at the sample position for a standard BASIS sample with ca. 10 cm2 area.9 At present, SNS typically operates at power levels between 1.4 and 1.7 MW, and eventually, 2.0 MW operation is envisaged for the first target station that provides neutrons for a suite of instruments, including BASIS, resulting in the concomitant increase of the neutron flux available. With a typical experiment duration of 3–5 days, up to 40–45 user experiments per year can be performed at BASIS. The scope and diversity of scientific studies carried out at BASIS to date are remarkable for a neutron backscattering spectrometer and can be attested by the long publication list featuring nearly four hundred papers in about a hundred journals, as BASIS is used to study a very broad range of materials (Fig. 1).
2. What does BASIS measure?
BASIS measures QENS signals from materials with stochastic dynamics in time (picoseconds to nanoseconds) and space (Angstroms to nanometres). The principles of QENS have been covered in many reviews and books.14–16 In short, a QENS-capable neutron spectrometer such as BASIS measures the double differential scattering cross-section, which is the intensity of neutrons of final energy (E) scattered from a material of a scattering cross-section (σ) in a given direction within a solid angle (Ω). The double differential cross section is given by:14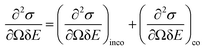 | (2) |
The measured intensity includes the contribution from both incoherent and coherent neutron scattering from a material. Incoherent scattering, which is very strong for hydrogen (but not deuterium) atoms, probes the single-particle dynamics, whereas coherent scattering probes the collective motion of the scattering particles. Most of the BASIS experiments are performed on materials rich in hydrogen; therefore, in most experiments, the coherent scattering contribution is small and oftentimes can be disregarded. In this situation, the measured intensity is related to the incoherent dynamic structure factor, Sinco(Q,E) as:14
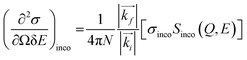 | (3) |
In eqn (3), N is the total number of scattering centers, kf and ki are the wave vectors of scattered and incident neutrons, which are related to the momentum transfer vector, Q = |(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )| = |(
)| = |(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i) − (
i) − (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f)|. It is the incoherent dynamic structure factor, Sinco(Q,E), that contains information about the dynamic processes in a material. Furthermore, the inverse Fourier transformation of Sinco(Q,E) in time gives intermediate scattering function, I(Q,t), which, upon further Fourier transformation in space, yields van Hove correlation function, G(r,t), that represents averaged over the entire sample self-correlation of the scattering particles at different times and distances. At BASIS, the measured QENS intensity, I(Q,E), is usually analyzed using the following expression:14
f)|. It is the incoherent dynamic structure factor, Sinco(Q,E), that contains information about the dynamic processes in a material. Furthermore, the inverse Fourier transformation of Sinco(Q,E) in time gives intermediate scattering function, I(Q,t), which, upon further Fourier transformation in space, yields van Hove correlation function, G(r,t), that represents averaged over the entire sample self-correlation of the scattering particles at different times and distances. At BASIS, the measured QENS intensity, I(Q,E), is usually analyzed using the following expression:14
| I(Q,E) = [X(Q)δ(E) + (1 − X(Q))Sinco(Q,E)] ⊗ R(Q,E) + B(Q,E) | (4) |
Here B(Q,E) is a background term (usually linear), R(Q,E) is the spectrometer's resolution spectrum normally collected from the same sample at a low temperature (∼20 K and below), δ(E) is the Dirac delta function to account for elastic scattering events, and X(Q) describes the elastic scattering fraction due to the contribution of immobile (within the spectrometer's sensitivity) species. Even when the signal from the immobile species can be subtracted, and only the mobile species are considered, the X(Q) is not necessarily zero if the particle's motion is spatially constrained; in this case, the X(Q) is referred to as elastic incoherent scattering factor (EISF). The quantity of interest that describes the diffusion dynamics, Sinco(Q,E), can be modeled to different model scattering functions, such as single and double Lorentzian,17 stretched exponential,18 Cole–Cole,19 and Cole–Davidson20 functional forms.
In QENS, inelastic peaks centered at finite energy transfers are not usually observed since they are typically outside of the accessible range of the energy transfers; therefore, Sinco(Q,E) in eqn (4) is primarily quasielastic in nature and can be referred to as SQE(Q,E), and called dynamic structure factor. The incoherent SQE(Q,E) carries the dynamics information on moving particles, which can be described by the van Hove formalism, and is given by self-correlation function, G(r,t), which provides the probability of finding a particle at a position r at time t which initially was at a position r = 0 at t = 0.
For long-range continuous (Fickian) self-diffusion the solution for G(r,t) is given by:21,22
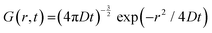 | (5) |
Spatial Fourier transformation of G(r,t) gives the intermediate scattering function, I(Q,t) as:
| I(Q,t) = exp(−DQ2t) | (6) |
Further time- Fourier transformation of the I(Q,t) gives SQE(Q,E), which is a Lorentz function of width, Γ(Q) (half width at half maximum), as:
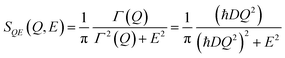 | (7) |
In this simplest approximation of Fickian diffusion, not often measured in practice, the scattering signal does not provide any spatial information, as the diffusion is assumed to occur through continuous infinitesimal jumps. In the limit of low Q (representing long distances), the linear dependence of Γ(Q) with the square of the momentum transfer:
| Γ(Q) = ħDQ2 | (8) |
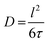 | (9) |
Thus, measurements of jump diffusion provide not only temporal, but also spatial information.
Depending on the distribution of jump-diffusion lengths, there may be several different jump-diffusion models:22,23
Chudley and Elliott model
This model considers a jump from one site to another site with a fixed jump length, (l). The Q-dependence of Γ(Q) is given by the following expression: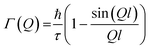 | (10) |
Hall and Ross model
This model assumes a Gaussian distribution of jump lengths and is given by: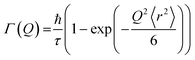 | (11) |
Singwi and Sjölander model
This model assumes an exponential distribution of jump lengths and relates to HWHM as: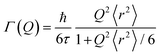 | (12) |
The mean square displacement (msd), 〈r2〉, in eqn (11) and (12) is related to D as D = 〈r2〉/6τ.
Jobic model21
This model modifies the Chudley and Elliott model by considering the delocalization of the molecules (r0) on its site after jumping a fixed length of l0, and is given by: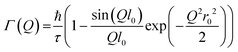 | (13) |
Sometimes it could be observed that measured Γ(Q) is either nearly independent of Q or exhibits diffusion-like Q-dependence at higher Q values but does not approach zero at Q = 0. The former scenario represents either so called rotational diffusion or spatially localized jumps over 2, 3, or more sites. Numerous models describing the corresponding Γ(Q) are available in the literature.14 Such processes are less often studied at BASIS because they tend to be too fast for the instrument energy transfer range (BASIS studies of methyl group rotations are a notable exception). On the other hand, the latter scenario represents diffusion that is translational, but spatially confined. That is, the particle does not move to infinite distance with time but instead is confined in a restricted geometry in space. Many studies at BASIS concern such scenario of diffusion in confinement. In either of these two scenarios, the measured QENS spectra provide another important parameter called elastic incoherent structure factor (EISF). Empirically, it is the fraction of the elastic signal with respect to the sum of the elastic and quasielastic signals, while its physical meaning is the probability for a moving particle to still remain within a volume defined by the Q value within a time defined by the spectrometer energy resolution. The EISF equals zero for purely long-range translational motion. Analysis of the Q-dependence of both Γ(Q) and EISF(Q) sheds light on the geometry of the rotational or spatially confined translational motions. More details about QENS and its data interpretation can be found elsewhere.14,21,24,25
It should be emphasized that, unlike periodic motions studied by INS, stochastic motions, either diffusional or relaxational, give rise to the QENS signal centered at E = 0 (elastic line). While INS is typically concerned with inelastic peak positions, QENS is concerned with the central peak shapes. As mentioned before, various functional forms, not restricted to a simple Lorentzian, provide the characteristic width of the quasielastic signal. Q-Dependence of the width suggests the character of the dynamics processes and gives the self-diffusivity of the mobile species. Temperature dependence of the self-diffusivity is then used to extract the activation energy of such dynamic processes. Furthermore, the Q-dependence of the measured EISF provides the geometry of the probed motions.17 BASIS has been employed to characterize a wide range of materials (Fig. 1), broadly classified into eight different groups, which will be covered in this review.
To summarize, energy-resolved neutron scattering techniques in general measure the length-specific (as determined via the signal Q dependence) scattering density fluctuations in the sample. These fluctuations could be periodic in time, with relatively well-defined vibration frequencies/energies as measured by INS, or stochastic, with a continuous distribution of frequencies/energies centered around the elastic line (E = 0) as measured by QENS. In turn, stochastic motions could be classified as either diffusional or relaxational. The former can be represented, in the simplest case of continuous (Fickian) diffusion, by the G(r,t), I(Q,t), and S(Q,E) as described by eqn (5)–(7). In this case, and even for more complex jump-diffusion processes, the self-diffusion coefficient, D, can be determined from the low-Q slope of the plot of the QENS broadening vs. Q2. The diffusion coefficient measured in such manner could be associated with either self-diffusion (as in the overwhelming majority of QENS experiments probing single-particle dynamics of hydrogen-bearing species that scatter neutrons predominantly incoherently) or transport diffusion (as in a minority of QENS experiments on the samples that scatter neutrons coherently).21 As far as the diffusion phenomena are concerned, QENS is the only technique that probes ensemble averages in macroscopically large samples on the Angstrom-to-nanometer scale. While pulsed field gradient NMR is often referred to as microscopic diffusion measurement technique, its probed lengths scale of ∼μm and time scale of ∼ms do not allow determination of atomic- and molecular level mechanisms of diffusion processes. QENS data, on the other hand, can be compared directly with simulation results providing information on the Angstrom-to-nanometer scale. Application of QENS to measurements of diffusion processes and its relationship to simulations has been extensively discussed21 and traditionally is one of the mainstays of neutron backscattering spectroscopy. On the other hand, the other type of stochastic motions, which are localized in space and thus not associated with long-range diffusion, in the past were often too fast to be measured at backscattering spectrometers, although they too give rise to QENS signal. When they could be measured, usually at coarser-resolution INS spectrometers, they were often described in terms of localized or spatially constrained diffusion processes, even though some of them were demonstrated to be non-diffusive in character.26,27 However, they can be universally classified as relaxations, and, accordingly, could be measured by a broad gamut of relaxation-probing spectroscopies, such as optical, IR, NMR, dielectric, etc. Through the Q-dependence of the signal, QENS measurements can reveal the geometry of relaxational processes in the way the other relaxation-probing spectroscopies cannot. BASIS was the first neutron backscattering spectrometer that could routinely measure both long-range diffusive motions and localized relaxations in the same spectrum. In BASIS studies, they were often referred to as “slow” and “fast” dynamics, respectively. Thus, interpretation of many QENS studies at BASIS had to rely on different ansatz compared to the earlier neutron backscattering spectrometers.
2.1. Water and aqueous materials
A relative majority of BASIS studies investigated dynamics in various forms of water and aqueous-based and hydrated materials. The low viscosity of pure water in its bulk state usually renders it more suitable to QENS studies at traditional time-of-flight (TOF) neutron spectrometers rather than QENS-dedicated backscattering neutron spectrometers, even though BASIS has been used in some measurements of bulk water28 in combination with a TOF spectrometer. Most seminal QENS results on bulk or loosely confined water dynamics were obtained on TOF neutron spectrometers.13,29–31 On the other hand, BASIS has excelled in studies of aqueous systems with the dynamics slowed down, either by tighter confinements (including in pores or on surfaces) or additives (e.g., salts) or supercooling. Often, a combination of the aforementioned factors has been explored, e.g., when confinement or additives enable water supercooling.Fig. 2 illustrates the new capabilities introduced by BASIS in probing dynamics of liquids, including many aqueous-based systems. The inset in Fig. 2 shows on the log–log scale the QENS data32 measured from (H2O)6(LiCl) as a function of neutron energy transfer, E, both as collected, I(E), open symbols, and converted into the dynamic susceptibility units, χ′′ = I(E)/(nB(E) + 1), filled symbols. Here nB(E) is the temperature-dependent Bose factor, nB(E) = (exp(E/kT) − 1)−1. Both plots in this inset represents the same data set. However, while it is difficult for the naked eye do discern various dynamic components from the standard I(E) representation, in the dynamics susceptibility representation, the position of the maxima corresponds to the characteristic frequencies (energies) in the system. The dynamic susceptibility data set in the inset exhibits, without relying on any data fitting, a maximum positioned in the μeV range, then a valley, and, finally, an increase in the intensity in the hundreds of μeV range, even though the position of the second maximum cannot be identified unambiguously because of the limited accessible energy transfer range. This demonstrates the presence of more than one dynamic component in the scattering spectrum. The main panel in Fig. 2 shows the same dynamics susceptibility data set rotated by 90 degrees and plotted as a function of measured characteristic time, τ = (h/2π)/E, where h is the Planck's constant. Just as when the susceptibility spectrum was plotted as a function of energy transfer, there is now a maximum positioned in the 0.1–1.0 ns range, then a valley, and finally, an increase in the intensity through the 0.001–0.01 ns range. That is, at a given length scale defined by the Q value (Q = 0.7 Å−1), BASIS measures two relaxational processes. It turns out that the slower process is related to the translational diffusion of water molecules, as could have been measured by any high-resolution neutron backscattering spectrometer. At the same time, the faster process, which would have been inaccessible to high-resolution neutron backscattering spectrometers predating BASIS, is associated with spatially localized relaxation of water molecules. Such “fast” dynamics is measurable by many relaxation-probing techniques, even though its origin was long debated. Regardless of the character of this motion, we note that the measured characteristic times (as the positions of the susceptibility maxima) map onto the proposed33 relaxation times diagram for the so-called “fragile”34 molecular glass-forming systems. At a given temperature (T = 240 K), there are two measurable characteristic relaxation times, as indicated by the crossing of the vertical (temperature) and two horizontal (relaxation times) dashed lines. The longer relaxation time is associated with the relaxation that gives rise to the long-range translational diffusion of the water molecules.
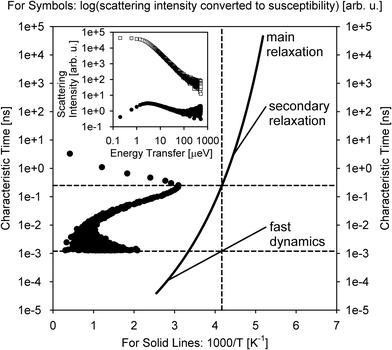 | ||
| Fig. 2 Inset: Open squares: the scattering intensity measured at T = 240 K from (H2O)6(LiCl) at Q = 0.7 Å−1 using BASIS. Filled circles: the same data set converted to the dynamic susceptibility units. These data sets, obtained from ref. 32 are plotted as a function of neutron energy transfer. Main panel: filled circles: the dynamic susceptibility data set, as presented in the inset, was replotted as a function of measured characteristic time (inverse energy transfer) and rotated by 90 degrees. Solid lines: a schematic map of dynamics (molecular center-of-mass) in glass-forming systems as proposed in ref. 33. Horizontal dashed lines: the characteristic relaxation times (dynamics susceptibility maxima positions) measured in the sample at T = 240 K (as presented by the vertical dashed line). Different relaxation processes present at the measurement temperature may give rise to more than one dynamic component in the spectrum (originated from the center-of-mass motion, besides possible dynamics processes from the side groups). | ||
According to this schematic diagram of relaxation times as presented in the main panel of Fig. 2, there may be other dynamic components (e.g., “secondary relaxation”) besides the main structural relaxation and “fast dynamics” that could be measurable in molecular glass-formers, such as supercooled water. The neutron scattering-based evidence for the “secondary relaxation” component, as presented in Fig. 2, has been demonstrated.35–38 However, it remains limited to date because it relies on challenging neutron spin-echo measurements. On the other hand, the “fast dynamics” component, as presented in Fig. 2, is commonly recognized, even though it is debated whether any characteristic frequency can be assigned to these motions representing rattling in the transient cage of the neighbor molecules that eventually dissipates via the main structural relaxation process.39 In water, this localized motion has been attributed to and is commonly known as molecular rotation29 until it was demonstrated13 that it is better described as localized diffusion within a spherical volume. On the other hand, large-jump non-diffusive reorientation of water molecules are also known as the mechanism associated with the localized water dynamics on the picosecond time scale.26,27 Accurate molecular-level description of water dynamics is complex, but we note that all the dynamic components presented as lines in Fig. 2 are associated with the molecular center-of-mass motion and thus should be exhibited even by a system of Lennard-Jones particles.40,41 That is, the “fast dynamics” motion is inevitably associated with reorientation of molecules (such as in water), but even a system of particles lacking intramolecular structure, without orientational degrees of freedom, would exhibit the “fast dynamics” in addition to the main structural relaxation. For such point-like particles (and for the center-of-mass of molecules), this “fast dynamics” is customarily described as rattling in the (transient) cage of neighbor particles, which, in turn, dissipates in the course of the main structural relaxation; the latter process leads to long-range translational diffusion. Any dynamics related to the intramolecular motion or the motion of side groups (in complex molecules) would be in addition to the center-of-mass dynamics that is presented schematically in Fig. 2. The split between the main relaxation and the “fast dynamics” requires two-component fits for many datasets obtained at BASIS, which was the first high-resolution neutron backscattering spectrometer capable of probing such multicomponent dynamics. Fig. 2 is important because it illustrates, using fit-free, model-free measurement of an aqueous solution as an example, the universality of the multicomponent description of QENS data from liquids. In liquid systems, BASIS is capable of measuring more than just structural relaxation associated with the long-range translational diffusion.
Even though BASIS was the first neutron backscattering spectrometer to detect routinely both the spatially localized, in-(transient)-cage rattling “fast dynamics” and the long-range mobility associated with the main structural relaxation in the same spectra, and fits with two dynamic components are very common for BASIS data, this approach is not universal. Sometimes, depending on the system and the measurement temperature, only one of the two dynamic components falls within the spectrometer's accessible range, or the two dynamic components may have merged, thus rendering a single-component data fit more appropriate. Such a data fit could use either a Debye-like model scattering function (a Lorentzian in the energy domain, as a Fourier transformation of exponential decay of the self-correlation function in the time domain) or a “stretched” model scattering function, such as a Fourier transformation into the energy domain of a stretched exponential, exp[−(t/τ)β] or a Cole–Cole function in the energy domain.42
The data presented in Fig. 2 provide an example of a bulk aqueous sample where supercooling is attained by adding salt. Several such studies have been carried out at BASIS using LiCl-based aqueous systems, based on the idea that many properties of water are less affected by adding LiCl to the bulk sample than by confining pure water in small pores.35,36,43,44 There are many striking similarities between pure water and aqueous solution of LiCl enabling studies of some water properties far below homogeneous nucleation temperature of 235 K without using confinement. Nevertheless, the disruption by LiCl of the water hydrogen-bonding network completion, which makes low-temperature studies possible, also leads to changes in the diffusion mechanism of the water molecules.32 Therefore, water confinement (see ref. 45 for a recent review of QENS studies of water in restricted geometries) was also utilized at BASIS to enable low-temperature studies of water properties, in particular, for water adsorbed on oxide surfaces, either external46–48 or those of the internal pores.49 Complementary to the earlier backscattering studies demonstrating that some bulk-like properties are acquired at the formation of the first disordered water layer atop the ordered water molecule layer(s),50 as already attained by exposure to ambient air,51 these BASIS measurements helped link common properties of water hydrating either inorganic surfaces or organic molecules.52 The latter case may have important implications for the connection between the hydration level and dynamics of hydrated biomolecules such as proteins.
With a possible exception of the surface/hydration water experiments, most of the studies of aqueous systems described above were focused primarily on the properties of water itself. In such studies, the presence of solute and/or confinement merely provides the means to suppress water crystallization. Different from these studies of general properties of surface/hydration water, BASIS experiments probing hydrated barite, BaSO4,53 and calcite, CaCO3,54 were aimed at the mineral-specific residence times/exchange rates of the water molecules in contact with the surface termination atoms. These studies took uncommon approach, where QENS data was utilized to validate simulations results, and the latter were used to discern residence times of water on the various ion surface sites, such as barium and sulfate in BaSO4 and calcium and carbonate in CaCO3. Likewise, in another BASIS experiment, material-specific properties of water interacting with super-hydrophilic CuO surfaces of special topography were of interest.55 The water in CuO exhibited two populations of molecules with distinct dynamic signatures, one (slow) in direct contact with the surface, another (faster, almost bulk-like) further way from the surface. BASIS measurements of more commonly studied three-dimensional water confining matrices were dominated by cement, concrete, and related materials.56–67 Many of these studies were of dual purpose, focusing on both the properties of supercooled confined water and the dynamics (and sometimes evolution with curing time) of the chemically bound, tightly confined, and loosely confined/free water populations. In this approach, the matrix-specific properties are of interest but take secondary importance to the properties of the confined water itself, as the cement/concrete matrix prevents crystallization of the confined water and allows measurements of dynamics over a broad temperature range. Such studies have implications for the fundamental properties of water such as the temperature-dependent dynamic crossover and the purported second critical point of water. However, some experiments focused on the performance of highly specific systems, e.g., high and low calcium fly ash-based geopolymer pastes.61 This study observed activation (polymerization) of the pastes at 60 °C but not at ambient temperature. The amount of chemically bound and constrained water increased through the initial activation period, and then remained approximately constant upon initiation of nucleation and growth period. The complexity of cement and concrete-related systems provides ample grounds for developing and testing various models describing the dynamics of the water molecules from different populations within the hydrated material. Elaborate models of water dynamics involving global fitting of the QENS data stemmed from some of such studies.66–68
Carbon and carbon-based systems were the second most popular class of hydrated materials for BASIS studies, sometimes involving aqueous solutions for electrochemical applications.69 In this work, QENS was instrumental in exploration of the effects of tuning the pore size and oxygen content in the very high surface area carbonaceous materials on the specific capacitance, as the measurements revealed processing-specific separation of the aqueous electrolyte into bulk-like mesopore and micropore populations. In contrast to this material-oriented work, most of the carbon-based studies focused on the behavior of the confined supercooled water itself as a function of temperature, pressure, or hydration level in porous carbon70–73 or carbon nanotubes.74 Such experiments conceptually have much in common with studies of water in more traditional confinements. While it is theorized that carbon provides hydrophobic confinement, in variance with silica- or cement-based matrices, it turns out that carbon-based materials that can be hydrated must be at least somewhat hydrophilic. Accordingly, the hydration level dependence of the microscopic dynamics of water adsorbed in carbon micropores exhibits many traits characteristic of water in hydrophilic matrices.73 For instance, the diffusion rate (related to the main structural relaxation time of hydration water) exhibits super-Arrhenius temperature dependence and becomes a stronger function of temperature as the hydration level is progressively increased. On the other hand, the study of water in graphene oxide75 was motivated mainly by the search for anisotropy in the dynamics of fluids in this two-dimensional material for water–ethanol separation. Other studies of two-dimensional materials at BASIS involved hydrated clays,76 MXenes,77,78 and MXene–TiO2 heterostructures.79 In particular, a highly cited study of water in MXenes has established the baseline for numerous subsequent QENS studies of various media confined in MXenes by revealing an important distinction between the intra-layer intercalated population of low or undetectable mobility and the intra-stack adsorbed population of a relatively high mobility (a fraction of the bulk value).77 QENS data on hydrated MXenes intercalated with various cations for electrochemical applications were highly complementary to the INS data probing the vibrational dynamics of water confined in these materials.80 Water in commonly studied silica or silicate matrices was also explored at BASIS using external stimuli such as electric field,81,82 or a combination of very high temperature and pressure.83 Some counterintuitive results on the enhancement of water mobility by a structure-breaking salt were also observed using silica as a confining matrix.84 In another example of a “hard” confining matrix, a complex nanoscale morphology of crystalline cellulose was found to give rise to rather complex multicomponent dynamics of its hydration water.85 Somewhat in analogy with water in MXenes, there a distinction between the two water populations of cellulose. The first population consists of cellulose-bound water molecules that gradually becomes mobile as the temperature is increased; essentially, surface water. The second population represents water that accumulates in the narrow spaces between the cellulose microfibrils. Unlike the non-freezing inter-stack water in MXenes, this water between the cellulose microfibrils melts at ca. 260 K, likely due to the larger confinement size that is sufficiently small to cause a freezing point depression but insufficiently small to suppress crystallization altogether. Besides traditional “hard” confining matrices, “soft” water hosts investigated at BASIS ranged from polymer materials86–89 to lyotropic liquid crystals90,91 and microemulsions.92
Finally, BASIS has been employed for studies of various aqueous solutions in the bulk form that, unlike the aforementioned LiCl-based aqueous systems, were not intended for probing the low-temperature behavior of water, but driven instead by electrochemical applications,20,93 complex waste management demands,94,95 and interest in the influence of structure making and structure breaking ions on water dynamics.96,97 One particularly remarkable example93 involved observation of correlated proton jumps between the molecules in pure and 85% aqueous phosphoric acid. The relaxational dynamics associated with these jumps was also observed in this work using dielectric spectroscopy and light scattering, but it required a probe with a spatial sensitivity, such as QENS corroborated by ab initio molecular dynamic simulations, to reveal that protons move by surprisingly short jumps of only 0.5–0.7 Å.
In the examples discussed above, the water molecules were disordered and constituted a “phase” characterized by some cooperative behavior. Other measurements of water at BASIS could be more appropriately classified as studies of confined water molecules, often, but not always, structurally ordered, that interact predominantly with the matrix but not the other water molecules. Because of that, some structural water molecules may exhibit fast rotational dynamics at cryogenic temperatures, where the mobility of interacting water molecules would have been long arrested.98 In this example, two thermally activated relaxation processes involving water molecules were observed in the temperature range between 70 and 130 K, one on a sub-picosecond time scale, another on a 10–100 ps time scale. The slower process was attributed to in-plane reorientation of the water molecule involving the breaking of hydrogen bonds with a framework. Despite the low temperatures involved, this slower process is analogous to rotational diffusion of water molecules in bulk water. The faster process was a localized motion of the water molecule with no apparent analogs among known bulk or confined phases of water. Other examples of BASIS studies of water molecules with limited interactions with one another include water molecules in molybdenum-oxide nanocages,99 uranyl fluoride hydrides,100–102 and core–shell polyoxometalates.103 BASIS experiments have also studied various hydrous transition metal oxides for electrochemical applications.104–106 The narrow channels of the mineral beryl, Be3Al2Si6O18, were used to probe anisotropy in the dynamics of the ultra-confined water molecules.107,108 This anisotropy was probed using dielectric spectroscopy, INS, and QENS. The latter technique presented some evidence of single-file diffusion of water molecules along the channels.107 Interestingly, while the reports of proton tunneling in bulk hexagonal ice109 could not be corroborated by BASIS measurements,110 highly unusual quantum tunneling of water molecules in beryl has been observed in INS experiments.111
Various spectroscopic techniques besides QENS can probe the same relaxation processes involving water molecules, whether isolated or in aqueous phases, but QENS possesses an important advantage of being a spatial-sensitive technique due do the signal Q-dependence. Analysis of the QENS spectra similar to those presented in Fig. 2 that were measured at different Q values could help distinguish between localized and translational dynamic components and quantify the geometry of the motions involved. Geometry analysis of the motion of a water molecule in the transient cage formed by its neighbor water molecules requires simultaneous detection of the “in-cage” rattling process and cage-dissipating structural relaxation process, which BASIS, with its large accessible dynamics range, excels at. Finding diffusion coefficients from QENS data is common among all neutron backscattering spectrometers, but BASIS is capable of measuring faster localized relaxation processes as well.
2.2. Biosystems and biomaterials
The placement of a section describing biological studies immediately following the section on water may not be intuitive if the narration is expected to progress gradually from the simplest to most complex systems, yet it is completely logical in view of the famously known inseparability of the dynamics of proteins and other biomacromolecules from their hydration water dynamics.33,112–117 A different line of reasoning, but adding to the same point, is that many BASIS studies of water that hydrates biomolecules, e.g., oriented substrate-supported lipid membranes,118–124 are conceptually very similar to BASIS studies of water that hydrates oriented inorganic surfaces.55 Likewise, water that hydrates even complex multicellular organisms in cryptobiosis (e.g., brine shrimp eggs in diapause) dynamically behaves just as water in regular inorganic matrices,125 as was also observed in BASIS measurements.126 Therefore, in many studies of hydrated powders of proteins and other biomacromolecules performed at BASIS,127–145 oftentimes in conjunction with other neutron spectrometers, it may be difficult to draw a line between analyses of the dynamics of biomolecule and its hydration water, the separation between which is enabled by partial or full deuteration of the molecule or use of D2O for hydration. Some of these studies were carried out as a function of applied electric field146 or pressure.147 Likewise, BASIS measurements of hydrated cellulose,148 lignin,149 and polysaccharides150 were conceptually related to those of water in cellulose.85 A few BASIS experiments addressed hybrid systems where hydrated biomolecules were incorporated into inorganic matrices, such as tRNA adsorbed on nanodiamonds151 or hepatitis B surface antigen encapsulated in silica,152 again with a direct link between the dynamics of biomolecules and their hydration water.Measurements performed at BASIS together with other neutron spectrometers reveal complex dynamics in water and hydrogen-bonding liquids153 even in their isotropic bulk state, whereas surface water hydrating biomolecules exhibit, due to broken isotropic symmetry, especially rich dynamics.154–156 Such dynamics further grow in complexity upon gradual transition from surface to bulk-like hydration levels,157,158 to which the hydrated biomolecules respond accordingly.159 Several BASIS studies of bulk-like solution samples concentrated on the symbiotic relationship between the chain group dynamics in solvated biomolecules and the innermost and other solvation layers in concentrated LiCl-based aqueous solutions,33,160–162 water,163 water–isopropanol,164 and non-aqueous, non-glass-forming carbon disulfide.42 Many other BASIS studies of proteins in bulk-like solutions were concerned with both side-chain protein dynamics and the global rotational/translational dynamics of protein as a whole.165–169
Lipid membranes represent another major class of biomaterials studied at BASIS. Due to their amphiphilic properties, the dynamics of solvated lipid assemblies are coupled to their aqueous solvent media, similarly to proteins, even though it is the hydrophobic lipid tails, not the hydrophilic solvated lipid headgroups, which typically dominate QENS signal from lipid systems. Unlike the aforementioned substrate-supported lipid single- or bilayers, lipid vesicles, which most closely mimic biological membranes, invariably give rise to a two-component QENS signal when measured at BASIS. In full analogy to the two-component QENS signal from liquids discussed in the previous section, the data fitting ansatz developed for solvated lipid assemblies such as vesicles170 includes the “fast dynamics” broad component describing spatially localized lipid motion and the narrow component associated with the slower lateral (long-range translational) lipid diffusion within the membrane. Just as in liquids,10–13 the geometry of the “fast dynamics” particle motion in the transient cage formed by the nearest neighbors (which will eventually dissipate by the structural relaxation associated with long-range diffusion) can be deduced from the Q-dependence of the relative spectral weight of the narrow dynamic component. In liquids such as water, this approach was used to prove that the spatially localized “fast dynamics” can be better described as localized diffusion within a transient spherical volume13 as opposed to isotropic rotation.29 In lipids, upon transition from the low-temperature gel phase to the high-temperature fluid phase, the “fast dynamics” changes its character from uniaxial lipid rotation to confined diffusion within the volumes that grow for the hydrogen atoms along the lipid's tail further away from the lipid's headgroup.170 Numerous BASIS studies explored the effect on the localized and lateral lipid motion in both gel and fluid membrane phases of various additives, such as cholesterol,171 α-Tocopherol,172 amyloid β peptide,173 aspirin,174 and nonsteroidal anti-inflammatory drugs.175 In variance with all the other additives studied, introduction of ergosterol changed the mechanism of the lateral lipid diffusion in a bilayer from the commonly observed continuous (Fickian) to jump diffusion.176
Similar to studies of supported membranes,121 several BASIS experiments explored the influence of an antimicrobial peptide melittin on lipid dynamics in vesicles.171,177 The effect of another antimicrobial peptide, aurein, on lipid dynamics in vesicles was also investigated.178 Other BASIS studies probed the effect of salts in the aqueous buffer on the lipid membrane dynamics.179,180 Most BASIS measurements of lipid assemblies in aqueous buffers involved unilamellar vesicles, but some studies were performed on multilamellar vesicle systems.181,182
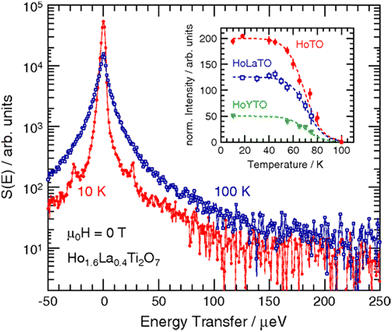
While the overwhelming majority of QENS studies of biomaterials at BASIS and elsewhere historically have been and are performed using model systems, more recently, strides have been made to probe the dynamics of intracellular water183–187 and intracellular biomacromolecules188–195 inside live cell cultures or spores.196 For such measurements of live cells, BASIS was employed to study the dynamics of water in cyanobacteria,197 and GroEL protein overexpressed in living deuterated E. coli cells.198 Besides, BASIS made contributions199,200 to the emergent studies of cancer cells.201–205 Furthermore, BASIS was employed in studies of live multicellular organisms.206–209 Such measurements, hardly feasible with beam probes other than neutrons,209 tend to resolve, despite the immense molecular complexity of the samples, the dynamics of (1) aqueous intra-organism constituents (e.g., cytoplasmic water or hemolymph) and (2) non-aqueous constituents (Fig. 3). The complexity of the organisms precludes unambiguous assignment of the “non-aqueous” signal component to a specific class of biomolecules, but arguments can be made that typical QENS spectra from such samples are dominated, besides the aqueous constituents, by lipid assemblies, as opposed to, e.g., proteins. It remains to be explored how far the complexity of the biological samples amenable to QENS measurements can reach.209
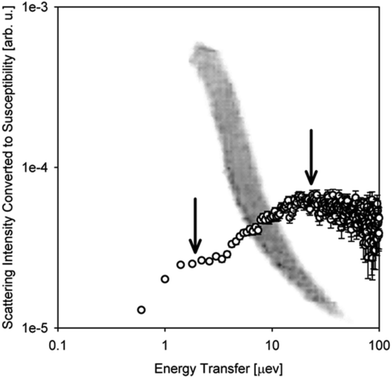 | ||
| Fig. 3 A photograph of one of the planarian flatworm specimens floating in water superimposed onto the scattering intensity data in the dynamic susceptibility form as measured on BASIS from live planarians in water at T = 304.1 K at Q = 0.3 Å−1. The measurements were described in ref. 206. The scattering intensity plot is presented after subtraction of the background signal from the bulk H2O medium. The vertical arrows indicate the two measurable dynamic components. The peak at ca. 10–20 μeV is from the water-in-specimen, whereas the shoulder at ca. 1–2 μeV is from the scattering by non-aqueous constituents in the flatworms. | ||
2.3. Polymers and polymer-nanocomposites
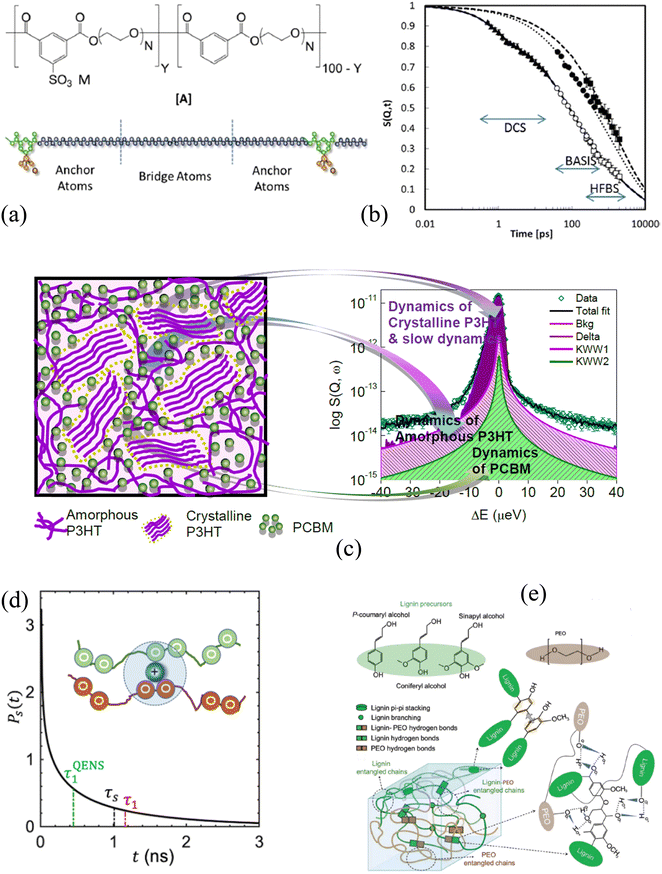
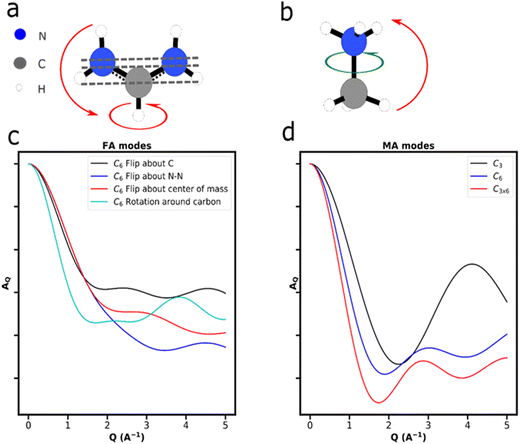
A comprehensive knowledge of the structure and dynamics of polymers and polymer nanocomposites at wide temporal and spatial scales is critical to tuning the polymer's architecture for their optimization in varied applications. This optimization realizes polymers with new properties resulting from enhanced complexities compared to a simple polymer chain. Polymers, which are macromolecules, exhibit many relaxation processes taking place at the molecular levels. Several spectroscopic techniques, such as dielectric spectroscopy,210,211 nuclear magnetic resonance,212 dynamic light scattering,213,214 X-ray photoelectron spectroscopy,215 and quasi-elastic neutron scattering (QENS),216,217 have investigated polymer dynamics in bulk and composites. Among them, QENS has distinct advantage over other techniques because it provides not only the time scales but also the geometry of the motion. Polymer dynamics span a wide range of time scales (Fig. 4b), capturing side chain vibrations and rotations as well as segmental motion and chain diffusion. Those motions determine polymers’ viscoelastic characteristics. A suite of neutron scattering spectrometers, having variable energy exchange coverages, has been implemented to capture the entire range of the relevant time scales.218–220 BASIS is a time-of-flight back-scattering spectrometer that probes dynamics from nano to picoseconds in polymers, polyelectrolytes, and their nanocomposites, mostly capturing the segmental and rotational motions. Any minor changes in the environment around these soft materials will significantly impact the properties on a macroscopic level.In a polyelectrolyte system comprising amine-terminated poly(amidoamine) dendrimers (PAMAM), a measurement at BASIS explored the internal dynamics in solution and at different hydration levels. It established that solvent interactions with polymer electrolyte counter ions enhance the local internal mobility of dendrimers, which is essential for the application of the material to transport drug molecules.221,222 Not limited to the biomedical field, the transport of chemical species is equally critical when using polymers as electrolytes in energy applications.223,224 Poly(ethylene oxide) (PEO), a polymer electrolyte, has been investigated at BASIS in pristine and composite forms to probe the segmental mobility of the polymer. PEO in its composite with alumina having two different surface chemistries (acid and neutral) in the presence of Li salt at eutectic concentration showed no impact on the segmental dynamics, but a slowing down of PEO motion by acidic particles compared to neutral particles in the absence of salt was observed.225 A reduced segmental mobility of PEO spacer in PEO-based ionomers (Fig. 4a) in the presence of three different meal ions was confirmed from a measurement at BASIS.226 However, the study of the dynamics of the sulfonated polystyrene (SPS) ionomers in deuterated-cyclohexane and deuterated-cyclohexane/d-ethanol (0.95/0.05) solution indicated that the ethanol does not break the ionic assemblies. Nevertheless, it affects the packing and motion of the ionic groups within the clusters and, in turn, increases the chain dynamics on all the length scales probed.227 A decrease in PEO's local segmental dynamics has also been reported when confined in nanopores of anodic aluminum oxide.228 Chen et al. also found a reduction in the segmental mobility, not only in the semicrystalline state of the PEO and LiTFSI salt mixture229 but also in the presence of OHARA ceramic with the salt, resulting in a 30% reduction in ionic conductivity230 from experiments at BASIS. Furthermore, a study of polyoxometalate–poly(ethylene glycol) (POM–PEG) hybrid nanocomposites at BASIS revealed the localized longitudinal motion of the PEG segments in confinement, thereby enhancing the proton conducting ability over the polymer backbone.231 Poly(alkylene oxide)s (PAOs), with a backbone similar to the PEO, have been studied at BASIS to probe the side chain dynamics. They exhibited a similar spectral shape for segmental dynamics to that of the PEO but of lower characteristic time, revealing the antiplasticization effect.220 A recent study at BASIS with poly(pentyl malonate) (PPM) poly electrolytes with LiTFSI revealed ultra-slow dynamics (ca. ∼ 0.22 ns) (Fig. 4d) of solvation shell breakup due to the formation of temporary cross-links between the Li ions and the polymer segments.232
BASIS has also contributed to understanding the charge transport mechanism in energy-harvesting materials where the dynamics of electron donor and acceptor materials play an essential role. Polythiophene (P3HT), a π-conjugated polymer, is one of the promising energy-harvesting materials for organic photovoltaics, which has been studied at BASIS under different conditions. A blend of P3HT with [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) (Fig. 4c) showed the presence of two distinct relaxation processes, one of each coming from P3HT and PCBM, compared to a single process dominating their bulk (pristine) counterparts. However, the dynamics of P3HT were found to be faster in the blend than in its bulk form due to the mixing of PCBM into the amorphous region of P3HT (Fig. 4c). Measurements at BASIS not only assisted in predicting the glass-transition temperatures of a series of semiconducting polymers with thiophene rings233 but also elucidated the microscopic dynamics234 as well as methyl and the methoxycarbonyl group rotations of dopant (p-type) on P3HT.235 They were also used to probe the side chain and ligand/methyl group dynamics in poly[2-methoxy-5-(20-ethyl-hexyloxy)-1,4-phenylene vinylene] (MEH-PPV) polymers236 and Polyoligosilsesquioxanes (POSS) hybrid molecule,237–239 respectively. Furthermore, experiments at BASIS on dielectric energy storage media, such as ferroelectric polymers, have investigated the impact of configurational changes on the dynamics of polyvinylidene fluoride (PVDF) and copolymers with trifluoro ethylene (TrFE) or tetrafluoroethylene, ferroelectric copolymers. The presence of two different dynamics processes was found; the slower one was associated with the jump-diffusion of the proton along the polymer backbone, whereas the faster one was attributed to the rotation of the methyl group.240 Similarly, QENS studies performed at BASIS supported the observation of the two different energy processes necessary for the ferroelectric to paraelectric phase transition in poled PVDF-TrFE ferroelectric copolymer films.241 A short-range faster process accounting for the molecular motion within the crystalline domains and the amorphous region in relaxor PVDF-based copolymers and terpolymers, respectively, was also reported.242 Besides studies of polymeric relaxor ferroelectric materials, BASIS was instrumental in revealing the freezing of the local dynamics, depending on the temperature and external electric field, in a relaxor ferroelectric PZN-4.5%PT single crystal.243
Nano-confined polymer materials have diverse properties, such as ferroelectric, transport, rheological, thermal, and more, compared to bulk polymers due to the different structural and dynamical behaviors of polymers in confinement. Confinement changes the polymer conformation, impacting the glass transition and the polymer chain dynamics. BASIS has been used to explore the dynamics of poly(ethylenimine) (PEI) confined into mesoporous SBA-15 silica particles of varied surface functionalities, which have a high affinity for CO2 adsorption.244,245 These studies have reported the presence of two relaxation times for the PEI molecules with a significant reduction, compared to the bulk, of the dynamics of the confined polymer. However, the functionalization of the silica wall with the hydrophobic group resulted in enhanced mobility (still slower than that of the bulk) of the PEI layer beyond the first interacting monolayers of the silica pores.26 On the other hand, a longer characteristic time to the PEI layer close to the attractive pore wall and a shorter time to the polymer away from the wall have been assigned.27 A dynamics study of polyethylene-alt-propylene confined in hydrophilic anodic alumina nanopores by Krutyeva et al. at BASIS showed that the local segmental dynamics of a polymer confined with the repulsive pore-wall remain unchanged.246 Similar behavior of the segmental dynamics of polyisoprene chains grafted on SiO2 particles has also been observed.247 However, a separate study at BASIS looked at the impact of the surface-polymer interactions on the dynamics of adsorbed PEI by grafting organosilanes with different chemical end groups to the SBA-15 silica.248 This study concluded that the chain mobility depends on the conformation of the surface-grafted chain and that of the PEI around the surface group. Besides the impact of the particle surface on the segmental dynamics of a polymer, one of the recent studies at BASIS investigated the effect of rigidity and miscibility on the segmental dynamics in dynamically asymmetric polymer blends containing no nanoparticles. Mbonu et al. studied the dynamics of poly(methyl acrylate) (PMA) chains when blended with poly(methyl methacrylate) (PMMA), polystyrene (PS), poly(ethylene oxide) (PEO).249 They found an increase in the segmental jump length of PMA due to an increase in free volume. They also observed the impacts of chain miscibility and rigidity in the segmental dynamics of PMA.
Many other complex polymers, polymer-nanocomposites, and hydrogel systems have been studied at BASIS to explore and understand the various factors impacting the macroscopic properties. For example, measurements performed at BASIS with poly(2-vinylpyridine) (P2VP)/silica nanocomposites and (PNCs) and P2VP-grafted-to-silica NPs (PGNs) had revealed that the control over the segmental mobility and the mechanical strength of the composite materials could be achieved by altering the local density and the chain stretching parameters at the interfacial layers of the nanoparticles.250 Furthermore, results obtained from an experiment using polystyrene exposed to toluene vapor were employed to understand the complex dynamical transition of hydrated protein resulting from a strong solvent–solute relationship controlling the protein functionalities.251 Replacing the hydration water with a polymer coating had similar, but enhanced, effect on the protein dynamics.252 BASIS has also contributed to probing the dynamics of more complex biomolecules, such as lignin, and its composites (Fig. 4e). Vural et al. investigated thermal history's impact on lignin dynamics. They found an extended lignin structure, resulting in a faster dynamic on cooling from a higher temperature. The effect was more pronounced at higher temperature and hydration levels.149 Similar temperature hysteresis after heating was also observed in the PEO-modified lignin complex (Fig. 4e), which showed slow structural rearrangement.253 Furthermore, an experiment at BASIS evaluated the curing dynamics of Tetrakis(phenylethynyl)benzene (TPEB) blended with a resorcinol-based PEEK™-like oligomeric phthalonitrile (Res) resin. The study showed a slowing down in the mobility of TPEB as one introduced the TPEB monomer with Res resin.254 Dynamics become complex when polymers form a three-dimensional network with a continuous phase of confined water, called hydrogels.255,256 QENS measurements of polyhydroxyethyl methacrylate (pHEMA) hydrogels at BASIS have demonstrated an increase in mobility of the polymer network at high hydration level256 providing information required to tune the transport properties of the hydrogels.
2.4. Bulk and confined ionic liquids
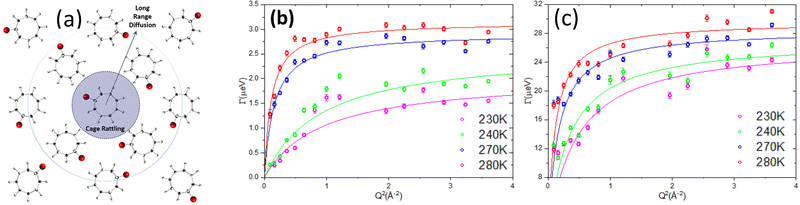
Ionic liquids are molten salts with organic cations and inorganic/organic anions. Many of them remain liquid at room temperature. Physio-chemical properties (high stability, low volatility, and non-flammability)257,258 originating from the molecular make-up of ionic liquids make them chemicals of choice for research in multiple scientific disciplines. Tunning of the molecular parameters allows control of the behavior of the liquids from microscopic to macroscopic levels259 for their optimization in different applications such as catalysis,260 separation science,261 biology,262,263 and energy storage and conversion.264,265 The structure and the dynamics of ionic liquids are critical, especially for energy applications. In energy-storing devices such as electrical double capacitors, the number of ions immobilized near the wall, which reflects the capacitance, is manifested in an increased fraction of the scattering signal that is perceived as elastic in a QENS measurement. For the ions that remain mobile, the mobility reflects the rate handling. An increased rate handling is manifested in a higher self-diffusivity of ions.266 Note that the fraction of elastic scattering in the signal originating from the attachment of the ions on the surface of the electrodes, which may remain completely static within the sensitivity of the BASIS spectrometer or show some localized motion, contributes to the elastic incoherent scattering factor (EISF), and can be correlated to the capacitance, while the self-diffusivity of ions in the electrolyte determines the rate handling capacity of the supercapacitors. Besides QENS, no technique can provide these two pieces of information from a single measurement. After the success of the very first QENS experiment on an ionic liquid performed at the FOCUS instrument at the SINQ installation,267 many ionic liquid systems have been probed using QENS.264,268,269 To this end, since the energy window and the instrument resolution of BASIS are well matched to examine various dynamic processes, many QENS experiments on bulk and confined ionic liquids have been performed at BASIS.A dynamics study of N,N,N′-tetramethyl guanidinium bis(perfuoroethylsulfonyl)imide ([H2NC(DMA)2][BETI]) as a function of temperature performed at BASIS explored the evolution of dynamics as a function of temperature.17 Two localized dynamics processes, one from the methyl group and another from –NH2, were observed below the melting temperature. Above the melting temperature, two processes, one fast and another slow, were observed. The fast process was attributed to the localized in-cage rattling motion, whereas the slow process was assigned to the long-range translational center of the mass motion of cations.12,17 BASIS's high resolution and wide energy transfer range allowed to capture one additional dynamics process associated with the protons of NH2 or CH2 groups in silver complex-based room-temperature ionic liquids, [Ag(1-pentene)+][Tf2N−] and [Ag(propylamine)2+][Tf2N−].270
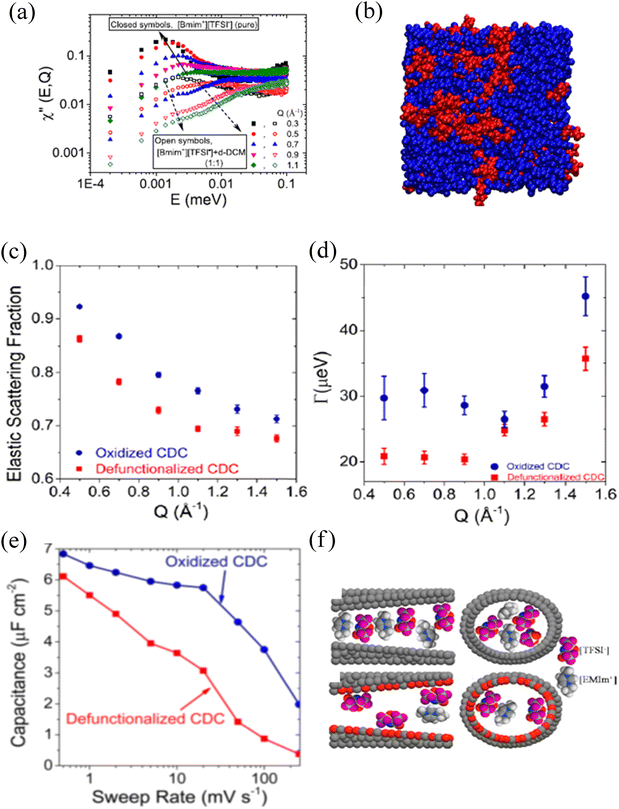
Even though considered designer solvents271 with potential applications as electrolytes in energy-storing devices, ionic liquids suffer significantly from their high viscosity, impacting the mobility of ions. An ionic liquid can be mixed with other organic solvents/salts to improve ion dynamics.272,273 An experiment at BASIS investigated the impact of organic solvent's dipole moment together with the concentration on the mobility of cation in 1-butyl-3-methyl-imidazolium bis-(trifluoromethylsulfonyl), [BMIM+][TFSI−], an ionic liquid.274 A clear nanophase separation, as indicated by the low and high energy transfer peaks of the dynamic susceptibility of QENS data (Fig. 5a), into ionic liquid-rich and solvent-rich phases (Fig. 5b) was observed. Furthermore, the self-diffusivity of the cation with hydrogen was linearly correlated with the dipole moment and the concentration of solvents. Besides the nanophase separation, which is universal for most ionic liquids, linearity on the long-range translational mobility of cation in [BMIM+][TFSI−] was also observed from a dynamic study on a mixture of an ionic liquid with organic solvents of nearly the same dipole moment but of different bulk diffusivities.275 A study at BASIS using 1,3 dimethylimidazolium bis(tri-fluoromethanesulfonyl)imide ([DMIM+][TFSI−]) and Lithium bis(trifluoromethane)sulfonimide (LiTFSI) salt mixture at low temperature allowed observation of quantum tunneling of the methyl groups.276 This phenomenon reflects the rotational potential barriers of methyl groups, which are high and broadly distributed in the disorder system, i.e., in the glassy state. (Dis)appearance of the methyl quantum tunneling peaks as a result of thermal cycling, mixing, and pressure application to investigate glassy and crystalline phases in ionic liquids were also observed at BASIS.277 On the other hand, a QENS study of an ionic liquid under a moderate pressure of 1 GPa at BASIS showed a solidification of the ionic liquid, 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMIM+][TFSI−]). Still, on decompression, ions with significantly reduced mobility, possibly due to the dimerization of ions, were observed.278 Furthermore, polymerized ionic (PolyILs) liquids, which are single-ion conductors having combined properties of ionic liquids and polymers,279,280 have been studied at BASIS to explore the role of segmental dynamics on ionic conductivity. From the QENS study on a series of PolyILs, Bocharova et al. reported that it is not the slow segmental mobility but the amplitude of the faster picosecond dynamics scaled with the ion size that controls the ionic conductivity in PolyILs.281 In addition, dynamics studies at BASIS also revealed a strong coupling between the side chain and localized ion dynamics in thermally polymerized diallylammonium mesylate, P(DAMAH+MsO−), protic ionic liquid membranes with a presence of nanoconfined and bulk-like water at high hydration levels.282
Ionic liquids behave differently in confinement than in their bulk states. Confinement alters the liquids’ physical properties, thereby impacting their applications.283 When used as electrolytes in energy storage devices, morphologies of the confining matrix, i.e., electrodes and interactions between the liquids and the surface of the electrodes, determine electrochemical performances. The surface electrolyte interactions (SEI) determine the amount of the charge absorbed together with the mobility of the ions inside the porous electrodes. The very first QENS experiment on a mesoporous (pore sizes = 8.5 nm) carbon-confined ionic liquid was performed at BASIS to look at the mobility of ions of [BMIM+][TFSI−] ionic liquid.284 Like with other bulk ionic liquids,17,274 they found two dynamic processes corresponding to faster localized and slower long-range translational self-diffusion of cations. However, the mobility of the confined ions is higher with a shorter relaxation time than in the bulk state due to the increased density of ions attached to the wall, leaving fewer ions with lower density in the middle of the pore. A similar observation was made by Chathoth et al.285 on an ionic liquid, [H2NC(DMA)2][BETI], confined in a carbon matrix of comparable pore sizes. However, in this [H2NC(DMA)2][BETI] confined system, they found a slowing down of the localized fast motion as a function of temperature, which they attributed to the structural modification of the absorbed ions on the surface of the wall at higher temperatures.
Modification on the surface chemistries of the carbon matrix influences the mobility of the confined ions. BASIS has contributed to understanding the impact of surface functional groups, pore sizes, and external perturbations on the structure and dynamics of nano-confined ions. Dyatkin et al.286 studied the effect of surface chemistry on the electrochemical preformation of carbon-derived carbon (CDC) electrodes with an ionic liquid, [EMIM+][TFSI−], as an electrolyte. They found an increase in the mobility of ions confined in oxidized CDC surfaces due to the accumulation of more of the cations on the wall next to an anion layer, giving higher EISF (Fig. 5c) and resulting in lower density of the ions in the center of the pore. Therefore, the ions have more freedom to diffuse, which gives much broader half width half maximum (HWHM) of QENS spectra (Fig. 5d). These ions accumulation and faster mobility were correlated with the higher capacitance and improved charging rate (Fig. 5e) in contrast to the electrochemical performance of defunctionalized pores. They also concluded that the surface functionalities influence the orientation of the ions (parallel vs perpendicular, Fig. 5f) on the surfaces, therefore impacting the dynamics. The same group observed higher capacitance in 1-octyl-3-methylimidazolium bis(-trifluoromethylsulfonyl)imide ionic liquid confined in defunctionalized bimodal molybdenum carbide-derived CDCs due to the dominance of the bulk-like behavior of ions present in larger pores.287 Besides the cation size influence,288 faster dynamics of confined cations with a shorter alkyl chain (ethyl) than butyl and hexyl side chains have also been reported from QENS measurements at BASIS.289 However, when the side chain is very long (dodecyl), a dynamic decoupling between the long alkyl chain from the imidazole ring of cations, 1-dodecyl-3-methylimidazolium, confined in ordered mesoporous carbon (OMC) has been reported.290 Effects of the pore size and the applied electric potential on the dynamics of an ionic liquid, [EMIM+][TFSI−], confined in carbon electrodes were also explored at BASIS. The ionic liquid confined in a carbon electrode of 1.5 nm pores showed an irreversible immobilization of the ions on the wall of the electrode after the potential application. However, the reversibility of the ion immobilization on altering the applied voltage was observed on the carbon electrode with larger (6.7 nm) pores.291 This reversibility was rationalized based on the significantly reduced long-range mobility of the ions adsorbed in the 1.5 nm pores under applied electric potential.292
Mixing an ionic liquid with other ionic liquids, organic/inorganic solvents, or some salts has been practiced to increase the ion's mobilities in electrochemical applications. A study performed at BASIS investigated the dynamics of cation in a mixture of two distinct ionic liquids, [EMIM+][TFSI−] and 1-ethyl-3-methylimidazolium tetrafluoroborate ([EMIM+][BF4−]) having common cation but different anions of different sizes in bulk and confined states.293 It was found that, irrespective of the mixing ratio, there was no change in the long-range translational cation mobility in the bulk liquid mixture. However, a higher cation self-diffusivity was observed for a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of [EMIM+][TFSI−]
1 volume ratio of [EMIM+][TFSI−]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [EMIM+][BF4−] confined in an onion-like carbon substrate. This higher mobility was correlated to the attachment of more cations to the carbon substrate wall, which already has a significant accumulation of smaller anions (first layer on the wall), leaving fewer cations with more volume to diffuse away from the wall. Once exposed to optimum humidity, dynamics of the confined ions of an ionic liquid are further increased due to the replacement of the cation by water molecules, which is further facilitated by the nanoporous carbon environment around the ions.294 The effect of the presence of salt on the structure and dynamics of ions in ionic liquids has also been investigated at BASIS. QENS study on two separate mixtures of ([EMIM+][TFSI−])295 and 3-methyl-1-methylimidazolium bis(trifluoromethanesulfonyl)imide ([DMIM+][TFSI−])296 with LiTFSI salt showed a slowing down of cations dynamics, but when a 0.5 M solution of LiTFSI in [EMIM+][TFSI−] was confined in a boron nitride (BN) matrix, an increase in the cation's self-diffusivity was observed.295 Not only with the salt, but polymer-grafted nanoparticles have also been found to impact the dynamics of ionic liquids. A study at BASIS explored the cation dynamics of 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([HMIM+][TFSI−]) mixed with deuterated poly(methyl methacrylate) (d-PMMA)-grafted nanoparticles.297 This study revealed an enhancement in the long-range translational mobility of HMIM+ ions due to the coupling with the polymer-grafted nanoparticles. Even in the absence of salts/nanoparticles, very fast mobility of 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM+][BF4−] ionic liquid confined in block copolymer-based porous carbon fibers (PCFs) has also been reported.298
[EMIM+][BF4−] confined in an onion-like carbon substrate. This higher mobility was correlated to the attachment of more cations to the carbon substrate wall, which already has a significant accumulation of smaller anions (first layer on the wall), leaving fewer cations with more volume to diffuse away from the wall. Once exposed to optimum humidity, dynamics of the confined ions of an ionic liquid are further increased due to the replacement of the cation by water molecules, which is further facilitated by the nanoporous carbon environment around the ions.294 The effect of the presence of salt on the structure and dynamics of ions in ionic liquids has also been investigated at BASIS. QENS study on two separate mixtures of ([EMIM+][TFSI−])295 and 3-methyl-1-methylimidazolium bis(trifluoromethanesulfonyl)imide ([DMIM+][TFSI−])296 with LiTFSI salt showed a slowing down of cations dynamics, but when a 0.5 M solution of LiTFSI in [EMIM+][TFSI−] was confined in a boron nitride (BN) matrix, an increase in the cation's self-diffusivity was observed.295 Not only with the salt, but polymer-grafted nanoparticles have also been found to impact the dynamics of ionic liquids. A study at BASIS explored the cation dynamics of 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([HMIM+][TFSI−]) mixed with deuterated poly(methyl methacrylate) (d-PMMA)-grafted nanoparticles.297 This study revealed an enhancement in the long-range translational mobility of HMIM+ ions due to the coupling with the polymer-grafted nanoparticles. Even in the absence of salts/nanoparticles, very fast mobility of 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM+][BF4−] ionic liquid confined in block copolymer-based porous carbon fibers (PCFs) has also been reported.298
BASIS has also contributed to revealing the behavior of ionic liquids confined in 2D materials, such as MXenes,299 which are immensely promising for energy applications.300 The first QENS experiment to study the dynamics of an ionic liquid, [EMIM+][TFSI−], confined in MXenes was performed at BASIS. These measurements demonstrated the presence of [EMIM+][TFSI−] in the inter-stack gaps of MXene with a half reduction of the self-diffusion coefficient compared to the bulk ionic liquid and revealed a mechanism of increased cation self-diffusivity upon humidity exposure.301 However, pre-intercalation of alkylammonium (AA) cations between MXene layers allowed [EMIM+][TFSI−] enter the interlayer gaps. Once they get between the layers, EMIM+ ions become immobilized/localized, therefore, not showing long-range self-diffusivity within the sensitivity of the spectrometer, as reflected from a QENS measurement performed at BASIS.302 In addition, when [EMIM+][TFSI−] was mixed with acetonitrile and used as an electrolyte, EMIM+ dynamics was found to be at its maximum in 25 wt. % solution, where a maximum number of cations are attached to the MXene electrode surface at a charged state.303
2.5. Organic molecules (bulk and confined)
The structure and dynamics of small organic molecules, hydrocarbons, or other solvents (polar and non-polar) in bulk and confinement are crucial for their practical industrial applications. Organic molecules undergo a phase transition from a liquid state to a supercooled liquid to crystal or glass as a function of temperature. Especially at a temperature below and above the glass transition, the relaxation processes of the organic molecules become complex and still are not understood very well. Similar to aqueous-based liquids discussed above, those relaxation processes were often captured using two components, one for slow, long-range translational motion and another for a fast in-cage rattling dynamics, as illustrated by a typical model fit of such QENS data (Fig. 6). Q-Dependence of the HWHMs of the quasielastic signals identifies the character of these two processes. Novak et al.304 observed those two distinct processes from the QENS data collected at BASIS from cyclohexanol and cyclooctanol (Fig. 6b and c) in plastic crystalline phases. Long-range translational diffusion, together with the faster localized in-cage motions inside the transient cage of the nearest neighbors (Fig. 6a), have been found in a deep eutectic solvent, glyceline, which is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of choline chloride to glycerol. Even though choline is larger than glycerol, BASIS data showed that choline cations experience looser confinement from the neighboring ions due to its superior hydrogen bonding capacity with chloride ions.305 At a sufficiently high temperature, only a single component is required to capture the center-of-mass diffusion of the liquid molecules, as Mamontov et al. demonstrated306 by measuring the diffusion dynamics on a series of organic aromatic liquids as a function of temperature at BASIS. This study reported that the faster cage relaxation and the slower cage-breaking components separate once the temperature is decreased. This separation temperature scales with the boiling temperature of the liquid. The same group also probed molecular dynamics in single-element liquids, gallium, and selenium, at the same spectrometer.11 They found a single long-range jump-type diffusion process in gallium, whereas selenium showed a presence of spatially localized faster β-relaxation and slow long-range α-relaxation. These processes are also generally present in confined water and ionic liquid systems. A spatially localized faster process and a slow long-range diffusion of phenanthrenequinone (PQ) molecules absorbed on the surface of onion-like carbon at high surface coverage have also been reported from a study conducted at BASIS.307 In a low surface coverage, where molecules are not uniformly distributed, both relaxation processes are found to be spatially localized. However, in a series of organic solvents (acetonitrile (ACN), tetrahydrofuran (THF), methanol (MeOH), dimethyl sulfoxide (DMSO), and propylene carbonate (PC)) and their 1 M solution with Lithium bis(trifluoromethane sulfonyl)imide (LiTFSI) measured at BASIS, Osti et al.308 reported a single Fickian-type diffusion process for the organic molecules in bulk with a 50% reduction in the mobility of the organic molecule in the solution. Likewise, in a BASIS study of liquid 1,2,3-triazole by Shinohara et al. a single jump-diffusion process was observed for the proton mobility.309
2 molar ratio of choline chloride to glycerol. Even though choline is larger than glycerol, BASIS data showed that choline cations experience looser confinement from the neighboring ions due to its superior hydrogen bonding capacity with chloride ions.305 At a sufficiently high temperature, only a single component is required to capture the center-of-mass diffusion of the liquid molecules, as Mamontov et al. demonstrated306 by measuring the diffusion dynamics on a series of organic aromatic liquids as a function of temperature at BASIS. This study reported that the faster cage relaxation and the slower cage-breaking components separate once the temperature is decreased. This separation temperature scales with the boiling temperature of the liquid. The same group also probed molecular dynamics in single-element liquids, gallium, and selenium, at the same spectrometer.11 They found a single long-range jump-type diffusion process in gallium, whereas selenium showed a presence of spatially localized faster β-relaxation and slow long-range α-relaxation. These processes are also generally present in confined water and ionic liquid systems. A spatially localized faster process and a slow long-range diffusion of phenanthrenequinone (PQ) molecules absorbed on the surface of onion-like carbon at high surface coverage have also been reported from a study conducted at BASIS.307 In a low surface coverage, where molecules are not uniformly distributed, both relaxation processes are found to be spatially localized. However, in a series of organic solvents (acetonitrile (ACN), tetrahydrofuran (THF), methanol (MeOH), dimethyl sulfoxide (DMSO), and propylene carbonate (PC)) and their 1 M solution with Lithium bis(trifluoromethane sulfonyl)imide (LiTFSI) measured at BASIS, Osti et al.308 reported a single Fickian-type diffusion process for the organic molecules in bulk with a 50% reduction in the mobility of the organic molecule in the solution. Likewise, in a BASIS study of liquid 1,2,3-triazole by Shinohara et al. a single jump-diffusion process was observed for the proton mobility.309
Dynamics in glass-forming molecules, mainly in the region where many fast relaxation processes arise and some get buried under the dominant alpha relaxation peak, give an excess wing on the susceptibility plot at a higher frequency.310,311 Even though the excess wings have been mainly investigated by light scattering and dielectric spectroscopy techniques, QENS performed at BASIS together with neutron spin echo experiments on glycerol revealed the length scale of fast and slow (resulting in an excess wing) secondary processes together with the center of mass relaxations in glass forming glycerol.38 BASIS was employed to explore the faster secondary relaxation process whereas NSE probed the slower structural relaxation process at a low temperature in the order of 100 ns at longer length scales. Note that NSE instruments, which measure I(Q,t) directly, have very high resolution (∼1 neV) compared to backscattering spectrometers including BASIS, and probe the dynamics in the order of nano to microsecond time scales, and therefore are used to explore slow relaxation modes in polymers, colloids, and proteins.312 Because the NSE experiment was performed on protonated sample, it measured the single particle dynamics complementing the single particle dynamics measured at BASIS. Similarly, a separate experiment with glycerol and LiCl–glycerol mixtures contributed to the understanding that the excess wing results from a faster process coming from the density–density fluctuations and some translational motions.37 Furthermore, a blend of 1.1 nm-sized polyhedral oligomeric silsesquioxane (POSS) molecules with glycerol was also found to significantly increase the broadening of the excess wing of the secondary relaxation compared to the amplitude of the structural relaxation at a temperature where both the processes take place.313 However, QENS data collected at BASIS from a strong glass former, Aspirin (acetylsalicylic acid (ASA)), was analyzed using a stretched exponential model, which suggested dynamics fluctuations as the system is brought to its supercooled state.314
The mobilities of organic molecules are greatly impacted when they are in tight confinement. BASIS has contributed to understanding the dynamics of many hydrocarbons (short to long chains) in bulk and confining matrixes of different porosity and surface chemistries under various experimental conditions. An experiment performed at BASIS investigated the diffusion and adsorption of methane on the surface of porous carbon aerogel as a function of pressure.315 The self-diffusion coefficient of methane under confinement was significantly reduced (by two orders of magnitude compared to bulk) with a non-monotonic pressure dependence of mobility due to the differences in the gas-filling mechanism inside micro and mesopores. However, the mobility of confined methane molecules was found to increase after CO2 addition under pressure due to the replacement of methane molecules by CO2 from the surface of the aerogel.316 Furthermore, BASIS has revealed the disorder effects on the tunneling multiplet transition in methane in its solid state II phase317 and the impact of molecular symmetry on the rotational tunneling using partially deuterated methane on the surface of MgO (100).318 Besides methane, many longer-chain hydrocarbon molecules under various conditions have been studied at BASIS. Gautam et al.319 investigated the temperature and pressure-dependent dynamics of propane confined in silica aerogel. They reported a pressure-dominated mobility of propane with a Fickian-like diffusion at low pressure transitioning to a jump-type diffusion at higher pressure, which increases on passing CO2 gas.320 However, a study to understand the influence of water on the dynamics of propane confined on 1.5 nm pores in MCM-41 at BASIS revealed a decrease in the mobility of propane molecules in the micropores due to the replacement of propane molecules by water from the surface, increasing molecular crowding.321 In all of these measurements involving the loading of organic molecules in porous matrices, QENS results have been interpreted without implementing a particular well-detailed simulation model. Even though those studies have demonstrated the spectrometer's capability to explore the self-diffusivity/transport diffusivity of small organic molecules in various types of geometrical confinement, model-based interpretation of QENS results, as summarized by Jobic et al. in their seminal review of the QENS study of diffusion in Zeolites,21 could be more helpful to understand the physics of small molecules in the confinement.
In addition, a QENS experiment at BASIS on covalently attached 1,3-diphenylpropane (DPP) on the walls of mesoporous MCM-41 modified with silyl-aryl-ether showed a localized diffusion inside a sphere of hydrogen atoms, which increased on moving away from the tether point of DPP from the surface modified walls.322 They also reported the highest self-diffusivity of DPP molecules in the largest pores (3 nm) with the highest DPP grafting density, at which the DPP molecules have more freedom to orient near the pore surface, leaving fewer molecules in the pore volume. In molecular metal oxide clusters, BASIS has revealed a severely restricted mobility of ligands due to strong confinement on the head and tail of the ligands resulting from their arrangement inside the cluster.323 In a biocompatible mesoporous silica matrix synthesized using diglycerylsilane (DGS) as a precursor, O’Neill et al.324 studied the dynamics of sodium benzoate and water encapsulated in the matrix using the QENS technique at BASIS. They concluded that benzoate suffers a 4-fold reduction in self-diffusion coefficient compared to its bulk value. However, even though the mobility of water was reduced, it was impacted more by the interaction of water with that of sodium benzoates; therefore, it depends on the compositional variation rather than on the confinement. Another experiment at the same spectrometer probed the molecular motion in a solid nano- to bulk-sized molecular crystal of alkane n-C32H66.325 They observed particle size-dependent phase transition temperatures with localized motion in plastic phases at two time scales, fast and slow, corresponding to uniaxial rotation and conformational modifications of the molecule, respectively.
Solvent-in-salt electrolyte (SISE) systems have gained much attention lately because they have the potential to overcome some of the limitations of current lithium-based batteries.326,327 In a SISE system, solvent dynamics resulting from its interaction with the ions play a major role in the electrochemical behavior. An approach of adding cosolvents to SISE systems to enhance the electrical conductivity by reducing the viscosity has been attempted. An experiment at BASIS explored the microscopic dynamics in LiTFSI salt with acetonitrile solvent in the presence of chloroform as a cosolvent.328 This study observed an increase in the mobility of chemical species resulting in higher conductivity, especially at low temperatures, at varied compositions of chloroform. However, a reduction in the ionic conductivity resulting from an enhancement in aggregate formation has been reported at higher concentrations. In addition, diffusivities of the organic species are found to be higher at low concentrations under confinement. Similarly, using acetone as a cosolvent, they have reported concentration-dependent solvent structures leading to higher conductivities in LiTFSI-Acetonitrile SIS electrolytes.329 In the same SISE systems, an experiment at BASIS evaluated the impact of cosolvents having different dielectric constants on the mobility of acetonitrile together with electrical conductivities. They have reported trends in the self-diffusivity of acetonitrile and conductivity of the electrolytes based on ordered/disordered structures formed depending on the nature of the interactions between Li+ and TFSI− with cosolvent of varied (low, moderate, and high) dielectric constants.330
2.6. Metal hydrides and confined hydrogen
The following section will discuss the diffusion of hydrogen in materials. In metals, protons (H+) are usually the mobile species and in some cases, such as alkali or alkali earth metals, hydride ion (H−) conductivity has been observed.331 QENS cannot differentiate between H+ and H−, thus only knowledge obtained elsewhere about the studied material could reveal this information. In some cases, the answer is not unambiguous, and when literature refers only to hydrogen diffusion or mobility, we will adapt to this terminology as well. Molecular hydrogen (H2) self-diffusivity is discussed at the end of this paragraph in the context of confinement. Metal hydride systems are a fascinating class of materials with diverse features, such as phases with different stoichiometry, electronic and crystal structures, or a mixture of physical and chemical properties. Their chemical bonding can adapt from ionic, to covalent, to metallic, depending on the electronic configuration of the associated metal. Furthermore, they offer a variety of application possibilities, particularly for energy production, e.g., reversible hydrogen storage, as hydride (H−) ion conductors, and moderation in nuclear reactors. QENS is a particularly useful technique for studying metal hydrides and some of their fundamental properties since it is sensitive to hydrogen dynamics on an atomic scale.Alkali and alkali earth metals usually form ionic bonds with hydrogen, their hydrides are thus ionic or saline hydrides. Lithium–beryllium metal hydrides have the highest hydrogen storage capacity by weight among the metal hydrides. LiBeH3 was studied at BASIS332 together with its parent compound, BeH2. Their crystallographic structure has not been determined conclusively, but in the BASIS study, hydrogen hopping mechanisms were observed in both studied materials.
Interestingly, lithium beryllium hydride exhibits a sharp increase in hydrogen mobility above 265 K, interpreted as a hydrogen sublattice disorder. This suggests that a transition so close to ambient temperature could offer invaluable insight into how to influence hydrogen uptake and release in this very lightweight hydrogen storage compound. Similarly, a structural phase transition from orthorhombic to hexagonal phase leads to a vast increase in hydride ion mobility in barium hydride, BaH2.333 In Fig. 7, the energy-resolved “elastic” neutron scattering intensity scan shows a sharp decrease in the elastic intensity at the phase transition temperature, indicating a rapid onset of hydride diffusion. Fig. 8(a) and (b) show the QENS spectra below and above the phase transition, where it can be noted how the width of the QENS component increases significantly above the phase transition temperature. This phase transition can be induced by increasing temperature or pressure. The hydride ion transport mechanism in BaH2 was studied at BASIS at elevated temperatures,334,335 and pressures.336 As shown in Fig. 8(c) and (d), the Chudley–Elliot model was used to describe the hydride ion jump diffusion. Observed jump lengths were found to correspond to H–H distances in the structures. In the orthorhombic phase, some H–H jumps were restricted, while in the hexagonal structure, these jumps were allowed. It is suggested that a similar phase transition, as occurs in BaH2 at high temperature and pressure, could possibly be induced in other metal hydrides by applying pressure or by doping, which could, in turn, lead to fast hydride diffusion. Moreover, metal hydrides have been considered optimal moderator alternatives for nuclear reactors that need higher operation temperatures than where regular water could be used. Various metal hydrides can maintain hydrogen density to temperatures greater than 500 °C. Potential metal hydrides for reactor moderation have been studied at BASIS; ThZr2Hx up to 750 K337 and YH1.87 up to 1173 K.338 YH1.87 was found to be stable up to high temperature, with translational diffusion onset at 1073 K. Hydrogen diffusion took place at lower temperatures in the case of ThZr2Hx. Both studies337,338 contribute to the development of nuclear reactors by understanding the hydrogen mobility in moderator materials. Moreover, dislocation hydrogen diffusion has been studied in palladium (PdHx, x ∼ 10−3),339,340 and steel (AISI 4130).341 Heuser et al.339 found experimental evidence of hydrogen dislocation pipe diffusion in palladium for the first time, which is elevated by one to two orders of magnitude compared to the bulk diffusion. These results were supported and corroborated by ab initio calculations.340 Further, several studies of molecular hydrogen dynamics in nanoporous carbon have been performed at BASIS.342–345
 | ||
| Fig. 7 Elastic intensity as a function of temperature from BaH2 measured at BASIS. Reprinted with permission from334 (Sci. Rep., 2022, 12, 6194). | ||
 | ||
| Fig. 8 The QENS measured for BaH2 at BASIS (a) at T = 710 K, and (b) at T = 850 K. (c) and (d) show the HWHM at measured temperatures modeled with the Chudley-Elliott model. Reprinted with permission from334 (Sci. Rep., 2022, 12, 6194). | ||
The diffusion of nano-confined hydrogen has attracted attention for fundamental and practical reasons, such as H2–D2 separation, catalysis, and hydrogen storage. Contescu et al. studied the dynamics and conversion of spin isomers of molecular hydrogen confined in nanoporous carbon at BASIS.345 Further, they studied the isotope effect on adsorbed hydrogen/deuterium in nanoporous carbon. Deuterium separation from an H2–D2 mixture can be achieved via preferential adsorption at low temperatures on porous materials. BASIS measurements of H2 and D2 in the same nanoporous carbon at temperatures below 40 K demonstrate extreme quantum sieving, with D2 diffusing up to 76 times faster. D2 diffusion is liquidlike, while H2 exhibits jump diffusion. This shows how the intermolecular interactions with the adsorption sites for H2 and D2 are very different due to quantum effects.343 Morris et al.344 studied how tuned pores can strongly enhance local adsorption and pore sizes can be used to tune adsorption characteristics. QENS measurements of molecular hydrogen at BASIS and similar spectrometers, such as OSIRIS,346 can shed light on the fundamental properties of hydrogen. Similar to the earlier neutron backscattering spectrometers, BASIS is well suited to probing the mobility of hydrogen species in hydrides. On the other hand, the mobility of molecular hydrogen in materials, even at very low temperatures, is usually too high for traditional backscattering spectrometers, but not BASIS. Unlike many classes of materials described in the previous sections, BASIS does not necessarily provide groundbreaking measurement capabilities for hydrogen species, the mobility of which could be measured at either neutron traditional backscattering or neutron time-of-flight spectrometers (on the latter class of spectrometers). On the other hand, BASIS can be a one-stop spectrometer for measuring the mobility of any species of hydrogen in materials, either atomic or molecular. Besides, below we will present examples of proton measurements where BASIS characteristics were imperative for capturing multi-component dynamics.
2.7. Solid state ionic conductors
Improved energy applications are needed for the transition towards cleaner renewable energy resources. The major challenge is the lack of efficient and safe materials; thus, developing new, better-performing materials is crucial. The use of advanced characterization techniques is needed to truly gain an understanding of the atomic scale processes that determine the bulk material properties and performance. Neutron scattering is a powerful technique for studying solid materials at the atomic scale since thermal neutrons have energies comparable to the energies of excitations in materials and wavelengths comparable to atomic distances in the solid state. Other techniques, such as infrared or Raman spectroscopy,347 X-ray pair-distribution analysis,348 X-ray absorption,349 or NMR350 could also be used, but they all lack the power neutrons have to penetrate bulk material and interact directly with elements without selection rules.Solid materials exhibiting protonic conductivity are sought for several energy-related applications, such as electrolytes for fuel cells. They have many benefits compared to other types of ion-conducting materials. For instance, oxide ion conductors generally require higher operating temperatures and possible fuel dilution with water vapor, which would lead to lower efficiency. Unlike polymers and other low-temperature materials, solid proton conductors do not require liquid water handling, which could cause electrode poisoning. Understanding the atomic scale mechanisms of proton dynamics in solid-state proton conductors is thus an important objective for improved future applications and for fundamental reasons. Solid oxide proton conductors normally contain protons (H+), but despite the low concentration due to high neutron scattering cross-section for hydrogen, they can still be detected in many samples. Over the past decades, a constant interest to study solid proton conductors by QENS has led for number of articles and book chapters that introduce the concept, offer perspectives, or give an overview.25,351–354
In solid oxides proton, diffusion consists of local reorientations and translational diffusion, which usually occurs as protons jumps through the crystal lattice. Local reorientations have typically residence time on the order of picoseconds, while translational jumps are more often found on the nanosecond scale. Most QENS spectrometers are not capable of measuring such a large spread of residence times, thus, atomic scale picture of proton diffusion remains incomplete. However, BASIS, with its high energy resolution and relatively large dynamic range, allows measurement of processes on both ns and ps timescales. For example, La1−xBa1+xGaO4−x/2 contains tetrahedral units of GaO4, where increasing the barium content at the expense of lanthanum will introduce oxygen vacancies. Protons from a humid atmosphere can be incorporated into the oxygen vacancies and become part of the composition. The material exhibits remarkable ionic conductivities, especially proton conduction at intermediate temperatures. The proton conduction mechanism was studied using impedance spectroscopy, neutron diffraction, and quasielastic neutron scattering.355,356 BASIS measurements were performed up to 500 K, and proton diffusion was found to consist of two steps. Protons jump between GaO4 units (inter-tetrahedral) and within GaO4 units (intra-tetrahedral). The intra-tetrahedral proton jump was found to be the rate-limiting step, and the activation energy was found to be about an order of magnitude higher than that of the inter-tetrahedral jump. Interestingly, both processes were observed in a single measurement. The QENS spectra and data fits are shown in Fig. 9. The narrow component has widths on the order of a few μeV and describes long-range diffusion, while the broader component has widths from about 100 to 200 μeV and corresponds to a localized reorientation of protons. A similar system, Ca-doped LaPO4, was studied at high temperatures up to 500 °C using furnace357 and an insert for humid gas handling to preserve the protonated state of the sample at higher temperatures.358 In this experiment, the sample was first measured in a humid atmosphere. Subsequently, the atmosphere was changed to dry for dehydration of the sample to obtain the background signal. A fast proton jump-diffusion process was observed in this sample with an activation energy of 0.09 eV. Generally, doped perovskites have been studied as potential proton conductors in the past decades. These materials have recently been considered potential hydride ion conductors, such as metal hydride-reduced BaTiO3, which was also studied at BASIS.359 The hydride ions undergo jump-diffusion, and the jump distance depends on the temperature. Ice, which is a common example of a pure proton conductor, was studied at BASIS after doping with HCl.360 This experiment revealed interesting behavior of protons in ice compared to liquid water, namely above 242 K, where the proton diffusion appears ten times faster than liquid water at room temperature.
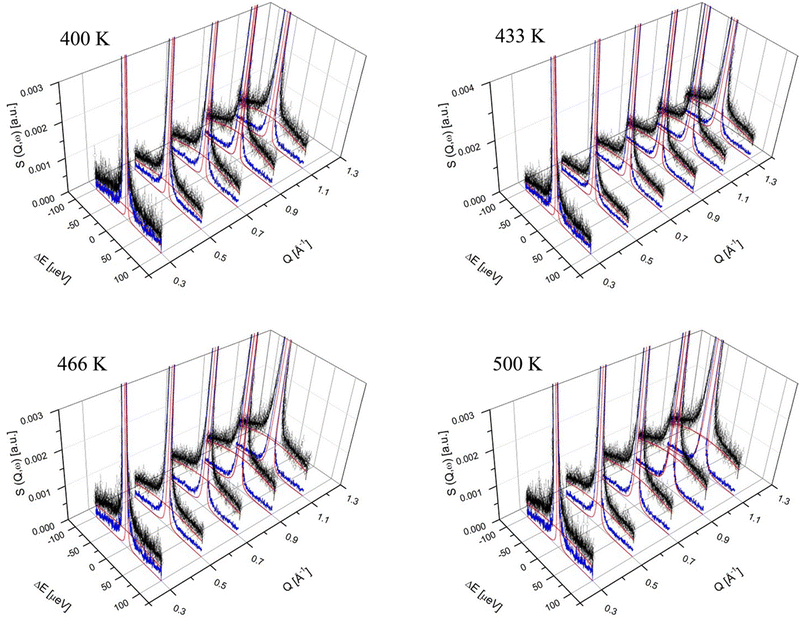 | ||
| Fig. 9 S(Q,ω) of La0.8Ba1.2GaO3.9 at 400, 433, 466, and 500 K. The open circles represent the experimental data. The fit comprises of the elastic peak (blue line) and the two QE components (red lines).355 Reprinted with permission from (Chem. Mater., 2013, 25, 2741–2748). Copyright (2020) American Chemical Society. | ||
Solid-state batteries are pursued as a future solution for energy storage. Liquid lithium-based batteries have been dominating the battery industry, but a need for alternative battery sources is apparent for safety reasons. Solid-state ionic conductors offer safer and possibly more economical options. Development of improved materials is in demand, and an optimal material with high energy density has yet to be discovered. BASIS has been used to study solid ionic conductors over the years, with increasing demand recently. The first study was conducted in 2012 on lithium ion conducting garnet-type oxide.361 This study provided a proof of principle on how diffusion of other ions besides protons could be successfully observed at BASIS. Inspired by that, nearly twenty published studies of solid-state ionic conductors, such as lithium,362–368 sodium,369–374 silver,375 copper376 and oxygen377 have been performed using BASIS. Lithium garnet oxides with general stoichiometry LixA3B2O12 (A and B refer to eight- and six-coordinated cation sites, respectively) are promising superionic conductors for all-solid-state lithium batteries as electrolyte materials. Li self-diffusion in Li5La3Ta2O12 was studied by combining backscattering QENS experiments and MD simulations. The Singwi-Sjölander jump-diffusion model described lithium diffusion, where ions are considered to jump between tetrahedral (24d) and octahedral (48g and 96h) sites. The residence times vary from nanoseconds to picoseconds with increasing temperatures from 400 to 1100 K as the Li jump distance becomes shorter at higher temperatures. A correlative neutron and electron spectroscopy method was used to identify garnet-type cubic Li6.25Al0.25La3Zr2O12 (LLZO) as a potential separation layer to enable the use of lithium metal anode towards high-performance aqueous lithium metal batteries.366,368 In this study, the conduction behavior of Li+ and H+ in H-LLZO (Li6.25−xHxAl0.25)La3Zr2O12 was explicitly differentiated using BASIS. H+ ions were found to be immobile, while Li+ ions maintain the desired mobility in H-LLZO at the operating temperature range of ALBs. Further lithium-ion correlations were investigated in LiAlGeO4 using QENS experiments and AIMD simulations.367 Structural and dynamical features critical to the lithium-ion diffusion process and their tuning were identified. It was concluded that tuning the host-structure flexibility and amorphizations is crucial to enable lithium ions to percolate through semirigid host structures. Besides, amorphous lithium ion conductors such as LixSi and xLi2SO4(1−x)LiPO3 were studied at BASIS.364,365 Sodium ion conductors have recently attracted much attention for their possible use in all-solid-state batteries due to more abundant resources and sodium's lower price than lithium. The first study of sodium ion diffusion at BASIS was published in 2020.374 Combining QENS, impedance spectroscopy, and DFT calculations, this work revealed the origin of distinct activation energies of Na-ion conduction in Na3SbS4 during the phase transition from tetragonal to cubic structure. From the experimental Arrhenius plot, the activation energy dramatically decreased from 0.224 eV for t-Na3SbS4 to 0.036 eV for c-Na3SbS4. Such distinct values of activation energies were shown to be associated with the Na-ion jump-diffusion process in crystalline structures. Cubic Na3SbS4 exhibited a shorter jump length (2.85 Å) and larger self-diffusion coefficient (2.07 × 10−10 m2 s−1) than tetragonal structure (4.83 Å and 1.25 × 10−10 m2 s−1). The sodium ion diffusion mechanism was also investigated in P2-type layered material Nax[Ni1/3Ti2/3]O2 at BASIS in combination with DFT calculations.369 Na ion diffusion behavior can be described as jump diffusion, with average jump lengths around 1.3–1.8 Å at 450–700 K, corresponding to the distance between the neighboring edge-share and face-share sites. Three polymorphic phases of NaAlSiO4 were studied at BASIS:370 nepheline (N-NASO; hexagonal), low-carnegieite (L-NASO; trigonal), and high-carnegieite (H-NASO; cubic). Localized diffusion of Na ions was found in L-NASO and N-NASO, but a long-range diffusion was observed in H-NASO. Excess Na ions in H-NASO enhance the host network flexibility and activate the AlO4/SiO4 tetrahedra rotational modes, thus enabling the long-range diffusion of Na via interstitial sites. While computer simulations have been proven to be very useful tools to support and complement QENS studies on ionic conductivity, also phonon measurements can offer invaluable additional information to understand the ionic conduction process on the atomic scale, as presented in ref. 371 and 373. Strongly anharmonic phonon modes enable Na ion diffusion along the minimum energy pathways in Na3PS4,376 while in Na3ZnGaX4 (X = S, Se),373 Na diffusion is topology-driven and soft phonon mode enabled. Correlations between Na ion diffusion and local and global structure were studied in Na2.9Sb0.9W0.1S4.372 The most recent BASIS study of Na diffusion as a function of interlayer cation ordering was performed on P2-type Na2/3Ni1/3Mn2/3O2 (PNNMO) family of materials.378
Oxygen diffusion was studied for bismuth oxide,377 that upon phase transition at ca. 740 °C becomes a fast ionic conductor. The BASIS measurements at the high-temperature phase show that translational diffusion of ions that scatter neutrons purely coherently, such as oxygen, can be studied by quasielastic neutron scattering. The measured oxygen diffusion jump length agrees with the nearest oxygen-vacancy distance of 2.83 Å. Cu-ion diffusion in the superionic argyrodite Cu7PSe6 was studied with INS and QENS measurements complemented with computer simulations.376 The results show how long-range diffusion is limited by inter-cluster jumps, controlled by selective anharmonic phonons of the crystalline framework. Moreover, scattering techniques and complementary simulations studied two-dimensional type I Ag+ superionic conductors (α-KAg3Se2).375 The QENS measurement shows how Ag+ ions are confined to sub-nanometer sheets. Yet another exotic experiment performed at BASIS involves measuring single-crystal BaTiO3 to study Ti ion dynamics using QENS.379
2.8. Hybrid perovskites
Organic–inorganic hybrid perovskites consist of an inorganic framework of corner-shared octahedra where an organic cation occupies the vacant space between the octahedra. These materials are interesting for possible use in photovoltaics, solid state lighting, and radiation detection. The organic cation dynamics play a critical role in the structure and properties of hybrid perovskites. Thus, QENS studies of these materials have been in demand during the past ten years.380–384 QENS offers a route to investigate the organic cation rotations in perovskites directly. Elastic Incoherent Structure Factor (EISF) can be extracted from the data, which can be modeled to describe the rotational dynamics, as shown in Fig. 10.384 This work represents a typical study of these materials at BASIS, where temperature-dependent QENS was measured in triple-cation (methylammonium-MA, formamidinium-FA, and Cs), lead mixed-halide perovskites as a function of bromide substitution.384 The inclusion of bromine was found to suppress low-energy rotations of FA. Inhibiting FA rotations correlates with a longer-lived carrier lifetime. When the fraction of bromine approaches 0.15 – a composition used extensively in the PSC literature – the fraction of actively rotating FA molecules is suppressed by more than 25% compared to the bromine-free perovskite. In another representative study, organic cation dynamics in layered hybrid halide perovskites (nBA)2PbBr4, (ODA)PbBr4, and (GABA)2 PbBr4 were measured at BASIS.382 Elastic incoherent structure factors were extracted from QENS data and fit by models to extract the dynamic radii. The results showed how the restricted organic cation dynamics caused smaller effective dynamic radii and affected the octahedral out-of-plane tilt angle. The increased tilt angle correlated to observing broadband emission as a single ensemble.2.9. Magnetic and quantum materials
Many studies have been performed at BASIS to shed light on nuclear spin dynamics and better understand magnetism and quantum materials. Fundamental knowledge about the nuclear spins of a system and how they can be manipulated is crucial for the development of spintronics or quantum devices such as quantum computers. Over the years, there has been a constant interest in studying spin dynamics at BASIS, which offers some unique advantages with its high energy resolution and access to low energy modes not accessible with other spectrometers. In addition, BASIS has a superior signal-to-noise-ratio that is essential to observing nuclear spin dynamics that often have rather weak signals.The spin ices have attracted much attention as interesting materials in the framework of frustrated magnetism. In the cubic pyrochlore oxides, A2B2O7 (A is a rare-earth ion, and B is a transition metal ion), both ion species occupy networks of corner-sharing tetrahedra, creating a lattice with frustration effects. When A = Ho, Dy, and B = Ti, Sn spin ice ground state can be formed. The spin ice phase usually occurs around T ∼ 1 K. It is characterized by non-collinear frozen disordered magnetic moments, associated with tetrahedral arrangements of magnetic moments coupled via antiferromagnetic exchange and large residual entropy. BASIS has established itself as a spectrometer where spin dynamics and spin–spin correlations can be studied. Indeed, one of the first experiments and published papers at BASIS was to understand spin correlations in diluted spin ice in Ho2−xLaxTi2O7 in 2008.385 This study showed that the spin–spin correlations are short-range and dynamic above macroscopic freezing. In addition to the pure spin ice, a second, faster relaxation process was observed. Inspired by the first study, a few follow up experiments were performed to understand better spin ice systems at various temperatures and magnetic fields.386,387 Ehlers et al. studied Ho2Ti2O7 and Dy2Ti2O7 and found a single nondispersive excitation at E0 = 26.3 μeV only for the Ho compound. Shown in Fig. 11 are the spectra measured at BASIS for Ho1.6La0.4Ti2O7 at 10 and 100 K.386 Further temperature dependence of the excitations is shown in the insert on the right-hand side. In another excellent example of BASIS capabilities, this figure illustrates the need of wider dynamics range, and high elastic energy resolution is necessary to study the evolution of large quasielastic component and small inelastic excitations simultaneously. Based on these observations, it was identified as an excitation between nuclear spin states, which have been split by a large hyperfine field known to be present in the spin ice compounds.
Upon discovering the hyperfine splitting in the above-mentioned Ho-containing spin ices, several further studies were conducted at BASIS to shed light on this phenomenon. Ho2Sn2O7 was studied388 and compared to other spin ices. The lattice was expanded by 3% relative to Ho2Ti2O7, but no significant changes were observed at the high-temperature properties. Ho2Sn2O7 enters the quantum phase at a somewhat higher temperature than Ho2Ti2O7 and has a more antiferromagnetic character. A weak inelastic mode was observed below 80 K at ±26.3 μeV arising from the Ho nuclear spin transition in a hyperfine field found to be ≈700 T. Chatterji et al. studied HoAl2,389 Ho390 and HoCrO3391,392 at BASIS. For HoAl2, low energy inelastic peaks due to the transitions from hyperfine-split nuclear levels were found at ±25.03 at T = 3 K. With increasing T, the energy continuously decreases and becomes zero at T ≈ 30 K. The energy of these excitations follows the order parameter of the ferromagnetic phase transition.389 A similar study was performed for Ho metal where excitations were found at ±26.59 μeV at T = 3 K. Still, they were preserved until a much higher temperature, namely until T ≈ 130 K.390 These results agreed with the conclusions made for the HoAl2 study, but to confirm the linear relationship for the Ho compounds, measurements on more Ho compounds are needed, especially for those with crystal-field reduced Ho moments. Finally, investigations of low-energy nuclear excitations of the strongly correlated electron compound HoCrO3 were performed.391,392 Peaks at ±22.18 μeV were observed from 1.5 K up to 40 K. A huge quasielastic broadening was observed at temperatures above 40 K. Together with specific heat measurements, this was attributed to the presence of short-range exchange interactions, which is understood to be contributing to the observed ferroelectricity.
Spin glass is a magnetic state characterized by randomness, except in freezing spins at a “freezing temperature” Tf. Spins align in the same direction in ferromagnetic solids, but spin glass is defined as a “disordered” magnetic state where spin states are random. Several studies at BASIS have been performed to understand the spin dynamics in spin glasses.393–396 Valldor et al. studied the transition metal-based oxide YBaCo3FeO7, a structurally related mineral to Swedenborgite SbNaBe4O7, a polar non-centrosymmetric crystal system.393 BASIS studies reveal that the spin correlations start to freeze in this material below ∼50 K. Combined with simulations, these results confirm that the geometric frustration in the Swedenborgite structure promotes quasi-one-dimensional partial order. Cobalt-based oxide compounds have attracted interest over the years due to the richness of the magnetic and electronic properties given by the strong correlation between spin, charge, and orbital degrees of freedom. Garlea et al. studied (BaSr)4−xLa2xCo4O15 (x = 0, 0.5, and 1) samples, and found competing ferro- and antiferromagnetic exchange interactions giving rise to a three-dimensional Heisenberg spin-glass state. On increasing the La concentration, spin-dynamics was slowed down, suggesting a reduction in charge randomness in the doped samples.394 Also, spin glass Tb2Mo2O7 was studied at BASIS, and a low-energy mode at 0.34 meV was measured, with the character of a crystalline electric field excitation.395 Samarakoon et al. experimented to categorize magnetic glassy materials into two distinct classes.396 Neutron scattering measurements were used to determine magnetic structure factor I(q) and to reveal the character of the magnetic nature of studied materials.
An individual example of a successful single crystal experiment at BASIS presents results of Yb2Ti2O7 measured between 0.3 and 2 K.397 This work demonstrates a dynamic scaling relation in the structure factor for inelastic neutron scattering for Yb2Ti2O7. The experimental results and simulations show how multiple-phase competition can have universal consequences beyond the ground state, manifesting in the spin dynamics of a correlated paramagnetic phase. The results suggest that dynamical scaling may be general to systems with competing ground states.
Few other condensed matter systems, including magnetic molecules, have been studied at BASIS. For instance, molecular spin cluster(Cr8)-cubane was measured in a magnetic field and at low temperatures to gain insight into the low-energy magnetic excitation spectrum and the field-induced level crossings.398 A study of the effect of magnetic fields on the methyl rotation in a paramagnetic cobalt(II) complex suggested that methyl groups do not behave as isolated units.399 A curious example of zero-field splitting was observed in naturally occurring MOF-type Stepanovite minerals.400 Furthermore, the evolution of quantum roton in nanoconfined liquid helium has also been studied at BASIS.401
3. Research to address COVID-19 pandemic
After a brief stay-home order issued in mid-March 2020, BASIS resumed operation in mid-April 2020 to carry out research addressing the quickly spreading COVID-19 pandemic caused by the virus SARS-CoV-2. The energy scale of BASIS is well suited for probing dynamics of small molecules thus, the existing drugs considered for repurposing to treat COVID-19 were studied at BASIS as well as two INS spectrometers at SNS, VISON402 and SEQUOIA.403 Besides the mobility of drug molecules in aqueous solutions, the drugs in the powder form (some of them hydrated) were investigated. For the powder samples, BASIS spectra were dominated by the stochastic rotational dynamics of methyl groups. A combination of QENS measurements of stochastic methyl rotations at physiological temperatures with INS measurements of methyl torsional vibrations at cryogenic temperatures provided a powerful cross-reference for probing the activation energies/barrier heights associated with methyl dynamics. In some cases, additional crosschecks could be provided by quantum rotation tunneling peaks, which appeared as very low energy INS peaks visible within the BASIS energy transfer range.At first, an abundantly available and easily accessible antimalaria and immunosuppressant drug hydroxychloroquine sulfate, was measured in various states of disorder introduced by hydration.404 The hydration-introduced disorder resulted in randomization and, on average, a significant reduction of the potential barriers for methyl rotations. Other drugs were initially available only in milligram quantities, and it took several weeks before another anti-inflammatory drug, dexamethasone sodium diphosphate, and an antiviral drug, remdesivir, could be obtained in quantities sufficient for reliable QENS and INS measurements. Again, the hydration-induced disorder was found to reduce the potential barriers for methyl rotations in water-solvable or hygroscopic drugs, sometimes even below the barrier values known for an isolated drug molecule.405 Finally, we studied two more drugs,406 an interleukin- and lipid kinase enzyme-inhibitor, apilimod, and a Ca2+ channel-blocking plant-derived alkaloid hanfangchin A, commonly known as tetrandrine, which have been identified in an extensive screening study of in vitro efficacy against SARS-CoV-2 using remdesivir as a benchmark.407 Interestingly, we found that apilimod and tetrandrine, which were known from the aforementioned screening study to be much more potent antiviral agents against SARS-CoV-2 than remdesivir, had much lower potential barriers for rotations of the most dynamically active methyl groups compared to those in remdesivir. While the main therapeutic action mechanisms are always drug-specific, at the molecular level, the small-amplitude atomic motions such as methyl rotations facilitate exploration of the configurational states of the energy landscape to sample the potentially thermodynamically favorable reaction states.114 Among the many compounds with low potential barriers for methyl rotations,408 only a few would demonstrate any therapeutic effect, but it is conceivable that within a pre-selected class of molecules with the desired therapeutic effect, bioactivity, in general, may benefit from the enhanced methyl dynamics associated with low potential barriers.406 The caveat is that the methyl rotational barriers in drugs in the clinically relevant molecular disorder state in vivo could be very different from the barriers in either drug powders or isolated molecules404,405 and might not be nearly as straightforward to calculate for drug prescreening.
When the Pfizer-BioNTech COVID-19 vaccine became available in 2021, we used BASIS to study the molecular-level dynamics of the vaccine.409 An original unopened vial with vaccine from the cold storage was placed into an indium-sealed outer aluminum sample holder following (1) scraping the vaccine paper label and its sticky residuals off the vial using a scalpel and ethanol and (2) placing a small sheath handmade of a flexible neutron-absorbing cadmium sheet over the top of the vial. These manipulations, performed in dry ice to keep the vaccine cold, were used to prevent exposure to the neutron beam of the hydrogen-rich sticky paper label and the vial rubber plug, which otherwise could have given rise to the QENS signal on their own, unlike the glass vial. The indium-sealed aluminum sample holder with the enclosed original vial containing the vaccine was then stored in dry ice before inserting the sample holder into the pre-cooled to T = 200 K sample environment equipment. Thus, the BASIS experiment commenced on the vaccine in the unopened vial that always remained in cold storage as prescribed by the manufacturer. Following cooling down to the baseline temperature of 20 K, a temperature scan of the “elastic” scattering intensity (the signal integrated over minus 3.7 μeV to plus 3.7 μeV range of the BASIS spectra) commenced at a heating rate of 5 K per hour. The data recorded at 2 K intervals (about every 24 min) were plotted using open symbols as one can see in the main panel of Fig. 12. While spikes in the “elastic” intensity might be indicative of partial sample crystallization on warming up from the low-temperature amorphous state that precedes melting,10 the sharp drops at 260 and 273 K indicated two-stage melting of the vaccine. The drop at 273 K indicated the melting of the bulk-like aqueous phase, whereas the drop at 260 K was due to the melting of another phase. This could be either a lipid phase or an aqueous-based phase with ca. 13 K melting point depression that might arise from the effect of water confinement (e.g., in vesicles) and/or the presence of solutes in water (e.g., sucrose). In any case, it was evident that the original vaccine from cold storage in an unopened vial had a two-phase morphology, with one of the phases being bulk-like water. Once the vaccine in the vial has been re-frozen following the melting, another heating cycle, as represented by the filled symbols in the main panel of Fig. 12, showed no melting step at 260 K, thus indicating the disappearance of the two-phase vaccine morphology. Likewise, the melted and re-frozen vaccine showed no signs of crystallization when warming up, unlike the original vaccine. The irreversible changes in the morphology and dynamics that the vaccine underwent upon melting and refreezing were corroborated by the INS data (Fig. 12 inset), showing the development of the very soft vibrational modes, below 3 meV, indicative of the molecular-level softening that can be expected to correlate inversely with the cold storage vaccine stability. Because the vaccine needs to be melted before dilution and administration, it is evident that the irreversible changes to the vaccine morphology upon melting do not lead by themselves to quick degradation of the active mRNA component. However, our results suggest that even prompt re-freezing of the vaccine after melting could not be used to extend its cold storage lifetime because such re-frozen vaccine already exhibits increased softness at the molecular level. This example showcases the remarkable capability of neutron scattering to probe pharmaceuticals stored in the original unopened containers in a non-destructive manner. This is because the interaction of a neutron beam at spectrometers such as BASIS is much stronger with the hydrogen-bearing contents than with the non-hydrogen-bearing container walls. Likewise, optical transparency of the container would not be necessary for neutron scattering studies of the contents. At the same time, the interaction of low-energy neutron probes with the sample is predominantly through scattering rather than ionization, which precludes possible probe damage to sensitive samples.
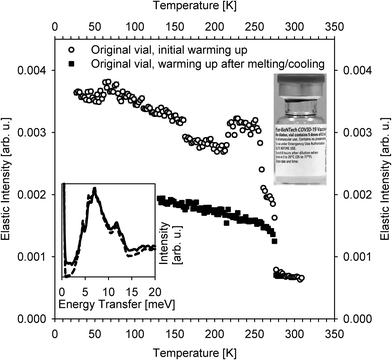 | ||
| Fig. 12 INS and QENS-derived data collected from the Pfizer-BioNTech COVID-19 vaccine kept in cold storage in an unopened vial, as presented in the inset image. The measurements were described in ref. 409. Main panel. QENS spectra-derived “elastic” scattering intensities measured at BASIS as a function of temperature on warming up from the as-received vaccine in a vial (open symbols) and vaccine in the same vial after melting/freezing (closed symbols). Inset. Zoomed-in INS spectra (the truncated elastic peak maxima have been normalized to unity) measured at VISION at 5 K from the as-received vaccine (dashed line) and the vaccine after melting/freezing (solid line). The effect of melting/freezing on the QENS and INS spectra is evident. | ||
4. Capabilities, limitations, and outlook
BASIS has been the first neutron backscattering spectrometer built at a spallation neutron source to perform QENS using Si111 crystal analyzers. This setup allows for high energy resolution in the micro-electron-volt range, approaching the resolution typically achieved with silicon crystal analyzers at reactor sources and a wide energy transfer range provided by spallation sources. The current specification of Si111-based measurement modes available at BASIS includes the continuous energy transfer ranges of −100 μeV to +100 μeV, −200 μeV to +200 μeV, and −100 μeV to +500 μeV (the latter two options come with one-half count rate), all with an energy resolution of ca. 3.5 μeV (full width at half maximum) and 0.2 Å−1 < Q < 2.0 Å−1 range of accessible momentum transfer. More relevant to the user community is a notion that BASIS is capable of probing dynamics on ca. picosecond to nanosecond time scale and ca. Angstrom to nanometer length scale. Since its inclusion in the user program in 2007, BASIS has been in high demand and has delivered valuable scientific output. It offers the scientific community access to information on dynamics across a diverse range of materials, such as soft matter, energy materials, catalysis, environmental sciences, and quantum/magnetic materials. The results of BASIS studies have contributed to the development of materials with optimized properties for their broad range of applications.The unusually broad for a neutron backscattering spectrometer scope of science addressed at BASIS may give the impression that studies of any material exhibiting dynamics on a pico- to nano-second time scale would benefit from the capabilities of this or some other QENS dedicated spectrometer. To some extent, this is true. However, as with any analysis technique, QENS has its limitations. One such limitation is fundamental and associated with the neutron scattering cross-sections of elements. The large, predominantly incoherent, neutron scattering cross-sections of hydrogen enable studies of hydrogen-bearing molecules in heavy elements matrices but, on the other hand, effectively precludes probing the dynamics of ions, such as Li, Na, K, and others, except in very dry, hydrogen-free materials. This problem is not readily mitigated even by using deuterated solvents. Indirect studies of solvated ion dynamics by measuring the QENS signal from the water molecules in the immediate hydration shells have been practiced for decades,410,411 but direct QENS measurements of ions in the presence of a solvent remain challenging. Likewise, QENS measurements of proton hopping in liquids, even in deuterated form, may be possible but very challenging.412 QENS experiments involving polarization analysis to distinguish between the single-particles and collective dynamics remain difficult and time-consuming.413,414 At the same time, there is a growing body of evidence that polarization-based QENS analysis may be imperative for the accurate interpretation of scattering data in systems ranging from water415,416 and organic solvents417 to proteins.418
However, many more of the current limitations arise from the present state of instrumentation rather than fundamentals. For example, reactor-based backscattering spectrometers, besides having somewhat better energy resolution, may continue providing better quality data for the temperature-dependent scans of the energy-resolved “elastic” scattering intensity due to their ability to “condense” a band of incident neutron energies into the narrow elastic intensity line.2 This type of measurements, which provides the data of impressive quality in systems with multiple distinct freezing points55,118–120,419 are as not easily performed at BASIS and other spallation source-based backscattering spectrometers. Besides, challenges encountered with the timely measurements at BASIS of the emergent candidates for COVID-19 treatment, initially available only in milligram quantities, illustrate the need for improved incident neutron flux and the reduced beam size for studies of small samples. When the candidate drugs became available in the tens and hundreds of milligram quantities, BASIS measurements faced additional challenges associated with studies of molecules with several methyl groups with different rotation barriers, which would be entering and exiting the spectrometer's energy transfer window at vastly different temperatures.406 In fact, many, if not most, measurements of protein dynamics at BASIS historically had to be combined with the measurements at other spectrometers to extend the accessible energy transfer window. Neutron backscattering spectrometers with an even larger accessible energy transfer range than BASIS have already become operational420–423 or are expected to become operational in several years,424,425 although BASIS at present retains the advantage of providing the broadest continuous range of accessible energy transfers. Nevertheless, BASIS, VISION, and SEQUOIA measurements of solvable drugs,404 in which hydrated powders might be undergoing time-dependent changes, further illustrate the compelling need to be able to perform not only the broadest range QENS but also simultaneous INS measurements from the sample in the given state. It is advantageous to perform simultaneous INS measurements in the “fingerprint” range of intramolecular vibrations, but even more essential to be able to measure, simultaneously with the QENS regime, the intermolecular INS excitations in the meV range, which blend with the stochastic dynamics measured by QENS. The intermolecular vibrations and stochastic motions can be naturally analyzed together in simulations,40,41 but at present, they must be measured at separate neutron spectrometers. To this end, the newly proposed BWAVES spectrometer for the SNS Second Target Station will cover energy transfers from ca. 10 μeV to ca. 1000 meV, enabling simultaneous measurement of QENS and INS spectra for samples available in milligram or microliter quantities.426,427 BWAVES is also expected to feature open access to the sample position, which is unusual among the existing QENS-dedicated spectrometers, including BASIS. As illustrated by Fig. 13, which shows the BASIS vessel outlook common among neutron backscattering spectrometers, the sample position is buried deep inside the vacuum vessel and is not easily accessible except from a meter or more above, where the flange-supported sample and sample environment equipment is installed. First time users of a neutron backscattering spectrometer such as BASIS, or a vibrational INS spectrometer such as VISION, who might have previously enjoyed open-geometry tabletop sample access at neutron reflectometers or small-angle diffractometers, are often surprised and somewhat disappointed to learn the any non-standard sample environment equipment must be extremely compact and custom-designed to be suspended on a long stick. Many types of complex sample environment equipment prove to be too bulky for such a restrictive sample access. However, there will be a wide-open access to the sample position at BWAVES. This will enable the application of versatile sample probes and stimuli as well as new sample environments simultaneously with neutron scattering measurements, further expanding the already broad scope of materials, systems, and phenomena presently amenable to studies by QENS.
Author contributions
All authors contributed equally to the manuscript.Data availability
No primary research results, software, or code have been included, and no new data were generated or analyzed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The neutron scattering experiments at Oak Ridge National Laboratory's (ORNL) Spallation Neutron Source were supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy (DOE). The beam time was allocated to BASIS on proposal number IPTS-18226. ORNL is managed by UT-Battelle, LLC, for the U.S. DOE under Contract No. DE-AC05-00OR22725.Notes and references
- B. Frick, A. Magerl, Y. Blanc and R. Rebesco, Phys. B, 1997, 234, 1177–1179 CrossRef.
- A. Meyer, R. M. Dimeo, P. M. Gehring and D. A. Neumann, Rev. Sci. Instrum., 2003, 74, 2759–2777 CrossRef CAS.
- J. Wuttke, A. Budwig, M. Drochner, H. Kämmerling, F. J. Kayser, H. Kleines, V. Ossovyi, L. C. Pardo, M. Prager, D. Richter, G. J. Schneider, H. Schneider and S. Staringer, Rev. Sci. Instrum., 2012, 83, 075109 CrossRef PubMed.
- C. J. Carlile and M. A. Adams, Phys. B, 1992, 182, 431–440 CrossRef CAS.
- M. T. F. Telling, S. I. Campbell, D. D. Abbley, D. A. Cragg, J. J. P. Balchin and C. J. Carlile, Appl. Phys. A: Mater. Sci. Process., 2002, 74, S61–S63 CrossRef CAS.
- M. T. F. Telling and K. H. Andersen, Phys. Chem. Chem. Phys., 2005, 7, 1255–1261 RSC.
- T. E. Mason, D. Abernathy, I. Anderson, J. Ankner, T. Egami, G. Ehlers, A. Ekkebus, G. Granroth, M. Hagen, K. Herwig, J. Hodges, C. Hoffmann, C. Horak, L. Horton, F. Klose, J. Larese, A. Mesecar, D. Myles, J. Neuefeind, M. Ohl, C. Tulk, X. L. Wang and J. Zhao, Phys. B-Condens. Matter, 2006, 385–386, 955–960 CrossRef CAS.
- K. W. Herwig and W. S. Keener, Appl. Phys. A: Mater. Sci. Process., 2002, 74, S1592–S1594 CrossRef CAS.
- E. Mamontov and K. W. Herwig, Rev. Sci. Instrum., 2011, 82, 085109 CrossRef CAS PubMed.
- E. Mamontov, H. Luo and S. Dai, J. Phys. Chem. B, 2009, 113, 159–169 CrossRef CAS PubMed.
- E. Mamontov, Chem. Phys. Lett., 2012, 530, 55–60 CrossRef CAS.
- E. Mamontov, R. W. Smith, J. J. Billings and A. J. Ramirez-Cuesta, Phys. B-Condens. Matter, 2019, 566, 50–54 CrossRef CAS.
- J. Qvist, H. Schober and B. Halle, J. Chem. Phys., 2011, 134, 144508 CrossRef PubMed.
- M. Bee, Quasielastic Neutron Scattering: Principles and Applications in Solid State Chemistry, Biology, and Materials Science, Adam Hilger, Bristol, 1998 Search PubMed.
- M. Kruteva, Adsorption, 2021, 27, 875–889 CrossRef CAS.
- N. C. Osti and E. Mamontov, Sustainable Energy Fuels, 2020, 4, 1554–1576 RSC.
- E. Mamontov, H. M. Luo and S. Dai, J. Phys. Chem. B, 2009, 113, 159–169 CrossRef CAS PubMed.
- D. L. Price, O. Borodin, M. Gonzalez, M. Kofu, K. Shibata, T. Yamada, O. Yamamuro and M. L. Saboungi, J. Phys. Chem. Lett., 2017, 8, 715–719 CrossRef CAS PubMed.
- Z. D. Deng and K. A. Mauritz, Macromolecules, 1992, 25, 2739–2745 CrossRef.
- I. Popov, R. L. Sacci, N. C. Sanders, R. A. Matsumoto, M. W. Thompson, N. C. Osti, T. Kobayashi, M. Tyagi, E. Mamontov, M. Pruski, P. T. Cummings and A. P. Sokolov, J. Phys. Chem. C, 2020, 124, 8457–8466 CrossRef CAS.
- H. Jobic and D. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- Q. Berrod, K. Lagrené, J. Ollivier and J.-M. Zanotti, EPJ Web Conf., 2018, 188, 05001 CrossRef.
- J. P. Embs, F. Juranyi and R. Hempelmann, Z. Phys. Chem., 2010, 224, 5–32 CrossRef CAS.
- M. T. F. Telling, A Practical Guide to Quasi-elastic Neutron Scattering, Royal Society of Chemistry, 2020 Search PubMed.
- R. Hempelmann, Structure and Diffusivity in Proton-Conducting Membranes Studied by Quasielastic Neutron Scattering, Wiley, 2012 Search PubMed.
- D. Laage, J. Phys. Chem. B, 2009, 113, 2684–2687 CrossRef CAS PubMed.
- D. Laage and W. Thompson, J. Chem. Phys., 2012, 136, 044513 CrossRef PubMed.
- A. Yahya, L. X. Tan, S. Perticaroli, E. Mamontov, D. Pajerowski, J. C. Neuefeind, G. Ehlers and J. D. Nickels, Phys. Chem. Chem. Phys., 2020, 22, 9494–9502 RSC.
- J. Teixeira, M. C. Bellissentfunel, S. H. Chen and A. J. Dianoux, Phys. Rev. A, 1985, 31, 1913–1917 CrossRef CAS PubMed.
- M. C. Bellissentfunel, S. H. Chen and J. M. Zanotti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4558–4569 CrossRef CAS PubMed.
- J. M. Zanotti, M. C. Bellissent-Funel and S. H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 3084–3093 CrossRef CAS.
- J. M. Borreguero and E. Mamontov, J. Phys. Chem. B, 2017, 121, 4168–4173 CrossRef CAS PubMed.
- E. Mamontov and X.-q Chu, Phys. Chem. Chem. Phys., 2012, 14, 11573–11588 RSC.
- C. A. Angell, Science, 1995, 267, 1924–1935 CrossRef CAS PubMed.
- E. Mamontov and M. Ohl, Phys. Chem. Chem. Phys., 2013, 15, 10732–10739 RSC.
- E. Mamontov, P. Zolnierczuk and M. Ohl, Phys. Chem. Chem. Phys., 2015, 17, 4466–4471 RSC.
- S. Gupta, N. Arend, P. Lunkenheimer, A. Loidl, L. Stingaciu, N. Jalarvo, E. Mamontov and M. Ohl, Eur. Phys. J. E, 2015, 38, 1–9 CrossRef PubMed.
- S. Gupta, E. Mamontov, N. Jalarvo, L. Stingaciu and M. Ohl, Eur. Phys. J. E, 2016, 39, 40 CrossRef CAS PubMed.
- M. Nakanishi, P. Griffin, E. Mamontov and A. P. Sokolov, J. Chem. Phys., 2012, 136, 124512 CrossRef PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626–4641 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 4134–4153 CrossRef CAS PubMed.
- E. Mamontov and H. O'Neill, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 3513–3519 CrossRef CAS PubMed.
- E. Mamontov, J. Phys. Chem. B, 2009, 113, 14073–14078 CrossRef CAS PubMed.
- E. Mamontov, A. De Francesco, F. Formisano, A. Laloni, L. Sani, B. M. Leu, A. H. Said and A. I. Kolesnikov, J. Phys.: Condens. Matter, 2012, 24, 064102 CrossRef CAS PubMed.
- N. C. Osti, A. Cote, E. Mamontov, A. Ramirez-Cuesta, D. J. Wesolowski and S. O. Diallo, Chem. Phys., 2016, 465, 1–8 CrossRef.
- E. Mamontov, D. J. Wesolowski, L. Vlcek, P. T. Cummings, J. Rosenqvist, W. Wang and D. R. Cole, J. Phys. Chem. C, 2008, 112, 12334–12341 CrossRef CAS.
- X.-Q. Chu, G. Ehlers, E. Mamontov, A. Podlesnyak, W. Wang and D. J. Wesolowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031505 CrossRef PubMed.
- T. T. Liu, S. Gautam, H. W. Wang, L. M. Anovitz, E. Mamontov, L. F. Allard and D. R. Cole, Phys. Chem. Chem. Phys., 2018, 20, 27822–27829 RSC.
- C. E. Bertrand, K.-H. Liu, E. Mamontov and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042312 CrossRef CAS PubMed.
- E. Mamontov, L. Vlcek, D. J. Wesolowski, P. T. Cummings, J. Rosenqvist, W. Wang, D. R. Cole, L. M. Anovitz and G. Gasparovic, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051504 CrossRef PubMed.
- E. Mamontov, J. Chem. Phys., 2005, 123, 171101 CrossRef CAS PubMed.
- E. Mamontov, H. O'Neill, Q. Zhang, W. Wang and D. J. Wesolowski, J. Phys.: Condens. Matter, 2012, 24, 064104 CrossRef CAS PubMed.
- A. G. Stack, J. M. Borreguero, T. R. Prisk, E. Mamontov, H.-W. Wang, L. Vlcek and D. J. Wesolowski, Phys. Chem. Chem. Phys., 2016, 18, 28819–28828 RSC.
- N. Rampal, H. W. Wang, A. B. Brady, J. M. Borreguero, D. Biriukov, E. Mamontov and A. G. Stack, RSC Adv., 2024, 14, 15743–15754 RSC.
- J. R. Torres, Z. N. Buck, H. Kaiser, E. Mamontov, M. Tyagi, F. Y. Hansen, K. W. Herwig, L. Daemen, M. K. Kidder and H. Taub, AIP Adv., 2022, 12, 065124 CrossRef CAS.
- Y. Zhang, M. Lagi, F. Ridi, E. Fratini, P. Baglioni, E. Mamontov and S. H. Chen, J. Phys.: Condens. Matter., 2008, 20, 504102 Search PubMed.
- S. H. Chen, Y. Zhang, M. Lagi, S. H. Chong, P. Baglioni and F. Mallamace, J. Phys.: Condens. Matter., 2009, 21, 504102 CrossRef CAS PubMed.
- Y. Zhang, M. Lagi, E. Fratini, P. Baglioni, E. Mamontov and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 040201 CrossRef PubMed.
- S. H. Chen, Y. Zhang, M. Lagi, X. Q. Chu, L. Liu, A. Faraone, E. Fratini and P. Baglioni, Z. Phys. Chem., 2010, 224, 109–131 CrossRef CAS.
- H. Li, E. Fratini, W.-S. Chiang, P. Baglioni, E. Mamontov and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061505 CrossRef PubMed.
- K. Kupwade-Patil, S. O. Diallo, D. Z. Hossain, M. R. Islam and E. N. Allouche, Constr. Build. Mater., 2016, 120, 181–188 CrossRef CAS.
- Z. Yi, P. N. Deng, L. L. Zhang and H. Li, Chin. Phys. B, 2016, 25, 106401 CrossRef.
- P. N. Deng, Z. Yi, L. L. Zhang and H. Li, Acta Phys. Sin., 2016, 65, 106101 CrossRef.
- P. Le, E. Fratini, K. Ito, Z. Wang, E. Mamontov, P. Baglioni and S.-H. Chen, J. Colloid Interface Sci., 2016, 469, 157–163 CrossRef CAS PubMed.
- P. Le, E. Fratini, L. Zhang, K. Ito, E. Mamontov, P. Baglioni and S.-H. Chen, J. Phys. Chem. C, 2017, 121, 12826–12833 CrossRef CAS.
- P. Le, E. Fratini and S. H. Chen, Colloids Surf., B, 2018, 168, 187–192 CrossRef CAS PubMed.
- Y. H. Chen, C. X. Xiao, H. Li, E. Fratini, P. Baglioni and S. H. Chen, Phys. B-Condens. Matter, 2022, 627, 413542 CrossRef CAS.
- P. S. Le, E. Fratini, L. L. Zhang, K. Ito, E. Mamontov, P. Baglioni and S. H. Chen, J. Phys. Chem. C, 2017, 121, 12826–12833 CrossRef CAS.
- T. Wang, R. T. Pan, M. L. Martins, J. L. Cui, Z. N. Huang, B. P. Thapaliya, C. L. Do-Thanh, M. S. Zhou, J. T. Fan, Z. Z. Yang, M. F. Chi, T. Kobayashi, J. Z. Wu, E. Mamontov and S. Dai, Nat. Commun., 2023, 14, 4607 CrossRef CAS PubMed.
- S. M. Chathoth, E. Mamontov, A. I. Kolesnikov, Y. Gogotsi and D. J. Wesolowski, EPL, 2011, 95, 56001 CrossRef.
- S. O. Diallo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012312 CrossRef CAS PubMed.
- S. O. Diallo, L. Vlcek, E. Mamontov, J. K. Keum, J. Chen, J. S. Hayes, Jr. and A. A. Chialvo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022124 CrossRef CAS PubMed.
- E. Mamontov, Y. Yue, J. Bahadur, J. Guo, C. I. Contescu, N. C. Gallego and Y. B. Melnichenko, Carbon, 2017, 111, 705–712 CrossRef CAS.
- S. O. Diallo, M. Jazdzewska, J. C. Palmer, E. Mamontov, K. E. Gubbins and M. Sliwinska-Bartkowiak, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022316 CrossRef CAS PubMed.
- G. R. Acharya, M. Tyagi, E. Mamontov and P. M. Hoffmann, J. Phys. Chem. B, 2023, 127, 7384–7393 CrossRef CAS PubMed.
- R. Ignazzi, W. P. Gates, S. Diallo, D. H. Yu, F. Juranyi, F. Natali and H. N. Bordallo, J. Phys. Chem. C, 2017, 121, 23582–23591 CrossRef CAS.
- N. C. Osti, M. Naguib, A. Ostadhossein, Y. Xie, P. R. C. Kent, B. Dyatkin, G. Rother, W. T. Heller, A. C. T. van Duin, Y. Gogotsi and E. Mamontov, ACS Appl. Mater. Interfaces, 2016, 8, 8859–8863 CrossRef CAS PubMed.
- M. L. Martins, T. S. Mathis, X. H. Wang, L. L. Daemen, Y. Gogotsi and E. Mamontov, Phys. Rev. Mater, 2022, 6, 034001 CrossRef CAS.
- K. Ganeshan, Y. K. Shin, N. C. Osti, Y. Sun, K. Prenger, M. Naguib, M. Tyagi, E. Mamontov, D. E. Jiang and A. C. T. van Duin, ACS Appl. Mater. Interfaces, 2020, 12, 58378–58389 CrossRef CAS PubMed.
- N. C. Osti, M. Naguib, K. Ganeshan, Y. K. Shin, A. Ostadhossein, A. C. T. van Duin, Y. Q. Cheng, L. L. Daemen, Y. Gogotsi, E. Mamontov and A. I. Kolesnikov, Phys. Rev. Mater, 2017, 1, 8 Search PubMed.
- S. O. Diallo, E. Mamontov, W. Nobuo, S. Inagaki and Y. Fukushima, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021506 CrossRef CAS PubMed.
- S. Diallo, E. Mamontov, A. Podlesnyak, G. Ehlers, N. Wada, S. Inagaki and Y. Fukushima, J. Phys. Soc. Jpn., 2013, 82, SA007 CrossRef.
- F. Yang, K.-U. Hess, T. Unruh, E. Mamontov, D. B. Dingwell and A. Meyer, Chem. Geol., 2017, 461, 152–159 CrossRef CAS.
- N. C. Osti, B. P. Thapaliya, S. Dai, M. Tyagi and E. Mamontov, J. Phys. Chem. Lett., 2021, 12, 4038–4044 CrossRef CAS PubMed.
- H. O'Neill, S. V. Pingali, L. Petridis, J. H. He, E. Mamontov, L. Hong, V. Urban, B. Evans, P. Langan, J. C. Smith and B. H. Davison, Sci. Rep., 2017, 7, 13 CrossRef PubMed.
- Z. Zhang, M. Ohl, S. O. Diallo, N. H. Jalarvo, K. Hong, Y. Han, G. S. Smith and C. Do, Phys. Rev. Lett., 2015, 115, 198301 CrossRef PubMed.
- N. C. Osti, T. N. Etampawala, U. M. Shrestha, D. Aryal, M. Tyagi, S. O. Diallo, E. Mamontov, C. J. Cornelius and D. Perahia, J. Chem. Phys, 2016, 145, 224901 CrossRef CAS PubMed.
- J. P. Melchior and N. H. Jalarvo, J. Phys. Chem. C, 2019, 123, 14195–14206 CrossRef CAS.
- B. Trusty, S. Berens, A. Yahya, J. C. Fang, S. Barber, A. P. Angelopoulos, J. D. Nickels and S. Vasenkov, Phys. Chem. Chem. Phys., 2022, 24, 10069–10078 RSC.
- G. L. Jackson, S. Mantha, S. A. Kim, S. O. Diallo, K. W. Herwig, A. Yethiraj and M. K. Mahanthappa, J. Phys. Chem. B, 2018, 122, 10031–10043 CrossRef CAS PubMed.
- G. L. Jackson, S. A. Kim, A. Jayaraman, S. O. Diallo and M. K. Mahanthappa, J. Phys. Chem. B, 2020, 124, 1495–1508 CrossRef CAS PubMed.
- T. L. Spehr, B. Frick, M. Zamponi and B. Stühn, Soft Matter, 2011, 7, 5745–5755 RSC.
- I. Popov, Z. H. Zhu, A. R. Young-Gonzales, R. L. Sacci, E. Mamontov, C. Gainaru, S. J. Paddison and A. P. Sokolov, Commun. Chem., 2023, 6, 77 CrossRef CAS PubMed.
- T. R. Graham, D. Semrouni, E. Mamontov, A. J. Ramirez-Cuesta, K. Page, A. Clark, G. K. Schenter, C. I. Pearce, A. G. Stack and H. W. Wang, J. Phys. Chem. B, 2018, 122, 12097–12106 CrossRef CAS PubMed.
- H. W. Wang, T. R. Graham, E. Mamontov, K. Page, A. G. Stack and C. I. Pearce, J. Phys. Chem. Lett., 2019, 10, 3318–3325 CrossRef CAS PubMed.
- P. Ben Ishai, E. Mamontov, J. D. Nickels and A. P. Sokolov, J. Phys. Chem. B, 2013, 117, 7724–7728 CrossRef CAS PubMed.
- P. Luo, Y. Q. Zhai, E. Senses, E. Mamontov, G. Y. Xu and A. Faraone, J. Phys. Chem. Lett., 2020, 11, 8970–8975 CrossRef CAS PubMed.
- T. R. Prisk, C. Hoffmann, A. I. Kolesnikov, E. Mamontov, A. A. Podlesnyak, X. Wang, P. R. C. Kent and L. M. Anovitz, Phys. Rev. Lett., 2018, 120, 6 CrossRef PubMed.
- A. Faraone, E. Fratini, S. Garai, A. Mueller, M. Tyagi, T. Jenkins, E. Mamontov, R. L. Paul, J. R. D. Copley and P. Baglioni, J. Phys. Chem. C, 2014, 118, 13300–13312 CrossRef CAS.
- A. Miskowiec, M. C. Kirkegaard, A. Huq, E. Mamontov, K. W. Herwig, L. Trowbridge, A. Rondinone and B. Anderson, J. Phys. Chem. A, 2015, 119, 11900–11910 CrossRef CAS PubMed.
- A. Miskowiec, M. C. Kirkegaard, K. W. Herwig, L. Trowbridge, E. Mamontov and B. Anderson, J. Appl. Phys., 2016, 119, 094308 CrossRef.
- A. Miskowiec, B. B. Anderson, A. Huq, E. Mamontov, K. W. Herwig, L. Trowbridge and A. Rondinone, Mol. Phys., 2016, 114, 61–71 CrossRef CAS.
- P. Yin, B. Wu, E. Mamontov, L. L. Daemen, Y. Cheng, T. Lo, S. Seifert, K. Hong, P. V. Bonnesen, J. K. Keum and A. J. Ramirez-Cuesta, J. Am. Chem. Soc., 2016, 138, 2638–2643 CrossRef CAS PubMed.
- J. B. Mitchell, N. R. Geise, A. R. Paterson, N. C. Osti, Y. Y. L. Sun, S. Fleischmann, R. Zhang, L. A. Madsen, M. F. Toney, D. E. Jiang, A. I. Kolesnikov, E. Mamontov and V. Augustyn, ACS Energy Lett., 2019, 4, 2805–2812 CrossRef CAS.
- S. Fleischmann, Y. Y. L. Sun, N. C. Osti, R. C. Wang, E. Mamontov, D. E. Jiang and V. Augustyn, J. Mater. Chem. A, 2020, 8, 412–421 RSC.
- J. B. Mitchell, M. Chagnot and V. Augustyn, Annu. Rev. Mater. Res., 2023, 53, 1–23 CrossRef CAS.
- L. M. Anovitz, E. Mamontov, P. ben Ishai and A. I. Kolesnikov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052306 CrossRef PubMed.
- A. I. Kolesnikov, L. M. Anovitz, E. Mamontov, A. Podlesnyak and G. Ehlers, J. Phys. Chem. B, 2014, 118, 13414–13419 CrossRef CAS PubMed.
- L. E. Bove, S. Klotz, A. Paciaroni and F. Sacchetti, Phys. Rev. Lett., 2009, 103, 165901 CrossRef CAS PubMed.
- A. I. Kolesnikov, G. Ehlers, E. Mamontov and A. Podlesnyak, Phys. Rev. B, 2018, 98, 5 CrossRef.
- A. I. Kolesnikov, G. F. Reiter, N. Choudhury, T. R. Prisk, E. Mamontov, A. Podlesnyak, G. Ehlers, A. G. Seel, D. J. Wesolowski and L. M. Anovitz, Phys. Rev. Lett., 2016, 116, 7802 CrossRef PubMed.
- P. W. Fenimore, H. Frauenfelder, B. H. McMahon and F. G. Parak, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16047–16051 CrossRef CAS PubMed.
- P. W. Fenimore, H. Frauenfelder, B. H. McMahon and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408–14413 CrossRef CAS PubMed.
- H. Frauenfelder, G. Chen, J. Berendzen, P. W. Fenimore, H. Jansson, B. H. McMahon, I. R. Stroe, J. Swenson and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5129–5134 CrossRef CAS PubMed.
- W. Doster and M. Settles, Biochim. Biophys. Acta, Proteins Proteomics, 2005, 1749, 173–186 CrossRef CAS PubMed.
- S. Khodadadi, S. Pawlus, J. H. Roh, V. G. Sakai, E. Mamontov and A. P. Sokolov, J. Chem. Phys., 2008, 128, 195106 CrossRef CAS PubMed.
- S. Khodadadi, J. H. Roh, A. Kisliuk, E. Mamontov, M. Tyagi, S. A. Woodson, R. M. Briber and A. P. Sokolov, Biophys. J., 2010, 98, 1321–1326 CrossRef CAS PubMed.
- M. Bai, A. Miskowiec, F. Y. Hansen, H. Taub, T. Jenkins, M. Tyagi, S. O. Diallo, E. Mamontov, K. W. Herwig and S.-K. Wang, EPL, 2012, 98, 48006 CrossRef.
- A. Miskowiec, Z. N. Buck, M. C. Brown, H. Kaiser, F. Y. Hansen, G. M. King, H. Taub, R. Jiji, J. W. Cooley, M. Tyagi, S. O. Diallo, E. Mamontov and K. W. Herwig, EPL, 2014, 107, 28008 CrossRef.
- A. Miskowiec, Z. N. Buck, F. Y. Hansen, H. Kaiser, H. Taub, M. Tyagi, S. O. Diallo, E. Mamontov and K. W. Herwig, J. Chem. Phys, 2017, 146, 125102 CrossRef CAS PubMed.
- Z. N. Buck, J. Torres, A. Miskowiec, E. Mamontov, H. Kaiser, F. Y. Hansen, H. Taub, M. Tyagi, L. Collins and K. W. Herwig, EPL, 2018, 123, 7 Search PubMed.
- C. L. Armstrong, M. D. Kaye, M. Zamponi, E. Mamontov, M. Tyagi, T. Jenkins and M. C. Rheinstadter, Soft Matter, 2010, 6, 5864–5867 RSC.
- F. Y. Hansen, G. H. Peters, H. Taub and A. Miskowiec, J. Chem. Phys, 2012, 137, 204910 CrossRef CAS PubMed.
- A. K. Ronnest, G. H. Peters, F. Y. Hansen, H. Taub and A. Miskowiec, J. Chem. Phys, 2016, 144, 144904 CrossRef CAS PubMed.
- E. C. Trantham, H. E. Rorschach, J. S. Clegg, C. F. Hazlewood, R. M. Nicklow and N. Wakabayashi, Biophys. J., 1984, 45, 927–938 CrossRef CAS PubMed.
- E. Mamontov, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 2382–2390 CrossRef CAS PubMed.
- S. Khodadadi, S. Pawlus and A. P. Sokolov, J. Phys. Chem. B, 2008, 112, 14273–14280 CrossRef CAS PubMed.
- Y. Zhang, M. Lagi, D. Liu, F. Mallamace, E. Fratini, P. Baglioni, E. Mamontov, M. Hagen and S.-H. Chen, J. Chem. Phys, 2009, 130, 135101 CrossRef PubMed.
- X.-q Chu, M. Lagi, E. Mamontov, E. Fratini, P. Baglioni and S.-H. Chen, Soft Matter, 2010, 6, 2623–2627 RSC.
- E. Mamontov, H. O'Neill and Q. Zhang, J. Biol. Phys., 2010, 36, 291–297 CrossRef CAS PubMed.
- L. Hong, N. Smolin, B. Lindner, A. P. Sokolov and J. C. Smith, Phys. Rev. Lett., 2011, 107, 148102 CrossRef PubMed.
- L. Hong, X. L. Cheng, D. C. Glass and J. C. Smith, Phys. Rev. Lett., 2012, 108, 238102 CrossRef PubMed.
- Y. L. Miao, Z. Yi, C. Cantrell, D. C. Glass, J. Baudry, N. Jain and J. C. Smith, Biophys. J., 2012, 103, 2167–2176 CrossRef CAS PubMed.
- J. D. Nickels, H. O'Neill, L. Hong, M. Tyagi, G. Ehlers, K. L. Weiss, Q. Zhang, Z. Yi, E. Mamontov, J. C. Smith and A. P. Sokolov, Biophys. J., 2012, 103, 1566–1575 CrossRef CAS PubMed.
- X.-q Chu, M. Gajapathy, K. L. Weiss, E. Mamontov, J. D. Ng and L. Coates, J. Phys. Chem. B, 2012, 116, 9917–9921 CrossRef CAS PubMed.
- Z. Yi, Y. L. Miao, J. Baudry, N. Jain and J. C. Smith, J. Phys. Chem. B, 2012, 116, 5028–5036 CrossRef CAS PubMed.
- X.-q Chu, E. Mamontov, H. O'Neill and Q. Zhang, J. Phys. Chem. Lett., 2013, 4, 936–942 CrossRef CAS PubMed.
- J. D. Nickels, Chem. Phys., 2013, 424, 7–11 CrossRef CAS.
- J. D. Nickels, V. G. Sakai and A. P. Sokolov, J. Phys. Chem. B, 2013, 117, 11548–11555 CrossRef CAS PubMed.
- Z. Wang, E. Fratini, M. Li, P. Le, E. Mamontov, P. Baglioni and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042705 CrossRef PubMed.
- S. Perticaroli, J. D. Nickels, G. Ehlers, E. Mamontov and A. P. Sokoov, J. Phys. Chem. B, 2014, 118, 7317–7326 CrossRef CAS PubMed.
- S. Perera, U. Chawla and M. F. Brown, J. Phys. Chem. Lett., 2016, 7, 4230–4235 CrossRef CAS PubMed.
- U. R. Shrestha, S. M. D. C. Perera, D. Bhowmik, U. Chawla, E. Mamontov, M. F. Brown and X.-Q. Chu, J. Phys. Chem. Lett., 2016, 7, 4130–4136 CrossRef CAS PubMed.
- Z. Liu, J. Huang, M. Tyagi, H. O'Neill, Q. Zhang, E. Mamontov, N. Jain, Y. Wang, J. Zhang, J. C. Smith and L. Hong, Phys. Rev. Lett., 2017, 119, 048101 CrossRef PubMed.
- D. Vural, X. H. Hu, B. Lindner, N. Jain, Y. L. Miao, X. L. Cheng, Z. Liu, L. Hong and J. C. Smith, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 3638–3650 CrossRef CAS PubMed.
- P. M. Favi, Q. Zhang, H. O'Neill, E. Mamontov and S. O. Diallo, J. Biol. Phys., 2014, 40, 167–178 CrossRef CAS PubMed.
- S. O. Diallo, Q. Zhang, H. O'Neill and E. Mamontov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042725 CrossRef CAS PubMed.
- L. Petridis, H. M. O'Neill, M. Johnsen, B. Fan, R. Schulz, E. Mamontov, J. Maranas, P. Langan and J. C. Smith, Biomacromolecules, 2014, 15, 4152–4159 CrossRef CAS PubMed.
- D. Vural, C. Gainaru, H. O'Neill, Y. Q. A. Pu, M. D. Smith, J. M. Parks, S. V. Pingali, E. Mamontov, B. H. Davison, A. P. Sokolov, A. J. Ragauskas, J. C. Smith and L. Petridis, Green Chem., 2018, 20, 1602–1611 RSC.
- J. D. Nickels, J. Atkinson, E. Papp-Szabo, C. Stanley, S. O. Diallo, S. Perticaroli, B. Baylis, P. Mahon, G. Ehlers, J. Katsaras and J. R. Dutcher, Biomacromolecules, 2016, 17, 735–743 CrossRef CAS PubMed.
- G. K. Dhindsa, D. Bhowmik, M. Goswami, H. O'Neill, E. Mamontov, B. G. Sumpter, L. Hong, P. Ganesh and X.-Q. Chu, J. Phys. Chem. B, 2016, 120, 10059–10068 CrossRef CAS PubMed.
- M. K. Rasmussen, J. E. M. Pereira, M. C. Berg, G. N. Iles, N. R. de Souza, N. H. Jalarvo, V. F. Botosso, O. A. Sant'Anna, M. C. A. Fantini and H. N. Bordallo, Eur. Phys. J.: Spec. Top, 2019, 227, 2393–2399 CAS.
- S. Perticaroli, B. Mostofian, G. Ehlers, J. C. Neuefeind, S. O. Diallo, C. B. Stanley, L. Daemen, T. Egami, J. Katsaras, X. L. Cheng and J. D. Nickels, Phys. Chem. Chem. Phys., 2017, 19, 25859–25869 RSC.
- P. Tan, Y. H. Liang, Q. Xu, E. Mamontov, J. L. Li, X. J. Xing and L. Hong, Phys. Rev. Lett., 2018, 120, 248101 CrossRef CAS PubMed.
- P. Tan, J. Li and L. Hong, Phys. B-Condens. Matter, 2019, 562, 1–5 CrossRef CAS.
- S. Li, P. Tan, J. Li, M. Tang and L. Hong, Phys. Rev. Res., 2022, 4, L022003 CrossRef CAS.
- P. Tan, J. Huang, E. Mamontov, V. G. Sakai, F. Merzel, Z. Liu, Y. Y. Ye and L. Hong, Phys. Chem. Chem. Phys., 2020, 22, 18132–18140 RSC.
- R. Li, Z. Liu, L. K. Li, J. Huang, T. Yamada, V. G. Sakai, P. Tan and L. Hong, Struct. Dyn., 2020, 7, 054703 CrossRef CAS PubMed.
- S. Perticaroli, G. Ehlers, N. Jalarvo, J. Katsaras and J. D. Nickels, J. Phys. Chem. Lett., 2015, 6, 4018–4025 CrossRef CAS PubMed.
- X. Q. Chu, E. Mamontov, H. O'Neill and Q. Zhang, J. Phys. Chem. Lett., 2012, 3, 380–385 CrossRef CAS PubMed.
- E. Mamontov, H. O'Neill, Q. Zhang and S. M. Chathoth, Chem. Phys., 2013, 424, 12–19 CrossRef CAS.
- E. Mamontov and H. O'Neill, Biopolymers, 2014, 101, 624–629 CrossRef CAS PubMed.
- S. Perticaroli, G. Ehlers, C. B. Stanley, E. Mamontov, H. O'Neill, Q. Zhang, X. Cheng, D. A. A. Myles, J. Katsaras and J. D. Nickels, J. Am. Chem. Soc., 2017, 139, 1098–1105 CrossRef CAS PubMed.
- M. R. Duff, J. M. Borreguero, M. J. Cuneo, A. Ramanathan, J. H. He, G. Kamath, S. C. Chennubhotla, F. Meilleur, E. E. Howell, K. W. Herwig, D. A. A. Myles and P. K. Agarwal, Biochemistry, 2018, 57, 4263–4275 CrossRef CAS PubMed.
- M. Grimaldo, F. Roosen-Runge, N. Jalarvo, M. Zamponi, F. Zanini, M. Hennig, F. Zhang, F. Schreiber and T. Seydel, EPJ Web Conf., 2014, 83, 02005 CrossRef.
- M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. J. Zhang, N. Jalarvo, M. Zamponi, F. Schreiber and T. Seydel, Phys. Chem. Chem. Phys., 2015, 17, 4645–4655 RSC.
- M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. J. Zhang, M. Zamponi, N. Jalarvo, F. Schreiber and T. Seydel, J. Phys. Chem. Lett., 2015, 6, 2577–2582 CrossRef CAS PubMed.
- M. Sarter, D. Niether, B. W. Koenig, W. Lohstroh, M. Zamponi, N. H. Jalarvo, S. Wiegand, J. Fitter and A. M. Stadler, J. Phys. Chem. B, 2020, 124, 324–335 CrossRef CAS PubMed.
- C. Beck, M. Grimaldo, M. K. Braun, L. Buhl, O. Matsarskaia, N. H. Jalarvo, F. J. Zhang, F. Roosen-Runge, F. Schreiber and T. Seydel, Soft Matter, 2021, 17, 8506–8516 RSC.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O'Neill and V. Urban, J. Phys. Chem. B, 2015, 119, 4460–4470 CrossRef CAS PubMed.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O'Neill and V. S. Urban, Soft Matter, 2015, 11, 6755–6767 RSC.
- V. K. Sharma, E. Mamontov, M. Tyagi and V. S. Urban, J. Phys. Chem. B, 2016, 120, 154–163 CrossRef CAS PubMed.
- D. K. Rai, V. K. Sharma, D. Anunciado, H. O’Neill, E. Mamontov, V. Urban, W. T. Heller and S. Qian, Sci. Rep., 2016, 6, 30983 CrossRef CAS PubMed.
- V. K. Sharma, E. Mamontov, M. Ohl and M. Tyagi, Phys. Chem. Chem. Phys., 2017, 19, 2514–2524 RSC.
- V. K. Sharma, E. Mamontov and M. Tyagi, Biochim. Biophys. Acta, Biomembr., 2020, 1862 Search PubMed.
- S. Qian, G. Nagy, P. Zolnierczuk, E. Mamontov and R. Standaert, J. Phys. Chem. Lett., 2024, 15, 4745–4752 CrossRef CAS PubMed.
- V. K. Sharma, E. Mamontov, M. Tyagi, S. Qian, D. K. Rai and V. S. Urban, J. Phys. Chem. Lett., 2016, 7, 2394–2401 CrossRef CAS PubMed.
- V. K. Sharma and S. Qian, Langmuir, 2019, 35, 4152–4160 CrossRef CAS PubMed.
- V. K. Sharma and E. Mamontov, J. Appl. Phys., 2022, 132, 074702 CrossRef CAS.
- V. K. Sharma, J. Gupta and E. Mamontov, Soft Matter, 2022, 19, 57–68 RSC.
- C. Z. Xie, S. M. Chang, E. Mamontov, L. R. Stingaciu and Y. F. Chen, Phys. Rev. E, 2020, 101, 012416 CrossRef CAS PubMed.
- D. Bolmatov, D. Soloviov, M. Zhernenkov, D. Zav'yalov, E. Mamontov, A. Suvorov, Y. Q. Cai and J. Katsaras, Langmuir, 2020, 36, 4887–4896 CrossRef CAS PubMed.
- M. Jasnin, M. Moulin, M. Haertlein, G. Zaccai and M. Tehei, EMBO Rep., 2008, 9, 543–547 CrossRef PubMed.
- A. M. Stadler, J. P. Embs, I. Digel, G. M. Artmann, T. Unruh, G. Büldt and G. Zaccai, J. Am. Chem. Soc., 2008, 130, 16852 CrossRef PubMed.
- M. Tehei, B. Franzetti, K. Wood, F. Gabel, E. Fabiani, M. Jasnin, M. Zamponi, D. Oesterhelt, G. Zaccai, M. Ginzburg and B. Z. Ginzburg, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 766–771 CrossRef CAS PubMed.
- A. Frölich, F. Gabel, M. Jasnin, U. Lehnert, D. Oesterhelt, A. M. Stadler, M. Tehei, M. Weik, K. Wood and G. Zaccai, Faraday Discuss., 2009, 141, 117–130 RSC.
- M. Jasnin, A. Stadler, M. Tehei and G. Zaccai, Phys. Chem. Chem. Phys., 2010, 12, 10154–10160 RSC.
- M. Jasnin, M. Moulin, M. Haertlein, G. Zaccai and M. Tehei, Biophys. J., 2008, 95, 857–864 CrossRef CAS PubMed.
- A. M. Stadler, I. Digel, G. M. Artmann, J. P. Embs, G. Zaccai and G. Büldt, Biophys. J., 2008, 95, 5449–5461 CrossRef CAS PubMed.
- V. Marty, M. Jasnin, E. Fabiani, P. Vauclare, F. Gabel, M. Trapp, J. Peters, G. Zaccai and B. Franzetti, J. R. Soc. Interface, 2013, 10, 20130003 CrossRef PubMed.
- J. Peters, N. Martinez, G. Michoud, A. Carlo, B. Franzetti, P. Oger and M. Jebbar, Z. Phys. Chem., 2014, 228, 1121–1133 CrossRef CAS.
- P. Vauclare, V. Marty, E. Fabiani, N. Martinez, M. Jasnin, F. Gabel, J. Peters, G. Zaccai and B. Franzetti, Extremophiles, 2015, 19, 1099–1107 CrossRef CAS PubMed.
- N. Martinez, G. Michoud, A. Cario, J. Ollivier, B. Franzetti, M. Jebbar, P. Oger and J. Peters, Sci. Rep., 2016, 6, 32816 CrossRef CAS PubMed.
- M. Salvador-Castell, M. Golub, N. Martinez, J. Ollivier, J. Peters and P. Oger, Soft Matter, 2019, 15, 8381–8391 RSC.
- M. Golub, N. Martinez, G. Michoud, J. Ollivier, M. Jebbar, P. Oger and J. Peters, Langmuir, 2018, 34, 10419–10425 CrossRef CAS PubMed.
- A. C. de la Noue, J. Peters, P. Gervais, N. Martinez, J. M. Perrier-Cornet and F. Natali, EPJ Web Conf., 2015, 83, 02003 CrossRef.
- M. Liberton, L. E. Page, W. B. O'Dell, H. O'Neill, E. Mamontov, V. S. Urban and H. B. Pakrasi, J. Biol. Chem., 2013, 288, 3632–3640 CrossRef CAS PubMed.
- D. B. Anunciado, V. P. Nyugen, G. B. Hurst, M. J. Doktycz, V. Urban, P. Langan, E. Mamontov and H. O'Neill, J. Phys. Chem. Lett., 2017, 8, 1899–1904 CrossRef CAS PubMed.
- M. L. Martins, A. B. Dinitzen, E. Mamontov, S. Rudic, J. E. M. Pereira, R. Hartmann-Petersen, K. W. Herwig and H. N. Bordallo, Sci. Rep., 2019, 9, 8704 CrossRef PubMed.
- M. L. Martins, H. N. Bordallo and E. Mamontov, Medicina, 2022, 58, 654 CrossRef PubMed.
- M. P. M. Marques, A. L. M. Batista de Carvalho, V. G. Sakai, L. Hatter and L. A. E. Batista de Carvalho, Phys. Chem. Chem. Phys., 2017, 19, 2702–2713 RSC.
- M. P. M. Marques, A. de Carvalho, A. P. Mamede, I. P. Santos, V. G. Sakai, A. Dopplapudi, G. Cinque, M. Wolna, P. Gardner and L. de Carvalho, J. Phys. Chem. B, 2019, 123, 6968–6979 CrossRef CAS PubMed.
- A. de Carvalho, A. P. Mamede, A. Dopplapudi, V. G. Sakai, J. Doherty, M. Frogley, G. Cinque, P. Gardner, D. Gianolio, L. de Carvalho and M. P. M. Marques, Phys. Chem. Chem. Phys., 2019, 21, 4162–4175 RSC.
- M. P. M. Marques, A. de Carvalho, A. P. Mamede, A. Dopplapudi, S. Rudic, M. Tyagi, V. G. Sakai and L. de Carvalho, Molecules, 2020, 25, 246 CrossRef CAS PubMed.
- M. P. M. Marques, L. de Carvalho, A. P. Mamede, S. Rudic, A. Dopplapudi and V. G. Sakai, Int. Rev. Phys. Chem., 2020, 39, 67–81 Search PubMed.
- E. Mamontov, Sci. Rep., 2018, 8, 4190 Search PubMed.
- E. Mamontov, Phys. B-Condens. Matter, 2019, 566, 23–29 CrossRef CAS.
- E. Mamontov, N. C. Osti and M. Tyagi, Sci. Rep., 2019, 9, 11646 CrossRef PubMed.
- E. Mamontov, Life, 2022, 12, 1219 CrossRef CAS PubMed.
- J. K. Liu, Z. J. Lv, Y. N. Fang, G. Z. Wu and Y. Lin, Polymer, 2023, 284, 126312 CrossRef CAS.
- K. Kunal, C. G. Robertson, S. Pawlus, S. F. Hahn and A. P. Sokolov, Macromolecules, 2008, 41, 7232–7238 CrossRef CAS.
- S. K. Kumar, R. H. Colby, S. H. Anastasiadis and G. Fytas, J. Chem. Phys., 1996, 105, 3777–3788 CrossRef CAS.
- Y. B. Zhang, J. F. Douglas, B. D. Ermi and E. J. Amis, J. Chem. Phys., 2001, 114, 3299–3313 CrossRef CAS.
- T. P. Lodge, Macromolecules, 1983, 16, 1393–1395 CrossRef CAS.
- P. Falus, M. A. Borthwick and S. G. J. Mochrie, Phys. Rev. Lett., 2005, 94, 016105 CrossRef CAS PubMed.
- A. Arbe, F. Alvarez and J. Colmenero, Polymers, 2020, 12, 3067 CrossRef CAS PubMed.
- J. Colmenero, A. Arbe and A. Alegria, Phys. Rev. Lett., 1993, 71, 2603–2606 CrossRef CAS PubMed.
- V. Arrighi and J. S. Higgins, Polymers, 2020, 12, 1884 CrossRef CAS PubMed.
- J. S. Higgins, Developments in Polymer Characterization, New York, vol. 4, 1983 Search PubMed.
- C. Gerstl, G. J. Schneider, A. Fuxman, M. Zamponi, B. Frick, T. Seydel, M. Koza, A. C. Genix, J. Allgaier, D. Richter, J. Colmenero and A. Arbe, Macromolecules, 2012, 45, 4394–4405 CrossRef CAS.
- X. Li, M. Zamponi, K. L. Hong, L. Porcar, C. Y. Shew, T. Jenkins, E. Liu, G. S. Smith, K. W. Herwig, Y. Liu and W. R. Chen, Soft Matter, 2011, 7, 618–622 RSC.
- B. Wu, Y. Liu, X. Li, E. Mamontov, A. I. Kolesnikov, S. O. Diallo, C. Do, L. Porcar, K. L. Hong, S. C. Smith, L. Liu, G. S. Smith, T. Egami and W. R. Chen, J. Am. Chem. Soc., 2013, 135, 5111–5117 CrossRef CAS PubMed.
- X. L. Xu, K. S. Hui, K. N. Hui, H. Wang and J. B. Liu, Mater. Horiz., 2020, 7, 1246–1278 RSC.
- W. H. Meyer, Adv. Mater., 1998, 10, 439 CrossRef CAS PubMed.
- L. Ganapatibhotla and J. K. Maranas, Macromolecules, 2014, 47, 3625–3634 CrossRef CAS.
- K. Sinha and J. Maranas, Macromolecules, 2014, 47, 2718–2726 CrossRef CAS.
- S. S. Mohottalalage, C. Kosgallana, M. Senanayake, S. Wijesinghe, N. C. Osti and D. Perahia, ACS Macro Lett., 2023, 12, 1118–1124 CrossRef CAS PubMed.
- M. Krutyeva, A. Wischnewski and D. Richter, EPJ Web Conf., 2015, 83, 02009 CrossRef.
- X. C. Chen, R. L. Sacci, N. C. Osti, M. Tyagi, Y. Y. Wang, J. K. Keum and N. J. Dudney, Front. Chem., 2021, 8, 592604 CrossRef PubMed.
- X. C. Chen, R. L. Sacci, N. C. Osti, M. Tyagi, Y. Y. Wang, M. J. Palmer and N. J. Dudney, Mol. Syst. Des. Eng., 2019, 4, 379–385 RSC.
- H. R. Wu, L. W. Li, M. Tsuboi, Y. Q. Cheng, W. Y. Wang, E. Mamontov, S. Uchida, Z. Wang and P. C. Yin, J. Phys. Chem. Lett., 2018, 9, 5772–5777 CrossRef CAS PubMed.
- N. J. Shah, C. Fang, N. C. Osti, E. Mamontov, X. P. Yu, J. Lee, H. Watanabe, R. Wang and N. P. Balsara, Nat. Mater., 2024, 23, 664–669 CrossRef CAS PubMed.
- A. Alesadi, Z. Q. Cao, Z. F. Li, S. Zhang, H. Y. Zhao, X. D. Gu and W. J. Xia, Cell Rep. Phys. Sci., 2022, 3, 100911 CrossRef CAS.
- C. M. Wolf, K. H. Kanekal, Y. Y. Yimer, M. Tyagi, S. Omar-Diallo, V. Pakhnyuk, C. K. Luscombe, J. Pfaendtner and L. D. Pozzo, Soft Matter, 2019, 15, 5067–5083 RSC.
- J. Li, C. Koshnick, S. O. Diallo, S. Ackling, D. M. Huang, I. E. Jacobs, T. F. Harrelson, K. Hong, G. Zhang, J. Beckett, M. Mascal and A. J. Moulé, Macromolecules, 2017, 50, 5476–5489 CrossRef CAS.
- N. C. Osti, E. Mamontov, L. Daemen, J. F. Browning, J. Keum, H. C. Ho, J. H. Chen, K. L. Hong and S. O. Diallo, J. Appl. Polym. Sci., 2019, 136, 47394 CrossRef.
- N. Jalarvo, M. Tyagi and M. K. Crawford, EPJ Web Conf., 2015, 83, 02007 CrossRef.
- N. Jalarvo, O. Gourdon, G. Ehlers, M. Tyagi, S. K. Kumar, K. D. Dobbs, R. J. Smalley, W. E. Guise, A. Ramirez-Cuesta, C. Wildgruber and M. K. Crawford, J. Phys. Chem. C, 2014, 118, 5579–5592 CrossRef CAS.
- J. M. Borreguero and V. E. Lynch, J. Chem. Theory Comput., 2016, 12, 9–17 CrossRef CAS PubMed.
- N. Jalarvo, A. Pramanick, C. Do and S. O. Diallo, Appl. Phys. Lett, 2015, 107, 4929693 CrossRef.
- A. Pramanick, S. Misture, N. C. Osti, N. Jalarvo, S. O. Diallo and E. Mamontov, Phys. Rev. B, 2017, 96, 174103 CrossRef.
- A. Pramanick, N. C. Osti, N. Jalarvo, S. T. Misture, S. O. Diallo, E. Mamontov, Y. Luo, J. K. Keum and K. Littrell, AIP Adv., 2018, 8, 5014992 Search PubMed.
- Z. J. Xu, J. S. Wen, E. Mamontov, C. Stock, P. M. Gehring and G. Y. Xu, Phys. Rev. B, 2012, 86, 144106 CrossRef.
- A. Holewinski, M. A. Sakwa-Novak and C. W. Jones, J. Am. Chem. Soc., 2015, 137, 11749–11759 CrossRef CAS PubMed.
- J. M. Y. Carrillo, M. A. Sakwa-Novak, A. Holewinski, M. E. Potter, G. Rother, C. W. Jones and B. G. Sumpter, Langmuir, 2016, 32, 2617–2625 CrossRef CAS PubMed.
- M. Krutyeva, S. Pasini, M. Monkenbusch, J. Allgaier, J. Maiz, C. Mijangos, B. Hartmann-Azanza, M. Steinhart, N. Jalarvo and D. Richter, J. Chem. Phys., 2017, 146, 4974836 Search PubMed.
- C. Mark, O. Holderer, J. Allgaier, E. Hübner, W. Pyckhout-Hintzen, M. Zamponi, A. Radulescu, A. Feoktystov, M. Monkenbusch, N. Jalarvo and D. Richter, Phys. Rev. Lett., 2017, 119, 047801 CrossRef CAS PubMed.
- H. J. Moon, J. M. Carrillo, J. Leisen, B. G. Sumpter, N. C. Osti, M. Tyagi and C. W. Jones, J. Am. Chem. Soc., 2022, 144, 11664–11675 CrossRef CAS PubMed.
- C. Mbonu, N. Osti, D. Wu and P. Akcora, J. Polym. Sci., 2024, 1, 1–9 Search PubMed.
- A. P. Holt, V. Bocharova, S. W. Cheng, A. M. Kisliuk, G. Ehlers, E. Mamontov, V. N. Novikov and A. P. Sokolov, Phys. Rev. Mater., 2017, 1, 062601 CrossRef.
- E. Mamontov, V. K. Sharma, J. M. Borreguero and M. Tyagi, J. Phys. Chem. B, 2016, 120, 3232–3239 CrossRef CAS PubMed.
- D. Russo, A. De Angelis, A. Paciaroni, B. Frick, N. de Sousa, F. R. Wurm and J. Teixeira, Langmuir, 2019, 35, 2674–2679 CrossRef CAS PubMed.
- N. A. Nguyen, C. C. Bowland, L. L. He, N. C. Osti, M. D. Phan, J. K. Keum, M. Tyagi, K. M. Meek, K. C. Littrell, E. Mamontov, J. Ankner and A. K. Naskar, Adv. Sustainable Syst., 2023, 7, 2300079 CrossRef CAS.
- M. Laskoski, B. Dyatkin, N. C. Osti, J. K. Keum, E. Mamontov and T. Butler, J. Polym. Sci., 2023, 61, 132–142 CrossRef CAS.
- H. Taheri-Afarani, E. Mamontov, W. R. Carroll and J. J. Biernacki, Gels, 2022, 8, 592 CrossRef CAS PubMed.
- D. Noferini, A. Faraone, M. Rossi, E. Mamontov, E. Fratini and P. Baglioni, J. Phys. Chem. C, 2019, 123, 19183–19194 CrossRef CAS.
- B. S. Wang, L. Qin, T. C. Mu, Z. M. Xue and G. H. Gao, Chem. Rev., 2017, 117, 7113–7131 CrossRef CAS PubMed.
- R. Gond, W. van Ekeren, R. Mogensen, A. J. Naylor and R. Younesi, Mater. Horiz., 2021, 8, 2913–2928 RSC.
- K. Dong, X. M. Liu, H. F. Dong, X. P. Zhang and S. J. Zhang, Chem. Rev., 2017, 117, 6636–6695 CrossRef CAS PubMed.
- Z. R. Zhang, J. L. Song and B. X. Han, Chem. Rev., 2017, 117, 6834–6880 CrossRef CAS PubMed.
- S. P. M. Ventura, F. A. E. Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. P. Coutinho, Chem. Rev., 2017, 117, 6984–7052 CrossRef CAS PubMed.
- Y. Wang, S. Gong, S. J. Wang, G. P. Simon and W. L. Cheng, Mater. Horiz., 2016, 3, 208–213 RSC.
- L. C. Tomé, L. Porcarelli, J. E. Bara, M. Forsyth and D. Mecerreyes, Mater. Horiz., 2021, 8, 3239–3265 RSC.
- N. C. Osti and E. Mamontov, Sustainable Energy Fuels, 2020, 4, 1554–1576 RSC.
- M. Watanabe, M. L. Thomas, S. G. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- A. C. Forse, J. M. Griffin, C. Merlet, J. Carretero-Gonzalez, A. R. O. Raji, N. M. Trease and C. P. Grey, Nat. Energy, 2017, 2, 16216 CrossRef.
- A. Triolo, O. Russina, V. Arrighi, F. Juranyi, S. Janssen and C. M. Gordon, J. Chem. Phys., 2003, 119, 8549–8557 CrossRef CAS.
- Y. Inamura, O. Yamamuro, S. Hayashi and H. O. Hamaguchi, Phys. B-Condens. Matter, 2006, 385, 732–734 CrossRef.
- O. Yamamuro, T. Yamada, M. Kofu, M. Nakakoshi and M. Nagao, J. Chem. Phys., 2011, 135, 3622598 CrossRef PubMed.
- E. Mamontov, G. A. Baker, H. M. Luo and S. Dai, ChemPhysChem, 2011, 12, 944–950 CrossRef CAS PubMed.
- T. Watkins, A. Kumar and D. A. Buttry, J. Am. Chem. Soc., 2016, 138, 641–650 CrossRef CAS PubMed.
- H. Yoon, P. C. Howlett, A. S. Best, M. Forsyth and D. R. MacFarlane, J. Electrochem. Soc., 2013, 160, A1629–A1637 CrossRef CAS.
- J. S. Wilkes, J. Mol. Catal. A: Chem., 2004, 214, 11–17 CrossRef CAS.
- N. C. Osti, K. L. Van Aken, M. W. Thompson, F. Tiet, D. E. Jiang, P. T. Cummings, Y. Gogotsi and E. Mamontov, J. Phys. Chem. Lett., 2017, 8, 167–171 CrossRef CAS PubMed.
- N. C. Osti, R. A. Matsumoto, M. W. Thompson, P. T. Cummings, M. Tyagi and E. Mamontov, J. Phys. Chem. C, 2019, 123, 19354–19361 CrossRef CAS.
- C. Do, X. G. Sun, C. J. Jafta, S. Dai, M. Ohl and E. Mamontov, Sci. Rep., 2018, 8, 10354 CrossRef PubMed.
- E. Mamontov, N. C. Osti and M. R. Ryder, Struct. Dyn., 2021, 8, 024303 CrossRef CAS PubMed.
- N. C. Osti, B. Haberl, N. Jalarvo, R. Boehler, J. J. Molaison, R. J. Goyette and E. Mamontov, Chem. Phys., 2020, 530, 110628 CrossRef.
- Z. Y. Dong, C. R. Zhang, H. W. Peng, J. Gong, H. Wang, Q. Zhao and J. Y. Yuan, Mater. Horiz., 2020, 7, 2683–2689 RSC.
- X. J. Lin, S. Y. Xu, Y. Q. Tong, X. S. Liu, Z. Y. Liu, P. Li, R. Q. Liu, X. M. Feng, L. Shi and Y. W. Ma, Mater. Horiz., 2023, 10, 859–868 RSC.
- V. Bocharova, A. C. Genix, A. Kisliuk, G. Sala, N. C. Osti, E. Mamontov and A. P. Sokolov, J. Phys. Chem. B, 2020, 124, 10539–10545 CrossRef CAS PubMed.
- A. Gallastegui, F. Foglia, P. F. McMillan, N. Casado, A. Gueguen and D. Mecerreyes, Polymer, 2023, 280, 126064 CrossRef CAS.
- S. G. Zhang, J. H. Zhang, Y. Zhang and Y. Q. Deng, Chem. Rev., 2017, 117, 6755–6833 CrossRef CAS PubMed.
- S. M. Chathoth, E. Mamontov, S. Dai, X. Wang, P. F. Fulvio and D. J. Wesolowski, EPL, 2012, 97, 66004 CrossRef.
- S. M. Chathoth, E. Mamontov, P. F. Fulvio, X. Wang, G. A. Baker, S. Dai and D. J. Wesolowski, EPL, 2013, 102, 16004 CrossRef.
- B. Dyatkin, Y. Zhang, E. Mamontov, A. I. Kolesnikov, Y. Q. Cheng, H. M. Meyer, P. T. Cummings and Y. Gogotsi, J. Phys. Chem. C, 2016, 120, 8730–8741 CrossRef CAS.
- B. Dyatkin, N. C. Osti, Y. Zhang, H. W. Wang, E. Mamontov, W. T. Heller, P. F. Zhang, G. Rother, P. T. Cummings, D. J. Wesolowski and Y. Gogotsi, Carbon, 2018, 129, 104–118 CrossRef CAS.
- K. L. Van Aken, J. K. McDonough, S. Li, G. Feng, S. M. Chathoth, E. Mamontov, P. F. Fulvio, P. T. Cummings, S. Dai and Y. Gogotsi, J. Phys.: Condens. Matter, 2014, 26, 284104 CrossRef PubMed.
- B. Dyatkin, N. C. Osti, A. Gallegos, Y. Zhang, E. Mamontov, P. T. Cummings, J. Wu and Y. Gogotsi, Electrochim. Acta, 2018, 283, 882–893 CrossRef CAS.
- N. C. Osti, B. Dyatkin, A. Gallegos, D. Voneshen, J. K. Keum, K. Littrell, P. F. Zhang, S. Dai, J. Z. Wu, Y. Gogotsi and E. Mamontov, J. Electrochem. Soc., 2019, 166, A507–A514 CrossRef CAS.
- S. M. Mahurin, E. Mamontov, M. W. Thompson, P. Zhang, C. H. Turner, P. T. Cummings and S. Dai, Appl. Phys. Lett, 2016, 109, 143111 CrossRef.
- E. Mamontov, S. M. Mahurin and S. Dai, AIP Conf. Proc., 2018, 1969, 020001 CrossRef.
- N. C. Osti, A. Gallegos, B. Dyatkin, J. Z. Wu, Y. Gogotsi and E. Mamontov, J. Phys. Chem. C, 2018, 122, 10476–10481 CrossRef CAS.
- N. C. Osti, B. Dyatkin, M. W. Thompson, F. Tiet, P. F. Zhang, S. Dai, M. Tyagi, P. T. Cummings, Y. Gogotsi, D. J. Wesolowski and E. Mamontov, Phys. Rev. Mater., 2017, 1, 035402 CrossRef.
- C. A. Bridges, M. L. Martins, C. J. Jafta, X. G. Sun, M. P. Paranthaman, J. Liu, S. Dai and E. Mamontov, J. Phys. Chem. B, 2021, 125, 5443–5450 CrossRef CAS PubMed.
- C. J. Jafta, C. Bridges, L. Haupt, C. Do, P. Sippel, M. J. Cochran, S. Krohns, M. Ohl, A. Loidl, E. Mamontov, P. Lunkenheimer, S. Dai and X. G. Sun, ChemSusChem, 2018, 11, 3512–3523 CrossRef CAS PubMed.
- S. Q. Liu, C. Liedel, N. V. Tarakina, N. C. Osti and P. Akcora, Nanoscale, 2019, 11, 19832–19841 RSC.
- J. P. Elliott, N. C. Osti, M. Tyagi, E. Mamontov, L. F. Liu, J. M. Serrano, K. Cao and G. L. Liu, ACS Appl. Mater. Interfaces, 2022, 14, 36980–36986 CrossRef CAS PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- K. A. S. Usman, S. Qin, L. C. Henderson, J. Z. Zhang, D. Y. Hegh and J. M. Razal, Mater. Horiz., 2021, 8, 2886–2912 RSC.
- N. C. Osti, M. W. Thompson, K. L. Van Aken, M. Alhabeb, M. Tyagi, J. K. Keum, P. T. Cummings, Y. Gogotsi and E. Mamontov, J. Phys. Chem. C, 2018, 122, 27561–27566 CrossRef CAS.
- K. Liang, R. A. Matsumoto, W. Zhao, N. C. Osti, I. Popov, B. P. Thapaliya, S. Fleischmann, S. Misra, K. Prenger, M. Tyagi, E. Mamontov, V. Augustyn, R. R. Unocic, A. P. Sokolov, S. Dai, P. T. Cummings and M. Naguib, Adv. Funct. Mater., 2021, 31, 2104007 CrossRef CAS.
- N. C. Osti, X. B. Lin, W. Zhao, X. H. Wang, C. F. Chen, Y. Gao, T. Torita, A. I. Kolesnikov, P. T. Cummings, Y. Gogotsi and E. Mamontov, 2D Mater., 2023, 10, 014014 CrossRef.
- E. Novak, N. Jalarvo, S. Gupta, K. Hong, S. Förster, T. Egami and M. Ohl, J. Phys. Chem. B, 2018, 122, 6296–6304 CrossRef CAS PubMed.
- D. V. Wagle, G. A. Baker and E. Mamontov, J. Phys. Chem. Lett., 2015, 6, 2924–2928 CrossRef CAS PubMed.
- E. Mamontov, J. Phys. Chem. B, 2013, 117, 9501–9507 CrossRef CAS PubMed.
- S. M. Chathoth, D. M. Anjos, E. Mamontov, G. M. Brown and S. H. Overbury, J. Phys. Chem. B, 2012, 116, 7291–7295 CrossRef CAS PubMed.
- N. C. Osti, B. P. Thapaliya, R. A. Matsumoto, A. Bansal, X. B. Lin, P. T. Cummings, M. Tyagi, S. Dai and E. Mamontov, J. Phys. Chem. Lett., 2022, 13, 2845–2850 CrossRef CAS PubMed.
- Y. Shinohara, T. Iwashita, M. Nakanishi, N. C. Osti, M. Kofu, M. Nirei, W. Dmowski and T. Egami, J. Phys. Chem. B, 2024, 128, 1544–1549 CrossRef CAS PubMed.
- A. Döss, M. Paluch, H. Sillescu and G. Hinze, Phys. Rev. Lett., 2002, 88, 095701 CrossRef PubMed.
- B. Guiselin, C. Scalliet and L. Berthier, Nat. Phys., 2022, 18, 468–472 Search PubMed.
- J. Gardner, G. Ehlers, A. Faraone and V. Sakai, Nat. Rev. Phys., 2020, 2, 103–116 Search PubMed.
- S. Gupta, J. K. H. Fischer, P. Lunkenheimer, A. Loidl, E. Novak, N. Jalarvo and M. Ohl, Sci. Rep., 2016, 6, 35034 Search PubMed.
- Y. Zhang, M. Tyagi, E. Mamontov and S. H. Chen, J. Phys.: Condens. Matter, 2012, 24, 064112 CrossRef PubMed.
- S. M. Chathoth, E. Mamontov, Y. B. Melnichenko and M. Zamponi, Microporous Mesoporous Mater., 2010, 132, 148–153 CrossRef CAS.
- S. M. Chathoth, L. He, E. Mamontov and Y. B. Melnichenko, Microporous Mesoporous Mater., 2012, 148, 101–106 CrossRef CAS.
- W. Press, I. Krasnow, M. Zamponi and M. Prager, J. Chem. Phys., 2011, 135, 224509 CrossRef PubMed.
- A. S. Hicks and J. Z. Larese, Chem. Phys., 2013, 427, 71–81 CrossRef CAS.
- S. Gautam, T. T. Liu, G. Rother, N. Jalarvo, E. Mamontov, S. Welch and D. Cole, AIP Conf. Proc., 2014, 1591, 1353–1355 CrossRef CAS.
- S. Gautam, T. T. Liu, G. Rother, N. Jalarvo, E. Mamontov, S. Welch, J. Sheets, M. Droege and D. R. Cole, J. Phys. Chem. C, 2015, 119, 18188–18195 CrossRef CAS.
- S. Gautam, T. T. B. Le, G. Rother, N. Jalarvo, T. T. Liu, E. Mamontov, S. Dai, Z. A. Qiao, A. Striolo and D. Cole, Phys. Chem. Chem. Phys., 2019, 21, 25035–25046 RSC.
- E. J. Kintzel, M. K. Kidder, A. C. Buchanan, P. F. Britt, E. Mamontov, M. Zamponi and K. W. Herwig, J. Phys. Chem. C, 2012, 116, 923–932 CrossRef CAS.
- Z. Wang, L. L. Daemen, Y. Q. Cheng, E. Mamontov, P. V. Bonnesen, K. L. Hong, A. J. Ramirez-Cuesta and P. C. Yin, Chem. - Eur. J., 2016, 22, 14131–14136 CrossRef CAS PubMed.
- H. O'Neill, S. M. Chathoth, M. B. Cardoso, G. A. Baker, E. Mamontov and V. S. Urban, J. Phys. Chem. C, 2012, 116, 13972–13979 CrossRef.
- S. K. Wang, E. Mamontov, M. Bai, F. Y. Hansen, H. Taub, J. R. D. Copley, V. G. Sakai, G. Gasparovic, T. Jenkins, M. Tyagi, K. W. Herwig, D. A. Neumann, W. Montfrooij and U. G. Volkmann, EPL, 2010, 91, 66007 CrossRef.
- S. Chereddy, P. R. Chinnam, V. Chatare, S. P. DiLuzio, M. P. Gobet, S. G. Greenbaum and S. L. Wunder, Mater. Horiz., 2018, 5, 461–473 RSC.
- L. M. Suo, Y. S. Hu, H. Li, M. Armand and L. Q. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed.
- M. L. Martins, R. L. Sacci, N. C. Sanders, J. L. Tyler, R. Matsumoto, I. Popov, W. Guo, S. Dai, P. T. Cummings, A. P. Sokolov and E. Mamontov, J. Phys. Chem. C, 2020, 124, 22366–22375 CrossRef CAS.
- M. L. Martins, R. L. Sacci, X. B. Lin, R. Matsumoto, I. Popov, J. L. Cui, T. Kobayashi, M. Tyagi, W. Guo, S. Dai, M. Pruski, P. T. Cummings, A. P. Sokolov and E. Mamontov, J. Phys. Chem. C, 2022, 126, 2788–2796 CrossRef CAS.
- M. L. Martins, X. B. Lin, C. Gainaru, J. K. Keum, P. T. Cummings, A. P. Sokolov, R. L. Sacci and E. Mamontov, J. Phys. Chem. B, 2023, 127, 308–320 CrossRef CAS PubMed.
- M. Verbraeken, E. Suard and J. Irvine, J. Mater. Chem., 2009, 19, 2766–2770 RSC.
- E. Mamontov, A. I. Kolesnikov, S. Sampath and J. L. Yarger, Sci. Rep., 2017, 7, 16244 CrossRef PubMed.
- M. C. Verbraeken, C. Cheung, E. Suard and J. T. S. Irvine, Nat. Mater., 2015, 14, 95–100 CrossRef CAS PubMed.
- E. Novak, L. Daemen, A. J. Ramirez-Cuesta, Y. Q. Cheng, R. Smith, T. Egami and N. Jalarvo, Sci. Rep., 2022, 12, 6194 CrossRef CAS PubMed.
- E. Novak, L. Daemen, K. Page, J. Neuefeind, M. Everett, T. Egami and N. Jalarvo, J. Phys. Chem. C, 2021, 125, 24328–24339 CrossRef CAS.
- E. Novak, B. Haberl, L. Daemen, J. Molaison, T. Egami and N. Jalarvo, Appl. Phys. Lett., 2020, 117, 051902 CrossRef CAS.
- K. A. Terrani, E. Mamontov, M. Balooch and D. R. Olander, J. Nucl. Mater., 2010, 401, 91–97 CrossRef CAS.
- E. Cakmak, M. N. Cinbiz, A. Sundar, E. Mamontov, J. G. Yu, X. X. Hu and K. D. Linton, J. Nucl. Mater., 2024, 593, 154972 CrossRef CAS.
- B. J. Heuser, D. R. Trinkle, N. Jalarvo, J. Serio, E. J. Schiavone, E. Mamontov and M. Tyagi, Phys. Rev. Lett., 2014, 113, 025504 CrossRef CAS PubMed.
- E. J. Schiavone and D. R. Trinkle, Phys. Rev. B, 2016, 94, 054114 CrossRef.
- Z. N. Buck, M. Connolly, M. L. Martin, D. Lauria, J. P. Killgore, P. Bradley, A. Slifka, Y. Chen and N. C. Osti, Microsc. Microanal., 2022, 28, 1626–1627 CrossRef.
- J. J. Guo, J. R. Morris, Y. Ihm, C. I. Contescu, N. C. Gallego, G. Duscher, S. J. Pennycook and M. F. Chisholm, Small, 2012, 8, 3283–3288 CrossRef CAS PubMed.
- C. I. Contescu, H. X. Zhang, R. J. Olsen, E. Mamontov, J. R. Morris and N. C. Gallego, Phys. Rev. Lett., 2013, 110, 236102 CrossRef PubMed.
- J. R. Morris, C. I. Contescu, M. F. Chisholm, V. R. Cooper, J. Guo, L. He, Y. Ihm, E. Mamontov, Y. B. Melnichenko, R. J. Olsen, S. J. Pennycook, M. B. Stone, H. Zhang and N. C. Gallego, J. Mater. Chem. A, 2013, 1, 9341–9350 RSC.
- C. I. Contescu, D. Saha, N. C. Gallego, E. Mamontov, A. I. Kolesnikov and V. V. Bhat, Carbon, 2012, 50, 1071–1082 CrossRef CAS.
- E. Bahn, O. Czakkel, B. Nagy, K. László, S. Villar-Rodil, J. Tascón, F. Demmel, M. Telling and P. Fouquet, Carbon, 2016, 98, 572–581 CrossRef CAS.
- M. Karlsson, A. Matic, C. S. Knee, I. Ahmed, S. G. Eriksson and L. Börjesson, Chem. Mater., 2008, 20, 3480–3486 CrossRef CAS.
- M. Coduri, S. Casolo, N. Jalarvo and M. Scavini, J. Appl. Crystallogr., 2019, 52, 712–721 CrossRef CAS.
- F. Giannici, D. Messana, A. Longo and A. Martorana, J. Phys. Chem. C, 2011, 115, 298–304 CrossRef CAS.
- Y. X. Xiang, G. R. Zheng, G. M. Zhong, D. W. Wang, R. Q. Fu and Y. Yang, Solid State Ionics, 2018, 318, 19–26 CrossRef CAS.
- P. Colomban and A. Slodczyk, Eur. Phys. J.: Spec. Top, 2012, 213, 171–193 CAS.
- M. Karlsson, Phys. Chem. Chem. Phys., 2015, 17, 26–38 RSC.
- R. Hempelmann, Phys. B, 1996, 226, 72–77 CrossRef CAS.
- C. Poinsignon, Solid State Ionics, 1989, 35, 107–113 CrossRef.
- N. Jalarvo, O. Gourdon, Z. H. Bi, D. Gout, M. Ohl and M. P. Paranthaman, Chem. Mater., 2013, 25, 2741–2748 CrossRef CAS.
- N. Jalarvo, L. Stingaciu, D. Gout, Z. H. Bi, M. P. Paranthaman and M. Ohl, Solid State Ionics, 2013, 252, 12–18 CrossRef CAS.
- A. al-Wahish, N. Jalarvo, Z. H. Bi, K. W. Herwig, C. Bridges, M. P. Paranthaman and D. Mandrus, J. Phys. Chem. C, 2014, 118, 20112–20121 CrossRef CAS.
- A. al-Wahish, D. Armitage, U. al-Binni, B. Hill, R. Mills, N. Jalarvo, L. Santodonato, K. W. Herwig and D. Mandrus, Rev. Sci. Instrum., 2015, 86, 095102 CrossRef PubMed.
- C. Eklöf-Österberg, R. Nedumkandathil, U. Häussermann, A. Jaworski, A. J. Pell, M. Tyagi, N. H. Jalarvo, B. Frick, A. Faraone and M. Karlsson, J. Phys. Chem. C, 2019, 123, 2019–2030 CrossRef.
- I. Presiado, J. Lal, E. Mamontov, A. I. Kolesnikov and D. Huppert, J. Phys. Chem. C, 2011, 115, 10245–10251 CrossRef CAS.
- H. Nozaki, M. Harada, S. Ohta, N. H. Jalarvo, E. Mamontov, I. Watanabe, Y. Miyake, Y. Ikedo and J. Sugiyama, J. Phys. Soc. Jpn., 2013, 82, SA004 CrossRef.
- H. Nozaki, M. Harada, S. Ohta, I. Watanabe, Y. Miyake, Y. Ikedo, N. H. Jalarvo, E. Mamontov and J. Sugiyama, Solid State Ionics, 2014, 262, 585–588 CrossRef CAS.
- M. J. Klenk, S. E. Boeberitz, J. Dai, N. H. Jalarvo, V. K. Peterson and W. Lai, Solid State Ionics, 2017, 312, 1–7 CrossRef CAS.
- R. L. Sacci, M. L. Lehmann, S. O. Diallo, Y. Q. Q. Cheng, L. L. Daemen, J. F. Browning, M. Doucet, N. J. Dudney and G. M. Veith, J. Phys. Chem. C, 2017, 121, 11083–11088 CrossRef CAS.
- T. Heitmann, G. Hester, S. Mitra, T. Calloway, M. S. Tyagi, A. Miskowiec, S. Diallo, N. Osti and E. Mamontov, Solid State Ionics, 2019, 334, 95–98 CrossRef CAS.
- X. M. Liu, Y. Chen, Z. D. Hood, C. Ma, S. H. Yu, A. Sharafi, H. Wang, K. An, J. Sakamoto, D. J. Siegel, Y. Q. Cheng, N. H. Jalarvo and M. F. Chi, Energy Environ. Sci., 2019, 12, 945–951 RSC.
- S. Kumar, M. K. Gupta, R. Mittal, N. H. Jalarvo, S. Mukhopadhyay, R. Shukla, S. N. Achary, A. I. Kolesnikov, A. K. Tyagi and S. L. Chaplot, ACS Appl. Energy Mater., 2022, 5, 14119–14126 CrossRef CAS.
- M. Chi, X. Liu, J. Hachtel, N. H. Jalarvo and J. S. Yongqiang Cheng, Microsc. Microanal., 2018, 24, 1496–1497 CrossRef.
- Q. Chen, N. H. Jalarvo and W. Lai, J. Mater. Chem. A, 2020, 8, 25290–25297 RSC.
- M. K. Gupta, R. Mittal, S. Kumar, B. Singh, N. H. Jalarvo, O. Delaire, R. Shukla, S. N. Achary, A. I. Kolesnikov, A. K. Tyagi and S. L. Chaplot, J. Mater. Chem. A, 2021, 9, 16129–16136 RSC.
- M. K. Gupta, J. X. Ding, N. C. Osti, D. L. Abernathy, W. Arnold, H. Wang, Z. Hood and O. Delaire, Energy Environ. Sci., 2021, 14, 6554–6563 RSC.
- O. Maus, M. T. Agne, T. Fuchs, P. S. Till, B. Wankmiller, J. M. Gerdes, R. Sharma, M. Heere, N. Jalarvo, O. Yaffe, M. R. Hansen and W. G. Zeier, J. Am. Chem. Soc., 2023, 145, 7147–7158 CrossRef CAS PubMed.
- S. Kumar, M. K. Gupta, R. Mittal, S. Sundaramoorthy, A. Choudhury, N. C. Osti, A. I. Kolesnikov, M. B. Stone, Y. Q. Cheng and S. L. Chaplot, J. Mater. Chem. A, 2023, 11, 23940–23949 RSC.
- Q. Zhang, C. Y. Zhang, Z. D. Hood, M. F. Chi, C. D. Liang, N. H. Jalarvo, M. Yu and H. Wang, Chem. Mater., 2020, 32, 2264–2271 CrossRef CAS.
- A. J. E. Rettie, J. X. Ding, X. Q. Zhou, M. J. Johnson, C. D. Malliakas, N. C. Osti, D. Y. Chung, R. Osborn, O. Delaire, S. Rosenkranz and M. G. Kanatzidis, Nat. Mater., 2021, 20, 1683 CrossRef CAS PubMed.
- M. K. Gupta, J. X. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Adv. Energy Mater., 2022, 12, 13 Search PubMed.
- E. Mamontov, Solid State Ionics, 2016, 296, 158–162 CrossRef CAS.
- E. Gabriel, Z. Wang, V. V. Singh, K. Graff, J. Liu, C. Koroni, D. Hou, D. Schwartz, C. Li, J. Liu, X. Guo, N. C. Osti, S. P. Ong and H. Xiong, J. Am. Chem. Soc., 2024, 146, 15108–15118 CrossRef CAS PubMed.
- A. Pramanick, X. P. Wang, C. Hoffmann, S. O. Diallo, M. R. V. Jorgensen and X. L. Wang, Phys. Rev. B, 2015, 92, 174103 CrossRef.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. H. Law, X. E. Li, F. Foglia, A. Walsh, B. C. O'Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- E. M. Mozur, A. E. Maughan, Y. Q. Cheng, A. Hug, N. Jalarvo, L. L. Daemen and J. R. Neilson, Chem. Mater., 2017, 29, 10168–10177 CrossRef CAS.
- A. A. Koegel, E. M. Mozur, I. W. H. Ostwald, N. H. Jalarvo, T. R. Prisk, M. Tyagi and J. R. Neilson, J. Am. Chem. Soc., 2022, 144, 1313–1322 CrossRef CAS PubMed.
- X. W. Gong, O. Voznyy, A. Jain, W. J. Liu, R. Sabatini, Z. Piontkowski, G. Walters, G. Bappi, S. Nokhrin, O. Bushuyev, M. J. Yuan, R. Comin, D. McCamant, S. O. Kelley and E. H. Sargent, Nat. Mater., 2018, 17, 550 CrossRef CAS PubMed.
- A. Johnston, G. Walters, M. I. Saidaminov, Z. R. Huang, K. Bertens, N. Jalarvo and E. H. Sargent, ACS Nano, 2020, 14, 15107–15118 CrossRef CAS PubMed.
- G. Ehlers, E. Mamontov, M. Zamponi, A. Faraone, Y. Qiu, A. L. Cornelius, C. H. Booth, K. C. Kam, R. Le Toquin, A. K. Cheetham and J. S. Gardner, J. Phys.: Condens. Matter, 2008, 20, 235206 CrossRef CAS PubMed.
- G. Ehlers, E. Mamontov, M. Zamponi, K. C. Kam and J. S. Gardner, Phys. Rev. Lett., 2009, 102, 016405 CrossRef CAS PubMed.
- G. Ehlers, E. Mamontov, M. Zamponi, K. C. Kam and J. S. Gardner, J. Phys.: Conf. Ser., 2009, 251, 012003 CrossRef.
- G. Ehlers, A. Huq, S. O. Diallo, C. Adriano, K. C. Rule, A. L. Cornelius, P. Fouquet, P. G. Pagliuso and J. S. Gardner, J. Phys.: Condens. Matter, 2012, 24, 076005 CrossRef CAS PubMed.
- T. Chatterji, N. Jalarvo and A. Szytula, Solid State Commun., 2013, 161, 42–45 CrossRef CAS.
- T. Chatterji and N. Jalarvo, J. Phys.: Condens. Matter, 2013, 25, 286003 CrossRef CAS PubMed.
- T. Chatterji, N. Jalarvo, C. M. N. Kumar, Y. Xiao and T. Brückel, J. Phys.: Condens. Matter, 2013, 25, 156002 CrossRef PubMed.
- C. M. N. Kumar, Y. Xiao, H. S. Nair, J. Voigt, B. Schmitz, T. Chatterji, N. H. Jalarvo and T. Brückel, J. Phys.: Condens. Matter, 2016, 28, 476001 CrossRef CAS PubMed.
- M. Valldor, R. P. Hermann, J. Wuttke, M. Zamponi and W. Schweika, Phys. Rev. B, 2011, 84, 224426 CrossRef.
- V. O. Garlea, R. Jin, E. Garlea, G. Ehlers, E. Mamontov, D. B. Myers, F. Xie and R. Custelcean, Phys. Rev. B, 2012, 86, 094434 CrossRef.
- J. S. Gardner, G. Ehlers and S. O. Diallo, Chin. J. Phys., 2012, 50, 256–261 CAS.
- A. M. Samarakoon, M. Takahashi, D. Zhang, J. Yang, N. Katayama, R. Sinclair, H. D. Zhou, S. O. Diallo, G. Ehlers, D. A. Tennant, S. Wakimoto, K. Yamada, G. W. Chern, T. J. Sato and S. H. Lee, Sci. Rep., 2017, 7, 12053 CrossRef CAS PubMed.
- A. Scheie, O. Benton, M. Taillefumier, L. D. C. Jaubert, G. Sala, N. Jalarvo, S. M. Koohpayeh and N. Shannon, Phys. Rev. Lett., 2022, 129, 217202 CrossRef CAS PubMed.
- D. Vaknin, V. O. Garlea, F. Demmel, E. Mamontov, H. Nojiri, C. Martin, I. Chiorescu, Y. Qiu, P. Kögerler, J. Fielden, L. Engelhardt, C. Rainey and M. Luban, J. Phys.: Condes. Matter, 2010, 22, 466001 CrossRef CAS PubMed.
- S. E. Stavretis, E. Mamontov, D. H. Moseley, Y. Q. Cheng, L. L. Daemen, A. J. Ramirez-Cuesta and Z. L. Xue, Phys. Chem. Chem. Phys., 2018, 20, 21119–21126 RSC.
- T. Xie, S. E. Nikitin, A. I. Kolesnikov, E. Mamontov, L. M. Anovitz, G. Ehlers, I. Huskic, T. Friscic and A. Podlesnyak, Phys. Rev. B, 2021, 103, 024402 CrossRef CAS.
- M. S. Bryan, T. R. Prisk, T. E. Sherline, S. O. Diallo and P. E. Sokol, Phys. Rev. B, 2017, 95, 144509 CrossRef.
- P. A. Seeger, L. L. Daemen and J. Z. Larese, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 604, 719–728 CrossRef CAS.
- G. E. Granroth, A. I. Kolesnikov, T. E. Sherline, J. P. Clancy, K. A. Ross, J. P. C. Ruff, B. D. Gaulin and S. E. Nagler, J. Phys.: Conf. Ser., 2010, 251, 012058 CrossRef.
- E. Mamontov, Y. Q. Cheng, L. L. Daemen, J. K. Keum, A. I. Kolesnikov, D. Pajerowski, A. Podlesnyak, A. J. Ramirez-Cuesta, M. R. Ryder and M. B. Stone, ACS Omega, 2020, 5, 21231–21240 CrossRef CAS PubMed.
- E. Mamontov, Y. Q. Cheng, L. L. Daemen, A. I. Kolesnikov, A. J. Ramirez-Cuesta, M. R. Ryder and M. B. Stone, J. Phys. Chem. Lett., 2020, 11, 10256–10261 CrossRef CAS PubMed.
- E. Mamontov, Y. Q. Cheng, L. L. Daemen, A. I. Kolesnikov, A. J. Ramirez-Cuesta, M. R. Ryder and M. B. Stone, Chem. Phys. Lett., 2021, 777, 138727 CrossRef CAS PubMed.
- L. Riva, S. F. Yuan, X. Yin, L. Martin-Sancho, N. Matsunaga, L. Pache, S. Burgstaller-Muehlbacher, P. D. De Jesus, P. Teriete, M. V. Hull, M. W. Chang, J. F. W. Chan, J. L. Cao, V. K. M. Poon, K. M. Herbert, K. Y. Cheng, T. T. H. Nguyen, A. Rubanov, Y. Pu, C. Nguyen, A. Choi, R. Rathnasinghe, M. Schotsaert, L. Miorin, M. Dejosez, T. P. Zwaka, K. Y. Sit, L. Martinez-Sobrido, W. C. Liu, K. M. White, M. E. Chapman, E. K. Lendy, R. J. Glynne, R. Albrecht, E. Ruppin, A. D. Mesecar, J. R. Johnson, C. Benner, R. Sun, P. G. Schultz, A. I. Su, A. García-Sastre, A. K. Chatterjee, K. Y. Yuen and S. K. Chanda, Nature, 2020, 586, 113 CrossRef CAS PubMed.
- M. Prager and A. Heidemann, Chem. Rev., 1997, 97, 2933–2966 CrossRef CAS PubMed.
- E. Mamontov, L. L. Daemen, E. Novak and M. B. Stone, Medicina, 2021, 57, 1343 CrossRef PubMed.
- P. Martel and B. M. Powell, Solid State Commun., 1981, 39, 107–110 CrossRef CAS.
- N. A. Hewish, J. E. Enderby and W. S. Howells, J. Phys. C: Solid State Phys., 1983, 16, 1777–1791 CrossRef CAS.
- M. L. Hoarfrost, M. Tyagi, R. A. Segalman and J. A. Reimer, J. Phys. Chem. B, 2012, 116, 8201–8209 CrossRef CAS PubMed.
- T. Burankova, R. Hempelmann, A. Wildes and J. P. Embs, J. Phys. Chem. B, 2014, 118, 14452–14460 CrossRef CAS PubMed.
- T. Burankova, J. F. M. Cardozo, D. Rauber, A. Wildes and J. P. Embs, Sci. Rep., 2018, 8, 16400 CrossRef PubMed.
- A. Arbe, P. de Molina, F. Alvarez, B. Frick and J. Colmenero, Phys. Rev. Lett., 2016, 117, 185501 CrossRef CAS PubMed.
- A. Arbe, G. Nilsen, J. Stewart, F. Alvarez, V. Sakai and J. Colmenero, Phys. Rev. Res., 2020, 2, 022015 CrossRef CAS.
- A. Arbe, G. Nilsen, M. Devonport, B. Farago, F. Alvarez, J. González and J. Colmenero, J. Chem. Phys., 2023, 158, 184502 CrossRef CAS PubMed.
- A. Nidriche, M. Moulin, P. Oger, J. R. Stewart, L. Mangin-Thro, W. Schmidt, G. Kneller and J. Peters, PRX Life, 2024, 2, 013005 CrossRef.
- E. Mamontov, D. R. Cole, S. Dai, M. D. Pawel, C. D. Liang, T. Jenkins, G. Gasparovic and E. Kintzel, Chem. Phys., 2008, 352, 117–124 CrossRef CAS.
- N. Takahashi, K. Shibata, Y. Kawakita, K. Nakajima, Y. Inamura, T. Nakatani, H. Nakagawa, S. Fujiwara, T. J. Sato, I. Tsukushi, F. Mezei, D. A. Neumann, H. Mutka and M. Arai, J. Phys. Soc. Jpn., 2011, 80, SB007 CrossRef.
- M. Arai, R. Kajimoto, M. Nakamura, Y. Inamura, K. Nakajima, K. Shibata, N. Takahashi, J. Suzuki, S. Takata, T. Yamada and S. Itoh, J. Phys. Soc. Jpn., 2013, 82, SA024 CrossRef.
- B. Frick, E. Mamontov, L. van Eijck and T. Seydel, Z. Phys. Chem., 2010, 224, 33–60 CrossRef CAS.
- M. Appel, B. Frick and A. Magerl, Phys. B-Condens. Matter, 2019, 562, 6–8 CrossRef CAS.
- N. Tsapatsaris, P. K. Willendrup, R. E. Lechner and H. N. Bordallo, EPJ Web Conf., 2014, 83, 03015 CrossRef.
- N. Tsapatsaris, R. E. Lechner, M. Markó and H. N. Bordallo, Rev. Sci. Instrum., 2016, 87, 4961569 CrossRef PubMed.
- E. Mamontov, C. Boone, M. J. Frost, K. W. Herwig, T. Huegle, J. Y. Y. Lin, B. McCormick, W. McHargue, A. D. Stoica, P. Torres and W. Turner, Rev. Sci. Instrum., 2022, 93, 0086451 CrossRef PubMed.
- E. Mamontov, H. N. Bordallo, O. Delaire, J. Nickels, J. Peters, G. J. Schneider, J. C. Smith and A. P. Sokolov, EPJ Web Conf., 2022, 272, 02003–02015 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |