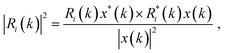Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coherent X-ray imaging of stochastic dynamics
Arnab
Sarkar
 and
Allan S.
Johnson
and
Allan S.
Johnson
 *
*
IMDEA Nanoscience, Calle Faraday 9, 28049, Madrid, Spain. E-mail: allan.johnson@imdea.org
First published on 25th June 2024
Abstract
Condensed phase systems often exhibit a mixture of deterministic and stochastic dynamics at the nanoscale which are essential to understanding their function, but can be challenging to study directly using conventional imaging methods. Coherent X-ray imaging has emerged as a powerful tool for studying both nanoscale stuctures and dynamics in condensed phase systems, including stochastic dynamics, but the requirement to obtain single-shot images in order to obtain freeze-frame images of the stochastic dynamics means the X-ray fluxes used must be very high, potentially destroying the samples. This prevents coherent imaging from being applied to complex systems like tracking the motion of charge carriers or domain fluctuations in quantum materials. Here we show that, by leveraging the coherence intrinsic to these methods, we can separate out the stochastic and deterministic contributions to a coherent X-ray scattering pattern, returning real space images of the deterministic contributions and the momentum spectrum of the stochastic contributions. We further show that, for several typical and important classes of fluctuations, we can return real space images of the mean fluctuations. We demonstrate this approach by numerically simulating the imaging of stochastic polaron seperation following photoexcitation and by recovering the spectral properties of fluctuating domain walls. Our versatile approach will enable the direct recovery of the spatial, spectral and temporal properties of stochastic material dynamics in a wide variety of systems currently unobtainable with existing methods.
Introduction
X-ray microscopy is a powerful tool for imaging nanoscale structure in a wide range of biological and materials systems. The ability to return real space images with nanometric resolution, chemical sensitivity and spectroscopic information has proved indispensable in understanding catalytic system, light-harvesting systems, structural mechanics and devices.1–4 Measuring dynamics at the sub-microsecond timescale in such systems, however, has proven much more challenging. X-ray optics are often incompatible with relevant sample geometries, and scanning methods, coherent or incoherent, require highly repeatable events to build up images of dynamical processes and are incapable of returning information on the real space dynamic fluctuations.5 Recently great progress has occurred in imaging dynamics using coherent lensless X-ray imaging methods, where X-ray optics are dispensed with and instead the spatial coherence of the beam is leveraged to obtain diffraction patterns which can be numerically inverted to return real space images.6 In the case of coherent diffractive imaging (CDI) this inversion is performed using iterative phase reconstruction algorithms,7,8 while in the related technique of Fourier transform holography (FTH), holographic reference holes add a local oscillator term and allow direct inversion via Fourier transform.9 As full-field imaging methods both return a complete picture of the object simultaneously, and so are well suited for imaging dynamical processes as well.5Both FTH and CDI have recently been leveraged to image real space dynamics in quantum materials,10,11 but acquiring videos of dynamical processes remains extremely challenging. In order to form an image of a dynamical process it is necessary to capture enough photons on the detector, while ensuring that they scattered from the sample within the time window of the event. For even quite slow nanoscale processes this becomes challenging, as the X-ray fluxes required would introduce tremendous heating and because imaging detectors are generally limited to, at best, kilohertz acquisition rates. The aforementioned studies10,11 and other X-ray imaging experiments12–18 have overcome this limitation by using stroboscopic (pump–probe) measurements. In such measurements the dynamical process is repeatedly initiated and a weak pulse of X-rays captures a partial frame each. These weak pulses can originate from various sources like an attenuated X-ray free electron laser,10 synchrotron facility12 or high-harmonic generation.11 The partial frames are then averaged to obtain sufficient signal to construct an image. The major limitation here is, of course, that it needs to be possible to repeatedly initiate the dynamical process.19 In case of pinned structures, either by defects or sample geometry, mean dynamics can be extracted from stroboscopic measurements10,12 but it rules out measurement of stochastic processes, where the system evolves through a different path in phase space during each measurement.
Such stochastic processes are widespread at the nanoscale, where thermal or quantum effects become highly significant.20–22 For instance quantum materials often show stochastic motion of charge carriers, vortices, or domain walls.21,23,24 Because of the difficulty in forming real space images of such stochastic processes, fluctuations are generally studied through alternative methods that return the statistical properties.25–28 Unlike imaging techniques of non-repeatable events with visible radiation (i.e. STAMP),29 single shot imaging in X-ray range is not feasible due to limitation of available optics. Established methods like fluctuation microscopy30 return only information on static fluctuations, i.e. deviations around a mean ordering and do not retrieve any information on temporal fluctuations. A fully coherent source returns a diffraction pattern in which fluctuations are directly represented in the speckle. X-ray photon correlation spectroscopy (XPCS) can be used to study dynamics of fluctuations by returning the speckle pattern as a function of time,31 but it makes no distinction between pinned and non-pinned defects and does not return real-space information on pinning. Only recently has real space imaging been attempted using coherent methods with the methodology of coherent correlation imaging (CCI),32 in which partial frames are taken faster than the timescale for the fluctuations. Similar frames are then grouped until the signal-to-noise is sufficient to reconstruct real images. CCI is a major methodological advance, but still requires enough flux in order to ensure the partial frames are sufficiently complete to allow for sorting, and furthermore requires a discrete number of different fluctuation parameters in order for the grouping procedure to be meaningful. Alternatively, the advent of high-intensity free-electron lasers has enabled single-shot imaging with femtosecond pulses,33 which should allow snapshots of fluctuations, though this may not be possible in many systems due to damage concerns.7 Single-shot measurements which destroy the sample are commonly performed at free-electron lasers,34 but cannot track events like pinning as defects or other events will not be identical across different samples. In systems where non-destructive single-shot imaging of the fluctuations is not feasible, the best case scenario would be to return real-space information on the deterministic part of states or reaction pathways, while simultaneously returning directly the statistical properties of the fluctuations independently.
Here, we demonstrate a new method for separating the stochastic and mean (deterministic) contributions in coherent imaging methods which we dub coherence isolated diffractive imaging (CIDI). By introducing fluctuation-free interferometric references to a coherent scattering pattern in an FTH arrangement, we show that the mean contribution is fully encoded in the coherent interferometry data. Conversely, the fluctuations are not reflected in the interferogram, allowing the mean and stochastic contributions to be separated post-hoc through a fully analytic algorithm. In particular CIDI allows us to recover the full momentum distribution of fluctuations as a function of external parameters like photon energy or pump–probe delay, allowing us to return important information on their size and properties. This information is not readily accessible with any existing methodology, and CIDI could have a unique role to play in understanding systems as diverse as light-harvesting complexes, superconductors, and catalytic systems.
Separation of coherent and incoherent contributions to X-ray holography
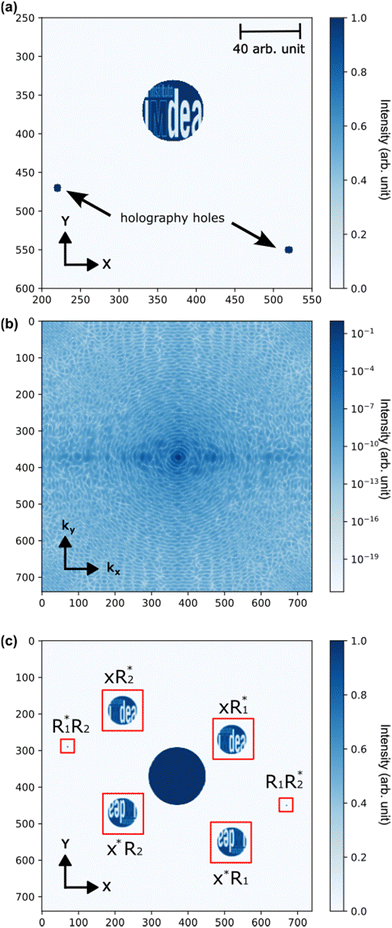
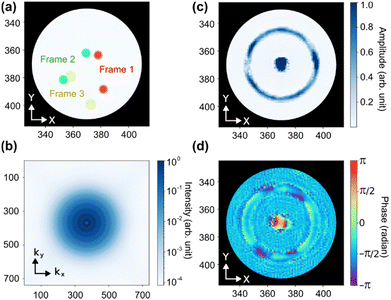
We consider the case where a coherent electromagnetic plane-wave scatters from a finite sample and the diffraction pattern is recorded on detector, in an FTH-like arrangement. In X-ray holography a mask constrains the object to an aperture of radius D. Small transmissive reference holes are milled all the way through the sample and mask at a position >4D away from the center. As the sample is milled through, there is no material to impart fluctuations onto the transmitted radiation and so the transmitted light through this hole forms a stable interferometric reference (Fig. 1a), allowing retrieval of the image directly from the corresponding diffraction pattern (Fig. 1b) by a simple Fourier transform (Fig. 1c).9 In the presence of stochastic dynamics occurring faster than the exposure time, or alternatively when averaging over multiple partial frames, the scattering pattern on the detector appears as the incoherent sum of the diffraction pattern of all the configurations.The simple intuitive idea behind CIDI is that the “static” or, more precisely, deterministic contributions lead to the same scattering pattern and fringe positions in each frame, while the stochastic portion leads to a changing fringe position between each exposure. This means the fringe visibility will be lost for the stochastic portion but remain for the deterministic portion. Because FTH is an interferometric technique, it is sensitive to interferometric fringes only and insensitive to the low-fringe contrast stochastic background.35 By applying FTH analysis we can then separate these two components and extract the scattering pattern of the stochastic contribution alone.
Analytic theory
The total electric field from the sample and holography holes can be written as a sum of three components:| E(r,t) = x(r) + R(r) + S(r,t). | (1) |
Here, x(r), R(r) and S(r,t) are contributions from deterministic part of the object, reference hole, and stochastic part, respectively, while r denotes the spatial coordinates and t time. Note that this could be either real time, in the case of an extended exposure,32 or frame number in the case of a stroboscopic measurement.10,11 Both the static and stochastic parts are restricted to the object aperture, i.e. x(r > D) = S(r > D) = 0. By definition the time average of the stochastic portion 〈S(r,t)〉 = 0; any non-vanishing contribution (for instance an overall decrease in transmission across the entire sample) is included in x(r).
The time averaged Fourier transform of electric field squared, which is the quantity actually measured at the detector in coherent imaging experiments, can be written as:
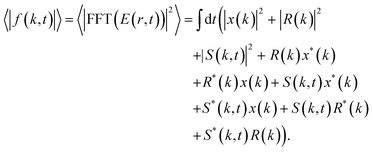 | (2) |
R(k) is the Fourier transform of the reference hole R(r), x(k) is the Fourier transform of the static contribution, S(k,t) is the Fourier transform of S(r,t), and 〈〉 denotes a time averaged quantity. The cross-correlations with the stochastic term vanish due to time averaging since 〈S(k,t)〉 = 0 and the expression simplifies to:
| 〈|FFT(E(r,t))|2〉 = |x(k)|2 + |R(k)|2 + |S(k)|2 + R(k)x*(k) + R*(k)x(k). | (3) |
| |S(k)|2 = 〈|FFT(E(r,t))|2〉 − |x(k)|2 + |R(k)|2 − R(k)x*(k) − R*(k)x(k). | (4) |
To evaluate this expression, we need to find the autocorrelation terms of static part of the sample and holography hole. This can be done by applying a simple holographic analysis which extracts R*(k)x(k) directly (Fig. 1c). In the limit where R(x) = δ(x), i.e. the standard holographic case,9 this also yields x(k) and the full expression can be evaluated, returning |S(k)|2.
A significant improvement can be obtained by considering the case where there are two holography holes36,37 (see Fig. 1a), which allows us to extract all the autocorrelation terms separately without the need for the small aperture approximation. Considering electric fields from two holographic apertures R1(r) and R2(r), we can rewrite the eqn (4):
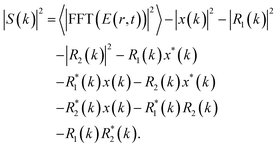 | (5) |
The first term of the right-hand side of this equation is the total diffraction pattern in presence of both the reference holes (Fig. 1b), while the others are the various cross and autocorrelation terms. All the cross-correlation terms can be directly extracted from different parts of the Fourier transform of retrieved holography image, as indicated in Fig. 1c. This then allows us to uniquely extract the autocorrelation terms as follows.
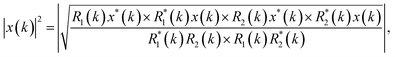 | (6) |
where the × operator is used to separate each pair of constituent cross-correlation terms that can be identified directly from the holography image. Thus, the fluctuation spectrum can fully be retrieved without any apriori assumptions.
The ability of an FTH experiment to directly return the fluctuation spectrum via CIDI analysis is the main finding of this article. While fluctuations are often studied via diffraction measurements, previous methods are unable to separate the contributions from the fluctuations and the average behaviour directly; for instance, electron diffraction studies25,27,38 on topological defects yield the spacing between the fluctuating topological defects, rather than the scattering from the defects themselves. As we will show in the rest of this article, CIDI allows us to extract the spatial and spectral properties of fluctuations directly. In particular, the fluctuation spectrum is intrinsically linked to the pair-distribution function of the fluctuations,39 and can in some circumstances be inverted directly to yield it, while the contrast mechanism of X-ray absorption naturally gives access to all the strengths of X-ray absorption spectroscopy like elemental selectivity and sensitivity to electronic and structural changes.5
Finally, we note that because the summation of the scattering patterns is incoherent (different frames) the signal levels of the stochastic and deterministic patterns both scale linearly with the number of exposures or overall signal level. All operations thereafter are linear, and so the relative signal levels of these two contributions are also linearly related to their actual contributions to the transmission of the object. Another interesting and perhaps counterintuitive feature is that while holographic imaging usually does not allow imaging of features smaller than the size of the holographic reference aperture d,37 the CIDI procedure isolates the fluctuation spectrum up to the maximum momentum k supported by the detector or wavelength of like. The main effect of the finite size of the reference aperture is to introduce zeros in the Fourier transform Ri(k) at k = 1/d. This introduces divergences which must be masked when extracting the autocorrelation features, but the momentum information at higher k remains meaningful, unlike in FTH where it introduces a phase ambiguity. Numerically, we routinely recover meaningful information at k far higher than 1/d.
Coherent diffractive imaging of a stochastic spectrum
While direct access to the momentum spectrum of the fluctuations is already a powerful new capability, enabling the extraction of important information like characteristic length scales, spectral dependencies and temporal evolution, the unique geometry used in X-ray holography actually allows us to go further still. Because the fluctuations are fully contained inside the mask, they naturally fulfil the confined sample requirement for CDI reconstruction.40,41 This gives the opportunity to, for certain types of fluctuations, retrieve the phase information of the fluctuating objects by using CDI algorithms and return real-space images of the fluctuations. This naturally depends on how well the average fluctuation spectrum |S(k)|2 corresponds to the spectrum of the fluctuation, since CDI requires the spectrum in k-space corresponds to a unique object in real space – a condition which does not have to be satisfied for an incoherent averaging.Nevertheless, there are two reasons to consider this approach. The first is that for a particular class of fluctuation – position only fluctuations – the correspondence between the average fluctuation spectrum |S(k)|2 and the spectrum of each individual fluctuation is exactly equal. This is because fluctuations in position, for example a quasiparticle nucleating in a different region each acquisition, means only fluctuations in phase in k-space, which are lost regardless. This, in normal CDI, leads to ambiguity in absolute positioning, but here allows to exactly reconstruct such fluctuations. The second reason CDI may be considered to yield interesting insight, even in the case where exact correspondence cannot be assured, is simply because CDI is well known practically to converge to representative mean solutions in many such cases.42 This can be seen in recent work where CDI reconstructions of fluctuating magnetic domain patterns converged to the mean pattern.32 Similar behaviour has long been known in the very closely related problem of numerical ultrafast pulse reconstruction.35
Numerical demonstrations
To verify the analytic theory, we have numerically simulated a variety of different scenarios and compare the output of the CIDI analysis to the input numerical data. In all cases we consider the FTH geometry shown in Fig. 1a, and then introduce fluctuations into the central image aperture. For simplicity we consider two perfectly circular reference holes with same radius, but the analysis is robust with respect to variation in these parameters. Unless otherwise stated, we average over 5000 frames in order to realize the statistical limit for the fluctuations.Single vortex dynamics
As a first example, we consider a single vortex (a two-dimensional Gaussian function) appearing at an arbitrary location inside the object mask. We model the case where the stochastic dynamics of the vortex are faster than the acquisition rate, and the probability of finding a single vortex at a particular point on the sample is random and uncorrelated. In Fig. 2a, a representative image of three frames is shown, where different colors (red, green and yellow) represent different snapshots of the vortex with the static background removed. In this case we don’t observe any spatial information for the vortex in the average image (not shown) – the effect of the vortex is just to change the average transmission of the sample. By applying the CIDI algorithm and numerically subtracting the static information, however, we isolate the momentum spectrum of the vortices as shown in Fig. 2c. The fluctuation spectrum calculated directly from the introduced fluctuations, without application of the CIDI procedure, is shown in Fig. 2b and matches exactly to the retrieved spectrum. The fluctuation spectrum in this case is a Gaussian distribution in momentum space with a dip at the center. This dip corresponds to the Airy disk resulting from the change in average transmission introduced by the vortices, which is reflected in |x(k)|2 rather than in |S(k)|2.As the fluctuations introduced here are in position only, we can next apply CDI to the retrieved spectrum. Using the known aperture size extracted from the holography analysis36 as our mask in the object plane, we apply 500 iterations of a modified relaxed alternating reflections algorithm.43 As described above, we mask regions where the retrieved fluctuation spectrum diverges due to zeroes in Ri(k) and allow the solution to vary freely in these regions. Good convergence is found for all reported CDI reconstructions within this article. Fig. 2d shows the reconstruction fluctuation object, which matches identically with the original vortex structure (red dotted line on side panels) apart from a small DC offset corresponding to the average transmission change.
Extending the same method to extract information about multiple uncorrelated vortices with arbitrary locations is straightforward. If we have more than one vortex, the resulting interference pattern depends on the specific configuration, and the fluctuation spectrum averages over these non-identical patterns. The high-frequency fringes, corresponding to the separation between different vortices, averages away over many configurations, while the overall Gaussian structure corresponding to the structure of each individual vortex survives this process.
Polaron and charge carrier pairs
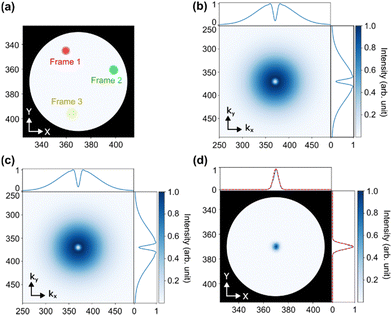
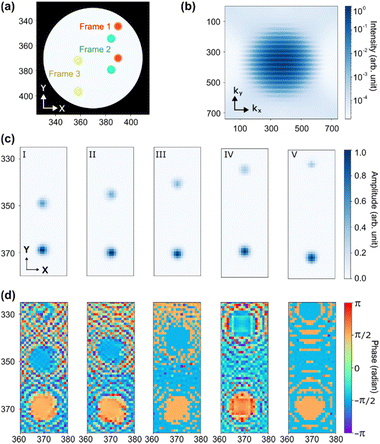
We next simulate a pair of particles, for instance polarons or other charge carriers.44 We represent them as two Gaussians with equal but opposite changes in X-ray transmission, roughly corresponding to the shifts in absorption expected for a positive and negative charge carrier.44 This is very general situation, and we simulate a variety of different configurations to understand the utility of the method under different scenarios. Initially we simulate a pair of polarons with opposite sign separated by a fixed distance along one spatial axis corresponding to, for instance, a snapshot of ballistic motion following photoexcitation. Fig. 3a shows three snapshot frames of the polaron pair subtracting the static background of the object. At each frame, the polaron pair appears at an arbitrary position but keeping the same relative distance and orientation. We do not, however, constrain both polarons to appear within the object aperture, and so there are frames in which only one polaron contributes to the X-ray scattering. After applying the CIDI algorithm we recover the scattering pattern shown in Fig. 3b. The fringe pattern is immediately reminiscent of that from a double slit experiment, with the fringes encoding the separation of the sources and their relative orientation. Note that here, because the net contribution of the positive and negative polarons to the transmission is zero, the Airy disk feature at k = 0 does not appear. We can then apply CDI to the recovered fringe pattern in Fig. 3b following the same procedure as for the single vortices. We successfully retrieve the amplitude and phase (Fig. 3c and d) of the polaron pairs, unambiguously showing the pattern results from a pair of sources with opposite sign, while also successfully recovering their size. We further consider the case of a pump–probe experiment in which at different delay times the polaron separation increases (I–V). As can be seen we clearly resolved the increasing separation, and CIDI can be used to track polaron motion in stroboscopic measurements.It is, however, fairly unlikely that most charge carriers or other paired particles will propagate along only one axis. Thus we simulated the case where the relative distance remains same but both the position and orientation of the polaron pairs is random for each frame, as shown in Fig. 4a. This is naturally a much more challenging scenario – it no longer corresponds to the case of a position only fluctuation, and so the fluctuation spectrum no longer maps to the momentum spectrum of a singular object as in the previous cases. In particular, the clear fringe pattern observed in Fig. 3b is blurred out by rotational averaging and we observe a series of rings in the fluctuation spectrum as shown in Fig. 4b. Nevertheless, clear oscillations in the radial momentum are still observable, encoding the relative separation of the polarons. We apply CDI reconstruction methods to this retrieved pattern and find that we are able to converge to a clear image, a central peak within a large ring (Fig. 4c and d). The radius of ring matches the separation of the polaron pairs, while the width of the ring and of the central aperture encodes the size of the polarons. The phase difference between the inner and outer ring furthermore matches the phase shift between the two polarons. Thus we are able to return a range of quantitative information even in this significantly more challenging scenario. We briefly note that in the case where the average separation of the polarons is also statistical, for instance in a diffusive scenario, the separation of the polarons and their relative sizes would be convolved, preventing such direct assignment, though properties such as velocity and relative phase would still be resolvable.
Extracting the properties of domain walls
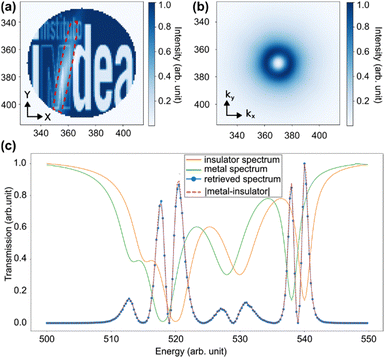
Finally we consider the case of fluctuating domain walls.45 Here we simulate the case of metallic domain walls forming at random locations between otherwise insulating domains,46 but these results are indicative of other important cases, for instance ferromagnetic domain walls between antiferromagnetic domains.47 In this case the fluctuation takes the form of a stripe with a strong aspect ratio corresponding to the (generally small) width of the domain wall and the (generally long) length of the insulating domain. In the case where the stripes are oriented, for instance along a particular crystal axis,23 it is possible to directly reconstruct the structure and recover the approximate size and shape of the domain walls. However, here we will consider the more general case of randomly oriented and positioned domain walls, as illustrated in Fig. 5a. In this case CDI reconstruction fails to return any relevant information. Nevertheless, CIDI analysis alone is able to return two important parameters about the domain walls: their spectral dependence (and thus metallic character) and their approximate width.We first show the retrieved fluctuation spectrum at one particular photon energy in which there exists contrast between the metallic domain wall and the insulating domains in Fig. 5b. For these simulations we average over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames. The pattern is radially symmetric due to the random orientation of the domain walls. However, we can see the radial distribution is relatively complex due to the DC offset Airy disk effect discussed earlier. In principle if one could uniquely assign the DC changes to the fluctuations, for instance in a static measurement where we cooled to a point where domain walls just begin to form, this term could be fit and removed. In general however, this pattern overlaps strongly with the scattering from the long-axis of the domain walls (vertical in Fig. 5a) and prevents quantitative information being extracted. The high k tails of the distribution, however, correspond to the thin width of the domain walls, and give a qualitative measure of this value. Such information is very difficult to extract from conventional measurements of fluctuations, which usually return the size of the normal, partially ordered background phase25,27,48 and no information on the walls themselves.
000 frames. The pattern is radially symmetric due to the random orientation of the domain walls. However, we can see the radial distribution is relatively complex due to the DC offset Airy disk effect discussed earlier. In principle if one could uniquely assign the DC changes to the fluctuations, for instance in a static measurement where we cooled to a point where domain walls just begin to form, this term could be fit and removed. In general however, this pattern overlaps strongly with the scattering from the long-axis of the domain walls (vertical in Fig. 5a) and prevents quantitative information being extracted. The high k tails of the distribution, however, correspond to the thin width of the domain walls, and give a qualitative measure of this value. Such information is very difficult to extract from conventional measurements of fluctuations, which usually return the size of the normal, partially ordered background phase25,27,48 and no information on the walls themselves.
We next turn to the spectral dependence of the fluctuations and the ability to extract the metallic nature of the domain walls.5 We introduce an absorption spectrum for the insulating phase and for the metallic phase, here characterized by a simple shift to lower photon energies for the metallic phase. We then repeat the simulation varying the transmission of the two phases according to these two spectra, and recover the fluctuation spectrum using CIDI at each photon energy. We note a new dataset is generated for each photon energy, and so the spatial behaviour of the fluctuations is uncorrelated between each photon energy. We then sum the recovered fluctuation spectrum over all k and plot the resulting transmission vs. photon energy. As can be seen, we recover that the spectrum of the fluctuations is the difference between the insulating background and metallic fluctuations. This is in sharp contrast to the average over the whole, pre-CIDI diffraction pattern, which instead returns a weighted average of the insulating and metallic spectra with a simple small shift to lower energies, obscuring the nature of the underlying metallic domain walls.
Partial coherence and other challenges
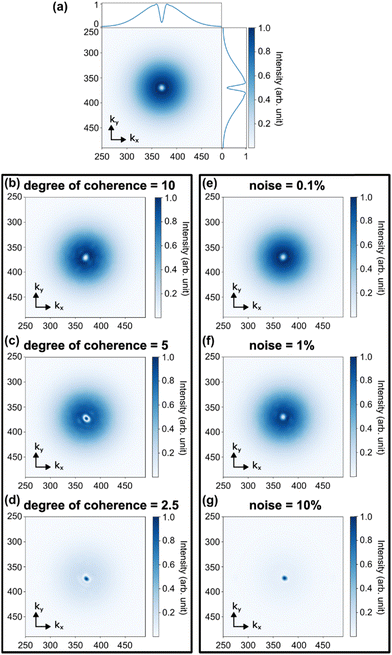
We now briefly discuss the effect of various imperfections in the experimental implementation on the CIDI analysis. Real experiments are characterized by partial coherence of the source and noise, which have been neglected in our simulations until this point.The partial coherence of the source can be quantified using a Gaussian coherence function characterized by a coherence length lcoh.42,49,50 By convoluting the Fourier transform of the coherence function with the otherwise fully coherent diffraction pattern |FFT(E(r,t))|2, we obtain the partially coherent diffraction pattern of the object. To remain dimensionless, we consider the degree of coherence, defined by the ratio (lcoh/L) of the coherence length and the size of the object L, here corresponding to the maximum radial distance of the holographic reference apertures.49 Fluctuation spectrum of a single vortex (Fig. 6a) is simulated for different degrees of coherence (Fig. 6b and c). For high degrees of coherence the reconstruction remains of very high quality, but as the coherence drops a DC peak begins to appear. This is because the primary effect of limited coherence is to suppress the Ri(k)R*j(k) terms, causing an inflation in the normalization of |x(k)|2 in eqn (6), and thus the DC term to eqn (5) to cancel incorrectly. The exact impact of this will depend sensitively on the relative weights of the deterministic and stochastic contributions, but in general degrees of coherence much greater than 1 should be used in order to ensure good normalization. Alternatively scaling factors could be introduced into eqn (5) to correct for this factor, ensuring that the DC component of the fluctuation spectrum is zero. As expected, CIDI thus relies heavily on the high spatial coherence of the source, a requirement which can be satisfied at 4th-generation synchrotron51 or X-ray free electron laser sources.52
We further explore CIDI in the presence of noise. In Fig. 6e–g we add white noise to the total diffraction pattern |FFT(E(r,t))|2 and see the effect on the recovered fluctuation spectrum. We consider different amplitudes of noise, defined with respect to the maximum of the fluctuation spectrum without noise (Fig. 6a). At low noise levels (Fig. 6e and f) the recovered pattern is relatively unperturbed, but at higher noise levels a DC peak appears instead. Both this and the coherence measurements show the importance to CIDI of retrieving accurately the Ri(k)R*j(k) normalization terms, which in turn requires high coherence and good signal to noise.
Conclusions
We have demonstrated a new methodology, CIDI, capable of separating the deterministic and stochastic contributions to a coherent scattering pattern. We show that, from averaged diffraction pattern of multiple snapshots, it is possible to isolate the stochastic part through a FTH-like analysis. Because the stochastic contribution is necessarily confined to a restricted aperture it becomes possible to apply a CDI analysis41 and return a mixture of qualitative and quantitative information regarding the real space behaviour (pair-distribution function) of these fluctuations. Furthermore CIDI can be combined with X-ray spectroscopy5 or other multidimensional studies to isolate the properties of the fluctuations from the deterministic variation of the sample in question. Although holographic apertures are used to provide phase stable references, the spatial resolution that can be obtained is set by the maximum-q captured, and the size of the holographic apertures only weakly affects the returned pattern via a discrete numbers of divergences in the recovered spatial pattern set by the zero of the corresponding Airy disk.37 We note that while here we have focused exclusively on the stochastic portion, the same analysis could be used to remove the stochastic contribution and improve CDI reconstruction of the deterministic part of the signal. CIDI also acts as a diagnostic for the presence of stochastic contributions, and could be used to validate the interpretation of previous experiments.10,11We have demonstrated CIDI in three representative test cases – uncorrelated point-like defects (vortices), polaron-like pairs, and metallic domain walls in an insulating matrix – but there are many more examples of fluctuations at the nanoscale available where CIDI could be applied. For time resolved studies CIDI could shed light if signals observed in recent imaging experiments10,11 are truly due to homogeneous melting of domains or due to stochastic domain changes. However, the use of CIDI to studying fast fluctuations does not actual require the use of femtosecond X-ray pulses; the limitation will be given by the coherence time of the light,53 which determines over what time window scattering contributions can add coherently at the detector. This means it may be possible to image femtosecond fluctuations using broadband continuous wave radiation, for instance the pink-beam of a synchrotron. In the future we foresee CIDI applied to a wide range of challenges where existing methods struggle.
Author contributions
ASJ conceived the study and performed the initial analytic calculations. AS performed the simulations and analysis of the results. Both authors contributed to writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Spanish AIE (projects PID2022-137817NA-I00 and EUR2022-134052). ASJ acknowledges the support of the Ramón y Cajal Program (Grant RYC2021-032392-I). IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centers of Excellence in R&D (MICIN, CEX2020-001039-S).Notes and references
- C. Cao, M. F. Toney, T. K. Sham, R. Harder, P. R. Shearing, X. Xiao and J. Wang, Emerging X-ray imaging technologies for energy materials, Mater. Today, 2019, 34, 132–147 CrossRef.
- E. de Smit, I. Swart, J. F. Creemer, G. H. Hoveling, M. K. Gilles, T. Tyliszczak, P. J. Kooyman, H. W. Zandbergen, C. Morin, B. M. Weckhuysen and F. M. F. de Groot, Nanoscale chemical imaging of a working catalyst by scanning transmission X-ray microscopy, Nature, 2008, 456, 222–225 CrossRef CAS PubMed.
- A. Sakdinawat and D. Attwood, Nanoscale X-ray imaging, Nat. Photonics, 2010, 4, 840–848 CrossRef CAS.
- J. N. Weker, X. Huang and M. F. Toney, In situ X-ray-based imaging of nano materials, Curr. Opin. Chem. Eng., 2016, 12, 14–21 CrossRef.
- A. S. Johnson, J. Valls Conesa, L. Vidas, D. Perez-Salinas, C. M. Günther, B. Pfau, K. A. Hallman, R. F. Haglund Jr, S. Eisebitt and S. Wall, Quantitative hyperspectral coherent diffractive imaging spectroscopy of a solid-state phase transition in vanadium dioxide, Sci. Adv., 2021, 7, eabf1386 CrossRef CAS PubMed.
- H. N. Chapman and K. A. Nugent, Coherent lensless X-ray imaging, Nat. Photonics, 2010, 4, 833–839 CrossRef CAS.
- J. Miao, T. Ishikawa, I. K. Robinson and M. M. Murnane, Beyond crystallography: Diffractive imaging using coherent x-ray light sources, Science, 2015, 348, 530–535 CrossRef CAS PubMed.
- T. Latychevskaia, Iterative phase retrieval in coherent diffractive imaging: practical issues, Appl. Opt., 2018, 57, 7187 CrossRef PubMed.
- S. Eisebitt, J. Lüning, W. F. Schlotter, M. Lörgen, O. Hellwig, W. Eberhardt and J. Stöhr, Lensless imaging of magnetic nanostructures by X-ray spectro-holography, Nature, 2004, 432, 885–888 CrossRef CAS PubMed.
- A. S. Johnson, D. Pérez-Salinas, K. M. Siddiqui, S. Kim, S. Choi, K. Volckaert, P. E. Majchrzak, S. Ulstrup, K. Hallman, R. F. H. Jr, C. M. Günther, B. Pfau, S. Eisebitt, D. Backes, F. Maccherozzi, A. Fitzpatrick, S. Dhesi, P. Gargiani, H. Choi, D. Jang, A. Katoch, S. Kwon, S. H. Park, H. Kim and S. E. Wall, Ultrafast X-ray imaging of the light-induced phase transition in VO2, Nat. Phys., 2023, 19, 215–220 Search PubMed.
- S. Zayko, O. Kfir, M. Heigl, M. Lohmann, M. Sivis, M. Albrecht and C. Ropers, Ultrafast high-harmonic nanoscopy of magnetization dynamics, Nat. Commun., 2021, 12, 6337 Search PubMed.
- C. Donnelly, S. Finizio, S. Gliga, M. Holler, A. Hrabec, M. Odstrčil, S. Mayr, V. Scagnoli, L. J. Heyderman, M. Guizar-Sicairos and J. Raabe, Time-resolved imaging of three-dimensional nanoscale magnetization dynamics, Nat. Nanotechnol., 2020, 15, 356–360 CrossRef CAS PubMed.
- S.-B. Choe, Y. Acremann, A. Scholl, A. Bauer, A. Doran, J. Stöhr and H. A. Padmore, Vortex Core-Driven Magnetization Dynamics, Science, 2004, 304, 420–422 CrossRef CAS PubMed.
- G. Dieterle, J. Förster, H. Stoll, A. S. Semisalova, S. Finizio, A. Gangwar, M. Weigand, M. Noske, M. Fähnle, I. Bykova, J. Gräfe, D. A. Bozhko, H. Y. Musiienko-Shmarova, V. Tiberkevich, A. N. Slavin, C. H. Back, J. Raabe, G. Schütz and S. Wintz, Coherent Excitation of Heterosymmetric Spin Waves with Ultrashort Wavelengths, Phys. Rev. Lett., 2019, 122, 117202 CrossRef CAS PubMed.
- Y. Zhu, Z. Cai, P. Chen, Q. Zhang, M. J. Highland, I. W. Jung, D. A. Walko, E. M. Dufresne, J. Jeong, M. G. Samant, S. S. P. Parkin, J. W. Freeland, P. G. Evans and H. Wen, Mesoscopic structural phase progression in photo-excited VO2 revealed by time-resolved x-ray diffraction microscopy, Sci. Rep., 2016, 6, 21999 CrossRef CAS PubMed.
- F. Büttner, C. Moutafis, M. Schneider, B. Krüger, C. M. Günther, J. Geilhufe, C. V. K. Schmising, J. Mohanty, B. Pfau, S. Schaffert, A. Bisig, M. Foerster, T. Schulz, C. A. F. Vaz, J. H. Franken, H. J. M. Swagten, M. Kläui and S. Eisebitt, Dynamics and inertia of skyrmionic spin structures, Nat. Phys., 2015, 11, 225–228 Search PubMed.
- S. Finizio, C. Donnelly, S. Mayr, A. Hrabec and J. Raabe, Three-Dimensional Vortex Gyration Dynamics Unraveled by Time-Resolved Soft X-ray Laminography with Freely Selectable Excitation Frequencies, Nano Lett., 2022, 22, 1971–1977 CrossRef CAS PubMed.
- R. M. Karl, G. F. Mancini, J. L. Knobloch, T. D. Frazer, J. N. Hernandez-Charpak, B. Abad, D. F. Gardner, E. R. Shanblatt, M. Tanksalvala, C. L. Porter, C. S. Bevis, D. E. Adams, H. C. Kapteyn and M. M. Murnane, Full-field imaging of thermal and acoustic dynamics in an individual nanostructure using tabletop high harmonic beams, Sci. Adv., 2018, 4, eaau4295 CrossRef CAS PubMed.
- J. Ravnik, M. Diego, Y. Gerasimenko, Y. Vaskivskyi, I. Vaskivskyi, T. Mertelj, J. Vodeb and D. Mihailovic, A time-domain phase diagram of metastable states in a charge ordered quantum material, Nat. Commun., 2021, 12, 2323 CrossRef CAS PubMed.
- F. Rao, K. Ding, Y. Zhou, Y. Zheng, M. Xia, S. Lv, Z. Song, S. Feng, I. Ronneberger, R. Mazzarello, W. Zhang and E. Ma, Reducing the stochasticity of crystal nucleation to enable subnanosecond memory writing, Science, 2017, 358, 1423–1427 CrossRef CAS PubMed.
- V. J. Emery and S. A. Kivelson, Importance of phase fluctuations in superconductors with small superfluid density, Nature, 1995, 374, 434–437 CrossRef CAS.
- B. Keimer and J. E. Moore, The physics of quantum materials, Nat. Phys., 2017, 13, 1045–1055 Search PubMed.
- L. Wu, Y. Shen, A. M. Barbour, W. Wang, D. Prabhakaran, A. T. Boothroyd, C. Mazzoli, J. M. Tranquada, M. P. M. Dean and I. K. Robinson, Real Space Imaging of Spin Stripe Domain Fluctuations in a Complex Oxide, Phys. Rev. Lett., 2021, 127, 275301 CrossRef CAS PubMed.
- K. Harada, T. Matsuda, H. Kasai, J. E. Bonevich, T. Yoshida, U. Kawabe and A. Tonomura, Vortex configuration and dynamics in Bi2Sr1.8CaCu2Ox thin films by Lorentz microscopy, Phys. Rev. Lett., 1993, 71, 3371–3374 CrossRef CAS PubMed.
- A. Zong, A. Kogar, Y. Q. Bie, T. Rohwer, C. Lee, E. Baldini, E. Ergeçen, M. B. Yilmaz, B. Freelon, E. J. Sie, H. Zhou, J. Straquadine, P. Walmsley, P. E. Dolgirev, A. V. Rozhkov, I. R. Fisher, P. Jarillo-Herrero, B. V. Fine and N. Gedik, Evidence for topological defects in a photoinduced phase transition, Nat. Phys., 2019, 15, 27–31 Search PubMed.
- S.-Z. Lin, X. Wang, Y. Kamiya, G.-W. Chern, F. Fan, D. Fan, B. Casas, Y. Liu, V. Kiryukhin, W. H. Zurek, C. D. Batista and S.-W. Cheong, Topological defects as relics of emergent continuous symmetry and Higgs condensation of disorder in ferroelectrics, Nat. Phys., 2014, 10, 970–977 Search PubMed.
- S. Vogelgesang, G. Storeck, J. G. Horstmann, T. Diekmann, M. Sivis, S. Schramm, K. Rossnagel, S. Schäfer and C. Ropers, Phase ordering of charge density waves traced by ultrafast low-energy electron diffraction, Nat. Phys., 2018, 14, 184–190 Search PubMed.
- F. Büttner, B. Pfau, M. Böttcher, M. Schneider, G. Mercurio, C. M. Günther, P. Hessing, C. Klose, A. Wittmann, K. Gerlinger, L. M. Kern, C. Strüber, C. von Korff Schmising, J. Fuchs, D. Engel, A. Churikova, S. Huang, D. Suzuki, I. Lemesh, M. Huang, L. Caretta, D. Weder, J. H. Gaida, M. Möller, T. R. Harvey, S. Zayko, K. Bagschik, R. Carley, L. Mercadier, J. Schlappa, A. Yaroslavtsev, L. Le Guyarder, N. Gerasimova, A. Scherz, C. Deiter, R. Gort, D. Hickin, J. Zhu, M. Turcato, D. Lomidze, F. Erdinger, A. Castoldi, S. Maffessanti, M. Porro, A. Samartsev, J. Sinova, C. Ropers, J. H. Mentink, B. Dupé, G. S. D. Beach and S. Eisebitt, Observation of fluctuation-mediated picosecond nucleation of a topological phase, Nat. Mater., 2020, 20, 30–37 CrossRef.
- K. Nakagawa, A. Iwasaki, Y. Oishi, R. Horisaki, A. Tsukamoto, A. Nakamura, K. Hirosawa, H. Liao, T. Ushida, K. Goda, F. Kannari and I. Sakuma, Sequentially timed all-optical mapping photography (STAMP), Nat. Photonics, 2014, 8, 695–700 CrossRef CAS.
- M. M. J. Treacy, J. M. Gibson, L. Fan, D. J. Paterson and I. McNulty, Fluctuation microscopy: a probe of medium range order, Rep. Prog. Phys., 2005, 68, 2899 CrossRef CAS.
- G. Grübel, G. B. Stephenson, C. Gutt, H. Sinn and T. Tschentscher, XPCS at the European X-ray free electron laser facility, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 262, 357–367 CrossRef.
- C. Klose, F. Büttner, W. Hu, C. Mazzoli, K. Litzius, R. Battistelli, S. Zayko, I. Lemesh, J. M. Bartell, M. Huang, C. M. Günther, M. Schneider, A. Barbour, S. B. Wilkins, G. S. D. Beach, S. Eisebitt and B. Pfau, Coherent correlation imaging for resolving fluctuating states of matter, Nature, 2023, 614, 256–261 CrossRef CAS PubMed.
- T. Wang, D. Zhu, B. Wu, C. Graves, S. Schaffert, T. Rander, L. Müller, B. Vodungbo, C. Baumier, D. P. Bernstein, B. Bräuer, V. Cros, S. de Jong, R. Delaunay, A. Fognini, R. Kukreja, S. Lee, V. López-Flores, J. Mohanty, B. Pfau, H. Popescu, M. Sacchi, A. B. Sardinha, F. Sirotti, P. Zeitoun, M. Messerschmidt, J. J. Turner, W. F. Schlotter, O. Hellwig, R. Mattana, N. Jaouen, F. Fortuna, Y. Acremann, C. Gutt, H. A. Dürr, E. Beaurepaire, C. Boeglin, S. Eisebitt, G. Grübel, J. Lüning, J. Stöhr and A. O. Scherz, Femtosecond Single-Shot Imaging of Nanoscale Ferromagnetic Order in Co/Pd Multilayers Using Resonant X-Ray Holography, Phys. Rev. Lett., 2012, 108, 267403 CrossRef PubMed.
- C. W. Siders, A. Cavalleri, K. Sokolowski-Tinten, C. Tóth, T. Guo, M. Kammler, M. H. V. Hoegen, K. R. Wilson, D. V. D. Linde and C. P. J. Barty, Detection of Nonthermal Melting by Ultrafast X-ray Diffraction, Science, 1999, 286, 1340–1342 CrossRef CAS PubMed.
- M. Rhodes, M. Mukhopadhyay, J. Birge and R. Trebino, Coherent artifact study of two-dimensional spectral shearing interferometry, J. Opt. Soc. Am. B, 2015, 32, 1881–1888 CrossRef CAS.
- O. Kfir, S. Zayko, C. Nolte, M. Sivis, M. Möller, B. Hebler, S. S. P. K. Arekapudi, D. Steil, S. Schäfer, M. Albrecht, O. Cohen, S. Mathias and C. Ropers, Nanoscale magnetic imaging using circularly polarized high-harmonic radiation, Sci. Adv., 2017, 3, eaao4641 CrossRef PubMed.
- J. Geilhufe, B. Pfau, C. M. Günther, M. Schneider and S. Eisebitt, Achieving diffraction-limited resolution in soft-X-ray Fourier-transform holography, Ultramicroscopy, 2020, 214, 113005 CrossRef CAS PubMed.
- D. Mihailovic, The Importance of Topological Defects in Photoexcited Phase Transitions Including Memory Applications, Appl. Sci., 2019, 9, 890 CrossRef CAS.
- S. J. L. Billinge and M. G. Kanatzidis, Beyond crystallography: the study of disorder, nanocrystallinity and crystallographically challenged materials with pair distribution functions, Chem. Commun., 2004, 749 RSC.
- J. C. H. Spence, U. Weierstall and M. Howells, Phase recovery and lensless imaging by iterative methods in optical, X-ray and electron diffraction, Philos. Trans. R. Soc., A, 2002, 360, 875–895 CrossRef CAS PubMed.
- J. R. Fienup, Reconstruction of an object from the modulus of its Fourier transform, Opt. Lett., 1978, 3, 27 CrossRef CAS PubMed.
- G. J. Williams, H. M. Quiney, A. G. Peele and K. A. Nugent, Coherent diffractive imaging and partial coherence, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–7 Search PubMed.
- R. Battistelli, D. Metternich, M. Schneider, L.-M. Kern, K. Litzius, J. Fuchs, C. Klose, K. Gerlinger, K. Bagschik, C. M. Günther, D. Engel, C. Ropers, S. Eisebitt, B. Pfau, F. Büttner and S. Zayko, Coherent X-ray magnetic imaging with 5 nm resolution, Optica, 2024, 11, 234–237 CrossRef.
- S. H. Park, A. Katoch, K. H. Chae, S. Gautam, P. Miedema, S. W. Cho, M. Kim, R.-P. Wang, M. Lazemi, F. de Groot and S. Kwon, Direct and real-time observation of hole transport dynamics in anatase TiO2 using X-ray free-electron laser, Nat. Commun., 2022, 13, 2531 CrossRef CAS.
- G. F. Nataf, M. Guennou, J. M. Gregg, D. Meier, J. Hlinka, E. K. H. Salje and J. Kreisel, Domain wall engineering: mastering topological defects in ferroelectric and ferroelastic materials, Nat. Rev. Phys., 2020, 2, 634–648 CrossRef CAS.
- S. R. Bakaul, W. Hu, T. Wu and T. Kimura, Intrinsic domain-wall resistivity in half-metallic manganite thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 184404 CrossRef.
- S. Da Col, S. Jamet, N. Rougemaille, A. Locatelli, T. O. Mentes, B. S. Burgos, R. Afid, M. Darques, L. Cagnon, J. C. Toussaint and O. Fruchart, Observation of Bloch-point domain walls in cylindrical magnetic nanowires, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 180405 CrossRef.
- W. S. Lee, Y. D. Chuang, R. G. Moore, Y. Zhu, L. Patthey, M. Trigo, D. H. Lu, P. S. Kirchmann, O. Krupin, M. Yi, M. Langner, N. Huse, J. S. Robinson, Y. Chen, S. Y. Zhou, G. Coslovich, B. Huber, D. A. Reis, R. A. Kaindl, R. W. Schoenlein, D. Doering, P. Denes, W. F. Schlotter, J. J. Turner, S. L. Johnson, M. Först, T. Sasagawa, Y. F. Kung, A. P. Sorini, A. F. Kemper, B. Moritz, T. P. Devereaux, D.-H. Lee, Z. X. Shen and Z. Hussain, Phase fluctuations and the absence of topological defects in a photo-excited charge-ordered nickelate, Nat. Commun., 2012, 3, 838 CrossRef CAS PubMed.
- D. H. Parks, X. Shi and S. D. Kevan, Partially coherent x-ray diffractive imaging of complex objects, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 063824 CrossRef.
- L. W. Whitehead, G. J. Williams, H. M. Quiney, D. J. Vine, R. A. Dilanian, S. Flewett, K. A. Nugent, A. G. Peele, E. Balaur and I. McNulty, Diffractive Imaging Using Partially Coherent X Rays, Phys. Rev. Lett., 2009, 103, 243902 CrossRef CAS PubMed.
- R. Khubbutdinov, A. P. Menushenkov and I. A. Vartanyants, Coherence properties of the high-energy fourth-generation X-ray synchrotron sources, J. Synchrotron Radiat., 2019, 26, 1851–1862 CrossRef CAS PubMed.
- I. A. Vartanyants, A. Singer, A. P. Mancuso, O. M. Yefanov, A. Sakdinawat, Y. Liu, E. Bang, G. J. Williams, G. Cadenazzi, B. Abbey, H. Sinn, D. Attwood, K. A. Nugent, E. Weckert, T. Wang, D. Zhu, B. Wu, C. Graves, A. Scherz, J. J. Turner, W. F. Schlotter, M. Messerschmidt, J. Lüning, Y. Acremann, P. Heimann, D. C. Mancini, V. Joshi, J. Krzywinski, R. Soufli, M. Fernandez-Perea, S. Hau-Riege, A. G. Peele, Y. Feng, O. Krupin, S. Moeller and W. Wurth, Coherence Properties of Individual Femtosecond Pulses of an X-Ray Free-Electron Laser, Phys. Rev. Lett., 2011, 107, 144801 CrossRef CAS PubMed.
- M. Born and E. Wolf, Principles of Optics, Cambridge University Press, Cambridge, 1999 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |