How lithium-ion batteries work conceptually: thermodynamics of Li bonding in idealized electrodes†
Received
26th February 2024
, Accepted 30th August 2024
First published on 10th September 2024
Abstract
A good explanation of lithium-ion batteries (LIBs) needs to convincingly account for the spontaneous, energy-releasing movement of lithium ions and electrons out of the negative and into the positive electrode, the defining characteristic of working LIBs. We analyze a discharging battery with a two-phase LiFePO4/FePO4 positive electrode (cathode) from a thermodynamic perspective and show that, compared to loosely-bound lithium in the negative electrode (anode), lithium in the ionic positive electrode is more strongly bonded, moves there in an energetically downhill irreversible process, and ends up trapped in the positive electrode. Only a sufficiently high charging voltage can drive it back to the other electrode. Since the stronger bonding in the positive electrode lowers the energy by ∼320 kJ mol−1, a lot of energy is released. This explanation is quantitatively supported by an analysis of cohesive-energy differences of the electrode materials. Since electrons are only intermediates in the discharge reaction and the chemical potential of the electron cannot be measured, electrons do not need to be assigned a distinct energetic role. The incorporation of Li+ and an electron into the cathode is accompanied by the reduction of another ion or atom, usually a transition metal such as Fe or Co. The metal's ionization energy in the corresponding oxidation step correlates with the cell voltage, based on a decomposition of cohesive energy into electronic and ionic components. We relate the differences in cohesive energies to the chemical potential of lithium atoms, which is quantified, for instance for a two-phase electrode. The analysis is extended to a single-phase LixCoO2 cathode, whose average voltage can be calculated from the cohesive-energy difference between LiCoO2 and CoO2.
Introduction
Lithium-ion batteries (LIBs) are electrochemical energy converters that play an important part in everyday life, powering computers, tablets, cell phones, electric cars, electric bicycles, and numerous other devices. They can also be used to store intermittently produced renewable energy. The lithium-ion battery's immense utility derives from its favorable characteristics: rechargeability, high energy per mass or volume relative to other battery types, a fairly long cycle life, moderate to good thermal stability, relatively low cost, and good power capability.1,2 These characteristics can be tuned to some extent by the use of different transition-metal oxides or phosphates in the positive electrode.2 In recognition of the importance of lithium-ion batteries, the 2019 Nobel Prize in Chemistry was awarded to Goodenough, Whittingham, and Yoshino.3
Descriptions of the chemical processes in LIBs are commonplace,1,2,4,5 but convincing explanations have been scarce. Why do positively charged lithium ions and electrons spontaneously move out of the negative into the positive electrode and release energy? These processes are the defining characteristics of a working LIB.5 A lowering in chemical potential is frequently invoked,2,4 but why the chemical potential goes down has not been explained. Since traditional thermodynamics often cannot quantify chemical potentials, but only their differences, discussions of chemical potentials2,4,6–12 in LIBs have mostly remained abstract2,4 or empirical.12 Some of the same treatments also offered partial explanations of cell voltages in terms of quantities that appear unrelated to lithium chemical-potential differences, such as electronegativity2,13 or point defects.4 The US Department of Energy5 tells us that LIBs work because “the electrolyte carries positively charged lithium ions from the anode to the cathode”, but such an active role of the electrolyte is not supported by the technical literature.
While analyses based on chemical thermodynamics4,6–11 have, with some success,6,7,11 relied on the difference in Gibbs free energy and the chemical potential of lithium atoms in the negative and positive electrode,8,12 other researchers14–16 have proposed an explanation of LIBs in terms of the chemical potential of the electron, which is the Fermi level familiar to physicists. However, this leaves out a contribution from the chemical potential of lithium ions, which we will show to be of considerable magnitude. It appears that the analysis in terms of the chemical potential of the electron has not led to reliably quantitative predictions.14–16 Some sources15,16 have equated the chemical potentials of electrons and ions to their work functions, but this results in incorrect predictions, as we document below. Given that explanations of lithium-ion batteries have been attempted based on a wide range of concepts, including the electrolyte,5 empirical reduction potentials,17 point defects,4 unexplained reductions in Gibbs free energy,6,7,11 electronegativity,2 work functions,15,16 and the chemical potential “in the[ir] electrodes”,2 of lithium,8,12 and of the electron,14–16 it appears that no explanation so far has been convincing enough to be widely accepted.
In prior work,18 we provided intuitive and quantitative explanations of the energetics of galvanic cells and several practical batteries in terms of cohesive energies per atom (i.e., the bonding of atoms) in metals and metal oxides as well as ionization energies in water.18 Here we develop a similar energetic analysis for discharging lithium-ion batteries with two-phase positive electrodes (cathodes), focusing on the widely used lithium iron phosphate,19 and discuss the driving forces for the movement of lithium ions and electrons, using a chemical approach7,18 that allows for analysis in terms of cohesive energies.18 This also results in an explanation of the correlation between cell voltage and the last ionization energy of the transition metal in the positive electrode. We establish the connection to the conventional formalism in terms of the chemical potential of the lithium atom4,6–12 and give quantitative, intuitive values of the chemical potentials of lithium and of electrode materials. Various problems with, and incorrect predictions of, the chemical potentials and work functions of electrons and lithium ions in the literature14–16 are also pointed out. Aging of LIBs and formation of disordered structures are important in practice but outside the scope of this paper.
Analysis
Components of a lithium-ion battery
While most household lithium-ion batteries consist of a single electrochemical cell generating a cell voltage of around 3.4 V, batteries providing higher voltages can be constructed from several such electrochemical cells in series. A typical cell, see Fig. 1, consists of two electrodes (negative and positive), a separator between the electrodes and an electrolyte that conducts ions but not electrons, as well as metallic current collectors on the electrodes that conduct electrons from the active materials to the external electrical circuit that allows the electrons to flow from the negative to the positive electrode.
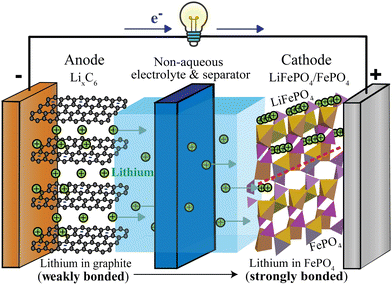 |
| | Fig. 1 Schematic of a discharging lithium-ion battery with a lithiated-graphite negative electrode (anode) and an iron–phosphate positive electrode (cathode). Since lithium is more weakly bonded in the negative than in the positive electrode, lithium ions flow from the negative to the positive electrode, via the electrolyte (most commonly LiPF6 in an organic, carbonate-based solvent20). At the positive electrode, lithium enters empty channels or tunnels in FePO4 near and parallel21–24 to the phase boundary with LiFePO4, whose tunnels are already filled with lithium (indicated by rows of lithium ions). The LiFePO4/FePO4 phase boundary, marked by the dashed red line, can be sharp22,23 or up to 20 nm wide.24 Electrons travel through the external circuit, where they perform electrical work; in the positive electrode, they are accepted mostly by iron of FePO4, in conjunction with the Li+ uptake. | |
Processes in a discharging lithium-ion battery
Fig. 1 shows a schematic of a discharging lithium-ion battery with a negative electrode (anode) made of lithiated graphite and a positive electrode (cathode) of iron phosphate. As the battery discharges, graphite with loosely bound intercalated lithium (LixC6(s)) undergoes an oxidation half-reaction, resulting in the release of a lithium ion and an electron. The lithium ion crosses the electrolyte-soaked separator and moves to the FePO4(s) cathode, where it enters and fills channels or tunnels in the iron phosphate, forming LiFePO4(s). Some details of this fascinating intercalation process are discussed in the ESI† (see Fig. S1). Since the separator and electrolyte are electrical insulators, the electron must travel through the external circuit, giving off the energy released in the chemical reaction. At the cathode, the electron is taken up by a transition-metal ion such as Fe3+, Co4+, or Mn4+, or by oxygen. This process is energetically downhill because the weakly bonded lithium in LixC6 is high in energy compared to more strongly bonded lithium in the positive electrode. Since lithium is bonded only relatively weakly to graphite sheets (see below),25 the lithiated graphite electrode stores a lot of chemical energy.
Explaining energy release in a battery
Release of electrical energy due to movement of lithium ions and electrons out of the negative into the positive electrode is the hallmark of a working lithium-ion battery. It is not the “chemical potential in their electrodes”2 but the Gibbs free energy of the cell that is lowered in this process, and we will explain how and why. The electrical energy released by an irreversibly discharging electrochemical cell is| | | wele = ΔrH − q ≈ ΔrG − qdiss | (1a) |
(see eqn (S4) and (S9) and their derivation from the first law of thermodynamics in Section 2 of the ESI†), with enthalpy decrease ΔrH, heat q, dissipative Ohmic heat loss qdiss in the battery, and the reduction in the Gibbs free energy, ΔrG, i.e. the difference between the Gibbs free energies of products and reactants. If the current is small and resulting Ohmic heating qdiss in the battery is minimal, we recover the universally accepted8,26 simple equality between electrical energy release and free-energy decrease,| | | wele ≈ ΔrG ≈ |ΔnLi(electrode)|ΔrG° | (1b) |
where ΔnLi(electrode) is the change in the amount (in mol) of lithium in one of the electrodes.
The same principle as in a Daniell cell, where the reactants are higher in energy than the products,18 applies to a lithium-ion battery; the low molar Gibbs free energy of lithium in the positive electrode means that lithium is more strongly bonded there and thus lower in energy than in the anode. In the following, we confirm that bonding-, i.e. cohesive-, energy differences between the negative and the positive electrode provide an intuitive, quantifiable explanation of the energy release in lithium-ion batteries.
Energetics of negative electrodes (anodes)
The negative electrode of a discharging lithium-ion battery is the anode (see Section 3 of the ESI† and Fig. S2 for a discussion of electrode terminology; for brevity, we will mostly use “anode” for “negative electrode”, and “cathode” for “positive electrode” in the following discussions of a discharging battery, as in most of the specialized literature). It consists of a conductive material where lithium is weakly bonded and easily released as a lithium ion while the electron is left behind in the electrode and passed on to the external circuit. Conceptually simplest is a lithium–metal anode, which is often used in theoretical analyses,4,6–10,14–16 including ours below.
In practice, lithiated graphite is the most widely used material for anodes. The intercalation of lithium from lithium metal into graphite27 can be written approximately as
| | | Li(s) + 6C(s) → LiC6(s) ΔrG° = −15 ± 6 kJ mol−1 | (2) |
(see eqn (S26), ESI
†). The negative free energy change indicates that the intercalation is spontaneous: lithium is bonded slightly more strongly in graphite than in metallic lithium. Nevertheless, as demonstrated in the next section, the difference is small (<5%) compared to the difference in lithium bonding energy between the anode and the strongly ionically bonded cathode materials. This confirms that lithium is relatively weakly bonded in a graphite anode.
Bonding energetics of positive electrodes (cathodes)
Among the variety of cathode materials that have been studied and applied,2 we focus here primarily on the widely used iron phosphate-based, two-phase cathode in conjunction with a lithium–metal anode. According to eqn (1), the electrical energy released per mole of lithium in the reaction| | | Li(s) + FeIIIPO4(s) → LiFeIIPO4(s) | (3) |
equals the free-energy change, ΔrG° = −331 kJ mol−1, calculated from literature data28 (see Scheme 1 and eqn (S11) for details, ESI†). The enthalpy change in the reaction is similar, ΔrH° = −337 kJ mol−1.28 The entropic contribution to the free-energy change, −298 K ΔrS° = +6 kJ mol−1, is less than 2% of ΔrG° and therefore quite insignificant.6 The strongly negative values confirm that discharge in a lithium iron phosphate battery is energetically strongly downhill. According to the well-known relation26| | 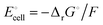 | (4) |
with the Faraday constant F = 96.5 kC mol−1, the cell voltage is 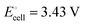 .
.
 |
| | Scheme 1 Cohesive energies (middle: enthalpies; bottom: free energies) per compound and per atom in an iron phosphate-based battery with a lithium–metal anode (see Section 4 of the ESI† for derivations). High (i.e. only slightly negative) energy values are highlighted in red. | |
Cell voltage from cohesive energies of electrode materials
The energetics of lithium bonding in the negative and the positive electrode can be quantified most clearly in terms of the cohesive energies 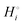 of the solid reactants and products, which can be calculated from the enthalpies of formation of the solids and their elemental compositions as shown in the ESI,† see eqn (S12). The results are summarized in Scheme 1. The cohesive energy
of the solid reactants and products, which can be calculated from the enthalpies of formation of the solids and their elemental compositions as shown in the ESI,† see eqn (S12). The results are summarized in Scheme 1. The cohesive energy 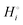 quantifies the strength of bonding in compound i relative to the free, unbonded atoms, which define the zero point of the energy scale.18,29 The same applies to the individual standard molar free energy,
quantifies the strength of bonding in compound i relative to the free, unbonded atoms, which define the zero point of the energy scale.18,29 The same applies to the individual standard molar free energy, 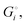 which is the cohesive free energy of the solid relative to the unbonded atoms.
which is the cohesive free energy of the solid relative to the unbonded atoms.
We can express the cell voltage explicitly in terms of the cohesive free energies 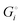 of the electrode materials from Scheme 1 and their stoichiometric coefficients νi (which are all 1 in eqn (3)):
of the electrode materials from Scheme 1 and their stoichiometric coefficients νi (which are all 1 in eqn (3)):
| | 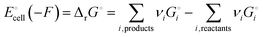 | (5a) |
| | 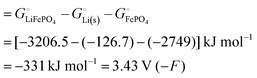 | (5b) |
and also approximately in terms of cohesive energies
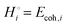
from
Scheme 1| | 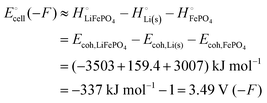 | (6) |
Eqn (6) provides a good approximation for the cell voltage expressed in terms of cohesive energies since the entropic contribution to the free energy change is only a few percent for this reaction only involving crystalline solids. In terms of
eqn (1a) and eqn (S8) (ESI
†), this means that for the electrical energy given off by the LIB, the heat
q released (−6 kJ mol
−1) is negligible compared to the change in bonding energetics, Δ
rH, due to the chemical reaction (−337 kJ mol
−1).
The cohesive (free) energies per formula unit and per atom in the reaction of eqn (3) are shown in Scheme 1. While the cohesive energy 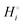 of a compound i with many atoms is always relatively large in magnitude, we can distinguish weak from strong bonding by comparing the cohesive energy per atom. Relatively strongly bonded, stable, low-energy compounds have a more negative
of a compound i with many atoms is always relatively large in magnitude, we can distinguish weak from strong bonding by comparing the cohesive energy per atom. Relatively strongly bonded, stable, low-energy compounds have a more negative 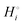 per atom than do more weakly bonded, high-energy compounds.18
per atom than do more weakly bonded, high-energy compounds.18
The crucial small magnitudes of the cohesive energy 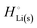 per atom (−159.4 kJ mol−1) and cohesive free energy
per atom (−159.4 kJ mol−1) and cohesive free energy 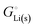 (−126.7 kJ mol−1) of lithium metal have already been pointed out.18 Due to its weak bonding, lithium metal is a high-energy material that reacts spontaneously even with a stable compound like H2O, and according to eqn (2), lithium intercalated in graphite is only slightly (−15 kJ mol−1) more stabilized.
(−126.7 kJ mol−1) of lithium metal have already been pointed out.18 Due to its weak bonding, lithium metal is a high-energy material that reacts spontaneously even with a stable compound like H2O, and according to eqn (2), lithium intercalated in graphite is only slightly (−15 kJ mol−1) more stabilized.
By contrast, according to Scheme 1, in the cathode Li is bonded by (−3503 − (−3007)) = −496 kJ mol−1, the difference in cohesive energies of LiFePO4 and FePO4, which is stronger by (−496 − (−159.4)) = −337 kJ mol−1 than in the Li(s) anode. (Compared to a lithiated graphite anode, the energy difference is only slightly smaller in magnitude, (−496 − (−159.4) + 15) = −322 kJ mol−1.) If we compare the cohesive energies per atom of LiFePO4(s) and Li(s) in Scheme 1, we find a difference of (−500.4 − 159.4) = −341 kJ mol−1 between the bonding energies of lithium in the cathode vs. the anode, very similar as before. All the variously calculated enthalpy and free-energy differences between lithium in the negative and positive electrode are found in a narrow range of −335 ± 13 kJ mol−1.
Why lithium ions move to the positive electrode
The data in Scheme 1 and Fig. 2 show that lithium is bound much more strongly (by −331 kJ mol−1) in the positive electrode (cathode) than in the negative electrode, which means that it can move only from its less stable, weakly bonded state in the negative electrode to the more stable, strongly bonding positive electrode; once lithium is trapped in the positive electrode, the reverse process cannot occur spontaneously. Transfer of lithium (as Li+ and e−) from a less to a more stable bonding environment is an irreversible movement from higher to lower energy, i.e. energetically downhill; the corresponding (free) energy difference is released as electrical energy. This picture is similar to a description in terms of the chemical potential of lithium12 (which is formally confirmed below), but the use of intuitive and quantifiable bonding concepts provides a more meaningful explanation of the discharge process and energy release in a lithium-ion battery. Lithium (as Li+ and e−) moving spontaneously from a weakly to a strongly bonded state is a robust principle that applies as long as the battery voltage is large enough (e.g. >2 V), even in the presence of disorder or amorphous structures, or after aging (because entropic contributions −TΔrS to the free energy change are always relatively minor (<100 kJ mol−1 or 1 eV) at 298 K).
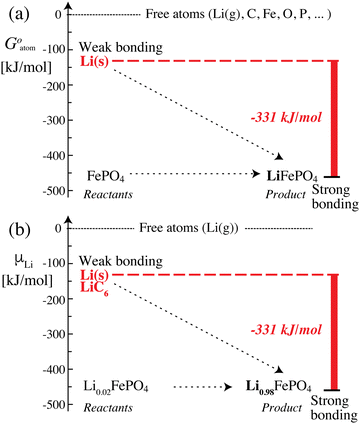 |
| | Fig. 2 Energetics and bonding of lithium in an iron phosphate-based lithium-ion battery. (a) Cohesive Gibbs free energy per atom. (b) Gibbs free energy per lithium atom, also known as the lithium (electro)chemical potential. The free-energy difference of −331 kJ mol−1 between the reactants and the product can be released as electrical energy. | |
Cathode charge neutrality after Li+ incorporation by transition-metal reduction
Lithium is incorporated into the positive electrode (cathode) as Li+, with a strong electrostatic interaction due to its small size. But it is not possible to simply add macroscopic amounts of Li+ into an otherwise unchanging cathode solid, since all solids must be nearly electrically neutral. This problem is solved by a reduction in oxidation state of a transition metal or other ion/atom in the cathode, with the cathode achieving this charge neutrality by taking up the needed electron from the external circuit. The effect of the energetics of the change in oxidation state on cell voltage is discussed below. This description also applies to the lithium–air battery:18 Li+ has strong ionic bonding in the cathode (Li2O2), and the oxidation state of oxygen in the cathode decreases.
Coexisting nonstoichiometric compositions
In a more detailed analysis (see eqn (S63), ESI†),10 one finds that due to a strong entropic driving force, a small amount of lithium will get incorporated uniformly into initially neat FePO4, forming Li0.02FePO4 throughout the cathode. The addition of more lithium leads to the formation of Li0.98FePO4, again deviating slightly from regular stoichiometry due to entropic effects. In a discharging battery, the two phases coexist until eventually the phase boundary has traversed every particle and converted all cathode material to Li0.98FePO4. Therefore, a more realistic description of the main discharge reaction is| | | 0.96Li(s) + Li0.02FePO4 → Li0.98FePO4 | (7a) |
This is equivalent to| | | Li(s) + 1.04Li0.02FePO4 → 1.04Li0.98FePO4 ΔrG° = −331 kJ mol−1 | (7b) |
a special case of the equation| | | Li(s) + Lix1FePO4/(x2 − x1) → Lix2FePO4/(x2 − x1) | (7c) |
of Urban et al.11 The off-stoichiometric compositions are stabilized by the strongly nonlinear entropy of mixing of Li+ + FeII and VacancyLi + FeIII.10 According to eqn (7), the change in the amounts (in moles) of the two phases is 4% larger than the amount of lithium transferred, but since the two off-stoichiometric phases are also about 2 + 2 = 4% less different in  than are FePO4 and LiFePO4,11 the Gibbs free energy change remains nearly the same, −331 kJ mol−1, as in eqn (5b) for the stoichiometric compounds, see also Fig. S3 (ESI†).10 The ∼2% larger value (3.51 eV = 339 kJ mol−1) reported by Phan et al.10 appears to be due to an inconsistency in Gibbs-energy referencing, see the ESI,† eqn (S67).
than are FePO4 and LiFePO4,11 the Gibbs free energy change remains nearly the same, −331 kJ mol−1, as in eqn (5b) for the stoichiometric compounds, see also Fig. S3 (ESI†).10 The ∼2% larger value (3.51 eV = 339 kJ mol−1) reported by Phan et al.10 appears to be due to an inconsistency in Gibbs-energy referencing, see the ESI,† eqn (S67).
Other cathode compositions
Fig. 3 shows that the cell voltages for other cathodes paired with a lithium–metal anode can also be calculated quantitatively from cohesive energies (enthalpies  neglecting entropic effects). The cohesive energy differences for the two end-member phases of layered LixCoO2 and LixMnO2 cathodes were calculated from their standard enthalpies of formation6,7,11,30,31 as shown in the ESI† (Scheme S1). While LixCoO2 is a single-phase cathode with decreasing voltage as x increases,30 the average voltage over a theoretical full discharge cycle, converting CoO2 to LiCoO2, can still be calculated simply from the difference in the cohesive energies of Li(s) + CoO2vs. LiCoO2 (from Scheme S1a, ESI†),6,11
neglecting entropic effects). The cohesive energy differences for the two end-member phases of layered LixCoO2 and LixMnO2 cathodes were calculated from their standard enthalpies of formation6,7,11,30,31 as shown in the ESI† (Scheme S1). While LixCoO2 is a single-phase cathode with decreasing voltage as x increases,30 the average voltage over a theoretical full discharge cycle, converting CoO2 to LiCoO2, can still be calculated simply from the difference in the cohesive energies of Li(s) + CoO2vs. LiCoO2 (from Scheme S1a, ESI†),6,11| | | Ecell(xLi = 0.5) ≈ average Ēcell = −ΔrG°/F ≈ −ΔrEcohes/F | (8) |
| = −(Ecoh,LiCoO2 − Ecoh,Li(s) − Ecoh,CoO2)/F |
| = −(−1762 − (−159 − 1213)) kJ/96.5 kC = 4.0 V |
as rederived below (eqn (53)); this is also the voltage near 50% lithium incorporation.32 The same applies for LixMnO2, where (see Scheme S1b, ESI†)| | | Ecell(xLi = 0.5) ≈ −(−1768 − (−159 − 1301)) kJ/96.5 kC = 3.2 V | (9) |
The good agreement of the experimental data points in Fig. 3 with the theoretical prediction (dashed line) confirms the theory as well as the consistency between thermodynamic data from calorimetry (horizontal axis) and electrochemical measurements (vertical). It also shows that disorder and amorphous states, of great concern to a reviewer, do not prevent the thermodynamic analysis for idealized electrodes from making correct predictions of the cell voltage and electrical energy release measured on real-world batteries.2 This is reasonable because, as proved in the Discussion, the cohesive energy of an amorphous phase differs from that of its crystalline counterpart only by a small margin.
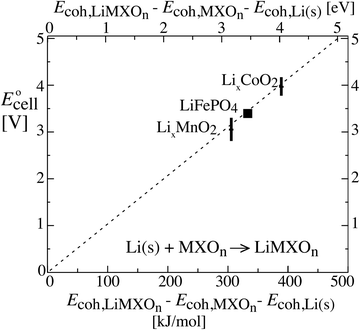 |
| | Fig. 3 Relation between the cell voltage and the difference in cohesive energies of a lithium–metal anode and the two phases in the cathode, for three types of cathodes. The theoretically expected relation (without a free factor) is indicated by the dashed line. Note that E stands for energy on the horizontal and for electromotive force on the vertical axis. For cohesive energies see Section 4 of the ESI,† while the cell voltage data were taken from ref. 2 and 10. | |
Charging a lithium-ion battery
While the movement of ions and electrons in a discharging battery is driven by chemical bonding forces and a reduction in free energy, in a charging battery it can be understood based on simple macroscopic electrostatics. Whereas in a discharging battery, the positive lithium ions move from the negative to the positive electrode, contrary to expectations from electrostatics, see Fig. 1, in a charging battery the applied voltage overcomes the favorable bonding of lithium in the positive electrode so that Li+ ions are pushed out by like-charge repulsion and pulled to the negative electrode by electrostatic attraction. The phosphate or oxide electrode becomes positive because the external voltage source pumps electrons out of the material, see Fig. S2b (ESI†), while graphite becomes more negative by electrons pushed into it by the external voltage source. It should be noted that the cathode in a discharging battery becomes the anode during charging but remains the positive electrode (see Section 3 of the ESI†).
Discussion
Cohesive energy and ionization energy
The cohesive energy of a solid is the energy released when a mole of atoms come together and form the solid, in reality or conceptually, at constant T and P. It is known with as many significant figures as the enthalpy of formation of the solid, see examples in Scheme 1 and ESI.† For instance, the cohesive energy of Li(s) is 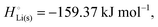 33 while that of LiCl(s) is
33 while that of LiCl(s) is 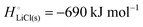 , see Fig. 4a. In magnitude, the cohesive energy is equal to the energy needed to dissociate the solid into atoms. It can therefore be considered as the binding or bonding energy of the solid. The cohesive energy also has the same magnitude as the energy of atomization or the enthalpy of sublimation, and for simple metals, the enthalpy of formation of the gaseous element.33 The corresponding cohesive free energy, e.g.
, see Fig. 4a. In magnitude, the cohesive energy is equal to the energy needed to dissociate the solid into atoms. It can therefore be considered as the binding or bonding energy of the solid. The cohesive energy also has the same magnitude as the energy of atomization or the enthalpy of sublimation, and for simple metals, the enthalpy of formation of the gaseous element.33 The corresponding cohesive free energy, e.g.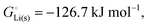 shows a moderately different value due to entropic effects.
shows a moderately different value due to entropic effects.
It is interesting to note that the cohesive energy of a metallic or ionic substance differs only little in its different condensed phases. For instance, the cohesive energy of liquid (molten, completely amorphous) lithium metal is different by only 3 kJ mol−1 (the enthalpy of fusion) or <3% from that of crystalline lithium metal (−159 kJ mol−1), while the cohesive energies of amorphous LiCl(l) and crystalline LiCl(s) differ by only 20 kJ mol−1 (the enthalpy of fusion) out of −690 kJ mol−1. The data reflect that the cohesive energy is due to local bonding. These observations imply that disorder or amorphous structuring do not have a major effect on the cohesive energy of a cathode material and the bonding energetics of lithium that are crucial for a working lithium-ion battery.
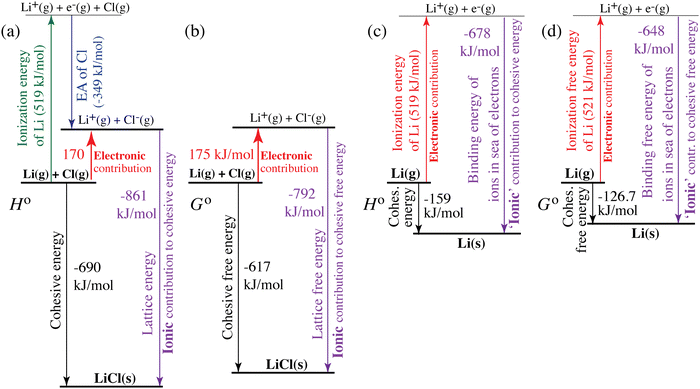 |
| | Fig. 4 Quantification of electronic (red, upwards) and ionic (purple, downwards) contributions to the cohesive energy of (a) and (b) LiCl(s) and (c) and (d) lithium metal. (a) and (c) Enthalpies; (b) and (d) free energies. The diagrams correspond to generalized Born–Haber cycles. | |
For ionic solids and metals, it may be instructive to split the cohesive energy into an ionic and an electronic part. For LiCl(s), for instance, the ionic part, i.e., the lattice energy,33 is −861 kJ mol−1, which is the energy released when Li+(g) and Cl−(g) ions form solid lithium chloride. The cohesive energy of 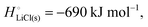 or −345 kJ per mol atoms, is released when neutral Li(g) and Cl(g) form solid LiCl. Converting Li(g) and Cl(g) to Li+(g) and Cl−(g) requires the input of the ionization energy of Li(g) (+519 kJ mol−1) and the release of the electron affinity of Cl(g) (−349 kJ mol−1), see Fig. 4a. The net energy input, 519–349 = 170 kJ mol−1, required for electron removal and re-uptake, can be considered as the electronic part of the cohesive energy. The cohesive free energy of LiCl(s) is
or −345 kJ per mol atoms, is released when neutral Li(g) and Cl(g) form solid LiCl. Converting Li(g) and Cl(g) to Li+(g) and Cl−(g) requires the input of the ionization energy of Li(g) (+519 kJ mol−1) and the release of the electron affinity of Cl(g) (−349 kJ mol−1), see Fig. 4a. The net energy input, 519–349 = 170 kJ mol−1, required for electron removal and re-uptake, can be considered as the electronic part of the cohesive energy. The cohesive free energy of LiCl(s) is 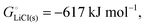 with an ionic part of −792 kJ mol−1 (considering the entropy difference of −245 J mol−1 K−1 between LiCl(s) and Li+(g) plus Cl−(g)) and an electronic part of 175 kJ mol−1.
with an ionic part of −792 kJ mol−1 (considering the entropy difference of −245 J mol−1 K−1 between LiCl(s) and Li+(g) plus Cl−(g)) and an electronic part of 175 kJ mol−1.
For simple metals such as Li(s), the “ionic” part of the cohesive energy is the energy of binding of the ion cores in the sea of conduction electrons (−678 kJ mol−1 for Li(s)), while the electronic part is the ionization energy of the atom (IELi(g) = +519 kJ mol−1);34 they add up to the cohesive energy  . The cohesive free energy of lithium metal is −126.7 kJ mol−1, with an electronic part of 521 kJ mol−1 and an “ionic” part (the free energy change when Li+(g) + e−(g) come together to form Li(s)) of −648 kJ mol−1 (less negative than the enthalpy change due to entropic favorability of gaseous Li+(g)). A corresponding expression in terms of chemical potentials is shown below (see eqn (25)).
. The cohesive free energy of lithium metal is −126.7 kJ mol−1, with an electronic part of 521 kJ mol−1 and an “ionic” part (the free energy change when Li+(g) + e−(g) come together to form Li(s)) of −648 kJ mol−1 (less negative than the enthalpy change due to entropic favorability of gaseous Li+(g)). A corresponding expression in terms of chemical potentials is shown below (see eqn (25)).
Cell voltage increase with the last ionization energy
Our analysis in the preceding section predicts that due to the larger ionization energy, a more ionized transition metal, i.e. in a higher oxidation state, has a larger, more destabilizing electronic contribution to the cohesive energy. (There will also be a more stabilizing ionic contribution due to the higher charge, but this effect should be nearly constant across olivines and across metal oxides, given that the nominal charge of the metal always increases by one unit and the variation in unit-cell volume for a given crystal structure is small.7) In the discharge reaction for a transition-metal phosphate cathode| | | Li(s) + MIIIPO4 → LiMIIPO4 | (10) |
we expect a systematic variation of the energy release with the difference in the energy of M2+ and M3+, i.e. the third ionization energy (IE3, in the gas phase). The bigger IE3, the more energy is released in the reverse process of converting MIII to MII according to eqn (10), i.e. the more favorable the discharge energetics and the larger the cell voltage. Accordingly, the plot of the cell voltage for transition-metal phosphate cathodes35 in Fig. 5a as a function of IE3 shows a clear correlation. Notably, Fe is not near Co and Ni, nor near Mn, in both cell voltage and IE3; both quantities dip significantly for Fe relative to the preceding and following elements, Mn and Co, respectively, which supports the correlation of voltage and IE3.
 |
| | Fig. 5 Plots of the change in cathode cohesive free energy upon lithiation and of the cell voltage of lithium-ion batteries with a Li(s) anode and a transition-metal-containing cathode, as a function of the 3rd or 4th ionization energy of the transition metal. (a) For phosphate cathodes with M2+/M3+ couples, cell voltage plotted as a function of the 3rd ionization energy of the transition metal M in the gas phase. Filled symbols: experimental data for LiMPO4/MPO4 olivines, as reviewed in ref. 35. Open symbols with large uncertainty ranges: data from quantum-chemical calculations for transition-metal phosphates.35 (b) For MO2 cathodes with M3+/M4+ couples, cell voltage plotted as a function of the 4th ionization energy of the transition metal M. Simple vertical bars: experimental data as compiled by Liu et al.2 Open squares: predicted cell voltages from quantum-chemical calculations.7 The observed trends (with R2 = 0.83 and 0.82 for (a) and (b), respectively, and dashed lines as guides to the eye) are qualitatively predicted in our analysis based on the electronic (ionization) component of the cohesive energy. | |
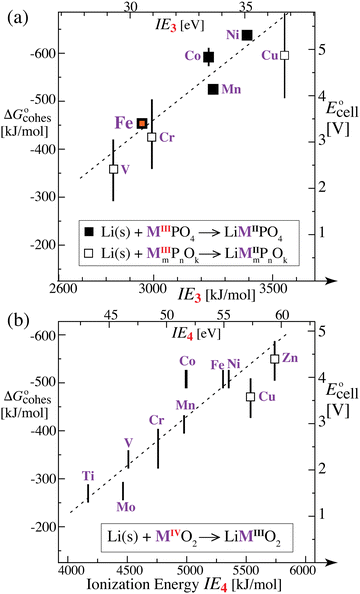
Similarly, in a discharge reaction for an oxide cathode
| | | Li(s) + MIVO2 → LiMIIIO2 | (11) |
the energy release should reflect the difference in the energy of M
3+ and M
4+,
i.e. the fourth ionization energy (IE
4).
Fig. 5b shows the cell voltages for transition-metal oxide cathodes
2,36 plotted as a function of IE
4. Again, a clear trend consistent with our prediction is observed. In particular, Mo (in the same group as Cr) lies closer to this curve than when ordered by the number of d-electrons.
2 The simple analysis underlying
Fig. 5 yields a more systematic correlation with cell voltage than does the change in electron chemical potential or Fermi level
μe−14 from band-structure calculations for the same oxides as in
Fig. 5b,
7 which exhibit weaker or even opposing trends with smaller
R2 values, see Fig. S4 (ESI
†).
The correlation of  with the nth ionization energy quantifies previous arguments2 that the cell voltage is increased when “electrons in the outer shells are more strongly attracted by atomic nuclei”2 of transition-metal cations with increasing atomic number (in the same oxidation state), due to increasing effective nuclear charge. We can now better understand why Li is strongly bonded in LiFePO4 (in addition to the electrostatic attraction of Li+ to PO43−): lithium intercalation lowers the energy of its environment, and therefore of lithium itself in this environment, by allowing the transition metal to reduce its energy by becoming less ionized.
with the nth ionization energy quantifies previous arguments2 that the cell voltage is increased when “electrons in the outer shells are more strongly attracted by atomic nuclei”2 of transition-metal cations with increasing atomic number (in the same oxidation state), due to increasing effective nuclear charge. We can now better understand why Li is strongly bonded in LiFePO4 (in addition to the electrostatic attraction of Li+ to PO43−): lithium intercalation lowers the energy of its environment, and therefore of lithium itself in this environment, by allowing the transition metal to reduce its energy by becoming less ionized.
Quantum-chemical calculations and analyses by Aydinol et al.7 have indicated that for transition-metal oxides, only about ¼ of one electron is transferred to the transition metal; this may go a long way towards explaining why in Fig. 5b the magnitude of the energy released is significantly smaller than the ionization energy. Dielectric screening of the electric field between the ion and the electron by intervening charged particles will also reduce their interaction energy.
The conceptually well-supported relation between the nth ionization energy and the cell voltage revealed here can be used to make predictions about relative cell potentials: generally, late transition metals are more difficult to ionize and therefore give higher voltages. More quantitative estimates are possible if some cell voltages for the same type of oxide or phosphate have already been measured.
No electrons in the overall reaction of a discharging battery
The process in a discharging lithium-ion battery with a lithiated graphite anode and an iron–phosphate cathode can be described by| | | LiC6(s) + FeIIIPO4(s) → 6C(s) + LiFeIIPO4(s) | (12) |
without electrons as reactants or products; they are only intermediates showing up in the half reactions. This absence of electrons in the overall reaction greatly simplifies the energetic analysis. It means that the chemical potential of electrons, sometimes considered a major driving force in lithium-ion batteries14–16 as discussed below, is of secondary importance. Fig. S5 (ESI†) shows that the chemical potentials of electrons in LiMO2 or MO2, as estimated by quantum-chemical calculations, only weakly correlate (R2 = 0.58 for a positive correlation and R2 = 0.42 for a weak anticorrelation, respectively) with the 4th ionization energy of the transition metal M. This also demonstrates that the electronic component of the cohesive energy discussed above does not correspond to μe−.
It may be important here to conceptually distinguish between an open lithium-ion cell on the one hand and a discharging, possibly reversible, cell on the other. In an open cell, electrons do show up in the overall reaction, see eqn (S69) (ESI†), but since they do not travel through an external circuit, no electrical energy is released. In a continuously discharging cell, the electrons released by the oxidation at the anode travel through the external circuit, performing electrical work, and end up in the cathode, where they are consumed in the reduction reaction. As a result, electrons disappear from the net reaction of a discharging cell.
The discharging battery: net Li atom transfer
Fig. 6 schematically shows a discharging lithium-ion battery and emphasizes that the simultaneous transfer of Li+ and an electron is equivalent to the transfer of a lithium atom. According to the path-independence of the change in free energy, which is a state function,33 and with eqn (1b), the energy release by the real process in Fig. 6a and the simpler hypothetical one in Fig. 6b is the same. This equivalence of the processes in Fig. 6a and b explains why the energetics of a discharging lithium-ion battery are determined by relatively simple differences in lithium-atom bonding energy and chemical potential μLi rather than differences in lithium-ion electrochemical potential ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+, which also depend on an unmeasurable37,38 difference in the Galvani (or inner) electrical potential ϕ. Fig. 6 again highlights that the energetics of electrons do not need to be considered separately in a discharging battery. This has also been emphasized by Ceder and coworkers in highly cited publications.6,7,11 The fundamental relation between lithium ions, electrons, and lithium atoms in materials is discussed below (see eqn (38)).
Li+, which also depend on an unmeasurable37,38 difference in the Galvani (or inner) electrical potential ϕ. Fig. 6 again highlights that the energetics of electrons do not need to be considered separately in a discharging battery. This has also been emphasized by Ceder and coworkers in highly cited publications.6,7,11 The fundamental relation between lithium ions, electrons, and lithium atoms in materials is discussed below (see eqn (38)).
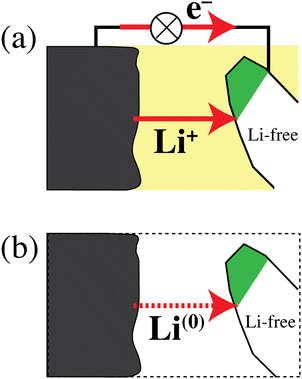 |
| | Fig. 6 (a) Schematic of a discharging lithium-ion battery. Li+ ions and electrons flow from a lithium metal anode to a cathode particle converting from the delithiated to the lithiated phase (shaded white and green, respectively). (b) Simplified process, chemically and energetically equivalent to that in (a), with a transfer of lithium atoms from anode to cathode. | |
Why the electrons flow
The electron flow in a discharging lithium-ion battery is driven by the chemical reaction. Electrons flow from the anode with a negative charge usually due to the chemically induced excess of electrons, left behind by Li atoms leaving the anode as Li+ ions, to the cathode where electrons from the external circuit get attracted to the positively charged freshly incorporated Li+. Equivalently, one can argue that the flow of lithium ions, usually driven by their different bonding strength in the two electrodes, produces an ionic current that must be accompanied by an electron current through the external circuit because circuits of current must always be closed (otherwise charge would accumulate excessively and stop the current due to electrostatic repulsion).
In an alternative view, the electron movement is driven by a difference in electron chemical potential.14–16 This statement is trivially true for the electron electrochemical potential ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−: like any chemical species, electrons move spontaneously from high to low electrochemical potential.26 Notably, a voltmeter measures the difference in electron electrochemical potential between its probe tips. In a good lithium-ion battery, the difference in electron electrochemical potential between the electrodes is mostly due to the electric potential difference Δϕ resulting from (chemically insignificant amounts of) excess charge on the electrodes that are maintained by the chemical reaction. The analysis in terms of the purely chemical parts of the electrochemical potentials, i.e. the electron and lithium-ion chemical potentials,14–16 which cannot be measured,37,38 is critically discussed below.
e−: like any chemical species, electrons move spontaneously from high to low electrochemical potential.26 Notably, a voltmeter measures the difference in electron electrochemical potential between its probe tips. In a good lithium-ion battery, the difference in electron electrochemical potential between the electrodes is mostly due to the electric potential difference Δϕ resulting from (chemically insignificant amounts of) excess charge on the electrodes that are maintained by the chemical reaction. The analysis in terms of the purely chemical parts of the electrochemical potentials, i.e. the electron and lithium-ion chemical potentials,14–16 which cannot be measured,37,38 is critically discussed below.
Chemical potentials in lithium-ion batteries
The description of the energetics of a discharging lithium-ion battery with two-phase cathodes in terms of bonding differences is intuitive and can be quantified as demonstrated in Scheme 1. Nevertheless, traditionally a formalism in terms of chemical potentials has been used instead, specifically focusing on the chemical potential of lithium atoms, μLi = (∂G/∂nLi)T,P,n′,4,6–10,14–16 (for basic aspects see the ESI,† starting at eqn (S33)), which we can rigorously relate to our analysis in terms of cohesive energies. The chemical potential of lithium is the (partial) molar Gibbs free energy of lithium. When lithium atoms move from high to low chemical potential μLi, the Gibbs free energy is reduced, which is allowed according to the second law of thermodynamics. A description of the chemical potential as a measure of how much Li(0) is “disliked” in a given phase4 may give the misleading impression that Li(0) is disliked more in pure metallic lithium than as an intercalant in a metal oxide or phosphate; in reality, lithium is stabilized (“liked”) by bonding in both environments, but much more so in the ionic oxide or phosphate, see Fig. 2b.
In the following, we show first that the chemical potential of lithium atoms in the cathode is equal to the difference in the molar Gibbs free energies, or chemical potentials, of FePO4 and LiFePO4, which are the cohesive free energies used in our analysis above. Then we express the cell voltage in terms of a difference of chemical potentials.
Chemical potentials in coexisting iron phosphates
The system under analysis in this section is a two-phase cathode consisting of FePO4 and LiFePO4 in various proportions. We start from well-established39| | 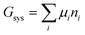 | (13a) |
where the ni are amounts in moles. Considering that lithium is contained only in LiFePO4 while Fe is part of both phases, we have| | | nLi = nLiFePO4 and nFePO4 + nLiFePO4 = nFe | (13b) |
This gives| | 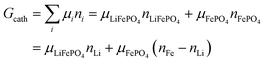 | (14a) |
The same result can be obtained from additivity of the Gibbs free energies of the two phases in the cathode:| | | Gcath = GLiFePO4 + GFePO4 = μLiFePO4nLi + μFePO4(nFe − nLi) | (14b) |
where we have used nFePO4 = (nFe − nLi) from eqn (13b).
From this dependence of G on the amount of lithium in the cathode, we can immediately derive the chemical potential of lithium in the cathode by taking the derivative:
| | | μLi(cathode) = (∂Gcath/∂nLi)T,P,n′ = μLiFePO4 − μFePO4 | (15) |
Since
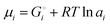
and the activity
ai of a pure solid is
apure![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solid
solid = 1,
26,39 we can equate
| | 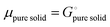 | (16) |
With
eqn (16) and (15) we obtain
| | 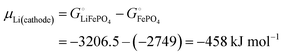 | (17) |
where we have used numerical values from
Scheme 1. This result makes sense: the equation matches the definition of the chemical potential of lithium in the cathode as the free-energy change when a mole of lithium is added to a large cathode, since adding lithium to the cathode converts FePO
4 to LiFePO
4, which results in the free-energy change
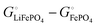
on the right-hand side of
eqn (17). This free-energy reduction per mole of Li incorporated is a good measure of the binding energy of lithium in the cathode, see
Fig. 2b.
The important result eqn (17) links our treatment in terms of the cohesive free energies 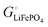 and
and 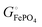 of the two phases in the cathode, explained using intuitive yet quantifiable bonding concepts, with the conventional formalism in terms of the chemical potential of lithium in the cathode.4,6–11 In the ESI,† a corresponding analysis in terms of coexisting Li0.02FePO4 and Li0.98FePO4 is presented. Its result, eqn (S44) (ESI†), essentially reproduces eqn (17).
of the two phases in the cathode, explained using intuitive yet quantifiable bonding concepts, with the conventional formalism in terms of the chemical potential of lithium in the cathode.4,6–11 In the ESI,† a corresponding analysis in terms of coexisting Li0.02FePO4 and Li0.98FePO4 is presented. Its result, eqn (S44) (ESI†), essentially reproduces eqn (17).
Note that relation (15) has not been apparent in the literature. A superficially similar-looking difference of chemical potentials in the literature,4
| | | −EcellF = μLi(α) − μLi(β) = μLi(cathode) − μLi(Li(s)) | (18) |
is of a quite different nature, referring not to two phases of the cathode, but to the anode and cathode. (The left-hand side of
eqn (15),
μLi(cathode), is only one of the terms on the right-hand side of
eqn (18).)
Lithium chemical potentials in anodes
For an anode consisting of lithium metal, trivially| | 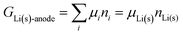 | (19) |
Given that in this simple system, nLi = nLi(s), we have| | | GLi(s)-anode = μLi(s)nLi | (20) |
and the chemical potential of lithium, according to its fundamental definition and on our scale with unbonded lithium atoms at zero free energy, is| | 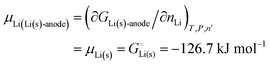 | (21) |
If we assume that an anode consists partially of graphite intercalated by lithium, with nLi = nLiC6(s), and partially of unintercalated graphite, then due to carbon balance,| | | 6nLiC6(s) + nC(s) = nC | (22) |
and we have| | 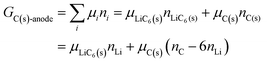 | (23) |
It follows (see also eqn (16) and eqn (S24), (S27), ESI†) that the chemical potential of lithium intercalating graphite is| | 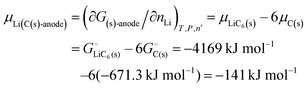 | (24) |
Ionic and electronic cohesive-energy contributions to the chemical potential of lithium
Above, we discussed a decomposition of the cohesive energy into an ionic and an electronic part. This decomposition is also valid when it comes to chemical potentials. The chemical potential of a neat stoichiometric solid, e.g. μLiCl(s), is equal to its cohesive free energy, 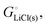 see eqn (16). Therefore, we can write (see also Fig. 4b)
see eqn (16). Therefore, we can write (see also Fig. 4b)| | 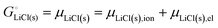 | (25) |
| | | −617 kJ mol−1 = μLiCl(s) = −792 kJ mol−1 + 175 kJ mol−1 | (26a) |
| | | μLiCl(s),ion = −792 kJ mol−1, μLiCl(s),el = 175 kJ mol−1 | (26b) |
This is a specific, quantitative example of the decomposition of a chemical potential into an ionic and an electronic component. Applying this concept to an iron–phosphate cathode, we can write| | 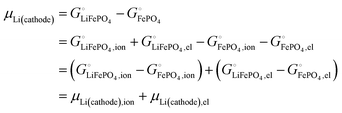 | (27) |
splitting the chemical potential of lithium in the cathode into an ionic and an electronic component, with the former given by| | 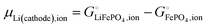 | (28) |
and the latter by| | 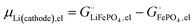 | (29) |
Chemical potentials and cell voltage
For a reversible electrochemical system40 under standard conditions, the cell voltage can be calculated from the standard molar change in free energy, ΔrG° according to eqn (4). This derives from the definition of voltage difference as electrical energy difference per charge, given that ΔrG° is the molar electrical work, and νeF is the charge transferred per mole of reaction. According to eqn (1), this remains a good approximation for a cell slowly and irreversibly discharging through a large external resistance. For a reaction involving only stoichiometric solid reactants and products near 1 bar pressure, standard conditions are automatically fulfilled.
More generally, for a system containing a lithium–metal anode and a cathode consisting of FePO4 and LiFePO4 in various proportions and undergoing the reaction of eqn (3), the change in Gibbs free energy at constant T and P is
| | 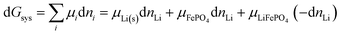 | (30) |
where d
nLi < 0 is a small amount of lithium transferred from the anode to the cathode. It relates directly to the change in the extent of reaction,
ξ,
39 according to
Via d
G =
μLiFePO4d
ξ −
μLi(s)d
ξ −
μFePO4d
ξ and formally dividing by d
ξ, we obtain a standard result in the thermodynamics of chemical reactions, with stoichiometric coefficients
νi (which are unity here),
| | 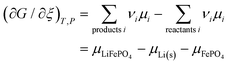 | (32) |
In advanced thermodynamics of electrochemical reactions, it can be shown (see eqn (S46), ESI
†) that the cell voltage, under standard or non-standard but still reversible conditions, relates to the slope of
G(
ξ) at constant
T and
P according to
| | | −νeFEcell = (∂G/∂ξ)T,P | (33) |
The number
νe of electrons transferred is
νe = 1. Combining
eqn (32), (33) and (16) (including
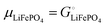
), we can relate the cell voltage to the free energies of the electrode materials, with data from
Scheme 1,
| | 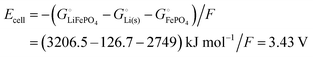 | (34) |
Eqn (32) and (33) can also be directly combined to express the cell voltage in terms of chemical potentials
| | | Ecell = −(μLiFePO4 − μLi(s) − μFePO4)/F | (35) |
Based on
eqn (15) and (21) relating the chemical potentials of the electrode materials to the chemical potential of lithium in these materials, this gives
| | | Ecell = −(μLi(cathode) − μLi(anode))/F = −ΔμLi/F | (36) |
a starting point of the conventional formalism in terms of the chemical potential of lithium atoms,
4,6–11 which is summarized in the ESI,
† starting at eqn (S53). Further relations between the cell voltage, the slope of
G(
xLi), and the chemical potential of lithium are derived in the ESI,
† starting at eqn (S61). They are applied below to show that in a single-phase cathode with gradually changing lithium concentration,
e.g. Li
xCoO
2, the average cell voltage can still be calculated from the difference in cohesive energies of the stoichiometric end-member compounds.
For a cell discharging according to eqn (12), the electrical energy released can be calculated from chemical potentials according to
| wele ≈ ΔrG = |ΔnLi|(μLiFePO4 + 6μC(s) − μLiC6 − μFePO4) |
| = |ΔnLi|(−3206.5 + 141.2 − (−2749)) kJ mol−1 |
| | | = |ΔnLi|(−316 kJ mol−1) = |ΔnLi|(−F)3.28 V | (37) |
with the change |Δ
nLi| in the amount of lithium in anode or cathode and the chemical potentials of products and reactants.
Lithium ions and atoms
To a good approximation, in LiCl(s), Li(s), LiFePO4(s), and LiC6(s) lithium exists as a Li+ ion core and an electron transferred to nearby space: into Cl−, into the space between ion cores, into (FeIIPO4)−, and into graphite layers, respectively. The transferred electron is distinct from electrons in atomic cores of Cl etc. in that it locally generates a net extra negative charge.
Nevertheless, in chemical formulas, including the four examples listed, and in energetic analyses, it is still more useful to refer to atomic Li than to ionic Li+. One writes LiCl, not Li+Cl−, and usually refers to the chemical potential μLi of Li(0), not to ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+. The relation between the cell voltage and the difference in chemical potential of lithium atoms in the two electrodes, Ecell = −ΔμLi/F, eqn (36), is an important example. Due to the approximate charge neutrality of condensed materials (the concentration of the uncompensated electrons and ions generating the electric potential difference in batteries is chemically insignificant, less than picomolar), almost every Li+ in a lithium-ion battery is accompanied by an electron, and treating both together as one neutral entity, a lithium atom, whose energy does not depend on the local electrical potential, simplifies the analysis. Thus, when we refer to “a lithium atom” in a material, we mean the combination of Li+ and a nearby “extra” electron in the material. As an equation, we can write
Li+. The relation between the cell voltage and the difference in chemical potential of lithium atoms in the two electrodes, Ecell = −ΔμLi/F, eqn (36), is an important example. Due to the approximate charge neutrality of condensed materials (the concentration of the uncompensated electrons and ions generating the electric potential difference in batteries is chemically insignificant, less than picomolar), almost every Li+ in a lithium-ion battery is accompanied by an electron, and treating both together as one neutral entity, a lithium atom, whose energy does not depend on the local electrical potential, simplifies the analysis. Thus, when we refer to “a lithium atom” in a material, we mean the combination of Li+ and a nearby “extra” electron in the material. As an equation, we can write
| | | “Li(material)” ≡ Li+(material) + e−(material) | (38) |
where “material” stands for a condensed material such as LiCl, Li(s), LiFePO
4, LiC
6,
etc. This important identity is fundamental and does not require equilibrium at the surface of the material. Note also that there is no such identity in the gas phase, where a lithium atom and a lithium ion plus a
distant free electron are distinct entities whose enthalpy differs by the ionization energy of 519 kJ mol
−1:
| | | Li(g) ≠ Li+(g) + e−(g). | (39) |
Naturally associated with the identity of
eqn (38) is the corresponding relation of chemical potentials,
| | | μLi(material) = μLi+(material) + μe−(material) | (40) |
Since lithium atoms are uncharged, their electrochemical and chemical potentials are equal according to eqn (S33b) (ESI
†),
| | μLi(material) = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li(material) = Li(material) = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+(material) + Li+(material) + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−(material) e−(material) | (41) |
The second equality in
eqn (41), which provides a useful relation to and between electrochemical potentials,
4 can be viewed as another consequence of
eqn (38); alternatively, one can consider that the ion and associated nearby excess electron experience the same inner potential
ϕ, whose contributions according to eqn (S33b) (ESI
†) therefore cancel so
eqn (40) is recovered. Evaluating the differences of the three (electro)chemical potentials in
eqn (41) between cathode and anode, we obtain
| | μLi(cathode) − μLi(anode) = ΔμLi = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li = Δ Li = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+ + Δ Li+ + Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− e− | (42) |
which directly leads to results useful in lithium-ion batteries: due to diffusion equilibrium of lithium ions between the two electrodes in an open or slowly discharging cell, we have
| | Li+(anode) ⇌ Li+(cathode) ⇔ Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+ = 0, Li+ = 0, | (43) |
which simplifies
eqn (42) to
| | Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = ΔμLi e− = ΔμLi | (44) |
The chemical potential of the electron, and its limitations
Repeatedly, attempts have been made to explain the processes in a lithium-ion battery by the difference in the chemical potential μe− of the electron in the two electrodes.14–16 This quantity has to be distinguished from the electrochemical potential ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− of the electron, already mentioned above, to which according to eqn (S33b) (ESI†) it is related by
e− of the electron, already mentioned above, to which according to eqn (S33b) (ESI†) it is related by| | ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = μe− − Fϕ e− = μe− − Fϕ | (45) |
and which is the immediate driving force of electron movement, with a large contribution from the inner or Galvani electrical potential ϕ. Fundamentally, the electromotive force or voltage of the cell is proportional to the difference in electrochemical potential of the electron between the electrodes:| | −EcellF = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = ΔμLi = ΔμLi+ + Δμe− e− = ΔμLi = ΔμLi+ + Δμe− | (46) |
where eqn (40) was used in the last step. The second equality results from eqn (44) and shows that the cell voltage is still proportional to the difference in the chemical potentials of lithium atoms in the two electrodes, as in eqn (36).
According to eqn (40), the chemical potential of lithium atoms, μLi, can be decomposed into the chemical potentials of lithium ions, μLi+, and electrons, μe−. However, this separation of the energy change of the lithium atom into an electronic and ionic part14–16 does not seem helpful since neither quantity is known independently. Indeed, McKinnon41 already concluded that the electronic and ionic intercalation energies (technically chemical potentials) are not independent. The focus on the electronic component μe−,14–16 presumably due to its familiarity to physicists as the Fermi level, has been justified with the assumption that the ionic component μLi+ is negligible compared to μe−, but this is unfounded. For instance, if μLi = 0 in elemental lithium in its standard state (i.e. in Li(s)),10 then eqn (40) gives
| | | 0 = μLi(Li(s)) = μLi+(Li(s)) + μe−(Li(s)) | (47) |
| ⇒ μLi+(Li(s)) = −μe−(Li(s)) |
which means that the ionic component would be equal in magnitude (and opposite in sign) to the electronic component. Below we will show that the interpretation of
μe− as the work function
15,16 leads to incorrect predictions and will quote literature strongly questioning whether
μe− can be measured at all.
For the two-phase electrodes that are the focus of this paper, the assumption of a single electron chemical potential14 in each electrode is not tenable, since the two phases have distinct μe− values, by as much as 2.3 eV,7 see also Fig. S4 (ESI†). With the electrons in the two phases in diffusion equilibrium, it is not at all clear which of the two μe− values is supposed to represent the driving force of electron movement.
Incorrect predictions from work functions as chemical potentials
The interpretation of the chemical potentials of electrons and of lithium ions as negative work functions Φe− (ref. 15 and 16) and ΦLi+,15 the energy needed to remove an electron or lithium ion, respectively, combined with eqn (47) leads to| | | μLi+(Li(s)) = −μe−(Li(s)) ≈ Φe−(Li(s)) > 2 eV ≈ 190 kJ mol−1 | (48a) |
| | | ΦLi+(Li(s)) ≈ −μLi+(Li(s)) < −190 kJ mol−1 ≪ 0 (‘Li+ emission’) | (48b) |
This would mean that removing lithium ions from lithium metal would not require energy input but rather release at least 190 kJ mol−1. This prediction of spontaneous emission of lithium ions from lithium metal at 298 K is clearly an incorrect result of this theory.
Due to these complications and others discussed below, we find it unhelpful to try to explain the processes in a discharging lithium-ion battery and the associated energy release by emphasizing that the electrons go to a lower energy state. An electron in a copper lead attached to the anode is higher in energy (free energy, or chemical potential) than in a copper lead attached to the cathode exclusively due to the electric potential difference between the electrodes, which is generated by excess charges in turn produced by the chemical reaction starting from neutral compounds. (This is the electrical-potential term −FΔϕ in the difference between the electrochemical potentials ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− of electrons in the electrode-attached copper leads.)
e− of electrons in the electrode-attached copper leads.)
The chemical potential of the electron cannot be measured
Various publications14,16,42 have attributed the movement of electrons in a lithium-ion battery to the difference in the chemical potential of the electron in the electrodes. However, the utility of this approach can be questioned.6,7,11,41 Importantly, the value of μe− cannot be measured, only calculated, as pointed out explicitly by Trasatti,37 referring to “μMe, which is not capable of either direct or, at present, even indirect measurement” (note that the concept of the work function was already well established at the time and also discussed by Trasatti37). This makes μe− distinct from μLi, the chemical potential of lithium atoms,4,6–10,14–16 which is well defined and can be quantified from experimental data with three to four significant figures, as we have shown in this paper, see eqn (17), (21) and (24). Note that a difference in μe− also cannot be measured, since according to eqn (45),| | Δμe− = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− + FΔϕ e− + FΔϕ | (49) |
so Δμe− is equal to the measurable Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = −EcellF plus the unmeasurable37,38 difference in the inner or Galvani potential ϕ, multiplied by F; only a difference in the outer or Volta potential ψ can be measured.37,38
e− = −EcellF plus the unmeasurable37,38 difference in the inner or Galvani potential ϕ, multiplied by F; only a difference in the outer or Volta potential ψ can be measured.37,38
The claimed15,16 equality of the chemical potential of the electron to the electron work function Φe−, which is experimentally accessible, is approximate at best.37,38 The −μe− values from highly cited quantum-chemical calculations7 are smaller than the measured Φe− values16 for LiCoO2 and LiNiO2 by as much as 1.6 eV, and the work-function predicted voltages16 still fall short of the measured values by at least 1.3 V. (Addition of the valence-band onset to the work function16 seems to have no basis in thermodynamic theory.37) Thus, less than half and maybe as little as 3.9–1.6–1.3 = 1 V of the ∼3.9 V cell voltage of LiCoO2 or LiNiO2 relative to lithium metal can realistically be attributed to differences in electron chemical potential, while the Li+ chemical-potential difference in eqn (46) accounts for the larger part of the voltage. Relative to a lithiated-graphite electrode with its larger (compared to lithium metal) Φe− > 3.5 V, the electronic contribution must be even smaller (safely <1.5 V out of ∼3.8 V). In other words, the movement of ions and electrons is driven mostly by the difference in the strength of bonding of Li+, not of the electrons, in anode and cathode.
Some sources have claimed explicitly42 or implicitly (e.g. in a figure)16,17 that
| | | −Ecell = Δμe−/F (not true) | (50) |
As shown in Fig. S4b (ESI
†), the data from highly cited simulations of transition-metal oxides
7 do not show the correlation predicted by
eqn (50), instead exhibiting a weak anticorrelation with
R2 = 0.40 and 0.24 for predicted and experimental voltages, respectively, thereby falsifying
eqn (50). Indeed,
eqn (50) is not a true equality. Instead, the cell voltage is the difference in the electrochemical potential of the electron (marked with a tilde) between anode and two-phase cathode in an open cell, according to
eqn (46):
14−Ecell = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−/F = Δμe−/F − Δϕ e−/F = Δμe−/F − Δϕ |
| | | = Δμe−/F + ΔμLi+/F = ΔμLi/F | (51) |
The last equality, with the chemical potential difference of lithium atoms,
4,6–10,14–16 is much easier to evaluate quantitatively than are approximate differences involving electrons and ions. And from cohesive energies, the stable cell voltage for two-phase cathodes can be calculated to two or three significant figures, as shown in
eqn (6),
Scheme 1 and
Fig. 3;
20 the cohesive energies, in turn, are amenable to both measurement by calorimetry and calculation from quantum chemistry.
6,7,11
Single-phase cathodes: average voltage from cohesive energies
So far, mostly two-phase cathodes have been discussed. These are instructive because they can be described in terms of a simple chemical reaction as in eqn (3). They also have the practical advantage of a stable voltage over a wide lithium concentration. The literature confirms that iron–phosphate cathodes can realistically be described as two-phase.22,23,43
Here we extend the analysis to single-phase cathodes, whose lithium content gradually increases as the battery discharges.11 We will consider LixCoO2 with CoO2 progressively converting to LiCoO2 as a specific sample reaction. Based on the linear dependence of the cell voltage on the chemical potential of lithium in the LixCoO2 cathode, μLi(cath) ≡ μLi(LixCoO2), which in turn relates to the molar Gibbs free energy10 or chemical potential of LixCoO2 according to
| | | μLi(cath) = (∂μLixCoO2/∂x) | (52) |
see eqn (S62) (ESI
†), we can show that the average voltage
Ēcell over a full discharge cycle, converting CoO
2 to LiCoO
2, can still be calculated simply from the difference in the cohesive energies of Li(s) + CoO
2(s)
vs. LiCoO
2(s). We start with
| Ēcell(−F) = average ΔμLi = average μLi(cath) − μLi(s) |
| | | = [average slope of μLixCoO2(x)] − μLi(s) | (53) |
According to a simple definition of averaging over the full composition range (
xLi from 0 to 1) applied to the slope of
μLixCoO2(
x) and then using the central theorem of calculus, we find for the average cell voltage
| | 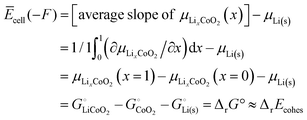 | (54) |
where
eqn (16),
e.g.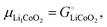
was used. A similar result holds for
xLi = 0.5: since both the entropy of mixing, proportional to
xLi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xLi
xLi + (1 −
xLi)ln(1 −
xLi), and the enthalpy of mixing in a regular solution model (eqn (S63), ESI
†), proportional to
xLi(1 −
xLi), have zero slope near
xLi = 0.5, at that central composition effects of mixing on the slope of
μLixCoO2(
x) are small and it remains approximately equal to Δ
rG° +
μLi(s). This means that
| Ecell(xLi = 0.5)(−F) = (∂μLixCoO2/∂x)|0.5 − μLi(s) |
i.e. not only the average voltage, but also the actual voltage for
xLi ≈ 50% lithium incorporation, can still be calculated from the cohesive energies of the stoichiometric end members. Note that in practice, the upper cutoff of the charging voltage is usually set such that
x in Li
xCoO
2 always stays above 0.5, because the cathode becomes unstable with a lithium content lower than
x = 0.5.
32 This also explains why the experimental voltage range for Li
xCoO
2 in
Fig. 3 is slightly below the prediction from the cohesive energies for
xLi = 0.5.
Conclusions
The hallmark of a working lithium-ion battery is the release of electrical energy due to the spontaneous movement of lithium ions and electrons out of the negative and into the positive electrode. These are the processes that must be convincingly accounted for in a good explanation of how LIBs work. We have shown that the energy release originates from lithium (as Li+ and e−) moving spontaneously from a weakly bonded (by ~−140 kJ mol−1) less stable state in the negative electrode to a more stable ionically bonded (by ∼−460 kJ mol−1) state in the positive electrode, where it remains trapped until driven back to the negative electrode by the macroscopic electrostatic forces of a sufficiently strong charging voltage overcoming the chemical-bonding forces. Charge neutrality requires that upon Li+ incorporation into the cathode, the oxidation state of a transition metal or other atom is reduced by an electron taken up from the external circuit. The corresponding ionization energy contributes to the cohesive energy difference of the lithium-free and lithiated cathode phases and therefore correlates with the cell voltage. The intuitive and quantifiable bonding description has been shown to be equivalent to the atomic-lithium chemical-potential formalism in the literature, and the chemical potential of lithium in a two-phase electrode has been quantified in terms of cohesive energies, in kJ mol−1. Electron flow is mostly driven by the chemical reaction and lithium-ion current; the chemical potential of the electron cannot be measured and does not correlate significantly with the cell voltage; it is therefore of secondary importance in a discharging, energy-releasing lithium-ion battery.
Author contributions
Sam Finkelstein: data curation; investigation; software; validation; visualization; writing – original draft, review & editing. Marco Ricci: conceptualization; data curation; investigation; visualization; validation; writing – review & editing. Tom Bötticher: conceptualization; visualization; writing – review & editing. Klaus Schmidt-Rohr: conceptualization; data curation; formal analysis; funding acquisition; investigation; methodology; project administration; resources; supervision; visualization; writing – original draft, review & editing.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
References
- G. E. Blomgren, J. Electrochem. Soc., 2016, 164, A5019–A5025 CrossRef.
- C. Liu, Z. G. Neale and G. Cao, Mater. Today, 2016, 19, 109–123 CrossRef CAS.
- Y.-S. Hu and Y. Lu, ACS Energy Lett., 2019, 4, 2689–2690 CrossRef CAS.
- J. Maier, Angew. Chem., Int. Ed., 2013, 52, 4998–5026 CrossRef CAS.
-
S. Minos, How Lithium-ion Batteries Work, 2023, https://www.energy.gov/energysaver/articles/how-lithium-ion-batteries-work, (accessed December 13) Search PubMed.
- G. Ceder, M. Aydinol and A. Kohan, Comput. Mater. Sci., 1997, 8, 161–169 CrossRef CAS.
- M. Aydinol, A. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 CrossRef CAS.
-
W. McKinnon and R. Haering, in Modern Aspects of Electrochemistry: No. 15, ed. R. E. White, J. O. M. Bockris and B. E. Conway, Springer US, Boston, MA, 1983, pp. 235–304 DOI:10.1007/978-1-4615-7461-3_4.
- W. Li, W. R. McKinnon and J. R. Dahn, J. Electrochem. Soc., 1994, 141, 2310–2316 CrossRef CAS.
- A. T. Phan, A. E. Gheribi and P. Chartrand, Can. J. Chem. Eng., 2019, 97, 2224–2233 CrossRef CAS.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 1–13 CrossRef.
- W. Li, J. R. Dahn and D. S. Wainwright, Science, 1994, 264, 1115–1118 CrossRef CAS PubMed.
- B. C. Melot and J.-M. Tarascon, Acc. Chem. Res., 2013, 46, 1226–1238 CrossRef CAS PubMed.
- H. Gerischer, F. Decker and B. Scrosati, J. Electrochem. Soc., 1994, 141, 2297–2300 CrossRef CAS.
- S. Schuld, R. Hausbrand, M. Fingerle, W. Jaegermann and K. M. Weitzel, Adv. Energy Mater., 2018, 8, 1–8 Search PubMed.
- G. Cherkashinin, R. Hausbrand and W. Jaegermann, J. Electrochem. Soc., 2019, 166, A5308–A5312 CrossRef CAS.
- A. Padhi, K. Nanjundaswamy, C. Masquelier, S. Okada and J. Goodenough, J. Electrochem. Soc., 1997, 144, 1609 CrossRef CAS.
- K. Schmidt-Rohr, J. Chem. Educ., 2018, 95, 1801–1810 CrossRef CAS.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- C. Wang, L. Yu, W. Fan, J. Liu, L. Ouyang, L. Yang and M. Zhu, ACS Appl. Energy Mater., 2018, 1, 2647–2656 CrossRef CAS.
- Z. Chen and J. Dahn, J. Electrochem. Soc., 2002, 149, A1184 CrossRef CAS.
- L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman, C. Masquelier and J. M. Tarascon, Chem. Mater., 2006, 18, 5520–5529 CrossRef CAS.
- C. Delmas, M. Maccario, L. Croguennec, F. Le Cras and F. Weill, Nat. Mater., 2008, 7, 665–671 CrossRef CAS.
- J. Niu, A. Kushima, X. Qian, L. Qi, K. Xiang, Y.-M. Chiang and J. Li, Nano Lett., 2014, 14, 4005–4010 CrossRef CAS.
- D. Allart, M. Montaru and H. Gualous, J. Electrochem. Soc., 2018, 165, A380–A387 CrossRef CAS.
-
R. G. Mortimer, Physical Chemistry, Elsevier, San Diego, 3rd edn, 2008 Search PubMed.
- J. Asenbauer, T. Eisenmann, M. Kuenzel, A. Kazzazi, Z. Chen and D. Bresser, Sustainable Energy Fuels., 2020, 4, 5387–5416 RSC.
- R. G. Iyer, C. Delacourt, C. Masquelier, J.-M. Tarascon and A. Navrotsky, Electrochem. Solid-State Lett., 2006, 9, A46–A48 CrossRef CAS.
- K. Schmidt-Rohr, J. Chem. Educ., 2015, 92, 2094–2099 CrossRef CAS.
- T. Abe and T. Koyama, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2011, 35, 209–218 CrossRef CAS.
- K. Jacob, A. Kumar, G. Rajitha and Y. Waseda, High Temp. Mater. Process, 2011, 30, 459–472 CAS.
- Z. Chen, Z. Lu and J. Dahn, J. Electrochem. Soc., 2002, 149, A1604 CrossRef CAS.
-
D. W. Oxtoby, H. P. Gillis and L. J. Butler, Principles of Modern Chemistry, CENGAGE Learning, Boston, MA, 8th edn, 2015 Search PubMed.
-
W. A. Harrison, Electronic structure and the properties of solids: the physics of the chemical bond, Dover Publications, New York, 1989 Search PubMed.
- G. Hautier, A. Jain, S. P. Ong, B. Kang, C. Moore, R. Doe and G. Ceder, Chem. Mater., 2011, 23, 3495–3508 CrossRef CAS.
-
A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database Ionization Energies Data, 2023, (accessed July 20) Search PubMed.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem, 1974, 52, 313–329 CrossRef CAS.
-
J. O. M. Bockris, A. K. N. Reddy and M. Gamboa-Aldeco, Modern Electrochemistry Fundamentals of Electrodics, Springer, New York, 2nd edn, 2000 Search PubMed.
-
D. A. McQuarrie and J. D. Simon, Molecular Thermodynamics, University Science Books, Sausalito, CA, 1999 Search PubMed.
- K. Schmidt-Rohr, Life, 2021, 11, 1191 CrossRef CAS PubMed.
-
W. R. McKinnon, in Chemical Physics of Intercalation, ed. A. P. Legrand and S. Flandrois, Springer Science & Business Media, New York, 1987, vol. 172, pp. 181–194 Search PubMed.
- Y. Zhang, J. A. Alarco, A. S. Best, G. A. Snook, P. C. Talbot and J. Y. Nerkar, RSC Adv., 2019, 9, 1134–1146 RSC.
- A. Andersson and J. O. Thomas, J. Power Sources, 2001, 97–98, 498–502 CrossRef CAS.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Marco
Ricci
a,
Marco
Ricci
 bc,
Tom
Bötticher
bc,
Tom
Bötticher
 d and
Klaus
Schmidt-Rohr
d and
Klaus
Schmidt-Rohr
 *a
*a

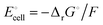
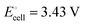 .
.

 of the solid reactants and products, which can be calculated from the enthalpies of formation of the solids and their elemental compositions as shown in the ESI,† see eqn (S12). The results are summarized in Scheme 1. The cohesive energy
of the solid reactants and products, which can be calculated from the enthalpies of formation of the solids and their elemental compositions as shown in the ESI,† see eqn (S12). The results are summarized in Scheme 1. The cohesive energy  quantifies the strength of bonding in compound i relative to the free, unbonded atoms, which define the zero point of the energy scale.18,29 The same applies to the individual standard molar free energy,
quantifies the strength of bonding in compound i relative to the free, unbonded atoms, which define the zero point of the energy scale.18,29 The same applies to the individual standard molar free energy, 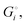 which is the cohesive free energy of the solid relative to the unbonded atoms.
which is the cohesive free energy of the solid relative to the unbonded atoms.
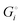 of the electrode materials from Scheme 1 and their stoichiometric coefficients νi (which are all 1 in eqn (3)):
of the electrode materials from Scheme 1 and their stoichiometric coefficients νi (which are all 1 in eqn (3)):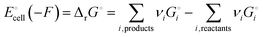
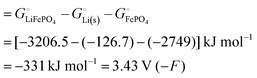
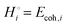 from Scheme 1
from Scheme 1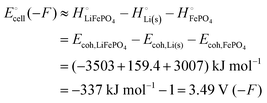
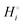 of a compound i with many atoms is always relatively large in magnitude, we can distinguish weak from strong bonding by comparing the cohesive energy per atom. Relatively strongly bonded, stable, low-energy compounds have a more negative
of a compound i with many atoms is always relatively large in magnitude, we can distinguish weak from strong bonding by comparing the cohesive energy per atom. Relatively strongly bonded, stable, low-energy compounds have a more negative 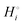 per atom than do more weakly bonded, high-energy compounds.18
per atom than do more weakly bonded, high-energy compounds.18 per atom (−159.4 kJ mol−1) and cohesive free energy
per atom (−159.4 kJ mol−1) and cohesive free energy  (−126.7 kJ mol−1) of lithium metal have already been pointed out.18 Due to its weak bonding, lithium metal is a high-energy material that reacts spontaneously even with a stable compound like H2O, and according to eqn (2), lithium intercalated in graphite is only slightly (−15 kJ mol−1) more stabilized.
(−126.7 kJ mol−1) of lithium metal have already been pointed out.18 Due to its weak bonding, lithium metal is a high-energy material that reacts spontaneously even with a stable compound like H2O, and according to eqn (2), lithium intercalated in graphite is only slightly (−15 kJ mol−1) more stabilized. than are FePO4 and LiFePO4,11 the Gibbs free energy change remains nearly the same, −331 kJ mol−1, as in eqn (5b) for the stoichiometric compounds, see also Fig. S3 (ESI†).10 The ∼2% larger value (3.51 eV = 339 kJ mol−1) reported by Phan et al.10 appears to be due to an inconsistency in Gibbs-energy referencing, see the ESI,† eqn (S67).
than are FePO4 and LiFePO4,11 the Gibbs free energy change remains nearly the same, −331 kJ mol−1, as in eqn (5b) for the stoichiometric compounds, see also Fig. S3 (ESI†).10 The ∼2% larger value (3.51 eV = 339 kJ mol−1) reported by Phan et al.10 appears to be due to an inconsistency in Gibbs-energy referencing, see the ESI,† eqn (S67).
 neglecting entropic effects). The cohesive energy differences for the two end-member phases of layered LixCoO2 and LixMnO2 cathodes were calculated from their standard enthalpies of formation6,7,11,30,31 as shown in the ESI† (Scheme S1). While LixCoO2 is a single-phase cathode with decreasing voltage as x increases,30 the average voltage over a theoretical full discharge cycle, converting CoO2 to LiCoO2, can still be calculated simply from the difference in the cohesive energies of Li(s) + CoO2vs. LiCoO2 (from Scheme S1a, ESI†),6,11
neglecting entropic effects). The cohesive energy differences for the two end-member phases of layered LixCoO2 and LixMnO2 cathodes were calculated from their standard enthalpies of formation6,7,11,30,31 as shown in the ESI† (Scheme S1). While LixCoO2 is a single-phase cathode with decreasing voltage as x increases,30 the average voltage over a theoretical full discharge cycle, converting CoO2 to LiCoO2, can still be calculated simply from the difference in the cohesive energies of Li(s) + CoO2vs. LiCoO2 (from Scheme S1a, ESI†),6,11
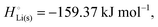 33 while that of LiCl(s) is
33 while that of LiCl(s) is 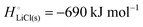 , see Fig. 4a. In magnitude, the cohesive energy is equal to the energy needed to dissociate the solid into atoms. It can therefore be considered as the binding or bonding energy of the solid. The cohesive energy also has the same magnitude as the energy of atomization or the enthalpy of sublimation, and for simple metals, the enthalpy of formation of the gaseous element.33 The corresponding cohesive free energy, e.g.
, see Fig. 4a. In magnitude, the cohesive energy is equal to the energy needed to dissociate the solid into atoms. It can therefore be considered as the binding or bonding energy of the solid. The cohesive energy also has the same magnitude as the energy of atomization or the enthalpy of sublimation, and for simple metals, the enthalpy of formation of the gaseous element.33 The corresponding cohesive free energy, e.g.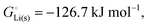 shows a moderately different value due to entropic effects.
shows a moderately different value due to entropic effects.
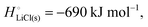 or −345 kJ per mol atoms, is released when neutral Li(g) and Cl(g) form solid LiCl. Converting Li(g) and Cl(g) to Li+(g) and Cl−(g) requires the input of the ionization energy of Li(g) (+519 kJ mol−1) and the release of the electron affinity of Cl(g) (−349 kJ mol−1), see Fig. 4a. The net energy input, 519–349 = 170 kJ mol−1, required for electron removal and re-uptake, can be considered as the electronic part of the cohesive energy. The cohesive free energy of LiCl(s) is
or −345 kJ per mol atoms, is released when neutral Li(g) and Cl(g) form solid LiCl. Converting Li(g) and Cl(g) to Li+(g) and Cl−(g) requires the input of the ionization energy of Li(g) (+519 kJ mol−1) and the release of the electron affinity of Cl(g) (−349 kJ mol−1), see Fig. 4a. The net energy input, 519–349 = 170 kJ mol−1, required for electron removal and re-uptake, can be considered as the electronic part of the cohesive energy. The cohesive free energy of LiCl(s) is 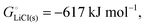 with an ionic part of −792 kJ mol−1 (considering the entropy difference of −245 J mol−1 K−1 between LiCl(s) and Li+(g) plus Cl−(g)) and an electronic part of 175 kJ mol−1.
with an ionic part of −792 kJ mol−1 (considering the entropy difference of −245 J mol−1 K−1 between LiCl(s) and Li+(g) plus Cl−(g)) and an electronic part of 175 kJ mol−1.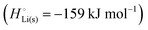 . The cohesive free energy of lithium metal is −126.7 kJ mol−1, with an electronic part of 521 kJ mol−1 and an “ionic” part (the free energy change when Li+(g) + e−(g) come together to form Li(s)) of −648 kJ mol−1 (less negative than the enthalpy change due to entropic favorability of gaseous Li+(g)). A corresponding expression in terms of chemical potentials is shown below (see eqn (25)).
. The cohesive free energy of lithium metal is −126.7 kJ mol−1, with an electronic part of 521 kJ mol−1 and an “ionic” part (the free energy change when Li+(g) + e−(g) come together to form Li(s)) of −648 kJ mol−1 (less negative than the enthalpy change due to entropic favorability of gaseous Li+(g)). A corresponding expression in terms of chemical potentials is shown below (see eqn (25)).
 with the nth ionization energy quantifies previous arguments2 that the cell voltage is increased when “electrons in the outer shells are more strongly attracted by atomic nuclei”2 of transition-metal cations with increasing atomic number (in the same oxidation state), due to increasing effective nuclear charge. We can now better understand why Li is strongly bonded in LiFePO4 (in addition to the electrostatic attraction of Li+ to PO43−): lithium intercalation lowers the energy of its environment, and therefore of lithium itself in this environment, by allowing the transition metal to reduce its energy by becoming less ionized.
with the nth ionization energy quantifies previous arguments2 that the cell voltage is increased when “electrons in the outer shells are more strongly attracted by atomic nuclei”2 of transition-metal cations with increasing atomic number (in the same oxidation state), due to increasing effective nuclear charge. We can now better understand why Li is strongly bonded in LiFePO4 (in addition to the electrostatic attraction of Li+ to PO43−): lithium intercalation lowers the energy of its environment, and therefore of lithium itself in this environment, by allowing the transition metal to reduce its energy by becoming less ionized.![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+, which also depend on an unmeasurable37,38 difference in the Galvani (or inner) electrical potential ϕ. Fig. 6 again highlights that the energetics of electrons do not need to be considered separately in a discharging battery. This has also been emphasized by Ceder and coworkers in highly cited publications.6,7,11 The fundamental relation between lithium ions, electrons, and lithium atoms in materials is discussed below (see eqn (38)).
Li+, which also depend on an unmeasurable37,38 difference in the Galvani (or inner) electrical potential ϕ. Fig. 6 again highlights that the energetics of electrons do not need to be considered separately in a discharging battery. This has also been emphasized by Ceder and coworkers in highly cited publications.6,7,11 The fundamental relation between lithium ions, electrons, and lithium atoms in materials is discussed below (see eqn (38)).
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−: like any chemical species, electrons move spontaneously from high to low electrochemical potential.26 Notably, a voltmeter measures the difference in electron electrochemical potential between its probe tips. In a good lithium-ion battery, the difference in electron electrochemical potential between the electrodes is mostly due to the electric potential difference Δϕ resulting from (chemically insignificant amounts of) excess charge on the electrodes that are maintained by the chemical reaction. The analysis in terms of the purely chemical parts of the electrochemical potentials, i.e. the electron and lithium-ion chemical potentials,14–16 which cannot be measured,37,38 is critically discussed below.
e−: like any chemical species, electrons move spontaneously from high to low electrochemical potential.26 Notably, a voltmeter measures the difference in electron electrochemical potential between its probe tips. In a good lithium-ion battery, the difference in electron electrochemical potential between the electrodes is mostly due to the electric potential difference Δϕ resulting from (chemically insignificant amounts of) excess charge on the electrodes that are maintained by the chemical reaction. The analysis in terms of the purely chemical parts of the electrochemical potentials, i.e. the electron and lithium-ion chemical potentials,14–16 which cannot be measured,37,38 is critically discussed below.
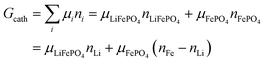
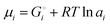 and the activity ai of a pure solid is apure
and the activity ai of a pure solid is apure![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solid = 1,26,39 we can equate
solid = 1,26,39 we can equate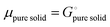
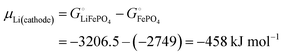
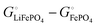 on the right-hand side of eqn (17). This free-energy reduction per mole of Li incorporated is a good measure of the binding energy of lithium in the cathode, see Fig. 2b.
on the right-hand side of eqn (17). This free-energy reduction per mole of Li incorporated is a good measure of the binding energy of lithium in the cathode, see Fig. 2b.
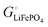 and
and 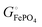 of the two phases in the cathode, explained using intuitive yet quantifiable bonding concepts, with the conventional formalism in terms of the chemical potential of lithium in the cathode.4,6–11 In the ESI,† a corresponding analysis in terms of coexisting Li0.02FePO4 and Li0.98FePO4 is presented. Its result, eqn (S44) (ESI†), essentially reproduces eqn (17).
of the two phases in the cathode, explained using intuitive yet quantifiable bonding concepts, with the conventional formalism in terms of the chemical potential of lithium in the cathode.4,6–11 In the ESI,† a corresponding analysis in terms of coexisting Li0.02FePO4 and Li0.98FePO4 is presented. Its result, eqn (S44) (ESI†), essentially reproduces eqn (17).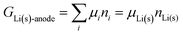
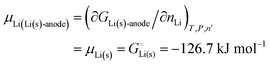
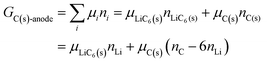
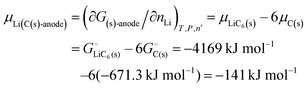
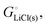 see eqn (16). Therefore, we can write (see also Fig. 4b)
see eqn (16). Therefore, we can write (see also Fig. 4b)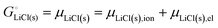
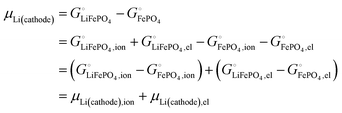
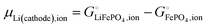
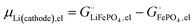
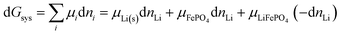
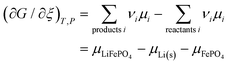
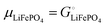 ), we can relate the cell voltage to the free energies of the electrode materials, with data from Scheme 1,
), we can relate the cell voltage to the free energies of the electrode materials, with data from Scheme 1,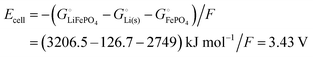
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+. The relation between the cell voltage and the difference in chemical potential of lithium atoms in the two electrodes, Ecell = −ΔμLi/F, eqn (36), is an important example. Due to the approximate charge neutrality of condensed materials (the concentration of the uncompensated electrons and ions generating the electric potential difference in batteries is chemically insignificant, less than picomolar), almost every Li+ in a lithium-ion battery is accompanied by an electron, and treating both together as one neutral entity, a lithium atom, whose energy does not depend on the local electrical potential, simplifies the analysis. Thus, when we refer to “a lithium atom” in a material, we mean the combination of Li+ and a nearby “extra” electron in the material. As an equation, we can write
Li+. The relation between the cell voltage and the difference in chemical potential of lithium atoms in the two electrodes, Ecell = −ΔμLi/F, eqn (36), is an important example. Due to the approximate charge neutrality of condensed materials (the concentration of the uncompensated electrons and ions generating the electric potential difference in batteries is chemically insignificant, less than picomolar), almost every Li+ in a lithium-ion battery is accompanied by an electron, and treating both together as one neutral entity, a lithium atom, whose energy does not depend on the local electrical potential, simplifies the analysis. Thus, when we refer to “a lithium atom” in a material, we mean the combination of Li+ and a nearby “extra” electron in the material. As an equation, we can write![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li(material) =
Li(material) = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+(material) +
Li+(material) + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−(material)
e−(material)![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li = Δ
Li = Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+ + Δ
Li+ + Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−
e−![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+ = 0,
Li+ = 0,![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = ΔμLi
e− = ΔμLi![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− of the electron, already mentioned above, to which according to eqn (S33b) (ESI†) it is related by
e− of the electron, already mentioned above, to which according to eqn (S33b) (ESI†) it is related by![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = μe− − Fϕ
e− = μe− − Fϕ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = ΔμLi = ΔμLi+ + Δμe−
e− = ΔμLi = ΔμLi+ + Δμe−![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− of electrons in the electrode-attached copper leads.)
e− of electrons in the electrode-attached copper leads.)![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− + FΔϕ
e− + FΔϕ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− = −EcellF plus the unmeasurable37,38 difference in the inner or Galvani potential ϕ, multiplied by F; only a difference in the outer or Volta potential ψ can be measured.37,38
e− = −EcellF plus the unmeasurable37,38 difference in the inner or Galvani potential ϕ, multiplied by F; only a difference in the outer or Volta potential ψ can be measured.37,38
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−/F = Δμe−/F − Δϕ
e−/F = Δμe−/F − Δϕ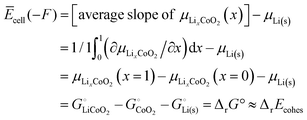
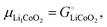 was used. A similar result holds for xLi = 0.5: since both the entropy of mixing, proportional to xLi
was used. A similar result holds for xLi = 0.5: since both the entropy of mixing, proportional to xLi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xLi + (1 − xLi)ln(1 − xLi), and the enthalpy of mixing in a regular solution model (eqn (S63), ESI†), proportional to xLi(1 − xLi), have zero slope near xLi = 0.5, at that central composition effects of mixing on the slope of μLixCoO2(x) are small and it remains approximately equal to ΔrG° + μLi(s). This means that
xLi + (1 − xLi)ln(1 − xLi), and the enthalpy of mixing in a regular solution model (eqn (S63), ESI†), proportional to xLi(1 − xLi), have zero slope near xLi = 0.5, at that central composition effects of mixing on the slope of μLixCoO2(x) are small and it remains approximately equal to ΔrG° + μLi(s). This means that


