Open Access Article
Open Access ArticleThe light-dependent pseudo-capacitive charging of conjugated polymer nanoparticles coupled with the depolarization of the neuronal membrane†
Greta
Chiaravalli
 ab,
Tiziana
Ravasenga
cd,
Elisabetta
Colombo
cd,
Jasnoor
ce,
Simona
Francia
cd,
Stefano
Di Marco
cd,
Riccardo
Sacco
f,
Grazia
Pertile
g,
Fabio
Benfenati
ab,
Tiziana
Ravasenga
cd,
Elisabetta
Colombo
cd,
Jasnoor
ce,
Simona
Francia
cd,
Stefano
Di Marco
cd,
Riccardo
Sacco
f,
Grazia
Pertile
g,
Fabio
Benfenati
 *cd and
Guglielmo
Lanzani
*cd and
Guglielmo
Lanzani
 *ab
*ab
aCenter for Nano Science Technology, Istituto Italiano di Tecnologia, Milano, Italy. E-mail: guglielmo.lanzani@iit.it
bPolitecnico di Milano, Physics Department, Milano, Italy
cCenter for Synaptic Neuroscience and Technology, Istituto Italiano di Tecnologia, Genova, Italy. E-mail: fabio.benfenati@iit.it
dIRCCS Ospedale Policlinico San Martino, Genova, Italy
eDepartment of Experimental Medicine, University of Genova, Genova, Italy
fPolitecnico di Milano, Mathematics Department, Milano, Italy
gDepartment of Ophthalmology, IRCCS Sacrocuore Don Calabria Hospital, Negrar, Verona, Italy
First published on 25th November 2023
Abstract
The mechanism underlying visual restoration in blind animal models of retinitis pigmentosa using a liquid retina prosthesis based on semiconductive polymeric nanoparticles is still being debated. Through the application of mathematical models and specific experiments, we developed a coherent understanding of abiotic/biotic coupling, capturing the essential mechanism of photostimulation responsible for nanoparticle-induced retina activation. Our modeling is based on the solution of drift-diffusion and Poisson–Nernst–Planck models in the multi-physics neuron-cleft-nanoparticle-extracellular space domain, accounting for the electro-chemical motion of all the relevant species following photoexcitation. Modeling was coupled with electron microscopy to estimate the size of the neuron-nanoparticle cleft and electrophysiology on retina explants acutely or chronically injected with nanoparticles. Overall, we present a consistent picture of electrostatic depolarization of the bipolar cell driven by the pseudo-capacitive charging of the nanoparticle. We demonstrate that the highly resistive cleft composition, due to filling by adhesion/extracellular matrix proteins, is a crucial ingredient for establishing functional electrostatic coupling. Additionally, we show that the photo-chemical generation of reactive oxygen species (ROS) becomes relevant only at very high light intensities, far exceeding the physiological ones, in agreement with the lack of phototoxicity shown in vivo.
1. Introduction
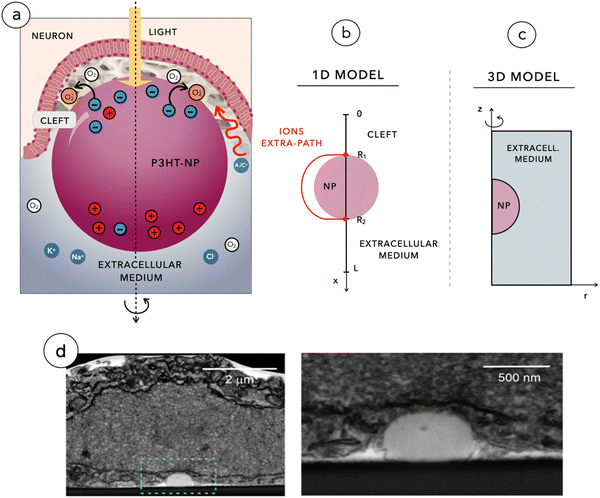
Degeneration of photoreceptors in the retina leads to visual impairment and eventually results in blindness in disorders such as retinitis pigmentosa (RP) and age-related macular degeneration. We have recently demonstrated that when injected within the subretinal space, organic photovoltaic nanoparticles (NPs) made of poly(3-hexylthiophene-2,5-diyl) (P3HT) can restore light sensitivity in blind rats.1,2 Once injected and captured in the subretinal space, NPs establish tight contacts with the plasma membrane of retinal neurons spared by degeneration. Upon illumination, NPs transduce light into a bioelectrical signal that stimulates the second order retinal neurons, namely bipolar and horizontal cells, thus reactivating the visual path. Importantly, NPs are not internalized by neurons but adhere to their membrane.2Light entering the eye is focused on the retina. In a healthy retina, photoreceptors located in the outer layer absorb light and hyperpolarize, phasically reducing their tonic synaptic glutamate release present in the dark. Bipolar cells in contact with photoreceptors respond to this modulation by starting a transduction cascade that reaches retinal ganglion cells (RGCs) in the inner retina, which funnel the signal into the optic nerve. In dystrophic retinas, photoreceptors are removed and the subretinally injected NPs decorate the surviving bipolar and horizontal cells.1 When the impinging light hits the semiconducting NPs, we assume that an exponential concentration gradient of charge carriers (electrons and holes) is established in space according to the Lambert–Beer law. This implies assuming a uniform absorption coefficient within the polymer NP, as it is standard in polymer films. While local intensity fluctuations due to inhomogeneity are probably occurring within each NP, smoothing them out seems to be a practical approximation that does not compromise the quality of the phenomenon. The large asymmetry in carrier mobility causes the electrical polarization of the NPs according to the photo-Dember effect: hole diffusion spreads positive charges homogeneously, while electrons are essentially fixed.4 At the illuminated side, where the negative charge accumulates, electrons transferring to hydrated oxygen generates a population of superoxide molecules that increases negative polarization, creating pseudo-capacitive charging.
The bio-organic interface was found to be diffused on tens of nm, due to the surface swelling of the polymer, and consists of a quasi-virtual cleft (thickness <20 nm, as determined by FIB/SEM analysis2) at the contacts between NPs and the apical dendrites and cell bodies of bipolar cells. This region is a secluded space filled by proteins and characterized by a very low concentration of ions. The well-established formation of a protein corona around NPs in the physiological environment5 has the essential feature of displacing free ionic charges at the interface that hamper electrical screening, favoring the formation of a tight electric coupling between the NP and the cell membrane that enhances the electrostatic effect induced by the accumulated charge. Each NP, acting as a nano-electrical synapse powered by light may induce a depolarization of a fraction of mV. However, the depolarization response of the bipolar cell is the result of temporal and spatial summation of individual membrane voltage changes caused by tens of NPs distributed along the neuronal membrane, as it occurs in any postsynaptic neuron in central chemical synapses.6 This effect is particularly relevant for the vast majority of bipolar cells which do not have a threshold to be reached to trigger action potential firing, being unable to generate action potential. Rather, they function in an “analogic” fashion by releasing glutamate at the synapses with RGCs based on subthreshold oscillations of their membrane potential.7 The depolarization integrated in time and space by the network of NPs yields a detectable membrane depolarization of bipolar cells and RGCs. This phenomenon has been proved to occur in the retina of blind rats and which mediates light restoration.1,2
The mechanism of photo-transduction that has been proposed in recent papers1,2,8–10 is here validated by a numerical model. We will show that the “photochemical” mechanism, associated with the generation of ROS, can be disregarded under expected retina conditions, and that the electrostatic effect caused by the accumulated charge is responsible for the perturbation of local membrane potential. Furthermore, measurements on explanted retinas treated with NPs acutely or chronically support the theoretical suggestion highlighting the role of the dielectric cleft that is formed over time within the tissue. The proposed model will provide a complete quantitative description of the full system taken into consideration, providing quantitative prediction of the most relevant effect triggered by the photo-modulation of P3HT NPs.
2. Methods
2.1. Mathematical modeling
For our analysis, we used two mathematical models: a 3D model of the photo-Dember effect in the NP and a 1D model of the biophysical events taking place at the interface between the NP and the neuronal membrane. The 3D model focuses on the study of the sole NP by considering the three-dimensional redistribution of charges across the spherical domain, leading to a non-uniform polarization of NPs. The 1D model instead aims at reproducing the full photo-transduction mechanism depicted in Fig. 1a and imaged through FIB/SEM as shown in Fig. 1d.Both simulations are based on the resolution of a system of partial differential equations (PDEs) according to the Poisson–Nernst–Planck model with the use of a fixed-point iteration algorithm, in the framework of the classic Gummel's map algorithm. Besides being computationally efficient, the fixed-point iteration has also the significant advantage of favoring the use of the most appropriate discretization schemes to approximate the dependent variables of the problem. In particular:
• Piecewise linear finite elements with mass lumping stabilization11 are used to numerically solve the PDEs. This prevents the occurrence of non-physical oscillations in the spatial distribution of the electric potential, especially in the neighborhood of material interfaces;
• Piecewise linear finite elements with Scharfetter-Gummel stabilization12 are used to numerically solve the continuity equations for carriers and ions. This preserves on the discrete level the strict positivity of the carrier number densities and ion molar density.
2.2. Experimental techniques
2.3. Statistics
The sample size needed for the planned experiments (n) was predetermined using the G*Power software for the ANOVA test with three experimental groups, considering an effect size = 0.25–0.40 with alpha (type-I error) = 0.05 and 1-β (type-II error) = 0.9, based on similar experiments and preliminary data. Peri-Stimulus Time Histograms (PSTHs) were realized with a 20 ms bin size and each bin is expressed by mean ± SEM. Data are represented as box plots, where the line depicts the median, the box extends from 25th to 75th percentile of the population, and the whiskers show the Tukey's limit for outliers definition. Normal distribution was assessed using D’Agostino–Pearson normality test, and one-way ANOVA followed by the Tukey's multiple comparison test was used. p < 0.05 was considered statistically significant.3. Results and discussion
According to the proposed model, we consider two phenomena that may occur at the neuron–NP interface: (i) the photo-electrostatic effect, due to the electric potential generated by the light-induced Dember polarization of the NP; (ii) the photo-chemical effect, which consists in the activation of cellular pathways secondary to the interaction of the membrane with O2−, produced at the interface with the NP. The NP polarization, according to the Dember effect, appears upon considering the Lambert–Beer carrier generation profile in space and the strongly asymmetric transport of electrons and holes inside the NP, as modeled and validated against electrochemical studies on P3HT thin films.4 To accurately account for this effect, we have studied it using a 2DAS model of the NP.The photo-chemical effect is accounted for in the 1D model by the introduction of boundary conditions for electron and O2− continuity equations at the interface between the NP and the external environment. The photo-cathodic reaction rate O2 + e− → O2− is described using the Marcus–Gerischer equation. In addition, to reproduce the long-lasting effect of P3HT-based retinal NP implants and their ability not to degrade over time, the 1D model accounts for a hole-surface-recombination effect, promoted by the presence of accumulated negative O2− at the interface.
3.1. The photo-Dember effect
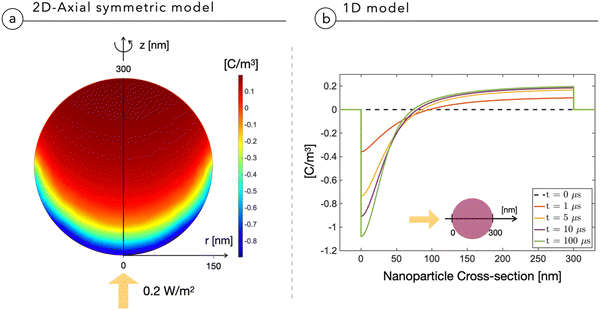
Fig. 2a shows the multidimensional drift-diffusion steady-state simulation of the charge density distribution in a NP with a radius of 150 nm irradiated from the bottom with a light power of 2 × 10−1 W m−2, estimated to be the physiological light intensity impinging onto the retina16 under normal daylight illumination conditions. Fig. 2b illustrates the net charge density profile across the NP, obtained using the 1D-model in a time-dependent simulation. Both models consistently indicate the formation of a dipole-like charge distribution, due to the difference in mobility between electrons, with a mobility of μn = 10−12 V m−2 s−1 limited by trapping caused by P3HT+:O2− complexes,17 and holes, with a mobility of μp = 10−8 V m−2 s−1.18,19 We note that the same effect well explains the electrochemical experiments on photovoltage in thin film electrodes.4 The modeling reduction from a 2DAS to a 1D description returns coherent quantitative results: for the sake of simplicity and computational costs, when dealing with time-dependency and coupling with the biological system, we will preferentially use the 1D description.The above-described NP polarization is not effective if the dielectric screening is at work. For this reason, the composition of the cleft region is crucial because it can enhance or completely hinder the screening effect. The first evidence for this phenomenon comes from a study of the normalized electric potential distribution around the NP in an empty medium with two distinct dielectric constants. 2DAS simulations of the steady state condition, reported in Fig. 3, show that a smaller dielectric constant of the surrounding medium corresponds to a larger region of the non-negligible electrical field, thus expanding the coupling range of the effect.
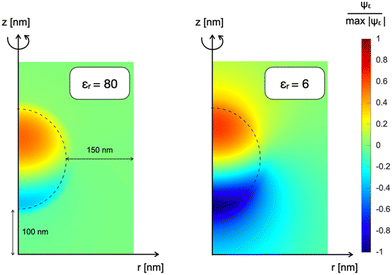 | ||
| Fig. 3 Normalized electrostatic potential Ψε distribution of a NP immersed in an empty medium characterized by different dielectric constants: on the left εr = 80; on the right εr = 6. | ||
In other words, in the electrolytic aqueous environment, the polarized NP would be able to induce sizable polarization at the neuron membrane only if positioned at few Debye lengths from the interface. The estimated Debye length is  , where ε0 and εr are the absolute and relative dielectric constants of the aqueous medium, respectively, kB is the Boltzmann constant, T is the temperature, q is the elementary charge and I is the ionic strength of the electrolyte. While the in vivo neuron/NP cleft is of several nm, it should be filled by proteins that decorate the NP (the so called “protein corona”20,21) and the neuronal membrane (adhesion proteins).22 A protein aggregate has high resistivity23 and would hamper ion penetration, contributing to create a “giga-seal” between the NP and the neuronal membrane that propagates electrostatic coupling.
, where ε0 and εr are the absolute and relative dielectric constants of the aqueous medium, respectively, kB is the Boltzmann constant, T is the temperature, q is the elementary charge and I is the ionic strength of the electrolyte. While the in vivo neuron/NP cleft is of several nm, it should be filled by proteins that decorate the NP (the so called “protein corona”20,21) and the neuronal membrane (adhesion proteins).22 A protein aggregate has high resistivity23 and would hamper ion penetration, contributing to create a “giga-seal” between the NP and the neuronal membrane that propagates electrostatic coupling.
3.2. The electrostatic coupling mechanism
Once we consider that ionic screening would hamper electrostatic coupling, the next step is to include in the 1D model in the presence of protein islands that partially fill the cleft, creating “tunnels” of the same size of the cleft region, across which polarization may be transmitted.22 To model this contribution also in the time domain, we applied the 1D time-dependent model (Section 2.1), which accounts for both the electronic transport across the NP and the ionic transport of bulk electrolytic ions in the aqueous regions.While the bulk electrolyte properties are well described by the classic Poisson–Nernst–Planck model, the properties of the cleft were obtained with a modification of the classic drift diffusion transport. To describe the effect of the protein on ion migration, we introduced an additional term regulating the ion flux that depends on the protein space filling and push ions towards empty space. This contribution does not depend on the charge sign of the ion, but it depends solely on the concentration gradient of the protein. The modified drift diffusion expression for the ion molar flux density Jα is:
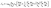 | (1) |
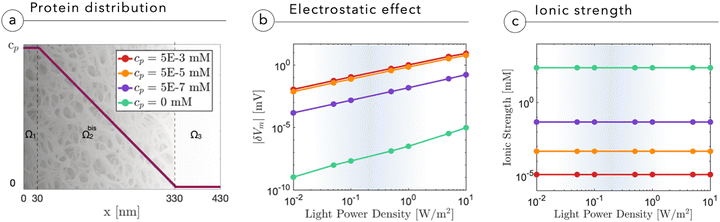
The presence of a proteinic cleft, hampering the ionic screening, allows an efficient electrostatic coupling with the neuronal membrane, which is expressed and evaluated in terms of variations in membrane potential Vm. The membrane potential Vm is defined as the electric potential difference between the intracellular and extracellular compartments, that is, Vm = ψN − ψcleft, where ψN is the electric potential inside the neuron and ψcleft is the electric potential in the cleft adjacent to the membrane, i.e. ψ(x = 0+). In Fig. 4b, we report the absolute variation of the membrane potential |δVm| = |Voffm − Vonm| induced upon switching-on the light for 100 ms, as a function of light intensity and protein concentration in the cleft. Increasing the light intensity leads to an almost linear growth of |δVm|. Electric field screening is quenched by the lack of mobile ions, until saturation sets in. The analysis shows that at cp ∼ 10−5 mM, the magnitude of |δVm| becomes relevant at physiological light intensities, around 0.1–1 W m−2. It is important to underline that the effect that we simulate is attributed to a single NP, whereas in vivo several tens of NPs constellate the neuron, thus providing multiple sources of depolarization around the membrane from the apical dendrite to the cell body. Also the effect of increasing size and micro-agglomeration, observed via high-resolution confocal microscopy in whole mount injected retinas,2 may lead to an increase in the depolarization effect as shown in the study by Chiaravalli et al.13 When light impinges on the neuron, the illuminated NP induces a negative potential in the cleft and reduces the membrane potential across the neuronal membrane, eliciting local depolarization. As light comes unidirectionally from the pupil, and the injected NPs remain concentrated in the outer retina without radially migrating to the inner layers,1,2 electrical polarization will be the same for all NPs, which will negatively charge their side facing the membrane of bipolar and horizontal cells.
From Fig. 4b we also see that without a dielectric cleft, the electrostatic coupling with the neuron remains negligible even at the highest light intensities (green curve). Fig. 4c shows the expected reduction in ion concentration upon cleft filling by proteins.
3.3. The photo-chemical coupling mechanism
To identify potential alternative mechanisms, we also consider the chemical effect induced by the diffusion of O2− across the cleft and the subsequent chemical reactions of secondary species. Indeed, even in the secluded cleft space, chemical reactions could convert superoxide into hydrogen peroxide, a common reactive oxygen species (ROS), and in turn affect membrane components, including ion channels such as Transient receptor potential vanilloid 1 (TRPV1) channels.24 Note that in our model, superoxide population is primarily a sort of “storage” of the charge. The negative oxygen ion is protected by a polaronic effect due to water molecule dressing that reduces back recombination. In the pseudo capacitive effect, superoxide molecules remain confined in the diffused interface and are doomed to recombine. Here we consider a different scenario in which the superoxide leaves the interface and diffuses in the cleft. If this happens, the conversion to ROS becomes a possible outcome of photostimulation.
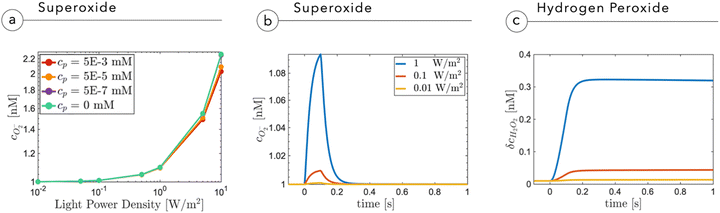
Fig. 5a shows the O2− concentration,  , as a function of light intensity and protein concentration in the cleft. We find that different from the electrostatic coupling described above, the superoxide concentration is only slightly affected by cleft composition, whereas it is markedly dependent on the light intensity, as more electrons at the interface enhance the photo-cathodic production of O2−. At the physiological values of ≃0.1–0.2 W m−2 light intensity and a time duration of 100 ms, the
, as a function of light intensity and protein concentration in the cleft. We find that different from the electrostatic coupling described above, the superoxide concentration is only slightly affected by cleft composition, whereas it is markedly dependent on the light intensity, as more electrons at the interface enhance the photo-cathodic production of O2−. At the physiological values of ≃0.1–0.2 W m−2 light intensity and a time duration of 100 ms, the  concentration increases by just few fractions of nM. The model also accounts for the ability of O2− to turn into hydrogen peroxide, whose concentration change secondary to a light pulse is reported in Fig. 5c. The concentration of hydrogen peroxide in the extracellular environment that can lead to oxidative eustress, (i.e., a mild oxidative condition that is not harmful to cells), is estimated to be about 100 nM. This value, however, can be reached only at high light intensities, over 10 W m−2.24 We also look at the possible accumulation of hydrogen peroxide as a function of time, plugging in a reasonable value for its lifetime in the kinetics, as described in the ESI.† The simulated effect of a prolonged stimulation at physiological light intensities supports the negligibility of the photo-chemical effect under these working conditions (see below Fig. 7). In conclusion, our simulations suggest that the use of P3HT-NPs in vivo hardly induces any oxidative eustress at physiological light intensities for the retina, because both superoxide and hydrogen peroxide do not reach significant concentrations in the cleft region (above 100 nM24). Moreover, the effects on RGC firing of NPs injected subretinally in blind retinal explants were not affected by the blockade of TRPV1 channels by ruthenium red (ref. 2). Furthermore, the calculations argue against the risk of phototoxicity because toxic ROS concentrations (≃1000 μM) would only be reached at light intensities well above the damage threshold of the retina.
concentration increases by just few fractions of nM. The model also accounts for the ability of O2− to turn into hydrogen peroxide, whose concentration change secondary to a light pulse is reported in Fig. 5c. The concentration of hydrogen peroxide in the extracellular environment that can lead to oxidative eustress, (i.e., a mild oxidative condition that is not harmful to cells), is estimated to be about 100 nM. This value, however, can be reached only at high light intensities, over 10 W m−2.24 We also look at the possible accumulation of hydrogen peroxide as a function of time, plugging in a reasonable value for its lifetime in the kinetics, as described in the ESI.† The simulated effect of a prolonged stimulation at physiological light intensities supports the negligibility of the photo-chemical effect under these working conditions (see below Fig. 7). In conclusion, our simulations suggest that the use of P3HT-NPs in vivo hardly induces any oxidative eustress at physiological light intensities for the retina, because both superoxide and hydrogen peroxide do not reach significant concentrations in the cleft region (above 100 nM24). Moreover, the effects on RGC firing of NPs injected subretinally in blind retinal explants were not affected by the blockade of TRPV1 channels by ruthenium red (ref. 2). Furthermore, the calculations argue against the risk of phototoxicity because toxic ROS concentrations (≃1000 μM) would only be reached at light intensities well above the damage threshold of the retina.
3.4. Pulsed light stimuli
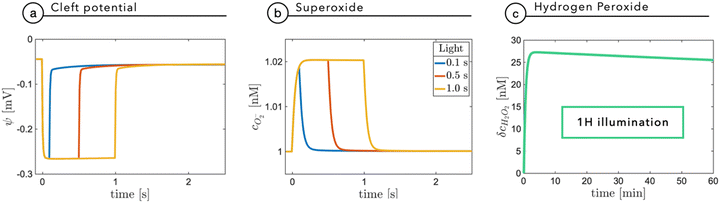
Fixation eye movements, including tremor and micro-saccades, counteract image fading and keep modulating the light intensity impinging on retinal photoreceptors, even when the observer stares steadily. This effectively provides a pulsed-like illumination of retinal photoreceptors or, alternatively, of the implanted NPs.25–27 In humans, the characteristic modulation time is in the order of 250 ms, while eye movement can be significantly faster, in the order of 10 ms. It is thus relevant to explore with specific time-dependent simulations the role of light pulse duration. As done before, for the sake of completeness, we will consider the build-up of superoxide as a fundamental agent in electrostatic coupling and the build-up of ROS, as a possible chemical agent.Fig. 6a reports the cleft potential variation following light stimuli of increasing duration: after few tens of milliseconds, at 0.2 W m−2, the potential reaches a plateau value and quickly recovers the initial value after switching-off the light. A similar trend is also observed by the superoxide concentration which, secondary to a prolonged stimulus, reaches an equilibrium value expressing the balance between its production rate at the NP interface and its evolution towards hydrogen peroxide (Fig. 6b). The observed plateau could in principle suggest that under prolonged exposure, hydrogen peroxide could build up to reach harmful concentrations. Fig. 6c shows that even for an non-physiological, prolonged and continuous light stimulation, hydrogen peroxide concentration does not exceed 30 nM, remaining far below the threshold for extracellular perturbations (that is at least one order of magnitude higher).24 These simulations again support the negligible and non-toxic role of the photo-cathodic behavior of P3HT-NPs within an oxygenated environment.
Fig. 7a shows the membrane potential as a function of time, during a train of light stimuli (100 ms each) with a 50% duty cycle with different values of the tunneling coefficient kt, a parameter that rules the efficiency of the photo-cathodic production of superoxide that is employed in the description of the Marcus–Gerischer reaction at the P3HT/electrolyte interface. We find that kt weakly affects the depolarization (Fig. 7a). The lower value, kt ≈ 10−30 m4 s−1 is in agreement with the data reported in the literature,28 and it is associated with the lowest production of superoxide. We observe that sequential stimuli lead to the build-up of a small background signal, possibly caused by incomplete recombination. It is reasonable to think that the slow time-constant of plateau formation, combined with its small intensity, can be easily compensated by neuron transmembrane ionic exchanges. By increasing kt, we see that the plateau is reduced. This can be ascribed to the reduced electrostatic effect localized in the NP and mainly caused by the pseudo-capacitive delocalization of the negative superoxide charge at the diffuse NP/cleft interface. The increased superoxide production is still below the concentration threshold for triggering physiological responses, as shown in Fig. 7b.
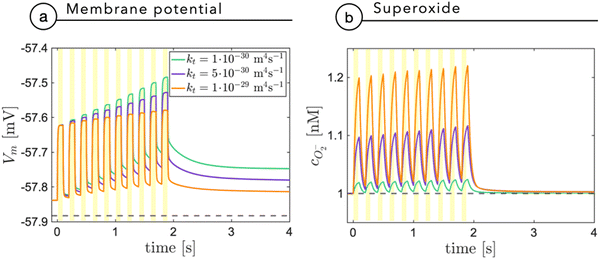 | ||
| Fig. 7 The membrane potential (a) and the superoxide concentration (b) are shown as a function of time secondary to a train of light stimuli with an on/off duty cycle of 100 ms. The results are reported for three different values of the tunneling coefficient kt, normally assumed equal to 10−30 m4 s−1, in agreement with the study by Rudolph et al.28 | ||
3.5. The role of the interface: experiment
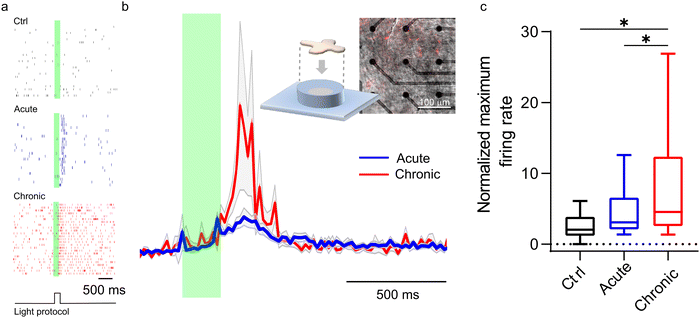
A confirmation of our model comes from ex vivo experiments on blind retinal explants from RCS rats, a well-known rodent model of retinitis pigmentosa. P3HT-NPs were either injected in the subretinal space of acutely dissected naïve RCS retinas or injected in vivo in RCS rats to explant the retinas one month later, allowing the complete formation of the NP–bipolar cell interface. Although the light intensity required to stimulate an ex vivo response in dissected retinas is typically higher than that needed in vivo, a comparison of the two conditions at constant light intensity can provide an indication of the nature of the coupling phenomenon towards a full merging of the abiotic component with the biotic component. As reported in Fig. 8, the recordings of RGC firing on acutely injected explants displayed significantly smaller responses with respect to the retinas which experienced a prolonged (1 month) in vivo contact with the NPs before being explanted. In addition, the data spreading is much larger when testing post in vivo explants, towards high-rate numbers. This is true when looking at both the normalized firing rate (Fig. 8a and b) and the maximum firing rate (Fig. 8c). The difference in the response of chronically and acutely injected retinas can be ascribed to the distinct interface conditions that are established at NP/bipolar cell contacts: when the injection is performed in vivo one month before the explant, in addition to the formation of a protein corona on the surface of the NPs, the neuronal membrane response to the NP contact/docking can lead to the formation of a tight NP–cell interface that in turn enhances the resistive nature of the cleft. While the full in vivo biological response cannot be reproduced on explants studied in vitro, these results support the model described above and the proposed role of proteins in the cleft. Consequently, in vivo the transduction efficiency is enhanced by biological mechanisms that do not take place under in vitro or ex vivo experimental conditions.4. Conclusions
Notwithstanding the remarkable success of the liquid retina prosthesis based on P3HT-NPs in rescuing vision in blind RP animal models, its working mechanism was incompletely understood.1,2 By applying several mathematical models, we propose here a coherent picture of abiotic/biotic coupling, capturing the essential ingredients that describe the photo-stimulation mechanism responsible for the electrical activation of the inner retina by the injected NPs.We explored both an electrostatic model and a photo-chemical model, finding that the two mechanisms reach the maximum efficiency under very different environmental conditions: (i) the photo-electrostatic effect is already relevant at physiological light intensities; (ii) the photo-chemical effect becomes relevant only at very high light intensities, far exceeding the physiological ones. This suggests that electrostatic coupling is the mechanism occurring during in vivo experiments and rules out possible phototoxic effects.
The pseudo-capacitive charging of the NP responsible for electrostatic coupling is appreciable only in the presence of a highly resistive cleft, where ionic screening is negligibly small (Debye length ≫ cleft thickness): if this condition is verified, even physiological light intensities (0.2 W m−2) will be able to induce an appreciable depolarization of second-order retinal neurons. The high electric resistance of the medium filling the cleft is ascribed to its minimal thickness and to the presence of adhesion proteins of the neuronal membrane and corona proteins coating the NP. Therefore, the presence of the protein corona, in addition to neuronal adhesion proteins, is suggested by the model as a fundamental ingredient to ensure coupling among neurons and NPs at low light intensities. This introduces the concept of “diffuse soft interface”, in contrast with the sharp boundary brought about by a metal electrode, validating the use of an organic semiconductor.
Experiments fully support this picture. Electron microscopy shows a cleft between a neuron membrane and a polymer nanoparticle that is less than 20 nm. Electrophysiology experiments show that the “incubation” time in vivo leads to sizable differences in the responses of blind retinas to light that can be reconciled by the in vivo formation of an efficient hybrid interface. These results also prove that in vitro experiments do not fully recapitulate the in vivo conditions, and that the prolonged contact between NPs and neurons, occurring in vivo, is necessary to build up a functional hybrid interface and fully elicit the physiological effects.
Author contributions
Chiaravalli performed the mathematical simulations and took lead in writing the manuscript. Sacco supervised the mathematical modeling contribution. Ravasenga and Jasnoor conducted ex vivo retina electrophysiology. Colombo performed data analysis, electron microscopy, supervision of the project and revision of the manuscript. Francia, Di Marco and Pertile performed surgery and in vivo nanoparticle microinjection. Lanzani and Benfenati conceived and supervised the project and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Drs M. M. La Vail (Beckman Vision Center, University of California San Francisco, CA) for kindly providing non-dystrophic RCS-rdy+ and dystrophic RCS rats; Angela Russo for her assistance in the subretinal microinjections; M. Cilli and L. Emionite (IRCCS Ospedale Policlinico San Martino, Genova, Italy) for their assistance in surgical procedures. The research was supported by Fondazione Cariplo (project 2018-0505 to GL, FB and GP), H2020-MSCA-ITN 2019 “Entrain Vision” (project 861423 to FB and GL), EuroNanoMed3 (project Nanolight 2019-132 to FB), the Italian Ministry of University and Research (PRIN2020WMSNBL to FB and PRIN2020XBFEMS to GL), the Italian Ministry of Health (RF-2021-12374404 to FB, GP and GL) and IRCCS Ospedale Policlinico San Martino (Ricerca Corrente and 5 × 1000 grants to FB and EC).References
- S. Francia, D. Shmal, S. Di Marco, G. Chiaravalli, J. F. Maya-Vetencourt, G. Mantero, C. Michetti, S. Cupini, G. Manfredi, M. L. DiFrancesco, A. Rocchi, S. Perotto, M. Attanasio, R. Sacco, S. Bisti, M. Mete, G. Pertile, G. Lanzani, E. Colombo and F. Benfenati, Nat. Commun., 2022, 13, 3677 CrossRef CAS PubMed.
- J. F. Maya-Vetencourt, G. Manfredi, M. Mete, E. Colombo, M. Bramini, S. Di Marco, D. Shmal, G. Mantero, M. Dipalo, A. Rocchi, M. L. DiFrancesco, E. D. Papaleo, A. Russo, J. Barsotti, C. Eleftheriou, F. Di Maria, V. Cossu, F. Piazza, L. Emionite, F. Ticconi, C. Marini, G. Sambuceti, G. Pertile, G. Lanzani and F. Benfenati, Nat. Nanotechnol., 2020, 15, 698–708 CrossRef CAS PubMed.
- D. Mishra, S. Gade, K. Glover, R. Sheshala and T. R. R. Singh, Curr. Eye Res., 2023, 48, 208–218 CrossRef CAS PubMed.
- G. Chiaravalli, G. Manfredi, R. Sacco and G. Lanzani, ACS Appl. Mater. Interfaces, 2021, 13, 36595–36604 CrossRef CAS PubMed.
- Y. He, R. Chen, W. Fa, B. Zhang and D. Wang, J. Chem. Phys., 2019, 151, 130902 CrossRef PubMed.
- J. H. Byrne, Postsynaptic Potentials and Synaptic Integration, Elsevier, Amsterdam, 2014 Search PubMed.
- R. Shiells, Photoreceptor-bipolar cell transmission, Springer, Dordrecht, 1995 Search PubMed.
- G. Bondelli, S. Sardar, G. Chiaravalli, V. Vurro, G. M. Paternò, G. Lanzani and C. D’Andrea, J. Phys. Chem. B, 2021, 125, 10748–10758 CrossRef CAS PubMed.
- J. F. Maya-Vetencourt, D. Ghezzi, M. R. Antognazza, E. Colombo, M. Mete, P. Feyen, A. Desii, A. Buschiazzo, M. Di Paolo, S. Di Marco, F. Ticconi, L. Emionite, D. Shmal, C. Marini, I. Donelli, G. Freddi, R. Maccarone, S. Bisti, G. Sambuceti, G. Pertile, G. Lanzani and F. Benfenati, Nat. Mater., 2017, 16, 681–689 CrossRef CAS PubMed.
- N. Martino, P. Feyen, M. Porro, C. Bossio, E. Zucchetti, D. Ghezzi, F. Benfenati, G. Lanzani and M. R. Antognazza, Sci. Rep., 2015, 5, 8911 CrossRef CAS PubMed.
- R. Sacco, F. Manganini and J. W. Jerome, Mol. Based Math. Biol., 2015, 3, 78 CAS.
- D. L. Scharfetter and H. K. Gummel, IEEE Trans. Electron Devices, 1969, 16, 64–77 Search PubMed.
- G. Chiaravalli, G. Lanzani and R. Sacco, Photonics, 2022, 9, 710 CrossRef CAS.
- A. A. Moya, Phys. Chem. Chem. Phys., 2015, 17, 5207–5218 RSC.
- M. A.-K. Urtenov, E. V. Kirillova, N. M. Seidova and V. V. Nikonenko, J. Phys. Chem. B, 2007, 111, 14208–14222 CrossRef CAS PubMed.
- E. Arnault, C. Barrau, C. Nanteau, P. Gondouin, K. Bigot, F. Viénot, E. Gutman, V. Fontaine, T. Villette, D. Cohen-Tannoudji, J. A. Sahel and S. Picaud, PLoS One, 2013, 8, e71398 CrossRef CAS PubMed.
- S. Bellani, D. Fazzi, P. Bruno, E. Giussani, E. V. Canesi, G. Lanzani and M. R. Antognazza, J. Phys. Chem. C, 2014, 118, 6291–6299 CrossRef CAS.
- A. J. Mozer, N. S. Sariciftci, A. Pivrikas, R. Österbacka, G. Juška, L. Brassat and H. Bässler, Phys. Rev. B, 2005, 71, 035214 CrossRef.
- T. Agostinelli, M. Caironi, D. Natali, M. Sampietro, P. Biagioni, M. Finazzi and L. Duò, J. Appl. Phys., 2007, 101, 114504 CrossRef.
- T. Kopac, Int. J. Biol. Macromol., 2021, 169, 290–301 CrossRef CAS PubMed.
- P. Breznica, R. Koliqi and A. Daka, Med. Pharm. Rep., 2020, 93, 342–350 Search PubMed.
- R. Changede and M. Sheetz, BioEssays, 2016, 39, 1–12 CrossRef PubMed.
- M. Natali, A. Campana, T. Posati, E. Benvenuti, F. Prescimone, D. O. Sanchez Ramirez, A. Varesano, C. Vineis, R. Zamboni, M. Muccini, A. Aluigi and S. Toffanin, Biosens. Bioelectron., 2019, 141, 111480 CrossRef CAS PubMed.
- H. Sies, Redox Biol., 2017, 11, 613–619 CrossRef CAS PubMed.
- R. G. Alexander, S. L. Macknik and S. Martinez-Conde, Front. Neurol., 2018, 9, 144 CrossRef PubMed.
- F. F. Ghasia and A. G. Shaikh, Exp. Brain Res., 2015, 233, 1089 CrossRef PubMed.
- R. Engbert and K. Mergenthaler, PNAS, 2006, 103, 7192–7197 CrossRef CAS PubMed.
- M. Rudolph and E. L. Ratcliff, Nat. Commun., 2017, 8, 1048 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04386j |
| This journal is © the Owner Societies 2024 |