Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Re-entrant relaxor ferroelectric behaviour in Nb-doped BiFeO3–BaTiO3 ceramics†
Ziqi
Yang
 a,
Bing
Wang
a,
Bing
Wang
 a,
Thomas
Brown
b,
Steven J.
Milne
a,
Thomas
Brown
b,
Steven J.
Milne
 b,
Antonio
Feteira
b,
Antonio
Feteira
 c,
Andreas
Wohninsland
c,
Andreas
Wohninsland
 d,
K. V.
Lalitha
d,
K. V.
Lalitha
 d,
Yizhe
Li
d,
Yizhe
Li
 a and
David A.
Hall
a and
David A.
Hall
 *a
*a
aDepartment of Materials, University of Manchester, M13 9PL, Manchester, UK. E-mail: david.a.hall@manchester.ac.uk
bSchool of Chemical and Process Engineering, University of Leeds, LS2 9JT, Leeds, UK
cMaterials and Engineering Research Institute, Sheffield Hallam University, Sheffield, S1 1WB, UK
dInstitute of Materials Science, Technische Universität Darmstadt, Darmstadt 64287, Germany
First published on 24th January 2023
Abstract
BiFeO3–BaTiO3 (BF–BT) solid solutions exhibit great promise as the basis for high temperature piezoelectric transducers and energy storage dielectrics, but the fundamental mechanisms governing their functional properties require further clarification. In the present study, both pure and niobium-doped 0.7BF–0.3BT ceramics are synthesized by solid state reaction and their structure–property relationships are systematically investigated. It is shown that substituting a low concentration of Ti with Nb at a level of 0.5 at% increases the resistivity of BF–BT ceramics and facilitates ferroelectric switching at high electric field levels. Stable planar piezoelectric coupling factor values are achieved with a variation from 0.35 to 0.45 over the temperature range from 100 to 430 °C. In addition to the ferroelectric-paraelectric phase transformation at the Curie point (∼430 °C), a frequency-dependent relaxation of the dielectric permittivity and associated loss peak are observed over the temperature range from −50 to +150 °C. These effects are correlated with anomalous enhancement of the remanent polarization and structural (rhombohedral) distortion with increasing temperature, indicating the occurrence of a re-entrant relaxor ferroelectric transformation on cooling. The results of the study provide new insight into the thermal evolution of structure and the corresponding functional properties in BF–BT and related solid solutions.
1. Introduction
Bismuth ferrite-based ceramics are considered as potential candidates for high temperature lead-free piezoelectric ceramics due to their high depoling temperatures and piezoelectric properties. Among various investigated BF-based solid solutions, a morphotropic phase boundary (MPB) was identified in the (1 − x)BiFeO3–xBaTiO3 (BF–BT) system around x = 0.3, where the rhombohedral and pseudo-cubic phases coexist and enhanced piezoelectric properties were achieved.1–3 As one of the most intensively studied compositions close to the MPB, 0.7BiFeO3–0.3BaTiO3 (0.7BF–0.3BT) solid solutions exhibit a high Curie temperature (TC > 400 °C), large remanent and saturation polarization (Pr, Ps) values together with high piezoelectric charge and coupling coefficients (d33, kp), which make them potential candidates for high temperature piezoelectric applications.4,5The high electrical conductivity of undoped BF–BT ceramics with high BF contents discourages the direct usage of such materials for piezoelectric applications and hinders the poling process that is necessary to impart piezoelectric properties. The origin of the high conductivity in BF–BT is commonly attributed to the presence of oxygen vacancies introduced due to volatilisation of bismuth oxide during sintering and the subsequent reoxidation on cooling, with associated formation of free electron holes.6,7 To address this issue, use of sintering additives and donor dopants or annealing in a reducing atmosphere have been reported to suppress the p-type electronic conductivity of BF–BT ceramics.8,9 Enhanced piezoelectric properties can also be achieved through quenching processes, during which the sintered ceramic pellets are cooled rapidly from elevated temperatures (700–1000 °C) to room temperature in air or water.10,11 On the other hand, the induced thermal shock can cause destructive fracture of sintered ceramics, which raises concerns over the feasibility of quenching as a heat treatment procedure in a commercial production process.
Control of the conductivity and functional properties of piezoceramics is commonly achieved by doping with both iso- and alio-valent cations, a method that has been successfully employed for many years in commercial lead zirconate titanate (PZT).12,13 Similar approaches have also been used in the BF–BT system by introducing various dopants, such as Sr2+, La3+, Mn4+, Ti4+, Nb5+.8,14–17 However, few reports have investigated the simultaneous control of resistivity and piezoelectric properties of BF–BT in response to donor substitution. As noted above, the resistivity can be improved by substituting donor-type Nb5+ cations for Fe3+ or Ti4+, but high Nb concentrations tend to suppress long-range ferroelectric ordering and induce ergodic relaxor ferroelectric behaviour.17,18 The corresponding ‘softening’ effect of Nb5+ doping, with the expected enhancement of ferroelectric and piezoelectric properties, was not generally observed and may have been overlooked in studies that employed relatively high Nb concentrations >1 at%.
Temperature- and frequency-dependent dielectric relaxation effects in BF–BT ceramics can be interpreted using the theories and models developed in previous studies on relaxor ferroelectrics. Such materials have been studied intensively since the properties of Pb(Mg1/3Nb2/3)O3 (PMN) were reported by Smolenskii et al. in 1959.19 In comparison with the long-range ordered domain configurations in traditional ferroelectric materials, relaxor ferroelectrics contain complex and dynamic polar nano-regions (PNRs), which are formed due to nanoscale chemical and structural heterogeneity. Many studies have been carried out and models proposed to describe the polarization switching mechanisms in different types of relaxor ferroelectrics.20–23 The mechanisms responsible for relaxor ferroelectricity have not been conclusively explained so far, but there is no doubt about the existence of PNRs and their importance in determining the dielectric and piezoelectric properties of such materials. In cryogenic dielectric experiments on PMN-0.30PT, the enhancement of piezoelectric properties was attributed to the unique structural characteristics in relaxors, such as nanoscale heterogeneous polar regions (NHPRs).24
To exploit the polarization mechanisms in relaxor ferroelectrics over various ranges of temperature and electric field, understanding of the relationships between crystal structure, ferroelectric and ferroelastic behaviour is critically important. This can be achieved through the investigation of temperature- and electric field-dependent X-ray (XRD) or neutron diffraction methods. The evolution of crystal structure, lattice parameters and texture due to variations in temperature and electric field can then be evaluated by appropriate analysis of the resulting diffraction data.25 In this respect, the ease of domain switching in polycrystalline ceramics is constrained by the elastic anisotropy and inter-granular residual stress induced by an electric field.26 Extrinsic contributions to the dielectric and piezoelectric properties also occur due to the motion of ferroelectric domain walls, which involves both local domain switching and domain wall vibration.27
The present investigation is concerned with Nb-doped 0.7BF–0.3BT ceramics (0.7BiFeO3–0.3BaTi0.995Nb0.005O3), near to the MPB between rhombohedral and pseudo-cubic phases and exhibiting a rhombohedral structure. Introducing a relatively low concentration of donor Nb5+ substitution for Ti4+ was found to be an effective way to increase electrical resistivity, but also led to the formation of a dielectric ‘plateau’ region above 100 °C, which is accompanied by enhanced ferroelectric and piezoelectric properties. These effects are correlated with an anomalous increase in rhombohedral lattice distortion at intermediate temperatures, leading to a form of re-entrant relaxor ferroelectric behaviour on cooling. The results of this investigation provide new insight into the effects of donor-doping in BF–BT ceramics and a route to design environmentally friendly high-temperature piezoelectric ceramics.
2. Experimental section
2.1. Sample preparation
0.7BiFeO3–0.3Ba(Ti0.995Nb0.005)O3 ceramics were synthesized by the conventional solid state reaction method. Stoichiometric amounts of Bi2O3 (99%), Fe2O3 (99%), BaCO3 (99%), TiO2 (99%) and Nb2O5 (99.99%) powders (Sigma-Aldrich) were weighed out according to the required stoichiometry followed by mixing and vibration ball milling using propan-2-ol and yttria-stabilized zirconia media for 24 h. No excess bismuth oxide content was used in the present study. Afterwards, the dried powders were calcined at 800 °C for 4 h in air and milled again for 24 h. Polyethylene glycol (PEG) solution was added into the calcined powders as a binder at a concentration of 2 wt% to improve compaction behaviour. The calcined powders were dried and uniaxially pressed into 10 mm diameter pellets at a pressure of 100 MPa. The ceramic pellets were sintered at 1010 °C for 3 h in air to obtain dense samples. For comparison purposes, a ‘pure’ undoped 0.7BiFeO3–0.3BaTiO3 ceramic was also prepared using the same processing procedures; in this case, test samples were annealed in Ar at 700 °C to suppress p-type electronic conductivity.The absolute bulk density, ρb, was measured by the Archimedes method, using deionised water as the immersion medium. By comparing with the theoretical density, ρth, calculated according to the full-pattern fits of XRD data, the relative density, ρr, was determined as the ratio ρb/ρth. Conductive electrodes were applied using a silver paste (GWENT C2130823D1), fired-on at 550 °C. Test samples for in situ high energy XRD poling experiments were prepared by cutting the pre-electroded ceramic disks into square-ended beam specimens, with approximate dimensions 10 mm × 1 mm × 1 mm. Afterwards, the specimens were annealed at 550 °C for 1 h in a closed alumina crucible to eliminate the residual stresses induced by diamond machining.
2.2. Structural and microstructural characterisation
Polished cross-sections of the as-sintered ceramic pellets were obtained by grinding with SiC paper, followed by polishing procedures with 3, 1, 0.25 μm diamond paste and 0.04 μm OPS silica colloidal suspension. A Tescan Mira3 SC scanning electron microscope (SEM) equipped with an energy-dispersive X-ray spectroscopy (EDS) system was used for microstructural and micro-chemical examination of the polished surfaces. Temperature-dependent XRD data of as-sintered samples were obtained with a Bruker D8 Discover in the 2θ range from 10 to 90° with a step size of 0.02°. The measurement temperature was increased from 25 to 500 °C, followed by cooling down to room temperature at a rate of 1 °C s−1 controlled by an Anton Paar HTK1200 High Temperature Stage.In situ high energy XRD experiments were carried out in transmission on beamline I15 at the Diamond Light Source, using a photon energy of 70 keV (λ = 0.177220 Å) and a Pilatus 2M detector, positioned approximately 1 m from the sample. The test specimens were placed under silicone oil in a polyimide sample holder with electrical contacts to a high voltage amplifier (Matsusada EC-10), allowing 2D diffraction patterns to be collected under an applied electric field up to 6 kV mm−1. The calibration and caking procedures for the 2-D images were performed with DAWN software, developed by Diamond Light Source.28 By this means, diffraction patterns were obtained over a range of orientations of the azimuthal angle, ψ, from ψ = 0° (parallel to the electric field direction) to ψ = 90° (perpendicular to the electric field direction).
2.3. Electrical property measurements
Ferroelectric hysteresis measurements were carried out using a function generator (HP 33120A) connected to a HV amplifier (Chevin Research, Otley, UK) to generate the desired high voltage. The samples were subjected to 4 cycles of a sinusoidal electric field with a frequency of 2 Hz. Polarization–electric field (P–E) hysteresis loops were constructed from the recorded electric potential and induced current waveforms, using the methods described by Stewart et al.29 Strain–electric field (S–E) loops were measured using an aixACCT TF 2000E tester with a frequency of 1 Hz at temperatures in the range from 25 °C to 125 °C.Dielectric measurements were carried out at fixed frequencies of 1, 10 and 100 kHz over the temperature range from −60 to 70 °C using a HP 4284 A impedance analyser in combination with an environmental chamber (TJR; Tenney Environmental-SPX, White Deer, PA) and from 70 to 650 °C with a Carbolite CWF1200 furnace. The complex electrical impedance was measured with a Solartron 1260 system (Solartron Analytical, UK) over the frequency range from 1 Hz to 1 MHz and at temperatures from 25 °C to 500 °C, in a Carbolite MTI12/388 tube furnace. The DC resistivity was obtained at a frequency of 1 Hz, where a plateau region was observed due to the dominance of the real part of impedance at low frequencies.
Thermal depolarization behaviour was determined by measurement of the pyroelectric current over the temperature range from 30 °C to 300 °C, using a HP34401A multi-meter in combination with a current amplifier.30,31 Samples were poled prior to the measurements by applying an AC field with amplitude of 6 kV mm−1. Two different poling temperatures, 25 °C and 100 °C, were employed to assess the influence of the changes in rhombohedral distortion and remanent polarization on thermal depolarization behaviour, in relation to the observed re-entrant relaxor ferroelectric behaviour.
3. Results and analysis
3.1. Structure and microstructure
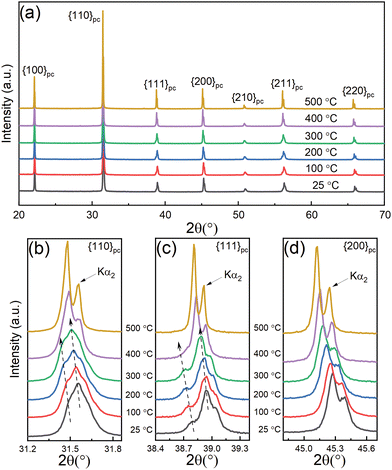
Temperature-dependent XRD results for the 0.5 at% Nb-doped 0.7BF–0.3BT sample are shown in Fig. 1. The XRD profiles are consistent with a single-phase rhombohedrally-distorted perovskite structure; splitting of the {110}pc and {111}pc peak profiles was observed, together with a single {200}pc peak (with Kα2 shoulder) as shown in Fig. 1(b)–(d). It is noteworthy that the single peak profile of (200) did not change significantly over the temperature range from 25 to 500 °C, whereas peak splitting of {110}pc and {111}pc reflections became more pronounced with increasing temperature and transformed into a single peak associated with the cubic phase at 500 °C. The general shift of the diffraction peak profiles to lower angles with increasing temperature is attributed to thermal expansion. These qualitative observations indicate that there is no obvious change of crystal structure below 500 °C, but an anomalous increase of the rhombohedral distortion occurs over the temperature range from 25 to 200 °C; similar behaviour was reported in a recent study of the ternary solid solution 0.3BaTiO3–0.1Bi(Mg1/2Ti1/2)O3–0.6BiFeO3.32 These observed structural variations are consistent with the temperature-dependence of dielectric, ferroelectric, piezoelectric, and pyroelectric properties reported in the following sections.The rhombohedral lattice distortion, 90-αpc,33 and pseudo-cubic unit cell volume, Vpc, for the 0.5 at% Nb-doped 0.7BF–0.3BT ceramics during heating and cooling at temperatures between 25 and 450 °C, were determined by Rietveld refinement using Topas,34 as shown in Fig. 2. Examples of the refined data corresponding to the rhombohedral R3c phase are presented in Fig. S1 (ESI†). On heating, an anomalous increase in the rhombohedral distortion was observed, from 0.167 to 0.196°, as temperature increased from 25 to 175 °C. The distortion angle exhibited a peak at 175 °C, contrary to general observations in classical ferroelectrics in which the structural distortion and spontaneous polarization both decrease monotonically with increasing temperature. The latter induces a stable and consistent negative pyroelectric coefficient.35 Similar anomalous variations in crystallographic parameters have also been reported in other BF-based ceramics,32,36 which suggests that such temperature-dependent structural changes could occur in other types of ferroelectric solid solutions. In the case of the BiFeO3–PbTiO3 system, it was suggested that this type of behaviour could be associated with the Néel temperature at the antiferromagnetic-paramagnetic transformation.36 It is shown below that these thermally-induced changes in crystallographic parameters for BF–BT can be correlated with corresponding variations in the spontaneous and remanent polarization, accompanied by a positive pyroelectric coefficient, which are characteristic of re-entrant relaxor ferroelectric behaviour.37
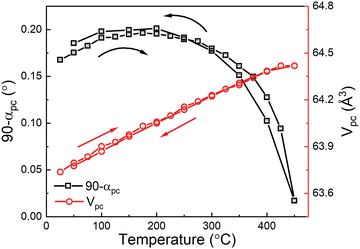 | ||
| Fig. 2 Temperature dependence of rhombohedral lattice distortion and pseudo-cubic cell volume of 0.7BiFeO3–0.3Ba(Ti0.995Nb0.005)O3 ceramics. | ||
The relative densities of the Nb-doped 0.7BF–0.3BT and undoped 0.7BF–0.3BT samples were determined as 96% and 95%, respectively. Residual porosity was mainly present in the grain boundary locations, as illustrated in Fig. 3. The presence of a chemically heterogeneous core–shell microstructure in some grains of the 0.7BiFeO3–0.3Ba(Ti0.995Nb0.005)O3 ceramics was revealed by a combination of back-scattered electron (BSE) imaging and EDS mapping, as shown in Fig. 3. It was observed that Ba and Ti were depleted in the core regions, while the signals corresponding to Bi and Fe were slightly enhanced, similar to previous observations in donor-doped BF–BT based ceramics.18,38 It was also shown previously that the BF-rich core regions exhibited high rhombohedral distortion and contained well-developed ferroelectric domain configurations in comparison with the BT-rich, relaxor-like pseudo-cubic shell regions.39
 | ||
| Fig. 3 SEM image (BSE mode) and EDS mapping of 0.7BiFeO3–0.3Ba(Ti0.995Nb0.005)O3 ceramic. The core regions in the red rectangular area are relatively deficient in Ba and Ti but enriched in Bi and Fe. | ||
Comparing undoped and Nb-doped 0.7BF–0.3BT ceramics, it was observed previously that single phase materials could be obtained for Nb substitution levels less than 1 at%, whereas secondary phases corresponding to Bi5Ti3FeO15 and BaNb2O6 were identified for dopant concentrations of greater than or equal to 1 at% Nb.18 In comparison with single component BiFeO3, where small changes in stoichiometry or impurity levels commonly lead to second phase formation,40 it is evident that the presence of BaTiO3 may help to stabilise the perovskite structure against decomposition in the presence of aliovalent dopants and/or impurities. The grain size was also progressively reduced with the increase in Nb concentration.18
On the other hand, Nb appeared to be distributed evenly across the examined area, although the validity of the results may be questionable in view of the limited sensitivity of the EDS detector for low dopant concentrations. There was little evidence of well-ordered ferroelectric domain configurations, such as those found in rhombohedral and tetragonal PZT ceramics,13 in the polished cross-sections, although irregular features with relatively light contrast were present in the images in back-scattered electron (BSE) mode.
3.2. Dielectric and ferroelectric properties
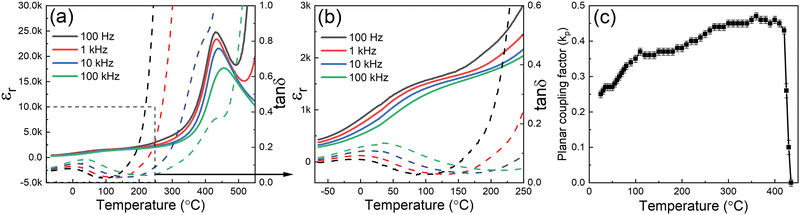
The temperature dependence of dielectric permittivity (εr) and loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the Nb-doped BF–BT and Ar annealed pure BF–BT ceramics are shown in Fig. 4(a) and Fig. S2 (ESI†), respectively. The presence of dielectric relaxation and a slight frequency dependence in the position of the dielectric peaks were apparent at temperatures around 420 °C, indicating the weak relaxor ferroelectric nature of the material and a tendency for increasing disorder in the polar state near to the ferroelectric-paraelectric transition. The rapid increase in dielectric loss at high temperatures and low frequencies is attributed to the increasing contribution from electrical conductivity at temperatures greater than 200 °C.41 Furthermore, upon cooling, a broad and frequency-dependent dielectric relaxation was observed over the temperature range from −50 to 150 °C, as shown in the Fig. 4(b), which was generally overlooked in previous reports on BF–BT based ceramics. The frequency-dependent variations in relative permittivity and dielectric loss are characteristic of a re-entrant relaxor ferroelectric transition, from a well-ordered ferroelectric state to a more disordered nanopolar state,37,42 which is consistent with the anomalous reduction in rhombohedral distortion upon cooling from 200 to 25 °C, as reported in section 3.1 above. Similar enhancement of dielectric and piezoelectric properties was previously reported in lead-based relaxor ferroelectrics by Li, who interpreted the temperature-dependent behaviour in terms of the evolution of polar nano-regions (PNR) associated with nano-scale chemical and structural heterogeneity.24
δ) of the Nb-doped BF–BT and Ar annealed pure BF–BT ceramics are shown in Fig. 4(a) and Fig. S2 (ESI†), respectively. The presence of dielectric relaxation and a slight frequency dependence in the position of the dielectric peaks were apparent at temperatures around 420 °C, indicating the weak relaxor ferroelectric nature of the material and a tendency for increasing disorder in the polar state near to the ferroelectric-paraelectric transition. The rapid increase in dielectric loss at high temperatures and low frequencies is attributed to the increasing contribution from electrical conductivity at temperatures greater than 200 °C.41 Furthermore, upon cooling, a broad and frequency-dependent dielectric relaxation was observed over the temperature range from −50 to 150 °C, as shown in the Fig. 4(b), which was generally overlooked in previous reports on BF–BT based ceramics. The frequency-dependent variations in relative permittivity and dielectric loss are characteristic of a re-entrant relaxor ferroelectric transition, from a well-ordered ferroelectric state to a more disordered nanopolar state,37,42 which is consistent with the anomalous reduction in rhombohedral distortion upon cooling from 200 to 25 °C, as reported in section 3.1 above. Similar enhancement of dielectric and piezoelectric properties was previously reported in lead-based relaxor ferroelectrics by Li, who interpreted the temperature-dependent behaviour in terms of the evolution of polar nano-regions (PNR) associated with nano-scale chemical and structural heterogeneity.24
Further investigations of the temperature-dependent planar coupling factor, kp, yielded a relatively stable value between 0.35 and 0.45 over the temperature range from 100 to 400 °C and confirmed a depoling temperature of approximately 420 °C, as shown in Fig. 4(c). These results demonstrate that the 0.5 mol% Nb-doped 0.7BF–0.3BT ceramics are well-suited for high temperature piezoelectric applications. The rapid increase in kp at temperatures around 75 °C coincides with the observation of temperature-dependent dielectric behaviour in the same temperature range, suggesting a common origin in improved polarizability.
Arrhenius plots of the volume resistivity, ρ, for pure and Nb-doped BF–BT ceramics are shown in Fig. S3 (ESI†). In the temperature range 20–500 °C, the resistivity of the Nb-doped BF–BT ceramic is several orders of magnitude higher than that of the pure BF–BT. The higher gradient of the ρ–T curve for the Nb-doped material also indicates a significantly higher activation energy of approximately 1.18 eV. In contrast, the Ar annealed pure BF–BT ceramic exhibits 2 different activation energies of 1.05 and 0.68 eV, which suggests the occurrence of different thermally activated conduction mechanisms for temperatures below or above 250 °C respectively. According to recent research on BiFeO3-based ceramics, the low- and high-temperature regions may correspond to predominantly electronic and ionic conduction regimes respectively.43 In summary, the substitution of Nb5+ for Ti4+ as a donor dopant in BF–BT ceramics suppresses the extrinsic p-type conductivity, which facilitates the poling procedure and induces piezoelectric properties that remain relatively stable for temperatures up to ∼400 °C.
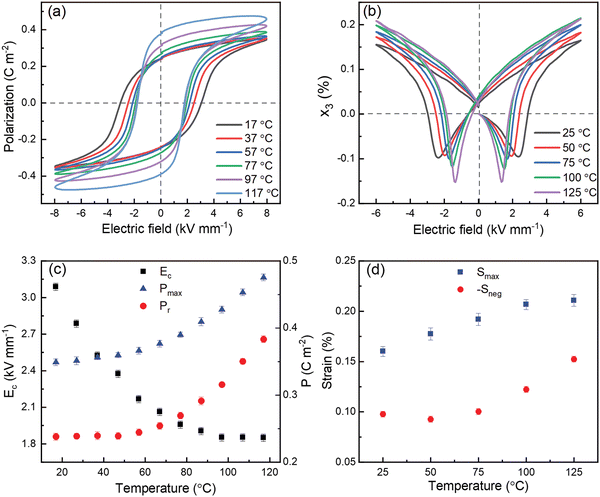
The temperature-dependent polarization–electric field (P–E) and longitudinal strain–electric field (S–E) hysteresis loops are presented in Fig. 5(a) and (b) respectively. In general, the remanent polarization (Pr) increased from 0.23 to 0.43 C m−2, while the coercive field (Ec) reduced from 3.10 to 1.85 kV mm−1 over the temperature range from 17 °C to 117 °C, as shown in Fig. 5(c). Although the coercive field decreased rapidly as the temperature increased from 17 to 60 °C, the values of Pr and Pmax remained relatively stable at 0.23 and 0.35 C m−2 respectively, which indicates that the activation energy for domain switching decreased, but the spontaneous polarization within each domain did not change significantly over this temperature range. These results also indicate that the maximum applied field, Emax, of 8 kV mm−1 should be sufficient for poling, since it is significantly larger than 2Ec for each of the temperatures investigated. The coercive field was reduced to a stable level around 1.85 kV mm−1 for temperatures beyond 75 °C, while the values of Pr and Pmax increased considerably, from 0.23 to 0.39 C m−2 and 0.35 to 0.48 C m−2 respectively, up to the maximum temperature of approximately 120 °C. A slight increase in leakage current, indicated by rounding of the P–E loop tips, may contribute to the enhancement of polarisation values at higher temperatures, but this is not considered to be a significant factor in view of the corresponding nature of the S–E loops which are not subject to this effect.
The anomalous increase in polarization with increasing temperature is consistent with the increase of rhombohedral distortion and re-entrant relaxor ferroelectric behaviour reported above. Conversely, the impairment of ferroelectric switching on cooling is associated with disruption of ferroelectric ordering and may induce a reduction of the stable domain dimension, tending towards polar nano-regions (PNRs) at low temperatures. Similar trends are also apparent in the x3–E relationships presented in Fig. 5(b) and (d), although the strain values increase more gradually with temperature. A slight reduction in the magnitude of Sneg at temperatures from 25 to 50 °C may indicate a weak domain stabilisation (ageing) effect after poling at room temperature. The enhancement of polarization and electro–strain values over the temperature range from 60 to 120 °C are discussed further in section 3.4 below.
3.3. Thermal depolarization and pyroelectric properties
The changes in remanent polarization for the Nb-doped BF–BT ceramics (poled either at room temperature or at 100 °C), determined by integration of the thermally-stimulated depolarization current (TSDC) measurements, are presented in Fig. 6. Upon initial heating, a gradual reduction in polarization, ΔP, developed gradually at temperatures up to 50 °C for both samples, which indicates that the remanent polarization values decreased initially with increasing temperature, as shown in Fig. 6(a), consistent with classical theories of the pyroelectric effect and previous observations in BT, NBT and PZT ceramics.35 This type of behaviour is common in ferroelectrics and indicates a negative pyroelectric coefficient, p, according to the following definition: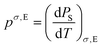 | (1) |
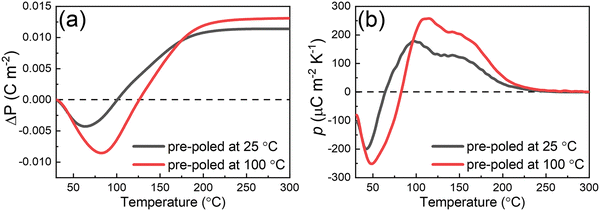 | ||
| Fig. 6 Temperature-dependent changes in (a) remanent polarization, ΔP, and (b) pyroelectric coefficient, p, of 0.5 mol% Nb-doped 0.7BF–0.3BT pre-poled at 25 and 100 °C. | ||
This observation is also in agreement with the relatively invariant Pr values obtained from room temperature to 50 °C, according to the results illustrated in Fig. 5(c).
Beyond this temperature, ΔP began to level off and increased significantly on further heating, yielding a positive pyroelectric coefficient for temperatures greater than 75 °C and consistent with the observed increase in Pr according to the ferroelectric P–E data presented in Fig. 5. These results provide direct evidence of the positive pyroelectric coefficient in BF–BT ceramics, which can be correlated with the negative electrocaloric effect (represented as dT/dE) in 0.68BiFeO3–0.32BaTiO3 reported by Liu et al.44 The magnitude of both the negative and positive pyroelectric coefficients was enhanced for the sample poled at 100 °C, which is attributed to the enhanced efficiency of ferroelectric domain switching at this temperature.
The unusual positive ΔP and p values from 70 to 200 °C are attributed to the enhancement of both rhombohedral distortion and unit cell volume with increasing temperature, which contribute to the direct (lattice distortion) and indirect (thermal expansion) pyroelectric effects respectively.45 The polarization values remained relatively stable at temperatures beyond 200 °C, leading to gradual reductions in the magnitude of the pyroelectric coefficient. TSDC measurements at higher temperatures, approaching Tm (temperature at maximum dielectric constant), were not feasible due to the influence of increasing electrical conductivity, which was found to destabilise the current amplifier in the present experimental setup. Further investigations, using a dynamic pyroelectric measurement technique at high temperatures,46 would be helpful to distinguish more clearly between the anomalous positive pyroelectric behaviour in the intermediate temperature range and the more pronounced thermal depolarization at the Curie temperature around 400 °C.
3.4. In situ electric field-dependent diffraction studies
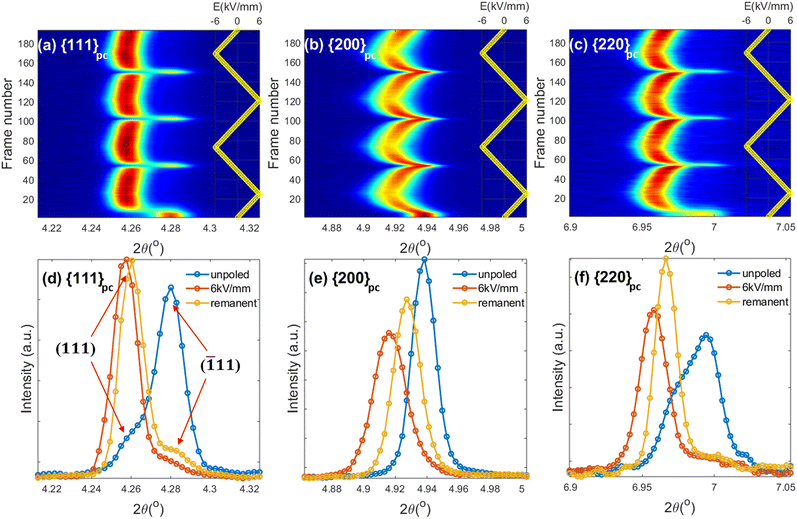
XRD contour plots of the {111}pc, {200}pc and {220}pc peak profiles at ψ = 0° (parallel to the direction of electric field) at 25 and 125 °C are shown in Fig. S4 (ESI†) and Fig. 7, respectively. Single {200}pc and double {111}pc and {220}pc peaks were observed for the initial unpoled state. On application of the electric field, the single {200}pc peak exhibits a shift to lower angles (tensile strain), which was most pronounced at the highest temperature of 125 °C. This was attributed to the combined effects of the piezoelectric/electrostrictive lattice strain and contributions from elastic interactions with the surrounding polycrystalline matrix, which is the so-called ‘intrinsic’ effect.47–49 The doublet {111}pc and {220}pc peak families exhibit variations in relative intensity under field due to ferroelectric domain switching during the poling process. The resulting ‘extrinsic’ contribution to electrostrain can be quantified in terms of the ratio of the lattice spacings, d111/d![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11, and the intensities, I111/I
11, and the intensities, I111/I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11. On the application of an electric field, the relative intensities of the split peaks varied dramatically due to the enhanced domain switching, as shown in Fig. 7. The dominance of the (111) peak for the direction parallel to the electric field (azimuthal angle, ψ = 0°) and of the (
11. On the application of an electric field, the relative intensities of the split peaks varied dramatically due to the enhanced domain switching, as shown in Fig. 7. The dominance of the (111) peak for the direction parallel to the electric field (azimuthal angle, ψ = 0°) and of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) peak in the orthogonal direction (ψ = 90°) is clearly evident in Fig. S5 (ESI†), indicating the occurrence of domain switching with the preferred polarisation direction towards the electric field direction.
11) peak in the orthogonal direction (ψ = 90°) is clearly evident in Fig. S5 (ESI†), indicating the occurrence of domain switching with the preferred polarisation direction towards the electric field direction.
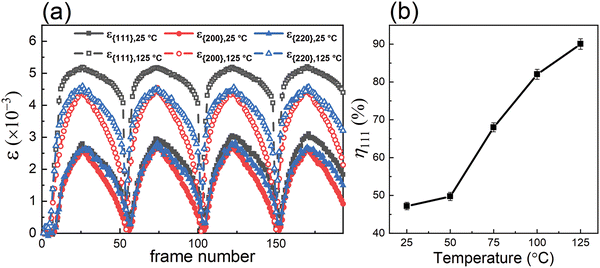
The effective (average) lattice strains vary in a cyclic manner with the applied electric field; εhkl values for {111}pc, {200}pc and {220}pc with ψ = 0° at temperatures of 25 and 125 °C were calculated using eqn (2), as shown in Fig. 8(a).
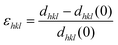 | (2) |
For d{111} and d{220}, it was calculated according to the following equations:
d{111} = η111 × d111 + (1 − η111) × d![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11 11 | (3) |
d{220} = η220 × d220 +(1 − η220) × d0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 2 2 | (4) |
The preferred orientation of ferroelectric domains is quantified in terms of the domain orientation fractions, ηhkl, given by eqn (5) and (6).
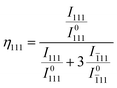 | (5) |
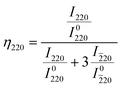 | (6) |
As shown in Fig. 8(a), each of the ε{hkl} values exhibit positive (tensile) strain for ψ = 0° in response to the applied electric field. At 25 °C, the differences between the effective lattice strains for different crystallographic orientations were negligible, while a clear anisotropy developed at 125 °C, with ε{111} being most pronounced due to the largest transformation strains associated with ferroelectric domain switching along the polar <111> directions.
The intensity of the (111) reflection at all temperatures was greatly enhanced relative to that of (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) due to ferroelectric domain switching along [111]. This results in an apparent shift of the relatively broad {111} peak to lower 2θ values, but the underlying change in peak intensities could be extracted by full-pattern fitting in MAUD52 using suitable domain and lattice strain orientation distribution functions. The anisotropic strain was estimated by a weighted strain orientation distribution function (WSODF) Popa–Balzar model, while the texture was described by a second order Harmonic function.53,54 It was found that the intensity ratio, I111/I
11) due to ferroelectric domain switching along [111]. This results in an apparent shift of the relatively broad {111} peak to lower 2θ values, but the underlying change in peak intensities could be extracted by full-pattern fitting in MAUD52 using suitable domain and lattice strain orientation distribution functions. The anisotropic strain was estimated by a weighted strain orientation distribution function (WSODF) Popa–Balzar model, while the texture was described by a second order Harmonic function.53,54 It was found that the intensity ratio, I111/I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11, in the poled state increased significantly with increasing temperature, indicating enhanced ferroelectric domain switching.
11, in the poled state increased significantly with increasing temperature, indicating enhanced ferroelectric domain switching.
The temperature dependence of η111 for the maximum field level is shown in Fig. 8(b). Initially, η111 increased slightly from 47 to 50% with increasing temperature from 25 to 50 °C, which is consistent with the slight increase in Pmax for P–E loops recorded over the same temperature range. A more dramatic increase in Δη111, from 50% to 90%, occurred above 50 °C, which is correlated with the enhancement of Pmax at elevated temperatures as shown in Fig. 5(c). The enlarged rhombohedral distortion and improved domain switching ability at higher temperatures are correlated with the re-entrant relaxor ferroelectric transformation and may result from a mechanism involving the development of a more uniform distribution of local polar Bi-displacements, as suggested by Kuroiwa.32 Further investigations of the local Bi-environment and its evolution with temperature would help to clarify this issue.
The contribution of the lattice strain to the macroscopic strain can be estimated from the weighted average of the effective lattice strains associated with different crystallographic orientations, according to Daymond,55 using the representative {111}pc, {200}pc and {220}pc reflections:
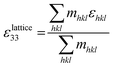 | (8) |
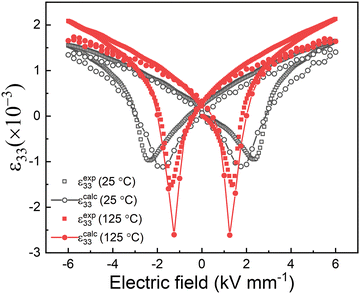
The average strain–electric field loops calculated according to the Daymond method, in comparison with the macroscopic strain measured experimentally, are illustrated in Fig. 9. The calculated and measured S–E loops both exhibit obvious enhancement of strain and reduced coercive field at higher temperatures. Differences between the calculated and directly measured macroscopic strain values are attributed primarily to the time scale (frequency) of the measurements. For the in situ XRD study, a relatively low frequency with a period of ∼600 s, was used for the bipolar electric field, in comparison with 60 s for the macroscopic measurement, providing greater efficiency for time-dependent domain switching processes and resulting in a lower coercive field.
4. Conclusions
The structure and functional properties of pure and Nb-doped 0.7BiFeO3–0.3BaTiO3 ceramics were investigated with respect to their application in piezoelectric transducers at high temperatures. Anomalous thermally-induced variations in the relative permittivity and loss, remanent polarization, electrostrain and rhombohedral inter-axial angle at temperatures from −50 to +175 °C were interpreted as evidence for re-entrant relaxor ferroelectric behaviour. The observed enhancement of the dielectric, ferroelectric and piezoelectric properties over this temperature range were attributed to improved ferroelectric ordering, which facilitated ferroelectric domain switching and provided more efficient poling. Stable kp values were achieved with a variation from 0.35 to 0.45 over the temperature range 100 to 430 °C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Yizhe Li and David Hall acknowledge financial support by the Engineering and Physical Sciences Research Council (Grant number EP/S028978/1). We thank Diamond Light Source for access to beamline I15-1 (proposal number CY24144-1) that contributed to the results presented here. The authors thank Gary Harrison (Department of Materials, University of Manchester) and Annette Kleppe (Diamond Light Source) for assistance with XRD measurements. Andreas Wohninsland thanks the Deutsche Forschungsgemeinschaft (DFG) for financial support under No. KO 5948/1-1 and KL 615/34-1 (Grant No. 414311761).References
- S. O. Leontsev and R. E. Eitel, J. Mater. Res., 2011, 26, 9–17 CrossRef CAS.
- H. Zhang, W. Jo, K. Wang and K. G. Webber, Ceram. Int., 2014, 40, 4759–4765 CrossRef CAS.
- S. O. Leontsev and R. E. Eitel, J. Am. Ceram. Soc., 2009, 92, 2957–2961 CrossRef CAS.
- S. Cheng, L. Zhao, B. P. Zhang and K. K. Wang, Ceram. Int., 2019, 45, 10438–10447 CrossRef CAS.
- B. W. Xun, N. Wang, B. P. Zhang, X. Y. Chen, Y. Q. Zheng, W. S. Jin, R. Mao and K. Liang, Ceram. Int., 2019, 45, 24382–24391 CrossRef.
- N. Maso and A. R. West, Chem. Mater., 2012, 24, 2127–2132 CrossRef CAS.
- L. Li, J. Kler, A. R. West, R. A. De Souza and D. C. Sinclair, Phys. Chem. Chem. Phys., 2021, 23, 11327–11333 RSC.
- M. H. Lee and T. K. Song, J. Eur. Ceram. Soc., 2019, 39, 4697–4704 CrossRef.
- L. Wang, R. Liang, Z. Zhou, M. Li, M. Gu, P. Wang and X. Dong, J. Eur. Ceram. Soc., 2019, 39, 4727–4734 CrossRef CAS.
- M. H. Lee, D. J. Kim, J. S. Park, S. W. Kim, T. K. Song, M. H. Kim, W. J. Kim, D. Do and I. K. Jeong, Adv. Mater., 2015, 27, 6976–6982 CrossRef CAS PubMed.
- L. K. Venkataraman, B. Wang, P. Ren, D. A. Hall and T. Rojac, Open Ceram., 2022, 100259 Search PubMed.
- W. Jaffe, Piezoelectric Ceramics, Academic Press, 1971 Search PubMed.
- D. Berlincourt, J. Acoust. Soc. Am., 1992, 91, 3034–3040 CrossRef.
- F. Kang, L. Zhang, B. Huang, P. Mao, Z. Wang, Q. Sun, J. Wang and D. Hu, J. Eur. Ceram. Soc., 2020, 40, 1198–1204 CrossRef CAS.
- C. Zhou, H. Yang, Q. Zhou, Z. Cen, W. Li, C. Yuan and H. Wang, Ceram. Int., 2013, 39, 4307–4311 CrossRef CAS.
- S. J. McCartan, I. Calisir, G. W. Paterson, R. W. Webster, T. A. Macgregor, D. A. Hall and I. MacLaren, J. Am. Ceram. Soc., 2021, 104, 2388–2397 CrossRef CAS.
- T. Wang, L. Jin, Y. Tian, L. Shu, Q. Hu and X. Wei, Mater. Lett., 2014, 137, 79–81 CrossRef CAS.
- Z. Yang, B. Wang, Y. Li and D. A. Hall, Materials, 2022, 15, 2872 CrossRef CAS PubMed.
- L. E. Cross, Ferroelectrics, 1987, 76, 241–267 CrossRef CAS.
- C. W. Ahn, C. H. Hong, B. Y. Choi, H. P. Kim, H. S. Han, Y. Hwang, W. Jo, K. Wang, J. F. Li and J. S. Lee, J. Korean Phys. Soc., 2016, 68, 1481–1494 CrossRef.
- A. Bokov and Z. G. Ye, J. Mater. Sci., 2006, 41, 31–52 CrossRef CAS.
- J. Hlinka, J. Adv. Dielectr., 2012, 2, 1241006 CrossRef.
- B. Dkhil, P. Gemeiner, A. Al-Barakaty, L. Bellaiche, E. Dul’kin, E. Mojaev and M. Roth, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064103 CrossRef.
- F. Li, S. Zhang, D. Damjanovic, L. Q. Chen and T. R. Shrout, Adv. Funct. Mater., 2018, 28, 1801504 CrossRef.
- L. E. Fuentes-Cobas, M. E. Montero-Cabrera, L. Pardo and L. Fuentes-Montero, Materials, 2015, 9, 14 CrossRef PubMed.
- L. Daniel, D. A. Hall and P. Withers, J. Phys. D: Appl. Phys., 2014, 47, 325303 CrossRef.
- A. Pramanick, D. Damjanovic, J. E. Daniels, J. C. Nino and J. L. Jones, J. Am. Ceram. Soc., 2011, 94, 293–309 CrossRef CAS.
- J. Filik, A. Ashton, P. Chang, P. Chater, S. Day, M. Drakopoulos, M. Gerring, M. Hart, O. Magdysyuk and S. Michalik, J. Appl. Crystallogr., 2017, 50, 959–966 CrossRef CAS PubMed.
- M. Stewart, M. G. Cain and D. A. Hall, Ferroelectric hysteresis measurement and analysis, NPL Report CMMT(A), 1999, 152, 1–57 Search PubMed.
- S. B. Lang and F. Steckel, Rev. Sci. Instrum., 1965, 36, 929–932 CrossRef CAS.
- S. Jachalke, E. Mehner, H. Stöcker, J. Hanzig, M. Sonntag, T. Weigel, T. Leisegang and D. Meyer, Appl. Phys. Rev., 2017, 4, 021303 Search PubMed.
- Y. Kuroiwa, S. Kim, I. Fujii, S. Ueno, Y. Nakahira, C. Moriyoshi, Y. Sato and S. Wada, Commun. Mater., 2020, 1, 1–8 CrossRef.
- G. Wang, D. A. Hall, Y. Li, C. A. Murray and C. C. Tang, J. Eur. Ceram. Soc., 2016, 36, 4015–4021 CrossRef CAS.
- BRUKER AXS GmbH, Karlsruhe, Diffrac Plus TOPAS V. 3.0 (Manual), 2006 Search PubMed.
- C. R. Bowen, J. Taylor, E. LeBoulbar, D. Zabek, A. Chauhan and R. Vaish, Energy Environ. Sci., 2014, 7, 3836–3856 RSC.
- T. P. Comyn, T. Stevenson, M. Al-Jawad, S. L. Turner, R. I. Smith, A. J. Bell and R. Cywinski, J. Appl. Phys., 2009, 105, 094108 CrossRef.
- A. A. Bokov and Z. Ye, Nanoscale Ferroelectrics and Multiferroics: Key Processing and Characterization Issues, and Nanoscale Effects, 2 Volumes, Reentrant phenomena in relaxors, John Wiley & Sons, 2016, pp. 729–764 Search PubMed.
- I. Calisir and D. A. Hall, J. Mater. Chem. C, 2018, 6, 134–146 RSC.
- I. Calisir, A. K. Kleppe, A. Feteira and D. A. Hall, J. Mater. Chem. C, 2019, 7, 10218–10230 RSC.
- M. Valant, A. K. Axelsson and N. Alford, Chem. Mater., 2007, 19, 5431–5436 CrossRef CAS.
- K. Härdtl, Ceram. Int., 1982, 8, 121–127 CrossRef.
- M. Fang, Y. Ji, Z. Zhang, Y. Yang, C. Liu, D. Wang, L. Zhang, J. Gao and X. Ren, NPG Asia Mater., 2018, 10, 1029–1036 CrossRef CAS.
- L. Li, J. Kler, A. R. West, R. A. De Souza and D. C. Sinclair, Phys. Chem. Chem. Phys., 2021, 23, 11327–11333 RSC.
- N. Liu, R. Liang, G. Zhang, Z. Zhou, S. Yan, X. Li and X. Dong, J. Mater. Chem. C, 2018, 6, 10415–10421 RSC.
- G. Velarde, S. Pandya, J. Karthik, D. Pesquera and L. W. Martin, APL Mater., 2021, 9, 010702 CrossRef CAS.
- M. Acosta, N. Novak, V. Rojas, S. Patel, R. Vaish, J. Koruza, G. Rossetti Jr and J. Rödel, Appl. Phys. Rev., 2017, 4, 041305 Search PubMed.
- Y. Li, Z. Zhang, Y. Chen and D. A. Hall, Acta Mater., 2018, 160, 199–210 CrossRef CAS.
- Y. Li, Y. Chen, Z. Zhang, A. Kleppe and D. A. Hall, Acta Mater., 2019, 168, 411–425 CrossRef CAS.
- M. Hoffmann, M. Hammer, A. Endriss and D. Lupascu, Acta Mater., 2001, 49, 1301–1310 CrossRef CAS.
- D. A. Hall, A. Steuwer, B. Cherdhirunkorn, T. Mori and P. Withers, Acta Mater., 2006, 54, 3075–3083 CrossRef CAS.
- J. L. Jones, E. B. Slamovich and K. J. Bowman, J. Appl. Phys., 2005, 97, 034113 CrossRef.
- L. Lutterotti, S. Matthies, H. R. Wenk, A. Schultz and J. Richardson Jr, J. Appl. Phys., 1997, 81, 594–600 CrossRef CAS.
- N. Popa and D. Balzar, J. Appl. Crystallogr., 2014, 47, 2113 CrossRef CAS.
- U. F. Kocks, C. N. Tomé and H.-R. Wenk, Texture and anisotropy: preferred orientations in polycrystals and their effect on materials properties, Cambridge university press, 2000 Search PubMed.
- M. R. Daymond, J. Appl. Phys., 2004, 96, 4263–4272 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc04702k |
| This journal is © The Royal Society of Chemistry 2023 |