Simultaneous optimization of the electrical and thermal transport properties of LuNiSb via aliovalent doping

Abstract

Rare earth-based half-Heusler compounds are potential thermoelectric materials with inherently low thermal conductivity. Here, LuNiSb-based compounds were successfully prepared and their electrical and thermal transport properties were simultaneously improved via aliovalent doping of Sn and Co. In addition to optimizing the carrier concentration, a huge suppression of lattice thermal conductivity κ_L (∼40% at 300 K) was observed, despite the atomic mass and radius of Sn and Co having only small differences compared with those of the substituted matrix atoms. With the help of first-principles calculations, it is discovered that the suppression of κ_L mainly originates from the deceleration of optical phonons and the enhancement of phonon–phonon (p–p) scattering phase space. Compared with Co-doped LuNiSb-based compounds, Sn-doped ones exhibit better electrical performance, which is probably because of the weaker perturbation of the valence band. Finally, a peak zT of about 0.4 was obtained at 775 K for LuNiSb_0.92Sn_0.08. This work highlights the simultaneous optimization of electrical and thermal transport properties only by aliovalent doping, which helps develop high-performance thermoelectrics.

---

Chenguang Fu

Dr Chenguang Fu is now a ZJU-100 Young Professor at the School of Materials Science and Engineering, Zhejiang University. He obtained his PhD (2016) in Materials Science from Zhejiang University. After that, he received the Humboldt Fellowship and worked as a subgroup leader on Thermoelectrics & Topology at the Max Planck Institute for Chemical Physics of Solids from 2016 to 2020. His current research interests include the understanding of the electron and phonon transport mechanism of thermoelectric materials, the development of new thermoelectric materials and devices, and anomalous transport in magnetic topological materials.

---

Introduction

Thermoelectric (TE) materials allow direct conversion of heat into electrical energy.¹ The figure of merit, zT = S²σT/(κ_e + κ_L), where S, σ, T, κ_e, and κ_L are the Seebeck coefficient, the electrical conductivity, the absolute temperature, and the electronic and lattice components of thermal conductivity, respectively, is used to gauge the conversion efficiency of TE materials.² Aiming at improving the TE performance of new semiconductor materials, choosing a suitable dopant to optimize carrier concentration (n) is usually the first and foremost step.² Further, enhancing the phonon scattering can be implemented to suppress the κ_L.³

Half-Heusler (HH) materials, which are thermally stable, non-toxic, and low cost, generally possess good electrical transport properties, but their high κ_L impedes the improvement of TE performance. Given this, numerous previous studies focused on the suppression of κ_L, by introducing point defect scattering,^4,5 phase separation,^6,7 and grain boundary scattering,^8,9 for instance. To date, several HH systems, including MNiSn (M = Ti, Zr, Hf),^10,11 RFeSb (R = V, Nb, Ta),^12–14 MCoSb^15–17 and R_1−δCoSb,⁴ have been discovered to be good TE materials.

ReNiSb-based (Re: rare earth elements) HH compounds, as another typical narrow-gap semiconductor system, were predicted to have inherently low κ_L and good electrical transport performance. Yang et al.¹⁸ carried out the theoretical evaluation of HH compounds as potential TE materials, in which n-type YNiSb was suggested to exhibit good electrical performance. Zhou et al.¹⁹ predicted high carrier mobility in ReNi(Sb,Bi). In 2021, by comparing the phonon spectra of YNiBi and LuNiBi, Hong et al.²⁰ anticipated the latter which consists of “two heavy and one light” atom will exhibit ultralow κ_L (∼0.7 W m⁻¹ K⁻¹ at 300 K). All of this aroused our interest in studying the TE performance of ReNiSb-based HH compounds with probably inherently low κ_L. However, owing to the challenge of synthesis and complex intrinsic defects, Re-based HH compounds have been rarely studied experimentally.²¹ In 2020, DyNiSb, ErNiSb, TmNiSb, and LuNiSb were successfully prepared by Ciesielski et al.,²² of which the κ_L were reported to be about 2.0–5.0 W m⁻¹ K⁻¹ at 300 K. The κ_L of YbNiSb, prepared by Huang et al.,²¹ was reported to be about 2.2 W m⁻¹ K⁻¹ at 300 K. Compared to other typical HH compounds (κ_L: 12 W m⁻¹ K⁻¹ for VFeSb,²³ 6 W m⁻¹ K⁻¹ for ZrNiSn,¹¹ 18 W m⁻¹ K⁻¹ for ZrCoSb²⁴), the experimentally reported low κ_Ls in ReNiSb-based HH compounds might be favorable for good TE performance. To verify this, more systematic studies on the optimization of TE performance should be carried out.

In this work, LuNiSb polycrystalline samples were successfully synthesized via levitation melting and high-energy mechanical alloying, followed by the spark plasma sintering (SPS) process. Considering the doping efficiency and solubility, Co and Sn, as the adjacent elements to the matrix Ni and Sb, respectively, were initially chosen to optimize the electrical performance of LuNiSb while it was surprisingly found that the κ_L was reduced effectively as well. First-principles calculations were further carried out and reveal that the reduction of group velocities of phonons in the high-energy range plays a key role in suppressing the κ_L. Meanwhile, it is found that the optimized power factor of Sn-doped LuNiSb compounds is better than that of the Co-doped ones. A peak zT of 0.4 was obtained at 775 K for LuNiSb_0.92Sn_0.08. This work highlights the simultaneous optimization of electrical and thermal transport properties via aliovalent doping.

Experimental and computational methods

Synthesis

Ingots with a nominal composition of LuNiSb_1−xSn_x and LuNi_1−yCo_ySb (x, y = 0, 0.02, 0.04, 0.06, 0.08, 0.12) were prepared by levitation melting of the stoichiometric amount of Lu (block, 99.99%), Ni (block, 99.99%), Sb (block, 99.99%), Sn (block, 99.99%), and Co (block, 99.99%) under an argon atmosphere for 3 minutes and excess Sb and Sn blocks of about 2% were added considering possible loss during the melting process. Each ingot was remelted three times to ensure homogeneity and no raw material remained. The ingots were manually ground into powders and mechanically milled (SPEX-8000D, PYNN Corporation) for an hour under argon protection. The fine powders were compacted by SPS (LABOX-650F, Sinter Land Inc.) at 1173 K under 65 MPa under vacuum for 15 minutes. Besides, LuNiSb_1−zBi_z (z = 0.2, 0.4, 0.6, 0.8, 1.0) ingots were prepared in two steps. The stoichiometric Lu (block, 99.99%) and Ni (block, 99.99%) were first weighed and melted to obtain the LuNi ingot, which was then cracked by hand milling. Then, stoichiometric Sb (powder, 99.99%) and Bi (powder, 99.99%) were subjected to the process of mechanical milling for 4 hours to obtain fine powders, and the following sintering steps are the same as those of LuNiSb_1−xSn_x.

Measurements

The phase structure of the powders and sintered bulks was studied by X-ray diffraction (XRD) on a PANalytical/Areis diffractometer using Cu Kα radiation (λ = 1.5406 Å). The Seebeck coefficient and electrical conductivity from 300 to 900 K were measured on a commercial Linseis LSR-3 system with an accuracy of ±5% and ±3%, respectively. The thermal conductivity κ was calculated by using κ = DρC_p, where ρ is the sample density estimated by the Archimedes method and D is the thermal diffusivity measured by a laser flash method on a Netzsch LFA457 instrument (the D of LuNiSb_1−xSn_x, LuNi_1−yCo_ySb, and LuNiSb_1−zBi_z are shown in Fig. S1†). The specific heat at constant pressure C_p was calculated from the measured sound velocity and density.¹⁶ Normal and shear ultrasonic measurements were performed at room temperature using input from a Panametrics 5052 pulser/receiver with a filter at 0.03 MHz. The response was recorded via a Tektronix TDS5054B-NV digital oscilloscope. The room temperature Hall coefficients were measured in a Mini Cryogen Free Measurement System (Cryogenic Limited, UK) under a variable magnetic field of ±4 T. The Hall carrier concentration (p_H) was calculated by p_H = 1/eR_H, where e is the unit charge and R_H is the Hall coefficient. The estimated error of the Hall coefficient is within ±10%. The carrier mobility μ_H was calculated by μ_H = σR_H. The chemical compositions of all sintered samples were checked using an electron probe microanalyzer (EPMA, JEOL JXA-8100) with a wavelength dispersive spectrometer (WDS). Raman active vibration modes were identified by Raman spectroscopy at room temperature with a solid-state argon laser at λ = 532 nm using a LabRAM HR (UV) system equipped with a CCD detector. The spectral resolution is around 1 cm⁻¹.

First-principles calculations

The ab initio calculations were performed by using the projector augmented wave method, as implemented in the Vienna ab initio simulation package (VASP).²⁵ The generalized gradient approximation²⁶ was used for the exchange–correlation function, and a plane-wave energy cutoff of 400 eV was adopted. The phonon density of states (DOS) and dispersions of LuNiSb_1−xSn_x (x = 0.00–0.12) were calculated by using the frozen phonon method, as implemented in the Phonopy package.²⁷ The phonon scattering rates and κ_Ls were obtained using the shengBTE²⁸ package, in which we considered the interactions between atoms to their fourth nearest neighbors. A 2 × 2 × 2 LuNiSb primitive cell, with 24 atoms in total, was adopted to accommodate 1/8 content of dopants in this work. For the structural optimization of the unit cell, the k-points were chosen as 4 × 4 × 4, and the convergence accuracy of force was 10⁻⁵ eV Å⁻¹. For the supercells with displacements (2 × 2 × 2 of the 24-atom-cell, 192 atoms in total), which were used in the calculations of second- and third-order force constants, only Γ point was considered. The energy convergence criterion was 10⁻⁷ eV throughout the work. Furthermore, the Quantum ESPRESSO²⁹ package and EPW³⁰ package with norm-conserving pseudopotentials³¹ and the Perdew–Burke–Ernzerhof exchange and correlation functional²⁶ were used to perform the electron–phonon (e–p) interaction of the 24-atom-cell (LuNiSn_0.875Sb_0.125). A plane wave cutoff of 100 Ry was employed, and the initial k and q meshes were both 4 × 4 × 4, which were interpolated to 15 × 15 × 15 meshes to calculate the e–p interaction matrix. Finally, we used a homemade code^32–35 to combine the phonon–phonon (p–p) and e–p scattering rates and calculate the lattice thermal conductivity.

Results and discussion

Crystal structure and thermal transport properties

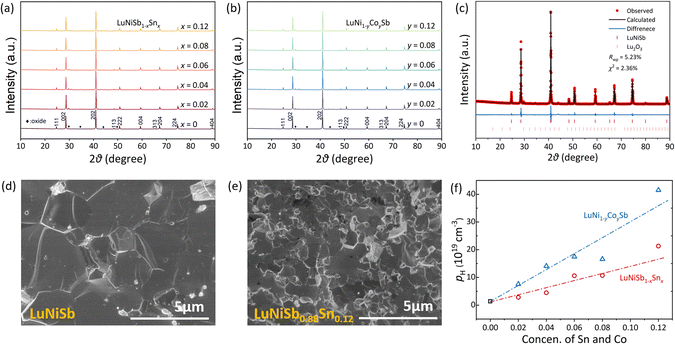
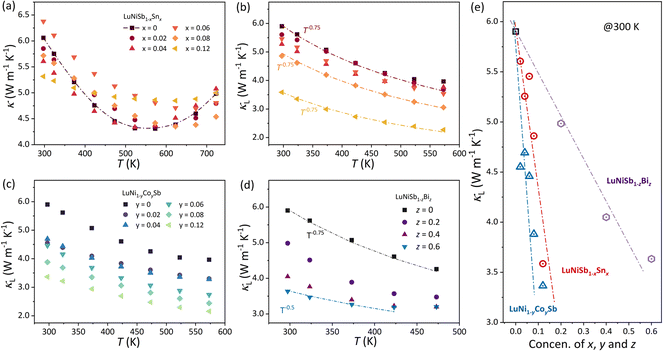
The powder XRD patterns of LuNiSb_1−xSn_x and LuNi_1−yCo_ySb samples are presented in Fig. 1a and b, respectively. Their main phases are indexed to the cubic MgAgAs-type half-Heusler structure. Owing to the similar atomic radius of matrix and dopant atoms (Sn in the Sb site and Co in the Ni site), the diffraction peaks of these samples do not shift noticeably. Additional tiny diffraction peaks, which are indexed to Lu₂O₃ (about 1.7 wt% according to the refinement result), are observed in the range of 30–50°. The Rietveld refinement (Fig. 1c) indicates the crystalline structure of LuNiSb corresponds to space group 216 with the Lu atom located at 4a (0,0,0), Ni at 4c (1/4,1/4,1/4), and Sb at 4d (1/2,1/2,1/2) Wyckoff positions. The lattice parameter of LuNiSb at room temperature was estimated to be 6.2256 Å, matching with the literature data.³⁶ The secondary electron morphology of the fracture surface was analyzed for LuNiSb and LuNiSb_0.88Sn_0.12, as shown in Fig. 1d and e, respectively. The analysis shows that the sample of LuNiSb has a grain size of a few micrometres, which is several times larger than that of the sample doped with 12% Sn. After the measurement of the Hall coefficient, it is found that n_H increases positively with the introduction of the dopant (Fig. 1f), which suggests that Sn and Co can adjust carrier concentration (n) effectively. Compared with Sn, the doping of Co gives a higher doping efficiency, and thus higher n_H is achieved at the same nominal doping concentration.

Fig. 1 The indexed laboratory XRD patterns of (a) LuNiSb_1−xSn_x and (b) LuNi_1−yCo_ySb. (c) Rietveld refinement of XRD patterns at room temperature with experimental (red dots), calculated (dark line), difference (blue line), and Bragg reflections (red and orange segment) of LuNiSb, and the indexed laboratory XRD patterns of LuNiSb_1−xSn_x. The secondary electron morphology of the fracture surface of (d) LuNiSb and (e) LuNiSb_0.88Sn_0.12. (f) The p_H of LuNi_1−yCo_ySb represented by empty blue triangles and empty red circles for LuNiSb_1−xSn_x.

The temperature dependence of total thermal conductivity κ and lattice thermal conductivity κ_L of LuNiSb_1−xSn_x is presented in Fig. 2a and b, respectively. The electronic thermal conductivity κ_e is obtained by the Wiedemann–Franz law: κ_e = LσT (Fig. S2†), where L is the Lorenz number calculated using the single parabolic band (SPB) model.³⁷ The κ_L of LuNiSb at room temperature is about 5.9 W m⁻¹ K⁻¹, which is relatively lower compared with other typical 18-electron HHs. With increasing temperature, the κ_L decreases and approaches a minimum value of about 3.9 W m⁻¹ K⁻¹ at 575 K. By increasing Sn doping from 0 to 12%, a sharp suppression of the room temperature κ_L by 39% is observed. A similar suppression in the κ_L occurs in the Co-doped LuNi_1−yCo_ySb (Fig. 2c). For instance, a drop of 42% is observed for LuNi_0.88Co_0.12Sb, resulting in a κ_L of about 3.4 W m⁻¹ K⁻¹ at 300 K.

Fig. 2 Temperature dependence of the κ (a) and κ_L (b) for LuNiSb_1−xSn_x. The temperature-dependent κ_L of (c) LuNi_1−yCo_ySb and (d) LuNiSb_1−zBi_z. (e) Nominal doping of alloying concentration dependence of κ_L for LuNiSb_1−xSn_x, LuNi_1−yCo_ySb and LuNiSb_1−zBi_z.

As the atomic mass and radius between the matrix and the dopants (Sb in the Sn site and Co in the Ni site) are similar, the significant reduction of κ_L in LuNiSb caused by doping is surprising. For LuNiSb_1−xSn_x, the κ_L of all the samples maintains a temperature dependence of T^−0.75, which suggests the point defect scattering brought about by Sn doping might not be serious.^38,39 A series of LuNiSb_1−zBi_z were further prepared to elucidate the effect of point defect scattering on the κ_L of LuNiSb,^40,41 and the phase characterization is presented in Fig. S3.† With increasing Bi alloying content, the κ_L is suppressed and the temperature dependence changes from T^−0.75 to T^−0.5 (Fig. 2d), which demonstrates the additional point defect scattering of phonons was induced. The κ_L of all the LuNiSb_1−xSn_x, LuNi_1−yCo_ySb, and LuNiSb_1−zBi_z at room temperature are presented together in Fig. 2e, from which one can find that the aliovalent doping of Co and Sn is a more effective method to reduce κ_L than the isoelectronic alloying of Bi. Based on the model proposed by Klemens and Abeles (eqn S1†),^42,43 the normalized disorder of mass field brought about by Sn doping and Bi alloying is presented in Fig. S4,† where LuNiSb_1−xSn_x can be found to have much lower mass fluctuations than those of LuNiSb_1−zBi_z. This suggests the lower κ_L observed in LuNiSb_1−xSn_x probably does not originate from the enhanced point defect scattering of phonons. The effect of grain boundary scattering was excluded as discussed in ESI Note 1 and Fig. S5 and S6.† Besides, it was recently found that aliovalent doping might play an important role in affecting the intrinsic phonon dispersion of the matrix compounds and thus their thermal transport.⁴⁴

In recent years, first-principles calculations of phonons have become an effective method for understanding the intrinsic phonon–phonon and electron–phonon interactions. For PbTe, the calculated thermal conductivity shows a six-times increase if the acoustic–optical scattering process was removed, which highlights the effect of the coupling between the low-lying transverse optical phonons and the longitudinal acoustic phonons.⁴⁵ In 2023, Dai et al.³² showed the different contributions of e–p scattering for several HH systems by calculating their EP coupling matrix. By means of thermal transport measurement, inelastic neutron scattering measurements, and first-principles calculations, Han et al.⁴⁴ found that aliovalent doping-induced optical phonon softening can significantly suppress phonon transport in NbFeSb. Herein, first-principles calculations are used to further analyze the intrinsic thermal transport characteristics for LuNiSb.

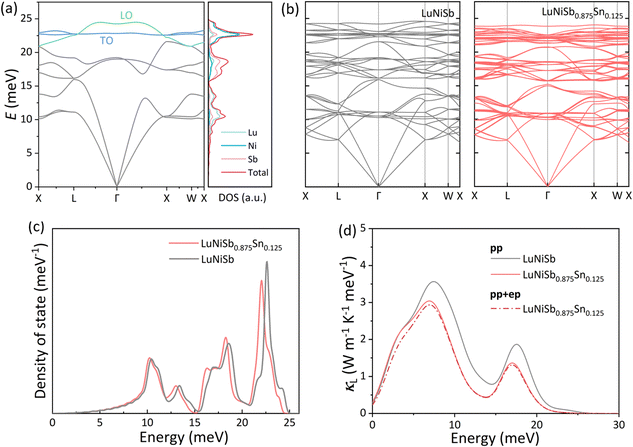
In polar materials, due to the long-range polarization field produced by the longitudinal optical (LO) phonon vibration, the degeneracy of the LO phonon and transverse optical (TO) phonon is lifted around the Brillouin zone center, corresponding to the LO–TO splitting.⁴⁶ For instance, free carriers brought by the Sb dopant in ZrNiSn screen the Coulomb interaction, resulting in the collapse of LO–TO splitting.⁴⁷ According to the calculated phonon dispersion (Fig. 3a), it is found that LO–TO splitting exists in LuNiSb as well. With 12.5% Sn doping into LuNiSb, high-energy optical phonon branches become flat and the collapse of LO–TO splitting appears (Fig. 3b). Moreover, a remarkable softening of the optical phonon branches occurs at the energy range of 15–25 meV which matches the movement of the two peaks (at ∼18 meV and ∼23 meV) presented in the total DOSs (Fig. 3c). At the same time, phonon softening is also captured by Raman spectroscopy, in which the redshift of the main Raman peaks with increasing Sn doping content for LuNiSb_1−xSn_x can be observed. Based on the expression of κ_L = 1/3C_vv_g²τ, where C_v is the heat capacity, v_g is the group velocity, and τ is the relaxation time, the calculated phonon energy-dependent κ_L is presented in Fig. 3d.

Fig. 3 (a) Calculated phonon dispersion of LuNiSb with total and partial DOS in a single cell. (b) Phonon dispersion of LuNiSb and LuNiSb_0.875Sn_0.125 in a 2 × 2 × 2 supercell. (c) Energy-dependent total DOSs and (d) room temperature κ_L of LuNiSb and LuNiSb_0.875Sn_0.125, where the solid lines were calculated only considering the p–p scattering event and the dotted line applies for both p–p and e–p scattering events.

With aliovalent Sn doping, the increased n ensures that the e–p scattering might not be ignored anymore.^33,48 Then, e–p scattering is further considered in the calculations of LuNiSb_0.875Sn_0.125 (dotted line in Fig. 3d). For LuNiSb_0.875Sn_0.125, the scattering rate of p–p scattering being considered varies from ∼10⁻² to ∼10⁴ ps⁻¹ while the counterpart of e–p just varies from ∼10⁻⁴ to ∼10⁻² ps⁻¹ (Fig. S8†). The large difference in the scattering rate between these two processes further suggests additional e–p scattering with Sn doping is weak, which only results in a weak suppression of κ_L (Fig. S9†). Compared to other HH materials, the inapparent e–p scattering in this system may be caused by the small 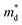and e–p coupling matrix.³²

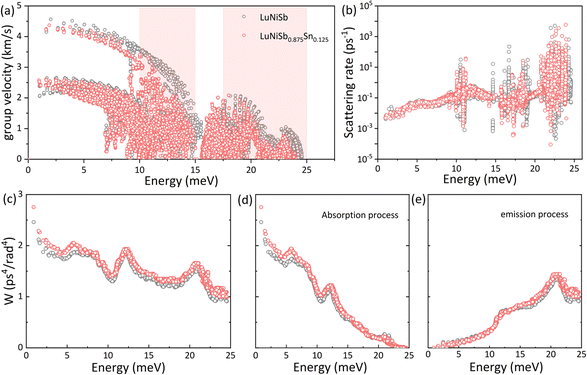
As discussed above, optical phonon softening is induced in LuNiSb with Sn doping, and this phenomenon will result in flattened optical branches at the same time. Owing to these two points, the optical phonons (v_g = dω/dk) are decelerated inevitably. When the energy-dependent group velocity for both LuNiSb and LuNiSb_0.875Sn_0.125 is presented in one figure, an obvious deceleration of the group velocity can be observed at the range of 10–15 meV and 17.5–25 meV (Fig. 4a), corresponding to the ranges where the κ_L declines significantly (Fig. 3d). Below 10 meV, the group velocity does not reduce obviously, corresponding to the negligible change of the measured sound velocities (Table S1†).

Fig. 4 Calculated group velocity (a) and scattering rate (b) versus the energy of phonon modes for LuNiSb and LuNiSb_0.875Sn_0.125. Energy dependence of p–p scattering phase space (c), the absorption process (d) and emission process (e).

The three-phonon process usually dominates the thermal transport of TE materials at elevated temperatures. The behavior of two phonons colliding and creating a new phonon beyond their primary Brillouin zone will produce thermal resistance under the law of conservation of energy and momentum: k₁ + k₂ = k₃ + G and ℏω_k1 + ℏω_k2 = ℏω_k3, where G is a reciprocal lattice vector. G = 0 refers to the normal (N) process with no direct generation of thermal resistance and G ≠ 0 refers to the Umklapp (U) process with thermal resistance. Determined by the energy conservation, new phonon k₃ can stay at the higher energy and whether the U process can occur depends on whether a phonon state exists at the corresponding energy or not. Therefore, with Sn doping in LuNiSb, phonon softening and optical branch flattening result in the rearrangement of phonon modes, which is going to change the probability of the three-phonon process. After calculating the energy-dependent p–p scattering rate of LuNiSb and LuNiSb_0.875Sn_0.125, the prominent variation of both scattering profiles is presented in Fig. 4b. What is hidden behind the variation of phonon scattering is the enhancement of phonon scattering phase space, which can be observed at almost all energy ranges (Fig. 4c). The p–p scattering is further resolved into two processes, i.e., the absorption and emission processes. The enlargement of phase scattering space occurs prominently at the range of <10 meV for the absorption process (Fig. 4d) and >15 meV for the emission process (Fig. 4e). That is, the rearrangement of phonon modes enhances the probability of the three-phonon process.

In short, with the help of first-principles calculations, it is discovered that the reduced group velocity and enhanced three-phonon process play a key role in the suppression of κ_L for Sn-doped LuNiSb_0.875Sn_0.125.

Electrical transport properties

The electrical transport properties of Sn- and Co-doped LuNiSb_1−xSn_x and LuNi_1−yCo_ySb are presented in Fig. 5. The positive S of pristine LuNiSb rises with increasing temperature and reaches the maximum at 475 K (Fig. 5a) while σ exhibits an opposite trend (Fig. 5b), which indicate that this compound is a typical p-type narrow-gap semiconductor. With the p-type dopant of Sn & Co, S shows a noticeable decrease while σ is enhanced (Fig. 5a, b, d and e), suggesting more holes are induced into the compounds. The power factor (PF = S²σ) for Sn- and Co-doped LuNiSb reaches a maximum value of about 27 × 10⁻⁴ W m⁻¹ K⁻² at 625 K (Fig. 5c) and about 22 × 10⁻⁴ W m⁻¹ K⁻² at 675 K (Fig. 5f), respectively. Compared with pristine LuNiSb (∼16 × 10⁻⁴ W m⁻¹ K⁻² at 575 K), an enhancement of PF by 68% is brought through Sn doping and 37.5% for Co doping.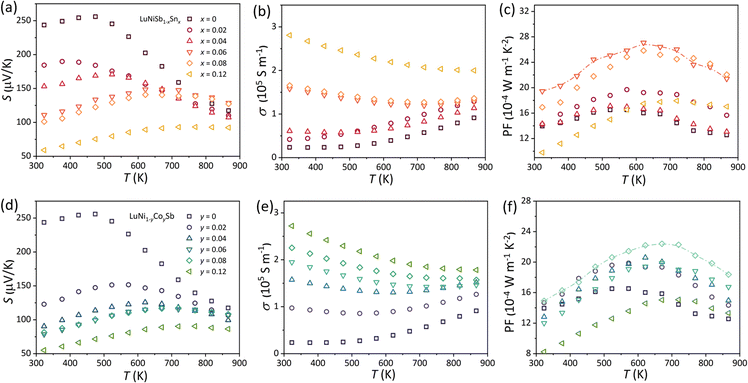

Fig. 5 Temperature-dependent (a and d) S, (b and e) σ, and (c and f) PF for LuNiSb_1−xSn_x and LuNi_1−yCo_ySb, respectively.

Hall measurements were carried out to further reveal the possible origin of the distinction in the electrical transport properties of Sn- and Co-doped LuNiSb. The μ_H of pristine LuNiSb is about 107 cm² V⁻¹ s⁻¹ at 300 K. Compared to LuNiSb_1−xSn_x, the μ_H of LuNi_1−yCo_ySb presents a larger drop (Fig. 6a), which finally results in the difference of their electrical PF (Fig. 5c and f). Generally, a lower μ_H may be caused by heavier effective mass or increased carrier scattering. The relationship between S and p_H of Sn-doped and Co-doped samples is presented in Fig. 6b, where all the experimental data match well with the Pisarenko curve calculated using the SPB model with 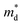of 1.2 m_e at room temperature, suggesting the electrical structure might not change obviously with doping of both Sn and Co. Considering the almost unchanged 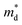, the enhanced carrier scattering becomes the most probable factor that results in the difference of electrical transport performance. From the calculated partial DOS of LuNiSb, it is discovered that compared with the Sb atom, the Ni atom contributes more to the top of the valence band (Fig. 6c and d). When Co is doped at the site of Ni, the periodic lattice field will be disturbed more seriously,⁴⁹ which might result in additional alloy scattering.

Fig. 6 (a) μ_H as a function of p_H and (b) the Pisarenko curves with 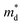≈ 1.2 m_e for LuNiSb_1−xSn_x and LuNi_1−yCo_ySb at room temperature. The projected band structure of (c) Ni and (d) Sb for LuNiSb.

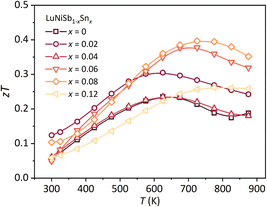
For pristine LuNiSb, the peak zT of 0.23 is obtained at 625 K (Fig. 7). Benefiting from Sn doping, an enhanced peak zT of 0.4 is obtained at 775 K for LuNiSb_0.92Sn_0.08. The enhanced zT value for LuNi_1−yCo_ySb is presented in Fig. S10.† These results suggest that the TE performance of ReNiSb can be optimized by doping with either Sn or Co, resulting from the suppression of κ_L and the optimization of PF at the same time.

Fig. 7 Temperature dependence of zT for LuNiSb_1−xSn_x.

Conclusions

In summary, rare-earth-based HH compound LuNiSb has been successfully prepared via levitation melting and high-energy mechanical alloying followed by SPS. A relatively low κ_L of ∼5.9 W m⁻¹ K⁻¹ at 300 K is obtained. Sn and Co dopants are found to simultaneously optimize the electrical performance and decrease κ_L. With first-principles calculations, it is found that the Sn doping induces the softening of optical phonons, resulting in reduced sound velocities and enhanced phonon scattering phase space, thereby suppressing κ_L effectively. Benefiting from the improved PF and reduced κ_L arising from Sn doping, a maximum zT of 0.4 is obtained at 775 K for LuNiSb_0.92Sn_0.08, a large improvement by 70% compared with that of LuNiSb. This work highlights the simultaneous optimization of the electrical and thermal transport properties of LuNiSb via aliovalent doping, which is probably also suitable for improving the thermoelectric performance of other rare-earth-based HH compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 52101275, 92163203, and 52172216). J. Yang acknowledges the support of the Key Research Project of Zhejiang Lab (No. 2021PE0AC02).

References

1. J. He and T. M. Tritt, Science, 2017, 357, eaak9997.
2. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
3. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418.
4. J. Yang, G. P. Meisner and L. Chen, Appl. Phys. Lett., 2004, 85, 1140–1142.
5. K. Xia, P. Nan, S. Tan, Y. Wang, B. Ge, W. Zhang, S. Anand, X. Zhao, G. J. Snyder and T. Zhu, Energy Environ. Sci., 2019, 12, 1568–1574.
6. M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872.
7. M. Sato, Y. W. Chai and Y. Kimura, ACS Appl. Mater. Interfaces, 2021, 13, 25503–25512.
8. A. Bahrami, P. Ying, U. Wolff, N. P. Rodríguez, G. Schierning, K. Nielsch and R. He, ACS Appl. Mater. Interfaces, 2021, 13, 38561–38568.
9. R. Bueno Villoro, M. Wood, T. Luo, H. Bishara, L. Abdellaoui, D. Zavanelli, B. Gault, G. J. Snyder, C. Scheu and S. Zhang, Acta Mater., 2023, 249, 118816.
10. X. Li, P. Yang, Y. Wang, Z. Zhang, D. Qin, W. Xue, C. Chen, Y. Huang, X. Xie, X. Wang, M. Yang, C. Wang, F. Cao, J. Sui, X. Liu and Q. Zhang, Research, 2020, 4630948.
11. X. Li, H. Yao, S. Duan, X. Bao, W. Xue, Y. Wang, F. Cao, M. Li, Z. Chen, Y. Wang, X. Lin, X. Liu, Z. Feng, J. Mao and Q. Zhang, Acta Mater., 2022, 118591.
12. J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313.
13. R. Bueno Villoro, D. Zavanelli, C. Jung, D. A. Mattlat, R. Hatami Naderloo, N. Pérez, K. Nielsch, G. J. Snyder, C. Scheu, R. He and S. Zhang, Adv. Energy Mater., 2023, 13, 2204321.
14. W. Li, B. Poudel, R. A. Kishore, A. Nozariasbmarz, N. Liu, Y. Zhang and S. Priya, Adv. Mater., 2023, 2210407.
15. Y. Liu, C. Fu, K. Xia, J. Yu, X. Zhao, H. Pan, C. Felser and T. Zhu, Adv. Mater., 2018, 30, 1800881.
16. Y. Xing, R. Liu, J. Liao, Q. Zhang, X. Xia, C. Wang, H. Huang, J. Chu, M. Gu, T. Zhu, C. Zhu, F. Xu, D. Yao, Y. Zeng, S. Bai, C. Uher and L. Chen, Energy Environ. Sci., 2019, 12, 3390–3399.
17. C. Hu, K. Xia, C. Fu, X. Zhao and T. Zhu, Energy Environ. Sci., 2022, 15, 1406–1422.
18. J. Yang, H. Li, T. Wu, W. Zhang, L. Chen and J. Yang, Adv. Funct. Mater., 2008, 18, 2880–2888.
19. J. Zhou, H. Zhu, T.-H. Liu, Q. Song, R. He, J. Mao, Z. Liu, W. Ren, B. Liao, D. J. Singh, Z. Ren and G. Chen, Nat. Commun., 2018, 9, 1721.
20. X. Yu and J. Hong, J. Mater. Chem. C, 2021, 9, 12420–12425.
21. J. Huang, R. Liu, Q. Ma, Z. Jiang, Y. Jiang, Y. Li and C. Wang, ACS Appl. Energy Mater., 2022, 5, 12630–12639.
22. K. Ciesielski, K. Synoradzki, I. Veremchuk, P. Skokowski, D. Szymański, Y. Grin and D. Kaczorowski, Phys. Rev. Appl., 2020, 14, 054046.
23. C. Fu, T. Zhu, Y. Pei, H. Xie, H. Wang, G. J. Snyder, Y. Liu, Y. Liu and X. Zhao, Adv. Energy Mater., 2014, 4, 1400600.
24. R. He, T. Zhu, Y. Wang, U. Wolff, J.-C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood, Z. Liu, L. Feng, N. P. Rodriguez, G. J. Snyder, J. C. Grossman, K. Nielsch and G. Schierning, Energy Environ. Sci., 2020, 13, 5165–5176.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
28. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
29. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
30. J. Noffsinger, F. Giustino, B. D. Malone, C.-H. Park, S. G. Louie and M. L. Cohen, Comput. Phys. Commun., 2010, 181, 2140–2148.
31. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
32. S. Dai, C. Liu, J. Ning, C. Fu, J. Xi, J. Yang and W. Zhang, Mater. Today Phys., 2023, 100993.
33. Z. Zhu, J. Xi and J. Yang, J. Mater. Chem. A, 2022, 10, 13484–13491.
34. J. Ding, C. Liu, L. Xi, J. Xi and J. Yang, J. Materiomics, 2021, 7, 310–319.
35. C. Liu, M. Yao, J. Yang, J. Xi and X. Ke, Mater. Today Phys., 2020, 15, 100277.
36. V. V. Romaka, L. Romaka, A. Horyn, P. Rogl, Y. Stadnyk, N. Melnychenko, M. Orlovskyy and V. Krayovskyy, J. Solid State Chem., 2016, 239, 145–152.
37. P. H. M. Böttger, G. S. Pomrehn, G. J. Snyder and T. G. Finstad, Phys. Status Solidi A, 2011, 208, 2753–2759.
38. J. Callaway, Phys. Rev., 1959, 113, 1046–1051.
39. J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154.
40. Y. Pei, L. Zheng, W. Li, S. Lin, Z. Chen, Y. Wang, X. Xu, H. Yu, Y. Chen and B. Ge, Adv. Electron. Mater., 2016, 2, 1600019.
41. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 2497.
42. P. G. Klemens, Phys. Rev., 1960, 119, 507–509.
43. C. L. Wan, W. Pan, Q. Xu, Y. X. Qin, J. D. Wang, Z. X. Qu and M. H. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 144109.
44. S. Han, S. Dai, J. Ma, Q. Ren, C. Hu, Z. Gao, M. Duc, D. Sheptyakov, P. Miao, S. Torii, T. Kamiyama, C. Felser, C. Fu and T. Zhu, arXiv, preprint, arXiv:2303.10899, 2023,  DOI:10.48550/arXiv.2303.10899.
45. Z. Tian, J. Garg, K. Esfarjani, T. Shiga, J. Shiomi and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184303.
46. B. Max and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, 1954.
47. Q. Ren, C. Fu, Q. Qiu, S. Dai, Z. Liu, T. Masuda, S. Asai, M. Hagihala, S. Lee, S. Torri, T. Kamiyama, L. He, X. Tong, C. Felser, D. J. Singh, T. Zhu, J. Yang and J. Ma, Nat. Commun., 2020, 11, 3142.
48. T. Zhu, G. Yu, J. Xu, H. Wu, C. Fu, X. Liu, J. He and X. Zhao, Adv. Electron. Mater., 2016, 2, 1600171.
49. H. Wang, X. Cao, Y. Takagiwa and G. J. Snyder, Mater. Horiz., 2015, 2, 323–329.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta02735j

‡ These authors contributed equally.

---