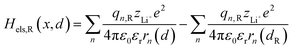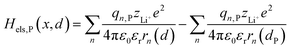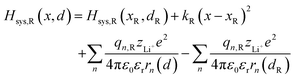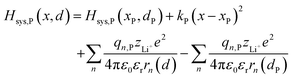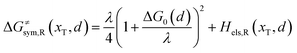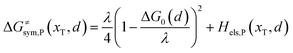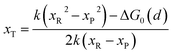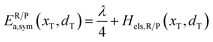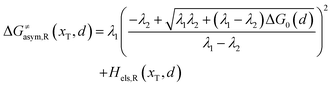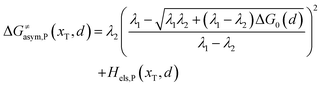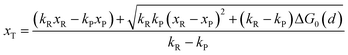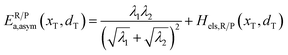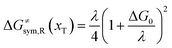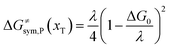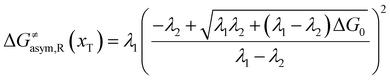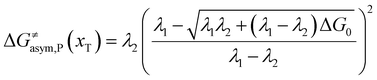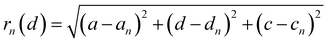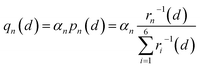DOI:
10.1039/D3SC04297A
(Edge Article)
Chem. Sci., 2023,
14, 13042-13049
The decisive role of electrostatic interactions in transport mode and phase segregation of lithium ions in LiFePO4†
Received
16th August 2023
, Accepted 24th October 2023
First published on 7th November 2023
Abstract
Understanding the mechanism of slow lithium ion (Li+) transport kinetics in LiFePO4 is not only practically important for high power density batteries but also fundamentally significant as a prototypical ion-coupled electron transfer process. Substantial evidence has shown that the slow ion transport kinetics originates from the coupled transfer between electrons and ions and the phase segregation of Li+. Combining a model Hamiltonian analysis and DFT calculations, we reveal that electrostatic interactions play a decisive role in coupled charge transfer and Li+ segregation. The obtained potential energy surfaces prove that ion–electron coupled transfer is the optimal reaction pathway due to electrostatic attractions between Li+ and e− (Fe2+), while prohibitively large energy barriers are required for separate electron tunneling or ion hopping to overcome the electrostatic energy between the Li+–e− (Fe2+) pair. The model reveals that Li+–Li+ repulsive interaction in the [010] transport channels together with Li+–e− (Fe2+)–Li+ attractive interaction along the [100] direction cause the phase segregation of Li+. It explains why the thermodynamically stable phase interface between Li-rich and Li-poor phases in LiFePO4 is perpendicular to [010] channels.
1. Introduction
Olivine LiFePO4 is one of the prevalent cathode materials in lithium-ion batteries for electric vehicle applications due to its distinctive advantages, such as low cost, high safety, and outstanding structural stability.1–3 However, LiFePO4 suffers from sluggish kinetics of charge transport, leading to poor intrinsic electronic conductivity (10−9–10−10 S cm−1) and ionic diffusivity (10−12–10−17 cm2 s−1).4–9 Substantial progress has been made over the past two decades to improve the rate performance of LiFePO4 by surface coating,10–12 ion doping,13–16 and control of grain size.17 It is worth noting that the electronic conductivity and ion diffusion rate increase simultaneously, which signifies a synergy between ion transport and electron transfer (ET).
Both experimental and computational studies have revealed the phenomenon of Li+ diffusion coupled ET in LiFePO4.18–23 Ellis et al.21 provided the first experimental clue to coupled Li+ and electron mobility based on Mössbauer spectrum measurements. The small electron polaron hopping is precisely related to Li+ disorder and vibrational (phonon) modes in the lattice. Maxisch et al.19 and Sun et al.20 clarified large binding energy and strong correlation between Li+ and e− in migration paths from first-principles calculations. Besides, Fraggedakis and Bazant24 developed a theory of ion–electron coupled transfer, revealing that ions and solvent molecules fluctuate cooperatively to facilitate non-adiabatic ET.
In our earlier research,6,25 we developed a kinetic model for Li+ transport in LiFePO4, which unravels that the ion mobility in LiFePO4 is coupled with electron transfer between Fe2+ and Fe3+. The electronic coupling effect is incorporated into the pre-exponential factor of the ionic diffusion coefficient (DLi+) by considering the electronic transmission coefficient (κel) in Landau–Zener theory,26–28 given by
| | 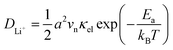 | (1) |
where
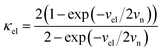
.
vn is the effective frequency of nuclear motion and
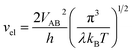
is the electron hopping frequency.
VAB is the electronic coupling matrix element, which describes the coupling strength between electron orbitals of the redox centers. This kinetic model quantitatively reveals that the very small value of
VAB in LiFePO
4 results in lower ionic diffusivity. Li
+ hopping is in conjunction with a nonadiabatic electron transfer. In the meantime, we employed a neural network-based deep potential (DP) to calculate hopping barriers of Li
+ with various Li–Li coordination environments.
4 The results show that the gradient distributions of Li
+ cause great asymmetry in the barriers of forward and backward ion hopping. It results in a very slow Li
+ diffusion rate and a diverse variation of
DLi+ based on the Kinetic Monte-Carlo (KMC) simulation.
Despite the abovementioned progress, a better understanding of the influence of electronic coupling on ion transport is needed. Specifically, the way electron transfer affects ion transport and its impact on the ion hopping barrier (Ea) remain unclear. Herein, we aim to develop a theoretical framework for exploring the mechanism of ion transport in the LiFePO4 lattice and further unveiling the effect of electronic coupling on the activation barrier. Properly considering the relaxation of the lattice structure and the electrostatic interaction between Li+ and e− (Fe2+), a model Hamiltonian is constructed for this purpose. Potential energy surfaces show that ion–electron coupled transfer is the optimal path with the lowest energy barrier. Additionally, the model is further employed to interpret the phase segregation behavior of LiFePO4 at equilibrium in terms of electrostatic interaction.
2. Theory development
2.1 Model specifications and Hamiltonians
Li+ transport in LiFePO4 corresponds to an ion-vacancy exchange process accompanied by an electron–hole exchange procedure, which is described as a self-exchange reaction.6,29–32| | | Li+iFe2+PO4(m) + Vi±1Fe3+PO4(m) → ViFe3+PO4(n) + Li+i±1Fe2+PO4(n) | (2) |
Li+i represents Li+ at the site i, and Vi±1 is a vacancy located at site i ± 1. Li+ can hop between the nearest-neighbor lattice sites (Fig. 1). m and n represent the lattice environment of Li+–e− (Fe2+)/V–hole (Fe3+) pairs, which is determined using the concentration and site of Li+ in LiFePO4. In the case of the same lattice environment before and after Li+ hopping, one has m = n, which is defined as the symmetric ion hopping process in LiFePO4. Otherwise, the process is referred to as the asymmetric ion hopping process.
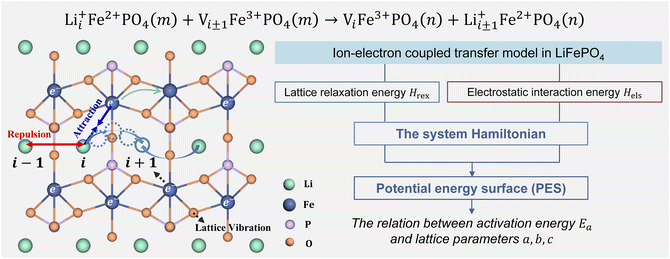 |
| | Fig. 1 Schematic illustration of ion hopping and electron transfer in LiFePO4 and the model framework. | |
Computational and experimental studies33–35 demonstrated that LiFePO4 has an olivine structure belonging to the space group Pnma, in which Li+ migrates along the b-axis ([010]) direction. Phosphorus ions occupy tetrahedral sites, and Li ions are located in chains of edge-sharing octahedral sites, which are adjacent to FeO6 octahedra. In the transition state, Li ions occupy tetrahedral sites. As shown in Fig. 1, the ion transport process includes Li+ hopping between different octahedral sites, electron transfer from Fe2+ to Fe3+, and the relaxation of the lattice framework, i.e. the vibration of P–O and Fe–O bonds. These processes induce changes in lattice relaxation energy and electrostatic interaction energy between ions and electrons, which are major origins of activation barriers for ion transport.
The ion transport process can be described by the coordinate of Li+, d, which is the b-axis lattice parameter, and the overall harmonic polarization reaction coordinate, x. Then, we construct model Hamiltonians of reactant and product systems as24
| | | Hsys,R(x,d) = Hsys,R(xR,dR) + Hrex,R(x) + Hels,R(x,d) | (3a) |
| | | Hsys,P(x,d) = Hsys,P(xP,dP) + Hrex,P(x) + Hels,P(x,d) | (3b) |
where
Hsys,R/P(
xR/P,
dR/P) is the equilibrium energy of the reactant/product system, corresponding to the state where both ions and electrons are located in the stable configuration of reactant R/product P. The change in volume and configuration entropy of LiFePO
4 is negligibly small throughout the ion transport process,
36,37 so the volumetric and entropic effects are not considered. The functions
Hrex and
Hels describe the change of the lattice relaxation energy and the electrostatic interaction energy, respectively.
2.1.1 Lattice relaxation energy term Hrex.
The change in P–O and Fe–O bond lengths triggered by electron transfer can be approximated as a simple harmonic vibration, so the lattice relaxation energy of reactant and product systems is represented by parabolic curves in terms of the polarization coordinate x in the near equilibrium region,| | | Hrex,R(x) = kR(x − xR)2 | (4a) |
| | | Hrex,P(x) = kP(x − xP)2 | (4b) |
where kR and kP are fixed force constants for reactants and products, respectively. The force constants relate directly to the configuration reorganization energies (λ) for the vibration of all bonds during ion transport and electron transfer.
2.1.2 Electrostatic interaction energy term Hels.
Based on coulomb forces or charge–charge interactions,38 the change of Li+–e− (Fe2+) electrostatic interaction energy reads| | 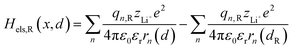 | (5a) |
| | 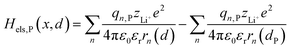 | (5b) |
where zLi+ is the charge of Li+ and qn represents the partial charges of an electron at different sites. ε0 and εr are the permittivity of vacuum and the dielectric medium. The channels of Li+ migration in LiFePO4 are similar to vacuum, thus εr = 1. r(d) is the distance between Li+ and e− (Fe2+). The lattice structure of FePO4 is regarded as an electrically neutral background. The first term on the right hand side (rhs) describes the electrostatic interaction energy of a Li+ at any position and an electron located in the stable configuration of reactant R/product P. The second term on the rhs refers to the electrostatic interaction energy of both a Li+ and an electron located in the stable configuration of reactant R/product P.
2.2 Model solution for the energy surface
Substituting eqn (4) and (5) into (3), the model Hamiltonians read,| | 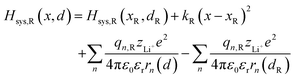 | (6a) |
| | 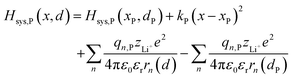 | (6b) |
The energy diagram can be represented by a two-dimensional surface, which is called the potential energy surface (PES).
2.2.1 Iso-energetic curve and activation energy.
Combining eqn (6a) and (6b), we can obtain the iso-energetic curve of reactants and products. It can also be defined as an activation energy curve. The details are discussed in Section 3. For the symmetric ion hopping in LiFePO4, the force constants kR = kP = k. The iso-energetic curve is expressed as| | 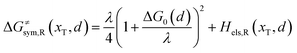 | (7a) |
| | 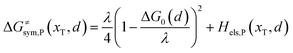 | (7b) |
with| | 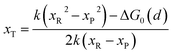 | (8) |
where ΔG0(d) is written as| | | ΔG0(d) = Hsys,P(xP,dP) − Hsys,R(xR,dR) + Hels,P(xP,d) − Hels,R(xR,d) | (9) |
In the transition state of the optimal reaction path, the ΔG≠sym,R/P(xT,d) arrives at one of the extrema, which is the minimum of the iso-energetic curve, that is, dΔG≠sym,R/P/dd = 0. Here, the value of ion coordinate d is expressed as dT. The minimum activation energy in the forward and backward directions reads
| | | ER/Pa,sym(xT,dT) = ΔG≠sym,R/P(xT,dT) | (10) |
which is the energy barrier of the optimal reaction path.
The structure of LiFePO4 is the same before and after the symmetric ion hopping process, meaning ΔG0(dT) = 0. Then, eqn (10) reduces to
| | 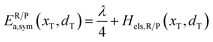 | (11) |
with
dT=(
dR +
dP)/2.
Similarly, for the asymmetric ion hopping process (kP ≠ kR), the iso-energetic curve is written as
| | 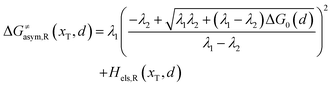 | (12a) |
| | 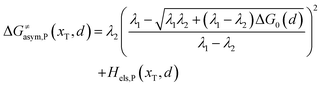 | (12b) |
with
| | 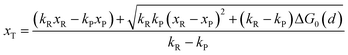 | (13) |
The activation energies of the optimal reaction path read
| | | ERa,asym(xT,dT) = ΔG≠asym,R(xT,dT) | (14a) |
| | | EPa,asym(xT,dT) = ΔG≠asym,P(xT,dT) | (14b) |
with
dT satisfying dΔ
G≠sym,R/P/d
d = 0.
If ΔG0(dT) = 0, eqn (12) reduces to
| | 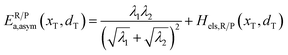 | (15) |
2.3 Comparison with classical charge transfer theories
The model Hamiltonian describes ion transport coupled non-adiabatic electron transfer. It returns to the classical charge transfer theories by ignoring ion effects, as shown in Fig. 2. For the symmetric electron transfer (kR = kP = k), eqn (7) is rewritten as| | 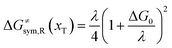 | (16a) |
| | 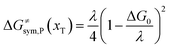 | (16b) |
with ΔG0 is a constant, ΔG0 = Hsys,P(xP,dP) − Hsys,R(xR,dR). Eqn (16) is the activation energy of non-adiabatic electron transfer in the classical Marcus theory,39–43 which was originally developed for homogeneous ET kinetics in solutions. It assumes a very weak electron coupling between active species.44 By contrast, the ET process proceeds in the adiabatic mode when electron coupling is sufficiently strong. It is described by introducing an electron transmission coefficient into the standard rate constant.6,41 Adiabatic ET had also been studied by Schmickler45 for electrocatalysis by combining the Anderson–Newns model46 and Marcus theory. Schmickler developed a theoretical model constituting an important straddle from weakly coupling systems, studied using the Levich–Dogonadze–Kuznetsov theory47 and the Marcus theory, to strongly coupling systems which electrocatalytic reactions belong to.48
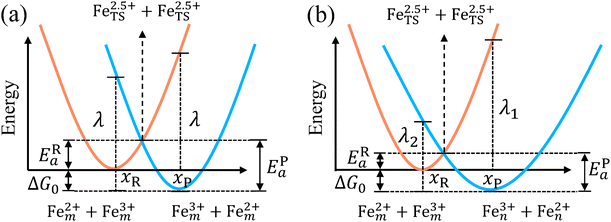 |
| | Fig. 2 Potential energy curves of reactant and product systems for (a) the symmetric and (b) the asymmetric electron transfer. | |
In the same way, for the asymmetric electron transfer (kR ≠ kP), eqn (12) reads
| | 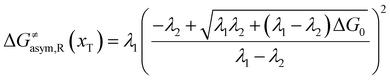 | (17a) |
| | 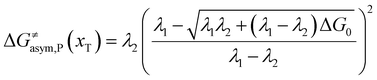 | (17b) |
The applicability of eqn (17) is not limited by the degree of difference between kR and kP. It is different from the activation energy of the asymmetric Marcus–Hush (AMH) model adopted by Compton et al. in their investigation of electrode processes.44,49–51 The AMH model takes into account the difference between inner-shell force constants of oxidized and reduced species by introducing an asymmetry parameter into the symmetric Marcus–Hush model. The accuracy is found to decrease as the difference between the force constants increases due to the first-order truncation of the approximating series from which it was derived.41,49,52
2.4 Model parameters
Model parameters are listed in Table S1.† To describe the potential energy surfaces, several parameters related to the lattice environment are detailed here. The force constants for reactants and products are calculated using reorganization energies, kR/P = λ1/2/(xP − xR)2. For the self-exchange reaction, eqn (2), the reorganization term is the sum of reorganization energy of individual reactants,31,32| | | λ1/2 = λFe2+→Fe3+ + λFe3+→Fe2+ | (18) |
where λFe2+→Fe3+ = EFePO4+Li − ELiFePO4 is the energy required to alter Fe–O bond length in LiFePO4 under equilibrium, x02, to the distance, x03, in the equilibrium state of FePO4. λFe3+→Fe2+ = ELiFePO4–Li − EFePO4 is the energy required to change the Fe–O bond length in FePO4 from x03 to x02. Here, EFePO4+Li is the energy of LiFePO4 in the FePO4 configuration and ELiFePO4 is the energy of stable LiFePO4 from the DFT calculations. Similarly, ELiFePO4–Li and EFePO4 are the energies of FePO4 in the LiFePO4 configuration and stable FePO4, respectively. More details are shown in Fig. S1† and can be found in the original papers.6
The distance of Li+ and e− (Fe2+), rn(d), is calculated using
| | 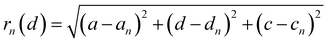 | (19) |
where (
a,
d,
c) and (
an,
dn,
cn) are the three-dimensional coordinates of Li
+ and e
− (Fe
2+). The trajectory of Li
+ is fitted with the Fourier series, as shown in Fig. S2.
†
It is essential to describe the distribution of an electron. Previous theoretical work19,53 and numerous experimental studies21,54 proved that charge carriers form small polarons in LiFePO4. The initial/final states of Li+ transport contain a Li+–e− pair with the electron located at a Fe site adjacent to the Li+. There are six adjacent Fe sites centered on the Li+ (Fig. 3). The Li+–e− pair corresponds to an assembly of a variety of microscopic states with the electron appearing at one of the six Fe sites.55 The probabilities of each microscopic state are different owing to the variable Li+–e− (Fe2+) distance during the Li+ transport. Steady-state DFT calculations only capture one of these microscopic states.55–58 For instance, the electron is localized on the Fe1 or Fe4 site for Lia and Fe4 or Fe7 site for Lib due to the minimum Li+–e− (Fe2+) distance, dFe1–Lia = dFe4–Lia = dFe4–Lib = dFe7–Lib = 3.317 Å (Fig. 3a). Nevertheless, when the electron is localized on the Fe4 site, it may not transfer during Li+ hopping from site a to site b. This disobeys the coupled ion–electron transfer mechanism. Over the dynamic course, the localized electron can transfer from one Fe atom to another in a period of time that is much shorter than that of Li+ transport. Macroscopically, Li+ is subjected to an average electrostatic effect from different Fe sites.
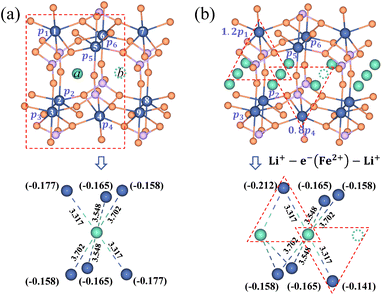 |
| | Fig. 3 Partial charges of an electron for (a) the isolated state and (b) the aggregated state of Li+ in the LiFePO4 structure. The dimension unit of Li+–e− (Fe2+) distance is Å. | |
Therefore, we approximately assign an electron localized on six Fe sites during Li+ hopping (Fig. 3). The charge distribution of electrons is assumed to follow two principles based on the short-range electrostatic interaction between Li+ and e− (Fe2+). Firstly, it can be inferred that the probability of an electron localized at a Fe site is inversely proportional to the distance of Li+ and e− (Fe2+). Secondly, electrons are more likely to be in the middle site of the two adjacent Li+. Consequently, the partial charge function of an electron, qn, is constructed as
| | 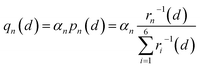 | (20) |
where
pn(
d) is the distribution probability of an electron being localized at one of six Fe sites closest to Li
+, which depends on the value of
rn(
d).
αn is the partition coefficient of electrons related to the aggregation state of Li
+. If there is an isolated Li
+,
αn = 1 for all Fe sites, as shown in
Fig. 3a. Two Fe sites in LiFePO
4 display point symmetry around the middle Li
+, thus partial charges at these two Fe sites are equal. When two sides of Li
+ are flanked by a Li
+ and a vacancy, the values of
αn take 1.2 and 0.8 for the Fe site located in the middle of two adjacent Li
+ and the middle of a Li
+ and a vacancy, respectively (
Fig. 3b). There is the structure of Li
+–e
− (Fe
2+)–Li
+.
3. Results and discussion
3.1 Symmetric ion hopping process
Ion transport in pure LixFePO4 and Li1−xFePO4 (x ≈ 0) are two typical examples. Li+ is isolated in FePO4, while there is the structure of Li+–e− (Fe2+)–Li+ in LiFePO4. We take the reactant system as the reference, namely, Hsys,R(xR,dR) = 0. DFT-calculated parameters are λFePO14 = λFePO24 = 1.167 eV and λLiFePO14 = λLiFePO24 = 1.380 eV. Two symmetric ion hopping processes are depicted in Fig. 4 and S3.†
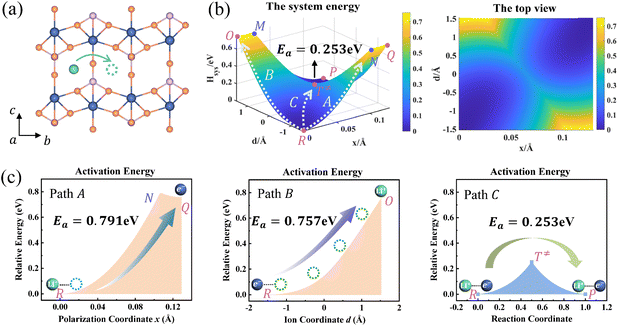 |
| | Fig. 4 (a) Structure diagram of Li+ hopping along the b-axis in FePO4. (b) Potential energy surface based on the Hamiltonian model (left) and its top view (right) for ion hopping and electron transfer. (c) Potential energy curves of paths A, B, and C. | |
The potential energy surface as a function of x and d is informative, as shown in Fig. 4b. The potential energy surface consists of two 2D parabolas corresponding to the energy of the reactant system and product system, respectively. The two lowest points are the equilibrium state R(xR,dR) and P(xP,dP). The intersection of two parabolic surfaces, M − T≠ − N, is the iso-energy curve described by eqn (7). In principle, electrons can tunnel from the reactant state to the product state for any value of ion coordinates d along the iso-energy curve. For example, in the case where d = dR there is a probability for electron transfer without ion hopping (Path A). The final state Q(xP,dR) is the configuration of the electron tunneled to the product state and Li+ located at the reactant state (Fig. S4†). The energy barrier is 0.791 eV, which is prohibitively large due to the short-range electrostatic interactions of the Li+ and e− (Fe2+) (Fig. 4c).
In contrast, there is also a chance for ion hopping without electron transfer (Path B), which must overcome the energy barrier of 0.757 eV. The final state O(xR,dP) represents that Li+ is located in the product state while the electron is still localized at the reactant state. The energies of states O(xR,dP) and Q(xP,dR) are both 0.757 eV higher than that of the initial state R(xR,dR). It is the electrostatic energy required to eliminate an ion–electron pair.
Reactant species fluctuate on the 2D energy surface during ion hopping and electron transfer. The fluctuating trajectory most likely follows the lowest energy path C. The transition state T≠(xT,dT) is the lowest point of the iso-energy curve. Along this optimal reaction pathway, ion hopping is coupled with electron transfer. As shown in Fig. S5,† partial charges are located at six Fe sites around Li+ in the initial state. The values of partial charges vary with the distance between Li+ and e− (Fe2+). Once Li+ arrives at the tetrahedral site and the lattice structure relaxes to the iso-energetic state of reactants and products, electron transfer will occur. Then Li+ hops to the final state with the redistribution of partial charges.
As shown in Fig. 4b and S3b,† the minimum activation energy of ion–electron coupled transfer is 0.253 eV and 0.336 eV for FePO4 and LiFePO4, respectively. The values are much lower than those of separate electron transfer (0.791 eV and 0.827 eV) or ion transport (0.757 eV and 0.816 eV). According to eqn (11), we calculate the value of Hels(xT,dT) in the transition state, which is the difference in the electrostatic interaction energy between the transition state and the initial state. The results are −0.0392 eV in FePO4 and −0.009 eV in LiFePO4. These negative values originate from a closer distance of Li+ and e− (Fe2+), rn(d), and the higher charges, qn, located in the nearest Fe site in the transition state than that in the initial state. Compared with the higher energy barriers of paths A and B, these results clearly illustrate that ion–electron coupled transfer is driven by the electrostatic attraction of Li+ and e− (Fe2+).
DFT calculated barriers correspond to the coupled ion–electron transfer process. The values serve as a reference for the model, while the model with an analytical nature can help understand the components of the DFT-calculated barriers. Different contributions, such as the configuration reorganization and the electrostatic interaction, can be separated and compared. The results in this model are in good agreement with those of NEB calculations (Fig. S6†), which are also close to literature values (0.24–0.27 eV for FePO4 and 0.32–0.39 eV for LiFePO4).6,59–61
3.2 Asymmetric ion hopping process
The charge transport in Li0.125FePO4 of a 3a × 2b × 1c supercell is depicted in Fig. 5. In the initial state, Li+ accumulate in the b-axis ([010]) transport channel, while the hopping Li+ is adjacent to another Li+ along the a-axis ([100]) at the final state. The partial charges at the initial and final states are shown in Table S4.† The reorganization energy λ is different for the two structures with λinitial = λ1 = 1.571 eV and λfinal = λ2 = 1.647 eV.
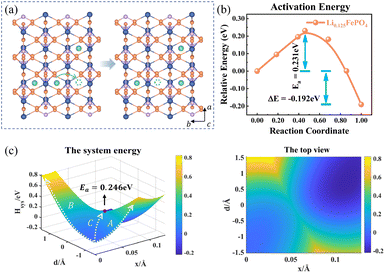 |
| | Fig. 5 (a) Structure diagram of the initial and final states of Li+ hopping. (b) The activation energy calculated using the NEB for asymmetric ion hopping in Li0.125FePO4, and (c) potential energy surface based on the Hamiltonian model (left) and its top view (right) for ion transport and electron transfer. | |
Fig. 5c displays the asymmetric potential energy surface of ion–electron coupled transfer. The activation energy of the optimal reaction path C is 0.246 eV, which is reasonably close to the 0.231 eV calculated using the NEB method (Fig. 5b). The value is much lower than those of path A (0.646 eV) and path B (0.817 eV) for separate electron transfer and ion hopping, as shown in Fig. S7.† The energy of the final state is about 0.192 eV less than that of the initial state, which indicates that the structure is more stable when Li+ amass in the [100] direction (a-axis) rather than the [010] direction (b-axis). This is mainly caused by the difference in electrostatic interactions in two directions, which is discussed in the next section.
3.3 The origin of ion aggregation in LiFePO4
In the [010] direction, the distance between two adjacent Li+ is 3.045 Å, which is smaller than all three kinds of distances between the Li+ and e− (Fe2+), 3.317 Å, 3.548 Å, and 3.702 Å (Fig. 6a). However, the distance between adjacent Li+ is 4.746 Å in the [100] direction, larger than the two kinds of distances between Li+ and e− (Fe2+), 3.548 Å and 3.702 Å (Fig. 6b). The complex electrostatic interactions include the electrostatic repulsion of the Li+–Li+ couple and the electrostatic attraction of the Li+–e− (Fe2+) pair. Based on the partial charge function, eqn (20), the electrostatic interaction energy between the two adjacent Li+ is calculated. In the [010] direction, the electrostatic interaction energy is 1.237 eV. The positive value indicates that the two Li+ are repulsive. In contrast, the two Li+ exhibit attractive interactions under the attraction of e− (Fe2+) when they collect in the [100] direction with the electrostatic interaction energy being −0.029 eV.
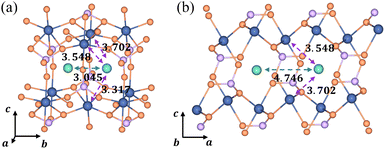 |
| | Fig. 6 Structural diagrams of Li+ aggregation (a) in the [010] direction and (b) in the [100] direction; purple and green arrows represent electrostatic attraction and repulsion, respectively. The dimension unit is Å. | |
The structure of Li+–e− (Fe2+)–Li+ is attractive in the [100] direction, which induces phase separation into Li-rich and Li-poor phases in LixFePO4, as reported in previous studies.62,63 Besides, the results also demonstrate that Li+ are more likely to amass in the [100] direction. It means that the phase interface of Li-rich and Li-poor phases is perpendicular to the [010] axis, which is consistent with observations of HRTEM images.64 In the meantime, it should be pointed out that the distance of layer to layer in the c-axis ([001]) is greater than 5 Å, which results in negligibly small interlayer interactions between Li ions.4 Therefore, the structure along the c-axis is not considered.
4. Conclusions
In summary, a simple model Hamiltonian has been developed to explore the mechanisms of ion transport and non-adiabatic electron transfer in LiFePO4. The model provides two analytical activation barriers as a function of lattice parameters for both symmetric and asymmetric ion hopping, respectively. The symmetric activation barrier is reduced to that of classical Marcus charge transfer theories by ignoring ion effects. Importantly, the model reveals that ion–electron coupled transfer is the optimal reaction path driven by the electrostatic attraction between Li+ and e− (Fe2+). Separate ion transport or electron transfer rarely occurs due to the extremely large energy barrier, which originates from the electrostatic interaction energy required to eliminate an ion–electron pair. In addition, the model shows that Li+–Li+ repulsive interaction in the [010] direction and Li+–e− (Fe2+)–Li+ attractive interaction in the [100] direction cause the phase segregation of LiFePO4. The results verify that the interface of Li-rich and Li-poor phases is perpendicular to the [010] channel. This work provides a new perspective on designing high-rate performance electrode materials. One can adjust the electrostatic interaction to improve the ionic and electronic conductivity by doping, coating, and other techniques.
Data availability
The data that support the findings of this study are available on request from the corresponding author.
Author contributions
S. L. C. conceived the project. X. X. W., J. H. and S. L. C. derived the model equations. X. X. W. performed the DFT calculations. Y. W. L. discussed the derivation and results. X. X. W., J. H. and S. L. C. wrote the paper. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (22272122, 21673163, and 21832004). J. H. is supported by the Initiative and Networking Fund of the Helmholtz Association under the award number VH-NG-1709. We gratefully thank the Supercomputing Center of Wuhan University and Wuhan Supercomputing Center for generous computing resources to support our research.
Notes and references
- J. B. Goodenough, Acc. Chem. Res., 2013, 46, 1053–1061 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- B. Kang and G. Ceder, Nature, 2009, 458, 190–193 CrossRef CAS PubMed.
- Y. C. Hu, X. X. Wang, P. Li, J. X. Chen and S. L. Chen, Sci. China: Chem., 2023, 1–10 Search PubMed.
- Z. Ma, Z. J. Zuo, L. Li and Y. N. Li, Adv. Funct. Mater., 2022, 32, 2108692 CrossRef CAS.
- Y. Gao, J. Huang, Y. W. Liu and S. L. Chen, Chem. Sci., 2022, 13, 257–262 RSC.
- K. Tang, X. Q. Yu, J. P. Sun, H. Li and X. J. Huang, Electrochim. Acta, 2011, 56, 4869–4875 CrossRef CAS.
- J. Xie, N. Imanishi, T. Zhang, A. Hirano, Y. Takeda and O. Yamamoto, J. Power Sources, 2009, 192, 689–692 CrossRef CAS.
- P. P. Prosini, M. Lisi, D. Zane and M. Pasquali, Solid State Ionics, 2002, 148, 45–51 CrossRef CAS.
- H. W. Zhang, J. Y. Li, L. Q. Luo, J. Zhao, J. Y. He, X. X. Zhao, H. Liu, Y. B. Qin, F. Y. Wang and J. J. Song, J. Alloys Compd., 2021, 876, 160210 CrossRef CAS.
- S. Heng, Q. Shi, X. Y. Zheng, Y. Wang, Q. T. Qu, G. Liu, V. S. Battaglia and H. H. Zheng, Electrochim. Acta, 2017, 258, 1244–1253 CrossRef CAS.
- Y. P. Xu and J. Mao, J. Mater. Sci., 2016, 51, 10026–10034 CrossRef CAS.
- H. Choi, J. Y. Seo and C. S. Kim, IEEE Trans. Magn., 2020, 57, 1–5 Search PubMed.
- O. M. Karakulina, N. R. Khasanova, O. A. Drozhzhin, A. A. Tsirlin, J. Hadermann, E. V. Antipov and A. M. Abakumov, Chem. Mater., 2016, 28, 7578–7581 CrossRef CAS.
- H. Q. Wang, A. J. Lai, D. Q. Huang, Y. Q. Chu, S. J. Hu, Q. C. Pan, Z. H. Liu, F. H. Zheng, Y. G. Huang and Q. Y. Li, New J. Chem., 2021, 45, 5695–5703 RSC.
- H. C. Liu, Y. M. Wang and C. C. Hsieh, Ceram. Int., 2017, 43, 3196–3201 CrossRef CAS.
- M. A. Alsamet and E. Burgaz, Electrochim. Acta, 2021, 367, 137530 CrossRef CAS.
- L. Hong, L. S. Li, Y.-K. Chen-Wiegart, J. J. Wang, K. Xiang, L. Y. Gan, W. J. Li, F. Meng, F. Wang and J. Wang, Nat. Commun., 2017, 8, 1194 CrossRef PubMed.
- T. Maxisch, F. Zhou and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- Y. Sun, X. Lu, R. J. Xiao, H. Li and X. J. Huang, Chem. Mater., 2012, 24, 4693–4703 CrossRef CAS.
- B. Ellis, L. K. Perry, D. H. Ryan and L. F. Nazar, J. Am. Chem. Soc., 2006, 128, 11416–11422 CrossRef CAS PubMed.
- R. Malik, A. Abdellahi and G. Ceder, J. Electrochem. Soc., 2013, 160, A3179 CrossRef CAS.
- G. H. Tao, J. Phys. Chem. C, 2016, 120, 6938–6952 CrossRef CAS.
- D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. R. Zhang, P. Bai, W. C. Chueh, Y. Shao-Horn and M. Z. Bazant, Electrochim. Acta, 2021, 367, 137432 CrossRef CAS.
- X. X. Wang, J. Huang and S. L. Chen, Curr. Opin. Electrochem., 2023, 101358 CrossRef CAS.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- B. S. Brunschwig, J. Logan, M. D. Newton and N. Sutin, J. Am. Chem. Soc., 1980, 102, 5798–5809 CrossRef CAS.
- J. Franck and E. Dymond, Trans. Faraday Soc., 1926, 21, 536–542 RSC.
- Z. M. Zhang, Y. Gao, S. L. Chen and J. Huang, J. Electrochem. Soc., 2019, 167, 013519 CrossRef.
- Y. Gao, J. Huang, Y. W. Liu, J. W. Yan, B. W. Mao and S. L. Chen, Sci. China: Chem., 2019, 62, 515–520 CrossRef CAS.
- S. Ghosh, A. V. Soudackov and S. Hammes-Schiffer, J. Chem. Theory Comput., 2016, 12, 2917–2925 CrossRef CAS PubMed.
- B. S. Brunschwig and N. Sutin, Coord. Chem. Rev., 1999, 187, 233–254 CrossRef CAS.
- Q. F. Zhao, S. Q. Zhang, M. Y. Hu, C. Wang and G. H. Jiang, Int. J. Electrochem. Sci., 2021, 16, 1–10 Search PubMed.
- C. L. Gong, Z. G. Xue, S. Wen, Y. S. Ye and X. L. Xie, J. Power Sources, 2016, 318, 93–112 CrossRef CAS.
- S. E. Boulfelfel, G. Seifert and S. Leoni, J. Mater. Chem., 2011, 21, 16365–16372 RSC.
- E. R. Logan and J. R. Dahn, J. Electrochem. Soc., 2021, 168, 120526 CrossRef CAS.
- K. Jalkanen, T. Aho and K. Vuorilehto, J. Power Sources, 2013, 243, 354–360 CrossRef CAS.
-
J. N. Israelachvili, in Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, San Diego, 3rd edn, 2011, pp. 53–70, DOI:10.1016/B978-0-12-375182-9.10003-X.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- S. L. Chen, Y. W. Liu and J. X. Chen, Chem. Soc. Rev., 2014, 43, 5372–5386 RSC.
- E. Laborda, M. C. Henstridge, C. Batchelor-McAuley and R. G. Compton, Chem. Soc. Rev., 2013, 42, 4894–4905 RSC.
- W. Schmickler, J. Electroanal. Chem. Interfacial Electrochem., 1986, 204, 31–43 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1961, 124, 41 CrossRef CAS.
- R. R. Dogonadze, A. M. Kuznetsov and T. A. Marsagishvili, Electrochim. Acta, 1980, 25, 1–28 CrossRef CAS.
- J. Huang, J. Chem. Phys., 2020, 153, 164707 CrossRef CAS PubMed.
- E. Laborda, M. C. Henstridge and R. G. Compton, J. Electroanal. Chem., 2012, 667, 48–53 CrossRef CAS.
- M. C. Henstridge, E. Laborda, Y. Wang, D. Suwatchara, N. Rees, Á. Molina, F. Martinez-Ortiz and R. G. Compton, J. Electroanal. Chem., 2012, 672, 45–52 CrossRef CAS.
- M. C. Henstridge, E. Laborda and R. G. Compton, J. Electroanal. Chem., 2012, 674, 90–96 CrossRef CAS.
- Y. Zeng, P. Bai, R. B. Smith and M. Z. Bazant, J. Electroanal. Chem., 2015, 748, 52–57 CrossRef CAS.
- S. P. Ong, V. L. Chevrier and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075112 CrossRef.
- K. Zaghib, A. Mauger, J. B. Goodenough, F. Gendron and C. M. Julien, Chem. Mater., 2007, 19, 3740–3747 CrossRef CAS.
- C. Cholsuk, S. Suwanna and K. Tivakornsasithorn, Mater. Today Commun., 2021, 26, 102043 CrossRef CAS.
- Y. Gu, M. Y. Weng, G. F. Teng, H. Zeng, J. S. Jie, W. J. Xiao, J. X. Zheng and F. Pan, Phys. Chem. Chem. Phys., 2019, 21, 4578–4583 RSC.
- V. A. Dinh, J. Nara and T. Ohno, Appl. Phys. Express, 2012, 5, 045801 CrossRef.
- T. W. Chen, Y. K. Ye, Y. Wang, C. Fang, W. C. Lin, Y. Jiang, B. Xu, C. Y. Ouyang and J. Zheng, Phys. Chem. Chem. Phys., 2023, 25, 8734–8742 RSC.
- G. G. Xu, K. H. Zhong, J. M. Zhang and Z. G. Huang, J. Appl. Phys., 2014, 116, 063703 CrossRef.
- H. Lin, Y. W. Wen, C. X. Zhang, L. L. Zhang, Y. H. Huang, B. Shan and R. Chen, Solid State Commun., 2012, 152, 999–1003 CrossRef CAS.
- Z. J. Liu and X. J. Huang, Solid State Ionics, 2010, 181, 907–913 CrossRef CAS.
- P. H. Xiao and G. Henkelman, ACS Nano, 2018, 12, 844–851 CrossRef CAS PubMed.
- F. Zhou, T. Maxisch and G. Ceder, Phys. Rev. Lett., 2006, 97, 155704 CrossRef PubMed.
- Y. J. Zhu, J. W. Wang, Y. Liu, X. H. Liu, A. Kushima, Y. H. Liu, Y. H. Xu, S. X. Mao, J. Li, C. S. Wang and J. Y. Huang, Adv. Mater., 2013, 25, 5461–5466 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *bc,
Yuwen
Liu
a and
Shengli
Chen
*bc,
Yuwen
Liu
a and
Shengli
Chen
 *a
*a
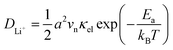
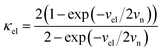 . vn is the effective frequency of nuclear motion and
. vn is the effective frequency of nuclear motion and 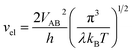 is the electron hopping frequency. VAB is the electronic coupling matrix element, which describes the coupling strength between electron orbitals of the redox centers. This kinetic model quantitatively reveals that the very small value of VAB in LiFePO4 results in lower ionic diffusivity. Li+ hopping is in conjunction with a nonadiabatic electron transfer. In the meantime, we employed a neural network-based deep potential (DP) to calculate hopping barriers of Li+ with various Li–Li coordination environments.4 The results show that the gradient distributions of Li+ cause great asymmetry in the barriers of forward and backward ion hopping. It results in a very slow Li+ diffusion rate and a diverse variation of DLi+ based on the Kinetic Monte-Carlo (KMC) simulation.
is the electron hopping frequency. VAB is the electronic coupling matrix element, which describes the coupling strength between electron orbitals of the redox centers. This kinetic model quantitatively reveals that the very small value of VAB in LiFePO4 results in lower ionic diffusivity. Li+ hopping is in conjunction with a nonadiabatic electron transfer. In the meantime, we employed a neural network-based deep potential (DP) to calculate hopping barriers of Li+ with various Li–Li coordination environments.4 The results show that the gradient distributions of Li+ cause great asymmetry in the barriers of forward and backward ion hopping. It results in a very slow Li+ diffusion rate and a diverse variation of DLi+ based on the Kinetic Monte-Carlo (KMC) simulation.