Open Access Article
Open Access ArticleTidying up the conformational ensemble of a disordered peptide by computational prediction of spectroscopic fingerprints†
Monika
Michaelis
 ab,
Lorenzo
Cupellini
ab,
Lorenzo
Cupellini
 *c,
Carl
Mensch
d,
Carole C.
Perry
*c,
Carl
Mensch
d,
Carole C.
Perry
 b,
Massimo
Delle Piane
b,
Massimo
Delle Piane
 *ae and
Lucio
Colombi Ciacchi
a
*ae and
Lucio
Colombi Ciacchi
a
aHybrid Materials Interfaces Group, Faculty of Production Engineering, Bremen Center for Computational Materials Science, Center for Environmental Research and Sustainable Technology (UFT), and MAPEX Center for Materials and Processes, University of Bremen, Am Fallturm 1, Bremen 28359, Germany. E-mail: massimo.dellepiane@polito.it
bBiomolecular and Materials Interface Research Group, Interdisciplinary Biomedical Research Centre, School of Science and Technology, Nottingham Trent University, Clifton Lane, Nottingham NG11 8NS, UK
cDipartimento di Chimica e Chimica Industriale, University of Pisa, Via G. Moruzzi 13, Pisa I-56124, Italy. E-mail: lorenzo.cupellini@unipi.it
dMolecular Spectroscopy Research Group, Department of Chemistry, University of Antwerp, Groenenborgerlaan 171, Antwerp 2020, Belgium
eDepartment of Applied Science and Technology, Politecnico di Torino, Corso Duca degli Abruzzi 24, Torino 10129, Italy
First published on 19th July 2023
Abstract
The most advanced structure prediction methods are powerless in exploring the conformational ensemble of disordered peptides and proteins and for this reason the “protein folding problem” remains unsolved. We present a novel methodology that enables the accurate prediction of spectroscopic fingerprints (circular dichroism, infrared, Raman, and Raman optical activity), and by this allows for “tidying up” the conformational ensembles of disordered peptides and disordered regions in proteins. This concept is elaborated for and applied to a dodecapeptide, whose spectroscopic fingerprint is measured and theoretically predicted by means of enhanced-sampling molecular dynamics coupled with quantum mechanical calculations. Following this approach, we demonstrate that peptides lacking a clear propensity for ordered secondary-structure motifs are not randomly, but only conditionally disordered. This means that their conformational landscape, or phase-space, can be well represented by a basis-set of conformers including about 10 to 100 structures. The implications of this finding have profound consequences both for the interpretation of experimental electronic and vibrational spectral features of peptides in solution and for the theoretical prediction of these features using accurate and computationally expensive techniques. The here-derived methods and conclusions are expected to fundamentally impact the rationalization of so-far elusive structure–spectra relationships for disordered peptides and proteins, towards improved and versatile structure prediction methods.
1 Introduction
Central to all biological processes are the tightly intertwined concepts of structure–activity relationships and molecular recognition.1,2 Traditionally, these concepts were developed for and applied to ordered biomolecules, presenting only one or a few strongly favoured conformations. However, biomolecules lacking an ordered structure have been shown to possess specific biological activity and recognition capability. E.g. proteins with more or less extended intrinsically-disordered regions3 mediate important signalling processes in eukaryotic cells.4,5 In cell signalling, disorder is advantageous because it allows a single protein to interact with multiple binding partners by adopting different structures.6 Also disordered oligopeptides are able to adapt their conformation to match interfacial features at surfaces of both biological and inorganic matter.7–9 Moreover, the activity of antimicrobial peptides results from their induced amphipathic conformation upon interaction with bacterial membranes.10 A fundamental phenomenon associated with this examples is the so-called ‘conformational selection’, namely a redistribution (or population shift) of the microscopic states in the biomolecular conformational ensemble as a consequence of the interaction.1 Understanding the solution structural ensemble provides insights into the conformational landscape accessible to the biomolecule, which plays a crucial role in both conformational selection and induced fit mechanisms. The biological significance of such processes cannot be understated, being for instance at the origin of the detrimental activities of amyloid peptides or prions.11,12 For this reason, the correct prediction of microstate populations and their interaction-induced redistribution in disordered conformational ensembles is crucial to rationalize and develop strategies against pathologies associated with misfolded and disordered peptides and proteins.13,14Addressing this issue at the molecular level poses great challenges both to experimental and theoretical approaches. Easily accessible experimental observables, such as light-absorption spectra of dissolved oligopeptides, are averaged over all ensemble microstates (conformers), each occurring with a probability specified by Boltzmann statistics. The issue here is that the free-energy landscapes in the conformational phase space of disordered peptides and proteins are wide and shallow, resulting in a very high number of conformers contributing almost equally to the ensemble average. Due to this, even the most advanced structure prediction methods, including AlphaFold,15 are powerless in exploring such a conformational ensemble16 and therefore the “protein folding problem”17 remains unsolved for preferentially disordered systems. Furthermore, theoretical methods capable of computing from first principles the spectral response of molecules are very demanding, limiting the number of conformers that can be investigated. As a consequence, interpretation of the behaviour of disordered peptide and protein systems in terms of structure–function relationships, or the molecular-scale elucidation of their biological recognition processes, requires a paradigm shift in the way experimental observables are predicted from atomistic simulations.
In this contribution we present a novel methodology that enables accurate calculations of ensemble observables, such as circular dichroism (CD), infrared (IR), Raman, and Raman optical activity (ROA) spectra, for disordered peptides. The methodology relies upon (i) prediction of the peptides' conformational ensembles by means of enhanced-sampling molecular dynamics (MD) methods;18–20 (ii) unbiased identification and characterization of a small number (order of 10 to 100) of representative conformers by means of clustering and dimensionality reduction methods; (iii) calculation and averaging of the spectral responses of those conformers with first-principle methods beyond the current state of the art. In particular, we calculated IR, Raman, and ROA spectra at a DFT level of theory, which is frequently used for accurate peptide spectra computation and comparison with experimental results, without employing fragmentation methods or approximations.21
CD is among the most important spectroscopic techniques for the study of protein secondary and tertiary structure.22 Specifically, the far-UV CD spectrum of ordered proteins is well correlated with the secondary structure, which has enabled the use of purely empirical methods for determining the secondary structure composition of a protein from its CD spectrum.23,24 Conversely, structure-based calculations using exciton models have proven successful in directly predicting CD signals that arise from the secondary structure elements, especially for helical proteins.25–30 These methods are based on the calculation of exciton interactions among peptide chromophores, and offer a physics-based way to compute the CD spectra.31,32 More recently, a structure-based exciton method was combined with machine learning predictions of the exciton parameters to enable an inexpensive determination of CD spectra.33 However, the empirical strategies have limitations in describing disordered peptides, which by definition lack specific secondary structure elements and cannot be described with one or few conformations. Furthermore, the structure-based calculations do not always agree with experiments,28 and they have been extensively tested only for ordered proteins.25,26,33
In order to tackle the prediction of CD spectra for Intrinsically Disordered Proteins (IDPs), more refined ab initio models are needed that can calculate the spectroscopic response independently of the conformation of the peptide. One such strategy is based on time-dependent (TD) density functional theory (DFT) calculations of the exciton parameters in a polarizable quantum mechanics/molecular mechanics (QM/MM) scheme.34 These calculations not only can capture the exciton interactions among peptide chromophores but also include the effect of the surrounding environment without the use of empirical parameters. Such strategy has proven successful in calculating the CD spectra of nucleic acids35,36 as well as the near-UV CD of proteins.37
Vibrational spectroscopies, such as IR, Raman, and ROA, have emerged as powerful tools for studying the structure of peptides and proteins.21,38,39 These techniques offer unique insights into the molecular structure and dynamics of these complex biomolecules, providing detailed information about their conformational landscapes, secondary structures, and even tertiary or disordered structure.21,39,40 The inherent sensitivity of these spectroscopic techniques to molecular vibrations makes them particularly suitable for discerning subtle changes in molecular structure and environment, as opposed to near-UV CD which samples electronic transitions.39,41 This is a crucial advantage for understanding the behavior and structure of peptides and proteins in solution, and to serve as reference techniques in the novel methodology presented here.
Numerous studies often employ a single spectroscopic method, despite the potential of a more robust analysis through the integration of multiple techniques, each with its unique structural sensitivities and advantages.42 By amalgamating the experimental methods CD, IR, Raman and ROA to refine an ensemble generated by enhanced-sampling MD, we can leverage the distinct strengths of each technique. This approach facilitates a comprehensive examination of protein solution structures without overtaxing computational resources, thereby offering a more efficient methodology.
Theoretical calculations are used to simulate the vibrational spectra of biomolecules, which can then be directly compared with the experimental spectra. This comparison yields the necessary insights into the molecular structures and dynamics that underlie the observed spectroscopic features.21,41 Recent research has therefore increasingly focused on the synergistic combination of experimental spectroscopic studies with theoretical approaches, particularly density functional theory (DFT) calculations.21,41,43 This combined approach allows for a more comprehensive and accurate interpretation of the spectroscopic data, enhancing our understanding of the structure and dynamics of peptides and proteins.
However, achieving a meaningful comparison between experimental and theoretical spectra often requires extensive DFT simulations, coupled with elaborate conformational sampling and solvent models.44–46 Given the complexity of peptides and proteins, and the myriad of conformational states they can adopt, specifically IDPs, a thorough exploration of their conformational space is necessary to capture the diversity of structures that contribute to the observed spectra. Similarly, accurate solvent models are crucial for capturing the effects of the solvent environment on the molecular structure and dynamics, which can significantly influence the vibrational spectra.45,47 These extensive simulations and models are often computationally demanding, but they are often necessary for obtaining a proper comparison between experiment and theory, and for advancing our understanding of peptide and protein structure. Hence, the development of a methodology like the one showcased here, which refines a conformational ensemble without overburdening computational resources, represents a cutting-edge endeavor.
As an example application of this strategy, we chose a representative dodecapeptide with sequence HSSHHQPKGTNP, which was identified as a strong binder to single-crystalline ZnO using phage-display techniques.48 By calculating multiple spectroscopic signals arising from electronic and vibrational degrees of freedom of the peptide, we set to achieve a robust characterization of the entire conformational ensemble. While previous studies have focused on the temporal evolution of a few vibrational observables,49 here we focus on the equilibrium ensemble of the peptide and its relationship with steady-state spectroscopy. Theoretically predicted and experimentally acquired spectroscopic spectra are compared, showing the advantages and limitations of the methodology developed here and of the methods employed to predict the spectral responses of individual conformers. To the very best of our knowledge, this is the first complete all-atom spectroscopic fingerprint of a disordered peptide in solution.
2. Results and discussion
2.1 The spectroscopic fingerprint of a disordered peptide
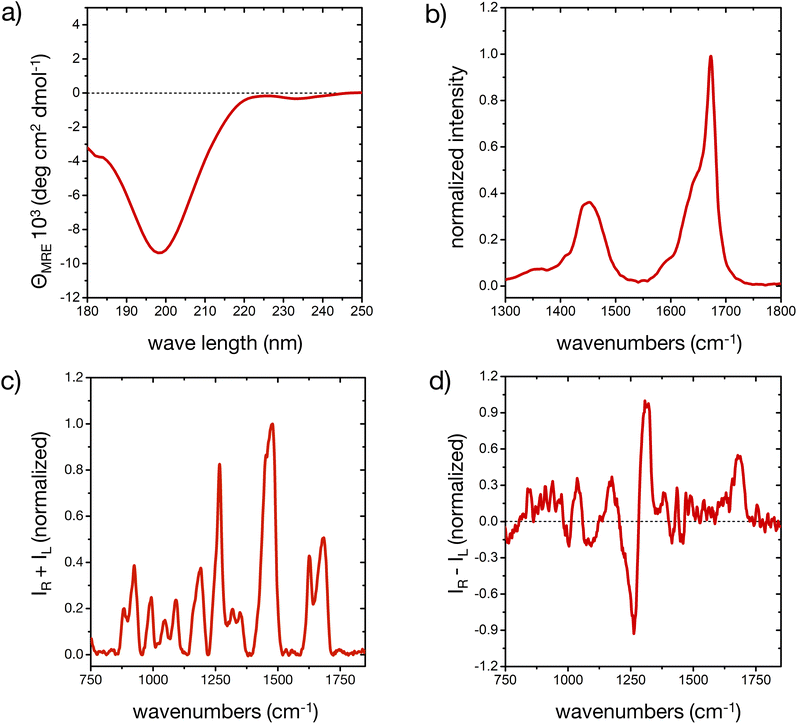
The different secondary structure elements in (poly)peptides, including intrinsically disordered ones,44,50,51 produce specific responses upon light excitation.52,53 The experimental CD, FT-IR, Raman and ROA spectroscopic fingerprint of our model peptide in water is reported in Fig. 1 (cf. ESI for experimental details†). The different signals prove that the peptide is mostly disordered, with some deviations that are consistent with a minor, but important amount of ordered microstates in the conformational ensemble.The CD spectrum (Fig. 1a) shows one pronounced minimum at 199 nm with intensities around −10 deg cm2 dmol−1. This spectral signature, albeit usually with an stronger intensity, is well-known for disordered conformations in peptides and proteins.51 Analysis of the secondary structure elements via BeStSel24 reveals contributions of about 25% of ‘anti-parallel β-sheet’, 20% of ‘turn’, and more than 50% of ‘other’ elements, which is an indication of a predominantly, but not completely disordered conformational ensemble.51
The broad amide I band in the IR spectrum between 1600 and 1700 cm−1 (Fig. 1b)54 and in the Raman spectrum at 1684 cm−1 57 (Fig. 1c) are supportive of a mostly disordered peptide structure. The maximum at 1673 cm−1 could indicate β-turn or β-sheet structure in the peptide's ensemble, while the shoulder around 1642 cm−1 is assigned to disordered structures.54,55 The peptide's side chains, such as histidine, lysine, asparagine and glutamine, contribute to the overall amide I′ shape, as well as the shoulder around 1590 cm−1.55,56 IR contributions in the lower amide I′ region (1600–1650 cm−1) stem from intra-molecular hydrogen bonding in turns and helical elements, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(ND2) stretching (around 1650 cm−1), COO− asymmetric stretching (1580–1600 cm−1), ND+3 deformations (around 1620 cm−1), different protonation states of the His residues, and hydrogen bonding to the solvent.55,56 A minor degree of order in our peptide may be inferred from the shape of the amide I′ IR peak, consistent with the CD result. The amide II region arises from C–N stretching coupled with N–D bending vibrations and is more complex than the amide I region in its interpretation. For this reason, while the amide II is also conformationally sensitive, it is less commonly used for conformational analysis.54
O(ND2) stretching (around 1650 cm−1), COO− asymmetric stretching (1580–1600 cm−1), ND+3 deformations (around 1620 cm−1), different protonation states of the His residues, and hydrogen bonding to the solvent.55,56 A minor degree of order in our peptide may be inferred from the shape of the amide I′ IR peak, consistent with the CD result. The amide II region arises from C–N stretching coupled with N–D bending vibrations and is more complex than the amide I region in its interpretation. For this reason, while the amide II is also conformationally sensitive, it is less commonly used for conformational analysis.54
In the ROA spectrum (Fig. 1d), a broad positive signal is observed at 1677 cm−1, which is also typical for mostly disordered peptides,39,40 whereas α-helical or β-sheet structures would display a ± couplet in this region.39 The amide III region in the Raman and ROA spectra (1240 to 1310 cm−1) arises from complex vibrational modes with out-of-phase N–D bending vibrations coupled with the amide Cα–D bond stretching mode.39 The coupling of these vibrations with Cα–D bending modes makes this spectral region very sensitive to the precise backbone conformation.39,41 The positive band at 1318 cm−1 in the ROA spectrum is typically observed for disordered peptides and proteins, mainly arising from the backbone's torsional angles clustering in the Ramachandran region of the left-handed polyproline II (PPII) helix (Φ ∼ 75° and ψ ∼ 145°).40,41,44
A more detailed interpretation of the spectroscopic fingerprint requires molecular-level information about the conformer population of the peptide, which we can predict from all-atom MD simulations, as described in the next section. In our study, experimental conditions were deliberately chosen to allow for a comparison with simulations; however, the experimental pH of the peptide solutions (6.4 ± 1.0), proximate to the pKa value of histidine side chains (6.0 ± 0.6),57 still created a complex environment in terms of the histidine protonation, an aspect thoroughly considered in our following approach.
2.2 Revealing the conformational ensemble of a disordered peptide
The conformational ensemble of the peptide is elucidated by means of Hamiltonian replica exchange with solute tempering (REST) MD simulations,58–60 in which the peptide is defined as the ‘solute’ (cf. ESI for computational details†). The geometric progression of temperatures applied to the solute61 ensures a nearly uniform overlap of the potential energy distributions and, thus, a uniform exchange probability across the replica ladder (Fig. 2a). The measurement of the experimental pH in ultrapure water can be affected by factors such as temperature, pressure, and exposure time. Due to potential variations in protonation states of histidines arising from the aforementioned factors, we conducted initial simulations with ε-protonated histidines (HIE protonation state), corresponding to pH ≈ 7, which we subsequently compared with the ensemble obtained with all histidines protonated (HIP protonation state), corresponding to a pH < 6, providing a more robust analysis of the peptide behavior under varying conditions. Regarding the HIE protonation state, acceptable convergence is reached early in the simulation (after about 150 ns, ESI Fig. S3†). We have further verified convergence by starting a new REST from a different initial conformation (i.e., fully extended all coil), resulting in a comparable conformational ensemble (cf. ESI Fig. S4†).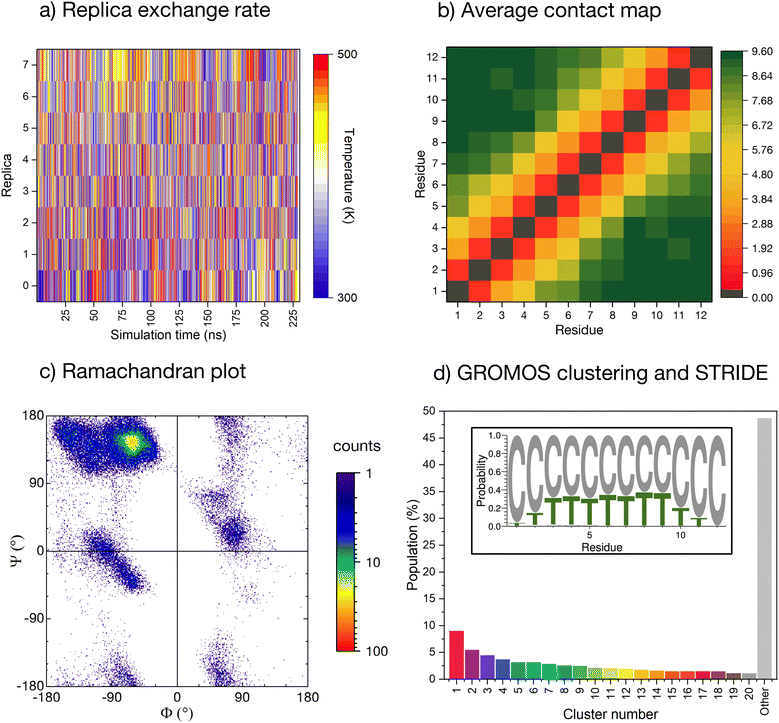 | ||
| Fig. 2 Enhanced-sampling MD simulation of the peptide in water. (a) Temperature position of each replica as the REST simulation progresses. (b) Pairwise inter-residue contact maps averaged along the whole simulation time. Distance computed for all heavy atoms with a resolution of 0.001 nm and truncated at 1.0 nm. (c) Cumulative Ramachandran plot for all residues for all frames in the ground temperature trajectory, colored according to the relative frequency (log scale). (d) Normalised cluster occupancy after cluster analysis with the GROMOS algorithm using an RMSD cut-off of 2.0 Å. The ‘other’ histogram bin collects clusters with populations smaller than 1%. The color associated to the cluster numbers is the same as in Fig. 3a. The insert depicts a weblogo-like representation of the secondary-structure propensity evaluated with STRIDE and averaged over the whole simulation (C: coil, T: turns). | ||
The REST trajectory of the room-temperature replica is analysed from multiple viewpoints focusing on different measures of order/disorder in the peptide (Fig. 2b–d and 3). A map of the contacts between the residues averaged over all conformers in the trajectory is shown in Fig. 2b. The map is populated only along its diagonal, consistent with either an elongated or a widely distributed peptide conformation. An analysis of the backbone radius of gyration (Rg) for all structures in the REST trajectory showed a wide distribution with an average Rg of 0.85 nm, indeed indicating that most structures are elongated. However, a significant population of structures exhibits Rg values below 0.6 nm, suggesting the presence of more compact conformations (cf. ESI Fig. S5a†).
As a further measure, the dihedral angles of the peptide residues collected along the trajectory are plotted together in a Ramachandran plot (Fig. 2c and ESI Fig. S6† for individual residues). While most of the accessible space is visited during the REST trajectory, the vast majority of the angles localize in the area around Φ = −75° and Ψ = +145°. This region corresponds to the conformation of the PPII helix, a reference structure for disordered conformations.40,44,51
The secondary structure propensity of the peptide conformers was also analyzed via STRIDE62 and averaged along the trajectory (Fig. 2d, inlet). All amino acids reveal a preferentially disordered conformation (‘coil’). Some amino acids, particularly in the center of the sequence, have a propensity <30% for a ‘turn’ motif.
More precise details about the conformer population are gained by means of a GROMOS cluster analysis (Fig. 2d),63 performed according to the differences in the root mean square deviation (RMSD) values of individual conformers, computed only for the peptide backbone with a cut-off of 2.0 Å (Fig. 2d). The RMSD values confirm the variability of sampled structures in the REST ground trajectory, ranging from less than 0.2 Å to around 10.5 Å, with an average of 4.2 Å separating the structures (cf. ESI Fig. S7†). This variability results in the most-populated cluster containing only 9% of the conformers, and to a smooth distribution of 20 clusters with conformer populations larger than 1%. Almost 50% of the conformers do not belong to these clusters and are grouped together in the histogram in Fig. 2d (grey bar labelled ‘other’).
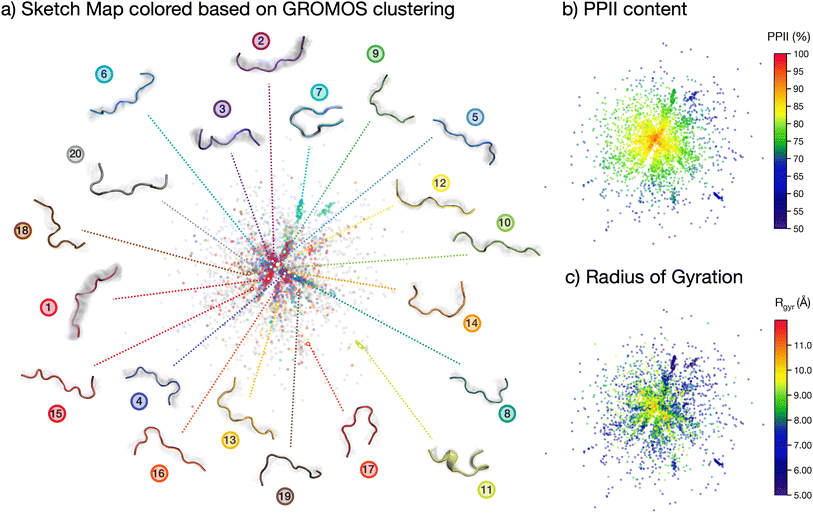
The analyses performed so far point towards a wide spread of peptide microstates in the conformational phase space, making it impossible to identify one or even a few ‘preferential conformations’ of the peptide in solution. However, the very uneven spread of the torsional angles in the Ramachandran plot clearly shows that the peptide, although ‘disordered’, is far from being ‘randomly disordered’. In order to shed light on the actual degree of order in the conformational ensemble, we plot a two-dimensional sketch map of the conformers in the high-dimensional space covered by all backbone dihedrals in the peptide sequence (Fig. 3).64,65 In this way, we obtain a visual representation of the structural differences (measured as distances in the phase-space of all dihedrals) among the conformers in the ensemble. We employed sketch map as a dimensionality reduction algorithm, since it focuses by definition on the relevant distances, allowing for a better representation of the ensemble. Indeed, we verified that a principal component analysis (PCA) on dihedrals was not able to capture the full structural complexity in our conformational ensemble (cf. ESI Fig. S8†).
The resulting sketch map is radial-symmetric and poorly structured. However, by coloring the conformers according to their PPII content and radius of gyration it is possible to identify some distinctive features. Namely, the center of the sketch map, which collects the most prevalent conformers, is mostly populated by stretched conformations with high (>90%) PPII content. This conclusion is consistent with the Ramachandran plot in Fig. 2c and the contact map in Fig. 2b, although stemming from a more general and unbiased analysis of the peptide's conformational phase space.
More information is gained by coloring the sketch map according to the cluster number (Fig. 2d) to which the conformer belongs, and visualizing the central backbone structures of the 20 most populated clusters around the sketch map (Fig. 3a). The majority of the most-populated clusters are located in the map center, but with member conformers (dots of the same color) scattered across the map rather than localized in a specific region of space. Only a few clusters contain members grouped together in the sketch map, signifying close structural similarity among the cluster's members. These are, in particular, cluster 7, 11 and 17. Cluster 11 shows conformers with partial helical folding, whereas clusters 7 and 17 show a preferential horseshoe-like structure. In general, folded and more ordered structures locate themselves at the far border of the map, far from the majority of non-folded and disordered conformers. By plotting (cf. ESI Fig. S5b†) the average Rg and standard deviation for each of the 20 most populated clusters in the REST trajectory we further highlighted this differences between elongated and disordered clusters (e.g., cluster 1) and compact, ordered clusters (e.g., clusters 7 and 11).
To explore the effect of different protonation states on our system, we conducted an additional REST simulation with all histidines protonated (HIP protonation state) and compared it with the original simulation using neutral histidines (HIE protonation state). This comparison revealed significant differences in structural properties. For instance, the protonated ensemble exhibited more structure than the neutral one, with 35%, of structures belonging to clusters with less than 1%, population, compared to 45%, in the neutral case. Furthermore, 50%, of the most populated clusters have a compact horseshoe-like conformation (cf. ESI Fig. S10a†). The average Rg is also smaller in the protonated case with a larger number of compact conformers (cf. ESI Fig. S10b†). Furthermore, mapping the fully protonated peptide ensemble using the PCA trained on the neutral ensembles resulted in a profile with no correlation to the original ensemble.
In summary, the conformational ensemble of the peptide is populated by conformers that span a wide and shallow free-energy landscape, independently on the protonation state. The distribution of conformers, however, is far from uniform in this phase space, giving rise to evident granularity in this reduced representation. We can therefore highlight a degree of structural order in some phase-space regions, which we expect to deliver specific and identifiable signatures in the peptide's spectroscopic fingerprint. The theoretical prediction of such spectroscopic fingerprints, in turn, should capitalize on these pieces of information and collect the spectroscopic responses from all of the most representative regions of the conformational phase space while composing ensemble averages that can be compared with the experimental observables. In particular, in view of our analysis, we expect that considering only one or two center structures of mostly populated clusters would certainly be misleading and insufficient in terms of phase-space sampling.
2.3 A structural basis set approach to interpret the peptide's CD fingerprint
We have shown that experimental CD spectra of ordered peptides and proteins can be well reproduced by the average of the computed CD spectra for all conformers in the ensemble,19,20 employing semi-empirical methods, e.g. with the DichroCalc server.27 However, it should be noted that DichroCalc has some known limitations which, in the case of this peptide, led to a very poor agreement with the experimental signal (cf. ESI Fig. S9†).To overcome these limitations, in this study, we deploy a novel, more accurate but computationally more demanding, method for the calculation of CD spectra for disordered ensembles (cf. ESI for computational details†). The approach is based on an excitonic model developed previously to predict optical spectra of multichromophoric systems,66,67 and applied to biopolymers and pigment–protein complexes.36,37,68–70 In this model, the properties of the single chromophoric units (here the peptide bonds, modelled as an N-methyl acetamide (NMA) fragments) are combined together to describe the excited states of the entire system. Each peptide bond is modeled in an idealized planar geometry and computed in the polarizable MM (MMPol) environment of the rest of the system. In this way, the resulting CD spectra depend both on the arrangement of the NMA chromophores (i.e. on the peptide's secondary structure) and on other effects captured by the MM embedding, such as the conformation of the side chains and the arrangement of the solvent around the backbone.
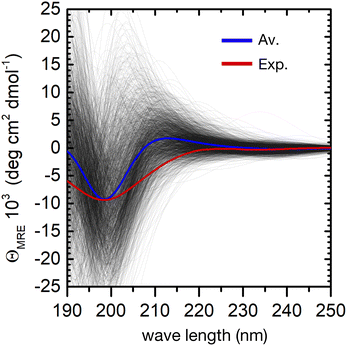
The individual spectra of 2000 evenly selected conformers in the ensemble show a very large variability (Fig. 4). This is not surprising, because the computed excitation energies of the NMA chromophoric units are very sensitive to the effect of the embedding field (for instance to the dipole orientations of the water solvent). In addition, the sign and position of the CD bands depend on the relative orientation of the peptide bonds. However, the calculated ensemble average reproduces well the general shape of the experimental CD spectrum. In particular, the strong negative π → π* band at about 200 nm shows a good agreement with the experimental CD spectrum. The largest deviation is a predicted positive band around 210 nm, which is absent in the experiment. This may arise from the neglect of side–chain transitions (e.g. histidine residues or the amide bonds of asparagine and glutamine), or to the underestimation of n → π*/π → π* mixing within each peptide bond. Finally, we note that the broadening of the negative band is underestimated in the simulations, possibly due to the neglect of vibronic structure in the π → π* band.20 A greater broadening may hide the positive contributions at around 210 nm.
Despite these minor deviations, our QM/MMPol approach predicts very well the peptide's CD spectroscopic fingerprint by computing an ensemble-average over thousands of individual conformers. However, the employed method is computationally rather expensive, and further improvements in its accuracy would make the calculation of such a large number of spectra impossible in practice. One can therefore wonder if, even in a preferentially disordered ensemble, there is a limited subset of conformers that can be chosen and averaged to obtain a simulated spectrum close enough to that of the full ensemble. The central structures of the first twenty most populated clusters might be a good choice, because they are spread evenly in the conformational phase space, Fig. 3.
Notably, the variability of computed CD spectra among the conformers in each of the clusters remain very large, as can be seen in Fig. 5a and S11 in ESI.† This is because in our approach the conformer similarity is assessed by aligning only the peptide backbone, and not the side chains, whose effect on the CD excitations is large and is taken into account in our calculations. Only for clusters 7 and 11, which present a predominantly ordered structure, is the spectral variability reduced (Fig. S11 in ESI†), in agreement with previous studies.20 However, despite the spectral variability, the CD spectrum of each central structure captures the main common features within its cluster, with only few exceptions (such as cluster 17 in ESI Fig. S11†).
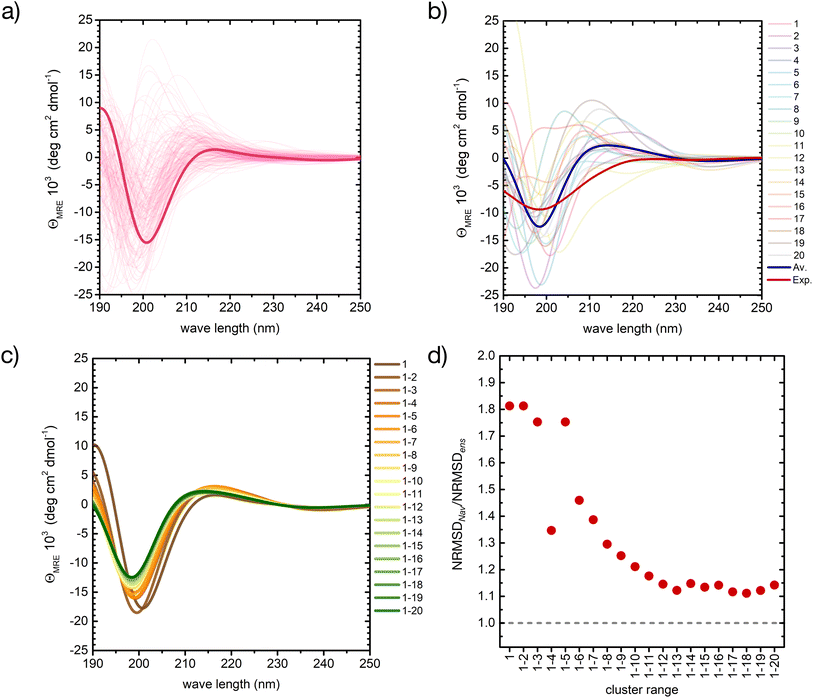 | ||
| Fig. 5 A basis set approach to reconstruct the CD fingerprint of the peptide. (a) Computed CD spectra for all conformers belonging to cluster 1 of the REST trajectory (Fig. 3), with the spectrum of the central structure drawn in bold. (b) Computed CD spectra of the central structures of the 20 most populated clusters of the REST trajectory (color code as in Fig. 3), with their weighted average (blue) compared to the experiment (red). (c) Evolution of the weighted-averaged CD spectrum by adding subsequent central structures of the 20 most populated clusters of the REST trajectory. (d) Evolution of the normalized root mean square deviation (NRMSD) between the weighted averaged CD spectra in (c) and the experimental spectrum, normalized to the NRMSD of the complete ensemble-average spectrum (Fig. 4). | ||
Also between different central structures, the variability among CD spectra is very large (Fig. 5b), reflecting differences in their secondary structure. Most spectra are characterized by a pronounced negative band at 190–200 nm and scattered positive band(s) between 205 and 220 nm. The helical cluster 11 also shows the typical negative shoulder between 210 and 230 nm (Fig. 5b and S11 in ESI†). Remarkably, if we average the CD spectra of these twenty structures weighted by their REST population, we obtain a very similar result to the average of the entire ensemble of 2000 conformers, although the negative intensity of the main minimum at around 200 nm is slightly overestimated (thick blue line in Fig. 5b).
Averaging the spectra of the first N cluster structures with increasing N from 1 to 20 reveals a smooth convergence towards the ensemble average (Fig. 5c). This convergence can be quantified by computing the normalized root mean squared deviation (NRMSD) of the computed spectra against the experimental one, as previously reported:24,71
 | (1) |
Whereas the NRMSD between the predicted ensemble-averaged and the experimental spectrum (NRMSDens) quantifies the intrinsic quality of the simulation approach, the ratio between the NRMSD of the average spectrum of the first N cluster structures (NRMSDNav) and NRMSDens is a measure of the convergence obtained with increasing N. This is plotted in Fig. 5d, showing large initial fluctuations for N < 6, followed by a smooth convergence behaviour afterwards. Limited improvement is observed for N > 12, and a 10% residual error remains up to N = 20. Although further increase of N is expected to improve the convergence, considering about 10 to 20 conformers instead of 2000 represents a huge advantage in terms of computational cost at the expense of a more than acceptable error.
We have employed the same approach to investigate the CD fingerprint of the ensemble of the peptide in all-HIP protonation state (cf. ESI Fig. S10c†). The weighted average of the 20 clusters is characterized by a single minimum at 199 nm with an intensity of −5 deg cm2 dmol−1, which is lower than the intensity of our original simulation (HIE protonation state). Another difference is the slightly positive values at around 190 nm. For this reason, the presence of more compact conformers among the most populated clusters is likely associated with the presence of more ordered secondary structures.
2.4 Validating the approach for FT-IR prediction
Considering only a small number of well-selected conformers is crucial to be able to compute IR, Raman and ROA spectra with accurate QM-based methods. In this section and the next ones we investigate whether the developed approach for the prediction of CD fingerprints can be transferred also to these other spectral observables. The computed IR spectra for the 20 cluster central structures are reported in Fig. 6 (cf. ESI† for computational details).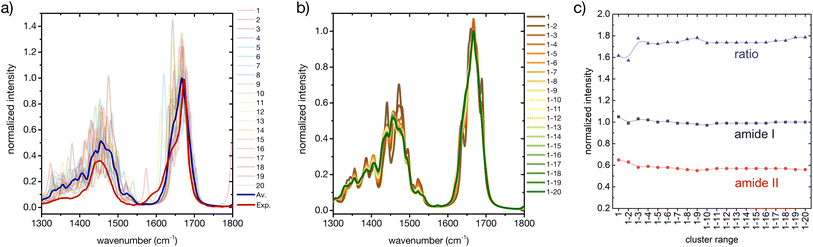 | ||
| Fig. 6 A basis set approach to reconstruct the FT-IR fingerprint of the peptide. (a) Computed FT-IR spectra of the central structures of the 20 most populated clusters of the REST trajectory (color code as in Fig. 3), their weighted average (blue), compared to the experiment (red). Only the amide I and amide II region is shown. Intensities are normalized at the maximum value of the computed weighted average and the experiment, respectively. (b) Evolution of the weighted averaged FT-IR spectrum by adding subsequent central structures of the 20 most populated clusters of the REST trajectory. (c) Convergence of the weighted averaged FT-IR spectrum by adding subsequent central structures of the 20 most populated clusters of the REST trajectory, showing the relative intensities of amide I and amide II and their ratio. | ||
Regarding the amide I′ band (the prime indicates that the labile protons are exchanged for deuterons, cf. ESI†), 18 of these clusters share the pronounced band at about 1670 cm−1 with the weighted average (Fig. 6a). Cluster 7 and cluster 11 are again two notable exceptions, cf. ESI Fig. S2.† Cluster 7 presents an additional amide I′ band at 1620 cm−1, due to hydrogen bonding of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in the amide bond between proline and asparagine with the N–D group in the amide bond between serine and histidine (N-terminus). Cluster 11 presents a pronounced peak at 1644 cm−1, which can be attributed to a partially α-helical structure, and two shoulders at 1612 cm−1 and 1669 cm−1. Indeed, the experimental amide I′ signal also shows prominent shoulders at wavenumbers lower than 1670 cm−1, which most probably stem from intramolecular hydrogen bonding in microstates with ordered secondary structures, as mentioned above (Fig. 1 and related text). Additionally, the precise amide I′ shape is determined also by the hydrogen bonding pattern with water (cf. ESI section Microsolvation and ESI Fig. S12 and S13†).45,72 By considering the evolution of the weighted-averaged IR spectrum by increasing the number N of central structures (Fig. 6b), we find little impact on the band position and intensity for the amide I signal. Regarding the amide II′ band, a much higher variability is found among the central cluster structures. However, the weighted average progressively approaches the shape of the experimental signal. Therefore, a rational consideration of the most important conformations assumed by the peptide in solution is essential in describing the ensemble-averaged IR signal. A good convergence with N is observed by looking at the ratio of the maximum intensities between the amide I′ and amide II′ main peaks (Fig. 6c), although the ratio remains overestimated in comparison with the experiment. In conclusion, our approach is able to reproduce reasonably well the overall IR band shapes, especially of the amide II′ band, but not some of the minor features and the precise peak ratio observed in the experiment. This suggests that including a larger number of ordered conformers, better quantifying the conformational degrees of freedom of the side chains, or explicit inclusion of solvent may be required to further improve the agreement.
O in the amide bond between proline and asparagine with the N–D group in the amide bond between serine and histidine (N-terminus). Cluster 11 presents a pronounced peak at 1644 cm−1, which can be attributed to a partially α-helical structure, and two shoulders at 1612 cm−1 and 1669 cm−1. Indeed, the experimental amide I′ signal also shows prominent shoulders at wavenumbers lower than 1670 cm−1, which most probably stem from intramolecular hydrogen bonding in microstates with ordered secondary structures, as mentioned above (Fig. 1 and related text). Additionally, the precise amide I′ shape is determined also by the hydrogen bonding pattern with water (cf. ESI section Microsolvation and ESI Fig. S12 and S13†).45,72 By considering the evolution of the weighted-averaged IR spectrum by increasing the number N of central structures (Fig. 6b), we find little impact on the band position and intensity for the amide I signal. Regarding the amide II′ band, a much higher variability is found among the central cluster structures. However, the weighted average progressively approaches the shape of the experimental signal. Therefore, a rational consideration of the most important conformations assumed by the peptide in solution is essential in describing the ensemble-averaged IR signal. A good convergence with N is observed by looking at the ratio of the maximum intensities between the amide I′ and amide II′ main peaks (Fig. 6c), although the ratio remains overestimated in comparison with the experiment. In conclusion, our approach is able to reproduce reasonably well the overall IR band shapes, especially of the amide II′ band, but not some of the minor features and the precise peak ratio observed in the experiment. This suggests that including a larger number of ordered conformers, better quantifying the conformational degrees of freedom of the side chains, or explicit inclusion of solvent may be required to further improve the agreement.
2.5 New challenges arise: Raman and ROA
The prediction of Raman and specifically ROA spectroscopic fingerprints of disordered oligopeptides represents a great challenge to current computational approaches, because they are very sensitive not only to the secondary-structure conformation of the backbone, but also to the solvation structure and the side-chain conformations.44,46 Indeed, as reported in Fig. 7a and c a large spectral variability is obtained among the 20 cluster central structures, especially for ROA. The evolution of the weighted-average Raman spectra with increasing the number N of included conformers reveals almost no changes in the amide I and II regions (Fig. 7c). More evident changes occur in the amide III region, which reflects its larger sensitivity to the extent of order in the ensemble microstates. The overall shape of the spectrum is progressively smoothened for larger N values, although important deviations with respect to the experimental spectrum remain. In particular, the calculations predict prominent peaks at about 1600 cm−1 and 1300 cm−1, which are absent in the experiment.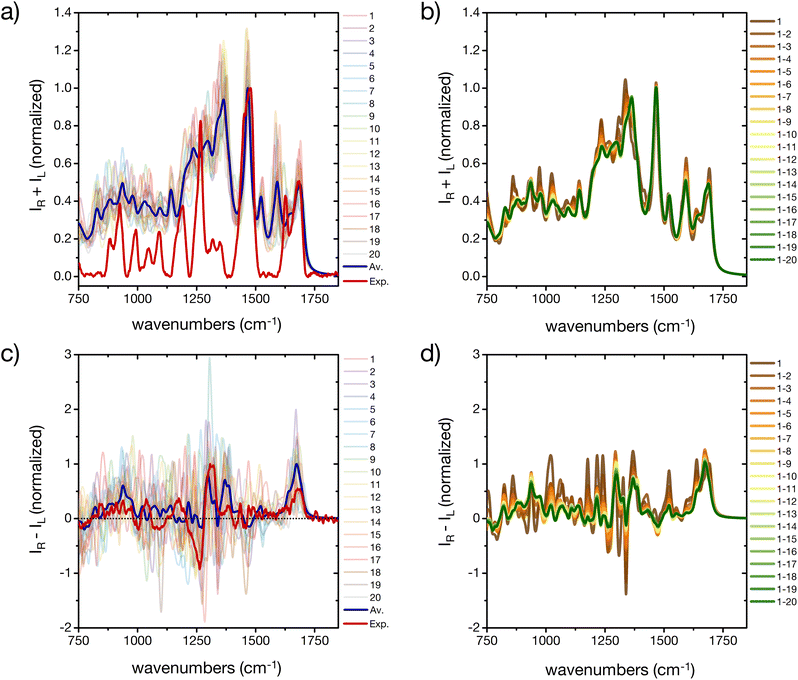 | ||
| Fig. 7 A basis set approach to reconstruct the Raman and ROA fingerprint of the peptide. (a) Computed Raman spectra of the central structures of the 20 most populated clusters of the REST trajectory (color code as in Fig. 3), their weighted average (blue), compared to the experiment (red). Intensities are normalized at the maximum value of the computed weighted average and the experiment, respectively. (b) Evolution of the weighted averaged Raman spectrum by adding subsequent central structures of the 20 most populated clusters of the REST trajectory. (c) Computed Raman optical activity spectra of the central structures of the 20 most populated clusters of the REST trajectory (color code as in Fig. 3), their weighted average (blue), compared to the experiment (red). Intensities are normalized at the maximum value of the computed weighted average and the experiment, respectively. (b) Evolution of the weighted averaged Raman optical activity spectrum by adding subsequent central structures of the 20 most populated clusters of the REST trajectory. | ||
Since contributions in these wavelength ranges may originate from Raman-active modes in the histidine rings, further simulations were performed with all imidazole rings of the peptide's side chains carrying an additional proton (ESI Fig. S14†). In fact, the pH of the experimental peptide solution is close to the pKa of the histidine side chain (6.0 ± 0.6).57 Reduced peaks are indeed obtained after protonation of all histidine residues, although at the present stage we cannot exclude other reasons for the deviation of some of the calculated spectral patterns from the experiment, such as interaction of the solvent (e.g. with the imidazole rings or other side chains, dependence on the DFT-level, etc.).
As far as the predicted ROA response is concerned, the weighted-average spectrum shows very limited convergence with increasing the number of averaged conformers (Fig. 7d). This is not surprising, given that a single calculated ROA spectrum is strongly influenced by contributions of the side chains conformations, while most contributions of the dynamic and achiral side chains cancel out.46,73 To achieve a better agreement with experiment, a larger number of conformers and side chain rotamers would be necessary. However, the positive band in the amide I region (at about 1680 cm−1) is observed in all calculated ROA spectra and in good agreement with the experiment, pointing towards an overall disordered structure of the peptide.74 This positive band in the amide I region of the ROA spectrum, as well the positive band around 1318 cm−1 in the amide III region, are typically assigned to short stretches of PPII backbone conformation of intrinsically disordered peptides and proteins.41,44,74 As a proof-of-concept, we used a regular PPII conformation (all Φ angles −75° and all Ψ angles 145°) of this peptide and created 20 different arrangements of the side chains (different rotamers) to better sample the side chain flexibility (ESI Fig. S15†). Comparing calculated IR and Raman spectra for the canonical PPII structures with rotational averaging of the side chains did not result in a considerable improvement. However, the resulting average ROA spectrum of this test set resembles the spectral features we observed in our experimental ROA spectrum (Fig. 1), such as the positive amide I band at 1680 cm−1 and the ± couplet at 1260/1318 cm−1, which are dominated by spectral features associated with PPII structures.41 Notably, some of these PPII backbone based rotamers show a negative signal in the amide III region, which is often not shown in PPII reference spectra, e.g. with poly-alanine reference structures,41 nor in the weighted average of the 20 cluster center structures (ESI Fig. S15†). Finally, we extended this side chain rotamer approach to the first four cluster center structures to verify how one specific side chain configuration of the peptide affects the simulated spectra (ESI Fig. S16†). While for IR each side chain configuration yields a specific spectrum, but with the same overall characteristic of the averaged one (ESI Fig. S16a†), Raman is found more sensitive to the signals arising from the side chains and their orientation (ESI Fig. S16b†). The ROA spectra are almost entirely determined by a specific side chain configuration (all χ-angles of all residues, ESI Fig. S16c†). Only the positive amide I signal is conserved in all calculations irrespective of the side chain conformation, and is thus a robust marker of the backbone conformation. This clearly demonstrates the need for thorough averaging over many conformations of both the backbone and side chain groups, as experimental ROA spectra show distinct patterns depending on the backbone conformation.41,74
The prediction of Raman and ROA spectra in agreement with experiments revealed more challenges, due to the higher sensitivity of the methods to the conformational degrees of freedom of the side chains and their solvation states. Regarding the Raman spectrum, the agreement is modestly improved after protonating the imidazole rings of all histidine residues, although such a high protonation state would not be expected under the pH conditions employed in the experiments. This demonstrates how challenging it is to properly model Raman and ROA spectra of peptides as the calculated spectrum is determined by all aspects of the considered model such as the protonation state, the side-chain conformations and dynamics, solvation, etc. The importance of incorporating conformational flexibility was especially clear for the ROA, for which not only the backbone conformation needs to be properly averaged over many conformations, but also many side chain rotamers need to be explicitly included to properly account for their contributions. Possibly, a clustering algorithm including both the backbone and the side-chain degrees of freedom might need to be developed and deployed to predict ROA observables in better agreement with experiments.
3 Conclusions
Our analysis clearly demonstrates that the investigated peptide48 presents a predominantly disordered, but not ‘randomly disordered’ conformational ensemble, possessing some ordered secondary-structure elements. Theoretical sampling and spectroscopic fingerprints hinted towards some contribution of ordered elements within the conformational ensemble, while the majority of conformers showed PPII-region torsional angles, typical of intrinsically disordered proteins.75 By means of a multidimensional analysis and clustering procedure, we have been able to ‘tidy up’ the conformational phase space and to filter out 20 representative conformers whose spectroscopic responses contribute in a major way to the ensemble-averaged observables. Only about 10% of these representatives displayed traditional secondary structure elements.Predicting structures of ordered systems, such as globular proteins with high amounts of β-sheets and α-helices,19,76 is theoretically demanding due to the associated calculation costs based on the system size, as is calculating their optical or vibrational spectra. However, the prediction of the conformational ensemble described by the free energy landscape is possible for short peptides with around 10 amino acids, via enhanced sampling methods. In contrast, truly disordered systems, like molten polymer chains, can be modeled more simply by assuming random conformations.77 The spectroscopic responses of specific conformational features are then averaged out by considering a sufficient number of random conformations, and continuum solvent models can adequately represent the surrounding environment. Disordered peptides represent a peculiar case of ‘conditionally disordered’ systems, and carry features of both these two worlds. The prediction of experimental observables requires an accurate conformer representation to take into account the responses of each important structural feature. However, ab initio methods are too costly to be applied to thousands of different conformers. Hence the necessity of rationally ‘tidying up’ the conformational phase space by means of clustering methods. Remarkably, once this is performed, the inclusion of more and more cluster central structures leads to a progressive convergence of the spectroscopic observables towards the ensemble average (Fig. 5d).
However, the accuracy of predicted observables hinges on three factors: (i) optimized force-fields for disordered structures;78 (ii) structural metrics and dimensionality-reduction algorithms for adequate visual representations (Fig. 3); (iii) high-level spectral response calculations. In particular, we could not reproduce the experimental CD spectrum using basis-set-based or semi-empirical approaches optimized for well-structured protein systems,24,26 as was possible for ordered peptides (cf. ESI Fig. S9†).20 While our novel QM/MMPol approach based on TD-DFT calculations provided good agreement with experimental CD spectra (Fig. 4 and 5). Raman and ROA spectra posed greater challenges due to their sensitivity to side-chain conformations, solvation states, and protonation.
Our approach offers valuable insights into the relationship between conformational ensembles and spectroscopic fingerprints of disordered peptides, and holds promise for studying dynamic processes such as protein folding or unfolding. The methods we have used for computing spectroscopic observables can be applied not only to equilibrium ensembles but also to out-of-equilibrium trajectories. For instance, these methods can be used to investigate the temporal evolution of spectral observables during temperature-induced protein unfolding. This would naturally involve addressing the challenge of accurately capturing the rates of transitions between different states in non-equilibrium simulations.
Moreover, our approach could aid in developing semi-empirical data-set-based methods41 for calculating light-absorption spectra, considering various spectroscopically relevant coil structures along with traditional ordered elements like α-helices and β-sheets. The clustering method and sketch map visualization of the conformational ensemble could be advantageous in future studies focused on rationalizing conformational-ensemble changes that peptides undergo upon solvent-exchange or adsorption at solid/liquid interfaces.
Finally, our approach could contribute to improving machine learning-based structure prediction methods15,79 and the development of enhanced force fields for biomolecules80 by generating a data-set of structure–spectra relationships, when extended to a larger collection of peptides.
Data availability
All computed spectra are included in ESI.† The datasets supporting this article are available at https://github.com/mdellepi/PeptideFingerprint.Author contributions
MM, MDP and LCC conceived this research. MM, CM and CP performed the experiments. MDP and MM developed the molecular models. MDP, LC and CM performed the simulations. MM, MDP, LC, CM, LCC analysed the results. CP and LCC supervised the work. MM, MDP, LC, CM, CP, LCC wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft under grants CO 1043/17-1 and GRK 2247 and funding from the Air Force Office of Scientific Research (AFOSR) grant FA9550-16-1-0213. The experimental CD spectrum was obtained at the DISCO Beamline at Synchrotron Soleil (Proposal 201702277) with support from beamline Scientist Frank Wien and beamline manager Matthieu Réfrégiers. Computational resources were provided by the North-German Supercomputing-Alliance (HLRN) and the VSC (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government.References
- D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796 CrossRef CAS PubMed.
- S. Brown, Nat. Biotechnol., 1997, 15, 269 CrossRef CAS.
- F. E. Thomasen and K. Lindorff-Larsen, Biochem. Soc. Trans., 2022, 50, 541–554 CrossRef CAS PubMed.
- S. E. Bondos, A. K. Dunker and V. N. Uversky, On the Roles of Intrinsically Disordered Proteins and Regions in Cell Communication and Signaling, 2021 Search PubMed.
- S. E. Bondos, A. K. Dunker and V. N. Uversky, Cell Commun. Signaling, 2022, 20, 1–26 CrossRef.
- P. E. Wright and H. J. Dyson, Nat. Rev. Mol. Cell Biol., 2015, 16, 18 CrossRef CAS PubMed.
- M. Hnilova, E. E. Oren, U. O. Seker, B. R. Wilson, S. Collino, J. S. Evans, C. Tamerler and M. Sarikaya, Langmuir, 2008, 24, 12440–12445 CrossRef CAS PubMed.
- J. Schneider and L. Colombi Ciacchi, J. Am. Chem. Soc., 2012, 134, 2407–2413 CrossRef CAS PubMed.
- A. Care, P. L. Bergquist and A. Sunna, Trends Biotechnol., 2015, 33, 259–268 CrossRef CAS PubMed.
- J.-P. S. Powers and R. E. Hancock, Peptides, 2003, 24, 1681–1691 CrossRef CAS PubMed.
- R. W. Carrell and B. Gooptu, Curr. Opin. Struct. Biol., 1998, 8, 799–809 CrossRef CAS PubMed.
- Y. Xu, J. Shen, X. Luo, W. Zhu, K. Chen, J. Ma and H. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 5403–5407 CrossRef CAS PubMed.
- Y. Zhao, W. Yang, C. Chen, J. Wang, L. Zhang and H. Xu, Curr. Opin. Colloid Interface Sci., 2018, 35, 112–123 CrossRef CAS.
- Y. Liang, X. Zhang, Y. Yuan, Y. Bao and M. Xiong, Biomater. Sci., 2020, 8, 6858–6866 RSC.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, et al. , Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- K. M. Ruff and R. V. Pappu, J. Mol. Biol., 2021, 433, 167208 CrossRef CAS PubMed.
- K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046 CrossRef CAS.
- A. Ardevol, G. A. Tribello, M. Ceriotti and M. Parrinello, J. Chem. Theory Comput., 2015, 11, 1086–1093 CrossRef CAS PubMed.
- N. Hildebrand, M. Michaelis, N. Wurzler, Z. Li, J. D. Hirst, A. Micsonai, J. Kardos, A. Gil-Ley, G. Bussi, S. Köppen, M. Delle Piane and L. C. Ciacchi, ACS Biomater. Sci. Eng., 2018, 4, 4036–4050 CrossRef CAS.
- M. Michaelis, N. Hildebrand, R. H. Meißner, N. Wurzler, Z. Li, J. D. Hirst, A. Micsonai, J. Kardos, M. Delle Piane and L. Colombi Ciacchi, J. Phys. Chem. B, 2019, 123, 6694–6704 CrossRef CAS.
- T. A. Keiderling, Chem. Rev., 2020, 120, 3381–3419 CrossRef CAS PubMed.
- R. W. Woody, Biomed. Spectrosc. Imaging, 2015, 4, 5–34 CAS.
- N. J. Greenfield, Nat. Protoc., 2007, 1, 2876–2890 CrossRef.
- A. Micsonai, F. Wien, L. Kernya, Y.-H. Lee, Y. Goto, M. Réfrégiers and J. Kardos, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E3095–E3103 CrossRef CAS.
- M. T. Oakley, B. M. Bulheller and J. D. Hirst, Chirality, 2006, 18, 340–347 CrossRef CAS.
- B. M. Bulheller, A. Rodger and J. D. Hirst, Phys. Chem. Chem. Phys., 2007, 9, 2020 RSC.
- B. M. Bulheller and J. D. Hirst, Bioinformatics, 2009, 25, 539–540 CrossRef CAS PubMed.
- R. W. Woody, J. Am. Chem. Soc., 2009, 131, 8234–8245 CrossRef CAS PubMed.
- Z. Li, D. Robinson and J. D. Hirst, Faraday Discuss., 2015, 177, 329–344 RSC.
- D. M. Rogers, S. B. Jasim, N. T. Dyer, F. Auvray, M. Réfrégiers and J. D. Hirst, Chem, 2019, 5, 2751–2774 CAS.
- N. Sreerama and R. W. Woody, Methods Enzymol., 2004, 383, 318–351 CAS.
- N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy: Instrumentation, Methodologies, and Theoretical Simulations, John Wiley & Sons, Hoboken, NJ, USA, 2012, vol. 1 Search PubMed.
- L. Zhao, J. Zhang, Y. Zhang, S. Ye, G. Zhang, X. Chen, B. Jiang and J. Jiang, JACS Au, 2021, 1, 2377–2384 CrossRef CAS PubMed.
- M. Bondanza, M. Nottoli, L. Cupellini, F. Lipparini and B. Mennucci, Phys. Chem. Chem. Phys., 2020, 19, 14433–14448 RSC.
- D. Loco, S. Jurinovich, L. Di Bari and B. Mennucci, Phys. Chem. Chem. Phys., 2016, 18, 866–877 RSC.
- D. Padula, S. Jurinovich, L. Di Bari and B. Mennucci, Chem.–Eur. J., 2016, 22, 17011–17019 CrossRef CAS PubMed.
- A. Ianeselli, S. Orioli, G. Spagnolli, P. Faccioli, L. Cupellini, S. Jurinovich and B. Mennucci, J. Am. Chem. Soc., 2018, 140, 3674–3682 CrossRef CAS.
- N. Kuhar, S. Sil and S. Umapathy, Spectrochim. Acta, Part A, 2021, 258, 119712 CrossRef CAS.
- L. Barron, L. Hecht, E. Blanch and A. Bell, Prog. Biophys. Mol. Biol., 2000, 73, 1–49 CrossRef CAS PubMed.
- C. Mensch, A. Konijnenberg, R. Van Elzen, A.-M. Lambeir, F. Sobott and C. Johannessen, J. Raman Spectrosc., 2017, 48, 910–918 CrossRef CAS.
- C. Mensch, L. D. Barron and C. Johannessen, Phys. Chem. Chem. Phys., 2016, 18, 31757–31768 RSC.
- E. D. Gussem, W. Herrebout, S. Specklin, C. Meyer, J. Cossy and P. Bultinck, Chem.–Eur. J., 2014, 20, 17385–17394 CrossRef PubMed.
- J. Kessler, J. Kapitán and P. Bouř, J. Phys. Chem. Lett., 2015, 6, 3314–3319 CrossRef CAS.
- C. Mensch, P. Bultinck and C. Johannessen, ACS Omega, 2018, 3, 12944–12955 CrossRef CAS PubMed.
- C. Mensch, P. Bultinck and C. Johannessen, Phys. Chem. Chem. Phys., 2019, 21, 1988–2005 RSC.
- C. Mensch and C. Johannessen, ChemPhysChem, 2019, 20, 42–54 CrossRef CAS.
- E. Ditler and S. Luber, Wiley Interdiscip. Rev.: Computat. Mol. Sci., 2022, 12, e1605 CAS.
- D. Rothenstein, B. Claasen, B. Omiecienski, P. Lammel and J. Bill, J. Am. Chem. Soc., 2012, 134, 12547–12556 CrossRef CAS.
- W. Zhuang, R. Z. Cui, D.-A. Silva and X. Huang, J. Phys. Chem. B, 2011, 115, 5415–5424 CrossRef CAS PubMed.
- V. N. Uversky, J. Biomol. Struct. Dynam., 2003, 21, 211–234 CrossRef CAS PubMed.
- J. L. S. Lopes, A. J. Miles, L. Whitmore and B. A. Wallace, Protein Sci., 2014, 23, 1765–1772 CrossRef CAS PubMed.
- J. T. Pelton and L. R. McLean, Anal. Biochem., 2000, 277, 167–176 CrossRef CAS PubMed.
- F. Zhu, N. W. Isaacs, L. Hecht and L. D. Barron, Structure, 2005, 13, 1409–1419 CrossRef CAS PubMed.
- H. Yang, S. Yang, J. Kong, A. Dong and S. Yu, Nat. Protoc., 2015, 10, 382–396 CrossRef CAS PubMed.
- A. Barth, Biochim. Biophys. Acta, Bioenerg., 2007, 1767, 1073–1101 CrossRef CAS PubMed.
- A. Barth, Prog. Biophys. Mol. Biol., 2000, 74, 141–173 CrossRef CAS PubMed.
- S. P. Edgcomb and K. P. Murphy, Proteins: Struct., Funct., Bioinf., 2002, 49, 1–6 CrossRef CAS PubMed.
- R. Affentranger, I. Tavernelli and E. E. Di Iorio, J. Chem. Theory Comput., 2006, 2, 217–228 CrossRef CAS.
- L. Wang, R. A. Friesner and B. J. Berne, J. Phys. Chem. B, 2011, 115, 9431–9438 CrossRef CAS.
- G. Bussi, Mol. Phys., 2013, 112, 379–384 CrossRef.
- N. Rathore, M. Chopra and J. J. de Pablo, J. Chem. Phys., 2005, 122, 024111 CrossRef PubMed.
- D. Frishman and P. Argos, Proteins: Struct., Funct., Bioinf., 1995, 23, 566–579 CrossRef CAS.
- X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. Van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240 CrossRef CAS.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023–13028 CrossRef CAS.
- G. A. Tribello, M. Ceriotti and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5196–5201 CrossRef CAS.
- S. Jurinovich, G. Pescitelli, L. Di Bari and B. Mennucci, Phys. Chem. Chem. Phys., 2014, 16, 16407 RSC.
- S. Jurinovich, L. Cupellini, C. A. Guido and B. Mennucci, J. Comput. Chem., 2018, 39, 279–286 CrossRef CAS PubMed.
- L. Cupellini, M. Bondanza, M. Nottoli and B. Mennucci, Biochim. Biophys. Acta, Bioenerg., 2020, 1861, 148049 CrossRef CAS PubMed.
- F. Segatta, L. Cupellini, M. Garavelli and B. Mennucci, Chem. Rev., 2019, 119, 9361–9380 CrossRef PubMed.
- V. Sláma, L. Cupellini and B. Mennucci, Phys. Chem. Chem. Phys., 2020, 22, 16783–16795 RSC.
- D. Mao, E. Wachter and B. Wallace, Biochemistry, 1982, 21, 4960–4968 CrossRef CAS PubMed.
- N. S. Myshakina, Z. Ahmed and S. A. Asher, J. Phys. Chem. B, 2008, 112, 11873–11877 CrossRef CAS PubMed.
- C. Mensch and C. Johannessen, ChemPhysChem, 2018, 19, 3134–3143 CrossRef CAS PubMed.
- F. Zhu, G. E. Tranter, N. W. Isaacs, L. Hecht and L. D. Barron, J. Mol. Biol., 2006, 363, 19–26 CrossRef CAS PubMed.
- V. Ozenne, R. Schneider, M. Yao, J.-r. Huang, L. Salmon, M. Zweckstetter, M. R. Jensen and M. Blackledge, J. Am. Chem. Soc., 2012, 134, 15138–15148 CrossRef CAS PubMed.
- T. Wollborn, M. Michaelis, L. C. Ciacchi and U. Fritsching, J. Colloid Interface Sci., 2022, 628, 72–81 CrossRef CAS PubMed.
- M. Mazars, Phys. Rev. E, 1996, 53, 6297 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell Jr, Nat. Methods, 2017, 14, 71 CrossRef CAS PubMed.
- G. Janson, G. Valdes-Garcia, L. Heo and M. Feig, Nat. Commun., 2023, 14, 774 CrossRef CAS.
- C. Empereur-Mot, L. Pesce, G. Doni, D. Bochicchio, R. Capelli, C. Perego and G. M. Pavan, ACS Omega, 2020, 5, 32823–32843 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Extended experimental and computational methods; supplementary data and figures on simulation convergence, all computed CD, IR, Raman, ROA spectra, investigation on the effect of microsolvation and protonation state of the His imidazole groups on IR, Raman, ROA spectra, proof-of-concept on the calculation of IR, Raman, ROA spectra on randomized rotamers. See DOI: https://doi.org/10.1039/d3sc02202a |
| This journal is © The Royal Society of Chemistry 2023 |