Open Access Article
Open Access ArticleReagent prediction with a molecular transformer improves reaction data quality†
Mikhail
Andronov
 *ae,
Varvara
Voinarovska
*ae,
Varvara
Voinarovska
 b,
Natalia
Andronova
b,
Natalia
Andronova
 c,
Michael
Wand
c,
Michael
Wand
 ad,
Djork-Arné
Clevert
ad,
Djork-Arné
Clevert
 e and
Jürgen
Schmidhuber
f
e and
Jürgen
Schmidhuber
f
aIDSIA, USI, SUPSI, 6900 Lugano, Switzerland. E-mail: mikhail.andronov@idsia.ch
bInstitute of Structural Biology, Molecular Targets and Therapeutics Center, Helmholtz Munich – Deutsches Forschungszentrum für Gesundheit und Umwelt (GmbH), 85764 Neuherberg, Germany
cVia Berna 9, 6900 Lugano, Switzerland
dInstitute for Digital Technologies for Personalized Healthcare, SUPSI, 6900 Lugano, Switzerland
eMachine Learning Research, Pfizer Worldwide Research Development and Medical, Linkstr.10, Berlin, Germany
fAI Initiative, KAUST, 23955 Thuwal, Saudi Arabia
First published on 1st March 2023
Abstract
Automated synthesis planning is key for efficient generative chemistry. Since reactions of given reactants may yield different products depending on conditions such as the chemical context imposed by specific reagents, computer-aided synthesis planning should benefit from recommendations of reaction conditions. Traditional synthesis planning software, however, typically proposes reactions without specifying such conditions, relying on human organic chemists who know the conditions to carry out suggested reactions. In particular, reagent prediction for arbitrary reactions, a crucial aspect of condition recommendation, has been largely overlooked in cheminformatics until recently. Here we employ the Molecular Transformer, a state-of-the-art model for reaction prediction and single-step retrosynthesis, to tackle this problem. We train the model on the US patents dataset (USPTO) and test it on Reaxys to demonstrate its out-of-distribution generalization capabilities. Our reagent prediction model also improves the quality of product prediction: the Molecular Transformer is able to substitute the reagents in the noisy USPTO data with reagents that enable product prediction models to outperform those trained on plain USPTO. This makes it possible to improve upon the state-of-the-art in reaction product prediction on the USPTO MIT benchmark.
1 Introduction
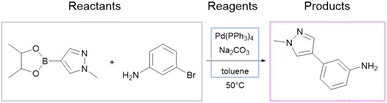
In pharmaceutical and other chemical industries, experts have to deal with organic synthesis problems all the time. Chemical reactions are the way substances are converted into each other, and the set of possible organic reactions comprises thousands of reaction types and millions of examples.1 In an attempt to facilitate the work with such a large number of options, chemists started creating automated computer-aided synthesis planning (CASP) systems. Currently, these systems, either based on expert-curated rules2,3 or machine learning techniques,4 demonstrate promising results in the prediction of organic reaction products5,6 and retrosynthesis paths.7,8However, there are caveats that are crucial for successful synthesis planning and often unaccounted for in CASP systems. Most importantly, one would like to take into account as much information about a chemical reaction as possible when modeling it. Among the most important aspects of a reaction besides reactants and products are reaction conditions (Fig. 1). The conditions comprise temperature, pressure, and other physical parameters as well as the chemical environment imposed by reagents, which are catalysts, solvents, and other molecules necessary for a reaction to occur. The conditions and reagents are integral to any reaction. The same reaction under different conditions can result in different outcomes.
In cheminformatics, all tasks of reaction modeling rely heavily on the datasets of known organic reactions. One of the most important of them at the moment is the USPTO dataset,9 which is publicly available and consists of reactions obtained by text mining from open-access texts from the United States Patents database. The reagents in this dataset are noisy, they may be often unspecified or incorrect, and the data does not report any temperature or pressure conditions. Therefore, the models for reaction product prediction or retrosynthesis cannot exactly benefit from full and reliable reaction information when developed using USPTO.
The reagent information is often overlooked in models for single-step retrosynthesis: even though some systems allow the prediction of retrosynthetic steps encompassing reagents,7 most of them only suggest reactants,10,11 leaving the chemist wondering about the actual procedure needed to conduct the proposed reaction. A separate reagent prediction model may help in this case.
1.1 Related work
In general, the proposal of suitable conditions for a novel or given reaction is a reaction modeling task machines can be used to solve. In fact, the conditions prediction subroutine is necessary for a successful CASP system that generates hundreds of plausible reactions that need to be validated.There have been substantial efforts to predict suitable reaction conditions or chemical contexts in various settings. For example, there are reports on using DFT to select suitable solvents for a reaction,12 or thermodynamic calculations to choose heterogeneous catalysts.13 Some focused on optimizing reaction conditions for particular reaction types using an expert system14 or machine learning.15–18 Gao et al.19 have used a fully connected neural network trained on the Reaxys20 data in the form of reaction fingerprints to predict reagents in a supervised classification manner. Also, Ryou et al.21 have extended this approach by using a graph network to encode the information in reaction graphs instead of using reaction fingerprints while also using Reaxys and treating the task as a supervised classification task.
The broad task of organic reaction modeling, whether it is reagent prediction, single-step retrosynthesis or product prediction, can be formulated as a sequence-to-sequence translation if the reactions are represented as reaction SMILES.22 The first attempts to use deep learning to predict reaction outcomes were made by Nam and Kim23 and Schwaller et al.24 This approach experienced significant advances with the adoption of the transformer25 as the deep learning model (transformers with “linearized self-attention” date back to 1992 (ref. 26)). The transformer performed very well in reaction prediction5,27 and single-step retrosynthesis7,28 and established state-of-the-art results in both these fields. A trained large-scale transformer can perform both single-step retrosynthesis and product prediction with impressive accuracy.29 The transformer has also been demonstrated to be suitable for multi-task reaction modeling: when trained in a BERT-like30 fashion to predict any masked tokens in a reaction, it can do both forward prediction and single-step retrosynthesis, as well as reagent prediction.31,32
1.2 Outline of the paper
This work proposes a deep learning method for reagent prediction. We treat the problem as a machine translation task and train a transformer25 model to predict the SMILES strings of reagents given the SMILES of reactants and products. Unlike the existing approaches designed specifically for reagent prediction, our formulation is not confined to a predefined set of possible reagents and allows the prediction of reagents for arbitrary reaction types. Whereas in principle our model is not the first transformer suitable for reagent prediction,31,32 it is the first one to be trained specifically for reagent prediction in a machine translation setting. We also demonstrate that the reagent prediction model can be used to improve a product prediction model trained on the USPTO dataset. First we predict missing reagents for not well-specified reactions in USPTO. Then we train a transformer for product prediction on the corrected USPTO and observe that it improves the accuracy of a basic Molecular Transformer,5 which is one of the state-of-the-art models, on the USPTO MIT benchmark.2 Materials and methods
2.1 Data
The largest and the most used open-access dataset of diverse organic chemical reactions at the moment is the dataset of about 2m reactions from US patents, commonly referred to as the USPTO dataset.9,33 It was assembled by text mining from openly accessible patents. The reactions in it are represented as reaction SMILES with atom mapping.Many machine learning tools for reaction modeling are trained on some preprocessed subsets of USPTO because it is an open dataset. Alternatively, there are proprietary reaction datasets. One of them, Reaxys, contains about 56 million hand-curated reactions. While researchers also use it to train ML models,19,34 the problem with it is that those models and data subsets are not allowed to be publicly shared.
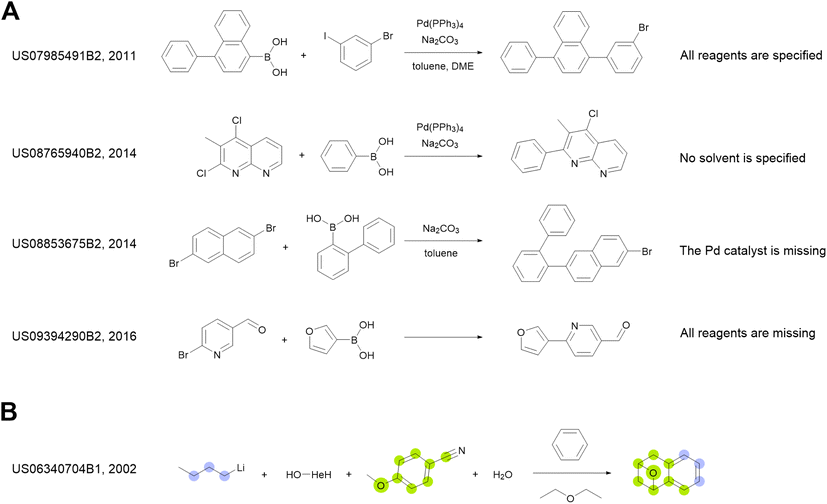
We use the whole USPTO as the training dataset for the reagent prediction model. To train and test the product prediction model, we use the subset of USPTO called USPTO MIT or USPTO 480K, which is a common benchmark for reaction product prediction.5,6 However, we do not use any subsets of USPTO as a test dataset for the reagent prediction model. The problem with the USPTO is that this dataset is assembled using text mining, so the reactions in it are recorded with a significant amount of noise. For example, different instances of the same reaction type may be written with different amounts of detail.35Fig. 2A shows examples of Suzuki coupling with the year and patent number. This reaction type makes up a significant portion of USPTO36 reactions. The Suzuki coupling generally requires a palladium catalyst, a base, and a suitable solvent. However, in many reactions of this type in USPTO the necessary reagents are not specified. This is also observed for other types of reactions. In addition, USPTO may contain reaction SMILES involving nonsensical molecules (Fig. 2B).
If such noisy reactions end up in the test dataset, it will not allow us to correctly evaluate the performance of the reagents model. Preliminary experiments in which we tested the reagents model on USPTO showed that often the model prediction does not match the ground truth sequence, even though the former is more sensible than the latter. To overcome this problem, we assembled our test set from the reactions in the Reaxys database. Since Reaxys is comprised of reactions manually extracted from scientific papers, we assume that the quality of reagents information there is ensured by human experts.
While gathering the Reaxys subset, we aimed at making it resemble the USPTO 50K37 dataset in its distribution of reaction types. The purpose of such a design is to make the test distribution close to the train distribution. We use USPTO 50K as a proxy for the training set because USPTO 50K is the only open subset of USPTO that contains reaction class labels. The subset of Reaxys used as the test comprises 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 reactions of 10 broad classes. Their distribution is displayed in Table 1. We aimed at making the class proportions in USPTO 50K and the Reaxys test set similar. The classes were determined using NameRXN software.38
729 reactions of 10 broad classes. Their distribution is displayed in Table 1. We aimed at making the class proportions in USPTO 50K and the Reaxys test set similar. The classes were determined using NameRXN software.38
| Reaction class | Proportion, USPTO 50K (%) | Proportion, Reaxys test (%) |
|---|---|---|
| Heteroatom alkylation and arylation | 28.73 | 28.11 |
| Acylation and related processes | 24.29 | 18.15 |
| Deprotections | 16.97 | 17.37 |
| C–C bond formation | 11.52 | 11.95 |
| Reductions | 9.72 | 11.10 |
| Protections | 1.35 | 4.53 |
| Functional group interconversion (FGI) | 3.89 | 4.13 |
| Functional group addition (FGA) | 0.51 | 2.46 |
| Oxidations | 1.70 | 2.10 |
| Heterocycle formation | 1.31 | 0.09 |
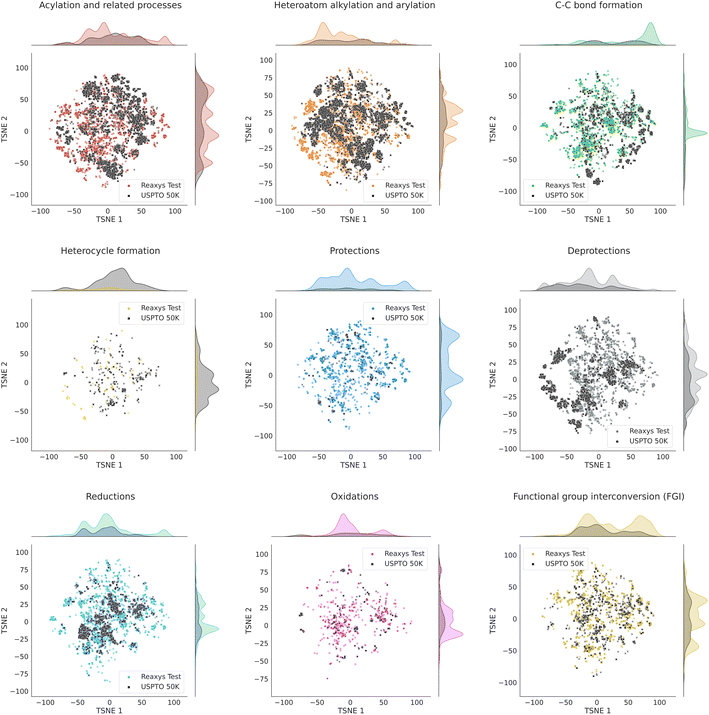
To further investigate the similarity of USPTO and the Reaxys subset we use, we employ the technique of parametric t-SNE, which is a dimensionality reduction method aiming at preserving closeness between points in higher-dimensional space. We represent each reaction as a reaction Morgan difference fingerprint39 of 2048 bits with both reagent- and non-reagent weight equal to 1. Using an implementation of parametric t-SNE from OpenTSNE,40 we project the fingerprint vectors of reactions in USPTO 50K on the 2D plane, and then use the same t-SNE model to obtain the projections of reactions in Reaxys. The absolute values of the coordinates of the t-SNE embeddings of reaction vectors bear no physical meaning. The closeness of the points in 2D reflects the closeness of the reaction vectors in the fingerprint space: similar reactions lie close together. Parametric t-SNE means that the coordinates of the 2D embeddings of reactions in Reaxys would lie close to those for similar reactions in USPTO 50K. In other words, the closeness of similar reactions will be preserved across datasets, not only within one dataset. The local structure of the second dataset is preserved but the absolute values of the coordinates of its points are determined by the coordinates of the points in the first dataset.
Fig. S1† in the ESI shows the t-SNE maps of USPTO 50K and our Reaxys test set. The maps for individual datasets are shown at the top of the figure. On the bottom, it demonstrates the overlap of those maps. One can see that the local structures of both datasets are similar: there is a significant overlap between the clusters of points in both datasets. Fig. 3 shows the overlapping t-SNE maps for individual classes of reactions. One can see that they also demonstrate a noticeable overlap, even though it is not ideal.
2.2 Model
For both reagents and product prediction we used the transformer25 — a deep learning model for autoregressive sequence-to-sequence modeling based entirely on the attention mechanism without using recurrent neural network layers. Although it was initially proposed for neural machine translation, it has been successfully adapted to work with chemical data in various cheminformatics problems.5,7,29,41The transformer is an encoder–decoder neural network architecture. The encoder is built of several layers which essentially consist of a multi-head attention part and a feed-forward layer. The multi-head attention updates the representations of every token in a batch according to eqn (1).
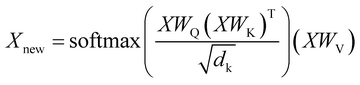 | (1) |
Here X is the matrix of the token embeddings, Xnew is the matrix of the token embeddings after a multi-head attention layer, WQ, WK, and WV are matrices of trainable parameters, and dk is the number of columns in WK. This mechanism resembles an update mechanism used in graph neural networks if we treat the batch of entries as nodes in a full graph.42 The decoder has a similar structure and learns the embeddings of tokens in the target sequence. Ultimately, the model uses the representations of all tokens both in the input sequence and the output sequence to predict the next token in the output sequence. The decoding stops when the model predicts the special “end-of-sequence” token. The ordering of the tokens is imposed by adding positional encodings (special periodic signals) to the token representations at the start of the training.25 By using a beam search, one can obtain several translations ordered by probability for an input sequence. The model produces output sequentially, token by token, treating the choice of each token as multi-class classification and conditioning this choice on the input sequence and the tokens already decoded for the given input sequence.
In our experiments, we used the OpenNMT43 implementation of the transformer for both the reagent and product prediction. We chose to use this particular solution to be consistent with Schwaller et al.5
2.3 Preprocessing of the training set
The transformer predicts the reagents for a reaction in the form of a SMILES string. As input, our model takes a reaction as a string with a “≫” separator, where to the left of the separator are the SMILES of the reactants separated by dots, and to the right are the SMILES of the products. The target sequence for each reaction is the SMILES of the reagents. This allows the model to predict reagents for a broad range of reactions without common restrictions: the number of reagents in a reaction and their particular roles are not predetermined.To train the reagents model, we take the copy of USPTO kindly provided by Schwaller et al.,5 but preprocess it to fit our setting. Instead of using the original train–validation–test split, we unite all those subsets together and choose 5000 reactions randomly for validation in this whole subset.
Our preprocessing pipeline for reagent prediction is as follows: for each reaction, we first remove all the auxiliary information written in the form of ChemAxon extended SMILES (CXSMILES). Then, we mix together all the molecules which are not products. The procedure of extracting the original data from patents included the detection of catalysts and solvents and placing them in the reagent section. However, we do not place our trust in it since it is quite imprecise and also does not account for other possible reagent types. Therefore, we separate reactants from reagents according to the fingerprint-based algorithm described by Schneider et al.37 and implemented in RDKit. A small number of all reactions, in this case, end up with no reactants whatsoever. For them, we decide on the separation based on the original atom mapping in USPTO: reactants are molecules with atom mapping labels that also appear in the products. We avoid using this approach for all reactions as the default atom mapping in USPTO is not reliable enough. Then, we canonicalize the SMILES of all molecules in a reaction, drop atom mapping and remove the isotope information if there are any. Finally, we order all molecules in the reaction: the molecules with the longest SMILES strings come first; strings of the same length are ordered alphabetically. We also tried implementing a step in which we remove all molecule duplicates in the reaction. This would make the reactions unbalanced but the reaction SMILES shorter while preserving the chemical context. However, this step did not prove to be useful and eventually, we did not include it in the preprocessing pipeline.
After processing every reaction in the described fashion, we proceed to remove rare reagents from the data, i.e. the reagents which appear in the training data less than 20 times. This lowers the number of unique reagents in the training set from 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602 (from which 26
602 (from which 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 were encountered only once) to 1314. The model is unlikely to learn to predict a reagent from such few examples even if they are correct, although the visual analysis shows that such rare reagents are in fact rather reactants in not well-specified reactions. For example, if a reaction includes several isomers of one reactant, only one of which is reported to become a product, all the other isomers get recognized as reagents. By removing rare reagents, we alleviate this problem. Finally, we drop duplicate reactions and the reactions where a product appears among reactants or reagents. In accordance with the common procedure of data augmentation in reaction modeling, we employ SMILES augmentation as implemented in the PySMILESutils Python package.44 Only the SMILES of reactants and products get augmented in the case of reagent prediction. In addition to that, we use “role augmentations”: some molecules from the side of the reagent have a chance to move to the reactants in an augmented example.
431 were encountered only once) to 1314. The model is unlikely to learn to predict a reagent from such few examples even if they are correct, although the visual analysis shows that such rare reagents are in fact rather reactants in not well-specified reactions. For example, if a reaction includes several isomers of one reactant, only one of which is reported to become a product, all the other isomers get recognized as reagents. By removing rare reagents, we alleviate this problem. Finally, we drop duplicate reactions and the reactions where a product appears among reactants or reagents. In accordance with the common procedure of data augmentation in reaction modeling, we employ SMILES augmentation as implemented in the PySMILESutils Python package.44 Only the SMILES of reactants and products get augmented in the case of reagent prediction. In addition to that, we use “role augmentations”: some molecules from the side of the reagent have a chance to move to the reactants in an augmented example.
All molecules in the target sequences are canonicalized and ordered by their detailed roles: catalysts come first, then redox agents, then acids and bases, then any other molecules and ions, but solvents come last. In this case, we utilize the model's autoregressive nature to predict the most important reagents first based solely on the input, and then the more interchangeable reagents based both on the input and the reagents suggested so far. A similar ordering of reagents by role was used by Gao et al.19 and it generally follows the line of thought of a chemist who would suggest reagents for a reaction based on their experience. The roles of the molecules are determined using the following heuristics:
(1) Every molecule in a SMILES string of reagents is assigned a role in the following order of decreasing priority: solvent, catalyst, oxidizing agent, reducing agent, acid, base, unspecified role.
(2) A molecule is a solvent if it is one of the standard 46 solvent molecules, like THF, hexane, benzene etc.
(3) A molecule is a catalyst if
(a) it is a free metal.
(b) it contains a cycle together with a metal or phosphorus atom.
(c) it is a metal halide.
(4) A molecule is an oxidizing agent if
(a) it contains a peroxide group.
(b) it contains at least two oxygen atoms and a transition metal or iodine atom.
(c) it is a standard oxidizing agent like free halogens.
(d) it is a standard halogenating agent.
(e) it contains both a positively charged atom and a negatively charged oxygen but is not a nitrate anion.
(5) A molecule is a reducing agent if it is one of the standard reducing agents or some hydride of boron, silicon or aluminum.
(6) A molecule is an acid if
(a) it is a derivative of sulphuric, sulfamic or phosphoric acid with the acidic –OH group intact.
(b) it is a carboxylic acid.
(c) it is a hydrohalic acid or a common Lewis acid like aluminium chloride.
(7) A molecule is a base if
(a) it is a tertiary or secondary amine.
(b) it contains a negatively charged oxygen atom and consists of only C, O, S, and P atoms.
(c) it consists only of lithium and carbon.
(d) it is the hydride ion or the hydroxide ion.
To tokenize our sequences, we employ the standard atomwise tokenization scheme.5 Additionally, we experimented with the scheme in which entire molecules get their own tokens, namely all solvents and some common reagents. However, this does not seem to improve the quality of a trained reagent prediction model, so we resort to standard atomwise tokenization in our final model.
For product prediction, we employ the same procedure that was employed by Schwaller et al.5 The tokenization is atomwise as well. Some of the current deep learning reaction prediction methods use explicit reagent information to make predictions,24,45,46 and some allow mixing all the precursors together, but the separation of reactant and reagent information improves the performance of such models.5,47,48 We trained product prediction models both in the separated setting (reactants and reagents are separated by the token “>” in the input sequences) and the mixed setting (all molecules are separated by dots in the input sequences). To evaluate the quality of the models, we used both the USPTO MIT test set and our Reaxys test set on which we tested the reagent prediction model. We did not use SMILES augmentations for product prediction.
2.4 Preprocessing of the test set
We use a subset of Reaxys data for testing purposes. To obtain it, we use the Reaxys web interface. In Reaxys, reaction SMILES do not contain reagents, which are enumerated separately by their IUPAC notation or common name and separated by semicolons. We employ the PubChemPy‡ package to retrieve SMILES of reagents from PubChem.49 We drop reactions in which reagents were absent or their SMILES could not be successfully retrieved. After constructing full reaction SMILES for all reactions, we canonicalize all molecules in the reactions and order them as we did with the training set. After proprocessing, every reaction in our test set has non-empty SMILES of reactants, reagents, and products. The final test set comprises 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 reactions.
729 reactions.
2.5 Training details
For both reagent and product prediction, we used the same transformer settings and hyperparameters used by Schwaller et al.:5 Adam optimizer,50 Noam learning rate schedule25 with 8000 warmup steps, a batch size of around 4096 tokens, accumulation count 4 and dropout rate 0.1. We did not conduct weight averaging across checkpoints. All the models were trained on an Nvidia GeForce GTX TITAN X GPU with 12 GB memory.3 Results and discussion
3.1 Model performance
Reagent prediction is not as straightforward as forward reaction prediction. A reaction may be carried out using different sets of reagents. To put it another way, there may be more than one plausible chemical context for a given reaction: catalysts, redox agents, acids, bases, and solvents in a reaction can be more or less replaceable. Therefore, multiple different sets of molecules might be correct predictions for a given transformation. Having that in mind, we chose the performance measures to be the following:(1) Exact match accuracy: the prediction of the model is considered correct if the symmetric difference between the set of predicted molecules and the set of the ground truth molecules is an empty set.
Example: A.C.B is an exact match to A.B.C.
(2) Partial match accuracy: the prediction counts as correct if the ground truth contains at least one of the predicted molecules.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Example: A.B is a partial match to A.C.D.
Example: A.B is a partial match to A.C.D.
(3) Recall: the number of the correctly predicted molecules divided by the number of molecules in the ground truth.
Example: A.B.C has 100% recall of A.C, A.D has 50% recall of A.B.C.D.
Here A, B, C, and D denote the SMILES strings of some molecules.
We use beam search with beam size 5 to obtain predictions from the transformer. Therefore, all performance metrics report the top-N predictions with N from 1 to 5. A correct top-N prediction means that the correct answer appeared among the first N sequences decoded with the beam search.
Additionally, our test set contains duplicate reactions with different reported reagent sets. While gathering performance statistics, we group predictions by unique reactions: if the model correctly predicts reagents for one of the duplicates, we count the reaction as correctly predicted.
The performance on the test set is summarized in Table 2.
| Metric | Top-1 | Top-2 | Top-3 | Top-4 | Top-5 |
|---|---|---|---|---|---|
| Exact match accuracy | 17.0 | 24.7 | 29.2 | 31.8 | 33.5 |
| Full recall | 19.2 | 28.4 | 35.1 | 39.3 | 42.8 |
| Partial match accuracy | 70.9 | 80.5 | 84.9 | 87.3 | 88.9 |
The model performs quite well on the test dataset. For each test reaction, each of the top-5 predictions is a valid SMILES string. An exact match of the prediction and the ground truth sequence is observed in 17.0% of the cases for top-1, 29.2% for top-3, and 33.5% for top-5. At the same time, full recall is higher at 19.2%, 28.4%, and 42.8%, respectively. As for the partial match between predictions and ground truth sequences, it is much higher at 70.9%, 84.9%, and 88.9% in the top-1, top-3, and top-5 cases, respectively. Thus, the model cannot correctly predict a single reagent for 11.1% of the reactions in the test dataset. In our evaluation, we do not use any methods to assess the plausibility of an incorrect prediction such as similarity metrics for interchangeable solvents, so the performance scores should be considered to be underestimates.
3.2 Model confidence
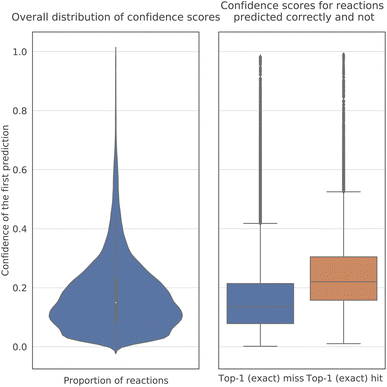
The confidence scores of the model are much lower than those5 of the Molecular Transformer for product prediction (Fig. 4). The probability of a decoded sequence is the product of the probabilities of all predicted tokens in it. In particular, their average value is between 0.1 and 0.2, whereas in reaction prediction most scores exceeded 0.9. The reason seems to be the nature of the problem, as several plausible sets of reagents may be proposed for a reaction, and the answer is not as unambiguous as in product prediction. Nonetheless, the confidence of the model is, on average, noticeably higher for correct predictions than for incorrect ones.3.3 Performance across publication years
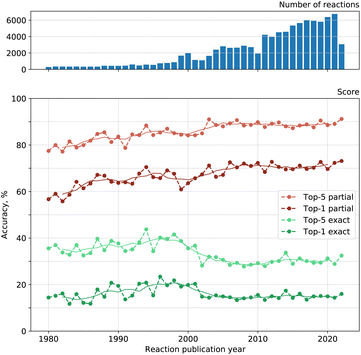
We looked into the dependence of the model on the publication date of reactions. As chemists discover new reaction types and new possible reagents for known reactions, the statistical knowledge gathered by a reagent model can become outdated.Fig. 5 shows both the exact and partial accuracy of our reagent model on reactions published every single year between 1980 and 2022. Solid lines illustrate the moving average of accuracy over five years with a centered window. Top-1 exact match accuracy tends to increase on average from 1980 to 1998, then we see a decrease until 2005 and a plateau after that. The picture is similar for top-5 exact accuracy and top-2 to top-4 as well. The dependence for total recall is alike. Top-1 partial match accuracy tends to increase on average from 1980 to 2008 and stagnate after that. Top-2 to top-5 accuracies demonstrate similar behavior as well.
3.4 Performance across reaction classes
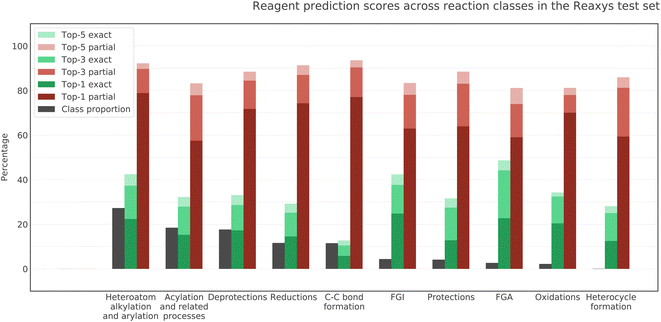
We investigated the performance of the model on different classes of reactions included in our test dataset. The middle and rightmost bars for each reaction class in Fig. 6 show the rate of exact and partial matches of the model prediction and ground truth. The leftmost bars reflect the relative proportion of each reaction class in the test dataset. We can see that the quality of the model predictions differs noticeably between classes. This difference in performance is most likely due to the difference between the data distribution in the train and in the test for different classes of reactions. The model demonstrates the best top-5 exact match accuracy for FGA, FGI, heteroatom alkylation and arylation and the best top-5 partial match accuracy for C–C bond formation. At the same time, C–C bond formation has the lowest exact match accuracy. The reason for that must be the wide variety of interchangeable reagents in this reaction class, especially metal-based catalysts. As we use USPTO 50K as a proxy for the training set, we assume that the least represented reaction classes in the former are also the least represented in the latter. The four least represented classes in USPTO 50K are FGA, oxidations, protections, and heterocycle formations. Interestingly, the model exhibits good generalization in all these classes.3.5 Performance across reagent roles
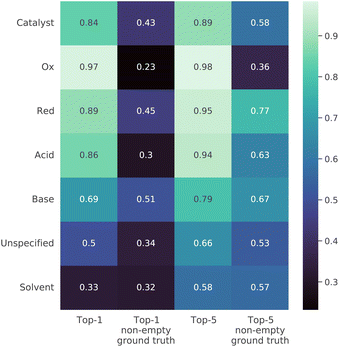
We also examined the quality of the model predictions for each reagent role (Fig. 7). The first and third columns in the table in the figure show that in both the top-1 and top-5 cases the solvents are the most difficult to predict. This is most likely due to the fact that they are often the most interchangeable. However, reactions need not involve reagents of every possible role, and the picture is somewhat different in the case where the roles in the ground truth sequence were strictly nonempty SMILES strings. In this case, it was most difficult to predict oxidizing agents. This effect is likely related to flawed heuristics for the classification of reagents or to the strong difference between the typical oxidizing agents in the train and in the test. The more detailed performance summary across both reagent roles and reaction classes is shown in Fig S2† in the ESI.3.6 Analysis of prevalence of reaction types
In the test set, there are 684 unique reaction types determined by NameRXN. These types can be split into five “bins” by occurrence frequency. The summary of those bins is given in Table 3. The most common types are those which occur more than a thousand times in the test set. There are only 20 such types. Among others, they include Suzuki coupling, Williamson ether synthesis, aldehyde reductive amination, N-Boc protection, and nitrile reduction. Heterocycle formation, oxidations, FGI, and FGA are not present among the common types. Out of all unique types, 245 are singular, meaning that they are represented in the test set by only one instance. Frequent types have 101 to 1000 instances, rare types have 11 to 100 instances and very rare types have from 2 to 10 reaction examples. The performance of the reagent model decreases with the decrease in type prevalence, which is expected.| Occurrence | N | Criterion | Reactions | Top-1 exact acc., % | Top-1 partial acc., % |
|---|---|---|---|---|---|
| Common | 20 | N > 1000 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 633 |
17.0 | 73.5 |
| Frequent | 67 | 100 < N ≤ 1000 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
16.2 | 65.1 |
| Rare | 120 | 10 < N ≤ 100 | 4219 | 13.5 | 60.3 |
| Very rare | 232 | 1 < N ≤ 10 | 947 | 14.2 | 53.1 |
| Singular | 245 | N = 1 | 245 | 13.5 | 62.4 |
In the “common” and “frequent” bins there are no reaction types with only a single possible reagent in any role. In the “rare” and “very rare” bins there is a small number of types in which it is the case. However, the analysis is limited by NameRXN and by the heuristics of role classification. If the type label is a name reaction, which is an infrequent case, then the reactions with that label may have a single option for one of the roles. For example, all instances of the rare “8.1.24 Ketone Swern oxidation” type have an oxidizing agent which is the same for all, and the instances of the rare “9.1.2 Appel chlorination” and the very rare “1.7.8 Ullmann condensation” types all have their one specific catalyst. Also, some “very rare” types may have only one option even for solvents in the test set, but it may be an accident due to under-representation. The reagent may or may not give a perfect top-1 prediction for all reactions of such types.
3.7 Improving product prediction
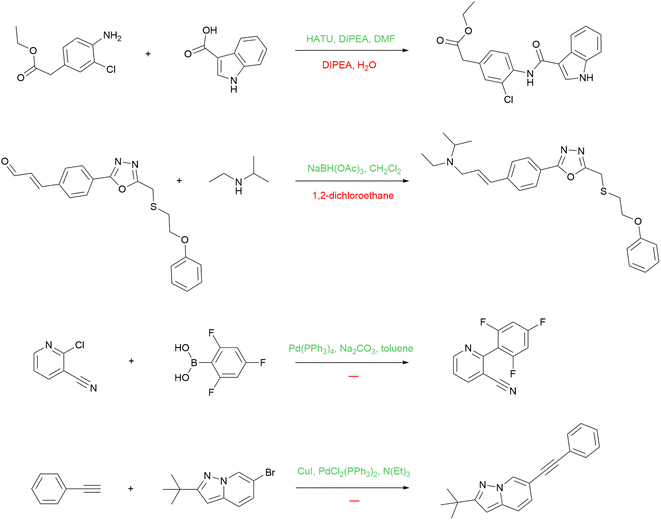
Besides predicting reagents per se, our model has another application: we can use it to augment USPTO with more reagents for reactions that are lacking them, and train a product prediction model on this augmented dataset. As noted above, many reactions in the USPTO contain reagents that are under-specified, yet many many reactions in USPTO contain the full set of reagents at the same time. This allows us to use a trained reagent prediction model to recover missing reagents in some reactions. We apply the model trained on the entire USPTO to the USPTO MIT subset. During training, we make sure that the USPTO MIT test set does not overlap with the training set for the reagent model.There can be various strategies for reagent string replacement. We apply the following rule: if the top-1 prediction of the model contains more molecules than the original string, then the prediction replaces that string. With that, we can improve the reactions with missing reagents without corrupting the good ones. We are aware, however, that this strategy is not ideal and we are convinced that better ones are possible. Some examples of the reactions with reagents improved after the reagent model inference are shown in Fig. 8.
The first reaction is an example of peptide coupling. The typical reagents in this case comprise HOBt or its analogs (e.g. HATU) usually used together with Hünig's base (DIPEA). The reagent model reintroduces the missing reagents to the reaction. The second one is an example of reductive amination, and the information about the solvent alone is not enough. The model proposed a suitable reducing agent, sodium triacetoxyborohydride. The last two reactions are Suzuki coupling and Sonogashira reaction, respectively. The model suggests the standard reagents that define these reaction types.
We compared two models, both of which were standard Molecular Transformers with the same hyperparameters but trained on different data. The first model, which we denote as “MT base”, was trained on the standard USPTO MIT. This is the model from the original Molecular Transformer paper.5 The second model, which we denote as “MT new”, was trained on USPTO MIT in which some of the reactions had reagents replaced according to the procedure described above. We chose top-1 exact match accuracy as the quality metric. Before testing on Reaxys, we reassigned the reactant–reagent partition in every test reaction with the role assignment algorithm.37 This was done to be consistent with the inference procedure, in which the reagents that will be replaced are the reagents determined by this algorithm. Additionally, we trained another Molecular Transformer for product prediction without any reagents in the source sequences. The performance summary of the models is presented in Table 4.
| Reaxys | USPTO MIT | |
|---|---|---|
| MT, no reagents | 77.3 | 84.0 |
| MT base, mixed | 82.0 | 87.7 |
| MT new, mixed | 83.0 | 88.3 |
| MT base, separated | 84.3 | 89.2 |
| MT new, separated | 84.6 | 89.6 |
The results of the base model are reproduced as described by Schwaller et al.5 without SMILES augmentations, checkpoint averaging, or model ensembling. The new model performs better than the old model on both Reaxys and USPTO in both separated and mixed settings. This performance improvement is statistically significant. To prove the statistical significance, we employed McNemar's test.51 The details are provided in the ESI.† The performance on Reaxys is worse than on USPTO because the distribution of data in Reaxys differs more from the distribution in the training set than in the USPTO test set. However, it is important to emphasize that the USPTO test set also underwent a reagent change to test the new model. The performance in the mixed setting is slightly worse than in the separated setting, which is expected.5 The score of the model trained with no reagents is expectedly the lowest both on Reaxys and USPTO. However, surprisingly, it is only 4.7 percentage points below the base model's score on Reaxys and 3.7 percentage points below the base model's score on USPTO. Therefore, we can conclude that even though the reagent information helps the product models trained on USPTO, which it should from a chemical perspective, the effect is not that drastic. However, we conjecture that such improvement will be much more noticeable on a larger scale, e.g. if all the models are trained on the entire Reaxys. We suggest that this is a manifestation of USPTO's flaws: the dataset does not contain many reactions in which the same reactant transforms into different products under different conditions.
4 Conclusions
A transformer neural network, which is one of the models used to achieve state-of-the-art results in reaction prediction, can also learn to successfully predict reagents for organic reactions, which is important for recommending reaction conditions. The reagent prediction model receives an atom-mapping-free reaction SMILES string with no reagents and suggests multiple possible sets of reagents for it. Our work is the first to use the strategy of training a reagent prediction model on USPTO and testing it on a Reaxys subset, demonstrating its generalization capabilities. We also used the reagent prediction model to improve the performance of a product prediction model on USPTO MIT in a self-supervised fashion. In order to do that, we used the reagent model to reconstruct the missing reagents to the reaction data before training the product prediction model on it. Since reagent information is important to predict reaction products, our approach allows a state-of-the-art model for reaction prediction to be outperformed while being model-agnostic. In our work, in particular, we improve upon the score of the Molecular Transformer on the USPTO MIT (USPTO 480K) benchmark dataset.Data availability
The link to the repository with the paper code: https://github.com/Academich/reagents. The links to access the USPTO data and Reaxys reaction ID's used in the experiments are provided in the ESI.†Author contributions
M. A. conceptualized the paper idea. M. A. and V. V. gathered and preprocessed the data for experiments. J. S., D. C. and M. W. acquired the research funding, administered the project and provided supervision. M. A. developed the software and carried out computational experiments. M. A. and N. A. developed the methodology, designed experiments, and validated the experimental results. M. A., V. V., M. W., and J. S. wrote the manuscript with inputs from all co-authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was funded by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Actions, grant agreement “Advanced machine learning for Innovative Drug Discovery (AIDD)” No. 956832.Notes and references
- P.-M. Jacob and A. Lapkin, React. Chem. Eng., 2018, 3, 102–118 RSC.
- T. Klucznik, B. Mikulak-Klucznik, M. P. McCormack, H. Lima, S. Szymkuć, M. Bhowmick, K. Molga, Y. Zhou, L. Rickershauser, E. P. Gajewska, A. Toutchkine, P. Dittwald, M. P. Startek, G. J. Kirkovits, R. Roszak, A. Adamski, B. Sieredzińska, M. Mrksich, S. L. Trice and B. A. Grzybowski, Chem, 2018, 4, 522–532 CAS.
- H. Gelernter, J. R. Rose and C. Chen, J. Chem. Inf. Comput. Sci., 1990, 30, 492–504 CrossRef CAS.
- K. Lin, Y. Xu, J. Pei and L. Lai, Chem. Sci., 2020, 11, 3355–3364 RSC.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- C. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Chem. Sci., 2020, 11, 3316–3325 RSC.
- C. Shi, M. Xu, H. Guo, M. Zhang and J. Tang, Proceedings of the 37th International Conference on Machine Learning, 2020 Search PubMed.
- Chemical reactions from US patents (1976-Sep-2016) dataset, https://figshare.com/articles/dataset/Chemical_reactions_from_US_patents_1976-Sep2016_/5104873, (accessed October 29, 2020).
- M. H. Lin, Z. Tu and C. W. Coley, J. Cheminf., 2022, 14, 15 Search PubMed.
- P. Seidl, P. Renz, N. Dyubankova, P. Neves, J. Verhoeven, J. K. Wegner, M. Segler, S. Hochreiter and G. Klambauer, J. Chem. Inf. Model., 2022, 62, 2111–2120 CrossRef CAS PubMed.
- H. Struebing, Z. Ganase, P. G. Karamertzanis, E. Siougkrou, P. Haycock, P. M. Piccione, A. Armstrong, A. Galindo and C. S. Adjiman, Nat. Chem., 2013, 5, 952–957 CrossRef CAS PubMed.
- H. Toulhoat and P. Raybaud, Catal. Sci. Technol., 2020, 10, 2069–2081 RSC.
- G. Marcou, J. Aires de Sousa, D. A. R. S. Latino, A. de Luca, D. Horvath, V. Rietsch and A. Varnek, J. Chem. Inf. Model., 2015, 55, 239–250 CrossRef CAS PubMed.
- M. R. Maser, A. Y. Cui, S. Ryou, T. J. DeLano, Y. Yue and S. E. Reisman, J. Chem. Inf. Model., 2021, 61, 156–166 CrossRef CAS PubMed.
- V. A. Afonina, D. A. Mazitov, A. Nurmukhametova, M. D. Shevelev, D. A. Khasanova, R. I. Nugmanov, V. A. Burilov, T. I. Madzhidov and A. Varnek, Int. J. Mol. Sci., 2022, 23, 248 CrossRef CAS PubMed.
- E. Walker, J. Kammeraad, J. Goetz, M. T. Robo, A. Tewari and P. M. Zimmerman, J. Chem. Inf. Model., 2019, 59, 3645–3654 CrossRef CAS PubMed.
- N. H. Angello, V. Rathore, W. Beker, A. Wołos, E. R. Jira, R. Roszak, T. C. Wu, C. M. Schroeder, A. Aspuru-Guzik, B. A. Grzybowski and M. D. Burke, Science, 2022, 378, 399–405 CrossRef CAS PubMed.
- H. Gao, T. J. Struble, C. W. Coley, Y. Wang, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2018, 4, 1465–1476 CrossRef CAS PubMed.
- Reaxys database, https://www.reaxys.com Search PubMed.
- S. Ryou, M. R. Maser, A. Y. Cui, T. J. DeLano, Y. Yue and S. E. Reisman, 2020, preprint, DOI: DOI:10.48550/arXiv.2007.04275.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- J. Nam and J. Kim, 2016, preprint, DOI: DOI:10.48550/arXiv.1612.09529.
- P. Schwaller, T. Gaudin, D. Lányi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- J. Schmidhuber, Neural Comput., 1992, 4, 131–139 CrossRef.
- G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- I. V. Tetko, P. Karpov, R. Van Deursen and G. Godin, Nat. Commun., 2020, 11, 5575–5585 CrossRef CAS PubMed.
- R. Irwin, S. Dimitriadis, J. He and E. J. Bjerrum, Mach. learn.: sci. technol., 2022, 3, 015022 Search PubMed.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, 2018, preprint, DOI:10.48550/arXiv.1810.04805.
- A. C. Vaucher, P. Schwaller and T. Laino, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.13273310.v1.
- J. Lu and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 1376–1387 CrossRef CAS PubMed.
- D. M. Lowe, Extraction of chemical structures and reactions from the literature. PhD Dissertation, University of Cambridge, Cambridge, UK, 2012 DOI:10.17863/CAM.16293.
- M. H. Segler and M. P. Waller, Chem. – Eur. J., 2017, 23, 5966–5971 CrossRef CAS PubMed.
- M. Andronov, M. V. Fedorov and S. Sosnin, ACS Omega, 2021, 6, 30743–30751 CrossRef CAS PubMed.
- A. Thakkar, T. Kogej, J.-L. Reymond, O. Engkvist and E. J. Bjerrum, Chem. Sci., 2020, 11, 154–168 RSC.
- N. Schneider, N. Stiefl and G. A. Landrum, J. Chem. Inf. Model., 2016, 56, 2336–2346 CrossRef CAS PubMed.
- NameRXN, https://www.nextmovesoftware.com/namerxn.html Search PubMed.
- N. Schneider, D. M. Lowe, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 39–53 CrossRef CAS PubMed.
- P. G. Poličar, M. Stražar and B. Zupan, bioRxiv, 2019, 731877, DOI:10.1101/731877.
- N. Frey, R. Soklaski, S. Axelrod, S. Samsi, R. Gomez-Bombarelli, C. Coley and V. Gadepally, 2022, preprint, DOI:10.26434/chemrxiv-2022-3s512.
- C. Joshi, The Gradient, 2020 Search PubMed.
- G. Klein, Y. Kim, Y. Deng, J. Senellart and A. Rush, Proceedings of ACL 2017, System Demonstrations, Vancouver, Canada, 2017, pp. 67–72 Search PubMed.
- E. Bjerrum, T. Rastemo, R. Irwin, C. Kannas and S. Genheden, ChemRxiv, 2021, preprint, DOI:10.26434/chemrxiv-2021-kzhbs.
- W. W. Qian, N. T. Russell, C. L. W. Simons, Y. Luo, M. D. Burke and J. Peng, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.11659563.v1.
- H. Bi, H. Wang, C. Shi, C. Coley, J. Tang and H. Guo, Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 904–913 Search PubMed.
- M. Sacha, M. Bła, P. Byrski, P. D
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) browski-Tumański, M. Chromiński, R. Loska, P. Włodarczyk-Pruszyński and S. Jastrzebski, J. Chem. Inf. Model., 2021, 61, 3273–3284 CrossRef CAS PubMed.
browski-Tumański, M. Chromiński, R. Loska, P. Włodarczyk-Pruszyński and S. Jastrzebski, J. Chem. Inf. Model., 2021, 61, 3273–3284 CrossRef CAS PubMed. - K. Do, T. Tran and S. Venkatesh, Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019, pp. 750–760 Search PubMed.
- Pubchem database, https://pubchem.ncbi.nlm.nih.gov/ Search PubMed.
- D. P. Kingma and J. Ba, arXiv, 2015 DOI:10.48550/arXiv.1412.6980.
- T. G. Dietterich, Neural Comput., 1998, 10, 1895–1923 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06798f |
| ‡ https://github.com/mcs07/PubChemPy |
| This journal is © The Royal Society of Chemistry 2023 |