Open Access Article
Open Access ArticleGraphene foam membranes with tunable pore size for next-generation reverse osmosis water desalination†
Duc Tam
Ho‡
 ,
Thi Phuong Nga
Nguyen
,
Arun
Jangir
and
Udo
Schwingenschlögl
,
Thi Phuong Nga
Nguyen
,
Arun
Jangir
and
Udo
Schwingenschlögl
 *
*
Physical Science and Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia. E-mail: udo.schwingenschlogl@kaust.edu.sa
First published on 31st May 2023
Abstract
The development of carbon-based reverse osmosis membranes for water desalination is hindered by challenges in achieving a high pore density and controlling the pore size. We use molecular dynamics simulations to demonstrate that graphene foam membranes with a high pore density provide the possibility to tune the pore size by applying mechanical strain. As the pore size is found to be effectively reduced by a structural transformation under strain, graphene foam membranes are able to combine perfect salt rejection with unprecedented water permeability.
New conceptsReverse osmosis is currently the leading technology for water desalination. However, conventional polyamide membranes suffer from the permeability-selectivity trade-off, i.e., high water permeability comes along with low salt rejection and vice versa, causing high energy costs. Alternative techniques based on carbon nanostructures cannot compete with the polyamide membranes due to challenges in controlling the pore density and size. In this study, we discover by molecular dynamics simulations that honeycomb and triangular graphene foam membranes can overcome these challenges by combining a high pore density (two orders larger than in the case of other carbon-based membranes) with the possibility to tune the pore size by applying strain. In particular, we find that strain triggers structural transformations that result in a significant reduction of the pore size. Consequently, honeycomb and triangular graphene foams reject salt perfectly with an unprecedented water permeability. Our work therefore solves the main bottle-neck of the next generation of reverse osmosis membranes. Furthermore, we broaden the fundamental understanding of nanoscale mechanical metamaterials, which will be of great interest to readers from many disciplines. |
Water scarcity is one of the largest global risks1 with 4.0 billion people living under conditions of severe water stress at least one month of the year during 1996–20062 and the number being predicted to increase to 5.6 billion people in 2050.3 Water desalination by reverse osmosis is a possible solution thanks to the availability of seawater. The method is currently used to produce 65.5 million m3 of desalinated water per day (69% of the total production).4 However, the employed polyamide membrane technology suffers from low fouling resistance, low mechanical, chemical, and thermal stabilities, and high energy consumption of 3–4 kW h m−3
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 due to the selectivity–permeability trade-off.6
5 due to the selectivity–permeability trade-off.6
Carbon-based nanostructures, including porous graphene, carbon nanotubes, and graphene oxide, provide high chemical and thermal stabilities as well as potential to achieve high salt rejection and water permeability, which is essential for reverse osmosis membranes.7 The high water permeability is due to the atomic thickness of porous graphene (mass transport inversely proportional to the membrane thickness according to the Hagen–Poiseuille law)8 and the atomically smooth pores (low friction) of carbon nanotubes9 and graphene oxide.10 While both experiments11 and molecular dynamics simulations8 show that the single pore water permeabilities are orders of magnitude higher, the effective water permeabilities of porous graphene and carbon nanotube membranes are comparable to those of polyamide membranes because of low pore densities.7 The pore size has to exceed a critical value for the water molecules to cross and has to stay below a critical value for the salt ions to be rejected. Unfortunately, control of the pore size is challenging, causing poor salt rejection as compared to polyamide membranes. Defects in porous graphene lead to large pore sizes of 10–150 Å,12 exceeding the sizes of hydrated Na+ (6.6 Å) and Cl− (7.2 Å),13 and carbon nanotube diameters below 8.1 Å for perfect salt rejection are difficult to achieve.14,15 While graphene oxide can be readily fabricated, it swells when subjected to moisture, losing the ability to reject salt ions.16
In this study, we use molecular dynamics simulations to investigate the water desalination performance of graphene foam membranes, which are stable according to solid state self consistent field17 and density functional theory18,19 predictions. Synthesis of graphene foam has been reported in ref. 20. We demonstrate for graphene foam excellent potential in water desalination due to high pore densities and the possibility to tune the pore size by applying strain. Pore areas from 66 to 396 Å2 are found to provide perfect salt rejection with water permeabilities from 14 to 122 l cm−2 day−1 MPa−1. Importantly, the proposed membranes can be cleaned from fouling by enlarging the pore size through the release of strain.
Results and discussions
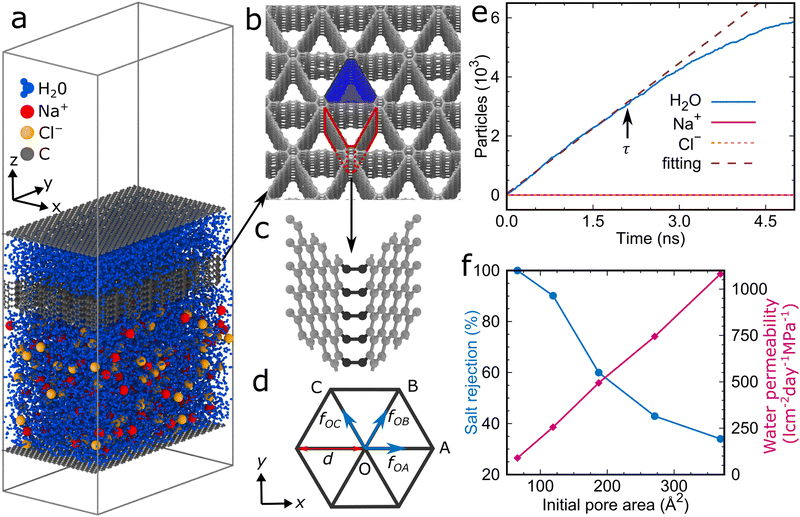
The simulation model (Fig. 1a) consists of the graphene foam membrane (Fig. 1b and 1c), the feed zone with 7921 water molecules, 117 Na+ ions, and 117 Cl− ions (corresponding to a salt concentration of 1.2 M, i.e., double that of seawater to reduce statistical effects by enhancing the interaction between the ions and membrane), the permeate zone with 2640 water molecules, and two graphene sheets acting as rigid pistons. The size of the simulation box is 50.3 Å in the x-direction and 87.1 Å in the y-direction. Periodic boundary conditions are applied in all directions, with a 110 Å vacuum layer added in the z-direction to avoid spurious interaction. We consider a graphene foam membrane with an initial pore area (colored blue in Fig. 1b) of 66 Å2 and a thickness of 12 Å.A molecular statics simulation is carried out initially using the conjugate gradient method with a total energy tolerance of 10−6 between successive iterations, followed by a molecular dynamics simulation at 300 K (canonical ensemble) with an upward/downward pressure of 100.0 MPa applied to the bottom/top piston for 200 ps. Then, the downward pressure is set to 0.1 MPa and the water molecules, Na+ ions, and Cl− ions in the permeate zone are counted as a function of the time (Fig. 1e). The water permeability is calculated as P = v/(AΔp), where v is the flow rate of water obtained as the slope of a linear fitting curve from time 0 to the moment τ when half of the water molecules have reached the permeate zone, A is the area of the membrane, and Δp is the pressure difference between the feed and permeate zones. The salt rejection is defined as R = (1 −Cp/Cf) × 100%, where Cp and Cf are the concentrations of salt ions in the permeate and feed zones at time τ, respectively. Further details can be found in the Simulation Methods and a video of the reverse osmosis process is provided as Supporting Information.
We obtain for the graphene foam membrane with an initial pore area of 66 Å2 and a thickness of 12 Å a water permeability of 90 l cm−2 day−1 MPa−1 with perfect salt rejection. In addition, similar to carbon nanotube membranes (where the atomic smoothness of the carbon nanotubes gives rise to a nearly frictionless transport),21 it turns out that the water permeability does not depend on the thickness of the graphene foam membrane, as, for example, we obtain the same numerical value when the thickness is multiplied by 10 (Fig. S3 in the ESI†).
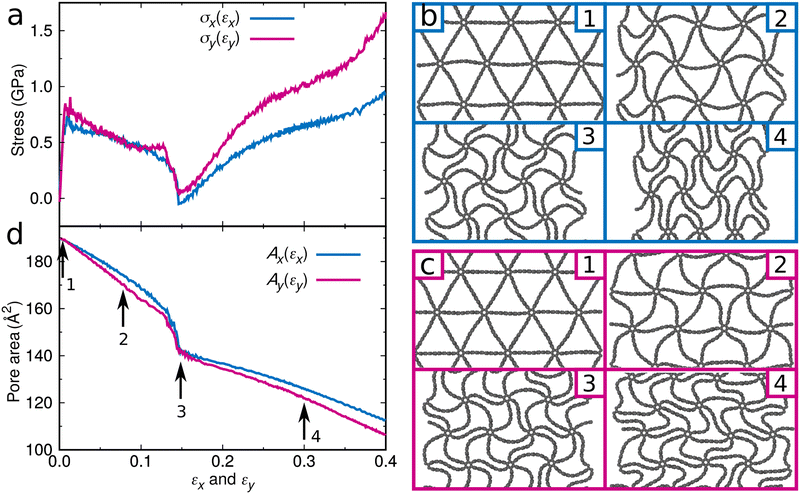
To study the effect of the initial pore area on the water desalination performance, we stepwise enlarge it to 369 Å2. Fig. 1f shows that the water permeability is enhanced to 1,081 l cm−2 day−1 MPa−1 (resembling the value of (1.35 × 10−16 m3 s−1)/(480 MPa × 246 Å2) = 988 l cm−2 day−1 MPa−1 obtained in ref. 22 for a graphene membrane with circular pores of 246 Å2 area and a flow rate of 1.35 × 10−16 m3 s−1 at a pressure of 480 MPa using molecular dynamics simulations and an analytical model, the difference in the required pore area being explained by the different pore shapes) but the salt rejection suffers dramatically (34%). We therefore tune the pore area by applying mechanical strain, see the Simulation Methods for details. Fig. 2 presents the response of the graphene foam membrane with an initial pore area of 187 Å2 to strain applied in the x- and y-directions. The stress–strain curves obtained for the two directions are similar with linear elasticity up to an applied strain of about 0.005 followed by a sudden drop of the stress (Fig. 2a).
The drop can be attributed to buckling of the graphene skeleton: We consider a continuum model based on the characterized length d of the pore (Fig. 1d). In the stress state (σx, σy, σxy) the forces per unit length (unit N m−1) on the elements OA, OB, and OC (Fig. 1d) are given by23
 | (1) |
 | (2) |
 | (3) |
 | (4) |
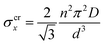 | (5) |
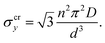 | (6) |
Classical plate theory cannot be used to calculate the bending stiffness directly from Young's modulus E and Poisson's ratio ν as D = Et3/12(1 −ν2), because the thickness t is not well-defined in the case of bending. Instead, the bending stiffness is obtained from the relation
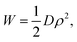 | (7) |
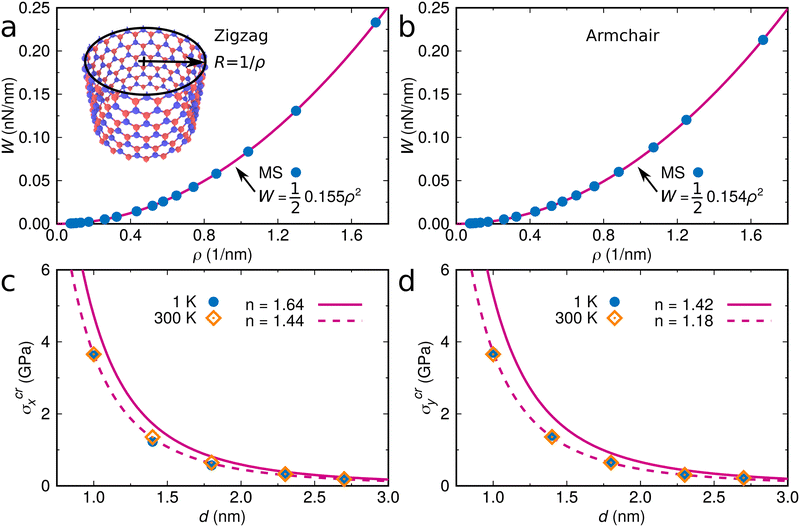
It turns out that Eqn (5) and (6) agree well with the trend (∝d−3) obtained by molecular dynamics simulations for the critical stress as a function of the characteristic length of the pore (Fig. 3c and d). Fitting of the data leads to n = 1.44 for loading in the x-direction and n= 1.18 for loading in the y-direction. These values are smaller than predicted by column-beam theory (1.64 and 1.42, respectively25), because the assumption of linearly connected elements is violated (ring-like connection; Fig. 1d). Note that temperature effects on the critical stresses are small (Fig. 3c and d).
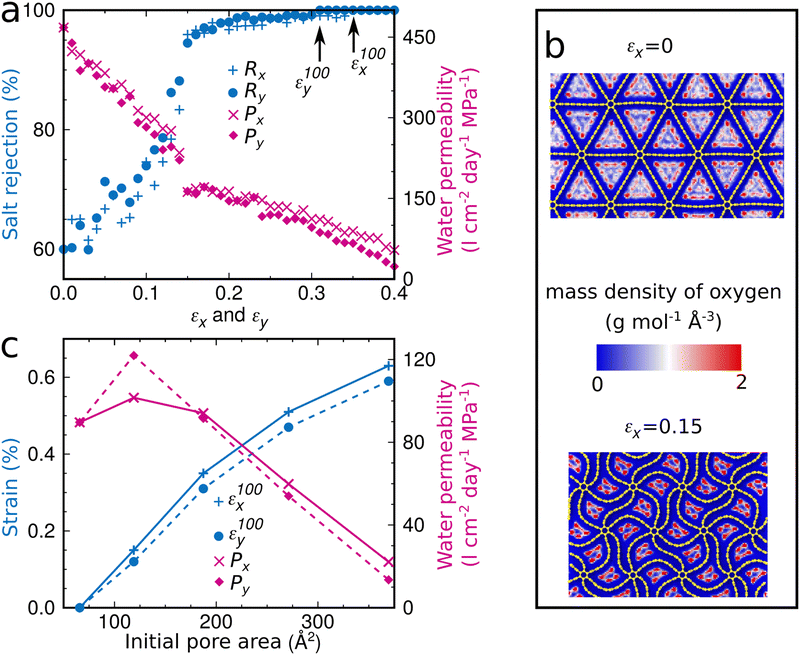
The buckling triggers a structural transformation in the graphene foam membrane when strain is applied (Fig. 2b and c). This localized and fully elastic (i.e., reversible) transformation is complete at an applied strain of about 0.15, while at higher applied strain the new shape is further accentuated. The buckling will affect the water desalination performance, as the pore area decreases (Fig. 2d). For example, strain of 0.015 applied in the x-direction of the graphene foam membrane with an initial pore area of 187 Å2 significantly enhances the salt rejection from 60% to 96%. Perfect salt rejection is achieved at εx100 = 0.35 (Fig. 4a), which corresponds to a pore area of 119 Å2 (Fig. 2d). Note that the salt rejection of the unstrained graphene foam membrane with an initial pore area of 119 Å2 is only 90% (Fig. 1f), indicating that the effective pore area under strain is much smaller. The reason is that the special pore shape (narrow at one end and wider at the other end) induced by the structural transformation allows passage only at the wider end (Fig. 4b). A similar behavior is observed for loading in the y-direction with perfect salt rejection achieved at εy100 = 0.31. The slightly lower water permeability and higher salt rejection as compared to loading in the x-direction are consistent with the slightly smaller pore area (Fig. 2d). While maintaining perfect salt rejection, ultrahigh water permeabilities of Px100 = 94 l cm−2 day−1 MPa−1 and Py100 = 92 l cm−2 day−1 MPa−1 are achieved for loading in the x- and y-directions, respectively. We also find that εx100 and εy100 increase when the initial pore area increases from 66 to 396 Å2, whereas Px100 and Py100 decrease (Fig. 4c). For a given initial pore area, the desalination conditions are best at εx100 and εy100 for loading in the x- and y-directions, respectively, because the salt rejection is perfect with the largest water permeability (Fig. 4a). Our simulation results therefore demonstrate that tuning of the pore area by applying mechanical strain is a highly effective strategy to obtain graphene foam membranes that combine perfect salt rejection with ultrahigh water permeability.
While the water permeability through a single pore is of the same order of magnitude as reported for graphyne,26 porous graphene,8 and carbon nanotube14 membranes, the intrinsic pore densities of graphene foam (from 0.7 × 1014 cm−2 to 1.5 × 1014 cm−2) and graphyne (9.3 × 1014 cm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26) membranes are much larger than the extrinsic pore densities of porous graphene (1.0 × 1012 cm−2
26) membranes are much larger than the extrinsic pore densities of porous graphene (1.0 × 1012 cm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11) and carbon nanotube (2.5 × 1011 cm−2
11) and carbon nanotube (2.5 × 1011 cm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9) membranes. As a result, the water permeabilities of the graphene foam and graphyne membranes are two orders of magnitude larger, and even three orders of magnitude as compared to conventional polyamide membranes27 (see Table 1 for a comparison). While tension can be used to enlarge the pores of graphene foam membranes and some two-dimensional materials,28,29 pore size reduction for perfect salt rejection (the most challenging issue of the next generation of membranes) by compression is only possible in the case of graphene foam membranes. While the pore size of graphene foam membranes can be controlled by compression due to buckling of the graphene skeleton (resulting from the atomic thickness of graphene), it is impossible to control the pore size of graphyne or any other two-dimensional material by compression due to the possibility of out-of-plane buckling. In contrast to the model employed in this study for describing graphene foam membranes, in reality the pores may not be perfectly directional and they may have different sizes and shapes, though highly directional pores were observed in graphene foam by high resolution transition electron microscopy.20 We find that the graphene skeleton buckles irrespective of the pore size (Fig. 4c). It also buckles irrespective of the pore shape and in the case of a non-uniform membrane with pores of different sizes and shapes (Fig. S4 in the ESI†), which implies that the pore size still can be tuned by strain.
9) membranes. As a result, the water permeabilities of the graphene foam and graphyne membranes are two orders of magnitude larger, and even three orders of magnitude as compared to conventional polyamide membranes27 (see Table 1 for a comparison). While tension can be used to enlarge the pores of graphene foam membranes and some two-dimensional materials,28,29 pore size reduction for perfect salt rejection (the most challenging issue of the next generation of membranes) by compression is only possible in the case of graphene foam membranes. While the pore size of graphene foam membranes can be controlled by compression due to buckling of the graphene skeleton (resulting from the atomic thickness of graphene), it is impossible to control the pore size of graphyne or any other two-dimensional material by compression due to the possibility of out-of-plane buckling. In contrast to the model employed in this study for describing graphene foam membranes, in reality the pores may not be perfectly directional and they may have different sizes and shapes, though highly directional pores were observed in graphene foam by high resolution transition electron microscopy.20 We find that the graphene skeleton buckles irrespective of the pore size (Fig. 4c). It also buckles irrespective of the pore shape and in the case of a non-uniform membrane with pores of different sizes and shapes (Fig. S4 in the ESI†), which implies that the pore size still can be tuned by strain.
In conclusion, graphene foam membranes are found to overcome the limitations of conventional polyamide membranes and existing carbon-based membranes for water desalination. The excellent performance of the graphene foams originates as follows: first, while low friction of water is common to carbon nanotubes and graphene foam, the high pore density of graphene foam results in ultrahigh water permeability. Second, due to the combination of periodic pores with the atomic thickness of graphene in a special three-dimensional geometry, graphene foam membranes undergo under mechanical strain a unique structural transformation based on buckling of the graphene skeleton, which results in tunability of the pore size. Third, while usually a large pore size is detrimental for the salt rejection, this does not apply to graphene foam membranes, because the pore size can be effectively reduced by applying mechanical strain. Importantly, the structural transformation is reversible, i.e., the initial (large) pore size can be restored for cleaning the membrane from fouling. These extraordinary properties let graphene foam membranes emerge as ideal candidates for reverse osmosis water desalination.
Simulation methods
Water is modeled using the SPC/E potential31 with the SHAKE algorithm (tolerance of 10−5)33 to keep the O–H distance at 1 Å and the H–O–H angle at 109.47°. The interaction between the C atoms is modelled by the AIREBO potential34 (which reproduces Young's modulus and Poisson's ratio of the graphene foam membrane and the interlayer binding energy of graphite obtained by first-principles calculations and experiment; see the Supporting Information for details). Other interactions are modelled by Lennard-Jones potentials V(r) = 4ε[(σ/r)12 − (σ/r)6] (where r is the distance, ε is the well depth, and V(σ) = 0) and Coulombic terms,30,32 using cutoff radii of 10.2 Å. We employ the parameters given in Table 2 and calculate those between different species by the Lorentz–Berthelot combination rules.35,36 The particle–particle particle-mesh method37 is employed to compute the long-range Coulombic interactions of the ions. The water-salt solutions are generated by PACKMOL.38 Two graphene sheets act as rigid pistons by setting the force components of each atom to zero in the x- and y-directions. The graphene foam membrane initially is relaxed at 300 K for 100 ps, using a isothermal-isobaric ensemble. Then compressive strain is applied in the x- or y-direction with a rate of 108 s−1 (where we assume that the pores are empty), using an isothermal-isobaric ensemble. The resulting stress in the y- or x-direction is controlled to be zero to simulate uniaxial stress. A Nose–Hoover thermostat39,40 is used to control the temperature and a Nose–Hoover barostat41,42 is used to control the pressure. All molecular dynamics simulations are performed by the LAMMPS code43 with a time step of 1 fs. During the reverse osmosis process, few atoms of the graphene foam membrane are fixed to prevent movement due to the applied pressure and for the others we fix the z-positions to decouple the deflection from the salt and water transport. Note that the deflection is reduced significantly in a thick graphene foam membrane according to plate theory.44 Estimation of statistical uncertainties by repetition of the molecular dynamics simulations is inhibited by the high consumption of computational resources.Data availability
The authors declare that the data supporting the findings of this study are available within the paper.Author contributions
D. T. H. performed the molecular statics and molecular dynamics simulations. A. J. performed the first-principles calculations. D. T. H. and T. P. N. N. wrote the initial draft of the manuscript. U.S. contributed to the data analysis and revised the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST). This work used computational resources of the Supercomputing Laboratory at KAUST.References
- The global risks report 2019, World Economic Forum.
- M. M. Mekonnen and A. Y. Hoekstra, Four billion people facing severe water scarcity, Sci. Adv., 2016, 2, e1500323 CrossRef PubMed.
- A. Boretti and L. Rosa, Reassessing the projections of the world water development report, npj Clean Water, 2019, 2, 15 CrossRef.
- E. Jones, M. Qadir, M. T. H. van Vliet, V. Smakhtin and S.-M. Kang, The state of desalination and brine production: A global outlook, Sci. Total Environ, 2019, 657, 1343–1356 CrossRef CAS PubMed.
- N. Ghaffour, T. M. Missimer and G. L. Amy, Technical review and evaluation of the economics of water desalination: Current and future challenges for better water supply sustainability, Desalination, 2013, 309, 197–207 CrossRef CAS.
- G. M. Geise, H. B. Park, A. C. Sagle, B. D. Freeman and J. E. McGrath, Water permeability and water/salt selectivity tradeoff in polymers for desalination, J. Membr. Sci., 2011, 369, 130–138 CrossRef CAS.
- E. Y. M. Ang, W. Toh, J. Yeo, R. Lin, Z. Liu, K. R. Geethalakshmi and T. Y. Ng, A review on low dimensional carbon desalination and gas separation membrane designs, J. Membr. Sci., 2020, 598, 117785 CrossRef CAS.
- D. Cohen-Tanugi and J. C. Grossman, Water desalination across nanoporous graphene, Nano Lett., 2012, 12, 3602–3608 Search PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Fast mass transport through sub-2-nanometer carbon nanotubes, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Unimpeded permeation of water through helium-leak-tight graphene-based membranes, Science, 2012, 335, 442–444 CrossRef CAS PubMed.
- Y. Yang, X. Yang, L. Liang, Y. Gao, H. Cheng, X. Li, M. Zou, R. Ma, Q. Yuan and X. Duan, Large-area graphene-nanomesh/carbon-nanotube hybrid membranes for ionic and molecular nanofiltration, Science, 2019, 364, 1057–1062 CrossRef CAS PubMed.
- S. C. O’Hern, D. Jang, S. Bose, J.-C. Idrobo, Y. Song, T. Laoui, J. Kong and R. Karnik, Nanofiltration across defect-sealed nanoporous monolayer graphene, Nano Lett., 2015, 15, 3254–3260 CrossRef PubMed.
- L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Fundamental transport mechanisms, fabrication and potential applications of nanoporous atomically thin membranes, Nat. Nanotechnol., 2017, 12, 509–522 CrossRef CAS PubMed.
- B. Corry, Designing carbon nanotube membranes for efficient water desalination, J. Phys. Chem. B, 2008, 112, 1427–1434 CrossRef CAS PubMed.
- Ihsanullah, Carbon nanotube membranes for water purification: Developments, challenges, and prospects for the future, Sep. Purif. Technol., 2019, 209, 307–337 Search PubMed.
- S. Zheng, Q. Tu, J. J. Urban, S. Li and B. Mi, Swelling of graphene oxide membranes in aqueous solution: Characterization of interlayer spacing and insight into water transport mechanisms, ACS Nano, 2017, 11, 6440–6450 CrossRef CAS PubMed.
- H. R. Karfunkel and T. Dressler, New hypothetical carbon allotropes of remarkable stability estimated by MNDO solid-state SCF computations, J. Am. Chem. Soc., 1992, 114, 2285–2288 CrossRef CAS.
- N. Park and J. Ihm, Electronic structure and mechanical stability of the graphitic honeycomb lattice, Phys. Rev. B, 2000, 62, 7614–7618 CrossRef CAS.
- M. Wu, X. Wu, Y. Pei, Y. Wang and X. C. Zeng, Three-dimensional network model of carbon containing only sp2 -carbon bonds and boron nitride analogues, Chem. Commun., 2011, 47, 4406–4408 RSC.
- N. V. Krainyukova and E. N. Zubarev, Carbon honeycomb high capacity storage for gaseous and liquid species, Phys. Rev. Lett., 2016, 116, 055501 CrossRef PubMed.
- A. Kalra, S. Garde and G. Hummer, Osmotic water transport through carbon nanotube membranes, Proc. Natl. Acad. Sci., 2003, 100, 10175–10180 CrossRef CAS PubMed.
- C. Sun, R. Zhou, Z. Zhao and B. Bai, Extending the classical continuum theory to describe water flow through two-simensional nanopores, Langmuir, 2021, 37, 6158–6167 CrossRef CAS PubMed.
- A.-J. Wang and D. L. McDowell, Yield surfaces of various periodic metal honeycombs at intermediate relative density, Int. J. of Plasticity, 2005, 21, 285–320 CrossRef.
- Q. Lu, M. Arroyo and R. Huang, Elastic bending modulus of monolayer graphene, J. Phys. D, 2009, 42, 102002 CrossRef.
- H. Fan, F. Jin and D. Fang, Uniaxial local buckling strength of periodic lattice composites, Mater. Des., 2009, 30, 4136–4145 CrossRef.
- M. Mehrdad and A. Moosavi, An efficient graphyne membrane for water desalination, Polymer, 2019, 175, 310–319 CrossRef CAS.
- M. M. Pendergast and E. M. V. Hoek, A review of water treatment membrane nanotechnologies, Energy Environ. Sci., 2011, 4, 1946–1971 RSC.
- Y. Yang, W. Li, H. Zhou, X. Zhang and M. Zhao, Tunable C2 N membrane for high efficient water desalination, Sci. Rep., 2016, 6, 29218 CrossRef CAS PubMed.
- M. Li, Y. Li, Y. Zhang, Y.-Q. Li, W. Li, M. Zhao and Y. Qu, Strain tunable nanoporous r-n-GDY membrane for efficient seawater desalination, J. Mater. Chem. A, 2022, 10, 16533–16540 RSC.
- T. Werder, J. H. Walther, R. L. Jaffe, T. Halicioglu and P. Koumoutsakos, On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes, J. Phys. Chem. B, 2003, 107, 1345–1352 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- D. Berthelot, Sur le mélange des gaz, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703–1855 Search PubMed.
- H. A. Lorentz, Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase, Ann. Phys., 1881, 248, 127–136 CrossRef.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles, Hilger, Bristol, 1988 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, The, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697 Search PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- W. Shinoda, M. Shiga and M. Mikami, Rapid estimation of elastic constants by molecular dynamics simulation under constant stress, Phys. Rev. B, 2004, 69, 134103 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- L. P. Kollár and G. Tarján, Plates, Mechanics of Civil Engineering Structures, Woodhead Publishing, Sawston, 2021, Chapter 10, pp. 365–428 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00475e |
| ‡ Current address: Department of Mechanical and Construction Engineering, Northumbria University, Newcastle upon Tyne NE1 8ST, UK. |
| This journal is © The Royal Society of Chemistry 2023 |