Halide (X = I, Br, Cl) doping to tune the electronic structure for conversion of Pb_0.6Sn_0.4Te into a high-performing thermoelectric material

Abstract

The fabrication of thermoelectric (TE) devices requires both p- and n-type legs with comparable performances. Pb_0.6Sn_0.4Te, which belongs to the class of topological crystalline insulator (TCI), has the potential to be a high-performing TE material due to its tunable electronic structure. Herein, we use first-principles electronic structure calculations for the very first time to study the electronic structure of halide-doped (X = I, Br and Cl) Pb_0.6Sn_0.4Te. We show through Boltzmann transport property calculations that the breaking of crystal mirror symmetry is not a necessary criterion for the enhancement of TE properties. A maximum attainable ZT of ∼1.42 to ∼1.51 at 800 K by tuning the chemical potential makes these materials worth studying further.

---

1. Introduction

The global energy crisis and environmental pollution have driven the need to search for alternative sources of energy generation. Thermoelectric (TE) materials, with their ability to scavenge waste heat, are increasingly attracting attention in various applications.^1–4 Various materials, such as oxides, half Heuslers, chalcogenides of Bi, Sn, Pb, Ge and silicides, are receiving immense importance.^5–17 Pb_0.6Sn_0.4Te, which is derived from PbTe and SnTe, is a well-known topological crystalline insulator (TCI).¹⁸ However, its performance as a TE material is extremely poor compared to that of PbTe- and SnTe-based materials.^19–22 Due to the extremely small band gap of Pb_0.6Sn_0.4Te, high bipolar conductivity is observed leading to poor performance at high temperatures.^23,24 Substitutional doping of Pb_0.6Sn_0.4Te has been carried out to improve its TE performance.^25,26 Breaking of the crystal mirror symmetry has been previously implemented to open the band gap of Pb_0.6Sn_0.4Te.^23–26 While doping Na and K has led to a maximum ZT of about 1 by opening the band gap, Mg was able to open the band gap as well as increase the number of degenerate valleys leading to a ZT of 2.^23–25 Recently, Zn was reported to introduce resonance levels, hyperconvergence and multiple electronic valleys in Pb_0.6Sn_0.4Te, improving its ZT to 1.57 at 840 K.²⁶ Due to advancements in high-performance computing, computational methods can be easily relied on to discover new TE materials with high performance.^27–30 For practical applications, it is essential to have both p- and n-type materials with comparable performances.^28,30 While the electronic structure modifications of TCI materials by cation doping have been studied using first-principles density functional theory (DFT) calculations, the effect of anion doping, and halide doping in Pb_0.6Sn_0.4Te in particular, has not been theoretically explored. Generally, it is very difficult to predict whether the doping can break the crystal mirror symmetry or not during synthesis. Hence, it is essential to find out if it is possible to improve TE performance without breaking the symmetry. Herein, we studied the effect of doping halides, namely I, Br and Cl, on the electronic structure of Pb_0.6Sn_0.4Te using first-principles DFT calculations. The transport property calculations using the Boltzmann equation predict a maximum ZT of ∼1.51 at 800 K for I-doped Pb_0.6Sn_0.4Te. The performances of Br- and Cl-doped TCI were also predicted to improve as the chemical potential moves towards positive values. This work predicts that Br-doped Pb_0.6Sn_0.4Te is the best n-type TE material among the three.

2. Computational details

In this study, Pb_0.6Sn_0.4Te was modelled using a fully relaxed most stable symmetric 2 × 2 × 1 supercell of Pb₁₀Sn₆Te₁₆.²⁶ I, Br and Cl were doped by substituting the Te atom at the center of the supercell, thus retaining the crystal mirror symmetry even after doping. We carried out DFT calculations using the Quantum ESPRESSO package using fully relativistic ultrasoft Perdew, Burke and Erzenhoff (PBE) pseudopotentials.^31,32 The wavefunctions were represented by a plane-wave basis set, which was truncated with an energy cutoff of 50 Ry and charge density cutoff of 400 Ry. Brillouin zone integrations were sampled using 10 × 10 × 20 k mesh for calculations of the total energy of the system. The electronic structures were determined along Γ–X–M–Γ–Z–R–A–Z high symmetry lines in the Brillouin zone.

3. Results and discussion

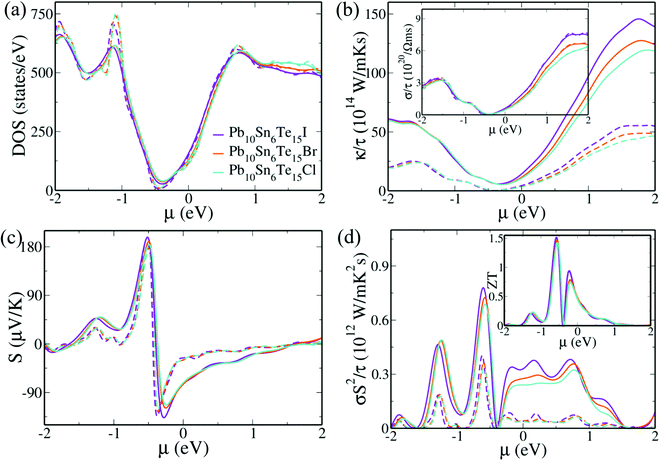
The efficiency of the TE material is largely dependent on the dimensionless quantity figure of merit ZT, which is directly proportional to the power factor and inversely proportional to the thermal conductivity.³³ Electrical conductivity and, in turn, the electronic thermal conductivity and the Seebeck co-efficient largely depend on the electronic structure of the material, while the lattice thermal conductivity can be independently tuned by using appropriate synthetic techniques.^19,28,30 While PbTe has a band gap of 0.3 eV and SnTe has a band gap of 0.18 eV, Pb_0.6Sn_0.4Te has an almost zero band gap.^34,35 Previously, we have determined the most stable symmetric configuration of Pb_0.6Sn_0.4Te out of 8008 possible configurations using the site occupancy disorder technique, which we further used in this work.^26,36

The simulated electronic structures of Pb₁₀Sn₆Te₁₆, Pb₁₀Sn₆Te₁₅I, Pb₁₀Sn₆Te₁₅Br and Pb₁₀Sn₆Te₁₅Cl reveal a principal band gap at Z point where the light hole valence and conduction band reside (Fig. 1). The heavy hole valence and conduction bands on the other hand reside at M + δ in the M → Γ direction.^20,35 We observe such a shift in the position from L and Σ points, where the light and heavy hole bands reside, respectively, in the parent PbTe and SnTe materials, which is due to the folding of bands during the construction of the supercell.^37,38 In the case of Pb₁₀Sn₆Te₁₆, we see a zero-band gap at Z point due to the penetration of the conduction band (CB) into the light hole valence band (VB), which peaks on either side of it with a hole-like character.²⁵ The bottom of the light carrier CB lies below the Fermi level and has an electron-like character. We see an energy offset of 0.13 eV between the valence sub-bands at Z′ and M + δ in the M → Γ direction. This energy offset value is smaller than that of SnTe (0.3 eV) due to the higher content of PbTe, which has a lower energy offset values.³³ The conduction sub-band energy offset on the other hand is estimated to be 0.61 eV, excluding their participation in the transport properties.

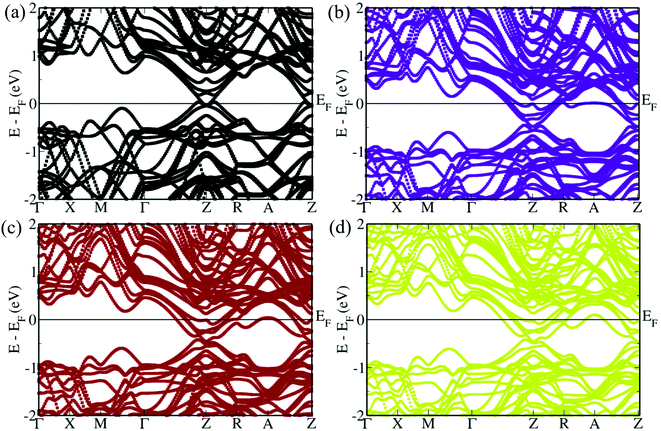Fig. 1 Electronic structure of (a) Pb₁₀Sn₆Te₁₆, (b) Pb₁₀Sn₆Te₁₅I, (c) Pb₁₀Sn₆Te₁₅Br and (d) Pb₁₀Sn₆Te₁₅Cl. Energy is shifted with respect to the Fermi level, which is set to zero.

Despite retaining the crystal mirror symmetry in doped samples, we observe that the band gap increases from 0 eV to 0.08 eV, 0.06 eV and 0.03 eV in I, Br and Cl-doped configurations, respectively, at Z point and around 0.1 eV, as we move slightly away from the Z point due to the loss of symmetry about the Z point along with Z → R and Z → Γ direction. This indicates that the breaking of crystal mirror symmetry is not an essential criterion for the increase in the band gap of TCI. We need to note here that the underestimation of the band gap is due to the existence of discontinuities with respect to the number of electrons in the derivative of energies in the DFT-based calculations.³⁹ The energy offset between the light and heavy hole valence sub-bands increases to 0.15 eV, 0.18 eV and 0.19 eV for I, Br and Cl doped Pb_0.6Sn_0.4Te, respectively between Z′ and M + δ in M → Γ direction. Similarly, the CB energy offsets increase to 0.627 eV, 0.629 eV and 0.638 eV in Pb₁₀Sn₆Te₁₅I, Pb₁₀Sn₆Te₁₅Br and Pb₁₀Sn₆Te₁₅Cl. This is contradictory to the case of Zn doping in Pb_0.6Sn_0.4Te where, in spite of Zn being a p-type dopant, it led to a the convergence of conduction sub-bands with an energy offset value of 0.51 eV.²⁶

Interestingly, in Pb₁₀Sn₆Te₁₆, a heavy hole sub-band also exists at R + δ′ in the R → A direction, one of which lies 0.36 eV below the VB maximum and the other 0.52 eV above the CB minimum. In the doped samples, this energy gap decreases in the order Cl (0.314 eV) > Br (0.311 eV) > I (0.296 eV) in the VB region and Cl (0.28 eV) < Br (0.29 eV) < I (0.41 eV) in the CB region. This reversal of behavior about the Z point is due to the higher loss of degeneracy in the case of Cl and Br compared to I-doped configurations, which drag degenerate orbitals apart. In the VB area, this leads to an asymmetry in the bands just below the VB maximum, wherein the bands are dragged lower in Z → Γ direction in comparison to the Z → R direction. Further, in the CB region, we see the appearance of newer valleys on either side of the Z point. This phenomenon results in the increase of the Seebeck co-efficient due to an increase in the electron transport channels. This feature was previously reported in p-type materials such as Zn-doped Pb_0.6Sn_0.4Te and Cd, Ge and Pb multi-doped SnTe but this is the first report on the occurrence of such feature in n-type materials.^26,40

Partial density of states (pDOS) sheds further light on this as we observe the behavior of various orbitals contributing to the VB and CB on either side of the Fermi level (Fig. 2). In undoped Pb_0.6Sn_0.4Te, while Te ‘p’ orbitals form the VB, the CB is formed by the ‘p’ orbitals of Sn and Pb. While Sn ‘p’ orbitals with a j value of 1.5 lies closer to the band edge, Pb ‘p’ orbitals with a j value of 1.5 lies slightly away from the band edge. In the halide-doped Pb_0.6Sn_0.4Te, while the contributions of Te ‘p’ orbitals and Pb ‘p’ orbitals with a j value of 1.5 remain more or less the same and ‘p’ orbitals of Sn and ‘p’ orbitals of Pb with a j value of 0.5 show different nature. We see that ‘p’ states of both Sn and Pb with a j value of 0.5 contribute closer to the CB edge with ‘p’ states of Pb forming the CB maxima in the undoped sample while ‘p’ states of Sn taking over the role in the doped samples. The ‘p’ states of I contribute immensely to the VB area and thus leading to a higher extent of convergence of valence sub-bands compared to conduction sub-bands, as observed in the electronic structure. The negligible loss of symmetry and degeneracy of the bands in Pb₁₀Sn₆Te₁₅I in comparison to the other two doped systems is apparent from the nature of the contribution of Sn ‘p’ states. We can observe that the contribution of Sn ‘p’ orbitals is completely different in Pb₁₀Sn₆Te₁₅Br and Pb₁₀Sn₆Te₁₅Cl near the Fermi energy. The hump-like plateau in pDOS near the Fermi level is due to the introduction of multiple valleys observed in the band structure due to the hybridization of ‘s’ orbitals of Br/Cl with ‘p’ orbitals of Sn. The ‘p’ states of Br/Cl contribute deep within the VB and hence the extent of convergence of valence sub-bands is lower compared to that in CB.

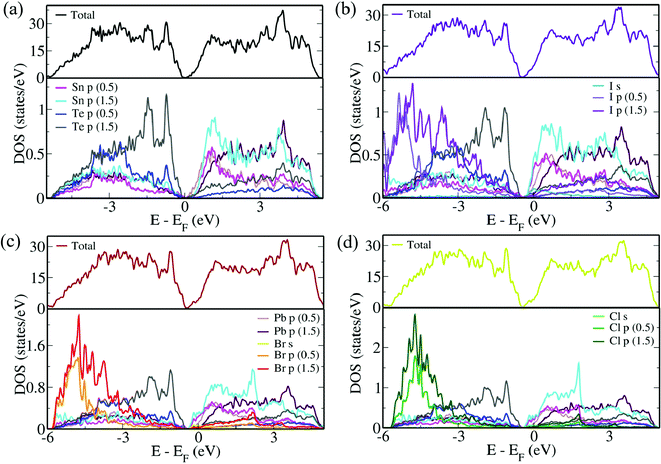Fig. 2 pDOS of (a) Pb₁₀Sn₆Te₁₆, (b) Pb₁₀Sn₆Te₁₅I, (c) Pb₁₀Sn₆Te₁₅Br and (d) Pb₁₀Sn₆Te₁₅Cl. Energy is shifted with respect to the Fermi level, which is set to zero.

We studied the transport properties within the rigid band approximation using Boltztrap code with constant scattering time approximation the details of which are given in previous reports.^41,42 While we observe that the DOS and electrical conductivity of the samples did not vary much with the temperature, the electronic thermal conductivity (κ) increased with the increase in the temperature from 300 K to 800 K (Fig. 3). While the values of κ were comparable for all three doped samples in the negative chemical potential ‘μ’ region, which corresponded to hole doping, in the positive potential region we observed higher values for the I-doped sample with Cl having the least κ values among the three, both, at 300 K and 800 K.⁴³ Further, the Seebeck values also changed the sign from positive to negative as the doping changed from the electron to hole. At zero ‘μ’, the Seebeck values were negative, indicating the material to be n-type. We see that for a large potential window in the positive region, the power factor (σS²) remains high enough. While the I-doped samples show higher power factor values among the three, both at 300 K and 800 K, the ZT values show a different trend. We observe that in the positive potential region, the ZT is higher for Br/Cl-doped samples due to the smaller thermal conductivity values in comparison to I-doped configurations. The generation of multiple electronic valleys in CB is responsible for the enhanced performance of these samples as the n-type material. It is interesting to note that by tuning the chemical potential in the negative region, we can attain a ZT of ∼1.51, ∼1.46 and ∼1.42 at 800 K for Pb₁₀Sn₆Te₁₅I, Pb₁₀Sn₆Te₁₅Br and Pb₁₀Sn₆Te₁₅Cl assuming a lattice thermal conductivity of 0.4 W m⁻¹ K⁻¹ at 800 K. Pb₁₀Sn₆Te₁₅Br configuration shows highest ZT at ‘μ’ of zero, which is strongly supported by the electronic structure modifications and indicates that it is a better n-type material. The added dopants are known to scatter the short-range phonons decreasing the lattice thermal conductivity.^30,44 By employing the nanostructuring approach during the synthesis, a further decrease in the lattice thermal conductivity and increase in the ZT could be attained.^45–48 A maximum ZT of 1.05 attained at 620 K by doping I in Te lattice in Pb_0.6Sn_0.4Te experimentally in the previous report supports the dual nature of the dopant by chemical tuning.⁴⁴

Fig. 3 (a) DOS; (b) thermal conductivity (inset: electrical conductivity); (c) Seebeck co-efficient; and (d) power factor (inset: ZT) of Pb₁₀Sn₆Te₁₅I, Pb₁₀Sn₆Te₁₅Br and Pb₁₀Sn₆Te₁₅Cl as a function of chemical potential at 300 K (dashed lines) and 800 K (solid lines). Electrical conductivity, thermal conductivity and power factor are reported by scaling them with τ. ZT is estimated by considering a lattice thermal conductivity value of 0.4 W m⁻¹ K⁻¹ at 800 K.

4. Conclusions

We carried out a detailed electronic structure study of halide doping in Pb_0.6Sn_0.4Te using the first-principle DFT calculations. We observed that despite not breaking the crystal mirror symmetry the I, Br, and Cl doped configurations show increased direct band gap and valence and conduction sub-band convergence. The introduction of multiple electronic valleys in the conduction band by aliovalent anion doping leads to enhanced TE properties. The transport property calculations predict a maximum ZT of ∼1.42 to ∼1.51 attainable at 800 K by tuning the chemical potential. Thus, this work harnesses the power of computational techniques in finding ways for the conversion of a TCI into a TE.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors gratefully acknowledge the financial support received from CSIR, Govt. of India in the form of R&D project grant and DST, Govt. of India for INSPIRE Faculty award.

References

1. L. Zhang, X. L. Shi, Y. L. Yang and Z. G. Chen, Flexible Thermoelectric Materials and Devices: From Materials to Applications, Mater. Today, 2021, 46, 62–108.
2. M. Dargusch, W. D. Liu and Z. G. Chen, Thermoelectric Generators: Alternative Power Supply for Wearable Electrocardiographic Systems, Adv. Sci., 2020, 7, 2001362.
3. Y. Sadia, T. O. Raz, O. B. Yehuda, M. Korngold and Y. Gelbstein, Criteria for Extending the Operation Periods of Thermoelectric Converters based on IV-VI Compounds, J. Solid State Chem., 2016, 241, 79–85.
4. J. Wei, L. Yang, Z. Ma, P. Song, M. Zhang, J. Ma, F. Yang and X. Wang, Review of Current High-ZT Thermoelectric Materials, J. Mater. Sci., 2020, 55, 12642–12704.
5. U. S. Shenoy and D. K. Bhat, Enhanced Thermoelectric Properties of Vanadium Doped SrTiO₃: A Resonant Dopant Approach, J. Alloys Compd., 2020, 832, 154958.
6. U. S. Shenoy and D. K. Bhat, Vanadium Doped BaTiO₃ as High Performance Thermoelectric Material: Role of Electronic Structure Engineering, Mater. Today Chem., 2020, 18, 100384.
7. T. Zilber, S. Cohen, D. Fuks and Y. Gelbstein, TiNiSn Half-Heusler Crystals Grown from Metallic Flux for Thermoelectric Applications, J. Alloys Compd., 2019, 781, 1132–1138.
8. J. N. Kahiu, U. S. Shenoy, S. K. Kihoi, H. Kim, S. Yi, D. K. Bhat and H. S. Lee, Optimized Electronic Performance in Half-Heusler Ti-doped NbFeSb Materials by Stoichiometric Tuning at the Fe and Sb Sites, J. Alloys Compd., 2021, 891, 162033.
9. O. Meroz and Y. Gelbstein, Thermoelectric Bi₂Te_3-xSe_x Alloys for Efficient Thermal to Electrical Energy Conversion, Phys. Chem. Chem. Phys., 2018, 20, 4092–4099.
10. Y. Wang, M. Hong, W. D. Liu, X. L. Shi, S. D. Xu, Q. Sun, H. Gao, S. Lu, J. Zou and Z. G. Chen, Bi_0.5Sb_1.5Te₃/PEDOT:PSS-based Flexible Thermoelectric Film and Device, Chem. Eng. J., 2020, 397, 125360.
11. Y. Gelbstein, Y. Rosenberg, Y. Sadia and M. P. Dariel, Thermoelectric Properties Evolution of Spark Plasma Sintered (Ge_0.6Pb_0.3Sn_0.1)Te Following a Spinodal Decomposition, J. Phys. Chem. C, 2010, 114, 13126–13131.
12. D. K. Bhat and U. S. Shenoy, Resonance Levels in GeTe Thermoelectrics: Zinc as a New Multifaceted Dopant, New J. Chem., 2020, 44, 17664–17670.
13. W. D. Liu, D. Z. Wang, Q. Liu, W. Zhou, Z. Shao and Z. G. Chen, High-performance GeTe-Based Thermoelectrics: From Materials to Devices, Adv. Energy Mater., 2020, 10, 2000367.
14. D. K. Bhat and U. S. Shenoy, Mg/Ca Doping Ameliorates the Thermoelectrics Properties of GeTe: Influence of Electronic Structure Engineering, J. Alloys Compd., 2020, 834, 155989.
15. Y. X. Chen, X. L. Shi, Z. H. Zheng, F. Li, W. D. Liu, W. Y. Chen, X. R. Li, G. X. Liang, J. T. Luo, P. Fan and Z. G. Chen, Two-dimensional WSe₂/SnSe p-n Junctions Secure Ultrahigh Thermoelectric Performance in n-type Pb/I Co-doped Polycrystalline SnSe, Mater. Today Phys., 2021, 16, 100306.
16. Y. Sadia, M. Elegrably, O. B. Nun, Y. Marciano and Y. Gelbstein, Sub-micron Features in Higher Manganese Silicide, J. Nanomater., 2013, 701268.
17. W. D. Liu, Z. G. Chen and J. Zou, Eco-Friendly Higher Manganese Silicide Thermoelectric Materials: Progress and Future Challenges, Adv. Energy Mater., 2018, 8, 1800056.
18. S. Y. Xu, C. Liu, N. Alidoust, M. Neupane, D. Qian, I. Belopolski, J. D. Denlinger, Y. J. Wang, H. Lin and L. A. Wray, et al., Observation of a Topological Crystalline Insulator Phase and Topological Phase Transition in Pb_1-xSn_xTe, Nat. Commun., 2012, 3, 1192.
19. U. S. Shenoy and D. K. Bhat, Bi and Zn Co-doped SnTe Thermoelectrics: Interplay of Resonance Levels and Heavy Hole Band Dominance Leading to Enhanced Performance and A Record High Room Temperature ZT, J. Mater. Chem. C, 2020, 8, 2036–2042.
20. D. K. Bhat and U. S. Shenoy, Enhanced Thermoelectric Performance of Bulk Tin Telluride: Synergistic Effect of Calcium and Indium Co-Doping, Mater. Today Phys., 2018, 4, 12–18.
21. L. You, J. Zhang, S. Pan, Y. Jiang, K. Wang, J. Yang, Y. Pei, Q. Zhu, M. T. Agne, G. J. Snyder, Z. Ren, W. Zhang and J. Luo, Realization of Higher Thermoelectric Performance by Dynamic Doping of Copper in n-type PbTe, Energy Environ. Sci., 2019, 12, 3089–3098.
22. U. S. Shenoy and D. K. Bhat, Selective Co-doping Improves the Thermoelectric Performance of SnTe: An Outcome of Electronic Structure Engineering, J. Alloys Compd., 2021, 892, 162221.
23. S. Roychowdhury, U. S. Shenoy, U. V. Waghmare and K. Biswas, Tailoring of Electronic Structure and Thermoelectric Properties of a Topological Crystalline Insulator by Chemical Doping, Angew. Chem., Int. Ed., 2015, 54, 15241–15245.
24. S. Roychowdhury, U. S. Shenoy, U. V. Waghmare and K. Biswas, Effect of Potassium Doping on Electronic Structure and Thermoelectric Properties of Topological Crystalline Insulator, Appl. Phys. Lett., 2016, 108, 193901.
25. S. Shenoy and D. K. Bhat, Enhanced Bulk Thermoelectric Performance of Pb_0.6Sn_0.4Te: Effect of Magnesium Doping, J. Phys. Chem. C, 2017, 121, 20696–20703.
26. U. S. Shenoy and D. K. Bhat, Electronic Structure Modulation of Pb_0.6Sn_0.4Te via Zinc Doping and Its Effect on the Thermoelectric Properties, J. Alloys Compd., 2021, 872, 159681.
27. J. J. G. Moreno, J. Cao, M. Fronzi and M. H. N. Assadi, A Review of Recent Progress in Thermoelectric Materials through Computational Methods, Mater. Renewable Sustainable Energy, 2020, 9, 16.
28. U. S. Shenoy and D. K. Bhat, Molybdenum as a Versatile Dopant in SnTe: A Promising Material for Thermoelectric Application, Energy Adv., 2022 10.1039/D1YA00003A.
29. Z. Ma, J. Wei, P. Song, M. Zhang, L. Yang, J. Ma, W. Liu, F. Yang and X. Wang, Review of Experimental Approaches for Improving ZT of Thermoelectric Materials, Mater. Sci. Semicond. Process., 2021, 121, 105303.
30. U. S. Shenoy and D. K. Bhat, Improving ZT of SnTe by Electronic Structure Engineering: Unusual Behavior of Bi dopant in the Presence of Pb as a Co-dopant, Mater. Adv., 2021, 2, 6267–6271.
31. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., Quantum ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
33. D. K. Bhat and U. S. Shenoy, SnTe Thermoelectrics: Dual Step Approach for Enhanced Performance, J. Alloys Compd., 2020, 834, 155181.
34. M. K. Brod and G. J. Snyder, Orbital Chemistry of High Valence Band Convergence and Low-dimensional Topology in PbTe, J. Mater. Chem. A, 2021, 9, 12119–12139.
35. D. K. Bhat and U. S. Shenoy, High Thermoelectric Performance of Co-Doped Tin Telluride Due to Synergistic Effect of Magnesium and Indium, J. Phys. Chem. C, 2017, 121, 7123–7130.
36. R. G. Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, Symmetry-Adapted Configurational Modeling of Fractional Site Occupancy in Solids, J. Phys.: Condens. Matter, 2007, 19, 256201.
37. U. S. Shenoy and D. K. Bhat, Electronic Structure Engineering of Tin Telluride Through Co-Doping of Bismuth and Indium for High Performance Thermoelectrics: A Synergistic Effect Leading to Record High Room Temperature ZT in Tin Telluride, J. Mater. Chem. C, 2019, 7, 4817–4821.
38. S. K. Kihoi, J. N. Kahiu, H. Kim, U. S. Shenoy, D. K. Bhat, S. Yi and H. S. Lee, Optimized Mn and Bi co-doping in SnTe based thermoelectric material: A case of band engineering and density of states tuning, J. Mater. Sci. Technol., 2021, 85, 76–86.
39. D. K. Bhat and U. S. Shenoy, Zn: A Versatile Resonant Dopant for SnTe Thermoelectrics, Mater. Today Phys., 2019, 11, 100158.
40. G. Xie, Z. Li, T. Luo, H. Bai, J. Sun, Y. Xiao, L. D. Zhao, J. Wu, G. Tan and X. Tang, Band Inversion Induced Multiple Electronic Valleys for High Thermoelectric Performance of SnTe with Strong Lattice Softening, Nano Energy, 2020, 69, 104395.
41. U. S. Shenoy and D. K. Bhat, Vanadium: A Protean Dopant in SnTe for Augmenting its Thermoelectric Performance, ACS Sustainable Chem. Eng., 2021, 9, 13033–13038.
42. G. K. H. Madsen and D. J. Singh, BoltzTrap. A code for Calculating Band Structure Dependent Quantities, Comput. Phys. Commun., 2006, 175, 67–71.
43. S. U. Shenoy and D. K. Bhat, Electronic Structure Engineering of SrTiO₃ via Rhodium doping: A DFT Study, J. Phys. Chem. Solids, 2021, 148, 109708.
44. S. Roychowdhury, M. Dutta and K. Biswas, Enhanced Thermoelectric Performance in Topological Crystalline Insulator n-type Pb_0.6Sn_0.4Te by Simultaneous Tuning of Band Gap and Chemical Potential, J. Mater. Chem. A, 2018, 6, 24216–24223.
45. S. K. Kihoi, U. S. Shenoy, D. K. Bhat and H. S. Lee, Complimentary Effect of Co-doping Aliovalent Elements Bi and Sb in Self-compensated SnTe-based Thermoelectric Materials, J. Mater. Chem. C, 2021, 9, 9922–9931.
46. H. A. Eivari, Z. Sohbatzadeh, P. Mele and M. H. N. Assadi, Low Thermal Conductivity: Fundamentals and Theoretical Aspects in Thermoelectric Applications, Mater. Today Energy, 2021, 21, 100744.
47. H. T. Liu, Q. Sun, Y. Zhong, C. L. Xia, Y. Chen, Z. G. Chen and R. Ang, Achieving High Performance n-type PbTe via Synergistically Optimizing Effective Mass and Carrier Concentration and Suppressing Lattice Thermal Conductivity, Chem. Eng. J., 2021, 428, 132601.
48. Z. H. Zheng, X. L. Shi, D. W. Ao, W. D. Liu, Y. X. Chen, F. Li, S. Chen, X. Q. Tian, X. R. Li, J. Y. Duan, H. L. Ma, X. H. Zhang, G. X. Liang, P. Fan and Z. G. Chen, Rational Band Engineering and Structural Manipulations Inducing High Thermoelectric Performance in n-type CoSb₃ Thin Films, Nano Energy, 2021, 81, 105683.

---