Developing a nitrile-based lithium-conducting electrolyte for low temperature operation†
Spencer A.
Langevin
,
Matthew M.
McGuire
,
Nam Q.
Le
,
Eugene
Ragasa
 ,
Tanner
Hamann
,
Gehn
Ferguson
,
Christine
Chung
,
Tanner
Hamann
,
Gehn
Ferguson
,
Christine
Chung
 ,
Janna
Domenico
,
Janna
Domenico
 and
Jesse S.
Ko
and
Jesse S.
Ko
 *
*
Research and Exploratory Development Department, Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723, USA. E-mail: jesse.ko@jhuapl.edu
First published on 23rd June 2022
Abstract
Lithium-ion (Li+) batteries are considered the most attractive for low temperature operation. Though Li+-conducting electrolytes predominately use carbonate solvents, we show that nitriles, such as 3-methoxypropyionitrile (MPN), are promising candidates for use at low temperatures. At a high salt concentration (2.5 molal), and combined with a fluoroethylene carbonate additive, this electrolyte enables −40 °C operation when configured in a graphite‖lithium cobalt oxide cell. We leverage molecular dynamics simulations and experimentally validate Li+ diffusivity/conductivity measurements to bolster our understanding of the MPN electrolyte in comparison with carbonates. At room temperature, cells demonstrate high rate capability (100 mA h g−1 discharge capacity at 2C), and also maintain >75% of their initial capacity up to 100 cycles when cycled at 0.2C. At −40 °C, >50% of the cell's room temperature discharge capacity is sustained, showing exemplary low temperature performance. By performing an impedance-based distribution of relaxation times analysis, we identify that interfacial kinetics at the anode surface and the cathode electrolyte interphase are the two underlying factors limiting low temperature operation. The results presented herein offer an exciting direction for the discovery and implementation of nitrile-based solvents that can withstand low temperatures.
1. Introduction
Lithium-ion batteries (LIBs) are ubiquitous in modern society and their application space continues to expand at an accelerating rate.1–3 A subset of these applications involve operating below room temperature, which is known to hinder the performance of LIBs due to decreased electrolyte ionic conductivity, sluggish lithium-ion (Li+) transport kinetics at the solid electrolyte interphase (SEI), increased polymer binder degradation, and decreased Li+ diffusivity within the electrode active material.4–6 Commercial state-of-the-art LIBs exhibit a notable decrease in capacity retention and rate capability below 0 °C and are often only recommended for use down to −20 °C, limiting applications for certain low-temperature extreme environments (e.g., space).7–13 At such low temperatures, the electrolyte is the greatest source of performance loss; thus, electrolyte engineering is essential to addressing the key challenges for low temperature operation.8–11Early studies identified electrolyte chemistry as one of the critical factors governing low temperature performance, a consensus that holds largely to the present day.4,14 An electrolyte comprises salts, solvents, and additives for the proper function of Li+ mobility across a porous separator. Such properties as ionic conductivity, Li+ transference number, dielectric permittivity, solvation/de-solvation, and stable SEI formation all contribute to the performance of LIBs.8–11,15 As a consequence, the effect of low operating temperature on these properties and the resulting LIB capacity retention must be studied. The bulk electrolyte should have a high ionic conductivity and a low liquidus point to maintain high performance at freezing temperatures. This in turn requires high dielectric permittivity and low dynamic viscosity to encourage strong dissociation of the lithium salt to form a highly conductive solution based on the Stokes–Einstein and Nernst–Einstein relations.16 Currently, mixtures of carbonate solvents (e.g., 1 M lithium hexafluorophosphate (LiPF6) in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethylene carbonate (EC)
1 ethylene carbonate (EC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dimethyl carbonate (DC)) are used to maintain high dielectric permittivity and low dynamic viscosity to achieve Li+ conductivities >10 mS cm−1.8–11 However, solvents with high dielectric permittivity tend to have high liquidus points, making such solvents more likely to freeze at low temperature and impede Li+ transport. For these reasons, bulk electrolytes are typically mixtures of multiple carbonate solvents and additives, combined in ratios that ensure that the most desirable properties of certain components balance out the less desirable properties of other components.
dimethyl carbonate (DC)) are used to maintain high dielectric permittivity and low dynamic viscosity to achieve Li+ conductivities >10 mS cm−1.8–11 However, solvents with high dielectric permittivity tend to have high liquidus points, making such solvents more likely to freeze at low temperature and impede Li+ transport. For these reasons, bulk electrolytes are typically mixtures of multiple carbonate solvents and additives, combined in ratios that ensure that the most desirable properties of certain components balance out the less desirable properties of other components.
Since the 1990's, the Jet Propulsion Laboratory has undertaken an expansive study of salt and solvent ratios to enable low temperature LIB operation for space applications.17–22 Ternary and quaternary carbonate solvent combinations were prepared and shown to improve low temperature performance. The motivation for using these complex mixtures was to extend the liquidus range and decrease the dynamic viscosity. For the ternary combination, the addition of diethyl carbonate (DEC) to an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC mixture was shown to prevent freezing of the electrolytes down to −40 °C, where ionic conductivities of ∼1 mS cm−1 were measured.17 The improved conductivity of the ternary system (1 M LiPF6 in EC
DMC mixture was shown to prevent freezing of the electrolytes down to −40 °C, where ionic conductivities of ∼1 mS cm−1 were measured.17 The improved conductivity of the ternary system (1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (1
DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v)) compared to the binary systems EC
1 v/v)) compared to the binary systems EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (3
DMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) and EC
7) and EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (3
DEC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) was attributed to the synergistic effects of the high dielectric permittivity of EC, the low freezing temperature of DEC, and the low dynamic viscosity of DMC. For the purposes of forming a stable SEI, ethyl methyl carbonate (EMC) was introduced in a ratio of EC
7) was attributed to the synergistic effects of the high dielectric permittivity of EC, the low freezing temperature of DEC, and the low dynamic viscosity of DMC. For the purposes of forming a stable SEI, ethyl methyl carbonate (EMC) was introduced in a ratio of EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC
DEC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (1
EMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 v/v) to achieve high performance down to −60 °C.21 Another promising solvent combination was propylene carbonate (PC) and DEC, where a high DEC content (>50%) resulted in a conductivity of ∼1 mS cm−1 at −40 °C.23,24 Comparable trends were also observed when changing the salt to lithium tetrafluoroborate (LiBF4), though the overall ionic conductivities were lower than electrolytes using LiPF6.25 For batteries equipped with lithium metal anodes, stable cycling ranging between −40 °C to even −85 °C has been achieved by leveraging unique combinations of fluorinated electrolytes.26,27 These results highlight the need for discovering new solvents or solvent combinations that can provide high dielectric permittivity, low dynamic viscosity, and interface stabilizing properties.
3 v/v) to achieve high performance down to −60 °C.21 Another promising solvent combination was propylene carbonate (PC) and DEC, where a high DEC content (>50%) resulted in a conductivity of ∼1 mS cm−1 at −40 °C.23,24 Comparable trends were also observed when changing the salt to lithium tetrafluoroborate (LiBF4), though the overall ionic conductivities were lower than electrolytes using LiPF6.25 For batteries equipped with lithium metal anodes, stable cycling ranging between −40 °C to even −85 °C has been achieved by leveraging unique combinations of fluorinated electrolytes.26,27 These results highlight the need for discovering new solvents or solvent combinations that can provide high dielectric permittivity, low dynamic viscosity, and interface stabilizing properties.
When assessing appropriate solvents to encourage the dissociation of lithium salts, only solvents with polar groups such as carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), nitrile (C
O), nitrile (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N), sulfonyl (S
N), sulfonyl (S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and ether-linkage (–O–) merit consideration.4,14 Nitriles, such as acetonitrile (AN), have been popular in the past due to their superior ionic conductivities (>30 mS cm−1 at 25 °C) compared to their carbonate counterparts (∼10 mS cm−1 at 25 °C).4,14 However, the narrow electrochemical stability window of AN, particularly when paired with a lithium metal anode, limited their applications for LIBs. Within the context of bulk electrolyte properties, nitriles such as 3-methoxypropionitrile (MPN)28 and 3-ethoxypropionitrile (EPN)/3-(2,2,2-trifluoro)ethoxypropionitrile (FEPN)29 offer low melting points (−43.8 to −57 °C), relatively high dielectric constants (∼36 at 25 °C), and low dynamic viscosities (0.37–1.1 cP at 25 °C). When a lithium salt, such as lithium bis(trifluorosulfonylimide) (LiTFSI), is dissolved, nitrile-based electrolytes provide a compelling electrolyte system for enabling high rate operation at room temperature. In particular, electrolytes prepared with MPN as the sole solvent possess the advantages of being environmentally benign, having a lower melting point, lower flammability, and lower volatility compared to commercial carbonate-based electrolytes.28 Wang et al., observed that 1 M LiTFSI in MPN exhibits an ionic conductivity of ∼8.5 mS cm−1 at room temperature and provides nearly a two-fold increase in rate capability compared to 1 M LiTFSI in EC
O), and ether-linkage (–O–) merit consideration.4,14 Nitriles, such as acetonitrile (AN), have been popular in the past due to their superior ionic conductivities (>30 mS cm−1 at 25 °C) compared to their carbonate counterparts (∼10 mS cm−1 at 25 °C).4,14 However, the narrow electrochemical stability window of AN, particularly when paired with a lithium metal anode, limited their applications for LIBs. Within the context of bulk electrolyte properties, nitriles such as 3-methoxypropionitrile (MPN)28 and 3-ethoxypropionitrile (EPN)/3-(2,2,2-trifluoro)ethoxypropionitrile (FEPN)29 offer low melting points (−43.8 to −57 °C), relatively high dielectric constants (∼36 at 25 °C), and low dynamic viscosities (0.37–1.1 cP at 25 °C). When a lithium salt, such as lithium bis(trifluorosulfonylimide) (LiTFSI), is dissolved, nitrile-based electrolytes provide a compelling electrolyte system for enabling high rate operation at room temperature. In particular, electrolytes prepared with MPN as the sole solvent possess the advantages of being environmentally benign, having a lower melting point, lower flammability, and lower volatility compared to commercial carbonate-based electrolytes.28 Wang et al., observed that 1 M LiTFSI in MPN exhibits an ionic conductivity of ∼8.5 mS cm−1 at room temperature and provides nearly a two-fold increase in rate capability compared to 1 M LiTFSI in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC or 1 M LiTFSI in AN when used with a lithium cobalt oxide (LCO) cathode and a lithium titanate (LTO) anode. Graphite anodes were found to be incompatible with MPN due to electrochemical instability, so MPN-based electrolytes are typically used with higher-potential anodes, such as LTO.44,45 It was also demonstrated that 1 M LiTFSI in EPN or FEPN supported comparable rate capabilities to 1 M LiTFSI in MPN.29
DMC or 1 M LiTFSI in AN when used with a lithium cobalt oxide (LCO) cathode and a lithium titanate (LTO) anode. Graphite anodes were found to be incompatible with MPN due to electrochemical instability, so MPN-based electrolytes are typically used with higher-potential anodes, such as LTO.44,45 It was also demonstrated that 1 M LiTFSI in EPN or FEPN supported comparable rate capabilities to 1 M LiTFSI in MPN.29
Another consideration is the use of additives for both low temperature operation and interface stabilization, particularly at the anode/electrolyte interface. Although additives have been shown to improve low temperature performance, their underlying function is to stabilize the electrode interfaces to chemical or morphological changes during formation of the SEI.9 Fluoroethylene carbonate (FEC) is a popular additive due to its favorable SEI-forming properties.4,30,31 Yoo et al. observed that 1.0 M LiPF6 in a mixture of butyronitrile, EC, and FEC formed a stable SEI comprising lithium nitride and lithium fluoride, which lowered the anode charge-transfer resistance and could be operated down to −40 °C.32 Another study demonstrated that acetonitrile, when combined with FEC, can also enhance compatibility with graphite anodes.33 These results advocate that the addition of FEC to nitrile-based electrolytes may stabilize interfaces and enable low temperature operation.
In the present study, we assess the viability of LiTFSI dissolved in MPN as the dominant component with an FEC additive (2.5 m LiTFSI in MPN + 5 wt% FEC; denoted as 2.5 m MPN) for operating at temperatures down to −40 °C. We comprehensively study the physical properties and electrochemical performance of this electrolyte for temperatures ranging from room temperature to −40 °C. To further elucidate bulk electrolyte properties, we also perform molecular dynamics simulations to simulate Li+ diffusion at low temperatures, which directly impacts Li+ conductivity. The computational efforts reported in this study further extend our understanding of complex electrolyte systems and how their behavior changes at low temperatures. We also perform an exhaustive impedance analysis by representing Nyquist plots in the form of relaxation times to identify the underlying interfacial processes responsible for low temperature operation.
2. Experimental
2.1. Chemicals
Lithium bis(trifluoromethanesulfonly)imide (LiTFSI, ≥98%), lithium hexafluorophosphate (LiPF6, ≥97%), and 4-fluor-2-oxo-1,3-dioxolane (FEC, ≥98%) were purchased from TCI America. Ethylene carbonate (EC, anhydrous ≥99%), dimethyl carbonate (DMC, anhydrous ≥99%), diethyl carbonate (DEC, anhydrous ≥99%), and 3-methoxypropionitrile (MPN, ≥98%) were purchased from Millipore Sigma. 2032-Coin cell components were purchased from MTI Corporation. Graphite and LCO electrode coatings with areal capacities of 1.21 and 1.1 mA h cm−2, respectively, were graciously provided by Saft America. All reagents were used as received with no further purification unless otherwise specified.2.2. Electrolyte synthesis and characterization
Three electrolyte types were synthesized in this study: 1.0 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (3
DMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) + 5 wt% FEC; 1.0 m LiPF6 in EC
7) + 5 wt% FEC; 1.0 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (1
DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); and X m LiTFSI in MPN + 5 wt% FEC (X = 1.0, 1.5, 2.0, 2.5). Electrolytes were prepared by adding the necessary molal amounts into a 20 mL glass vial. The solvents were continuously stirred at room temperature until all solid material was dissolved, which typically required 30 min of stirring. Samples were prepared in a glovebox (H2O and O2 levels maintained <0.5 ppm) and transferred into a dry room (humidity maintained <100 ppm) to be used to prepare coin cells.
1); and X m LiTFSI in MPN + 5 wt% FEC (X = 1.0, 1.5, 2.0, 2.5). Electrolytes were prepared by adding the necessary molal amounts into a 20 mL glass vial. The solvents were continuously stirred at room temperature until all solid material was dissolved, which typically required 30 min of stirring. Samples were prepared in a glovebox (H2O and O2 levels maintained <0.5 ppm) and transferred into a dry room (humidity maintained <100 ppm) to be used to prepare coin cells.
To measure the total conductivities of the electrolyte solutions, liquid electrolyte was soaked into glass fiber separators (18 mm dia., 190 μm thick), sandwiched between two stainless steel discs (15.5 mm dia., 0.5 mm thick, Gelon Lib Group), placed into a 2032-coin cell case with one stainless steel wave spring (Gelon Lib Group), and crimped at 700 psi (MTI MSK-110 Hydraulic Crimping Machine). Coin cells were placed into an ESPEC BTZ-133 environmental chamber, after which Electrochemical Impedance Spectroscopy (EIS) measurements were performed at 25 °C, 0 °C, −20 °C, and −40 °C (20 mV RMS, 100 kHz to 0.2 Hz, Gamry Instruments Reference 3000 Potentiostat/Galvanostat/ZRA). The coin cells were allowed to equilibrate at each temperature for 30 min before measurement. Reference measurements of the short-circuited setup were performed using the same EIS settings and temperature profile. “Electrolyte + setup” resistance was taken from the high frequency intercept of the electrolyte Nyquist plots, while “setup” resistance was taken from the low frequency intercept of the reference Nyquist plots. After subtracting the “setup” resistance from the “electrolyte + setup” resistance, the calculated “electrolyte” resistance was converted to “electrolyte” total conductivity using the glass fiber separator thickness and the stainless steel disc diameter.
Differential scanning calorimetry (DSC) was performed using the TA Instruments 2500 to identify the freezing/melting transitions of the electrolyte solutions. Samples were removed from the dry room and prepared for DSC. The DSC aluminum pan mass was measured, 30 mg of electrolyte solution was pipetted into the pan, and the pan mass was measured again to determine the sample mass. The lid was then crimped closed using the Tzero Sample Encapsulation Press. Samples were punctured to create a pinhole opening and loaded onto the DSC auto sampler. All samples underwent the same measurement program, with an isothermal hold for 5 min at 25 °C, followed by ramping down to −100 °C at a rate of 1 °C min−1, and then ramping up to 25 °C at a rate of 1 °C min−1.
2.3. Electrochemical characterization
Li+ coin cells (CR2032) were used for all electrochemical characterization experiments. For corrosion measurements, chronoamperometry was performed at 4.5 V vs. Li/Li+ for 5 h for 1.0, 1.5, 2.0, and 2.5 m MPN electrolytes using a coin cell configuration of liquid electrolyte soaked into a glass fiber separator, lithium metal as the anode, and a 14 mm dia. aluminum foil disk as the working electrode. A Zeta-20 optical profiler was used to obtain optical micrographs of the aluminum foil current collectors before and after corrosion tests. For electrochemical stability window tests, the coin cell configuration was liquid electrolyte soaked into a glass fiber separator, lithium metal as the anode, and a stainless steel disc as the working electrode. Linear sweep voltammetry was performed at a scan rate of 5 mV s−1 from open circuit potential to 5 V vs. Li/Li+ with one cell, and from open circuit potential to 0 V for the other cell.Full cells comprising lithium cobalt oxide (LCO) as the cathode and graphite (gr) as the anode were constructed using a N/P (negative/positive) capacity ratio of 1.1 (LCO: 1.1 mA h cm−2; gr: 1.21 mA h cm−2). A glass fiber separator soaked in the respective electrodes was used as the separator. Room-temperature rate capability tests were carried out for 5 cycles at each of the following C-rates: C/10, C/5, C/2, 1C, and 2C, then returned to C/10 for 5 more cycles. For cycle life tests, cells were first cycled at C/10 for 5 cycles, then cycled at C/5 for a total of 100 cycles. Temperature-controlled experiments ranging from room temperature down to −40 °C were conducted using an Espec BTZ-133 environmental chamber. EIS measurements were performed on the full cells at multiple temperatures (20 mV RMS, 100 kHz to 0.2 Hz, Gamry Instruments Reference 3000 Potentiostat/Galvanostat/ZRA). At room temperature (25 °C), the cells were cycled for three formation cycles before EIS measurements were performed in the discharged state. For 0, −20 °C, and −40 °C, cells were held at the desired temperature for 2, 4, and 8 h, respectively, before EIS measurements were performed in the discharged state. In between each EIS measurement, cells were returned to room temperature, charged to 100% SOC, and held at room temperature for 8 h before returning to the target temperature for discharging.
Distribution of relaxation times (DRT) analysis was used to identify characteristic distribution of typical EIS timescales, where the experimental data were fitted against a model (ZDRT), which is obtained from the following relationship (eqn (1)):34
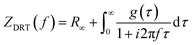 | (1) |
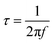 | (2) |
The Matlab GUI, DRTtools, developed by Ciucci, et al., was used to fit the impedance data based on the Tikhonov regularization.34 Since the frequency data was collected on a logarithmic scale, eqn (1) can then be expressed as eqn (3):34
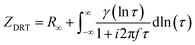 | (3) |
Here, γ[ln(τ)] = τg(τ); so the term “ln[γ(τ)]” is then another representation of the distribution of relaxation times.
2.4. Molecular dynamics simulations
All-atom molecular dynamics (MD) simulations were used to model ionic diffusivities and conductivities of electrolyte solutions corresponding to the three systems measured experimentally, excepting the FEC additive for stabilization of the solid–electrolyte interphase: 1 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (3
DMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 v/v), 1 m LiPF6 in EC
7 v/v), 1 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (1
DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v), and 2.5 m LiTFSI in MPN. Structures and force field parameters for Li+, PF6−, and the carbonates (EC, DMC, DEC) were adapted based on OPLS-AA.35–37 Structures and force field parameters for TFSI− and MPN were obtained using the Automated Topology Builder (ATB)38 based on GROMOS 54A7.39 Since non-polarizable force fields are known to significantly underestimate diffusivities when using full ionic charges, the charges of all salt ions were scaled by a standard correction factor of 80%.40 Simulation domains with composition corresponding to each electrolyte system were prepared using Moltemplate41 and MD simulations were run using LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator).42
1 v/v), and 2.5 m LiTFSI in MPN. Structures and force field parameters for Li+, PF6−, and the carbonates (EC, DMC, DEC) were adapted based on OPLS-AA.35–37 Structures and force field parameters for TFSI− and MPN were obtained using the Automated Topology Builder (ATB)38 based on GROMOS 54A7.39 Since non-polarizable force fields are known to significantly underestimate diffusivities when using full ionic charges, the charges of all salt ions were scaled by a standard correction factor of 80%.40 Simulation domains with composition corresponding to each electrolyte system were prepared using Moltemplate41 and MD simulations were run using LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator).42
Each simulation domain was initialized using Moltemplate to randomly distribute 512 total molecules consisting of salt and electrolyte to match experimental concentrations excepting FEC. A sequence of five sequential phases was used in each MD simulation at temperature T: (1) energy minimization, (2) NPT at 300 K for 1 ns, (3) NVT at T for 400 ps, (4) NPT at T for 400 ps, and finally (5) data collection under NVT at T for 10 ns. The diffusivity for each cation and anion species i was calculated as 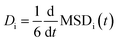 , using a linear model fit to the mean squared displacement MSDi(t) = <|ri(t) − ri(0)|2>i based on the last 5 ns of the trajectory from the data collection phase. The total conductivity was then estimated using the Nernst–Einstein equation κ = (D+ + D−)ce2NA/(kBT),43 where D+ and D− are the diffusivities of the cation and anion, c is the molar salt concentration, e is the elementary charge, NA is Avogadro's number, kB is Boltzmann's constant, and T is the system temperature.
, using a linear model fit to the mean squared displacement MSDi(t) = <|ri(t) − ri(0)|2>i based on the last 5 ns of the trajectory from the data collection phase. The total conductivity was then estimated using the Nernst–Einstein equation κ = (D+ + D−)ce2NA/(kBT),43 where D+ and D− are the diffusivities of the cation and anion, c is the molar salt concentration, e is the elementary charge, NA is Avogadro's number, kB is Boltzmann's constant, and T is the system temperature.
3. Results and discussion
The three electrolytes studied in this work are (i) 1.0 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (3
DMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) + 5 wt% FEC; (ii) 1.0 m LiPF6 in EC
7) + 5 wt% FEC; (ii) 1.0 m LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (1
DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); and (iii) 2.5 m MPN + 5 wt% FEC. To facilitate the discussion, these electrolytes will be referred to as STD1, STD2, and 2.5 m MPN, respectively. The STD1 electrolyte is ubiquitous in current LIB technologies while the STD2 electrolyte is one of the first discovered low temperature electrolytes, so these were chosen as references to compare against 2.5 m MPN.17 The 2.5 m MPN electrolyte was selected for its optimum balance of conductivity and stability. Table 1 summarizes the key physical characteristics of the solvents used for this series of electrolytes. The melting point of native MPN is −63 °C, which is lower than that of each of the carbonate solvents studied here (e.g., EC, DMC, and DEC). This is desirable for ensuring that the native solvent is unlikely to freeze at low temperatures. The flash point of MPN is higher than that of DMC, which may offer slightly better safety (though MPN remains a flammable solvent and should still be handled with care). Though the viscosity of MPN is similar to that of EC, the much higher dielectric permittivity compared to DMC and DEC enables this solvent to be used without the addition of other nitriles.
1); and (iii) 2.5 m MPN + 5 wt% FEC. To facilitate the discussion, these electrolytes will be referred to as STD1, STD2, and 2.5 m MPN, respectively. The STD1 electrolyte is ubiquitous in current LIB technologies while the STD2 electrolyte is one of the first discovered low temperature electrolytes, so these were chosen as references to compare against 2.5 m MPN.17 The 2.5 m MPN electrolyte was selected for its optimum balance of conductivity and stability. Table 1 summarizes the key physical characteristics of the solvents used for this series of electrolytes. The melting point of native MPN is −63 °C, which is lower than that of each of the carbonate solvents studied here (e.g., EC, DMC, and DEC). This is desirable for ensuring that the native solvent is unlikely to freeze at low temperatures. The flash point of MPN is higher than that of DMC, which may offer slightly better safety (though MPN remains a flammable solvent and should still be handled with care). Though the viscosity of MPN is similar to that of EC, the much higher dielectric permittivity compared to DMC and DEC enables this solvent to be used without the addition of other nitriles.
| Solvent | Melting point (°C) | Boiling point (°C) | Flash point (°C) | Viscosity (cP) | Dielectric constant (ε) |
|---|---|---|---|---|---|
| Ethylene carbonate (EC) | 36.4 | 248 | 143 | 1.92 | 89.8 (40 °C) |
| Dimethyl carbonate (DMC) | 0.5 | 90.5 | 19 | 0.585 | 3.09 (25 °C) |
| Diethyl carbonate (DEC) | −43 | 127 | 77 | 0.827 | 2.82 (25 °C) |
| 3-Methoxypropionitrile (MPN) | −63 | 165 | 66 | 2.5 | 36 (25 °C) |
Literature studies have shown that LiTFSI at low concentrations (<2.0 M) corrodes the aluminum current collector, which leads to significant capacity fade or shorting of the cell.44,45 At higher concentrations of LiTFSI, a cathode electrolyte interphase (CEI) can readily form to protect against parasitic reactions.44,45 To identify the optimized concentration of LiTFSI in MPN, the corrosion behavior of the aluminum current collector was tested by imposing a constant potential of 4.5 V vs. Li/Li+ for 5 h when exposed to electrolyte solutions with 1.0, 1.5, 2.0, and 2.5 m LiTFSI in MPN (Fig. 1a). For 1.0 m concentration, high current generation of ∼7.5 mA cm−2 is observed within the first 30 min. At higher concentrations (1.5 and 2.0 m), we observe less current generation of 1.8 and 0.7 mA cm−2, respectively. At 2.5 m, no peaks were detected, and the current maintained <0.2 mA cm−2 for the entire 5 h duration. This decrease in current generation advocates corrosion mitigation at higher concentrations of LiTFSI. To corroborate these electrochemical measurements, optical micrographs were taken of the current collectors to visualize the presence of pitting and crevice attack that are indicative of corrosion; the micrograph of pristine aluminum foil is shown as a control (Fig. 1b). For 1.0 m concentration, severe pitting and crevice corrosion was observed (Fig. 1c). For 1.5 and 2.0 m concentration, slightly less crevice corrosion is observed; however, there is extensive pitting of both aluminum foils (Fig. 1d and e). At 2.5 m concentration, the edge of the aluminum foil is comparable to that of the pristine aluminum current collector, and only slight pitting occurred (Fig. 1f). Moreover, with the addition of 5 wt% FEC, the decomposition currents at low potentials (0–1.5 V vs. Li/Li+) yielded comparable trends to STD1 and STD2, suggesting that a stable SEI was formed (Fig. S1†). Based on these results, the 2.5 m MPN electrolyte solution was down-selected to be the most desirable candidate for electrochemical testing.
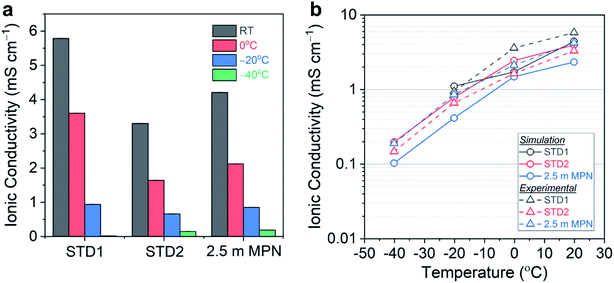
The total conductivity of this series of electrolytes was measured at the following temperatures: (i) room temperature (25 °C); (ii) 0 °C; (iii) −20 °C; and (iv) −40 °C (Fig. 2a). Tabulated values of the conductivity measurements are listed in Table S1.† At room temperature, STD1 yielded the highest conductivity of 5.79 mS cm−1. The conductivity of STD2 was slightly lower (3.30 mS cm−1), which was attributed to the higher viscosity of DEC. The 1.0 m MPN achieved a conductivity of 5.38 mS cm−1 comparable to STD1, while the 2.5 m MPN exhibited a slightly lower conductivity of 4.21 mS cm−1. At 0 °C, STD1 maintained the highest conductivity of 3.60 mS cm−1, with the next highest being 2.5 m MPN (2.12 mS cm−1), and the lowest conductivity being STD2 (1.64 mS cm−1). At −20 °C, STD1 and 2.5 m MPN yielded comparable conductivities (∼1.0 mS cm−1), while STD2 was 0.66 mS cm−1. At −40 °C, STD1 froze and EIS could not provide a meaningful measurement. In contrast, STD2 and 2.5 m MPN exhibited a conductivity of ∼0.2 mS cm−1, which suggested both of these systems should be good candidates for low temperature operation.
MD simulations were performed to corroborate the experimental conductivity trends and to simulate the diffusion process for 2.5 m MPN in comparison to the carbonate-based electrolytes. Values of ionic conductivity estimated from MD simulations were reported alongside experimentally measured values in Fig. 2b for the three electrolyte systems. The conductivities from simulation and experiment are in qualitative agreement. Furthermore, simulations performed at T = −40, −20, 0, and 20 °C also reproduce the correct temperature trends for this series of electrolytes. These trends are driven by the temperature dependence in calculated ionic diffusivities, which are reported in Fig. S2.† Both the measured and simulated transport properties for STD1 and STD2 are consistent with literature values in similar carbonate systems: conductivities of ∼10 mS cm−1 and diffusivities of 10−6 cm2 s−1 at room temperature.46–48 The conductivity in MPN was also consistent with prior measurements for the LiClO4 salt (∼5.0 mS cm−1 at 20 °C).49 To the best knowledge of the authors, the results reported in this work are the first MD simulations of ion transport in MPN-based electrolytes. Quantitatively, the simulated conductivity of MPN underestimates the experimental values and with a larger error than the carbonate-based systems. This difference is likely due to shortcomings in the GROMOS-based parameters for MPN from ATB, in contrast with the more-established OPLS-AA parameters for the carbonates. Therefore, there is a need to develop improved molecular models for more detailed modeling of diffusion mechanisms in MPN and other solvents in future work.
Taken together, the simulation results corroborate the experimental observations that ion transport in MPN exhibits similar temperature dependence to STD2, albeit lower overall conductivity values, down to −40 °C. This suggests that significant opportunities remain to further optimize nitrile-based solvents as an alternative to carbonates, particularly for low temperature operation. Future studies will continue to build towards this goal by using complementary experimental and modeling efforts, performing more extensive analysis of the transport mechanisms in the carbonate versus nitrile systems, and by expanding the parameter space for optimizing low temperature performance.
The freezing point of the electrolyte solution is another critical factor to be useful for LIBs operating at low temperatures. Differential scanning calorimetry measurements were performed for this series of electrolytes from 25 °C down to −100 °C to identify the freezing point, then returned to 25 °C to identify the melting point, using a heating/cooling rate of 1 °C min−1. As shown in Fig. 3, both STD1 and STD2 exhibited a freezing point of roughly −33 °C. This is consistent with reported freezing points in the literature, where STD1 was 100% solid at roughly −40 °C while STD2 displayed coexistence of solid and liquid phases at −42.5 °C.6 For 2.5 m MPN, no freezing point was observed down to −100 °C, which is a promising attribute for low temperature operation.
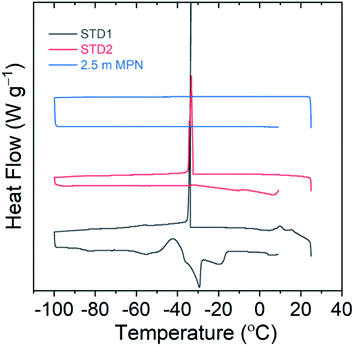 | ||
| Fig. 3 Differential scanning calorimetry curves to identify possible freezing points using a scan range of 25 °C to −100 °C. | ||
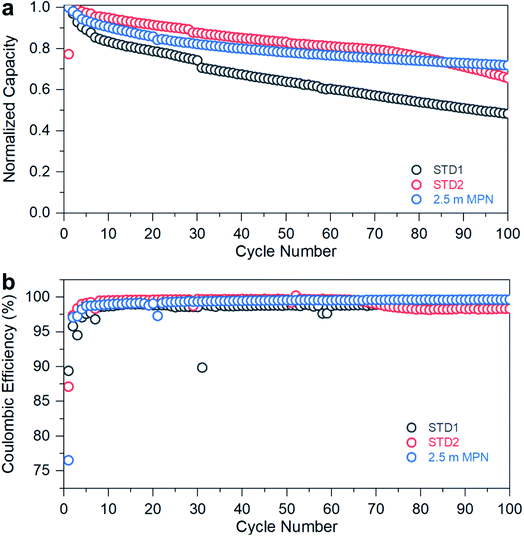
Electrochemical performance was assessed in a technologically-relevant cell configuration: graphite‖LiCoO2 (gr‖LCO). First, the rate capability and cycle life retention of cells utilizing these electrolytes were measured at room temperature for C-rates ranging from 0.1C to 2C (Fig. 4a–c). The rate capability performance of STD1, STD2, and 2.5 m MPN are in agreement with the high conductivity trends at room temperature. The specific capacities for these three cells (based on the active mass of LCO) all yielded near-theoretical values (135–138 mA h g−1). At an imposed rate of 2C, a capacity of ∼100 mA h g−1 is still supported by all electrolytes. The initial coulombic efficiencies of STD1 and STD2 were both >82%, whereas for 2.5 m MPN is ∼78%. However, after the 1st cycle, all cells yielded high coulombic efficiencies, reaching up to >99% from C/5 to 2C, and ∼98% at C/10.
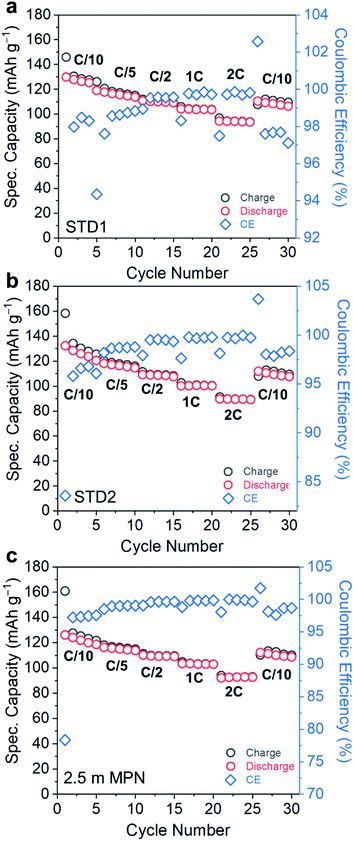 | ||
| Fig. 4 Rate capability performance of gr‖LCO cells when subjected to C-rates ranging from C/10 to 2C and utilizing (a) STD1, (b) STD2, and (c) 2.5 m MPN electrolytes. | ||
The performance of the standard and MPN formulations was further evaluated to assess long-term stability when subjected to a C-rate of 0.2C (Fig. 5a) at room temperature. The STD1 electrolyte exhibited rapid capacity fade, dropping below 60% of its initial discharge capacity after 100 cycles. The STD2 electrolyte showed improved capacity retention up to 85 cycles, then began to decay. The 2.5 m MPN solution, though initially exhibiting a more rapid decrease in capacity over the first 80 cycles versus STD2, yielded the greatest capacity retention after 100 cycles (>75%). When examining the coulombic efficiencies (Fig. 5b), STD1 yielded an efficiency of ∼97%, while STD2 maintained ∼100%, but began to drop to ∼97% after the 85th cycle, correlating well with the decay in discharge capacity. For 2.5 m MPN, the efficiency was maintained at ∼100% throughout the entire duration, demonstrating that this electrolyte can be used as a drop-in replacement for potential commercial use. Overall, STD2 and 2.5 m MPN offer the best combination of rate performance and cycle stability at room temperature. Though both are nearly comparable to each other, with the more challenging gr‖LCO cell configuration, a significant improvement in stability was observed with the addition of 5 wt% FEC to the nitrile-based electrolyte. Otherwise, a LTO anode would be needed to maintain both high-rate capability and long-term stability.
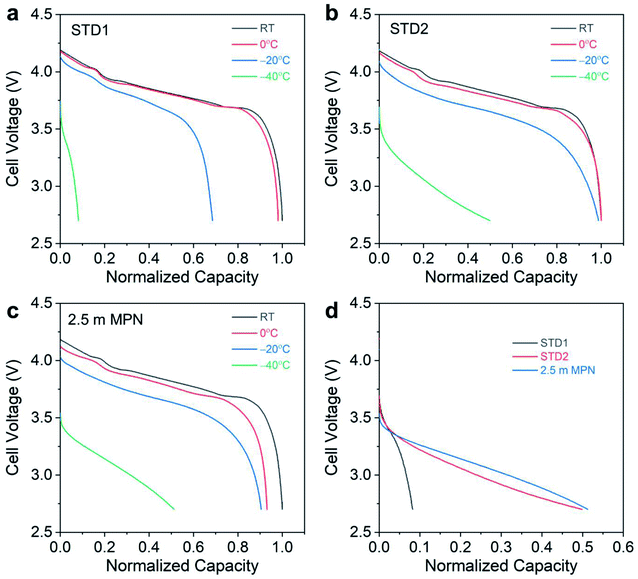
To further analyze the electrochemical performance, low temperature testing was performed, ranging from room temperature to −40 °C (Fig. 6). At room temperature and at 0 °C, both STD1 and STD2 exhibited comparable performance with negligible capacity loss (Fig. 6a and b). However, at −20 °C, STD1 showed a significant capacity drop of ∼30% relative to its room temperature discharge capacity, while STD2 retained nearly 100% of its room temperature discharge capacity. Between STD1 and STD2, the discharge capacity at −40 °C was much higher for STD2 (∼50% retention), which was to be expected due STD1 freezing. The 2.5 m MPN electrolyte showed a capacity drop of ∼10% at −0 °C and an additional ∼5% decay at −20 °C relative to its room temperature discharge capacity. At −40 °C, the 2.5 m electrolyte retained >50% capacity, comparable to STD2 (Fig. 6c). To probe deeper into the distinct advantage of the 2.5 m MPN electrolyte, the mid-point discharge voltage was tracked, which relates to the ohmic polarization of the cells during discharge (overlaid discharge curves shown in Fig. 6d). Though the 2.5 m MPN electrolyte showed comparable capacity retention to STD2, it in fact had a higher mid-point voltage (3.07 V) at −40 °C compared to STD2 (2.98 V) (Table 2). This implies that 2.5 m MPN showed less resistance at −40 °C compared to STD2 and can exhibit higher power at −40 °C, traits that are important for practical applications under such extreme conditions. Under continuous charge/discharge operation at −40 °C, high initial discharge capacity retention was observed for both STD2 and 2.5 m MPN, though subsequent cycling led to decreasing discharge capacities (Fig. S3†), suggesting that charging at low temperatures was the limiting factor in delivering high capacities.
| Electrolyte | Mid-point discharge voltage (V) | |||
|---|---|---|---|---|
| Room temperature | 0 °C | −20 °C | −40 °C | |
| STD1 | 3.85 | 3.79 | 3.59 | 3.00 |
| STD2 | 3.81 | 3.78 | 3.65 | 2.98 |
| 2.5 M MPN | 3.85 | 3.79 | 3.66 | 3.07 |
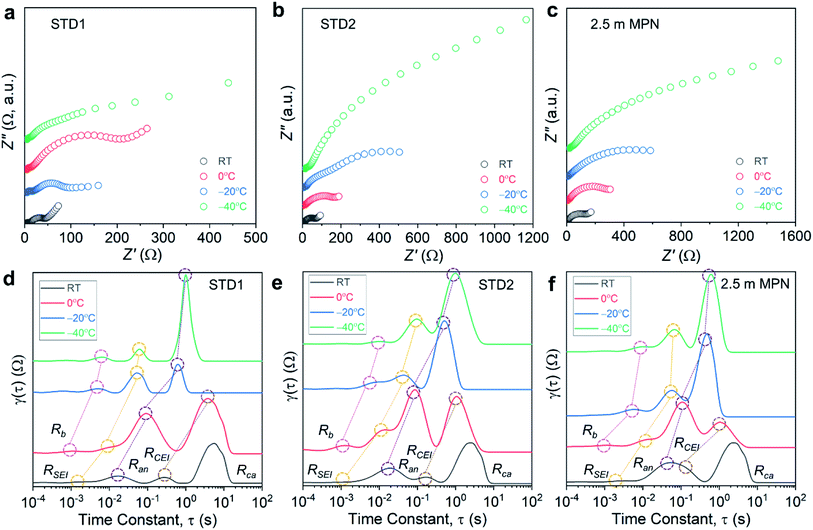
Impedance measurements were performed on the full cells for a range of operating temperatures (Fig. 7a–c), and the bulk resistance (Rb) and the charge-transfer resistances of the anode and cathode (Ran and Rca, respectively) were quantified using a Rb − Ran|Qan − Rca|Qca equivalent circuit. For all three electrolytes, a commensurate increase in Rb was observed, which is consistent with the decrease in conductivity measured experimentally (Table S2†). At −40 °C, 2.5 m MPN had the highest Rb (22.1 Ω) compared to STD1 (5.67 Ω) and STD2 (15.44 Ω). For all three types of full cells, the resistance values for Rca were nearly one order-of-magnitude higher than the resistance values for Ran (Table S3†). STD1 and STD2 yielded comparable values of Ran, which increased from ∼15 Ω at room temperature to ∼70 Ω at −40 °C. For Rca, values >1000 Ω were observed at −40 °C for STD2 and 2.5 m MPN (Table S4†). Though the resistance values of STD2 and 2.5 m MPN were higher than that of STD1, these two electrolytes maintained a higher level of capacity retention when compared to their room temperature performance. This shows that while charge-transfer processes are slower at low temperature, the performance of the LIB is to a large degree dependent on maintaining a liquid phase.
The distribution of relaxation times (DRT) method is a complementary electroanalytical tool used to interpret electrochemical systems as a continuous distribution of RQ elements with a range of relaxation times.34,50–53 By taking advantage of the different responses of the anode and cathode to changing temperatures, the interfacial processes in full cells could be separated into (i) electrolyte (Rb); (ii) passive film processes (anode SEI, RSEI; and cathode electrolyte interphase, RCEI); (iii) charge transfer at the anode (Ran); and (iv) charge transfer at the cathode (Rca).54 All tabulated τ values are summarized in Table S5.†
The DRT plots for STD1 initially showed four peaks at room temperature that corresponded to RSEI, Ran, RCEI, and Rca, which shifted to Rb, RSEI, Ran, and RCEI for 0 °C to −40 °C (Fig. 7d). The DRT method can only be applied to processes in the frequency range of the impedance measurement (100 kHz to 0.2 Hz), so faster processes (e.g., bulk electrolyte transport at room temperature) or slower processes (e.g., charge transfer at the cathode for 0 °C to −40 °C) cannot be evaluated accurately.54,55 When examining Rb, τ increased from 1.0 ms to 6.0 ms when the temperature decreased from 0 to −40 °C, respectively. This slight increase indicated that the bulk electrolyte began to exhibit slower reaction kinetics at lower temperatures. Similarly, τ for RSEI increased slightly from 10 ms to 60 ms for the same temperature range. The greatest change was observed for Ran, which represented the charge-transfer reaction at the graphite surface. The τ values increased two orders-of-magnitude from 10 ms to 1.0 s when the temperature decreased from 0 to −40 °C, respectively. Similarly, RCEI increased by an order-of-magnitude from 0.27 to 3.7 s when the temperature decreased from room temperature to 0 °C, respectively.
These results indicated that the cell kinetics are most strongly limited by Ran and RCEI. The DRT analysis of STD2 and 2.5 m MPN focused on these two parameters. For STD2, τ for Ran at 0 °C (0.18 s) was higher than that for STD1 and increased to 1.0 s at −40 °C, suggesting STD2 had a similar anode response time to STD1 (Fig. 7e). For 2.5 m MPN, τ for Ran was 0.05 s at 0 °C, but only increased to 0.59 s at −40 °C (Fig. 7f), demonstrating the improved low temperature interfacial kinetics of the 2.5 m MPN electrolyte. For both STD2 and 2.5 m MPN, τ for RCEI was 0.16 s at room temperature and increased to 1.1 s at 0 °C, which was two times lower than that for STD1 (3.7 s). Overall, the DRT method identified that the limiting interfacial kinetics most affected by lower temperatures occurred at the anode (e.g. gr) and cathode (e.g. CEI) surfaces, lower temperatures.
4. Conclusions
Nitrile-based solvents are a promising candidate for low temperature lithium-ion battery operation. In the present study, we demonstrate that 3-methoxypropionitrile (MPN) mixed at a 2.5 m concentration with LiTFSI, enables operation under low temperature environments (−40 °C). With the addition of an interface stabilizing–additive (FEC), gr‖LCO full cells demonstrated high cycling rates and stable cycling capacities at room temperature, accompanied by high capacity retention at low temperatures. Leveraging impedance spectroscopy, particularly the DRT method, we identified that interfacial processes at the graphite surface and the cathode electrolyte interphase are the two underlying limitations to low temperature performance. By characterizing the physical properties of the studied electrolytes, we also demonstrate that molecular dynamics simulations can semi-quantitatively reproduce diffusion and conductivity mechanisms in nitrile-based systems, as well as more established carbonate-based systems, while identifying quantitative shortcomings to be addressed in force field development. This unique combination of theoretical and experimental assessments provide insight into novel chemistries that can be leveraged for novel low temperature electrolytes. Future studies will focus on identifying other nitrile-based solvents and solvent combinations that enable low temperature operation below −40 °C, with the aid of simulation-based predications and experimental validation.Author contributions
S. A. L. and J. S. K. conceived and designed this work. S. A. L., M. M. M., T. H., and J. S. K. prepared the electrolytes and carried out electrochemical measurements. G. F. and C. C. measured the physical characteristics of the electrolytes. N. Q. L., E. R., and J. D. carried out the molecular dynamics simulations and calculations. S. A. L. and J. S. K. wrote the manuscript. All authors assisted in the discussions to improve the paper and made revisions.Conflicts of interest
There are no conflicts of interests to declare.Acknowledgements
This work was supported by the Johns Hopkins University Applied Physics Laboratory Independent Research and Development Program. The authors would like to thank Dr Rengaswamy Srinivasan, Dr Christopher Stiles, Dr Konstantinos Gerasopoulos, and Dr Bing Tan for insightful discussions.References
- M. Winter, B. Barnett and K. Xu, Before Li ion batteries, Chem. Rev., 2018, 118(23), 11433–11456 CrossRef CAS PubMed.
- J. B. Goodenough, How we made the Li-ion rechargeable battery, Nat. Electron., 2018, 1, 204 CrossRef.
- J. B. Goodenough and K.-S. Park, The Li-ion rechargeable battery: A perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176 CrossRef CAS PubMed.
- K. Xu, Electrolyte and interphases in Li-ion batteries and beyond, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- J. Hou, M. Yang, D. Wang and J. Zhang, Fundamentals and challenges of lithium ion batteries at temperatures between –40 and 60°C, Adv. Energy Mater., 2020, 10, 1904152 CrossRef CAS.
- C.-K. Huang, J. S. Sakamoto, J. Wolfenstine and S. Surampudi, The limits of low-temperature performance of Li-ion cells, J. Electrochem. Soc., 2000, 147(8), 2893–2896 CrossRef CAS.
- G. Zhu, K. Wen, W. Lv, X. Zhou, Y. Liang, F. Yang, Z. Chen, M. Zou, J. Li, Y. Zhang and W. He, Materials insights into low-temperature performances of lithium-ion batteries, J. Power Sources, 2015, 300, 29–40 CrossRef CAS.
- N. Zhang, T. Deng, S. Zhang, C. Wang, L. Chen, C. Wang and X. Fan, Critical review on low-temperature Li-ion/metal batteries, Adv. Mater., 2022, 2107899 CrossRef CAS PubMed.
- D. Hubble, D. Emory Brown, Y. Zhao, C. Fang, J. Lau, B. D. McCloskey and G. Liu, Liquid electrolyte development for low-temperature lithium-ion batteries, Energy Environ. Sci., 2022, 15, 550–578 RSC.
- A. Gupta and A. Manthiram, Designing advanced lithium-based batteries for low-temperature conditions, Adv. Energy Mater., 2020, 10, 2001972 CrossRef CAS PubMed.
- N. Piao, X. Gao, H. Yang, Z. Guo, G. Hu, H.-M. Cheng and F. Li, Challenges and development of lithium-ion batteries for low temperature environments, eTransportation, 2022, 11, 100145 CrossRef.
- T. L. Kulova and A. M. Skundin, A critical review of electrode materials and electrolytes for low-temperature lithium-ion batteries, Int. J. Electrochem. Sci., 2020, 15, 8638–8661 CrossRef.
- M. Armand and J.-M. Tarascon, Building better batteries, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- K. Xu, Nonaqueous liquid electrolytes for lithium-based rechargeable batteries, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- S. S. Zhang, K. Xu and T. R. Jow, The low temperature performance of Li-ion batteries, J. Power Sources, 2003, 115, 137–140 CrossRef CAS.
- O. V. Bushkova, T. V. Yaroslavtseva and Y. A. Dobrovolsky, New lithium salts in electrolytes for lithium-ion batteries (review), Russ. J. Electrochem., 2017, 53(7), 677–699 CrossRef CAS.
- M. C. Smart, B. V. Ratnakumar and S. Surampudi, Electrolytes for low-temperature lithium batteries based on ternary mixtures of aliphatic carbonates, J. Electrochem. Soc., 1999, 146(2), 486–492 CrossRef CAS.
- M. C. Smart, B. V. Ratnakumar, S. Surampudi, Y. Wang, X. Zhang, S. G. Greenbaum, A. Hightower, C. C. Ahn and B. Fultz, Irreversible capacities of graphite in low-temperature electrolytes for lithium-ion batteries, J. Electrochem. Soc., 1999, 146(11), 3963–3969 CrossRef CAS.
- E. J. Plichta, M. Hendrickson, R. Thompson, G. Au, W. K. Behl, M. C. Smart, B. V. Ratnakumar and S. Surampudi, Development of low temperature Li-ion electrolytes for NASA and DoD applications, J. Power Sources, 2001, 94, 160–162 CrossRef CAS.
- B. V. Ratnakumar, M. C. Smart, C. k. Huang, D. Perrone, S. Surampudi and S. G. Greenbaum, Lithium ion batteries for Mars exploration missions, Electrochim. Acta, 2000, 45, 1513–1517 CrossRef CAS.
- M. C. Smart, B. V. Ratnakumar, L. D. Whitcanack, K. B. Chin, S. Surampudi, H. Croft, D. Tice and R. Staniewicz, Improved low-temperature performance of lithium-ion cells with quaternary carbonate-based electrolytes, J. Power Sources, 2003, 119–121, 349–358 CrossRef CAS.
- M. C. Smart, B. V. Ratnakumar, R. C. Ewell, S. Surampudi, F. J. Puglia and R. Gitzendanner, The use of lithium-ion batteries for JPL's Mars missions, Electrochim. Acta, 2018, 268, 27–40 CrossRef CAS.
- M. S. Ding, Electrolytic conductivity and glass transition temperature as functions of salt content, solvent composition, or temperature for LiPF6 in propylene carbonate + diethyl carbonate, J. Chem. Eng. Data, 2003, 48, 519–528 CrossRef CAS.
- M. S. Ding and T. R. Jow, Conductivity and viscosity of PC-DEC and PC-EC solutions of LiPF6, J. Electrochem. Soc., 2003, 150(5), A620–A628 CrossRef CAS.
- M. S. Ding, Electrolytic conductivity and glass transition temperatures as functions of salt content, solvent composition, or temperature for LiBF4 in propylene carbonate + diethyl carbonate, J. Chem. Eng. Data, 2004, 48, 1102–1109 CrossRef.
- D. Zhang, D. Zhu, W. Guo, C. Deng, Q. Ju, H. Li and Y. Min, The fluorine-rich electrolyte as an interface modifier to stabilize lithium metal battery at ultra-low temperature, Adv. Funct. Mater., 2022, 32, 2112764 CrossRef CAS.
- X. Fan, X. Ji, L. Chen, J. Chen, T. Deng, F. Han, J. Yue, N. Piao, R. Wang, X. Zhou, X. Xiao, L. Chen and C. Wang, All-temperature batteries enabled by fluorinated electrolytes with non-polar solvents, Nat. Energy, 2019, 4, 882–890 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, I. Exnar and M. Grätzel, 3-Methoxypropionitrile-based novel electrolytes for high-power Li-ion batteries with nanocrystalline Li4Ti5O12 anode, J. Electrochem. Soc., 2004, 151(10), A1598–A1603 CrossRef CAS.
- Q. Wang, P. Pechy, S. M. Zakeeruddin, I. Exnar and M. Grätzel, Novel electrolytes for Li4Ti5O12-based high power lithim ion batteries with nitrile solvents, J. Power Sources, 2005, 146, 813–816 CrossRef CAS.
- C. Wang, Y. S. Meng and K. Xu, Fluorinating interphases, J. Electrochem. Soc., 2019, 166(3), A5184–A5186 CrossRef CAS.
- B. Liu, B. Li and S. Guan, Effect of fluoroethylene carbonate additive on low temperature performance of Li-ion batteries, Electrochem. Solid-State Lett., 2012, 15(6), A77–A79 CrossRef CAS.
- D.-J. Yoo, Q. Liu, O. Cohen, M. Kim, K. A. Persson and Z. Zhang, Understanding the role of SEI layer in low-temperature performance of lithium-ion batteries, ACS Appl. Mater. Interfaces, 2022, 14, 11910–11918 CrossRef CAS PubMed.
- P. Hilbig, L. Ibing, B. Streipert, R. Wagner, M. Winter and I. Cekic-Laskovic, Acetonitrile-based electrolytes for lithium-ion battery application, Curr. Top. Electrochem., 2018, 20, 1–13 CrossRef.
- T. H. Wan, M. Saccoccio, C. Chen and F. Ciucci, Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools, Electrochim. Acta, 2015, 182, 483–499 CrossRef.
- T. Hou, K. D. Fong, J. Wang and K. A. Persson, The solvation structure, transport properties, and reduction behavior of carbonate-based electrolytes of lithium-ion batteries, Chem. Sci., 2021, 12, 14740–14751 RSC.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirad-Rives and W. L. Jorgensen, Evaluation and reparameterization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides, J. Phys. Chem. B, 2001, 105(28), 6474–6487 CrossRef CAS.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, An automated force field topology builder (ATB) and respository: Version 1.0, J. Chem. Theory Comput., 2011, 7(12), 4026–4037 CrossRef CAS PubMed.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Definition and testing of the GROMOS force-field versions 54A7 and 54B7, Eur. Biophys. J., 2011, 40, 843–856 CrossRef CAS PubMed.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. Mackerell Jr, B. Roux and C. Schröder, Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields, Chem. Rev., 2019, 119(13), 7940–7995 CrossRef CAS PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, Moltemplate: A tool for coarse-grained modeling of complex biological matter and soft condensed matter physics, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- A. P. Thompson, H. Metin Aktulga, R. Berger, D. S. Bolintineanu, W. Michael Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. Dac Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- F. Hanke, N. Modrow, R. L. C. Akkermans, I. Korotkin, F. C. Mocanu, V. A. Neufeld and M. Veit, J. Electrochem. Soc., 2020, 167, 013522 CrossRef CAS.
- K. Matsumoto, K. Inoue, K. Nakahra, R. Yuge, T. Noguchi and K. Utsugi, Suppression of aluminum corrosion by using high concentration LiTFSI electrolyte, J. Power Sources, 2013, 231, 234–238 CrossRef CAS.
- D. W. McOwen, D. M. Seo, O. Borodin, J. Vatamanu, P. D. Boyle and W. A. Henderson, Concentrated electrolytes: Decrypting electrolyte properties and reassessing Al corrosion mechanisms, Energy Environ. Sci., 2014, 7, 416 RSC.
- S. Hwang, D.-H. Kim, J. H. Shin, J. E. Jang, K. H. Ahn, C. Lee and H. Lee, Ionic conduction and solution structure in LiPF6 and LiBF4 propylene carbonate electrolytes, J. Phys. Chem. C, 2018, 122(34), 19438–19446 CrossRef CAS.
- L. Ole Valøen and J. N. Reimers, Transport properties of LiPF6-based Li-ion battery electrolytes, J. Electrochem. Soc., 2005, 152, A882 CrossRef.
- C. Capiglia, Y. Saito, H. Yamamoto, H. Kageyama and P. Mustarelli, Electrochim. Acta, 2000, 45, 1341–1345 CrossRef CAS.
- H. Shim, Ö. Budak, V. Haug, M. Widmaier and V. Presser, Electrochim. Acta, 2020, 337, 135760 CrossRef CAS.
- E. Ivers-Tiffée and A. Weber, Evaluation of electrochemical impedance spectra by the distribution of relaxation times, J. Ceram. Soc. Jpn., 2017, 125, 193–201 CrossRef.
- M. A. Danzer, Generalized distribution of relaxation times analysis for the characterization of impedance spectra, Batteries, 2019, 5, 53 CrossRef CAS.
- M. Hahn, S. Schindler, L.-C. Triebs and M. A. Danzer, Optimized process parameters for a reproducible distribution of relaxation times analysis of electrochemical systems, Batteries, 2019, 5, 43 CrossRef CAS.
- E. Espinoza-Villatoro, J. Nelson Weker, J. S. Ko and E. Quiroga-González, Tracking the evolution of processes occurring in silicon anodes in lithium ion batteries by 3D visualization of relaxation times, J. Electroanal. Chem., 2021, 892, 115309 CrossRef.
- J. Zhu, M. Knapp, X. Liu, P. Yan, H. Dai, X. Wei and H. Ehrenberg, Low-temperature separating lithium-ion battery interfacial polarization based on distribution of relaxation times (DRT) of impedance, IEEE Transactions on Transportation Electrification, 2021, 7, 410–421 Search PubMed.
- P. Shafiei Sabet, A. J. Warnecke, F. Meier, H. Witzenhausen, E. Martinez-Laserna and D. U. Sauer, Non-invasive yet separate investigation of anode/cathode degradation of lithium-ion batteries (nickel–cobalt–manganese vs. graphite) due to accelerated aging, J. Power Sources, 2020, 449, 227369 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta03240f |
| This journal is © The Royal Society of Chemistry 2022 |