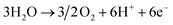Impact of the dopant-induced ensemble structure of hetero-double atom catalysts in electrochemical NH3 production†
Seung-hoon
Kim
 ab,
Ho Chang
Song
c,
Sung Jong
Yoo
ab,
Ho Chang
Song
c,
Sung Jong
Yoo
 ade,
Jonghee
Han‡
*ab,
Kwan-Young
Lee
ade,
Jonghee
Han‡
*ab,
Kwan-Young
Lee
 *bf and
Hyung Chul
Ham
*bf and
Hyung Chul
Ham
 *c
*c
aCenter for Hydrogen and Fuel Cell Research, Korea Institute of Science and Technology (KIST), 5, Hwarangno 14-gil, Seongbuk-gu, Seoul, 02792, Republic of Korea
bGraduate School of Energy and Environment, Korea University, 145, Anam-ro, Seongbuk-gu, Seoul, 02841, Republic of Korea
cDepartment of Chemistry and Chemical Engineering, Education and Research Center for Smart Energy and Materials, Inha University, 100, Inha-ro, Michuhol-gu, Incheon, 22212, Republic of Korea. E-mail: ham.hyungchul@inha.ac.kr
dKHU-KIST Department of Converging Science and Technology, Kyung Hee University, Seoul 02447, Republic of Korea
eDivision of Energy & Environment Technology, KIST School, University of Science and Technology (UST), Seoul 02792, Republic of Korea
fDepartment of Chemical and Biological Engineering, Korea University, 145, Anam-ro, Seongbuk-gu, Seoul, 02841, Republic of Korea. E-mail: kylee@korea.ac.kr
First published on 11th January 2022
Abstract
Using spin-polarized density functional theory (DFT) calculations, we examined electrochemical N2 reduction (N2RR) toward NH3 production on hetero-RuM (M = 3d transition metals) double atom catalysts supported on defective graphene by means of analysis on the geometric ensemble structure, the N2RR mechanism, the decoupling of strain, dopant and configurational effects and the d-orbital resolved density of states (ORDOS) (dz2, dxz, dyz, dxy, and dx2–y2) on the hetero-double atoms. In addition, we computationally screened novel catalysts by exploring 4d, 5d and p block metals as the hetero-M metals in the RuM system. First, we found the significantly enhanced N2RR activity of inclined pentagon M (Fe, Mn, and Sc) double atom catalysts (RuFe has the highest activity) compared to the homo-Ru2 double atom catalyst. Our DFT calculations on the interplay of strain, dopant and configurational effects in the inclined pentagon M (Fe, Mn, and Sc) double atom catalysts predicted that (1) the dopant effect was the promoter to improve the N2RR activity of RuSc and RuMn, (2) the tensile strain (RuSc) tended to reduce the NH3 productivity via the N2RR, while the effect of compressive strain (RuFe and RuMn) was insignificant, and (3) the dopant-support interaction induced a unique inclined pentagon M double atom ensemble structure, which leads to the large reduction of the N2RR activity of the hetero-RuSc double atom but the activity increases for the hetero-RuFe and RuMn cases. Finally, our DFT calculation on the analysis of the p–d (dz2, dxz, dyz, dxy, and dx2–y2) orbital overlap identified the key d orbitals in determining the descriptor (NH2 adsorption energy) for representing the N2RR. That is, the orbitals (dz2, dxz, and dyz) having an orientation toward the z direction in the horizontal Ru2 double atom played an important role in determining the NH2 adsorption process, while for the inclined pentagon M double atoms (RuFe, RuSc, and RuMn), the dxz and dxy orbitals were found to be essential for the modification of NH2 adsorption energy. Finally, a descriptor based DFT search additionally discovered promising hetero-RuOs and RuIr double atom catalysts. This study highlights that the dopant engineering of hetero-double atom catalysts supported on defective graphene can significantly modify the electrochemical reactivity, particularly by the dopant type and geometric ensemble structure.
Introduction
To reduce global warming, many studies are being actively conducted around the world to reduce anthropogenic carbon dioxide (CO2) emissions and find new clean energy sources to replace fossil fuels. Among the candidates for new energy media, hydrogen (H2) is being spotlighted.1 H2 is the most bountiful chemical substance in the universe, and it is colourless, non-toxic and highly combustible. It can be produced without carbon emission through electrolysis of water using renewable electricity and used as a power source for fuel cells that can produce electricity for ships, airplanes, automobiles, and drones.2–4 When H2 is consumed in a fuel cell, it only emits water as a byproduct.5 However, its low volumetric energy density, wide range of flammability limits, and high transportation cost are obstacles to using it directly as an energy medium.Recently, ammonia (NH3) has been prominent as a promising candidate for storage and transportation of H2 due to its several advantages. It can be readily liquefied under 8 bar at ambient temperature,6 and its relatively high autoignition temperature (651 °C, compared to 254 °C for diesel) enables us to use it safely from fire and explosion.7–9 Zamfirescu et al. reported that NH3 is competitive compared to other common fuels such as gasoline, liquefied petroleum gas (LPG) and methanol due to its high volumetric and gravimetric H2 storage density and low energy costs.7 It is already widely used for industrial use and has a distributional infrastructure to transport it in amounts larger than 100 million tons yearly or more.10
In industrial NH3 production so far, the Haber–Bosch process constitutes the dominant route.11,12 However, this process consumes a huge amount of energy due to its high operating temperatures (400–500 °C) and pressure (150–300 bar) to break the intermolecular N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, which is equivalent to about 2% of the worldwide energy use.13,14 Moreover, natural gas (mainly methane) is used as a source of H2, releasing massive amounts of CO2 as a by-product.
N bond, which is equivalent to about 2% of the worldwide energy use.13,14 Moreover, natural gas (mainly methane) is used as a source of H2, releasing massive amounts of CO2 as a by-product.
In contrast, electrochemical NH3 production through the N2 reduction reaction (N2RR) can synthesize NH3 directly from N2 and H2 without carbon emission, and it can be operated by supplying renewable electricity such as solar and wind power. In general, electrolytic cells based on a solid electrolyte membrane are used for this process as they allow easy separation of the H2 feed from the NH3 product.15,16 The basic equations for electrochemical NH3 production using electrolytic cells under acidic conditions are as follows:
Anode:
Cathode:
| N2 + 6H+ + 6e− → 2NH3 |
Overall:
In the anode, water (H2O) is oxidized through the oxygen evolution reaction, giving protons and electrons and releasing oxygen. These protons and electrons are transferred to the cathode via the membrane and electric potential, respectively. In the cathode, NH3 is produced by the N2RR, in which gaseous N2 is sequentially combined with protons and electrons.
Group VIII elements (Fe, Ru and Os) have been known to have excellent activity in electrochemical NH3 production.17–22 In addition, the catalyst research has been expanded to noble metals (e.g. Rh, Pd, Au, Ru, Pt and their oxides, nitrides, and sulphides), non-noble metals (e.g. Ti, Fe, Ni, Mo, V, W and their oxides, nitrides and sulphides), and carbon-based non-metal catalysts.23–39 Among those species, Ru has been reported to be the most active catalyst. For example, according to Nørskov's study, there is a volcanic relationship between the number of valence electrons and the NH3 productivity, indicating that Ru has optimal valence electrons for NH3 production through N2 reduction.20 Ru has exhibited a high reactivity toward electrochemical NH3 production under room temperature and pressure conditions.11,15,16,21,22 However, Ru still shows poor NH3 productivity for the commercialization of electrochemical NH3 production.
To deal with this issue, the concept of single atom catalysts (SACs) has been recently introduced to make a breakthrough in activity for electrochemical NH3 production, since it can improve activity beyond the existing volcanic curve, maximize the number of active sites, and achieve economic feasibility by reducing catalyst loading.40–47 Zhao et al. theoretically reported that single Mo exhibited the lowest N2RR onset potential (−0.35 V) among SACs embedded in defective boron nitride sheets,40 and Lü et al. claimed that the active site for the N2RR on an Fe catalyst anchored to an N-doped carbon framework is Fe–N–C, in which a single Fe atom is bonded to four N atoms.42 For Ru-based SACs, Geng et al. reported that Ru–N–C SACs showed a lower overpotential [ΔG(Ru1–N3) = 0.73 eV and ΔG(Ru1–N4) = 0.77 eV] compared to the Ru (101) catalyst [ΔG = 0.91 eV] by using calculations and experiments.47 This study showed that Ru SACs supported on N-doped graphene have better activity than metallic Ru catalysts for the N2RR. However, they did not discuss the origin of the enhanced N2RR activity in detail.
In the catalytic design, the introduction of hetero-atoms into a pure metal (so-called alloy or multi-metallic catalysts) has been known as a salient approach for the enhancement of catalyst activity and durability: for example, core@shell, surface alloys, and intermetallic alloys.48–50 Nonetheless, a study on the heteroatom addition strategy has not yet been conducted to tune the activity of a single atom catalyst.
In this study, the electrochemical activity of Ru-based SACs, homo-Ru2 double atom catalysts (DACs), and hetero-RuM DACs having Ru and M (M = 3d transition metal) was investigated using quantum mechanics computation based on spin-polarized density functional theory (DFT). We calculate the structural stability, reaction mechanism and activity of the N2RR on homo- and hetero-Ru DACs. In addition, the decoupling of strain, dopant and configurational effects and the d-orbital resolved density of states (ORDOS) (dz2, dxz, dyz, dxy, and dx2–y2) on the hetero-double atoms are presented for a clear understanding of enhanced catalysis. Finally, using the descriptor we have identified, we computationally screen for a novel catalyst composition by exploring more search spaces (4d, 5d, and p block metals) for boosting NH3 production via N2 reduction.
Computational details
All of the calculations were performed on the basis of spin-polarized density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP).51–53 The projector augmented wave (PAW) method using a plane wave basis set was implemented to describe the interaction between core and valence electrons.54 The Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional within the generalized gradient approximation (GGA) was employed.55 For the plane wave expansion of the electronic eigenfunctions, an energy cutoff of 400 eV was used.To model the RuM/C catalysts, we first built a periodic geometry of monolayer graphene consisting of 60 carbon atoms from a P63/mmc-structured graphite supercell by removing all layers except one and stretching the z vector to 20 Å.56 After modelling of pristine graphene, two adjacent carbon atoms were removed to create unsaturated carbon to provide embeddable sites for Ru and 3d transition metal (M) atoms.
Here, we chose defective graphene as the supporting material for DACs instead of pristine graphene. Note that the interaction between pristine graphene and DACs is not strong enough to prevent the aggregation of DACs.57 According to Jamie H. Warner et al., an Fe double atom in defective graphene has been successfully incorporated via the defect-assisted doping method by electron beam irradiation.58 That is, the Fe precursor (FeCl3) solutions are added on the surface of graphene via drop-casting and in turn vacancy sites are created through irradiation with a focused electron beam using an aberration-corrected transmission electron microscope (AC-TEM), leading to an Fe dimer (Fe double atom) embedded into defective graphene.59,60 In addition, Pt dimers can be prepared on defect-rich graphene using atomic layer deposition (ALD), through the creation of nucleation sites, single Pt atom deposition and attachment of a second Pt atom selectively on the single Pt one.61 Following these considerations and computational validation, the RuM/C catalysts were modelled by using mono- and diatomic clusters anchored to defective graphene with double vacancies (see Fig. S1†).
To find the optimized geometry and the total energy of hetero-RuM DACs, all of the atoms were fully relaxed using the conjugate gradient method until residual forces on all the constituent atoms became smaller than 5 × 10−2 eV Å−1.62 For Brillouin zone integration, we chose a (4 × 4 × 1) Monkhorst–Pack mesh of k-points to determine the equilibrium geometries and total energies of RuM/C catalysts.63 To calculate the electronic structure, average energy and occupancy of the d-band, and atomic charge density of the catalysts, we increased the mesh size to (10 × 10 × 1).
In the total N2RR process (N2 + 6(H+ + e−) → 2NH3), N2 is reduced to NH3 through six net coupled proton and electron (CPE) transfer steps, and each step involves the transfer of a CPE from solution to an adsorbed intermediate.39 To calculate the Gibbs free energy change (ΔG) of every step for the N2RR, we introduced a computational hydrogen electrode (CHE) model as pioneered by Nørskov.64 In this model, the free energy of a CPE is equivalent to half that of gaseous H2 [G(H+ + e−) = 1/2G(H2)] under standard reaction conditions (T = 298.15 K, P = 1 bar, and pH = 0) with no external potential. According to this method, the ΔG value can be determined using the following equation;
| ΔG = ΔE − TΔS + ΔZPE − neU |
Results and discussion
Mechanism of electrochemical NH3 production on Ru single and double atom catalysts
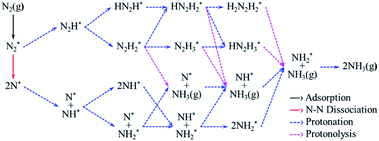
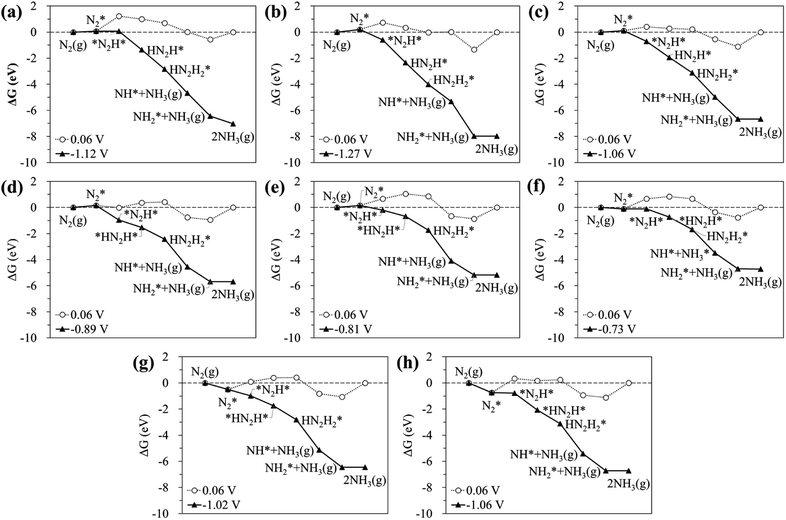
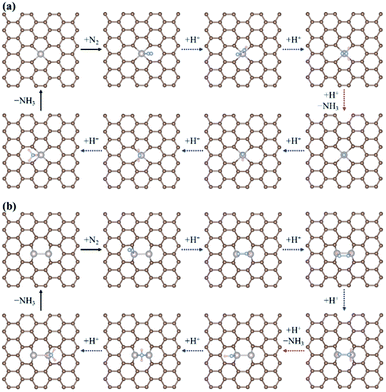
According to previous studies,13,45,46,67–69 the NH3 formation paths from the electrochemical N2RR on a SACs can be mainly classified into two reaction routes: the dissociative and associative mechanisms, which are shown in Fig. 1. The first step for both the dissociative and associative mechanisms is the adsorption of a gaseous N2 molecule in the catalyst [(1) N2(g) → N2*] (the asterisk * denotes the end-on adsorption state). In the dissociative mechanism, the adsorbed N2 molecule (N2*) is dissociated into two N* atoms on the catalytic surface [(2) N2* → 2N*], which can then undergo three successive protonation reactions, leading to NH3 production [(3) N* + (H+ + e−) → NH*, (4) NH* + (H+ + e−) → NH2*, and (5) NH2* + (H+ + e−) → NH3(g)]. On the other hand, in the associative mechanism, N2* is protonated to form N2H* [(6) N2* + (H+ + e−) → N2H*], which undergoes protonation or protonolysis (the cleavage of the N–N bond by the addition of H+) for NH3 formation. Here, depending on the type of catalyst, the reduction of N2H to NH3 follows one of the following three reaction pathways: (A) alternating path [(7) N2H* + (H+ + e−) → HN2H*, (8) HN2H* + (H+ + e−) → HN2H2*, (9) HN2H2* + (H+ + e−) → H2N2H2*, and (10) H2N2H2* + (H+ + e−) → NH2* + NH3(g)], (B) distal path [(11) N2H* + (H+ + e−) → N2H2* and (12) N2H2* + (H+ + e−) → N* + NH3(g)] and (C) enzymatic path (unlike alternating and distal paths, N2 is adsorbed on the catalyst surface via a side-on configuration) [(13) *N2H* + (H+ + e−) → *HN2H*, (14) *HN2H* + (H+ + e−) → *HN2H2*, (15) *HN2H2* + (H+ + e−) → *H2N2H2*, and (16) *H2N2H2* + (H+ + e−) → NH2* + NH3(g) (note that double asterisks ** denote the side-on states of adsorbates)]. In addition, the N2RR can also follow a mixed mechanism of alternating, distal and enzymatic pathways [(17) *HN2H2* + (H+ + e−) → NH* + NH3(g) and (18) N2H2* + (H+ + e−) → HN2H2*].Here, we considered the NH2* + (H+ + e−) → NH3(g) reaction as the final reaction step in the N2RR, where the NH3 desorption energy is indirectly included in the NH2* protonation reaction. Note that the NH2* + (H+ + e−) → NH3(g) reaction is considered to be the combination of NH2* + (H+ + e−) → NH3* and NH3* → NH3(g), which makes it possible to understand the electrode potential effect on the NH3 desorption process.69
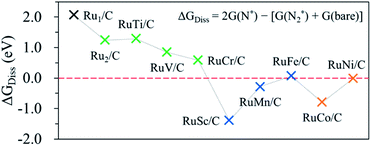
In this study, we first attempt to determine the preference of the dissociative mechanism in the N2RR by calculating the free energy change for the N2(g) → N* + N* reaction (ΔGdiss) using the following equation.
| ΔGdiss = 2G(N*) − [G(N2) + 2G(bare)] |
If the ΔGdiss value (which can be used to understand what type of N2RR mechanism takes place more favourably) on the catalytic surface is positive (endothermic process), the dissociative mechanism may not be possible for the N2RR to NH3. A negative ΔGdiss value means that N* is more stable than N2*, indicating that the N2RR may follow the dissociative mechanism. Here, we further confirm whether the catalyst having a negative ΔGdiss value goes through the dissociative mechanism by calculating the barrier (ΔGbarr) for the N2 dissociation reaction into 2N*.
Fig. 2 displays the most favourable N2RR pathways and optimized geometric structures of intermediates in each reaction step on the Ru1 SACs and homo-Ru2 DACs. For the Ru1 SAC case, the N2RR is found to follow the associative ‘Distal’ mechanism (note that ΔGdiss = 2.07 eV, indicating that the dissociative mechanism is unfavourable). First, a N2 molecule is adsorbed on top of the Ru atom in an end-on configuration [(1) N2(g) → N2*] and then undergoes two successive protonation reactions to form *N2H* with a side-on configuration [(6) N2* + (H+ + e−) → *N2H*] and N2H2* [(11) *N2H* + (H+ + e−) → N2H2*] with an end-on configuration. Here, the N–N bond length of N2(g), N2*, *N2H*, and N2H2* is 1.12 Å, 1.13 Å, 1.25 Å, and 1.31 Å, respectively. Next, the adsorbed N2H2* dissociates into N* and NH3(g) by protonolysis [(12) N2H2* + (H+ + e−) → N* + NH3(g)]. Finally, NH3(g) is formed by three successive protonation reactions of adsorbed N*. This is consistent with prior reports on single atom catalysis.40–42,45–47
 | ||
| Fig. 2 The optimized geometric structures of N2RR intermediates along the most favourable reaction pathway on (a) the Ru SAC and (b) the homo-Ru2 DAC. | ||
On the other hand, our DFT calculation predicts that the homo-Ru2 DAC follows a mixed mechanism of ‘Alternating’ or ‘Distal’ and ‘Enzymatic’ pathways (note that ΔGdiss = 1.24 eV). First, a N2 molecule is adsorbed on top of a single Ru atom in the Ru2 DAC with an end-on configuration, which leads to side-on *N2H* formation by protonation. Next, *N2H* undergoes two successive protonation reactions to form *HN2H* [(7) *N2H* + (H+ + e−) → *HN2H*] and *HN2H2* [(8) *HN2H* + (H+ + e−) → *HN2H2*]. The N–N bond length in N2*, N2H*, HN2H*, and HN2H2* is 1.14 Å, 1.28 Å, 1.37 Å, and 1.46 Å, respectively. Finally, *HN2H* is decomposed into NH3(g) + NH* by the protonolysis of the N–N bond [(17) *HN2H2* + (H+ + e−) → NH* + NH3(g)] and then NH* is converted into NH3(g) via two successive protonation reactions.
The calculated free energy diagrams for the N2RR to NH3 on the Ru SAC and homo-Ru2 DAC are displayed in Fig. 3. The adsorption energies (ΔEads) are calculated as follows: [ΔEads(X) = EX* − (E(bare) + E(X))], where EX*, E(bare), and E(X) denote the total energy of the X-adsorbed surface, the bare surface, and the isolated X species, respectively. E(X) was calculated in a cubic vacuum unit cell of size a = 20 Å, and the calculated E(X) values are shown in Table S1.† For both the Ru1 SAC and the homo-Ru2 DAC, the N2 adsorption under thermodynamic equilibrium potential conditions (0.06 V) is predicted to be an endothermic process, which comes from the large loss of entropy due to the formation of a bound state.68 Note that ΔG = 0.54 eV and ΔEads(N2) = −0.46 eV for the Ru1 SAC, and ΔG = 0.21 eV and ΔEads(N2) = −0.84 eV for the homo-Ru2 DAC. For the N2RR under thermodynamic equilibrium potential conditions for both the Ru1 SAC and homo-Ru2 DAC, the first step [(6) N2* + (H+ + e−) → *N2H*] is calculated to be the most endothermic [note that ΔG = 1.14 eV (Ru1 SAC) and 0.91 eV (Ru2 DAC)] among all the steps for the most favourable N2RR pathway. This indicates that the first N2 protonation [which is defined as the potential limiting step (PLS)] determines the NH3 production potential. Consequently, for the Ru1 SACs and homo-Ru2 DACs, we predict an over-potential of 1.19 V and 0.96 V, respectively, suggesting the higher N2RR activity of a homo-Ru2 DAC than a Ru1 SAC. This is higher than previous single Ru atom calculation results,47 which shows that the overpotentials for Ru1–N3 and Ru1–N4 are predicted to be 0.79 V and 0.83 V, respectively. This difference is related to the presence of N atoms in the defective graphene support. In our DFT study, a single Ru atom is embedded into a defective graphene support (forming a Ru–C bond), while, in the previous calculation, single Ru atoms are associated with three N atoms (Ru1–N3) or four N atoms (Ru1–N4) in the defective graphene support (forming a Ru–N bond). Due to the higher electronegativity of the N atom (3.04) than the carbon case (2.55), the Ru in the Ru–N bond loses more electrons than that in the Ru–C case, which may lead to the increase of adsorption strength in reaction intermediates and in turn the enhancement of N2RR activity.
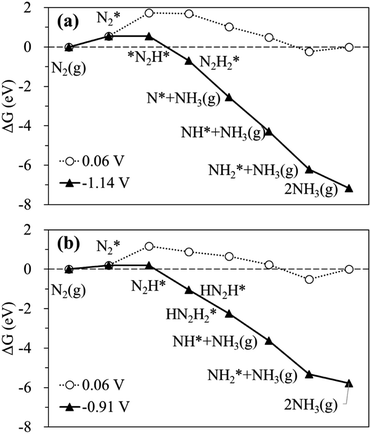 | ||
| Fig. 3 Calculated free energy profiles at equilibrium (○) and limiting (▲) potentials for the N2RR on (a) the Ru SAC and (b) the homo-Ru2 DAC via the most favourable pathway. | ||
Next, we examine the effect of the addition of a hetero-M atom (M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni) into a Ru1 SAC in order to enhance the N2RR activity toward NH3 formation.
Geometric ensemble structure of hetero-RuM double atom catalysts
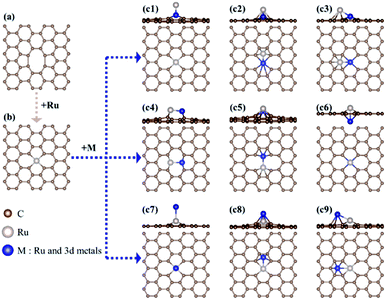
First, we investigate the structural stability of hetero-RuM DACs supported on defective graphene by calculating the formation energy (indicated as ΔEf) for the addition of a hetero-M atom onto a Ru SAC [a negative (exothermic) ΔEf value means the stable formation of hetero-RuM DACs from Ru SACs, and vice versa] as follows:| ΔEf(RuM/C) = E(RuM/C) − [E(Ru/C) + E(M)] |
Here, to find the most stable geometric ensemble of hetero-RuM DACs, we compare the calculated ΔEf values of nine possible ensemble geometries (referred to as c1, c2, c3, c4, c5, c6, c7, c8, and c9) (see Fig. 4 and Table 1). For the comparison, the homo-Ru2 DAC case is also presented. We see that the most stable geometric ensemble of the RuM/C system is classified into three groups. That is, (1) group I (c4 geometry) (we call horizontal double atom); the Ru–M dimer [M = Ru (ΔEf = −3.69 eV), Ti (ΔEf = −4.49 eV), V (ΔEf = −3.96 eV), and Cr (ΔEf = −1.72 eV)] is nearly horizontally adsorbed at two carbon vacant sites, leading to chemical bond formation between a Ru (or M) atom and two C atoms and (2) group II (c8 geometry) (we call inclined pentagon M double atom); the Ru–M dimer [M = Sc (ΔEf = −4.23 eV), Mn (ΔEf = −1.82 eV), and Fe (ΔEf = −2.41 eV)] are connected to one carbon vacant and hollow carbon sites. Here, Ru and M atoms are associated with rectangular- and pentagonal-shaped four carbons, respectively, leading to the formation of an inclined RuM structure. (3) Group III (c9 geometry) (we call inclined hexagon M double atom); the configuration of the Ru–M dimer [M = Co (ΔEf = −2.49 eV) and Ni (ΔEf = −2.87 eV)] is similar to that in the group II case, except that M atoms are bound to hexagon-shaped five carbons, respectively. Here, group III also shows an inclined RuM structure. The optimized ensemble geometries of all hetero-Ru DACs are shown in Fig. S2.† In the following section, we investigate the electrocatalytic activity of hetero-RuM DACs toward NH3 formation in the most stable models.
| c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | |
|---|---|---|---|---|---|---|---|---|---|
| Ru2/C | −2.98 | −3.22 | −3.39 | −3.69 | −2.02 | −3.23 | — | — | — |
| RuTi/C | 1.09 | — | — | −2.58 | −1.30 | −4.14 | −2.74 | −4.23 | −4.13 |
| RuV/C | −0.92 | −2.83 | — | −4.49 | −2.52 | −4.04 | −2.90 | −4.42 | −4.23 |
| RuCr/C | −1.78 | −2.97 | −2.55 | −3.96 | −1.99 | −2.93 | −2.16 | −3.09 | −3.19 |
| RuSc/C | −0.39 | −1.07 | −0.79 | −1.72 | −0.03 | −1.27 | −1.04 | −1.46 | −1.37 |
| RuMn/C | −0.28 | −0.98 | −0.94 | −1.75 | 0.20 | −1.45 | −1.20 | −1.82 | −1.71 |
| RuFe/C | −0.90 | −1.74 | −1.64 | −2.26 | −0.71 | −1.81 | −1.83 | −2.41 | −2.35 |
| RuCo/C | −0.80 | −1.97 | −2.36 | −2.31 | −0.56 | −2.00 | −1.91 | −2.40 | −2.49 |
| RuNi/C | — | −2.16 | −2.00 | −2.15 | — | −2.48 | −2.51 | −2.73 | −2.87 |
Reactivity of hetero-RuM double atom catalysts
Fig. 5 shows the calculated ΔGdiss for the N2(g) → N* + N* reaction on the surface of the hetero-RuM DACs. We observe the endothermic process when M is Ti, V, Cr, and Fe in RuM/C [note that ΔGdiss = 1.29 eV (Ti), ΔGdiss = 0.85 eV (V), ΔGdiss = 0.58 eV (Cr), and ΔGdiss = 0.07 eV (Fe)], suggesting that the N2RR via the dissociative mechanism is energetically unfavourable. On the other hand, the RuSc/C, RuMn/C, RuCo/C, and RuNi/C cases exhibit negative ΔGdiss values [−1.39 eV (Sc), −0.28 eV (Mn), −0.79 eV (Co), and −0.01 eV (Ni)], indicating that there is a possibility for the dissociative N2RR on those catalysts. Even if the ΔGdiss value is less than zero, the dissociative NRR will not occur if the barrier (ΔGbarr) is insurmountably high under the reaction conditions. The ΔGdiss value on the stepped Ru (0001) surface, which is known to be capable of the dissociative N2RR under standard temperature and pressure conditions, is 0.78 eV.21,72 Zhao et al. reported that they did not consider the dissociative N2RR because the dissociation barrier of N2* in their catalyst (Mo SAC on BN) was as high as 4.25 eV.40 To clearly determine which mechanism to follow on hetero-RuM/C, we calculate ΔGbarr for the RuSc/C, RuMn/C, and RuCo/C catalysts with substantial negative values of ΔGdiss, as well as for the RuNi/C and RuFe/C catalysts with near zero values of ΔGdiss (see Fig. S3†). We find that all the ΔGbarr values are above 2.2 eV [note that ΔGbarr(Sc), ΔGbarr(Mn), ΔGbarr(Fe), ΔGbarr(Co), and ΔGbarr(Ni) are 2.92 eV, 2.43 eV, 2.71 eV, 2.40 eV, and 2.22 eV, respectively], suggesting that the N2RR via the dissociative mechanism cannot occur on the RuSc/C, RuMn/C, RuCo/C, RuNi/C and RuFe/C surfaces under the reaction conditions.Fig. 6 displays the Gibbs free energy diagram for the favourable pathway for the N2RR on the hetero-RuM DACs. The PLS for the N2RR on the Ru1 SAC and homo-Ru2 DAC is the protonation of N2* to form N2H* (see Fig. 3). However, in the case of hetero-RuM DACs, the PLS is changed to the protonation of NH2* except for hetero-RuFe and RuTi DACs. We also find that the onset potential for NH3 formation strongly depends on the type of M, and hetero-RuM DACs show a less negative onset potential than the Ru1 SAC (−1.14 V) except for the hetero-RuV DAC. In particular, the hetero-RuSc, RuMn, and RuFe in group II (inclined pentagon M double atom) have a less negative onset potential [−0.89 V (RuSc/C), −0.81 V (RuMn/C), and −0.73 V (RuFe/C), where RuFe exhibits the best activity toward NH3 production] than the homo-Ru2 DAC [−0.91 V], indicating a reduced over-potential and in turn enhanced NH3 productivity for the hetero-RuSc, RuMn, and RuFe DACs. In contrast, for the hetero-RuTi, RuV, and RuCr DACs in group I (horizontal double atom) [−1.12 V (RuTi/C), −1.27 V (RuV/C), and −1.06 V (RuCr/C)], and RuCo and RuNi DACs in group III (inclined hexagon M double atom) [−1.02 V (RuCo/C) and −1.06 V (RuNi/C)], the opposite is true.
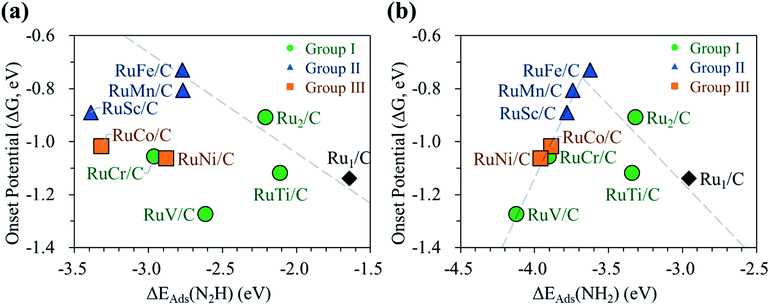
Next, we display the change of the onset potentials of the Ru1 SAC, homo-Ru DAC, and hetero-RuM DACs for NH3 production as a function of the adsorption energy of N2H and NH2 (see Fig. 7). The calculated ΔEads(N2H) and ΔEads(NH2) are summarized in Table S2.†
We see a clear volcanic relationship between the onset potential of the N2RR and ΔEads(NH2), whereas there is no correlation between the onset potential and ΔEads(N2H). The strong dependence of N2RR activity in the RuM system on ΔEads(NH2) [rather than ΔEads(N2H)] is related to the PLS we have identified. For most RuM (M = V, Cr, Sc, Mn, Co, Ni) cases, the PLS is NH2* protonation [(4) NH2* + (H+ + e−) → NH3(g)], where the level of ΔEads(NH2) determines the reactivity toward NH3 production. That is, the strong binding of NH2 to the catalyst leads to a decrease in reaction potential and vice versa. Thus, ΔEads(NH2) can be used for the representation of NH3 productivity via the N2RR, which is called as the descriptor.
Looking closely at the volcano plot of Fig. 7(b), the lowering of the descriptor values [ΔEads(NH2)] compared to the Ru1 SAC increases the activity (onset potential) of hetero-RuM DACs (M = Ru, Ti, and Fe) toward NH3 production until the ΔEads(NH2) value approaches about −3.68 eV (which is defined as the peak position of the volcanic activity-descriptor plot). After that, the N2RR activity is reduced (onset potential is lowered) as descriptor values are further lowered. Here, the opposition correlation between the right and left sides of the volcano plot is related to the type of PLS. On the left leg of the volcano plot, the PLS is the protonation of NH2* [(5) NH2* + (H+ + e−) → NH3(g)] regardless of its mechanism, where the level of NH2 adsorption energy (descriptor value) determines the reactivity toward NH3 production. That is, the strong binding of NH2 to the catalyst leads to a decrease in the reaction potential. On the other hand, on the right leg of the volcano plot, the N2RR occurs via the associative mechanism due to the weak ability to bind the reaction intermediates such as NH2, where the increase of NH2 affinity enhances the NH3 productivity.
Origin of the enhanced N2RR catalysis for hetero-RuM double atom catalysts
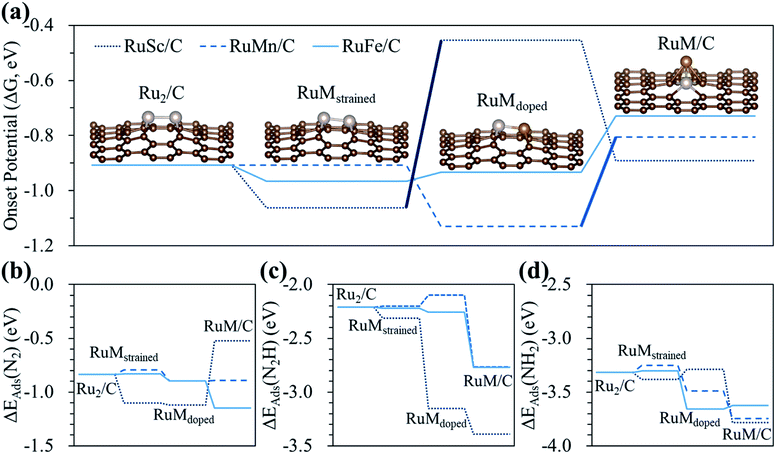
To clearly understand the relative role of strain, dopant and configurational effects in determining NH3 productivity in the hetero-RuM DACs in group II catalysts (here, we choose group II catalysts which exhibit higher N2RR activity compared to the group I and III cases), we decoupled these three effects as shown in Fig. 8 and Table S3.† We also displayed optimized N2-, N2H-, and NH2-adsorbed geometries in Fig. S4.†
First, we attempt to only extract the strain effect from the total N2RR catalysis by calculating the onset potential for strained homo-Ru2 DACs having the same geometric configuration as the homo-Ru2 DAC but having a different Ru–Ru bond distance (indicated by RuMstrained). To model RuMstrained, we use the optimized atomic position from hetero-RuM DACs with the geometry of horizontal double atom (group I). Compared to the homo-Ru2 DAC case (2.276 Å), the Ru–Ru bond distance for the RuScstrained, RuMnstrained, and RuFestrained models is 2.300, 2.135 and 2.142 Å, respectively, which are under a tensile strain of +1.05% and compressive strain of −6.20% and −5.90%, respectively, (note that ‘+’ and ‘−’ signs represent the tensile and compressive strain, respectively). Our DFT calculation predicts a substantial decrease of onset potential by 0.15 V for the RuScstrained catalyst, but a small variation for the RuFestrained (onset potential decreases by 0.05 V) and RuMnstrained (onset potential decreases by ∼0 V) catalysts [see Fig. 8(a)], suggesting that the tensile strain tends to reduce the NH3 productivity via the N2RR, while the effect of compressive strain is insignificant. The large decrease of onset potential in the RuScstrained catalyst is related to the decrease of N2 adsorption energy (increase of N2 affinity) [see Fig. 8(b)] from −0.84 V (homo-Ru2 DAC) to −1.10 V and little change of N2H adsorption energy [see Fig. 8(c)], which only raise the level of reactant energy for the potential limiting step [(6) N2* + (H+ + e−) → N2H*] and in turn increase the endothermicity of the reaction.
Next, for the calculation of the contribution of the dopant effect to the NH3 formation, we prepared RuScdoped, RuMndoped, and RuFedoped models by replacing a Ru atom by a Sc, Mn, and Fe atom in RuScstrained, RuMnstrained, and RuFestrained models, respectively. Here, the change of onset potential from the RuMstrained model to the RuMdoped model indicates the contribution of the dopant effect to total catalysis. We find different aspects for all three catalysts due to the dopant effect. For the RuScdoped case, the onset potential is significantly increased to −0.45 V compared to the RuScstrained model, which is related to the dramatic increase of N2H affinity [ΔEads(N2H) = −3.15 eV] and almost no change of N2 binding energy [ΔEads(N2) = −1.12 eV] compared to the RuScstrained model [ΔEads(N2H) = −2.31 eV and ΔEads(N2) = −1.10 eV] [see Fig. 8(b) and (c)]. Consequently, this induces the shift of the PLS from [(6) N2* + (H+ + e−) → N2H*] to [(5) NH2* + (H+ + e−) → NH3(g)]. In the case of RuMndoped, the onset potential is decreased to −1.13 V by the dopant effect compared to the RuMnstrained model. Unlike the RuScdoped case, this is mainly connected to the stronger N2 adsorption and weaker N2H adsorption [ΔEads(N2) = −0.90 eV and ΔEads(N2H) = −2.10 eV]. However, the N2RR onset potential (−0.93 V) and the adsorption energies of N2 [ΔEads(N2) = −0.90 eV] and N2H [ΔEads(N2H) = −2.26 eV] on the RuFedoped model are changed little by the dopant effect compared to the RuFestrained models [−0.96 V (onset potential), ΔEads(N2) = −0.83 eV] and [ΔEads(N2H) = −2.22 eV].
For the contribution of the configurational effect to the total N2RR catalysis, we calculate the difference of the onset potentials between the RuMdoped models and hetero-RuM DACs. Notice that the configurational effect induces the geometric ensemble configuration change of the hetero-RuSc, RuMn, and RuFe DACs from group I (horizontal double atom) to group II (inclined pentagon M double atom), which affects the N2RR catalysis. We find that for the hetero-RuSc DAC, the N2RR activity (onset potential) is reduced by 0.44 V since the NH2 adsorption energy is decreased from −3.29 eV to −3.78 eV by the configurational effect. For the RuMn and RuFe DAC cases, the onset potential is increased from −1.13 V and −0.93 V to −0.81 V and −0.73 V, respectively, which is related to the increase of N2H affinity by 0.67 eV and 0.51 eV compared to the respective RuMndoped and RuFedoped models. Especially for the RuMn case, the potential limiting step is shifted to (5) NH2* + (H+ + e−) → NH3(g) due to the strong NH2 adsorption. These results demonstrate that the strain, dopant and configurational effects play an important role in determining NH3 productivity via electrochemical N2 reduction. In particular, the dopant and configurational effects are responsible for the enhancement of NH3 production.
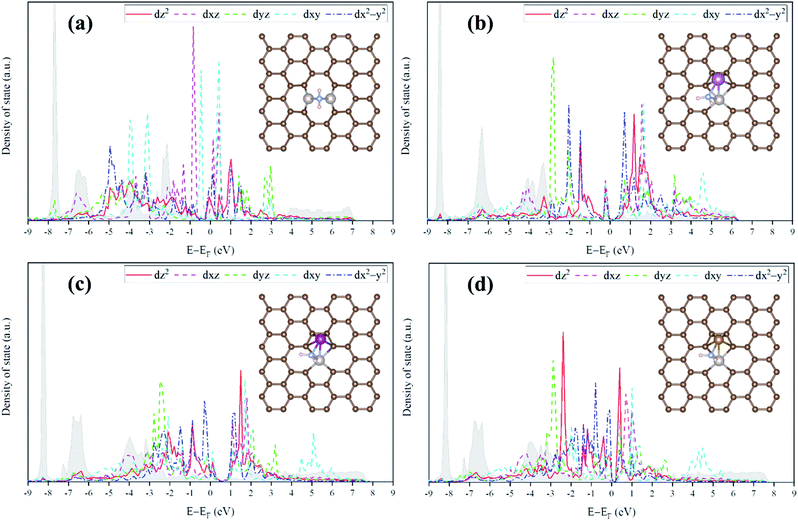
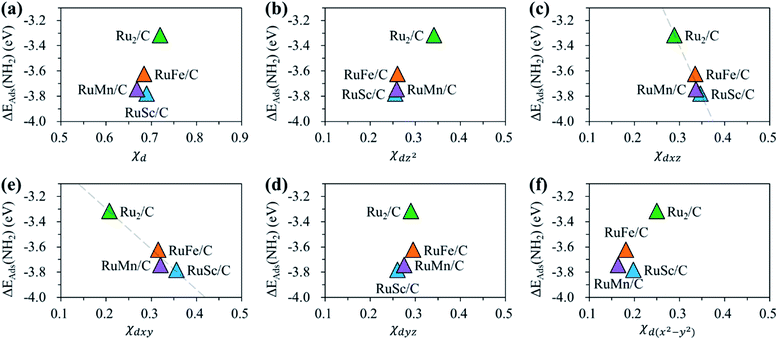
For the homo-Ru2 DAC case, we see strong interatomic mixing between the p orbital of N in adsorbed NH2 and the dz2, dxz, dyz, dxy, and dx2–y2 orbitals of Ru2 DAC in the energy ranges from −7.0 eV to −6.0 eV, from −4.5 eV to −3.5 eV and from −3.0 eV to −1.5 eV. To quantitatively understand the degree of interatomic mixing between each d orbital and p orbital, we calculate the fraction of p–d orbital overlap in the total p orbital of the N atom (referred to as χd) (see Fig. 10). Our DFT calculation shows that the order of overlap between p and d orbitals is dz2 (χdz2 = 0.341) > dxz (χdxz = 0.289), dyz (χdyz = 0.290) > dx2–y2 (χdx2–y2 = 0.250) > dxy (χdxy = 0.208). This suggests that the orbitals (dz2, dxz, and dyz) having an orientation toward the z direction in the Ru2 double atom [which is horizontally placed in the x–y plane; group I] have a higher impact in determining the adsorption of NH2 with the catalyst than dx2–y2 and dxy.
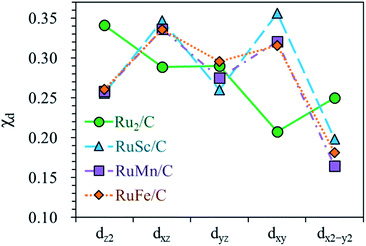 | ||
| Fig. 10 Fraction of p–d orbital overlap in the total p orbital of the N atom (indicated by χd) according to the variation of the type of d orbital (dz2, dxz, dyz, dxy, and dx2–y2). | ||
On the other hand, for the hetero-RuFe DAC case, we find a strong overlap between the p orbital and d orbitals in the range from −4.5 eV to −2.5 eV (see Fig. 9(d)). In particular, unlike the homo-Ru2 DAC case (key orbitals in bonding are in the order of dz2 > dxz > dyz), the dxz and dxy orbitals exhibit larger interatomic mixing with p orbital cases, suggesting that the orbitals (dxz and dxy) having an orientation toward the x direction play an important role in stabilizing a NH2 adsorbate on the hetero-RuFe DAC. Note that dxz (χdxz = 0.336) > dxy (χdxy = 0.315) > dyz (χdyz = 0.296) > dz2 (χdz2 = 0.261) > dx2–y2 (χdx2–y2 = 0.182) (see Fig. 10). Here, the different nature of p–d orbital overlap between the homo-Ru2 DAC and hetero-RuFe DAC is related to the geometric ensemble difference of double atoms induced by the strong hetero-dopant-support effect. That is, unlike the homo-Ru2 DAC [whose two atoms are horizontally placed in the x direction; group I (horizontal double atom)], the hetero-RuFe DAC [group II (inclined pentagon M double atom)] has an inclined geometric ensemble structure in the y-direction where each Ru and M atom has a different z position in the normal direction of the x–y plane (see Fig. S2†). This makes the dxz and dxy orbitals more favourable for the interaction with the p orbital of NH2 than the dz2, dx2–y2 and dyz orbitals, leading to the tilted adsorption configuration of NH2 on the RuFe DAC. For the RuSc and RuMn DACs, we see a similar p–d orbital overlap to the RuFe case, that is, the p orbital mixing mainly with dxz and dxy in the range from −5.0 eV to −2.7 eV (from −7.0 eV to −6.0 eV) for the RuSc DAC and from −4.7 eV to −2.6 eV for RuMn DAC. This demonstrates that the dopant and configurational effects in a hetero-RuM double atom induce an inclined RuM geometric ensemble configuration and in turn activate the dxz and dxy orbitals for NH2 adsorption (rather than the dz2 and dxy + dx2–y2 orbitals), leading to the modification of NH2 binding energy.
Fig. 11 shows the relationship between ΔEads(NH2) and χd for the RuM (M = Sc, Mn, Fe) DACs. We find that for the dxz and dxy orbitals, the increase of p–d orbital overlap (χd) enhances the NH2 affinity linearly, while for the dz2, dx2–y2 and dyz orbitals, no clear relationship is observed. This indicates that the dxz and dxy orbitals have a higher impact in determining the NH2 adsorption process, which is in line with the larger p–d overlap of the dxz and dxy orbitals than the dz2, dx2–y2 and dyz orbitals as discussed above.
HER activity
In addition to the N2RR studies on the RuM DACs, we calculate the onset potential of the hydrogen evolution reaction (HER), which is one of the reasons for lowering the faradaic efficiency of NH3 production.13,42,45 The calculated onset potentials of the N2RR (ΔGNRR) and HER (ΔGHER) and the difference of onset potentials between the N2RR and HER (indicated by ΔΔG = ΔGNRR − ΔGHER) on the Ru1 SAC, homo-Ru2 DAC, and hetero-DACs are shown in Table 2. Our DFT calculation shows the enhanced selectivity (ΔΔG = −0.31 eV) of the most active hetero-ReFe double atom catalyst toward the N2RR over the HER compared to the Ru1 SAC (ΔΔG = −0.91 eV) and homo-Ru DAC (ΔΔG = −0.54 eV) cases. However, the onset potentials of the N2RR for all RuM catalysts are still lower than the HER onset potential.| Ru1/C | Group I | Group II | Group III | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ru2/C | RuTi/C | RuV/C | RuCr/C | RuSc/C | RuMn/C | RuFe/C | RuCo/C | RuNi/C | ||
| ΔGNRR | −1.14 | −0.91 | −1.12 | −1.27 | −1.06 | −0.89 | −0.81 | −0.73 | −1.02 | −1.06 |
| ΔGHER | −0.22 | −0.37 | −0.20 | −0.77 | −0.55 | −0.36 | −0.29 | −0.42 | −0.81 | −0.80 |
| ΔΔG | −0.91 | −0.54 | −0.92 | −0.51 | −0.51 | −0.53 | −0.52 | −0.31 | −0.21 | −0.26 |
Screening for additional hetero-RuM double atom catalysts
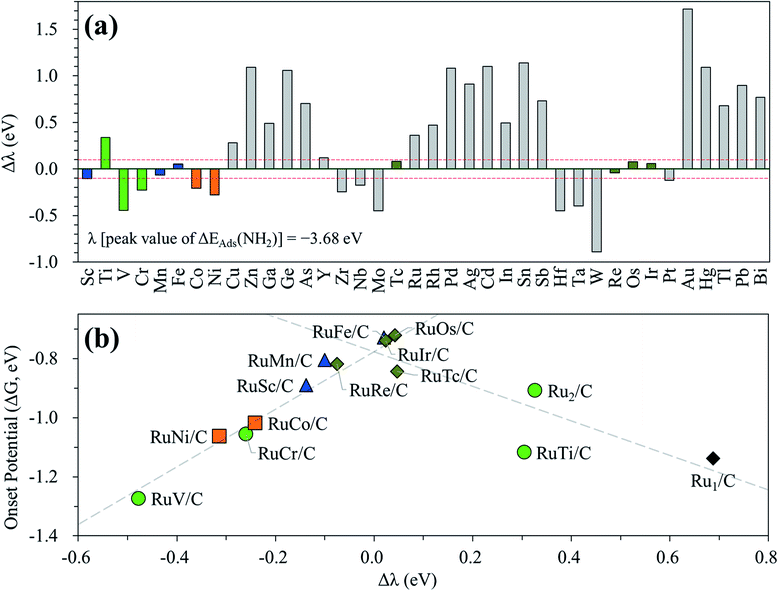
In the above investigation of the hetero-RuM DACs (whose M is a 3d transition metal) for NH3 production, we concluded that a hetero-RuFe DAC is the best catalyst. To find out if there is a catalyst with better activity than a hetero-RuFe DAC, we further screen the candidate materials by engineering the chemical composition of RuM (M = 4d, 5d, and p blocks) using the descriptor (which is NH2 adsorption energy and is indicated by λ) to predict the onset potential. First, the most stable geometry of the expanded hetero-RuM DACs was investigated using the same procedure as that in the case of 3d transition metals, and these results are shown in Table S4.† Using this optimized hetero-RuM DAC geometry, we further calculated the adsorption energy of NH2, the descriptor for N2RR activity we found. Fig. 12(a) displays the relative descriptor (denoted as Δλ) compared to the descriptor value of the peak position in the volcano plot (λ = −3.68 eV) identified in the above section (see Fig. 7(b)). We find that the descriptor value depends on the chemical composition and tends to increase as M moves to the right of the periodic table in the hetero-RuM DACs. Here, based on −0.1 eV < Δλ < 0.1 eV, we select four candidates (hetero-RuTc, RuRe, RuOs, and RuIr DACs), which can be expected to enhance NH3 production via electrochemical N2 reduction. The calculated onset potentials for these candidates are shown in Fig. 12(b). We see a higher NH3 production reactivity (in particular, hetero-RuOs and RuIr DACs, whose onset potentials are −0.72 V and −0.74 V, respectively) than that of the homo-Ru2 DAC case (−0.91 V), which is close to the onset potential of the hetero-RuFe DAC (−0.73 V).We also calculate the onset potentials of the HER (ΔGHER) on the additional four candidates and compared with the onset potential of the N2RR (ΔGNRR) to evaluate N2RR selectivity (see Table S5†). However, ΔGHER on all those candidates is also lower than ΔGNRR. Improving the selectivity by increasing the N2RR onset potential over the HER remains one of the biggest challenges to be addressed in the subsequent study.
Conclusions
In this study, using spin-polarized DFT calculations, we investigated NH3 production catalysis via the electrochemical N2 reduction (N2RR) on hetero-RuM (M = 3d transition metal) double atom catalysts supported on defective graphene and computationally screened novel catalysts by exploring 4d, 5d and p block metals as the hetero-M metals.First, we investigated the geometric ensemble structure of the hetero-RuM double atom catalysts on carbon vacant graphene. Depending on the type of hetero-atom, we identified three possible ensemble configurations; (1) group I: the horizontal double atom (Ru2, RuTi, RuV, and RuCr), (2) group II: the inclined pentagon M double atom (RuSc, RuMn, and RuFe), and (3) group III: the inclined hexagon M double atom (RuCo and RuNi).
Second, our DFT calculation predicted the significantly enhanced N2RR activity (reduced over-potential) of the inclined pentagon M double atom catalysts (group II) (such as RuFe, RuMn, and RuSc) (RuFe has the highest activity) compared to the homo-Ru2 double atom case. By looking at the potential limiting step, we found that the NH2 binding energy (so-called descriptor) was suitable for representing the N2RR onset potential on the hetero-RuM double atom catalyst. In addition, from the volcanic activity-descriptor plot, we found that the peak position for a descriptor was around about −3.68 eV. We further searched for the catalyst candidate using the descriptor to represent onset potential by varying the chemical composition of RuM (M = 4d, 5d, and p blocks), which leads to the discovery of promising hetero-RuOs and RuIr double atom catalysts, whose onset potentials were close to the onset potential of the hetero-RuFe catalyst.
Third, the study on the relative role of strain, dopant and configurational effects in the inclined pentagon M double atom catalysts (RuFe, RuMn, and RuSc) demonstrated that the strain, dopant and configurational effects play an important role in determining NH3 productivity via electrochemical N2 reduction. That is, (1) the tensile strain (RuSc) tended to reduce the NH3 productivity via the N2RR, while the effect of compressive strain (RuFe and RuMn) was insignificant, (2) the dopant effect was found to have a significant effect on N2RR activity, that is, a beneficial effect for the RuSc and RuFe cases and a detrimental effect for the RuMn case, and (3) the dopant-support interaction induced the change of the ensemble structure from the horizontal double atom to the inclined pentagon M double atom, where the N2RR activity on the RuSc double atoms was substantially reduced, while for the RuFe, and RuMn cases, the change in the ensemble structure resulted in the enhancement of N2RR activity.
Finally, our DFT calculation for the analysis of the p–d (dz2, dxz, dyz, dxy, and dx2–y2) orbital overlap identified the key d orbitals in determining the affinity of the descriptor NH2. That is, the orbitals (dz2, dxz, and dyz) having an orientation toward the z direction in the horizontal Ru2 double atom played an important role in determining the NH2 adsorption process, while for the inclined pentagon M double atom [RuFe, RuSc, and RuMn, where each Ru and M (Fe, Sc, and Mn) atom has a substantially different z position in the normal direction of the x–y plane], the dxz and dxy orbitals were found to be essential for the modification of NH2 binding energy.
Our theoretical study provides the fundamental mechanism of NH3 production catalysis on hetero-double atom catalysts and gives physical and chemical intuition (in particular, interplay of strain, dopant and configurational effects) for next generation multi-metallic atom catalysts for hydrogen storage applications.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2020R1A2C1099711 and NRF-2018M1A2A2061975). This work was also supported by the National Supercomputing Center with supercomputing resources including technical support (KSC-2021-CRE-0264).Notes and references
- H.-J. Neef, International overview of hydrogen and fuel cell research, Energy, 2009, 34, 327–333 CrossRef CAS.
- L. van Biert, M. Godjevac, K. Visser and P. V. Aravid, A review of fuel cell systems for maritime applications, J. Power Sources, 2016, 327, 345–364 CrossRef CAS.
- J. W. Pratt, L. E. Klebanoff, K. Munoz-Ramos, A. A. Akhil, D. B. Curgus and B. L. Schenkman, Proton exchange membrane fuel cells for electrical power generation on-board commercial airplanes, Appl. Energy, 2013, 101, 776–796 CrossRef CAS.
- F. Ustolin and R. Taccani, Fuel cells for airborne usage: energy storage comparison, Int. J. Hydrogen Energy, 2018, 43, 11853–11861 CrossRef CAS.
- S. S. Kumar and V. Himabindu, Hydrogen production by PEM water electrolysis – a review, Mater. Sci. Energy Technol., 2019, 2, 442–454 Search PubMed.
- F. Jiao and B. Xu, Electrochemical ammonia synthesis and ammonia fuel cells, Adv. Mater., 2019, 31, 1805173 CrossRef PubMed.
- C. Zamfirescu and I. Dincer, Ammonia as a green fuel and hydrogen source for vehicular applications, Fuel Process. Technol., 2009, 90, 729–737 CrossRef CAS.
- R. Metkemeijer and P. Achard, Ammonia as a feedstock for a hydrogen fuel cell; reformer and fuel cell behaviour, J. Power Sources, 1994, 49, 271–282 CrossRef CAS.
- W. Wang, J. M. Herreros, A. Tsolakis and A. P. E. York, Ammonia as hydrogen carrier for transportation; investigation of the ammonia exhaust gas fuel reforming, Int. J. Hydrogen Energy, 2013, 38, 9907–9917 CrossRef CAS.
- C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Towards an ammonia-mediated hydrogen economy?, Catal. Today, 2006, 111, 140–144 CrossRef CAS.
- V. Kyriakou, I. Garagounis, A. Vourros, E. Vasileiou and M. Stoukides, An electrochemical Haber-Bosch process, Joule, 2020, 4, 142–158 CrossRef CAS.
- J. Hymphreys, R. Lan and S. Tao, Development and recent progress on ammonia synthesis catalysts for Habor-Bosch process, Advanced Energy and Sustainability Research, 2021, 2, 2000043 CrossRef.
- J. Kong, A. Lim, C. Yoon, J. H. Jang, H. C. Ham, J. Han, S. Nam, D. Kim, Y.-E. Sung, J. Choi and H. S. Park, Electrochemical synthesis of NH3 at low temperature and atmospheric pressure using a γ-Fe2O3 catalyst, ACS Sustainable Chem. Eng., 2017, 5, 10986–10995 CrossRef CAS.
- N. Saadatjou, A. Jafari and S. Sahebdelfar, Ruthenium nanocatalysts for ammonia synthesis: a review, Chem. Eng. Commun., 2018, 202, 420–448 CrossRef.
- N. Cao and G. Zheng, Aqueous electrocatalytic N2 reduction under ambient conditions, Nano Res., 2008, 11, 2992–3008 CrossRef.
- S. Giddey, S. P. S. Badwal and A. Kulkarni, Review of electrochemical ammonia production technologies and materials, Int. J. Hydrogen Energy, 2019, 38, 14576–14594 CrossRef.
- J. K. Nørskov, Electronic factors in catalysis, Prog. Surf. Sci., 1991, 38, 103–144 CrossRef.
- H. Iriawan, S. Z. Andersen, X. Zhang, B. M. Comer, J. Barrio, P. Chen, A. J. Medford, I. E. L. Stephens, I. Chorkendorff and Y. Shao-Horn, Methods for nitrogen activation by reduction and oxidation, Nature Reviews Methods Primers, 2021, 1, 56 CrossRef.
- L. Forni, D. Molinari, I. Rossetti and N. Pernicone, Carbon-supported promoted Ru catalyst for ammonia synthesis, Appl. Catal., A, 1999, 185, 269–275 CrossRef CAS.
- G. Ertl, Primary steps in catalytic synthesis of ammonia, J. Vac. Sci. Technol., A, 1983, 1, 1247–1253 CrossRef CAS.
- V. Kordali, G. Kyriacou and C. Lambrou, Electrochemical synthesis of ammonia at atmospheric pressure and low temperature in a solid polymer electrolyte cell, Chem. Commun., 2000, 17, 1673–1674 RSC.
- K. Imamura and J. Kubota, Electrochemical membrane cell for NH3 synthesis from N2 and H2O by electrolysis at 200 to 250 °C using a Ru catalyst, hydrogen-permeable Pd membrane and phosphate-based electrolyte, Sustainable Energy Fuels, 2018, 2, 1278–1286 RSC.
- K. Kugler, M. Luhn, J. A. Schramm, K. Rahimi and M. Wessling, Galvanic deposition of Rh and Ru on randomly structured Ti felts for the electrochemical NH3 synthesis, Phys. Chem. Chem. Phys., 2015, 17, 3768–3782 RSC.
- G. Marnellos, S. Zisekas and M. Stoukides, Synthesis of ammonia at atmospheric pressure with the use of solid state proton conductors, J. Catal., 2000, 193, 80–87 CrossRef CAS.
- J. Wang, L. Yu, L. Hu, G. Chen, H. Xin and X. Feng, Ambient ammonia synthesis via palladium-catalyzed electrohydrogenation of dinitrogen at low over-potential, Nat. Commun., 2018, 9, 1795 CrossRef PubMed.
- S. Li, D. Bao, M.-M. Shi, B.-R. Wulan, J.-M. Yan and Q. Jiang, Amorphizing of Au nanoparticles by CeOx–RGO hybrid support towards highly efficient electrocatalyst for N2 reduction under ambient conditions, Adv. Mater., 2017, 29, 1700001 CrossRef.
- R. Manjunatha and A. Schechter, Electrochemical synthesis of ammonia using ruthenium–platinum alloy at ambient pressure and low temperature, Electrochem. Commun., 2018, 90, 96–100 CrossRef CAS.
- Y. Abghoui and E. Skúlason, Computational predictions of catalytic activity of zincblende (110) surfaces of metal nitrides for electrochemical ammonia synthesis, J. Phys. Chem. C, 2017, 121, 6141–6151 CrossRef CAS.
- M.-M. Shi, D. Bao, B.-R. Wulan, Y.-H. Le, Y.-F. Zhang, J.-M. Yan and Q. Jiang, Au Sub-nanoclusters on TiO2 toward highly efficient and selective electrocatalyst for N2 conversion to NH3 at ambient conditions, Adv. Mater., 2017, 29, 1606550 CrossRef PubMed.
- S. Chen, S. Perathoner, C. Ampelli, C. Mebrahtu, D. Su and G. Centi, Electrocatalytic Synthesis of Ammonia at Room Temperature and Atmospheric Pressure from Water and Nitrogen on a Carbon-Nanotube-Based Electrocatalyst, Angew. Chem., Int. Ed., 2017, 56, 2699–2703 CrossRef CAS PubMed.
- X. Zhao, F. Yin, N. Liu, G. Li, T. Fan and B. Chen, Highly efficient metal–organic-framework catalysts for electrochemical synthesis of ammonia from N2 (air) and water at low temperature and ambient pressure, J. Mater. Sci., 2017, 52, 10175–10185 CrossRef CAS.
- K. Kim, C.-Y. Yoo, J.-N. Kim, H. C. Yoon and J.-I. Han, Electrochemical synthesis of ammonia from water and nitrogen in ethylenediamine under ambient temperature and pressure, J. Electrochem. Soc., 2016, 163, F1523–F1526 CrossRef CAS.
- D. Yang, T. Chen and Z. Wang, Electrochemical reduction of aqueous nitrogen (N2) at a low over-potential on (110)-oriented Mo nanofilm, J. Mater. Chem. A, 2017, 5, 18967–18971 RSC.
- L. Zhang, X. Ji, X. Ren, Y. Ma, X. Shi, Z. Tian, A. M. Asiri, L. Chen, B. Tang and X. Sun, Electrochemical ammonia synthesis via nitrogen reduction reaction on a MoS2 satalyst: theoretical and experimental studies, Adv. Mater., 2018, 30, 1800191 CrossRef.
- X. Zhang, R.-M. Kong, H. Du, L. Xia and F. Qu, Highly efficient electrochemical ammonia synthesis via nitrogen reduction reactions on a VN nanowire array under ambient conditions, Chem. Commun., 2018, 54, 5323–5325 RSC.
- X. Ma, J. Hu, M. Zheng, D. Li, H. Lv, H. He and C. Huang, N2 reduction using single transition-metal atom supported on defective WS2 monolayer as promising catalysts: A DFT study, Appl. Surf. Sci., 2019, 489, 684–692 CrossRef CAS.
- Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen, H. Yu, H. Zhao, Y. Zhang and J. Zhao, Facile ammonia synthesis from electrocatalytic N2 reduction under ambient conditions on N-doped porous carbon, ACS Catal., 2018, 8, 1186–1191 CrossRef CAS.
- C. Lv, Y. Qian, C. Yan, Y. Ding, Y. Liu, G. Chen and G. Yu, Defect Engineering Metal-Free Polymeric Carbon Nitride Electrocatalyst for Effective Nitrogen Fixation under Ambient Conditions, Angew. Chem., Int. Ed., 2018, 57, 10246–10250 CrossRef CAS PubMed.
- S. Mukherjee, D. A. Cullen, S. Karakalos, K. Liu, H. Zhang, S. Zhao, H. Xu, K. L. More, G. Wang and G. Wu, Metal-organic framework-derived nitrogen-doped highly disordered carbon for electrochemical ammonia synthesis using N2 and H2O in alkaline electrolytes, Nano Energy, 2018, 48, 217–226 CrossRef CAS.
- J. Zhao and Z. Chen, Single Mo atom supported on defective boron nitride monolayer as an efficient electrocatalyst for nitrogen fixation: a computational study, J. Am. Chem. Soc., 2017, 139, 12480–12487 CrossRef CAS.
- B. Huang, N. Li, W.-J. Ong and N. Zhou, Single atom-supported MXene: how single-atomic-site catalysts tune the high activity and selectivity of electrochemical nitrogen fixation, J. Mater. Chem. A, 2019, 7, 27620–27631 RSC.
- F. Lü, S. Zhao, R. Guo, J. He, X. Peng, H. Bao, J. Fu, L. Han, G. Qi, J. Luo, X. Tang and X. Liu, Nitrogen-coordinated single Fe sites for efficient electrocatalytic N2 fixation in neutral media, Nano Energy, 2019, 61, 420–427 CrossRef.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Single-atom catalysis of CO oxidation using Pt1/FeOx, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed.
- K. Liu, Y. Lei and G. Wang, Correlation between oxygen adsorption energy and electronic structure of transition metal macrocyclic complexes, J. Chem. Phys., 2013, 139, 204306 CrossRef PubMed.
- C. Liu, Q. Li, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, Conversion of dinitrogen to ammonia on Ru atoms supported on boron sheets: a DFT study, J. Mater. Chem. A, 2019, 7, 4771–4776 RSC.
- C. Choi, S. Back, N. Kim, J. Lim, Y. Kim and Y. Jung, Suppression of hydrogen evolution reaction in electrochemical N2 reduction using single-atom catalysts: a computational guideline, ACS Catal., 2018, 8, 7517–7525 CrossRef CAS.
- Z. Geng, Y. Liu, X. Kong, P. Li, K. Li, Z. Liu, J. Du, M. Shu, R. Si and J. Zeng, Achieving a Record-High Yield Rate of 120.9 μgNH3 mgcat.-1 h-1 for N2 Electrochemical Reduction over Ru Single-Atom Catalysts, Adv. Mater., 2018, 30, 1803498 CrossRef.
- R. Burch, Importance of ligand effects in metal alloy catalysts, Acc. Chem. Res., 1982, 15, 24–31 CrossRef CAS.
- B. Li, J. Wang, X. Gao, C. Qin, D. Yang, H. Lv, Q. Xiao and C. Zhang, High performance octahedral PtNi/C catalysts investigated from rotating disk electrode to membrane electrode assembly, Nano Res., 2019, 12, 281–287 CrossRef CAS.
- S. Kim, J. Jung, E. Yang, K.-Y. Lee and D. J. Moon, Hydrogen production by steam reforming of biomass-derived glycerol over Ni-based catalysts, Catal. Today, 2014, 228, 145–151 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 124, 11169–11186 CrossRef.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. P. Bundy and J. S. Kasper, Hexagonal diamond—a new form of carbon, J. Chem. Phys., 1967, 46, 3437–3446 CrossRef CAS.
- H. Sevinçli, M. Topsakal, E. Durgun and S. Ciraci, Electronic and Magnetic Properties of 3d Transition-Metal Atom Adsorbed Graphene and Graphene Nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195434 CrossRef.
- Z. He, K. He, A. W. Robertson, A. I. Kirkland, D. Kim, J. Ihm, E. Yoon, G.-D. Lee and J. H. Warner, Atomic Structure and Dynamics of Metal Dopant Pairs in Graphene, Nano Lett., 2014, 14, 3766–3772 CrossRef CAS PubMed.
- Y. Li, H. Su, S. H. Chan and Q. Sun, CO2 Electroreduction Performance of Transition Metal Dimers supported on Graphene: A Theoretical Study, ACS Catal., 2015, 5, 6658–6664 CrossRef CAS.
- A. W. Robertson, C. S. Allen, Y. A. Wu, K. He, J. Olivier, J. Neethling, A. I. Kirkland and J. H. Warner, Spatial Control of Defect Creation in Graphene at the Nanoscale, Nat. Commun., 2012, 3, 1144 CrossRef PubMed.
- H. Yan, Y. Lin, H. Wu, W. Zhang, Z. Sun, H. Cheng, W. Liu, C. Wang, J. Li, X. Huang, T. Yao, J. Yang, S. Wei and J. Lu, Bottom-up precise synthesis of stable platinum dimers on graphene, Nat. Commun., 2017, 8, 1070 CrossRef PubMed.
- H. Jiang and W. Yang, Conjugate-gradient optimization method for orbital-free density functional calculations, J. Chem. Phys., 2004, 121, 2030–2036 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Anderson, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the over-potential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, Modeling the electrochemical hydrogen oxidation and evolution reactions on the basis of density functional theory calculations, J. Phys. Chem. C, 2010, 114, 18182 CrossRef.
- NIST Standard Reference Database Number 69, https://webbook.nist.gov/chemistry/ Search PubMed.
- Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, Electroreduction of N2 to ammonia at ambient conditions on mononitrides of Zr, Nb, Cr, and V: a DFT guide for experiments, ACS Catal., 2016, 6, 635–646 CrossRef CAS.
- X. Li, Q. Li, J. Cheng, L. Liu, Q. Yan, Y. Wu, X. Zhang, Z. Wang, Q. Qiu and Y. Luo, Conversion of dinitrogen to ammonia by FeN3-embedded graphene, J. Am. Chem. Soc., 2016, 138, 8706–8709 CrossRef CAS PubMed.
- H. Niu, X. Wang, C. Shao, Z. Zhang and Y. Guo, Computational Screening Single-Atom Catalysts Supported on g-CN for N2 Reduction: High Activity and Selectivity, ACS Sustainable Chem. Eng., 2020, 8, 13749–13758 CrossRef CAS.
- X. Zhai, L. Li, X. Liu, Y. Li, J. Yang, D. Yang, J. Zhang, H. Yan and G. Ge, A DFT screening of single transition atoms supported on MoS2 as highly efficient electrocatalysts for the nitrogen reduction reaction, Nanoscale, 2020, 12, 10035–10043 RSC.
- Z. Xu, R. Song, M. Wang, X. Zhang, G. Liu and G. Qiao, Single atom-doped arsenene as electrocatalyst for reducing nitrogen to ammonia: a DFT study, Phys. Chem. Chem. Phys., 2020, 22, 26223–26230 RSC.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Effect of Strain on the Reactivity of Metal Surfaces, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Lattice-strain control of the activity in dealloyed core–shell fuel cell catalysts, Nat. Chem., 2010, 2, 454–460 CrossRef CAS PubMed.
- A. Khorshidi, J. Violet, J. Hashemi and A. A. Peterson, How strain can break the scaling relations of catalysis, Nat. Catal., 2018, 1, 263–268 CrossRef.
- T. Bligaard and J. K. Nørskov, Ligand effects in heterogeneous catalysis and electrochemistry, Electrochim. Acta, 2007, 52, 5512–5516 CrossRef CAS.
- A. A. Jeffery, S.-Y. Lee, J. Min, Y. Kim, S. Lee, J. H. Lee, N. Jung and S. J. Yoo, Surface engineering of Pd-based nanoparticles by gas treatment for oxygen reduction reaction, Korean Journal of Chemical Engineering, 2020, 37(8), 1360–1364 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08358a |
| ‡ Current address: Korea Institute of Energy Technology (KENTECH), Naju-si, Jeollanam-do, 58330, Republic of Korea. E-mail: E-mail: jhan@kentech.ac.kr |
| This journal is © The Royal Society of Chemistry 2022 |