Open Access Article
Open Access ArticleEnsemble representation of catalytic interfaces: soloists, orchestras, and everything in-between
Robert H.
Lavroff
 ,
Harry W. T.
Morgan
,
Harry W. T.
Morgan
 ,
Zisheng
Zhang
,
Zisheng
Zhang
 ,
Patricia
Poths
,
Patricia
Poths
 and
Anastassia N.
Alexandrova
and
Anastassia N.
Alexandrova
 *
*
Department of Chemistry and Biochemistry, University of California, Los Angeles, Los Angeles, California 90095-1569, USA. E-mail: ana@chem.ucla.edu
First published on 24th May 2022
Abstract
Catalytic systems are complex and dynamic, exploring vast chemical spaces on multiple timescales. In this perspective, we discuss the dynamic behavior of fluxional, heterogeneous thermal and electrocatalysts and the ensembles of many isomers which govern their behavior. We develop a new paradigm in catalysis theory in which highly fluxional systems, namely sub-nano clusters, isomerize on a much shorter timescale than that of the catalyzed reaction, so macroscopic properties arise from the thermal ensemble of isomers, not just the ground state. Accurate chemical predictions can only be reached through a many-structure picture of the catalyst, and we explain the breakdown of conventional methods such as linear scaling relations and size-selected prevention of sintering. We capitalize on the forward-looking discussion of the means of controlling the size of these dynamic ensembles. This control, such that the most effective or selective isomers can dominate the system, is essential for the fluxional catalyst to be practicable, and their targeted synthesis to be possible. It will also provide a fundamental lever of catalyst design. Finally, we discuss computational tools and experimental methods for probing ensembles and the role of specific isomers. We hope that catalyst optimization using chemically informed descriptors of ensemble nature and size will become a new norm in the field of catalysis and have broad impacts in sustainable energy, efficient chemical production, and more.
Introduction
Catalysis is the study of change. When a chemical reaction occurs in the presence of a catalyst, the substrate undergoes drastic structural transformations. Definitions of a catalyst generally agree that such a substance should be unchanged by the overall reaction, though a transformation to the active form of the catalyst in the reaction conditions is also accepted. However, in the dynamic environment of reactions, why should we assume that a fluxional catalyst does not undergo rapid reversible changes during the reaction?It is well established that the pristine material surfaces we think of as heterogeneous catalysts undergo sintering, morphological changes, surface alloying, and much more as a result of reaction conditions.1,2 More often than not, when painting a picture of a catalytic reaction, we assume that the catalyst is staying put once transformed into its steady state form, neglecting the continuing dynamic effects on the catalyst. However, when the catalyst is fluxional, at realistic reaction temperatures, low-lying isomeric structures can be accessed by the catalytic system, each of these structures possessing its own properties.3 Hence, the catalyst will constantly isomerize, i.e. never stop moving. The accessible isomers will form a statistical ensemble of states. In the thermodynamic limit, the prevalence of each structure can be determined by a Boltzmann probability, and it has been shown that the most probable structure (the global energy minimum, GM) is quite frequently not the most active or selective.3,4 In extreme cases of this dynamism, sub-nano clusters and their ensembles of many isomers can lead to strong deviations from the behavior of “normal” catalysts, vide infra. This is relevant to so-called single cluster catalysis.5–8 However, the phenomenon, while possibly somewhat tamed or changed to being regional rather than global, is also present in other types of catalytic interfaces, including larger nanoparticles undergoing morphological (and sometimes oscillatory) changes in reaction conditions, as well as amorphous thermal and electrocatalytic bulk interfaces.9–12 The relative time-scales of the various coupled events, such as reconstruction of the surface, adsorbate migration, adsorption/desorption, and the reaction itself, is key to accessing the true relevant active sites; this remains an outstanding problem in the field. For the exceptionally fluxional catalysts that have been our focus, we hypothesize that large ensembles containing isomers with diverse properties can be detrimental for catalytic selectivity. In some cases, however, ensembles can be surprisingly small. If the small ensemble has the desired catalytic properties, the situation is quite ideal. The key questions, therefore, are: why and when are ensembles large or small, and how can their size and nature be controlled to result in just perfect activity and selectivity for the catalytic process of interest? Can we purposefully synthesize such catalysts that would possess the desired ensemble characteristics? What would be the relevant levers of ensemble tuning in this seemingly uncontrollable situation?
The ensemble composition will depend on the reaction conditions, such as temperature and potential, so to predict the behavior of these dynamic systems we must understand the influence of these conditions in detail. In this perspective we will examine the complex relationship between cluster stoichiometry and ensemble size, paving the way toward controlling the latter, outline some key catalytic properties which depend strongly on ensemble composition, discuss relevant fundamentals of bonding, thermodynamics, and kinetics, explore the effects of different reaction conditions on ensemble size, and finally describe methods for studying catalytic ensembles.
Effects of fluxionality and ensemble size
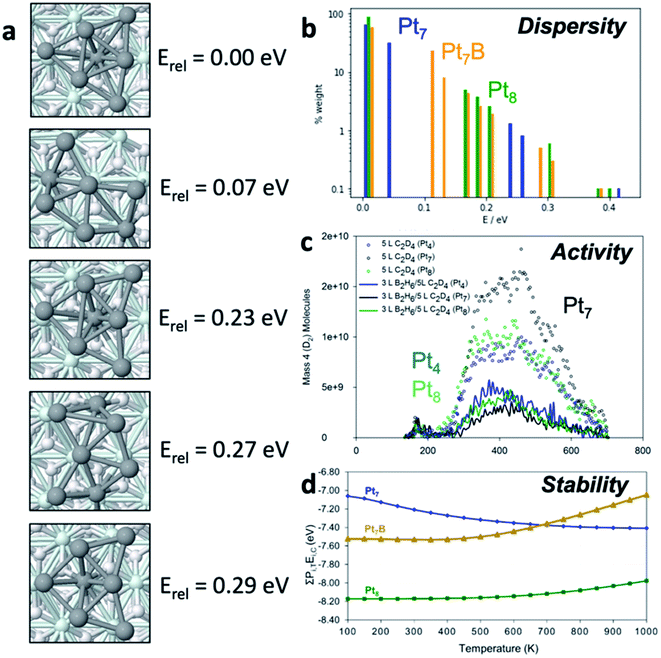
To begin our discussion of catalytic cluster ensembles we will consider Ptn clusters adsorbed onto Al2O3, a classic thermal catalyst for dehydrogenation of alkanes,13 as well as tractable model catalyst for larger Pt particles used in industrial processes.14,15 We consider four closely related clusters – Pt4, Pt7, Pt7B, and Pt8 – to see the dramatic effects of small changes in composition. Fig. 1a shows the low-lying states of Pt7 which comprise most of the ensemble for this cluster and their energies relative to the lowest energy structure, the GM. Two main structural types are clearly visible: the quasi-three-fold-symmetric global minimum, and the quasi-planar fan-shaped lowest-energy local minimum (LM1). Particularly important is the energy of this LM1 state – at only 0.07 eV above the GM this structure will be significantly populated at reaction temperatures.The dispersion of isomers for Pt7, Pt7B and Pt8 are shown on a histogram of energies in Fig. 1b, relative to the GM for their composition, and fractional population, or ensemble weight, at 700 K (calculated via simple Boltzmann statistics). The weight axis (y) is plotted on a log scale to improve visibility of isomers with small weights. Pt8 exists predominantly as its GM isomer, with the first LM appearing around 0.2 eV above the ground state, accessible only at elevated temperatures. For Pt7 the low-lying LM1 geometry is clearly accessible (second blue peak), comprising around 25% of the ensemble at 700 K, and will be significantly populated at relatively mild temperatures. Pt7B has a very broad distribution of isomers, contrasting with both Pt7 and Pt8. Thus, property predictions for these systems must be done on the statistical ensemble of states, not just the ground state (i.e. GM).
To see the chemical consequences of ensembles, Fig. 1c describes the catalytic activity of Pt4, Pt7 and Pt8 clusters for ethylene (C2D4) dehydrogenation by showing the rate of D2 desorption in temperature-programmed desorption (TPD) experiments. Clearly, activity varies unpredictably with cluster composition. It is particularly significant that the most active cluster is Pt7, which was shown in Fig. 4a to have a thermally accessible isomer at low temperature. This isomer is in fact more active than the GM, and it also becomes more prevalent in the ensemble upon ethylene binding (i.e. reagents reshape the ensemble). LM1 causes the activity enhancement of Pt7 over Pt4 and Pt8 above 300 K, highlighting the need to study the reactivities of all members of an ensemble.
Besides the activity, selectivity, or susceptibility to poisoning, are also clear functions of ensembles. Fig. 1d provides computational insight into the coking susceptibility of platinum clusters by plotting the binding energy of a carbon atom as a function of temperature – a more negative value implies more exothermic coking. The temperature dependence arises from the accessible isomeric population. From the upward and downward trends, we can deduce that Pt7 becomes more susceptible to coking as temperature increases while Pt8 and Pt7B become more resistant. This means that the higher-lying isomers of Pt7 are more prone to coking than the GM, while the reverse is true for Pt8 and Pt7B. Prediction of temperature-dependent properties requires particular focus on ensemble size as the percentage of the GM structure can change significantly and in a system-specific manner.
Bonding models
With the importance of isomeric ensembles in catalysis established, there is a pressing need to predict the properties and sizes of these ensembles. A fundamental way to approach this problem is through the details of chemical bonding. The idea that chemical behavior can be understood by counting electrons has been key in chemistry for over a century. This idea inspired pioneering work on atomic structure and valence by Lewis16 and Langmuir,17 appears in familiar forms like the octet and 18-electron rules, and underpins the structure of the periodic table itself. Modern chemists continue to use electron counting methods to understand complex chemical behavior, from Hückel aromaticity in conjugated cyclic systems to the Wade–Mingos rules18,19 for electron-deficient clusters.In platinum chemistry, magnetism and reactivity in Pt13 and hydrogen-adsorbed derivatives have been explained through superatom character.20,21 Particularly interesting for catalyst design is the finding that ORR catalytic activity of “magic-number” Pt13 clusters was less than half that of less-symmetrical, non-superatom Pt12 clusters.22 Reactivity effects in response to local aromaticity have also been found in the B8 island on B-rich WB(001) for electrocatalytic hydrogen evolution reaction (HER), where each hydrogenation step leads to massive charge redistribution.23
Electron counting schemes may provide powerful tools to explain isomeric diversity, so we can formulate a key question: if a cluster ground state is well-described by a particular bonding model, can that model make predictions about the isomer distribution? In the following discussion we will continue to focus on the superatom model, but the concepts are applicable to other bonding models.
The chemical stability implied by a superatom configuration may indicate a paucity of low-lying isomers, because other isomers would violate the symmetry and stability of the superatomic configuration. Inversely, we might expect a non-superatom cluster to have a broader isomeric distribution. However high-spin superatomic arrangements may exhibit the opposite, since stability could be gained by symmetry-breaking and electron-pairing. This remains to be demonstrated, however. The relationships are complex between isomer distribution and catalytic qualities of activity, selectivity, and stability, so specific study of electron-precise clusters is warranted. Pt12 has been shown to be a more active ORR catalyst than superatomic Pt13, but the role of low-lying isomers in either system is currently unknown. Beyond simply considering the dispersity of the isomeric ensemble, assuming that superatomic clusters are not all well-described by a single structure, we may also wish to use bonding models to predict the properties of those isomers. The superatom model is intimately connected to structure by the spherically symmetric potential which stabilizes particular electron counts, so it is unclear how well the model will deal with deviations from spherical symmetry in higher-lying isomers. Oblate and prolate distortions in gold clusters have been explained by superatomic p2 and p4 configurations,24 where p0 and p6 configurations would be spherical. This invites the intriguing possibility of relating excited geometries of a superatom cluster to excited electronic configurations, from which reactivity predictions may follow.
Chemical bonding ideas are central to chemistry, as this is the way we rationalize the chemical world, but much development is still needed to apply existing or new bonding concepts to catalytic clusters. Then can we begin to make use of bonding analysis in predictions of relative stabilities of isomers and, ultimately, catalytic properties.
Thermodynamic and kinetic control
In our paradigm, we assume that ensembles of sub-nano clusters and surface states are populated based on their Boltzmann weights, therefore assuming that the ensemble is entirely thermally equilibrated. We know that this is the case for Pt7/Al2O3, where we have explicitly calculated all the barriers for isomerization within the ensemble. Based on these barriers, at 700 K the entire ensemble will be visited within nanoseconds.25 We use this same approximation for ensembles of surface sites that develop under reaction conditions, such as the formation of off-stoichiometric boron oxide surface layers for the oxidative dehydrogenation of propane,26 or for the surface restructuring of WB under electrocatalytic HER conditions.23It is presently unclear whether the assumption of thermal equilibration at all reactions stages applies universally, or whether some systems may have low-lying isomers which are kinetically inaccessible. There is the example of a cationic Au6+ cluster, where the barrier between different isomers decreases with the chemisorption and physisorption of H2O and CO,27 so adsorbate coverage and type could play a role in determining whether the entire ensemble is thermodynamically accessible. It has been seen that larger nanoparticles (NPs) can readily restructure under reaction conditions and induce structural change in the support closest to them.28,29 This suggests that typically dynamic rearrangement even of large NPs and surfaces could be facile on industrially relevant timescales, but possibly confined to the top few layers at the NP surface, i.e. the NP ensembles can be restricted. In general, the question of kinetic accessibility of all thermodynamically accessible states of the catalyst remains open.
The kinetics of rapidly interconverting isomers with unequal reaction barriers is well described in physical organic chemistry by the Curtin–Hammett principle. The distribution of products in such a system is determined by the difference in transition state energies, which can be written as a combination of the energy difference between the conformers and the barrier heights as shown in Fig. 2a. This means that neither the Boltzmann populations nor the reaction barriers alone are sufficient to predict the relative reactivities of members of an ensemble. Understanding the Curtin–Hammett principle will be essential to any successful attempt to optimize a catalytic ensemble. It is worth noting that this principle was developed in organic chemistry to predict the distributions of stereoisomers; our studies of small-molecule reactivity have so far offered no opportunity to observe an equivalent distribution, but future work could include searching for such an ensemble. Fig. 2b describes this schematically for a hypothetical dehydrogenation catalyst with two active isomers, each of which reacts with butane to give a different isomer of butene. For such a system, correct prediction of the product distribution would require analysis according to the Curtin–Hammett principle, accounting for the relative energies and reaction barriers of both isomers of the catalyst.30
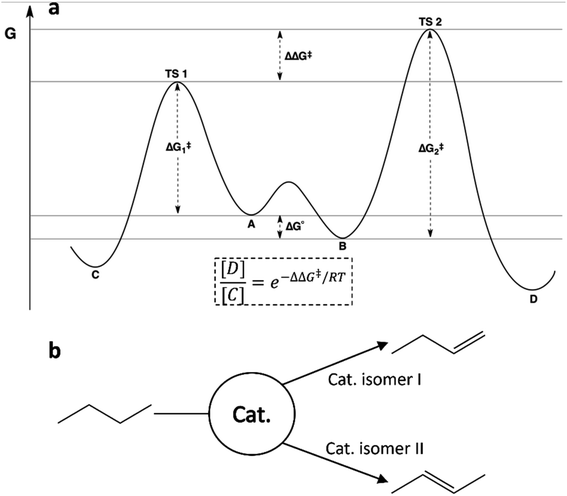 | ||
| Fig. 2 (a) Reaction scheme illustrating the Curtin–Hammett principle for two interconverting isomers where the more stable isomer (B) reacts through the higher energy transition state (TS 2). The equation for the product ratio [D]/[C] is given in terms of the difference in transition state energies. (b) Schematic illustrating a possible consequence of the Curtin–Hammet principle in catalytic butane dehydrogenation, where members of an ensemble may selectively produce different isomers of the product.31 | ||
Establishing the true, complex nature of active catalysts in reaction conditions, whether by experiment or computation, is only part of the battle. Upon determination of the ensemble of structures within the system, we can begin to assess which structures serve as excellent active sites and which are bystanders or even adversaries to our desired reaction. For instance, isomeric diversity can conceivably be detrimental to the selectivity of a catalyst. Looking forward, this begs the question: can we tune our catalyst and its surroundings to meet the needs of the target transformation? Establishing these needs is already possible; what remains to be seen is whether they can be “hand-picked.”
Classifying fluxionality and its descriptors
While a series of nano/sub-nano catalysts and amorphous surfaces have been shown to be fluxional under reaction, the characteristics of their fluxionality, which underlies the nature of the ensemble, can differ greatly.32 We proposed that fluxionality begs some classification, enabling its fundamental understanding. In Fig. 3a, we classify the catalyst fluxionality at realistic temperature into four categories based on their PES landscapes: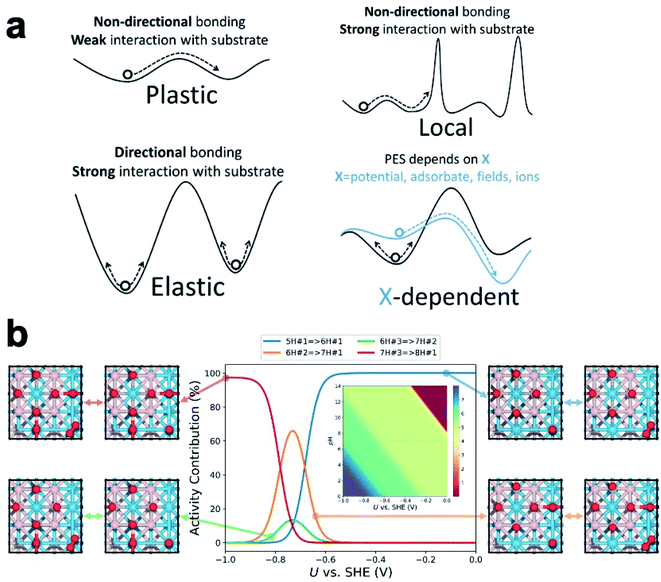 | ||
| Fig. 3 (a) A depiction of the four classifications of fluxionality. (b) Isomer distribution of tungsten boride surface states for HER as a function of applied potential and pH. | ||
(i) Plastic fluxionality is the case where the PES is so flat/anharmonic that the restructuring barriers are of a similar magnitude as thermal fluctuations. The catalyst can then readily transform into LMs in neighboring shallow wells, thereby populating a large ensemble of accessible states. Systems with plastic fluxionality are expected to have non-directional bonding within the restructuring region (metal) and weak interaction with the substrate (or in isolated gaseous form).
(ii) Elastic fluxionality occurs when the PES features deep wells throughout, forming high barriers to isomerization that the system cannot cross within a realistic timescale. Although the local curvature at the bottom of the well might be small to allow significant structural deformation, the high restructuring barriers prevent the initial configuration from accessing other LMs, and it can only oscillate around the equilibrium configuration. This is often the case for systems with more rigid and directional bonding (e.g., oxides) or those that interact too strongly with the substrate.
(iii) Local fluxionality is a mixture of plastic and elastic cases where there are several flat regions separated by high barriers.25 As a result, the catalyst will only be allowed to access local LMs within its flat surroundings, while the pathways to other regions are blocked, or at least significantly hindered. This can be a result of non-directional bonding (local flatness) and a strong-interacting substrate. Most oxide-supported metal clusters should fall into this category.
(iv) X-dependent fluxionality is the case where the PES of the catalyst can be reshaped by an external factor such as applied potential, adsorbate coverage/configuration, external fields, or near-surface ions. The external factor may lower restructuring barriers and shift the GM to another configuration, but it may also deepen the wells and collapse the ensemble into fewer structures.
In thermal catalysis, ensemble size is determined by the amplitude of the thermal fluctuations and the local PES around the initial configuration. Systems with plastic functionality access the LMs globally with little kinetic hindrance, which yields a large ensemble obeying Boltzmann statistics. Systems with elastic fluxionality, however, are usually kinetically trapped in their initial configuration, leading to unpredictable non-Boltzmann distributions. It is also possible to recover the thermodynamic distribution by annealing the system to a sufficiently high T or deliberately populating a thermodynamic metastable state. These techniques can translate to local fluxionality, constructing an ensemble with a desired size based on understanding of the density of local minima within each separated PES region.
In electrocatalysis, in contrast, the operating temperature is usually near room temperature. Since the restructuring barriers are usually much higher than the thermal energy at room temperature, one would expect most catalysts to exhibit elastic fluxionality and inability to restructure. However, the isomers in the ensemble could vary significantly in redox properties and dipole moment, giving their free energies different dependences on the applied field. As the electrode potential changes, the PES reshapes accordingly, making the ensemble evolve away from the neutral state distribution. In other words, electrochemical cycling at low temperature can cause fluxional behavior of the catalyst and resize the ensemble of accessible states (Fig. 3b, vide infra). The difference in potential dependence of the isomers originates in the different redox potentials (or potential of zero charge) and interfacial capacitances for different geometries and adsorbate configurations.
We now describe the various interdependent factors that influence the extent and type of fluxionality in cluster catalysts, as well as some ways to influence the resultant ensemble size through chemical composition and reaction conditions.
Adsorbates and ions
At a catalytic interface, the catalyst is in constant adsorbate exchange with the gas/liquid environment, so it is crucial to include adsorbate coverage and configurations into the theoretical model. This is done by treating the system as a grand canonical ensemble, i.e. a system of variable composition. Indeed, the catalyst under heavy adsorbate coverage can differ from the bare case qualitatively. For example, the already mentioned bare Pt7 supported on α-Al2O3 flattens under the coverage of ethylene. Pt8 supported on γ-Al2O3 tends to adopt a compact shape with a large interface with the support. Under a higher H coverage, the metal–adsorbate interaction outcompetes the metal–support interaction, reshaping the cluster core into a stretched 3D shape and partially detaching it from the support.33 At very high H coverages (i.e. high partial pressure of H2), the cluster core could be immobilized due to formation of hydride-like motifs, and multiple accessible surface states could share a common core shape.34 However, this does not mean a smaller ensemble and weakened X-dependent fluxionality. Even on the same core shape, catalytic sites with diverse reactivity can emerge out of different adsorbate coverages and configurations,35 and the fluxionality takes on the form of adsorbate binding, desorption, migration, and rearrangement. A more extreme, nonmetal example is the B8 island on B-rich WB(001) surface in condition of electrocatalytic hydrogen evolution reaction (HER).23 Despite structural similarity with planar metal clusters, the B8 island features localized bonding and local aromaticity, which leads to drastic charge redistribution across the surface upon each hydrogenation step. With the configuration of W and B staying the same, the binding free energy of H on the catalyst ranges from −0.9 to +0.7 eV. The population of the surface states (with different H coverages and configurations) is dependent on the pH and applied potential (Fig. 3b), and the HER activity can be broken down to contributions from different surface states. For more complicated reactions, there can be a mixture of relevant adsorbates, or even chemisorbed or dissociated solvent molecules, on the catalyst.36 Since the adsorbates can differ in their vibrational amplitude and timescale, the configurational sampling can be highly nontrivial, and core–shell decoupling treatment may be necessary to address the distinct atomic mobility.34The role of chemically inert cation or anion additives in tuning the activity and selectivity of electrocatalysis has been reported. Some ions can indirect or directly interact with polar reaction intermediates to promote specific reaction steps.37 The concentration of hydrated ions in the electric double layer at an electrified interface leads to a stronger local electric field, which influences the energy of reaction intermediates via dipole–field interactions.38 In addition, the near-surface ions can significantly deform (in the case of large, soft ions) or enforce (for small, hard ions) local order of the H-bond network, affecting the solvation environment of the reaction intermediates.39 Since supported clusters extrude out of the surface and are positioned partially inside the inner Helmholtz plane (IHP), they are expected to be more heavily influenced by the discussed effects than the bare surfaces.
Breaking linear scaling relations
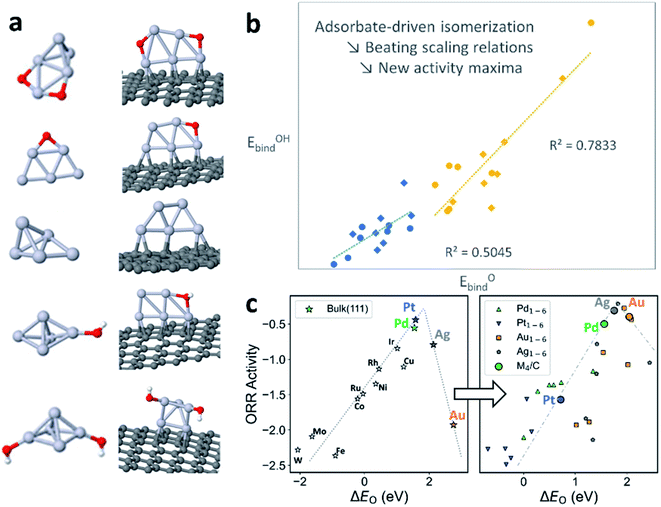
On bulk metal surfaces, it has been observed that the binding energies of a series of chemically-related adsorbates linearly correlate with each other, due to the similar bonding modes and sites that they share.40 This correlating behavior also extends to the activation energies through the Brønsted–Evans–Polanyi (BEP) relation.41 Hence, the reaction energies and activation barriers can be expressed by using linear combinations of adsorbate binding energies as “basis parameters”, reducing the dimensionality of the chemical space to be explicitly explored. The as-known linear scaling relations (LSR), in both thermodynamic and kinetic senses, have been successfully applied to catalyst design by interpolation/extrapolation of the LSRs, high-throughput catalyst screening, and microkinetic modelling of complex reaction networks at a reduced cost.42 However, in the systems where fluxionality prevails, the catalyst can adapt its geometry to more effectively bind each different adsorbate, which routinely breaks the LSRs without elaborate geometric or electronic engineering of the catalyst.43Take the oxygen reduction reaction (ORR) as an example. For metal surfaces, the binding energies of O, OH, and OOH, as well as activation barriers, have been shown to linearly correlate with each other.44,45 This can be attributed to the similar adsorbate–surface interaction for all reaction intermediates on a rigid surface with well-defined active sites. However, on sub-nano metal clusters (Pt5 in Fig. 4a), the core of the cluster isomerizes in response to different adsorbates, coverage, and supports. Such behavior is attributed to the exceptionally flat potential energy surfaces of the clusters and, hence, the abundance of structural diversity in the low-energy thermally accessible region. On different cluster isomers, the reagent binding mode and sites vary, thereby breaking down the geometric and electronic prerequisite of LSRs (Fig. 4b).
The breakdown of the LSR in the sub-nano regime also shakes the activity volcano model derived from LSR and Sabatier analysis, which generally offers an intuitive picture for catalyst design: the catalyst–adsorbate interaction must be neither too strong nor too weak, to prevent over-binding of product (Fig. 3c, left) or failure to activate the reactant (Fig. 4c, right). When we venture into the dynamic sub-nano regime, firstly, the linear segments of the volcano are no longer linear due to the decoupling of the energetics of reaction steps, as can be seen from the M1–6 (M = Pd, Pt, Ag, Au) data points in the right panel of Fig. 3c. Secondly, the fluxional catalysts generally possess more freedom in varying their coordination structures, causing overall over-binding of the adsorbates compared to their bulk counterparts, shifting the elements that under-bind in bulk form (Ag, Au) closer to the apex of the activity volcano. The apex-shifting is slightly weakened but persists even after deposition of the cluster onto supports (M4/C datapoints in the right panel of Fig. 4c). This explains the exceptional activity of downsized Au NPs and provides a rational route to utilize cluster fluxionality as a design tool, and to activate elements in catalysis usually considered inert.46
Intimately related to the size-dependent ability of clusters to restructure and break LSRs is the phenomenon of the reaction thermodynamics and kinetics not linearly scaling with cluster size (the “each atom counts” effect47). The non-directional nature of metal–metal bonds makes the geometric and electronic rearrangements unpredictable as the size increases. As a result, certain cluster sizes could form an ensemble that is favorable for a certain reaction and stand out as reactive “magic numbers”, such as Pt4 supported on indium tin oxide for methanol oxidation48 and Pt7 on alumina for ethylene dehydrogenation.49 Hence, rational design of sub-nano cluster catalysts can be achieved by size-selective preparation, guided by understanding of the ensemble properties obtained from theory. Heteroatom doping and alloying of the cluster can allow ensemble tuning beyond simple size-selection.50–52
Control via self-limiting poisoning
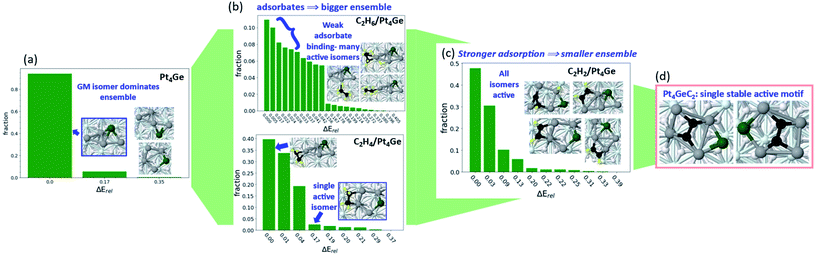
This is a recently found effect related to strong adsorption, and whose generality need to be further explored. In Fig. 1, we saw interesting changes in ensemble size for Pt7, Pt8, and Pt7B, and how those impacts the reaction mechanism. However, the catalytic process itself in turn impacts the catalyst ensemble, and in what follows – can collapse it even to a single structure. In our recent work investigating the particular stability and selectivity towards alkane dehydrogenation to alkene of Pt4Ge/Al2O3 clusters,53 we were primarily interested in understanding the fundamental chemical cause of improved dehydrogenation selectivity from nano-alloying Pt with Ge. The step-by-step investigation of dehydrogenation illuminated some new factors influencing the ensemble size of this C2Hx/Pt4Ge/Al2O3 system, and especially how the ensemble size and reactivity interact.The initial ensemble of bare supported Pt4Ge is heavily dominated by the GM structure (Fig. 5). The two other thermally accessible structures (within 0.4 eV energy cutoff) contribute ∼6% to the total ensemble at a catalytically relevant 700 K. Ethane binding to Pt4Ge is weak, resulting in a large ensemble where the core cluster structure and relative isomer ordering is unperturbed. The lowest energy ethane binding mode consists of less than 12% of the total ensemble, indicating the spread of the ensemble over many structures and binding modes of ethane. In contrast, strongly binding adsorbates appear to reduce ensemble sizes. Ethylene binds much more strongly to Pt4Ge via its π orbitals, reducing the ensemble size, and particularly stabilizing the ring-like structure that favors dehydrogenation-prone di-σ binding mode for ethylene.54–60 Under ethylene, the lowest binding mode comprises approximately 38% of the ensemble. Acetylene binds even more strongly to Pt4Ge, reducing the ensemble size further. Not only does acetylene binding induce further stabilization of the ring-like structure, but it also triggers isomerization of the metal core to structures not seen in the bare ensemble, as the acetylene binding to the cluster maximizes. This binding strength enables dehydrogenation of acetylene, which ultimately forms Pt4GeC2. The Pt4GeC2 ensemble consists of a single stable isomer, where Pt–C bonding is maximized by incorporating the intact C2 unit into the center of the cluster (Fig. 5d). Despite the presence of carbon, which would act as a poison for pure Pt catalyst, the C2 unit interacts electronically with the Ge such that the system is a stable and selective catalyst for ethane dehydrogenation. Notably, one particular isomer motif (Fig. 6d) is the single active cluster type. While the fully sampled ensemble of Pt4GeC2 contains structures with dissociated C2, those isomers are not active with respect to ethane and ethylene C–H activation, and are destabilized relative to the isomers with the intact C2 unit. Furthermore, the barrier for the dissociation of the C–C bond of the bare cluster is high enough that it will not occur under reaction conditions, or in the presence of adsorbates. Throughout this example we see how considering an ensemble of bare clusters is not enough to fully understand their reactivity-a full accounting of how they can restructure in the presence of adsorbates is essential in understanding their evolution throughout the reaction, and how this may influence the final ensemble of active sites.
These observations inform us that, once the adsorbate binds strongly, the ensemble might collapse into a few structures or even just a single structure or active structure type. Here is where we raise the question—where do we draw the line between a strongly bound adsorbate, compared to a dopant? Adsorbates that bind too strongly are considered poisons, as they block further activity. But in the case of Pt4GeC2, we see that a classical dopant, in this case Ge, can work in synergy with a classical poison, coke, in order to modulate the behavior of the system, resulting in a better catalyst. In this particular case, we might consider C and Ge to even be co-dopants of the system. The collapse of the ensemble to one active structure type that we see as a result of adsorbate binding worked in favor of selective catalysis, in this particular case. The goal of future research in this area should thus be investigating synergy between different possible dopants and poisons in order to reduce poisoning while retaining reactivity of the initial system and improving its selectivity and stability.
Surfaces and supports
Choice of surface varies greatly across electro- and thermal cluster catalysis, each affecting ensemble size differently. The strength of the interaction between cluster and surface, measurable by charge transfer for example, is a key indicator of ensemble size. Strong binding of cluster to surface will generally lead to deep potential energy wells (i.e. local elastic fluxionality) whereas weak binding generally correlates to local plastic fluxionality. However, these correlations are poorly understood, and more chemical insight into the relationships between surface chemistry and ensemble size is needed. Given the range of supports used in catalytic applications, extensive research in this area is warranted in the near future.For example, for electrocatalysis, graphitic carbon materials are the most common supports, due to their electric conductance and facile preparation. Owing to the large π-conjugation system, the defect-free graphitic carbon surface has only few dangling bonds, which minimizes the cluster–support interaction. Therefore, the metal–metal interaction within the cluster outcompetes the interaction with support, and the cluster will exhibit global plastic fluxionality, forming an ensemble dictated by this bonding.61 However, it also leads to a lower migration barrier which promotes sintering into larger particles via coalescence, which can cause stability issues at higher metal loading. This issue can be mitigated by using materials with built-in anchoring sites, such as graphdiyne and graphitic C3N4, to strengthen the metal–support binding. Otherwise, one may also artificially construct the anchoring sites by introduction of defects or vacancies (for graphene, borophene, phosphene etc.).62 Realistic carbonaceous material may be quite amorphous, with porous microstructures containing 5- or 7-member rings within the deformed sheets.63 Therefore, the common model of graphite may overestimate the crystallinity and cleanness of the surface, while underestimating the metal–support interaction.
The support may also undergo changes in the reaction conditions, leading to strengthening or weakening the metal–support interactions. Conducting oxide thin films are known to undergo significant hydroxylation by dissociating chemisorbed water molecules in aqueous media.64 After hydroxylation, the metal–support interaction will be considerably weakened compared to oxo-terminations. Under oxidative conditions, some transition metal phosphides and chalcogenides are known to transform into an oxide phase which can interact more strongly with supported clusters.65 Studies of cluster ensembles on chemically active surfaces face great challenges in the dimensionality of the chemical space, so new modelling techniques may be required to understand such systems in depth.
For thermal catalysis, metal clusters are most commonly supported by metal oxides. An important factor to consider when assessing the ensemble size of an oxide-supported cluster whether the oxide is reducible or irreducible. Metals on reducible supports can change oxidation state upon cluster deposition, offering stronger interaction which can trigger elastic fluxionality.66,67 In addition to binding strength, ensemble size may be drastically affected by support reduction, leading to a massive increase in its grand-canonical chemical space.2 Pristine alumina68 and magnesia69 supports are highly resistant to reduction, though cases of increasing catalytic activity by forced reduction and vacancy formation have been shown,70 but other oxides such as titania2,71 and ceria72–74 can undergo major surface reconstruction. Whether this reconstruction results in expansion or collapse of the ensemble is an active area of computational research. The trend could be toward larger ensemble sizes due to surface reconstruction, or instead toward smaller sizes due to stronger binding to the support that would single out most stable shapes.
Generalizing the relationship between surface characteristics and ensemble size is further complicated by metal oxide clusters on metal surfaces. While we often think of effective thermal catalysts as metal clusters on oxide surfaces, “inverse” catalysts have shown excellent performance,75 being as or more reactive in CO2 reduction to methanol,76–78 as well as the water–gas shift reaction (WGSR),79,80 and CO oxidation.81 These systems are also of interest for giving insight into their “non-inverse” counterparts as, unlike irreducible metal oxides, metal surfaces allow for use of photoemission, ion scattering, and other charged-particle probes of atomic composition and electronic structure.82 Inverse systems in computational studies can further represent oxide-decorated metal nanoparticles designed to maximize the surface area of metal–oxide interfaces important for reactions such as Fischer–Tropsch synthesis.83
In general, gas phase ensembles for metal oxide clusters are smaller than those for metal clusters.84–87 This can be attributed to the metal (M) atoms' affinity for oxygen, leading to M–O–M–O–… motifs. Specifics of restructuring under reaction conditions is not well understood and an active area of research. Surface effects on ensemble size are highly dependent on the metal surface and its atomic properties. For example, highly electronegative surfaces like Au (111), though too costly to use for anything other than a model catalyst, will draw electron density out of oxide clusters,88 whereas other metals such as copper will donate electrons to the cluster instead.89 Additionally, much like reducible oxides, metal supports may be prone to local oxidation, leading to surface reconstruction and sharp increase in chemical space.
Size-dependent sintering
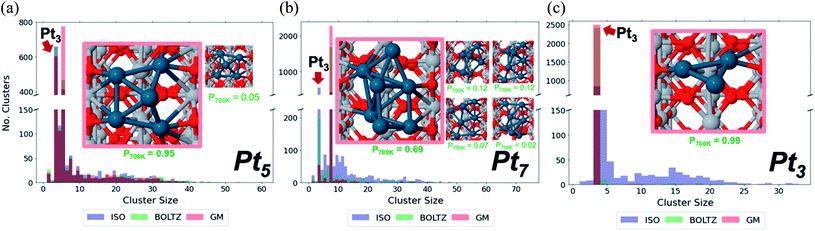
Sintering eliminates the least stable cluster sizes, and as such stands as inescapable in attempting to control the ensemble sizes. This topic is also linked to the support type. Importantly, sintering at the nano-scale exhibits fluxionality-induced cluster size-dependence.90 In thermal catalysis, we have shown that including isomeric diversity when accounting for the sintering of perfectly monodisperse cluster size distributions accelerates sintering significantly. This behavior is in contrast to larger NPs whose sintering resistance increases at size uniformity, by statistical argument within the Ostwald theory. Furthermore, the degree to which cluster sintering is accelerated is not uniform across sizes. We can classify the different sizes into three categories—the first, where isomeric diversity dramatically accelerates sintering compared to the hypothetical scenario in which the system consists only of the GM structures; the second, where the isomer-driven sintering acceleration is small but non-negligible; and the third, where isomeric diversity makes virtually no difference to sintering rate.Fig. 6a–c shows Monte Carlo sintering simulations of Pt3, Pt5 and Pt7 on rutile, each initialized with three different isomer distributions: GM, with all clusters starting in the GM; BOLTZ, with isomer distributions determined by the Boltzmann distribution at 700 K; ISO, where all isomers within 0.4 eV of the GM are equally prevalent at the start but become Boltzmann in the course of the simulation. GM is therefore a low-temperature limit, while BOLTZ and ISO are simplified high-temperature limits. Simulations were terminated after a fixed number of steps to prevent complete sintering to NPs. The histograms of the final cluster size distribution show distinct stratification based on initial isomeric diversity. Pt5 has the three histograms largely superimposed, implying that the starting configuration had little effect on sintering, while Pt7 and Pt3 show greater differences between simulations with different starting configurations. We can therefore see that the dependence of the final size distributions on the nature of the initial distribution increases in the order Pt5, Pt7, Pt3. Additionally, the histograms reveal the presence of particular cluster sizes as “magic” sinter-resistant cluster sizes. Note that the term “magic” is typically applied to mass-selection of clusters at milder temperatures, whereas here we refer specifically to their thermal stability. In each histogram for all the cluster sizes, the peak for Pt3 is, if not the dominant peak, the second most dominant, even when Pt3 is not initially present. This dominance points to the exceptional stability of Pt3 on TiO2 relative to the other cluster sizes. The final cluster size distribution for Pt3 supports this as well: in BOLTZ simulations, the system hardly sinters. Only when the initial configuration contains an artificially high population of high-energy isomers (ISO) does the size-selected Pt3 system sinter.
We have to conclude that sintering stability and thermal ensemble size exhibit only lose correlation. Instead, the size-dependent behavior is described by the “competing pathways” mechanism, in which we compare the energetic (un)favorability of combining various isomers of different cluster sizes in either sintering or reverse sintering monomer motion steps. The balance of forward vs. reverse sintering is then considered by weighting each isomer combination by the probability of it happening, and whether or not it is favorable. Comparing the GM-only combinations with the entire ensemble is what dictates the degree to which isomeric diversity impacts sintering. Ultimately, these results indicate that the theory of Ostwald ripening, based solely on surface energies, requires updating to account for the isomeric diversity of small fluxional clusters and nanoparticles.
Exploring ensembles via computation and experiment
Determination of the low-lying isomers of catalytic systems is not trivial, particularly in the case of surface-deposited, small metal clusters where the chemical bonding is not well understood. Thus, a large chemical space must be sampled to ensure as many configurations as possible are considered and evaluated energetically by electronic structure calculations. Effective computational methods for this purpose fall under the category of global optimization (GO) and include particle swarm optimization,91–93 random searching,94,95 genetic algorithms,96–100 basin hopping,101–103 and simulated annealing.104 In addition, simulation under pressures of gasses and adsorbates, which often cause significant restructuring, can be accomplished by minimizing free energy under chemical potentials as opposed to electronic (i.e. density functional theory) energy only.26,33 These treatments, such as grand canonical genetic algorithms (GCGA), drastically expand the space sampled by GO, however. This is important to consider for keeping these calculations computationally tractable. In the case of systems which have been studied extensively in the past, machine learning (ML) can be employed to sample potential energy surfaces. As recently shown for carbon monoxide on large, stepped Pt surfaces, ML can be extremely useful for accelerated sampling and sampling systems too high in electron count for a high number of ab initio calculations.105Identifying ensembles and ensemble sizes with experiment only is presently difficult, as current methods cannot provide the required spatial, temporal, or atomistic resolution. However, we can validate the existence of ensembles by comparing predictions from our ensemble paradigm to experiment. We have aided experiment in explaining size–reactivity relationships of Pt4,7,8 clusters using temperature programmed desorption (TPD).49 Size-selected clusters, synthesized via atom-layer deposition,51,56,106 are used to identify the size-dependent behavior of the system, and to simplify modelling of the ensemble we can focus on the ensemble of a single composition. The size-dependent TPD measurements can only be explained by accounting for the ensemble of each cluster, rather than the global minima alone, as discussed above for Pt7,8 on Al2O3.49 Multiple cycles of TPD can assess the stability of the system over many cycles in a catalytic reaction, and this has played an important role in our investigation of changes to stability and selectivity as we dope Pt clusters with main group elements such as B,51 Si,55 Sn,52,56,106 and Ge.53,54 This is an indirect way to access ensembles in experiment, by explaining the behavior of the system as an ensemble effect.
There are more direct ways to access ensembles in catalysis, however. Ensemble-based spectroscopic techniques exist, such as X-ray absorption spectroscopy, X-ray photoelectron spectroscopy, X-ray scattering and IR-absorption spectroscopy. These techniques are versatile as they can be used either ex situ, to characterize as-prepared or post-catalysis samples, or used in situ/operando to probe dynamic changes in catalysts triggered by reaction conditions.107 They are considered ensemble techniques because their spectra contain signals that are both spatially and temporally averaged. This can give information about how ensembles change with time and reaction conditions, but makes it difficult to deconvolute the spectra of the individual components. For systems consisting of bulk-like mixtures, this can be determined with X-ray absorption near-edge spectroscopy (XANES), for instance, by taking pure bulk standards and performing linear combination fitting with those standards on the XANES of the mixed system, thereby determining which fraction can be attributed to what bulk material. However, this approach does not work on systems of sub-nano clusters: they deviate so much from bulk that no sensible information can be obtained. Thus, we globally optimize said sub-nano clusters and use their computed XANES spectra as standards.108,109 Further collaboration between experimental and computational researchers is required to improve the interpretability of XANES spectra of sub-nano clusters.
Localized microscopy techniques, such as TEM and STM, allow for atom-level resolution, in contrast to ensemble-averaged methods. These can provide images of clusters and show dynamic behavior, emphasizing that catalysis must be understood through the lens of multiple interconverting active sites. While these techniques are highly localized, and cannot provide whole-ensemble information to the same degree as X-ray-based techniques, we can get time-averaged information via dynamic behavior. TEM can show, for example, the isomerization of Pt4 clusters,110 emphasizing the importance of a dynamic ensemble when evaluating Pt4 clusters for catalysis. Furthermore, this dynamic behavior has been shown to couple to the catalytic reaction, such as the case of CO oxidation on CeO2-supported Pt NPs.28 Aberration corrections are required for optimal atomic resolution, especially for supports containing heavy atoms, with the use of in situ set-ups (environmental/electrochemical sample holder) and elemental mapping (EELS, EDS).2 Ultimately, ensembles can be probed through experiment in a number of ways, and theorists must embrace ensembles in order to provide meaningful interpretation of experimental results.
Conclusion and future prospects
We have described the ensemble paradigm of sub-nano catalysis, in which macroscopic chemical properties arise from individual clusters interconverting between isomeric states and outlined its consequences for activity and stability. Four classes of fluxionality have been defined in terms of potential energy surface topology, and their impact on ensemble size has been discussed. We have examined chemical and environmental factors which influence ensemble size including composition, adsorbates, and supports. By incorporating realistic reaction conditions into computational models, we can explore differences between ensembles and make predictions about catalytic reactivity.Tremendous progress has been made, but urgent and difficult questions remain. Deeper chemical insights into the factors influencing ensemble size and the nature of the ensemble states forming under reaction conditions will afford a better understanding of existing fluxional catalysts and accelerate discovery of catalysts in the future. In particular, the interaction between surface and catalyst is a promising focus of research for scientists approaching the topic from all directions. A shared aim for all researchers is the determination of chemical trends and the discovery of qualitative or quantitative descriptors of catalytic behavior, by which we can direct the search for new catalysts intelligently and reduce the need for costly and challenging investigations. Such descriptors may be derived from fundamentals, such as the bonding concepts discussed above, or phenomenologically, by careful examination of known and novel systems. In parallel, strategies for manipulation of ensembles must be developed, towards the goal of biasing ensembles in favor of isomers with desirable properties. This is exemplified by the serendipitous discovery of Pt4GeC2, a stable catalyst which forms from a Pt4Ge precursor under reaction conditions, so we should seek inspiration from it on our search for bespoke ensembles. Broad questions are still outstanding – when is the ideal catalyst a solo isomer, and when does harmonious fluxionality create catalytic activity? Also, how can we synthesize a catalyst that creates the desired catalytic states in abundance, under reaction conditions?
In conclusion, we must reiterate the absolute necessity of collaboration in this field. Fluxional catalytic ensembles are subtle, where small changes have big consequences, so chemical insight and technical expertise must bridge disciplinary boundaries if we are to understand their intricacies. The challenge is unquestionably worthwhile; catalysis touches every aspect of our lives, and further developments in tuning fluxionality-triggered ensembles could have far-reaching consequences.
Author contributions
Robert H. Lavroff: investigation, visualization, supervision, writing – original draft, writing – review & editing. Harry W. T. Morgan: investigation, visualization, writing – original draft, writing – review & editing. Zisheng Zhang: investigation, visualization, writing – original draft. Patricia Poths: investigation, visualization, writing – original draft. Anastassia N. Alexandrova: conceptualization, supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The funding for the works summarized in this article is from Air Force Office of Scientific Research grant AFOSR FA9550-19-1-0261, and the U.S. Department of Energy Office of Basic Sciences grants DE-SC0019152 and DE-SC0020125.References
- K. F. Kalz, R. Kraehnert, M. Dvoyashkin, R. Dittmeyer, R. Gläser, U. Krewer, K. Reuter and J. D. Grunwaldt, ChemCatChem, 2017, 9(1), 17–29 CrossRef CAS PubMed.
- A. Beck, X. Huang, L. Artiglia, M. Zabilskiy, X. Wang, P. Rzepka, D. Palagin, M. G. Willinger and J. A. van Bokhoven, Nat. Commun., 2020, 11(1), 3220 CrossRef CAS.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53(2), 447–458 CrossRef CAS PubMed.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7(3), 1905–1911 CrossRef CAS.
- J. C. Liu, X. L. Ma, Y. Li, Y. G. Wang, H. Xiao and J. Li, Nat. Commun., 2018, 9, 1610, DOI:10.1038/s41467-018-03795-8.
- X. L. Ma, J. C. Liu, H. Xiao and J. Li, J. Am. Chem. Soc., 2018, 140, 46–49 CrossRef CAS PubMed.
- C. C. Hou, H. F. Wang, C. Li, Q. Xu, Q. Xu and Q. Xu, Energy Environ. Sci., 2020, 13, 1658–1693 RSC.
- C. Yao, N. Guo, S. Xi, C. Q. Xu, W. Liu, X. Zhao, J. Li, H. Fang, J. Su, Z. Chen, H. Yan, Z. Qiu, P. Lyu, C. Chen, H. Xu, X. Peng, X. Li, B. Liu, C. Su, S. J. Pennycook, C. J. Sun, J. Li, C. Zhang, Y. Du and J. Lu, Nat. Commun., 2020, 11, 4389 CrossRef CAS PubMed.
- P. Grosse, D. Gao, F. Scholten, I. Sinev, H. Mistry and B. Roldan Cuenya, Angew. Chem., 2018, 57, 6192–6197 CrossRef CAS.
- F. Dattila, R. Garclá-Muelas and N. López, ACS Energy Lett., 2020, 5, 3176–3184 CrossRef CAS.
- J. M. Venegas, Z. Zhang, T. O. Agbi, W. P. McDermott, A. Alexandrova and I. Hermans, Angew. Chem., Int. Ed., 2020, 14, 16527–16535 CrossRef PubMed.
- Y. Li, M. Kottwitz, J. L. Vincent, M. J. Enright, Z. Liu, L. Zhang, J. Huang, S. D. Senanayake, W. C. D. Yang, P. A. Crozier, R. G. Nuzzo and A. I. Frenkel, Nat. Commun., 2021, 12(1), 914 CrossRef CAS.
- S. Vajda, M. J. Pellin, J. P. Greeley, C. L. Marshall, L. A. Curtiss, G. A. Ballentine, J. W. Elam, S. Catillon-Mucherie, P. C. Redfern, F. Mehmood and P. Zapol, Nat. Mater., 2009, 8, 213–216 CrossRef CAS PubMed.
- O. A. Bariås, A. Holmen and E. A. Blekkan, J. Catal., 1996, 158, 1–12 CrossRef.
- M. Santhosh Kumar, D. Chen, A. Holmen and J. C. Walmsley, Catal. Today, 2009, 142, 17–23 CrossRef CAS.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38(4), 762–785 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1919, 41(6), 868–934 CrossRef CAS.
- K. Wade, J. Chem. Soc. D, 1971, 15, 792–793 RSC.
- D. M. P. Mingos, Nature (London), Phys. Sci., 1972, 236, 99–102 CrossRef CAS.
- N. Watari and S. Ohnishi, J. Chem. Phys., 1997, 106, 7531 CrossRef CAS.
- E. Roduner, C. Jensen, J. Vanslageren, R. A. Rakoczy, O. Larlus and M. Hunger, Angew. Chem., Int. Ed., 2014, 53(17), 4318–4321 CrossRef CAS PubMed.
- T. Imaoka, H. Kitazawa, W. J. Chun, S. Omura, K. Albrecht and K. Yamamoto, J. Am. Chem. Soc., 2013, 135(35), 13089–13095 CrossRef CAS PubMed.
- Z. Zhang, Z. H. Cui, E. Jimenez-Izal, P. Sautet and A. N. Alexandrova, ACS Catal., 2020, 10(23), 13867–13877 CrossRef CAS.
- D. M. P. Mingos, Dalton Trans., 2015, 44, 6680–6695 RSC.
- H. Zhai and A. N. Alexandrova, J. Phys. Chem. Lett., 2018, 9, 1696–1702 CrossRef CAS.
- Z. Zhang, E. Jimenez-Izal, I. Hermans and A. N. Alexandrova, J. Phys. Chem. Lett., 2019, 10, 20–25 CrossRef CAS PubMed.
- X. Xing, X. Li, B. Yoon, U. Landman and J. H. Parks, Int. J. Mass Spectrom., 2015, 377, 393–402 CrossRef CAS.
- J. L. Vincent and P. A. Crozier, Nat. Commun., 2021, 12, 5789 CrossRef CAS PubMed.
- P. L. Hansen, J. B. Wagner, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen and H. Topsøe, Science, 2002, 295, 2053–2055 CrossRef CAS PubMed.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, 2007 Search PubMed.
- S. Arlow, Own work, 2011 Search PubMed.
- G. Sun and P. Sautet, Acc. Chem. Res., 2021, 54, 4595 CrossRef CAS PubMed.
- G. Sun, A. N. Alexandrova and P. Sautet, J. Chem. Phys., 2019, 151, 194703 CrossRef PubMed.
- H. Zhai, P. Sautet and A. N. Alexandrova, ChemCatChem, 2020, 12, 762–770 CrossRef CAS.
- G. Sun and P. Sautet, J. Am. Chem. Soc., 2018, 140, 2812–2820 CrossRef CAS.
- G.-J. Xia and Y.-G. Wang, J. Catal., 2021, 404, 537–550 CrossRef CAS.
- M. C. O. Monteiro, F. Dattila, N. López and M. T. M. Koper, J. Am. Chem. Soc., 2022, 144(4), 1589–1602 CrossRef CAS PubMed.
- S. Ringe, E. L. Clark, J. Resasco, A. Walton, B. Seger, A. T. Bell and K. Chan, Energy Environ. Sci., 2019, 12, 3001–3014 RSC.
- B. Huang, R. R. Rao, S. You, K. Hpone Myint, Y. Song, Y. Wang, W. Ding, L. Giordano, Y. Zhang and T. Wang, JACS Au, 2021, 1, 1674–1687 CrossRef CAS.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 16105 CrossRef CAS PubMed.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- A. J. Medford, A. C. Lausche, F. Abild-Pedersen, B. Temel, N. C. Schjødt, J. K. Nørskov and F. Studt, Top. Catal., 2014, 57, 135–142 CrossRef CAS.
- J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- Z. Zhang, B. Zandkarimi, J. Munarriz, C. E. Dickerson and A. N. Alexandrova, ChemCatChem, 2022, e20220345 Search PubMed.
- U. Heiz, A. Sanchez, S. Abbet and W.-D. Schneider, J. Am. Chem. Soc., 1999, 121, 3214–3217 CrossRef CAS.
- A. von Weber, E. T. Baxter, S. Proch, M. D. Kane, M. Rosenfelder, H. S. White and S. L. Anderson, Phys. Chem. Chem. Phys., 2015, 17, 17601–17610 RSC.
- E. T. Baxter, M.-A. Ha, A. C. Cass, A. N. Alexandrova and S. L. Anderson, ACS Catal., 2017, 7, 3322–3335 CrossRef CAS.
- E. T. Baxter, M.-A. Ha, A. C. Cass, H. Zhai, A. N. Alexandrova and S. L. Anderson, J. Phys. Chem. C, 2018, 122, 1631–1644 CrossRef CAS.
- M. A. Ha, E. T. Baxter, A. C. Cass, S. L. Anderson and A. N. Alexandrova, J. Am. Chem. Soc., 2017, 139, 11568–11575 CrossRef CAS PubMed.
- B. Zandkarimi, T. J. Gorey, G. Li, J. Munarriz, S. L. Anderson and A. N. Alexandrova, Chem. Mater., 2020, 32, 8595–8605 CrossRef CAS.
- G. Li, P. Poths, T. Masubuchi, H. W. T. Morgan, A. N. Alexandrova and S. L. Anderson, ArXiv: chemrxiv-2022-l10k7, 1–32.
- E. Jimenez-Izal, J. Y. Liu and A. N. Alexandrova, J. Catal., 2019, 374, 93–100 CrossRef CAS.
- E. Jimenez-Izal, H. Zhai, J.-Y. Liu and A. N. Alexandrova, ACS Catal., 2018, 8, 8346–8356 CrossRef CAS.
- T. J. Gorey, B. Zandkarimi, G. Li, E. T. Baxter, A. N. Alexandrova and S. L. Anderson, ACS Catal., 2020, 10, 4543–4558 CrossRef CAS.
- A. F. Carlsson and R. J. Madix, J. Chem. Phys., 2001, 115, 8074–8082 CrossRef CAS.
- M. Neurock and R. A. van Santen, J. Phys. Chem. B, 2000, 104, 11127–11145 CrossRef CAS.
- L. O. Paz-Borbón, A. Hellman, J. M. Thomas and H. Grönbeck, Phys. Chem. Chem. Phys., 2013, 15, 9694–9700 RSC.
- J. Stöhr, F. Sette and A. L. Johnson, Phys. Rev. Lett., 1984, 53, 1684 CrossRef.
- T. Imaoka, T. Toyonaga, M. Morita, N. Haruta and K. Yamamoto, Chem. Commun., 2019, 55, 4753–4756 RSC.
- J.-C. Liu, H. Xiao and J. Li, J. Am. Chem. Soc., 2020, 142, 3375–3383 CrossRef CAS PubMed.
- S. Monti, G. Barcaro, W. A. Goddard III and A. Fortunelli, ACS Nano, 2021, 15, 6369–6385 CrossRef CAS PubMed.
- A. Marikutsa, M. Rumyantseva, E. A. Konstantinova and A. Gaskov, Sensors, 2021, 21, 2554 CrossRef CAS PubMed.
- Z. Wu, L. Huang, H. Liu, M. Li and H. Wang, Nano Res., 2021, 14, 2264–2267 CrossRef CAS.
- H. Wu and L. F. Liotta, RSC Catalysis Series, 2014 Search PubMed.
- F. M. Pinto, V. Y. Suzuki, R. C. Silva and F. A. la Porta, Front. Mater., 2019, 6 DOI:10.3389/fmats.2019.00260.
- A. Beniya, S. Higashi, N. Ohba, R. Jinnouchi, H. Hirata and Y. Watanabe, Nat. Commun., 2020, 11, 1888 CrossRef CAS PubMed.
- S. Jin, H. Byun and C. H. Lee, J. Catal., 2021, 400, 195–211 CrossRef CAS.
- A. R. Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7(10), 6493–6513 CrossRef.
- Y. G. Wang, Y. Yoon, V. A. Glezakou, J. Li and R. Rousseau, J. Am. Chem. Soc., 2013, 135(29), 10673–10683 CrossRef CAS.
- F. R. Negreiros, M. F. Camellone and S. Fabris, J. Phys. Chem. C, 2015, 119(37), 21567–21573 CrossRef CAS.
- M. W. Chang, L. Zhang, M. Davids, I. A. W. Filot and E. J. M. Hensen, J. Catal., 2020, 392, 39–47 CrossRef CAS.
- Y. Q. Su, G. J. Xia, Y. Qin, S. Ding and Y. G. Wang, Chem. Sci., 2021, 12, 8260–8267 RSC.
- J. A. Rodríguez and J. Hrbek, Surf. Sci., 2010, 604, 241–244 CrossRef.
- R. M. Palomino, P. J. Ramírez, Z. Liu, R. Hamlyn, I. Waluyo, M. Mahapatra, I. Orozco, A. Hunt, J. P. Simonovis, S. D. Senanayake and J. A. Rodriguez, J. Phys. Chem. B, 2018, 122(2), 794–800 CrossRef PubMed.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355(6331), 1296–1299 CrossRef CAS PubMed.
- Y. Ma, J. Wang, K. R. Goodman, A. R. Head, X. Tong, D. J. Stacchiola and M. G. White, J. Phys. Chem. C, 2020, 124(40), 22158–22172 CrossRef CAS.
- J. A. Rodriguez, J. Graciani, J. Evans, J. B. Park, F. Yang, D. Stacchiola, S. D. Senanayake, S. Ma, M. Perez, P. Liu, J. F. Sanz and J. Hrbek, Angew. Chem., Int. Ed., 2009, 48(43), 8047–8050 CrossRef CAS PubMed.
- J. A. Rodriguez, S. Ma, P. Liu, J. Hrbek, J. Evans and M. Pérez, Science, 2007, 318(5857), 1757–1760 CrossRef CAS PubMed.
- F. Yang, J. Graciani, J. Evans, P. Liu, J. Hrbek, J. F. Sanz and J. A. Rodriguez, J. Am. Chem. Soc., 2011, 133(10), 3444–3451 CrossRef CAS PubMed.
- Y. Yang, J. Zhou, M. Nakayama, L. Nie, P. Liu and M. G. White, J. Phys. Chem. C, 2014, 118(25), 13697–13706 CrossRef CAS.
- R. Zhang, M. Athariboroujeny, G. Collinge, V. Iablokov, K. D. Shumilov, L. Kovarik, A. N. Alexandrova, N. Kruse and J. S. McEwen, ACS Catal., 2020, 10(24), 14722–14731 CrossRef CAS.
- W. J. Chen, H. J. Zhai, Y. F. Zhang, X. Huang and L. S. Wang, J. Phys. Chem. A, 2010, 114(19), 5958–5966 CrossRef CAS PubMed.
- S. Ganguly, M. Kabir, C. Autieri and B. Sanyal, J. Phys.: Condens. Matter, 2015, 27(5), 056002 CrossRef CAS PubMed.
- S. Li and D. A. Dixon, J. Phys. Chem. A, 2010, 114(7), 2665–2683 CrossRef CAS PubMed.
- S. Hamad, C. R. A. Catlow, S. M. Woodley, S. Lago and J. A. Mejías, J. Phys. Chem. B, 2005, 109(33), 15741–15748 CrossRef CAS PubMed.
- K. R. Goodman, J. Wang, Y. Ma, X. Tong, D. J. Stacchiola and M. G. White, J. Chem. Phys., 2020, 152, 054714 CrossRef CAS PubMed.
- M. Xue, M. Nakayama, P. Liu and M. G. White, J. Phys. Chem. C, 2017, 121(40), 22234–22247 CrossRef CAS.
- B. Zandkarimi, P. Poths and A. N. Alexandrova, Angew. Chem., 2021, 90095, 11973–11982 CrossRef PubMed.
- Q. Tong, J. Lv, P. Gao and Y. Wang, Chin. Phys. B, 2019, 28, 106105 CrossRef CAS.
- G. Avendaño-Franco and A. H. Romero, J. Chem. Theory Comput., 2016, 12(7), 3416–3428 CrossRef PubMed.
- S. T. Call, D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28(7), 1177–1186 CrossRef CAS PubMed.
- C. J. Pickard and R. J. Needs, Phys. Status Solidi B, 2009, 246(3), 536–540 CrossRef CAS.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288, DOI:10.1103/PhysRevLett.75.288.
- J. B. A. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, Nanoscale, 2015, 7, 14032–14038 RSC.
- R. P. F. Kanters and K. J. Donald, J. Chem. Theory Comput., 2014, 10(12), 5729–5737 CrossRef CAS PubMed.
- A. N. Alexandrova and A. I. Boldyrev, J. Chem. Theory Comput., 2005, 1(4), 566–580 CrossRef CAS PubMed.
- A. N. Alexandrova, J. Phys. Chem. A, 2010, 114(48), 12591–12599 CrossRef CAS PubMed.
- H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731 CrossRef CAS PubMed.
- A. R. Oganov, Modern Methods of Crystal Structure Prediction, 2010 Search PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101(28), 5111–5116 CrossRef CAS.
- J. Wang, L. Ma, J. Zhao and K. A. Jackson, J. Chem. Phys., 2009, 130, 214307 CrossRef PubMed.
- V. Sumaria and P. Sautet, Chem. Sci., 2021, 12, 15543–15555 RSC.
- G. Li, B. Zandkarimi, A. C. Cass, T. J. Gorey, B. J. Allen, A. N. Alexandrova and S. L. Anderson, J. Chem. Phys., 2020, 152, 024702 CrossRef CAS PubMed.
- A. Bergmann and B. Roldan Cuenya, ACS Catal., 2019, 9, 10020–10043 CrossRef CAS.
- B. Zandkarimi, G. Sun, A. Halder, S. Seifert, S. Vajda, P. Sautet and A. N. Alexandrova, J. Phys. Chem. C, 2020, 124, 10057–10066 CrossRef CAS.
- P. Poths, G. Sun, P. Sautet and A. N. Alexandrova, J. Phys. Chem. C, 2022, 1972–1981 CrossRef CAS.
- T. Imaoka, T. Toyonaga, M. Morita, N. Haruta and K. Yamamoto, Chem. Commun., 2019, 55, 4753–4756 RSC.
| This journal is © The Royal Society of Chemistry 2022 |