Open Access Article
Open Access ArticleMechanical compression in cofacial porphyrin cyclophane pincers†
Chunwei
Hsu‡
 a,
Werner M.
Schosser‡
a,
Werner M.
Schosser‡
 b,
Patrick
Zwick‡
b,
Patrick
Zwick‡
 c,
Diana
Dulić
c,
Diana
Dulić
 d,
Marcel
Mayor
d,
Marcel
Mayor
 *cef,
Fabian
Pauly
*cef,
Fabian
Pauly
 *b and
Herre S. J.
van der Zant
*b and
Herre S. J.
van der Zant
 *a
*a
aKavli Institute of Nanoscience, Delft University of Technology, Lorentzweg 1, Delft 2628 CJ, The Netherlands. E-mail: h.s.j.vanderzant@tudelft.nl
bInstitute of Physics, University of Augsburg, 86135 Augsburg, Germany. E-mail: fabian.pauly@uni-a.de
cDepartment of Chemistry, University of Basel, St. Johanns-Ring 19, 4056 Basel, Switzerland. E-mail: marcel.mayor@unibas.ch
dDepartment of Physics, Department of Electrical Engineering, Faculty of Physical and Mathematical Sciences, University of Chile, Avenida Blanco Encalada 2008, Santiago 8330015, Chile
eInstitute for Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), P. O. Box 3640, 76021 Karlsruhe, Germany
fLehn Institute of Functional Materials (LIFM), School of Chemistry, Sun Yat-Sen University (SYSU), 510275 Guangzhou, China
First published on 13th June 2022
Abstract
Intra- and intermolecular interactions are dominating chemical processes, and their concerted interplay enables complex nonequilibrium states like life. While the responsible basic forces are typically investigated spectroscopically, a conductance measurement to probe and control these interactions in a single molecule far out of equilibrium is reported here. Specifically, by separating macroscopic metal electrodes, two π-conjugated, bridge-connected porphyrin decks are peeled off on one side, but compressed on the other side due to the covalent mechanical fixation. We observe that the conductance response shows an exceptional exponential rise by two orders of magnitude in individual breaking events during the stretching. Theoretical studies atomistically explain the measured conductance behavior by a mechanically activated increase in through-bond transport and a simultaneous strengthening of through-space coupling. Our results not only reveal the various interacting intramolecular transport channels in a molecular set of levers, but also the molecules' potential to serve as molecular electro-mechanical sensors and switches.
Introduction
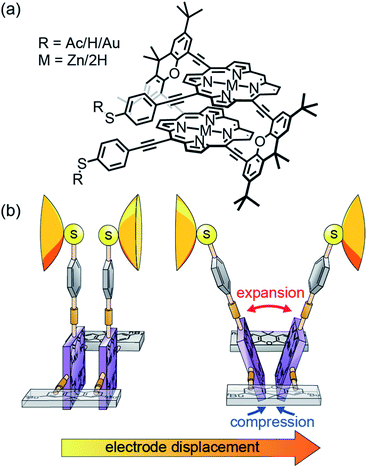
In recent years it has been demonstrated that by stretching molecular junctions, their conductance can change from a few times to even a few orders of magnitude.1–18 This mechanosensitivity is interpreted either as arising from mechanical manipulation of the molecule–electrode contact or from mechanically triggered structural variations of the integrated molecule. The origin, however, is not always clear. For example, the mechanosensitivity in ferrocene derivatives has been attributed to both redox activity1 and destructive quantum interference.2 Other examples are conductance measurements of thiophene based molecular rods and a benzil derivative.3,4 While both exhibit a very similar two order-of-magnitude conductance change, the former has been explained by hemilabile ligands,4 the latter as the folding of the 1,2-dione subunit.3 A well-controlled and careful study of single-molecule mechanosensitivity is thus key to gain insights into inter- and intramolecular transport phenomena and the related interactions. This requires a molecular design tailoring either the flexibility of the molecular subunit arrangement or the structural configuration in the molecular junction. For instance, the overlap of molecular orbitals can be controlled mechanically either via changing the relative position or the angle between π-orbitals.10,12–14,18 The underlying changes in transport mechanisms, resulting from quantum interference10,12,13,18 and the size of tunnel couplings,14 are revealed by single-molecule measurements.To explore the interplay between through-bond and through-space intramolecular transport pathways under nonequilibrium conditions, we have created porphyrin cyclophanes as mechanosensitive model compounds.19 From the perspective of molecular design, these porphyrin cyclophanes are particularly attractive because of the extended π-orbital system with the possibility of further tuning the building blocks' physicochemical properties, e.g. by coordinating different metals.20
In the model compounds 2HPC2 and ZnPC2 studied here, two porphyrin planes are cofacially arranged in a three-dimensional cyclophane architecture (see Fig. 1a). While a pair of rigid xanthene bridges separates the two porphyrin planes, these subunits are interconnected by acetylenes as revolving joints. This combination of planar rigid building blocks and revolving linkers provides the intended mechanosensitivity. Both porphyrin decks are further expanded on the same side of the cyclophane, laterally to the bridge, with rigid-rod type phenylacetylenes, exposing each a thioacetate as the anchoring group. The nature and the position of the terminal acetyl-masked thiol anchoring groups are of particular importance for the experiments reported in this paper, as the thiol–gold bonds formed upon deprotection are robust enough to allow substantial mechanical manipulation of the immobilized compound. When the molecule is embedded in a mechanically controlled break junction (MCBJ), pulling on the anchoring groups triggers the rotation of both porphyrin planes around aforementioned revolving acetylene joints. In this mechanically controlled process, the porphyrin planes are turned out of their cofacial orientation and, like operating a pair of pincers, the decks are separated in the part above the bridges, while the inter-plane distance below the bridges is decreased (see Fig. 1b). This change is reflected in the breaking traces by a unique conductance upturn, reaching up to two orders of magnitude. We explain the related changes in transport pathways through detailed atomistic calculations.
Results & discussion
Single-molecule characterization
The ZnPC2 molecule studied in this manuscript, see Fig. 1a, is synthesized following a reported protocol, and its identity is corroborated by a complete characterization including the solid-state structure of a derivate.19 To characterize its mechanosensitive response, we use the MCBJ technique to perform single-molecule conductance measurements as a function of electrode displacement under dark ambient conditions. A schematic of a MCBJ sample and details of the MCBJ technique can be found in SI.1.1† and in previous reports.21,22 First, to examine the possibility to integrate ZnPC2 into a single-molecule junction and characterize its single-molecule conductance, we perform fast-breaking experiments (see Methods). Data of the fast-breaking measurements with ZnPC2, comprising 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive traces, is presented in a two-dimensional (2D) density plot of conductance versus electrode displacement in Fig. 2a, at a bias voltage of V = 250 mV. Additional fast-breaking results at V = 100 mV or without zinc in the porphyrin centers can be found in SI.1.2 and SI.1.4.† In Fig. 2a we observe two main signatures. First, the conductance decreases as a function of displacement, representing the gold-to-gold direct tunneling transport (region I). Second, a broad plateau with a length of around 2.8 nm appears at conductance values between 10−5G0 and 10−6G0 (region II), where G0 = 2e2/h is the conductance quantum, e is the electron charge and h is the Planck constant. For further study of the molecular traces, we use a reference-free clustering algorithm to filter out the gold-to-gold direct tunneling traces, yielding the density plot shown in Fig. 2b (ref. 23) and the remainder classes, discussed in SI.1.3.†
000 consecutive traces, is presented in a two-dimensional (2D) density plot of conductance versus electrode displacement in Fig. 2a, at a bias voltage of V = 250 mV. Additional fast-breaking results at V = 100 mV or without zinc in the porphyrin centers can be found in SI.1.2 and SI.1.4.† In Fig. 2a we observe two main signatures. First, the conductance decreases as a function of displacement, representing the gold-to-gold direct tunneling transport (region I). Second, a broad plateau with a length of around 2.8 nm appears at conductance values between 10−5G0 and 10−6G0 (region II), where G0 = 2e2/h is the conductance quantum, e is the electron charge and h is the Planck constant. For further study of the molecular traces, we use a reference-free clustering algorithm to filter out the gold-to-gold direct tunneling traces, yielding the density plot shown in Fig. 2b (ref. 23) and the remainder classes, discussed in SI.1.3.†
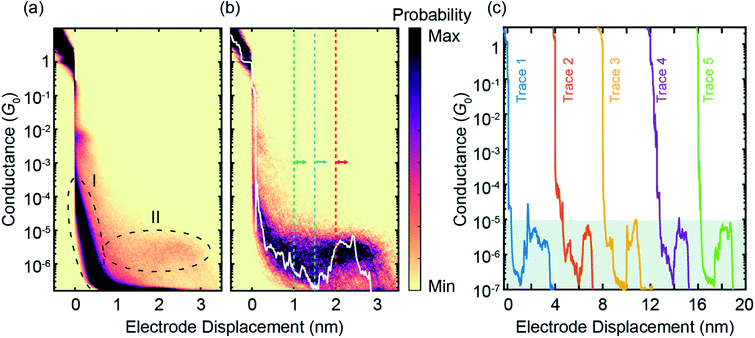 | ||
Fig. 2 (a), Raw data of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive fast-breaking traces, illustrated in a 2D density plot of conductance versus electrode displacement. (b) Same as panel (a) but for 596 molecular traces, corresponding to around 6% of all junctions formed, where pure tunneling traces without molecular conductance signatures are filtered out by a reference-free clustering method23 (see also Fig. S4†). A representative individual breaking trace (white) is plotted, illustrating features visible in the 2D plot. A characteristic rise in the conductance as a function of electrode displacement can be observed after around 1.5 nm. The dashed lines indicate the initial positions of the modulation experiments discussed later. (c), Examples of individual fast-breaking traces. The traces are horizontally offset by 4 nm for clarity. Traces feature a clear conductance increase after a steep initial drop. This conductance increase reaches two orders of magnitude, from G = 10−7G0 to 10−5G0 (shaded in green). 000 consecutive fast-breaking traces, illustrated in a 2D density plot of conductance versus electrode displacement. (b) Same as panel (a) but for 596 molecular traces, corresponding to around 6% of all junctions formed, where pure tunneling traces without molecular conductance signatures are filtered out by a reference-free clustering method23 (see also Fig. S4†). A representative individual breaking trace (white) is plotted, illustrating features visible in the 2D plot. A characteristic rise in the conductance as a function of electrode displacement can be observed after around 1.5 nm. The dashed lines indicate the initial positions of the modulation experiments discussed later. (c), Examples of individual fast-breaking traces. The traces are horizontally offset by 4 nm for clarity. Traces feature a clear conductance increase after a steep initial drop. This conductance increase reaches two orders of magnitude, from G = 10−7G0 to 10−5G0 (shaded in green). | ||
The extracted molecular traces show a minimum in conductance at an electrode displacement of around 1.5 nm, a subsequent rise and a shorter plateau with a length of 1 nm. These features are robust over many junction configurations, as no further data selection has been applied, and they are evident in the representative individual traces shown in Fig. 2c. From the minimum to the subsequent plateau, the conductance increase may amount up to two orders of magnitude in individual breaking events, rivaling the highest switching factor reported for single-molecule junctions of ortho-pentaphenylene foldamers.14 It is worth noting that a conductance increase upon electrode separation has only been documented in a few reports.8,9,11,24 Generally, they show conductance enhancement by less than a factor of 10. Particularly in the cases of germanium and silicon molecular wires, it is a contact effect rather than an intrinsic molecular feature.8,9 This conductance upturn is distinct from the conductance decrease upon electrode separation in ortho-pentaphenylene and other single molecules with large mechanosensitivity studied so far.6,7,14 Evidently, the conductance increase with increasing electrode spacing excludes an explanation involving direct tunneling transport but necessitates transport mechanisms sensing complex rearrangements inside the molecular structure.
To further quantify the conductance response of the single-molecule junctions, we perform electrode displacement modulation experiments. In the modulation measurement (see also Methods), we modulate the electrode separation with an amplitude of 2.5 Å at different initial electrode displacements, sampling different regions of a molecular breaking trace. After collecting thousands of these modulation traces for the ZnPC2 molecule at different initial displacements, we analyze the gauge factor (GF) to quantify the conductance variations. In the GF analysis we apply a Fourier transform on the conductance data, which specifies both the magnitude and complex phase of a conductance change for a corresponding change in electrode displacement, see SI.1.5† for more details. For example, a molecular junction with a large in-phase conductance modulation, i.e., an increase of conductance with increasing electrode displacement, is characterized by a large positive GF. Based on the conductance-displacement traces in Fig. 2b, we expect the size and sign of the GF to depend on the initial displacement.
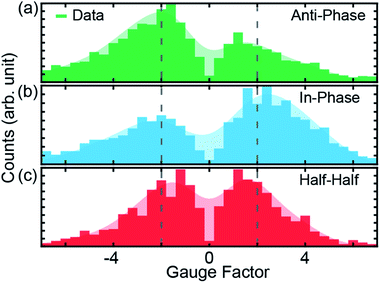 | ||
| Fig. 3 (a–c), Gauge factors for the different initial electrode displacements, indicated in Fig. 2b by dashed colored lines. The starting positions for modulations are 1.0, 1.5 and 2.0 nm for (a), (b) and (c), respectively. In all cases, the modulation amplitude is 2.5 Å at a frequency of 5 Hz, applied for a duration of 15 s. The shaded areas represent the smoothed distribution, from which the peak positions are determined. Dotted vertical lines indicate |GF| = 2. | ||
GFs of the modulation experiments with initial electrode displacements of 1.0, 1.5 and 2.0 nm, indicated by the green, blue and red dotted vertical lines in Fig. 2b, are displayed in Fig. 3. Notably, each initial electrode displacement corresponds to a different prevalent phase relation in the GF. In the case of an initial electrode displacement of 1.0 nm we observe more anti-phase (negative) GFs. This means that the conductance statistically decreases when the molecular junction is opened, in agreement with the negative slope observed in Fig. 2b. Similarly, when in-phase behavior (positive GF) predominates at an initial displacement of 1.5 nm, molecular conductance essentially increases with increasing electrode separation, corresponding to the upturn in conductance. For the modulation starting in the flat region at 2.0 nm, we find that the GF exhibits an equal weight between anti-phase and in-phase behaviors. We classify this situation as “half–half”. When considering the peak positions of GF distributions, we observe that 2 > |GF| ≳ 1 for the conductance plateau, i.e. GFs are smaller as compared to the previous two cases, for which |GF| ≳ 2. We note that there are statistical variations in the GF histograms as there are many possible junction configurations for the molecule. By taking a large set of modulation measurements without data selection, GFs at different initial displacements demonstrate statistically the conductance features of ZnPC2, revealing the exponential conductance decay, increase and plateau.
DFT and transport analysis
To understand the underlying transport mechanisms of the observed conductance changes during stretching, we model geometries of ZnPC2 single-molecule junctions during the unfolding process and describe the related electronic transport as phase-coherent and elastic in terms of the Landauer scattering theory.25 We compute the conductance at room temperature via the linear response expression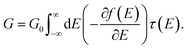 | (1) |
We obtain junction geometries from DFT through energy optimization as follows: First, the isolated ZnPC2 molecule, see Fig. 1a, is optimized in the gas phase. Second, the molecule is placed between two Au20 clusters, see Fig. 4, forming the extended central cluster of the molecular junction.26 In this step, the molecule and the four gold atoms of the two innermost layers of each gold pyramid closest to the molecule are optimized, while other gold atoms in the two outermost layers of each metal cluster are kept fixed in a face-centered cubic bulk lattice configuration, see Fig. 4a. Third, the stretching process is started from the initial geometry and continued until the point of rupture. During the process the two outermost fixed layers of the gold clusters are separated in steps of 0.1 Å, and the geometry is optimized in each step in the same way, as described before under point two. This yields the simulated junction geometries that are visualized via snapshots at various electrode displacements, d, in Fig. 4.
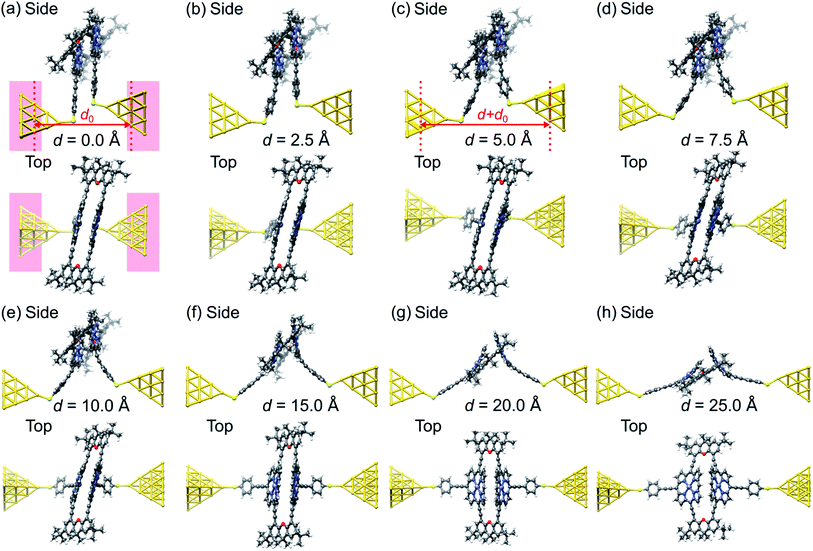 | ||
| Fig. 4 (a–h), Geometries obtained for a simulated unfolding process of a ZnPC2 single-molecule junction. The junction geometries are shown in side and top views at various displacements d of the gold electrodes. The displacement d is defined as the horizontal shift between the fixed layers of the gold electrodes with respect to their initial separation d0, see panels (a) and (c). For d = 0 Å the red background indicates, which atoms of the extended central cluster are kept fixed, while the rest is optimized. Panels (a) and (b) belong to geometries in region (i), (c) and (d) to region (ii), (e) and (f) to region (iii), and (f)–(h) to region (iv), as defined in Fig. 5. | ||
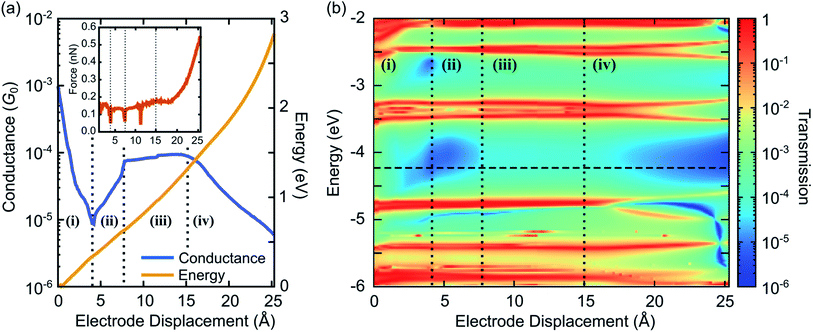
We calculate the transmission τ(E) and the conductance G at T = 300 K from eqn (1), using the electronic structure of the obtained geometries. Fig. 5 characterizes electrical and mechanical properties of the simulated ZnPC2 single-molecule junction. Fig. 5a visualizes the conductance G and the total DFT energy of the system in dependence on the electrode displacement d. The conductance behavior can be divided into four regions: (i) exponential decrease from G = 10−3G0 to 6 × 10−6G0 for d = 0 Å to 4.4 Å, (ii) exponential increase from 6 × 10−6G0 to 8 × 10−5G0, by more than one order of magnitude, for 4.4 Å to 7.8 Å, (iii) plateau from 8 × 10−5G0 to 9 × 10−5G0 for 7.8 Å to 15 Å, (iv) exponential decrease from 9 × 10−5G0 to 5 × 10−6G0 for 15 Å to the point of rupture at 25.3 Å. Throughout the unfolding process the total energy rises rather monotonically. Taking the derivative of the total DFT energy with respect to the electrode displacement yields the tensile force, shown in the inset of Fig. 5a. The force is rather constant in regions (i)–(iii), while it increases sharply towards the end in region (iv), where the molecule is far away from its equilibrium configuration. At the point of rupture, the force amounts to 0.57 nN.
For a better understanding of electronic transport, the energy- and distance-dependent transmission of the molecular junction is displayed in Fig. 5b. Vertical dashed lines separate the four conductance regions, introduced in Fig. 5a. Transmission values are relatively high for small electrode displacements around d = 0 Å at all energies inside the HOMO–LUMO gap, which is located between the horizontal red resonance lines of frontier orbitals at about −4.7 eV and −3.8 eV. Interestingly, a blue area of suppressed transmission is visible that extends between regions (i) and (ii), while the transmission is comparatively high at all energies inside the HOMO–LUMO gap in region (iii). The transmission finally decays in region (iv). This plot shows that the overall conductance behavior of Fig. 5a is expected to be robust, since even for other choices of Fermi energies or level alignments, i.e., a constant shift of molecular and metallic levels, a similar conductance behavior is expected. Remarkably, the theoretically predicted behavior with the four regions (i)–(iv) agrees well with the experimental observations reported in Fig. 2 of a fast conductance decay, revival, plateau and final decay.
Let us now relate the different conductance regions of Fig. 5 to the complex atomic motion inside the junction, shown in Fig. 4. For this purpose we provide additional information in SI.2.1,† including transmissions as a function of energy at different electrode displacements d, corresponding to vertical cuts in Fig. 5b, and an analysis of various intramolecular distance changes. Furthermore, a video in the ESI† establishes the link between the simultaneous evolution of conductance and junction geometry.
The fast initial conductance decay in region (i) arises from the separation of para-ethynylbenzenethiol linkers, see in particular the side views in Fig. 4a–c. This is accompanied by the decay of an energy independent background of the transmission inside the HOMO–LUMO gap, resulting from the removal of the direct through-space tunneling pathway.
Region (ii) is characterized by a constant position of transmission resonances, but a changing energetic broadening, while para-ethynybenzenethiols are separated further, see Fig. 4c and d. Region (ii) starts and ends with fast molecular reconfigurations, which lead to the dips in the tensile force in Fig. 5a at d = 4.4 Å and 7.8 Å. They originate from sudden rotations of the left and right anchoring benzene rings, which consecutively align favorably to the Au electrodes and to the porphyrin's π-system, as the bending of the porphyrin–acetylene–benzene connections increase, see SI.2.3.† We attribute the rising conductance to a combined effect of an increasing through-bond coupling within each deck and the strengthened through-space coupling between the decks. They result on the one hand from the alignment of the anchoring benzenes with the porphyrins and on the other hand from the simultaneous compression of the two porphyrins on the opposed side of the mechanically fixing xanthene bridges, while the porphyrin–porphyrin interaction area remains basically constant. Essentially, these mechanically induced reconfigurations make the conduction pathway through the porphyrin pincers the dominant one.
In region (iii), where energy–dependent transmission curves remain basically unchanged inside the HOMO–LUMO gap for different displacements d, porphyrins are peeled off. While the upper part of the porphyrin double decker is compressed, c.f. the side views in Fig. 4d–f, the lower part separates. These competing effects of separation and compression nearly compensate, leading to a weak growth of the conductance. A dip in the tensile force arises in the middle of region (iii) at d = 11.7 Å, when the porphyrins align rather abruptly to the pulling direction, while they are initially canted, see the top views in Fig. 4a–e in comparison to Fig. 4f. At this point, a small kink is visible in the conductance in Fig. 5a.
In region (iv) all such canting and twists inside the molecule are removed due to tensile stress. Further separation of the electrodes decreases the region of porphyrin–porphyrin overlap, leading to the collapse of the conduction pathway within the porphyrin pincers and a fast overall decay of the conductance. Ultimately, the pulling apart of the porphyrins is limited by the rigid xanthene bridges.
Fig. 6 visualizes the wave functions of the left-incoming transmission eigenchannels with the highest transmission at the Fermi energy for selected electrode separations d within each of the four regions (i)–(iv).27,28 We find that the wave functions of the eigenchannels in regions (i)–(iii), see Fig. 6a–c, spread over the whole molecule. Remarkably the direct tunneling from one para-ethynylbenzenethiol to the other is directly visible in region (i), see Fig. 6a. In region (iv) at d = 20 Å, see Fig. 6d, the weight of the wave function quickly decays along the molecule instead. Here, we find a high weight only on the porphyrin deck that is directly connected through a sulfur anchor to the left electrode, while the weight on the right molecular deck is substantially reduced. Since the π-orbitals of the porphyrins at d = 20 Å stand nearly perpendicular to each other and the wave function is no longer efficiently propagated through the xanthene linkers, the intramolecular electronic coupling is low.
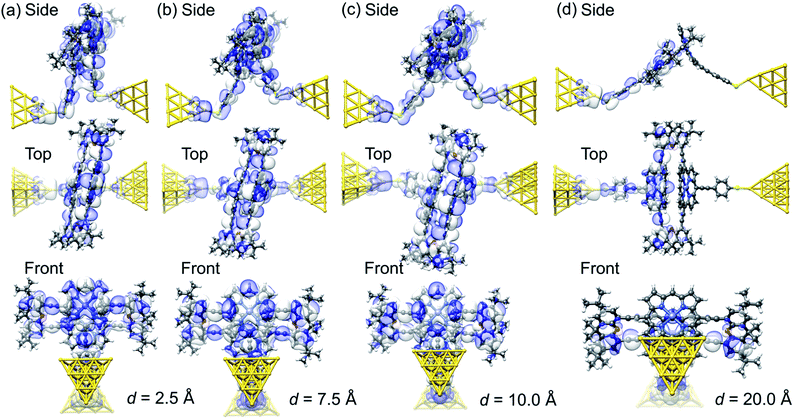 | ||
| Fig. 6 (a–d), Wave function of the most transparent left-incoming transmission eigenchannel in side, top and front views for several electrode displacements, d, as indicated below the panels. The transmission eigenchannels are evaluated at the Fermi energy EF. Panel (a) belongs to a geometry in region (i), (b) to region (ii), (c) to region (iii), and (d) to region (iv), as defined in Fig. 5. | ||
The above transmission calculations elucidate the four conductance regions as a result of changes in intramolecular conduction pathways. Initially the charge takes a shortcut via through-space tunneling, while it later on takes a much longer pathway through the porphyrin pincers, leading to the characteristic behavior of the conductance upturn upon electrode separation, plateau region and subsequent final decay. Two regions in the unfolding process are particularly interesting. One is related to the fast rotation of benzene rings and the other to the unfolding of porphyrin pincers, pivoting at the central xanthene bridges. The former suggests that by including components such as acetylenes in a molecular design, rotations under mechanical bending can act as a switch for through-space and through-bond conduction. The latter indicates that by changing the pivot points of a co-facial π-system with anchoring on the same sides, intramolecular interactions can be controlled, thereby serving as a starting point for more complex folded molecular origami designs.
Conclusions
We have presented a combined experimental and theoretical study of charge transport through a cofacial porphyrin cyclophane as a model compound representing molecular pincers. We have experimentally demonstrated a large mechanosensitivity of this molecule, exhibiting a conductance upturn by two orders of magnitude upon increasing distance between the electrodes in individual breaking traces. While separating the electrodes, four regions have been identified: (i) exponentially decreasing conductance, (ii) exponentially increasing conductance, (iii) constant conductance, and (iv) exponential decay before the contacts finally break. Compellingly, DFT-based calculations reproduce the four characteristic conductance regions during the molecular rearrangement in the junctions and rationalize the effects by atomistic simulations. We find that the conduction pathways are mechanically controlled as a result of a subtle balance between through-bond and through-space contributions in intramolecular transport. The study highlights the precise unfolding that metal electrodes can evoke on single molecules, bringing the molecular system out of its natural equilibrium. We are currently interested in tuning the extent of the different transport contributions by improved molecular designs. In particular, increased mechanosensitivity and analyte-mechanosensitive model compounds are crucial for a better understanding of molecular unfolding processes, paving the way to new sensing concepts relevant to biological systems or bioanalytics.Methods
MCBJ fast-breaking measurement
In the fast-breaking measurement, a constant DC bias voltage from 100 mV to 250 mV is applied across the junction and the current I is measured, which is subsequently converted into the electrical conductance G = I/V. While monitoring the electrical conductance, the gold junction is opened by bending the substrate. Once the gold metallic junction is broken, a molecule in the vicinity can bridge the gap, indicated by a conductance plateau corresponding to the molecular length. We repeat this cycle of breaking and forming gold junctions thousands of times to collect a statistically significant distribution of conductance-displacement curves.Electrode displacement modulation experiment
An electrode displacement modulation experiment starts by stretching the gold electrodes, until a conductance of 2G0 is reached. At this point the narrow metallic junction breaks by itself due to surface tension and thermally activated atomic motion.29 When the metallic wire is broken, the junction is further opened to a well-defined initial electrode displacement, and the gap size between the electrodes is modulated with an amplitude of 2.5 Å at a frequency of 5 Hz. The initial displacement determines, which part of the molecular breaking trace is sampled by the periodic modulation. The conductance of the junction is recorded during the modulation experiment over a time interval of 15 s. More details of the modulation experiment are described in ref. 12.DFT calculation
DFT calculations are performed with the quantum chemistry code TURBOMOLE,30 employing the def-SV(P) Gaussian basis set31 for all atoms, the PBE exchange-correlation functional32 and the DFT-D dispersion correction.33 Total energies are converged to an accuracy of better than 10−8 a.u., while geometries are optimized until the change of the maximum norm of the Cartesian gradient is below 10−5 a.u. The transport program34 used for computing the elastic transmission is custom-built and interfaced with TURBOMOLE. For evaluating the transmission function, we employ 32 × 32 transverse k-points to properly describe the semi-infinite gold electrodes. The DFT description of quasiparticle energies of molecular junctions is frequently improved by using the DFT+Σ method.35,36 In order to avoid such calculations for every stretching step, we apply this method only for a single representative junction geometry at an electrode displacement of 1.0 Å to correct the Fermi energy in the standard DFT calculations. In detail, we position the Fermi energy, EF, in the standard DFT calculations in a similar way as in the DFT+Σ calculations. For the junction with the correction applied, the Fermi energy of the gold electrodes is known to be located at EF,corr = −5.00 eV with respect to vacuum. The position of EF in the standard DFT calculations is then adjusted in such a way that the ratios of the differences of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energies, as indicated by the resonances in the corresponding transmission plots, to the respective Fermi energy are the same: (EF− EHOMO)/(ELUMO− EF) = (EF,corr− EHOMO,corr)/(ELUMO,corr− EF,corr). This procedure yields EF = −4.24 eV.Data availability
Experimental data for the main text is available online at https://doi.org/10.4121/20059988. Theoretical results are available upon reasonable request (F. P.). Any other supporting data can be made available upon request to the corresponding author.Author contributions
P. Z., D. D., H. S. J. v. d. Z. and M. M. conceived the project and the molecular design. C. H. performed the experimental single-molecule study and data analysis. W. M. S. carried out the DFT calculations and their analysis. P. Z. synthesized the studied molecules. H. S. J. v. d. Z., F. P. and M. M. supervised the project. All authors contributed to discussions and the writing of this manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
Part of this work was supported by the EU and FET open project QuIET (number 767187). H. S. J. v. d. Z. and C. H. acknowledge financial support through the Dutch Organisation for Scientific Research (NWO) (Grant ID: 680.92.18.01), while M. M. acknowledges the Swiss National Science Foundation (SNF grant number 200020-207744) and the 111 project (90002-18011002). D. D. thanks Fondecyt 1220984, Fondequip EQM140055 and EQM180009 for funding her research.Notes and references
- Y. Li, N. L. Haworth, L. Xiang, S. Ciampi, M. L. Coote and N. Tao, J. Am. Chem. Soc., 2017, 139, 14699–14706 CrossRef CAS PubMed.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. Inkpen, G. Lovat, E. D. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef.
- C. Wu, D. Bates, S. Sangtarash, N. Ferri, A. Thomas, S. J. Higgins, C. M. Robertson, R. J. Nichols, H. Sadeghi and A. Vezzoli, Nano Lett., 2020, 20, 7980–7986 CrossRef CAS PubMed.
- N. Ferri, N. Algethami, A. Vezzoli, S. Sangtarash, M. McLaughlin, H. Sadeghi, C. J. Lambert, R. J. Nichols and S. J. Higgins, Angew. Chem., Int. Ed., 2019, 58, 16583–16589 CrossRef CAS PubMed.
- S. Kobayashi, S. Kaneko, M. Kiguchi, K. Tsukagoshi and T. Nishino, J. Phys. Chem. Lett., 2020, 11, 6712–6717 CrossRef CAS.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- J. S. Meisner, M. Kamenetska, M. Krikorian, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nano Lett., 2011, 11, 1575–1579 CrossRef CAS PubMed.
- T. A. Su, H. Li, V. Zhang, M. Neupane, A. Batra, R. S. Klausen, B. Kumar, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, J. Am. Chem. Soc., 2015, 137, 12400–12405 CrossRef CAS PubMed.
- T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7, 215–220 CrossRef CAS.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099–1104 CrossRef CAS.
- R. Frisenda, G. D. Harzmann, J. A. Celis Gil, J. M. Thijssen, M. Mayor and H. S. J. van der Zant, Nano Lett., 2016, 16, 4733–4737 CrossRef CAS PubMed.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988 CrossRef CAS PubMed.
- K. Reznikova, C. Hsu, W. M. Schosser, A. Gallego, K. Beltako, F. Pauly, H. S. J. van der Zant and M. Mayor, J. Am. Chem. Soc., 2021, 143, 13944–13951 CrossRef CAS PubMed.
- J. Li, P. Shen, S. Zhen, C. Tang, Y. Ye, D. Zhou, W. Hong, Z. Zhao and B. Z. Tang, Nat. Commun., 2021, 12, 167 CrossRef CAS.
- I. Franco, C. B. George, G. C. Solomon, G. C. Schatz and M. A. Ratner, J. Am. Chem. Soc., 2011, 133, 2242–2249 CrossRef CAS.
- D. Stefani, M. Perrin, C. Gutiérrez-Cerón, A. C. Aragonès, J. Labra-Muñoz, R. D. Carrasco, Y. Matsushita, Z. Futera, J. Labuta, T. H. Ngo, K. Ariga, I. Díez-Pérez, H. S. J. van der Zant, D. Dulić and J. P. Hill, ChemistrySelect, 2018, 3, 6473–6478 CrossRef CAS.
- J. Nejedlý, M. Šámal, J. Rybáček, I. G. Sánchez, V. Houska, T. Warzecha, J. Vacek, L. Sieger, M. Buděšínský, L. Bednárová, P. Fiedler, I. Císařová, I. Starý and I. G. Stará, J. Org. Chem., 2020, 85, 248–276 CrossRef.
- W. M. Schosser, C.-W. Hsu, P. Zwick, K. Beltako, D. Dulić, M. Mayor, H. S. J. van der Zant and F. Pauly, Nanoscale, 2022, 14, 984–992 RSC.
- P. Zwick, C. Hsu, M. El Abbassi, O. Fuhr, D. Fenske, D. Dulić, H. S. J. van der Zant and M. Mayor, J. Org. Chem., 2020, 85, 15072–15081 CrossRef CAS PubMed.
- P. Zwick, D. Dulić, H. S. J. van der Zant and M. Mayor, Nanoscale, 2021, 13, 15500–15525 RSC.
- C. A. Martin, D. Ding, H. S. J. van der Zant and J. M. van Ruitenbeek, New J. Phys., 2008, 10, 065008 CrossRef.
- C. A. Martin, R. H. M. Smit, R. van Egmond, H. S. J. van der Zant and J. M. van Ruitenbeek, Rev. Sci. Instrum., 2011, 82, 053907 CrossRef.
- D. Cabosart, M. El Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. van der Zant and M. L. Perrin, Appl. Phys. Lett., 2019, 114, 143102 CrossRef.
- P. Shen, M. Huang, J. Qian, J. Li, S. Ding, X. Zhou, B. Xu, Z. Zhao and B. Z. Tang, Angew. Chem., Int. Ed., 2020, 59, 4581–4588 CrossRef CAS.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, Singapore, 2nd edn, 2017 Search PubMed.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117 CrossRef.
- M. Bürkle, J. K. Viljas, D. Vonlanthen, A. Mishchenko, G. Schön, M. Mayor, T. Wandlowski and F. Pauly, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075417 CrossRef.
- M. Tsutsui, K. Shoji, M. Taniguchi and T. Kawai, Nano Lett., 2008, 8, 345–349 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- M. Bürkle, J. K. Viljas, T. J. Hellmuth, E. Scheer, F. Weigend, G. Schön and F. Pauly, Phys. Status Solidi B, 2013, 250, 2468–2480 CrossRef.
- S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482 CrossRef CAS.
- L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Details concerning transport calculations and measurements, results especially for PC2 molecular junctions, and summary of chemical synthesis. See https://doi.org/10.1039/d2sc00937d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |