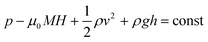Ferrofluids and bio-ferrofluids: looking back and stepping forward
V.
Socoliuc
a,
M. V.
Avdeev
*b,
V.
Kuncser
c,
Rodica
Turcu
 d,
Etelka
Tombácz
*ef and
L.
Vékás
d,
Etelka
Tombácz
*ef and
L.
Vékás
 *ag
*ag
aRomanian Academy – Timisoara Branch, Center for Fundamental and Advanced Technical Research, Laboratory of Magnetic Fluids, Mihai Viteazu Ave. 24, 300223 Timisoara, Romania. E-mail: vekas.ladislau@gmail.com; ladislau.vekas@academiatm.ro
bFrank Laboratory of Neutron Physics, Joint Institute for Nuclear Research, Joliot-Curie Str. 6, 141980 Dubna, Moscow Reg., Russia. E-mail: avd@dubna.ru
cNational Institute of Materials Physics, Bucharest-Magurele, 077125, Romania
dNational Institute for Research and Development of Isotopic and Molecular Technologies (INCDTIM), Donat Str. 67-103, 400293 Cluj-Napoca, Romania
eUniversity of Szeged, Faculty of Engineering, Department of Food Engineering, Moszkvai krt. 5-7, H-6725 Szeged, Hungary. E-mail: E.Tombacz@chem.u-szeged.hu
fUniversity of Pannonia – Soós Ernő Water Technology Research and Development Center, H-8800 Zrínyi M. str. 18, Nagykanizsa, Hungary
gPolitehnica University of Timisoara, Research Center for Complex Fluids Systems Engineering, Mihai Viteazul Ave. 1, 300222 Timisoara, Romania
First published on 24th February 2022
Abstract
Ferrofluids investigated along for about five decades are ultrastable colloidal suspensions of magnetic nanoparticles, which manifest simultaneously fluid and magnetic properties. Their magnetically controllable and tunable feature proved to be from the beginning an extremely fertile ground for a wide range of engineering applications. More recently, biocompatible ferrofluids attracted huge interest and produced a considerable increase of the applicative potential in nanomedicine, biotechnology and environmental protection. This paper offers a brief overview of the most relevant early results and a comprehensive description of recent achievements in ferrofluid synthesis, advanced characterization, as well as the governing equations of ferrohydrodynamics, the most important interfacial phenomena and the flow properties. Finally, it provides an overview of recent advances in tunable and adaptive multifunctional materials derived from ferrofluids and a detailed presentation of the recent progress of applications in the field of sensors and actuators, ferrofluid-driven assembly and manipulation, droplet technology, including droplet generation and control, mechanical actuation, liquid computing and robotics.
1 Introduction
Ferrofluids or magnetic (nano)fluids – a category of magnetically controllable fluids – are rather attractive for a large variety of applications, which require simultaneously fluid and magnetic properties. Among the first attempts to achieve this ambitious goal was the patent filed in 1963 by Steven Papell of NASA,1 who used long term ball milling of a mixture of large particles of magnetite (Fe3O4), a carrier liquid and a surfactant to obtain a magnetizable liquid rocket fuel. Ferrofluids, highly stable magnetic colloids incorporating magnetic particles with a size of the order of 10 nm, use a surface-active layer coating on each nanoparticle to provide a short-range repulsion, preventing them from sticking to each other. Early results on the composition, physico-chemical make-up and magnetic properties of the ferrofluids characterizing the particle size, colloidal stability, diffusive properties, magnetization curve, and viscosity2–6 enforced intensive research on the science of magnetic fluids. Rosensweig and Neuringer proposed a mathematical theory broadening the Navier-Stokes equation to include the force on a magnetic fluid regarded as a continuum, developing the basics of ferrohydrodynamics,7 the name given to magnetohydrodynamics of ferrofluids with a very rich new phenomenology.8–10 The discovery of the normal field instability is perhaps the best known and most characteristic response of a ferrofluid.11World interest in ferrofluids was highly stimulated by the first commercial application of ferrofluids, the leakage-free rotating seals,12 an excellent component of many recent high-tech devices. Moving coil speakers with magnetic fluid damping and cooling demonstrated another highly successful commercial development.13,14 Due to continuous progress in the science of magnetic fluids, these proved to be today fully involved in nanotechnology contributions to industrial progress and development of smart devices, all improving everyone's quality of life. More recently, intensive research concerning biocompatible ferrofluids – bio-ferrofluids – is fully motivated by the huge interest for their applications in biotechnology and nanomedicine, practically a new field of research, also accounted for in the present review. The scientific and technological progress in the field is illustrated by the highly positive trend of publications focused on magnetic fluids/ferrofluids. According to Web of Science Core Collection the number of papers increased more than three times in the last two decades; especially, due to ferrofluid improved smart audio devices, biomedical applications and the increasing applicability of magnetically operated sensors, the global market for ferrofluids is expected to have a compound annual growth rate (CAGR) of 5.5% until 2025 and to attain a valuation of US$ 73.9 Mn by the end of 2025.15 Except the Introduction, the paper is structured as follows:
Section 2 is dedicated to the presentation and evaluation of the most efficient synthesis procedures of engineering and biocompatible ferrofluids, respectively, also including various aspects of up-scaled manufacturing. The similarities and differences between the two classes of ferrofluids are thoroughly discussed with reference to composition, particle size, surface coating and volume concentration of magnetic nanoparticles, as well as biocompatibility and colloidal stability in application related conditions.
Section 3 concerning advanced characterization of engineering and biocompatible ferrofluids is the most extended part of the paper. There will be reviewed results of high-resolution electron microscopy (HRTEM), static light scattering (SLS), dynamic light scattering (DLS), X-ray photoelectron spectroscopy (XPS), Mössbauer spectroscopy, X-ray scattering techniques (small-angle X-ray scattering (SAXS), small-angle neutron scattering (SANS), polarization analyzed SANS (SANSPOL, PASANS), very small-angle neutron scattering (VSANS) and neutron reflectometry), magnetometry, and rheo- and magneto-rheometry, all the techniques essentially contributing to the qualification of ferrofluids to the highest requirements of envisaged applications.
Section 4 refers to ferrohydrodynamics, interfacial instabilities, pattern formation, droplet formation and manipulation, and microfluidics. A brief summary of equations of ferrohydrodynamics is presented in their continuum or macroscopic description, to provide the framework for an overview of ferrohydrodynamic phenomena described by the generalized Bernoulli relationship. Interfacial instabilities and patterning phenomena, droplet formation and manipulation are summarized to show the way towards magnetically controlled ferrofluid droplet populations and new features of digital microfluidics. Spin-up flow and flow in confined geometries are considered taking into account the microscopic make-up of ferrofluids.
The most successful and, also, some of the most promising applications are reviewed in Section 5. Tunable and adaptive multifunctional materials derived from ferrofluids, ferrofluid-driven assembly, ferrofluid enabled surfaces and interfaces, sensors, actuators and ferrofluid droplet technology illustrate the huge applicative potential of ferrofluids. It is a comprehensive overview, but far from being a complete one. Among others, there are missing applications of ferrofluids in heat transfer processes, energy harvesting or in adaptive optics; we refer in this respect to recent papers16–22 and also to the book chapter23 and the book.24
Not the last, the famous Rosensweig instabilities paved the way to kinetic art, in particular to liquid sculptures constantly changing shape controlled by magnetic fields.25 Ferrofluid spikes formed and moving in non-uniform time-varying fields (Fig. 1a) and an inspired combination of ferrofluids with water colors shaped by a magnetic field (Fig. 1b)26 provide a convincing illustration of how nanomaterials, in particular magnetic fluids, can expand the expressive vocabulary of artists today.27
 | ||
| Fig. 1 Ferrofluids-inspiration for arts. (a) Ferrofluid spikes in a non-uniform time-varying field between two magnetic poles28 and (b) mixing ferrofluid with watercolor (reproduced from ref. 26 with permission from APS Division of Fluid Dynamics, copyright 2020). | ||
The review is aimed at attracting young scientists and introducing them to the broad field of engineering and bio-ferrofluids, while providing newcomers with a selected collection of literature references.
2 Synthesis procedures
2.1 Optimal size range of magnetic nanoparticles in ferrofluids and bio-ferrofluids
Colloidal magnetic fluids are stable suspensions of generally spherical shape magnetic nanoparticles in a carrier liquid; that is, the particles have to be homogeneously distributed in the volume of the sample and have to avoid sedimentation for a long period of time even in a strong magnetic field. While fabrication of multi (temperature, pH and ionic strength) stimuli-responsive nanoparticle systems is a real challenge today,29 in which particle aggregation is driven by the manipulation of colloidal stability, magnetic fluids require well-stabilized colloid state under variable conditions where external stimuli, such as magnetic field, changing pH, ionic strength and protein content in the case of aqueous systems for biomedical purposes, do not lead to a loss of colloidal stability. Colloidal stability of magnetic fluids with aqueous and organic carriers involves besides the forces between charged colloidal particles described by the classical Derjaguin–Landau–Verwey–Overbeek (DLVO) theory,30,31 also non-DLVO forces,32 magnetic dipolar attractive interactions and steric repulsion forces.33–36 If the repulsive (electrostatic and steric) forces exceed the attractive (van der Waals and magnetic dipolar) forces during the random (thermal motion) or forced (in shear, gravitational or magnetic field) collision of the particles, they cannot stick together; they remain independent. The colloidal stability of a magnetic fluid is achieved if the thermal energy of the particles is able to keep them distributed in a liquid carrier as mentioned above; that is, the thermal energy has to be larger than their energy in the gravitational field or in a magnetic field gradient, respectively.34,37–39 A typical case refers to magnetite nanoparticles, which conduct to a range of particle sizes between 5 and 15 nm to ensure optimal magnetic behavior and long-term colloidal stability of ferrofluids in gravitational and/or intense and non-uniform magnetic fields. During the last years intensive research on applications in the biomedical field widely extended the above-mentioned size range of iron-oxide nanoparticles in the composition of ferrofluids. Bio-ferrofluids, i.e. biocompatible ferrofluids,40,41 refer to ferrofluids with mostly multicore nanoparticles with sizes well above 10 nm designed for nanomedicine and biotechnology42–45 and, also to ferrofluids with particle sizes less than 5 nm synthesized especially for MRI contrast agents.46,47 There are essential differences compared to conventional ferrofluids. For very small particle sizes, below 5 nm, the magnetization of particles is abruptly reduced due to spin canting in the surface layer.48,49The multicore particles keep the superparamagnetic behavior, but do not have permanent magnetic moment, only field dependent induced magnetic moment, which could provide an improved magnetic response in applied magnetic field. The dispersed particles are mainly iron oxide nanoparticle (IONP) clusters with relatively big size (several tens of nm or even higher); therefore, the colloidal stability of this kind of bio-ferrofluid is significantly reduced. Following the discussion about ideal and real ferrofluids in ref. 50, the typical IONP size ranges for ideal, real and bio-ferrofluids are summarized in Fig. 2. Actually, referring to the large diversity of ferrofluids synthesized for biomedical applications, the particle sizes are mainly in the size ranges I and IV but nanoparticles of other sizes are also encountered. At the same time engineering devices require the use of ideal or at most conventional (real) ferrofluids, say engineering ferrofluids, with much restricted particle sizes.
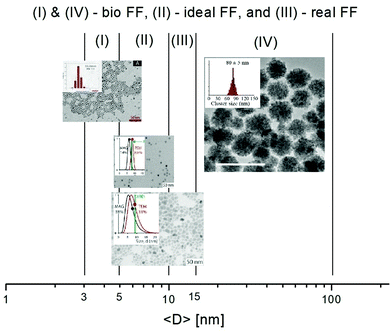 | ||
| Fig. 2 Particle size ranges for ferrofluids and bio-ferrofluids: (I) bio-ferrofluids (2–5 nm) (reproduced from ref. 47 with permission from MDPI, copyright 2020), (II) ideal ferrofluids (5–10 nm), (III) conventional (real) ferrofluids (5–15 nm), and (IV) bio-ferrofluids (15–100 nm) (reproduced from ref. 44 with permission from Am. Chem. Soc., copyright 2020). | ||
2.2 Synthesis of magnetic nanoparticles for ferrofluids
The bottom-up synthesis is actually a self-assembly in solution of atomic and molecular precursors51 giving rise to colloidal nanoparticles of various shape and composition. According to the model of LaMer and Dinegar52–54 the synthesis of monodisperse nanoparticles requires a net separation of nucleation and growth.This theory is based on nucleation-growth mechanisms and considers nucleation as the limiting step in the process. The LaMer diagram describes the evolution of the monomer concentration vs. time, involving the interplay of free-energy barrier and thermal energy and can be divided in three stages (Fig. 3): (1) increasing monomer concentration until nuclei are continuously being formed and dissolved; (2) nuclei formation partially reduces supersaturation, leading to a decrease of nucleation rate; (3) the growth by diffusion of stable nuclei into discrete particles, if the system remains supersaturated.
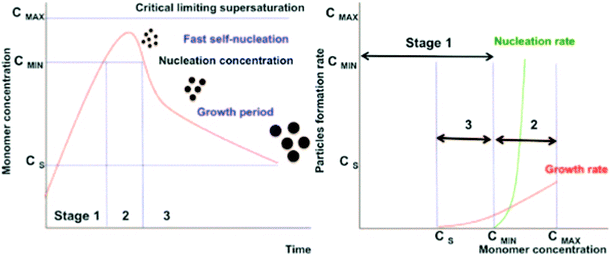 | ||
| Fig. 3 Nucleation and growth model according to LaMer's theory (left) (reproduced from ref. 52 with permission from Am. Chem. Soc, copyright 1950). Comparison of nucleation and growth rates versus monomer concentration (right) (reproduced from ref. 54 with permission from Royal Soc. Chem., copyright 2018). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 using a base.38,57 The reaction is complex and involves the conversion of the hydroxide particles to magnetite58 according to the reaction Fe2+ + 2Fe3+ + 8OH− → Fe3O4 + 4H2O. The control of the mole ratio Fe3+
1 using a base.38,57 The reaction is complex and involves the conversion of the hydroxide particles to magnetite58 according to the reaction Fe2+ + 2Fe3+ + 8OH− → Fe3O4 + 4H2O. The control of the mole ratio Fe3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe2+, their concentrations, nature and concentration of the alkaline medium, as well as of the precipitation temperature, rate of heating and addition of surfactant to the reaction medium and the magnetite crystal growth time59–65 can determine the nature and size of iron oxide particles. Oxidation of Fe2+ leads to the stoichiometry of the particles not being purely magnetite which can be circumvented by performing the synthesis under a non-oxidizing environment (e.g. Ar62 or N2
Fe2+, their concentrations, nature and concentration of the alkaline medium, as well as of the precipitation temperature, rate of heating and addition of surfactant to the reaction medium and the magnetite crystal growth time59–65 can determine the nature and size of iron oxide particles. Oxidation of Fe2+ leads to the stoichiometry of the particles not being purely magnetite which can be circumvented by performing the synthesis under a non-oxidizing environment (e.g. Ar62 or N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63,66) or by adjusting the ratio of the Fe2+ to Fe3+ concentrations.56,63,67 In an oxidizing environment taking into account the oxidation of Fe2+ to Fe3+ an initial molar ratio Fe3+
63,66) or by adjusting the ratio of the Fe2+ to Fe3+ concentrations.56,63,67 In an oxidizing environment taking into account the oxidation of Fe2+ to Fe3+ an initial molar ratio Fe3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe2+ = 1.5–1.7 is considered to be optimal.68,69 An essential feature related to the synthesis of magnetite ferrofluids is to ensure the optimum temperature of 80–82 °C61,63,70 for co-precipitation and stabilization (usually with oleic acid) in order to obtain only magnetite nanoparticles with an adequate chemisorbed stabilizing layer. The possible mechanisms to restore magnetization in the surface layer of nanoparticles closer to bulk values are related to the nature of surfactant,71 to the number density of organic acid molecules in the stabilizing layer for high temperature synthesized magnetite NPs72–74 or to the nature of coprecipitation agents.75
Fe2+ = 1.5–1.7 is considered to be optimal.68,69 An essential feature related to the synthesis of magnetite ferrofluids is to ensure the optimum temperature of 80–82 °C61,63,70 for co-precipitation and stabilization (usually with oleic acid) in order to obtain only magnetite nanoparticles with an adequate chemisorbed stabilizing layer. The possible mechanisms to restore magnetization in the surface layer of nanoparticles closer to bulk values are related to the nature of surfactant,71 to the number density of organic acid molecules in the stabilizing layer for high temperature synthesized magnetite NPs72–74 or to the nature of coprecipitation agents.75
The synthesis of magnetite nanoparticles by chemical co-precipitation is a scalable and cost-effective procedure as it does not need or produce toxic intermediates, and does not require precursor complexes and it proceeds at moderate temperatures below 100 °C.76–78
An interesting type of multicore magnetic nanoparticle is nanoflowers, the assembly of monocrystalline grains to be used as the magnetoresponsive component of a bio-ferrofluid. Nanoflowers have an exceptional hyperthermic efficacy, and their specific loss power (SLP) is one order of magnitude higher than that reported for the single core MNPs of the same size under the same AC field exposure, so they have shown outstanding interest since their first discovery. This novel structure was synthetized first by applying a modified “polyol” protocol,79 where alkaline hydrolysis of stoichiometric Fe(II) and Fe(III) salt mixture was performed in the mixture of diethyleneglycol (DEG) and N-methyldiethanolamine (NMDA) and the precipitate was aged at high temperature. Colloidal stability of the dispersion was provided by citric acid addition. Some years later, microwave radiation was used in a similar, coprecipitation process.80 According to the authors their process is of good reproducibility, produces stable multi-core MNPs and is potentially scalable.
Efficient size control of magnetite nanoparticles was achieved by an approach involving the extended LaMer mechanism,86 in the thermal decomposition of iron oleate in high boiling point solvents. This synthesis procedure is based on the constant addition of a precursor to the reaction solution which results in uniform and continuous growth of nanoparticles to arbitrarily large sizes. Control of particle size monitored by SAXS is achieved by varying the volume of added precursor, i.e. the reaction duration, leading to highly crystalline nanoparticles with sub nanometer size precision and very low size dispersity. The procedure proved to be highly reproducible, as a consequence of the simplified kinetics of the steady state growth stage.86
Following the procedure described in ref. 85, the thermal decomposition of iron pentacarbonyl in the presence of oleic acid was investigated via in situ small-angle X-ray scattering,87 allowing for following by direct observation the reaction kinetics and precursor states with high time resolution and statistical significance. By the advanced monitoring there were identified six phases of the synthesis process: (i) heat-up lag phase; (ii) decomposition of the precursors to form iron oleate; (iii) formation of clusters or prenuclei (precursors); (iv) a second heating lag phase; (v) burst nucleation; and (vi) core growth with narrowing of the size distribution. The final iron-oxide nanoparticle size was found to be directly related to a phase of inorganic cluster formation that takes place between precursor decomposition and particle nucleation. The main factors identified to influence the size and concentration of clusters are the precursor-to-surfactant ratio and heating rate. The resulting oleic acid coated IONPs have very reduced polydispersity.88 Focusing on the biomedical application, single-crystalline iron oxide nanoparticles with small physical size but large dipole moment, hence advantageous magnetic properties (e.g. high values: 74 Am2 kg−1 magnetic saturation, SAR 209 W per gFe and ILP 6.1 nHm2 kg−1, low 98.2 K blocking temperature), were synthetized by the extended LaMer thermal decomposition synthesis from iron oleate through the controlled addition of little amount of molecular oxygen.89
Core–shell type nanoparticles with different shapes (spherical, cubic and octopode) were synthesized by thermal decomposition, leading to the formation of an antiferromagnetic inner core Fe1−xO surrounded by a ferrimagnetic Fe3−xO4 shell, a hydrophilic dendron coating ensuring good water dispersibility of the composite particles.90
The composition and shape determine favorable anisotropy properties for biomedical applications of the resulting bio-ferrofluids. Size and shape controlled nanocubes of mixed zinc–cobalt–ferrite in the size range 8–15 nm were prepared, initially with a hydrophobic coating and dispersed in chloroform, followed by a phase transfer procedure to water by polymer coating of particles, to provide bio-ferrofluids with favorable magnetic fluid hyperthermia performances.91
The shape-controlled MNP synthesis has recently been thoroughly reviewed.92 It has been stated that synthesis of high-quality nanoparticles is still unresolved; the protocols are not robust enough, since the mechanisms of nucleation and growth are still not well-understood. If synthesis of monodisperse nanoparticles is aimed, the nucleation and growth stages must be separated in time and temperature; otherwise, polydisperse products with various morphologies form. Two basically different routes (starting from either iron(II) and/or iron(III) salts or organic precursors) of direct magnetite synthesis are evaluated. A mild reducing or oxidizing agent is present in the reaction mixture in most cases to get the accurate Fe3O4 composition. In the shaped-controlled synthesis, preferential adsorption of designed ligands on specific facets of the iron oxide nucleus inhibits growth in the specified direction. Preparation of several monodisperse, shape-controlled Fe3O4 such as nanocubes, nanoctahedrons, elongated nanostructures (spindles, nanobelts, nanorods and nanowhiskers), disks, nanoflowers, nanostars, tetrapods, nanoprisms and hollow nanostructures is evaluated. Regarding their colloidal stability in aqueous media, the authors concluded that it is important that the ligands/polymers are needed to stabilize them in water, and there is plenty of work to improve dispersibility.
Different synthesis strategies based on the partial oxidation of Fe(OH)2, polyol-mediated synthesis or thermal decomposition of iron acetylacetonate were studied93 to obtain multi-core, flower-shaped MNPs in the size range of 25–100 nm. The same research group clarified their design strategies and published two clear strategies for the synthesis of the 3D flower-like magnetite MNPs with different sizes: the polyol route and thermal decomposition.92 The authors emphasized that colloidal stability of MNPs is of importance and prepared chemically bound ligands/polymers for better stability in aqueous media. It has been stated that the hierarchical magnetic nanostructure in nanoflowers is built up from densely packed aggregates of ferrimagnetic nanocrystallites; these building blocks are superferromagnetically coupled, enhancing magnetic hyperthermia performance.94 The collective characteristics of the interacting crystallites permit a large magnetic moment while retaining the faster dynamics typically associated with smaller particles.95
The chemical coprecipitation and thermal decomposition synthesis are the most relevant and efficient methods for preparing MNPs for ferrofluids. The same conclusion was reached in a most recent review on SPION synthesis for magnetic particle imaging.96 Although the authors emphasized that the details of SPION synthesis do not fall within the scope of the review, they summarized it very concisely and purposefully, comparing the five well-established synthesis methods (co-precipitation, thermal decomposition, hydrothermal, microemulsion and sol–gel), and describing the mostly beneficial properties of co-precipitation and thermal decomposition. Namely, co-precipitation is a cost-effective, simple, scalable, environmentally friendly method with high-yielding, but polydisperse products with a low degree of crystallinity. In turn, the products of thermal decomposition have a very narrow size distribution and excellent crystallinity. However, the organoiron precursors are decomposed in organic solvents at high temperature, in the presence of hydrophobic surfactants. The stabilizing layer of the latter must be altered with hydrophilic coating agents to obtain the biocompatible, water dispersible nanoparticles.97–99 This expensive method is not environmentally friendly; it requires generally toxic chemicals and organic solvents.
As shown before, MNPs synthesized by coprecipitation usually have a wide size distribution because the growth of crystal is only governed by kinetic factors. In case of thermal decomposition, the size of MNPs can be finely controlled by varying the reaction condition, such as the types of solvent, heating rate, surfactant, and reaction time, or by a seed mediated growth process. In Fig. 4 a comparison of the two procedures is summarized, including transition-metal doped ferrites, FePt nanoparticles and also some commercial IONP samples.102
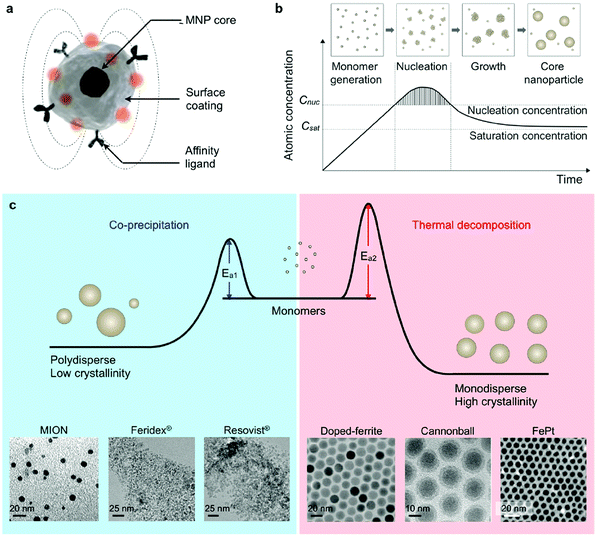 | ||
| Fig. 4 Synthesis of core MNPs. (a) Representative structure of a MNP. (b) Crystal-growth diagram. When the monomers are supersaturated and exceed the nucleation concentration, seed nucleation is induced and monomers are continuously aggregated onto the seeds, leading to crystal growth. Cnuc, nucleation concentration; Csat, saturation concentration. (c) Comparison of coprecipitation and nonhydrolytic thermal decomposition methods. The coprecipitation method results in kinetically favored MNPs which generally have a polydisperse size and relatively low crystallinity. Conversely, the thermal decomposition method produces thermodynamically stable MNPs with a monodisperse size and high crystallinity. Examples of transmission electron microscope (TEM) images of MNPs synthesized by coprecipitation (MION, Feridex, and Resovist) or thermal decomposition methods (doped ferrite, cannonball, and FePt) are shown.82,100,101 (Reproduced from ref. 102 with permission from Am. Chem. Soc., copyright 2015.) | ||
For most of the ferrofluid applications the magnetic properties of individual particles are critical as they determine the macroscopic magnetic behavior, TEM size monodispersity therefore is not the only criterion for a successful synthesis. Low TEM size polydispersity of magnetic nanoparticles does not guarantee low polydispersity of the magnetic dipole moment. Crystal defects, such as twinning and dislocations, can have a highly detrimental effect on the strength and low polydispersity of the magnetic properties. Sometimes crystallite sizes from XRD, volume-averaged TEM and magnetogranulometry for iron oxide nanoparticles synthesized by aqueous coprecipitation and thermal decomposition processes could show significant differences between geometric and magnetic sizes.103
The bottom-up synthesis procedures of iron oxide nanoparticles, especially for preparation of bio-ferrofluids, were thoroughly analyzed;104 the advantages and disadvantages evaluated taking into account the most important conditions and parameters, as well as the production yield, are summarized in Table 1. The proper choice of the synthesis method is determined by the envisaged application and costs involved.
| Synthesis methods | Synthesis conditions | T (°C) | Reaction time | Solvent | Size (nm) | Size distribution | Morphology control | Yield |
|---|---|---|---|---|---|---|---|---|
| Co-precipitation | Very easy | 20–90 | Minutes | Water | <40 | Average | Average | Very high |
| Microemulsion | Complex | 20–50 | 10 min | Water/organic | <50 | Quite narrow | Good | Low |
| Polyol method | Very easy | >180 | 10 min | Organic | <10 | Quite narrow | Very good | Average |
| Hydrothermal method | Simple but under high pressure | >200 | Hours | Water/ethanol | <1000 | Quite narrow | Very small | Average |
| Thermal decomposition | Complex | 200–400 | Hours | Organic | <20 | Narrow | Very good | High |
The scale-up synthesis of bio-ferrofluids for magnetic hyperthermia was recently considered in a complex investigation concerning the reproducibility and scalability of the thermal decomposition procedure involving kilograms of reagents and cheap commercial precursors.105 To obtain large quantities of single core and multi-core magnetite nanoparticles the scale-up procedure applied refers to the decomposition of iron(III) acetylacetonate 99% in benzyl ether in the presence of oleic acid and 1,2-dodecanediol 90%, with substantial modifications of the lab-scale synthesis, such as the extension of the high temperature step from minutes to hours. The results of large-scale synthesis were evaluated by thorough comparative analyses of the solvodynamic size average values and magnetic heating characteristics under different field conditions measured for toluene-based suspensions of oleic acid stabilized magnetite nanoparticles.
A continuous flow system was built-up to investigate the influence of concentration and nature of surfactants, temperature, pressure, residence time, and capillary inner diameter on the thermal decomposition synthesis of very small, less than 5 nm size, iron-oxide nanoparticles.47 The high flow rate (up to 2 mL min−1) synthesis process demonstrated its efficacy in producing highly stable single-core MNPs, the colloidal magnetic nanoparticles having well-designed magnetic and relaxometric properties for T1-weighted magnetic resonance imaging (MRI). The output of the continuous flow synthesis process proved to be higher than that of the usual batch methods.
The flow chemistry approach seems to provide a solution also to the kinetic problem of MNP synthesis, i.e., the separation of nucleation and growth over time. This dynamic method has been developed to reveal the early stages of Fe(II) and Fe(III) salt co-precipitation via in situ measurement of small angle X-ray scattering and synchrotron X-ray diffraction106 and also via in situ magnetometry (flow susceptometry).107 The authors stated that most crystalline phase forms in some seconds, and the aggregation of nanoparticles takes place simultaneously, and subsequent addition of a stabilizer (citric acid) can prevent aggregation, and even disintegrate already formed agglomerates. This scalable synthesis route was optimized for laboratory size by designing a multistage flow reactor to produce iron oxide nanoparticles continuously. This flow reactor has been used to produce monodisperse and non-aggregated small iron oxide nanoparticles suitable for MRI diagnosis purpose.108 The authors emphasized that this type of flow reactor is suitable for larger scale reproducible production.
Application oriented continuous manufacturing of bioferrofluids is a challenging task. A microreactor with 3D flow focusing for coprecipitation synthesis and biphosphonate functionalization of IONPs was combined with an online NMR relaxation characterization unit, to provide a continuous flow automated production system.109 The primary nanoparticle sizes varied between 24.6 and 12.3 nm when the pH value increased from 10 to 12, respectively. Following peptization and colloidal stabilization iron oxide nanoparticle clusters resulted with hydrodynamic sizes from 38 nm (at pH 1.08) to 344 nm (at pH 3.45), allowing for controlling the functionalized cluster size to achieve the optimal transversal or longitudinal relaxation rate.
A recently published review110 gives the fundamental information to design LoC (lab on a chip) systems for the synthesis of magnetic nanoparticles. Two main types of microreactors are used, namely single-phase (continuous-flow microfluidics) and multi-phase flow (droplet-based microfluidics). A droplet-based microfluidic device was already used to synthesize MNPs in 2008.111 In 2010, a book chapter was published about this flow method for MNP synthesis.112 The oxidation of green roast from FeSO4 hydrolysis was controlled in an inert, oxidant, or reductant gas segmented microfluidic device, and the desired crystalline phase and shape of the resulting nanostructures were reproducibly prepared in less than 2 min reaction time.113 These flow methods became popular for MNP synthesis in the last years; however, they require further improvements for colloidally stable ferrofluid synthesis.
2.3 Preparation of magnetic fluids
The stability of aqueous colloidal dispersions of ionic magnetic nanoparticles is a function of pH as the interparticle interactions may be tuned through pH variations. The addition of an electrolyte to the ferrofluid destabilizes the colloid, which results in phase separation in two liquid phases of different concentrations,117 the larger size particles going preferably to the dense phase. Scanning the whole pH scale from acidic to alkaline medium different states are evidenced by magnetooptical effects: sol, thixotropic gel, and floc (around the point of zero charge).
Exploring a very wide range of particle volume fraction values, 1–30%,118 a critical volume fraction Φ* was determined expressing the freezing of the rotational dynamics of magnetic nanoparticles. Φ* depends on the size of nanoparticles and the ionic strength of the dispersion. For volume fractions Φ > Φ* the effective spheres of the particles (particles with surrounding ionic cloud) interpenetrate and the system is becoming glass forming. Magnetic field is a powerful control parameter of the glass transition process. Time resolved X-ray photon correlation spectroscopy evidenced highly anisotropic cooperativity on interparticle length scales induced by the applied magnetic field.119
A slightly modified version of the Massart synthesis procedure120 led to a concentrated ferrofluid with very high saturation magnetization and initial susceptivity, Ms = 1000 G and χi = 3.3.121 The average diameter of the iron oxide nanocrystals was 4.6 nm with a standard deviation of 0.35 nm. The hydrodynamic size of electrostatically stabilized particles is only slightly greater than the physical size; therefore, the main advantage of this kind of fluid is the reduction of the total suspended material at constant magnetic volume fraction compared with a sterically stabilized fluid, which explains the very high saturation magnetization achieved. However, their high sensitivity against changes of the pH-value of the carrier medium can easily lead to a complete destabilization of electrostatically stabilized ferrofluids, which could be a drawback both for engineering39 and biomedical applications.122 However, chemically induced destabilization of citric acid stabilized ferrofluids, followed by magnetic manipulation of clustered MNPs,123 is possible to be the key for successful biotechnology applications, such as immunoassays, protein purification and, especially, water remediation.124 Cationic methylene blue (MB) organic dyes as model pollutants added to citrate stabilized ferrofluids are adsorbed onto the IONP surface and reduce the repulsive interactions between them. This partial screening initiates the primary aggregation of nanoparticles, increasing the magnetic content of the resulting clusters, which form large secondary agglomerates due to induced dipole–dipole interactions in the applied magnetic field. The induced clusterization process creates favourable conditions for magnetic separation in gradient magnetic fields. The mechanism of primary aggregation of IONPs is evidenced by DLS measurements which show an exponential increase of the hydrodynamic size due to MB adsorption, the mechanism of the adsorption/destabilization process being still investigated.
Remarkable colloidal stability was achieved under extreme field conditions for dilute aqueous citrate stabilized ferrofluids designed for multifraction magnetic density separation on an industrial scale.77,78 The colloidal stability of the citrate coated maghemite ferrofluid was tested at fields of up to 10 T and gradients of up to 100 T m−1. The ferrofluids with particles in the 5–10 nm diameter range (ideal ferrofluid) show no aggregation and only low sedimentation rates which are compatible with their use in large-scale magnetic density separation.
The electrostatic stabilization mechanism was extended to a non-aqueous highly polar solvent dimethyl sulfoxide (DMSO)125 and also to various ionic liquids.126–129 DMSO and ionic liquids have a permittivity lower than that of water, and consequently the stabilization of magnetic nanoparticles by electrostatic repulsion is expected to be more difficult than in water. Long term (several years) colloidal stability, even at relatively high temperatures (up to 200 °C), was achieved recently by adapting the interfacial properties of magnetic nanoparticles to pure ionic liquid carriers.130
The hydrophobic (e.g. OA coated) magnetite particles are not dispersible in alcohols (such as propanol, butanol, pentanol, hexanol, heptanol, etc. with εr well above 5 (NBS(USA)-AD-A278956(1994)), diesters (DOA = dioctyl adipate (bis(2-ethylhexyl)adipate), C22H42O4; DOF = dioctyl phthalate (bis(ethylhexyl)phthalate), C24H38O4, and DOS = dioctyl sebacate (bis(2-ethylhexyl)sebacate), C26H50O4), high vacuum oil (HVO (KW, Merck)), dichlorometane or ketones (acetone, methyl–ethyl–ketone); therefore, in the case of polar carriers, the colloidal stability is achieved by applying appropriate primary or also secondary stabilizers.142–145 The efficiency of appropriate secondary stabilizers is well illustrated in the case of a series of alcohol based MFs, from propanol to decanol,143 having saturation magnetization up to 920 G, the highest value attained for these polar carriers. The method of double layer sterical stabilization proved to be successful also for most polar solvents, such as water62,68,146 or methyl–ethyl ketone144,147 or even acetone,145 a destabilizing agent. Aqueous ferrofluids synthesized by chemical coprecipitation achieved high saturation magnetization (up to 600 G) with oleic acid double layer electro-steric stabilization.121 The stabilization mechanism, in particular, the weakly bonded physisorbed second oleic acid layer which increases the overall thickness of the coating, greatly influences the surface properties, hydrodynamic and magnetic size, colloidal behavior and structuring of particles, as well as the magnetic properties and magnetorheological behavior. A thinner, irreversibly adsorbed hydrophilic stabilizing layer highly increases the colloidal stability of aqueous bio-ferrofluids even in very intense magnetic fields (9.4 T in MRI facilities).148
Steric stabilization was applied for dispersing magnetic nanoparticles also in ionic liquid carriers. A double layer of oleic acid proved to be efficient in stabilizing magnetite nanoparticles in 1-ethyl-3-methylimidazolium ethylsulphate ([EMIM][EtSO4]) ionic liquid, while citric acid and humic acid were poor stabilizers in the same carrier.149
Synthesis of stable FFs of superparamagnetic 7 ± 2 nm magnetite (Fe3O4) nanoparticles in the hydrophobic ionic liquid 1alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([CRMIM][NTf2]) was achieved150 using designed and synthesized 1-butyl-3-(10-carboxydecyl)-1H-imidazol-3-ium bromide (ILC10-COOH) surfactant that combines the same imidazole moiety as the ionic liquid. The surfactant with a long alkyl chain ensured compatibility with the ionic liquid and increased the steric repulsion between the magnetite nanoparticles sufficiently such that long-term stable relatively concentrated (50 wt%) ferrofluids resulted which passed stability tests in the presence of a magnetic field (0.5–1 Tesla), being foreseen to be used in rotating magnetic fluid seals (e.g., in ultra-high vacuum space applications).
Stable dispersion of maghemite NPs in fluorinated oils, among the most difficult cases in ferrofluid synthesis, was achieved by a two-step chemical route starting with aqueous Massart synthesis of maghemite NPs. The procedure involves perfluoropoly(ether) surfactant coating, ligand exchange, sol–gel reaction and silanization to obtain individually dispersed maghemite nanoparticles in any fluorinated oil. The result is a true highly stable ferrofluid; it remains monophasic up to a magnetic field of 7 T.151
2.4 On the colloidal stability of ferrofluids and bioferrofluids
A ferrofluid is a colloidal dispersion of magnetic nanoparticles having diameters between 5 and 15 nm in a carrier fluid, and as such it is inherently thermodynamically unstable due to the effort to minimize surface free energy. As is well known in colloid science,152 an increasing surface to volume ratio of particles is accompanied by an increase in surface free energy. Therefore, the particles especially in the nano size range are constantly roughening: their size is growing over time because of the surface energy loss while reaching the state of energy minimum. The nanomaterial systems have only kinetic stability, and consequently their colloidal state is limited in time; sometimes, they exist for a very long time after preparation (an example of the stability of FF for nearly four decades given in 2.4.2).As far as colloidal stability of ferrofluids is concerned, in addition to the magnetic specificities and interactions, it is essentially related to both their fabrication and application, as we have mentioned several times in this section. Here we intend to summarize the main facts.
First, the theoretical aspects of colloidal stability have been discussed for decades [e.g., ref. 33, 34 and 153]. These approximations mainly discuss the combination of DLVO forces involving electrostatic repulsion and van der Waals attraction with non-DLVO forces such as Born and steric repulsion at very close vicinities and farther from the particle surface, respectively, and the magnetic attraction forces due to externally applied magnetic fields. In a recently published theoretical article,154 the authors have solved the problem of the DLVO approach at small intersurface separation and also the limitation of the EDL model, which has long been known in colloid science and has failed to describe ferrofluids. Analytical formulas of an extended DLVO model considering electrostatic, steric and Born–Mayer repulsions and a term for magnetic bipolar interactions were introduced in the proposed approach. In comparison with the total interaction energy calculations, Monte Carlo simulations performed in parallel provide very good results. It was concluded that the proposed modifications of DLVO allow for manifesting the effect of magnetic interparticle interactions on the colloid structure of ferrofluids.
Colloidal stability, i.e. aggregation stability, is ensured by a balance among all these interactions to ensure an overall repulsive force between the suspended nanoparticles.31,34,37,39,155,156 This basic requirement is achieved by optimizing the size distribution of magnetic nanoparticles and by coating them by stabilizing layers of surfactants or/and ions to avoid inter-particle contact and to decrease or compensate for the attractive dipole–dipole interactions. The magnetic dipolar energy over the thermal energy at close contact between particles, 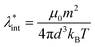 , and also the ratio between the magnetic dipolar energy and thermal energy in a homogeneous ferrofluid of particle volume fraction φ (sometimes denoted also by Φ),
, and also the ratio between the magnetic dipolar energy and thermal energy in a homogeneous ferrofluid of particle volume fraction φ (sometimes denoted also by Φ), 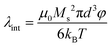 , are the main parameters generally used to characterize the magnetic interactions; here, m-particle magnetic dipole moment; Ms – saturation magnetization of the material; d-particle diameter; kB – Boltzmann constant; T-temperature (°K); μ0 – magnetic permeability of vacuum. The parameter λint is a function of the mean interparticle distance determined by the volume fraction φ. Note that
, are the main parameters generally used to characterize the magnetic interactions; here, m-particle magnetic dipole moment; Ms – saturation magnetization of the material; d-particle diameter; kB – Boltzmann constant; T-temperature (°K); μ0 – magnetic permeability of vacuum. The parameter λint is a function of the mean interparticle distance determined by the volume fraction φ. Note that 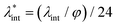 , the ratio λint/φ corresponding to the potential between two orientated dipoles at contact, taking into account the thicknesses of surface coating and non-magnetic (random spin orientation) layers when it is the case. To conclude, the field-induced particle aggregation is governed by the particle volume fraction φ, dipolar coupling parameter λint and the ratio of the energy of interaction of a magnetic particle with an external magnetic field to thermal energy represented by the Langevin parameter ξ. The parameters λint and ξ are proportional to the volume of particles, i.e. to d3, the particle interactions being strongly size dependent and consequently, ferrofluid structure, aggregate formation and phase behavior are highly influenced by polydispersity.157–159
, the ratio λint/φ corresponding to the potential between two orientated dipoles at contact, taking into account the thicknesses of surface coating and non-magnetic (random spin orientation) layers when it is the case. To conclude, the field-induced particle aggregation is governed by the particle volume fraction φ, dipolar coupling parameter λint and the ratio of the energy of interaction of a magnetic particle with an external magnetic field to thermal energy represented by the Langevin parameter ξ. The parameters λint and ξ are proportional to the volume of particles, i.e. to d3, the particle interactions being strongly size dependent and consequently, ferrofluid structure, aggregate formation and phase behavior are highly influenced by polydispersity.157–159
Second, more importantly the practical aspects of colloid stability need to be addressed in both production and application [e.g., ref. 160 and 161]. Although good colloidal stability is crucial for ferrofluid behavior, the situation is relatively simple; since ferrofluids are manufactured for the given purpose with specific requirements, no further change is required, and the shelf life can be guaranteed. The designed magnetic cores are coated with often fatty acids via chemical bonds, and dispersed in organic carriers. Chemical and colloidal stability of magnetic materials is acquired by the coating. This protective layer is thick enough to provide steric stabilization against aggregation during random or forced collision of particles even in a strong magnetic field and its large gradient.The organic carrier media are very favorable, because chemical transformation except e.g., the well-known maghemite formation from magnetite nanoparticles is unlikely and, also, dissolution, corrosion cannot take place. It is well-known that a stable ferrofluid reacts quickly as a whole to a magnet, while the magnetophoretic motion of individual particles begins in a poorly stabilized system and needs longer time. Very good colloidal stability is required and can be tested by monitoring sedimentation in a strong magnetic field even at 10 T.77,78 The lack of magnetoviscous effect also indicates the ideal behavior of “true” ferrofluids.162,163
In the case of aqueous bio-ferrofluids, however, one faces several extra problems. Water is an aggressive medium, the spontaneous aqueous processes (corrosion, iron leaching, etc.) can be only hindered during storage, and thus shelf life is shorter than that of ferrofluids with organic carriers. In our opinion, however, the source of most problems is that aqueous media in which MNPs are dispersed change dramatically during administration. One must consider the significant changes in the composition of aqueous milieu. First of all, bio-ferrofluids are diluted with biofluids with different pH, salt and protein content (e.g., physiological salt concentration, pH ∼ 7.4, platelets, red and white blood cells, antibody proteins, coagulation factors, globulins, and fibrinogens in blood), and interact with bio entities (proteins, cell membranes, etc.). Moreover, even biological requirements like exclusion of toxicity, iron leaching and non-specific interactions must be taken into account when designing bio-ferrofluids. The crucial issues are biocompatibility and colloidal stability which involve nano-bio interactions164–166 governed by the solid–liquid interface that forms on NPs’ surface in the surrounding milieu and comes into contact with biological entities, protein corona formation,167–169 immune response,170,171etc.
The question is how to test and measure whether bio-ferrofluids meet the requirements or not. Unfortunately, there is no answer yet, and there are no agreement on what and how to test and no proposals for uniformly usable protocols. There are widespread methods in the literature, mainly in vitro cytotoxicity measurements (e.g., flow cytometry and MTT tests) and in vivo methods using animals available for experiments often without prior testing of chemical and colloidal stability of the newly developed MNP products, though a scheme has been proposed for IONPs.172
In general, the hydrodynamic size is usually measured by dynamic light scattering (DLS) and it is given as DLS size without solution compositions and description of experimental conditions such as dilution, ultrasonication, the time of treatment and waiting prior to the measurement crucial in a not perfectly stabilized system, and even the method of data analysis especially for polydisperse samples where the number, volume, intensity and Z average values differ greatly. The colloidal stability was characterized in different physiological media by DLS measurements, and at least the conditions of biologically relevant solutions were given to some extent in the supplementary materials in an article published recently.173
In colloid science, the coagulation kinetics measurement and analysis of kinetic data to determine the critical coagulation concentration (ccc), i.e. the lowest concentration of electrolyte that induces fast coagulation is a widely accepted method to characterize colloid stability; the ccc value and the stability plot are comparable to DLVO theory.174 We have introduced this method for correct colloidal stability characterization of bio-ferrofluids, i.e., to measure the electrolyte tolerance of dilute samples at constant pHs.175 Unfortunately, this method has not been widely used, although it was qualified recently as a method for measuring colloidal stability.29
As colloidal parameters, the zeta potential and hydrodynamic size of commercially available IONPs with different coatings, dispersed in distilled water, saline phosphate buffer solution and human blood plasma, were measured in order to find the criteria for the selection of coatings suitable for nanoparticles for in vivo tests.176 According to the authors the selection criteria are the hydrophilicity, and the net surface charge of the nanoparticle coating in aqueous media. The key roles of coatings are to preserve colloidal stability (i) in the media required for injection, (ii) in blood and (iii) inside the cells as well. The latter was also concluded in a very recent paper177 in which magnetic nanoparticles have been used for magneto-mechanical actuation in a low frequency alternating magnetic field to damage cancer cells. Haemocompatibility tests have been also introduced to support qualification for good and bad MNP manufacturing; the latter ‘promises’ fatal outcome in vivo. A routine diagnostic test, the blood smear, proved to be the most sensitive.178
3 Advanced characterization
3.1 Electron microscopy, X-ray diffraction and light scattering techniques: particle sizes and interactions
The size of even isometric particles in the nanometer size range cannot be given in a common way, since it depends on the measuring method such as electromicroscopy (TEM and SEM – sample taken in very small quantity, projected images), X-ray diffraction (XRD via the Scherrer equation – only crystalline phase) for physical sizes, dynamic light scattering (DLS – diluted samples, highly influenced by the composition of medium and by polydispersity either as prepared or due to aggregation in a given medium) for hydrodynamic size, and magnetic measurements for magnetic size. The latter is the uniqueness of magnetic nanoparticles and involves magnetogranulometry based on the full magnetization curves of the nanoparticle system, discussed in section 3.6. Usually, the magnetic size of a nanoparticle is somewhat smaller than its physical (solid) size due to spin-canting in the surface layer, while the hydrodynamic size, which includes the surface coating stabilizing layer(s), exceeds both the previous sizes. These sizes and size distributions differ accordingly even for mono- or slightly polydisperse samples as already discussed in detail in the relevant literature [e.g., ref. 179 and 180]. The size investigation techniques are thoroughly used together with other characterization methods (such as SAXS and SANS), as it will be evidenced throughout the paper.The size distribution of magnetic nanoparticles is an essential feature of ferrofluids developed for engineering and biomedical applications. Particle size determines the magnetic moment and the resulting magnetic interactions between the constituent magnetic nanoparticles and, consequently, the size distribution is the most important factor influencing the long-term stability of a magnetic colloid. Particle correlations in ferrofluids are governed by attractive and repulsive forces, in particular by magnetic dipole–dipole (anisotropic), as well as hard core, van der Waals, steric and/or electrostatic (isotropic) interactions. Ferrofluids are characterized by having a large number of approx. 10 nm size magnetic particles in unit volume, even at low volume fraction; therefore, particle number density (n) and the relative distance between particle surfaces (δip) taking into account the surface coating stabilizing layer, i.e. the hydrodynamic volume fraction (φh), are relevant for magnetic and hydrodynamic interactions between particles.161 Neglecting the influence of Brownian motion, external shear stress and magnetic fields, the particle density and relative distance δip can be estimated181 considering random distribution of monodisperse particles. According to the estimation in Fig. 5 of the magnetic and hydrodynamic interactions, in particular the possibility of formation of particle clusters has to be considered depending on the particle size, already for φh > 0.1%.161 For sufficiently low particle sizes 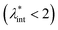 and low volume fractions φ the magnetic fluids can be considered as a gas of hard spheres, well described by one-particle models in the low coupling regime (ideal ferrofluid). For large
and low volume fractions φ the magnetic fluids can be considered as a gas of hard spheres, well described by one-particle models in the low coupling regime (ideal ferrofluid). For large 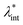 and φ values particle interactions are important and chains and more complex particle aggregates are developed in real ferrofluids, largely influencing their magnetic and flow properties.182–187 Upon systematically increasing particle size, i.e.
and φ values particle interactions are important and chains and more complex particle aggregates are developed in real ferrofluids, largely influencing their magnetic and flow properties.182–187 Upon systematically increasing particle size, i.e.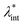 , an abrupt transition occurs in the case of an iron nanoparticle ferrofluid from separate Fe particles to randomly oriented linear aggregates and even branched networks in zero field.188,189 The aggregation tendency evidenced for Fe nanocolloids is significant also in the case of magnetite ferrofluids when the dipolar potential exceeds thermal fluctuations; that is, for a dipolar coupling constant
, an abrupt transition occurs in the case of an iron nanoparticle ferrofluid from separate Fe particles to randomly oriented linear aggregates and even branched networks in zero field.188,189 The aggregation tendency evidenced for Fe nanocolloids is significant also in the case of magnetite ferrofluids when the dipolar potential exceeds thermal fluctuations; that is, for a dipolar coupling constant 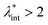 .190
.190
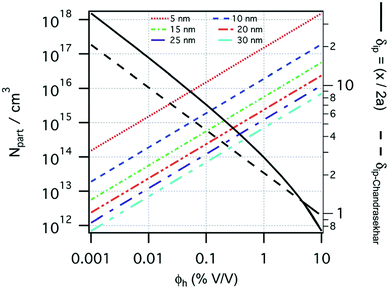 | ||
| Fig. 5 Number of particles (Npart) per cubic centimeter in a ferrofluid and the relative distance (δip) between the particle surfaces as a function of the hydrodynamic volume fraction (φh), where x is the distance between the particle surfaces and a is the hydrodynamic particle radius, estimated considering a monodisperse particle size distribution, neglecting the influence of Brownian motion, external shear stress, or magnetic field. Particle sizes considered from 5 to 30 nm (reproduced from ref. 161 with permission from Royal Soc. Chem., copyright 2014). | ||
3.2 X-ray photoelectron spectroscopy: surface chemical analysis
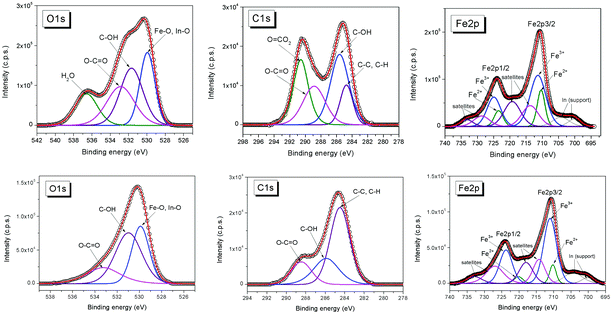
X-ray photoelectron spectroscopy (XPS) is a surface analysis method which enables the determination of the elemental composition of the surface, as well as the valence states, oxidation degree, and ligands of the atoms, therefore highly contributing especially to the advanced characterization and functionalization strategies of bio-ferrofluids.191The surface chemistry affects the magnetic properties of the nanoparticles. Various anchoring groups such as carboxylate, phosphonate, catechol, and silane104 interact in a different way with the nanoparticle surface and influence the magnetic properties.42,72,192–198 XPS is one of the most powerful techniques to quantitatively analyze the chemical composition of the coating layer of magnetic nanoparticles.199–203 XPS can determine the oxidation state of the metal in the magnetic core, differentiate between magnetite (Fe3O4) and maghemite (γ-Fe2O3), and identify possible additional phases that could alter the magnetic properties of the nanoparticles. These oxidation states of iron can be determined from the XPS Fe 2p spectrum employing chemical shifts and multiplet splitting and the characteristic satellites.65,121,204–207 XPS is the most appropriate method to evaluate the formation of surface complexes. Stabilization of magnetic nanoparticles is often accomplished in such a way that the magnetic contribution of the particle surface layer is maintained. For example, phosphatation of magnetite nanoparticles proved to be among the most efficient procedures for MNP stabilization, while keeping the magnetic contribution of the particle surface layer.104,208 XPS, in concert with other characterization techniques such as X-ray diffraction, Mössbauer and infrared spectroscopies, can be used to investigate the type of phosphate complex formed at the surface of the magnetite nanoparticles. For example, XPS spectra indicate that the Fe 2p bands in phosphate-coated magnetite nanoparticles are similar to those of magnetite.104 This similarity suggests that some FeII ions remain at the surface of phosphate-coated magnetite but also that the amount of FeIII increases with increasing concentrations of phosphate ligand. The contribution of surface species has been analyzed from XPS spectra. This analysis indicates that the contribution of the Fe–OH bond was replaced by the contribution of a Fe–O–P bond and a P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. XPS and Mössbauer techniques concluded that the phosphate-coated nanoparticles are magnetite with a small deviation from stoichiometry (Fe2.90±0.02O4). The phosphates interact with FeIII in octahedral sites via the formation of monoprotonated binuclear species.208 XPS was also used to characterize magnetite nanoparticles coated with poly(glycidyl methacrylate) (pGMA), a precursor for further functionalization via nucleophilic ring opening of glycidyl–oxirane moieties.202 Core–shell magnetic nanoparticles can also be prepared by adsorption of monomers followed by their in situ surface polymerization. This approach combines the advantages of physicochemical surface modification and chemical binding.201 For instance, gallic acid was adsorbed onto magnetite nanoparticles and in situ surface polymerized, resulting in a polygallate coating that protects the magnetic nanoparticles from aggregation at physiological pH and salt concentration. The polymer gives the nanoparticles the colloidal and chemical stability necessary for biomedical applications. XPS was used to elucidate the mechanism of surface-induced polymerization of gallic acid. The high-resolution XPS spectra of O, C, and Fe in a polygallate-coated magnetic nanoparticle sample are shown in Fig. 6. The FeIII/FeII atomic ratio at the surface of polygallate-coated magnetic nanoparticles, as calculated from the FeIII and FeII 2p peak areas, decreases from 2 in bulk magnetite (Fe(III)2Fe(II)O4) to 1.77.
O bond. XPS and Mössbauer techniques concluded that the phosphate-coated nanoparticles are magnetite with a small deviation from stoichiometry (Fe2.90±0.02O4). The phosphates interact with FeIII in octahedral sites via the formation of monoprotonated binuclear species.208 XPS was also used to characterize magnetite nanoparticles coated with poly(glycidyl methacrylate) (pGMA), a precursor for further functionalization via nucleophilic ring opening of glycidyl–oxirane moieties.202 Core–shell magnetic nanoparticles can also be prepared by adsorption of monomers followed by their in situ surface polymerization. This approach combines the advantages of physicochemical surface modification and chemical binding.201 For instance, gallic acid was adsorbed onto magnetite nanoparticles and in situ surface polymerized, resulting in a polygallate coating that protects the magnetic nanoparticles from aggregation at physiological pH and salt concentration. The polymer gives the nanoparticles the colloidal and chemical stability necessary for biomedical applications. XPS was used to elucidate the mechanism of surface-induced polymerization of gallic acid. The high-resolution XPS spectra of O, C, and Fe in a polygallate-coated magnetic nanoparticle sample are shown in Fig. 6. The FeIII/FeII atomic ratio at the surface of polygallate-coated magnetic nanoparticles, as calculated from the FeIII and FeII 2p peak areas, decreases from 2 in bulk magnetite (Fe(III)2Fe(II)O4) to 1.77.
 | ||
| Fig. 6 O 1s, C 1s, and Fe 2p spectra of the (top row) original and (bottom row) acidified polygallate-containing magnetic nanoparticles (bottom row) aged for 4 weeks at pH ∼ 6.5 in 10 mM NaCl (reproduced from ref. 201 with permission from Am. Chem. Soc., copyright 2014). | ||
This decrease indicates that iron is reduced at the surface of the nanoparticle by gallic acid. The C 1s peaks of polygallate-coated nanoparticles were assigned to aromatic carbons (C–C, 284.72 eV), phenolic OH groups (C–O, 285.6 eV, alcohols and ethers), carboxylic groups (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O, 288.87 eV, carboxylic acids and esters) and carbonates (O–CO2, 290.58 eV). The carbonate contamination in the polygallate-coated magnetic nanoparticle is due to the prolonged surface polymerization process under ambient conditions. The carbonate was successfully removed by acidifying the dispersions to pH ∼ 4 using HCl (Fig. 6, bottom row). Iron reduction is accompanied by the oxidation of gallic acid as inferred from the doubling of the O
C–O, 288.87 eV, carboxylic acids and esters) and carbonates (O–CO2, 290.58 eV). The carbonate contamination in the polygallate-coated magnetic nanoparticle is due to the prolonged surface polymerization process under ambient conditions. The carbonate was successfully removed by acidifying the dispersions to pH ∼ 4 using HCl (Fig. 6, bottom row). Iron reduction is accompanied by the oxidation of gallic acid as inferred from the doubling of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O/C–O ratio in the coating layer relative to its original value in gallic acid: 0.675 and 0.33, respectively. These XPS results elucidated the mechanism of chemical stabilization of iron oxide nanoparticles by polygallate.
C–O/C–O ratio in the coating layer relative to its original value in gallic acid: 0.675 and 0.33, respectively. These XPS results elucidated the mechanism of chemical stabilization of iron oxide nanoparticles by polygallate.
The biomedical applications of magnetic nanoparticles are strongly dependent on their size, coating layer, morphology, colloidal stability, magnetic and electronic properties, biocompatibility and biodegradability.42,192,193,209,210 The functionalization of magnetic nanoparticles with different biocompatible molecules influences the cytotoxicity and interaction with biological cells.211 The differences in the cytotoxicity on HeLa cells of magnetite nanoparticles functionalized with succinic acid(I), L-arginine(II), oxalic acid(III), citric acid(IV) and glutamic acid(V) have been evidenced. XPS analysis of the chemical composition and the chemical states of the elements at the surface of MNP coated with different molecules highlighted the main peculiarities responsible for the differences in the cytotoxicity of these nanoparticles.
A correlation between the surface properties of functionalized MNP and the cytotoxicity tests on HeLa cells has been found.211 The cytotoxicity of functionalized MNP with different coating layers decreases in the following order: oxalic acid > succinic acid > glutamic acid > citric acid > L-arginine. The highest cytotoxicity was obtained for MNP coated with a smaller thickness of molecular layers with the highest content of oxygen and carbon–oxygen groups, the highest ratio of O2− and OH− to C sp2 hybridization on the surface, and the highest ratio of adsorbed O−and OH− to C sp2 hybridization.211
Because the nature of surface coating influences the properties of nanomaterials, the XPS analysis of the chemical states of surface atoms is very important to evaluate the appropriate coating layer to provide a high level of biocompatibility, colloidal stability of the nanoparticles, and functional groups for specific applications.
Compositional tuning of magnetic nanoparticles is a promising strategy to tailor their magnetic properties and to improve the performances for magnetic hyperthermia application. Recently, ferrofluids composed of magnetite (Fe3O4, MION) and cobalt-doped magnetite (Cox-MION, x = 3, 5, and 10% mol of cobalt) coated with a biocompatible organic layer carboxymethylcellulose (CMC) have been reported.212 The highest hyperthermia efficiency was observed for Co10-MION@CMC nanocolloids due to the increase of magnetic anisotropy. The cobalt doping of iron oxide nanoparticles may represent a valuable strategy to improve the magnetic hyperthermia performance of nanoparticles for applications in cancer therapy.
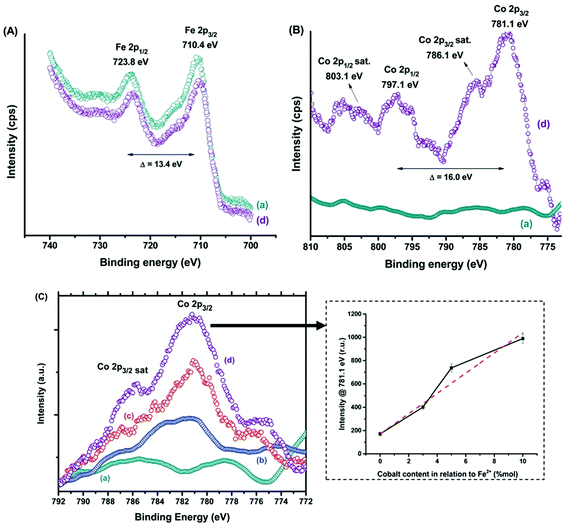
Fig. 7 shows both Fe(II) and Fe(III) species, the spin–orbit components (Fe 2p3/2 and Fe 2p1/2) being separated by a binding energy interval of approximately 13.4 eV. The XPS spectrum of Fe 2p for the sample Co10-MION@CMC is similar to the spectrum for MION@CMC (Fig. 7A, spectra (a) and (d)). Due to the substitution of iron by cobalt, a slight decrease in the intensities of the Fe 2p peaks is observed for the sample Co10-MION@CMC. In Fig. 7B the spectrum (d) of Co10-MION@CMC shows two peaks located at 781.1 eV (Co 2p3/2) and 797.1 eV (Co 2p1/2) ascribed to Co 2p transitions in cobalt doped magnetite nanoparticles. The satellite peaks for Co 2p3/2 and Co 2p1/2 located at 786.1 eV and 803.1 eV, respectively, confirm the presence of divalent cobalt.213 A comparison of Co 2p3/2 spectra (Fig. 7C) for MION@CMC (a), Co3-MION@CMC (b), Co5-MION@CMC (c) and Co10-MION@CMC (d) evidences that with the cobalt content increase, the Co2p3/2 peak becomes stronger and sharper which was well correlated by linear regression (Fig. 7C, inset).
 | ||
| Fig. 7 XPS spectra of (A) Fe 2p and (B) Co 2p regions for (a) MION@CMC and (d) Co10-MION@CMC. (C) Spectra of the Co 2p3/2 region for (a) MION@CMC, (b) Co3-MION@CMC, (c) Co5-MION@CMC, and (d) Co10-MION@CMC. Inset: evolution of intensity at the Co 2p3/2 peak with increasing cobalt content (reproduced from ref. 212 with permission from Royal Soc. Chem., copyright 2021). | ||
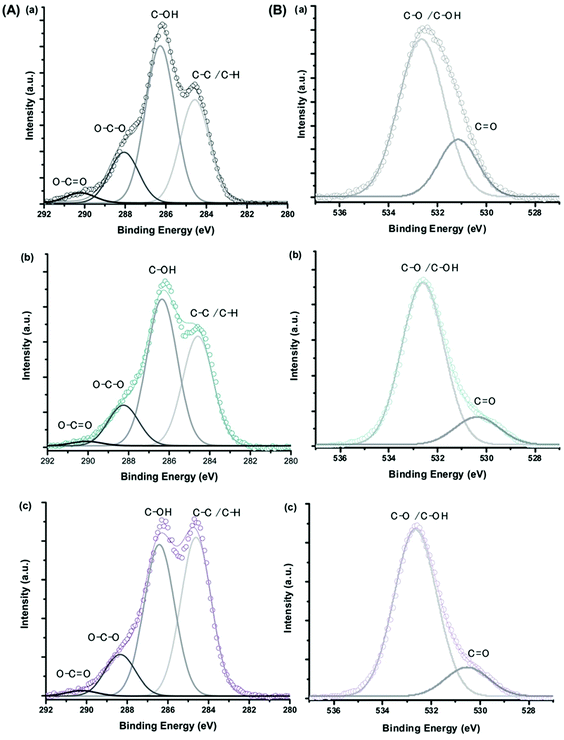
The XPS spectra of C 1s and O 1s for CMC polymer, MION@CMC and Co10-MION@CMC samples (Fig. 8) show the different chemical states of carbon (C–C/C–H, C–OH, O–C–O, and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O) and oxygen (C–O/C–OH and C
C–O) and oxygen (C–O/C–OH and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) ascribed to the CMC polymer.214 The changes in the relative intensities of the component peaks evidenced the interactions between the functional groups of the polymer and metallic ions at the nanointerfaces.
O) ascribed to the CMC polymer.214 The changes in the relative intensities of the component peaks evidenced the interactions between the functional groups of the polymer and metallic ions at the nanointerfaces.
 | ||
| Fig. 8 XPS spectra of (A) C 1s and (B) O 1s regions obtained for (a) CMC ligand, (b) MION@CMC, and (c) Co10-MION@CMC (reproduced from ref. 212 with permission from Royal Soc. Chem., copyright 2021). | ||
3.3 Mössbauer spectroscopy
Most of the applications of ferrofluids are related to sensoristic and actuating capabilities of magnetic nanoparticles and therefore depend on two main issues: their magnetization values and specific relaxation behavior. Although pure metals especially Fe possess the highest saturation magnetization, they are toxic and sensitive to the subsequent oxidation and aging effects and therefore are not relevant especially for bio-medical applications.215 This is why mainly Fe oxide nanoparticles (e.g. different types of ferrites, MFe2O4 with M = Fe, Co, Zn, Ni, Mn, or γ-Fe2O3) were considered as the most appropriate magnetic constituents of ferrofluids for more than 50 years, being at the same time stable and easy to properly functionalize. Actually, Fe oxide nanoparticles are additionally covered by an organic (polyethylene glycol, polyvinyl alcohol, dextran-based coatings, and chitosan) or inorganic (gold and silica) coating, assuring not only an enhanced colloidal stability but also increased bio-medical safe compatibility.216 It is worth mentioning here that the mix of specific size and surface effects due to nanoparticle coating as well as the substitutional degree of transition metal ions M in various ferrites may lead to a large flexibility in tuning the associated magnetic properties of the constituent nanoparticles and hence the magnetic response of the ferrofluid.Having in mind that ferrofluids are mainly based on Fe containing nanoparticles, 57Fe Mössbauer spectroscopy represents a powerful technique for the investigation of the magnetic properties of nanoparticles in ferrofluids, in close relation to the local structure and atomic configuration responsible for such properties. 57Fe (2% natural abundance) is the most convenient Mössbauer isotope concerning both the resolution of the Mössbauer spectra and the magnitude of the effect.217 Mössbauer spectroscopy is a nuclear resonance spectroscopy which is based on the resonant emission/absorption of the γ radiation without loss of energy due to the recoil of the nucleus. In classical configuration, the tuning of the frequency of incoming photon over the resonance energy/frequency is realized by the Doppler effect. The spectrum consists of the intensity of the absorbed/reemitted radiation (following Mössbauer events) versus the relative velocity between an oscillatory moving radioactive source (e.g.57Co in Rh matrix) and the absorber (Fe oxide nanoparticles from a dried ferrofluid or even a frozen ferrofluid). A nuclide with identical local configuration as in the source would absorb the incident radiation at zero relative velocity between the source and absorber. A different local configuration of Fe in the sample gives rise to very small additional shifts or splittings of the nuclear levels, due to the additional hyperfine interactions of the nucleus with the specific electron surroundings. Only the range of these perturbations induced by the hyperfine interactions is tuned via the Doppler effect. One (singlet), two (doublet), or six (sextet) resonant absorption lines can appear, depending on the specific electronic configuration of the Fe atom/ion. These specific patterns of the Mössbauer spectrum are described by the so-called hyperfine parameters: isomer shift (δ), measured via the shift of the single absorption line or of the symmetry center of the doublet with respect to a reference velocity, quadrupole splitting (Δ), measured via the splitting of the doublet, and hyperfine magnetic field (Bhf), measured via the magnetic splitting of a sextet.
In the case of ferrite nanoparticles, due to the different electronic configurations of Fe (Fe2+ or Fe3+ ions, octahedral or tetrahedral configurations, surface versus bulk positions, etc.) the Mössbauer spectra can be decomposed into different spectral components and fully analyzed with respect to the associated hyperfine parameters. Isomer shifts offer information about the valence state and local atomic configuration of the central Fe, whereas the quadrupole splittings offer information about the components of the electric field gradients, counting therefore on various distortions of the electronic configurations as well as of the crystal field components. The magnetic hyperfine field is specific only to the sextet pattern and can be uniquely determined from the nuclear magnetic splitting, caused by the interaction between the nuclear spin and the local magnetic field, Bhf, generated at the nucleus by the surrounding electrons. This hyperfine magnetic field, Bhf, is proportional to the iron net magnetic moment and is anti-parallel to it, if the Fermi contact term is highly dominant.218 In the magnetic ordered state, the relative intensity of the second and fifth Mössbauer lines of the sextet is influenced by the direction of the local magnetic moment (Fe spin) with respect to the direction of the incident γ-radiation. Quantitatively, the angular spin configuration may be analyzed starting from the intensity ratio between the second (or fifth line) and the third (or the fourth) line of the sextet component: R23 = I2/I3 = 4sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/(1 + cos2
θ/(1 + cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) with θ the angle between the Fe spin direction and the γ-ray direction.219 In a perpendicular geometry (γ-radiation perpendicular to the sample plane), R23 = 4 shows Fe spins perpendicular to the direction of the γ-radiation (θ = 90 deg), whereas for R23 = 0 the spins are oriented along the direction of the γ-radiation (θ = 0 deg). Intermediate orientations of the spins are reflected by R23 values between 0 and 4. Hence, any magnetic texture in the sample connected to the possible magnetic anisotropy axis can be deduced by Mössbauer experiments. On the other hand, the proportionality between Bhf and the electronic magnetic moment of the involved Fe atom/ion can be translated also in terms of the magnetic moment dynamics/relaxation. Typically, the magnetic relaxation phenomena are induced by increasing the temperature of the sample. A faster dynamics activated at higher temperatures may lead to a time averaged magnetic moment approaching zero, which is equivalent to a collapsing behavior of the Mössbauer spectral component from a sextet-like to a doublet/singlet-like pattern with increasing temperature. Therefore, 57Fe Mössbauer spectroscopy is a powerful investigation technique of magnetic nanoparticles in ferrofluids which provides direct information about the iron distribution and phase composition of nanoparticles in the sample, as well as on the angular and temporal evolutions of the different magnetic configurations of Fe. Mössbauer spectroscopy can be applied only in the case of bonding the sensitive Fe nuclei in the solid state. In the case of very fine nanoparticles (a few nm in size) dispersed in the liquid state, the Brownian movement and the weakness of bindings lead to quite reduced Mössbauer effects, especially in ferrofluids of low volume fractions and hence to prohibitive acquisition times of convenient spectra. While the magnetic relaxation behavior is investigated by the temperature evolution of the acquired spectra, the overall investigation time becomes prohibitive and the methodology for the separation of the Brownian versus Néel relaxation effects is quite complex. However, at this moment, both suitable methodologies for the investigation of the Brownian relaxation effects and fast acquisition by synchrotron-based Mössbauer techniques (time and energy resolved as well) are available.
θ) with θ the angle between the Fe spin direction and the γ-ray direction.219 In a perpendicular geometry (γ-radiation perpendicular to the sample plane), R23 = 4 shows Fe spins perpendicular to the direction of the γ-radiation (θ = 90 deg), whereas for R23 = 0 the spins are oriented along the direction of the γ-radiation (θ = 0 deg). Intermediate orientations of the spins are reflected by R23 values between 0 and 4. Hence, any magnetic texture in the sample connected to the possible magnetic anisotropy axis can be deduced by Mössbauer experiments. On the other hand, the proportionality between Bhf and the electronic magnetic moment of the involved Fe atom/ion can be translated also in terms of the magnetic moment dynamics/relaxation. Typically, the magnetic relaxation phenomena are induced by increasing the temperature of the sample. A faster dynamics activated at higher temperatures may lead to a time averaged magnetic moment approaching zero, which is equivalent to a collapsing behavior of the Mössbauer spectral component from a sextet-like to a doublet/singlet-like pattern with increasing temperature. Therefore, 57Fe Mössbauer spectroscopy is a powerful investigation technique of magnetic nanoparticles in ferrofluids which provides direct information about the iron distribution and phase composition of nanoparticles in the sample, as well as on the angular and temporal evolutions of the different magnetic configurations of Fe. Mössbauer spectroscopy can be applied only in the case of bonding the sensitive Fe nuclei in the solid state. In the case of very fine nanoparticles (a few nm in size) dispersed in the liquid state, the Brownian movement and the weakness of bindings lead to quite reduced Mössbauer effects, especially in ferrofluids of low volume fractions and hence to prohibitive acquisition times of convenient spectra. While the magnetic relaxation behavior is investigated by the temperature evolution of the acquired spectra, the overall investigation time becomes prohibitive and the methodology for the separation of the Brownian versus Néel relaxation effects is quite complex. However, at this moment, both suitable methodologies for the investigation of the Brownian relaxation effects and fast acquisition by synchrotron-based Mössbauer techniques (time and energy resolved as well) are available.
Two different situations can be considered in the case of Fe oxide/ferrite nanoparticles in ferrofluids at low temperatures, corresponding to the magnetic frozen regime: (i) a finite number of Fe configurations can be distinctly observed in well crystallized nanoparticles and (ii) poorly crystallized very fine nanoparticles where the Fe configurations present a quite continuous electronic distribution. Note that in both cases one deals with magnetic monodomain nanoparticles while the specific size of Fe oxide/ferrite nanoparticles used in classical ferrofluids is always lower than 60 nm, as a prerequisite of magnetic monodomain behavior.219,220 The two different cases differ by only the way of suitable fitting and interpretation of the Mössbauer spectra (distinct Mössbauer components versus hyperfine field distributions) under conditions that a similar methodology of investigation is used, as follows: (i) Mössbauer measurements at low enough temperature are performed for assuring the magnetic frozen regime (no magnetic relaxation is in action) in order to provide information about the intimate spin structure responsible for a suitable magnetic response and (ii) temperature dependent Mössbauer spectra are collected for in depth investigation of magnetic relaxation phenomena of nanoparticles in specifically engineered ferrofluids.
The first discussed case is ferrite nanoparticles, of large enough size (some 60 nm) in order to neglect the surface effects and to provide a distinct number of crystalline configurations and a blocking temperature much higher than RT as well. Mössbauer spectra of hydrophilic magnetite Fe3O4 and Mn ferrite MnFe2O4 nanoparticles, where the initial hydrophobic oleic acid surfacted shell has been transformed by a simple and environmentally friendly oxidative scission method into an azelaic acid (AZA) shell,221 are shown in Fig. 9.
 | ||
| Fig. 9 Mössbauer spectra of hydrophilic Fe3O4–AZA (left) and MnFe2O4–AZA magnetic nanoparticles (right) at various temperatures in the magnetic frozen regime. In the middle there are the hysteresis loops collected at 10 K on Fe3O4–AZA (A1) and MnFe2O4–AZA (B1) (reproduced from ref. 221 with permission from Am. Chem. Soc., copyright 2021). | ||
The spinel structure of general formula AB2O4 consists of a face centered cubic oxygen (O) array with 8 formula units and with divalent or trivalent transition metal cations on the 8 tetrahedral (A) and 16 octahedral (B) positions.219 In the case of spinel ferrites, MFe2O4, Fe is the trivalent transition metal cation, whereas the other transition metal M is a divalent cation. There are two structural limits of such compounds: (i) the normal spinel ferrite, with Fe3+ ions located on all the 16 octahedral positions and with M2+ ion on all the 8 tetrahedral (B) positions, and (ii) the inverse spinel ferrite, with Fe3+ ions on all the 8 tetrahedral positions and the 16 octahedral positions equally shared by Fe3+ and M2+ cations. Usual spinel ferrites as magnetite, Mn or Co ferrite show theoretically an inverse spinel structure. In these conditions, as a direct example, the formula unit (f.u.) of magnetite can be symbolically written in order to show also the theoretical cation occupancy as Fe3+[Fe3+ Fe2+]O4, with the octahedral positions in brackets. From the magnetic point of view, the oxygen mediated exchange interactions among the magnetic ions lead to ferromagnetic coupling between Fe ions which occupy cation positions of the same type (either tetrahedral or octahedral) and antiferromagnetic coupling between Fe neighbors belonging to different positions. As a consequence, in the case of inverse spinels (as most of the ferrite nanoparticles used in ferrofluids are) the formula unit is composed of the two Fe3+ ions (on A and B positions) which compensate for their magnetic moments, and the divalent metal (Fe2+ or Mn2+ or Co2+) which gives also the overall magnetic moment per formula unit. At low temperature, the magnetic moment of Fe3+ ions (and hence, their hyperfine magnetic field) is slightly higher on the octahedral positions than in the tetrahedral ones, and even much larger than that of the Fe2+ ions (e.g. 5μBvs. 4μB), making a clear distinction between the different configurations of the Fe ions in the spectra. The 3 spectral components observed in the Mössbauer spectra collected at 6 K on the 2 illustrative samples Fe3O4-AZA and MnFe2O4-AZA correspond to octahedral Fe3+ (the most external sextet), tetrahedral Fe3+ (the next external sextet) and octahedral Fe2+ (the inner sextet). The occupancy of these positions can be estimated from the relative spectral area of the components. An additional electronic aspect can be investigated by the interpretation of the Mössbauer spectra collected at higher temperatures, but still in the magnetic frozen regime. It can be observed that above 150 K the spectra can be suitably fitted by only 2 spectral components, assigned this time to trivalent Fe on tetrahedral positions (the most external sextet) and Fe ions with intermediate valence (between 2 and 3) on octahedral positions (the inner sextet). That is due to the typical Verwey transition which can appear in such compounds if the particle size is not too small. At temperatures higher than the Verwey transition temperature (e.g. 120 K in bulk magnetite, but lower in magnetite nanoparticles of nanometer size) the thermal energy activates the delocalization of an electron between the Fe2+ and Fe3+ neighbours on the octahedral positions. Hence, above the Verwey transition, the relative area of the 2 spectral components provides direct information on only the occupancy of the tetrahedral and octahedral positions, which coupled with the additional information on site occupancy by the type of Fe ions, obtained below the Verwey transition, offers a first hint on the inversion degree in the studied ferrite nanoparticles. Finally, by corroboration of all the above results on site occupancy (provided by Mössbauer spectroscopy) and spontaneous magnetization (provided by the magnetization curves presented also in the same Fig. 9) and taking into account the type of magnetic coupling between ions on different sites as well as the values of their atomic magnetic moments, the following configurations per formula unit are deduced:221 [Fe0.32+Fe0.73+]Tetra[(Fe0.72+Fe0.73+)Fe0.63+]OctaO4 in the case of Fe3O4-AZA and, respectively, [Mn0.22+Fe0.83+]tetra[(Mn0.82+Fe0.83+)Fe0.43+]octaO4 in the case of MnFe2O4-AZA.
The full magnetic configurations of the above spinel structures were obtained due to the possibility to observe in the low temperature Mössbauer spectra distinct Mössbauer components assigned to different Fe positions both below and above the Verwey transition. However, in the case of ferrite nanoparticles of much lower size (below 10–15 nm) the crystalline structure becomes more defective and the Verwey transition is canceled out. Hence, the correct separation of the Mössbauer spectral components is hardly achievable and a much easier and reliable interpretation of the Mössbauer data can be obtained only in high applied magnetic fields. Two are the main consequences of the applied magnetic field on the low temperature Mössbauer spectra:222 (i) an almost complete reorientation of the net magnetic moments along the field direction is produced in high enough magnetic field and (ii) an effective magnetic field is measured, as composed by the vectorial sum of the applied magnetic field and the internal hyperfine magnetic field. In the case of the ferrite nanoparticles, once the net magnetic moment of the ferrimagnetic structure is oriented along the field direction, the effective fields on the two positions of Fe (octahedral and tetrahedral) with opposite directions of hyperfine magnetic fields (order of 50 T) with respect to the applied magnetic field (order of T) are obtained as follows: the effective field for the position with the internal field pointing along the applied magnetic field is obtained by adding the applied field to the hyperfine magnetic field, whereas the effective field for the position with the internal field pointing against the applied magnetic field is obtained by subtracting the applied field from the hyperfine magnetic field. As a result of the applied magnetic field, two Mössbauer spectral components which are rather superposing under zero applied field transform into one more split component and one less split component, depending on the site occupation (octahedral versus tetrahedral).
This procedure was initially applied on 3 different samples:223 FF1 (ferrofluid of Co ferrite nanoparticles of average size of 3.3 nm), FF2 (ferrofluid of Co ferrite nanoparticles of average size of 7 nm) and PR2 (the precursor of FF2 consisting of powder of Co ferrite nanoparticles of average size of 7 nm, covered by an organic surfactant). The Mössbauer spectra collected at 10 K, without and with a 6 T applied magnetic field along the propagation direction of the γ rays, have been fitted by two sextet components, the most intense assigned to octahedral positions and the less intense to tetrahedral positions. As expectedly, under the applied field the magnetic splitting of Fe on octahedral positions is diminishing (the octahedral positions provide the effective magnetic moment per u.f. which is oriented along the field direction, with the antiparallel hyperfine magnetic field pointing against the field direction), whereas the magnetic splitting of Fe on tetrahedral positions is increasing. The larger the particle size, the larger the component separation and the lower the intensity of second/fifth lines in the spectrum, both aspects pointing to a better classical antiferromagnetic spin structure of larger nanoparticles. The fact that even under 6 T applied field, there are still finite intensities of the second/fifth lines (of much larger values for finer nanoparticles) stands on the fact that not all the spins in the nanoparticles are aligned along the applied field, which can be correlated with the presence of a dead magnetic layer (with random spin orientation) at the particle surface, thicker for lower sized nanoparticles. Such spin canted shells at the nanoparticle surface can nevertheless influence the spontaneous magnetization of nanoparticles and hence their magnetic response.
A more detailed analysis refers to the nanoscale size effects on surface spin canting in Fe oxide nanoparticles.224 Fe oxide nanoparticles with spinel structures of various mean diameters between 3 nm and 9 nm, without and with a capping layer of organic surfactant molecules, have been prepared by the microemulsion route. The Mössbauer spectra acquired at 4.2 K and in 5 T applied magnetic field on such samples are shown in Fig. 10. The interpretation of the authors was for a best fit obtained via 3 spectral components, with the most intense sextets as due to trivalent Fe in tetrahedral positions (the most external one) and in octahedral positions (the next split one), respectively. The most inner and less intense sextet was attributed to divalent Fe in octahedral positions of magnetite. Due to the much lower relative area of the last component than expected from an inverse spinel structure (e.g. 33% according to the formula Fe3+[Fe3+Fe2+] it was concluded on the formation of a thin maghemite (γ-Fe2O3) shell at the surface of magnetite nanoparticles (by an enhanced surficial oxidation of magnetite). While maghemite contains only Fe3+ ions, the Mössbauer spectra will be characterized by a much enhanced relative fraction of trivalent ions with the deviation of the relative spectral area of the divalent Fe from the standard 33% value, providing information on the thickness of the more oxidized shell. At the limit, its relative spectral area approaching 33% means almost no oxidized shell, whereas the relative spectral area approaching 0% means completely oxidized maghemite nanoparticles. Indeed, it is observed that increasing the mean particle size, the relative spectral area of this component is slightly increasing, supporting the formation of a maghemite shell of about 1 nm at the nanoparticle surface. On the other hand, the same trend of the intensity of second/fifth absorption lines in the Mössbauer spectra as in the case of ref. 223 has been reported. The intensity of these lines is decreasing toward zero with increasing mean size of nanoparticles, showing specific spin configurations approaching the ideal ferrimagnetic one for 9 nm average size of the nanoparticle.
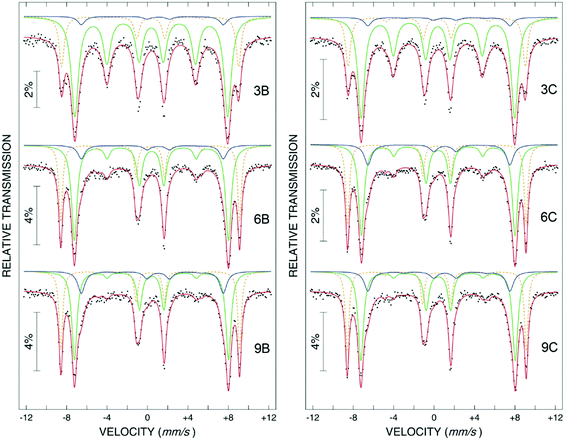 | ||
| Fig. 10 Mössbauer spectra of Fe oxide nanoparticles collected at 4.2 K in 5 T applied field along the direction of γ rays, as corresponding to samples xB (without caping layer) and xC (with caping layer), where x = 3 or 6 or 9, represents the mean diameter of nanoparticles in nm (reproduced from ref. 224 with permission from IOP Publishing, copyright 2012). | ||
It has been proven by computing R23 that the mean canting angle relative to the applied field is increasing with decreasing the size of the nanoparticles, by increasing the number of atoms at the particle surface relative to the bulk atoms. Moreover, an insignificant effect of the capping layer over the mean canting angle of the spins has been shown. It is of note that the interpretation of the less intense and less split sextet is different from the one provided by ref. 225 where this component was directly assigned to a dead surface layer with randomly distributed spins. However, the physical assignation of the spin configuration in such low size nanoparticles, especially in the case of continuously distributed atomic configurations, is challenging and still under debate. What is important for applications is the influence of the local spin configurations on the spontaneous magnetization and in this respect the main information is related to the relative number of the spins in the octahedral and tetrahedral sites with antiferromagnetic coupling and also to the relative number of spins in an eventually dead magnetic layer at the particle surface. Therefore, a general fitting procedure also has been developed for the Mössbauer spectra of defective spin ferrite nanoparticles in applied magnetic field, which is able to provide such information, Fig. 11.226
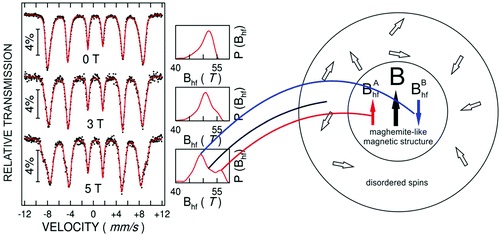 | ||
| Fig. 11 Mössbauer spectra of Fe oxide nanoparticles of 6 nm mean size, collected at 3 K under increasing magnetic fields up to 5 T applied perpendicular on the direction of γ rays and corresponding schematic representation of the spin structure of a nanoparticle. On the left side there are hysteresis loops of this sample, collected at different temperatures. Adapted with permission (reproduced from ref. 226 with permission from Nature, copyright 2020). | ||
The Fe oxide nanoparticles with a mean size of 6 nm have been obtained by laser pyrolysis and the Mössbauer measurements have been performed at 3 K in increasing applied fields. In the case of no applied magnetic field, the Mössbauer spectrum in the magnetic frozen regime does not show evidence for distinct Mössbauer spectral components and therefore has been fitted by a continuous distribution of Fe positions with distributed hyperfine fields. The distribution of probability for the involved hyperfine magnetic field is shown on the right side of each spectrum and the interpretation of the spectra has to be done in terms of either average or highest probable hyperfine magnetic field. The 5 T magnetic field applied this time perpendicular to the direction of gamma radiation induces the almost complete reorientation of the net magnetic moments of the ferrimagnetic structure along the field direction, an effect which is also clearly evidenced by the increased intensity of the second and fifth absorption lines of the sextet. The two resulting effective fields corresponding to the two local maxima in the probability distribution have to correspond to Fe spins opposite to the external field (B1 = 47 T) and along the external field (B2 = 57 T), respectively. In both cases the effective field is obtained by subtracting/adding the external field of 5 T to the internal hyperfine field of 52 T, specific to the maghemite-like structure and clearly evidenced by the single local maximum of the hyperfine field distribution in the zero-field case. For a defected spinel-like structure (cation deficient) as maghemite, the highest number of Fe3+ ions belongs to octahedral-like B and expectedly the corresponding effective field is the one with the lowest value. However, except the two types of spins leading in the probability distributions to the local maxima centered at 57 T and 47 T, respectively, there is still a finite probability to find Fe positions characterized in averaged by an effective field equating the internal magnetic field. This is possible only if the orientation of those spins is randomly distributed and a first assumption is for a magnetic dead layer formed at the particle surface. It is only a matter of suitable decomposition of the probability distribution of the hyperfine magnetic field under 5 T applied field in order to find the contribution of the spins in B-like sites, A-like sites and in the magnetic dead layer and to correlate such data with a spontaneous magnetization of only 30 emu g−1, provided by magnetic measurements.226 Accordingly, some 20% of the Fe3+ spins are in the magnetic dead layer, 55% with the spins along the applied field and 25% with the spins opposite to the applied magnetic field (to note the antiparallel orientation of the hyperfine magnetic field versus the direction of the spin/magnetic moment). Hence, only some 30% of Fe3+ spins contribute to the net magnetization (net magnetic moment per f.u.), in agreement with the observed spontaneous magnetization. Moreover, an exchange bias field of some 400 Oe is observed by in field cooling the sample at 5 K, which is direct evidence for an interfacial interaction between the magnetically disordered shell and the ferrimagnetic core of net magnetization of the nanoparticle. However, such hybrid magnetic nanoparticles with core–shell configuration and interfacial magnetic interactions provide versatile platforms for efficient hyperthermia applications via specific mechanisms described in ref. 227.
On the extended debate on the mechanism responsible for the reduction of the magnetization in fine Fe oxide nanoparticles (magnetic dead layer at the nanoparticle surface versus the uniform reduction of the magnetization in the nanoparticle core due to an overall spin canted structure), a recent study228 pointed to the so called antiphase boundary mechanism consisting in a shift of the Fe sublattice into an unchanged oxygen lattice, taking place everywhere in the volume of the nanoparticle. The presence of the antiphase boundaries was observed in surfacted iron oxide nanoparticles with a nominal size of 15 nm by high resolution transmission electron microscopy, being shown by Mössbauer spectroscopy at 4.2 K, the lack of a significant magnetic dead layer able to explain the much-reduced magnetization.
The heat transfer is counted by a power deposition term which in turn depends on the volume fraction of the nanoparticles in the ferrofluid, φ. The power deposition term, qp, which characterizes the energy transfer from the AC magnetic field to the ferrofluid (or specific tissue loaded by MNPs), is directly related to the so called specific absorption rate (SAR), with the usual meaning of power absorbed per mass unit of ferrofluid (W kg−1). Accordingly, SAR = P/m = c × ΔT/Δt = qp/ρ, with P being the power absorbed by the ferrofluid/tissue of mass m. Terms c and ρ are the specific heat and the density of the ferrofluid/tissue, respectively, and ΔT/Δt represents the rate of the temperature increment. SAR can be simply evaluated if the rate of the temperature increment is experimentally estimated in adiabatic like-systems.229
Whereas in the case of the heat transfer through hysteretic losses, only AC magnetometry can provide suitable explanation, in the case of the non-interacting magnetic nanoparticles in the dynamical magnetic regime (superparamagnetic regime), it has been shown in230 that only a susceptibility loss mechanism has to be considered (P ∼ χ″ where χ″ is the out of phase component of the magnetic susceptibility). Accordingly, the volumetric power is given by P = μ0πfH02χ0 × 2πfτ/(1 + (2πfτ)2) where τ is the effective relaxation time related to Brownian231 and Néel232,233 relaxation mechanisms characterized by the specific relaxation times τB and τN (1/τ = 1/τB + 1/τN). Further on, f and H are the frequency and the amplitude of the applied AC magnetic field, μ0 is the air permittivity and χ0 is the equilibrium susceptibility. The magnetic NP rotational mechanisms and equilibrium timescales in ferrofluids9,234,235 strongly depend on the physical and hydrodynamic sizes of particles. The Brownian relaxation time is given by τB = 3Vhη/(kBT), where Vh is the hydrodynamic volume, η is the carrier viscosity and kBT is the thermal energy. Introducing σ = KV/(kBT) – the nondimensional anisotropy energy (K-anisotropy constant and V-particle volume), the Néel relaxation time has the expression 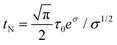 , where τ0 = Ms/(2αγK), α-damping constant (0.1−1.0), and γ-gyromagnetic ratio. Both Néel and Brownian relaxation times increase with the particle volume and decreases with temperature, but the involved dependences of the Néel relaxation time start to be much sharper above a critical volume, due to the exponential dependence (see more details in section 3.6.2). Therefore, depending on temperature and nanoparticle volume and magnetic parameters, one relaxation mechanism can dominate over the other mechanism, as graphically detailed in ref. 230. In the case of spherical magnetite nanoparticles at RT, the Néel relaxation strongly dominates for particle sizes lower than about 10 nm, whereas the Brownian relaxation dominates for sizes larger than 20 nm. In the case of ellipsoidal nanoparticles, not only the size, but also the aspect ratio dictates the magnetic relaxation regime and the heat transfer mechanism in ferrofluids can be optimized in respect to both geometric and magnetic parameters of nanoparticles.236
, where τ0 = Ms/(2αγK), α-damping constant (0.1−1.0), and γ-gyromagnetic ratio. Both Néel and Brownian relaxation times increase with the particle volume and decreases with temperature, but the involved dependences of the Néel relaxation time start to be much sharper above a critical volume, due to the exponential dependence (see more details in section 3.6.2). Therefore, depending on temperature and nanoparticle volume and magnetic parameters, one relaxation mechanism can dominate over the other mechanism, as graphically detailed in ref. 230. In the case of spherical magnetite nanoparticles at RT, the Néel relaxation strongly dominates for particle sizes lower than about 10 nm, whereas the Brownian relaxation dominates for sizes larger than 20 nm. In the case of ellipsoidal nanoparticles, not only the size, but also the aspect ratio dictates the magnetic relaxation regime and the heat transfer mechanism in ferrofluids can be optimized in respect to both geometric and magnetic parameters of nanoparticles.236
From the above discussions, it is clear that the realistic determination and tuning of the magnetic relaxation times (either Néel or Brownian) are crucial for the optimization of ferrofluids in respect to the desired applications. However, there are no direct experimental methods for their determination but only indirect ones and Mössbauer spectroscopy has been proven to be one of the most convenient.
The indirect way in the determination of the relaxation time in the case of the Néel relaxation is to correlate the temperature induced dynamics of magnetic moments to a specific trace in the temperature dependence of a convenient experimental parameter. In the case of magnetic monodomain nanoparticles the dynamics of each atomic magnetic moment (proportional to Bhf) is similar to that of the magnetic moments of nanoparticles which, in case of uniaxial magnetic anisotropy of the nanoparticle, may oscillate between two energy minima along the magnetic easy axis separated by the anisotropy energy barrier KV. Two regimes are considered for the thermally induced fluctuations over the anisotropy energy barrier, depending on the ratio r = kT/KV:219 (i) the regime of collective excitations for r < 0.1 when the magnetic moment oscillates slightly along the easy axis at the bottom of one energy minimum and (ii) the regime of superparamagnetic relaxation for r > 0.1, when the magnetic moment jumps over the energy barrier with the jumping frequency related to the inverse of the relaxation time. In the last case, for a particle of anisotropy energy K, the relaxation time, τN, equates the measuring time window τM at a certain temperature called the blocking temperature, TB. It is this TB the experimental parameter which can be derived from the experimental data in order to be related to the relaxation time or more precisely to specific parameters (e.g. τ0 and KT) defining uniquely the temperature dependent relaxation time. Whereas the blocking temperature can be obtained from the maximum of the zero field cooled magnetization curve or the in phase component of AC susceptibility curve,237 it can be also alternatively obtained from the temperature dependent Mössbauer spectra. The advantage in the last case refers mainly to applications of ferrofluids involving high frequency AC actuating magnetic fields (over hundreds of kHz), when the Mössbauer time window (5 × 10−9 s) is much closer to the inverse of the frequency. There are two ways of finding TB from the temperature dependent Mössbauer spectra in the collapsing regime from a sextet-like pattern to a singlet/doublet like one. The classical one238 assumes the fitting of the Mössbauer spectra collected at increasing temperature by a superposition of the sextet (dominant below TB) and singlet/doublet (dominant above TB) with TB derived as the temperature where the relative area of the sextet equates the relative area of the singlet/doublet components. The second one239 assumes the fitting of the temperature dependent spectra via a hyperfine field distribution and takes TB as the temperature where the reduced averaged hyperfine magnetic field <Bhf> decreases at half of its maximum value in the static regime at low temperature, <B0>, or where the relative width of the distribution reaches a maximum (Fig. 12).
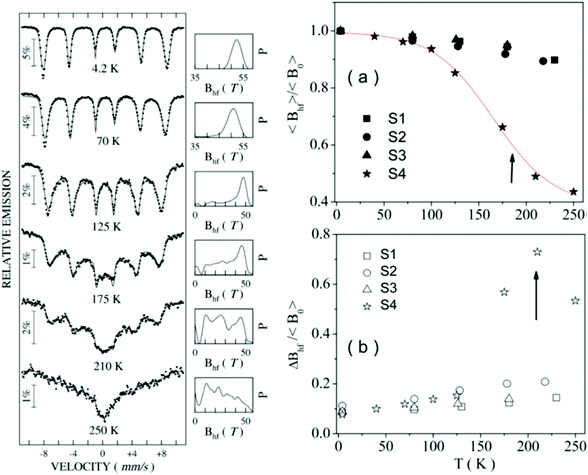 | ||
| Fig. 12 Temperature dependent Mössbauer spectra of a ferrofluid sample consisting of magnetite nanoparticles (about 10 nm size) dispersed in water (0.04 volume fraction) and covered by a double layer of auric acid (sample S4). The corresponding hyperfine magnetic field distribution probability is shown on the right size of each spectrum. Additional samples consisting of either magnetite (S2) or Co ferrite (S1 and S3) NPs with other coating double layers were measured. The temperature dependence of the relative average hyperfine magnetic field (a) and relative width of the hyperfine magnetic field distribution (b) are also presented and the specific trace leading to TB is presented by an arrow. Adapted and reproduced from ref. 239 with permission from IOP Publishing, copyright 2007. | ||
Once TB is experimentally derived via a measurement technique of known time window, τM, the specific equation of the Néel relaxation time is applied under the imposed conditions of T = TB and τN = τM. An equation connecting τ0 and KV results straightforwardly. It allows either the determination of the anisotropy energy KV, if τ0 is assumed, or of τ0 if KV is deduced by other means. The procedure is general and independent of the method of deriving TB, but the advantage of Mössbauer spectroscopy is the possibility to derive the anisotropy energy KV as well, by simply using the dynamic regime of collective excitation. By a suitable exploitation of the spectra at temperatures much lower than TB according to the second fitting procedure, the average hyperfine magnetic field or the width of the hyperfine magnetic field distribution is obtained along the early stage of relaxation. It has been proven that in this case both the reduced average hyperfine magnetic field and the reduced distribution width as well depend linearly on the temperature (see the corresponding temperature dependence of these parameters below 50–60 K in Fig. 12), with the corresponding slopes providing direct information on the average anisotropy energy <KV> and the relative dispersion of the anisotropy energy δ(kV)/<KV>, respectively.219 Hence, using Mössbauer spectroscopy in different relaxation regimes, a full set of parameters (the average anisotropy energy and its dispersion, the attempt time τ0, etc.) which characterize the Néel relaxation time is obtained. It is worth mentioning that these possibilities are valid in conditions of non-interacting nanoparticles (e.g. for ferrofluids of relatively low volume fractions), where the Néel expression of relaxation time is respected. By increasing the particle concentration, the interparticle interactions may modify the relaxation time and at the limit may lead to a new collective magnetic behavior (superferromagnetism, superspinglass) of the NPs in the ferrofluid.237 A critical discussion on the way that the superparamagnetic relaxation process governed by the Néel relaxation law can suffer due to interparticle interactions was reported in ref. 229. Under reasonable strong interparticle interactions (mainly of dipolar type) the Néel relation remains valid if two alternative corrections are applied: (i) the interactions are modelled by an increased anisotropy energy (KV)* meaning an equivalent increased effective anisotropy constant or effective magnetic volume of NP due to the interaction or (ii) the interactions are modelled by an additional temperature term T0, leading to an increased transition temperature to the superparamagnetic state. Keeping the procedure of defining TB from Mössbauer spectroscopy, increased effective anisotropy energies are expected in the case of increased interparticle interactions. It has been proven in the cases of three ferrofluid samples consisting of 10 nm size magnetite NPs coated with oleic acid and dispersed in a non-polar organic solvent that the effective anisotropy energy per nanoparticle as well as the way the nanoparticles become structured during the de-freezing process depends strongly on the volume fraction.240 The zero field cooling-field cooling (ZFC-FC) magnetization curves, representative temperature dependent Mössbauer spectra and the temperature evolution of the relative average hyperfine magnetic field of three samples FF1, FF2 and FF3 with volume fractions of 0.04, 0.15 and 0.2 were reported in that paper.
Using the slope of the linear decrease of the reduced average hyperfine magnetic field versus temperature in the regime of collective excitations, it has been shown that the effective anisotropy energy increases from 0.66 × 10−20 J in sample FF1 to 0.79 × 10−20 J in sample FF3, in close agreement with an increase of the TB deduced from magnetometry from about 95 K to about 120 K. It is worth mentioning that subsequent experimental and theoretical studies have proved that the interparticle interactions lead, in addition to an increased effective anisotropy energy, to an unexpected decreased attempt time τ0.229,241
Not only the Néel relaxation but also the Brownian relaxation can be studied by Mössbauer spectroscopy. Starting from the Einstein equation which expresses the average square displacement <x2(t)> of particles due to the Brownian movement (proportional to an infinitesimal short time t and the diffusion coefficient, D), an average velocity can be computed and transferred in terms of a second order Doppler shift. Due to the random movement of nanoparticles (and associated Fe atoms) an increased linewidth, ΔΓ, of the Mössbauer spectral line should be observed at increased temperature, due to the proportionality of the absorption line broadening to temperature. The slope of this increment is inversely proportional to both the hydrodynamic diameter of NPs and viscosity η of the ferrofluid, as main parameters which dictates also the Brownian relaxation time. Therefore, the suitable exploitation of the line broadening in the temperature dependent Mössbauer spectra can offer information about the Brownian relaxation within the condition to control an additional change of the spectral line shape due to the complementary Néel relaxation process. Different methodologies have been developed in this respect in the last years, according to reports.242–244
3.4 Magneto-optics: light scattering
Transmission electron microscopy investigations are limited to highly diluted and dried/vitrified samples; therefore, these refer mainly to particle size distributions, without details concerning structuring processes themselves, which require the use of various scattering techniques (Fig. 13). The ferrofluid structure–optical property relationship is closely tuned by composition, concentration and applied magnetic field.245–254 By applying a magnetic field, a preferential direction is established, leading to an optical anisotropy of the magnetic fluid. Magneto-optical effects, such as field induced birefringence, dichroism and light scattering, are in strong correspondence with particle morphology, magnetic relaxation processes, magnetic dipole–magnetic field and long-range dipole–dipole interactions,37,246,255,256 as well as formation of particle chains and more complex anisotropic structures.245,249–251,257,258 Unless highly diluted, the large number of dispersed particles makes ferrofluids opaque; however, when confined to optical paths of several hundreds of micrometers or less, they acquire the above mentioned magnetically controlled optical properties.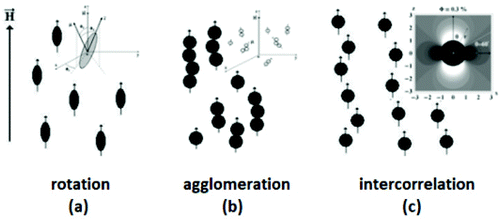 | ||
| Fig. 13 The three main magnetically induced structuring mechanisms on the nanoscale in ferrofluids: (a) rotation, (b) agglomeration, and (c) interparticle correlation. | ||
Magnetically induced optical anisotropy of ferrofluids is caused by three distinct structuring mechanisms: rotation, formation and correlation. The rotation mechanism (Fig. 13a) is due to hard (for Brown nanoparticles) or soft (for Néel nanoparticles) coupling between the nanoparticle's magnetic moment and anisotropy axis (shape and/or crystalline). Pure rotation theoretical models of ideal ferrofluids, i.e. non-aggregated ferrofluids, for magneto-optical phenomena (linear and circular dichroism and birefringence) were developed for Brown nanoparticles,246 and for Néel nanoparticles.259 The formation mechanism (Fig. 13b) is due to field oriented magnetically induced nanoparticle linear chains. Already early investigations245,260–265 revealed that chains or more complex rod-like aggregates formed in magnetic field convey reversible optical anisotropy properties to ferrofluids. If particles have anisotropic shapes, chains influence the induced birefringence only when the ferrofluid concentration is high enough.266 However, if the magnetic component of the ferrofluid consists in spherical nanoparticles the only source of optical anisotropy can be attributed to chains of nanoparticles.249,251,264,267–269 The correlation mechanism (Fig. 13c) is due to magnetically induced anisotropy of the nanoparticles’ pair correlation function.258,270–273
In the case of high colloidal stability low concentration ferrofluids particle clusters are practically absent; therefore, the rotation mechanism is the most plausible. During preparation nanoparticles with a non-ideal morphology result whose form can be approximated by an ellipsoid of revolution. In the rigid dipole model, it is usually assumed that the frozen magnetic moment is directed along the long axis of the particle. By applying a magnetic field, the orientational ordering of particles with Brownian relaxation confers anisotropic properties to the ferrofluid;37,246,255,256,259 hence, its polarization properties at optical frequencies may be described by the dielectric permeability tensor. To achieve a high degree of orientation a high magnetic field (the Langevin parameter ξ much higher than 1) and to the same extent, a high magnetic anisotropy of particles are necessary, σ ≫ 1. The field-induced magneto-optical effects in ferrofluids are 5–7 orders of magnitude higher than those observed in the case of molecular liquids.255,264 In the case of maghemite or magnetite ferrofluids only the particles with great enough sizes (8–10 nm or greater) have magnetic anisotropy energy of the order of thermal energy kBT (σ ≈ 1; soft dipole limit), while in ferrofluids with cobalt-ferrite nanoparticles (σ ≫ 1) these behave as rigid magnetic dipoles. The anisotropy field (Hani) linked to the anisotropy energy37 is much higher for Co-ferrite than for maghemite or magnetite nanoparticles274 and closely determines their mechanical response in solution (alignment of the particle body along the field) and the magneto-optic behavior, but in zero magnetic field both types of ferrofluids are optically isotropic. For highly stable diluted ferrofluids (up to 1–2% vol fraction) the field induced static birefringence Δn is proportional to the particle volume fraction and Δn ∼ H2,275 both dependences strongly indicating that in such colloids the effect is not due to a cooperative (agglomeration) process but to a single particle effect. The nonlinear fit of dichroism data from a ferrofluid with 2% volume magnetite nanoparticles dispersed in transformer oil, with the models for Brown246 and Néel259 rotation, proved the validity of the latter, leading to a realistic and closer to TEM value of the nanoparticle ellipticity.276 Dynamic magneto-optic effects in the case of cobalt-ferrite and maghemite MF samples with anisotropy fields differing by an order of magnitude reveal essential differences in what concerns the magnetic field dependence of the characteristic relaxation time.274 Magnetic field dependence of relaxation time is quite different for σ ≫ 1 compared to σ ≈ 1. The induced birefringence is linear with respect to the probing field and a model with linear response approximation, considering suspended nanoparticles with finite magnetic anisotropy of the easy axis type, describes well the experimental data.277 The significant difference between magneto-optical dynamical birefringence and low-field complex susceptibility278 or relaxation of magnetization279 measurements is that it only probes the mechanical rotation of the grains, being not directly sensitive to the Néel process.274
A common feature of the rotation models is the linear dependence of the effect on the nanoparticle volume fraction (Φ): Δn ∼ Φ. Experimental refutation of this feature led to early proof for the magnetically induced nanoparticle agglomeration.247,249,280 The influence of particle concentration on static birefringence and dichroism in the case of double layer steric stabilized diester based magnetic fluid samples reveals the effect of particle interactions already at 1% vol fraction, the departure from the ideal orientation theory increasing significantly for higher particle concentrations and quality of the colloidal stabilization.249,281,282
Full account of the nanoparticle aggregates’ contribution to the magnetically induced optical anisotropy in ferrofluids requires knowledge on both aggregate statistics and aggregate optical shape anisotropy. The first formation theoretical model of linear dichroism in ferrofluids249 was based on the statistical theory for rigid chain-like aggregates,283 the bidisperse nanoparticle distribution284 and the approximation of chains as revolution ellipsoids. The bidisperse distribution reduces the continuous distribution to two fractions, the small particles and the large ones, each fraction consisting of identical particles with the constant magnetic moment, and only the large particles aggregate in chains. The model, limited at low magnetic fields and by the rigid chain assumption, provides a good qualitative description of the nanoparticle concentration dependence of the magnetically induced dichroism in ferrofluids. A bidisperse nanoparticle birefringence model251 was limited to low and high magnetic field values. Applying the model in the case of two electrostatic stabilized samples investigated in ref. 259, the main fractions (90%–95%) consist of small particles with a magnetic core diameter of 7–9 nm, while the second fractions consist of a small number (5%–10%) of large particles of 15–18 nm. The model favors chains of up to 5 nanoparticles, which have in composition, besides large size particles, at most 2 small particles of less than 10 nm size and give a good correspondence with measured birefringence data.251,259 In the framework of a birefringence model limited to nanoparticle dimers, i.e. two nanoparticle chains,268 the fit of the theoretical estimate of birefringence to experimental data, the dependence on applied field and on the particle volume fraction both confirm the role of dimers in magnetic field induced anisotropy of highly diluted Co ferrofluids. A breakthrough in the analytical modeling of nanoparticle chaining in ferrofluids285 provides a full range magnetic field and ferrofluid concentration statistics of arbitrary long flexible nanoparticle chains. This model was used267 to calculate the influence of magnetically induced chains on polarized light extinction in ferrofluids, with the goal to explain experimentally measured field dependence of extinction of light polarized at 54.73° with respect to the magnetic field, which, according the orientation theory developed in ref. 286, should not depend on the external magnetic field. A further development of the analytical model of MNP chaining285 refers to the theory of magnetically induced dichroism in ferrofluids with bidisperse nanoparticle flexible chain-like aggregates.269 This improved model was used to fit dichroism experimental data from highly diluted and concentrated ferrofluid samples and thus determine the magnetic field dependence of (a) the n-particle chains’ mass weight, (b) average number of particles per chain, and (c) total chains’ mass weight. The total chains’ mass weight increased from 2.5% to 4% in the 0–300 kA m−1 field range, thus proving the sensitivity of the dichroism to the magnetically induced nanoparticle chain formation. Chains with up to 5 particles have significant mass weight and thus influence the magnetically induced optical anisotropy of the concentrated ferrofluid sample.
In the case of non-aggregated magnetic nanoparticles in concentrated ferrofluids the coupling between the magnetic dipole-field and the long-range dipole–dipole interactions leads to a magnetically induced anisotropy of the particle pair correlation function, which causes magnetically induced optical anisotropy.258,270–273 The specific dichroism in the case of a steric stabilized ferrofluid shows a concave shape dependence on solid volume fraction: it increases with increasing volume fraction in the region of diluted samples, but above Φmax volume fraction the specific dichroism decays, going negative above Φ0. Using the general theory for the influence of the pair correlation function on the optical anisotropy in ferrofluids,258 a bidisperse model was developed273 based on the bidisperse pair correlation theory.287 The bidisperse model accounts for the magnetic field dependence of Φmax and Φ0, which was not achieved by a monodisperse model.272,273
In real magnetic fluids with great polydispersity the particle sizes are usually in the interval 3–20 nm and the fraction of large size particles could induce the formation of clusters and also of more extended agglomerates. Clusters of magnetic nanoparticles of medium size, 20 < d < 100 nm, are frequently encountered especially in water based magnetic fluids.68,288–290 These “particles” are usually porous nanoclusters composed of smaller 10 nm superparamagnetic nanoparticles.291 The kinetics of aggregation for diluted water based ferrofluids (8 × 10−4–0.3%vol) was directly evidenced already in the presence of a very weak magnetic field (∼1 kA m−1) using a transmission light microscope.
Phase separation was observed in external uniform magnetic field manifesting by appearance of long needlelike aggregates extended along the direction of the applied field and growing with elapsed time. Two distinct phases are distinguished, the growth of individual aggregates by absorption of single MNPs from ambient fluid and the coalescence of neighboring aggregates occurring at longer elapsed times.291
Light scattering techniques are used also to probe the aggregation kinetics of magnetic colloidal systems in what concerns the formation and characteristic time of particle aggregates of various degrees of complexity. The time required for aggregation of individual particles and of linear aggregates (secondary aggregation) in a carrier liquid for a given external field is determined by the competing magnetic and viscous forces68,253,288,292–297 and depends on the particle size, number of particles in linear aggregates and external field strength, whereas the viscous force depends on the particle or aggregate size and viscosity of the carrier liquid (Fig. 14a). The randomly oriented dispersed Brownian particles undergo head-to-tail aggregation, forming chains aligned along the field direction, followed by lateral coalescence of the chains resulting in columns formed by secondary aggregation,257,298 a mechanism described in the framework of an extended version of the Halsey–Toor model of coarsening,299–302 proper to weak colloidal stability ferrofluids, magnetic emulsions and MR fluids. The aggregation kinetics of Brownian suspensions is described by the Vicsek–Family model of diffusion-limited aggregation of clusters (DLCA);303 the cluster size distributions as a function of cluster size and time obey a dynamic scaling form. In the case of non-Brownian particles of large sizes (14 μm) the dynamic scaling exponent z for the average cluster length S(t) ∼ tz was found to be strongly dependent on the magnetic-field strength;304 the scaling exponents smaller than 1/3 for values over 1000 of the dimensionless interaction strength λ are shown to be inconsistent with the DLCA model.
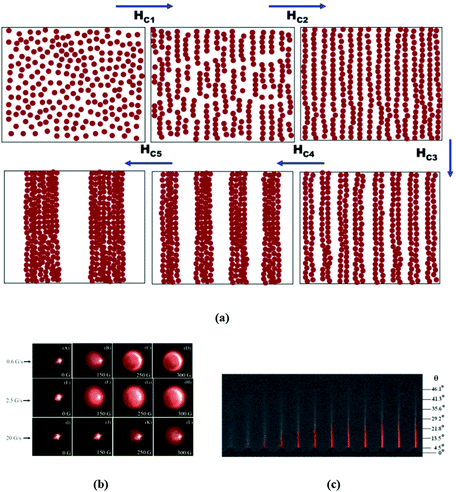 | ||
| Fig. 14 Primary and secondary particle aggregation. (a) Schematic of the arrangement of magnetic nanoparticles in the dispersion before and after aggregation at different critical fields HC1, HC2, HC3, HC4, and HC5 (reproduced from ref. 257 with permission from Am. Phys. Soc., copyright 2009). (b) Light scattering patterns from the nanofluid at different magnetic field values (during decrease) on a screen placed perpendicular to the field direction of incident light for ramp rates 0.6 G s−1 (A–D and M–P), 2.5 G s−1 (E–H), and 20 G s−1 (I–L)253 (reproduced from ref. 253 with permission from Am. Phys. Soc., copyright 2010). (c) Time evolution of the forward scattered light in transverse configuration at several values of the applied magnetic field (reproduced from ref. 305 with permission from Royal Soc. Chem., copyright 2013). | ||
In longitudinal scattering configuration, where the light propagation vector is parallel to the magnetic field direction (Fig. 14b), the scattered patterns and their corresponding surface plots at different magnetic field values for three different ramp rates, on decreasing the magnetic field to zero value, finally go back to the original diffused spot, indicating the reversibility of the aggregation process. Depending on the ramp rate a certain degree of hysteresis in the transmitted intensity curves is observed during the increase and decrease of magnetic field. Experiments in transverse scattering configuration, where the light propagation vector is perpendicular to the magnetic field direction with typical scattering patterns (Fig. 14c), were also used to probe the kinetics of the magnetically induced phase condensation in ferrofluids and bio-ferrofluids.68,288,305–307 The asymptotic critical condensation proposed in ref. 308 was experimentally observed in an aqueous ferrofluid: the critical temperature was 42.5 °C.306 Using the time evolution saturation values of the light extinction, the field dependence of the magnetic supersaturation (i.e. the total amount of magnetic material contained in the condensed phase) in a bio-ferrofluid can be calculated based on a model for the forward light scattering on the condensed phase drops [ref. 305, ESI]. Magnetically induced aggregation in a bio-ferrofluid under the action of high frequency (100 kHz) magnetic fields with amplitude as low as 4 mT was recently observed using light scattering experiments.307
3.5 Small-angle scattering and reflectometry
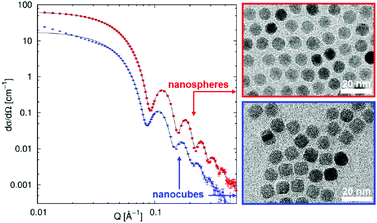 | ||
| Fig. 15 SAXS curves from diluted solutions of oleic acid-capped maghemite nanospheres and nanocubes in toluene combined with TEM image from dried samples (reproduced from ref. 314 with permission from IOP Publishing – Open Access, copyright 2012). | ||
Magnetic particles with shape anisotropy are of current interest. 2D scattering patterns become anisotropic after the particles are oriented in external magnetic fields. Thus, 2D SAXS from hematite spindle shaped particles in water revealed316 the elongation of the scattering pattern parallel to the applied field which corresponds to a preferential orientation of the long (polar) shape axis perpendicular to the applied field. So, this is the direct evidence that the particle magnetization is perpendicular to the long particle axis. These particles were additionally oriented in a magnetorheological setup combined with SANS.317
In SANS experiments, two contributions to the scattering are present, which are nuclear scattering (interaction of neutrons with atomic nuclei) and magnetic scattering (interaction of magnetic moments of neutrons and atoms).318 They are determined by the distributions of the nuclear and magnetic scattering contrasts, respectively. The distributions corresponding to the nuclear scattering can be varied with keeping the same chemical structure by isotope (hydrogen/deuterium) substitution in the system. In partially or fully deuterated carriers, the peculiarities corresponding to the hydrogen-containing components (such as particle coatings) become visible, thus opening more possibilities for studying the distribution of the scattering densities within particles. At the same time the magnetic contribution becomes significant and should be taken into account. As the first step, the SANS contrast variation with the measurements at different molar ratios H/D in the carrier can be applied to polydisperse ferrofluids using the extended classical approach based on modified basic functions.319,320 This way is valid for purely superparamagnetic systems in which no interference between nuclear and magnetic scattering takes place. The last property determines the fact that the magnetic scattering contribution is contrast independent, so the information about the nuclear and magnetic structures can be separated in the experiments on the contrast variation which is made for non-magnetized samples. Regarding the particle structure, the approach is most informative for organic ferrofluids with a single coating (chemisorption) of MNPs and minimum free surfactant in the carrier. Some parameters of complex particles, such as surfactant shell thickness and the volume fractions of the core and shell in the particles, are determined independently of the models (both for nuclear and magnetic scattering) probed in the treatment of the scattering curves in the next step, thus giving additional criteria of the self-consistency of the description of the particle nuclear structure. For ferrofluids with colloidal aggregation, the main contribution to the scattering comes from the aggregates. The obtaining of the information about single particles at different contrasts is possible only by modeling scattering curves (with assuming corresponding contrast distribution) at sufficiently large q-values, at which the aggregate effect is minimum. If such q-interval is resolved, with the simultaneous treatment of the scattering curves in the frame of one model one increases the reliability of the model probed, as well as achieving better precision of the varied parameters. The additional change in the contrasts can be achieved in the combined SAXS/SANS experiments with the same system. Two techniques have different contrast combinations between components for the same (from the viewpoint of the chemical structure) system under study. Moreover, other complementary data can be included in combined numerical modeling. An example is the combined analysis of the SAXS/SANS data together with the data of static light scattering (SLS) and isothermal magnetization from multi-core iron oxide nanoparticles (single core diameter of about 9 nm) embedded in poly(styrene) spheres (160 nm) immobilized and dispersed in water.321 This extended analysis of SAXS/SANS data (made in terms of the pair distance distribution functions obtained by numerical inversion, a special approach for the realization of the indirect Fourier transform method) strongly indicated that the cores were mostly accumulated in the surface layers of the poly(styrene) spheres.
SANS experiments concentrated on the analysis of magnetic scattering from ferrofluids are carried out in two modes: with non-polarized and polarized neutron beams. In both cases, non-magnetized samples give isotropic scattering patterns due to disorientation of the magnetic moments. When magnetized in an external magnetic field perpendicular to the neutron beam, due to the anisotropy of the magnetic scattering component, the scattering patterns become anisotropic and, using this anisotropy, it is possible to separate the nuclear and magnetic components of the scattering. Still, the two components do not interfere. When one employs a polarized neutron beam, the interference between two components appears which depends on the relative orientations of the beam polarization and sample magnetization. As a rule, two scattering patterns are measured with different relative orientations of the neutron spin (S = 1/2) regarding the external magnetic field. The analysis of the change in the neutron spin during scattering is not performed to save statistics. This option is known as SANSPOL. Now, one has two equations for the same system for separating the nuclear and magnetic scattering components, which gives more reliable results. However, due to polarization, the intensity of the initial beam is half less than the intensity of a non-polarized beam, which leads to a loss of statistics and requires more experimental time and better background conditions. This fact limits the SANSPOL application referred to the magnetic structure of single particles, since diluted samples with suppressed particle interaction are of interest. Also, for the most effective use of the SANSPOL option based on the interference between nuclear and magnetic scattering the polydispersity should be as small as possible to avoid the smearing of the interference effects. The classical ferrofluids with separated and well-defined composite nanoparticles seem ideal systems for fundamental studies on clarification of the reasons for reduced specific magnetization of magnetic nanoparticles as compared to bulk values. In particular, several attempts were made to resolve a magnetically dead layer in the near-surface vicinity of the particles due to a potential spin canting predicted earlier in some theoretical works.
Thus, SANSPOL was recently applied to organic (deuterated toluene) low-concentrated (<1 vol%) ferrofluids with oleic acid-capped maghemite nanospheres and truncated nanocubes314 and monodisperse iron oxide nanoparticles.228 The experiments showed a magnetically depleted surface layer about 0.3 nm thick with canted spins; however, the observed reduction in specific magnetization cannot be explained by this surface layer alone. So, a uniform reduction of the magnetization over the magnetic core volume was also concluded. In ref. 228, the precision was provided by the additional contrast variation and simultaneous fitting of the scattering curves obtained at five H/D contents in the solvent (Fig. 16). Antiphase boundaries in iron oxide nanocrystals were considered as the main contributors to the uniform reduction of the magnetization saturation based on the complementary data, which included extended magnetization analysis, HR-TEM of isolated nanoparticles and powder X-ray diffraction. To a lesser extent the effect was also related to iron cation vacancies in nanoparticles.
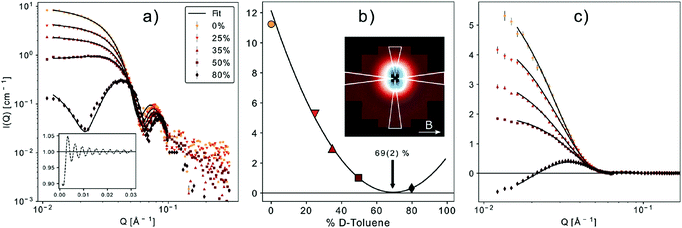 | ||
| Fig. 16 (a) SANSPOL from oleic acid coated iron oxide MNPs in toluene with 5 different contrasts (volume fraction of d-toluene is given in legends). The black line represents the best fit of a core–shell model with a sticky hard sphere structure factor (inset on the lower left). (b) Contrast matching. The minimum of the parabolic fit corresponds to the match point resulting in a core SLD of 6.8(2) × 10−6 Å−2. The inset shows the 2D-detector image for 50% d-toluene. (c) Fit of the magnetic-nuclear interference terms for the 5 contrasts. The only fit parameters are the magnetic scattering length density and thickness of a magnetically dead shell (reproduced from ref. 228 with permission from Royal Soc. Chem., copyright 2021). | ||
The magnetic contrast variation method extends the capabilities of the SANSPOL technique.322 In this case, only the Langevin function is varied in the expression for the magnetic scattering contribution with the external magnetic field growth, so one can fit different scattering curves simultaneously with the constraint of identical scattering amplitudes and the same particle size distribution for all curves, thus significantly increasing the precision of the structural parameters derived.
In some cases, despite comparatively low statistics, full polarization analysis in SANS is applicable to ferrofluids. For example, this concerns the comparison of multi-core bio-ferrofluids showing a strong difference in the internal magnetic (intracore) structure. Such kind of particle is of current interest for regulated magnetic hyperthermia (MHT). In ref. 323 commercial bio-ferrofluids were studied using unpolarized SANS combined with polarization analyzed SANS (PASANS). The systems under study comprised a mixture of Fe3O4 and γ-Fe2O3 with a shell or matrix of dextran suspended in water (total hydrodynamic diameter of about 115 nm). Analyzed by TEM the magnetic cores of the nanoparticles comprise several crystallites of magnetic iron oxide aggregated to form a single dense core having a nominal diameter from ≈50–60 nm to ≈100 nm, suggesting a diffuse loosely bound structure. Dynamic light scattering and even transmission electron microscopy data do not offer detailed information about the internal structure of composite nanoparticles. Intra-core magnetic interactions have to be properly accounted for a desired end-use – magnetic hyperthermia, magnetic drug targeting or magnetic separation – in order to ensure a proper balance among interaction strength, exchange coupling, and external magnetic field. Actually, the intra-core structure of magnetic particles of bio-ferrofluids has to be tailored by synthesis to the requirements of each application. As it is followed from the comparison of the magnetic scattering contributions, magnetic structures differ significantly among the particles, being responsible for both the mechanism of reorientation and the resulting energy dissipation in time varying magnetic field.
Recently, the same approach was applied324 to specific multicore particles with a dextran coating known as nanoflowers – densely packed aggregates of several iron oxide crystallites. Again, this type of particle has emerged as a promising candidate for MHT, providing phenomenal heating behavior due to the exchange coupling between the cores (superferromagnetic magnetization state). The comprehensive analysis including SANSPOL showed that the multi-core particles (size of about 39 nm) had an irregular shape with slight anisotropy. They preferentially magnetized along their longest dimension (due to shape anisotropy), but with a slight internal spin disorder/misalignment.
The better way to enhance the contrast in nanosystems is multiple-energy anomalous small-angle X-ray scattering (ASAXS). This technique takes advantage of the fact that for X-rays whose energy is close to the absorption edge of an element, the atomic scattering factor of that element is strongly reduced as compared to its value far from the edge, so that a contrast variation can be made by simply varying the energy of the incident X-ray photons. An example is composite magnetic nanoparticles in which an Fe3O4 core, as assumed, is surrounded by a (MnxFe1−x)3O4 shell.325 Here, SANS data even at high contrast ratio are not sufficient to distinguish whether their structure is closer to homogeneous or core–shell type. ASAXS data evidence the core–shell structure revealing the (MnxFe1−x)3O4 shell with a graded composition, ranging from x ≈ 0.40 at the inner shell to x ≈ 0.46 at the surface.
3.5.2.1 Particle interaction. For the analysis of various interactions in liquid colloidal systems, the structure factor S(q), Fourier transform of the radial distribution function, is experimentally obtained as a ratio between the scattering intensities for concentrated and diluted systems. In real (polydisperse) ferrofluids, this is mostly qualitative analysis of the characteristic spatial correlations, since modeling (like in the case of particle form-factor) faces principal difficulties. Nevertheless, such kind of analysis115,326–328 proved to be useful. The interaction of one-domain magnetic nanoparticles in a liquid carrier of ferrofluids can be considered in the first approximation in terms of the theory of dipolar liquids, in which magnetic dipole-dipole interaction competes with the Brownian repulsion strengthened in some cases with electrostatic repulsion (water-based ferrofluids with charged stabilization). The qualitative diagram of the states of a dipolar liquid, coupling parameter against particle volume fraction, for sterically stabilized ferrofluids327,329 shows several modes of interaction. From the point of view of the small-angle scattering experiment, each of the modes gives a specific structure-factor, which modulates the form-factor of individual spherical-like particles. A theoretical prediction is that even in the absence of the external magnetic field, there are thermodynamically stable chain-like aggregates, which takes place at a sufficiently strong coupling parameter. At low particle concentrations, the chain concentration is small, and they do not interact with each other. At high concentrations, it is difficult to analyze the chain interaction. That is why most of the structural experiments are made either for low concentration or for low coupling parameter. The hard sphere approximation (polydiperse case) proved to be applicable only for ferrofluids with rather thick surfactant coatings, such as magnetite with double layer (oleic acid plus dodecylbenzenesulphonic acid) coatings in alcohol (pentanol) and concentration below 5 vol%.147 Just only from the analysis of the structure-factor, which gave the total (magnetic core plus surfactant shell) size, the effective thickness of the coating was found to be smaller than the total length of the two surfactants, thus suggesting the overlapping of the surfactant layers. For higher concentration, the ‘softening’ (non-proportional growth) of the structure-factor peak (whose position corresponds to the inverse effective radius of interaction) is observed, indicating the effective interpenetration of the shells when the particles are in contact.
Regarding the structure-factor effects for ferrofluids with a low-coupling parameter, SANSPOL was applied to a classical type of low-polarity polydisperse ferrofluid (single coating of magnetite nanoparticles, size of about 10 nm, deuterated organic solvents).328,330 The nuclear and magnetic correlations were revealed and compared for the systems with moderate (about 1 vol%) concentrations. A main conclusion is that in this kind of system magnetic correlations between particles take place when the structure factor effect in the particle location is negligible. This fact was associated with the polydispersity of particles: the magnetic moment of small particles, which are in the vicinity of large particles and affected by their local dipole field, experiences an effect opposite to that of an external magnetic field. The situation was found331 to be opposite in aqueous polydisperse ferrofluids, where magnetic particles are electrostatically stabilized with adsorbed ions. The charge repulsion in them resulted in greater interparticle distances, so magnetic correlations were suppressed. But a strong structure-factor in nuclear scattering was observed, which is typical for charged particles. This example clearly shows that even in diluted ferrofluids the magnetic and nuclear correlations are complex and depend on the stabilization method.
In the cases when the magnetic scattering contribution is absent (SAXS) or can be neglected (SANS from fully protonated systems), for concentrated non-magnetized ferrofluids with good stabilization (low coupling parameter) and comparatively hard shells (single layered stabilization in low-polarity solvents or electrostatic stabilization in water), the repulsive component in the interaction potential results in the appearance of a pronounced peak in the structure-factor corresponding to the effective radius of short-range interaction. If the long-range attraction is not suppressed, then a central (q = 0) peak appears in the structure-factor. In low-polarity ferrofluids with sterical stabilization S(q) is dependent only on the particle concentration328 (Fig. 17a). In water-based ferrofluids with electrostatic stabilization the particle interactions can be continuously tuned by varying the ionic strength so that at some point the repulsive character is changed to the attractive one (Fig. 17b). Thus, at low ionic strength, the particle interaction potential is a strongly repulsive Yukawa potential, while for high ionic strength a globally attractive Lennard-Jones type potential results.332 The limit q = 0 for S(q) in this kind of ferrofluid is well used for estimating the osmotic compressibility of ensembles of nanoparticles in colloidal dispersions, which is used in the extended characterization of their concentration dependent properties, e.g. ref. 129. Under an external magnetic field, the structure-factor becomes anisotropic.119,333,334 The presence of such anisotropy (Fig. 17c) shows that there is a preferable positioning of the particles along the field direction around a reference particle, the effect of interaction of the oriented magnetic dipoles. In water-based ferrofluids with electrostatic stabilization, the anisotropy increases with increasing the ratio γ/Φ (ratio of Langevin parameter to particle volume fraction), thus allowing for a tuning of the amplitude of the magnetic field effect by varying both the particle concentration and magnetic moment. For such kind of ferrofluid, the ‘softening’ of the structure-factor is observed in extremely concentrated (∼30% vol.) samples (glassy samples). Still, the asymmetry in the structure-factor in the glassy state conserves (Fig. 17d).
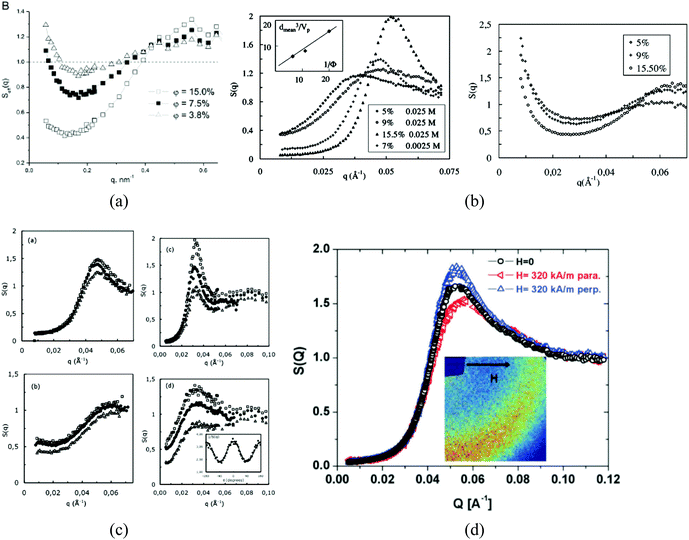 | ||
| Fig. 17 Effective structure-factors in 1D SANS in the absence of external magnetic field for (a) low-polarity ferrofluids (reproduced from ref. 328 with permission from Elsevier, copyright 2014) and (b) ionic water-based ferrofluids with low and high ionic strength (reproduced from ref. 332 with permission from Am. Phys. Soc., copyright 2003). Components of the effective structure-factors in 2D SANS parallel and perpendicular to external magnetic field for (c) ionic water-based ferrofluids (reproduced from ref. 333 with permission from Am. Chem. Soc., copyright 2006) and (d) glassy samples (reproduced from ref. 334 with permission from Royal Soc. Chem., copyright 2015). | ||
When magnetic scattering contribution is significant (SANS experiments with deuterated carriers), the total structure factor is a complex mixture of two correlated (nuclear and magnetic) components. The additional complication for the analysis is particle polydispersity. The character of the total structure factor in non-magnetized organic ferrofluids strongly depends on the particle concentration and coupling parameter.328 Despite the complex behavior of the structure-factor, in some cases its qualitative analysis makes it possible to conclude about the processes in ferrofluids including biological systems. An example is the combined SAXS/SANS studies of the adsorption and desorption of the cytostatic mitoxantrone (MTO) to lauric acid-albumin hybrid coated magnetic nanoparticles in water.335 Such MTO-loaded nanoparticles have shown very promising results in in vivo animal models before, while the exact binding mechanism of the drug was unknown. The complex particles have shown better stability under drug loading in comparison with uncoated nanoparticles and sustainable drug release compared with protein solution. Adsorption of MTO leads to a decrease of absolute value of zeta potential and repulsive interaction among particles, which points to the location of separate molecules of MTO on the outer surface of the shell.
The equilibrium chain aggregates were recently observed in SAXS experiments (Fig. 18) when two organic (polydisperse) ferrofluids with strongly different coupling parameters were placed in the saturating magnetic field.336 The low particle concentration of the two samples provided the equilibrium state under magnetic field. 2D SAXS patterns became anisotropic and did not change in time. The structure-factor in this case is associated with the chain-like aggregates which are oriented under magnetic field. From the scattering component parallel to the magnetic field direction the size distribution of the particles in chains was derived for comparison with that obtained from the scattering curves from non-magnetized samples. The scattering component perpendicular to the magnetic field direction was analyzed in monodisperse approximation to estimate the mean particles per chain, as well as the fraction of particles in the chains. It was shown that the stable samples based on organic solvents (monolayer surfactant stabilization) behave in full agreement with the theoretical predictions for dipolar fluids with respect to the formation of chain-like particle associates. The experimentally estimated chain length and the aggregation rate correlate with the coupling parameter for magnetic interaction between nanoparticles in the systems.
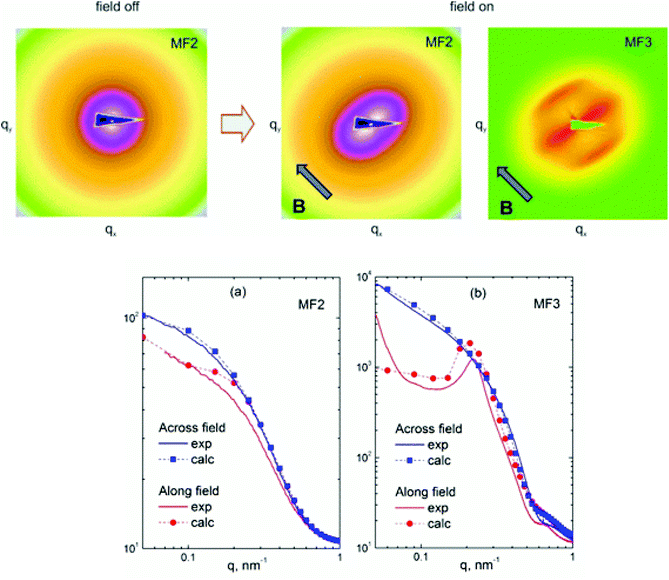 | ||
| Fig. 18 Illustration of evolution of experimental 2D SAXS scattering patterns (logarithmic scale) in external magnetic field for magnetic fluids with different coupling parameters: magnetite (MF2) and cobalt (MF3) nanoparticles coated with oleic acid in toluene. All patterns are very similar for the ‘field off” state; as an example, the pattern for the MF2 fluid is shown. For the ‘field on” state q-cuts of 2D experimental patterns along and perpendicular to the direction of the saturating magnetic field for two ferrofluids under study are shown. The model calculations (solid lines) take into account the formation of thermodynamically stable chains oriented along the field (reproduced from ref. 336 with permission from Elsevier, copyright 2018). | ||
3.5.2.2 Ordering. Environmental changes leading to the effective amplification of the particle attraction can cause orderings of various types in ensembles of magnetic particles, which is well reflected as specific changes in small-angle scattering curves. Thus, the cooling of ferrofluids (magnetite coated with a double layer of oleic acid oleylamine in decalin, size from 10 to 20 nm, concentration from 0.1 to 1.5 vol%) under saturating magnetic field results in the formation of dipolar chains combined then into packed hexagonal structures.337 Such kinds of ordering were observed in cooled thin films by cryo-TEM. They are also concluded from the symmetry of the diffraction peaks observed in 2D SANS patterns (Fig. 19), thus proving that this ordering starts to form in bulk as well. The separation and comparison of nuclear and magnetic scattering components in the SANSPOL experiments showed that the nuclear and magnetic structure-factors responsible for diffraction peaks are the same.
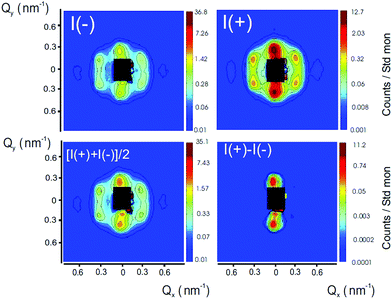 | ||
| Fig. 19 SANSPOL from frozen ferrofluids magnetite/oleic acid + oleylamine in decalin. In a homogeneous magnetic field of 0.2 T, a transition occurs to equal-spaced columns that exhibit hexagonal symmetry (reproduced from ref. 337 with permission from Am. Phys. Soc., copyright 2007). | ||
An increase in the particle concentration of strongly interacting particle ferrofluids leads to the increase in the chain concentration and, hence, their interaction, which becomes more intensive under an external magnetic field. Due to the large total magnetic moments oriented along the field, the chains are combined into close-to-hexagonal planes, such as for concentrated cobalt ferrofluids (up to 6 vol% Co). The ordered structures were evidenced by small-angle scattering using polarized neutrons and synchrotron X rays;338,339 the combination of these techniques allows the separation of the magnetic and nuclear form factors from the structure factors. A recent example of magnetic field induced self-assembly of magnetic nanoparticles340 concerns the formation of superlattices of magnetic nanoparticles formed in classical ferrofluids with comparatively large particle sizes (17 nm) under moderate magnetic fields (from 0.1 to 2.2 T). Using SANSPOL analysis including 2D patterns the 3D long-range ordered superlattice of MNPs was identified to be face-centered cubic.
Time-resolved SANS techniques allow for dynamical studies of the formation and disintegration of magnetic structures on the nanoscale in ferrofluids, by extending time resolution into the micro-second range.341 The analysis of time-dependent SANS data as a function of frequency, field and temperature allows (1) for proving the validity of the Langevin statistics describing the particle moment orientation, (2) for extraction of the effect of field-induced interparticle correlations, (3) for monitoring the slowing down of the dynamics of moment rotation with decreasing temperature, (4) for studying the effect of freezing of the solvent on the dynamics of the particle moments, and (5) for deciding between the possible relaxation mechanisms (Néel and Brownian).342 Applying a continuous neutron flux allows for achieving the shortest time range of about 3 ms by the stroboscopic SANS technique in an oscillating magnetic field,343,344 while the use of the pulsed beam (TISANE) technique extends the time resolution to the microsecond range.341 The stroboscopic small-angle neutron scattering technique consists in application of a cyclic perturbation to the sample by an oscillating magnetic field, allowing for extraction of the polarization-dependent scattering cross-sections as a time dependent response.342,344
In ferrofluids based on dielectric carriers, the formation of anisotropic aggregates of magnetic nanoparticles can be induced by direct current (dc) electric field, with a strong dependence on the field intensity, which was evidenced by SANS.345,346 The anisotropic aggregates preferably orient in the direction of the applied electric field, giving rise to an electrorheological effect, analogous to the magnetic field induced viscosity increase.346 The reason is the electric polarization of particles by the field.
Aggregation stability and phase separation are important questions for ionic liquid based ferrofluids with electrostatic stabilization. A microstructural study of ethylammonium nitrate (EAN) ionic liquid based ferrofluids with initially citrate coated MNPs shows that the nature of the initial counterion in water (here sodium, lithium or ethylammonium) and the amount of added water (<20 vol%) modulate the interparticle repulsion.126,127,347
3.5.2.3 Colloidal aggregates: diagnostics. Colloidal aggregation in ferrofluids produces parasitic effects related to their properties employed in an application; especially, it concerns potential side effects of biological ferrofluids. In this sense, the diagnostics of the aggregates including their inner structure and magnetic properties in various environments is of current interest. The SAXS/SANS analysis of the aggregates is well combined with the modelling particle form-factors and finding parameters of the SLD distribution in the particles.49 The same, like in the case of separate particles, analysis of the structure-factor in the SAXS/SANS curves makes it possible to conclude about the interaction of aggregates in solutions.121,348
The inner structure of aggregates in ferrofluids is studied by SAXS/SANS in the same way like for single particles. Thus, it was demonstrated that the modified function approach in the frame of the SANS contrast variation is useful for determining the average shape of the aggregates, relative content of the surfactant in them and the presence of the surfactant shell at the particles on the outer surface of the aggregates.233,348–350 The additional feature is that the method resolves the free surfactant micelles which can form in doubly stabilized water-based ferrofluids with a surfactant excess.
Regarding the particle aggregation, essential differences concerning the structure of steric stabilized aqueous and non-polar and polar organic solvent based ferrofluids were first observed in ref. 351 by small-angle neutron scattering and dynamic and static light scattering investigations, making use also of the contrast variation technique. The SANS curves for low concentration (2.5 wt%) aqueous (double layer steric stabilization; decanoic acid (C10) + dodecanoic acid (C12)) and non-polar organic carrier (hexane; monolayer steric stabilization (C10)) ferrofluids differ markedly depending on the contrast ratio and, for the aqueous systems, on whether the two surfactant layers are both protonated or one is protonated and the other deuterated. A core–shell model fitted to the rich data set allowed the determination of the iron oxide core size and size distribution, the thicknesses of the surfactant shells, and the spatial arrangement of the individual particles. At the same time, it was concluded that weak interactions in the organic-solvent-based systems resulted in the formation of the developed (fractal) aggregates with small fractal dimensions and significantly stronger interparticle interactions in aqueous magnetic fluids resulted in larger and more compact clusters with higher fractal dimensions. Fractal clusters often form after preparation of ferrofluids. They are well detected by small-angle scattering. The clusters with explicit fractal organization show the power-law type dependence I ∼ q−D, where D is the fractal dimension of the clusters. Thus, fractal clusters in double layer steric stabilized water based ferrofluids are dependent on the surfactant combinations.147,352 A transition from compact aggregates to developed structures of the fractal type when modifying the synthesis was reported349 for electrosterically stabilized water-based ferrofluids where initially magnetite nanoparticles were coated by a double layer of sodium oleate, to which polyethylene glycol (PEG) was added349 for improving the biocompatibility of this kind of ferrofluid.
From recent research, fractal clusters were observed309 (SAXS combined with SLS) in ferrofluids with multi-core superparamagnetic maghemite nanoparticles synthesized by the thermal decomposition procedure and stabilized with dimercaptosuccinic acid according to ref. 353 (Fig. 20). The mass fractals are close to dense associates with a fractal dimension of 2.9. The size characteristics of clusters found made it possible to estimate the characteristic aggregation number; each cluster contains 117 and 186 primary nanoparticles, respectively.
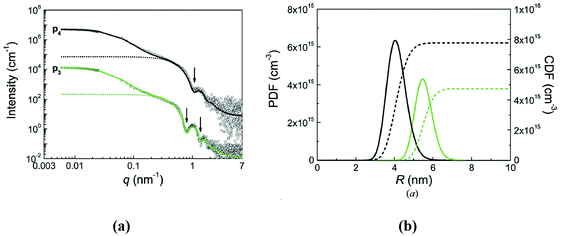 | ||
| Fig. 20 (a) Combined SAXS and SLS analyses of multi-core water based magnetic nanoparticle systems. Curve fits according to the relation scattering intensity = particle form factor multiplied by structure factor are given (solid lines). The mass fractal structure factor in the equation of scattering intensity is used for consideration of the multi-core structure. The scattering profiles of the particles alone without structure factor are given as dotted lines. (b) Size distributions of the cores of the primary particles in number-weighted form. Displayed are the partial differential functions (PDF-solid lines) and cumulative distribution functions (CDF-dashed lines) (reproduced from ref. 309 with permission from International Union of Crystallography, copyright 2017). | ||
Fractal clusters in magnetic fluids arise most probably from small primary aggregates formed during synthesis. This statement was recently confirmed in SAXS/SANS studies350 of the temperature dependent fractal structure of the aggregates in water based ferrofluids.
The secondary structuring at the aggregate level induced by magnetic fields can take place in ferrofluids. Thus, “colloidal” anisotropies presumably originating from the competition between steric repulsion and magnetostatic attraction were evidenced by magnetometry and SANS in the case of diluted bio-ferrofluids having dextran coated magnetite NPs with 44 ± 13 nm mean core size.354 The magnetic field induced anisotropy of cluster solutions (manganese ferrite with a maghemite shell in water, particle size of about 7 nm, pH = 2, volume fraction of 2%), which satisfy good superparamagnetic behavior, was recently observed355 by 2D SAXS and related to the anisotropic secondary aggregation of the magnetized clusters. The existing residue after the anisotropic aggregate preparation explains the anisotropic growth of clusters in magnetic fields even in ferrofluids with weak particle interaction, which is reflected well in 2D SAXS patterns.356
In early works on these kinds of studies, the regular adsorption of nanoparticles from ferrofluids on the silicon surface was concluded.360
The application of neutron reflectometry to water-based MFs (magnetite/sodium oleate/D2O) with extremely high for this type of ferrofluid concentration of 10 vol% revealed layered structures of MNPs on the silicon surface, which gave quasi-diffraction peaks in the reflectivity curves. The enhanced ordering was observed for external magnetic field application (with certain non-uniformity) both perpendicular and parallel to the surface; the number of layers fixed at the surface could exceed ten. The important fact, however, is that these effects occurred only in concentrated (conventionally ‘oversaturated’) samples. Such kind of response to magnetic fields means that water-based ferrofluids at such concentrations are not so well stable in magnetic fields. Similar effects of ‘oversaturation’ can be observed at the interface ‘air–ferrofluid’ when drying the sample. This was done by X-ray reflectometry;361 the formation and growth of a periodic structure was detected during the solvent evaporation. More extended studies with application of grazing incidence SAXS (GISAX) were performed362 for evaporation-induced assembly during drop casting of superparamagnetic, oleate-capped γ-Fe2O3 nanospheres dispersed in toluene. The superlattice growth was revealed and associated with the movement of a drying front across the surface of the droplet. The rapid formation of large, highly ordered superlattices was explained by the capillary-induced fluid flow.
The question how strong MNP are adsorbed from highly stable MFs of different types was clarified in the work.363 In particular, for non-polar ferrofluids (benzene-based, oleic acid coating of nanomagnetite, concentration of about 10 vol%, adsorption on silicon) and polar water-based ferrofluids (double coating by sodium oleate of nanomagnetite, concentration of about 2 vol%, adsorption on silicon oxide) the deviations from the reflectivity curve corresponding to the interface between two uniform media were observed. This means that slight but resolvable structuring at the substrate surface takes place. It was not sensitive to the application of the external magnetic field, proving high stability of the samples studied, even at rather high particle concentration. The SLD depth profiles from both types of ferrofluids revealed the formation of one adsorbed layer with the particle density naturally increasing with the particle concentration in bulk. The single adsorption layer (wetting layer) was observed364 for commercial water-based ferrofluids (double coating of nanomagnetite by oleic acid). It is interesting that this layer is stable under shear flow applied along the substrate surface. A depletion layer between the wetting layer and the moving ferrofluid was observed. Once the flow is stopped, the wetting layer becomes more pronounced with dense packing and is accompanied by a looser packed second layer. An adsorption enhancement up to two-three adsorbed layers in highly stable organic ferrofluids (single layer coating by oleic acid in transformer oil) was achieved by applying gradient magnetic field perpendicular to the substrate surface.365
A key question in the interface structuring of ferrofluids is the influence of aggregates on this process. It is especially important for water-based ferrofluids in which often colloidal aggregates form and develop during and after the preparation. The aggregation in bulk ferrofluids can be well controlled by SAXS/SANS. Neutron specular reflectivity was shown to be sensitive to the aggregate state of ferrofluids as well. Thus, for PEG-modified water-based ferrofluids (initial double coating of magnetite by sodium oleate) the reorganization of initially smaller and compact clusters into large fractal aggregates in the modified ferrofluids (first revealed by SANS; see Fig. 21) affected the single adsorption layer of MNP by destroying it.366 It was concluded that the number of single (non-aggregated) particles in the modified sample which can be adsorbed in a well-defined and sufficiently dense layer was significantly reduced. The reflectivity curve corresponded to the interface from two uniform media. This information complemented that obtained from SANS; in the SANS experiment the aggregate size in the modified sample was not resolved, which complicated the estimate of the fraction of particles in the aggregation state.
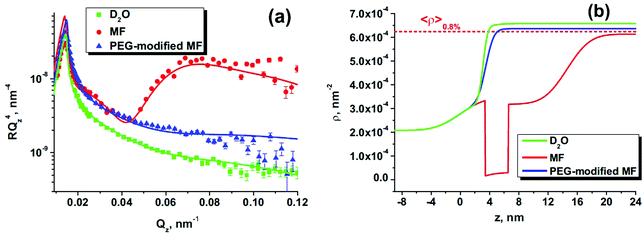 | ||
| Fig. 21 (a) Experimental reflectivity curves (Fresnel representation) together with fits (solid lines) for pure D2O (green squares), initial aqueous MF (red circles) and PEG-modified MF (blue triangles); (b) found from experimental data SLD profiles for three studied kinds of solid/liquid interfaces. The calculated mean SLD for the initial ferrofluid (concentration 0.8%) is shown (dashed line) for comparison (reproduced from ref. 366 with permission from Elsevier, copyright 2017). | ||
The linier aggregation can help in enhancement of the particle adsorption on substrates. This idea was tested in ref. 367 for water-based ferrofluids with double stabilization with an external magnetic field applied parallel to the substrate surface. The prolate particles in ferrofluids experience a torque and are aligned with their long axes along the silicon surface which leads to a higher particle density. To enhance the particles adsorption, in ref. 367 magnetite particle cores were coated with a monolayer of oleic acid and a monolayer of an amphiphilic polymer with carboxylic acid (Fig. 22). This kind of coating makes them very stable in water and also provides anchors for attaching to a functionalized substrate surface (APTES). The SANS analysis of such kind of modified ferrofluid showed that the particles are mostly (about 90%) in dimer state; that is, there are prolate particles in the solution. This fact together with the presence of anchors on the substrate surface significantly strengthened the formation of the dense layers on the substrate surface under parallel magnetic field due to the orientation of the dimers. The application of the reflectivity of polarized neutrons made it possible to conclude about the planar domain structure of the layered MNP ensemble, a result of pure dipole–dipole interaction in the system with close to 2D structuring. This study helps to understand the mechanism of the formation of packed surface structures from ferrofluids with high coupling parameter. The surface modification approach was also extended368 to the perpendicular magnetic field. Different kinds of the functionalized substrate surface (APTES, OTS, and piranha treatment) were compared. It was shown that the formation of the single wetting layer from non-magnetized ferrofluids is strongly dependent on the modification type. It is important to obtain by chemisorption good seed layers of MNP for further growth of well-defined structures. Again, the coupling parameter is the key factor for the formation of dense layers. Application of the perpendicular magnetic field promotes further particle layering.
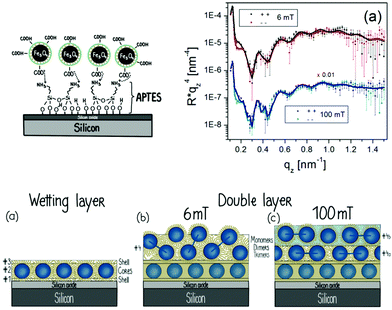 | ||
| Fig. 22 Schematic drawing of the chemically functionalized interface for better adsorption of MNP from water solutions. Polarized NR data (Fresnel representation) taken when applying parallel magnetic fields of 6 and 100 mT. Schematic drawing of NP-ordering determined from the results of SANS and polarized NR (reproduced from ref. 367 with permission from Am. Chem. Soc., copyright 2018). | ||
The direct ‘sticking’ of MNP from diluted ferrofluids on a magnetic film (ferrimagnetic substrate Tb15Co85) with perpendicular (out-of-plane) anisotropy (in-plane domains) was recently observed by polarized NR.49 The self-assembled layers are firmly attached and stable even after a thorough cleaning of the substrate, thus indicating their pinning at the domain walls of the substrate.
3.6 Magnetometry
If the volume fraction of the magnetic particles is not too high (usually less than 5%), effects of magnetic interparticle interaction can be neglected and the ferrofluid can be treated as a system of small thermally agitated permanent nanomagnets in the carrier liquid. Consequently, the magnetic behavior of the ferrofluid will have superparamagnetic character372,373 and can thus be described using Langevin's equation for the equilibrium magnetization of a paramagnetic system, M(H) = nmL(ξ) where n-particle number in unit volume, m-magnetic moment of the particle, L(ξ) = cth(ξ) − 1/(ξ)-the Langevin function and ξ-the Langevin parameter.34,39,234Ms = nm = φM0 denotes the saturation magnetization of the ferrofluid given by the product of the volume concentration φ of the suspended magnetic material and its spontaneous magnetization M0, which is less than the saturation magnetization of the bulk (M0 = 4.5 × 105 A m−1 for magnetite), due to specific nanoparticle surface layer effects discussed in ch.2. As mentioned above, the magnetic moment m entering the Langevin parameter ξ is not the magnetic moment of a single molecule but the magnetic moment of the whole magnetic particle, about four orders of magnitude larger than the values familiar from normal paramagnetic systems. The initial susceptibility of a magnetite ferrofluid could attain several units, while its saturation magnetization 90–100 kA m−1. Moreover, due to high magnetic susceptibility, 90% of the saturation magnetization can be easily reached with magnetic fields common for laboratory use having a strength of about 50 kA m−1, favorable for design and construction of various devices exploiting the unique properties of ferrofluids. As expected, the full magnetization curve of highly stable ferrofluids described in section 2 does not show any hysteresis and provides data about their magnetostatic properties and composition, such as initial susceptibility, saturation magnetization, particle volume fraction and mean particle size, by supposing log–normal size distribution374 or by applying the Tikhonov375 regularization method162,376,377 (Fig. 23a). The method using the Tikhonov regularization procedure in the case of a commercial ferrofluid and of a laboratory prepared sample61 is presented in ref. 162 and 377.
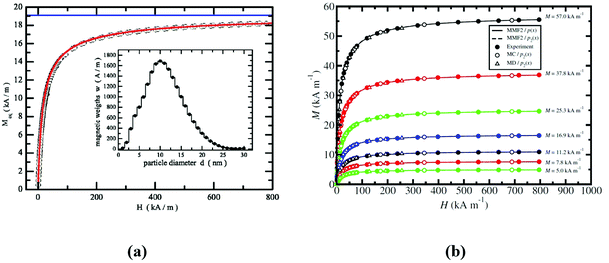 | ||
Fig. 23 (a) Equilibrium magnetization Meq as a function of the internal field H for the ferrofluid AGP 933 of Ferrotec. The horizontal line marks the saturation magnetization Msat FF = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 A m−1. The inset shows the distribution of the magnetic weights w as a function of the magnetic particle diameter d (in nanometers) as deduced from Meq(H) using Tikhonov's regularization method (reproduced from ref. 377 with permission from Am. Phys. Soc., copyright 2006); (b) complete magnetization curves, M(H), for ferrofluids of the same set. Filled circles are from experiment, open circles are from MC simulations with p2(x), open triangles are from MD simulation with p2(x), solid lines are from MMF2 theory with p(x), and dashed lines (almost coincident with solid lines) are from MMF2 theory with p2(x). The statistical uncertainties in the simulation points are smaller than the symbol size; MMF2-second-order modified mean-field theory, MC-Monte Carlo simulation, and MD-molecular dynamics simulation. Reproduced from ref. 378 with permission from Am. Phys. Soc., copyright 2006. 108 A m−1. The inset shows the distribution of the magnetic weights w as a function of the magnetic particle diameter d (in nanometers) as deduced from Meq(H) using Tikhonov's regularization method (reproduced from ref. 377 with permission from Am. Phys. Soc., copyright 2006); (b) complete magnetization curves, M(H), for ferrofluids of the same set. Filled circles are from experiment, open circles are from MC simulations with p2(x), open triangles are from MD simulation with p2(x), solid lines are from MMF2 theory with p(x), and dashed lines (almost coincident with solid lines) are from MMF2 theory with p2(x). The statistical uncertainties in the simulation points are smaller than the symbol size; MMF2-second-order modified mean-field theory, MC-Monte Carlo simulation, and MD-molecular dynamics simulation. Reproduced from ref. 378 with permission from Am. Phys. Soc., copyright 2006. | ||
Size polydispersity and particle interactions becoming significant at higher volume fraction values were considered in more developed approaches. Considered as dipolar liquids,379 the effective interactions of magnetic nanoparticles are often modeled by dipolar hard sphere (DHS),380,381 dipolar Yukawa382 or Stockmayer383 interaction potentials. To describe the structure determined magnetic properties of ferrofluids mean field theories,384,385 thermodynamic perturbation theory,380 integral equation theories386–388 and various density functional theories (DFTs)389–393 were applied.
Initial susceptibility and the magnetization of polydisperse magnetic colloids with interacting dipolar particles were described using the mean effective (Weiss) field and considering the log–normal size distribution function.281,394,395 Using the mean spherical approximation (MSA),396 the applicability of MSA was extended to the calculation of magnetizations of ferrofluids.387 In physical terms, the modified mean-field (MMF) theories380,397 provide a means of including the effective field experienced by a particle due to the external field and all of the other particles. By approximating the pair-correlation function in various ways, e.g., through virial-type expansions and thermodynamic perturbation theory, a systematic approach to magnetic susceptibility χ and magnetization M(H) can be established. Developed on the basis of thermodynamic perturbation theory, the second-order modified mean-field (MMF2) theory380 was compared with Monte Carlo (MC) and molecular dynamics (MD) simulation data, as well as with experimental magnetization data378 (Fig. 23b) for systems with discretized versions of the magnetic-core diameter distribution function p(x) corresponding as closely as possible to that of the real ferrofluid. The experimental results (taken at T = 293 K) for ferrofluids at seven different concentrations having the saturation magnetization values in the order of increasing concentration 5.0, 7.8, 11.2, 16.9, 25.3, 37.8, and 57.0 kA m−1 are from ref. 398. p1(x) and p2(x) are the discretized simulation distributions, while p(x) denotes the exact magnetic-core diameter distribution.
There is very good agreement between experiment and second order mean field theory (MMF2) with p(x) over the whole range of ferrofluid concentrations considered; indeed, it was found that the distribution does not vary with the concentration of a ferrofluid with fixed composition.378
The influence of particle interaction parameter λ and particle volume fraction Φ on the initial susceptibility χi of aggregate-free ferrofluids obtained by chemical size-fractionation of a high colloidal stability cyclohexane based ferrofluid (FFR) was demonstrated.399 The difference in initial slope of the magnetization curves is a consequence of the difference in particle size between samples.
The concentration-dependence of the initial susceptibility at low volume fraction values is similar at weak and strong interaction strengths, which correspond to the models of Langevin,9,400,401 Onsager,379,402,403 Weiss,401,403,404 perturbation theory380,405,406 and mean spherical model (MSM),379,407 while at higher concentrations significant deviations exist from theoretical model dependences and need second and third order polynomial approximation.399 In order to describe the equilibrium magnetization of concentrated polydisperse ferrofluids, a Born–Mayer cluster expansion approach developed for monodisperse systems408 was extended also to polydisperse systems.409
The dependence of the zero-field susceptibility χ0 on the Langevin susceptibility χL for polydisperse dipolar hard sphere (DHS) fluids was derived in.410,411 The MSA-based DFT (continuous line) provides a master curve which is the same for various polydisperse systems. For low polydispersity (a = ∞ (monodisperse), 104 and 52) the agreement between DFT and the simulation data is rather good. For high polydispersity (a = 26) the agreement is reasonable only for lower values of the Langevin susceptibilities.410 Indeed, the comparison between theoretical predictions and experimental data for two ferrofluids with calculated Langevin susceptibilities of 4πχL ≈ 1 and 4πχL ≈ 4 shows good agreement only for ferrofluid I with the lower susceptibility value.
Nonmonotonic temperature dependence of the initial magnetic susceptibility was evidenced first in very low concentration magnetic fluids,412 and it was confirmed later to take place for linoleic acid stabilized light hydrocarbon based ferrofluids.413 The observation of a maximum of the initial susceptibility on cooling was interpreted, when both the temperature and the density are very low, by particle ring formation and, consequently, by the exclusion of a significant fraction of particles from the collective magnetic response.414 The excluded particles might be considered to form “magnetic holes”, reducing this way the effective concentration of dipolar particles contributing to the magnetic response of the system.
Temperature dependence in the range 210K–390 K of magnetic susceptibility of strong, moderate, and low concentrated magnetite-based ferrofluids (hydrodynamic volume fraction ϕhydr from 0.2 to 0.5) was analyzed415 using the following theoretical models: (1) second-order modified mean-field theory (MMF2);380 (2) correction of MMF2 for polydisperse ferrofluids arising from Mayer-type cluster expansion and taking into account the first terms of the polydisperse second virial coefficient416 and (3) a new theory based on MMF2 combined with the first terms of the polydisperse second and third virial contributions to susceptibility. The temperature dependences of the initial magnetic susceptibility χ(T) were measured for twelve samples with different particle concentrations and of the same granulometric composition prepared using an oleic acid stabilized concentrated ferrofluid.413 It turns out that the applicability of theoretical approaches (1) for ϕhydr < 0.3, (2) for ϕhydr > 0.4 and (3) for ϕhydr ∼ 0.3–0.4 depends on the experimental sample concentration; consequently, a universal formula predicting a ferrofluid susceptibility over a broad range of concentrations and temperatures remains a challenge.415
According to the most common picture of ferrofluids, the magnetic nanoparticles are supposed to be spherical and the field they create can be approximated by that of a point dipole at the sphere's center. Different shapes and compositions of magnetic nanoparticles, such as magnetic ellipsoids and magnetic rods,417 magnetic core–shell,418,419 magnetic cap,420,421 magnetic superball422,423 and shifted dipole (SD) type particles,424–426 were considered in order to tailor the particle interactions and the overall properties of ferrofluids. In the case of SD particles, they are spherical but the dipole moment is not located at their centers, being shifted radially towards the particle surface.
The SD particle model actually closely approximates the magnetic cap type particles.425 The shift parameter s = 0 refers to a particle with a central dipole and s = 1 refers to the dipole being located at the particle's surface. The effective interaction parameter λ* compares the lowest energy for two SD-particles in close contact for a given shift to the thermal energy. Changes in nanostructure induce also a different magnetic response.426 In contrast to suspensions of particles with central dipoles, a reduction of cluster size with increasing field is observed for some parameters. The magnetization curve is well above the Langevin curve for zero shift, while for increasing shift values it shows a decreasing tendency, going even below the Langevin curve as the cluster size decreases and neighboring particles tend to have more anti-parallel orientations. In this particular SD particle model, the initial susceptibility can fall below the Langevin value for non-interacting dipoles depending on the chosen parameters, an unusual behavior for magnetic suspensions.
Analytical and computational investigations of the shape of magnetic nanoparticle assemblies show that by increasing the shape parameter427 of the resulting clusters, i.e. by going from a spherical to cubic shape, could show the way toward the aim of producing more field-responsive magnetic liquids.422 Taking into account that chains are a much more field favorable cluster topology than rings, the transition between these configurations is of practical interest. The general trend observed for each particle shape was increasing χ0 with growing λ for fixed φ, as to be expected. The observed decrease in χ0, for fixed λ, as the shape factor is increased has to be reconsidered as a superball particle becomes more cubic the chain to ring transition, observed in the ground state of spherical particles, occurs at an increasingly larger cluster size.423
In Fig. 24a, the values of static initial susceptibility of a usual, nonconfined magnetic fluid (MF) and of a system of nanoparticles entrapped in liposomes are compared; the measured values are smaller for the magnetoliposome (ML) sample, but both ML and MF values are higher than that corresponding to the non-interacting Langevin model. The experimental data are close to the calculated values using the Mendelev–Ivanov model285 for the dipole–dipole interaction parameter λ = 5,428 the Monte-Carlo simulations corresponding to a strongly interacting magnetic nanoparticle system. The chain distributions for the two cases in Fig. 24b indicate a lower degree of aggregate formation (corresponding to a lower magnetic susceptibility) for the ML sample for low volume fractions, being close to the Langevin dependence. For higher volume fraction values more complex aggregates resulted in the ML sample, which could correspond to flux closure (ring shaped) particle arrangements,414 implying a reduction of magnetic susceptibility.
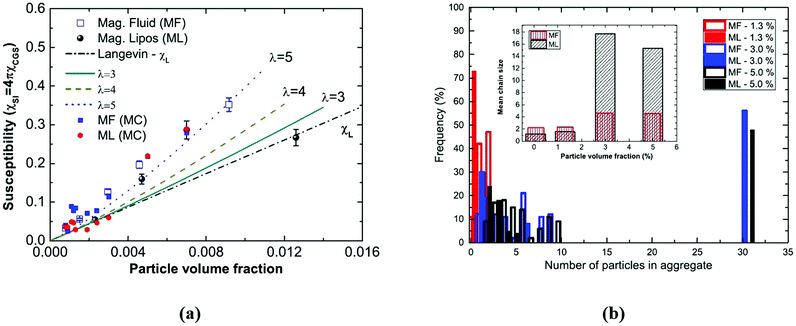 | ||
| Fig. 24 (a) Initial susceptibility as a function of particle volume fraction for magnetic fluids (squares) and magnetoliposomes (spheres). The red line represents a Langevin calculation. (b) Histograms of the cluster size distribution for the magnetic fluid (MF) and magnetoliposome samples (ML), for 0.0013, 0.03, and 0.05 particle volume fractions (indicated in %), considering a 0.3 T magnetic field. In the inset, mean chain size as a function of particle volume fraction includes the 0.00075 (or 0.075%) data (reproduced from ref. 428 with permission from Am. Phys. Soc., copyright 2016). | ||
Magnetogranulometry is the method to determine the concentration and magnetic diameter statistics of the nanoparticles from the magnetization data. Two main methods of magnetogranulometry are being used: (1) diameter distribution free, and (2) with parametric diameter distribution probability density function (PDF). Diameter distribution free magnetogranulometry162,376,377 provides the magnetic diameter distribution in pre-established bins (see. Fig. 23a), as a result of the optimization of the fit between experimental data and Langevin response. Parametric PDF magnetogranulometry is based on the assumption of a particular magnetic diameter PDF, log–normal and gamma distributions being the most widely used. Thus, most often, three parameters need to be determined: the nanoparticle density (n) and two diameter PDF parameters. The first parametric magnetogranulometry technique319 is equating three characteristics of the experimental magnetization curve (M(H)) with the corresponding theoretical expression based on Langevin magnetic response: the initial susceptibility, the saturation magnetization and the zero asymptotic field (H0) of M(1/H). In ref. 281 Chantrell's theoretical model was refined by the introduction of the saturation magnetization dependence on the diameter PDF and the nanoparticle concentration. Magnetogranulometry at low magnetic fields with induced nanoparticle chains429 is using a statistical model of MNP chaining.283 Long range interparticle interaction models were introduced378,380,430 for the magnetization of ferrofluids with polydisperse nanoparticle size, with applicability to full magnetic field intensity range and low to medium (∼15% volume fraction) concentrated samples. The theoretical models are dependent on the ferrofluid structural and composition parameters: nanoparticle diameter distribution and nanoparticle density respectively. The nonlinear fit of the magnetization data (see. Fig. 23b) with the parametric theoretical model provides quantitative estimates of the nanoparticle diameter distribution and density.431 A recent advance in the attempt to increase the fit accuracy180 incorporated the paramagnetic contribution of the dead magnetic layer at the surface of the nanoparticles.
The Néel relaxation time grows exponentially with the particle size, the respective time constant for the Brownian process scales only linearly in particle volume and therefore a transition occurs at a critical particle size where the Brownian relaxation becomes faster than the Néel process. In the transition region around the critical diameter the actual relaxation time is given by the geometric mean τ of the times for the single processes.9,437 The anisotropy constant, applied field and dipolar interactions through τN, while the carrier liquid viscosity and stabilizer coating thickness through τB, all influence the effective relaxation time of magnetization.438 The frequency-dependent magnetic susceptibility of a ferrofluid in a first order modified mean field model MMF1,439 having monodisperse constituent particles with only Brownian relaxation (with relaxation times on the order of τB ∼ 1–100 μs) and taking into account the interparticle dipole–dipole interactions, has the following important characteristics440 (Fig. 25): (1) in the low-concentration, noninteracting regime, it gives the correct single-particle Debye-theory results (i.e. the Langevin susceptibility); (2) it yields the exact leading-order results in the zero-frequency limit; (3) it includes particle polydispersity correctly from the outset. The theory is in quantitative agreement with the simulation results as long as λ = 1 and starts to deviate for larger values of the particle interaction parameter. The simulation results with χL ≤ 1 are not dependent on the particular choices of ρ* and λ, and hence the leading-order corrections to the Langevin and Debye theories are accounted for correctly. At higher values of χL, the systems simulated at ρ* exhibit dynamical properties that deviate from the MMF1 predictions, and from the simulated properties with λ = 1 (Fig. 25). For higher values of λ chain formation has to be considered, which involves longer orientational relaxation times and influences the susceptibility spectrum by shifting the absorption peak to lower frequencies.441 In concentrated ferrofluids the coupling of Brownian and Néel processes and the resulting effective relaxation time have a significant influence on the magnetization dynamics, in particular on the theoretical modelling and interpretation of magnetic susceptibility and magnetorelaxometry data, as the dipolar interactions lead to significant deviations from the Debye behavior of non-interacting systems.442
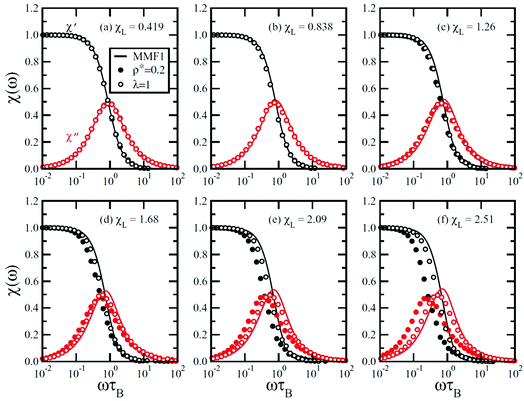 | ||
| Fig. 25 Normalized susceptibility spectra χ(ω) of interacting particles at ρ* = 0.20 and with 0.50 ≤ λ ≤ 3.00 (solid circles), at 0.10 ≤ ρ* ≤ 0.60 and with λ = 1 (open circles), and from MMF1 theory (solid lines). All simulation points are from systems with N = 216 particles. The Langevin susceptibilities are (a) χL = 0.419, (b) χL = 0.838, (c) χL = 1.26, (d) χL = 1.68, (e) χL = 2.09, and (f) χL = 2.51. For clarity, only 1 in 20 simulation points is shown. ρ* denotes the reduced density and λ the particle interaction parameter (reproduced from ref. 440 with permission from Am. Phys. Soc., copyright 2016). | ||
In the case of bio-ferrofluids nonlinear magnetization of SPIONs (single-and multicore) and their response to time-varying magnetic fields by Néel and/or Brownian relaxation process make them of high interest for imaging techniques, in particular for magnetic particle imaging (MPI), and also for magnetic fluid hyperthermia.209,235,443,444 The particle sizes (magnetic and hydrodynamic) and particle environment factors, like viscosity and pH, strongly influence the rotation mechanism and magnetization dynamics of MNP tracers. By separate reconstruction of the signals provided by different particles in different surrounding bio-environments, each of them corresponding to one color, a multicolor image can be generated, highly improving the sensitivity and resolution of the MPI technique.235,445
The influence of polarizing field on the ferromagnetic resonance frequency fres, in the case of a high magnetization ferrofluid (Ms = 760 Gauss; carrier Isopar M; stabilizer oleic acid), was investigated. For the real and imaginary parts of complex susceptibility, the variation of the polarizing field, H0, over the range 0–100 kA m−1 resulted in fres increasing from 1.6 GHz to 5.0 GHz (Fig. 25c).435,436 Initially, both components reduce with increasing H0 as a result of the contribution of the relaxational components to the susceptibility. Beyond approximately 400 MHz a relaxation to resonance transition occurs with the χ′ component going through zero at the resonant frequency fres, while the value of fmax corresponds to the maximum in the value of χ″(ω) (loss peak). The application of H0 to the sample effectively results in an increase in the anisotropy energy barrier KV (and hence σ = KV/kT) which the magnetic moment of the particles must overcome. The increase in H0 results in a shift of fmax from 1.0 GHz to 4.7 GHz and of fres from 1.6 GHz to 5.0 GHz.
The result of this is that the value of fmax corresponding to the maximum in the value of χ″(ω) (loss peak) approaches the value of fres as resonance becomes the dominant process. A mean value of the anisotropy field HA is determined from the intercept as being equal to 41 kA m−1.435
In particular, in the case of bio-ferrofluids in which clusters and single particles coexist,42,447,448 the coexistence of cluster rotation and individual particle rotations in the clustered-particle system gives rise to field-strength-dependent relaxation of magnetization,446 evidenced by applying the Cole–Cole symmetric model449 and the Cole–Davidson asymmetric model of relaxation.450 At low field strength the dominance of cluster rotation is due to strong dipolar interactions between individual particles, while at higher field strength a shorter relaxation time results which denotes smaller hydrodynamic size and preponderant individual particle relaxation (Fig. 26), the relaxation process being controlled by the relative strength of interparticle vs. particle-field interactions. Dipolar interactions between cores within a multicore particle could have non-zero resultant magnetic moment which enables Brownian relaxation of the cluster and the effective relaxation time.451 Depending on the cluster size and morphology, a kind of collective behavior of the constituent core particles appears as a large effective core with a long Néel relaxation time constant.
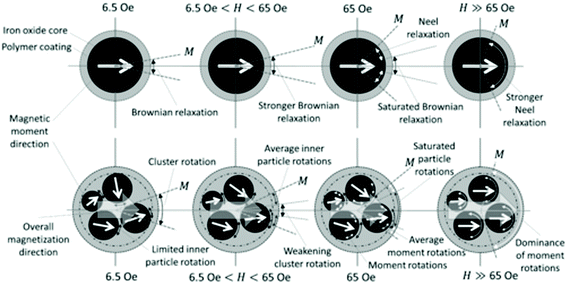 | ||
| Fig. 26 Field-strength-dependent relaxation dynamics of dispersed particles and clustered particles at low frequency and constant temperature describing the evolution of relaxation modes. Brownian relaxations (black two-headed arrows) are gradually replaced by Néel relaxation (white two-headed arrows) at higher field strength. In the case of a clustered-particle system, cluster friction should be less than individual particle friction to allow cluster rotation (reproduced from ref. 446 with permission from Am. Phys. Soc., copyright 2014). | ||
The ferromagnetic properties of this colloid are due to the interplay of the nematic elastic interaction and the magnetic dipolar interaction, the shape of suspended particles (nanoplatelets of bariumhexaferrite) being identified to be a critical issue. The magnetic dipolar interactions favor the appearance of spontaneous magnetization of anisotropic magnetic nanoplatelets dispersed in a nematic liquid crystal, ferromagnetic ordering and magnetic hysteresis being observed (Fig. 27A). It is worth mentioning in this context that exchange interactions between spins responsible for ferromagnetic ordering in the case of a solid ferromagnetic are essentially isotropic, while magnetic dipolar interactions which are highly anisotropic can also provide ferromagnetic ordering in liquid crystal based ferrofluids.458 Small-angle neutron scattering investigations (SANS, SANSPOL) show that in the absence of an external magnetic field, short range positional and orientational order already exist at relatively low volume fractions, the plate-like morphology of the magnetic particles favoring the dipolar interactions and, consequently, the stabilization of ferromagnetic ordering giving rise to ferromagnetic ferrofluids (Fig. 27B).457
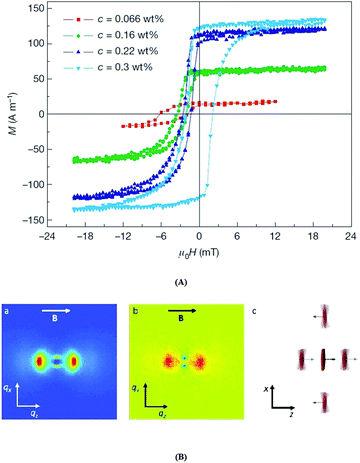 | ||
| Fig. 27 (A) Magnetization curves of monodomain samples show the switching behavior of magnetic nanoplatelets in an ordered nematic suspension. Magnetization curves are shown for four different platelet concentrations c (key at top left). At lower platelet concentrations, the magnetization in zero field returns to its initial value, whereas in the sample with a concentration of 0.3 wt%, the magnetization curve is centered around zero (reproduced from ref. 456 with permission from Springer Nature, copyright 2013). (B) SANSPOL in a suspension with Φ = 0.07. (a) Total SANS intensity I↑ + I↓ showing positional correlations. The peaks in the horizontal direction correspond to ∼30 nm, while the ones in the vertical direction to ∼90 nm. (b) SANSPOL intensity difference I↑ − I↓ showing magnetic correlations. The blue peaks correspond to antiferromagnetic correlations, and the red peaks to ferromagnetic correlations. (c) Scheme of positional and magnetic correlations of the neighbouring platelets. B = 0.19 mT (reproduced from ref. 457 with permission from Royal Soc. Chem., copyright 2019). | ||
Interfacial jamming of magnetic nanoparticles459 is another possible mechanism of liquid phase ferromagnetic ordering. Magnetic nanoparticles are assembled at the water–oil interface of an aqueous ferrofluid in toluene (water dispersion of carboxylated 22 nm-diameter MNPs (Fe3O4–CO2H) in a solution of amine-modified polyhedral oligomeric silsesquioxane (POSS-NH2) in toluene), providing a reversible paramagnetic-to-ferromagnetic transformation of ferrofluid droplets, which exhibit a finite coercivity and remanent magnetization (Fig. 28A–D).460,461 The two-dimensional layer of magnetic nanoparticles generated on the curved interface between two immiscible liquids is the result of the restriction of translational and rotational degrees of freedom and increased dipolar interactions between close packed nanoparticles.462
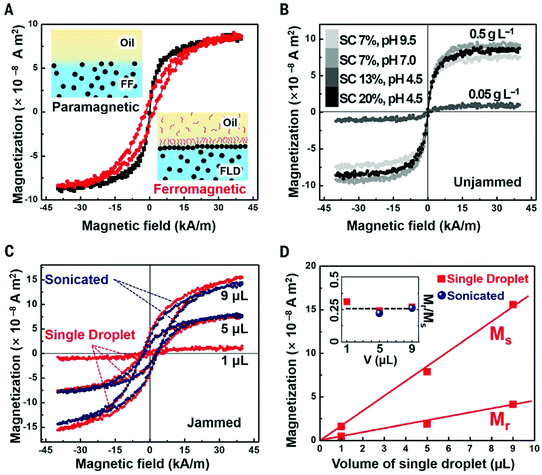 | ||
| Fig. 28 Tunable transformation of a paramagnetic ferrofluid (FF) into a ferromagnetic liquid droplet (FLD) by the interfacial jamming of magnetic nanoparticle (MNP)–surfactants (MNPS). (A) Magnetic hysteresis loops of droplets with (red line) and without (black line) an interfacial layer of jammed MNP–surfactants measured with a vibrating sample magnetometer. Two schematics of aqueous FF and FLD, containing Fe3O4–CO2H MNPs (0.5 g L−1) at pH 4.5, immersed in toluene without and with POSS–NH2 ligands (1.0 g L−1). (B) Hysteresis loops of individual 5 mL aqueous droplets, with 0.5 g L−1 and 0.05 g L−1 Fe3O4–CO2H MNPs at different pH, immersed in 0.01 g L−1 ligand solution. Surface coverage (SC) of droplets is ∼7 to ∼20% where MNPS assemblies are not jammed. (C) Hysteresis loops of single, jammed aqueous droplets with 0.5 g L−1 MNPs at pH 4.5 immersed in a 1.0 g L−1 solution of POSS–NH2 in toluene and hysteresis loops of the same system after being sonicated. (D) Mr and Ms of the droplets as a function of droplet volume. In the inset, the remanence ratio Mr/Ms as a function of initial droplet volume (single droplet or droplet sonicated into multiple smaller droplets) remains constant at ∼0.25 (reproduced from ref. 460 with permission from The American Association for the Advancement of Science, copyright 2019). | ||
3.7 Rheometry: field induced effects
Soon after the synthesis of the first ferrofluid samples, their flow properties in applied magnetic field started to be of great interest for most of the envisaged applications. The results of the first measurements published by McTague463 referred to a highly diluted ferrofluid (0.05 vol% of Co-particles with a mean diameter of at least 6 nm in a low viscous carrier) and evidenced a field induced enhancement of viscosity. A first theoretical explanation due to Hall and Busenberg464 interpreted the observed effect in terms of rotational viscosity by adding a correction term to Einstein's formula for the viscosity of diluted suspensions. Supposing that the magnetic nanoparticle is a rigid dipole, the action of the magnetic field leads to a hindrance of the free rotation of the magnetic particle in the flow, which is at the origin of rotational viscosity described theoretically by Shliomis using the concept of internal angular momentum.465–467Capillary flow effective viscosity measurements on a medium concentration laboratory prepared magnetite ferrofluid (saturation magnetization 258 G; mean particle diameter determined from Langevin fit 12.9 nm; stabilizing agent oleic acid) as a function of applied magnetic field oriented in the perpendicular direction of the flow are in close agreement with the Shliomis expression of rotational viscosity468 derived on the basis of the effective field method.469 This formula agrees with the expression of rotational viscosity obtained in ref. 465 in the low- and high-field limits and deviates from that at most on 15% in the entire range of the Langevin argument.
For concentrated commercial ferrofluids a strong increase of effective viscosity in magnetic field was observed,467,470,471 which denotes the dominant role of interparticle interactions and chain formation in flow properties. These particle interaction effects are basically different from the microscopic reason of rotational viscosity; therefore, the term magnetoviscous effect (MVE) was introduced472 for effective viscosity increase induced by structuring phenomena in concentrated ferrofluids induced by a fraction of large particles.183,471 The influence of applied field and shear rate183 and of fraction of large particles473 is a proof of the dominant contribution of interparticle interactions and particle agglomerates to the observed magnetoviscous effect determined by particle microstructural details of ferrofluids,162,163 such as particle concentration and field induced chain formation121 and phase separation.474–476 Very high hydrodynamic volume fraction (up to 30%) aqueous magnetic fluids with electrosteric (oleic acid (OA) bilayer) and electrostatic (citric acid (CA) stabilization show different flow behavior: the OA stabilized samples manifest shear-thinning (pseudoplastic) behavior both in zero and non-zero magnetic fields, while the samples using CA have approximately Newtonian behavior in both magnetic field conditions, due to composition induced microstructural differences.121 Theoretical calculations concerning the formation and breaking of chain-like aggregates of magnetic particles186,477–479 show that the interaction between larger particles is strong enough to form chain-like structures, which in turn dominate the flow behavior. Particle agglomerates are responsible for high magnetoviscous effect; successive refinement of commercial ferrofluids and elimination of particle agglomerates reduce the effect to a negligible level.480 Thick chainlike clusters in a simple shear flow, captured by Stokesian dynamic simulations,481 dissociate into some short clusters which are relatively stable and do not decrease significantly any more. Equilibrium and non-equilibrium Brownian dynamics simulations of a ferrofluid model system with sufficiently strong effective dipolar interaction strengths λ* > 3 indicate the formation of chain-like structures in the presence of a magnetic field.479 The cluster sizes are exponentially distributed which in the presence of a shear flow are shifted towards smaller values, providing numerical evidence for flow-induced rupture of chains responsible for pronounced shear thinning behavior observed experimentally.184,186 Particle chaining and large agglomerates in concentrated water based MFs prepared by the ball milling procedure produce strongly non-Newtonian magnetorheological behavior, including significant yield stress under magnetic field.482 The stress varies linearly with shear rate and in the absence of the applied magnetic field it goes through zero. A non-zero applied field gives rise to an offset of the stress, i.e. to a magnetic field induced yield stress typical for a Bingham fluid.472,483 In the case of ferrofluids the field induced yield stress is very small, usually well below 1 N m−2, compared to 50–100 kN m−2 specific to magnetorheological fluids.
In the case of bidisperse ferrofluids according to theoretical evaluations the presence of small particles has a strong influence on the aggregation of large particles,182 having a “poisoning” influence on particle chaining and magnetoviscous effect.484 Two specially designed Co ferrofluids with small (FF5: 5.27 nm mean magnetic core size) and large (FFF20: 19.21 nm mean magnetic core size) particles, with mean dipolar coupling constants λ = 0.43 and λ = 9.41 respectively, were used to tailor a bidisperse sample A0.75, to compare its magnetoviscous behavior with that of the sample A0 having only large particles (Fig. 29). The two pure basic ferrofluid samples were mixed in three different ratios “i” to provide the fluid samples A0.75 (iA0.75 = 0.75), B0.9 (iB0.9 = 0.9) and C0.97 (iC0.97 = 0.97), keeping constant the fraction of large particles.
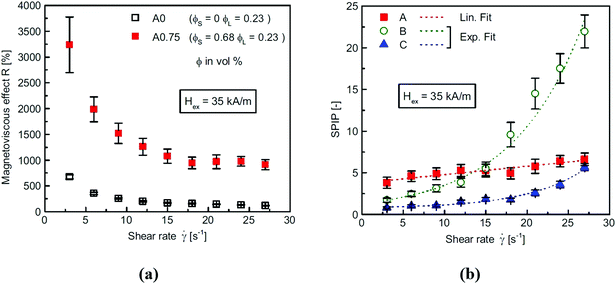 | ||
| Fig. 29 Magnetoviscous behavior of bidisperse ferrofluids. (a) Magnetoviscous effect vs. shear rate under the influence of an external magnetic field strength of 35 kA m−1. Shown are the ferrofluid samples A0 containing only large particles and A0.75 where small particles are added (mixing ratio i = 0.75). (b) The change of the magnetoviscous effect forced by the presence of small particles – expressed using the small particle influence parameter SPIP – plotted against shear rate in the presence of an external magnetic field Hex = 35 kA m−1. Datapoints of A, B, and C denote respectively the relations of the fluid samples A0 and A0.75, B0 and B0.9, and C0 and C0.97. The dotted lines represent a linear fit for the sample set A (SPIPA) and an exponential fit for sample sets B (SPIPB) and C (SPIPC) (reproduced from ref. 485 with permission from Elsevier, copyright 2015). | ||
In contrast to the expected decrease due to the predicted “poisoning” of the chain growth, the experiments reveal a highly significant result for the application orientated design of ferrofluids: the magneto-viscous effect is more than three times higher (R ≈ 3300% to R ≈ 900%) than that of the fluid containing only large particles (A0), evidencing this way the enhanced interaction of the large particles in a magnetic background fluid expressed by the small particle influence parameter SPIP (Fig. 29b).485
The magnetoviscous effect in ferrofluids is highly dependent on the orientation of the magnetic field with respect to the fluid flow. The viscosity changes in a different way depending on the relative orientation of the magnetic field and the velocity gradients, evidencing the anisotropic character of the magnetoviscous effect.185,463,478,486,487 An idealized isothermal many-particle model of perfectly oriented magnetic moments (in the bulk), which interact through soft-sphere repulsion and dipolar interaction,486 offers a qualitative description of the magnetorheological behavior of ferrofluids in strong magnetic field. Dynamical mean field model simulations479 favor the role of chain-like aggregates especially in strongly interacting ferrofluids (λ > 1). The shear and field dependent magnetoviscous effect in a cobalt ferrofluid with strong interparticle interaction (interaction parameter λ ∼ 10) for three orientations of the magnetic field488 shows that the strongest effect occurs for the magnetic field orientation parallel to the shear gradient (Δη2), i.e. perpendicular to the flow and to the vorticity. The shear modulus in the direction of the field is 2–4 times larger than in the perpendicular direction in the case of a magnetic colloid of polymer nanocomposite particles, close to what we call bio-ferrofluids.
An outstanding experimental set-up was dedicated to evidence the fundamental role of particle agglomerates in the flow properties of ferrofluids in magnetic field.489 A specially designed cone-plate rheometer allowed for involving small-angle neutron scattering in establishing the direct correlation between the ferrofluid microstructure and magnetoviscous effect. The scattered neutron beam intensity was correlated with the applied magnetic field and shear rate induced changes of the microstructure, as well as of the flow behavior.
In the case of a ferrofluid considered as a non-interacting magnetic nanoparticle system with no structures in the absence of the field, chains are formed under the influence of the applied magnetic field evidenced by the scattering patterns for ferrofluids at rest and under shear flow.184 In order to evidence only the relevant changes in microstructure induced by chain formation, for each magnetic field strength used in the experiments, the reference scattering pattern (for shear rate 0 s−1 or 200 s−1) corresponding to the single particle system has been subtracted from the scattering patterns obtained for all other measured shear rates, giving rise to difference scattering patterns.
The unique joint MR and SANS investigation on a cobalt-based ferrofluid, Co87_03, having a mean particle diameter of about 10 nm, 0.35 vol% magnetic material and interaction parameter λ* = 5.26, much higher than 1, shows a strong shear rate dependent magnetoviscous effect due to intense field induced chain formation evidenced by SANS. The magnetoviscous effect in the case of two different ferrofluids, a commercial magnetite based fluid (APG513A, Ferrotec Co.) with λ* = 0.5 and a cobalt based fluid (VS1-017; synthesized by S Behrens and A Gorschinski490) with λ* = 2.5, is considerably higher for the cobalt ferrofluid, as a consequence of more intense interparticle interactions and structure formation.491
Pre-existent clusters (surface coated multicore particles),492 specific for bio-ferrofluids or the use of stearic acid (a “bad” stabilizer132) instead of oleic acid as a particle coating layer493 provides ferrofluids with much enhanced magnetoviscous effect. A ferrofluid having well-stabilized particles that resists chain formation, and another ferrofluid with poorly stabilized particles, which readily form dynamic chains upon application of a magnetic field, while the particle interaction parameter for both FFs is below 1, show very different magnetorheological behavior:494 a shear and magnetic field-dependent viscosity and the appearance of magnetic field-dependent viscoelasticity in the less well stabilized sample. This behavior evidences that the average description considering only the interaction parameter for mean particle size, without details on stabilization and polydispersity, could be misleading.187 Polydispersity and the existence of a fraction of large particles with intense particle interactions are at the origin of particle chaining and formation of dense, drop-like bulk aggregates, influencing magnetic and rheological behavior of concentrated ferrofluids.183,480,495–500 Chain formation should give rise to the appearance of viscoelastic effects in ferrofluids;283,497,501 in particular, it can explain the appearance of normal stress differences, the Weissenberg effect502 in ferrofluids.503 Surface elevation determined in microgravity conditions ensured by parabolic flights with 5 × 10−3 g residual acceleration evidences the strength of the Weissenberg effect measured as a function of the shear rate and magnetic field intensity, which correspond qualitatively to the chain model of ferrofluids.503
Magnetizable fluids with clustered iron oxide particles, such as some type of bio-ferrofluids, show time-dependent rheological properties492,504,505 due to complex structure formation and relaxation processes which depend strongly on the strength of the applied magnetic field and shear rate.506 Due to these processes the time needed for the viscosity to reach the steady state was found to take several minutes. Due to their large size and magnetization, interaction of coated clusters of iron oxide (multi-core) nanoparticles at a certain magnetic field strength exceeds the stress, which leads to the appearance of a weak dynamic yield stress. During the flow some drop-like aggregates are destroyed and not all of them are restored; therefore, the residual stress τr is less than the yield stress τs, the two stress values being of the same order of magnitude.506 In the case of a ferrofluid with several micrometer size drop-like aggregates in a thin channel placed into a normal magnetic field, the appearance of drop-like particle structures treated as the classical van der Waals ‘gas–liquid’ phase transition can account for the appearance of significant elastic and yield stress effects.507
Bio-ferrofluids with multi-core iron-oxide nanoparticles, while with very low volume fraction (0.293%), show a Herschel–Bulkley behavior (Fig. 30I) and have a several orders of magnitude relative increase of effective viscosity (R) in magnetic field,40Fig. 30II, similar to magnetorheological fluids. The strong influence of multicore iron-oxide nanoparticles on the flow behavior is evidenced in Fig. 30III. By adding a small amount (5% mass concentration) of magnetic nanoclusters to a practically structureless highly stable ferrofluid the resulting composite fluid (MNCS5) shows a 100 times increase of the effective viscosity at a low shear rate (8.73 s−1), i.e. a pronounced magnetoviscous effect.508 The magnetorheology of good colloidal stability bio-ferrofluids with well defined and negligible remanence multi-core superparamagnetic nanoparticle clusters in the water carrier shows specific features between ferrofluids with low interaction strength and magnetorheological fluids with extremely strong magnetic coupling. A comprehensive experimental and theoretical analysis of the region of intermediate magnetic coupling strength between colloidal ferrofluids and magnetorheological suspensions509 provides evidence that the yielding of multi-core aqueous suspensions should proceed via the layered (lamellar) phase, details of the yielding behavior being summarized in Fig. 30IV.
 | ||
Fig. 30 (I) Flow curves and (II) magnetoviscous effect of a bio-ferrofluid (fluidMAG-D-200 nm; manufactured by Chemicell GmbH) for several magnetic field strength values, depending on the shear rate. The lines represent fits using the Herschel–Bulkley model (reproduced from ref. 40 with permission from IOP Publishing, copyright 2014). (III) The magnetoviscous effect for a high colloidal stability transformer oil based ferrofluid (empty symbols) (Ms = 120 G; physical volume fraction of magnetite nanoparticles = 2.8%) and for the same ferrofluid with magnetite nanoclusters added (full symbols) (mean size of nanoclusters = 280 nm; mass concentration of nanoclusters = 5%) (reproduced from ref. 508 with permission from IOP Publishing, copyright 2019); (IV) yielding behavior of bio-ferrofluids-aqueous dispersions of multicore nanoparticles. (A) Emergence of dynamic yield stress τ for γ → 0 as a function of dipolar interaction strength λ: (a) suspension of nanoclusters, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of nanoclusters and nanochains, and (c) suspension of nanochains. (B) Schematic representation of the magnetically coupled hexagonal network of chain bundles emerging in the rheometer gap according to numerical simulations, which causes the appearance of yield stress in the preyielded regime and reciprocal [η] ∝ Mn−1 dependence of intrinsic viscosity; right – a chain bundle spanning the rheometer gap, self-assembled by lateral attraction of magnetic nanoparticle chains. (C) Schematic representation of the yielding scenario; hydrodynamic stresses reorganize the chain bundles into flowing layers of chains interleaved by the carrier fluid; the inset shows the delaminated phase calculated from numerical simulations (λ = 7, Mn = 10–3) (reproduced from ref. 509 with permission from Elsevier, copyright 2020). 1 mixture of nanoclusters and nanochains, and (c) suspension of nanochains. (B) Schematic representation of the magnetically coupled hexagonal network of chain bundles emerging in the rheometer gap according to numerical simulations, which causes the appearance of yield stress in the preyielded regime and reciprocal [η] ∝ Mn−1 dependence of intrinsic viscosity; right – a chain bundle spanning the rheometer gap, self-assembled by lateral attraction of magnetic nanoparticle chains. (C) Schematic representation of the yielding scenario; hydrodynamic stresses reorganize the chain bundles into flowing layers of chains interleaved by the carrier fluid; the inset shows the delaminated phase calculated from numerical simulations (λ = 7, Mn = 10–3) (reproduced from ref. 509 with permission from Elsevier, copyright 2020). | ||
The application of an alternating linearly polarized magnetic field can induce an additional viscosity contribution to the rotational viscosity of a ferrofluid. For a certain range of the frequency and field strength of the applied field this gives rise to a “negative viscosity” effect,255 which can be understood as a transfer of energy from the magnetic field into rotational motion of the particles510 that manifests itself in a reduction of the total viscosity. In a simplified model these particles with only Brownian relaxation act as nanosize motors reducing the friction between neighboring fluid layers.511 The effect can be also accounted for without referring to the angular momentum of individual magnetic nanoparticles,512,513 a hydrodynamic approach which is different from the mesoscopic model of internal angular momentum255,437 and uses only macroscopic quantities, the two models being analyzed comparatively in ref. 514. The negative viscosity effect was for the first time experimentally confirmed in the case of a concentrated (20%vol) water based ferrofluid with cobalt-ferrite rigid dipole nanoparticles of 10 nm mean size in the Poiseuille flow and subjected to an axial oscillating magnetic field, the data indicating a decrease of magnetoviscosity to −19 cP at H ∼ 2000 Oe and frequency greater than 700 Hz.515
The experimental dependence of magnetoviscosity on the flow vorticity in an oscillating magnetic field for a ferrofluid in the Couette flow511 reveals that the field-dependent part of viscosity can be positive or negative, as argued also theoretically in ref. 516. The dynamics of the magnetic moment in the oscillating field in a mesoscopic model using a Fokker–Planck equation gives rise to a hierarchy of equations for the different moments, describing the relaxation of the magnetic moment.517 The model results in the dissipated power and the viscosity which is a non-monotonous function of the frequency of the field and up to the first order in the field agree with the corresponding ones obtained in ref. 511 based on the phenomenological equation of Shliomis. Analogous to the torque measurements on a commercial ferrofluid in rotating magnetic fields518 shows negative viscosity for high values of Langevin parameter and frequency under corotating magnetic field;519 again, the observed effect corresponds to the simplified model of nanosized rotors that reduce the friction between adjacent fluid layers,511 leading to a decrease in the effective viscosity of the suspension.
4 Ferrohydrodynamics, interfacial instabilities, pattern formation, droplet formation and manipulation, and flow in confined geometries
4.1 Ferrohydrodynamics
Coupling of the fluid magnetization with the fluid dynamics is due to a specific relation between magnetic and rotational degrees of freedom of suspended magnetic nanoparticles in a carrier liquid. A complete set of constitutive equations consists of the equation of ferrofluid motion, the Maxwell equations, and the magnetization equation, giving rise to magnetohydrodynamics of ferrofluids, known as ferrohydrodynamics.7,9,10,34,37,39,161,234,520–523 For isothermal incompressible ferrofluids in the continuum approximation, having spatially uniform distribution of spherical, rigid, and monodisperse particles, the equation of motion has the form161Here ρ is the density, v is the translational velocity, ω is the so-called spin velocity related to the rotational degrees of freedom of suspended rigid dipole particles, p is the pressure, g is the gravitational acceleration, μ0 is the vacuum permeability, M is the ferrofluid magnetization vector, and H is the intensity of the applied magnetic field. Also, λ represents the bulk viscosity, η is the shear viscosity, while ζ denotes the vortex viscosity. The conversion between internal and external angular momentum is related to the antisymmetric part of the stress tensor. The rate of change of the internal angular momentum density ρIω is given by the following equation:
introduced by Shliomis and thoroughly discussed in.9 The effective relaxation time τ is related to the Neél and Brownian relaxation times,
 , while Meq is the equilibrium (Langevin) magnetization of the ferrofluid.
, while Meq is the equilibrium (Langevin) magnetization of the ferrofluid.
As the magnetization is collinear with the local field, it means that the magnetization relaxation time is considered to be zero in the quasistationary regime. Under isothermal conditions the magnetic force is a potential one, allowing for a generalized Bernoulli equation in irrotational flow:34
The rich ferrohydrodynamic phenomena described by the generalized Bernoulli relationship are illustrated by the classical Quincke experiment,523,524 the conical meniscus formed by the free surface of a ferrofluid around a vertical current carrying rod,34,520,525,526 the levitation of a nonmagnetic body in a magnetized fluid,8,523 the self-levitation of a permanent magnet immersed in a beaker with a ferrofluid523,527 and by the reduction of the cross section of a jet induced by a magnetic field.34,520
Note that the stable levitation of a nonmagnetic body immersed in a magnetic liquid by applying a suitable nonuniform magnetic field is possible, circumventing the classical Earnshaw theorem.528 The generalized Bernoulli relationship brings together most of the basic ferrofluid phenomenology and inspired along several decades the development of devices operating with ferrofluids.161,523
The initial linear approach of the stability of the equilibrium of small interface deflections in response to a gravitational force, interfacial tension and applied magnetic field, considering a magnetic fluid with air and water interfaces,11,34 has been further developed to include the influence of viscosity and finite thickness of the ferrofluid layer.529–532 The instability of a flat interface between a very concentrated (relative permeability approx. 40) and a diluted ferrofluid shows a first order transition between a flat interface and the observed regular pattern of peaks,474 the observed effect having a large hysteresis due to the high value of the relative permeability of the concentrated ferrofluid. The linear analysis is unable to predict the amplitude of surface deflections or to describe transition from a hexagonal to square pattern, aspects investigated in further experiments and nonlinear analyses.533–541 The energy-variational method533 considering the total energy as a sum of the gravitational energy, surface energy and magnetic field energy recovers in the linear limit the onset relations of Cowley and Rosensweig.11
Strongly localized soliton-like structures of ferrofluids (“ferrosolitons”) were evidenced in a stationary magnetic field542 by applying an X-ray imaging technique,543 capable of recording the full surface relief in the center of the vessel, far away from distortions by the edges.544 A local perturbation of the stationary magnetic field produced a stable non-decaying structure – a ferrosoliton – remaining intact for days, the amplitude of the pattern depending on the magnetic induction. The multi-soliton cluster evolves towards the Rosensweig hexagonal pattern.545 Above a critical value of the magnetic field a hexagonal array of peaks is formed, followed by a morphological transition from the hexagonal array to a square array above a second threshold of the applied magnetic field, triggered by penta–hepta defects, present in the hexagonal pattern. The stability domains of competing hexagons and squares and wave number selection541,546,547 are a function of the relative magnetic permeability of the fluid.533,540
The growth rate and characteristics of Rosensweig instability patterns depends on ferrofluid viscosity,531 finite depth of the container,548 microgravity or hypergravity conditions549 and also on non-linear field dependence of magnetization550,551 evidenced experimentally in ref. 552–554.
Using a highly viscous magnetic fluid, obtained by cooling down a commercial sample (APG E32, Ferrotec Co), the growth rate of the Rosensweig instability can be slowed down by more than 2000 times554–556 and, consequently, the growth of the pattern takes several tens of seconds, allowing for measurements with high temporal resolution using a 2D X-ray imaging technique.543 The plain surface and domain-covering regular up-hexagonal (i.e. hexagons whose maximum amplitude is positive) patterns are bistable, as shown by the bifurcation diagram in Fig. 31A(a),556 which stems from a fit to about 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 measured data points.555 Direct computation with a finite element method557 concluded that the hexagonal pattern is not a result of the geometry of the boundaries as a square domain can also generate a hexagonal configuration. Fig. 31A(b) displays an experimental realization of the domain-covering hexagonal pattern observed at the upper branch. By slowing down the formation of Rosensweig patterns due to the high viscosity ferrofluid the magnetic induction B (the control parameter) and the pattern amplitude A can be varied almost independently in order to explore the region around the unstable branch of the instability, where homoclinic snaking558 is expected to develop from the side (Fig. 31A).556 In Fig. 31B there are displayed the numerical results for µr = 2 which show that radial spots bifurcate subcritically at onset from the flat state and undergo a subsequent fold. Here, the steady-state free-surface is given by z = ζ(x,y), with ζ = 0 corresponding to the flat state and ∥ζ∥22 is the normalized L2 norm of the interface. Experimental findings confirmed a linear scaling of the growth rate with the magnetic inductions (Fig. 31C(a)), as predicted,553 while the rates of growth and decay are slightly different (Fig. 31C(b)), due to the formation of chains of magnetic particles in the static spikes and their subsequent destruction during the decay indicated by the observed magnetically enhanced shear thinning.554 Large scale numerical simulation of magnetic field induced patterns using specific techniques (fast multipole method; smoothed particle hydrodynamics) allows for an accurate simulation of surface shape/topology considering ferrofluids as a deformable and paramagnetic continuum with surface tension.559
000 measured data points.555 Direct computation with a finite element method557 concluded that the hexagonal pattern is not a result of the geometry of the boundaries as a square domain can also generate a hexagonal configuration. Fig. 31A(b) displays an experimental realization of the domain-covering hexagonal pattern observed at the upper branch. By slowing down the formation of Rosensweig patterns due to the high viscosity ferrofluid the magnetic induction B (the control parameter) and the pattern amplitude A can be varied almost independently in order to explore the region around the unstable branch of the instability, where homoclinic snaking558 is expected to develop from the side (Fig. 31A).556 In Fig. 31B there are displayed the numerical results for µr = 2 which show that radial spots bifurcate subcritically at onset from the flat state and undergo a subsequent fold. Here, the steady-state free-surface is given by z = ζ(x,y), with ζ = 0 corresponding to the flat state and ∥ζ∥22 is the normalized L2 norm of the interface. Experimental findings confirmed a linear scaling of the growth rate with the magnetic inductions (Fig. 31C(a)), as predicted,553 while the rates of growth and decay are slightly different (Fig. 31C(b)), due to the formation of chains of magnetic particles in the static spikes and their subsequent destruction during the decay indicated by the observed magnetically enhanced shear thinning.554 Large scale numerical simulation of magnetic field induced patterns using specific techniques (fast multipole method; smoothed particle hydrodynamics) allows for an accurate simulation of surface shape/topology considering ferrofluids as a deformable and paramagnetic continuum with surface tension.559
 | ||
Fig. 31 Rosensweig instability patterns in a highly viscous ferrofluid. (A) (a) The bifurcation diagram (black line) of this pattern is obtained by a fitting procedure of amplitude equations described in ref. 555 to about 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 measured data. Via the path indicated by the arrows, one obtains localized patches, as shown in (c). The magnetic induction B is kept fixed during (1) for a time delay of τ1, and then B is switched to (2) for a time delay of τ2 before finally being switched to (3) until equilibrium is reached at point (3b). (b) A reconstruction of the height field of the domain-covering hexagons at point (1b). (c) Gives a reconstruction of the height field of a three-spike patch at point (3b) in the bifurcation diagram. (B) Emergence of a fully localized hexagon patch (dashed purple) bifurcating from a single spike (green) with µr = 2. There are also plotted the snaking regions of the 〈10〉 (blue) and 〈11〉 planar fronts (red); here, ε denotes the bifurcation parameter, which depends on the relative permeability of the ferrofluid, µr (reproduced from ref. 556 with permission from Cambridge Univ. Press, copyright 2015). (C) Grow and decay of the Rosensweig pattern in the case of a highly viscous ferrofluid. (a) The linear growth rates ω2 (■) from the experiment and the maximal growth rate ω2,m (solid black line) from theory as a function of the magnetization M. (b) The growth (■) and decay (●) rates ω2 of the pattern amplitude as a function of the magnetization M. The symbols represent the measured data. The black dashed line shows a fit of expression of scaling law for ω2 to the experimental growth and decay rates (reproduced from ref. 554 with permission from Am. Phys. Soc., copyright 2016). 000 measured data. Via the path indicated by the arrows, one obtains localized patches, as shown in (c). The magnetic induction B is kept fixed during (1) for a time delay of τ1, and then B is switched to (2) for a time delay of τ2 before finally being switched to (3) until equilibrium is reached at point (3b). (b) A reconstruction of the height field of the domain-covering hexagons at point (1b). (c) Gives a reconstruction of the height field of a three-spike patch at point (3b) in the bifurcation diagram. (B) Emergence of a fully localized hexagon patch (dashed purple) bifurcating from a single spike (green) with µr = 2. There are also plotted the snaking regions of the 〈10〉 (blue) and 〈11〉 planar fronts (red); here, ε denotes the bifurcation parameter, which depends on the relative permeability of the ferrofluid, µr (reproduced from ref. 556 with permission from Cambridge Univ. Press, copyright 2015). (C) Grow and decay of the Rosensweig pattern in the case of a highly viscous ferrofluid. (a) The linear growth rates ω2 (■) from the experiment and the maximal growth rate ω2,m (solid black line) from theory as a function of the magnetization M. (b) The growth (■) and decay (●) rates ω2 of the pattern amplitude as a function of the magnetization M. The symbols represent the measured data. The black dashed line shows a fit of expression of scaling law for ω2 to the experimental growth and decay rates (reproduced from ref. 554 with permission from Am. Phys. Soc., copyright 2016). | ||
The radioscopy technique evidenced the formation of Rosensweig surface instabilities, on a much slower time scale than for ferrofluids, also in a layer of thermoreversible ferrogel exposed to a vertical static and time dependent magnetic field.560In situ imaging provided direct evidence of spontaneous transition from an unstructured superfluid to an ordered arrangement of droplets in an atomic dysprosium Bose–Einstein condensate, i.e. in a quantum ferrofluid, which are long-lived and show a hysteretic behavior, in close analogy to the Rosensweig instability.561
4.1.1.1 Labyrinthine instabilities. The labyrinthine pattern forms in thin layers of magnetic liquid confined together with an immiscible nonmagnetic liquid by applying a magnetic field perpendicular to the layer.34,520,562
A related configuration arises in the case of a ferrofluid drop confined between closely placed walls; by increasing the applied magnetic field the shape successively changes from a circular drop to a multiply bifurcated configuration.34,563,564 Varying systematically the wall spacing of horizontal cells and increasing the intensity of applied magnetic field resulted in more finely convoluted patterns.565 Labyrinthine, hexagonal, or dispersed columnar structures are formed in a thin layer of a partially miscible ferrofluid–nonferrofluid mixture under the influence of a perpendicular magnetic field.566 A hybrid ferrohydrodynamic instability arises by reducing the thickness of the ferrofluid layer and by the miscible nature of the sample and the surrounding nonmagnetic liquid.567 The concomitant emergence of both Rosensweig and labyrinthine instabilities, i.e. a mixed pattern formation in a uniform magnetic field perpendicular to the layer, is governed by diffusion, flow, convection, and magnetic effects.568
A thin film of a ternary mixture of liquids including a ferrofluid, an ester based ferrofluid/2,6-lutidine/silicone mixture, undergoes a sequence of transitions in a magnetic field (Fig. 32A(a–g)) starting from a critical demixing of the fluid in cylindrical droplets (minority phase) immersed in an extended majority phase, followed by destabilization and transformation into a labyrinth pattern and by a third wrinkling transition at even higher field if the liquid has a liquid/air interface.569 Wrinkles are a result of two coupled materials that grow with different rates.570 In Fig. 32B there is a plot of wrinkle numbers, wr0 and wr4, of the red droplet of Fig. 32Aversus the external magnetic induction.
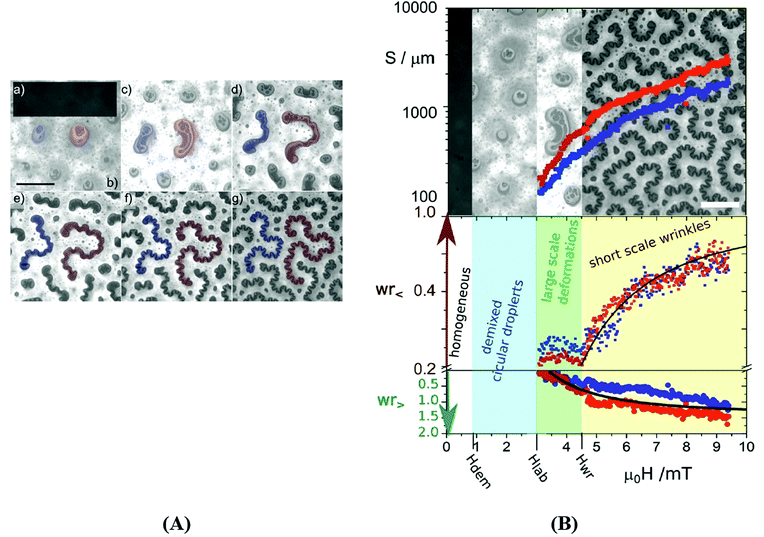 | ||
Fig. 32 (A) Reflection microscopy image of the surface of a ferrofluid/2,6-lutidine/silicone (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture at an external magnetic induction of (a) μ0H = 0 mT, (b) μ0H = 2.4 mT, (c) μ0H = 3.6 mT, (d) μ0H = 4.8 mT, (e) μ0H = 6.3 mT, (f) μ0H = 7.9 mT, and (g) μ0H = 9.3 mT normal to the film having a silicone oxide support and a free liquid/air surface at the top. (a) Exhibits a homogeneous image with no texture. The demixing of the fluid into ferrofluid rich and ferrofluid poorer phases occurs between (a) and (b). Cylindrical droplets get deformed into a labyrinth of droplets as one increases the field. The onset of the large-scale shape transition is between (b) and (c). Between (c) and (1d) the labyrinth starts to wrinkle. Wrinkles and large-scale bending of the droplets can be distinguished very clearly as the droplets grow (d–g). Scale bar in figure (b) is 100 micrometers. The two droplets in the center that are marked in blue and red correspond to the data shown in the next plot. (B) Plot of the surface path length S, the small-scale wrinkle number wr0, and the large-scale wrinkle number wr4versus the external magnetic field for the structures marked with red and blue in (A). Small scale wrinkles only occur after the circle versus dogbone/labyrinth transition. The black lines are fits to the theoretical expressions obtained for wrinkle numbers. Scale bar in the images is 100 micrometers (reproduced from ref. 569 with permission from Royal Soc. Chem., copyright 2017). 1) mixture at an external magnetic induction of (a) μ0H = 0 mT, (b) μ0H = 2.4 mT, (c) μ0H = 3.6 mT, (d) μ0H = 4.8 mT, (e) μ0H = 6.3 mT, (f) μ0H = 7.9 mT, and (g) μ0H = 9.3 mT normal to the film having a silicone oxide support and a free liquid/air surface at the top. (a) Exhibits a homogeneous image with no texture. The demixing of the fluid into ferrofluid rich and ferrofluid poorer phases occurs between (a) and (b). Cylindrical droplets get deformed into a labyrinth of droplets as one increases the field. The onset of the large-scale shape transition is between (b) and (c). Between (c) and (1d) the labyrinth starts to wrinkle. Wrinkles and large-scale bending of the droplets can be distinguished very clearly as the droplets grow (d–g). Scale bar in figure (b) is 100 micrometers. The two droplets in the center that are marked in blue and red correspond to the data shown in the next plot. (B) Plot of the surface path length S, the small-scale wrinkle number wr0, and the large-scale wrinkle number wr4versus the external magnetic field for the structures marked with red and blue in (A). Small scale wrinkles only occur after the circle versus dogbone/labyrinth transition. The black lines are fits to the theoretical expressions obtained for wrinkle numbers. Scale bar in the images is 100 micrometers (reproduced from ref. 569 with permission from Royal Soc. Chem., copyright 2017). | ||
Labyrinthine (fingering) instabilities in a Hele-Shaw cell with miscible magnetic fluids-surrounding non-magnetic fluids were investigated under different experimental conditions.571–575 The evolution of magnetic-field-driven micro-convection, in particular the initial fast fingering process followed by the subsequent decay of the flow due to the diffusion of the nanoparticles was investigated by particle image velocimetry and also by numerical simulation.574 The observed intensification of mixing by magnetic nanoparticles envisages applications in microfluidics from the mixing process within a microdroplet576 to local flows in the gaps of ferrofluidic seals and bearings.577 In the case of a rotating Hele-Show cell the growth of instabilities is strongly influenced by the rotation speed and magnetic field strength, evidencing also the Coriolis effect on labyrinthine instabilities.575 In the case of electroferrofluids-weakly charged superparamagnetic iron oxide nanoparticles in a nonpolar solvent-the application of an electric field induces the migration of the magnetic NPs to form concentration gradients.578
These translate to electrically controlled magnetic properties and pattern formation to be compared to the classical magnetic field induced instabilities (Fig. 33).
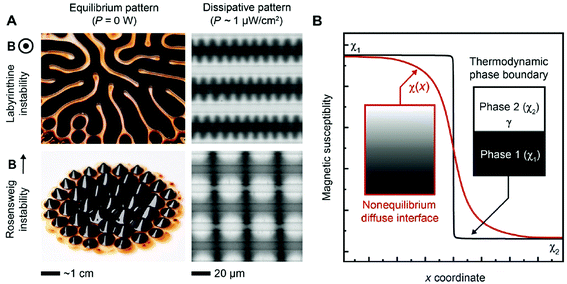 | ||
| Fig. 33 Comparison to classic equilibrium patterns and quantification of dissipation. (A) Images of the classic equilibrium Rosensweig and labyrinthine patterns and their dissipative analogs in electroferrofluids. (B) A schematic plot of the magnetic susceptibility near an equilibrium thermodynamic interface and a dissipative diffuse interface. The formation of the Rosensweig-like and labyrinthine-like patterns at B = 6 mT and, respectively, E = 0.3 V μm−1 (reproduced from ref. 578 with permission from American Association for the Advancement of Science, copyright 2021). | ||
4.2 Ferrofluid droplets
Droplet generation and manipulation techniques, precise control of droplet volumes and reliable manipulation of individual droplets579–582 are particularly interesting in the case of ferrofluid droplets262,564,583–592 due to their unique magnetic properties, giving rise to fascinating applications reviewed in Section 5.The overall phenomenology of aqueous maghemite ferrofluid59 drops deposited on a hydrophobic PDMS (polydimethylsiloxane) surface is outlined in Fig. 34I:593 magnetic forces up to 100 times the gravitational one and magnetic gradients up to 1 T cm−1 produce the observed changes in morphology and contact angle.
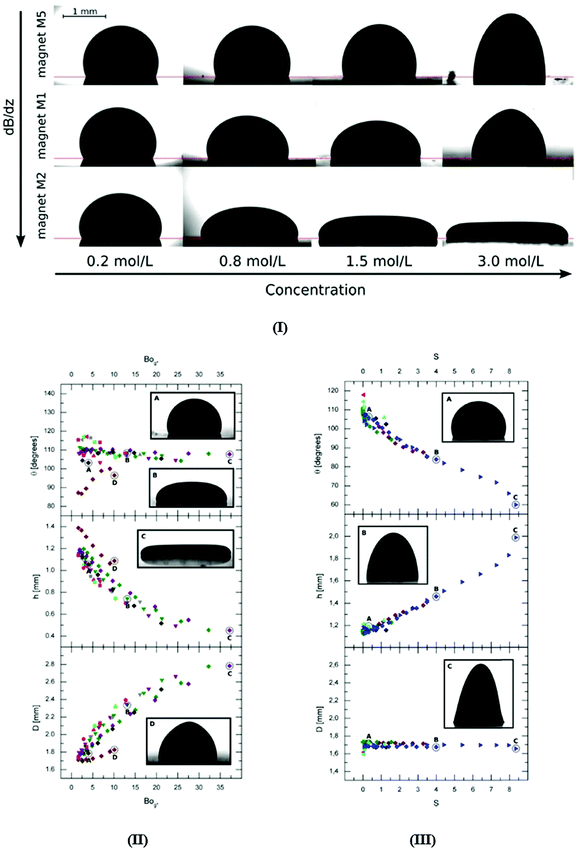 | ||
| Fig. 34 Ferrofluid drop on a flat solid surface (PDMS coated glass slide). (I) Images of ferrofluid drops with various concentrations placed on polydimethylsiloxane (PDMS) surface at a distance of 1 mm from three permanent magnets having very different values of the axial gradient dB/dz. The value for magnet M5 is dB/dz = 1.34 ± 0.04 T m−1, for magnet M1 dB/dz = 17.4 ± 0.4 T m−1, and for magnet M2 dB/dz = 86± 2 T m−1. (II) Contact angle (top), maximum height (middle), and diameter of the contact line (bottom) of ferrofluid drops of volume V = 2.5 μL as a function of the effective Bond number. The symbols represent different concentrations of the ferrofluidic solutions: ◁ 0.2 mol L−1, □ 0.4 mol L−1, ○ 0.8 mol L−1, △ 1.5 mol L−1, ∇ 2 mol L−1, ◊ 3 mol L−1, and ▷ 4 mol L−1. Different colors are associated with the magnets according to the following palette: maroon and red: magnet M1, dark green and light green: magnet M2, purple and pink: magnet M3, black and gray: magnet M4, and blue and aqua blue: magnet M5, where the first (second) color corresponds to measurements done changing the distance of the magnet from the sample (with the magnet in contact with the substrate). (III) Contact angle (top), maximum height (middle), and diameter of the contact line (bottom) of ferrofluid drops of volume V = 2.5 μL as a function of the S number. The symbols represent different concentrations of the ferrofluid solutions: ◁ 0.2 mol L−1, □ 0.4 mol L−1, ○ 0.8 mol L−1, △ 1.5 mol L−1, ∇ 2 mol L−1, ◊ 3 mol L−1, and ▷ 4 mol L−1. Different colors are associated with the magnets according to the following palette: maroon and red: magnet M1, dark green and light green: magnet M2, purple and pink: magnet M3, black and gray: magnet M4, and blue and aqua blue: magnet M5, where the first (second) color corresponds to measurements done changing the distance of the magnet from the sample (with the magnet in contact with the substrate) (reproduced from ref. 593 with permission from American Chemical Society, copyright 2016). | ||
All of the drops have the same volume V = 2.5 μL but different molar concentrations and are placed at a distance of 1 mm from three different magnets (M1, M2, and M5) having very different field gradient values indicated in Fig. 34I; for each concentration, increasing the field gradient causes a flattening of the drop by varying the contact angle. The observed effects can be conveniently described593 in terms of the effective Bond number Bog* (effective drop attraction vs. the capillary force) (Fig. 34II) and by the dimensionless number S (Fig. 34III) which compares the pressure jump at the ferrofluid interface due to the magnetization with the capillary pressure. In a vertical uniform magnetic field, the droplet aspect ratio increases along the field. In the non-uniform field of a permanent magnet the initial approximatively spherical shaped droplet first deforms and breaks up when the magnetic field increases above the critical field.
The division of a FF droplet, while related to the normal-field instability of ferrofluids, does not take place in a homogeneous magnetic field but it is due to a combination of high magnetic field and high vertical magnetic field gradient,588,589Fig. 35A and B. Moreover, the Rosensweig pattern is reversible (the pattern decays when the field is removed), but the patterns in Fig. 35B proved to be irreversible: the droplets do not coalesce back to a single droplet when the static magnetic field is switched off (Fig. 35C). Magnetic field (from high (P1) to low (P2)) controls the lattice constant in the kinetically trapped patterns (Fig. 35D–F). Dynamic self-assembly is a way to reduce the number of droplets and, in contrast to division instability, it is the mechanism to overcome the irreversibility of the droplet formation in static self-assembly.
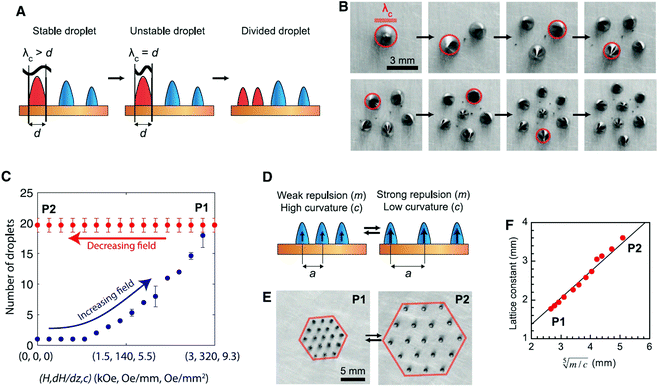 | ||
| Fig. 35 Self-assembled aqueous FF droplet patterns on a superhydrophobic surface in axisymmetric magnetic field. (A) Scheme of the division instability: λc, critical wavelength; d, diameter. (B) Photographs of the stepwise division and self-assembly of a 10 microliter droplet. The largest droplet is marked with a red circle. Magnetic field strength was increased from 1.0 kOe (dH/dz 82 Oe mm−1) for one droplet to 1.9 kOe (dH/dz 193 Oe mm−1) for eight droplets. (C) Number of droplets as a function of increasing and decreasing magnetic field, showing hysteresis due to the kinetic trapping. P1, high magnetic field; P2, low magnetic field. Error bars indicate standard deviation of three data sets. (D) Scheme of controlling the lattice constant in the kinetically trapped patterns by adjusting the magnetic field curvature (c) and the magnetic moment of the droplets (m). a, nearest-neighbor distance. (E) Snapshots of a 19-droplet pattern with two extreme periodicities at high and low magnetic fields. (F) The corresponding nearest-neighbor distance as a function of (m/c)1/5. Red dots denote experimental measurements; the black line indicates the best linear fit (reproduced from ref. 589 with permission from American Association for the Advancement of Science, copyright 2013). | ||
When a magnetic liquid drop deposited on a superhydrophobic substrate is subjected to vertical vibrations (Fig. 36a) without applied field (Fig. 36b) and in the presence of a static magnetic field (Fig. 36c), the magnetic field contribution (Fig. 36c and d) is equivalent to adding an effective negative surface tension to the drop.594
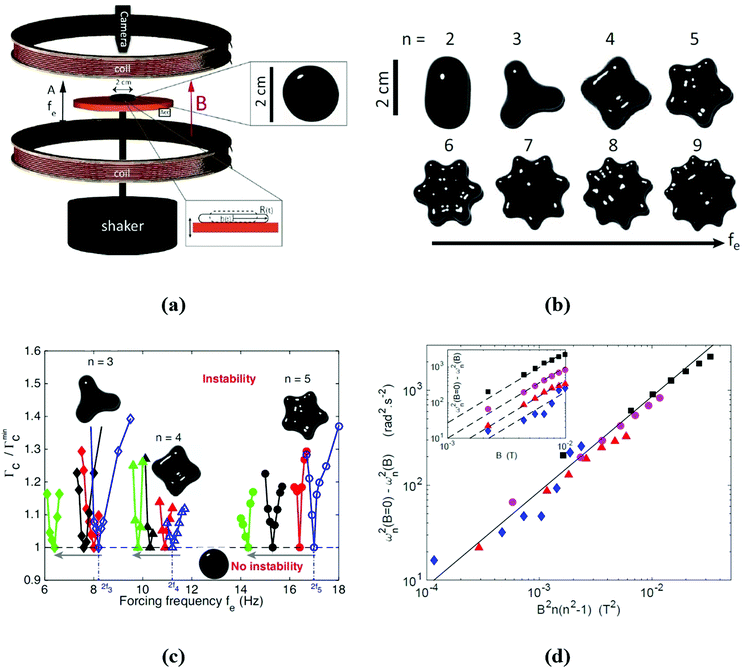 | ||
Fig. 36 Magnetic liquid drop subjected to vertical vibrations in the presence of a magnetic field. (a) Experimental setup. The bottom inset shows a schematic of the puddle at two phases of the vibration. Top inset: top view of the ferrofluid puddle at rest. (b) Top view of the azimuthal pattern displayed around the drop as a function of fe. Above a critical acceleration of vibration, an azimuthal pattern is observed normal to the vibration direction. When the forcing frequency fe is increased (0 ≤ fe ≤ 52 Hz), the number n of lobes, oscillating radially at fe/2, increases from n = 2 to 9 (from left to right and top to bottom). Magnetic field B = 0. Volume V = 1 ml. (c) Phase diagram of normalized rescaled critical acceleration Γc/Γmin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cvs. fe. Curves are marginality curves separating stable and unstable zones for different mode numbers n = 3 (◆), 4 (△) and 5 (○). No instability occurs for Γ ≤ Γc, whereas an azimuthal pattern around the puddle occurs within tongues. Open symbols correspond to B = 0, full symbols to B ≠ 0: B = 44 G (red, dark gray), 77 G (black) and 99 G (green, light gray). When B is increased (see arrows), the tongues are shifted towards a lower frequency, for each mode n. (d) Eigenfrequency shift ωn2(B = 0) − ωn2(B) as a function of B2n(n2 − 1) for different modes n = 3 (◆), 4 (▲), 5 (●) and 7 (■). The solid line is the prediction from the theoretical relationship obtained based on the Rayleigh model,595 with no fitting parameter. Inset: Un-rescaled frequency shift vs. B. Dashed lines have a slope of 2 (reproduced from ref. 594 with permission from Am. Phys. Soc., copyright 2016). cvs. fe. Curves are marginality curves separating stable and unstable zones for different mode numbers n = 3 (◆), 4 (△) and 5 (○). No instability occurs for Γ ≤ Γc, whereas an azimuthal pattern around the puddle occurs within tongues. Open symbols correspond to B = 0, full symbols to B ≠ 0: B = 44 G (red, dark gray), 77 G (black) and 99 G (green, light gray). When B is increased (see arrows), the tongues are shifted towards a lower frequency, for each mode n. (d) Eigenfrequency shift ωn2(B = 0) − ωn2(B) as a function of B2n(n2 − 1) for different modes n = 3 (◆), 4 (▲), 5 (●) and 7 (■). The solid line is the prediction from the theoretical relationship obtained based on the Rayleigh model,595 with no fitting parameter. Inset: Un-rescaled frequency shift vs. B. Dashed lines have a slope of 2 (reproduced from ref. 594 with permission from Am. Phys. Soc., copyright 2016). | ||
By adding magnetic nanoparticles to a water drop, i.e. by considering a ferrofluid droplet, its eigenfrequencies can be shifted by tuning the magnetic field strength, the experimental results being well accommodated594 (Fig. 36d) by extending the Rayleigh model of capillarity.595 Related to ferrofluid droplet dynamics on superhydrophobic surfaces, the collision and post-impact dynamics of ferrofluid droplets show asymmetric spreading regimes and rebound suppression under the influence of a horizontal magnetic field.596
4.3 Magnetic fluids with internal rotations: asymmetric stress tensor
The Shliomis model465 introduced the volume density of the angular momentum of ferrofluids which consists of the external (“orbital”) part associated with the translational motion and the internal (“spin”) part corresponding to the rotational motion of magnetic nanoparticles in the viscous carrier. In this model the magnetic moment is strongly coupled with the particle and due to the finite relaxation time the magnetization vector M is not always collinear with H. Particle rotation occurs with respect to the surrounding carrier liquid and, consequently, besides the magnetic force density (M·∇)H, the ferrofluid can undergo a magnetic torque of the density M × H and asymmetric stresses arise.34,520 The internal angular momentum is an independent variable along with the fluid velocity, density, and pressure. A complete set of constitutive equations consists of the equation of ferrofluid motion, the Maxwell equations, and the magnetization equation,161,234 as summarized in section 4.1. The magnetization equation can be obtained phenomenologically using the classical Debye relaxation equation597 applied to rotating magnetic nanoparticles or derived microscopically by the Fokker–Planck equation.437 Irreversible thermodynamics provides a consistent description of dissipative processes based on entropy production and provides a complete set of constitutive equations, leading to the same phenomenological magnetization equation.522 The rotating or spin-up flow of a ferrofluid in a stationary container induced by a rotating magnetic field was first evidenced by Moskowitz and Rosensweig.598 The theoretical approach of structured continua599–601 is used to describe the phenomena related to antisymmetric stress and the interchange of internal and external angular momentum of ferrofluids, involving the diffusion or spread of spin velocity parametrized by the spin viscosity, as well as the vortex viscosity and the equation of magnetic field taking into account the spin velocity and vorticity beside the usual magnetic terms.34,520,602–604The existing experimental data and the fundamental role of spin viscosity were recently reevaluated by Shliomis.623 The spin viscosity was found to be much smaller than any formerly calculated values and, consequently, the concept of spin diffusion cannot be used to explain the experimental findings. The rotational motion of the free-surface layer was found to be strongly related to the shape of the ferrofluid meniscus in the cylindrical vessel determined by the contact angle. The sign of the surface deformation determines the direction of fluid rotation (corotation or counter rotation relative to the rotating field), in agreement with experimental data (Fig. 37).613
 | ||
| Fig. 37 The distribution of azimuthal velocity u/u0 of the ferrofluid surface in a cylinder of R = 2.33 cm, angular velocity 60 Hz. The symbols mark the experimental data: ○ – H = 100 Oe, Δ – H = 200 Oe,613 and the solid line is for the theoretical values found by Shliomis (reproduced from ref. 623 with permission from Am. Phys. Soc., copyright 2021). | ||
The non-zero bulk flow observed in experiments was attributed to forces which could arise even from minor values of magnetic field and magnetization inhomogeneities in a ferrofluid exposed to a rotating field; therefore, spin viscosity is no more necessary to explain the data. The above reinterpretation of existing experimental data adds new arguments to the long-term debate concerning spin viscosity and spin-up flow of ferrofluids in rotating magnetic field.
4.4 Flow in confined geometries
Analogously, in quantum ferrofluids561,633,634 (Bose–Einstein condensates of Cr,635 Dy636 or Er atoms637) with dominantly dipolar interactions coherent vortex structures are formed, and the emerging quasi-classical quantum turbulence is controlled also by magnetic field.638 By extending the investigations to ferrofluid flow in time-varying magnetic field, the Brownian and Néel relaxation times come into play. The laminar and turbulent fractional pressure drop (ΔP(H)/ΔP(0) − 1) results are well described by ferrohydrodynamic equations when the effective magnetic susceptibility is allowed to depend on the magnetic field intensity and relaxation time.639 The theoretical description considering the existence of chain-like aggregates and the dependence of magnetic susceptibility and Brownian relaxation time on the ferrofluid flow rate provides a satisfactory fit516 to experimental data.639 Due to magnetic field induced spinning of rigid dipole particles in ferrofluids their angular velocity is not necessarily one-half the vorticity, as the magnetic torque in the internal angular momentum equation influences the flow.640 The magnetic torque for large magnetic field values (ξ > 1) depends on the choice of the particular magnetization equation437,465,641 and the Taylor and Kolmogorov turbulence scales642 show relatively large changes of averaged turbulence length scales in steady magnetic field. Numerical simulation evidences the effect of the choice of a particular magnetization equation on the time development of spatially averaged root-mean-square magnetic torque and vortex viscous dissipation rate.640 The pressure drop required to maintain a constant flow rate for a ferrofluid increases with the applied magnetic field strength. For channel flow the pressure drop required to maintain a constant flow rate at a frequency of 1000 Hz of the applied magnetic field corresponding to ΩτB = 0.06 relating particle relaxation time and characteristic time of oscillating field is less than that when the magnetic field is steady.643 Similar to pipe flow,639 in low Reynolds number turbulent flow the excess pressure drop increases with magnetic field and varies only slightly with frequency. The k–ε model,644 with k the turbulent kinetic energy and ε the rate of viscous dissipation of turbulent kinetic energy, correlates well the mean velocity profiles, the turbulent kinetic energy, Reynolds stresses, spin, and torque.643,645 The axial ferrofluid pipe flow in a constant axial magnetic field becomes unstable via spontaneous symmetry breaking and a concentric, two-phase swirling flow appears.646 The effect predicted takes place above some critical pressure drop and magnetic field strength due to the shear rate dependence of effective viscosity. The resulting ferrofluid swirling flow, instability similar to Rosensweig instabilities, has no classical analogy and it is the result of the competition between magnetic and viscous torques acting upon magnetic particles.
The change of ferrofluid viscosity in magnetic field stabilizes the Couette flow and, by exploiting the high sensitivity of the onset of turbulence653 to variation of viscosity, the rotational viscosity was determined in axial, radial and azimuthal magnetic fields.471,654,655
A Taylor–Couette system162 with four magnetic field coils in a Fanselau-type arrangement656 and with ultrasound Doppler velocimetry657 evidenced changes in the flow structure (Taylor-vortex flow and stabilization of the circular Couette flow due to axial and transverse magnetic fields in the case of two ferrofluid samples with significantly different microstructural characteristics).163 The Taylor-vortex flow structure, i.e. number of vortex pairs n and flow wave number k, in the case of a non-aggregating magnetite ferrofluid sample is much less influenced by axial magnetic field in comparison with the sample with strongly aggregating cobalt nanoparticles.
The onset of turbulence in Taylor–Couette ferrofluidic flow at a critical magnetic field strength can be accurately controlled via an external magnetic field,658 in contrast to classical fluid turbulence which involves a high degree of uncertainty.659 Computational ferrohydrodynamics through a detailed investigation of transitions in the flow structure in the presence of a magnetic field transverse to the symmetry axis of the system concluded that turbulence can occur at Reynolds numbers that are at least one order of magnitude smaller than those in conventional fluids.658 An estimate, involving the Niklas parameter,651 in the case of a commercial ferrofluid (APG933, Ferrotec Co) expects the onset of turbulence to occur for a critical magnetic field strength less than 80 kA m−1. Computational studies of flow dynamics evidenced transient behaviors to occur between multi-cell states, e.g., between two-cell and three-cell flow states, passing through two critical thresholds in a strength of an axial (transverse) magnetic field.660
5 Recently developed applications
5.1 Looking back: two highly successful ferrofluid applications
Initially developed for space applications, ferrofluids proved to be today an essential component of a very large number of high-tech devices and processes.161,661–663 Ferrofluids are fully involved in nanotechnology contributions to industrial progress and environmental protection and to the overall improvement of everyone's quality of life. Tiny quantities of specially designed and manufactured ferrofluids produced a real revolution in leakage-free rotating seal technology and high-fidelity audio engineering.39,664–667 Ferrofluid O-rings provide hermetic sealing of gaseous media and utterly free of mechanical wear, an extremely large variety of dynamical seals being used from the semiconductor industry to nuclear energetics. Also, highly improved centering, cooling and viscous damping of moving coil loudspeakers is a well-established ferrofluid-based technology applied in present day high-fidelity audio devices.5.2 Tunable and adaptive multifunctional materials derived from ferrofluids
Ferrofluids are fundamentally different from MR fluids,684 such as particle sizes and flow behavior. However, ferrofluids are part of promising new MR fluid formulations. Using a ferrofluid, i.e. a magnetizable carrier for MR fluids,140,627,685,686 results in an extremely bimodal suspension with highly improved MR behavior and kinetic stability.687 A very large size ratio (about 1000) exists between the small magnetite NPs (approx. 10 nm mean size) and the Fe particles; therefore, the ferrofluid carrier behaves as an effective continuum for the large micrometer size particles,688,689 implying a viscosity reduction of the overall suspension compared to the monodisperse case.690,691 The non-zero magnetic susceptivity of the carrier increases the magnetic interactions between the Fe particles, favoring structure formation and increasing the yield stress.627 The two fractions behave independently, allowing for an increase of the total particle volume fraction at close packing well above the maximum value for monodisperse spherical particles (0.64 at random close packing689). The favorable sedimentation/redispersion behavior and the observed increase of yield stress are most probably due to the formation of heterogeneous iron–magnetite structures that avoid the irreversible aggregation between iron particles and facilitate field-induced chaining.140,692 At the same magnetic particle volume fraction (40%), the MR behavior of a ferrofluid based MR fluid is more pronounced compared to a conventional MR fluid.693 Due to the very large particle size ratio the effective total hydrodynamic volume fraction of particles in a concentrated ferrofluid based MR fluid attained 0.85, for 0.44 volume fraction of micrometer size Fe particles suspended in the ferrofluid carrier,694 which is close to the theoretical upper limit corresponding to infinite size ratio.695
The non-dimensional apparent viscosity (ηapp/η∞) dependence on the Mason number (Mn) for MR fluid samples having F100, F500, and F1000 transformer oil based ferrofluids as carriers with 100, 500, and 1000 G nominal saturation magnetization for different values of the volume fraction of micron size Fe particles (ΦFe) and that of magnetite nanoparticles (φ) offer a useful correlation of magnetic and flow properties. Using the Casson model and drawing the curves ηapp/η∞ = f(Mn/Mn* = 1/Ca) (Mn*-critical Mason number corresponding to the transition from magnetic to hydrodynamic control of the suspension structure; Ca-Casson number) for all the magnetic field values for samples with different ΦFe and φ, the data collapse on a master curve, Fig. 38a.696 This master curve indicates the concentration–magnetization superposition in the case of FF-MRFs. The characteristic magnetic stress, defined as a function of the FF-MRF magnetization and of the ferrofluid carrier magnetization, can be used for any value of the external magnetic field; it allows the description of static yield stress as a function of volume fraction of iron microparticles and the applied magnetic field using a single variable, τchar. The characteristic magnetic stress values τchar, calculated using a finite element method, are well correlated with experimental data, providing a more general master curve, Fig. 38b.697 The master curves offer valuable information for adequate tuning of the composition of ferrofluid-based MR fluids to the specific requirements of various MR devices. A requirement of FF-MRFs is to avoid the formation of any magnetic nanoparticle aggregates which could prolong the very fast transition time of the magnetic field induced reversible change from fluid to quasi-solid state; therefore, the high colloidal stability of the ferrofluid carrier is an essential feature.
 | ||
| Fig. 38 Ferrofluid based MR fluids. (a) The dependence ηapp/η∞ = f(Mn/Mn* = 1/Ca) for different values of the Fe particle volume fraction ΦFe and of the magnetic nanoparticle volume fraction φ. Fit lines: ηapp/η∞ = Ca + 2Ca1/2 + 1. Fit parameter values are given in ref. 696; (b) master curve obtained for all samples with different nano and micro concentrations, at different values of magnetic field induction. aΦ and bM are horizontal and vertical translation coefficients of experimental data (reproduced from ref. 697 with permission from The Society of Rheology, copyright 2018). | ||
In the case of a ternary solid–ferrofluid–liquid magnetorheological fluid obtained by dispersing carbonyl iron particles in a water-in-oil emulsion of an aqueous ferrofluid,698 the FF droplets are attracted by the primary chain-like structures formed by the CI particles in applied magnetic field and move to fill in the gaps between the CI particles (Fig. 39a), the complex structuring mechanism being evidenced by bright light and fluorescence microscopy images. The apparent yield stress exhibits a maximum with the FF concentration (Fig. 39b-left) and, similarly, a maximum is evidenced for the magnetic field dependence of the storage modulus (G′) (Fig. 39b-right). The storage modulus attains a maximum and for very large magnetic fields levels off, reaching a constant value, as a consequence of the magnetic saturation of CI particles.698
 | ||
| Fig. 39 (a) Schematics of the FF bridges under magnetic fields; (b) left: apparent yield stress (τ0) as a function of FF concentration for 5 vol% CI suspensions at H = 100 kA m−1. Right: Storage modulus (G′) as a function of external magnetic field strength (H) for 5 vol% CI suspensions with different FF concentration levels. The vertical arrow corresponds to the magnetic field strength for microscopy observations (56 kA m−1) (reproduced from ref. 698 with permission from IOP Publishing, copyright 2018). | ||
The density mismatch between the ferrofluid carrier (density up to approx. 1.8 g cm−3) and Fe particles (7.8 g cm−3) is relatively high. To improve the kinetic stability of the composite MR fluid the multidomain Fe particles were replaced by nanocomposite particles consisting of a mixture of oleic acid coated magnetite nanoparticles of about 6 nm and Al2O3 coated FeCo particles of about 50 nm average size.699 The reduced density (3.3 g cm−3) 100–300 nm size compactly packed nanocomposite particles with relatively high saturation magnetization (130 emu g−1) dispersed in a ferrofluid carrier provided a promising MR response, among others for semiactive seismic damper applications.
 | ||
| Fig. 40 Hierarchical assembly of 3-particle ring structures is illustrated on the underlying ring templates: (a) MN4 ring, which was observed for φ = 0.1%, NL/NM = 4; (b) MN3 ring, which was observed for φ = 0.1–0.2%, NL/NM = 3; (c) MN2 ring, which was observed for φ = 0.1–0.2%, NL/NM = 2; (d) MN ring, which was observed for φ = 0.1–0.2%, NL/NM = 1; (e) M2N2 crystallite, which was observed for φ = 0.2–0.3%, NL/NM = 1; (f) M2N ring, which was observed for φ = 0.1–0.2%, NL/NM = 2; (g) M3N ring, which was observed for φ = 0.3–0.4%, NL/NM = 3; and (h) M4N ring, which was observed for φ = 0.4%, NL/NM > 4. The illustrations depict the crystal structures, in which the 1 μm particles (S) are red, 2.7 μm particles (M) are dark brown, and 4.8 μm particles (L) are green. The scale bars are 10 μm. The notation MxNy is used to refer to the stoichiometry of a structure in which a unit cell contains x paramagnetic particles and y diamagnetic particles (reproduced from ref. 706 with permission from Am. Chem. Soc., copyright 2013). | ||
For rodlike (i.e. nonspherical) nonmagnetic particles dispersed in a ferrofluid the assembly process by the magnetic hole mechanism acquires new features due to the orientational degree of freedom of particles.707 The anisotropic shape of rods favors the tip-toe arrangement in chain-like structures, the assembly process following a power law time-dependence (Fig. 41).
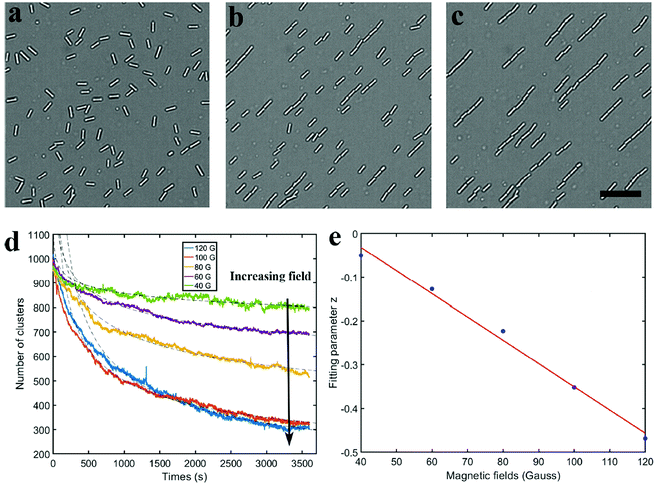 | ||
| Fig. 41 Self-assembly of silica rods in ferrofluids under different magnetic field strengths. (a−c) Optical images showing the chain formation under 40 G at (a) t = 0, (b) 500, and (c) 3600 s. The scale bar is 15 μm. (d) Number of clusters in an area of 550 × 550 μm2 as a function of time under different magnetic field strengths; the black dashed lines are fittings using N ∼ tz. (e) Power-law exponent z as a function of the field strength. The solid line is a linear fit (reproduced from ref. 707 with permission from Am. Chem. Soc., copyright 2021). | ||
The magnetic hole mechanism was extended using magnetic and also hydrodynamic forces in a ferrofluid for the shape and assembly of non-magnetic polymer particles in a continuous flow process. When an external magnetic field gradient is applied in a ferrofluid droplet microfluidic device the manufacturing process of polymer particles is controlled by the flow rate and magnetic means708 (Fig. 42).
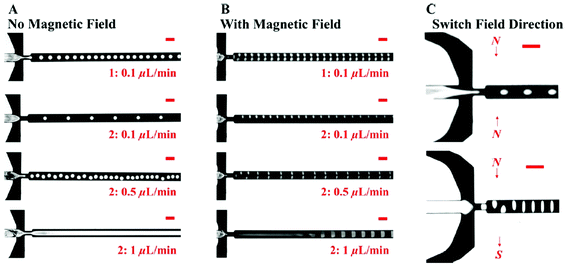 | ||
| Fig. 42 Continuous shape and assembly of polymer particles. (A) Spherical polymer droplet generation with no magnetic field. The sizes of the droplets can be controlled by adjusting the flow rate ratio between the polymer phase and the continuous ferrofluid phase. (B) Nonspherical polymer droplet generation with magnetic fields induced by attractively placed magnets. (C) Polymer droplets are either compressed or stretched into an ellipsoidal shape by arranging magnets differently (in an attractive manner or in a repulsive manner, as indicated by the arrows). The continuous phase is a commercial water-based magnetite ferrofluid (EMG 705, Ferrotec Co., Bedford, NH). The volume fraction of the magnetite particles for this particular ferrofluid is 5.8%. Scale bars in A–C are 200 μm (reproduced from ref. 708 with permission from Am. Chem. Soc., copyright 2015). | ||
The magnetic field directed assembly process of dielectric spheres, schematically presented in Fig. 43a,709 is also an application of the first order magnetofluidic levitation effect (magnetic hole mechanism). By using a ferrofluid of Fe3O4 nanoparticles in water (10 nm, 0.25% to 0.5% volume fraction) and by precisely designing the local field gradient around diamagnetic microspheres, various coupled photonic structures for optoelectronic applications can be produced. The process of magnetic field induced assembly of colloids is illustrated for fluorescent dye-doped PS microspheres (large 15 µm, small 10 µm) in images captured by optical microscopy (Fig. 43b).
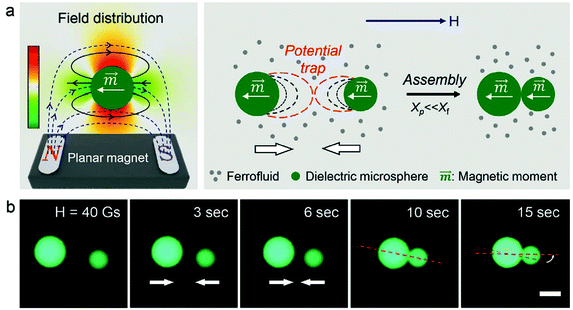 | ||
| Fig. 43 Ferrofluid-driven assembly of dielectric microspheres: (a) schematic illustration of the field distribution around a polystyrene (PS) microsphere on top of a planar magnet (left) and the potential trap of magnetostatic forces between microspheres dispersed in a ferrofluid. (b) Optical microscopy images of a pair of PS microspheres in a ferrofluid under a magnetic field of 40 Gs. Scale bar is 10 µm (reproduced from ref. 709 with permission from John Wiley and Sons, copyright 2021). | ||
Water droplets, while non-magnetic, can be controlled by magnetic fields when immersed in a non-miscible oil based ferrofluid.710 Permalloy tracks displaced in the substrate of a Hele-Shaw cell are magnetized by an in-plane rotating magnetic field, while the ferrofluid by an orthogonal field. The local field gradients ensure the synchronous generation and propagation of water droplets. An array of hydrophobic ferrofluid spikes formed by a non-uniform magnetic field can be used to transport a water droplet by the combined action of surface tension and magnetic force developed by a moving magnet (Fig. 44), resulting in a basic process in a noncontact and biocompatible magnetic manipulation technique of non-magnetic droplets.711
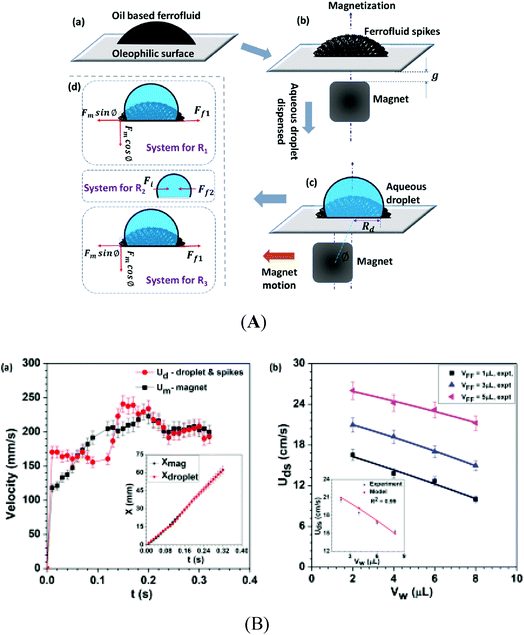 | ||
| Fig. 44 Magnetofluidic transport of an aqueous droplet. (A) (a) Schematic of an oil-based ferrofluid (FF) droplet dispensed on a rigid oleophilic substrate. (b) Formation of an array of FF spikes after incorporation of a normal magnetic field. (c) Aqueous droplet dispensed over the array of FF spikes, encapsulating the FF spikes, where ϕ is the angle between the axis of magnetization (magnet) and the axis of the droplet. (d) Force balance for the respective system in various regimes. (B) (a) Variation of the magnet velocity Um and aqueous droplet (Vw = 4 μL) velocity Ud (which is the same as the FF spike velocity) for VFF = 3 μL with time t; variation of the location x of the magnet and the aqueous droplet (and the FF spikes) with time t is shown in the inset. (b) Variation of maximum velocity of aqueous droplets Uds with aqueous droplet volume Vw, for different ferrofluid volumes VFF, for VFF = 3 μL; a comparison between the model predictions and experimental data is also shown, θ = 70° (reproduced from ref. 711 with permission from Am. Chem. Soc., copyright 2019). | ||
A gallium-based iron NP ferrofluid, called transitional ferrofluid (TF), was made to provide switchable interlocking force during phase change to achieve magnetic manipulation of non-magnetic objects.712 The transitional ferrofluid is a unique temperature- and magneto-responsive remote controlled liquid gripper which enables intimate contact with arbitrarily shaped objects, as illustrated in Fig. 45.
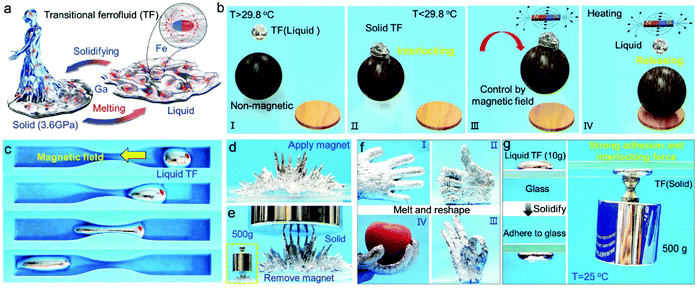 | ||
| Fig. 45 The reversible phase transition of a transitional ferrofluid (TF) and the mechanism of magnetic manipulation of nonmagnetic objects. (a) Diagram showing a reversible phase change between a solid and liquid of TF. (b) A diagram demonstrating the switchable magnetic grasp of non-magnetic objects by the phase transition of the TF. In a liquid state (T > Tm = 29.8 °C), the transformable TF can come into contact with the target objects intimately (I); the TF solidifies at room temperature (T = 25 °C < Tm) and tightly interlocks the embedded objects without external energy consumption (II); utilizing the magnetism of the TF, the embedded objects can be grasped remotely by a magnetic field (III); after delivery to the designated spot, the objects are freed from the bonds by melting the TF again upon moderate heating (IV). (c) The liquid TF droplet can easily transform its shape on a large scale and pass through narrow channels under control of the magnetic field; (d) when a strong magnetic field is applied at the bottom of the liquid TF, the transformable TF presents macroscopic protuberances immediately because of the formation of a chain-like alignment of iron particle; (e) the multi-thorn structure formed can bear more than 500 grams of weight; (f) The artificial hand made by rubber and TF (I) can mimic the different gestures of a real hand such as “thumbs up (II)”, “OK (III)” and grasping the fruit (IV) through melting TF, reshaping and solidifying. (g) Solidification of TF enables a strong adhesion force to glass and an interlocking force to the weight (500 g) (reproduced from ref. 712 with permission from John Wiley and Sons, copyright 2021). | ||
 | ||
| Fig. 46 Droplet transport with a ferrofluid liquid infusion. (A) Magnetic flux density over an array of rod-shaped magnets computed with finite element analysis. This magnetic flux density generates the surface topography formed by the ferrofluid infused on the soft carpet. The planes xz and xy indicate the side and top views, respectively. (B) Finite element analysis of the magnetic scalar potential formed on top of a magnet array. The polarization direction (N/S depicts the north and south pole of the magnet, respectively) along the z-axis of each magnet in the array is indicated in the sketch. (C) Schematics depicting the case of excess ferrofluid in the layer used to infuse the soft carpet. Here, the system stays at the slip state, as the pillar edges are constantly covered by the infusion layer. (D) The motion of the surface topography with a moving magnetic wave carries the 20 μL droplet along the same direction of the wave motion. Snapshots show the droplet transport at the slip state over time. (E) A sketch depicting the case of a soft carpet infused with a layer poor in ferrofluid. Here, the surface exhibits both pin and slip states. Droplets pin quickly, and the strokes of these pinning pillars drive the droplet motion. (F) The strokes of the pinning pillars push the 60 μL droplet in an opposite direction to the moving magnetic field wave. Snapshots show the droplet transport at the pin state over time. (G) A rotor-shaped magnet array manipulates ten 50 μL droplets with a ferrofluid infusion. Magnetic flux density of the rotor-shaped magnet array placed under the infused substrate (H) and time lapse of a 50 μL water droplet being manipulated on a circular path (I) (scale bars, 5 mm) (reproduced from ref. 714 with permission from PNAS, copyright 2021). | ||
A hierarchical magnetoresponsive composite surface, made by infiltrating a ferrofluid into a microstructured matrix (ferrofluid-containing liquid-infused porous surfaces-FLIPS), offers substantial versatility in designing dynamic surfaces with multiscale topographical responses at three different length scales:715 self-assembly of colloidal particles on the micrometer scale (Fig. 47A); regulated flow of liquid droplets on the millimeter scale (Fig. 47B); and switchable adhesion and friction, liquid pumping and removal of biofilms on the centimetre scale (Fig. 47C). FLIPS are envisaged to be used as part of integrated control systems for the manipulation and transport of matter, thermal management, microfluidics and fouling-release materials.
 | ||
| Fig. 47 Applications of ferrofluid-containing liquid-infused porous surfaces-FLIPS. (A) Manipulation of non-magnetic colloidal particles on FLIPS (application of FLIPS on the micrometer scale). (a and b) Schematics (top) and confocal fluorescence images (bottom) of 10 μm-diameter melamine colloidal particles floating on the flat surface of FLIPS in the absence of a magnetic field (a) and confined in micro-topography of FLIPS when the ferrofluid has been locally depleted from the microstructures using a magnet (b). (c) Schematics showing colloidal particles staying stationary in the absence of a magnetic-field gradient (∇H0 = 0; top) and moving in the presence of a magnetic-field gradient that is created by a magnet on the right (direction of ∇H0 indicated by the arrow; bottom). (d) Optical images showing the transport of colloidal particles along the micro-topographical region. Four particles are labelled to depict their movement within a 10 s interval. (e) Schematic illustrating the mechanism behind the transport of non-magnetic colloidal particles in a magnetic field: the transport of ferrofluid induces a flow of the water near the ferrofluid–water interface, leading to the transport of the colloidal particles. (f) Plot of relative colloidal positions along the channels as a function of time; the green shaded areas indicate the times when the magnet field is turned on. (B) Control of droplet flow and droplet manipulation (application of FLIPS on the millimeter scale). (a) Top, schematic showing the configuration of the experimental set-up in (b) and (c). The FLIPS is tilted and placed at a distance d above the magnet. Bottom, simulated magnetic pressure distribution (pm) around the magnet. The upper and lower scales of the color scale correspond to (c) and (b), respectively. (b) Two photographs showing a water droplet pinned on the micro-topographical area and its subsequent release after the magnet is lowered to allow the ferrofluid to flow back and submerge the micro-topography. (c) Five photographs showing different clustering behaviors of 15 μl water droplets on the macro-topographical feature at five different distances d. This FLIPS used a diluted ferrofluid and hence did not have a micro-topographical area. (d) Schematic showing the unwrapping of a thin ferrofluid layer around a water droplet by changing the surrounding medium from air to a hydrocarbon liquid. (e) Five photographs showing the unwrapping of a thin layer of ferrofluid around a water droplet after the addition of dodecane. (f) Four photographs showing the delayed mixing of two liquid droplets in the presence of wrapping layers. The white and red droplets are the suspension of 10 μm-diameter polystyrene colloids in an ethanol–water mixture and in water dyed with rhodamine B, respectively. They were brought together by a stationary alternating-current electromagnet at the center beneath the FLIPS. (g) Three photographs showing instant mixing of two droplets in the absence of wrapping layers. The left droplet is an aqueous solution of sodium bicarbonate and the right droplet is an aqueous solution of 2 M hydrochloric acid. The right image shows the CO2 bubble formed after the coalescence of the droplets. (C) Adhesion, pumping and biofilm removal (application of FLIPS on the centimeter scale). (a) Adhesion. The top left schematic shows the set-up for adhesion measurement. The test surface is brought into contact with FLIPS at a speed of 0.1 mm s−1, held still for 10 s and then lifted at 1 mm s−1. An example of the resulting force–distance curve is shown at top right. The test surface in this example is a smooth PTFE. The photographs at the bottom demonstrate switchable adhesion. (b) Pumping. The top is a schematic of the pumping mechanism. The pair of magnets moves the ferrofluid plug along the FLIPS pipe, which in turn drives the liquid (blue) flow inside the pipe. The bottom photographs show that an ethanol solution of rhodamine B is pumped from the right vial to the left vial. (c) A green algae biofilm is removed by swirling a magnet under FLIPS. Note that the fluorocarbon-based ferrofluids used in these experiments are not toxic, as indicated by the green color of the algal biofilm (reproduced from ref. 715 with permission from Springer Nature, copyright 2018). | ||
The liquid-in-liquid approach in microfluidics acquires highly valuable new features-self-healing, non-clogging, anti-fouling and near-frictionless flow-when the solid wall of the flow channel is replaced by a non-miscible ferrofluid layer stabilized by a permanent magnet configuration providing, for example, a water “antitube”, Fig. 48.716 Applications of the liquid-in-magnetic liquid approach envisage, among others, magnetostaltic human blood pumping in heart–lung machines during cardiopulmonary bypass surgery to avoid damage (haemolysis) by shear forces.
 | ||
| Fig. 48 Wall-less magnetic confinement in a fluidic channel. (a) Permanent magnets (red, blue) in an in-plane quadrupolar configuration create a low-field zone at the centre, where an antitube of water (yellow) is stabilized inside an immiscible magnetic liquid (white). (b) Contour plot of the magnetic field. (c) Synchrotron X-ray tomographic reconstruction of a water antitube (yellow) with a diameter of 81 μm, surrounded by a ferrofluid (blue). (d) Optical end view of a water antitube in a ferrofluid. (e) X-ray end-view cross-section from tomographic data at y = 4 mm. (f) X-ray side-view cross-section from tomographic data at x = 1 mm. Scale bars (black/white), 2 mm. A set of 5 commercial ferrofluids were used in experiments (reproduced from ref. 716 with permission from Springer Nature, copyright 2020). | ||
Droplet interface bilayers with an engineered protein pore with diode-like properties in droplet networks could form devices with electrical properties (e.g., a current limiter, a half-wave rectifier and a full-wave rectifier) with collective properties that cannot be produced by droplet pairs.717 Droplet interface bilayer (DIB) networks by the incorporation of a ferrofluid within the droplet phases allow for remote manipulation of the interfacial bilayer properties, resulting in magnetically responsive DIB arrays.718 Ferrofluid droplets were assembled into larger DIB structures by an external applied magnetic field, and the resulting membrane and structure remained stable after removing the field and allow for the combination of water and ferrofluid droplets in DIB clusters.
Preparation of magnetic liposomes using ferrofluids acquired much interest for drug encapsulation and MRI detection, allowing for magnetic actuation and controlled release of the active substance stored either in the bilayer or in the aqueous core of vesicles.719–723 Taking into account the width of a lipid bilayer of 4–6 nm, the incorporation of magnetite NPs in such a thin layer requires ferrofluids with practically monodisperse and very small (3–5 nm) mean size IONPs in order to achieve a significant loading efficiency without disrupting the bilayer.724,725 The organization of SPIONs within glyceryl monooleate (GMO)/water mesophases shows locally enhanced SPION concentration and improved magnetic response. SAXS investigations of the thermotropic and magnetotropic behavior reveal that already small amounts of IONPs with a hydrophobic (oleic acid) coating alter the phase behaviour and promote cubic to hexagonal phase transition, which is produced also by an alternating magnetic field. The rheological measurements show the role of long-range dipolar interactions inducing a solid-like behavior, these interactions controlling the mechanical properties of the lipid structure. The magnetic field responsiveness and rheological behavior are allowing for spatio-temporal control of the confined drug release.725,726
The magnetic field configured templates starting from a ferrofluid are extremely flexible and easily adjustable to provide a rich morphology mimicking even a biological surface architecture.727 Negative microhole array moldings with precise sizes and angles were manufactured by adjusting the magnetic field strength and orientation driving the ferrofluid, paving the way for the feasible and cost-effective production of microneedle arrays by replicating the moldings.728
5.3 Sensors
Following dynamic sealing and damping applications, the first and second order levitation effects and outstanding magnetic properties specific to ferrofluids inspired from the beginning research on sensing applications.664For acceleration/inclination measurements using ferrofluidic levitation the sensor proof mass is a non-magnetic body (first order levitation effect) or a permanent magnet (second order levitation effect) suspended in a ferrofluid, the displacement being monitored (by an inductive or capacitive means or by a Hall probe)666,729–732 and assisted by a magnetic field source (permanent magnet) for non-magnetic seismic mass, as well as by an electronic control unit. According to the operating principle the friction-free movement of the proof mass in the axial direction is balanced electromagnetically. Essentially, the force balance concept is that the proof mass is maintained as much as possible in a fixed position relative to the housing using a high gain amplifier to ensure the required forcing current. For inclination angle the output voltage vs. output voltage characteristics are linear, while the highest sensitivity achieved attains 147 mV/0,732 while for acceleration sensors sensitivity values of 10−6 to 10−9 m s−2 were attained.729 Applications of ferrofluidic inertial sensors refer to inclination angle measurements of oil well bores and steering of drill bits,665 as well as to calibration of sea and land gravimeters and horizontal acceleration measurements for seismic noise monitoring.729 A bio-inspired tactile sensor also based on the ferrofluidic levitation effect733 relates the external mechanical stimuli producing the deflection of a submerged rod in a ferrofluid volume to a certain distortion of the magnetic field detected by a Hall sensor.
Inductive sensors fully exploit the magnetic properties and liquid nature of a ferrofluid used as sensing component in a two-coil arrangement.664,665,734,735 The ferrofluid behaves like a liquid magnetic core and increases the inductance of each coil; initially, when there is no any pressure difference or non-zero inclination angle/non-zero angular displacement, both coils are filled to the same level and thus, the inductance values are the same. An inductive-differential type inclination sensor has a fine resolution of 0.01 mm m−1, while the measured linearity is better than 1.5%.735 In a different approach a small volume, a drop of ferrofluid, subjected to a magnetic field was used as a sensing element of an inertial sensor.736 The inclinometer uses a free sliding ferrofluid mass in a glass channel with an actuation coil and two sensing coils to monitor the time elapsed during transitions of the ferrofluid mass between two fixed positions which correspond to the inclination angle, the electronic control and data acquisition system, providing a frequency output approximatively proportional to the tilt angle.737 The magnetic fluid filled coil inductive sensor elements can be arranged to measure a differential pressure or a gas flow rate (with inclination angle compensation). The highly sensitive differential pressure sensor (of the order of μmH2O) and specially developed laminar flow measuring elements allow for considering ferrofluidic inductive sensors operating from low (several cm3 min−1) to high (hundreds of m3 h−1) flow rate values.734
Magnetic nanoparticle relaxation processes by Néel and Brown mechanisms typical for ferrofluids234 are fully exploited by magnetic particle spectroscopy (MPS)-based lateral flow immunoassays. The non-linear magnetic response of MNPs to time-varying excitation fields is monitored by pick-up coils to extract the MPS spectra for analysis.738–740 For volume-based MPS platforms MNPs serve as high-specificity probes to capture target analytes from biofluid samples. The successful recognition and binding events on biofunctionalized MNPs cause increased hydrodynamic volume and reduced Brownian rotational freedom of MNPs, the key feature in high precision (mean error 1.3 ng) quantification of magnetic nanoparticles in biological fluids.741 By monitoring the larger phase lags between the magnetic moments and external fields using a frequency mixing technique, a successful immunoassay was achieved for cytometry740 (Fig. 49I). Highly sensitive diagnostically relevant analyses were developed using bio-ferrofluids for ultrasensitive circulating tumour cell (Fig. 49II), blood cell, biomolecule or pathogen detection/separation.742–748
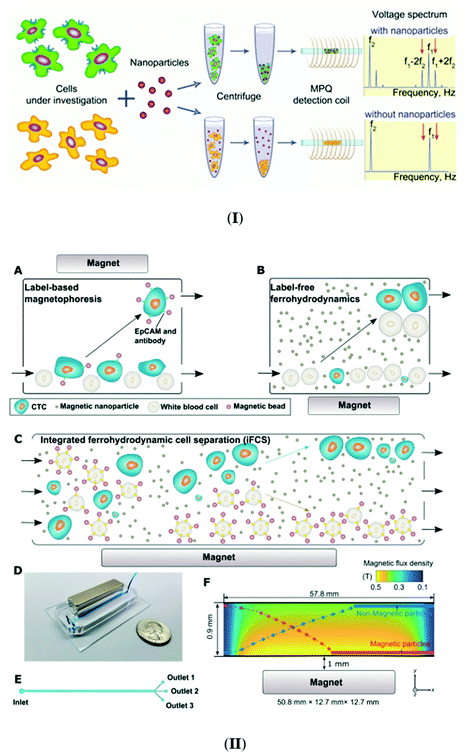 | ||
| Fig. 49 (I) Scheme of the MPQ-cytometry workflow: cell labeling and detection of cell-bound nanoparticles. The cells under investigation are incubated with the nanoparticle suspension (bio-ferrofluid), and unbound nanoparticles are then removed from the cells by centrifugation. The quantity of nanoparticles bound to the cells is measured using the magnetic particle quantification (MPQ) technique at combinatorial frequencies (reproduced from ref. 740 with permission from Royal Soc. Chem., copyright 2016); (II) overview of integrated ferrohydrodynamic cell separation (iFCS) and its prototype. (A) Schematic illustration of traditional label-based magnetophoresis for circulating tumor cell (CTC) separation, in which CTCs were labeled via specific biomarkers such as the epithelial cell adhesion molecule (EpCAM) through functionalized magnetic particles to be separated by magnetic force towards the magnetic field maxima in a continuous-flow manner. (B) Schematic illustration of label-free ferrohydrodynamic cell separation of CTCs. CTCs with increased physical sizes in the ferrofluid experienced increased magnetic buoyance force via diamagnetophoresis and were pushed towards the magnetic field minimum. (C) Schematic illustration of an integrated ferrohydrodynamic cell separation (iFCS) scheme for CTC isolation. Unlabeled CTCs of different sizes and magnetically labeled WBCs were pushed towards opposite directions via different mechanisms (diamagnetophoresis for CTCs and magnetophoresis for white blood cells (WBCs)), resulting in a spatial separation at the end of the device. (D) A prototype iFCS device. (E) Top view of the iFCS microchannel with labels of the inlet and outlets. (F) Simulated magnetic flux density distribution and trajectories of 11.8 μm magnetic beads and 15 μm diamagnetic beads in the microchannel (L × W × H, 57.8 mm × 0.9 mm × 0.15 mm) with a neodymium permanent magnet (L × W × H, 50.8 mm × 12.7 mm × 12.7 mm). The dimensions of the microchannel and the magnet were not drawn to scale. Particles were simulated using 0.05% (v/v) ferrofluid and a flow rate of 200 μL min−1 (reproduced from ref. 742 with permission from Royal Soc. Chem., copyright 2021). | ||
Ferrofluids are used, by exploiting highly sensitive detection and imaging techniques based on nonlinear properties of nanomagnets or various liquid-phase adsorption/magnetic separation processes, to extract toxic and harmful analytes from different matrices.123,124,749–753 A ferrofluid-based biosensor for histamine detection in red wines is a combination of magnetic competitive lateral flow immunoassay strips and an inductive sensor using recombinant protein functionalized 10 nm mean size superparamagnetic iron-oxide NPs for the magnetic quantification of the toxic component.754 The ferrofluid aided inductive biosensor was validated against ultra-high-performance liquid chromatography analyses and proved to be successful as a histamine point-of-use analytical technique. Signal amplification was obtained by clustering of 3–5 lauric acid double-layer coated and streptavidin functionalized magnetite NPs, increasing this way the magnetic moment of the resulting nanolabel. The lauric acid coated nanoclusters in aqueous bioferrofluids proved to be highly performant nanolabels for lateral flow immunoassays and their magnetic quantification.755
Ferrofluids due to their high magnetic field sensitivity, fluidity and optical fiber compatibility756–758 are the basic component of various magneto-optic devices,759 among them a large variety of magnetic field sensors exploiting specific field induced effects, such as birefringence, dichroism, Faraday rotation or refractive index variation246,760–762 and magnetic fluids coupled with optical fiber technology.763 Magnetic field sensors were developed by combining magnetic fluids with an etched fiber Bragg grating,764 with a Sagnac interferometer,761,765 with a Mach–Zehnder interferometer and photonic crystal fiber,766 and with a Michelson767 or a Fabry–Pérot interferometer.768 An optical fiber magnetic field sensor based on the single-mode–multimode–single-mode (SMS) structure and magnetic fluid gives the magnetic field strength either by measuring the dip wavelength shift of the transmission spectrum or by detecting the transmission loss at a specific wavelength with high sensitivities given by the central wavelength shift of 905 pm mT−1 or by the transmission loss of 0.748 dB mT−1.769 Microstructured optical fibers770 with ferrofluids filled into their air holes consist in versatile platforms for developing compact optofluidic devices.771 A compact fiber-optic vector magnetometer consists in a tilted fiber Bragg grating coated with a nanometer scale gold film placed together with a water-based magnetite ferrofluid (EMG705, Ferrotec, Japan, with saturation magnetization of 22 mT and effective refractive index of 1.385) inside a capillary.772 The orientation (2 nm deg−1) and the intensity (1.8 nm mT−1) of the measured magnetic fields result from the tilted fiber Bragg grating spectrum.
An optical loss based magnetic field sensor with ferrofluid infiltrated microstructured polymer optical fiber (MPOF)773 is primarily based on the effect of the magnetic field on the transmission loss properties of the light hydrocarbon based ferrofluid; in particular, the short wavelength cut-off absorption band of the ferrofluid undergoes large spectral red-shifts under magnetic field excitation.
The direction and intensity of the magnetic field can be measured by monitoring the wavelength shift of the transmission spectra of a Mach–Zehnder interferometer making use of the anisotropic aggregation of magnetic nanoparticles (Fig. 50A.a–d) in an air-bubble-caused nonconsecutive MF film (Fig. 50A.e and f) of a fiber-optic vector magnetometer.762 The sensing mechanism relies on the magnetism-controllable effective refractive index modification and gives a wavelength shift as a function of magnetic field (H) (Fig. 50B.e and f), which allows for an intensity sensitivity of 222.0 pm mT−1. Even higher sensitivity was achieved for a magnetic field sensor based on a microfiber coupler (MFC) combined with an aqueous magnetic fluid (MF) (IO-A10-1; Cytodiagnostics Inc., Canada) in a Sagnac loop formed from a polarization maintaining fiber (PMF):774 a magnetic field sensitivity of −488 pm mT−1 in the range from 0 to 200 mT has been experimentally obtained with a MFC of small waist diameter (∼2.6 μm) and PMF length of 20 cm.
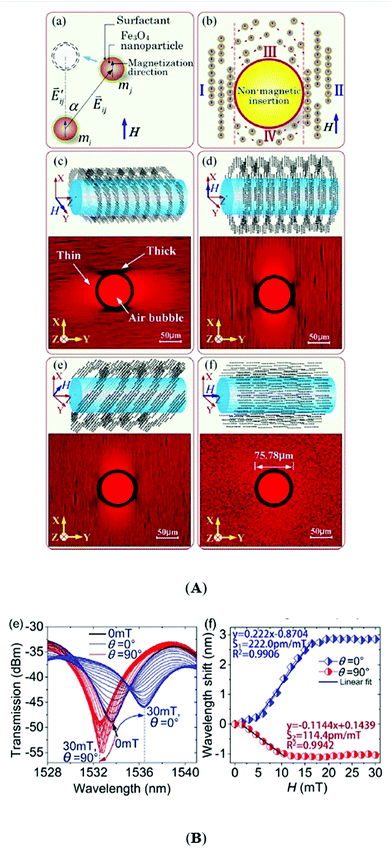 | ||
| Fig. 50 Fiber-optic magnetic fluid-based vector magnetometer. (A) Magnetic nanoparticle behavior: (a) schematic diagram of dual-magnetic-dipole interactions under the magnetic field. (b) A schematic view illustrating anisotropic nanochain cluster formation of Fe3O4 nanoparticles in the non-continuous MF film. Anisotropic nanochain-clusters of magnetic nanoparticles with different magnetic field directions (c) along the Y-axis, (d) along the X-axis, (e) making ∼45° with respect to the Z-axis, and (f) along the Z-axis; the upper images are the schematic diagrams of anisotropic aggregation around a fiber; the lower micrographs exhibit the anisotropic formation of nanochain-clusters around an air bubble. (B) (e) The spectra response curves and (f) wavelength shift as the magnetic field intensity increases from 0 mT to 30 mT (reproduced from ref. 762 with permission from AIP Publishing, copyright 2017). | ||
A temperature-compensated variant of the magnetic field sensor is based on a ring erbium-doped fiber laser combined with a fiber Bragg grating and a Sagnac loop containing a microfiber coupler and a water based magnetic fluid (IO-A10-1; Cytodiagnostics Inc., Canada), providing a maximum sensitivity of 102 pm mT−1 in the magnetic field range from 0 to 60 mT.775 A cost-effective and relatively simple fiber magnetic field sensor can be constructed by immersing microfiber into a magnetic fluid (produced by Hangzhou Jikang New Materials CO.) and exploiting the magneto-optical dichroism and the non-circular symmetric distribution of the magnetic field induced nanoparticle clusters around the microfiber.776 Degree and direction of light polarization provide the information on magnetic field intensity and orientation up to 88 Oe with a sensitivity of 3.36 × 10−4 per Oersted.
The ferrofluid-based fiber magnetometers have the advantage of magnetically tunable optical effects and of their basic design involving magnetic fluid as a layer outside the magneto-optical coupling device or as a liquid filler in the micro-hole-arrays of photonic crystal fibers. Magnetic fluids employed in these sensors are mostly aqueous ferrofluids which have to show well-controlled reversible magnetic field induced structuring of steric stabilized magnetite/maghemite nanoparticles, providing intense magneto-optical effects. To keep the favorable aggregating tendency in magnetic field and, at the same time, to ensure long-term colloidal stability of water-based magnetic fluids is a delicate issue, involving high quality requirements. Irreversible aggregate formation could have a strong negative influence on the sensor characteristics.
Due to high sensitivity, fast response, and low power consumption optical fiber ferrofluidic magnetometers are envisaged to be applied in many areas, among others in information storage, environmental monitoring, hazard forecasts, and aeronautics.
5.4 Actuators
Microfluidics777–779 highly benefit from the use of ferrofluids which respond to external localized magnetic forces, conform to the channel shape and offer leakage-free sealing, providing easy magnetic actuation in various flow configurations on the microscale to promote micromixing, pumping, focusing, sorting and transfer phenomena applications.780–783 Lab-on-a-chip (LOC) technology requires miniature fluid handling devices,778 which put forward various pumping mechanisms using non-uniform magnetic field ferrofluid actuation.782 The magnetocaloric effect controls the position or movement of tiny volumes of ferrofluid to fulfill the role of a plug, a valve or a piston. Ferrofluidic micropumps have characteristic sizes from several mm to a few tens of mm and flow rate of the order of several tens of microliter per min and can ensure a backpressure of about 1000 Pa,784 with promising applications in micro fluid handling, such as for polymerase chain reaction (PCR),785 lab-on-a-chip, micro total analysis and drug delivery systems.780,786,787 In the case of micro-scale gear pumps, the extremely low efficiency is due to volumetric loss which can be reduced almost completely (approx. 90%) by introducing a magnetorheological fluid between gear and housing providing an efficient dynamic sealing effect, without introducing larger friction, tighter manufacturing tolerances, or vulnerability to vibrations.788A completely different mechanism relies on spatially traveling, sinusoidally time-varying magnetic fields and dynamic particle chain formation, which provides direct body pumping of ferrofluids in closed-loop geometries without any moving parts. The pumping effect is a result of formation of particle chains exposed to a locally rotating field with a radial gradient in magnitude, creating a radial shear that drives ferrofluid flow. A maximum flow rate of 0.69 ml s−1 and a no-flow pressure of 4.8 Pa were achieved at 12 A current amplitude and 1 kHz.789 This mechanism powered by rotating magnetic fields to increase diffusion-limited NP transport by enhancing local fluid convection was recently applied for magnetoresponsive microrobots (artificial bacterial flagellum or magnetotactic bacteria (MTB))-a kind of “living ferrofluid” designed to overcome a lot of physiological barriers existing in drug delivery by ferrohydrodynamics driven solutions, such as non-magnetic NP transport.790
Fig. 51 offers a comparison between the ferrohydrodynamic pumping mechanisms of suspensions of magnetotactic bacteria (MTB) and multicore IONPs to evaluate their performance as mediators of magnetically induced fluid flow for pumping and transport. Taking into account the magnetic volume fraction values of the two kinds of bio-ferrofluids, the “living” ferrofluid with MTB was found to produce more homogeneous and efficient flow when exposed to a uniform rotating magnetic field (RMF).791
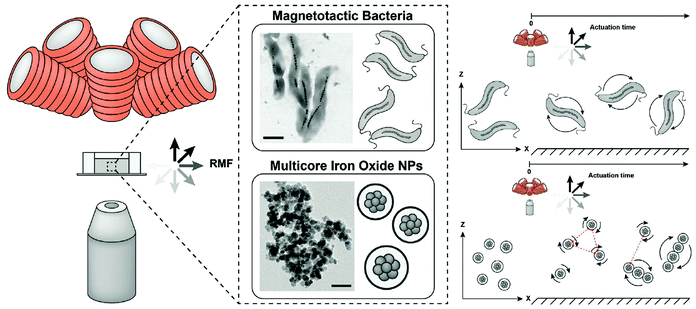 | ||
| Fig. 51 Integrated magnetic manipulation and imaging setup to analyze the magnetically induced flow of a living ferrofluid based on suspensions of magnetotactic bacteria (top, scale bar 500 nm) and a synthetic ferrofluid based on suspensions of multicore iron oxide nanoparticles (bio-ferrofluid fluidMAG-PVA (Chemicell 4120-5)) (bottom, scale bar 50 nm). Samples are located between the objective lens and electromagnetic coils generating a uniform rotating magnetic field. Ferrohydrodynamic coupling occurs by actuating MTB and IONP suspensions under rotating magnetic field. MTB start to rotate individually in response to the applied field and IONPs self-assemble into chain-like microstructures while rotating upon exposure to the same magnetic stimulus. RMF-uniform rotating magnetic field (reproduced from ref. 791 with permission from John Wiley and Sons, copyright 2020). | ||
Highly localized traps in a ferrofluid created by a magnetized/demagnetized magnetically soft micropen allow for magnetofluidic tweezing of nonmagnetic objects of 1–50 µm in size and, also, for controlling in a reversible manner entire colloidal formations.792
A ferrofluidic manipulator was set-up that exploits the magnetically controllable air-ferrofluid interface for automatic moving of nonmagnetic objects (Fig. 52).793 The ferrofluid based device controls the motion of non-magnetic particles along predefined paths using a linear-programming-based control algorithm.
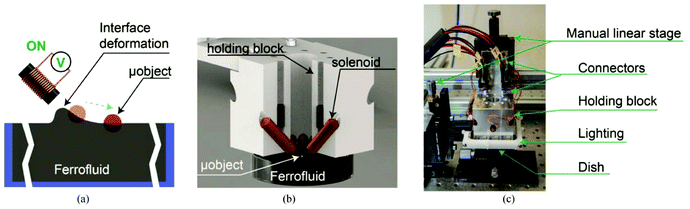 | ||
| Fig. 52 Ferrofluid manipulator: the concept and interacting components for automatic manipulation of small-scale nonmagnetic objects at the air–ferrofluid interface. Illustration not to scale. (a) Concept of two-dimensional manipulation of a nonmagnetic object: e.g., polyethylene particle. (b) Computer-aided design (CAD) rendered image of the mechanical assembly consisting of solenoids within a holding block located on top of a dish containing the ferrofluid and a particle at the air–ferrofluid interface. (c) Photograph of the ferrofluidic manipulator showing the aluminum holder with the solenoids, a ring LED light, and a Petri dish containing a ferrofluid sitting on a 2-D goniometer stage. Manipulation platform resides on an antivibration table (reproduced from ref. 793 CC Creative Commons license). | ||
5.5 Ferrofluid droplet technology
Droplet-based microfluidics is an emerging liquid handling technology579,794–796 which refers to the generation, precise control and manipulation of discrete droplets (usually of nanoliter to picoliter volume) inside microchannels and microdevices.797–800Among various passive and active methods of droplet generation801 formation of microdroplets involving ferrofluids,588,589,802i.e. the possibility of remote actuation of droplets on surfaces, which was not possible using conventional microfluidics, adds another level of controllability in modulating droplet formation and transport with the aid of additional energy input by an external magnetic field.801,803–805 Magnetowetting, a new feature specific to ferrofluid droplets806 and ferrofluid thin films,807 could provide an efficient way to manipulate magnetic or non-magnetic droplets for digital microfluidics and lab-on-a-chip applications.593,663,710,742,805,806,808–810
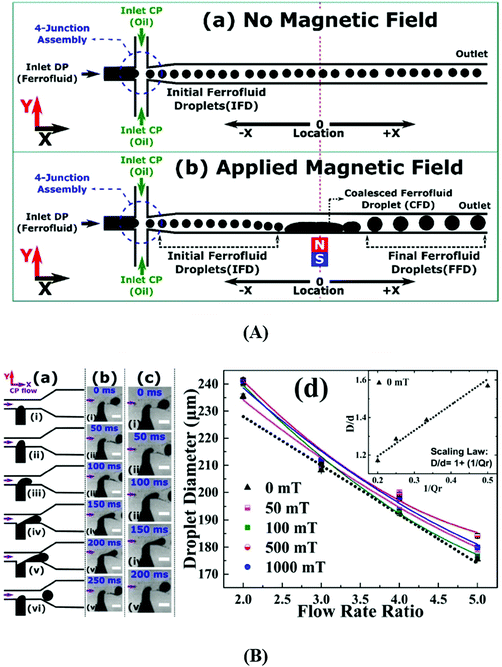 | ||
| Fig. 53 Ferrofluid droplet generation. (A) Influence of magnetic field. Schematic of (a) initial ferrofluid droplet (IFD) generation by a 4-junction assembly with no magnetic field and (b) effect of an applied magnetic field on IFDs resulting in the formation of the final ferrofluid droplets (FFD). A permanent magnet was used to apply the magnetic field. Center of the magnet was selected as the reference location x = 0, denoted by the dotted red line. In the negative x region (x < 0), IFDs are generated. Near x = 0, IFDs coalesce and the formation of a coalesced ferrofluid droplet (CFD) takes place. The FFDs are then released from the CFD, with a larger diameter than the IFDs. The diameter of the FFDs can be tuned by the applied magnetic field and the flow rate ratio (reproduced from ref. 811 with permission from Elsevier, copyright 2017). (B) Generation of ferrofluid droplets in a uniform magnetic field. Influence of flow rate. (a–c) Droplet generation at the flow rate ratio of 2 (Q2). (a) Schematic. (b and c) Experimental micrographs at (b) H = 0 mT and (c) H = 500 mT, scale bar = 250 μm. (d) Droplet size vs. flow rate ratio (Qr) at magnetic field H = 0, 50, 100, 500, and 1000 mT. Solid lines denote polynomial fits and the dotted line shows a linear fit. The inset shows the graph for the scaling law D/d = 1 + 1/Qr at H = 0 mT, for droplet diameter D, channel width d and flow rate ratio Qr = Qcp/Qdp. The purple arrow indicates the direction of the CP flow (x-direction). The magnetic field is in the y-direction. Ferrofluid: EMG 807 (Ferrotec Co.) (reproduced from ref. 582 with permission from Springer Nature, copyright 2016). | ||
Magnetic-field-induced instability in the case of citrate stabilized aqueous ferrofluid immersed in an immiscible solvent is producing splitting and self-assembly of ferrofluid microdroplets, as illustrated in Fig. 54.812 Droplet splitting occurs at a critical field strength and gradient and successively gives rise to satellite droplets with orders of magnitude smaller volumes than the initial ones. Varying the ferrofluid concentration and interfacial tension allows for the creation of self-assembled droplet populations in a controlled manner. The size and frequency of FF droplet generation at a T-junction can be controlled by a non-uniform time-dependent magnetic field, a suitable alternative for moving magnets or an array of micro-coils.813,814
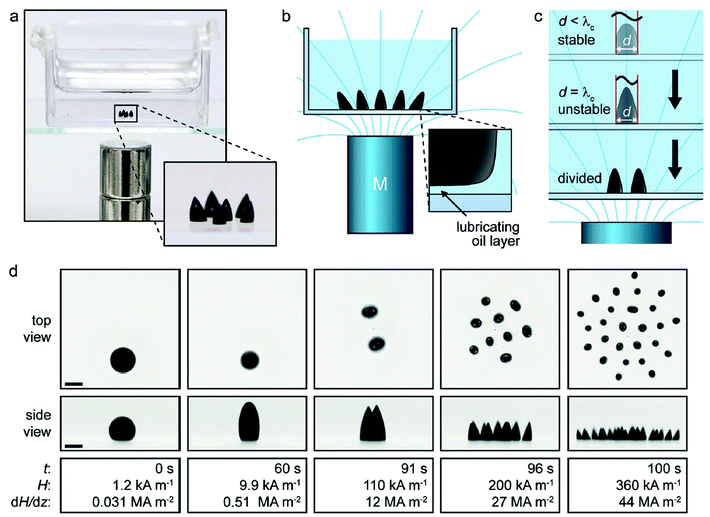 | ||
| Fig. 54 Magnetic-field-induced ferrofluid droplet splitting in an immiscible liquid. (a) Photo of ferrofluid droplets in a polystyrene container filled with silicone oil and a stack of two cylindrical magnets (diameter and height = 9.5 mm) underneath. (b) Schematic of a droplet population in a magnetic field (field lines in cyan) created by a permanent magnet. The inset shows a lubricating oil layer between the droplet and the substrate. (c) Schematic of droplet splitting in an increasing magnetic field (λc: critical wavelength, d: droplet diameter). (d) Top and side views of ferrofluid droplet splitting in silicone oil (t: time, H: external magnetic field, and dH/dz: vertical field gradient). The distance between the magnet (diameter = 20 mm, height = 42 mm) and the droplets is reduced from 102.8 to 2.8 mm at a speed of 1 mm s−1. Scale bar: 1 mm (reproduced from ref. 812 CC Creative Commons licence). | ||
Nonuniform magnetic field induced ferrofluid droplet splitting presented above creates a large liquid surface area, a magnetically tunable, hydrophobic, liquid substrate. Functionalized by a fusion protein the ferrofluid interface is capable of capturing antibody molecules, which are released when the pH of the solution is decreased (Fig. 55).815
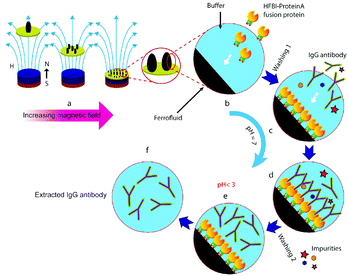 | ||
| Fig. 55 Ferrofluid droplet splitting for the antibody extraction process-schematics. (a) The process starts with magnetic-field-induced splitting of the ferrofluid droplets. (b) The droplets are decorated with HFBI-Protein A fusion protein, after which excess HFBI-Protein A is washed out of the system (Washing 1). (c) Immunoglobulin G (IgG) antibody molecules with possible impurities are added to the buffer solution. (d) IgG molecules are caught by Protein A. After that the excess IgG molecules and any impurities are washed out (Washing 2). (e) IgG molecules are released from Protein A by decreasing the pH of the solution. (f) The purified antibody molecules are collected (reproduced from ref. 815 CC Creative Commons licence). | ||
A similar ferrofluid magnetic field splitted droplet structure forms negative microhole array moldings with various geometrical characteristics. The magnetically programmed moldings could serve for cost-effective manufacturing of biocompatible polymer based isotropic and anisotropic needle arrays for biomedical applications.728
Ferrofluid droplets can be used as mechanical actuators and micro-rheometers to apply controlled forces and quantify endogenous mechanical properties in developing 3D tissues and organs.816 Such a multifunctional single probe consists in a fluorocarbon ferrofluid droplet (Fig. 56A) acted by a magnetic field (up to 1 kG) of a permanent magnet array to generate a magnetic force in the investigated tissue (zebrafish embryo) (Fig. 56B).
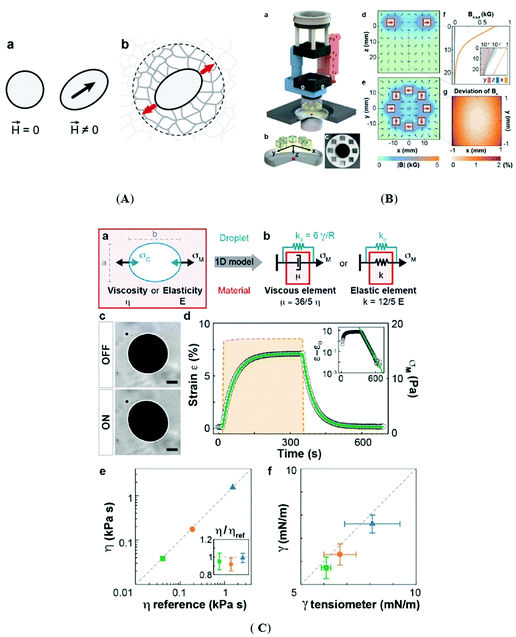 | ||
| Fig. 56 Ferrofluid droplet actuator and measuring unit. (A) Ferrofluid microdroplets as mechanical actuators. (a) A ferrofluid oil droplet, spherical in the absence of a magnetic field (H = 0), deforms into an ellipsoid elongated along the axis defined by the direction (black arrow) of an externally applied, uniform magnetic field (H ≠ 0). (b) When a ferrofluid oil droplet, inserted between the cells forming a tissue, is actuated by applying a uniform magnetic field, it deforms and generates a local force dipole (red arrows) in the tissue. Imaging the droplet deformation over time upon controlled actuation allows for the quantification of the local tissue mechanical properties in a small neighborhood around the droplet (dashed circle). (B) Module for ferrofluid droplet actuation. (a) 3D drawing of the module. The uniform magnetic field is generated using an array consisting of eight permanent magnets (yellow). The magnitude and direction of the magnetic field on the sample are specified by controlling the distance between the magnet array and the sample using a piezo stage (red) and the magnet array orientation using a rotatory motor (blue), respectively. (b) Magnified sketch of the system geometry, including the magnets, glass-bottom dish (gray) and sample (red). (c) Picture of the magnet array mounted on a 3D-printed holder. (d and e) Finite element simulation of the magnetic flux density B (direction, blue arrows; magnitude, color coded), or equivalently the magnetic field H = B/μ0, generated by the magnet array in the xz (d) and xy planes (e). Homogeneous magnetic fields of up to 1 kG (0.1 T) are achieved at the center of the array (e; red arrows). (f) Measured values of the three components of the magnetic flux density (Bx, By, Bz) at the center of the array (x = y = 0) along the z axis (inset: log–linear scale; error bands indicate the s.d.). (g) Measured deviation of Bx in the xy plane at z = 0 from its value at the center (x = y = 0). The dashed circle indicates the typical size of a zebrafish embryo (∼0.6 mm). The reported values of the magnetic field correspond to the average of N = 1024 measurements at 100 μm increments in z (f) and in x and y (g). (C) Measuring mechanical properties using ferrofluid droplets. (a) Sketch of a ferrofluid droplet (blue) in a material (red) characterized by viscosity η or stiffness E. Magnetic stresses σM deform the ferrofluid droplet into an ellipsoid with major and minor axes b and a, respectively, and are resisted by capillary stress σC. (b) Effective 1D diagrams representing the combined system of the droplet within a Newtonian fluid or elastic material, characterized by viscous (μ) and elastic elements (k), respectively. (c) Fluorocarbon-based ferrofluid oil droplet in an immiscible, Newtonian hydrocarbon oil, with (on) and without (off) magnetic field. The strain ε is obtained from the droplet's aspect ratio, b/a, by detecting the droplet's elliptical contour (white ellipse). Scale bar, 100 μm. (d) Strain evolution (black circles) upon actuation of the droplet in (c) with a controlled magnetic stress σM (orange dashed line), showing an exponential relaxation (inset: log–linear scale). A single (N = 1) droplet actuation cycle is shown. The green line represents the fit to the solution of the 1D rheological model for a Newtonian fluid. (e) Viscosity values of three reference Newtonian hydrocarbon oils (N15000, green square; N62000, orange circle; N450000, blue triangle; online methods) measured using ferrofluid droplets and compared to their reference viscosity values (N = 4 samples and 4 actuations per sample). The inset shows the ratio of measured to reference viscosities; error bars indicate the s.d. (f) Interfacial tension of the ferrofluid droplet in the same reference hydrocarbon oils measured using the ferrofluid drop deformation (N = 7) and compared to independent bulk measurements using a pendant drop tensiometer (N = 7). Error bars indicate the s.d. In all cases, N indicates the number of samples (reproduced from ref. 816 with permission from Springer Nature, copyright 2017). | ||
Ferrofluid droplets for in situ measurements were calibrated using a pendant drop tensiometer and a parallel plate rheometer, as well as known properties of materials (hydrocarbon oil and polyacrylamide gel). Direct in vivo measurements of tissue mechanics performed by a multifunctional ferrofluid droplet (Fig. 56C), application exemplified for developing zebrafish tailbud tissues, are capable of relating biomaterial behavior on the intermediate stress relaxation time scale at supracellular scales (tissue level) with that specific to the characteristic time scale of subcellular level.816
A universal synchronous scheme using ferrofluids, which does not rely on pressure-based flow controllers, implements logic gates by exploiting nonlinear magnetic and hydrodynamic interactions between fluid droplets.823 The principle of operation outlined in Fig. 57A relies on creating local energy minima or “potential wells” (Fig. 57Aa) on a planar (2D) Hele-Shaw flow geometry to set ferrofluid droplets in motion on permalloy patterns magnetized with an in-plane rotating field (Fig. 57A b and c). The system consists of aqueous ferrofluid droplets immersed in silicone oil between two glass plates-the fluidic chip (Fig. 57A d and e).
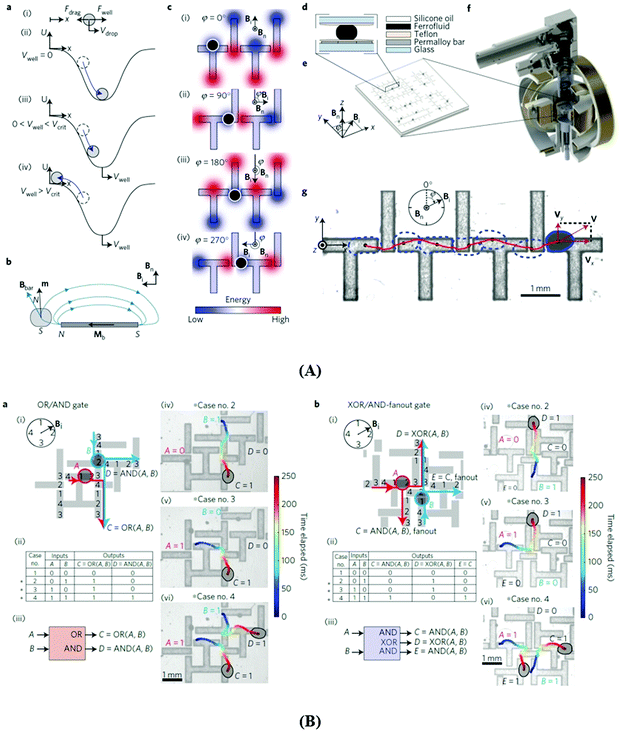 | ||
| Fig. 57 Ferrofluid droplet logic. (A) Principle of operation. (a) (i) Free body diagram of a droplet with velocity Vdrop in a 1D potential well U(x) with velocity Vwell, where Fwell = −dU/dx is the force due to the well and Fdrag is the hydrodynamic force. (ii) Droplet equilibrium case Vwell = 0: the droplet settles at the centre of the well. (iii) 0 < Vwell < Vcrit: the droplet moves with the well Vdrop = Vwell at a relative position where Fnet = Fdrag + Fwell = 0. (iv) Vwell > Vcrit: the droplet falls behind the well because Vwell is higher than the critical Vcrit, such that Fdrag(Vcrit) > max(Fwell). (b) Schematic of a ferrofluid droplet with a magnetic dipole moment m (induced by a field Bn) inside a field Bbar by a permalloy bar with magnetization Mb (induced by Bi). The magnetostatic energy U = −mBbar is minimized when opposite poles of the droplet and the bars are paired. (c) Schematic top view of the droplet (shown as a black dot) on ‘T-bars’ and ‘I-bars’. During a full rotation of Bi, the droplet follows the potential wells formed for each φ = (0°, 90°, 180°, and 270°), and thus moves rightwards. (d) Schematic side view of Hele–Shaw geometry of a fluidic chip. (e) Perspective view of a fluidic chip with magnetic fields Bi and Bn. (f) Experimental set-up including electromagnetic coils combined with a microscope system. (g) Video snapshot where a droplet propagates rightwards under a clockwise rotating field Bi and a fixed Bn. The droplet trajectory is marked in red and the instantaneous droplet shapes are marked with blue dashed lines. (B) Combinational droplet logic: basic gates. Logic gates with junction geometries where droplets interact through a repulsive magnetic force to perform logic operations. ‘1’ and ‘0’ are assigned to the presence and absence of a droplet at a given inlet or outlet port of the junction geometry. The junctions act as combinational logic gates; the input droplets at the inlet ports ‘compute’ the output droplets at the outlet ports. (a) OR/AND logic gate. (i) Schematic where the black numbers 1–4 denote the potential wells activated by the angular orientations of Bi, prescribing the droplet trajectories (corresponding droplet-trajectory pairs have the same colour). (ii) A truth table. (iii) Block representation of the logic gate. (iv–vi) Experimental realizations of logic cases, corresponding to the asterisks in (ii). The background images are presented as semi-transparent and the droplet boundaries are marked in black. The colour of the trajectories represents the elapsed time. (b) XOR/AND-fanout gate. Items (i–vi) have the same meanings as in (a). The XOR is a supercase of logic NOT, for example, for B = 1, XOR(A, 1) = NOT(A) shown in cases 2, 4 in (v, vi). The XOR/AND-fanout gate has two identical outputs or fanouts, C = E = AND(A, B), which, for example, can duplicate input A using B = 1 so that C = E = AND(A, 1) = A. The XOR/AND-fanout is capable of universal logic—that is, it can be combined to perform any Boolean logic computation. All experiments are performed at f = 6 Hz, Bi = 40 G, and Bn = 250 G (reproduced from ref. 823 with permission from Springer Nature, copyright 2015). | ||
The rotating field induces a synchronous motion of the droplets, while the out-of-plane magnetic field a magnetic repulsion between them, allowing for designing logic gates (Fig. 57A.f) which result in well-defined droplet trajectories (Fig. 57A.g). In Fig. 56B there are represented an OR/AND gate (Fig. 57B.d) and an XOR/AND-fanout gate (Fig. 57B.b) designed by applying ferrofluid droplet technology. The XOR/AND-fanout gate can be combined to perform any Boolean logic operation; consequently, this gate is capable of universal digital logic. The key features are the rotating magnetic field, a kind of global clock to synchronize the motion of arbitrary numbers of ferrofluid droplets and the nonlinear magnetic and hydrodynamic interaction forces between droplets.823
In Fig. 58a and b there are illustrated several advanced ferrofluid droplet actuation mechanisms used to perform in a programmable manner diverse and massively parallelized and sequential microfluidic operations, such as splitting and merging for liquid-cargo delivery, fluidic-mixing, navigating through narrow channels and versatile manipulation of delicate objects. Ferrofluid droplet robotics is a highly relevant field for biomedicine, pharmaceutics and biotechnology, among them for point-of-care diagnostics, drug development, and chemical/material synthesis.
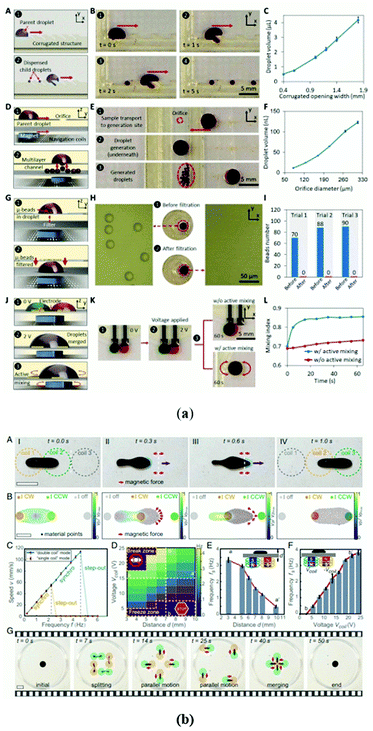 | ||
| Fig. 58 Advanced magnetic field controlled operations with ferrofluid droplets. (a) (A) Schematic illustration of the droplet dispensing mechanism involving the transportation of the package against a corrugated microfluidic wall. (B) Sequential optical images of the droplet dispensing process. (C) Characterization of the dispensed droplets’ size for different corrugated opening widths. Error bars, SE (n = 10). (D) Schematic illustration of the droplet generation process involving the droplet transportation to a vertical interconnect access (VIA-like) orifice. (E) Sequential optical images of the droplet generation process. (F) Characterization of the generated droplets’ volume for different orifice diameters. Error bars, SE (n = 20). (G) Schematic illustration of the filtration mechanism. (H) Optical image of the solution sample before and after filtration. (I) Bead counts before and after filtration (three trials). (J) Schematic illustration of droplet merging and mixing mechanisms. (K) Optical images to visualize the droplet merging (upon applying 2 V) and mixing process (with and without active mixing). (L) Comparison of the progressive mixing index for the two cases of with and without active mixing. Bio-ferrofluid used: Feraheme (AMAG Pharmaceuticals, MA, USA) (reproduced from ref. 825 with permission from The American Association for the Advancement of Science, copyright 2020). (b) Actuation mechanism and characterization of the single-body and coordinated motions of ferrofluid droplet robots (FDRs). (A) Snapshots of the dynamic motion of an FDR actuated in the double-coil mode. The white dashed lines indicate the boundary line of neighboring coils. The red arrows near the white dashed lines indicate that the magnetic pulling forces change their directions. The purple arrows and blue dots mark the motion and shape of the FDR, respectively (scale bar, 20 mm). (B) Simulated velocity Vp of an FDR under the spatiotemporal magnetic pulling forces. The applied current I in each coil is marked as clockwise (CW), counterclockwise (CCW), or “off” (scale bar, 10 mm). (C) Speed of an FDR as a function of the actuation frequency f in the double-coil (blue lines) and single-coil (yellow lines) modes. Error bars represent the SD for n = 3 measurements. (D) The step-out frequency fs of an FDR in the double-coil mode as a function of the applied voltages in the electromagnet array (equivalent to |Bext|) and the actuation distance d from the electromagnet array to the actuation plane in water. In the “freeze zone”, FDRs cannot move. In the “break zone”, FDRs split. (E) The step-out frequency for an FDR as a function of d along the line aa′ in D. (F) The step-out frequency for an FDR as a function of the applied voltage along the line bb′ in D. (G) Sequential snapshots of the splitting, coordinated navigation, and merging behaviors of FDRs. Red arrows indicate the moving directions of FDRs. The yellow and green dots denote coils with currents in the CW and CCW directions, respectively (scale bar, 20 mm). In all experiments, ferrofluids with a dynamic viscosity of 8 mPa s, type EMG 901 from Ferrotec Corporation, were used (reproduced from ref. 826 with permission from PNAS, copyright 2020). | ||
6 Conclusion and outlook
Looking back to ferrofluid science and technology, the progress after more than five decades is well established and highly promising for future prospects. Due to their outstanding magnetic response, ferrofluids continue to be an exciting topic of fundamental research and a fertile ground for further technological development. This review covers the field of ferrofluids, significantly enlarged during the last period of time by biocompatible ferrofluids having an impressive applicative potential in biotechnology and nanomedicine. The most efficient and reproducible synthesis procedures of engineering and bio-ferrofluids were analysed and evaluated with a special focus on stabilization mechanisms and long-term colloidal stability in magnetic field and biological environment, essential aspects for applications. The comprehensive presentation of the advanced structural, physico-chemical, magnetic and rheological characterization of ferrofluids offers a deep insight into the most relevant features and difficulties of the application orientated design of engineering and bio-ferrofluids. As a highly attractive type of external stimuli nanosystem, bio-ferrofluids show several advantages towards remotely controlled therapeutic performances and pave the way to promising solutions for the unsolved needs of conventional biomedical sciences. The basic results of ferrohydrodynamics, interfacial instabilities, pattern formation, droplet formation and manipulation and ferrofluid microfluidics provide a solid platform for the development of new engineering applications. Following a brief recall of the most successful commercial applications in leakage-free dynamic sealing technology and HiFi audio engineering, the overview on tunable and adaptive multifunctional materials derived from ferrofluids, sensors and actuators with ferrofluids and ferrofluid droplet technology, including liquid computing and robotics, provides the reader with convincing arguments that ferrofluids continue to be an exciting research area with high technological impact in the forthcoming decades.Author contributions
Writing—original draft and writing—review and editing, M. V. A., R. T. and V. K.; conceptualization, writing—original draft, and writing—review and editing, V. S., E. T. and L. V.; conceptualization, writing—original draft, writing—review and editing, and supervision, E. T. and L. V. All authors have read and agree to the published version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work of V. S. and L. V. was supported by the RA-TB/CFATR/LMF multiannual research program 2021–2025. The support of the Romanian Ministry of Research and Innovation, CCCDI-UEFISCDI through project number PN-III-PI-1.2-PCCDI-2017-0871, contract 47PCCDI/2018v and of the JINR Dubna-RO project no. 35/04-4-1142-2021/2025 is also acknowledged. The work of R. T. was funded by the Romanian Ministry of Research and Innovation, Core Project PN-19-35-02-03 and of V. K. by Core Project PN19-03 and PED486/2020. L. V. is grateful to Prof. Emil Burzo (Romanian Academy, Cluj-Napoca, Romania) for his advice and encouragement in writing a review on ferrofluids.References
- S. S. Papell, Low viscosity magnetic fluid obtained by the colloidal suspension of magnetic particles, US Pat., 3215572, 1965 Search PubMed.
- R. E. Rosensweig, J. W. Nestor and R. S. Timmins, Proc. AIChE – IChemE Symposium Series No. 5, London, 1965, 104–118; discussion, 133–137.
- R. E. Rosensweig and R. Kaiser, Study of ferromagnetic liquid, Phase I. NTIS Rep. No. NASW-1219, NASA Rep. NASA-CR-91684. NASA Office of Advanced Research and Technology, Washington, D. C., 1967.
- R. Kaiser and G. Miskolczy, Magnetic properties of stable dispersions of subdomain magnetic particles, J. Appl. Phys., 1970, 41(3), 1064–1072 CrossRef CAS.
- G. W. Reimers and S. E. Khalafalla, Preparing magnetic fluids by a peptizing method, Bureau of Mines, US Dept. Int., Technical Progress Report-59, 1972.
- R. Chubachi, K. Nakatsuka and J. Shimoiizaka, Influence of Temperature and pH on the Dispersion Stability in Water Base Magnetic Fluids, J-STAGE, 1976, 23(6), 211–215, DOI:10.2497/jjspm.23.211.
- J. L. Neuringer and R. E. Rosensweig, Ferrohydrodynamics, Phys. Fluids, 1964, 7, 1927 CrossRef.
- R. E. Rosensweig, Fluidmagnetic buoyancy, AIAA J., 1966, 4(10), 1751–1758 CrossRef.
- M. I. Shliomis, Sov. Phys. Usp., 1974, 112, 153 CrossRef.
- R. E. Rosensweig, Fluid dynamics and science of magnetic liquids, in Advances of Electronics and Electron Physics, ed. M. Martin, Academic Press, New York, 1979, vol. 48, pp. 103–199 Search PubMed.
- M. D. Cowley and R. E. Rosensweig, The interfacial stability of a ferromagnetic fluid, J. Fluid Mech., 1967, 30, 671–688 CrossRef CAS.
- R. E. Rosensweig, Magnetic fluid seals, US Pat., 3260584, 1971 Search PubMed.
- W. Bottenberg, L. Melillo and K. Raj, The dependence of loudspeaker design parameters on the properties of magnetic fluids, J. Audio Eng. Soc., 1980, 28, 17 Search PubMed.
- K. Raj and R. Moskowitz, A review of damping applications of ferrofluids, IEEE Trans. Magn., 1980, 16(2), 358–364 CrossRef.
- Persistence Market Research (PMR): Ferro Fluids Market: Global Industry Analysis 2012–2016 and Forecast 2017–2025, https://www.persistencemarketresearch.com/market-research/ferro-fluids-market.asp.
- S. Pathak, K. Jain, P. Kumar, X. Wang and R. P. Pant, Improved thermal performance of annular fin-shell tube storage system using magnetic fluid, Appl. Energy, 2019, 239, 1524–1535 CrossRef.
- H. M. Buschmann, Critical review of heat transfer experiments in ferrohydrodynamic pipe flow utilising ferronanofluids, Int. J. Therm. Sci., 2020, 157, 106426 CrossRef.
- G. N. G. Jia, C. Stanley, N.-T. Nguyen and G. Rosengarten, Ferrofluids for heat transfer enhancement under an external magnetic field, Int. J. Heat Mass Transfer, 2018, 123, 110–121 CrossRef.
- M. A. Khairul, E. Doroodchi, R. Azizian and B. Moghtaderi, Advanced applications of tunable ferrofluids in energy systems and energy harvesters: A critical review, Energy Convers. Manage., 2017, 149, 660–674 CrossRef CAS.
- M.-L. Seol, S.-B. Jeon, J.-W. Han and Y.-K. Choi, Ferrofluid-based triboelectric-electromagnetic hybrid generator for sensitive and sustainable vibration energy harvesting, Nano Energy, 2017, 31, 233–238 CrossRef CAS.
- A. Dudus, R. Blue and D. Uttamchandani, Single mode fiber variable optical attenuator based on a ferrofluid shutter, Appl. Opt., 2015, 54(8), 1952–1957 CrossRef CAS PubMed.
- Z. Wu, X. Kong, Z. Zhang, J. Wu, T. Wang and M. Liu, Magnetic Fluid Deformable Mirror with a Two-Layer Layout of Actuators, Micromachines, 2017, 8, 72 CrossRef.
- E. Blums, Heat and mass transfer phenomena, in Ferrofluids. Magnetically controllable fluids and their applications, Lecture notes in Physics 594, ed. S. Odenbach, Springer Verlag Berlin, Heidelberg, New York, 2002, pp. 124–142 Search PubMed.
- V. G. Bashtovoy, B. M. Berkovsky and A. N. Vislovich, Introduction to Thermomechanics of Magnetic Fluids, Hemisphere, Washington, 1988 Search PubMed.
- S. Kodama, Dynamic ferrofluid sculpture: Organic shape-changing art forms, Commun. ACM, 2008, 51(6), 79–81 CrossRef (see also https://www.artfutura.org/v3/en/sachiko-kodama/).
- A. Eslam-Panah, C. Kovar, L. Panczner and H. Reuter, Fluid dynamics of millefiori: Mixing ferrofluid with watercolor, Phys. Rev. Fluids, 2020, 5, 110510 CrossRef.
- A. K. Yetisen, A. F. Coskun, G. England, S. Cho, H. Butt, J. Hurwitz, M. Kolle, A. Khademhosseini, A. J. Hart, A. Folch and S. H. Yun, Art on the Nanoscale and Beyond, Adv. Mater., 2016, 28, 1724–1742 CrossRef CAS PubMed.
- Ferrofluid properties illustrating device-Lab, Magnetic Fluids Timisoara & ROSEAL Co. Odorheiu Secuiesc (Romania), http://roseal.eu/index.php/cercetare/fluid-magnetice; first presented by the Romanian Space Agency at the Exhibition organized on the occasion of the Third United Nations Conference on the Exploration and Peaceful Uses of Outer Space (UNISPACE III) Vienna, Austria, 19–30 July, 1999.
- L. Johnson, D. M. Gray, E. Niezabitowska and T. O. McDonald, Multi-stimuli-responsive aggregation of nanoparticles driven by the manipulation of colloidal stability, Nanoscale, 2021, 13, 7879 RSC.
- M. Quesada-Perez, J. Callejas-Fernandez and R. Hidalgo-Alvarez, Interaction potentials, structural ordering and effective charges in dispersions of charged colloidal particles, Adv. Colloid Interface Sci., 2002, 95, 295 CrossRef CAS.
- J. C. Bacri, R. Perzynski, D. Salin, V. Cabuil and R. Massart, Ionic ferrofluids: a crossing of chemistry and physics, J. Magn. Magn. Mater., 1990, 85, 27–32 CrossRef CAS.
- B. W. Ninham, On progress in forces since the DLVO theory, Adv. Colloid Interface Sci., 1999, 83, 1 CrossRef CAS.
- N. Buske, H. Sonntag and T. Götze, Magnetic fluids – their preparation, stabilization and applications in colloid science, Colloids Surf., 1984, 12, 195–202 CrossRef CAS.
- R. E. Rosensweig, Ferrohydrodynamics, Cambridge Univ. Press, Cambridge, 1985, p. 344, reprinted with slight corrections by Dover, Mineola, New York, 1997 Search PubMed.
- S. W. Charles and J. Popplewell, Properties and applications of magnetic liquids, in Handbook of Magnetic Materials, ed. K. H. J. Buschow, 1986, vol. 2 Search PubMed.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, UK, 1989 Search PubMed.
- E. Blums, A. Cebers and M. M. Maiorov, Magnetic Fluids, Walter de Gruyter, Berlin New York, 1997, pp. 416 Search PubMed.
- S. W. Charles, The preparation of magnetic fluids, in Ferrofluids. Magnetically controllable fluids and their applications (Lecture Notes in Physics, 594), ed. S. Odenbach, Springer-Verlag, 2002, pp. 3–18 Search PubMed.
- S. Odenbach, Ferrofluids, in Handbook of Magnetic Materials, ed. K. H. J. Buschow, Elsevier, Amsterdam, The Netherlands, 2006, vol. 16, pp. 127–208 Search PubMed.
- J. Nowak, F. Wiekhorst, L. Trahms and S. Odenbach, The influence of hydrodynamic diameter and core composition on the magnetoviscous effect of biocompatible ferrofluids, J. Phys.: Condens. Matter, 2014, 26, 176004 CrossRef CAS PubMed.
- J. Zaloga, C. Janko, J. Nowak, J. Matuszak, S. Knaup, D. Eberbeck, R. Tietze, H. Unterweger, R. P. Friedrich, S. Duerr, R. Heimke-Brinck, E. Baum, I. Cicha, F. Dörje, S. Odenbach, S. Lyer, G. Lee and C. Alexiou, Development of a lauric acid/albumin hybrid iron oxide nanoparticle system with improved biocompatibility, Int. J. Nanomed., 2014, 9, 4847–4866 CrossRef PubMed.
- E. Tombácz, R. Turcu, V. Socoliuc and L. Vekas, Magnetic iron oxide nanoparticles: Recent trends in design and synthesis of magnetoresponsive nanosystems, Biochem. Biophys. Res. Commun., 2015, 468(3), 442–453 CrossRef PubMed.
- V. Socoliuc, D. Peddis, V. I. Petrenko, M. V. Avdeev, D. Susan-Resiga, T. Szabó, R. Turcu, E. Tombácz and L. Vekas, Magnetic nanoparticle systems for nanomedicine–A materials science perspective, Magnetochemistry, 2020, 6, 2 CrossRef CAS.
- Z. Xiao, Q. Zhang, X. Guo, J. Villanova, Y. Hu, I. Külaots, D. Garcia-Rojas, W. Guo and V. L. Colvin, Libraries of Uniform Magnetic Multicore Nanoparticles with Tunable Dimensions for Biomedical and Photonic Applications, ACS Appl. Mater. Interfaces, 2020, 12(37), 41932–41941 CrossRef CAS PubMed.
- R. P. Friedrich, I. Cicha and C. Alexiou, Iron Oxide Nanoparticles in Regenerative Medicine and Tissue Engineering, Nanomaterials, 2021, 11, 2337 CrossRef CAS PubMed.
- Z. Li, P. W. Yi, Q. Sun, H. Lei, H. L. Zhao, Z. H. Zhu, S. C. Smith, M. B. Lan and G. Q. Lu, Ultrasmall Water-Soluble and Biocompatible Magnetic Iron Oxide Nanoparticles as Positive and Negative Dual Contrast Agents, Adv. Funct. Mater., 2012, 22(11), 2387–2393 CrossRef CAS.
- T. Vangijzegem, D. Stanicki, A. Panepinto, V. Socoliuc, L. Vekas, R. N. Muller and S. Laurent, Influence of Experimental Parameters of a Continuous Flow Process on the Properties of Very Small Iron Oxide Nanoparticles (VSION) Designed for T1-Weighted Magnetic Resonance Imaging (MRI), Nanomaterials, 2020, 10(4), 757 CrossRef CAS PubMed.
- B. H. Kim, M. J. Hackett, J. Park and T. Hyeon, Synthesis, Characterization, and Application of Ultrasmall Nanoparticles, Chem. Mater., 2014, 26(1), 59–71 CrossRef CAS.
- A. Saini, J. A. Borchers, S. George, B. B. Maranville, K. L. Krycka, J. A. Dura, K. Theis-Bröhl and M. Wolff, Layering of Magnetic Nanoparticles at Amorphous Magnetic Templates with Perpendicular Anisotropy, Soft Matter, 2020, 16, 7676 RSC.
- M. T. Lopez-Lopez, A. Gómez-Ramírez, L. Rodríguez-Arco, J. D. G. Durán, L. Iskakova and A. Zubarev, Colloids on the frontier of ferrofluids. Rheological properties, Langmuir, 2012, 28, 6232–6245 CrossRef CAS PubMed.
- W. Parak, Complex colloidal assembly, Science, 2011, 334, 1359–1360 CrossRef CAS PubMed.
- V. K. LaMer and R. H. Dinegar, Theory, production and mechanism of formation of monodispersed hydrosols, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- J. Polte, Fundamental growth principles of colloidal metal nanoparticles – a new perspective, CrystEngComm, 2015, 17, 6809–6830 RSC.
- D. Stanicki, L. Vander Elst, R. N. Muller and S. Laurent, Synthesis of Iron Oxide Nanoparticles, in New Developments in NMR No. 13, Contrast Agents for MRI: Experimental Methods, ed. V. C. Pierre and M. J. Allen, The Royal Society of Chemistry, 2018, ch. 4.2, pp. 331–339 Search PubMed.
- S. E. Khalafalla and G. W. Reimers, Magnetofluids and their manufacture, US Pat, 3764540, 1973 Search PubMed.
- S. E. Khalafalla and G. W. Reimers, Preparation of dilution-stable aqueous magnetic fluids, IEEE Trans. Magn., 1980, 16, 178–183 CrossRef.
- J.-P. Jolivet, C. Chaneac and E. Tronc, Iron oxide chemistry. From molecular clusters to extended solid networks, Chem. Commun., 2004, 481–487 CAS.
- R. M. Cornell and U. Schwertmann, Iron oxides in the Laboratory: Preparation and Characterization, VCH Publishers, Weinheim, 1991 Search PubMed.
- R. Massart, Preparation of aqueous magnetic liquids in alkaline and acidic media, IEEE Trans. Magn., 1981, 17(2), 1247–1248 CrossRef.
- K. J. Davies, S. Wells and S. W. Charles, The effect of temperature and oleate adsorption on the growth of maghemite particles, J. Magn. Magn. Mater., 1993, 122, 24–28 CrossRef CAS.
- D. Bica, Preparation of magnetic fluids for various applications, Rom. Rep. Phys., 1995, 47(3–5), 265–272 CAS.
- L. Shen, P. E. Laibinis and T. A. Hatton, Bilayer Surfactant Stabilized Magnetic Fluids: Synthesis and Interactions at Interfaces, Langmuir, 1999, 15, 447–453 CrossRef CAS.
- D. K. Kim, M. Mikhaylova, Y. Zhang and M. Muhammed, Protective Coating of Superparamagnetic Iron Oxide Nanoparticles, Chem. Mater., 2003, 15, 1617–1627 CrossRef CAS.
- G. Gnanaprakash, J. Philip, T. Jayakumar and B. Raj, Effect of Digestion Time and Alkali Addition Rate on Physical Properties of Magnetite Nanoparticles, J. Phys. Chem. B, 2007, 111, 7978–7986 CrossRef CAS PubMed.
- H.-C. Roth, S. P. Schwaminger, M. Schindler, F. E. Wagner and S. Berensmeier, Influencing factors in the Co-precipitation process of superparamagnetic iron oxide nano particles: a model based study, J. Magn. Magn. Mater., 2015, 377, 81–89 CrossRef CAS.
- A. K. Gupta and M. Gupta, Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications, Biomaterials, 2005, 26, 3995–4021 CrossRef CAS PubMed.
- D. Maity and D. C. Agrawal, Synthesis of iron oxide nanoparticles under oxidizing environment and their stabilization in aqueous and non-aqueous media, J. Magn. Magn. Mater., 2007, 308, 46–55 CrossRef CAS.
- D. Bica, L. Vékás, M. V. Avdeev, O. Marinică, V. Socoliuc, M. Bălăşoiu and V. M. Garamus, Sterically stabilized water based magnetic fluids: Synthesis, structure and properties, J. Magn. Magn. Mater., 2007, 311, 17–21 CrossRef CAS.
- G. Gnanaprakash, S. Mahadevan, T. Jayakumar, P. Kalyanasundaram, J. Philip and B. Raj, Effect of initial pH and temperature of iron salt solutions on formation of magnetite nanoparticles, Mater. Chem. Phys., 2007, 103, 168–175 CrossRef CAS.
- G. D. Moeser, K. A. Roach, W. H. Green, P. E. Laibinis and T. A. Hatton, Water-Based Magnetic Fluids as Extractants for Synthetic Organic Compounds, Ind. Eng. Chem. Res., 2002, 41, 4739–4749 CrossRef CAS.
- T. J. Daou, J. M. Greneche, G. Pourroy, S. Buathong, A. Derory, C. Ulhaq-Bouillet, B. Donnio, D. Guillon and S. Begin-Colin, Coupling Agent Effect on Magnetic Properties of Functionalized Magnetite-Based Nanoparticles, Chem. Mater., 2008, 20, 5869–5875 CrossRef CAS.
- J. Salafranca, J. Gazquez, N. Pérez, A. Labarta, S. T. Pantelides, S. J. Pennycook, X. Batlle and M. Varela, Surfactant Organic Molecules Restore Magnetism in Metal-Oxide Nanoparticle Surfaces, Nano Lett., 2012, 12, 2499–2503 CrossRef CAS PubMed.
- P. Guardia, B. Batlle-Brugal, A. G. Roca, O. Iglesias, M. P. Morales, C. J. Serna, A. Labarta and X. Batlle, Surfactant effects in magnetite nanoparticles of controlled size, J. Magn. Magn. Mater., 2007, 316, e756–e759 CrossRef CAS.
- P. Guardia, N. Perez, A. Labarta and X. Batlle, Controlled Synthesis of Iron Oxide Nanoparticles over a Wide Size Range, Langmuir, 2010, 26(8), 5843–5847 CrossRef CAS PubMed.
- C. Pereira, A. M. Pereira, M. Rocha, C. Freire and C. F. G. C. Geraldes, Architectured Design of Superparamagnetic Fe3O4 Nanoparticles for Application as MRI Contrast Agents: Mastering Size and Magnetism for Enhanced Relaxivity, J. Mater. Chem. B, 2015, 3, 6261–6273 RSC.
- V. Socoliuc and L. Vekas, Hydrophobic and hydrophilic magnetite nanoparticles: synthesis by chemical coprecipitation and physico-chemical characterization, in Upscaling of Bio-Nano-Processes. Selective Bioseparation by Magnetic Particles, ed. H. Nirschl and K. Keller, Springer Verlag, 2014, pp. 39–56 Search PubMed.
- A. M. van Silfhout, H. Engelkamp and B. H. Erné, Colloidal Stability of Aqueous Ferrofluids at 10 T, J. Phys. Chem. Lett., 2020, 11, 5908–5912 CrossRef CAS PubMed.
- A. M. van Silfhout, H. Engelkamp and B. H. Erné, Magnetic Sedimentation Velocities and Equilibria in Dilute Aqueous Ferrofluids, J. Phys. Chem. B, 2020, 124, 7989–7998 CrossRef CAS PubMed.
- H. Pierre, L. Michael, A. Damien, L. Lenaïc, D. Emmanuelle, C. Valérie, R. Christian, R. Stéphane, W. Claire, G. Florence and B. Rana, Iron Oxide Monocrystalline Nanoflowers for Highly Efficient Magnetic Hyperthermia, J. Phys. Chem. C, 2012, 116(29), 15702–15712 CrossRef.
- C. Blanco-Andujar, D. Ortega, P. Southern, Q. A. Pankhurst and N. T. K. Thanh, High performance multi-core iron oxide nanoparticles for magnetic hyperthermia: microwave synthesis, and the role of core-to-core interactions, Nanoscale, 2015, 7, 1768–1775 RSC.
- S. Sun and H. Zeng, Size-Controlled Synthesis of Magnetite Nanoparticles, J. Am. Chem. Soc., 2002, 124, 8204–8205 CrossRef CAS PubMed.
- M. Chen, J. P. Liu and S. Sun, One-Step Synthesis of Fept Nanoparticles with Tunable Size, J. Am. Chem. Soc., 2004, 126, 8394–8395 CrossRef CAS PubMed.
- T. Hyeon, Chemical synthesis of magnetic nanoparticles, Chem. Commun., 2003, 927–934 RSC.
- T. Hyeon, S. S. Lee, J. Park, Y. Chung and H. B. Na, Synthesis of Highly Crystalline and Monodisperse Maghemite Nanocrystallites without a Size-Selection Process, J. Am. Chem. Soc., 2001, 123(51), 12798–12801 CrossRef CAS PubMed.
- J. Park, K. An, Y. Hwang, J.-G. Park, H.-J. Noh, J.-E. Kim, J.-G. Park, N.-M. Hwang and T. Hyeon, Ultra-large-scale syntheses of monodisperse nanocrystals, Nat. Mater., 2004, 3, 891–895 CrossRef CAS PubMed.
- E. C. Vreeland, J. Watt, G. B. Schober, B. G. Hance, M. J. Austin, A. D. Price, B. D. Fellows, T. C. Monson, N. S. Hudak, L. Maldonado-Camargo, A. C. Bohorquez, C. Rinaldi and D. L. Huber, Enhanced nanoparticle size control by extending LaMer's mechanism, Chem. Mater., 2015, 27(17), 6059–6066 CrossRef CAS.
- A. Lassenberger, T. A. Grünewald, P. D. J. van Oostrum, H. Rennhofer, H. Amenitsch, R. Zirbs, H. C. Lichtenegger and E. Reimhult, Monodisperse Iron Oxide Nanoparticles by Thermal Decomposition: Elucidating Particle Formation by Second-Resolved in Situ SmallAngle X-ray Scattering, Chem. Mater., 2017, 229, 4511–4522 CrossRef PubMed.
- A. Lassenberger, A. Scheber, A. Stadlbauer, A. Stiglbauer, T. Helbich and E. Reimhult, Individually Stabilized, Superparamagnetic Nanoparticles with Controlled Shell and Size Leading to Exceptional Stealth Properties and High Relaxivities, ACS Appl. Mater. Interfaces, 2017, 9, 3343–3353 CrossRef CAS PubMed.
- M. Unni, A. M. Uhl, S. Savliwala, B. H. Savitzky, R. Dhavalikar, N. Garraud, D. P. Arnold, L. F. Kourkoutis, J. S. Andrew and C. Rinaldi, Thermal Decomposition Synthesis of Iron Oxide Nanoparticles with Diminished Magnetic Dead Layer by Controlled Addition of Oxygen, ACS Nano, 2017, 11, 2284–2303, DOI:10.1021/acsnano.7b00609.
- A. Walter, C. Billotey, A. Garofalo, C. Ulhaq-Bouillet, C. Lefevre, J. Taleb, S. Laurent, L. Vander Elst, R. N. Muller, L. Lartigue, F. Gazeau, D. Felder-Flesch and S. Begin-Colin, Mastering the shape and composition of dendronized iron oxide nanoparticles to tailor magnetic resonance imaging and hyperthermia, Chem. Mater., 2014, 26, 5252–5264 CrossRef CAS.
- N. Silvestri, H. Gavilán, P. Guardia, R. Brescia, S. Fernandes, A. C. S. Samia, F. J. Teran and T. Pellegrino, Di- and tri-component spinel ferrite nanocubes: synthesis and their comparative characterization for theranostic applications, Nanoscale, 2021, 13, 13665–13680 RSC.
- A. G. Roca, L. Gutiérrez, H. Gavilán, M. E. F. Brollo, S. Veintemillas-Verdaguer and M. Puerto Morales, Design strategies for shape-controlled magnetic iron oxide nanoparticles, Adv. Drug Delivery Rev., 2019, 138, 68–104 CrossRef CAS PubMed.
- H. Gavilan, A. Kowalski, D. Heinke, A. Sugunan, J. Sommertune, M. Varon, L. K. Bogart, O. Posth, L. Zeng, D. Gonzalez-Alonso, C. Balceris, J. Fock, E. Wetterskog, C. Frandsen, N. Gehrke, C. Gruttner, A. Fornara, F. Ludwig, S. Veintemillas-Verdaguer, C. Johansson and M. P. Morales, Colloidal Flower-Shaped Iron Oxide Nanoparticles: Synthesis Strategies and Coatings, Part. Part. Syst. Charact., 2017, 34, 1700094 CrossRef.
- P. Bender, D. Honecker and L. F. Barquín, Supraferromagnetic correlations in clusters of magnetic nanoflowers, Appl. Phys. Lett., 2019, 115, 132406 CrossRef.
- A. Karpavicius, A. Coene, P. Bender and J. Leliaert, Advanced analysis of magnetic nanoflower measurements to leverage their use in biomedicine, Nanoscale Adv., 2021, 3, 1633–1645 RSC.
- S. Harvell-Smith, L. D. Tung and N. T. K. Thanh, Magnetic particle imaging: tracer development and the biomedical applications of a radiation-free, sensitive, and quantitative imaging modality, Nanoscale, 2022 10.1039/D1NR05670K.
- W. W. Yu, E. Chang, C. M. Sayes, R. Drezek and V. L. Colvin, Aqueous dispersion of monodisperse magnetic iron oxide nanocrystals through phase transfer, Nanotechnology, 2006, 17, 4483–4487 CrossRef CAS.
- L. Lartigue, C. Innocenti, T. Kalaivani, A. Awwad, M. S. Duque, Y. Guari, J. Larionova, C. Guerin, J.-L. Georges Montero, V. Barragan-Montero, P. Arosio, A. Lascialfari, D. Gatteschi and C. Sangregorio, Water-Dispersible Sugar-Coated Iron Oxide Nanoparticles. An Evaluation of their Relaxometric and Magnetic Hyperthermia Properties, J. Am. Chem. Soc., 2011, 133, 10459–10472 CrossRef CAS PubMed.
- A. Lak, J. Dieckhoff, F. Ludwig, J. M. Scholtyssek, O. Goldmann, H. Lünsdorf, D. Eberbeck, A. Kornowski, M. Kraken, F. J. Litterst, K. Fiege, P. Mischnick and M. Schilling, Highly stable monodisperse PEGylated iron oxide nanoparticle aqueous suspensions: A nontoxic tracer for homogeneous magnetic bioassays, Nanoscale, 2013, 5(23), 11447–11455 RSC.
- R. Weissleder, M. Nahrendorf and M. J. Pittet, Imaging Macrophages with Nanoparticles, Nat. Mater., 2014, 13, 125–138 CrossRef CAS PubMed.
- R. M. Ferguson, A. P. Khandhar and K. M. Krishnan, Tracer Design for Magnetic Particle Imaging, J. Appl. Phys., 2012, 111, 07B318 CrossRef PubMed.
- H. Lee, T.-H. Shin, J. Cheon and R. Weissleder, Recent Developments in Magnetic Diagnostic Systems, Chem. Rev., 2015, 115(19), 10690–10724 CrossRef CAS PubMed.
- B. Luigjes, S. M. C. Woudenberg, R. de Groot, J. D. Meeldijk, H. M. Torres Galvis, K. P. de Jong, A. P. Philipse and B. Erne, Diverging geometric and magnetic size distributions of iron oxide nanocrystals, J. Phys. Chem. C, 2011, 115, 14598–14605 CrossRef CAS.
- A. Walter, A. Garofalo, A. Parat, H. Martinez, D. Felder-Flesch and S. Begin-Colin, Functionalization strategies and dendronization of iron oxide nanoparticles, Nanotechnol. Rev., 2015, 4(6), 581–593 CAS.
- J. G. Ovejero, A. Gallo-Cordova, A. G. Roca, M. P. Morales and S. Veintemillas-Verdaguer, Reproducibility and Scalability of Magnetic Nanoheater Synthesis, Nanomaterials, 2021, 11, 2059 CrossRef CAS PubMed.
- M. O. Besenhard, A. P. LaGrow, A. Hodzic, M. Kriechbaum, L. Panariello, G. Bais, K. Loizou, S. Damilos, M. M. Cruz, N. T. K. Thanh and A. Gavriilidis, Co-precipitation synthesis of stable iron oxide nanoparticles with NaOH: New insights and continuous production via flow chemistry, Chem. Eng. J., 2020, 399, 125740 CrossRef CAS.
- M. O. Besenhard, D. Jiang, Q. A. Pankhurst, P. Southern, S. Damilos, L. Storozhuk, A. Demosthenous, N. T. K. Thanh, P. Dobson and A. Gavriilidis, Development of an in-line magnetometer for flow chemistry and its demonstration for magnetic nanoparticle synthesis, Lab Chip, 2021, 21, 3775 RSC.
- M. O. Besenhard, L. Panariello, C. Kiefer, A. P. LaGrow, L. Storozhuk, F. Perton, S. Begin, D. Mertz, N. T. K. Thanh and A. Gavriilidis, Small iron oxide nanoparticles as MRI T1 contrast agent: scalable inexpensive water-based synthesis using a flow reactor, Nanoscale, 2021, 13, 8795–8805 RSC.
- J. Bemetz, A. Wegemann, K. Saatchi, A. Haase, U. O. Hafeli, R. Niessner, B. Gleich and M. Seidel, Microfluidic-Based Synthesis of Magnetic Nanoparticles Coupled with Miniaturized NMR for Online Relaxation Studies, Anal. Chem., 2018, 90(16), 9975–9982 CrossRef CAS PubMed.
- R. Abedini-Nassab, M. P. Miandoab and M. Sasmaz, Microfluidic Synthesis, Control, and Sensing of Magnetic Nanoparticles: A Review, Micromachines, 2021, 12, 768 CrossRef PubMed.
- L. Frenz, A. E. Harrak, M. Pauly, S. Begin-Colin, A. D. Griffiths and J.-C. Baret, Droplet-Based Microreactors for the Synthesis of Magnetic Iron Oxide Nanoparticles, Angew. Chem., Int. Ed., 2008, 47, 6817 CrossRef CAS PubMed.
- A. Abou-Hassan, O. Sandre and V. Cabuil, Microfluidics for the synthesis of iron oxide nanoparticles, in Microfluidic Devices in Nanotechnology: Applications, ed. C. S. S. R. Kumar, John Wiley & Sons, Hoboken NJ, 2010, ch. 9, pp. 323–360 Search PubMed.
- A. Larrea, V. Sebastian, A. Ibarra and M. Arruebo, Santamaria J: Gas Slug Microfluidics: A Unique Tool for Ultrafast, Highly Controlled Growth of Iron Oxide Nanostructures, Chem. Mater., 2015, 27, 4254–4260 CrossRef CAS PubMed.
- R. Massart, E. Dubois, V. Cabuil and E. Hasmonay, Preparation and properties of monodisperse magnetic fluids, J. Magn. Magn. Mater., 1995, 149, 1–5 CrossRef CAS.
- G. Meriguet, E. Wandersman, E. Dubois, A. Cebers, J. de Andrade Gomes, G. Demouchy, J. Depeyrot, A. Robert and R. Perzynski, Magnetic fluids with tunable interparticle interaction: monitoring the under-field local structure, Magnetohydrodynamics, 2012, 48, 415–425 CrossRef.
- J. Lyklema, Adsorption of small ions, in Adsorption from solution at the solid/liquid interface, ed. G. D. Parfitt and C. H. Rochester, Academic Press, New York London, 1983 Search PubMed.
- J.-C. Bacri, R. Perzynski, V. Cabuil and R. Massart, Phase diagram of an ionic magnetic colloid: Experimental study of the effect of ionic strength, J. Colloid Interface Sci., 1989, 132(1), 43–53 CrossRef CAS.
- E. Wandersman, E. Dubois, V. Dupuis, A. Duri, A. Robert and R. Perzynski, Heterogeneous dynamics and aging in a dense ferro-glass, J. Phys.: Condens. Matter, 2008, 20, 204124 CrossRef CAS PubMed.
- E. Wandersman, Y. Chuskhin, E. Dubois, V. Dupuis, A. Robert and R. Perzynski, Field induced anisotropic cooperativity in a magnetic colloidal glass, Soft Matter, 2015, 11, 7165–7170 RSC.
- Y. Sahoo, A. Goodarzi, M. T. Swihart, T. Y. Ohulchanskyy, N. Kaur, E. P. Furlani and P. N. Prasad, Aqueous Ferrofluid of Magnetite Nanoparticles: Fluorescence Labeling and Magnetophoretic Control, J. Phys. Chem. B, 2005, 109, 3879–3885 CrossRef CAS PubMed.
- C. Vasilescu, M. Latikka, K. D. Knudsen, V. M. Garamus, V. Socoliuc, R. Turcu, E. Tombacz, D. Susan-Resiga, R. H. A. Ras and L. Vekas, High concentration aqueous magnetic fluids: structure, colloidal stability, magnetic and flow properties, Soft Matter, 2018, 14(32), 6648–6666 RSC.
- T. L. Moore, L. Rodriguez-Lorenzo, V. Hirsch, S. Balog, D. Urban, C. Jud, B. Rothen-Rutishauser, M. Lattuada and A. Petri-Fink, Nanoparticle colloidal stability in cell culture media and impact on cellular interactions, Chem. Soc. Rev., 2015, 44, 6287–6305 RSC.
- D. Talbot, J. Queiros Campos, B.-L. Checa-Fernandez, J. A. Marins, C. Claire Lomenech, C. Hurel, G. D. Godeau, M. Raboisson-Michel, G. Verger-Dubois, L. Obeid, P. Kuzhir and A. Bee, Adsorption of Organic Dyes on Magnetic Iron Oxide Nanoparticles. Part I: Mechanisms and Adsorption-Induced Nanoparticle Agglomeration, ACS Omega, 2021, 6(29), 19086–19098 CrossRef CAS PubMed.
- J. Queiros Campos, B. L. Checa-Fernandez, J. A. Marins, C. Lomenech, C. Hurel, G. Godeau, M. Raboisson-Michel, G. Verger-Dubois, A. Bee, A. Talbot and P. Kuzhir, Adsorption of Organic Dyes on Magnetic Iron Oxide Nanoparticles. Part II: Field-Induced Nanoparticle Agglomeration and Magnetic Separation, Langmuir, 2021, 37(35), 10612–10623 CrossRef CAS PubMed.
- C. L. Filomeno, M. Kouyaté, V. Peyre, G. Demouchy, A. F. C. Campos, R. Perzynski, F. A. Tourinho and E. Dubois, Tuning the Solid/Liquid Interface in Ionic Colloidal Dispersions: Influence on Their Structure and Thermodiffusive Properties, J. Phys. Chem. C, 2017, 121, 5539–5550 CrossRef CAS.
- M. Mamusa, J. Sirieix-Plénet, F. Cousin, R. Perzynski, E. Dubois and V. Peyre, Microstructure of colloidal dispersions in the ionic liquid ethylammonium nitrate: influence of the nature of the nanoparticles’ counterion, J. Phys.: Condens. Matter, 2014, 26, 284113 CrossRef CAS PubMed.
- M. Mamusa, J. Sirieix-Plenet, R. Perzynski, F. Cousin, E. Dubois and V. Peyre, Concentrated assemblies of magnetic nanoparticles in ionic liquids, Faraday Discuss., 2015, 181, 193–209 RSC.
- C. L. Filomeno, M. Kouyaté, F. Cousin, G. Demouchy, E. Dubois, L. Michot, G. Mériguet, R. Perzynski, V. Peyre, J. Sirieix-Plénet and F. A. Tourinho, Ionic magnetic fluids in polar solvents with tuned counter-ions, J. Magn. Magn. Mater., 2017, 431, 2–7 CrossRef.
- T. Fiuza, M. Sarkar, J. C. Riedl, A. Cebers, F. Cousin, G. Demouchy, J. Depeyrot, E. Dubois, F. Gelebart, G. Meriguet, R. Perzynski and V. Peyre, Thermodiffusion anisotropy under a magnetic field in ionic liquid-based ferrofluids, Soft Matter, 2021, 17, 4566–4577 RSC.
- J. C. Riedl, M. Sarkar, T. Fiuza, F. Cousin, J. Depeyrot, E. Dubois, G. Mériguet, R. Perzynski and V. Peyre, Design of concentrated colloidal dispersions of iron oxide nanoparticles in ionic liquids: structure and thermal stability from 25 to 200 °C, J. Colloid Interface Sci., 2022, 607, 584–594 CrossRef CAS PubMed.
- M. T. Lopez-Lopez, J. D. G. Duran, A. V. Delgado and F. Gonzalez-Caballero, Stability and magnetic characterization of oleate-covered magnetite ferrofluids in different nonpolar carriers, J. Colloid Interface Sci., 2005, 291, 144–151 CrossRef CAS PubMed.
- R. Tadmor, R. E. Rosensweig, J. Frey and J. Klein, Resolving the puzzle of ferrofluid dispersants, Langmuir, 2000, 16, 9117–9120 CrossRef CAS.
- M. V. Avdeev, D. Bica, L. Vékás, O. Marinică, M. Bălăşoiu, V. L. Aksenov, L. Rosta, V. M. Garamus and A. Schreyer, On the possibility of using short chain length mono-carboxylic acids for stabilization of magnetic fluids, J. Magn. Magn. Mater., 2007, 311, 6–9 CrossRef CAS.
- M. V. Avdeev, D. Bica, L. Vekas, V. L. Aksenov, A. V. Feoktystov, O. Marinica, L. Rosta, V. M. Garamus and R. Willumeit, Comparative structure analysis of non-polar organic ferrofluids stabilized by saturated mono-carboxylic acids, J. Colloid Interface Sci., 2009, 334, 37–41 CrossRef CAS PubMed.
- S. N. Lysenko, S. A. Astaf'eva, D. E. Yakusheva and M. Balasoiu, Novel parameter predicting stability of magnetic fluids for possible application in nanocomposite preparation, Appl. Surf. Sci., 2019, 463, 217–226 CrossRef CAS.
- G. A. van Ewijk, G. J. Vroege and B. W. M. Kuipers, Phase Behavior of Magnetic Colloid-Polymer Mixtures: 2. A Magnetic Sensing Coil Study, Langmuir, 2002, 18, 382–390 CrossRef CAS.
- R. Lenin and P. A. Joy, Role of Primary and Secondary Surfactant Layers on the Thermal Conductivity of Lauric Acid Coated Magnetite Nanofluids, J. Phys. Chem. C, 2016, 120, 11640–11651 CrossRef CAS.
- V. I. Petrenko, M. V. Avdeev, L. A. Bulavin, L. Almasy, N. A. Grigoryeva and V. L. Aksenov, Effect of Surfactant Excess on the Stability of Low-Polarity Ferrofluids Probed by Small-Angle Neutron Scattering, Crystallogr. Rep., 2016, 61(1), 121–125 CrossRef CAS.
- D. Susan-Resiga and L. Vekas, From high magnetization ferrofluids to nano-micro composite magnetorheological fluids: properties and applications, Rom. Rep. Phys., 2018, 70, 508 Search PubMed.
- M. T. Lopez-Lopez, P. Kuzhir, S. Lacis, G. Bossis, F. Gonzalez-Caballero and J. D. G. Duran, Magnetorheology for suspensions of solid particles dispersed in ferrofluids, J. Phys.: Condens. Matter, 2006, 18, S2803–S2813 CrossRef CAS.
- D. Susan-Resiga, V. Socoliuc, T. Boros, T. Borbáth, O. Marinică, A. Han and L. Vekas, The influence of particle clustering on the rheological properties of highly concentrated magnetic nanofluids, J. Colloid Interface Sci., 2012, 373, 110–115 CrossRef CAS PubMed.
- D. Bica and L. Vékás, Preparations and properties of a series of alcohol based magnetic fluids, Magnetohydrodynamics, 1994, 30(3), 194–196 Search PubMed.
- D. Bica, L. Vékás and M. Raşa, Preparation and magnetic properties of concentrated magnetic fluids on alcohol and water carrier liquids, J. Magn. Magn. Mater., 2002, 252, 10–12 CrossRef CAS.
- D. Bica, L. Vékás, M. V. Avdeev, M. Bălăşoiu, O. Marinică, D. F. Stoian, D. Susan-Resiga, G. Török and L. Rosta, Magnetizable colloids on strongly polar carriers – preparation and manifold characterization, Prog. Colloid Polym. Sci., 2004, 125, 1–9 CAS.
- M. S. A. Darwish, S. Machunsky, U. Peuker, U. Kunz and T. Turek, Magnetite core-shell nano-composites with chlorine functionality: preparation by miniemulsion polymerization and characterization, J. Polym. Res., 2011, 18, 79–88 CrossRef CAS.
- A. Wooding, M. Kilner and D. B. Lambrick, Studies of the Double Surfactant Layer Stabilization of Water-Based Magnetic Fluids, J. Colloid Interface Sci., 1991, 144(1), 236–242 CrossRef CAS.
- M. V. Avdeev, V. L. Aksenov, M. Bălăşoiu, V. Garamus, A. Schreyer, G. Török, D. Hasegan, A. Schreyer, L. Rosta, D. Bica and L. Vékás, Comparative analysis of the structure of sterically stabilized ferrofluids on polar carriers by small-angle neutron scattering, J. Colloid Interface Sci., 2006, 295(1), 100–107 CrossRef CAS PubMed.
- A. Lassenberger, A. Scheber, A. Stadlbauer, A. Stiglbauer, T. Helbich and E. Reimhult, Individually Stabilized, Superparamagnetic Nanoparticles with Controlled Shell and Size Leading to Exceptional Stealth Properties and High Relaxivities, ACS Appl. Mater. Interfaces, 2017, 9, 3343–3353 CrossRef CAS PubMed.
- L. Rodriguez-Arco, M. T. Lopez-Lopez, J. D. G. Duran, A. Zubarev and D. Chirikov, Stability and magnetorheological behaviour of magnetic fluids based on ionic liquids, J. Phys.: Condens. Matter, 2011, 23, 455101 CrossRef PubMed.
- L. Mestrom, J. J. M. Lenders, R. de Groot, T. Hooghoudt, N. A. J. M. Sommerdijk and M. Vilaplana Artigas, Stable ferrofluids of magnetite nanoparticles in hydrophobic ionic liquids, Nanotechnology, 2015, 26, 285602 CrossRef PubMed.
- K. Zimny, B. Mascaro, T. Brunet, O. Poncelet, C. Aristegui, J. Leng, O. Sandre and O. Mondain-Monval, Design of a fluorinated magneto-responsive material with tuneable ultrasound scattering properties, J. Mater. Chem. B, 2014, 2, 1285–1297 RSC.
- R. J. Hunter, Foundations of colloid science, Clarendon Press, Oxford, UK, 1989, vol. 1 Search PubMed.
- F. Qu, D. R. Santos, Jr. and P. C. Morais, Colloidal stability in magnetic fluids: effects of the intrinsic dipolar magnetic field in magnetic semiconductors, J. Phys.: Condens. Matter, 2008, 20, 204114 CrossRef.
- L. L. Castro, C. C. C. Amorim, J. P. V. Miranda, T. S. A. Cassiano and F. L. O. Paula, The role of small separation interactions in ferrofluid structure, Colloids Surf., A, 2022, 635, 128082 CrossRef.
- E. Dubois, V. Cabuil, F. Boue and R. Perzynski, Structural analogy between aqueous and oily magnetic fluids, J. Chem. Phys., 1999, 111(15), 7147–7160 CrossRef CAS.
- L. Vekas, M. V. Avdeev and D. Bica, Magnetic nanofluids: synthesis and structure, in NanoScience in Biomedicine, ed. D. Shi, Springer, USA, 2009, ch. 25, pp. 645–704 Search PubMed.
- A. F. Pshenichnikov and A. A. Fedorenko, Chain like aggregates in magnetic fluids, J. Magn. Magn. Mater., 2005, 292, 332–344 CrossRef CAS.
- C. Holm and J.-J. Weis, The structure of ferrofluids: A status report, Curr. Opin. Colloid Interface Sci., 2005, 10, 133–140 CrossRef CAS.
- V. Cabuil, Phase behavior of magnetic nanoparticles dispersions in bulk and confined geometries, Curr. Opin. Colloid Interface Sci., 2000, 5, 44–48 CrossRef CAS.
- C. Scherer and A. M. Figuereido Neto, Ferrofluids: properties and applications, Braz. J. Phys., 2005, 35, 718–727 CrossRef CAS.
- I. Torres-Diaz and C. Rinaldi, Recent progress in ferrofluids research: novel applications of magnetically controllable and tunable fluids, Soft Matter, 2014, 10, 8584–8602 RSC.
- M. Reindl and S. Odenbach, Influence of a homogeneous axial magnetic field on Taylor–Couette flow of ferrofluids with low particle–particle interaction, Exp. Fluids, 2011, 50, 375–384 CrossRef.
- M. Reindl and S. Odenbach, Effect of axial and transverse magnetic fields on the flow behavior of ferrofluids featuring different levels of interparticle interaction, Phys. Fluids, 2011, 23, 093102 CrossRef.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Understanding biophysicochemical interactions at the nano-bio interface, Nat. Mater., 2009, 8(7), 543–557 CrossRef CAS PubMed.
- L. Abarca-Cabrera, P. Fraga-García and S. Berensmeier, Bio-nano interactions: binding proteins, polysaccharides, lipids and nucleic acids onto magnetic nanoparticles, Biomater. Res., 2021, 25, 12 CrossRef CAS PubMed.
- S. Khizar, N. M. Ahmad, N. Zine, N. Jaffrezic-Renault, A. Errachid-el-salhi and A. Elaissari, Magnetic Nanoparticles: From Synthesis to Theranostic Applications, ACS Appl. Nano Mater., 2021, 4(5), 4284–4306 CrossRef CAS.
- A. Jedlovszky-Hajdu, F. Baldelli Bombelli, M. P. Monopoli, E. Tombácz and K. A. Dawson, Surface Coatings Shape the Protein Corona of SPIONs with Relevance to Their Application in Vivo, Langmuir, 2012, 28, 14983–14991 CrossRef CAS PubMed.
- P. Ke, S. Lin, W. Parak, T. Davis and F. Caruso, A decade of the protein corona, ACS Nano, 2017, 11, 11773–11776 CrossRef CAS PubMed.
- M. Schroffenegger, N. S. Leitner, G. Morgese, S. N. Ramakrishna, M. Willinger, E. M. Benetti and E. Reimhult, Polymer Topology Determines the Formation of Protein Corona on Core–Shell Nanoparticles, ACS Nano, 2020, 14(10), 12708–12718 CrossRef CAS PubMed.
- H.-W. Cheng, H.-Y. Tsao, C.-S. Chiang and S.-Y. Chen, Advances in Magnetic Nanoparticle-Mediated Cancer Immune-Theranostics, Adv. Healthcare Mater., 2021, 10, 2001451 CrossRef CAS PubMed.
- T. J. Carter, G. Agliardi, F.-Y. Lin, M. Ellis, C. Jones, M. Robson, A. Richard-Londt, P. Southern, M. Lythgoe, M. Z. Thin, V. Ryzhov, R. T. M. de Rosales, C. Gruettner, M. R. A. Abdollah, R. B. Pedley, Q. A. Pankhurst, T. L. Kalber, S. Brandner, S. Quezada, P. Mulholland, M. Shevtsov and K. Chester, Potential of Magnetic Hyperthermia to Stimulate Localized Immune Activation, Small, 2021, 2005241 CrossRef CAS PubMed.
- M. Szekeres, I. Y. Tóth, E. Illés, A. Hajdú, I. Zupkó, K. Farkas, G. Oszlánczi, L. Tiszlavicz and E. Tombácz, Chemical and Colloidal Stability of Carboxylated Core-Shell Magnetite Nanoparticles Designed for Biomedical Applications, Int. J. Mol. Sci., 2013, 14(7), 14550–14574 CrossRef PubMed.
- G. Cotin, C. Blanco-Andujar, F. Perton, L. Asin, J. M. de la Fuente, W. Reichardt, D. Schaffner, D. Nguyen, D. Mertz, C. Kiefer, F. Meyer, S. Spassov, O. Ersen, M. Chatzidakis, G. Botton, C. Henoumont, S. Laurent, J. Grenèche, F. J. J. Teran, D. Ortega, D. Felder-Flesch and S. Begin-Colin, Unveiling the role of surface, size, shape and defects for theranostic applications of iron oxide nanoparticles, Nanoscale, 2021, 13, 14552–14571 RSC.
- M. Elimelech, J. Gregory and X. Jia, Particle Deposition and Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, 2013, p. 458 Search PubMed.
- A. Hajdú, M. Szekeres, I. Y. Tóth, R. A. Bauer, J. Mihály, I. Zupkó and E. Tombácz, Enhanced stability of polyacrylate coated magnetite nanoparticles in biorelevant media, Colloids Surf., B, 2012, 94, 242–249 CrossRef PubMed.
- A. Aires, D. Cabrera, L. C. Alonso-Pardo, A. L. Cortajarena and F. J. Teran, Elucidation of the Physicochemical Properties Ruling the Colloidal Stability of Iron Oxide Nanoparticles under Physiological Conditions, ChemNanoMat, 2017, 3(3), 183–189 CrossRef CAS.
- A. R. Iliasov, T. R. Nizamov, V. A. Naumenko, A. S. Garanina, S. S. Vodopyanov, A. A. Nikitin, A. G. Pershina, A. A. Chernysheva, Y. Kan, P. S. Mogilnikov, O. N. Metelkina, I. V. Schetinin, A. G. Savchenko, A. G. Majouga and M. A. Abakumov, Non-magnetic shell coating of magnetic nanoparticles as key factor of toxicity for cancer cells in a low frequency alternating magnetic field, Colloids Surf., B, 2021, 206, 111931 CrossRef CAS PubMed.
- E. Tombácz, K. Farkas, I. Földesi, M. Szekeres, E. Illés, I. Y. Tóth, D. Nesztor and T. Szabó, Polyelectrolyte coating on superparamagnetic iron oxide nanoparticles as interface between magnetic core and biorelevant media, Interface Focus, 2016, 6, 20160068 CrossRef PubMed.
- M. M. Modena, B. Rühle, T. P. Burg and S. Wuttke, Nanoparticle Characterization: What to Measure?, Adv. Mater., 2019, 1901556 CrossRef PubMed.
- A. Bertran, S. Sandoval, J. Oro-Sole, A. Sanchez and G. Tobias, Particle size determination from magnetization curves in reduced graphene oxide decorated with monodispersed superparamagnetic iron oxide nanoparticles, J. Colloid Interface Sci., 2020, 566, 107–119 CrossRef CAS PubMed.
- S. Chandrasekhar, Stochastic Problems in Physics and Astronomy, Rev. Mod. Phys., 1943, 15, 1–89 CrossRef.
- Z. Wang and C. Holm, Structure and magnetic properties of polydisperse ferrofluids: a molecular dynamics study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041401 CrossRef PubMed.
- S. Odenbach and S. Thurm, Magnetoviscous Effects in Ferrofluids, in Ferrofluids. Magnetically controllable fluids and their applications. Lecture Notes in Physics 594, ed. S. Odenbach, Springer, 2002, pp. 185–201 Search PubMed.
- L. M. Pop and O. Odenbach, Investigation of the microscopic reason for the magnetoviscous effect in ferrofluids studied by small angle neutron scattering, J. Phys.: Condens. Matter, 2006, 18, S2785–S2802 CrossRef CAS.
- S. Mahle, P. Ilg and M. Liu, Hydrodynamic theory of polydisperse chain-forming ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 016305 CrossRef PubMed.
- P. Ilg and S. Odenbach, Ferrofluid structure and rheology, in Lecture Notes in Physics 763, Colloidal Magnetic Fluids. Basics, Development and Application of Ferrofluids, ed. S. Odenbach, Springer, 2009, pp. 249–325 Search PubMed.
- A. Mertelj, A. Rešetič, S. Gyergyek, D. Makovec and M. Čopič, Anisotropic microrheological properties of chain-forming magnetic fluids, Soft Matter, 2011, 7, 125–131 RSC.
- K. Butter, P. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, Direct observation of dipolar chains in iron ferrofluids by cryogenic electron microscopy, Nat. Mater., 2003, 2, 88–91 CrossRef CAS PubMed.
- K. Butter, P. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, Direct observation of dipolar chains in ferrofluids in zero field using cryogenic electron microscopy, J. Phys.: Condens. Matter, 2003, 15, S1451–S1470 CrossRef CAS.
- M. Klokkenburg, C. Vonk, M. Claesson, J. Meeldijk, B. Erné and A. P. Philipse, Direct imaging of zero-field dipolar structures in colloidal dispersions of synthetic magnetite, J. Am. Chem. Soc, 2004, 126, 16706–16707 CrossRef CAS PubMed.
- S. E. Sandler, B. Fellows and O. T. Mefford, Best Practices for Characterization of Magnetic Nanoparticles for Biomedical Applications, Anal. Chem., 2019, 91, 14159–14169 CrossRef CAS PubMed.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Magnetic iron oxide nanoparticles: synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed.
- E. Amstad, M. Textor and E. Reimhult, Stabilization and functionalization of iron oxide nanoparticles for biomedical applications, Nanoscale, 2011, 3, 2819–2843 RSC.
- G. Muscas, N. Yaacoub, G. Concas, F. Sayed, R. Sayed Hassan, J. M. Greneche, C. Cannas, A. Musinu, V. Foglietti, S. Casciardi, C. Sangregorio and D. Peddis, Evolution of the magnetic structure with chemical composition in spinel iron oxide nanoparticles, Nanoscale, 2015, 7, 13576–13585 RSC.
- S. Sathish and S. Balakumar, Influence of physicochemical interactions of capping agent on magnetic properties of magnetite nanoparticles, Mater. Chem. Phys., 2016, 173, 364–371 CrossRef CAS.
- R. Di Corato, A. Aloisi, S. Rella, J. M. Greneche, G. Pugliese, T. Pellegrino, C. Malitesta and R. Rinaldi, Maghemite Nanoparticles with Enhanced Magnetic Properties: One-Pot Preparation and Ultrastable Dextran Shell, ACS Appl. Mater. Interfaces, 2018, 10, 20271–20280 CrossRef CAS PubMed.
- M. Harada, M. Kuwa, R. Sato, T. Teranishi, M. Takahashi and S. Maenosono, Cation Distribution in Monodispersed MFe2O4 (M = Mn, Fe, Co, Ni, and Zn) Nanoparticles Investigated by X-ray Absorption Fine Structure Spectroscopy: Implications for Magnetic Data Storage, Catalysts, Sensors, and Ferrofluids, ACS Appl. Nano Mater., 2020, 3, 8389–8402 CrossRef CAS.
- Y. Sang-Mook, P. Jin-Sung, L. Ke, J. Ki-Baek, A. H. Joy and K. Young-Rok, Modulation of the peroxidase-like activity of iron oxide nanoparticles by surface functionalization with polysaccharides and its application for the detection of glutathione, Carbohydr. Polym., 2021, 267, 118164 CrossRef PubMed.
- R. Turcu, V. Socoliuc, I. Craciunescu, A. Petran, A. Paulus, M. Franzreb, E. Vasile and L. Vekas, Magnetic microgels, a promising candidate for enhanced magnetic adsorbent particles in bioseparation: Synthesis, physicochemical characterization, and separation performance, Soft Matter, 2015, 11, 1008–1018 RSC.
- Y. V. Kolenko, M. Bañobre-López, C. Rodríguez-Abreu, E. Carbó-Argibay, A. Sailsman, Y. Piñeiro-Redondo, M. Fátima Cerqueira, D. Y. Petrovykh, K. Kovnir, O. I. Lebedev and J. Rivas, Large-Scale Synthesis of Colloidal Fe3O4 Nanoparticles Exhibiting High Heating Efficiency in Magnetic Hyperthermia, J. Phys. Chem. C, 2014, 118, 8691–8701 CrossRef CAS.
- I. Y. Toth, M. Szekeres, R. Turcu, S. Saringer, E. Illes, D. Nesztor and E. Tombacz, Langmuir, 2014, 30, 15451 CrossRef CAS PubMed.
- A. Nan, T. Radu and R. Turcu, Poly(glycidyl methacrylate)-functionalized magnetic nanoparticles as platforms for linking functionalities, bioentities and organocatalysts, RSC Adv., 2016, 6, 43330–43338 RSC.
- M. Mazur, A. Barras, V. Kuncser, A. Galatanu, V. Zaitzev, K. V. Turcheniuk, P. Woisel, J. Lyskawa, W. Laure, A. Siriwardena, R. Boukherrouba and S. Szunerits, Iron oxide magnetic nanoparticles with versatile surface functions based on dopamine anchors, Nanoscale, 2013, 5, 2692–2702 RSC.
- A. L. Willis, N. J. Turro and S. O'Brien, Spectroscopic Characterization of the Surface of Iron Oxide Nanocrystals, Chem. Mater., 2005, 17, 5970–5975 CrossRef CAS.
- T. J. Daou, G. Pourroy, S. Begin-Colin, J. M. Greneche, C. Ulhaq-Bouillet, P. Legare, P. Bernhardt, C. Leuvrey and G. Rogez, Hydrothermal synthesis of monodisperse magnetite nanoparticles, Chem. Mater., 2006, 18, 4399–4404 CrossRef CAS.
- D. Wilson and M. A. Langell, XPS analysis of oleylamine/oleic acid capped Fe3O4 nanoparticles as a function of temperature, Appl. Surf. Sci., 2014, 303, 6–13 CrossRef CAS.
- S. P. Schwaminger, D. Bauer, P. Fraga-García, F. E. Wagner and S. Berensmeier, Oxidation of magnetite nanoparticles: impact on surface and crystal properties, CrystEngComm, 2017, 19, 246 RSC.
- T. J. Daou, S. Begin-Colin, J. M. Greneche, F. Thomas, A. Derory, P. Bernhardt, P. Legare and G. Pourroy, Phosphate Adsorption Properties of Magnetite-Based Nanoparticles, Chem. Mater., 2007, 19, 4494–4505 CrossRef CAS.
- H. Etemadi and P. G. Plieger, Magnetic Fluid Hyperthermia Based on Magnetic Nanoparticles: Physical Characteristics, Historical Perspective, Clinical Trials, Technological Challenges, and Recent Advances, Adv. Ther., 2020, 2000061 CrossRef.
- Clinical Applications of Magnetic Nanoparticles Design to Diagnosis Manufacturing to Medicine, ed. N. T. K. Thanh, CRC Press Taylor & Francis Group, Boca Raton, FL, USA, 2018 Search PubMed.
- B. Lesiak, N. Rangam, P. Jiricek, I. Gordeev, J. Toth, L. Kover, M. Mohai and P. Borowicz, Surface study of Fe3O4 nanoparticles functionalized with biocompatible adsorbed molecules, Front. Chem., 2019, 7, 642 CrossRef CAS PubMed.
- A. G. Leonel, A. A. P. Mansur, S. M. Carvalho, L. E. F. Outon, J. D. Ardisson, K. Krambrock and H. S. Mansur, Tunable magnetothermal properties of cobalt-doped magnetite–carboxymethylcellulose ferrofluids: smart nanoplatforms for potential magnetic hyperthermia applications in cancer therapy, Nanoscale Adv., 2021, 3, 1029 RSC.
- H. Liu, G. Wei, Z. Xu, P. Liu and Y. Li, Appl. Surf. Sci., 2016, 389, 438–446 CrossRef CAS.
- P. X. Sheng, Y.-P. Ting, J. P. Chen and L. Hong, J. Colloid Interface Sci., 2004, 275, 131–141 CrossRef CAS PubMed.
- N. Tran and T. J. Webster, Magnetic nanoparticles: biomedical applications and challenges, J. Mater. Chem., 2010, 20, 8760–8767 RSC.
- S. Laurent, S. Dutz, U. O. Hafeli and M. Mahmoudi, Magnetic fluid hyperthermia: focus on superparamagnetic iron oxide nanoparticles, Adv. Colloid Interface Sci., 2011, 166, 8–23 CrossRef CAS PubMed.
- N. N. Greenwood and T. G. Gibb, Mössbauer Spectroscopy, Chapman and Hall Ltd, London, 1971 Search PubMed.
- M. F. Thomas and C. E. Johnson, Mössbauer Spectroscopy of Magnetic Solids, in Mössbauer Spectroscopy, ed. D. P. E. Dickson and F. J. Berry, Cambridge University Press, Cambridge, U. K., 1986, ch. 4, pp. 143–197 Search PubMed.
- V. Kuncser, P. Palade, A. Kuncser, S. Greculeasa and G. Schinteie, Engineering Magnetic Properties of Nanostructures via Size Effects and Interphase Interactions, in Size Effects in Nanostructures, Springer Series in Materials Science 205, ed. V. Kuncser and L. Miu, Springer Verlag, 2014, ch. 7, pp. 169–237. DOI:10.1007/978-3-662-44479-5_7.
- C. M. Sorensen, Magnetism, in Nanoscale Materials in Chemistry, ed. J. K. Klabunde, John Wiley and Sons Inc., New York, 2001 Search PubMed.
- I. Craciunescu, P. Palade, N. Iacob, G. M. Ispas, A. E. Stanciu, V. Kuncser and R. P. Turcu, High-Performance Functionalized Magnetic Nanoparticles with Tailored Sizes and Shapes for Localized Hyperthermia Applications, J. Phys. Chem. C, 2021, 125(20), 11132–11146 CrossRef CAS.
- V. Kuncser, M. Rosenberg, G. Principi, U. Russod, A. Hernando, E. Navarro and G. Filoti, Magnetic interactions in nanocrystalline FeRh alloys studied by in field Mössbauer spectroscopy, J. Alloys Compd., 2000, 308, 21–29 CrossRef CAS.
- P. Didukh, J. M. Greneche, A. Slawska-Waniewska, P. C. Fannin and L. I. Casas, Surface effects in CoFe2O4 magnetic fluids studied by Mossbauer Spectroscopy, J. Magn. Magn. Mater., 2002, 242–245, 613–616 CrossRef CAS.
- M. Darbandi, F. Stromberg, J. Landers, N. Reckers, B. Sanyal, W. Keune and H. Wende, Nanoscale size effect on surface spin canting in iron oxide nanoparticles synthesized by the microemulsion method, J. Phys. D: Appl. Phys., 2012, 45, 195001 CrossRef.
- E. C. Sousa, H. R. Rechenberg, J. Depeyrot, J. A. Gomes, R. Aquino, F. A. Tourinho, V. Dupuis and R. Perzynski, J. Appl. Phys., 2009, 106, 093901 CrossRef.
- S. G. Greculeasa, P. Palade, G. Schinteie, A. Leca, F. Dumitrache, I. Lungu, G. Prodan, A. Kuncser and V. Kuncser, Tuning structural and magnetic properties of Fe oxide nanoparticles by specific hydrogenation treatments, Sci. Rep., 2020, 10, 17174 CrossRef CAS PubMed.
- G. C. Lavorato, R. Das, J. A. Masa, M.-H. Phan and H. Srikanth, Hybrid magnetic nanoparticles as efficient nanoheaters in biomedical applications, Nanoscale Adv., 2021, 3, 867–888 RSC.
- T. Kohler, A. Feoktystov, O. Petraci, E. Kentzinger, T. Bhatnagar-Schöffmann, M. Feygenson, N. Nandakumaran, J. Landers, H. Wende, A. Cervellino, U. Rücker, A. Kovács, R.-E. Dunin-Borkowski and T. Brückel, Mechanism of magnetization reduction in iron oxide nanoparticles, Nanoscale, 2021, 13, 6965–6976 RSC.
- N. Iacob, G. Schinteie, C. Bartha, P. Palade, L. Vekas and V. Kuncser, Effects of magnetic dipolar interactions on the specific time constant in superparamagnetic nanoparticle systems, J. Phys. D: Appl. Phys., 2016, 49, 295001 CrossRef.
- R. E. Rosensweig, Heating magnetic fluid with alternating magnetic field, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- W. F. Brown, Thermal fluctuations of a single-domain particle, Phys. Rev., 1963, 130, 1677 CrossRef.
- L. Néel, Theorie du traınage magnetique des ferromagnetiques en grains fins avec applications aux terres cuites, Ann. Geophys., 1949, 5(2), 99–136 Search PubMed.
- L. Néel, J. Phys. Soc. Jpn., 1962, 17(Suppl. B-1), 676 Search PubMed.
- M. I. Shliomis, Ferrohydrodynamics: Retrospective and Issues, in Ferrofluids. Magnetically controllable fluids and their applications, Lecture notes in Physics 594, ed. S. Odenbach, Springer Verlag Berlin, Heidelberg, New York, 2002, pp. 85–111 Search PubMed.
- C. Shasha and K. M. Krishnan, Nonequilibrium Dynamics of Magnetic Nanoparticles with Applications in Biomedicine, Adv. Mater., 2020, 1904131 Search PubMed.
- N. Iacob, A. Kuncser, C. Comanescu, P. Palade and V. Kuncser, Optimization of magnetic fluid hyperthermia with respect to nanoparticle shape-related parameters: case of magnetite ellipsoidal nanoparticles, J. Nanopart. Res., 2020, 22, 138 CrossRef CAS.
- S. Bedanta and W. Kleemann, Supermagnetism, J. Phys. D: Appl. Phys., 2009, 42, 013001 CrossRef.
- J. L. Dormann, D. Fiorani and E. Tronc, in Magnetic Relaxation in Fine Partocle Systems, Advances in Chemical Physics, ed. I. Progogine and A. Stuart Rice, John Wiley & Sons Inc., 1997, vol. XCVIII Search PubMed.
- V. Kuncser, G. Schinteie, B. Sahoo, W. Keune, D. Bica, L. Vekas and G. Filoti, Magnetic interactions in water based ferrofluids studied by Mossbauer spectroscopy, J. Phys.: Condens. Matter, 2007, 19, 016205 CrossRef.
- G. Schinteie, P. Palade, L. Vekas, N. Iacob, C. Bartha and V. Kuncser, Volume fraction dependent magnetic behaviour of ferrofluids for rotating seal applications, J. Phys. D: Appl. Phys., 2013, 46, 395501 CrossRef.
- A. Kuncser, N. Iacob and V. Kuncser, On the relaxation time of interacting superparamagnetic nanoparticles and implications for magnetic hyperthermia, Beilstein J. Nanotechnol., 2019, 10, 1280–1289 CrossRef CAS PubMed.
- J. Landers, S. Salamon, H. Remmer, F. Ludwig and H. Wende, Simultaneous Study of Brownian and Néel Relaxation Phenomena in Ferrofluids by Mössbauer Spectroscopy, Nano Lett., 2016, 16, 1150–1155 CrossRef CAS PubMed.
- J. Landers, S. Salamon, H. Remmer, F. Ludwig and H. Wende, In-Field Orientation and Dynamics of Ferrofluids Studied by Mössbauer Spectroscopy, ACS Appl. Mater. Interfaces, 2019, 11, 3160–3168 CrossRef CAS PubMed.
- R. Gabbasova, A. Yurenya, A. Nikitin, V. Cherepanova, M. Polikarpova, M. Chueva, A. Majouga and V. Panchenko, Study of Brownian motion of magnetic nanoparticles in viscous media by Mössbauer spectroscopy, J. Magn. Magn. Mater., 2019, 475, 146–151 CrossRef.
- S. Taketomi, M. Ukita, M. Mizukami, H. Miyajima and S. Chikazumi, Magnetooptical Effects of Magnetic Fluid, J. Phys. Soc. Jpn., 1987, 56, 3362–3374 CrossRef CAS.
- J. J. M. Janssen and J. A. A. J. Perenboom, Magneto-optical phenomena in magnetic fluids: The influence of orientation of anisotropic scatterers, J. Magn. Magn. Mater., 1989, 81(1–2), 14–24 CrossRef CAS.
- M. Xu and P. J. Ridler, Linear dichroism and birefringence effects in magnetic fluids, J. Appl. Phys., 1997, 82, 326 CrossRef CAS.
- F. Donatini, D. Jamon, J. Monin and S. Neveu, Experimental investigation of longitudinal magneto-optic effects in four ferrite ferrofluids in visible-near infrared spectrum, IEEE Trans. Magn., 1999, 35, 4311–4317 CrossRef CAS.
- V. Socoliuc, Investigation of Concentration and Surfactant Quality Influence on Magnetic Particle Agglomeration in Ferrofluids from Static Linear Dichroism Experiments, J. Magn. Magn. Mater., 1999, 207, 146–157 CrossRef CAS.
- H. E. Horng, C.-Y. Hong, S. Y. Yang and S. C. Yang, Novel properties and applications in magnetic fluids, J. Phys. Chem. Solids, 2001, 62, 1749–1764 CrossRef CAS.
- A. O. Ivanov and S. S. Kantorovich, Chain aggregate structure and magnetic birefringence in polydisperse ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 021401 CrossRef PubMed.
- R. V. Mehta, R. Patel, R. Desai, R. V. Upadhyay and K. Parekh, Experimental Evidence of Zero Forward Scattering by Magnetic Spheres, Phys. Rev. Lett., 2006, 96, 127402 CrossRef CAS PubMed.
- J. M. Laskar, J. Philip and B. Raj, Experimental investigation of magnetic-field-induced aggregation kinetics in nonaqueous ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021402 CrossRef PubMed.
- H. Bhatt, R. Patel and R. V. Mehta, Energy transport velocity in bidispersed magnetic colloids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011401 CrossRef PubMed.
- Y. L. Raikher and M. I. Shliomis, The Effective-Field Method in the Orientational Kinetics of Magnetic Fluids and Liquid-Crystals, Adv. Chem. Phys., 1994, 87, 595–751 CAS , rearranged and corrected by Y. L. Raikher in 2002 as: the effective field method in the orientational kinetics of magnetic fluids.
- J.-C. Bacri and R. Perzynski, Optical properties of magnetic fluids, in Magnetic fluids and applications Handbook, ed. B. Berkovski and V. Bashtovoy, Begell House Inc., New York-Wallingford, 1996, pp. 79–129 Search PubMed.
- J. M. Laskar, J. Philip and B. Raj, Experimental evidence for reversible zippering of chains in magnetic nanofluids under external magnetic fields, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041401 CrossRef PubMed.
- V. Socoliuc and L. B. Popescu, The influence of long range interparticle correlations on the magnetically induced optical anisotropy in magnetic colloids, Phys. A, 2011, 390, 569–578 CrossRef CAS.
- E. Hasmonay, E. Dubois, J.-C. Bacri, R. Perzynski, L. Raikher Yu and V. I. Stepanov, Static magneto-optical birefringence of size-sorted γ-Fe2O3 nanoparticles, Eur. Phys. J. B, 1998, 5, 859–867 CrossRef CAS.
- A. Martinet, Biréfringence et dichroïsme linéaire des ferrofluides sous champ magnétique, Rheol. Acta, 1974, 13(2), 260–264 CrossRef CAS.
- P. C. Scholten, Origin of magnetic birefringence and dichroism in magnetic fluids, IEEE Trans. Magn., 1980, 16(2), 221–225 CrossRef.
- J.-C. Bacri and D. Salin, Optical scattering on ferrofluid agglomerates, J. Phys., Lett., 1982, 43, L771–L777 CrossRef.
- J. P. Llewellyn, Form birefringence in ferrofluids, J. Phys. D: Appl. Phys., 1983, 16(1), 95 CrossRef CAS.
- S. Taketomi, Magnetic Fluid's Anomalous Pseudo-Cotton Mouton Effects about 107 Times Larger than That of Nitrobenzene, Jpn. J. Appl. Phys., 1983, 22, 1137–1143 CrossRef CAS.
- W. Reed and J. H. Fendler, Anisotropic aggregates as the origin of magnetically induced dichroism in ferrofiuids, J. Appl. Phys., 1986, 59, 2914–2924, DOI:10.1063/1.336952.
- S. Neto K, A. F. Bakuzis, P. C. Morais, A. R. Pereira, R. B. Azevedo, L. M. Lacava and Z. G. M. Lacava, The influence of aggregates and relative permeability on the magnetic birefringence in ionic magnetic fluids, J. Appl. Phys., 2001, 89, 3362 CrossRef.
- V. Socoliuc and L. B. Popescu, Extinction of polarized light in ferrofluids with different magnetic particle concentrations, J. Magn. Magn. Mater., 2012, 324, 113–123 CrossRef CAS.
- J. Szczytko, N. Vaupoti, M. A. Osipov, K. Madrak and E. Gorecka, Effect of dimerization on the field-induced birefringence in ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062322 CrossRef PubMed.
- V. Socoliuc and L. B. Popescu, Determination of the statistics of magnetically induced particle chains in concentrated ferrofluids, J. Magn. Magn. Mater., 2020, 502, 166532 CrossRef CAS.
- L. B. Popescu, V. Socoliuc and D. Bica, Magnetically-induced dichroism in ferrocolloids, Rom. J. Phys., 2006, 51(7–8), 791–797 CAS.
- A. Zubarev, L. Yu and Y. Iskakova, On the theory of optical birefringence in ferrofluids, Magnetohydrodynamics, 2009, 45(1), 15–24 CrossRef.
- V. Socoliuc and L. B. Popescu, The role of the magnetically induced anisotropy of the pair correlation function in the dichroism of magnetic fluids, J. Magn. Magn. Mater., 2013, 347, 146–452 CrossRef CAS.
- E. A. Elfimova, A. O. Ivanov, L. B. Popescu and V. Socoliuc, Transverse magneto-optical anisotropy in bidisperse ferrofluids with long range particle correlations, J. Magn. Magn. Mater., 2017, 431, 54–58 CrossRef CAS.
- E. Hasmonay, E. Dubois, S. Neveu, J.-C. Bacri and R. Perzynski, Alternating magneto-birefringence of ionic ferrofluids in crossed fields, Eur, Phys. J. B, 2001, 21, 19–29 CAS.
- S. Taketomi, N. Inaba, H. Takahashi and H. Miyajima, Field dependence of magnetic birefringence of magnetic fluid in low-magnetic-field region, J. Phys. Soc. Jpn., 1990, 59(9), 3007–3080 CrossRef.
- V. Socoliuc and D. Bica, The influence of the Neel rotation on the magnetic induced dichroism in magnetic fluids, J. Magn. Magn. Mater., 2005, 289, 177–180 CrossRef CAS.
- Y. L. Raikher, V. I. Stepanov, J.-C. Bacri and R. Perzynski, Orientational dynamics of ferrofluids with finite magnetic anisotropy of the particles: Relaxation of magneto-birefringence in crossed fields, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021203 CrossRef PubMed.
- P. C. Fannin and S. W. Charles, The study of a ferrofluid exhibiting both Brownian and Néel relaxation, J. Phys. D: Appl. Phys., 1989, 22, 187 CrossRef CAS.
- R. Kötitz, P. C. Fannin and L. Trahms, Investigation of Brownian and Néel relaxation in magnetic fluids, J. Magn. Magn. Mater., 1999, 149, 42 CrossRef.
- L. Sakhnini and J. Popplewell, J. Magn. Magn. Mater., 1993, 122, 146 CrossRef CAS.
- M. Rasa, Magnetic properties and magneto-birefringence of magnetic fluids, Eur. Phys. J. E, 2000, 2, 265–275 CrossRef CAS.
- V. Socoliuc and D. Bica, The influence of the degree of colloidal stabilization and concentration on the magnetic particle aggregation in ferrofluids, J. Magn. Magn. Mater., 2002, 252, 26–28 CrossRef CAS.
- Z. A. Yu and I. L. Yu, On the theory of physical properties of magnetic fluids with chainy aggregates, J. Exp. Theor. Phys., 1995, 80, 857 Search PubMed.
- A. O. Ivanov, J. Magn. Magn. Mater., 1996, 66, 154 Search PubMed.
- V. S. Mendelev and A. O. Ivanov, Ferrofluid aggregation in chains under the influence of a magnetic field, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051502 CrossRef PubMed.
- P. Kopcansky, D. Macko, D. Horvath, M. Kasparkova and T. Tima, Study of magneto-optical effects in a damping-oil-based magnetic fluid in the infrared region, J. Magn. Magn. Mater., 1993, 122, 150–153 CrossRef CAS.
- E. Nekhoroshkova Yu, O. A. Goldina, E. A. Elfimova and A. O. Ivanov, J. Exp. Theor. Phys., 2014, 118(3), 442–456 CrossRef.
- V. Socoliuc and D. Bica, Experimental investigation of magnetic-induced phase separation kinetics in aqueous ferrofluids, Prog. Colloid Polym. Sci., 2001, 117, 131 CAS.
- M. V. Avdeev, B. Mucha, K. Lamszus, L. Vékás, V. M. Garamus, A. V. Feoktystov, O. Marinica, R. Turcu and R. Willumeit, Structure and in vitro biological testing of water-based ferrofluids stabilized by monocarboxylic acids, Langmuir, 2010, 26(11), 8503–8509 CrossRef CAS PubMed.
- S. L. Saville, R. C. Woodward, M. J. House, A. Tokarev, J. Hammers, B. Qi, J. Shaw, M. Saunders, R. R. Varsani, T. G. St Pierre and O. T. Mefford, The effect of magnetically induced linear aggregates on proton transverse relaxation rates of aqueous suspensions of polymer coated magnetic nanoparticles, Nanoscale, 2013, 5(5), 2152–2163 RSC.
- H. Ezzaier, J. A. Marins, I. Razvin, M. Abbas, A. Ben Haj Amara, A. Zubarev and P. Kuzhir, Two-stage kinetics of field-induced aggregation of medium-sized magnetic nanoparticles, J. Chem. Phys., 2017, 146, 114902 CrossRef CAS PubMed.
- M. Fermigier and A. P. Gast, J. Colloid Interface Sci., 1992, 154, 522 CrossRef CAS.
- J. Promislow, A. P. Gast and M. Fermigier, Aggregation kinetics of paramagnetic colloidal particles, J. Chem. Phys., 1995, 102, 5492 CrossRef CAS.
- G. Helgesen, A. T. Skjeltorp, P. M. Mors, R. Botet and R. Jullien, Aggregation of Magnetic Microspheres: Experiments and Simulations, Phys. Rev. Lett., 1988, 61, 1736 CrossRef PubMed.
- G. Helgesen and A. T. Skjeltorp, An experimental system for studying dynamic behavior of magnetic microparticles, J. Appl. Phys., 1991, 69, 8277, DOI:10.1063/1.347436.
- S. Melle, M. A. Rubio and G. G. Fuller, Time scaling regimes in aggregation of magnetic dipolar particles: scattering dichroism results, Phys. Rev. Lett., 2001, 87, 115501 CrossRef CAS PubMed.
- C. P. Reynolds, K. E. Klop, F. A. Lavergne, S. M. Morrow, D. G. A. L. Aarts and R. P. A. Dullens, Deterministic aggregation kinetics of superparamagnetic colloidal particles, J. Chem. Phys., 2015, 143, 214903, DOI:10.1063/1.4936323.
- C. Rablau, P. Vaishnava, C. Sudakar, R. Tackett, G. Gavin Lawes and R. Naik, Magnetic-field-induced optical anisotropy in ferrofluids: A time-dependent light-scattering investigation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051502 CrossRef PubMed.
- T. C. Halsey and W. Toor, Structure of electrorheological fluids, Phys. Rev. Lett., 1990, 65, 2820 CrossRef CAS PubMed.
- J. E. Martin, J. Odinek and T. C. Halsey, Phys. Rev. Lett., 1992, 69, 1524 CrossRef CAS PubMed.
- J. E. Martin, K. M. Hill and C. P. Tigges, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5676 CrossRef CAS PubMed.
- E. M. Furst and A. P. Gast, Dynamics and lateral interactions of dipolar chains, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 6916 CrossRef CAS PubMed.
- T. Vicsek and F. Family, Dynamic scaling for aggregation of clusters, Phys. Rev. Lett., 1984, 52(19), 1669–1672 CrossRef.
- J. Cernak, G. Helgesen and A. Skjeltorp, Aggregation dynamics of nonmagnetic particles in a ferrofluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 031504 CrossRef PubMed.
- V. Socoliuc, L. Vekas and R. Turcu, Magnetically induced phase condensation in an aqueous dispersion of magnetic nanogels, Soft Matter, 2013, 9(11), 3098–3105 RSC.
- V. Socoliuc, D. Bica and L. Vekas, Magnetically induced phase condensation with asymptotic critical temperature in an aqueous magnetic colloid, Magnetohydrodynamics, 2011, 47(2), 201–206 CrossRef.
- V. Socoliuc and R. Turcu, Large scale aggregation in magnetic colloids induced by high frequency magnetic fields, J. Magn. Magn. Mater., 2020, 500, 166348 CrossRef.
- A. Cebers, Basic physical, mathematical and computer simulation models, in Magnetic Fluids and Applications Handbook, ed. B. Berkovski and V. Bashtovoy, Begell House, New York & Wallingford, UK, 1996, pp. 253 Search PubMed.
- W. Szczerba, R. Costo, S. Veintemillas-Verdaguer, M. Puerto Morales and A. F. Thunemann, SAXS analysis of single- and multi-core iron oxide magnetic nanoparticles, J. Appl. Crystallogr., 2017, 50, 481–488 CrossRef CAS PubMed.
- S. Muhlbauer, D. Honecker, E. A. Périgo, F. Bergner, S. Disch, A. Heinemann, S. Erokhin, D. Berkov, C. Leighton, M. R. Eskildsen and A. Michels, Magnetic small-angle neutron scattering, Rev. Mod. Phys., 2019, 91, 015004 CrossRef.
- B. R. Pauw, A. J. Smith, T. Snow, N. J. Terrill and A. F. Thüneman, The modular small-angle X-ray scattering data correction sequence, J. Appl. Crystallogr., 2017, 50, 1800–1811 CrossRef CAS PubMed.
- J. Watt, G. C. Bleier, Z. W. Romero, B. G. Hance, J. A. Bierner, T. C. Monson and D. L. Huber, Gram Scale Synthesis of Fe/Fe, Py Core-Shell Nanoparticles and their Incorporation into Matrix-Free Superparamagnetic Nanocomposites, Mater. Res., 2018, 33, 2156–2167 CrossRef CAS.
- M. Unni, S. Savliwala, B. D. Partain, L. Maldonado-Camargo, Q. Zhang, S. Narayanan, E. M. Dufresne, J. Ilavsky, P. Grybos, A. Koziol, P. Maj, R. Szczygiel, K. D. Allen and C. M. Rinaldi-Ramos, Sci. Adv., 2021, 7, eabf8467 CrossRef CAS PubMed.
- S. Disch, E. Wetterskog, R. P. Hermann, A. Wiedenmann, U. Vainio, G. Salazar-Alvarez, L. Bergström and T. Brückel, Quantitative spatial magnetization distribution in iron oxide nanocubes and nanospheres by polarized small-angle neutron scattering, New J. Phys., 2012, 14, 013025 CrossRef.
- A. Kabelitz, A. Guilherme, M. Joester, U. Reinholz, M. Radtke, R. Bienert, K. Schulz, R. Schmack, R. Kraehnert and F. Emmerling, Time-resolved in situ studies on the formation mechanism of iron oxide nanoparticles using combined fast-XANES and SAXS, CrystEngComm, 2015, 17, 8463 RSC.
- D. Zakutna, Y. Falke, D. Dresen, S. Prévost, P. Bender, D. Honecker and S. Disch, Morphological and crystallographic orientation of hematite spindles in an applied magnetic field, Nanoscale, 2019, 11, 7149–7156 RSC.
- D. Zakutna, K. Graef, D. Dresen, L. Porcar, D. Honecker and S. Disch, In situ magnetorheological SANS setup at Institut Laue-Langevin, Colloid Polym. Sci., 2021, 299, 281–288 CrossRef CAS.
- B. Grabcev, M. Balasoiu, A. Tirziu, A. I. Kuklin and D. Bica, Application of contrast variation method in SANS experiments with ferrofluids, J. Magn. Magn. Mater., 1999, 201, 140–143 CrossRef CAS.
- M. V. Avdeev, Contrast variation in small-angle scattering experiments on polydisperse and superparamagnetic systems: basic functions approach, J. Appl. Crystallogr., 2007, 40, 56–70 CrossRef CAS.
- M. V. Avdeev and V. L. Aksenov, Small-angle neutron scattering in structure research of magnetic fluids, Phys.-Usp., 2010, 53(10), 971–993 CrossRef CAS.
- P. Bender, L. K. Bogart, O. Posth, W. Szczerba, S. E. Rogers, A. Castro, L. Nilsson, L. J. Zeng, A. Sugunan, J. Sommertune, A. Fornara, D. González-Alonso, L. Fernández Barquín and C. Johansson, Structural and magnetic properties of multi-core nanoparticles analysed using a generalised numerical inversion method, Sci. Rep., 2017, 7, 45990, DOI:10.1038/srep45990.
- A. Heinemann, A. Wiedenmann, M. Kammel, H. Bonnemann and N. Matoussevitch, High-quality structure parameter for magnetic liquids obtained by small-angle scattering of polarized neutrons, Appl. Organomet. Chem., 2004, 18, 561–564 CrossRef CAS.
- C. L. Dennis, K. L. Krycka, J. A. Borchers, R. D. Desautels, J. van Lierop, N. F. Huls, A. J. Jackson, C. Gruettner and R. Ivkov, Internal Magnetic Structure of Nanoparticles Dominates Time-Dependent Relaxation Processes in a Magnetic Field, Adv. Funct. Mater., 2015, 25, 4300–4311 CrossRef CAS.
- P. Bender, J. Fock, C. Frandsen, M. F. Hansen, C. Balceris, F. Ludwig, O. Posth, E. Wetterskog, L. K. Bogart, P. Southern, W. Szczerba, L. Zeng, K. Witte, C. Grüttner, F. Westphal, D. Honeker, D. González-Alonso, L. F. Barquín and C. Johansson, Relating Magnetic Properties and High Hyperthermia Performance of Iron Oxide Nanoflowers, J. Phys. Chem. C, 2018, 122(5), 3068–3077 CrossRef CAS.
- L. Krycka K, A. Borchers J, G. Salazar-Alvarez, A. López-Ortega, M. Estrader, S. Estradé, E. Winkler, R. D. Zysler, J. Sort, F. Peiró, M. D. Baró, C.-C. Kao and J. Nogués, Resolving Material-Specific Structures within Fe3O4|γ-Mn2O3 Core|Shell Nanoparticles Using Anomalous Small-Angle X-ray Scattering, ACS Nano, 2013, 7(2), 921–931 CrossRef PubMed.
- F. Gazeau, F. Boue, E. Dubois and R. Perzynski, Static and quasi-elastic small angle neutron scattering on biocompatible ionic ferrofluids: magnetic and hydrodynamic interactions, J. Phys.: Condens. Matter, 2003, 15, S1305–S1334 CrossRef CAS.
- E. Pyanzina, S. Kantorovich, J. J. Cerda, A. Ivanov and C. Holm, How to analyse the structure factor in ferrofluids with strong magnetic interactions: a combined analytic and simulation approach, Mol. Phys., 2009, 107, 571–590 CrossRef CAS.
- M. V. Avdeev, Particle interaction in polydisperse magnetic fluids: Experimental aspects of small-angle neutron scattering applications, J. Mol. Liq., 2014, 189, 68–73 CrossRef CAS.
- J. Cerda, E. Elfimova, V. Ballenegger, E. Krutikova, A. O. Ivanov and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011501 CrossRef PubMed.
- M. V. Avdeev, M. Balasoiu, V. L. Aksenov, V. M. Garamus, J. Kohlbrecher, D. Bica and L. Vekas, On the magnetic structure of magnetite/oleic acid/benzene ferrofluids by small-angle neutron scattering, J. Magn. Magn. Mater., 2004, 270, 371–379 CrossRef CAS.
- M. V. Avdeev, E. Dubois, G. Meriguet, E. Wandersman, V. M. Garamus, A. V. Feoktystov and R. Perzynski, Small-angle neutron scattering analysis of a water based magnetic fluid with charge stabilization: contrast variation and scattering of polarized neutrons, J. Appl. Crystallogr., 2009, 42, 1009–1019 CrossRef CAS.
- F. Cousin, E. Dubois and V. Cabuil, Tuning the interactions of a magnetic colloidal suspension, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021045 CrossRef PubMed.
- G. Meriguet, F. Cousin, E. Dubois, F. Boue, A. Cebers, B. Farago and R. Perzynski, What tunes the structural anisotropy of magnetic fluids under a magnetic field?, J. Phys. Chem. B, 2006, 110, 4378–4386 CrossRef CAS PubMed.
- E. Wandersman, A. Cebers, E. Dubois, G. Mériguet, A. Robert and R. Perzynski, The cage elasticity and under-field structure of concentrated magnetic colloids probed by small angle X-ray scattering, Soft Matter, 2013, 9, 11480–11489 RSC.
- J. Zaloga, A. Feoktystov, V. M. Garamus, W. Karawacka, A. Ioffe, T. Brückel, R. Tietze, C. Alexiou and S. Lyer, Studies on the adsorption and desorption of mitoxantrone to lauric acid/albumin coated iron oxide nanoparticles, Colloids Surf., B, 2018, 161, 18–26 CrossRef CAS PubMed.
- A. A. Veligzhanin, D. I. Frey, A. V. Shulenina, A. Gruzinov, V. Y. Zubavichus Ya and M. V. Avdeev, Characterization of aggregate state of polydisperse ferrofluids: Some aspects of anisotropy analysis of 2D SAXS in magnetic field, J. Magn. Magn. Mater., 2018, 459, 285–289 CrossRef CAS.
- E. Klokkenburg M., B. H. Wiedenmann A, A. V. Petukhov and A. P. Philipse, Dipolar structures in magnetite ferrofluids studied with small-angle neutron scattering with and without applied magnetic field, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051408 CrossRef PubMed.
- A. Wiedenmann, A. Hoell, M. Kammel and P. Boesecke, Field-induced pseudocrystalline ordering in concentrated ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 031203 CrossRef CAS PubMed.
- A. Wiedenmann, Polarized SANS for probing magnetic nanostructures, Phys. B, 2005, 336, 246–253 CrossRef.
- Z. Fu, Y. Xiao, A. Feoktystov, V. Pipich, M.-S. Appavou, Y. Su, E. Feng, W. Jin and T. Brückel, Field-induced self-assembly of iron oxide nanoparticles investigated using small-angle neutron scattering, Nanoscale, 2016, 8, 18541 RSC.
- A. Wiedenmann, U. Keiderling, K. Habicht, M. Russina and R. Gähler, Dynamics of Field-Induced Ordering in Magnetic Colloids Studied by New Time-Resolved Small-Angle Neutron-Scattering Techniques, Phys. Rev. Lett., 2006, 97, 057202 CrossRef CAS PubMed.
- A. Wiedenmann, R. Gähler, R. P. May, U. Keiderling, K. Habicht, S. Prévost, M. Klokkenburg, B. Erné and J. Kohlbrecher, Stroboscopic Small Angle Neutron Scattering Investigations of Microsecond Dynamics in Magnetic Nanomaterials, in Studying Kinetics with Neutrons, Springer Series in Solid-State Sciences, 2009, vol. 161, pp. 241–263 Search PubMed.
- A. Wiedenmann, U. Keiderling, M. Meissner, D. Wallacher, R. Gähler, R. P. May, S. Prévost, M. Klokkenburg, B. H. Erné and J. Kohlbrecher, Low-temperature dynamics of magnetic colloids studied by time-resolved small-angle neutron scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184417 CrossRef.
- A. Wiedenmann, R. Gähler, C. D. Dewhurst, U. Keiderling, S. Prévost and J. Kohlbrecher, Relaxation mechanisms in magnetic colloids studied by stroboscopic spin-polarized small-angle neutron scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 214303 CrossRef.
- M. Rajnak, V. I. Petrenko, M. V. Avdeev, O. I. Ivankov, A. Feoktystov, B. Dolnik, J. Kurimsky, P. Kopcansky and M. Timko, Direct observation of electric field induced pattern formation and particle aggregation in ferrofluid, Appl. Phys. Lett., 2015, 107, 073108 CrossRef.
- M. Rajnak, M. Timko, P. Kopcansky, K. Paulovicova, J. Tothova, J. Kurimsky, B. Dolnik, R. Cimbala, M. V. Avdeev, V. I. Petrenko and A. Feoktystov, Structure and viscosity of a transformer oil-based ferrofluid under an external electric field, J. Magn. Magn. Mater., 2017, 431(1), 99–102 CrossRef CAS.
- M. Mamusa, J. Siriex-Plenet, F. Cousin, E. Dubois and V. Peyre, Tuning the colloidal stability in ionic liquids by controlling the nanoparticles/liquid interface, Soft Matter, 2013, 10, 1097–1101 RSC.
- A. V. Nagornyi, Y. Shlapa, M. V. Avdeev, S. O. Solopan, A. G. Belous, A. V. Shulenina, O. I. Ivankov and L. A. Bulavin, Structural characterization of aqueous magnetic fluids with nanomagnetite of different origin stabilized by sodium oleate, J. Mol. Liq., 2020, 312, 113430 CrossRef CAS.
- M. V. Avdeev, A. V. Feoktystov, P. Kopcansky, G. Lancz, V. M. Garamus, R. Willumeit, M. Timko, M. Koneracka, V. Zavisova, N. Tomasovicova, A. Jurikova, K. Csach and L. A. Bulavin, Structure of water-based ferrofluids with sodium oleate and polyethylene glycol stabilization by small-angle neutron scattering: contrast-variation experiments, J. Appl. Crystallogr., 2010, 43, 959–969 CrossRef CAS.
- O. V. Tomchuk, M. V. Avdeev, V. L. Aksenov, A. V. Shulenina, O. I. Ivankova, V. Ryukhtin, L. Vekas and L. A. Bulavin, Temperature-dependent fractal structure of particle clusters in aqueous ferrofluids by small-angle scattering, Colloids Surf., A, 2021, 613, 126090 CrossRef CAS.
- L. Shen, A. Stachowiak, S.-E. K. Fateen, P. E. Laibinis and T. A. Hatton, Structure of Alkanoic Acid Stabilized Magnetic Fluids. A Small-Angle Neutron and Light Scattering Analysis, Langmuir, 2001, 7, 288–299 CrossRef.
- A. Balasoiu M, M. V. Aksenov and V. L, SANS Study of Clusters in Aqueous Magnetic Fluids, Crystallogr. Rep., 2007, 52(3), 505–511 CrossRef.
- G. Salas, C. Casado, F. J. Teran, R. Miranda, C. J. Serna and M. Puerto Morales, Controlled synthesis of uniform magnetite nanocrystals with high-quality properties for biomedical applications, J. Mater. Chem., 2012, 22, 21065–21075 RSC.
- C. L. Dennis, A. J. Jackson, J. A. Borchers, C. Gruettner and R. Ivkov, Correlation between physical structure and magnetic anisotropy of a magnetic nanoparticle colloid, Nanotechnology, 2018, 29, 215705 CrossRef CAS PubMed.
- F. L. O. Paula, SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters, Condens. Matter, 2019, 4(2), 55, DOI:10.3390/condmat4020055.
- Z. Rozynek, A. Jozefczak, K. D. Knudsen, A. Skumiel, T. Hornowski, J. O. Fossum, M. Timko, P. Kopcansky and M. Koneracka, Structuring from nanoparticles in oil-based ferrofluids, Eur. Phys. J. E, 2011, 34, 28 CrossRef CAS PubMed.
- M. Wang, L. He and Y. Yin, Magnetic field guided colloidal assembly, Mater. Today, 2013, 16(4), 110–116 CrossRef CAS.
- Y. Wu, N. Dong, S. Fu, J. D. Fowlkes, L. Kondic, M. A. Vincenti, D. de Ceglia and P. D. Rack, Directed Liquid Phase Assembly of Highly Ordered Metallic Nanoparticle Arrays, ACS Appl. Mater. Interfaces, 2014, 6, 5835 CrossRef CAS PubMed.
- J. Faraudo, J. S. Andreu, C. Calero and J. Camacho, Predicting the Self-Assembly of Superparamagnetic Colloids under Magnetic Fields, Adv. Funct. Mater., 2016, 26, 3837 CrossRef CAS.
- A. Vorobiev, J. Major, H. Dosch, G. Gordeev and D. Orlova, Phys. Rev. Lett., 2004, 93, 267203 CrossRef CAS PubMed.
- I. V. Gapon, V. I. Petrenko, O. Soltwedel, N. Khaydukov Yu, M. Kubovcikova, P. Kopcansky, L. A. Bulavin and M. V. Avdeev, J. Phys.: Conf. Ser., 2018, 994, 012008 CrossRef.
- E. Josten, E. Wetterskog, A. Glavic, P. Boesecke, A. Feoktystov, E. Brauweiler-Reuters, U. Rücker, G. Salazar-Alvarez, T. Brückel and L. Bergström, Superlattice growth and rearrangement during evaporationinduced nanoparticle self-assembly, Sci. Rep., 2017, 7, 2802 CrossRef PubMed.
- M. V. Avdeev, V. I. Petrenko, I. V. Gapon, L. A. Bulavin, A. A. Vorobiev, O. Soltwedel, M. Balasoiu, L. Vekas and P. Kopcansky, Comparative structure analysis of magnetic fluids at interface with silicon by neutron reflectometry, Appl. Surf. Sci., 2015, 352, 49–53 CrossRef CAS.
- K. Theis-Bröhl, P. Gutfreund, A. Vorobiev, M. Wolff, B. P. Toperverg, J. A. Dura and J. A. Borchers, Self assembly of magnetic nanoparticles at silicon surfaces, Soft Matter, 2015, 11, 4695–4704 RSC.
- A. V. Nagornyi, V. I. Petrenko, M. Rajnak, I. V. Gapon, M. V. Avdeev, B. Dolnik, L. A. Bulavin, P. Kopcansky and M. Timko, Appl. Surf. Sci., 2019, 473, 912–917 CrossRef CAS.
- M. Kubovcikova, V. Igor, I. V. Gapon, V. Zavisova, M. Koneracka, V. I. Petrenko, O. Soltwedel, L. Almasy, M. V. Avdeev and P. Kopcansky, On the adsorption properties of magnetic fluids: Impact of bulk structure, J. Magn. Magn. Mater., 2017, 427, 67–70 CrossRef CAS.
- K. Theis-Bröhl, E. C. Vreeland, A. Gomez, D. L. Huber, A. Saini, M. Wolff, B. B. Maranville, E. Brok, K. L. Krycka, J. A. Dura and J. A. Borchers, Self-Assembled Layering of Magnetic Nanoparticles in a Ferrofluid, on Silicon Surfaces, ACS Appl. Mater. Interfaces, 2018, 10, 5050–5060 CrossRef PubMed.
- A. Saini, K. Theis-Bröhl, A. Koutsioubas, K. L. Krycka, J. A. Borchers and M. Wolff, Magnetic Particle Self-Assembly at Functionalized Interfaces, Langmuir, 2021, 37(14), 4064–4071 CrossRef CAS PubMed.
- Q. A. Pankhurst and R. J. Pollard, Fine-particle magnetic oxides, J. Phys.: Condens. Matter, 1993, 5, 8487–8508 CrossRef CAS.
- P. C. Fannin, Magnetic Spectroscopy as an Aide in Understanding Magnetic Fluids, in Ferrofluids. Magnetically Controllable Fluids and Their Applications, Lecture Notes in Physics 594, ed. S. Odenbach, Springer Verlag, 2002, pp. 19–32 Search PubMed.
- V. Socoliuc, V. Kuncser, R. Turcu and L. Vekas, Magnetic Characterization, in New Developments in NMR No. 13, Contrast Agents for MRI: Experimental Methods, ed. V. C. Pierre and M. J. Allen, The Royal Society of Chemistry, 2018, ch. 4.5, pp. 391–426 Search PubMed.
- C. P. Bean and J. D. Livingston, Superparamagnetism, J. Appl. Phys., 1959, 30(4), S120–S129 CrossRef.
- W. T. Coffey and Y. P. Kalmykov, Thermal fluctuations of magnetic nanoparticles: fifty years after brown, J. Appl. Phys., 2012, 112, 121301 CrossRef.
- R. W. Chantrell, J. Popplewell and S. W. Charles, Measurements of particle size distribution parameters in ferrofluids, IEEE Trans. Magn., 1978, 14(5), 975–977 CrossRef.
- A. N. Tikhonov and V. Y. Arsenin, Solutions of Ill-Posed Problems, Wiley, New York, 1977 Search PubMed.
- T. Weser and K. Stierstadt, Discrete Particle Size Distribution in Ferrofluids, Z. Phys. B: Condens. Matter, 1985, 59, 253–256 CrossRef CAS.
- J. P. Embs, S. May, C. Wagner, A. V. Kityk, A. Leschhorn and M. Lücke, Measuring the transverse magnetization of rotating ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 036302 CrossRef CAS PubMed.
- A. O. Ivanov, S. S. Kantorovich, E. N. Reznikov, C. Holm, A. F. Pshenichnikov, A. V. Lebedev, A. Chremos and P. J. Camp, Magnetic properties of polydisperse ferrofluids: A critical comparison between experiment, theory, and computer simulation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061405 CrossRef PubMed.
- B. Huke and M. Lucke, Magnetic properties of colloidal suspensions of interacting magnetic particles, Rep. Prog. Phys., 2004, 67, 1731–1768 CrossRef CAS.
- A. O. Ivanov and O. B. Kuznetsova, Magnetic properties of dense ferrofluids: An influence of interparticle correlations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041405 CrossRef CAS PubMed.
- Y. A. Buyevich and A. O. Ivanov, Phys. A, 1992, 190, 276 CrossRef CAS.
- I. Szalai and S. Dietrich, Magnetization and susceptibility of ferrofluids, J. Phys.: Condens. Matter, 2008, 20, 204122 CrossRef CAS PubMed.
- V. Russier and M. Douzi, On the Utilization of the Stockmayer Model for Ferrocolloids: Phase Transition at Zero External Field, J. Colloid Interface Sci., 1994, 162, 356–371 CrossRef CAS.
- P. Debye, Einige Resultate einer kinetischen Theorie der Isolatoren, Z. Phys., 1912, 13, 97 CAS.
- K. Sano and M. Doi, Theory of agglomeration of ferromagnetic particles in magnetic fluids, J. Phys. Soc. Jpn., 1983, 52, 2810–2815 CrossRef CAS.
- G. A. R. Martin, A. Bradbury and R. W. Chantrell, J. Magn. Magn. Mater., 1987, 65, 177 CrossRef.
- K. I. Morozov and A. V. Lebedev, The effect of magneto-dipole interactions on the magnetization curves of ferrocolloids, J. Magn. Magn. Mater., 1990, 85, 51 CrossRef CAS.
- S. Klapp and F. Forstmann, Phase behavior of dipolar hard spheres: integral equations and density functional results, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 3183 CrossRef CAS PubMed.
- P. I. Teixeira and M. M. Telo da Gama, J. Phys.: Condens. Matter, 1991, 3, 111 CrossRef CAS.
- P. Frodl and S. Dietrich, Bulk and interfacial properties of polar and molecular fluids, Phys. Rev. A, 1992, 45, 7330 CrossRef CAS PubMed.
- B. Groh and S. Dietrich, Ferroelectric phase in Stockmayer fluids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 3814 CrossRef CAS PubMed.
- B. Groh and S. Dietrich, Structural and thermal properties of orientationally ordered dipolar fluids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 2509 CrossRef CAS PubMed.
- I. Szalai and S. Dietrich, Eur. Phys. J. E, 2009, 28, 347 CrossRef CAS PubMed.
- A. O. Ivanov, Magnetostatic properties of moderately concentrated ferrocolloids, Magnetohydrodynamics, 1992, 28(4), 353–359 Search PubMed.
- L. Vekas, M. Rasa and D. Bica, Physical properties of magnetic fluids and nanoparticles from magnetic and magneto-rheological measurements, J. Colloid Interface Sci., 2000, 231(2), 207–405 CrossRef PubMed.
- M. S. Wertheim, Exact Solution of the Mean Spherical Model for Fluids of Hard Spheres with Permanent Electric Dipole Moments, J. Chem. Phys., 1971, 55, 4291, DOI:10.1063/1.1676751.
- A. O. Ivanov and O. B. Kuznetsova, Magnetogranulometric analysis of ferrocolloids: Second-order modified mean field theory, Colloid J., 2006, 68, 430 CrossRef CAS.
- A. F. Pshenichnikov, V. V. Mekhonoshin and A. V. Lebedev, Magneto-granulometric analysis of concentrated ferrocolloids, J. Magn. Magn. Mater., 1996, 161, 94–102 CrossRef CAS.
- G. A. van Ewijk, G. J. Vroege and A. P. Philipse, Susceptibility measurements on a fractionated aggregate-free ferrofluid, J. Phys.: Condens. Matter, 2002, 14, 4915–4925 CrossRef CAS.
- P. Langevin, Magnétisme et théorie des electrons, Ann. Chim. Phys., 1905, 5, 70–127 Search PubMed.
- D. Jiles, Introduction to Magnetism and Magnetic Materials, Springer-Science+Business Media, B.V., 1991, p. 440 Search PubMed.
- L. Onsager, Electric moments of molecules in liquids, J. Am. Chem. Soc., 1936, 58, 1486 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1939, 7, 911 CrossRef CAS.
- P. J. Weiss, Hypothesis of the molecular field and ferromagnetic properties, J. Phys. Radium, 1907, 4, 661 Search PubMed.
- I. Szalai, K.-Y. Chan and D. Henderson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 8846 CrossRef CAS PubMed.
- G. S. Rushbrooke, Mol. Phys., 1979, 37, 761 CrossRef CAS.
- M. S. Wertheim, Exact Solution of the Mean Spherical Model for Fluids of Hard Spheres with Permanent Electric Dipole Moments, J. Chem. Phys., 1971, 55, 4291, DOI:10.1063/1.1676751.
- B. Huke and M. Lucke, Magnetization of ferrofluids with dipolar interactions: A Born–Mayer expansion, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62(5), 6875–6890 CrossRef CAS PubMed.
- B. Huke and M. Lucke, Magnetization of concentrated polydisperse ferrofluids: cluster expansion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051403 CrossRef CAS PubMed.
- I. Szalai, S. Nagy and S. Dietrich, Comparison between theory and simulations for the magnetization and the susceptibility of polydisperse ferrofluids, J. Phys.: Condens. Matter, 2013, 25, 465108 CrossRef CAS PubMed.
- I. Szalai and S. Dietrich, Magnetization of multicomponent ferrofluids, J. Phys.: Condens. Matter, 2011, 23, 326004 CrossRef CAS PubMed.
- A. Tari, J. Popplewell and S. Charles, Observation of spin glass behaviour in ferrofluids, J. Magn. Magn. Mater., 1980, 15, 1125 CrossRef.
- A V. Lebedev, Low-temperature magnetic fluid stabilized with mixed fatty acids, Colloid J., 2010, 72(6), 815–819 CrossRef CAS.
- S. Kantorovich, A. O. Ivanov, L. Rovigatti, J. M. Tavares and F. Sciortino, Nonmonotonic Magnetic Susceptibility of Dipolar Hard-Spheres at Low Temperature and Density, Phys. Rev. Lett., 2013, 110, 148306 CrossRef PubMed.
- A. Y. Solovyova, O. A. Goldina, A. O. Ivanov, A. V. Lebedev and E. A. Elfimova, The initial magnetic susceptibility of polydisperse ferrofluids: A comparison between experiment and theory over a wide range of concentration, J. Chem. Phys., 2016, 145, 084909, DOI:10.1063/1.4961405.
- A. O. Ivanov and E. A. Elfimova, Low-temperature magnetic susceptibility of concentrated ferrofluids: The influence of polydispersity, J. Magn. Magn. Mater., 2015, 374, 327–332 CrossRef CAS.
- F. Vereda, J. de Vicente and R. Hidalgo-Alvarez, Physical properties of elongated magnetic particles: Magnetization and friction coefficient anisotropies, ChemPhysChem, 2009, 10(8), 1165 CrossRef CAS PubMed.
- A. P. Philipse, M. P. B. van Bruggen and C. Pathmamanoharan, Magnetic silica dispersions: preparation and stability of surface-modified silica particles with a magnetic core, Langmuir, 1994, 10, 92 CrossRef CAS.
- K. L. Krycka, R. A. Booth, C. R. Hogg, Y. Ijiri, J. A. Borchers, W. C. Chen, S. M. Watson, M. Laver, T. R. Gentile, L. R. Dedon, S. Harris, J. J. Rhyne and S. A. Majetich, Core-Shell Magnetic Morphology of Structurally Uniform Magnetite Nanoparticles, Phys. Rev. Lett., 2010, 104, 207203 CrossRef CAS PubMed.
- G. Steinbach, D. Nissen, M. Albrecht, E. Novak, P. Sanchez, S. Kantorovich, S. Gemming and A. Erbs, Bistable self-assembly in homogeneous colloidal systems for flexible modular architectures, Soft Matter, 2016, 12, 2737–2743 RSC.
- E. V. Novak and S. S. Kantorovich, Self-assembly of colloids with magnetic caps, J. Magn. Magn. Mater., 2017, 431, 214–217 CrossRef CAS.
- J. G. Donaldson, E. S. Pyanzina and S. S. Kantorovich, Nanoparticle Shape Influences the Magnetic Response of Ferro-Colloids, ACS Nano, 2017, 11, 8153–8166, DOI:10.1021/acsnano.7b03064.
- J. G. Donaldson, P. Linse and S. S. Kantorovich, How cube-like must magnetic nanoparticles be to modify their self-assembly?, Nanoscale, 2017, 9, 6448, 10.1039/C7NR01245D.
- S. Kantorovich, R. Weeber, J. J. Cerda and C. Holm, Ferrofluids with shifted dipoles: ground state structures, Soft Matter, 2011, 7(11), 5217–5227 RSC.
- M. Klinkigt, R. Weeber, S. Kantorovich and C. Holm, Cluster formation in systems of shifted-dipole particles, Soft Matter, 2013, 9, 3535–3546 RSC.
- R. Weeber, M. Klinkigt, S. Kantorovich and C. Holm, Microstructure and magnetic properties of magnetic fluids consisting of shifted dipole particles under the influence of an external magnetic field, J. Chem. Phys., 2013, 139, 214901 CrossRef PubMed.
- L. Rossi, V. Sonia, D. J. Ashton, D. J. Pine, A. P. Philipse, P. M. Chaikin, M. Dijkstra, S. Sacanna and W. T. M. Irvine, Shape-sensitive crystallization in colloidal superball fluids, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(17), 5286–5290 CrossRef CAS PubMed.
- M. A. Salvador, A. S. Costa, M. Gaeti, L. P. Mendes, E. M. Lima, A. F. Bakuzis and R. Miotto, Characterization, nanoparticle self-organization, and Monte Carlo simulation of magnetoliposomes, Phys. Rev. E, 2016, 93, 022609 CrossRef PubMed.
- V. Socoliuc, D. Bica and L. Vekas, Estimation of Magnetic Particle Clustering in Magnetic Fluids from Static Magnetization Experiments, J. Colloid Interface Sci., 2003, 264(1), 141–147 CrossRef CAS PubMed.
- I. Szalai, S. Nagy and S. Dietrich, Linear and nonlinear magnetic properties of ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042314 CrossRef CAS PubMed.
- V. Socoliuc and C. N. Marin, The effect of long time exposure to light of a water-based ferrofluid on its low frequency complex magnetic permeability, J. Magn. Magn. Mater., 2021, 523, 167635 CrossRef CAS.
- M. I. Shliomis and V. I. Stepanov, Theory of dynamic susceptibility of magnetic fluids, in: Relaxation Phenomena in Condensed Matter (Ed. W.T. Coffey), Adv. Chem. Phys., 1994, 87, 1–30 CAS.
- W. T. Coffey, Yu.P. Kalmykov and S. V. Titov, Itinerant Oscillator Models of Fluids, Adv. Chem. Phys., 2003, 126, 131–186 CrossRef CAS.
- C. Scherer and H.-G. Matuttis, Rotational dynamics of magnetic particles in suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 011504 CrossRef PubMed.
- P. C. Fannin, Magnetic Spectroscopy as an Aide in Understanding Magnetic Fluids, in Ferrofluids. Magnetically Controllable Fluids and Their Applications, Lecture Notes in Physics, ed. S. Odenbach, Springer Verlag, 2002, vol. 594, pp. 19–32 Search PubMed.
- P. C. Fannin and W. T. Coffey, contribution of particle inertia effects to resonance in ferrofluids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 6129–6140 CrossRef CAS PubMed.
- M. A. Martsenyuk, Y. L. Raikher and M. I. Shliomis, Kinetics of magnetization of suspensions of ferromagnetic particles, Sov. Phys. JETP, 1974, 38, 413 Search PubMed.
- K. Wu, R. Saha, D. Su, V. D. Krishna, J. Liu, M. C.-J. Cheeran and J.-P. Wang, Magnetic-Nanosensor-Based Virus and Pathogen Detection Strategies before and during COVID-19, ACS Appl. Nano Mater., 2020, 3(10), 9560–9580 CrossRef CAS.
- A. O. Ivanov, V. S. Zverev and S. S. Kantorovich, Revealing the signature of dipolar interactions in dynamic spectra of polydisperse magnetic nanoparticles, Soft Matter, 2016, 12, 3507–3513 RSC.
- J. I. Sindt, P. J. Camp, S. S. Kantorovic, E. A. Elfimova and A. O. Ivanov, Influence of dipolar interactions on the magnetic susceptibility spectra of ferrofluids, Phys. Rev. E, 2016, 93, 063117 CrossRef PubMed.
- A. O. Ivanov, S. S. Kantorovich, E. A. Elfimova, V. S. Zverev, J. O. Sindt and P. J. Camp, The influence of interparticle correlations and self-assembly on the dynamic initial magnetic susceptibility spectra of ferrofluids, J. Magn. Magn. Mater., 2017, 431, 141–144 CrossRef CAS.
- P. Ilg and M. Kroger, Dynamics of interacting magnetic nanoparticles: effective behavior from competition between Brownian and Néel relaxation, Phys. Chem. Chem. Phys., 2020, 22, 22244–22259 RSC.
- P. W. Goodwill, E. U. Saritas, L. R. Croft, T. N. Kim, K. M. Krishnan, D. V. Schaffer and S. M. Conolly, X-space MPI: magnetic nanoparticles for safe medical imaging, Adv. Mater., 2012, 24, 3870–3877 CrossRef CAS PubMed.
- A. Rivera-Rodriguez and C. M. Rinaldi-Ramos, Emerging Biomedical Applications Based on the Response of Magnetic Nanoparticles to Time-Varying Magnetic Fields, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 163–185 CrossRef CAS PubMed.
- J. Rahmer, A. Halkola, B. Gleich, I. Schmale and J. Borgert, First experimental evidence of the feasibility of multi-color magnetic particle imaging, Phys. Med. Biol., 2015, 60, 1775–1791 CrossRef CAS PubMed.
- S. B. Trisnanto and Y. Kitamoto, Field-dependent Brownian relaxation dynamics of a superparamagnetic clustered-particle suspension, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032306 CrossRef CAS PubMed.
- D. Eberbeck, F. Wiekhorst, U. Steinhoff and L. Trahms, Aggregation behaviour of magnetic nanoparticle suspensions investigated by magnetorelaxometry, J. Phys.: Condens. Matter, 2006, 18(38), S2829–S2846 CrossRef CAS.
- C. Ravikumar, S. Kumar and R. Bandyopadhyaya, Aggregation of dextran coated magnetic nanoparticles in aqueous medium: Experiments and Monte Carlo simulation, Colloids Surf., A, 2012, 403, 1–6 CrossRef CAS.
- K. S. Cole and R. H. Cole, Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics, J. Chem. Phys., 1941, 9, 341, DOI:10.1063/1.1750906.
- D. W. Davidson and R. H. Cole, Dielectric Relaxation in Glycerol, Propylene Glycol, and n–Propanol, J. Chem. Phys., 1951, 19, 1484, DOI:10.1063/1.1748105.
- S. K. Trisnanto and Y. Takemura, Effective Néel relaxation time constant and intrinsic dipolar magnetism in a multicore magnetic nanoparticle system, J. Appl. Phys., 2021, 130, 064302 CrossRef CAS.
- F. Brochard and P. G. de Gennes, Theory of magnetic suspensions in liquid crystals, J. Phys., 1970, 31, 691–708 CrossRef CAS.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Novel Colloidal Interactions in Anisotropic Fluids, Science, 1997, 275(5307), 1770–1773, DOI:10.1126/science.275.5307.1770.
- P. Kopcansky, N. Tomašovičová, M. Koneracká, V. Závišová, M. Timko, A. Džarová, A. Šprincová, N. Éber, K. Fodor-Csorba, T. Tóth-Katona, A. Vajda and J. Jadzyn, Structural changes in the 6CHBT liquid crystal doped with spherical, rodlike, and chainlike magnetic particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011702 CrossRef PubMed.
- P. Kopcansky, N. Tomasovicova, M. Koneracka, V. Zavisova, M. Timko, M. Hnatic, N. Eber, T. Toth-Katona, J. Jadzyn, J. Honkonen, E. Beaugnon and X. Chaud, Magnetic-Field Induced Isotropic to Nematic Phase Transition in Ferronematics, IEEE Trans. Magn., 2011, 47(10), 4409–4412 CAS.
- A. Mertelj, D. Lisjak, M. Drofenik and M. Copic, Ferromagnetism in suspensions of magnetic platelets in liquid crystal, Nature, 2013, 504, 237–241 CrossRef CAS PubMed.
- A. Mertelj, B. Lampret, D. Lisjak, J. Klepp, J. Kohlbrecher and M. Čopič, Evolution of nematic and ferromagnetic ordering in suspensions of magnetic nanoplatelets, Soft Matter, 2019, 15, 5412–5420 RSC.
- M. Shuai, A. Klittnick, Y. Shen, G. P. Smith, M. R. Tuchband, C. Zhu, R. G. Petschek, A. Mertelj, D. Lisjak, M. Copic, J. E. Maclennan, M. A. Glaser and N. A. Clark, Spontaneous liquid crystal and ferromagnetic ordering of colloidal magnetic nanoplates, Nat. Commun., 2016, 7, 10394 CrossRef CAS PubMed.
- M. Cui, T. Emrick and T. P. Russell, Stabilizing Liquid Drops in Nonequilibrium Shapes by the Interfacial Jamming of Nanoparticles, Science, 2013, 342, 460–463 CrossRef CAS PubMed.
- X. Liu, N. Kent, A. Ceballos, R. Streubel, Y. Jiang, Y. Chai, P. Y. Kim, J. Forth, F. Hellman, S. Shi, D. Wang, B. A. Helms, P. D. Ashby, P. Fischer and T. P. Russell, Reconfigurable ferromagnetic liquid droplets, Science, 2019, 365, 264–267 CrossRef CAS PubMed.
- R. Streubel, X. Liu, X. Wu and T. P. Russell, Perspective: Ferromagnetic Liquids, Materials, 2020, 13, 2712 CrossRef CAS PubMed.
- X. Wu, R. Streubel, X. Liu, P. Y. Kim, Y. Chai, Q. Hu, D. Wang, P. Fischer and T. P. Russell, Ferromagnetic liquid droplets with adjustable magnetic properties, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(8), e2017355118 CrossRef CAS PubMed.
- J. P. McTague, Magnetoviscosity of Magnetic Colloids, J. Chem. Phys., 1969, 51, 133 CrossRef CAS.
- W. F. Hall and S. N. Busenberg, Viscosity of Magnetic Suspensions, J. Chem. Phys., 1969, 51, 137 CrossRef CAS.
- M. I. Shliomis, Effective Viscosity of Magnetic Suspensions, Sov. Phys. JETP, 1972, 34, 1291–1294 Search PubMed.
- M. I. Shliomis and K. I. Morozov, Negative viscosity of ferrofluid under alternating magnetic field, Phys. Fluids, 1994, 6, 2855–2861 CrossRef CAS.
- S. Odenbach, Magnetoviscous and viscoelastic effects in ferrofluids, Int. J. Mod. Phys. B, 2000, 14(16), 1615–1631 CrossRef CAS.
- R. Patel, R. V. Upadhyay and R. V. Mehta, Viscosity measurements of a ferrofluid: comparison with various hydrodynamic equations, J. Colloid Interface Sci., 2003, 263(2), 661–664 CrossRef CAS PubMed.
- M. I. Shliomis, Ferrohydrodynamics: Testing a third magnetization equation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 060501(R) CrossRef PubMed.
- R. E. Rosensweig, R. Kaiser and G. Miskolczy, Viscosity of magnetic fluid in a magnetic field, J. Colloid Interface Sci., 1969, 29, 680–686 CrossRef CAS.
- O. Ambacher, S. Odenbach and K. Stierstadt, Rotational viscosity in ferrofluids, Z. Phys. B: Condens. Matter, 1992, 86, 29–32 CrossRef.
- S. Odenbach, Magnetoviscous Effects in Ferrofluids. Lecture Notes in Physics m71, Springer-Verlags, Berlin, Heidelberg, New York, 2002, p. 151 Search PubMed.
- S. Odenbach, Recent progress in magnetic fluid research, J. Phys.: Condens. Matter, 2004, 16, R1135–R1150 CrossRef CAS.
- J.-C. Bacri and D. Salin, First-order transition in the instability of a magnetic fluid interface, J. Phys., Lett., 1984, 45(11), 559–564 CrossRef.
- J.-C. Bacri and R. Perzynski, Optical properties of magnetic fluids, in Magnetic fluids and applications Handbook, ed. B. Berkovski and V. Bashtovoy, Begell House Inc., New York-Wallingford, 1996, pp. 79–129 Search PubMed.
- S. Odenbach, Microstructure and rheology of magnetic hybrid materials, Arch. Appl. Mech., 2016, 86, 269–279 CrossRef.
- S. Thurm and S. Odenbach, Particle size distribution as key parameter for the flow behavior of ferrofluids, Phys. Fluids, 2003, 15, 1658 CrossRef CAS.
- P. Ilg, M. Kröger and S. Hess, Magnetoviscosity of semidilute ferrofluids and the role of dipolar interactions: Comparison of molecular simulations and dynamical mean-field theory, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 031205 CrossRef PubMed.
- P. Ilg, E. Coquelle and S. Hess, Structure and rheology of ferrofluids: simulation results and kinetic models, J. Phys.: Condens. Matter, 2006, 18, S2757–S2770 CrossRef CAS.
- S. Odenbach and K. Raj, The influence of large particles and agglomerates on the magnetoviscous effect in ferrofluids, Magnetohydrodynamics, 2000, 36(4), 379–386 CrossRef.
- A. Satoh, R. W. Chantrell, G. F. Coverdale and S. Kamiyama, Stokesian Dynamics Simulations of Ferromagnetic Colloidal Dispersions in a Simple Shear Flow, J. Colloid Interface Sci., 1998, 203(2), 233–248 CrossRef CAS PubMed.
- R. Y. Hong, A. Q. Ren, Y. P. Han, H. Z. Li, Y. Zheng and J. Ding, Rheological properties of water-based Fe3O4 ferrofluids, Chem. Eng. Sci., 2007, 62, 5912–5924 CrossRef CAS.
- H. Shahnazian and S. Odenbach, Rheological investigations of ferrofluids with a shear stress controlled rheometer, J. Colloid Interface Sci., 2008, 20, 204137 Search PubMed.
- S. S. Kantorovich, Chain aggregate structure in polydisperse ferrofluids: different applications, J. Magn. Magn. Mater., 2005, 289, 203–205 CrossRef CAS.
- E. Siebert, V. Dupuis, S. Neveu and S. Odenbach, Rheological investigations on the theoretical predicted “Poisoning” effect in bidisperse ferrofluids, J. Magn. Magn. Mater., 2015, 374, 44–49 CrossRef CAS.
- M. Kroger, P. Ilg and S. Hess, Magnetoviscous model fluids, J. Phys.: Condens. Matter, 2003, 15, S1403–S1423 CrossRef CAS.
- M. Gerth-Noritzsch, D. Y. Borin and S. Odenbach, Anisotropy of the magnetoviscous effect in ferrofluids containing nanoparticles exhibiting magnetic dipole interaction, J. Phys.: Condens. Matter, 2011, 23(34), 346002 CrossRef CAS PubMed.
- J. M. Linke and S. Odenbach, Anisotropy of the magnetoviscous effect in a ferrofluid with weakly interacting magnetite nanoparticles, J. Phys.: Condens. Matter, 2015, 27, 176001 CrossRef CAS PubMed.
- L. M. Pop, S. Odenbach, A. Wiedenmann, N. Matoussevitch and H. Bönnemann, Microstructure and rheology of ferrofluids, J. Magn. Magn. Mater., 2005, 289, 303–306 CrossRef CAS.
- S. Behrens, H. Bönnemann, N. Matoussevitch, A. Gorschinski, E. Dinjus, W. Habicht, J. Bolle, S. Zinoveva, N. Palina, J. Hormes, H. Modrow, S. Bahr and V. Kempter, Surface engineering of Co and FeCo nanoparticles for biomedical application, J. Phys.: Condens. Matter, 2006, 18, S2543–S2561 CrossRef CAS.
- D. Y. Borin and S. Odenbach, Magnetic measurements on frozen ferrofluids as a method for estimating the magnetoviscous effect, J. Phys.: Condens. Matter, 2009, 21, 246002 CrossRef PubMed.
- D. Borin, A. Zubarev, D. Chirikov, R. Müller and S. Odenbach, Ferrofluid with clustered iron nanoparticles: Slow relaxation of rheological properties under joint action of shear flow and magnetic field, J. Magn. Magn. Mater., 2011, 323(10), 1273–1277 CrossRef CAS.
- D. Y. Borin, V. V. Korolev, A. G. Ramazanova, S. Odenbach, O. A. Balmasova, V. I. Yashkova and D. V. Korolev, Magnetoviscous effect in ferrofluids with different dispersion media, J. Magn. Magn. Mater., 2016, 416, 110–116 CrossRef CAS.
- D. I. Santiago-Quinones, K. Raj and C. Rinaldi, A comparison of the magnetorheology of two ferrofluids with different magnetic field-dependent chaining behavior, Rheol. Acta, 2013, 52, 719–726 CrossRef CAS.
- K. I. Morozov and M. I. Shliomis, Magnetic fluid as an assembly of flexible chains, Lecture Notes in Physics, Springer-Verlag, 2002, vol. 594, pp. 162–184 Search PubMed.
- K. I. Morozov and M. I. Shliomis, Ferrofluids: flexibility of magnetic particle chains, J. Phys.: Condens. Matter, 2004, 16, 3807–3818 CrossRef CAS.
- A. Yu Zubarev, Statistical physics on non-dilute ferrofluids, Lecture Notes in Physics, Springer-Verlag, 2002, vol. 594, pp. 143–161 Search PubMed.
- O. Muller, D. Hahn and M. Liu, Non-Newtonian behaviour in ferrofluids and magnetization relaxation, J. Phys.: Condens. Matter, 2006, 18, S2623–S2632 CrossRef.
- A. Y. Zubarev and L. Y. Iskakova, Rheological properties of ferrofluids with drop-like aggregates, Phys. A, 2007, 37, 38–50 CrossRef.
- D. N. Chirikov, S. P. Fedotov, L. Y. Iskakova and A. Y. Zubarev, Viscoelastic properties of ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051405 CrossRef CAS PubMed.
- A. Y. Zubarev and L. Y. Iskakova, Effect of chainlike aggregates on dynamical properties of magnetic liquids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5415 CrossRef CAS.
- K. Weissenberg, A continuum theory of rheological phenomena, Nature, 1947, 159, 310–311 CrossRef CAS PubMed.
- S. Odenbach, T. Rylewicz and H. Rath, Investigation of the Weissenberg effect in suspensions of magnetic nanoparticles, Phys. Fluids, 1999, 11(10), 2901–2905 CrossRef CAS.
- C. Balan, D. Broboana, E. Gheorghiu and L. Vekas, Rheological characterization of complex fluids in electro-magnetic fields, J. Non-Newtonian Fluid Mech., 2008, 154, 22–30 CrossRef CAS.
- D. Borin and S. Odenbach, Rheology of novel ferrofluids, Int. J. Mod. Phys. B, 2011, 25, 963 CrossRef CAS.
- D. Y. Borin, A. Y. Zubarev, D. N. Chirikov and S. Odenbach, Stress relaxation in a ferrofluid with clustered nanoparticles, J. Phys.: Condens. Matter, 2014, 26, 406002 CrossRef PubMed.
- A. Y. Zubarev and L. Y. Iskakova, Rheological properties of ferrofluids with microstructures, J. Phys.: Condens. Matter, 2006, 18, S2771–S2784 CrossRef CAS.
- D. Susan-Resiga, V. Socoliuc, A. Bunge, R. Turcu and L. Vekas, From high colloidal stability ferrofluids to magnetorheological fluids: tuning the flow behavior by magnetite nanoclusters, Smart Mater. Struct., 2019, 28, 115014 CrossRef CAS.
- D. Zablotsky, S. Kralj and M. M. Maiorov, Features of magnetorheology of biocompatible chain-forming ferrofluids with multi-core magnetic nanoparticles: Experiment and simulation, Colloids Surf., A, 2020, 603, 125079 CrossRef CAS.
- R. E. Rosensweig, “Negative viscosity” in a magnetic fluid, Science, 1996, 271, 614–615 CrossRef CAS.
- F. Gazeau, C. Baravian, J.-C. Bacri, R. Perzynski and M. I. Shliomis, Energy conversion in ferrofluids: Magnetic nanoparticles as motors or generators, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 614 CrossRef CAS.
- H. W. Muller and M. Liu, Structure of ferrofluid dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061405 CrossRef CAS PubMed.
- H. W. Muller and M. Liu, Ferrofluid Dynamics, in Ferrofluids. Lecture Notes in Physics, ed. S. Odenbach, Springer, Berlin, Heidelberg, 2002, vol. 594, pp. 112–123 Search PubMed.
- H. W. Muller and A. Engel, Dissipation in ferrofluids: Mesoscopic versus hydrodynamic theory, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60(6), 7001–7009 CrossRef CAS PubMed.
- J.-C. Bacri, R. Perzynski, M. I. Shliomis and G. I. Burde, “Negative – viscosity” effect in a magnetic fluid, Phys. Rev. Lett., 1995, 75, 2128–2131 CrossRef PubMed.
- A. P. Krekhov, M. I. Shliomis and S. Kamiyama, Ferrofluid pipe flow in an oscillating magnetic field, Phys. Fluids, 2005, 17, 033105 CrossRef.
- A. Perez-Madrid, T. Alarcón, J. M. G. Vilar and J. M. Rubi, A mesoscopic approach to the “negative” viscosity effect in ferrofluids, Phys. A, 1999, 270(3–4), 403–412 CrossRef.
- C. Rinaldi, F. Gutman, X. A. D. He, A. D. Rosenthal and M. Zahn, Torque measurements on ferrofluid cylinders in rotating magnetic fields, J. Magn. Magn. Mater., 2005, 289, 307 CrossRef CAS.
- J. H. Sanchez and C. Rinaldi, Magnetoviscosity of dilute magnetic fluids in oscillating and rotating magnetic fields, Phys. Fluids, 2010, 22, 043304 CrossRef.
- R. E. Rosensweig, Directions in ferrohydrodynamics, J. Appl. Phys., 1985, 57, 4259 CrossRef.
- R. E. Rosensweig, Magnetic fluids, Annu. Rev. Fluid Mech., 1987, 19, 437–453 CrossRef.
- R. E. Rosensweig, Continuum equations for magnetic and dielectric fluids with internal rotations, J. Chem. Phys., 2004, 121, 1228 CrossRef CAS PubMed.
- K. Stierstadt and M. Liu, Maxwell's stress tensor and the forces in magnetic liquids, Z. Angew. Math. Mech., 2014, 1–34 Search PubMed.
- T. B. Jones, Theory and application of ferrofluid seals, in Thermomechanics of magnetic fluids, ed. B. Berkovsky, Hemisphere, Washington DC, 1978, pp. 255–298 Search PubMed.
- T. John, M. May and R. Stannarius, Meniscus of a ferrofluid around a vertical cylindrical wire carrying electrical current, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 056308 CrossRef PubMed.
- P.-B. Eissmann, A. Lange and S. Odenbach, Meniscus of a magnetic fluid in the field of a current-carrying wire: two-dimensional numerical simulations, Magnetohydrodynamics, 2011, 47(2), 149–157 CrossRef.
- R. E. Rosensweig, Buoyancy and stable levitation of a magnetic body immersed in a magneti zable fluid, Nature, 1966, 210(5036), 613–614 CrossRef.
- S. Earnshaw, On the nature of the molecular forces which regulate the constitution of the luminferous ether, Trans. Cambridge Philos. Soc., 1842, 7, 97–112 Search PubMed.
- R. E. Zelazo and J. R. Melcher, Dynamics and stability of ferrofluids: surface interactions, J. Fluid Mech., 1969, 39, 1 CrossRef CAS.
- J.-P. Brancher, Interfacial instability in viscous ferrofluids, IEEE Trans. Magn., 1980, 16, 1331 CrossRef.
- D. Salin, Wave vector selection in the instability of an interface in a magnetic or electric field, Europhys. Lett., 1993, 21, 667 CrossRef.
- B. Abou, G. Neron de Surgy and J.-E. Wesfreid, Dispersion relation in a ferrofluid layer of any thickness and viscosity, J. Phys. II, 1997, 7, 1159 CrossRef CAS.
- A. Gailitis, Formation of the hexagonal pattern on the surface of a ferromagnetic fluid in an applied magnetic field, J. Fluid Mech., 1977, 82, 401 CrossRef.
- D. Allais and J.-E. Wesfreid, Instabilite de surface dans les ferrofluides, Bull. Soc. Geol. Fr., Suppl., 1985, 57, 20 Search PubMed.
- V. G. Bashtovoy, B. M. Berkovsky and A. N. Vislovich, Introduction to Thermomechanics of Magnetic Fluids, Hemisphere, Washington, 1988 Search PubMed.
- A. G. Boudouvis, J. L. Puchalla, L. E. Scriven and R. E. Rosensweig, Normal field instability and patterns in pools of ferrofluid, J. Magn. Magn. Mater., 1987, 65, 307 CrossRef.
- M. Silber and E. Knobloch, Pattern selection in ferrofluids, Phys. D, 1988, 30(1–2), 83–98 CrossRef.
- F. Elias, C. Flament, J.-C. Bacri and S. Neveu, Macro-Organized Patterns in Ferrofluid Layer: Experimental Studies, J. Phys. I, 1997, 7(5), 711–728 CrossRef CAS.
- T. Mahr and I. Rehberg, Nonlinear dynamics of a single ferrofluid-peak in an oscillating magnetic field, Phys. D, 1998, 111(1), 335–346 CrossRef CAS.
- B. Abou, J.-E. Wesfried and S. Roux, The normal field instability in ferrofluids: hexagon–square transition mechanism and wavenumber selection, J. Fluid Mech., 2000, 416, 217–237 CrossRef CAS.
- R. Friedrichs and A. Engel, Pattern and wave number selection in magnetic fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021406 CrossRef CAS PubMed.
- R. Richter and I. Barashenkov, Two-dimensional solitons on the surface of magnetic fluids, Phys. Rev. Lett., 2005, 94, 184503 CrossRef PubMed.
- R. Richter and J. Blasing, Measuring surface deformations in magnetic fluid by radioscopy, Rev. Sci. Instrum., 2001, 72, 1729 CrossRef CAS.
- C. Gollwitzer, G. Matthies, R. Richter, I. Rehberg and L. Tobiska, The Surface Topography of a Magnetic Fluid-a Quantitative Comparison between Experiment and Numerical Simulation, J. Fluid Mech., 2007, 571, 455–474 CrossRef.
- R. Richter and A. Lange, Surface instabilities of ferrofluids, in Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids, Lecture Notes in Physics, ed. S. Odenbach, Springer Berlin Heidelberg, 2009, vol. 763, pp. 157–247 Search PubMed.
- H. Herrero, C. Perez-Garcıa and M. Bestehorn, Stability of fronts separating domains with different symmetries in hydrodynamical instabilities, Chaos, 1994, 4, 15 CrossRef PubMed.
- C. Kubstrup, H. Herrero and C. Perez-Garcıa, Fronts between hexagons and squares in a generalized Swift–Hohenberg equation, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 1560 CrossRef CAS PubMed.
- J. Weilepp and H. R. Brand, Competition between the Bénard-Marangoni and the Rosensweig Instability in Magnetic Fluids, J. Phys. II, 1996, 6, 419–441 CrossRef CAS.
- T. Y. Chong, K. L. Ho and B. H. Ong, Investigations of field instability of ferrofluid in hypergravity and microgravity, AIP Adv., 2012, 2, 012138 CrossRef.
- H. Knieling, R. Richter, I. Rehberg, G. Matthies and A. Lange, Growth of surface undulations at the Rosensweig instability, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 066301 CrossRef PubMed.
- M. D. Groves, D. J. B. Lloyd and A. Stylianou, Pattern formation on the free surface of a ferrofluid: spatial dynamics and homoclinic bifurcation, Phys. D, 2017, 350, 1–12 CrossRef.
- A. Lange, B. Reimann and R. Richter, Wave number of maximal growth in viscous magnetic fluids of arbitrary depth, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5528 CrossRef CAS PubMed.
- A. Lange, Scaling behaviour of the maximal growth rate in the Rosensweig instability, Europhys. Lett., 2001, 55, 327 CrossRef CAS.
- A. Lange, C. Gollwitzer, R. Maretzki, I. Rehberg and R. Richter, Retarding the growth of the Rosensweig instability unveils a new scaling regime, Phys. Rev. E, 2016, 93, 043106 CrossRef PubMed.
- C. Gollwitzer, I. Rehberg and R. Richter, From phase space representation to amplitude equations in a pattern-forming experiment, New J. Phys., 2010, 12, 093037 CrossRef.
- D. J. B. Lloyd, C. Gollwitzer, I. Rehberg and R. Richter, Homoclinic snaking near the surface instability of a polarisable fluid, J. Fluid Mech., 2015, 783, 283–305 CrossRef CAS.
- Y. Cao and Z. J. Ding, Formation of hexagonal pattern of ferrofluid in magnetic field, J. Magn. Magn. Mater., 2014, 355, 93–99 CrossRef CAS.
- J. Burke and E. Knobloch, Homoclinic snaking: Structure and stability, Chaos, 2007, 17, 037102 CrossRef PubMed.
- L. Huang, T. Hädrich and D. L. Michels, On the Accurate Large-scale Simulation of Ferrofluids, ACM Trans. Graph., 2019, 38(4), 93 Search PubMed.
- C. Gollwitzer, M. Krekhova, G. Lattermann, I. Rehberg and R. Richter, Surface instabilities and magnetic soft matter, Soft Matter, 2009, 5, 2093–2100 RSC.
- H. Kadau, M. Schmitt, M. Wenzel, C. Wink, T. Maier, I. Ferrier-Barbut and T. Pfau, Observing the Rosensweig instability of a quantum ferrofluid, Nature, 2016, 530, 194–197 CrossRef CAS PubMed.
- L. T. Romankiw, M. M. G. Slusarczyk and D. A. Thompson, IEEE Trans. Magn., 1975, 11, 25 CrossRef.
- A. Cebers and M. M. Maiorov, Magnetostatic instabilities in plane layers of magnetizable liquids, Magnetohydrodynamics, 1980, 16(1), 21–27 Search PubMed.
- C.-Y. Chen, W.-L. Wu and J. A. Miranda, Magnetically induced spreading and pattern selection in thin ferrofluid drops, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 056321 CrossRef PubMed.
- R. E. Rosensweig, M. Zahn and R. Shumovich, Labyrinthine instability in magnetic and dielectric fluids, J. Magn. Magn. Mater., 1983, 39(1–2), 127–132 CrossRef.
- R. Rungsawang, J. da Silva, C.-P. Wu, E. Sivaniah, A. Ionescu, C. H. W. Barnes and N. J. Darton, Magnetically Induced Pattern Formation in Phase Separating Polymer-Solvent–Nanoparticle Mixtures, Phys. Rev. Lett., 2010, 104, 255703 CrossRef PubMed.
- C.-Y. Chen, W.-K. Tsai and J. A. Miranda, Hybrid ferrohydrodynamic instability: Coexisting peak and labyrinthine patterns, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 056306 CrossRef PubMed.
- C.-Y. Chen, Y.-S. Yang and J. A. Miranda, Miscible ferrofluid patterns in a radial magnetic field, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016314 CrossRef PubMed.
- N. Wilke, J. Bugase, L.-M. Treffenstadt and T. M. Fischer, Wrinkled labyrinths in critical demixing ferrofluid, Soft Matter, 2017, 13, 7307–7307 RSC.
- E. Cerda and L. Mahadevan, Geometry and physics of wrinkling, Phys. Rev. Lett., 2003, 90, 074302 CrossRef CAS PubMed.
- A. Cebers, Stability of diffusion fronts of magnetic particles in porous media (Hele-Shaw cell) under the action of an external magnetic field, Magn. Gidrodin. 33(1), 67 (1997), Magnetohydrodynamics, 1997, 33, 48 Search PubMed.
- C.-Y. Chen and C.-Y. Wen, Numerical simulations of miscible magnetic flows in a Hele-Shaw cell. Radial flows, J. Magn. Magn. Mater., 2002, 252, 296 CrossRef CAS.
- M. Igonin and A. Cebers, Labyrinthine instability of miscible magnetic fluids, Phys. Fluids, 2003, 15, 1734, DOI:10.1063/1.1568949.
- K. Erglis, A. Tatulcenkov, G. Kitenbergs, O. Petrichenko, F. Ergin, B. Watz and A. Cebers, Magnetic field driven micro-convection in the Hele-Shaw cell, J. Fluid Mech., 2013, 714, 612 CrossRef CAS.
- M.-Y. Chen, L.-Q. Chen, H. Li and C.-Y. Wen, Labyrinthine instabilities of miscible magnetic fluids in a rotating Hele-Shaw cell, Phys. Fluids, 2017, 29, 024109 CrossRef.
- M. A. Maleki, M. Soltani, N. Kashaninejad and N.-T. Nguyen, Effects of magnetic nanoparticles on mixing in droplet-based microfluidics, Phys. Fluids, 2019, 31, 032001 CrossRef.
- W. Yang, B. Fang, B. Liu and Z. Yang, Promotion of ferrofluid microchannel flows by gradient magnetic fields, J. Non-Newtonian Fluid Mech., 2022, 300, 104730 CrossRef CAS.
- T. Cherian, F. Sohrabi, C. Rigoni, O. Ikkala and J. V. I. Timonen, Electroferrofluids with nonequilibrium voltage-controlled magnetism, diffuse interfaces, and patterns, Sci. Adv., 2021, 7, eabi8990 CrossRef CAS PubMed.
- R. Seemann, M. Brinkmann, T. Pfohl and T. Herminghaus, Droplet based microfluidics, Rep. Prog. Phys., 2012, 75(1), 016601 CrossRef PubMed.
- P. Aussillous and D. Queare, Liquid marbles, Nature, 2001, 411, 924–927 CrossRef CAS PubMed.
- D. Yamamoto, C. Nakajima, A. Shioi, M. P. Krafft and K. Yoshikawa, The evolution of spatial ordering of oil drops fast spreading on a water surface, Nat. Commun., 2015, 6, 7189 CrossRef PubMed.
- V. B. Varma, A. Ray, Z. M. Wang, Z. P. Wang and R. V. Ramanujan, Droplet Merging on a Lab-on-a Chip Platform by Uniform Magnetic Fields, Sci. Rep., 2016, 6, 37671 CrossRef CAS PubMed.
- V. I. Arkhipenko, Y. D. Barkov and V. G. Bashtovoi, Shape of a drop of magnetized fluid in a homogeneous magnetic field, Magn. Gidrodin., 1979, 14, 131–134 Search PubMed.
- J.-C. Bacri and D. Salin, Dynamics of the shape transition of a magnetic ferrofluid drop, J. Phys., Lett., 1983, 44, L-415–L-420 CrossRef.
- J. P. Brancher and D. Zouaoui, Equilibrium of a magnetic liquid drop, J. Magn. Magn. Mater., 1987, 65(2), 311–314 CrossRef.
- S. Afkhami, A. J. Tyler, Y. Renardy, M. Renardy, T. G. St. Pierre, R. C. Woodward and J. S. Riffle, Deformation of a hydrophobic ferrofluid droplet suspended in a viscous medium under uniform magnetic fields, J. Fluid Mech., 2010, 663, 358–384 CrossRef CAS.
- G.-P. Zhu, N.-T. Nguyen, R. V. Ramanujan and X.-Y. Huang, Nonlinear deformation of a ferrofluid droplet in a uniform magnetic field, Langmuir, 2011, 27(24), 14834–14841 CrossRef CAS PubMed.
- J. V. I. Timonen, M. Latikka, O. Ikkala and R. H. A. Ras, Free-decay and resonant methods for investigating the fundamental limit of superhydrophobicity, Nat. Commun., 2013, 4, 2398 CrossRef PubMed.
- J. V. I. Timonen, M. Latikka, L. Leibler, R. H. A. Ras and O. Ikkala, Switchable Static and Dynamic Self-Assembly of Magnetic Droplets on Superhydrophobic Surfaces, Science, 2013, 341, 253–257 CrossRef CAS PubMed.
- P. Rowghanian, C. D. Meinhart and O. Campàs, Dynamics of ferrofluid drop deformations under spatially uniform magnetic fields, J. Fluid Mech., 2016, 802, 245–262 CrossRef CAS.
- T. Vieu and C. Walter, Shape and fission instabilities of ferrofluids in non-uniform magnetic fields, J. Fluid Mech., 2018, 840, 455–497 CrossRef CAS.
- U. Banerjee, A. Raj and A. K. Sen, Dynamics of aqueous ferrofluid droplets at coflowing liquid-liquid interface under a nonuniform magnetic field, Appl. Phys. Lett., 2018, 113, 143702 CrossRef.
- C. Rigoni, M. Pierno, G. Mistura, D. Talbot, R. Massart, J.-C. Bacri and A. A. Abou-Hassan, Static Magnetowetting of Ferrofluid Drops, Langmuir, 2016, 32(30), 7639–7646 CrossRef CAS PubMed.
- T. Jamin, Y. Djama, J.-C. Bacri and E. Falcon, Tuning the resonant frequencies of a drop by a magnetic field, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2016, 1, 021901(R) Search PubMed.
- L. Rayleigh, On the Capillary Phenomena of Jets, Proc. R. Soc. London, 1879, 29, 71–97 CrossRef.
- N. Sahoo, G. Khurana, D. Samanta and P. Dhar, Collisional ferrohydrodynamics of magnetic fluid droplets on superhydrophobic surfaces, Phys. Fluids, 2021, 33, 012012 CrossRef CAS.
- P. Debye, Polar Molecules, The Chemical Catalogue Company, New York, 1929; reprinted by Dover Publications, New York 1945; 1960 Search PubMed.
- R. Moskowitz and R. E. Rosensweig, Nonmechanical torque driven flow of a ferromagnetic fluid by an electromagnetic field, Appl. Phys. Lett., 1967, 11(10), 301–303 CrossRef.
- S. J. Dahler and L. E. Scriven, Angular momentum of continua, Nature, 1961, 192, 36 CrossRef.
- S. J. Dahler and L. E. Scriven, Theory of structured continua. I. General considerations of angular momentum and polarization, Proc. R. Soc. London, Ser. A, 1963, 275, 504 Search PubMed.
- D. W. Condiff and J. S. Dahler, Fluid mechanical aspects of antisymmetric stress, Phys. Fluids, 1964, 69, 842–854 CrossRef.
- S. Feng, A. L. Graham, J. R. Abbott and H. Brenner, Antisymmetric stresses in suspensions: vortex viscosity and energy dissipation, J. Fluid Mech., 2006, 563, 97–122 CrossRef.
- B. A. Finlayson, Spin-up of ferrofluids: The impact of the spin viscosity and the Langevin function, Phys. Fluids, 2013, 25, 073101 CrossRef.
- I. Torres-Diaz, A. Cortes, Y. Cedeño-Mattei, O. Perales-Perez and C. Rinaldi, Flows and torques in Brownian ferrofluids subjected to rotating uniform magnetic fields in a cylindrical and annular geometry, Phys. Fluids, 2014, 26, 012004 CrossRef.
- V. N. Zaitsev and M. I. Shliomis, Entrainment of ferromagnetic suspension by rotating magnetic field, J. Appl. Mech. Tech. Phys., 1969, 10(5), 696–700 CrossRef.
- J. T. Jenkins, Some simple flows of a para-magnetic fluid, J. Phys., 1971, 32(11–12), 931–938 CrossRef.
- R. Mailfert and A. Martinet, Flow regimes for a magnetic suspension under a rotating magnetic field, J. Phys., 1973, 34(2–3), 197–201 CrossRef CAS.
- I. Y. Kagan, V. G. Rykov and E. I. Yantoovskii, Flow of a dielectric ferromagnetic suspension in a rotating magnetic field, Magnetohydrodynamics, 1973, 9, 135 Search PubMed.
- O. A. Glazov, Motion of a ferrosuspension in rotating magnetic fields, Magn. Gidrodin., 1975, 11, 16 Search PubMed.
- O. A. Glazov, Role of higher harmonics in ferrosuspension motion in a rotating magnetic field, Magn. Gidrodin., 1975, 11, 31 Search PubMed.
- G. H. Calugaru, C. Cotae, R. Badescu, V. Badescu and E. Luca, A new aspect of the movement of ferrofluids in a rotating magnetic field, Rev. Roum. Phys., 1976, 21, 439 CAS.
- I. Anton, L. Vekas, I. Potencz and E. Suciu, Ferrofluid flow under the influence of rotating magnetic fields, IEEE Trans. Magn., 1980, 16(2), 283–287 CrossRef.
- R. E. Rosensweig, J. Popplewell and R. J. Johnston, Magnetic fluid motion in rotating field, J. Magn. Magn. Mater., 1990, 85, 171 CrossRef.
- A. F. Pshenichnikov, A. V. Lebedev and M. I. Shliomis, On the rotational effect in nonuniform magnetic fluids, Magnetohydrodynamics, 2000, 36(4), 275–281 CrossRef.
- R. Krauss, B. Reimann, R. Richter, I. Rehberg and M. Liu, Fluid pumped by magnetic stress, Appl. Phys. Lett., 2005, 86, 024102 CrossRef.
- A. Chaves, I. Torres-Diaz and C. Rinaldi, Flow of ferrofluid in an annular gap in a rotating magnetic field, Phys. Fluids, 2010, 22, 092002 CrossRef.
- A. Chaves and C. Rinaldi, Interfacial stress balances in structured continua and free surface flows in ferrofluids, Phys. Fluids, 2014, 26, 042101 CrossRef.
- R. Krauss, M. Liu, B. Reimann, R. Richter and I. Rehberg, Pumping fluid by magnetic surface stress, New J. Phys., 2006, 8, 18 CrossRef.
- A. Chaves, C. Rinaldi, S. Elborai, X. He and M. Zahn, Bulk flow in ferrofluids in a uniform rotating magnetic field, Phys. Rev. Lett., 2006, 96, 194501 CrossRef CAS PubMed.
- I. Torres-Diaz, C. Rinaldi, S. Khushrushahi and M. Zahn, Observations of ferrofluid flow under a uniform rotating magnetic field in a spherical cavity, J. Appl. Phys., 2012, 111, 07B313 CrossRef.
- C. Rinaldi and M. Zahn, Effects of spin viscosity on ferrofluid flow profiles in alternating and rotating magnetic fields, Phys. Fluids, 2002, 14, 2847 CrossRef CAS.
- A. Chaves-Guerrero, V. A. Peña-Cruz, C. Rinaldi and D. Fuentes-Díaz, Spin-up flow in non-small magnetic fields: Numerical evaluation of the predictions of the common magnetization relaxation equations, Phys. Fluids, 2017, 29, 073102 CrossRef.
- M. I. Shliomis, How a rotating magnetic field causes ferrofluid to rotate, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2021, 6, 043701 Search PubMed.
- V. Soni, E. S. Bililign, S. Magkiriadou, S. Sacanna, D. Bartolo, M. J. Shelley and W. T. M. Irvine, The odd free surface flows of a colloidal chiral fluid, Nat. Phys., 2019, 15, 1188 Search PubMed.
- H. Massana-Cid, D. Levis, R. J. Hernández Hernández, I. Pagonabarraga and P. Tierno, Arrested phase separation in chiral fluids of colloidal spinners, Phys. Rev. Res., 2021, 3, L042021 Search PubMed.
- B. C. van Zuiden, J. Paulose, W. T. M. Irvine, D. Bartolo and V. Vitelli, Spatiotemporal order and emergent edge currents in active spinner materials, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(46), 12919–12924 CrossRef CAS PubMed.
- G. Bossis, O. Volkova, S. Lacis and A. Meunier, Magnetorheology: Fluids, Structures and Rheology, in Ferrofluids: Magnetically controllable fluids and their applications, Lecture Notes in Physics, ed. S. Odenbach, Springer-Verlag, 2002, vol. 594, pp. 202–232 Search PubMed.
- A. O. Cebers, Flow of dipole fluids in external fields, Magnetohydrodynamics, 1974, 10(4), 381–393 Search PubMed.
- K. Sudou, Y. Tomita, R. Yamane, Y. Ishibashi and H. Otawa, Ferromagnetic fluid flow through a circular channel, Bull. JSME, 1983, 26(222), 2120–2128 CrossRef.
- A. I. Anton, Measurements of Turbulence Suppression due to a Transverse Magnetic Field Applied on a Ferrofluid Motion, J. Magn. Magn. Mater., 1990, 85, 137–140 CrossRef CAS.
- S. Kamiyama and K. Koike, Pipe flow problems, in ed. and Berkovski B. and Bashtovoy, Magnetic fluids and Applications Handbook, Begell House (USA), 1996, pp. 471–503 Search PubMed.
- S. Kamiyama and A. Satoh, Pipe-flow problems and aggregation phenomena of magnetic fluids, J. Magn. Magn. Mater., 1990, 85, 121–124 CrossRef CAS.
- I. Ferrier-Barbut, H. Kadau, M. Schmitt, M. Wenzel and T. Pfau, Liquid quantum droplets of ultracold magnetic atoms, Phys. Rev. Lett., 2016, 116, 215301 CrossRef PubMed.
- M. Schmitt, M. Wenzel, F. Böttcher, I. Ferrier-Barbut and T. Pfau, Self-bound droplets of a dilute magnetic quantum liquid, Nature, 2016, 539, 259–262 CrossRef CAS PubMed.
- A. Griesmaier, J. Werner, S. Hensler, J. Stuhler and T. Pfau, Bose-Einstein condensation of chromium, Phys. Rev. Lett., 2005, 94, 160401 CrossRef PubMed.
- M. Lu, N. Q. Burdick, S. H. Youn and B. L. Lev, A Strongly Dipolar Bose-Einstein Condensate of Dysprosium, Phys. Rev. Lett., 2011, 107, 190401 CrossRef PubMed.
- K. Aikawa, A. Frisch, M. Mark, S. Baier, A. Rietzler, R. Grimm and F. Ferlaino, Bose-Einstein Condensation of Erbium, Phys. Rev. Lett., 2012, 108, 210401 CrossRef CAS PubMed.
- T. Bland, G. W. Stagg, L. Galantucci, A. W. Baggaley and N. G. Parker, Quantum ferrofluid turbulence, Phys. Rev. Lett., 2018, 121(17), 174501 CrossRef CAS PubMed.
- K. Schumacher, I. Sellien, G. Knoke, T. Cader and B. Finlayson, Experiment and simulation of laminar and turbulent ferrofluid pipe flow in an oscillating magnetic field, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 26308 CrossRef PubMed.
- K. R. Schumacher, J. J. Riley and B. A. Finlayson, Homogeneous turbulence in ferrofluids with a steady magnetic field, J. Fluid Mech., 2008, 599, 1–28 CrossRef CAS.
- B. U. Felderhof and H. J. Kroh, Hydrodynamics of magnetic and dielectric fluids in interaction with the electromagnetic field, J. Chem. Phys., 1999, 110, 7403–7411 CrossRef CAS.
- M. T. Landahl and E. Mollo-Christensen, in Turbulence and Random Processes in Fluid Mechanics, Cambridge, 2 edn, 1992 Search PubMed.
- K. R. Schumacher, J. J. Riley and B. A. Finlayson, Turbulence in ferrofluids in channel flow with steady and oscillating magnetic fields, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 016307 CrossRef PubMed.
- B. E. Launder and D. B. Spalding, The numerical computation of turbulent flows, Comput. Meth. Appl. Mech. Eng., 1974, 3(2), 269–289 CrossRef.
- K.-Y. Chien, Predictions of Channel and Boundary-Layer Flows with a Low-Reynolds-Number Turbulence Model, AIAA J., 1982, 20(1), 33–38 CrossRef CAS.
- A. Krekhov and M. Shliomis, Spontaneous Core Rotation in Ferrofluid Pipe Flow, Phys. Rev. Lett., 2017, 118, 114503 CrossRef PubMed.
- M. Couette, Etudes sur le frottement des liquides, Ann. Chim. Phys., 1890, 6, 433–510 Search PubMed.
- G. I. Taylor, Stability of a viscous liquid contained between two rotating cylinders, Philos. Trans. R. Soc. London, A, 1923, 223, 289–343 Search PubMed.
- P. Chossat and G. Iooss, The Couette–Taylor Problem, Applied Mathematical Sciences, Springer, Berlin, 1994, vol. 102, p. 234 Search PubMed.
- S. Altmeyer, Y. Do and S. Ryu, Transient behavior between multi-cell flow states in ferrofluidic Taylor-Couette flow, Chaos, 2017, 27, 113112, DOI:10.1063/1.5002771.
- M. Niklas, Influence of magnetic fields on Taylor vortex formation in magnetic fluids, Z. Phys. B: Condens. Matter, 1987, 68, 493–501 CrossRef.
- S. Altmeyer, C. Hoffmann, M. Heise, J. Abshagen, A. Pinter, M. Lücke and G. Pfister, End wall effects on the transitions between Taylor vortices and spiral vortices, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 066313 CrossRef CAS PubMed.
- J. P. Gollub and H. L. Swinney, Onset of turbulence in a rotating fluid, Phys. Rev. Lett., 1975, 35(14), 927–930 CrossRef.
- M. Holderied, L. Schwab and K. Stierstadt, Rotational viscosity of ferrofluids and the Taylor instability in a magnetic field, Z. Phys. B: Condens. Matter, 1988, 70, 431433 CrossRef.
- S. Odenbach and H. Gilly, Taylor vortex flow of magnetic fluids under the influence of an azimuthal magnetic field, J. Magn. Magn. Mater., 1996, 152(1–2), 123–128 CrossRef CAS.
- G. Fanselau, Die Erzeugung weitgehend homogener Magnetfelder durch Kreisströme, Z. Phys., 1929, 54(3–4), 260–269 CrossRef.
- H. Kikura, Y. Takeda and F. Durst, Velocity profile measurement of the Taylor vortex flow of a magnetic fluid using the ultrasonic Doppler method, Exp. Fluids, 1999, 26(3), 208–214 CrossRef CAS.
- S. Altmeyer, Y. Do and Y.-C. Lai, Transition to turbulence in Taylor-Couette ferrofluidic flow, Sci. Rep., 2015, 5, 10781 CrossRef CAS PubMed.
- U. Frisch, Turbulence, Cambridge Univ. Press, Cambridge, UK, 1996 Search PubMed.
- S. Altmeyer, Y. Do and S. Ryu, Transient behavior between multi-cell flow states in ferrofluidic Taylor-Couette flow, Chaos, 2017, 27, 113112, DOI:10.1063/1.5002771.
- A. Joseph and S. Mathew, Ferrofluids: Synthetic Strategies, Stabilization, Physicochemical Features, Characterization, and Applications, ChemPlusChem, 2014, 79(10), 1382–1420 CrossRef CAS.
- X. Zhang, L. Sun, Y. Yu and Y. Zhao, Flexible Ferrofluids: Design and Applications, Adv. Mater., 2019, 1903497 CrossRef CAS PubMed.
- X. Liu, Y. Tian and L. Jiang, Manipulating Dispersions of Magnetic Nanoparticles, Nano Lett., 2021, 21(7), 2699–2708 CrossRef CAS PubMed.
- K. Raj and R. Moskowitz, Commercial applications of ferrofluids, J. Magn. Magn. Mater., 1990, 85, 233–245 CrossRef CAS.
- K. Raj, B. Moskowitz and R. Casciari, Advances in ferrofluid technology, J. Magn. Magn. Mater., 1995, 149, 174–180 CrossRef CAS.
- K. Raj, Magnetic fluids and devices: a commercial survey, in ed. B. Berkovski and V. Bashtovoy, Magnetic fluids and applications handbook, Begell House, Inc., New York, Wallingford, 1996, ch. 5, pp. 657–754 Search PubMed.
- S. Odenbach, Ferrofluids and their applications, MRS Bull., 2013, 38, 921–924 CrossRef.
- Z. Nosrati, N. Li, F. Michaud, S. Ranamukhaarachchi, S. Karagiozov, G. Soulez, S. Martel, K. Saatchi and U. O. Hafeli, Development of a Coflowing Device for the Size-Controlled Preparation of Magnetic-Polymeric Microspheres as Embolization Agents in Magnetic Resonance Navigation Technology, ACS Biomater, Sci. Eng., 2018, 4, 1092–1102 CAS.
- T. Krasia-Christoforou, V. Socoliuc, K. D. Knudsen, E. Tombácz, R. Turcu and L. Vekas, From single-core nanoparticles in ferrofluids to multi-core magnetic nanocomposites: Assembly strategies, structure and magnetic behavior, Nanomaterials, 2020, 10, 2178 CrossRef CAS PubMed.
- Y. Li, N. Wang, X. Huang, F. Li, T. P. Davis, R. Qiao and D. Ling, Polymer-Assisted Magnetic Nanoparticle Assemblies for Biomedical Applications, ACS Appl. Biol. Mater., 2020, 3, 121–142 CrossRef CAS PubMed.
- Z. Hou, Y. Liu, J. Xu and J. Zhu, Surface Engineering of Magnetic Iron Oxide Nanoparticles by Polymer Grafting: Synthesis Progress and Biomedical Applications, Nanoscale, 2020, 12, 14957–14975 RSC.
- T. Kahmann and F. Ludwig, Magnetic field dependence of the effective magnetic moment of multi-core nanoparticles, J. Appl. Phys., 2020, 127, 233901 CrossRef CAS.
- S. Müssig, B. Kuttich, F. Fidler, D. Haddad, S. Wintzheimer, T. Kraus and K. Mandel, Reversible magnetism switching of iron oxide nanoparticle dispersions by controlled agglomeration, Nanoscale Adv., 2021, 3, 2822l RSC.
- S. Müssig, J. Reichstein, J. Prieschl, S. Wintzheimer and K. Mandel, A Single Magnetic Particle with Nearly Unlimited Encoding Options, Small, 2021, 17(2021), 2101588 CrossRef PubMed.
- Z. Xiao, L. Zhang, V. L. Colvin, Q. Zhang and G. Bao, Synthesis and Application of Magnetic Nanocrystal Clusters, Ind. Eng. Chem. Res. DOI:10.1021/acs.iecr.1c04879.
- J. D. Carlson, MR fluids and devices in the real world, Int. J. Mod. Phys. B, 2005, 19, 1463–1470 CrossRef.
- J. D. Carlson, What makes a good MR fluid?, J. Intell. Mater. Syst. Struct., 2002, 13, 431–435 CrossRef.
- S. A. Wahid, I. Ismail, S. Aid and M. S. A. Rahim, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 114, 012101 Search PubMed.
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Magnetorheological fluids: a review, Soft Matter, 2011, 7, 3701–3710 RSC.
- Y. P. Seo, S. Han, J. Choi, A. Takahara, H. J. Choi and Y. Seo, Searching for a Stable High-Performance Magnetorheological Suspension, Adv. Mater., 2018, 30, 1704769 CrossRef PubMed.
- J. R. Morillas and J. de Vicente, Magnetorheology: a review, Soft Matter, 2020, 16, 9614–9642 RSC.
- Q. Lu, K. Choi, J.-D. Nam and H. J. Choi, Magnetic Polymer Composite Particles: Design and Magnetorheology, Polymers, 2021, 13, 512 CrossRef CAS PubMed.
- J. R. Morillas, A. J. F. Bombard and J. de Vicente, Enhancing magnetorheological effect using bimodal suspensions in the single-multidomain limit, Smart Mater. Struct., 2018, 27, 07LT01 CrossRef.
- L. Vekas, Ferrofluids and Magnetorheological Fluids, Adv. Food Sci. Technol., 2008, 54, 127–136 CAS.
- J. M. Ginder, L. D. Elie and L. C. Davis, Magnetic fluid-based magnetorheological fluids, US Pat., 5549837, 1996 Search PubMed.
- Y. Yang, L. Li and G. Chen, Static yield stress of ferrofluid-based magnetorheological fluids, Rheol. Acta, 2009, 48(4), 457–466 CrossRef CAS.
- R. E. Rosensweig, Magnetorheological particle clouds, J. Magn. Magn. Mater., 2019, 479, 301–306 CrossRef CAS.
- H. J. H. Brouwers, Viscosity of a concentrated suspension of rigid monosized particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051402 CrossRef CAS PubMed.
- R. S. Farr, Simple heuristic for the viscosity of polydisperse hard spheres, J. Chem. Phys., 2014, 141, 214503 CrossRef PubMed.
- R. J. Farris, Prediction of the Viscosity of Multimodal Suspensions from Unimodal Viscosity Data, Trans. Soc. Rheol., 1968, 12, 281–301 Search PubMed.
- C. Chang and R. L. Powell, Effect of Particle Size Distributions on the Rheology of Concentrated Bimodal Suspensions, J. Rheol., 1994, 38(1), 85–98 CrossRef CAS.
- M. T. Lopez-Lopez, J. de Vicente, G. Bossis, F. González-Caballero and J. D. G. Durán, Preparation of stable magnetorheological fluids based on extremely bimodal iron–magnetite suspensions, J. Mater. Res., 2005, 20(4), 874–881 CrossRef CAS.
- D. Susan-Resiga, D. Bica and L. Vekas, Flow behaviour of extremely bidisperse magnetizable fluids, J. Magn. Magn. Mater., 2010, 322, 3166–3172 CrossRef CAS.
- D. Susan-Resiga and L. Vekas, Ferrofluid-based magnetorheological fluids: tuning the properties by varying the composition at two hierarchical levels, Rheol. Acta, 2016, 55(7), 581–595 CrossRef CAS.
- R. S. Farr and R. D. Groot, Close packing density of polydisperse hard spheres, J. Chem. Phys., 2010, 131, 244104 CrossRef PubMed.
- D. Susan-Resiga and L. Vekas, Ferrofluid based composite fluids: Magnetorheological properties correlated by Mason and Casson numbers, J. Rheol., 2017, 61(3), 401–408 CrossRef CAS.
- D. Susan-Resiga and P. Barvinschi, Correlation of rheological properties of ferrofluidbased magnetorheological fluids using the concentration-magnetization superposition, J. Rheol., 2018, 62(3), 739–752 CrossRef CAS.
- J. Yang, F. Vereda, J. R. Morillas and J. de Vicente, Ternary solid-ferrofluid-liquid magnetorheological fluids, Smart Mater. Struct., 2018, 27, 075017 CrossRef.
- I. Craciunescu, E. Chiţanu, M. M. Codescu, N. Iacob, A. Kuncser, V. Kuncser, V. Socoliuc, D. Susan-Resiga, F. Bălănean, G. Ispas, T. Borbáth, I. Borbáth, R. Turcu and L. Vékás, High performance magnetorheological fluids: very high magnetization FeCo-Fe3O4 nanoclusters in ferrofluid carrier, Soft Matter, 2022, 18, 626–639 RSC.
- B. B. Yellen, O. Hovorka and G. Friedman, Arranging matter by magnetic nanoparticle assemblers, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(25), 8860–8864 CrossRef CAS PubMed.
- R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello and B. B. Yellen, Magnetic assembly of colloidal superstructures with multipole symmetry, Nature, 2009, 457, 999–1002 CrossRef CAS PubMed.
- G. Friedman and B. Yellen, Magnetic separation, manipulation and assembly of solid phase in fluids, Curr. Opin. Colloid Interface Sci., 2005, 10, 158–166 CrossRef CAS.
- A. T. Skjeltorp, One- and Two-Dimensional Crystallization of Magnetic Holes, Phys. Rev. Lett., 1983, 51, 2306 CrossRef CAS.
- K. H. Li and B. B. Yellen, Magnetically tunable self-assembly of colloidal rings, Appl. Phys. Lett., 2010, 97, 083105 CrossRef.
- K. S. Khalil, A. Sagastegui, Y. Li, M. A. Tahir, J. E. S. Socolar, B. J. Wiley and B. B. Yellen, Binary colloidal structures assembled through Ising interactions, Nat. Commun., 2012, 3, 794 CrossRef PubMed.
- Y. Yang, L. Gao, G. P. Lopez and B. B. Yellen, Tunable Assembly of Colloidal Crystal Alloys UsingMagnetic Nanoparticle Fluids, ACS Nano, 2013, 7(3), 2705–2716 CrossRef CAS PubMed.
- S. Wang, Y. Chen, X. Zhou, L. Lei, Z. H. Shah, G. Lin and Y. Gao, Magnetic Manipulation and Assembly of Nonmagnetic Colloidal Rods in a Ferrofluid, Langmuir, 2021, 37, 1429–1437 CrossRef CAS PubMed.
- T. Zhu, R. Cheng, G. R. Sheppard, J. Locklin and L. Mao, Magnetic-Field-Assisted Fabrication and Manipulation of Nonspherical Polymer Particles in Ferrofluid-Based Droplet Microfluidics, Langmuir, 2015, 31, 8531–8534 CrossRef CAS PubMed.
- B. Yin, W. Wu, C. Dai, H. Jia, C. Zhang and J. Yao, Magnetically Controlled Assembly of Dielectric Microspheres toward Photonic Molecules, Adv. Funct. Mater., 2021, 2103945 CrossRef CAS.
- G. Katsikis, A. Breant, A. Rinberg and M. Prakash, Magnetophoretic synchronous control of water droplets in bulk ferrofluid, Soft Matter, 2018, 14, 681–692 RSC.
- C. Mandal, U. Banerjee and A. K. Sen, Transport of a Sessile Aqueous Droplet over Spikes of Oil Based Ferrofluid in the Presence of a Magnetic Field, Langmuir, 2019, 35, 8238–8245 CAS.
- H. Wang, S. Chen, H. Li, X. Chen, J. Cheng, Y. Shao, C. Zhang, J. Zhang, L. Fan, H. Chang, R. Guo, X. Wang, N. Li, L. Hu, Y. Wei and J. Liu, A Liquid Gripper Based on Phase Transitional Metallic Ferrofluid, Adv. Funct. Mater., 2021, 2100274 CrossRef CAS.
- K. S. Khalil, S. R. Mahmoudi, N. Abu-dheir and K. K. Varanasi, Active surfaces: Ferrofluid-impregnated surfaces for active manipulation of droplets, Appl. Phys. Lett., 2014, 105, 041604 CrossRef.
- A. F. Demirors, S. Aykut, S. Ganzeboom, Y. A. Meier and E. Poloni, Programmable droplet manipulation and wetting with soft magnetic carpets, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(46), e2111291118 CrossRef CAS PubMed.
- W. Wang, J. V. I. Timonen, A. Carlson, D.-M. Drotlef, C. T. Zhang, S. Kolle, A. Grinthal, T.-S. Wong, B. Hatton, S. H. Kang, S. Kennedy, J. Chi, R. T. Blough, M. Sitti, L. Mahadevan and J. Aizenberg, Multifunctional ferrofluid-infused surfaces with reconfigurable multiscale topography, Nature, 2018, 559, 77–82 CrossRef CAS PubMed.
- P. Dunne, T. Adachi, A. Arun Dev, A. Sorrenti, L. Giacchetti, A. Bonnin, C. Bourdon, P. H. Mangin, J. M. D. Coey, B. Doudin and T. M. Hermans, Liquid flow and control without solid walls, Nature, 2020, 581, 58–62 CrossRef CAS PubMed.
- G. Maglia, A. J. Heron, W. L. Hwang, M. A. Holden, E. Mikhailova, Q. Li, S. Cheley and H. Bayley, Droplet networks with incorporated protein diodes show collective properties, Nat. Nanotechnol., 2009, 4, 437–440 CrossRef CAS PubMed.
- M. Makhoul-Mansour, W. Zhao, N. Gay, C. O'Connor, J. S. Najem, L. Mao and E. C. Freeman, Ferrofluid-Based Droplet Interface Bilayer Networks, Langmuir, 2017, 33, 13000–13007 CrossRef CAS PubMed.
- M.-S. Martina, J.-P. Fortin, C. Menager, O. Clement, G. Barratt, C. Grabielle-Madelmont, F. Gazeau, V. Cabuil and S. Lesieur, Generation of Superparamagnetic Liposomes Revealed as Highly Efficient MRI Contrast Agents for in Vivo Imaging, J. Am. Chem. Soc., 2005, 127, 10676–10685 CrossRef CAS PubMed.
- Y. Namiki, T. Namiki, H. Yoshida, Y. Ishii, A. Tsubota, S. Koido, K. Nariai, M. Mitsunaga, S. Yanagisawa, H. Kashiwagi, Y. Mabashi, Y. Yumoto, S. Hoshina, K. Fujise and N. Tada, A novel magnetic crystal–lipid nanostructure for magnetically guided in vivo gene delivery, Nat. Nanotechnol., 2009, 4, 598–606 CrossRef CAS PubMed.
- G. Bealle, R. Di Corato, J. Kolosnjaj-Tabi, V. Dupuis, O. Clément, F. Gazeau, C. Wilhelm and C. Ménager, Ultra magnetic liposomes for MR imaging, targeting, and hyperthermia, Langmuir, 2012, 28(32), 11834–11842 CrossRef CAS PubMed.
- C. Montis, B. Castroflorio, M. Mendozza, A. Salvatore, D. Berti and P. Baglioni, Magnetocubosomes for the delivery and controlled release of therapeutics, J. Colloid Interface Sci., 2015, 449, 317–326 CrossRef CAS PubMed.
- O. Bixner and E. Reimhult, Controlled magnetosomes: Embedding of magnetic nanoparticles into membranes of monodisperse lipid vesicles, J. Colloid Interface Sci., 2016, 466, 62–71 CrossRef CAS PubMed.
- E. Amstad, J. Kohlbrecher, E. Müller, T. Schweizer, M. Textor and E. Reimhult, Triggered Release from Liposomes through Magnetic Actuation of Iron Oxide Nanoparticle Containing Membranes, Nano Lett., 2011, 11(4), 1664–1670 CrossRef CAS PubMed.
- M. Mendozza, C. Montis, L. Caselli, M. Wolf, P. Baglioni and D. Berti, On the thermotropic and magnetotropic phase behavior of lipid liquid crystals containing magnetic nanoparticles, Nanoscale, 2018, 10, 3480–3488 RSC.
- M. Mendozza, L. Caselli, C. Montis, S. Orazzini, E. Carretti, P. Baglioni and D. Berti, Inorganic nanoparticles modify the phase behavior and viscoelastic properties of non-lamellar lipid mesophases, J. Colloid Interface Sci., 2019, 541(2019), 329–338 CrossRef CAS PubMed.
- L. Shang, Y. Yu, W. Gao, Y. Wang, L. Qu, Z. Zhao, R. Chai and Y. Zhao, Bio-Inspired Anisotropic Wettability Surfaces from Dynamic Ferrofluid Assembled Templates, Adv. Funct. Mater., 2018, 1705802 CrossRef.
- X. Zhang, F. Wang, Y. Yu, G. Chen, L. Shang, L. Sun and Y. Zhao, Bio-inspired clamping microneedle arrays from flexible ferrofluid-configured moldings, Sci. Bull., 2019, 64, 1110–1117 CrossRef CAS.
- M. I. Piso, Applications of magnetic fluids for inertial sensors, J. Magn. Magn. Mater., 1999, 201, 380–384 CrossRef CAS.
- R. Olaru and D. Dragoi, Inductive tilt sensor with magnets and magnetic fluid, Sens. Actuators, A, 2005, 120, 424–428 CrossRef CAS.
- J. Yao, S. Liu, Z. Li and D. Li, A Novel Ferrofluid Inclinometer Exploiting a Hall Element, IEEE Sens. J., 2016, 16(22), 7986–7991 CAS.
- J. Yao, Y. Chen, Z. Li, T. Zhang and D. Li, A novel accelerometer based on the first kind of ferrofluid levitation principle, Smart Mater. Struct., 2016, 25, 095016 CrossRef.
- T. I. Volkova, V. Böhm, V. A. Naletova, T. Kaufhold, F. Becker, I. Zeidis and K. Zimmermann, A ferrofluid based artificial tactile sensor with magnetic field control, J. Magn. Magn. Mater., 2017, 431, 277–280 CrossRef CAS.
- N. C. Popa, I. De Sabata, I. M. Anton, I. Potencz and L. Vékás, Magnetics fluids in aerodynamic measuring devices, J. Magn. Magn. Mater., 1999, 201, 385–390 CrossRef CAS.
- O. Baltag, D. Costandache and A. Salceanu, Tilt measurement sensor, Sens. Actuators, A, 2000, 81, 336–339 CrossRef CAS.
- B. Ando, S. Baglio and A. Beninato, A low-cost inertial sensor based on shaped magnetic fluids, IEEE Trans. Instrum. Meas., 2012, 61, 231–236 Search PubMed.
- B. Ando, S. Baglio and A. Beninato, A ferrofluid inclinometer with a Time Domain Readout strategy, Sens. Actuators, A, 2013, 202, 57–63 CrossRef CAS.
- P. I. Nikitin, P. M. Vetoshko and T. I. Ksenevich, New Type of Biosensor Based on Magnetic Nanoparticle Detection, J. Magn. Magn. Mater., 2007, 311, 445–449 CrossRef CAS.
- H.-J. Krause, N. Wolters, Y. Zhang, A. Offenhausser, P. Miethe, M. H. Meyer, M. Hartmann and M. Keusgen, Magnetic Particle Detection by Frequency Mixing for Immunoassay Applications, J. Magn. Magn. Mater., 2007, 311, 436–444 CrossRef CAS.
- V. O. Shipunova, M. P. Nikitin, P. I. Nikitin and S. M. Deyev, MPQ-cytometry: a magnetism-based method for quantification of nanoparticle–cell interactions, Nanoscale, 2016, 8, 12764–12772 RSC.
- Y. Shi, D. Jyoti, S. W. Gordon-Wylie and J. B. Weaver, Quantification of magnetic nanoparticles by compensating for multiple environment changes simultaneously, Nanoscale, 2020, 12(1), 195–200 RSC.
- Y. Liu, W. Zhao, R. Cheng, B. N. Harris, J. R. Murrow, J. Hodgson, M. Egan, A. Bankey, P. G. Nikolinakos, T. Laver, K. Meichnerg and L. Mao, Fundamentals of integrated ferrohydrodynamic cell separation in circulating tumor cell isolation, Lab Chip, 2021, 21, 1706–1723 RSC.
- M. P. Nikitin, A. V. Orlov, I. L. Sokolov, A. A. Minakov, P. I. Nikitin, J. Ding, D. S. Bader, E. A. Rozhkova and V. Novosad, Ultrasensitive Detection Enabled by Nonlinear Magnetization of Nanomagnetic Labels, Nanoscale, 2018, 10, 11642–11650 RSC.
- S. L. Znoyko, A. V. Orlova, V. A. Bragina, M. P. Nikitin and P. I. Nikitin, Nanomagnetic lateral flow assay for high-precision quantification of diagnostically relevant concentrations of serum TSH, Talanta, 2020, 216, 120961 CrossRef CAS PubMed.
- W. Zhao, T. Zhu, R. Cheng, Y. Liu, J. He, H. Qiu, L. Wang, T. Nagy, T. D. Querec, E. R. Unger and L. Mao, Label-Free and Continuous-Flow Ferrohydrodynamic Separation of HeLa Cells and Blood Cells in Biocompatible Ferrofluids, Adv. Funct. Mater., 2016, 26(22), 3990–3998 CrossRef CAS PubMed.
- V. Uskokovic, S. Tang and V. M. Wu, Targeted magnetic separation of biomolecules and cells using earthicle-based ferrofluids, Nanoscale, 2019, 11, 11236–11253 RSC.
- K. Wu, R. Saha, D. Su, V. D. Krishna, J. Liu, M. C.-J. Cheeran and J.-P. Wang, Magnetic-Nanosensor-Based Virus and Pathogen Detection Strategies before and during COVID-19, ACS Appl. Nano Mater., 2020, 3(10), 9560–9580 CrossRef CAS.
- E. L. Rosch, J. Zhong, A. Lak, Z. Liu, M. Etzkorn, M. Schilling, F. Ludwig, T. Viereck and B. Lalkens, Point-of-need detection of pathogen-specific nucleic acid targets using magnetic particle spectroscopy, Biosens. Bioelectron., 2021, 192, 113536 CrossRef PubMed.
- W. Li, J. T. Mayo, D. N. Benoit, L. Troyer, Z. A. Lewicka, B. J. Lafferty, J. G. Catalano, S. S. Lee, V. L. Colvin and J. D. Fortner, Engineered superparamagnetic iron oxide nanoparticles for ultra-enhanced uranium separation and sensing, J. Mater. Chem. A, 2016, 4, 15022–15029 RSC.
- R. Gonzalez-Martin, A. Gutierrez-Serpa and V. Pino, The Use of Ferrofluids in Analytical Sample Preparation: A Review, Separations, 2021, 8, 47 CrossRef CAS.
- J. Chen, Q. Cao and X. Han, Smart water-based ferrofluid with stable state transition property: Preparation and its application in anionic dye removal, J. Cleaner Prod., 2021, 287, 125003 CrossRef CAS.
- J. I. Tapia, E. Alvarado-Gomez and A. Encinas, Non-expensive hydrophobic and magnetic melamine sponges for the removal of hydrocarbons and oils from water, Sep. Purif. Technol., 2019, 222, 221–229 CrossRef CAS.
- R. Nayebi and F. Shemirani, Ferrofluids-based microextraction systems to process organic and inorganic targets: The state-of-the-art advances and applications, Trends Anal. Chem., 2021, 138, 116232 CrossRef CAS.
- A. Moyano, M. Salvador, J. C. Martínez-García, V. Socoliuc, L. Vékás, D. Peddis, M. A. Alvarez, M. Fernández, M. Rivas and M. C. Blanco-López, Magnetic immunochromatographic test for histamine detection in wine, Anal. Bioanal. Chem., 2019, 411, 6615–6624 CrossRef CAS PubMed.
- M. Salvador, J. L. Marqués-Fernández, J. C. Martínez-García, D. Fiorani, P. Arosio, M. Avolio, F. Brero, F. Balanean, A. Guerrini, C. Sangregorio, V. Socoliuc, L. Vekas, D. Peddis and M. Rivas, Double-Layer Fatty Acid Nanoparticles as a Multiplatform for Diagnostics and Therapy, Nanomaterials, 2022, 12, 205 CrossRef CAS PubMed.
- H. V. Thakur, S. M. Nalawade, S. Gupta, R. Kitture and S. N. Kale, Photonic crystal fiber injected with Fe3O4 nanofluid for magnetic field detection, Appl. Phys. Lett., 2011, 99(16), 161 CrossRef.
- L. Luo, S. Pu, J. Tang, X. Zeng and M. Lahoubi, Highly sensitive magnetic field sensor based on microfiber coupler with magnetic fluid, Appl. Physl Lett., 2015, 106, 193507 CrossRef.
- S. Pissadakis, Lab-in-a-fiber sensors: A review, Microelectron. Eng., 2019, 217, 111105 CrossRef CAS.
- Y. Zhao, R. Lv, Y. Zhang and Q. Wang, Novel optical devices based on the transmission properties of magnetic fluid and their characteristics, Opt. Lasers Eng., 2012, 50(9), 1177–1184 CrossRef.
- F. Martinez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernandez, Aggregation of magnetic polystyrene particles: a light scattering study, Colloids Surf., A, 2005, 270–271, 317–322 CrossRef CAS.
- P. Zu, C. C. Chan, L. W. Siang, Y. Jin, Y. Zhang, L. H. Fen, L. Chen and X. Dong, Magneto-optic fiber Sagnac modulator based on magnetic fluids, Opt. Lett., 2011, 36(8), 1425–1427 CrossRef PubMed.
- J. Yin, P. Yan, H. Chen, L. Yu, J. Jiang, M. Zhang and S. Ruan, All-fiber-optic vector magnetometer based on anisotropic magnetism-manipulation of ferromagnetism nanoparticles, Appl. Phys. Lett., 2017, 110, 231104 CrossRef.
- N. Alberto, D. M. Fátima, M. Carlos, A. Paulo and A. Paulo, Optical Fiber Magnetic Field Sensors Based on Magnetic Fluid: A Review, Sensors, 2018, 18, 4325 CrossRef PubMed.
- J. X. Dai, M. H. Yang, X. B. Li, H. L. Liu and X. L. Tong, Magnetic field sensor based on magnetic fluid clad etched fiber Bragg grating, Opt. Fiber Technol., 2011, 17(3), 210–213 CrossRef CAS.
- P. Zu, C. C. Chan, W. S. Lew, Y. Jin, Y. Zhang, H. F. Liew, L. H. Chen, W. C. Wong and X. Dong, Magneto-optical fiber sensor based on magnetic fluid, Opt. Lett., 2012, 37(3), 398–400 CrossRef PubMed.
- P. Zu, C. C. Chan, W. S. Lew, L. Hu, Y. Jin, H. F. Liew, L. H. Chen, W. C. Wong and X. Dong, Temperature-Insensitive Magnetic Field Sensor Based on Nanoparticle Magnetic Fluid and Photonic Crystal Fiber, IEEE Photonics J., 2012, 4(2), 491–498 Search PubMed.
- M. Deng, X. Sun, M. Han and D. Li, Compact magnetic-field sensor based on optical microfiber Michelson interferometer and Fe3O4 nanofluid, Appl. Opt., 2013, 52, 734 CrossRef CAS PubMed.
- R.-Q. Lv, Y. Zhao, D. Wang and Q. Wang, Magnetic Fluid-Filled Optical Fiber Fabry–Pérot Sensor for Magnetic Field Measurement, IEEE Photonics Technol. Lett., 2014, 26(3), 217–219 Search PubMed.
- Y. Chen, Q. Han, T. Liu, X. Lan and H. Xiao, Optical fiber magnetic field sensor based on single-mode-multimode-single-mode structure and magnetic fluid, Opt. Lett., 2013, 38(20), 3999–4001 CrossRef PubMed.
- P. S. J. Russell, Photonic-Crystal fibers, J. Lightwave Technol., 2006, 24(12), 4729–4749 Search PubMed.
- S. Z. Malynych, A. Tokarev, S. Hudson, G. Chumanov, J. Ballato and K. G. Kornev, Magneto-controlled illumination with opto-fluidics, J. Magn. Magn. Mater., 2010, 322, 1894–1897 CrossRef CAS.
- Z. Zhang, T. Guo, X. Zhang, J. Xu, W. Xie, M. Nie, Q. Wu, B.-Q. Guan and J. Albert, Plasmonic fiber-optic vector magnetometer, Appl. Phys. Lett., 2016, 108, 101105 CrossRef.
- A. Candiani, A. Argyros, S. G. Leon-Saval, R. Lwin, S. Selleri and S. Pissadakis, A loss-based, magnetic field sensor implemented in a ferrofluid infiltrated microstructured polymer optical fiber, Appl. Phys. Lett., 2014, 104, 111106 CrossRef.
- F. Wei, A. K. Mallik, D. Liu, Q. Wu, G.-D. Peng, G. Farrell and Y. Semenova, Magnetic field sensor based on a combination of a microfiber coupler covered with magnetic fluid and a Sagnac loop, Sci. Rep., 2017, 7, 4725 CrossRef PubMed.
- F. Wei, D. Liu, A. K. Mallik, G. Farrell, Q. Wu, G.-D. Peng and Y. Semenova, Temperature-compensated magnetic field sensing with a dual-ring structure consisting of microfiber coupler-Sagnac loop and fiber Bragg grating-assisted resonant cavity, Appl. Opt., 2019, 58(9), 2334–2339 CrossRef CAS PubMed.
- X. Li, R. Ma and Y. Xia, Magnetic Field Sensor Exploiting Light Polarization Modulation of Microfiber With Magnetic Fluid, J. Lightwave Technol., 2018, 36(9), 1620–1625 CAS.
- N. T. Nguyen and S. T. Wereley, Fundamentals and Applications of Microfluidics, Artech House, 2nd edn, 2006, p. 488 Search PubMed.
- N. T. Nguyen, X. Y. Huang and K. C. Toh, MEMS–micropumps: a review, J. Fluids Eng., 2002, 124, 384–392 CrossRef.
- M. Kakuta, F. G. Bessoth and A. Manz, Microfabricated devices for fluid mixing and their application for chemical synthesis, Chem. Rec., 2001, 1, 395–405 CrossRef CAS PubMed.
- L. Mao and H. Koser, Towards ferrofluidics for μ-TAS and lab on-a-chip applications, Nanotechnology, 2006, 17, S34 CrossRef CAS PubMed.
- R. Ganguly and I. K. Puri, Microfluidic transport in magnetic MEMS and bioMEMS, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2010, 2(4), 382–399 CAS.
- N.-T. Nguyen, Micro-magnetofluidics: interactions between magnetism and fluid flow on the microscale, Microfluid. Nanofluid., 2012, 12(1–4), 1–16 CrossRef.
- R.-J. Yang, H.-H. Hou, Y.-N. Wang and L.-M. Fu, Micro-magnetofluidics in microfluidic systems: A review, Sens. Actuators, B, 2016, 224, 1–15 CrossRef CAS.
- B. Liu, Z. Zhang, J. Yang, J. Yang and D. Li, A rotary ferrofluidic vane micropump with C shape baffle, Sens. Actuators, B, 2018, 263, 452–458 CrossRef CAS.
- K. S. Lok, Y. C. Kwok, P. P. F. Lee and N. T. Nguyen, Ferrofluid plug as valve and actuator for whole cell PCR on chip, Sens. Actuators, B, 2012, 166–167, 893–897 CrossRef CAS.
- A. Nisar, N. Afzulpurkar, B. Mahaisavariya and A. Tuantranont, MEMS-based micropumps in drug delivery and biomedical applications, Sens. Actuators, B, 2008, 130, 917–942 CrossRef CAS.
- F. Amirouche, Y. Zhou and T. Johnson, Current micropump technologies and their biomedical applications, Microsyst. Technol., 2009, 15, 647–666 CrossRef CAS.
- Y. Liang, J. R. Alvarado, K. D. Iagnemma and A. E. Hosoi, Dynamic Sealing Using Magnetorheological Fluids, Phys. Rev. Appl., 2018, 10, 064049 CrossRef CAS.
- L. Mao, S. Elborai, X. He, M. Zahn and H. Koser, Direct observation of closed-loop ferrohydrodynamic pumping under traveling magnetic fields, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104431 CrossRef.
- S. Schuerle, A. P. Soleimany, T. Yeh, G. M. Anand, M. Häberli, H. E. Fleming, N. Mirkhani, F. Qiu, S. Hauert, X. Wang, B. J. Nelson and S. N. Bhatia, Synthetic and living micropropellers for convection-enhanced nanoparticle transport, Sci. Adv., 2019, 5, eaav4803 CrossRef CAS PubMed.
- N. Mirkhani, M. G. Christiansen and S. Schuerle, Living, Self-Replicating Ferrofluids for Fluidic Transport, Adv. Funct. Mater., 2020, 2003912 CrossRef CAS.
- J. V. I. Timonen, A. F. Demirörs and B. A. Grzybowski, Magnetofluidic Tweezing of Nonmagnetic Colloids, Adv. Mater., 2016, 28, 3453–3459 CrossRef CAS PubMed.
- Z. Cenev, P. A. D. Harischandra, S. Nurmi, M. Latikka, V. Hynninen, R. H. A. Ras, J. V. I. Timonen and Q. Zhou, Ferrofluidic Manipulator: Automatic Manipulation of Nonmagnetic Microparticles at the Air–Ferrofluid Interface, IEEE ASME Trans. Mechatron., 2021, 26(4), 1932–1940 Search PubMed.
- G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Droplet microfluidics, Lab Chip, 2008, 8, 198–220 RSC.
- K. Choi, A. H. C. Ng, R. Fobel and A. R. Wheeler, Digital Microfluidics, Annu. Rev. Anal. Chem., 2012, 5, 413–440 CrossRef CAS PubMed.
- H. A. Stone, A. D. Stroock and A. Ajdari, Engineering flows in small devices: Microfluidics Toward a Lab-on-a-Chip, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Formation of droplets and bubbles in a microfluidic T-junction—scaling and mechanism of break-up, Lab Chip, 2006, 6, 437–446 RSC.
- T. S. Kaminski and P. Garstecki, Controlled droplet microfluidic systems for multistep chemical and biological assays, Chem. Soc. Rev., 2017, 46, 6210–6226 RSC.
- L. Shang, Y. Cheng and Y. Zhao, Emerging Droplet Microfluidics, Chem. Rev., 2017, 117, 7964–8040 CrossRef CAS PubMed.
- P. Zhu and L. Wang, Passive and active droplet generation with microfluidics: a review, Lab Chip, 2017, 17, 34–35 RSC.
- A. Al-Azawi, M. Latikka, V. Jokinen, S. Franssila and R. H. S. Ras, Friction and Wetting Transitions of Magnetic Droplets on Micropillared Superhydrophobic Surfaces, Small, 2017, 1700860 CrossRef PubMed.
- Z. G. Guo, G. F. Zhou, J. C. Hao, Y. M. Liang, W. M. Liu and W. T. S. Huck, “Stick and slide” ferrofluidic droplets on superhydrophobic surfaces, Appl. Phys. Lett., 2006, 89, 081911 CrossRef.
- H. W. Koh, K. S. Lok and N.-T. Nguyen, A Digital Micro Magnetofluidic Platform For Lab-on-a-Chip Applications, J. Fluids Eng., 2013, 135, 021302 CrossRef.
- G. Huang, M. Li, Q. Yang, Y. Li, H. Liu, H. Yang and F. Xu, Magnetically Actuated Droplet Manipulation and Its Potential Biomedical Applications, ACS Appl. Mater. Interfaces, 2017, 9(2), 1155–1166 CrossRef CAS PubMed.
- M. Latikka, M. Backholm, J. V. I. Timonen and R. H. A. Ras, Wetting of ferrofluids: Phenomena and control, Curr. Opin. Colloid Interface Sci., 2018, 36, 118–129 CrossRef CAS.
- S. Tenneti, S. G. Subramanian, M. Chakraborty, G. Soni and S. DasGupta, Magnetowetting of Ferrofluidic Thin Liquid Films, Sci. Rep., 2017, 7, 44738 CrossRef PubMed.
- N. T. Nguyen, G. Zhu, Y. C. Chua, V. N. Phan and S. H. Tan, Magnetowetting and sliding motion of a sessile ferrofluid droplet in the presence of a permanent magnet, Langmuir, 2010, 26(15), 12553–12559 CrossRef CAS PubMed.
- Y. Zhao, Z. Xu, H. Niu, X. Wang and T. Lin, Magnetic Liquid Marbles: Toward “Lab in a Droplet”, Adv. Funct. Mater., 2015, 25, 437–444 CrossRef CAS.
- C. Yang and G. Li, A novel magnet-actuated droplet manipulation platform using a floating ferrofluid film, Sci. Rep., 2017, 7, 15705 CrossRef PubMed.
- A. Ray, V. B. Varma, P. J. Jayaneel, N. M. Sudharsan, Z. P. Wang and R. V. Ramanujan, On demand manipulation of ferrofluid droplets by magnetic fields, Microfluid. Nanofluid., 2017, 3, 245–281 Search PubMed.
- M. Latikka, M. Backholm, A. Baidya, A. Ballesio, A. Serve, G. Beaune, J. V. I. Timonen, T. Pradeep and R. H. A. Ras, Ferrofluid Microdroplet Splitting for Population-Based Microfluidics and Interfacial Tensiometry, Adv. Sci., 2020, 2000359 CrossRef CAS PubMed.
- M. A. Bijarchi, A. Favakeh, E. Sedighi and M. B. Shafii, Ferrofluid droplet manipulation using an adjustable alternating magnetic field, Sens. Actuators, A, 2020, 301, 111753 CrossRef CAS.
- M. A. Bijarchi, A. Favakeh, S. Alborzi and M. B. Shafii, Experimental investigation of on-demand ferrofluid droplet generation in microfluidics using a Pulse-Width Modulation magnetic field with proposed correlation, Sens. Actuators, B, 2021, 329, 129274 CrossRef CAS.
- H. H. Al-Terke, M. Latikka, J. V. I. Timonen, L. Vékás, A. Paananen, J. Joensuu and R. H. A. Ras, Functional Magnetic Microdroplets for Antibody Extraction, Adv. Mater. Interfaces, 2022, 9, 2101317 CrossRef CAS.
- F. Serwane, A. Mongera, P. Rowghanian, D. A. Kealhofer, A. A. Lucio, Z. M. Hockenbery and O. Campàs, In vivo quantification of spatially varying mechanical properties in developing tissues, Nat. Methods, 2017, 14, 181–186 CrossRef CAS PubMed.
- L. F. Cheow, L. Yobas and D.-L. Kwong, Digital microfluidics: Droplet based logic gates, Appl. Phys. Lett., 2007, 90, 054107 CrossRef.
- M. Prakash and N. Gershenfeld, Microfluidic bubble logic, Science, 2007, 315, 832–835 CrossRef CAS PubMed.
- M. J. Fuertman, P. Gartecki and G. M. Whitesides, Coding/decoding and reversibility of droplet trains in microfluidic networks, Science, 2007, 315, 828–832 CrossRef PubMed.
- O. Cybulski and P. Garstecki, Dynamic memory in a microfluidic system of droplets travelling through a simple network of microchannel, Lab Chip, 2010, 10, 484–493 RSC.
- T. Tesla, U.S. Patent No., 1329559, 1920 Search PubMed.
- A. Adamatzky, A brief history of liquid computers, Philos. Trans. R. Soc., B, 2019, 374, 20180372, DOI:10.1098/rstb.2018.0372.
- G. Katsikis, J. S. Cybulski and M. Prakash, Synchronous universal droplet logic and control, Nat. Phys., 2015, 11(7), 588–596 Search PubMed.
- G. M. Whitesides, Soft Robots, Angew. Chem., Int. Ed., 2018, 57, 2–18 CrossRef.
- W. Yu, H. Lin, Y. Wang, X. He, N. Chen, K. Sun, D. Lo, B. Cheng, C. Yeung, J. Tan, D. Di Carlo and S. Emaminejad, A ferrobotic system for automated microfluidic logistics, Sci. Robot., 2020, 5, eaba4411 CrossRef PubMed.
- X. Fan, X. Dong, A. C. Karacakol, H. Xie and M. Sitti, Reconfigurable multifunctional ferrofluid droplet robots, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(45), 27916–27926 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |