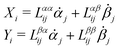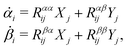DOI:
10.1039/D0SM02076A
(Paper)
Soft Matter, 2021,
17, 3634-3653
Onsager's variational principle in active soft matter
Received
21st November 2020
, Accepted 4th January 2021
First published on 5th January 2021
Abstract
Onsagers variational principle (OVP) was originally proposed by Lars Onsager in 1931 [L. Onsager, Phys. Rev., 1931, 37, 405]. This fundamental principle provides a very powerful tool for formulating thermodynamically consistent models. It can also be employed to find approximate solutions, especially in the study of soft matter dynamics. In this work, OVP is extended and applied to the dynamic modeling of active soft matter such as suspensions of bacteria and aggregates of animal cells. We first extend the general formulation of OVP to active matter dynamics where active forces are included as external non-conservative forces. We then use OVP to analyze the directional motion of individual active units: a molecular motor walking on a stiff biofilament and a toy two-sphere microswimmer. Next we use OVP to formulate a diffuse-interface model for an active polar droplet on a solid substrate. In addition to the generalized hydrodynamic equations for active polar fluids in the bulk region, we have also derived thermodynamically consistent boundary conditions. Finally, we consider the dynamics of a thin active polar droplet under the lubrication approximation. We use OVP to derive a generalized thin film equation and then employ OVP as an approximation tool to find the spreading laws for the thin active polar droplet. By incorporating the activity of biological systems into OVP, we develop a general approach to construct thermodynamically consistent models for better understanding the emergent behaviors of individual animal cells and cell aggregates or tissues.
1 Introduction
Active matter represents a novel type of nonequilibrium systems that contain a large number of self-propelling particles or creatures moving in fluids or more complex environments.1–10 The self-propelling units are considered to be active in the sense that they are capable of continuously converting fuel or chemical energy (stored internally or in the ambient) into directional motion or mechanical work. Active matter containing self-propelled units is ubiquitous in biology and in many artificial systems. Examples in biology are abundant and occur at all length scales, ranging from bacteria suspensions3,9–12 to animal cells,2,4 animal cell aggregates (or tissues),13–17 bird and fish flocks,18,19 and pedestrian crowds.20,21 Artificially made active matter3 includes layers of vibrated granular rods,1,22 collections of robots,23 and suspensions of colloidal or nanoscale particles24–26 that are propelled through catalytic activities at their surfaces.
A distinctive feature of active matter is that the system is locally driven out of equilibrium by active units at the length scale of a constituent component.1–3,27 This is distinct from those nonequilibrium systems that are driven at the system boundaries.28 The presence of self-propelled units in active matter breaks the detailed balance and time-reversal symmetry (TRS),1,3,5,8 resulting in a wealth of intriguing macroscopic structures and behaviors, such as spontaneous flows,3,4 motility-induced phase separation,3,6,8 unusual mechanical and rheological properties,2,10 wave propagation and sustained oscillations even in the absence of inertia,29–31etc. One of the most interesting questions in the nonequilibrium dynamics of active matter is how the local driving forces operating at the small scale of individual active unit can produce the observable macroscopic emergent phenomena at the large scale of the whole system. Answering this question will not only shed new light on the fundamental statistical mechanics,3,6,8,26 but also deepen our understanding of biological processes,1–4 and help design new generations of biomimetic active materials that balance structural flexibility and stability.1,3,5
The study of active matter can be brought into the framework of condensed matter physics based on the consideration that the collective behaviors of active matter emerge from the interactions among the constituent self-propelling units and the dissipation mechanisms operating inside the system. In particular, soft condensed matter physics provides many useful model systems for reference to active matter,2,5e.g. the wetting of substrates by liquid droplets,32–34 the dynamics of colloid suspensions,35,36 the dynamics of nematic liquid crystals,37 the dynamics and rheology of polymer gels,38,39 and the phase segregation of surfactants,40,41etc. The major challenge is to couple these model systems with active and molecularly specific processes, such as the active force generation by self-propelling units, and the binding and unbinding of transmembrane adhesion receptors on solid substrates.2,5 Over the last decade, several soft matter systems have been revisited with a focus on this point of view.2 The physical understanding for the emergent structures and behaviors of active soft matter has been rapidly growing,1–10 with particular attention paid to dry active matter,3,18 active polar fluids,42 active nematics,43 active gels,44 and active membranes.45
Theoretically there have been two major approaches to the study of active soft matter: particle-based models3,6–8,26,46 and continuum phenomenological models.1,2,4–6,14,15,43 In particle-based models, the active units are usually modeled as self-propelled particles with fixed or variable speed and random orientation moving in an inert background, following the seminal work of Vicsek et al.47 It provides a straightforward approach to the study of active soft matter with an emphasis on the order and fluctuations rather than the forces and mechanics.3,7,8,26 In continuum phenomenological models, active units are represented by a smooth density field rather than individually resolved particles. A continuum model for active soft matter is usually constructed by modifying the dynamic model of a proper reference soft matter system.1,2,4–6,43 This is typically accomplished by adding a minimal set of extra terms that cannot be derived from any free energy or dissipation functions. This is an effective way to introduce the activity and break the TRS such as active forces, active fluxes, and active chemical potentials.1,43,48,49 However, there is another more systematic way of including activity by introducing the mechanochemical coupling between passive dissipative processes and some relevant biochemical reactions1,4 in Onsager's framework of irreversible thermodynamics.50,51 The two theoretical approaches are complementary. The particle-based approach involves only a small number of parameters for each active unit, and therefore the theoretical predictions can be readily compared with experiments for some model active systems such as self-propelled colloids.52 However, the model for interacting self-propelled particles sometimes oversimplifies the problem, and hence may lose some generality and applicability of its conclusions when applied to real systems, especially in vivo biological systems.1,2,4,43 By contrast, the formulation of phenomenological models is based upon symmetry consideration, conservation laws of mass, momentum, and angular momentum, and laws of thermodynamics. This gives the continuum approach a large range of applicability and generality when applied to real biological processes.1,2,4,43 In this work, we focus on the continuum phenomenological models and show that Onsagers variational principle, which has been widely used in the study of soft matter dynamics,53 can be extended for the study of active soft matter.
Onsager's variational principle (OVP) was originally proposed by Lars Onsager in his seminar papers in 1931.54,55 He showed that for irreversible processes in a near-equilibrium thermodynamic system, the thermodynamic fluxes can be written as linear combinations of conjugate thermodynamic forces, and the proportionality coefficient matrix must be positive-definite and symmetric according to Onsager's reciprocal relations (ORR). The ORR lay the foundation for the theoretical framework of linear irreversible thermodynamics. In the end of his paper, Onsager proposed OVP as a variational principle that is equivalent to the linear force–flux relations in describing dissipative dynamics. In addition, OVP can be regarded as an extension of “the principle of the least dissipation of energy” proposed by Lord Rayleigh.56 For isothermal systems, OVP takes a simple form as follows.53,57,58 The irreversible processes described by the thermodynamic fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) follow the dynamic path that minimizes the function:
follow the dynamic path that minimizes the function:
Here the function
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
is called the Rayleighian as suggested by Doi and Edwards,
59Φ is the dissipation function which is quadratic in
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
when the system is close to equilibrium, and
Ḟ is the rate of change of the free energy in the isothermal system. Onsager later used his principle to study the diffusion in electrolyte solutions.
57 However, OVP has not been widely recognized and applied to describe irreversible processes for a long time until 1953 when Onsager and Machlup
60 established the statistical mechanical foundation of OVP. Since then, OVP and its relationship with other thermodynamic variational principles have been extensively studied and identified.
61 In recent years, OVP has been widely used as an indispensable and powerful tool for the study of nonlinear and nonequilibrium phenomena of soft matter.
53,58,62–65
OVP can be used to derive many transport equations for soft matter dynamics,53,62e.g., the Stokes equation for incompressible low-Reynolds-number flows,58 the diffusion equation,53,62 the reaction-diffusion equations for (low molecular weight) multi-component solutions,51,64,65 the thin film evolution equations,63,66–68 the phase field model for two-phase hydrodynamics,58,69 the electrorheological hydrodynamic equation,70 the two-fluid model for the phase separation dynamics in colloids and polymers,53,62,63 the dynamics of polymer gels,39,63 the dynamic equations of lipid membrane,71–73etc. Moreover, OVP also provides a very convenient way to derive thermodynamically consistent boundary conditions that supplement the transport equations in the bulk region.58,69 Examples include the generalized Navier boundary condition (GNBC) for the contact line hydrodynamics,58 the generalized nemato-hydrodynamic boundary conditions for liquid crystals,74 and the boundary conditions for block copolymer solution films,75etc. In addition, Doi and his collaborators have recently proposed that OVP can be used as a direct variational method to find approximate solutions for complex soft matter dynamics.63,68,76 This approximation method has been successfully used to study the evolution of droplets and thin films,63,67,77,78 the dynamics of the beads-on-string structure of viscoelastic polymer filaments,63,79 the sedimentation in colloidal suspensions,80 and the translocation of a vesicle through a narrow hole,81etc. Although OVP has been widely applied with great successes in the study of inert soft matter dynamics, it is rarely used in the study of active soft matter dynamics.65,82–84 In the present work, we will show that OVP can be readily extended to include biochemical activity and conveniently applied to study the emergent structures and behaviors of active soft matter. OVP can not only be applied to formulate thermodynamically consistent models, but also be used to generate approximate solutions for the complex dynamics of active soft matter.
This paper is organized as follows. In Section 2, a brief review of OVP is provided, and a simple extension of OVP is presented for applications to active matter, in which the active forces are treated as non-conservative forces that cannot be derived from any free energy and dissipation functions. In the next three sections, we apply OVP and its extended form to three representative active matter problems motivated by the biology of bacteria and animal cells. In Section 3, we present the first application of OVP to the directional motion of an individual active unit, e.g., a molecular motor walking on a stiff biofilament and a toy two-sphere microswimmer moving in a viscous fluid. In Section 4, we consider the two-phase hydrodynamics for active polar droplets. We use OVP to formulate a diffuse-interface model for an active polar droplet on a solid substrate. This hydrodynamic model is thermodynamically consistent and consists of hydrodynamic equations in the bulk region and boundary conditions at the solid surface. In Section 5, we consider a thin active polar droplet moving on a solid substrate in two dimensions. Under the lubrication approximation, we firstly apply OVP to derive the classical thin film equation that has been obtained previously. We then use OVP as an approximation tool to find the scaling laws for the spreading of a thin active droplet in the respective limits of negligible activity and strong activity. In Section 6, we summarize our major results, make some general remarks, and envision a few potential applications of OVP to more realistic biological problems.
2 Variational principles for active matter dynamics
In this section, we show that the original variational principle of Onsager54,60 can be easily modified to study the dynamics of active soft matter by including active forces as non-conservative forces that can not be derived from any free energy function. Since we are mostly interested in the flow, diffusion, and biochemical reactions in active soft matter, we, therefore, limit our discussions to isothermal systems where temperature is assumed to be constant.
2.1 Onsager's variational principle and Onsager–Machlup variational principle
Consider a non-equilibrium isothermal system that is characterized by a set of coarse-grained, slow state variables, α ≡ {α1,α2,…,αN}. The dynamics of the system is then described by the time evolution of α(t) which is governed, in the linear response regime near equilibrium, by the general (overdamped) Langevin equation60| | 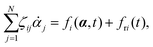 | (2) |
in which ζ = {ζij} is the friction coefficient matrix that generally depends on the state variables65α. Here we assume that all the state variables α have the same time parity, and therefore, according to Onsager's reciprocal symmetry, the friction matrix ζ is not only positive definite (due to the second law of thermodynamics) but also symmetric,54i.e., ζij = ζji. State variables with different time parities have been discussed briefly in the Appendix Section A.2. The stochastic force fr(t) is assumed to be an uncorrelated white noise| | | 〈fri(t)〉 = 0, 〈fri(t)frj(t′)〉 = 2ζijkBTδ(t − t′), | (3) |
with kB denoting the Boltzmann constant and T the temperature. The generalized force fi, in general, includes two types of forces: fi(α,t) = fci(α) + fai(α,t), in which the conservative force fci(α) can be derived from some free energy F(α) by| | 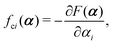 | (4) |
and fai(α,t) is the active force, a non-conservative force that cannot be derived from any energy function. Physically, the active forces arise from the persistent consumption of chemical energy and they continuously drive the system out of equilibrium locally at the small scale of individual active unit. For example, the active forces can be generated by biochemical reactions such as ATP hydrolysis in animal cells/tissues,1,4 or by external fields such as light acting on active colloids with photosensitive coatings.3,7 The active forces also break the time-reversal symmetry (TRS) of the system (in a sense different from the breakdown of TRS due to friction).8,43,48,85 For example, the self-propelling force in active colloids drives the persistent motion of colloids in some direction, resulting in the intrinsic breakdown of TRS.43
From the Langevin eqn (2), we calculate the transition probability60P(α′,t + dt|α,t) from the state α at time t to α′ at t + dt:
| | 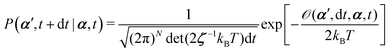 | (5) |
for
α′ close to
α, and d
t is an infinitesimal time interval. Here the Onsager–Machlup function
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
is defined by
| | 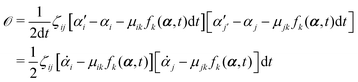 | (6) |
with the rates
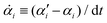
and
μij being the mobility coefficient matrix that is positive definite and symmetric, and satisfies
ζijμjk =
δik. From the transition probability
P(
α′,
t + d
t|
α,
t) in
eqn (5), the most probable transition occurring between
α and nearby
α′ is the one which minimizes the Onsager–Machlup function
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
or equivalently the function
| | ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ( (![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ( ;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) , ,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ( ) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa( ;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) ;α) | (7) |
with respect to
α′ or equivalently, the rates
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
for prescribed
α. Here
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
is called the Rayleighian,
62,63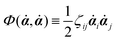
is the positive-definite dissipation-function,
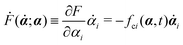
is the change rate of free energy, and
Ẇa(
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
;
α) =
fai(
α,
t)
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) i
i is the work power done by the active force,
fa. The Euler–Lagrange equation for minimizing
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
in
eqn (7) with respect to
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
is
| | 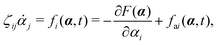 | (8) |
as expected from the Langevin
eqn (2) for dynamic processes where the stochastic forces and fluctuations can be neglected.
† The dynamic equations in
eqn (8) state the balance among the dissipative (frictional) forces, the conservative forces derived from the free energy, and the active forces that are non-conservative and generated by biochemical reactions. This variational principle of minimizing the Rayleighian
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
with respect to the rates
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
was originally proposed by Lars Onsager in 1931
54,60 and usually referred to as The principle of least dissipation of energy or simply Onsager's variational principle (OVP).
We would like to give some remarks on OVP as follows.
(i) A term 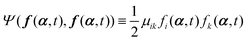 appearing in the Onsager–Machlup function
appearing in the Onsager–Machlup function ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) in eqn (6) does not contribute to the Rayleighian
in eqn (6) does not contribute to the Rayleighian ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) because we are considering the most probable state α′ at an immediate future time close to t, which is to be determined from the prescribed state α and hence the prescribed forces f(α,t) and Ψ(f(α,t),f(α,t)).
because we are considering the most probable state α′ at an immediate future time close to t, which is to be determined from the prescribed state α and hence the prescribed forces f(α,t) and Ψ(f(α,t),f(α,t)).
(ii) The active matter may also be subject to the influence of some external forces that do not arise locally from the consumption of chemical energy of the system. This can be treated by subtracting the work power Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) done by the external forces from the Rayleighian
;α) done by the external forces from the Rayleighian ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) in eqn (7):
in eqn (7):
| | ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ( (![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ( ;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) , ,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ( ) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa( ;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇext( ;α) − Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α). ;α). | (9) |
Minimization of
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
leads to an Euler–Lagrange equation that includes the external forces, in a form generalized from
eqn (8).
(iii) In a continuum model of active matter, the set of slow variables α can represent the field variables both in the bulk and at the boundary. Then eqn (8) derived from OVP gives the dynamic equations both in the bulk and at the boundary, with the latter becoming dynamic boundary conditions. Furthermore, if there are external forces applied at the system boundary, then their contributions may be described by Ẇext in the Rayleighian in eqn (9).
(iv) It is important to note that OVP is a local principle that can be used to find the most probable state only in the immediate future (without additional constraints). To locate the most probable paths that can take the system to the far future under various constraints,60,87 we can divide the long time interval (say, t − t0) into Nt sub-intervals with dt = (t − t0)/Nt, then
| | 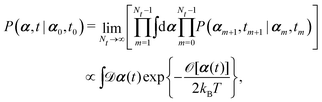 | (10) |
where
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
[
α(
t)] is called the Onsager–Machlup functional or integral defined by
| | 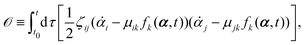 | (11) |
or equivalently, into the following quadratic form
| | 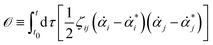 | (12) |
with
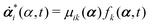
being the actual rates of the system at state
α and time
t. Note that
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
is defined by the time derivative of the state variables
α, while
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
* is defined by the force
f(
α,
t) and depends only on the state variable
α and time
t. The Onsager–Machlup integral is non-negative definite and equals to zero (the minimum) only when
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
equals to the actual kinetic path,
i.e.,
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
=
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
*. Hence the variational principle can be stated that nature chooses the kinetic path which minimizes the Onsager–Machlup functional
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
[
α(
t)] with respect to the state variables
α(
t). This variational principle is called Onsager–Machlup variational principle (OMVP).
63,68 In contrast to OVP, a local principle that predicts the most probable state in the immediate future, the OMVP is a global principle that can determine the most probable path taking the system to the far future under various constraints. For example, it can be used to determine the long-time behaviors such as the steady-states.
63,68 It can also be used to locate the most probable transition pathway that takes the system from one free energy minimum to another.
87,88
2.2 Direct variational methods for approximation solutions
The variational principles introduced previously can be used to obtain thermodynamically-consistent dynamic equations as well as matching boundary conditions. However, the resulting equation systems are usually difficult to solve both analytically and numerically. This subsection deals with some direct variational methods of finding approximate solutions that are obtained directly from above variational principles for the system dynamics in both short and long time scales.63,68,76,89
Variational principles have been proposed in various fields of physics and several variational methods have been developed accordingly to find approximation solutions such as Ritz method and the least-squares method.89 Recently, Doi developed a Ritz-type variational method based on OVP76 by assuming that state variables α(t) is a certain function of a small number of parameters denoted by a = (a1,a2,…), i.e., α(t) = α(a(t)). Then the rate of the state variables ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) can be written as
can be written as
| | 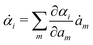 | (13) |
and the Rayleighian is then a function of the rates of parameters
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
(
ȧ). The dynamics of the system described by the temporal evolution of the parameters
a(
t) is determined by minimizing
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
with respect to
ȧ.
Similarly, direct variational method can also be developed based on the OMVP to approximate the long time kinetic paths or states of the system.68 We consider certain kinetic path which involves a parameter set α(a(t)). The best guess for the actual path is the path which gives the smallest value of the Onsager–Machlup functional ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [α(a(t))] with respect to the parameter functions a(t). This variational method is similar to the least-square method but with a target function that is more physically meaningful based on physical principles.68,89
[α(a(t))] with respect to the parameter functions a(t). This variational method is similar to the least-square method but with a target function that is more physically meaningful based on physical principles.68,89
These direct variational methods are useful particularly when we have an idea for the probable kinetic path and can write down the functions α(a(t)). It has been applied successfully to many problems in soft matter dynamics. In this work, we will show that these approximation methods can also be used to study the dynamics of active soft matter.
2.3 Advantages of variational approaches
The above variational principles are equivalent to Onsagers kinetic equations in eqn (8) with kinetic coefficients satisfying Onsager's reciprocal relations, but these variational principles and the direct variational methods have several advantages to investigate the dynamics of non-equilibrium systems as follows.
• Scalar formulation. The variational principles involve only physical quantities that can be defined without reference to a particular set of generalized coordinates, namely the dissipation function, free energy, and active work power. This formulation is therefore automatically invariant with respect to the choice of coordinates for the system, which allows us a great flexibility in choosing state variables and rates.
• Thermodynamic consistency. The variational principles incorporate the intrinsic structure of Onsagers theory of non-equilibrium thermodynamics clearly. They provide compact invariant ways of obtaining thermodynamically-consistent dynamic equation systems where the pairs of rates and forces are obtained automatically.
• Direct variational approximation tools. The direct Ritz-type variational method of finding approximation solutions for the system dynamics bypasses the derivation of the Euler–Lagrange equations and goes directly from a variational statement of the problem to the solution of the Euler–Lagrange equations. This approximation method helps to pick up the most important dynamic behaviors and to simplify the calculations significantly from complicated partial differential equation systems to simple ordinary differential equations. In addition, the direct least-square-type variational method based on OMVP of minimizing the Onsager–Machlup integral further optimizes the search for more realistic kinetic paths and provides a new method of studying long-time steady-state dynamics of the system.
The above variational principles have been successfully applied to the diffusion in electrolyte solutions by Onsager himself in 1940s,57 and more recently applied to various soft matter systems such as multiphase flows,58,69 electrorheological fluids,70 colloid suspensions,80 polymer solutions,53,62,63 polymer gels,39,63 liquid crystals,62,74 vesicles,81 membranes71–73 and so on. This indicates that OVP is an important principle in soft matter dynamics.62,63,68 In this work, we present its applications to active soft matter dynamics that is mostly motivated by biological applications.
Before ending this section, we would like to summarize the general steps for applying OVP to the dynamics of active soft matter for which the dynamic equations are not yet known or still controversial.62,63
(i) Choose a set of coarse-grained, slow variables, α ≡ {α1,α2,…}, to describe the time evolution of the macroscopic state of the system.
(ii) Construct the free energy function, F(α), and calculate the rate of change of the free energy, Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α).
;α).
(iii) Construct the dissipation function, Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ), which is quadratic in the rates/fluxes
), which is quadratic in the rates/fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) .
.
(iv) Find the work power done by the active forces, Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α), based on the specific activity considered, and find the work power done by some other external forces, Ẇext(
;α), based on the specific activity considered, and find the work power done by some other external forces, Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α). The external forces are usually applied at the system boundary and do not arise locally from the consumption of chemical energy of the system.
;α). The external forces are usually applied at the system boundary and do not arise locally from the consumption of chemical energy of the system.
(v) Minimize the Rayleighian in eqn (9): ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (
(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ(
;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ(
) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa(
;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇext(
;α) − Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α), with respect to the rates/fluxes
;α), with respect to the rates/fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) . Note that some additional constraints on the system dynamics may need to be imposed by using Lagrange multipliers.
. Note that some additional constraints on the system dynamics may need to be imposed by using Lagrange multipliers.
Furthermore, if we have an idea about the most probable kinetic path, then we can write down the slow variables α = α(a(t)) as functions of a small number of parameters, a = (a1,a2,…). We can follow the above steps and obtain the Rayleighian as a function of ȧ and a as ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (ȧ;a). The minimization of
(ȧ;a). The minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to ȧ will then provide an approximate description for the active matter dynamics directly.
with respect to ȧ will then provide an approximate description for the active matter dynamics directly.
3 Applications 1: directional motion of individual active units
Activity in biology or in some artificial active systems usually arises from the consumption of ATP and the mechanochemical cross-coupling, but sometimes activity appears simply as time-dependent constraints in geometric shapes. In this section, we consider the first applications of OVP to the directional motion of an individual active unit as shown in Fig. 1: a molecular motor walking on a polar biofilament and a toy two-sphere microswimmer swimming in a viscous fluid.
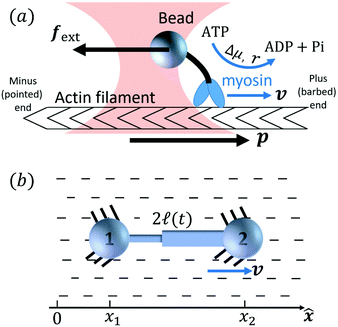 |
| | Fig. 1 Directional motion of individual active units. (a) A myosin motor catalyzes ATP hydrolysis and converts the released chemical energy into its directional motion on an actin filament94 toward the plus (barbed) end. Meanwhile, an external force, fext, is applied on the myosin through optical trapping of a nano-bead attached to the motor. (b) A toy two-sphere microswimmer swims in viscous fluids. The body length, 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t), of the microswimmer oscillates cyclically and the friction coefficient, ζ, is asymmetric for forward motion (with smaller friction) and backward motion (with larger friction), as shown in eqn (23). The front-back asymmetry in friction is indicated by inclined thorns on the microspheres. (t), of the microswimmer oscillates cyclically and the friction coefficient, ζ, is asymmetric for forward motion (with smaller friction) and backward motion (with larger friction), as shown in eqn (23). The front-back asymmetry in friction is indicated by inclined thorns on the microspheres. | |
3.1 Molecular motors walking on biofilaments: mechano-chemical cross-coupling
Molecular motor proteins are enzymes that bind adenosine triphosphate (ATP) and catalyze its hydrolysis to adenosine diphosphate (ADP) and inorganic phosphate (Pi):90The chemical energy released from this ATP hydrolysis is partially converted into mechanical work or directional motion of motors along some stiff biofilaments that are made of other proteins. Animal cells in vivo contain over a hundred different motor proteins, which can be classified into three different families: myosins moving along actin filaments, kinesins and dyneins moving along tubulin filaments. The underlying biofilaments are usually periodic and fairly rigid structures with a period ξ ∼ 10 nm. They are moreover polar or asymmetric, so that one can define a “plus” end and a “minus” end. A given motor always moves in the same deterministic direction: myosin moves along actin filaments towards their plus end, and kinesins and dyneins move along tubulin filaments towards their plus and minus ends, respectively. Motor molecules play a key role in cell contraction, cell division, intracellular transport, and material transport along the axons of nerve cells, etc.90
In this subsection, we use OVP to formulate a thermodynamic description in the linear (near-equilibrium) regime for the directional motion of a translationary molecular motor along a polar filament against an external force, as shown in Fig. 1a. This Onsager-type description is pioneered by Kedem & Caplan91 and extended by Chen & Hill.92 We take our thermodynamic system to include the molecular motor and the surrounding solution of ATP, ADP, and Pi. The system is coupled to a heat reservoir and a work reservoir, which can apply external forces on the motor, for example, by optical tweezers, that is, optical trapping of a nano-probe attached to the motor (see Fig. 1a). The states of the thermodynamic system can be described by the average motor position x, the polarization vector p (describing the polarity of the filament and assuming to point from minus end to plus end), and the average number Nα of chemical components involved in ATP hydrolysis with α = ATP, ADP, and Pi.
The reaction free energy for ATP hydrolysis takes the form of
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r = r = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r(NATP,NADP,NPi), r(NATP,NADP,NPi), | (15) |
from which we find the rate of the change of free energy as
4| | 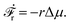 | (16) |
Here
r ≡ d
ξ/d
t is the reaction rate of ATP hydrolysis with
ξ being the reaction extent, d
ξ ≡ d
Nα/
να = −d
NATP = d
NADP = d
NPi, and
να being the stoichiometric coefficients (negative for reactants and positive for products, here
νATP = −1,
νADP = +1, and
νPi = +1). Δ
μ is the reaction affinity of ATP hydrolysis, given by
| | 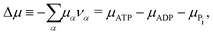 | (17) |
which measures the free-energy change for the hydrolysis of each ATP molecule. At chemical equilibrium Δ
μ = 0, whereas it is positive when ATP is in excess and negative when ADP is in excess. Under
in vivo conditions, ATP is usually in excess with Δ
μ > 0; the reason may be that ATP has evolved as a biological hydrotrope to keep biomolecules soluble at high concentrations and subsequently used a the “energy currency” of the cell due to its high energy phospho-diester bonds.
93
The irreversible dynamics of the thermodynamic motor/filament system is characterized by two rates: the reaction rate r and the average motor velocity v = ẋ. In the linear response regime close to equilibrium, the dissipation function is a quadratic function of the rates given by
| | 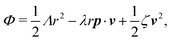 | (18) |
and the rate of work done by the external force
fext to the motor is given by
Here
Λ and
ζ are generalized friction coefficients, and
λ is the mechanochemical coupling coefficient, which is nonzero only if the filaments are polar and can be either positive or negative.
95 The positive-definiteness of the dissipation function requires
Λ,
ζ > 0 and
Λζ −
λ2 > 0. The degree of mechanochemical cross-coupling can be quantified by
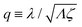
(with −1 <
q < 1), as suggested by Kedem and Caplan.
91
Using the Rayleighian 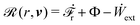 in the presence of the external force and eqn (16)–(19), we minimize
in the presence of the external force and eqn (16)–(19), we minimize ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to r and v and obtain
with respect to r and v and obtain
Here we have taken
v and
fext to be in parallel with
p; a positive
v (or
fext) means the motion of the motor (or the direction of the external force) is along the direction of
p, pointing toward plus end as assumed. Note that the Onsager reciprocal relation for mechanochemical cross-coupling is automatically satisfied. Physically,
eqn (20b) can be written as a balance equation
fext +
fa +
ffric = 0 for the external force
fext, the active force
fa =
λr, and the frictional force
ffric = −
ζv.
To be specific, for the in vivo motion of myosin motors along actin filaments, ATP is usually in excess with a constant Δμ > 0 and myosin motor always move towards to the plus end of the actin filament. Therefore, the load-free motor velocity 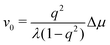 (for fext = 0) must be positive (and hence λ > 0 and 0 < q < 1). In this case, we can identify the following four regimes from eqn (20):
(for fext = 0) must be positive (and hence λ > 0 and 0 < q < 1). In this case, we can identify the following four regimes from eqn (20):
(i) For fext > 0, we have v > 0 and r > 0 (hence fextv > 0 and rΔμ > 0), the external force pulls the motor to the plus end. Meanwhile, the excess ATP hydrolyzes and the chemical energy is consumed to drive the motor along the same direction to the plus end.
(ii) For small negative force fext < 0 and fext > fstall,v, we still have v > 0 and r > 0 (hence fextv < 0 and rΔμ > 0), the excess ATP hydrolyzes and the released chemical energy is converted into mechanical work. Here fstall,v = −λΔμ/Λ < 0 is called stall force of myosin motion and when fext = fstall,v, the motor is stationary with v = 0.
(iii) For fstall,r < fext < fstall,v, the moving direction of the motor is reversed with v < 0 and hence fextv > 0. That is, the external force is doing positive work on the motor moving along the plus end. However, we still have r > 0 and hence rΔμ > 0. That is, the excess ATP hydrolyzes and the released chemical energy also drives the motion the motor towards the same plus end. Here fstall,r = −Δμζ/λ < 0 is called stall force of ATP hydrolysis and when fext = fstall,r, the ATP hydrolysis is inhibited with r = 0.
(iv) For fext < fstall,r < 0, we have v < 0 and r < 0, hence fextv > 0 and rΔμ < 0. That is, the external force is doing positive work on the motor and produces ATP that is already in excess; the system then works as an ATP pump.
Therefore, the motor/filament system is a reversible machine: it can not only convert chemical energy into mechanical work, but can also convert mechanical work into chemical energy. In this work, we are particularly interested in the regime (ii), in which ATP hydrolysis occurs spontaneously and the released chemical energy is used to drive the system out of equilibrium continuously.
Now let's consider a practical limit at which the ATP hydrolysis rate r (or equivalently the active force fa = λr) is taken as a given positive parameter that measures the activity of the system. That is, the effect of mechanical forces on the ATP hydrolysis is neglected and the rate of ATP hydrolysis is determined dominantly by the chemical affinity as r ≈ Λ−1Δμ > 0. This leads to a reduced description in which the position of the molecular motor in directional motion becomes the only state variable, while the amounts of the reactants and products in the ATP hydrolysis are no longer involved. As a result, the Rayleighian reduces to its extended form in eqn (9) as
| | 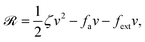 | (21) |
in which
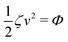
is the dissipation function,
fav =
Ẇa is the rate of work done by the active force to the reduced system, and
fextv =
Ẇext is the rate of work done by the external force. Minimizing this Rayleighian gives the force balance equation −
ζv +
fa +
fext = 0.
Finally, we would like to point out that the results obtained here from thermodynamic description for the motion of molecular motors on polar filaments are completely independent of any underlying microscopic mechanisms. However, the above linear-response theory applies only to the linear regime near equilibrium where Δμ/kBT ≪ 1 and fextξ/kBT ≪ 1 with ξ being the typical molecular size of relevant proteins. In real life, molecular motors mostly operate far from equilibrium (with Δμ ∼ 10kBT) and the velocity v(fext,Δμ) and the rate of ATP consumption r(fext,Δμ) are in general highly nonlinear. Therefore, more specific models such as a minimal two-states model for molecular motors should be constructed to arrive at a more comprehensive understanding of the specificity and robustness of the directional motion of motors in highly fluctuating environment.95
3.2 A toy two-sphere microswimmer: active shape changes
Many animals and cells can actively change their shape in some periodic or cyclic manner to migrate on frictional substrates or swim in their surrounding viscous fluid environment.9,10,96–98 For example, snakes and some worms migrate on the ground by generating body waves to change their shapes.96 Some bacteria such as Escherichia coli, swims in fluids through bundling and rotating their flagella as driven by rotary motors.9,10 Many types of animal cells can also migrate on substrates by dramatic periodical shape changes97 as primarily driven by their active cellular cortex that consumes chemical energy. It is interesting to note that in most of the cell migration driven by active shape changes, the cell migration velocity shows highly nonlinear dependence on the active force or the active shape-changing velocity of the cell. This seems to go far beyond the linear-response regime and be out of the scope of OVP. However, we will show that OVP developed in the linear-response regime can still be employed if we expand the set of state variables63 to include not only the center-of-mass position of the cell but also the fast changing body length which describes the shape change.
Specifically, to show how periodic shape changes can generate directional self-propulsion, here we consider a toy microswimmer that is composed of two microspheres99 as shown in Fig. 1b. Let x1 and x2 denote the coordinates of these two microspheres. Then the directional motion and the shape changes of the microswimmer can be described by the temporal evolution of the center-of-mass position 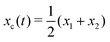 and the half-body-length of the swimmer
and the half-body-length of the swimmer 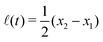 , which are taken as the two slow variables. The toy microswimmer can actively change its shape by periodically changing its body length (or the distance between the two spheres) 2
, which are taken as the two slow variables. The toy microswimmer can actively change its shape by periodically changing its body length (or the distance between the two spheres) 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) as
(t) as
where
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0 is the half of the average body length of the microswimmer,
a and
ω are the amplitude and frequency of the shape oscillations, respectively, and the shape-oscillation period is
T![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
= 2π/
ω.
The toy microswimmer subjected to the periodic shape oscillations can achieve directional motion only when there exists some mechanisms that break the front-back symmetry. Here we consider an asymmetry in the viscous friction, defined by fv = −ζ(ẋ)ẋ, in which the friction coefficient ζ(ẋ) depends on the moving direction of each microsphere according to:
| | 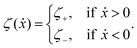 | (23) |
The dynamics of the microswimmer is characterized by the velocities (the rates),
ẋ1 and
ẋ2, of the two spheres. To the leading order in the two rates, the dissipation function is given by
| | 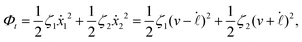 | (24) |
where
v =
ẋc is the center-of-mass velocity of the microswimmer,
ζ1 and
ζ2 are the frictional coefficients given in
eqn (23) that depend on the signs of
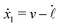
and
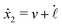
, respectively. Note that the dissipation function
Φt is actually not quadratic in dissipative rates any more but highly nonlinear; a highly nonlinear dissipation function has been discussed in classical mechanics of particles before.
100
In most microswimmers, it is natural to assume that there is a clear separation of time scales between their shape oscillations and the directional motion. The directional motion of the microswimmer is usually much slower than its shape oscillations, i.e., ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/v ≫ T
0/v ≫ T![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . We can, therefore, integrate out the relatively fast varying variable, the half-body-length
. We can, therefore, integrate out the relatively fast varying variable, the half-body-length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t), in one cycle of shape oscillation and arrive at a time-averaged dissipation function of the slow variable, the center-of-mass velocity v, by
(t), in one cycle of shape oscillation and arrive at a time-averaged dissipation function of the slow variable, the center-of-mass velocity v, by 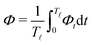 as
as
| | 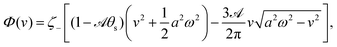 | (25) |
where
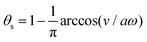
for |
v| ≤
aω and
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
= 1 −
ζ+/
ζ− is a dimensionless parameter measuring the degree of the front-back asymmetry in the friction coefficients. Note that this dissipation function is not quadratic but highly nonlinear in the rate
v. We can define the Rayleighian
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
(
v) =
Φ −
Φ(
v = 0) to determine the time-averaged directional motion of the toy microswimmer. Minimization of
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
(
v) gives the cell migration velocity
v as a function of the active velocity
aω of the periodic shape change, and this function can be compared to experimental observations. Furthermore, in the limit of small
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
, we have |
v| ≪
aω and the Rayleighian can be approximated, to the leading order, by
| | 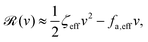 | (26) |
where
ζeff =
ζ− +
ζ+ is the effective frictional coefficient and
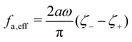
is a time-averaged effective active force that drives the directional self-propulsion of the microswimmer. Minimization of
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
gives the directional velocity of the microswimmer as
which approaches
v =
aω![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
/π in the limit of weak asymmetry with
ζ+/
ζ− → 1
− or
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
→ 0
+.
We would like to give some remarks on the directional motion of the toy two-sphere microswimmer as follows.
(i) Most dynamic behaviors of biological systems show strong nonlinearity. For example, in the toy two-sphere microswimmer, the swimmer migration velocity shows highly nonlinear dependence on the active force or the active shape-changing velocity of the swimmer. However, in many cases, OVP can still be employed if we expand the set of slow state variables properly.63 For example, here our set of slow variables includes not only the center-of-mass position of the swimmer but also its fast-changing body length.
(ii) The dissipation function is non-zero even for symmetric microswimmers (with ζ = ζ− = ζ+) when there is no average directional motion (i.e., v = 0): 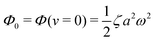 . It arises in the symmetric microswimmer from the viscous dissipation due to the fast shape-oscillation in viscous fluids.
. It arises in the symmetric microswimmer from the viscous dissipation due to the fast shape-oscillation in viscous fluids.
(iii) Similar to the walk of molecular motors in the previous example, the active shape changes of microswimmers are also driven by spontaneous ATP hydrolysis. Then the irreversible dynamics of the microswimmer should be characterized by the rate of ATP hydrolysis r in addition to the sphere velocities, ẋ1 and ẋ2. The rate of the change of free energy is given in eqn (16) by 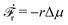 . The dissipation function is given, to the leading order in the rates, by
. The dissipation function is given, to the leading order in the rates, by
| | 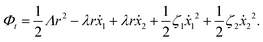 | (28) |
Also as mentioned in the previous example, in many practical cases we can take a limit at which the ATP hydrolysis rate
r and hence the active force
fa =
λr is a given positive parameter. This leads to a reduced description in which the dynamics of the microswimmer is described only by the sphere velocities. In this case, the Rayleighian takes to the general form of
eqn (7) as
| | 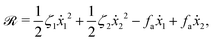 | (29) |
in which the first two terms compose the dissipation function
Φ(
ẋ1,
ẋ2), the last two terms compose the rate of work done by the active forces to the system with
Ẇa =
faẋ1+ (−
fa)
ẋ2. Minimizing this Rayleighian with respect to
ẋ1 and
ẋ2 gives the force balance equations for each sphere:
| | | fa − ζ1ẋ1 = 0, −fa − ζ2ẋ2 = 0, | (30) |
respectively. Here the pair of active forces
fa and −
fa forms a force dipole on the microswimmer. If the rate of the ATP hydrolysis
r is oscillating and the resulted active force
fa =
λr takes the form of
| | 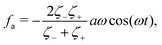 | (31) |
then it will drive a shape oscillation defined in
eqn (22). Note that the effective active force
fa,eff in
eqn (26) is not a simple time-average of the oscillating active force
fa in
eqn (31), but is the “net” active force that drives the directional motion of the microswimmer.
Finally, we would like to point out that in our toy two-sphere microswimmer, the two necessary conditions for a steady directional motion are the active shape oscillations as the energy input and the frictional asymmetry that breaks the front-back symmetry. Similarly, for a long thin swimming micro-filament, the hydrodynamic friction is anisotropic: it experiences less friction when moving along its axis than perpendicular to it. In this case, a cyclic beat pattern on the filament will be able to drive directional propulsion in a similar manner as in the above one-dimensional toy microswimmer‡.
4 Applications 2: active polar fluid models for collectives of active units
Let's now consider an active fluid that includes collectives of active units with anisotropic shapes and polarity such as rod-like self-propelled colloids,3 rod-like bacteria,3,9,10 and the active networks of stiff filaments in the cytoskeleton of living cells.1,2 The constituting active units can assume chemical energy to apply (extensile or contractile) dipole forces to their surrounding inert environment that drive the system locally out of equilibrium, as schematically shown in Fig. 2. Such active fluids are in contrast to more familiar passive (inert) non-equilibrium systems which are usually driven externally at their boundaries.28
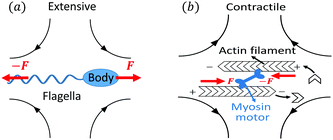 |
| | Fig. 2 Active stresses generated by active units: (a) extensile force dipoles generated by the bacterial microswimmer, and (b) contractile force dipoles generated by the actomyosin filament. | |
4.1 Active polar fluid regarded as a reactive fluid
Active fluids with polar constituent agents often show phase separation (with coexisting dilute and dense phases) and collective orientational or polar order (with collective alignment on average).1,43 Such an active polar fluid can be viewed as a reactive fluid where viscous flows and diffusion are closely coupled with biochemical reactions.1,4 A generalized hydrodynamic theory has been developed to describe the dynamics of such active polar fluids, phenomenologically based on conservation laws and symmetry considerations,1,4 which is in complete compatibility with micro-reversibility and Onsager's reciprocal relations. This is in contrast to other methods of modeling active polar fluids where some active (non-equilibrium) terms are selectively added to the dynamical equations for their passive counterparts to break TRS.43,48,85,101 In these methods, the rates of biochemical reactions in the active fluids are implicitly assumed to be a constant that is independent of the surrounding mechanical environment and simply determined by some preset reaction affinity. In this case, the active terms arising from biochemical reactions can not be derived from any free energy or dissipation function, and hence can only be added in an ad hoc manner.
In this subsection, we present an alternative derivation of the generalized hydrodynamic model for an active polar fluid that is regarded as a reactive fluid involving the ATP hydrolysis/synthesis. In the next subsection, we will show that in the same active polar fluid, if the effects of polarization and flow on the ATP hydrolysis are negligible, then the rate of ATP hydrolysis becomes a constant simply determined by the preset constant chemical affinity Δμ. The activities, driven by the spontaneous ATP hydrolysis, are then represented by local external non-conservative force fields that are added as the active terms to the dynamic model of a passive polar fluid.
To be specific, here we use OVP to derive a diffuse-interface model for a droplet of active polar fluids moving on a solid substrate, as schematically shown in Fig. 3a. The states of such an active polar droplet can be described by the following slow field variables: the scalar composition field ϕ(r,t) (distinguishing the coexisting passive isotropic phase from the active polar phase), the polarization vector field p(r,t) (describing the average orientation of active polar agents), the average fluid velocity field v(r,t), and the density field nα(r,t) of chemical components involved in ATP hydrolysis (eqn (14)) with α = ATP, ADP, and Pi. For an active polar fluid that is confined between solid substrates or flows at the solid surfaces, the total free energy includes four contributions, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [ϕ,p,nα] =
[ϕ,p,nα] = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ϕ +
ϕ + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p +
p + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r +
r + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) s, as respectively given by
s, as respectively given by
| | 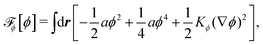 | (32a) |
| | 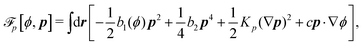 | (32b) |
| | 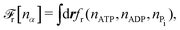 | (32c) |
| | 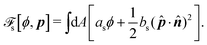 | (32d) |
Here
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ϕ
ϕ is the free energy for the two (isotropic and polar) phase coexistence, in which a and the stiffness parameter
Kϕ are both constants.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p
p is the free energy for polar liquid crystallinity, in which for simplicity, we employ the approximation of one elastic constant
37,102Kp and we take
b1(
ϕ) = −
b0ϕ with
b0 > 0 that controls the isotropic-to-polar phase transition:
b1 < 0 in the polar phase (with
ϕ = 1) and
b1 > 0 in the isotropic phase (with
ϕ = −1). Note that the last cross-coupling term in
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p
p represents the cases of perpendicular anchoring at the isotropic-polar phase interfaces and defines the orientation of
p: if
c > 0,
p points from polar phase to isotropic phase.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r
r is the reaction free energy for ATP hydrolysis: if d
fr/d
nATP > 0 (that is, ATP is in excess), the forward ATP hydrolysis is exergonic, occurs spontaneously, and can be used to drive the changes in the motor configurations and generate mechanical motion, resulting in active dipole forces on the the surrounding passive polar fluids (see
Fig. 2). In this case, the polar fluid will never reach thermodynamic equilibrium states and will be driven locally out of equilibrium by the active units or the motors that consumes ATP.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) s
s is the surface energy at the substrate surfaces (with
as and
bs being constants, and
A being the surface area), which characterizes the adhesion strength of active units to the surface and the anchoring conditions for the agent orientation. Note that such a free energy
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
will stabilize a droplet of active polar phase (
ϕ ≃ 1 and |
p| ≃ 1) in coexistence with surrounding fluids of passive isotropic phase (
ϕ ≃ −1 and |
p| ≃ 0), or
vice versa.
43
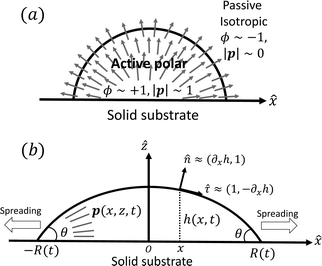 |
| | Fig. 3 A droplet containing a large number of active units on a solid substrate. (a) A general two-phase diffuse-interface model of an active droplet moving on solid substrates. A droplet of active polar phase is stabilized to coexist with surrounding fluids of passive isotropic phase. (b) Spreading of a thin active droplet on a solid substrate. Planar or homogeneous anchoring condition is assumed at all bounding surfaces with which the active units are in contact. | |
The composition variable, ϕ, is a conserved phase parameter and its dynamics follows the following conservation equation
However, the polarization vector
p is not conserved and its rate of change is defined by
ṗ ≡ ∂
p/∂
t +
v·∇
p. Furthermore, the density fields
nα (with
α = ATP, ADP, and P) are also not conserved due to the presence of chemical reaction of ATP hydrolysis or synthesis, and
nα follows the dynamic equation of the form
| | | ∂tnα = −∇·(nαv) + rνα. | (34) |
Here
να is the stoichiometric coefficients (see the discussion about ATP hydrolysis after
eqn (16)). The reaction rate
r ≡ d
ξ/d
t depends on the concentrations of all chemical components. (This dependence is one of the constitutive relations to be derived later from OVP and given in
eqn (45c).) However, in the present work, we do not intend to go into the specific expression of this concentration dependence because our purpose is to show that accompanying the chemical reaction, a mechanical force arises from the mechanochemical coupling as the active force. It is also noted that the general dynamics of ATP hydrolysis should be described by reaction-diffusion equations. However, for simplicity, here we neglect the diffusion processes, assuming that the density of each component is simply advected by the flow and produced or consumed by the chemical reaction.
Using eqn (33) and (34) and the definition of ṗ, we obtain the change rate of free energy from eqn (32) as
| | 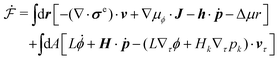 | (35) |
where
σe is the Ericksen stress tensor
37,62,74 given by
| | σe = −![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) I − Kϕ∇ϕ∇ϕ − Kp∇pk∇pk − cp∇ϕ, I − Kϕ∇ϕ∇ϕ − Kp∇pk∇pk − cp∇ϕ, | (36) |
and
σe satisfies the generalized Gibbs–Duhem relation
| | 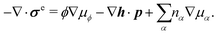 | (37) |
Here
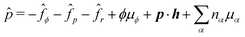
is the generalized pressure with
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) m
m (
m =
ϕ,
p,
r) being the volume density of free energy in
eqn (32),
μα ≡ ∂
fr/∂
nα being the chemical potential, and the reaction affinity, Δ
μ, of ATP hydrolysis given in
eqn (17). The chemical potentials
μϕ in the bulk and
L at the solid surfaces are, respectively, given by
| | 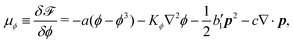 | (38) |
| | L ≡ as + Kϕ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·∇ϕ + c ·∇ϕ + c![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·p, ·p, | (39) |
with
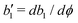
denoting the derivative of
b1. The molecular field
h in the bulk and
H at the solid surfaces are, respectively, given by
| | 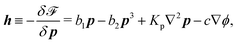 | (40) |
The energy dissipation function Φ is a quadratic function of three dissipative rates: the shear rate 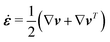 , the rate of change of polarization ṗ, and the rate of ATP hydrolysis r. These rates have the same time parity and from symmetry considerations, Φ can be written into the following invariant scalar form as62
, the rate of change of polarization ṗ, and the rate of ATP hydrolysis r. These rates have the same time parity and from symmetry considerations, Φ can be written into the following invariant scalar form as62
| | 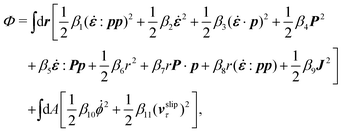 | (42) |
where the frictional coefficients
β1,…,
β11 are constants and the resulted frictional coefficient matrix,
β, is positive definite. That is, the diagonal coefficient terms in
β are all positive, but the off-diagonal coefficient terms that describe the cross-coupling effects between two dissipative processes can be negative (although some other inequality relations have to be satisfied to keep the positive-definiteness of
β). Note that the proper dissipative rates that are present in
Φ and associated with the orientational dynamics of
p is not
ṗ but the convected co-rotational time derivative
37,62,63,74 of
p:
| | | P ≡ ṗ − ω × p = ṗ + Ω·p, | (43) |
which characterizes the rotation of
p relative to the rotation of surrounding fluids with
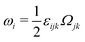
being the vorticity, and
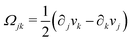
being the antisymmetric part of the velocity gradient tensor. Moreover, for simplicity, we have neglected the cross coupling among the transport of
ϕ, the dynamics of polarization, and the ATP hydrolysis in the bulk fluid. This coupling can represent the treadmilling dynamics of the constituting components.
103 We have also ignored the possible dissipative relaxation processes associated with the anchoring of
p at the solid surfaces. In addition, we would like to point out that the choice of dissipative rates in active polar fluids is not unique.
50,51 Another set of rates has been taken by Marchetti
et al.:
1 the viscous stress
σv (or the momentum flux),
r and
P. In this case, the time parity of
σv is different from the other two rates
r and
P. A brief discussion about the consequences of different choices of dissipative rates or thermodynamic fluxes on the symmetry of Onsager coupling matrix and the applications of OVP has been presented in the Appendix Section A.2.
Then the Rayleighian is given by
| | 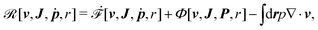 | (44) |
where the local incompressibility constraints, ∇·
v = 0, have been taken into account with the pressure
p being the Lagrange multiplier. Minimization of
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
[
v,
J,
ṗ,
r] with respect to the rates gives the dynamic equations for two-phase active polar flows as
| | | −∇p + ∇·(σe + σv + σa) = 0, | (45a) |
| | h = γ1P + γ2p·![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) − ha, − ha, | (45b) |
| | Δμ = −λp·P − ![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) pp: pp:![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + Λr, + Λr, | (45c) |
together with the incompressibility condition ∇·
v = 0, the dynamic equations for
ϕ in
eqn (33) and for
nα in
eqn (34). The stress tensors,
σe,
σv, and
σa, are, respectively, given by
eqn (36), and
| | σv = α1(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) :pp)pp + α2pP + α3Pp + α4 :pp)pp + α2pP + α3Pp + α4![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + α5pp· + α5pp·![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + α6 + α6![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) ·pp, ·pp, | (46a) |
| | σa = −![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) rpp, rpp, | (46b) |
with
αi being the Leslie viscosity coefficients. Note that
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif)
in
σe in
eqn (36) can be absorbed into
p in
eqn (45a) due to the incompressibility of the active polar fluids. The active molecular field
ha is driven by ATP hydrolysis and is defined
viaThe diffusion flux in
eqn (33) is given by
J = −
M∇
μϕ. Note that the mechanochemical cross-coupling indicated in
eqn (45) is similar (although more complex) to
eqn (20) for the mechanochemical coupling in the motor/filament system in Section 3.1. The general discussions there about the reversible conversion of chemical energy and mechanical work also apply here in active polar fluids. We will also focus on the regime where ATP is in excess and its hydrolysis occurs spontaneously and the released chemical energy is used by the suspending active units to drive the surrounding inert polar fluids out of equilibrium continuously.
Furthermore, from the minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [v,J,ṗ,r], we can also obtain the thermodynamically-consistent boundary conditions at the solid surfaces that supplements the dynamic equations in the bulk fluids:
[v,J,ṗ,r], we can also obtain the thermodynamically-consistent boundary conditions at the solid surfaces that supplements the dynamic equations in the bulk fluids:
| | | ∂tϕ + vτ·∇τϕ = −ΓL(ϕ,p), | (48a) |
| | 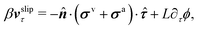 | (48b) |
together with the impermeability boundary conditions,
| | ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·v = 0, ·v = 0, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·J = 0, ·J = 0, | (48c) |
and the equilibrium anchoring boundary condition,
| | H ≡ bsp·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) + Kp + Kp![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·∇p = 0. ·∇p = 0. | (48d) |
Here the subscript
τ denotes the tangential component in the plane of the substrate. Note that the boundary condition for the tangential velocity in
eqn (48a) is similar to the generalized Navier boundary condition (GNBC) formulated for immiscible two-phase flows at solid surfaces.
58 The frictional coefficient
β now depends on the adhesion strength of the active fluids on the substrate surfaces.
The phenomenological coefficients in the above equation systems are functions of the frictional coefficients βi in the dissipation function Φ in eqn (42) as62
| | 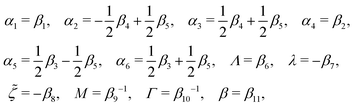 | (49) |
with
γ1 =
α3 −
α2 and
γ2 =
α6 −
α5. Note that the Parodi relation
α2 +
α3 =
α6 −
α5 and the symmetry of coefficients for cross-coupling effects are all automatically satisfied.
4.2 Active polar fluid regarded as a passive polar fluid under local external non-conservative fields
In the last part of Section 3.1, we have considered a practical and useful limit at which the effect of mechanical forces on the ATP hydrolysis can be neglected and the rate of ATP hydrolysis is determined dominantly by the chemical affinity as a constant parameter. Here we consider the same limit of the above general dynamics of active polar fluids: the effects of polarization and flow on the ATP hydrolysis are negligibly small, and the rate r in eqn (45c) is constant and simply determined by the reaction affinity or the change of reaction free energy, i.e., r ≈ Λ−1Δμ. In this case, the rate of change of the free energy and the dissipation function reduce to| | 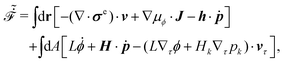 | (50) |
| | 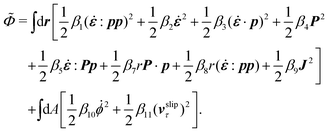 | (51) |
It is interesting to note that the two mechanochemical cross-coupling terms (the two terms with coefficients β7 and β8) in ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) , parametrized by the constant reaction rate r, can be rewritten as
, parametrized by the constant reaction rate r, can be rewritten as 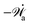 ,
,| | 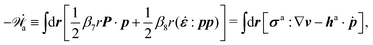 | (52) |
in which the active stress σa defined in eqn (46b) and the active molecular field ha defined in eqn (47) now becomewith ζ ≡ ![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) Λ−1Δμ and ζh ≡ λΛ−1Δμ. The cross-coupling coefficients β7 and β8 (hence ζ and ζh) can be either positive or negative as long as they can preserve the positive definiteness of the dissipation function. For example, negative and positive values of ζ correspond to contractile and extensile active stresses, respectively, as schematically shown in Fig. 2.
Λ−1Δμ and ζh ≡ λΛ−1Δμ. The cross-coupling coefficients β7 and β8 (hence ζ and ζh) can be either positive or negative as long as they can preserve the positive definiteness of the dissipation function. For example, negative and positive values of ζ correspond to contractile and extensile active stresses, respectively, as schematically shown in Fig. 2.
We would like to further point out that eqn (52) indicates that in the limit of constant reaction rate of ATP hydrolysis, the ATP-induced activity in the active polar fluid can be regarded simply as some local non-conservative fields applied externally on the passive polar fluid. The active characteristic of these external fields is reflected in the fact that the active stress σa and the active molecular field ha both depend on the local state variable (the polarization), p. Furthermore, these active fields driven by spontaneous ATP hydrolysis break the time-reversal symmetry of the polar fluids.
It follows that according to the general form of eqn (7), the Rayleighian in eqn (44) can be rewritten as
| | 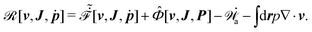 | (54) |
Here
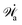
represents the work power done on the passive polar fluids by the active stress
σa and the active molecular field
ha. The dissipation function
![[capital Phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a9.gif)
for the passive polar fluid is given by
| | 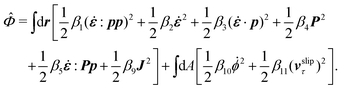 | (55) |
Minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) gives the following simplified dynamic equation system:
gives the following simplified dynamic equation system:
(i) The dynamic equations for v: the incompressibility condition ∇·v = 0, the generalized Stokes' equation in eqn (45a) with the stress tensors σe, σv, and σa, given in eqn (36), (46a), and (53a), respectively;
(ii) The dynamic equation for ϕ: the conservation equation in eqn (33) with J = −M∇μϕ;
(iii) The dynamic equations for p:
| | P = γ1−1h − γ1−1γ2p·![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + γ1−1ha, + γ1−1ha, | (56) |
with the active molecular field
ha given in
eqn (53b) and the passive molecular field
h given in
eqn (40);
(iv) The boundary conditions in eqn (48) still apply to the present case.
We would like to point out that in Section 4.1, a complete model is constructed to incorporate the chemical reaction and explicitly describe the mechanochemical coupling. In this description, the time-reversal symmetry (TRS) is preserved, and so is Onsagers reciprocal relation (ORR) for mechanochemical coupling. In Section 4.2, the limit of constant reaction rate is taken, and a simplified model is obtained from the complete one in Section 4.1. In this limit, the TRS is lost, and so is ORR for mechanochemical coupling. However, the Parodi relation for the cross coupling in the passive polar fluid is still preserved.
Finally, we note that the dynamic equation system for two-phase active polar flows on solid substrates is similar to that for two-phase passive polar flows on solid substrates, but is supplemented by some extra active terms (here the active stress σa and the active molecular field ha) that break the TRS. This type of diffuse-interface model has been solved numerically as a minimal model for cell motility.49,104
5 Applications 3: dynamics of thin active droplets on solid substrates
In this section, we consider a thin droplet of active polar fluids moving on a solid substrate in a simple two dimensions (xz plane), as schematically shown in Fig. 3b. The detailed dynamics of such a droplet can be described by the full dynamic equation system that is derived in the previous Section 4. However, here we present a thin film description of the active droplet on solid substrates where the lubrication approximation applies.101,102,105–107 In this case, the shape of the droplet is described by its thickness h(x,t) in the vertical z direction as a function of horizontal position x at time t, as shown in Fig. 3b. The hydrodynamic velocity field and the average orientation of the active polar filaments inside the two-dimensional drop are represented by v(x,z,t) = (u,w), and the polarization vector p(x,z,t), respectively. Similar problems have been studied by several groups108–110 for thin films of passive liquid crystals, by Kitavtsev et al.111 for thin films of active liquid crystals, by Sankararaman & Ramaswamy105 for thin films of active polar fluids, and by Joanny & Ramaswamy102 for thin drops of active polar fluids. Here we use OVP to provide an alternative derivation of thin film equations for active polar droplets and to find approximate scaling laws for the spreading or dewetting of the droplet on solid substrate.
5.1 Thin film equations for active polar fluids
We firstly use OVP to derive the thin film equations for a thin active polar droplet moving on a solid substrate. To be specific and simple, we make several assumptions as follows.
(i) The active fluid is incompressible, satisfying the incompressibility condition, ∇·v = ∂xu + ∂zw = 0, from which we get the local mass conservation equation for the evolution of film height as
| | 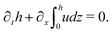 | (57) |
Here and in the following, we use ∂
α to denote the partial derivatives with respect to the variable
α such as time
t, coordinates
x and
z.
(ii) The lubrication approximation66,77,112,113 is applied to the thin-film dynamics of the active polar droplet on the solid substrate. In the long-wave limit, the characteristic film thickness h0 is much smaller than the length scale R0 for variations in the x direction, i.e., h0/R0 ≪ 1. It follows that the film thickness varies slowly in space with |∂xh| ≪ 1. Given h0/R0 ≪ 1 and ∇·v = 0, we obtain that the flow velocity v is approximately along the x direction with w ≪ u.
(iii) The equilibrium contact angle of the droplet θe is very small such that Young's equation is approximated as
| | 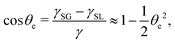 | (58) |
where
γ is fluid–gas surface tension,
γSG solid–gas surface tension, and
γSL solid–fluid surface tension.
(iv) We only consider droplet dynamics with left-right symmetry and the droplet shape is mainly determined by its interfacial energy and the effects of nematic elastic energy can be neglected. This arises when the characteristic thickness of the droplet is much larger than hK ∼ Kp/γ with Kp being the elastic constant defined in eqn (32b). Then the total energy functional of the droplet is given by
| | 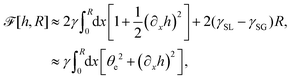 | (59) |
where
R is half of the contact length of the droplet with the solid substrate. The rate of change of the total energy is easily obtained as
| | 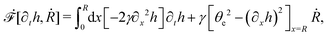 | (60) |
where we have used the identity ∂
th +
Ṙ∂
xh = 0 (obtained from
h(
x =
R(
t),
t) = 0) at the contact line
x =
R.
(v) The active filaments inside the droplet lack a head–tail polarity, that is, p and −p are equivalent, but they can show average nematic alignment. Furthermore, in the case of thin active droplets, the z dependence of p = (px,pz) is determined by the equilibrium equations,
which are obtained from the minimization of nematic elastic energy,
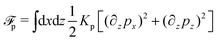
, similarly as defined in
eqn (32b) under the approximation of one elastic constant,
Kp, and fixed magnitude of
p.
(vi) We assume the planar anchoring conditions at any bounding surfaces with which the active filaments are in contact, that is, the polarization vector p is parallel to the tangent direction of all the bounding surfaces. Here we then have: p = ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) at z = 0 and p =
at z = 0 and p = ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b8.gif) ≈ (1,∂xh) at the free surface z = h, in which
≈ (1,∂xh) at the free surface z = h, in which ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) is the unit vector along the x-direction and
is the unit vector along the x-direction and ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b8.gif) is the unit tangent vector of the free surface of the droplet. This anchoring boundary condition is mainly motivated by the stress-fiber structure in adherent cells2 and by the experimental observations114 on thin films of amoeboid cells, in which the cells lie in the plane of the glass slide on which they spread and form nematic liquid-crystal structures. The planar anchoring conditions at the free surface have been employed in many previous works.98,102,105,106 In contrast, in our diffuse-interface model of active polar droplets in Section 4, we have assumed planar anchoring condition at the solid surface but perpendicular anchoring condition at the free interface, which mimics the orientation of actin filaments in the lamellipodium of migrating cells. Such anchoring boundary conditions have also been used in many previous works.43,49,101,104
is the unit tangent vector of the free surface of the droplet. This anchoring boundary condition is mainly motivated by the stress-fiber structure in adherent cells2 and by the experimental observations114 on thin films of amoeboid cells, in which the cells lie in the plane of the glass slide on which they spread and form nematic liquid-crystal structures. The planar anchoring conditions at the free surface have been employed in many previous works.98,102,105,106 In contrast, in our diffuse-interface model of active polar droplets in Section 4, we have assumed planar anchoring condition at the solid surface but perpendicular anchoring condition at the free interface, which mimics the orientation of actin filaments in the lamellipodium of migrating cells. Such anchoring boundary conditions have also been used in many previous works.43,49,101,104
Then based on the assumptions in (v) and the planar anchoring conditions in (vi), we can solve the polarization vector p from eqn (61) independently of the flow velocity v for a given drop profile h(x,t) and obtain102,105
| | | px ≈ 1, pz ≈ (z/h)∂xh. | (62) |
(vii) We consider only the dynamic limit of active polar fluids discussed in Section 4.2, at which the effects of polarization and flow on the ATP hydrolysis are negligibly small, and the rate r ≈ Λ−1Δμ is a constant parameter. In this case, the active stress σa = −ζpp in eqn (53a) is only a function of the local polarization vector p and it breaks the TRS, driving the system out of equilibrium locally. The work power done by σa on the thin droplet is approximated to the leading order as
| | 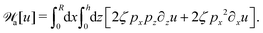 | (63) |
(viii) Using the lubrication approximation, the dissipation functional is given to the leading order by66,77,112,113
| | 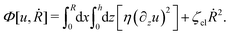 | (64) |
Here we have neglected the dissipation from the fluid slip at the solid surface (away from the contact line). The first term in
Φ represents the usual hydrodynamic viscous dissipation under the lubrication approximation with
η being the shear viscosity of the fluid. The second term represents the extra energy dissipation associated with the dynamics near the contact line region,
77,112 which can be very complex for the suspension droplets of active filaments.
101 The phenomenological parameter
ζcl is the frictional coefficient at the contact line, which is infinitely large for a pinned contact line, and is zero for a freely moving contact line.
From the above discussions, we then obtain the Rayleighian as
| | 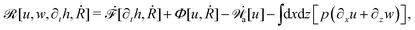 | (65) |
where
p is the pressure (a Lagrange multiplier) that imposes the incompressibility constraint. Minimizing
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif)
with respect to the rates,
u,
w, ∂
th, and
Ṙ, give a closed dynamic equation system for the thin droplets moving on solid substrates as follows. In the bulk, the dynamic equations are
| | 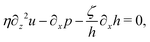 | (66a) |
which are supplemented with the no-slip condition
u = 0 at the solid surface
z = 0, the boundary conditions at the free surface
z =
h:
| | | p(x,h,t) = p0 − γ∂x2h, | (67a) |
and the boundary conditions at the contact line
x =
R and
z = 0:
| | 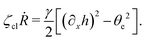 | (68) |
Here
p0 is the pressure in the surrounding gas; we have also used the impermeability condition
w = 0 at the solid surface
z = 0, and the kinematic boundary condition
w = ∂
th +
u∂
xh at the free surface
z =
h.
As in the classical problems of thin film fluids,66,107,115 the solution of the above closed equation system gives a parabolic profile for u(x,z,t) in the form of
| | 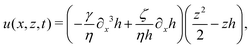 | (69) |
from which we find the thickness-averaged velocity
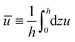
as
| | 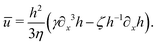 | (70) |
Substituting
eqn (70) into the mass conservation
eqn (57), one obtains the thin film equation for active droplets:
| | 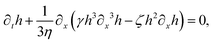 | (71) |
which is supplemented with the boundary condition
(68) at the contact line
x =
R(
t). The static solutions of this thin film equation yield the steady-state shape of the active droplet and the dynamic scaling properties of the solutions lead to the spreading or dewetting laws for the active droplet.
32,33
We would like to comment and compare our model for the thin active droplets on solid substrates with other models in the literature101,102,106 as follows.
(i) In comparison to the thin-film model by Joanny & Ramaswamy,102 we have neglected the effect of nematic elastic energy in determining the droplet shape. As a result, our thin film equation is a limiting case of their model when the droplet thickness is much larger than hK ∼ Kp/γ as discussed above near eqn (59). However, if hK is not very small, our boundary condition (68) in the vicinity of the contact line with hK > h ∼ 0 may be problematic and elastic contributions have to be included.
(ii) In the thin-film model by Loisy et al.,106 the flows inside the active droplets are induced by the winding of the polarization field. This winding introduces a dramatic change in the orientation of the polarization p along the thickness z-direction: 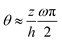 , in which θ is the angle of p relative to the x-axis and ω is an integer winding number that counts the number of quarter turns of p across the drop height. In comparison, in the present work, we have not considered such internal polarization winding and the orientation of p varies along z as θ ∼ pz/px ≈ (z/h)∂xh (see eqn (62)). Such difference in the variation of p orientation leads to the difference in the final form of thin film equation between the present work and that by Loisy et al.106
, in which θ is the angle of p relative to the x-axis and ω is an integer winding number that counts the number of quarter turns of p across the drop height. In comparison, in the present work, we have not considered such internal polarization winding and the orientation of p varies along z as θ ∼ pz/px ≈ (z/h)∂xh (see eqn (62)). Such difference in the variation of p orientation leads to the difference in the final form of thin film equation between the present work and that by Loisy et al.106
(iii) In the recent work by Trinschek et al.,101 the authors have proposed a more complete model for active polar droplets, which is similar to our model presented in Section 4 but have introduced one additional active contribution from the treadmilling or self-propulsion of active units in the direction of their polarization. Using their more complete free energy, we can still apply our variational approach and the lubrication approximation to study the more complicated thin film dynamics by following similar methods that we have done for thin films of binary mixtures before.66
5.2 Spreading laws for thin active fluid droplets
Now we consider the spreading dynamics of thin active droplets on solid substrates. We do not try to solve the thin film eqn (71) directly, but use OVP as an approximation method to solve the scaling laws for the droplet spreading.
We assume that the height profile of the droplet h(x,t) is given by a parabolic function
| | 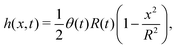 | (72a) |
and the velocity
u(
x,
z,
t) inside the droplet takes the following parabolic profile along the
z-direction as
| | 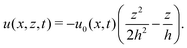 | (72b) |
The reason of choosing these function forms is apparent if we compare
eqn (72b) with the velocity profile in
eqn (69), and remember that the equilibrium shape of a thin droplet takes the form of
eqn (72a) with
θ(
t) =
θe being the equilibrium contact angle and
R(
t) =
Re being (half of) the contact length between the droplet and the solid substrate at equilibrium. Note that
θ(
t) defined from the parabolic height profile in
eqn (72a) is the apparent contact angle interpolated away from the microscopic contact line, which is different from the contact angle
θ = |∂
xh| defined in the previous subsection locally in the close vicinity of the contact line.
To achieve an approximate description of the droplet dynamics, the time-dependent parameters θ(t), R(t), and u0(x,t) must be determined by OVP. However, note that these parameters are not independent. Firstly, from the conservation of the droplet area (or mass), A0, that is, 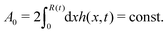 , we have
, we have
| | 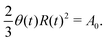 | (73) |
Secondly, from the mass conservation
eqn (57) for droplet height, we obtain
| | 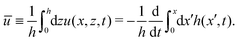 | (74) |
Substituting the approximate profile of
h(
x,
t) and
u(
x,
z,
t) in
eqn (72) into
eqn (74) we obtain
| | 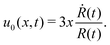 | (75) |
Therefore, the dynamics of the droplet can be described by one time-dependent parameter and here we take
R(
t).
Substituting the droplet profile h(x,t) in eqn (72a) into eqn (59), we obtain the total free energy
| | 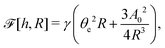 | (76) |
from which we find the rate of change of the total energy as
| | 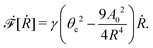 | (77) |
Similarly, we find the energy dissipation function
Φ as
| | 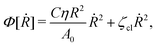 | (78) |
and the work power done by active stress,
σa, as
| | 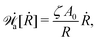 | (79) |
which are obtained by substituting the approximate profile of
h(
x,
t) and
u(
x,
z,
t) in
eqn (72) into the dissipation function in
eqn (64) and the active work power function in
eqn (63), respectively. Here
C ≡ 2[ln(2
R/
ε) − 2] and
ε is the molecular cutoff length that is introduced to remove the divergence in the energy dissipation near the contact line.
Then from eqn (77)–(79), we obtain the Rayleighian 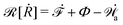 . Minimizing
. Minimizing ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to Ṙ gives the following evolution equation
with respect to Ṙ gives the following evolution equation
| | 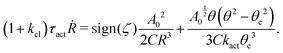 | (80) |
Here sign(
ζ) is the sign function of
ζ with sign(
ζ) = +1 for extensile active units and sign(
ζ) = −1 for contractile active units as shown in
Fig. 2. The contact angle
θ is a function of
R as given by
eqn (73). The dimensionless parameter
kcl ≡
ζcl/
ζhydro is a material parameter determined by the droplet and the substrate, which can be treated as a constant and characterizes the importance of the additional friction
ζcl near the contact line relative to the normal hydrodynamic friction
ζhydro = 3
Cη/2
θ in the bulk fluids of the droplet. Two time scales are introduced and defined as
| | 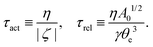 | (81) |
The time
τact represents the characteristic time for the droplet to reach steady-state motion driven by active stresses, and
τrel represents the relaxation time needed for the droplet to reach the equilibrium contact angle
θe. The dimensionless parameter
kact defined by
| | 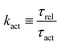 | (82) |
characterizes the strength of activity in the active fluids. If
kact is small, the equilibration of the droplet shape and contact angle is very fast and the droplet spreading is mainly driven by surface energy. On the other hand, if
kact is large, the activity is strong and the activity-driven droplet motion is much faster than the energy-driven equilibration of the droplet, that is, the droplet spreading is mainly driven by active stress and a large capillary-number flow will be induced.
Particularly, for kact ≪ 1, the first term on the right-hand side of eqn (80) can be ignored, and the evolution equation for R becomes
| | 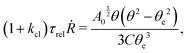 | (83) |
which gives (for
θe → 0) the classical Tanner's spreading law for two-dimensional droplets:
32–34| | 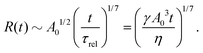 | (84) |
On the other hand, if
kact ≫ 1, the second term on the right-hand side of
eqn (80) can be ignored, and the equation becomes
| | 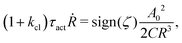 | (85) |
from which we obtain the spreading law (or dewetting law from very small initial contact angle) predicted by Joanny & Ramaswamy
102 for two-dimensional droplets of extensile active units with sign(
ζ) = +1 (or of contractile active units with sign(
ζ) = −1):
| | 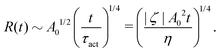 | (86) |
Note that as mentioned by Joanny & Ramaswamy,102 the effects of activity on the droplet spreading enter at the same order in gradients as those of gravity, but with a different dependence on the film height. Furthermore, similar dynamic equation as eqn (80) for thin droplets on solid substrates has been obtained in a very different scenario where evaporation occurs at the free surface of the droplet.77 The effects of activity on the droplet spreading enter at the same order as those of evaporation, but with a different dependence on the droplet radius or contact length.
In addition, the formulation and calculations presented here can be readily extended to the thin-film dynamics of three-dimensional droplets on solid substrates, particularly for the spreading dynamics of a droplet with cylindrical symmetry. Furthermore, the effects of nematic energy on the spreading dynamics can also be considered by including nematic elastic energy,102 which takes the simple form of 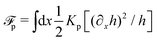 .
.
6 Conclusions
Onsagers variational principle (OVP) has recently become an indispensable and powerful tool in the study of the nonlinear and nonequilibrium phenomena of many inert soft matter systems, such as liquid droplets, colloid suspensions, nematic liquid crystals, polymer gels, and surfactants, etc. In this work, we present a simple extension of OVP for the dynamic modeling of active soft matter such as suspensions of bacteria and aggregates of animal cells. In this extended OVP, the active forces generated locally by individual active units are treated as non-conservative forces that cannot be derived from any free energy and dissipation functions. We then apply this extended form of OVP to three representative active matter problems, which are motivated by the biology of bacteria and animal cells. We show that OVP can not only help to formulate thermodynamically-consistent models, but can also be used to find approximate solutions for the emergent structures and complex dynamics of active soft matter.
The first application of OVP presented in Section 3 is about the directional motion of individual active units: a molecular motor walking on a stiff biofilament and a toy two-sphere microswimmer moving in a viscous fluid. In the motor/filament system, we consider the mechanochemical cross-coupling which indicates that the system is a reversible machine: it can not only convert chemical energy into mechanical work, but can also convert mechanical work into chemical energy. In the toy microswimmer, we show how directional self-propulsion can be generated by cyclic body-shape oscillations together with front-back asymmetry in hydrodynamic friction. It is shown that mechanochemical cross-coupling in biological systems can be considered in Onsager's framework of non-equilibrium thermodynamics. Activity and the broken time reversal symmetry in active matter are basically resulted from the persistent consumption and conversion of chemical energy, released during spontaneous ATP hydrolysis, into motion or mechanical work.
The second application presented in Section 4 is about the two-phase hydrodynamics for a droplet of active polar fluids, which is composed of suspending contractile or extensile active units such as bacteria, actomyosin units, and animal cells. We use OVP to formulate a diffuse-interface model for an active polar droplet moving on a solid substrate. This hydrodynamic model is thermodynamically consistent in both hydrodynamic equations in the bulk fluid and matching boundary conditions at the solid surface.
The third application presented in Section 5 is about the motion of a thin active polar droplet on a solid substrate in two dimensions. Using the lubrication approximation, we firstly apply OVP to derive the classical thin film equation that has been obtained previously. We then use OVP as an approximation tool to find two scaling laws for the spreading (or dewetting) of the thin active droplet in the respective limits of negligible activity and strong activity. It is interesting to note that the reduced equation obtained for the spreading (or dewetting) dynamics of thin active droplets takes a similar form as that has been obtained previously for the dewetting dynamics of an evaporating droplet on solid substrates.
Below we make a few general remarks and outlook.
(i) Near-equilibrium assumption of OVP. OVP is proposed in Onsager's linear-response framework of non-equilibrium thermodynamics, which is based on the near-equilibrium assumption. However, biological systems are usually far away from equilibrium. Therefore, the validity and the range of the OVP applications should be and can only be justified by solving real biological problems and comparing with quantitative experiments.1,4
(ii) Relationships between OVP/OMVP and other approaches in nonequilibrium thermodynamics. Following the pioneering works of Onsager, there have been various approaches developed for nonequilibrium thermodynamics. In particular, there have been various variational principles formulated for the study of irreversible processes.116 More recently, the general equation for non-equilibrium reversible-irreversible coupling (GENERIC) formalism has been proposed as an extension of Hamiltonian's formalism of classical mechanics to nonequilibrium thermodynamic systems with both reversible and irreversible dynamics.117 However, a general discussion on the relationships among the various approaches is beyond the scope of this work.
(iii) Applications of Onsager–Machlup variational principle (OMVP). In the end of Section 2.1, we have mentioned that Onsager and Machlup60 introduced OMVP in their study of the statistical fluctuations of kinetic paths in the framework of Langevin equation. They have shown that the most probable kinetic path over a certain long-time period is determined by the minimization of a time integral, i.e., the Onsager–Machlup integral in eqn (12). Recently, Doi et al.68 proposed that OMVP can be used to approximate the long-time dynamics of nonequilibrium systems. However, in this work, we have not given applications of using OMVP to find approximate solutions for long-time behaviors such as steady states. We mention two potential applications of OMVP as follows: the steady-state for the wave propagation and sustained oscillations observed in migrating cells;29–31 the steady-state (spontaneous) retraction dynamics of an injured axon118 or a laser-cutting stress-fiber bundle in adherent cells.119
(iv) Applications of OVP and OMVP to more specific biological problems. The applications considered in this work are mostly toy models or simplified models of mostly theoretical interests. We are now trying to apply the extended form of OVP to more specific biological problems such as cell spreading, cell curvotaxis, wound closure, tissue folding, and so on. However, in these real systems, we usually need to involve many more complex active processes16 in addition to active forces and cyclic body-shape oscillations, such as tensional homeostasis,2 cell division and apoptosis,13 topological cell rearrangements,16 memory effects.1,17
In summary, the variational method proposed in this work about incorporating biochemical activity into OVP will help to construct thermodynamically-consistent models and to find approximate dynamic solutions in active soft matter. Particularly, this will help to deepen our understanding of the emergent structure and dynamic behaviors of real in vivo biological systems such as bacteria suspensions, individual animal cells and cell aggregates (or tissues).1,2,13
Conflicts of interest
There are no conflicts to declare.
A Some additional notes on the choice of thermodynamic fluxes and forces
In Onsager's theory of non-equilibrium thermodynamics, the choice of thermodynamic fluxes and forces is not unique.50,51 For example, for active polar fluids, two different sets of fluxes and forces can be chosen as follows:
(i) Fluxes are chosen to be r, P, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) (or the flow velocity v) and the corresponding forces are Δμ, h, σv, respectively, as taken in Section 4 of this work. Here all the three fluxes have the same time parity.
(or the flow velocity v) and the corresponding forces are Δμ, h, σv, respectively, as taken in Section 4 of this work. Here all the three fluxes have the same time parity.
(ii) Fluxes are chosen to be r, P, σv (the momentum flux) and the corresponding forces are Δμ, h, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) , respectively, as taken by Marchetti et al.1 Here the time parity of the flux σv is different from the other two fluxes r and P. Furthermore, note that in this case, the new pair of flux σv and force
, respectively, as taken by Marchetti et al.1 Here the time parity of the flux σv is different from the other two fluxes r and P. Furthermore, note that in this case, the new pair of flux σv and force ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) is a swap of the pair of flux
is a swap of the pair of flux ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) and force σv in the first choice (i).
and force σv in the first choice (i).
The symmetry of Onsager matrix coupling fluxes and forces depends on the time parity (i.e., the time-reversal signature) of the fluxes:1,50 the Onsager coupling matrix is symmetric for fluxes of the same time parity and is antisymmetric for fluxes of opposite time parity. Therefore, for the first choice (i) with fluxes of the same time parity, the Onsager coupling matrix is symmetric. In comparison, for the second choice (ii), the cross-coupling coefficients between the flux σv and the flux r or between the flux σv and the flux P are both antisymmetric as shown in Marchetti et al.1
Given the non-unique choice of flux–force pairs, we will make some general discussions in this Appendix about the consequences of different choices of thermodynamic fluxes and forces.
A.1 Changes in the symmetry of Onsager coupling matrix by swapping some of fluxes and forces
We discuss the changes in the symmetry of Onsager coupling matrix when we swap some of fluxes with forces, as in the above two choices of force–flux pairs in active polar fluids. To this end, let's consider two pairs of fluxes and forces: ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X1,
1 and X1, ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2 and X2. Suppose that the two fluxes
2 and X2. Suppose that the two fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and
1 and ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2 have the same time parity, and hence the two forces X1 and X2 also have the same time parity but opposite to that of the corresponding fluxes. In this case, the linear force–flux relations are then given by:
2 have the same time parity, and hence the two forces X1 and X2 also have the same time parity but opposite to that of the corresponding fluxes. In this case, the linear force–flux relations are then given by:| | 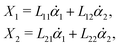 | (A1) |
in which the Onsager coupling matrix Lij is symmetric and positive definiteness, that is, L12 = L21, L11, L22 > 0, and L11L22 − L122 > 0.
If alternatively, we swap X2 with ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2, that is, we choose the fluxes to be
2, that is, we choose the fluxes to be ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X2, and the corresponding forces are X1 and
1 and X2, and the corresponding forces are X1 and ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2. Then the time parities of the two fluxes
2. Then the time parities of the two fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X2 are now different. In this case, the linear force–flux relations become
1 and X2 are now different. In this case, the linear force–flux relations become
| | 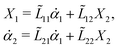 | (A2) |
in which
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 11
11 = (
L11L22 −
L122)/
L22,
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 12
12 =
L12/
L22,
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 21
21 = −
L21/
L22,
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 22
22 = 1/
L22. Note that now
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 21
21 = −
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 12
12, that is, the Onsager coupling matrix
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ij
ij is antisymmetric. From this simple example, we show that although there exists some flexibility in choosing fluxes and forces, we can safely use the time parity of the chosen fluxes to determine the symmetry of the Onsager coupling matrix in the linear force–flux relations.
A.2 Onsager's variational principle for thermodynamic fluxes of different time parities
Suppose that there are two sets of slow state variables, α and β and they have opposite time parity. Then the free energy is ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (α,β) and the rate of change of the free energy is given by
(α,β) and the rate of change of the free energy is given by| | 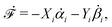 | (A3) |
in which ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) and
and 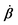 are two fluxes, and
are two fluxes, and| | Xi ≡ − ∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /∂αi, Yi ≡ − ∂ /∂αi, Yi ≡ − ∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /∂βi /∂βi | (A4) |
are the corresponding conjugate forces. Since α and β have opposite time parities, then the time parities of ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) and
and 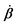 , and that of X and Y are both opposite, respectively. In this case, we can decompose the two forces into reactive and dissipative parts as
, and that of X and Y are both opposite, respectively. In this case, we can decompose the two forces into reactive and dissipative parts as| | | X = Xd + Xr, Y = Yd + Yr. | (A5) |
Here Xd and Yd arise from dissipative couplings that can be derived from dissipation function, while Xr and Yr derive from reactive couplings:| | 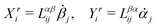 | (A6) |
with the friction matrix Lαβij = −Lβαji being antisymmetric. The reactive couplings do not contribute to dissipation and therefore can not be derived from dissipation functions. Substituting eqn (A5) into the rate of change of the free energy in eqn (A3), using eqn (A6) and Lαβij = −Lβαji, we obtain| | 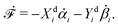 | (A7) |
The dissipation function is given by
| | 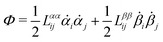 | (A8) |
with the friction matrix
Lααij =
Lααji and
Lββij =
Lββji being symmetric. Using
eqn (A5)–(A8) and minimizing the Rayleighian
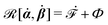
, we obtain
| | 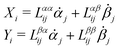 | (A9) |
or equivalently by taking the inverse:
| | 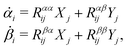 | (A10) |
where the mobility matrix
R is the inverse of the friction matrix
L. Note that only the dissipative part of the thermodynamic forces can be considered and derived from the minimization of the Rayleighian, which is simply because the reactive forces don't contribute to the dissipation function and the Rayleighian.
Acknowledgements
We thank Masao Doi at Beihang University for many fruitful discussions, particularly during his visit in Xu's group in 2019. Great thanks should also be given to Len Pismen and Yariv Kafri at Technion for their valuable comments and suggestions. T. Q. acknowledges support of the Hong Kong RGC CRF (No. C1018-17G). X. X. is supported in part by National Natural Science Foundation of China (NSFC, No. 12004082), by Provincial Science Foundation of Guangdong (No. 2019A1515110809), by Guangdong Province Universities and Colleges Pearl River Scholar Funded Scheme (2019), by 2020 Li Ka Shing Foundation Cross-Disciplinary Research Grant (No. 2020LKSFG08A), by Guangdong Basic and Applied Basic Research Foundation (No. 2020B1515310005), and by Featured Innovative Projects (No. 2018KTSCX282), Youth Talent Innovative Platforms (No. 2018KQNCX318) in Universities in Guangdong Province and Science and Technology Innovation Program 2020 (No. ST002).
Notes and references
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- J. Prost, F. Jülicher and J.-F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- A. M. Menzel, Phys. Rep., 2015, 554, 1–45 CrossRef CAS.
- G. De Magistris and D. Marenduzzo, Phys. A, 2015, 418, 65–77 CrossRef.
- D. Marenduzzo, Eur. Phys. J.: Spec. Top., 2016, 225, 2065–2077 Search PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS.
- J. Gachelin, A. Rousselet, A. Lindner and E. Clement, New J. Phys., 2014, 16, 025003 CrossRef.
- H.-P. Zhang, A. Beer, E.-L. Florin and H. L. Swinney, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13626–13630 CrossRef CAS.
- J. Ranft, M. Basan, J. Elgeti, J.-F. Joanny, J. Prost and F. Jülicher, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20863–20868 CrossRef CAS.
- M. H. Köpf and L. M. Pismen, Soft Matter, 2013, 9, 3727–3734 RSC.
- S. He, Y. Green, N. Saeidi, X. Li, J. J. Fredberg, B. Ji and L. M. Pismen, J. Mech. Phys. Solids, 2020, 137, 103860 CrossRef.
- M. Popović, A. Nandi, M. Merkel, R. Etournay, S. Eaton, F. Jülicher and G. Salbreux, New J. Phys., 2017, 19, 033006 CrossRef.
-
S. Banerjee and M. C. Marchetti, in Cell Migrations: Causes and Functions, ed. C. A. M. La Porta and S. Zapperi, Springer, Cham, 2019, pp. 45–66 Search PubMed.
- J. Toner and Y. Tu, Phys. Rev. Lett., 1995, 75, 4326–4329 CrossRef CAS.
- C. K. Hemelrijk and H. Hildenbrandt, Interface Focus, 2012, 2, 726–737 CrossRef.
- D. Helbing, Rev. Mod. Phys., 2001, 73, 1067 CrossRef.
- C. Castellano, S. Fortunato and V. Loreto, Rev. Mod. Phys., 2009, 81, 591 CrossRef.
- I. S. Aranson, D. Volfson and L. S. Tsimring, Phys. Rev. E, 2007, 75, 051301 CrossRef.
- C. Scholz, M. Engel and T. Pöschel, Nat. Commun., 2018, 9, 1–8 CrossRef.
- J. Zhang, E. Luijten, B. A. Grzybowski and S. Granick, Chem. Soc. Rev., 2017, 46, 5551–5569 RSC.
- Z. Lin, C. Gao, M. Chen, X. Lin and Q. He, Curr. Opin. Colloid Interface Sci., 2018, 35, 51–58 CrossRef CAS.
- Z. Ma, M. Yang and R. Ni, Adv. Theory Simul., 2020, 3, 2000021 CrossRef CAS.
- A. Grosberg and J.-F. Joanny, Phys. Rev. E, 2015, 92, 032118 CrossRef CAS.
- M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys., 1993, 65, 851–1112 CrossRef CAS.
- G. Gerisch, T. Bretschneider, A. Müller-Taubenberger, E. Simmeth, M. Ecke, S. Diez and K. Anderson, Biophys. J., 2004, 87, 3493–3503 CrossRef CAS.
- O. D. Weiner, W. A. Marganski, L. F. Wu, S. J. Altschuler and M. W. Kirschner, PLoS Biol., 2007, 5, e221 CrossRef.
- N. Inagaki and H. Katsuno, Trends Cell Biol., 2017, 27, 515–526 CrossRef CAS.
- L. Leger and J.-F. Joanny, Rep. Prog. Phys., 1992, 55, 431 CrossRef CAS.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS.
- H. Tanaka, Faraday Discuss., 2012, 158, 371–406 RSC.
- R. G. Winkler, D. A. Fedosov and G. Gompper, Curr. Opin. Colloid Interface Sci., 2014, 19, 594–610 CrossRef CAS.
-
P.-G. De Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, 1993 Search PubMed.
- S. B. Ross-Murphy, Polym. Gels Networks, 1994, 2, 229–237 CrossRef CAS.
- M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001 CrossRef.
- M. Cates and S. Candau, J. Phys.: Condens. Matter, 1990, 2, 6869–6892 CrossRef CAS.
- S. Safran, P. Pincus, D. Andelman and F. MacKintosh, Phys. Rev. A, 1991, 43, 1071–1078 CrossRef CAS.
- A. Baskaran and M. C. Marchetti, J. Stat. Mech.: Theory Exp., 2010, 2010, P04019 Search PubMed.
- M. E. Cates and E. Tjhung, J. Fluid Mech., 2018, 836, P1 CrossRef.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef.
- J. Prost and R. Bruinsma, Europhys. Lett., 1996, 33, 321–326 CrossRef CAS.
- E. Woillez, Y. Zhao, Y. Kafri, V. Lecomte and J. Tailleur, Phys. Rev. Lett., 2019, 122, 258001 CrossRef CAS.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS.
- R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- E. Tjhung, A. Tiribocchi, D. Marenduzzo and M. Cates, Nat. Commun., 2015, 6, 1–9 Search PubMed.
-
S. R. de Groot and P. Mazur, Non-equilibrium Thermodynamics, Dover, New York, 1984 Search PubMed.
-
I. Gyarmati, Non-equilibrium Thermodynamics, Springer, Berlin, 1970 Search PubMed.
- H. Li, X.-Q. Shi, M. Huang, X. Chen, M. Xiao, C. Liu, H. Chaté and H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 777–785 CrossRef CAS.
-
M. Doi, Soft Matter Physics, Oxford University Press, 2013 Search PubMed.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS.
- L. Onsager, Phys. Rev., 1931, 38, 2265–2279 CrossRef CAS.
- J. W. Strutt, Proc. London Math. Soc., 1871, 1, 357–368 CrossRef.
- L. Onsager, Ann. N. Y. Acad. Sci., 1945, 46, 241–265 CrossRef CAS.
- T. Qian, X.-P. Wang and P. Sheng, J. Fluid Mech., 2006, 564, 333–360 CrossRef CAS.
-
M. Doi and S. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1986 Search PubMed.
- L. Onsager and S. Machlup, Phys. Rev., 1953, 91, 1505–1512 CrossRef CAS.
- S. Ono, Adv. Chem. Phys., 1961, 3, 267–321 Search PubMed.
- M. Doi, J. Condens. Matter Phys., 2011, 23, 284118 CrossRef.
- M. Doi, Prog. Polym. Sci., 2021, 112, 101339 CrossRef CAS.
-
Y. Wang, C. Liu, P. Liu and B. Eisenberg, 2020, arXiv:2001.10149.
-
Q. Wang, in Frontiers and Progress of Current Soft Matter Research, ed. X.-Y. Liu, Springer, Singapore, 2020, pp. 101–132 Search PubMed.
- X. Xu, U. Thiele and T. Qian, J. Phys.: Condens. Matter, 2015, 27, 085005 CrossRef.
- Y. Di, X. Xu, J. Zhou and M. Doi, Chin. Phys. B, 2018, 27, 024501 CrossRef.
- M. Doi, J. Zhou, Y. Di and X. Xu, Phys. Rev. E, 2019, 99, 063303 CrossRef CAS.
- X. Xu and T. Qian, Procedia IUTAM, 2017, 20, 144–151 CrossRef.
- P. Sheng, J. Zhang and C. Liu, Prog. Theor. Phys. Suppl., 2008, 175, 131–143 CrossRef.
- T. V. Sachin Krishnan, R. Okamoto and S. Komura, Phys. Rev. E, 2016, 94, 062414 CrossRef CAS.
- Y. Oya and T. Kawakatsu, J. Chem. Phys., 2018, 148, 114905 CrossRef.
-
M. Arroyo, N. Walani, A. Torres-Sánchez and D. Kaurin, The Role of Mechanics in the Study of Lipid Bilayers, Springer, Cham, 2018, pp. 287–332 Search PubMed.
- A. Fang, T. Qian and P. Sheng, Phys. Rev. E, 2008, 78, 061703 CrossRef.
- X. Xu, X. Man, M. Doi, Z.-C. Ou-Yang and D. Andelman, Macromolecules, 2019, 52, 9321–9333 CrossRef CAS.
- M. Doi, Chin. Phys. B, 2015, 24, 20505 CrossRef.
- X. Man and M. Doi, Phys. Rev. Lett., 2016, 116, 066101 CrossRef.
- X. Man and M. Doi, Phys. Rev. Lett., 2017, 119, 044502 CrossRef.
- J. Zhou and M. Doi, Phys. Rev. Fluids, 2018, 3, 084004 CrossRef.
- J. Sui, M. Doi and Y. Ding, Soft Matter, 2018, 14, 8956–8961 RSC.
- P. Khunpetch, X. Man, T. Kawakatsu and M. Doi, J. Chem. Phys., 2018, 148, 134901 CrossRef.
- F. J. Vernerey and U. Akalp, Phys. Rev. E, 2016, 94, 012403 CrossRef.
- Y.-H. Zhang, M. Deserno and Z.-C. Tu, Phys. Rev. E, 2020, 102, 012607 CrossRef CAS.
- X. Yang, J. Li, M. G. Forest and Q. Wang, Entropy, 2016, 18, 202 CrossRef.
- A. Tiribocchi, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 115, 188302 CrossRef.
- S. Gu, T. Qian, H. Zhang and X. Zhou, Chaos, 2020, 30, 053133 CrossRef CAS.
- Q. Du, T. Li, X. Li and W. Ren, Sci. China Math., 2020, 1–42 Search PubMed.
- H. Touchette, Phys. Rep., 2009, 478, 1–69 CrossRef CAS.
-
J. N. Reddy, Energy Principles and Variational Methods in Applied Mechanics, John Wiley & Sons, 2017 Search PubMed.
-
B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, London, 5th edn, 2007 Search PubMed.
- O. Kedem and S. R. Caplan, Trans. Faraday Soc., 1965, 61, 1897–1911 RSC.
- Y.-D. Chen and T. L. Hill, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 1982–1986 CrossRef CAS.
- A. Patel, L. Malinovska, S. Saha, J. Wang, S. Alberti, Y. Krishnan and A. A. Hyman, Science, 2017, 356, 753–756 CrossRef CAS.
-
R. Phillips, J. Kondev, J. Theriot and H. Garcia, Physical Biology of the Cell, Garland Science, 2012 Search PubMed.
- F. Jülicher, A. Ajdari and J. Prost, Rev. Mod. Phys., 1997, 69, 1269–1281 CrossRef.
- H. C. Astley, C. Gong, J. Dai, M. Travers, M. M. Serrano, P. A. Vela, H. Choset, J. R. Mendelson, D. L. Hu and D. I. Goldman, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6200–6205 CrossRef CAS.
- D. L. Bodor, W. Pönisch, R. G. Endres and E. K. Paluch, Dev. Cell, 2020, 52, 550–562 CrossRef CAS.
- A. Loisy, J. Eggers and T. B. Liverpool, Soft Matter, 2020, 16, 3106–3124 RSC.
-
K. Zimmermann, I. Zeidis and C. Behn, Mechanics of Terrestrial Locomotion: with a Focus on Non-Pedal Motion Systems, Springer, 2009 Search PubMed.
-
A. Lurie, Analytical Mechanics, Springer, 2002 Search PubMed.
- S. Trinschek, F. Stegemerten, K. John and U. Thiele, Phys. Rev. E, 2020, 101, 062802 CrossRef CAS.
- J.-F. Joanny and S. Ramaswamy, J. Fluid Mech., 2012, 705, 46 CrossRef.
- A. C. Callan-Jones and F. Jülicher, New J. Phys., 2011, 13, 093027 CrossRef.
- E. Tjhung, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12381–12386 CrossRef CAS.
- S. Sankararaman and S. Ramaswamy, Phys. Rev. Lett., 2009, 102, 118107 CrossRef.
- A. Loisy, J. Eggers and T. B. Liverpool, Phys. Rev. Lett., 2019, 123, 248006 CrossRef CAS.
- W. Ren, D. Hu and W. E, Phys. Fluids, 2010, 22, 102103 CrossRef.
- M. Ben Amar and L. Cummings, Phys. Fluids, 2001, 13, 1160–1166 CrossRef CAS.
- S. Mechkov, A.-M. Cazabat and G. Oshanin, J. Condens. Matter Phys., 2009, 21, 464131 CrossRef CAS.
- T.-S. Lin, L. J. Cummings, A. J. Archer, L. Kondic and U. Thiele, Phys. Fluids, 2013, 25, 082102 CrossRef.
- G. Kitavtsev, A. Münch and B. Wagner, Proc. R. Soc. A, 2018, 474, 20170828 CrossRef CAS.
- H. Wang, D. Yan and T. Qian, J. Phys.: Condens. Matter, 2018, 30, 435001 CrossRef.
- R. V. Craster and O. K. Matar, Rev. Mod. Phys., 2009, 81, 1131 CrossRef CAS.
- R. Kemkemer, V. Teichgräber, S. Schrank-Kaufmann, D. Kaufmann and H. Gruler, Eur. Phys. J. E, 2000, 3, 101–110 CrossRef CAS.
- A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931–980 CrossRef CAS.
- M. Ichiyanagi, Phys. Rep., 1994, 243, 125–182 CrossRef.
-
H. C. Öttinger, Beyond equilibrium thermodynamics, John Wiley & Sons, 2005 Search PubMed.
- X. Shao, R. You, T. H. Hui, C. Fang, Z. Gong, Z. Yan, R. C. C. Chang, V. B. Shenoy and Y. Lin, Biophys. J., 2019, 117, 193–202 CrossRef CAS.
- A. Besser, J. Colombelli, E. H. Stelzer and U. S. Schwarz, Phys. Rev. E, 2011, 83, 051902 CrossRef.
Footnotes |
| † It is interesting to mention that in active matter, the presence of active forces and the breakdown of TRS can significantly change the statistical behaviors of the system such as the distribution of α and barrier crossing kinetics. The dynamics of downhill and uphill processes are very different even for passive systems, and hence must be treated using their respective variational approaches. In this work, we are interested in the active dynamics that would reduce to downhill processes if the activity vanishes. However, the fluctuation effects can still be investigated in a variational framework.46,86 |
| ‡ Private communications with M. Doi. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Tiezheng
Qian
ab,
Tiezheng
Qian
 c and
Xinpeng
Xu
c and
Xinpeng
Xu
 *ab
*ab
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) follow the dynamic path that minimizes the function:
follow the dynamic path that minimizes the function:![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (
(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) = Φ(
) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ(
) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α).
;α).![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is called the Rayleighian as suggested by Doi and Edwards,59Φ is the dissipation function which is quadratic in
is called the Rayleighian as suggested by Doi and Edwards,59Φ is the dissipation function which is quadratic in ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) when the system is close to equilibrium, and Ḟ is the rate of change of the free energy in the isothermal system. Onsager later used his principle to study the diffusion in electrolyte solutions.57 However, OVP has not been widely recognized and applied to describe irreversible processes for a long time until 1953 when Onsager and Machlup60 established the statistical mechanical foundation of OVP. Since then, OVP and its relationship with other thermodynamic variational principles have been extensively studied and identified.61 In recent years, OVP has been widely used as an indispensable and powerful tool for the study of nonlinear and nonequilibrium phenomena of soft matter.53,58,62–65
when the system is close to equilibrium, and Ḟ is the rate of change of the free energy in the isothermal system. Onsager later used his principle to study the diffusion in electrolyte solutions.57 However, OVP has not been widely recognized and applied to describe irreversible processes for a long time until 1953 when Onsager and Machlup60 established the statistical mechanical foundation of OVP. Since then, OVP and its relationship with other thermodynamic variational principles have been extensively studied and identified.61 In recent years, OVP has been widely used as an indispensable and powerful tool for the study of nonlinear and nonequilibrium phenomena of soft matter.53,58,62–65
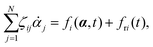
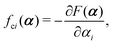
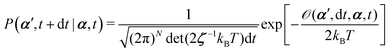
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is defined by
is defined by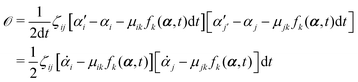
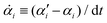 and μij being the mobility coefficient matrix that is positive definite and symmetric, and satisfies ζijμjk = δik. From the transition probability P(α′,t + dt|α,t) in eqn (5), the most probable transition occurring between α and nearby α′ is the one which minimizes the Onsager–Machlup function
and μij being the mobility coefficient matrix that is positive definite and symmetric, and satisfies ζijμjk = δik. From the transition probability P(α′,t + dt|α,t) in eqn (5), the most probable transition occurring between α and nearby α′ is the one which minimizes the Onsager–Machlup function ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) or equivalently the function
or equivalently the function![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (
(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ(
;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ(
) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa(
;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α)
;α)![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) for prescribed α. Here
for prescribed α. Here ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is called the Rayleighian,62,63
is called the Rayleighian,62,63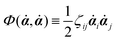 is the positive-definite dissipation-function,
is the positive-definite dissipation-function, 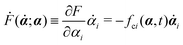 is the change rate of free energy, and Ẇa(
is the change rate of free energy, and Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = fai(α,t)
;α) = fai(α,t)![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) i is the work power done by the active force, fa. The Euler–Lagrange equation for minimizing
i is the work power done by the active force, fa. The Euler–Lagrange equation for minimizing ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) in eqn (7) with respect to
in eqn (7) with respect to ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) is
is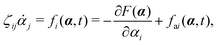
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to the rates
with respect to the rates ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) was originally proposed by Lars Onsager in 193154,60 and usually referred to as The principle of least dissipation of energy or simply Onsager's variational principle (OVP).
was originally proposed by Lars Onsager in 193154,60 and usually referred to as The principle of least dissipation of energy or simply Onsager's variational principle (OVP).
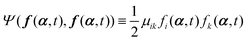 appearing in the Onsager–Machlup function
appearing in the Onsager–Machlup function ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) in eqn (6) does not contribute to the Rayleighian
in eqn (6) does not contribute to the Rayleighian ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) because we are considering the most probable state α′ at an immediate future time close to t, which is to be determined from the prescribed state α and hence the prescribed forces f(α,t) and Ψ(f(α,t),f(α,t)).
because we are considering the most probable state α′ at an immediate future time close to t, which is to be determined from the prescribed state α and hence the prescribed forces f(α,t) and Ψ(f(α,t),f(α,t)).![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) done by the external forces from the Rayleighian
;α) done by the external forces from the Rayleighian ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) in eqn (7):
in eqn (7):![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (
(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ(
;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ(
) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa(
;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇext(
;α) − Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α).
;α).![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) leads to an Euler–Lagrange equation that includes the external forces, in a form generalized from eqn (8).
leads to an Euler–Lagrange equation that includes the external forces, in a form generalized from eqn (8).
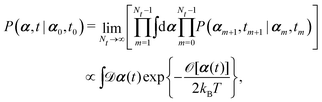
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [α(t)] is called the Onsager–Machlup functional or integral defined by
[α(t)] is called the Onsager–Machlup functional or integral defined by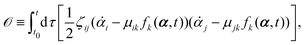
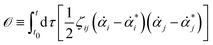
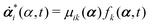 being the actual rates of the system at state α and time t. Note that
being the actual rates of the system at state α and time t. Note that ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) is defined by the time derivative of the state variables α, while
is defined by the time derivative of the state variables α, while ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) * is defined by the force f(α,t) and depends only on the state variable α and time t. The Onsager–Machlup integral is non-negative definite and equals to zero (the minimum) only when
* is defined by the force f(α,t) and depends only on the state variable α and time t. The Onsager–Machlup integral is non-negative definite and equals to zero (the minimum) only when ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) equals to the actual kinetic path, i.e.,
equals to the actual kinetic path, i.e., ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) =
= ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) *. Hence the variational principle can be stated that nature chooses the kinetic path which minimizes the Onsager–Machlup functional
*. Hence the variational principle can be stated that nature chooses the kinetic path which minimizes the Onsager–Machlup functional ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [α(t)] with respect to the state variables α(t). This variational principle is called Onsager–Machlup variational principle (OMVP).63,68 In contrast to OVP, a local principle that predicts the most probable state in the immediate future, the OMVP is a global principle that can determine the most probable path taking the system to the far future under various constraints. For example, it can be used to determine the long-time behaviors such as the steady-states.63,68 It can also be used to locate the most probable transition pathway that takes the system from one free energy minimum to another.87,88
[α(t)] with respect to the state variables α(t). This variational principle is called Onsager–Machlup variational principle (OMVP).63,68 In contrast to OVP, a local principle that predicts the most probable state in the immediate future, the OMVP is a global principle that can determine the most probable path taking the system to the far future under various constraints. For example, it can be used to determine the long-time behaviors such as the steady-states.63,68 It can also be used to locate the most probable transition pathway that takes the system from one free energy minimum to another.87,88
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) can be written as
can be written as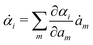
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (ȧ). The dynamics of the system described by the temporal evolution of the parameters a(t) is determined by minimizing
(ȧ). The dynamics of the system described by the temporal evolution of the parameters a(t) is determined by minimizing ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to ȧ.
with respect to ȧ.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [α(a(t))] with respect to the parameter functions a(t). This variational method is similar to the least-square method but with a target function that is more physically meaningful based on physical principles.68,89
[α(a(t))] with respect to the parameter functions a(t). This variational method is similar to the least-square method but with a target function that is more physically meaningful based on physical principles.68,89![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α).
;α).![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ), which is quadratic in the rates/fluxes
), which is quadratic in the rates/fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) .
.![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α), based on the specific activity considered, and find the work power done by some other external forces, Ẇext(
;α), based on the specific activity considered, and find the work power done by some other external forces, Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α). The external forces are usually applied at the system boundary and do not arise locally from the consumption of chemical energy of the system.
;α). The external forces are usually applied at the system boundary and do not arise locally from the consumption of chemical energy of the system.![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (
(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) = Φ(
;α) = Φ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ,
,![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ) + Ḟ(
) + Ḟ(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇa(
;α) − Ẇa(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α) − Ẇext(
;α) − Ẇext(![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) ;α), with respect to the rates/fluxes
;α), with respect to the rates/fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) . Note that some additional constraints on the system dynamics may need to be imposed by using Lagrange multipliers.
. Note that some additional constraints on the system dynamics may need to be imposed by using Lagrange multipliers.![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (ȧ;a). The minimization of
(ȧ;a). The minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to ȧ will then provide an approximate description for the active matter dynamics directly.
with respect to ȧ will then provide an approximate description for the active matter dynamics directly.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t), of the microswimmer oscillates cyclically and the friction coefficient, ζ, is asymmetric for forward motion (with smaller friction) and backward motion (with larger friction), as shown in eqn (23). The front-back asymmetry in friction is indicated by inclined thorns on the microspheres.
(t), of the microswimmer oscillates cyclically and the friction coefficient, ζ, is asymmetric for forward motion (with smaller friction) and backward motion (with larger friction), as shown in eqn (23). The front-back asymmetry in friction is indicated by inclined thorns on the microspheres.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r =
r = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r(NATP,NADP,NPi),
r(NATP,NADP,NPi),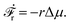
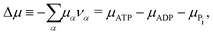
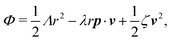
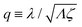 (with −1 < q < 1), as suggested by Kedem and Caplan.91
(with −1 < q < 1), as suggested by Kedem and Caplan.91
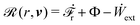 in the presence of the external force and eqn (16)–(19), we minimize
in the presence of the external force and eqn (16)–(19), we minimize ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to r and v and obtain
with respect to r and v and obtain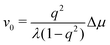 (for fext = 0) must be positive (and hence λ > 0 and 0 < q < 1). In this case, we can identify the following four regimes from eqn (20):
(for fext = 0) must be positive (and hence λ > 0 and 0 < q < 1). In this case, we can identify the following four regimes from eqn (20):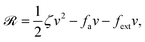
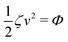 is the dissipation function, fav = Ẇa is the rate of work done by the active force to the reduced system, and fextv = Ẇext is the rate of work done by the external force. Minimizing this Rayleighian gives the force balance equation −ζv + fa + fext = 0.
is the dissipation function, fav = Ẇa is the rate of work done by the active force to the reduced system, and fextv = Ẇext is the rate of work done by the external force. Minimizing this Rayleighian gives the force balance equation −ζv + fa + fext = 0.
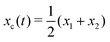 and the half-body-length of the swimmer
and the half-body-length of the swimmer 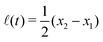 , which are taken as the two slow variables. The toy microswimmer can actively change its shape by periodically changing its body length (or the distance between the two spheres) 2
, which are taken as the two slow variables. The toy microswimmer can actively change its shape by periodically changing its body length (or the distance between the two spheres) 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) as
(t) as![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) =
(t) = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 + a
0 + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(ωt),
sin(ωt),![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is the half of the average body length of the microswimmer, a and ω are the amplitude and frequency of the shape oscillations, respectively, and the shape-oscillation period is T
0 is the half of the average body length of the microswimmer, a and ω are the amplitude and frequency of the shape oscillations, respectively, and the shape-oscillation period is T![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2π/ω.
= 2π/ω.
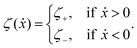
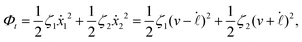
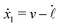 and
and 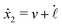 , respectively. Note that the dissipation function Φt is actually not quadratic in dissipative rates any more but highly nonlinear; a highly nonlinear dissipation function has been discussed in classical mechanics of particles before.100
, respectively. Note that the dissipation function Φt is actually not quadratic in dissipative rates any more but highly nonlinear; a highly nonlinear dissipation function has been discussed in classical mechanics of particles before.100
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/v ≫ T
0/v ≫ T![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . We can, therefore, integrate out the relatively fast varying variable, the half-body-length
. We can, therefore, integrate out the relatively fast varying variable, the half-body-length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t), in one cycle of shape oscillation and arrive at a time-averaged dissipation function of the slow variable, the center-of-mass velocity v, by
(t), in one cycle of shape oscillation and arrive at a time-averaged dissipation function of the slow variable, the center-of-mass velocity v, by 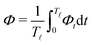 as
as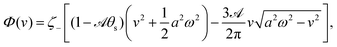
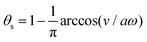 for |v| ≤ aω and
for |v| ≤ aω and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 1 − ζ+/ζ− is a dimensionless parameter measuring the degree of the front-back asymmetry in the friction coefficients. Note that this dissipation function is not quadratic but highly nonlinear in the rate v. We can define the Rayleighian
= 1 − ζ+/ζ− is a dimensionless parameter measuring the degree of the front-back asymmetry in the friction coefficients. Note that this dissipation function is not quadratic but highly nonlinear in the rate v. We can define the Rayleighian ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (v) = Φ − Φ(v = 0) to determine the time-averaged directional motion of the toy microswimmer. Minimization of
(v) = Φ − Φ(v = 0) to determine the time-averaged directional motion of the toy microswimmer. Minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (v) gives the cell migration velocity v as a function of the active velocity aω of the periodic shape change, and this function can be compared to experimental observations. Furthermore, in the limit of small
(v) gives the cell migration velocity v as a function of the active velocity aω of the periodic shape change, and this function can be compared to experimental observations. Furthermore, in the limit of small ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , we have |v| ≪ aω and the Rayleighian can be approximated, to the leading order, by
, we have |v| ≪ aω and the Rayleighian can be approximated, to the leading order, by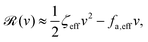
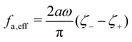 is a time-averaged effective active force that drives the directional self-propulsion of the microswimmer. Minimization of
is a time-averaged effective active force that drives the directional self-propulsion of the microswimmer. Minimization of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) gives the directional velocity of the microswimmer as
gives the directional velocity of the microswimmer as![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) /π in the limit of weak asymmetry with ζ+/ζ− → 1− or
/π in the limit of weak asymmetry with ζ+/ζ− → 1− or ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) → 0+.
→ 0+.
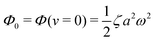 . It arises in the symmetric microswimmer from the viscous dissipation due to the fast shape-oscillation in viscous fluids.
. It arises in the symmetric microswimmer from the viscous dissipation due to the fast shape-oscillation in viscous fluids.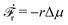 . The dissipation function is given, to the leading order in the rates, by
. The dissipation function is given, to the leading order in the rates, by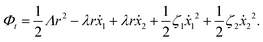
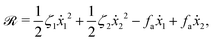
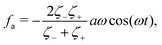

![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [ϕ,p,nα] =
[ϕ,p,nα] = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ϕ +
ϕ + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p +
p + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r +
r + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) s, as respectively given by
s, as respectively given by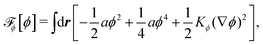
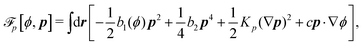
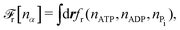
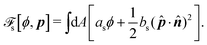
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ϕ is the free energy for the two (isotropic and polar) phase coexistence, in which a and the stiffness parameter Kϕ are both constants.
ϕ is the free energy for the two (isotropic and polar) phase coexistence, in which a and the stiffness parameter Kϕ are both constants. ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p is the free energy for polar liquid crystallinity, in which for simplicity, we employ the approximation of one elastic constant37,102Kp and we take b1(ϕ) = −b0ϕ with b0 > 0 that controls the isotropic-to-polar phase transition: b1 < 0 in the polar phase (with ϕ = 1) and b1 > 0 in the isotropic phase (with ϕ = −1). Note that the last cross-coupling term in
p is the free energy for polar liquid crystallinity, in which for simplicity, we employ the approximation of one elastic constant37,102Kp and we take b1(ϕ) = −b0ϕ with b0 > 0 that controls the isotropic-to-polar phase transition: b1 < 0 in the polar phase (with ϕ = 1) and b1 > 0 in the isotropic phase (with ϕ = −1). Note that the last cross-coupling term in ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) p represents the cases of perpendicular anchoring at the isotropic-polar phase interfaces and defines the orientation of p: if c > 0, p points from polar phase to isotropic phase.
p represents the cases of perpendicular anchoring at the isotropic-polar phase interfaces and defines the orientation of p: if c > 0, p points from polar phase to isotropic phase. ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r is the reaction free energy for ATP hydrolysis: if dfr/dnATP > 0 (that is, ATP is in excess), the forward ATP hydrolysis is exergonic, occurs spontaneously, and can be used to drive the changes in the motor configurations and generate mechanical motion, resulting in active dipole forces on the the surrounding passive polar fluids (see Fig. 2). In this case, the polar fluid will never reach thermodynamic equilibrium states and will be driven locally out of equilibrium by the active units or the motors that consumes ATP.
r is the reaction free energy for ATP hydrolysis: if dfr/dnATP > 0 (that is, ATP is in excess), the forward ATP hydrolysis is exergonic, occurs spontaneously, and can be used to drive the changes in the motor configurations and generate mechanical motion, resulting in active dipole forces on the the surrounding passive polar fluids (see Fig. 2). In this case, the polar fluid will never reach thermodynamic equilibrium states and will be driven locally out of equilibrium by the active units or the motors that consumes ATP. ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) s is the surface energy at the substrate surfaces (with as and bs being constants, and A being the surface area), which characterizes the adhesion strength of active units to the surface and the anchoring conditions for the agent orientation. Note that such a free energy
s is the surface energy at the substrate surfaces (with as and bs being constants, and A being the surface area), which characterizes the adhesion strength of active units to the surface and the anchoring conditions for the agent orientation. Note that such a free energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) will stabilize a droplet of active polar phase (ϕ ≃ 1 and |p| ≃ 1) in coexistence with surrounding fluids of passive isotropic phase (ϕ ≃ −1 and |p| ≃ 0), or vice versa.43
will stabilize a droplet of active polar phase (ϕ ≃ 1 and |p| ≃ 1) in coexistence with surrounding fluids of passive isotropic phase (ϕ ≃ −1 and |p| ≃ 0), or vice versa.43
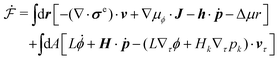
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) I − Kϕ∇ϕ∇ϕ − Kp∇pk∇pk − cp∇ϕ,
I − Kϕ∇ϕ∇ϕ − Kp∇pk∇pk − cp∇ϕ,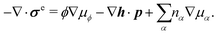
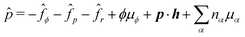 is the generalized pressure with
is the generalized pressure with ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) m (m = ϕ, p, r) being the volume density of free energy in eqn (32), μα ≡ ∂fr/∂nα being the chemical potential, and the reaction affinity, Δμ, of ATP hydrolysis given in eqn (17). The chemical potentials μϕ in the bulk and L at the solid surfaces are, respectively, given by
m (m = ϕ, p, r) being the volume density of free energy in eqn (32), μα ≡ ∂fr/∂nα being the chemical potential, and the reaction affinity, Δμ, of ATP hydrolysis given in eqn (17). The chemical potentials μϕ in the bulk and L at the solid surfaces are, respectively, given by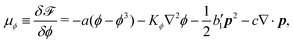
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·∇ϕ + c
·∇ϕ + c![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·p,
·p,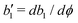 denoting the derivative of b1. The molecular field h in the bulk and H at the solid surfaces are, respectively, given by
denoting the derivative of b1. The molecular field h in the bulk and H at the solid surfaces are, respectively, given by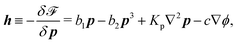
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) + Kp
+ Kp![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·∇p.
·∇p.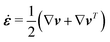 , the rate of change of polarization ṗ, and the rate of ATP hydrolysis r. These rates have the same time parity and from symmetry considerations, Φ can be written into the following invariant scalar form as62
, the rate of change of polarization ṗ, and the rate of ATP hydrolysis r. These rates have the same time parity and from symmetry considerations, Φ can be written into the following invariant scalar form as62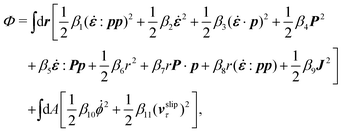
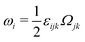 being the vorticity, and
being the vorticity, and 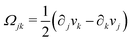 being the antisymmetric part of the velocity gradient tensor. Moreover, for simplicity, we have neglected the cross coupling among the transport of ϕ, the dynamics of polarization, and the ATP hydrolysis in the bulk fluid. This coupling can represent the treadmilling dynamics of the constituting components.103 We have also ignored the possible dissipative relaxation processes associated with the anchoring of p at the solid surfaces. In addition, we would like to point out that the choice of dissipative rates in active polar fluids is not unique.50,51 Another set of rates has been taken by Marchetti et al.:1 the viscous stress σv (or the momentum flux), r and P. In this case, the time parity of σv is different from the other two rates r and P. A brief discussion about the consequences of different choices of dissipative rates or thermodynamic fluxes on the symmetry of Onsager coupling matrix and the applications of OVP has been presented in the Appendix Section A.2.
being the antisymmetric part of the velocity gradient tensor. Moreover, for simplicity, we have neglected the cross coupling among the transport of ϕ, the dynamics of polarization, and the ATP hydrolysis in the bulk fluid. This coupling can represent the treadmilling dynamics of the constituting components.103 We have also ignored the possible dissipative relaxation processes associated with the anchoring of p at the solid surfaces. In addition, we would like to point out that the choice of dissipative rates in active polar fluids is not unique.50,51 Another set of rates has been taken by Marchetti et al.:1 the viscous stress σv (or the momentum flux), r and P. In this case, the time parity of σv is different from the other two rates r and P. A brief discussion about the consequences of different choices of dissipative rates or thermodynamic fluxes on the symmetry of Onsager coupling matrix and the applications of OVP has been presented in the Appendix Section A.2.
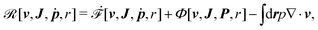
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [v,J,ṗ,r] with respect to the rates gives the dynamic equations for two-phase active polar flows as
[v,J,ṗ,r] with respect to the rates gives the dynamic equations for two-phase active polar flows as![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) − ha,
− ha,![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) pp:
pp:![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + Λr,
+ Λr,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) :pp)pp + α2pP + α3Pp + α4
:pp)pp + α2pP + α3Pp + α4![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + α5pp·
+ α5pp·![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + α6
+ α6![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) ·pp,
·pp,![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) rpp,
rpp,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) in σe in eqn (36) can be absorbed into p in eqn (45a) due to the incompressibility of the active polar fluids. The active molecular field ha is driven by ATP hydrolysis and is defined via
in σe in eqn (36) can be absorbed into p in eqn (45a) due to the incompressibility of the active polar fluids. The active molecular field ha is driven by ATP hydrolysis and is defined via![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [v,J,ṗ,r], we can also obtain the thermodynamically-consistent boundary conditions at the solid surfaces that supplements the dynamic equations in the bulk fluids:
[v,J,ṗ,r], we can also obtain the thermodynamically-consistent boundary conditions at the solid surfaces that supplements the dynamic equations in the bulk fluids: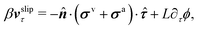
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·v = 0,
·v = 0, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·J = 0,
·J = 0,![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) + Kp
+ Kp![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·∇p = 0.
·∇p = 0.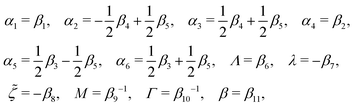
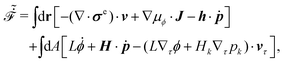
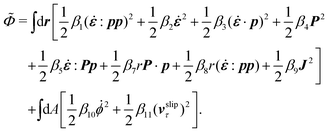
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) , parametrized by the constant reaction rate r, can be rewritten as
, parametrized by the constant reaction rate r, can be rewritten as 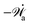 ,
,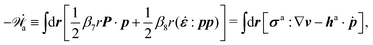
![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) Λ−1Δμ and ζh ≡ λΛ−1Δμ. The cross-coupling coefficients β7 and β8 (hence ζ and ζh) can be either positive or negative as long as they can preserve the positive definiteness of the dissipation function. For example, negative and positive values of ζ correspond to contractile and extensile active stresses, respectively, as schematically shown in Fig. 2.
Λ−1Δμ and ζh ≡ λΛ−1Δμ. The cross-coupling coefficients β7 and β8 (hence ζ and ζh) can be either positive or negative as long as they can preserve the positive definiteness of the dissipation function. For example, negative and positive values of ζ correspond to contractile and extensile active stresses, respectively, as schematically shown in Fig. 2.
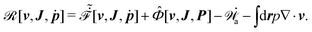
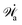 represents the work power done on the passive polar fluids by the active stress σa and the active molecular field ha. The dissipation function
represents the work power done on the passive polar fluids by the active stress σa and the active molecular field ha. The dissipation function ![[capital Phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a9.gif) for the passive polar fluid is given by
for the passive polar fluid is given by
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) gives the following simplified dynamic equation system:
gives the following simplified dynamic equation system:![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) + γ1−1ha,
+ γ1−1ha,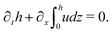
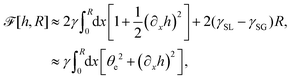
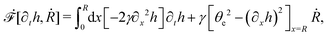
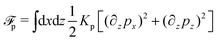 , similarly as defined in eqn (32b) under the approximation of one elastic constant, Kp, and fixed magnitude of p.
, similarly as defined in eqn (32b) under the approximation of one elastic constant, Kp, and fixed magnitude of p.
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) at z = 0 and p =
at z = 0 and p = ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b8.gif) ≈ (1,∂xh) at the free surface z = h, in which
≈ (1,∂xh) at the free surface z = h, in which ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) is the unit vector along the x-direction and
is the unit vector along the x-direction and ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b8.gif) is the unit tangent vector of the free surface of the droplet. This anchoring boundary condition is mainly motivated by the stress-fiber structure in adherent cells2 and by the experimental observations114 on thin films of amoeboid cells, in which the cells lie in the plane of the glass slide on which they spread and form nematic liquid-crystal structures. The planar anchoring conditions at the free surface have been employed in many previous works.98,102,105,106 In contrast, in our diffuse-interface model of active polar droplets in Section 4, we have assumed planar anchoring condition at the solid surface but perpendicular anchoring condition at the free interface, which mimics the orientation of actin filaments in the lamellipodium of migrating cells. Such anchoring boundary conditions have also been used in many previous works.43,49,101,104
is the unit tangent vector of the free surface of the droplet. This anchoring boundary condition is mainly motivated by the stress-fiber structure in adherent cells2 and by the experimental observations114 on thin films of amoeboid cells, in which the cells lie in the plane of the glass slide on which they spread and form nematic liquid-crystal structures. The planar anchoring conditions at the free surface have been employed in many previous works.98,102,105,106 In contrast, in our diffuse-interface model of active polar droplets in Section 4, we have assumed planar anchoring condition at the solid surface but perpendicular anchoring condition at the free interface, which mimics the orientation of actin filaments in the lamellipodium of migrating cells. Such anchoring boundary conditions have also been used in many previous works.43,49,101,104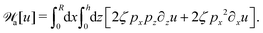
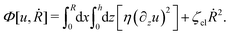
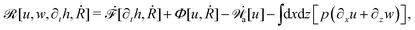
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to the rates, u, w, ∂th, and Ṙ, give a closed dynamic equation system for the thin droplets moving on solid substrates as follows. In the bulk, the dynamic equations are
with respect to the rates, u, w, ∂th, and Ṙ, give a closed dynamic equation system for the thin droplets moving on solid substrates as follows. In the bulk, the dynamic equations are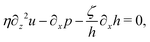
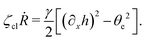
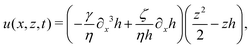
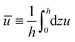 as
as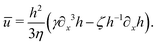
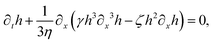
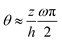 , in which θ is the angle of p relative to the x-axis and ω is an integer winding number that counts the number of quarter turns of p across the drop height. In comparison, in the present work, we have not considered such internal polarization winding and the orientation of p varies along z as θ ∼ pz/px ≈ (z/h)∂xh (see eqn (62)). Such difference in the variation of p orientation leads to the difference in the final form of thin film equation between the present work and that by Loisy et al.106
, in which θ is the angle of p relative to the x-axis and ω is an integer winding number that counts the number of quarter turns of p across the drop height. In comparison, in the present work, we have not considered such internal polarization winding and the orientation of p varies along z as θ ∼ pz/px ≈ (z/h)∂xh (see eqn (62)). Such difference in the variation of p orientation leads to the difference in the final form of thin film equation between the present work and that by Loisy et al.106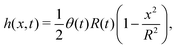
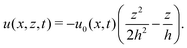
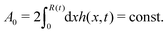 , we have
, we have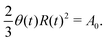
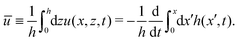
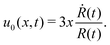
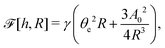
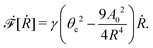
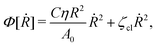
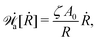
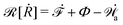 . Minimizing
. Minimizing ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) with respect to Ṙ gives the following evolution equation
with respect to Ṙ gives the following evolution equation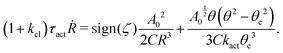
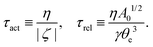
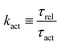
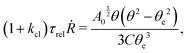
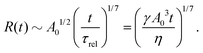
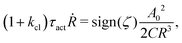
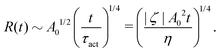
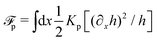 .
.![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) (or the flow velocity v) and the corresponding forces are Δμ, h, σv, respectively, as taken in Section 4 of this work. Here all the three fluxes have the same time parity.
(or the flow velocity v) and the corresponding forces are Δμ, h, σv, respectively, as taken in Section 4 of this work. Here all the three fluxes have the same time parity.![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) , respectively, as taken by Marchetti et al.1 Here the time parity of the flux σv is different from the other two fluxes r and P. Furthermore, note that in this case, the new pair of flux σv and force
, respectively, as taken by Marchetti et al.1 Here the time parity of the flux σv is different from the other two fluxes r and P. Furthermore, note that in this case, the new pair of flux σv and force ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) is a swap of the pair of flux
is a swap of the pair of flux ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) and force σv in the first choice (i).
and force σv in the first choice (i).![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X1,
1 and X1, ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2 and X2. Suppose that the two fluxes
2 and X2. Suppose that the two fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and
1 and ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2 have the same time parity, and hence the two forces X1 and X2 also have the same time parity but opposite to that of the corresponding fluxes. In this case, the linear force–flux relations are then given by:
2 have the same time parity, and hence the two forces X1 and X2 also have the same time parity but opposite to that of the corresponding fluxes. In this case, the linear force–flux relations are then given by: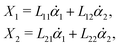
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2, that is, we choose the fluxes to be
2, that is, we choose the fluxes to be ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X2, and the corresponding forces are X1 and
1 and X2, and the corresponding forces are X1 and ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 2. Then the time parities of the two fluxes
2. Then the time parities of the two fluxes ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14c.gif) 1 and X2 are now different. In this case, the linear force–flux relations become
1 and X2 are now different. In this case, the linear force–flux relations become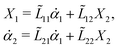
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 11 = (L11L22 − L122)/L22,
11 = (L11L22 − L122)/L22, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 12 = L12/L22,
12 = L12/L22, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 21 = −L21/L22,
21 = −L21/L22, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 22 = 1/L22. Note that now
22 = 1/L22. Note that now ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 21 = −
21 = −![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 12, that is, the Onsager coupling matrix
12, that is, the Onsager coupling matrix ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ij is antisymmetric. From this simple example, we show that although there exists some flexibility in choosing fluxes and forces, we can safely use the time parity of the chosen fluxes to determine the symmetry of the Onsager coupling matrix in the linear force–flux relations.
ij is antisymmetric. From this simple example, we show that although there exists some flexibility in choosing fluxes and forces, we can safely use the time parity of the chosen fluxes to determine the symmetry of the Onsager coupling matrix in the linear force–flux relations.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (α,β) and the rate of change of the free energy is given by
(α,β) and the rate of change of the free energy is given by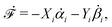
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) and
and  are two fluxes, and
are two fluxes, and![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /∂αi, Yi ≡ − ∂
/∂αi, Yi ≡ − ∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /∂βi
/∂βi![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) and
and 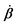 , and that of X and Y are both opposite, respectively. In this case, we can decompose the two forces into reactive and dissipative parts as
, and that of X and Y are both opposite, respectively. In this case, we can decompose the two forces into reactive and dissipative parts as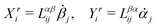
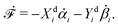
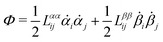
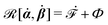 , we obtain
, we obtain