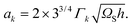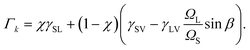DOI:
10.1039/D1CE00743B
(Paper)
CrystEngComm, 2021,
23, 5284-5292
Surface energy driven miscibility gap suppression during nucleation of III–V ternary alloys
Received
4th June 2021
, Accepted 5th July 2021
First published on 6th July 2021
Abstract
The existence of a miscibility gap limits the range of solid compositions which are possible to achieve under near-equilibrium growth conditions. Circumventing the miscibility gap is of paramount importance for device fabrication. We propose that one of the suppression mechanisms is the nucleus surface energy and explain how the surface energy influences the miscibility gap during nucleation from a liquid melt. By doing this, we start with the formation of the critical nucleus of a ternary alloy considering its surface energy as a combination of the binary ones. For certain nucleation scenarios in the InGaAs materials system we show that the compositional independence of the surface energy term is a good approximation due to similar values for InAs and GaAs pairs. However, a large difference in the surface energies of the two materials may lead to a significant modification of the liquid–solid composition dependence and a complete suppression of the miscibility gap.
Introduction
Growth of ternary alloys formed by mixing two binary compounds is of paramount importance in materials science and engineering.1 This is due to the possibility to tune one or more properties (band gap and lasing wavelength, lattice constant, magnetic properties) of the structure by varying its composition. Among structures of ternary alloys of different dimensions and morphology, ternary nanowires2–4 have attracted great attention due to a broad spectrum of its possible application in optoelectronics, biotechnology and energy harvesting.5 In contrast to elemental and binary compound semiconductors, the emission wavelength of optoelectronic devices based on ternary alloys can be adjusted by choosing from a continuous range determined by the two binaries.6,7 Mastering the optoelectronic device design is impossible without an accurate composition control. Nevertheless, having the ideal growth technique, in many cases not all the solid compositions can be achieved for all materials combinations because of the miscibility gap, resulting in a wide range of thermodynamically forbidden compositions.8 The reason for the miscibility gap is a net repulsion between dissimilar atoms and is, in the regular solution model,9 described by the pseudobinary interaction parameter in the solid, ωS. It can readily be shown that the miscibility gap appears in ternary alloys with ωS > 2RT, where R is the gas constant and T is the temperature in Kelvin.10
The composition tuning range is limited in (In,Ga)As (ref. 11) and (In,Ga)N (ref. 12) alloys due to prominent miscibility gaps. In some cases such as In(As,Sb), the miscibility gap is shifted and non-symmetrical because of the composition-dependent pseudobinary interaction parameter.13 The miscibility gap shrinks with temperature. However, high growth temperatures are often unfeasible because of the increased decomposition rate of the solid. For example, the miscibility gap in InGaAs materials system disappears at 543 °C,14 while typical growth temperature of InGaAs nanowires by the molecular beam epitaxy and vapor phase epitaxy methods is in the range of 400–500 °C.4 Thus, a large composition range of certain ternary alloys is thermodynamically forbidden. Understanding how to tune the composition of solid solutions over the entire range is needed to improve the quality of modern devices and to design promising structures such as vertical quantum wires.15
Considering the immiscibility in bulk alloys,16 growth of nanostructures with compositions inside the miscibility gap is often possible via formation of metastable states. For example, the miscibility gap in thin films can be suppressed by elastic stress.17,18 In the case of growth of axial nanowire heterostructures at temperatures lower than the critical one,14 the wide range of thermodynamically forbidden compositions should lead to the formation of an atomically abrupt interface. However, a compositionally graded interface over the entire compositional range is observed in heterostructured nanowires of materials systems with a high pseudobinary interaction parameter which proves either the metastable state formation inside the miscibility gap, or the suppression of the miscibility gap.19,20 Despite a number of experimental investigations on the growth of nanowires with composition inside the miscibility gap,21,22 the suppression mechanism in these nanostructures remain unclear. Some kinetic theories23,24 assume that the miscibility gap might shrink under relatively high supersaturations in the liquid. Indeed, it has been shown that high concentrations of group V elements in the droplet can “straighten” the initially S-shaped liquid–solid composition dependence curve. Another possible explanation is the size-dependent effect of spinodal decomposition,25 or the chemical-potential-dependent surface reactions resulting in a miscibility gap shrinkage with reducing particle size.26
The composition-independence of the surface energy term of the critical nucleus is a standard assumption substantiated by the investigation by Wilemski,27 where it was assumed that the component with the lower surface energy segregates to the surface so readily so that the nucleus always obtains the surface energy of that component. This is used in the majority of kinetic models based on the incorporation rate,23,24,28 mass balance models,29 equilibrium models30 and nucleation-limited models.14,31 The omitted surface energy term is a good approximation for the relatively large size of the stable growing clusters, making the surface energies insignificant. Using the Butler equations32 for calculation of the composition-dependent interface energies, the robustness of the existence of the saddle point is presented in.33 Finally, the effect of a composition-dependent edge energy on the interface profiles of the axial heterostructures in nanowires has been studied by Glas34 for the (Al,Ga)As materials system, in which the growth temperatures are far above the miscibility gap.
In the current paper, we aim to analytically explore the miscibility gap suppression driven by the surface energy of the ternary nucleus. The nucleus surface energy is introduced in a general way giving an opportunity to consider the Vegard's law case, the Wilemski approach, and their intermediate cases as well as a convex (second degree polynomial) model which resembles the Butler equations case. We construct the miscibility gap and analyse it with respect to the composition of group V elements and the effective surface energy ratio.
There are a number of simplifications and assumptions utilized in this paper. (i) The investigation is based on classical nucleation theory and implies the capillarity approximation35–37 within which molecular clusters are treated as macroscopic objects. This is a basic model and might lead to some invalid results such as overestimation of the nucleation rate of crystalline monolayers.38 No renormalization because of the finite size of the considered system is utilized. Such self-consistency renormalization of the Zeldovich nucleation rate for calculation of nanowire elongation rates and description of crystal structure can be found in.39 The critical nucleus size depending on the supersaturation could be relatively large (>200 atoms (ref. 33)). However, more accurate calculations involve quantum corrections and consideration of the nanoscale nature.40,41 (ii) The Gibbs–Thomson effect of elevated chemical potential in the droplet due to a curved surface42 is not considered. Its effect can often be ignored for liquid particles with sizes larger than about 20 nm. (iii) The obtained results describe the composition of the critical nucleus. Thus, it applies to nucleation-limited growth. At high supersaturation the final composition might differ from the one of the critical nucleus.24 (iv) Finally, there is an uncertainty in the estimated values of the surface energies and the concentration of group V elements in the liquid. Despite these shortcomings, classical nucleation theory has proven to be valuable for modelling and understanding several aspects of nanowire growth.14,31,43,44
Due to the theoretical nature of our work, we are able to vary the parameters whose values are very difficult to study experimentally, namely the surface energy ratio and concentration of group V elements. This allows us to discuss some general trends, which can be of high value to experimentalists. Moreover, we have estimated the effect of the uncertainty of surface energy values on the liquid–solid composition dependence and miscibility gap.
Calculations
Conceptually, there are two main approaches to fabricate micro- and nanostructures.45 The first one is the top-down approach which implies the surface patterning by electron beam lithography,46 nanoimprint lithography47 and other methods followed by etching. The second one is the bottom-up approach in which structures are synthesized by stacking atoms of provided semiconductor materials onto each other. Nucleation occurs from the liquid phase within vapor–liquid–solid growth or from the vapor within vapor–solid–solid growth.
To fabricate ternary alloy structures, bottom-up approach with the involved liquid phase is the most suitable because the solid composition can be accurately controlled by composition of the liquid while the layer-by-layer growth process provides excellent crystal quality. Therefore, in this paper we consider the formation of a critical nucleus of a ternary AxB1−xD alloy from a quaternary liquid droplet which contain A, B, D, and U, where U is gold or another catalyst. The foreign catalyst changes the chemical potential in the liquid and simplifies nanostructure growth. In the context of nanowires, liquid catalyst droplets act as collection sites for semiconductor material resulting in selective growth which can be ordered if the patterned mask is used or randomly distributed otherwise. It is also possible to synthesize nanowires without a foreign metal. This is the so called self-catalyzed growth48 where the liquid droplets contain only the group III nanowire constituent and small amount of group V constituent.
Nucleation is schematically presented in Fig. 1. Nucleation occurs at the liquid–solid interface while the ratio of incorporated A and B atoms determines the solid composition x. The presented model allows us to discuss growth of both bulk structures and nanowires from the liquid phase. Assuming the droplet and substrate to be “infinitely” large, the theory can be applied for the description of bulk structures grown by the liquid phase epitaxy.49 For the nanoscale droplet particles, the model is applicable for nanowires grown via the vapor–liquid–solid (VLS) mechanism.50 This is an attractive bottom-up approach of nanostructure fabrication that involves nucleation and growth from supersaturated liquid droplets. The difference between nucleation at the triple phase line and in the center of the liquid–solid interface is determined by the vertical edge of the 2D nucleus. It is a weighted sum of the vapor-solid, liquid–solid and liquid–vapor surface energies at the triple phase line nucleation, while it is a function of the liquid–solid surface energy in the case of nucleation in the center of the liquid–solid interface (see Appendix A).
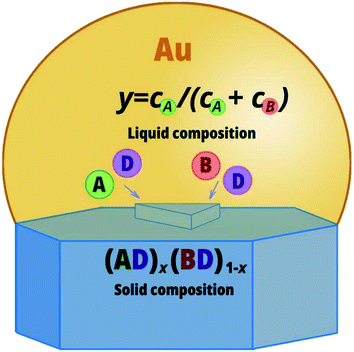 |
| | Fig. 1 Schematic illustration of the formation of an AxB1−xD nucleus from the quaternary liquid phase at nucleation in the center of the liquid–solid interface. | |
The change of Gibbs energy during nucleation is composed of three parts. The first one decreases linearly with the nucleus size s with the chemical potential as proportionality factor. The second term increases with the nucleus perimeter due to the formation of new surfaces. The last term is VLS specific and refers to the transformation of the liquid drop surface due to the nucleus formation and is often ignored because of its small value. Thus, the nucleus formation energy is given by
| | 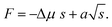 | (1) |
Here
a is the effective surface energy of the nucleus of a ternary alloy and Δ
μ is the chemical potential difference between the quaternary liquid melt and the solid (see Appendix A). The form of the chemical potentials which contain the ternary and composition-dependent binary interaction parameters can be found in.
31
According to classical, two-component nucleation theory, the size and composition of a critical nucleus can be found from the simultaneous solution of the following system of differential equations:
| | 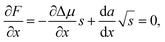 | (2) |
| | 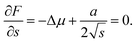 | (3) |
The critical size is a result of maximization of the formation energy in the size and can be expressed from
eqn (3), yielding
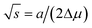
. Then, the nucleation barrier required for the formation of the nucleus of the critical size is
F* = a
2/4Δ
μ. Now, one should minimize the nucleation barrier
F* in the solid composition. This procedure is equivalent to elimination of the nucleus size in
eqn (2), and gives the relationship between the terms related to the phase transition and the nucleus surface energy in the form
| | 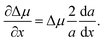 | (4) |
As a consequence of the chemical potential being a partial molar property of a binary system, the derivative of the chemical potential difference with respect to solid composition equals the chemical potential difference of the AD (Δ
μAD) and BD (Δ
μBD) pairs, ∂Δ
μ/∂
x = Δ
μAD − Δ
μBD. Thus,
eqn (4) might be reduced to
| | 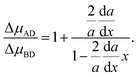 | (5) |
In this form, it is clearly seen that in the general case, there is no equality between the chemical potential difference of AD and BD pairs. This equality (being equivalent to ∂Δ
μ/∂
x = 0 considered in ref.
14 and
31) is only the case if d
a/d
x = 0.
To combine all the considered cases, the surface energy of the ternary nucleus can be presented as
with Δ
a =
aAD −
aBD. The composition-dependent function
g(
x) defines a particular model. So, a linear relationship can be obtained at
It is clearly seen that the Vegard's law case
a =
aADx +
aBD (1 −
x) is implemented at
δ = 0, while the Wilemski case
a =
aAD corresponds to
δ = 1. All the linear intermediate cases lying between the first and second curves can be described by 0 <
δ < 1.
For the convex relationship, the function is given by
where the bowing parameter
α defines the quadratic term and, thus, describes the deviation from linearity. Then the derivatives of the nucleus surface energy with respect to the solid composition are
| | 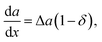 | (9) |
| | 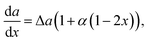 | (10) |
In the linear case of the Vegard's law (
δ = 0), the derivative of the nucleus surface energy with respect to the solid composition is the surface energy difference of the binaries d
a/d
x = Δ
a. In this case the solid composition of a ternary alloy can be found from the following equation
| | (ΔμyADaBD − ΔμyBD(aAD + Δa)) − (ΔμyAD − ΔμyBD)xΔa = (RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + ωs(1 − x)2)(aBD − xΔa) − (RT x + ωs(1 − x)2)(aBD − xΔa) − (RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − x) + ωSx2)(aAD + (1 − x)Δa). ln(1 − x) + ωSx2)(aAD + (1 − x)Δa). | (11) |
Eqn (11) can be written as
f(
y) +
u(
y)
x =
g(
x). The superscript
y in the chemical potential difference is explained in Appendix A. This mixing of solid and liquid compositions results in a complex dependence where the miscibility gap is a function of several parameters including As and Au concentrations in the droplet, growth temperature and the ratio of the binary surface energy terms. The In/III concentration ratio the liquid is denoted by
y.
Considering the nucleus surface energy, the miscibility gap is shifted and not symmetrical around x = 0.5 anymore. Its width at the fixed liquid composition can be found using the Maxwell construction or the Hessian determinant,
| | 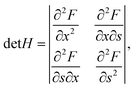 | (12) |
which in our case is given by
| | 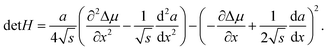 | (13) |
In
eqn (13),
∂2Δ
μ/∂
x2 = 2
ωs −
RT/(
x/(1 −
x)),
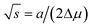
, and d
2a/d
x2 = 0 for the linear model and d
2a/d
x2 = −2
αΔ
a for the convex model. The spinodal is defined by the equation det
H = 0. The maximum of the Hessian determinant as a function of
x corresponds to the largest instability of the system and gives the center of the miscibility gap.
The critical temperature Tc corresponds to the critical point where the binodal and spinodal curves coincide. In the case of x-independent nucleus surface energy, 2RTc = ωS (Tc). Otherwise, to find the critical temperature as a function of the effective surface energy ratio at fixed concentrations of D and U, it is necessary to solve the equations d(detH)/dx = 0 and detH = 0 simultaneously with x being the composition of the critical nucleus.
Results and discussion
We start the discussion with an overview of the different approaches to the surface energy of an arbitrary ternary nucleus. All the main cases calculated at aBD/aAD = 2 are summarized in Fig. 2. The first curve (i) represents the Vegard's law where the surface energy term is a linear combination of the binary ones implemented at δ = 0. Another extreme case (ii) corresponds to δ = 1 meaning the independence of the surface energy on the solid composition (da/dx = 0). This approach was introduced by Wilemski27 and is motivated by a phase segregation situation where the binary with lower surface energy concentrates at the nucleus periphery. In spite of the lack of justification for its application for solids51 it remains very popular for modelling vapor–liquid–solid nucleation due to its simplicity.14,24,31 The curve (iii) corresponds to the intermediate case calculated at δ = 0.5. Finally, a non-linear case can be considered within the convex model (iv) calculated at α = 1, while the curve coincides with the Vegard's law case at α = 0. Due to the quadratic form in the convex model at non-zero α, the results are expected to be similar to the Butler equation case.33
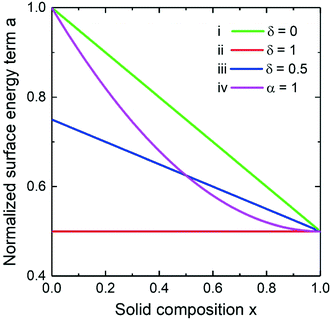 |
| | Fig. 2 Normalized surface energy term of a ternary nucleus for aBD/aAD = 2 in the (i) Vegard's law case, (ii) Wilemski approach, (iii) their intermediate case and the convex model (iv). | |
The liquid–solid composition dependence can be obtained from eqn (11) by finding the crossings of functions f(y) + u(y)x and g(x). Under the condition of aGaAs/aInAs = 1, the function g(x) coincides with the previously considered case of g(x) = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(x/(1 − x)) − 2ωS(x − 1/2)14 while the decrease or increase of the ratio determines shifting the function up or down correspondingly. Fig. 3 shows the functions f(y) + u(y)x and g(x) calculated for different y at fixed aGaAs/aInAs = 1.3, T = 450 °C, cAs = 0.01 and cAu = 0.28. As seen from Fig. 3, there is only one solution in a wide y range except of y ≈ 0.9506 near which the curve f(y) + u(y)x crosses the curve g(x) three times. At such liquid compositions there is a miscibility gap.
ln(x/(1 − x)) − 2ωS(x − 1/2)14 while the decrease or increase of the ratio determines shifting the function up or down correspondingly. Fig. 3 shows the functions f(y) + u(y)x and g(x) calculated for different y at fixed aGaAs/aInAs = 1.3, T = 450 °C, cAs = 0.01 and cAu = 0.28. As seen from Fig. 3, there is only one solution in a wide y range except of y ≈ 0.9506 near which the curve f(y) + u(y)x crosses the curve g(x) three times. At such liquid compositions there is a miscibility gap.
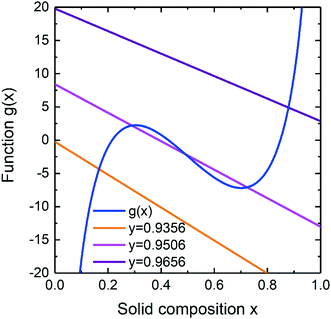 |
| | Fig. 3 Illustration of the y(x) selection rule for InGaAs materials system. The blue solid curve is g(x) function; the tilted lines are f(y) + u(y)x calculated for different y and at fixed aGaAs/aInAs = 1.3. | |
Now let us consider the effect of the surface energy on the ternary nucleus formation in vapor–liquid–solid growth. Fig. 4a shows the liquid–solid composition dependence calculated within the Vegard's law for the critical InxGa1−xAs nucleus at different surface energies. The parameters are cAs = 0.01, cAu = 0.28 and T = 450 °C. It is seen that the liquid–solid composition dependence is significantly modified with increasing aGaAs/aInAs. It leads to a narrowing of the miscibility gap and to higher In content in the solid at fixed liquid composition. At the large enough ratio of aGaAs/aInAs = 1.5, the miscibility gap is completely suppressed, while at aGaAs/aInAs ≈ 2 the solid composition is almost equal to the liquid composition (x ≈ y).
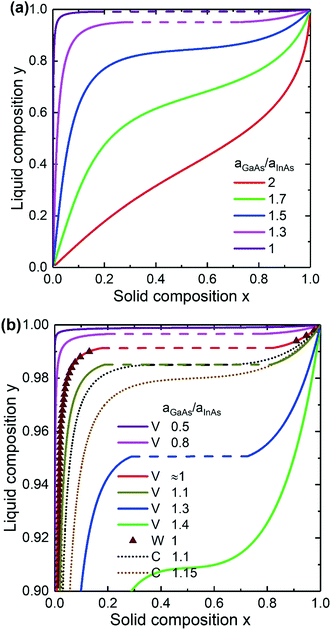 |
| | Fig. 4 Liquid–solid composition dependences of InGaAs alloy for different surface energy ratio calculated within the Vegard model (a) and within Vegard (V), Wilemski (W) and convex (C) models (b). Triangles correspond to the Wilemski approach. The solid curves are the Vegard's law case and dots are the convex model with α = 0.5. The dashed lines correspond to the miscibility gap. | |
A comparison of the composition dependences calculated within different models is presented in Fig. 4b. The parameters are the same as in Fig. 4a. For center nucleation43 of a InGaAs nucleus, the values of the surface energy terms (see Appendix A for definitions) for InAs (ref. 52) and GaAs (ref. 53) pairs are similar, namely aGaAs/aInAs = 1.0002. Thus the liquid–solid composition dependence is expected to be identical to the one in the Wilemski approach.31 Modelling of nucleation from a quaternary liquid melt hampers the calculations because the surface energy of GaAs pairs at the solid–liquid interface increases by an order of magnitude during the transition from Au-catalyzed growth to self-catalyzed one.43,54 However, in this paper the surface energy at the solid–liquid interface is treated as independent on the group III concentration since this phenomenon is poorly studied.
As seen from Fig. 4b the composition dependences corresponding to the Vegard's law at aGaAs/aInAs = 1.0002 and the Wilemski approach are almost identical. This justifies the assumption of composition-independence of the surface energy for the InGaAs materials system. It is remarkable that within Vegard's law, the miscibility gap disappears at surface energy ratios quite far from 1 (aGaAs/aInAs ≈ 0.5 and aGaAs/aInAs ≈ 1.4 under the chosen conditions), while the surface energy ratio has larger impact within the convex model. Here the solid composition can be tuned throughout the entire range at aGaAs/aInAs = 1.15. The shape of the curve is similar to the result obtained in33 using the Butler equations at c3 ≡ cIn + cGa = 0.7, T = 477 °C, cAs = 0.02 and the ratio of the pure InAs and GaAs surface energies of 1.15. It is important to note that in the case of nucleation at the triple phase line, aGaAs/aInAs ≈ 1.15, which was the considered case in ref. 33. So, the miscibility gap is slightly modified in the Vegards law case and completely suppressed within the convex model. Thus, at the triple phase line nucleation the choice of model is crucial.
As it is widely known, for a composition independent ωS the temperature of the binodal can be written as Tb = ωS(1 − 2x)/(R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((1 − x)/x)). Introducing the surface energy, it is impossible to explicitly express the binodal temperature as a function of solid composition in a similar closed form. Moreover, including the surface energies, Tb depends on the chemical potential in the liquid which is a strong function of group V element concentration. Fig. 5 shows the miscibility gap in an InGaAs alloy calculated for the Vegard's law case for different surface energy ratios at fixed cAs = 0.01 and cAu = 0.28. The largest binodal region corresponds to aGaAs/aInAs = 1 and narrows the more this ratio deviates from 1. So, the critical temperature above which all the solid compositions are stable is T = 543 °C at aGaAs/aInAs = 1, T ≈ 505 °C at aGaAs/aInAs = 1.3 and T = 432 °C at aGaAs/aInAs = 1.4.
ln((1 − x)/x)). Introducing the surface energy, it is impossible to explicitly express the binodal temperature as a function of solid composition in a similar closed form. Moreover, including the surface energies, Tb depends on the chemical potential in the liquid which is a strong function of group V element concentration. Fig. 5 shows the miscibility gap in an InGaAs alloy calculated for the Vegard's law case for different surface energy ratios at fixed cAs = 0.01 and cAu = 0.28. The largest binodal region corresponds to aGaAs/aInAs = 1 and narrows the more this ratio deviates from 1. So, the critical temperature above which all the solid compositions are stable is T = 543 °C at aGaAs/aInAs = 1, T ≈ 505 °C at aGaAs/aInAs = 1.3 and T = 432 °C at aGaAs/aInAs = 1.4.
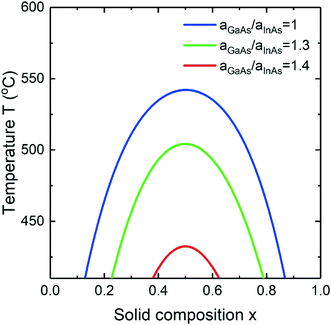 |
| | Fig. 5 The miscibility gap in InxGa1−xAs alloy at cAs = 0.01 for different surface energy ratios. | |
The dependence of the miscibility gap of InGaAs alloy on the As concentration at aGaAs/aInAs = 1.3 and cAu = 0.28 is presented in Fig. 6. As seen with increasing As concentration the miscibility gap decreases. Changing the As concentration by an order of magnitude from cAs = 0.01 to cAs = 0.1 results in shift of the critical temperature by 64 °C from T ≈ 505 °C to T ≈ 441 °C. Simplifying, the chemical potentials in the solid μsAD and μsBD are responsible for the binary separation and the appearance of the miscibility gap in a ternary alloy. Their difference is an essential part of the chemical potential term in the nucleus formation energy and has the largest impact on the thermodynamically forbidden compositional range. By including a composition dependence of the nucleus surface energy in the formation energy, the miscibility gap might be reduced in two possible ways. They are the increase of the second term in eqn (1) with raising the difference of the interface energies of the two binaries (Fig. 5) and the decrease of the first term in eqn (1) with raising the group V concentration in the liquid which leads to higher supersaturation (Fig. 6). Thus, even in ternary alloys with a high value of the pseudobinary interaction parameter, the miscibility gap might be suppressed completely at temperatures relevant for growth. It is interesting that the surface energy driven suppression mechanism acts at the nucleation stage in contrast to the kinetic growth picture previously discussed.23,24,28
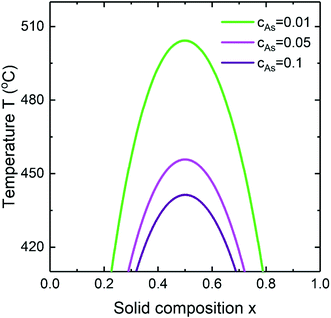 |
| | Fig. 6 The miscibility gap in InGaAs alloy at aGaAs/aInAs = 1.3 for different As concentrations. | |
The critical temperature Tc at which the miscibility gap vanishes is determined by both the composition of the liquid and the effective surface energy ratio. Fig. 7 shows the dependence of the critical temperature on aGaAs/aInAs for the InGaAs nucleus at fixed cAu = 0.28 calculated for different As concentrations within the Vegard's law model. It is clearly seen that both curves reach the maximum at equal surface energies (aGaAs/aInAs = 1). Then the critical temperature decreases rapidly and almost symmetrically on both sides of aGaAs/aInAs = 1. So, if aGaAs/aInAs ≈ 1.38 and cAs = 0.01, the miscibility gap disappears at Tc = 450 °C which is a relevant growth temperature for vapor phase deposition. The U-shaped curve of the critical temperature against effective surface energy ratio explains the liquid–solid composition dependence presented in Fig. 4b: the solid phase exists over the entire compositional range at both high and low enough values of the effective surface energy ratio (the violet and green solid lines). Increasing the As concentration, the critical temperature decreases.
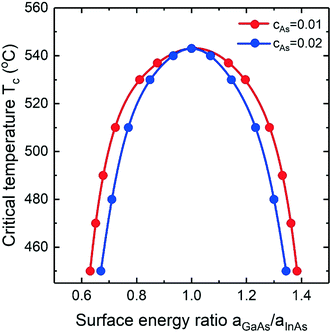 |
| | Fig. 7 Critical temperature versus the ratio of binary surface energy terms for InGaAs materials system at fixed As concentration of cAs = 0.01 (red curve) and cAs = 0.02 (blue curve). The dots represent numerical calculations and the solid curves are polynomial fits. | |
Finally, we discuss the impact of the uncertainty of the surface energies. The estimated error of the surface energy found in the literature is about 10%.55 It influences both the critical nucleus size which is not calculated here and the liquid–solid composition dependence and the miscibility gap through the ratio of the surface energies. Assuming the error is 10%, the surface energy ratio is in a range of 0.9–1.1. As seen from Fig. 4b (compare the solid red and dark yellow curves), the liquid–solid composition dependence is slightly shifted to the bottom while the miscibility gap and the critical temperature (see Fig. 7) are almost the same. However, within the convex model (compare the solid red and dotted black curves), the miscibility gap is twice as small. Thus, in the context of the miscibility gap, the Vegard's law case is less sensitive to the surface energy error than the convex model.
Conclusions
To summarize, the surface energy contribution in the formation energy of a two-component ternary alloy nucleus is considered. By doing this, we solve the system of equations which define the saddle point of the nucleus formation energy and eliminate the nucleus size. Within this model based on two-component nucleation theory, the composition of ternary alloys nucleating from a liquid melt is obtained as a function of the composition of the melt. The surface energy term of the ternary nucleus is a combination of the corresponding binary terms. In this regard, we analyse one convex model and three linear models, namely the Vegard's law case, the Wilemski approach and their intermediate case. Modelling the example of InGaAs VLS nanowire system shows that at the central nucleation the surface energy contribution is small and almost does not change the miscibility gap and the liquid–solid composition dependence because of the similar values of InAs and GaAs surface energy terms. This justifies the usage of the Wilemski approach which simplifies the calculations. For nucleation at the triple phase line, the convex and linear models give different results: in contrast to the Vegard's law case, the miscibility gap is completely suppressed within the convex model at aGaAs/aInAs = 1.15. In any case, a sufficient increase of the surface energy ratio results in a complete suppression of the miscibility gap. The model might be useful for the optimization of growth parameters for the fabrication of III–V semiconductor nanowires and bulk structures growing from the liquid phase with a specified ternary composition. Thus, the model could be applied to InxGa1−xN, InAsxSb1−x or InxGa1−xSb alloys for instance. By doing this, one should find and substitute in the corresponding places of eqn (11)–(13) the values of Gibbs free energies, interaction parameters and surface energies of the chosen material system. Moreover, the model might be used for modelling solid composition of material systems without miscibility gap at relevant growth temperatures because a large surface energy contribution may modify the liquid–solid composition dependence. With relevant chemical potentials and surface energies, our approach can also be generalized to other scenarios, such as direct vapor-solid nucleation and growth. However, care should be taken when applying the model and the obtained results because of the uncertainty in the surface energies.
Appendix A
The difference of the chemical potentials between liquid and solid is given by| | | Δμ = xΔμAD + (1 − x)ΔμBD, | (A1) |
where the chemical potential differences of AD and BD pairs in the liquid and in the solid state are given by| | | ΔμAD = μLA + μLD − μsAD, | (A2) |
| | | ΔμBD = μLB + μLD − μsBD. | (A3) |
The chemical potentials in the liquid of the corresponding component are given by| | μLA = μ0A + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cA + φA, cA + φA, | (A4) |
| | μLB = μ0B + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cB + φB, cB + φB, | (A5) |
| | μLD = μ0D + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cD + φD. cD + φD. | (A6) |
Here μ0 is the Gibbs free energy of the corresponding pure element, φ is a sum of products of corresponding interaction parameters and concentrations.23,31
The chemical potentials in the solid of AD and BD binary species are given by
| | μsAD = μ0AD + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + ωS(1 − x)2, x + ωS(1 − x)2, | (A7) |
| | μsBD = μ0BD + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − x) + ωSx2, ln(1 − x) + ωSx2, | (A8) |
with
ωS being the pseudobinary interaction parameter and
μs is the Gibbs free energy of the corresponding binary compound. We use the following notation:
| | | ΔμyAD = μLA + μLD − μ0AD, | (A9) |
| | | ΔμyBD = μLB + μLD − μ0BD. | (A10) |
Next, the interface energy ak with k = (AD,BD) is a product of a geometrical factor and Γk being the effective surface energy of the vertical edge of the corresponding binary nucleus:
| | 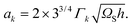 | (A11) |
Here
ΩS is the volume of a pair in the solid and
h is the 2D nucleus thickness.
Γk is a function of the surface energies of the solid–liquid (
γSL), solid–vapor (
γSV), and liquid–vapor (
γLV) interfaces and is given by
| | 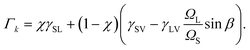 | (A12) |
Here
ΩL is the volume of a pair in the liquid and
β is the wetting angle between the catalyst particle and the liquid–solid interface. Parameter
χ = 1 for nucleation in the center and
χ = 2/3 for triple line nucleation. It should be noted that in this paper we don't take into account the dependence of the surface energy of the solid–liquid interface
γSL on composition of the liquid droplet
39 because it is poorly studied. The parameter values in the cases of nucleation at the triple phase line and in the center of the liquid–solid interface can be found in ref.
56.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
This research was funded by the European Union's Horizon 2020 research and innovation program, the Marie Skłodowska-Curie grant 722176 (project acronym INDEED) and by NanoLund.
References
-
T. Vasyl, Ternary Alloys Based on III-V Semiconductors, CRC Press, Boca Raton, 1st edn, 2017, p. 408 Search PubMed.
- C.-Z. Ning, L. Dou and P. Yang, Bandgap engineering in semiconductor alloy nanomaterials with widely tunable compositions, Nat. Rev. Mater., 2017, 2, 17070 CrossRef CAS.
- B. Liu, J. Li, W. Yang, X. Zhang, X. Jiang and Y. Bando, Semiconductor Solid-Solution Nanostructures: Synthesis, Property Tailoring, and Applications, Small, 2017, 13, 1701998 CrossRef PubMed.
- M. Ghasemi, E. D. Leshchenko and J. Johansson, Assembling your nanowire: an overview of composition tuning in ternary III-V nanowires, Nanotechnology, 2021, 32, 072001 CrossRef CAS.
- E. Barrigon, M. Heurlin, Z. Bi, B. Monemar and L. Samuelson, Synthesis and Applications of III-V Nanowires, Chem. Rev., 2019, 119, 9170–9220 CrossRef CAS.
- R. R. LaPierre, M. Aagesen, P. Kuyanov and B. A. Wood, GaAsP nanowire-on-Si tandem solar cell, J. Photonics Energy, 2017, 7, 042502 Search PubMed.
- Y. Zhang, J. Wu, M. Aagesen and H. Liu, III–V nanowires and nanowire optoelectronic devices, J. Phys. D: Appl. Phys., 2015, 48, 463001 CrossRef.
-
R. DeHoff, Thermodynamics in Materials Science, 2006 Search PubMed.
- J. H. Hildebrand, Solubility, Xii, Regular Solutions1, J. Am. Chem. Soc., 1929, 51, 66–80 CrossRef CAS.
-
U. W. Pohl, Epitaxy of Semiconductors, Graduate Texts in Physics, 2013 Search PubMed.
- E. Kuphal, Phase diagrams of InGaAsP, InGaAs and InP lattice-matched to (100)InP, J. Cryst. Growth, 1984, 67, 441–457 CrossRef CAS.
- I. H. Ho and G. B. Stringfellow, Solid phase immiscibility in GaInN, Appl. Phys. Lett., 1996, 69, 2701–2703 CrossRef CAS.
- J. B. Li, W. Zhang, C. Li and Z. Du, A thermodynamic assessment of the In-As-Sb system, J. Phase Equilib., 1998, 19, 473–478 CrossRef CAS.
- V. G. Dubrovskii, A. A. Koryakin and N. V. Sibirev, Understanding the composition of ternary III-V nanowires and axial nanowire heterostructures in nucleation-limited regime, Mater. Des., 2017, 132, 400–408 CrossRef CAS.
- Q. Zhu, E. Pelucchi, S. Dalessi, K. Leifer, M. A. Dupertuis and E. Kapon, Alloy Segregation, Quantum Confinement, and Carrier Capture in Self-Ordered Pyramidal Quantum Wires, Nano Lett., 2006, 6, 1036–1041 CrossRef CAS.
- D. Kohen, X. S. Nguyen, R. I. Made, C. Heidelberger, K. H. Lee, K. E. K. Lee and E. A. Fitzgerald, Preventing phase separation in MOCVD-grown InAlAs compositionally graded buffer on silicon substrate using InGaAs interlayers, J. Cryst. Growth, 2017, 478, 64–70 CrossRef CAS.
- G. B. Stringfellow, The importance of lattice mismatch in the growth of GaxIn1−xP epitaxial crystals, J. Appl. Phys., 1972, 43, 3455–3460 CrossRef CAS.
- Y. Li, G. C. Weatherly and M. Niewczas, TEM studies of stress relaxation in GaAsN and GaP thin films, Philos. Mag., 2005, 85, 3073–3090 CrossRef CAS.
- M. Paladugu, J. Zou, Y.-N. Guo, X. Zhang, Y. Kim, H. J. Joyce, Q. Gao, H. H. Tan and C. Jagadish, Nature of heterointerfaces in GaAs/InAs and InAs/GaAs axial nanowire heterostructures, Appl. Phys. Lett., 2008, 93, 101911 CrossRef.
- K. A. Dick, J. Bolinsson, B. M. Borg and J. Johansson, Controlling the abruptness of axial heterojunctions in III-V nanowires: beyond the reservoir effect, Nano Lett., 2012, 12, 3200–3206 CrossRef CAS.
- I. Regolin, D. Sudfeld, S. Lüttjohann, V. Khorenko, W. Prost, J. Kästner, G. Dumpich, C. Meier, A. Lorke and F. J. Tegude, Growth and characterisation of GaAs/InGaAs/GaAs nanowhiskers on (111) GaAs, J. Cryst. Growth, 2007, 298, 607–611 CrossRef CAS.
- L. Li, D. Pan, Y. Xue, X. Wang, M. Lin, D. Su, Q. Zhang, X. Yu, H. So, D. Wei, B. Sun, P. Tan, A. Pan and J. Zhao, Near Full-Composition-Range High-Quality GaAs1-xSbx Nanowires Grown by Molecular-Beam Epitaxy, Nano Lett., 2017, 17, 622–630 CrossRef CAS.
- E. Roche, Y. Andre, G. Avit, C. Bougerol, D. Castelluci, F. Reveret, E. Gil, F. Medard, J. Leymarie, T. Jean, V. G. Dubrovskii and A. Trassoudaine, Circumventing the miscibility gap in InGaN nanowires emitting from blue to red, Nanotechnology, 2018, 29, 465602 CrossRef PubMed.
- E. D. Leshchenko and J. Johansson, Role of Thermodynamics and Kinetics in the Composition of Ternary III-V Nanowires, Nanomaterials, 2020, 10, 2553 CrossRef CAS PubMed.
- J. W. Cahn, On spinodal decomposition, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- D. Burch and M. Z. Bazant, Size-dependent spinodal and miscibility gaps for intercalation in nanoparticles, Nano Lett., 2009, 9, 3795–3800 CrossRef CAS PubMed.
- G. Wilemski, Revised classical binary nucleation theory for aqueous alcohol and acetone vapors, J. Phys. Chem., 1987, 91, 2492–2498 CrossRef CAS.
- J. Johansson and M. Ghasemi, Kinetically limited composition of ternary III-V nanowires, Phys. Rev. Mater., 2017, 1, 040401 CrossRef.
- V. G. Dubrovskii, Fully Analytical Description for the Composition of Ternary Vapor–Liquid–Solid Nanowires, Cryst. Growth Des., 2015, 15, 5738–5743 CrossRef CAS.
- G. Priante, F. Glas, G. Patriarche, K. Pantzas, F. Oehler and J. C. Harmand, Sharpening the Interfaces of Axial Heterostructures in Self-Catalyzed AlGaAs Nanowires: Experiment and Theory, Nano Lett., 2016, 16, 1917–1924 CrossRef CAS.
- E. D. Leshchenko, M. Ghasemi, V. G. Dubrovskii and J. Johansson, Nucleation-limited composition of ternary III–V nanowires forming from quaternary gold based liquid alloys, CrystEngComm, 2018, 20, 1649–1655 RSC.
- J. A. V. Butler, The thermodynamics of the surfaces of solutions, Proc. R. Soc. London, Ser. A, 1997, 135, 348–375 Search PubMed.
- J. Johansson and M. Ghasemi, Composition of Gold Alloy Seeded InGaAs Nanowires in the Nucleation Limited Regime, Cryst. Growth Des., 2017, 17, 1630–1635 CrossRef CAS.
- F. Glas, Comparison of Modeling Strategies for the Growth of Heterostructures in III–V Nanowires, Cryst. Growth Des., 2017, 17, 4785–4794 CrossRef CAS.
- G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations, Chem. Rev., 2016, 116, 7078–7116 CrossRef CAS.
- A. Laaksonen and I. Napari, Breakdown of the Capillarity Approximation in Binary Nucleation: A Density Functional Study†, J. Phys. Chem. B, 2001, 105, 11678–11682 CrossRef CAS.
- J. F. Lutsko and M. A. Duran-Olivencia, Classical nucleation theory from a dynamical approach to nucleation, J. Chem. Phys., 2013, 138, 244908 CrossRef PubMed.
- D. Kashchiev, Toward a better description of the nucleation rate of crystals and crystalline monolayers, J. Chem. Phys., 2008, 129, 164701 CrossRef PubMed.
- V. G. Dubrovskii and J. Grecenkov, Zeldovich Nucleation Rate, Self-Consistency Renormalization, and Crystal Phase of Au-Catalyzed GaAs Nanowires, Cryst. Growth Des., 2014, 15, 340–347 CrossRef.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, A Review of Classical and Nonclassical Nucleation Theories, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- V. I. Kalikmanov, Binary nucleation beyond capillarity approximation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 050601 CrossRef CAS PubMed.
- V. G. Dubrovskii, N. V. Sibirev, G. E. Cirlin, I. P. Soshnikov, W. H. Chen, R. Larde, E. Cadel, P. Pareige, T. Xu, B. Grandidier, J. P. Nys, D. Stievenard, M. Moewe, L. C. Chuang and C. Chang-Hasnain, Gibbs-Thomson and diffusion-induced contributions to the growth rate of Si, InP, and GaAs nanowires, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205316 CrossRef.
- F. Glas, J. C. Harmand and G. Patriarche, Why does wurtzite form in nanowires of III-V zinc blende semiconductors?, Phys. Rev. Lett., 2007, 99, 146101 CrossRef PubMed.
-
V. G. Dubrovskii, Nucleation Theory and Growth of Nanostructures, NanoScience and Technology, 2014 Search PubMed.
- J. A. Liddle and G. M. Gallatin, Lithography, metrology and nanomanufacturing, Nanoscale, 2011, 3, 2679–2688 RSC.
-
M. Stepanova and S. Dew, Nanofabrication, 2012 Search PubMed.
- L. J. Guo, Nanoimprint Lithography: Methods and Material Requirements, Adv. Mater., 2007, 19, 495–513 CrossRef CAS.
- A. Fontcuberta i Morral, C. Colombo, G. Abstreiter, J. Arbiol and J. R. Morante, Nucleation mechanism of gallium-assisted molecular beam epitaxy growth of gallium arsenide nanowires, Appl. Phys. Lett., 2008, 92, 063112 CrossRef.
-
S. Dost and B. Lent, Liquid Phase Epitaxy, in Single Crystal Growth of Semiconductors from Metallic Solutions, 2007, pp. 131–203 Search PubMed.
-
J. M. Redwing, X. Miao and X. Li, Vapor-Liquid-Solid Growth of Semiconductor Nanowires, in Handbook of Crystal Growth: Thin Films and Epitaxy, 2015, Elsevier Inc., pp. 399–439 Search PubMed.
- V. Kurasov, Gibbs Thermodynamics of the Renninger-Wilemski Problem, J. Thermodyn., 2015, 2015, 1–13 CrossRef.
- N. Moll, M. Scheffler and E. Pehlke, Influence of surface stress on the equilibrium shape of strained quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 4566–4571 CrossRef CAS.
- N. Moll, A. Kley, E. Pehlke and M. Scheffler, GaAs equilibrium crystal shape from first principles, Phys. Rev. B: Condens. Matter, 1996, 54, 8844–8855 CrossRef CAS PubMed.
- F. Glas, M. R. Ramdani, G. Patriarche and J.-C. Harmand, Predictive modeling of self-catalyzed III-V nanowire growth, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195304 CrossRef.
- S. De Waele, K. Lejaeghere, M. Sluydts and S. Cottenier, Error estimates for density-functional theory predictions of surface energy and work function, Phys. Rev. B, 2016, 94, 235418 CrossRef.
- J. Johansson and E. D. Leshchenko, Zinc blende and wurtzite crystal structure formation in gold catalyzed InGaAs nanowires, J. Cryst. Growth, 2019, 509, 118–123 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

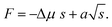
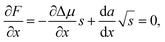
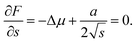
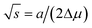 . Then, the nucleation barrier required for the formation of the nucleus of the critical size is F* = a2/4Δμ. Now, one should minimize the nucleation barrier F* in the solid composition. This procedure is equivalent to elimination of the nucleus size in eqn (2), and gives the relationship between the terms related to the phase transition and the nucleus surface energy in the form
. Then, the nucleation barrier required for the formation of the nucleus of the critical size is F* = a2/4Δμ. Now, one should minimize the nucleation barrier F* in the solid composition. This procedure is equivalent to elimination of the nucleus size in eqn (2), and gives the relationship between the terms related to the phase transition and the nucleus surface energy in the form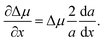
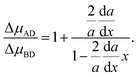
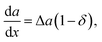
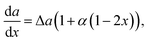
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + ωs(1 − x)2)(aBD − xΔa) − (RT
x + ωs(1 − x)2)(aBD − xΔa) − (RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − x) + ωSx2)(aAD + (1 − x)Δa).
ln(1 − x) + ωSx2)(aAD + (1 − x)Δa).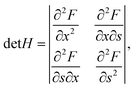
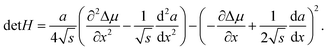
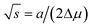 , and d2a/dx2 = 0 for the linear model and d2a/dx2 = −2αΔa for the convex model. The spinodal is defined by the equation detH = 0. The maximum of the Hessian determinant as a function of x corresponds to the largest instability of the system and gives the center of the miscibility gap.
, and d2a/dx2 = 0 for the linear model and d2a/dx2 = −2αΔa for the convex model. The spinodal is defined by the equation detH = 0. The maximum of the Hessian determinant as a function of x corresponds to the largest instability of the system and gives the center of the miscibility gap.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(x/(1 − x)) − 2ωS(x − 1/2)14 while the decrease or increase of the ratio determines shifting the function up or down correspondingly. Fig. 3 shows the functions f(y) + u(y)x and g(x) calculated for different y at fixed aGaAs/aInAs = 1.3, T = 450 °C, cAs = 0.01 and cAu = 0.28. As seen from Fig. 3, there is only one solution in a wide y range except of y ≈ 0.9506 near which the curve f(y) + u(y)x crosses the curve g(x) three times. At such liquid compositions there is a miscibility gap.
ln(x/(1 − x)) − 2ωS(x − 1/2)14 while the decrease or increase of the ratio determines shifting the function up or down correspondingly. Fig. 3 shows the functions f(y) + u(y)x and g(x) calculated for different y at fixed aGaAs/aInAs = 1.3, T = 450 °C, cAs = 0.01 and cAu = 0.28. As seen from Fig. 3, there is only one solution in a wide y range except of y ≈ 0.9506 near which the curve f(y) + u(y)x crosses the curve g(x) three times. At such liquid compositions there is a miscibility gap.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((1 − x)/x)). Introducing the surface energy, it is impossible to explicitly express the binodal temperature as a function of solid composition in a similar closed form. Moreover, including the surface energies, Tb depends on the chemical potential in the liquid which is a strong function of group V element concentration. Fig. 5 shows the miscibility gap in an InGaAs alloy calculated for the Vegard's law case for different surface energy ratios at fixed cAs = 0.01 and cAu = 0.28. The largest binodal region corresponds to aGaAs/aInAs = 1 and narrows the more this ratio deviates from 1. So, the critical temperature above which all the solid compositions are stable is T = 543 °C at aGaAs/aInAs = 1, T ≈ 505 °C at aGaAs/aInAs = 1.3 and T = 432 °C at aGaAs/aInAs = 1.4.
ln((1 − x)/x)). Introducing the surface energy, it is impossible to explicitly express the binodal temperature as a function of solid composition in a similar closed form. Moreover, including the surface energies, Tb depends on the chemical potential in the liquid which is a strong function of group V element concentration. Fig. 5 shows the miscibility gap in an InGaAs alloy calculated for the Vegard's law case for different surface energy ratios at fixed cAs = 0.01 and cAu = 0.28. The largest binodal region corresponds to aGaAs/aInAs = 1 and narrows the more this ratio deviates from 1. So, the critical temperature above which all the solid compositions are stable is T = 543 °C at aGaAs/aInAs = 1, T ≈ 505 °C at aGaAs/aInAs = 1.3 and T = 432 °C at aGaAs/aInAs = 1.4.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cA + φA,
cA + φA,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cB + φB,
cB + φB,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cD + φD.
cD + φD.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + ωS(1 − x)2,
x + ωS(1 − x)2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − x) + ωSx2,
ln(1 − x) + ωSx2,