One-dimensional electronic systems: metal-chain complexes and organic conductors†
Yukihiro
Yoshida
 * and
Hiroshi
Kitagawa
* and
Hiroshi
Kitagawa
 *
*
Division of Chemistry, Graduate School of Science, Kyoto University, Kitashirakawa-Oiwakecho, Sakyo-ku, Kyoto 606-8502, Japan. E-mail: yoshiday@ssc.kuchem.kyoto-u.ac.jp; kitagawa@kuchem.kyoto-u.ac.jp
First published on 24th July 2020
Abstract
One-dimensional (1D) metal-chain complexes and organic conductors show many similarities as well as striking differences in structural and electronic properties, although constituent elements and orbitals that contribute to charge transfer in these systems are quite different. In this review, we highlighted the structural and electronic properties of neutral MMX-chain complexes (M = Pt2+/3+, X = I−) and tetramethyltetrathiafulvalene-based cation radical salts as typical examples of each group while comparing them with each other. This review primarily aims to construct a coherent body of knowledge of 1D electronic materials that might have been separately investigated. We have proposed future directions for the exploration of new and more advanced electronic materials not only having 1D character, but also residing in the dimensional crossover regime.
1. Introduction
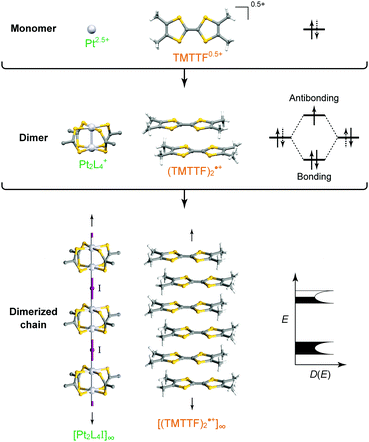
Intuitively, one-dimensional (1D) electronic systems seem to be extremely simple, but they have long been a central subject in solid-state sciences because of their totally different chemistry and physics from those of their higher-dimensional counterparts.1–3 This is primarily because these systems offer a rich variety of exotic quantum phenomena such as charge/spin-soliton, polaron/bipolaron, bond-order wave, charge/spin-density wave, and Tomonaga–Luttinger liquid (non-Fermi liquid). In principal, 1D structures allow the formation of various kinds of ordered phases, which sometimes break the translational symmetry of lattice, charge, or spin degrees of freedom. Although quantum fluctuations, which play a prominent role in 1D systems, suppress long-range ordering at finite temperatures, transverse interactions, which are usually present in actual systems, lead to an ordered state. Because anisotropic p and d orbitals of components as well as directional interactions, such as hydrogen and π–π interactions, between components are dominant factors in determining the anisotropic packing motif in metal-complex and molecular solids, it is apparent that these compounds are a promising platform for investigating low-dimensional electronic systems showing phase transitions as a function of temperature and pressure. In fact, the first spin-Peierls transition, which has been predicted to occur in certain compounds composed of spin-1/2 antiferromagnetic chains, was found in a molecular solid, TTF·Cu(tfd)2 (TTF: tetrathiafulvalene, tfd: 1,2-bis(trifluoromethyl)ethene-1,2-dithiolate), in 1975,4 more than a decade prior to the first discovery of an inorganic spin-Peierls compound, CuGeO3.5In 1D metal complexes, an axial overlapping of the dz2 orbitals of group 10 metals, such as Ni, Pd, and Pt, is indispensable for securing conduction pathways. A representative example is prototype Krogmann's salt, K2Pt(CN)4Br0.3·3H2O (so-called KCP(Br)),6 which involves a 1D chain comprising square-planar PtCl4 subunits arranged through Pt⋯Pt interactions. A marked overlap between the 5dz2 orbitals of Pt results in band formation, and 0.3 holes per Pt (i.e., Pt2.3+) serve as carriers in the solid with a partially filled band. In 1974, it was found that this complex behaves as metallic above approximately 250 K,7 below which the conductivity becomes thermally activated due to Peierls instability arising from the electron–phonon interactions in the 1D system. On the other hand, in molecular solids, such as that comprising electron-donating TTF and electron-accepting 7,7,8,8-tetracyano-p-quinodimethane (TCNQ) discovered independently by two groups in 1973,8,9 each component constructs a π-stacking column through π-orbital overlap, and the inter-column charge transfer (CT) interactions between TTF and TCNQ cause the generation of carriers within both columns. TTF·TCNQ with a partial CT (0.59) is currently regarded as the first molecular or synthetic metal and also shows complicated phase transitions associated with the Peierls instabilities at low temperatures.10 In both systems, itineracy depends largely on the balance between transfer energy (t ≈ W/4 in 1D electronic systems; W: bandwidth), on- or inter-site Coulomb repulsion energy (U or V, respectively), and site-diagonal (or intra-site) and site-off-diagonal (or inter-site) electron–phonon coupling energy (S).11 This review covers recent developments in each system after providing a general introduction to some materials comprehensively discussed in earlier review articles1–3,12–14 and compares the electronic behavior of 1D metal-chain complexes and organic conductors to provide a deeper understanding of how molecular and crystal structures affect the electronic properties. We mainly focused on neutral MMX-chain complexes, in which binuclear metal subunits (MM) are connected by a halogen (X), and cation radical salts, (TMTTF)2X (TMTTF: tetramethyl-TTF, X: monoanion), in which cationic TMTTF0.5+ molecules form a weakly dimerized π-stacking column, as examples of 1D metal-complex and molecular solids, respectively (Fig. 1), because both systems are increasingly recognized to be full of examples of the relevance of electronic behavior to lattice, charge, and spin degrees of freedom.
2. MMX-chain complex family
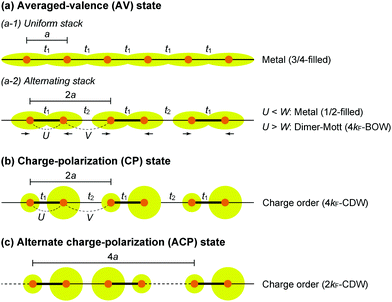
The first halogen-bridged MX-chain complex, in which metal (M) and halogen (X) species are arranged in an alternating manner through the antibonding combination of M(dz2) and X(pz) orbitals, was synthesized by Wolfram more than a century ago.15 In [Pt(EtNH2)4Cl]Cl2·2H2O, the so-called Wolfram's red salt, mixed valence Pt2+(d8) and Pt4+(d6) ions are arranged alternately primarily due to the significant site-diagonal electron–phonon interactions (U < S; negative-U effect;16Fig. 2(a)).17 Such a mixed valence state is accompanied by opening of the energy gap (Δ) resulting in nonmagnetic insulating behavior. Replacing Pt with a lighter homologous element, i.e. Ni, provides an averaged valence state of +3, in which the unpaired electron is localized due to the on-site Coulomb interactions (U > W; Fig. 2(b)) while maintaining a spin degree of freedom. Regardless of their origin, all the MX-chain complexes reported to date show insulating behavior. Instead, the efforts in synthesizing chain complexes based on binuclear metal subunits (MMs) have been devoted to exploring diverse electronic states mainly because of the reduced electron–electron correlations. In MMX-chain complexes, a halogen (X) serves as a bridge between MMs, each of which is assembled by four bidentate ligands in a paddle-wheel fashion. In a PtPt subunit, the Pt2+(d8) ions adopt a planar four-coordinate geometry with no Pt2+–Pt2+ bond within the subunit, whereas Pt3+(d7) ions adopt an octahedral coordination geometry to form an intra-subunit Pt3+–Pt3+ bond.12,18 Therefore, each Pt3+ ion can form a covalent bond with a bridging iodine, i.e., the iodine is displaced from the central position between two adjacent subunits depending on the valence state and approaches closer to Pt3+. As shown in Fig. 3, four types of valence states appear in the MMX chain depending primarily on the valence states of Pt ions: (a) averaged-valence (AV) state: uniform chain composed of Pt2.5+– Pt2.5+ homovalent dimers, showing metallic (U < W) or Mott insulating (U > W) behavior; (b) charge-density wave (CDW) state: alternating chain comprising Pt2+–Pt2+ and Pt3+–Pt3+ homovalent dimers; (c) charge-polarization (CP) state: uniform chain composed of Pt2+–Pt3+ heterovalent dimers with a parallel orientation; (d) alternate charge-polarization (ACP) state: alternating chain comprising Pt2+–Pt3+ heterovalent dimers with an antiparallel orientation. It should be noted that the valence states Pt2+ and Pt3+ are more accurately represented by Pt(2+δ)+ and Pt(3−δ)+, respectively, where the δ value (0 < δ < 0.5) significantly depends on the degree of orbital hybridization. The CP state retains the periodicity of the original AV state, whereas the CDW and ACP states described as Peierls and spin-Peierls states, respectively, deform their chain structures to produce a doubled periodicity as –Pt–Pt–I–Pt–Pt–I–. The spin degree of freedom, which is maintained in the AV and CP states, is essentially frozen in the CDW and ACP states in the extreme case (δ = 0) due to the opening of the spin gap. The CP state with a permanent dipole moment has the potential to show ferroelectric behavior at a glance. In actual solids, these chains interact only weakly with each other through van der Waals forces, thereby identifying with a 1D electronic system.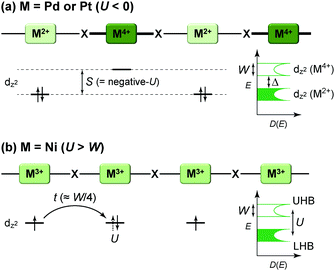 | ||
| Fig. 2 Schematic electronic structures of (a) mixed-valence (M = Pd or Pt) and (b) Mott–Hubbard (M = Ni) insulating states in MX-chain complexes (UHB: upper Hubbard band, LHB: lower Hubbard band) related to physical parameters such as on-site Coulomb repulsion energy (U), bandwidth (W) or transfer energy (t ≈ W/4 in 1D electronic systems), and electron–phonon coupling energy (S).18,25S is proportional to a spatial distortion from the equilibrium structure with a coefficient β (i.e., site-diagonal electron–phonon coupling constant), whereas t becomes smaller in proportional to the spatial distortion with a coefficient α (i.e., site-off-diagonal electron–phonon coupling constant).27,28,30 | ||
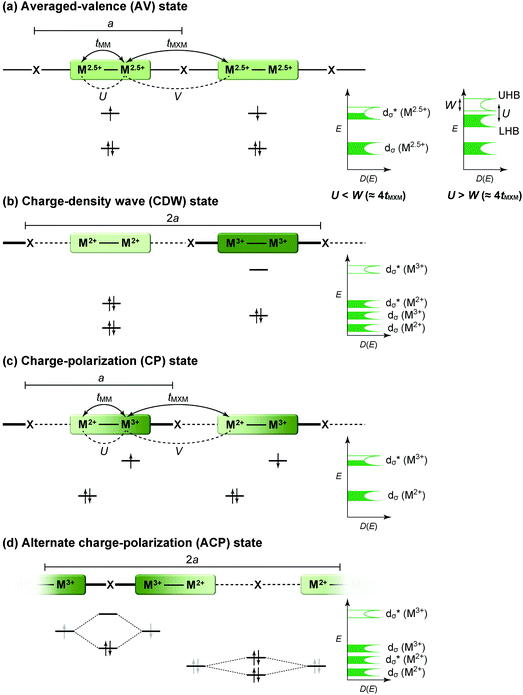 | ||
| Fig. 3 Schematic electronic structures of the typical states in MMX-chain complexes: (a) averaged-valence (AV) state, (b) charge-density wave (CDW) state, (c) charge-polarization (CP) state, and (d) alternate charge-polarization (ACP) state (a: periodicity of an –M–M–I– unit, tMM: transfer energy within an MM subunit, tMXM: transfer energy between the subunits, V: inter-site Coulomb repulsion energy).18 | ||
The first MMX-chain complex, Pt2(MeCS2)4I, was synthesized by Bellitto et al. in 1983.19 In this solid, four bidentate dithiocarboxylate ligands (RCS2−; R: alkyl group) are attached to two Pt ions in a square planar coordination for each Pt, and the paddle-wheel-shaped building units are assembled in a linear fashion by the bridging iodines. It is apparent that the ligands are responsible for the spatial isolation of the chains from each other, producing a 1D electronic state. To date, several MMX-chain complexes have been synthesized using RCS2− ligands with different alkyl chain lengths. Another extensively studied line of research is A4[Pt2(pop)4I]·nH2O (A: monocation, pop: P2H2O52−), which is already the subject of some reviews12,20,21 and therefore will not be dealt with here. Typically, Pt2(RCS2)4I can be prepared by the thermal treatment of a Pt2+ dimer complex, Pt2(RCS2)4, and a Pt3+ dimer complex, Pt2(RCS2)4I2, in toluene or toluene/hexane solution, where the acidic ligands RCS2H are commonly synthesized by the reaction of appropriate alkyl Grignard reagents with carbon disulfide in tetrahydrofuran/diethyl ether solution at low temperatures.22 It is well-known that Pt2(MeCS2)4I with R = Me can also be prepared by the iodine oxidation of Pt2(MeCS2)4 (Pt/I molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in toluene solution.19
1) in toluene solution.19
Pt2(MeCS2)4I is not only the second example, after KCP(Br), of the transition-metal complex showing metallic behavior under ambient pressure but also the first example of metallic neutral chain complex. Its metallic behavior could be observed only when a high-purity single crystal was used for the transport measurements.23,24 At room temperature, the complex belongs to the monoclinic space group C2/c, and each infinite chain running along the b axis includes one –Pt–Pt–I– unit in a unit cell (Fig. 4).18,19,25 Along the side-by-side direction (‖c), there are heteroatomic S⋯S contacts with a distance (ca. 3.8 Å) slightly longer than the sum of van der Waals radii (3.60 Å). Provided that the intra-subunit transfer energy (tMM) is comparable to the inter-subunit transfer energy (tMXM), the dz2 band is originally three-quarter-filled, (5dz2)2(5dz2)1. However, the possible condition tMM > tMXM results in the splitting of dz2 into bonding dσ and antibonding d*σ due to dimerization, latter of which is in the half-filled state (Fig. 3(a)). It is noteworthy that contrary to the dσ orbital, the d*σ orbital possibly expands towards the outside of the subunit, which facilitates electron transfer between the subunits (i.e., tMXM). The conductivity of Pt2(MeCS2)4I along the chain direction is ca. 13 S cm−1 at room temperature and shows metallic behavior above approximately 300 K (Fig. 5(a)). A temperature-independent thermoelectric power above room temperature strongly suggests that the complex has a half-filled metallic state in this temperature range. The observation of a single C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) S stretching band in the infrared (IR) spectra is firm evidence for the formation of the AV state. The insulating phase caused by a metal–insulator transition can be readily assigned to the CP state (Fig. 3(c)) because of its significant magnetic susceptibility (Fig. 5(b)) as well as the splitting of the C
S stretching band in the infrared (IR) spectra is firm evidence for the formation of the AV state. The insulating phase caused by a metal–insulator transition can be readily assigned to the CP state (Fig. 3(c)) because of its significant magnetic susceptibility (Fig. 5(b)) as well as the splitting of the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) S stretching mode (trapped-valence states Pt2+ and Pt3+). The 129I Mössbauer spectra showing two different iodine sites below 80 K indicate that the electronic state formed below 80 K is the ACP state (Fig. 3(d)), which is consistent with that predicted by theoretical studies.26–28 Because it is reasonable to expect that the Pt–I bonds are more compressible than the Pt–Pt bonds in MMX-chains, the tMXM approaches the tMM as the temperature is decreased. Thus, the degree of dimerization in the MMX-chain (i.e., difference between tMM and tMXM) weakens upon cooling, which could have a favorable effect on the stability of a charge-ordered (CO) state as compared to that on a dimer-Mott state.29 Although the increase in V owing to lattice compression must stabilize the CP state, the emergence of the ACP state at lower temperatures might be associated with the magnetic energy gain due to the opening of the spin gap. In this regard, site-off-diagonal electron–phonon interactions that modulate the transfer energies, especially tMXM in this system, must be beneficial for realizing an ACP state with redistributed tetramers.27,30
S stretching mode (trapped-valence states Pt2+ and Pt3+). The 129I Mössbauer spectra showing two different iodine sites below 80 K indicate that the electronic state formed below 80 K is the ACP state (Fig. 3(d)), which is consistent with that predicted by theoretical studies.26–28 Because it is reasonable to expect that the Pt–I bonds are more compressible than the Pt–Pt bonds in MMX-chains, the tMXM approaches the tMM as the temperature is decreased. Thus, the degree of dimerization in the MMX-chain (i.e., difference between tMM and tMXM) weakens upon cooling, which could have a favorable effect on the stability of a charge-ordered (CO) state as compared to that on a dimer-Mott state.29 Although the increase in V owing to lattice compression must stabilize the CP state, the emergence of the ACP state at lower temperatures might be associated with the magnetic energy gain due to the opening of the spin gap. In this regard, site-off-diagonal electron–phonon interactions that modulate the transfer energies, especially tMXM in this system, must be beneficial for realizing an ACP state with redistributed tetramers.27,30
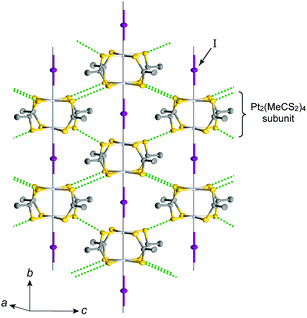 | ||
| Fig. 4 Crystal structure of Pt2(MeCS2)4I at room temperature,18,19 where green dotted lines show heteroatomic S⋯S contacts between adjacent chains. Hydrogen atoms are omitted for clarity. | ||
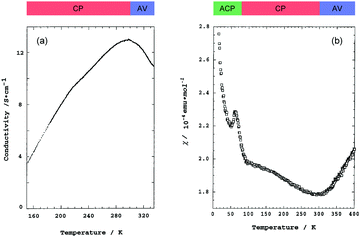 | ||
| Fig. 5 Temperature dependence of (a) conductivity and (b) magnetic susceptibility (χ) of Pt2(MeCS2)4I (AV: averaged-valence state, CP: charge-polarization state, ACP: alternate charge-polarization state). Adapted with permission from ref. 18. Copyright 1999 American Chemical Society. | ||
Pt2(EtCS2)4I (space group: C2/c), in which the methyl groups of ligands in Pt2(MeCS2)4I are replaced with longer ethyl groups, was synthesized by Mitsumi et al. via the reaction of Pt2(EtCS2)4 with Pt2(EtCS2)4I2 in toluene.31 The complex shows a room-temperature conductivity of 5–30 S cm−1, comparable to that of Pt2(MeCS2)4I, and a conductivity maximum at 205 K. Because the X-ray diffuse scattering lines corresponding to the 2-fold periodicity along the chain direction start to grow below 160 K, it is likely that the conductivity change at 205 K occurs due to a phase transition from the metallic AV to the Mott-insulating AV or charge-ordered CP state (Raman spectra suggest the coexistence of these states32). X-ray structural refinement revealed that the low-temperature phase (<160 K) with a 2-fold –Pt–Pt–I– unit repetition is identical to the ACP state, i.e., –Pt2+–Pt3+–I–Pt3+–Pt2+–I– (space group: P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ).33 The emergence of the ACP state was confirmed by 129I Mössbauer spectroscopy, which estimates the charge of iodine bridging the Pt3+ ions to be −0.4 and that of iodine bridging the Pt2+ ions to be −0.3.34 This structural feature is seemingly inconsistent with the magnetic susceptibility data, which indicate the presence of the spin degree of freedom even below 160 K (Fig. 6). This discrepancy can probably be explained by the difference between the degrees of lattice deformation within the chain. In fact, the difference between the Pt2+–I and Pt3+–I bond lengths (0.02–0.03 Å) is significantly smaller than that in the case of Pt2(n-BuCS2)4I (ca. 0.07 Å),33 which shows a rapid drop in magnetic susceptibility associated with the first-order transition, as expected from the ideal ACP state (Fig. 6). As above-mentioned, the observation of ferroelectric behavior in the CP state is of fascinating interest. The distorted ESR spectra shown in Fig. 7 is indicative of the significantly reduced cavity quality factor, which is inversely proportional to dielectric loss, tan
).33 The emergence of the ACP state was confirmed by 129I Mössbauer spectroscopy, which estimates the charge of iodine bridging the Pt3+ ions to be −0.4 and that of iodine bridging the Pt2+ ions to be −0.3.34 This structural feature is seemingly inconsistent with the magnetic susceptibility data, which indicate the presence of the spin degree of freedom even below 160 K (Fig. 6). This discrepancy can probably be explained by the difference between the degrees of lattice deformation within the chain. In fact, the difference between the Pt2+–I and Pt3+–I bond lengths (0.02–0.03 Å) is significantly smaller than that in the case of Pt2(n-BuCS2)4I (ca. 0.07 Å),33 which shows a rapid drop in magnetic susceptibility associated with the first-order transition, as expected from the ideal ACP state (Fig. 6). As above-mentioned, the observation of ferroelectric behavior in the CP state is of fascinating interest. The distorted ESR spectra shown in Fig. 7 is indicative of the significantly reduced cavity quality factor, which is inversely proportional to dielectric loss, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, possibly due to the emergence of ferroelectricity.35 The temperature range of the distorted spectra (130–140 K) is below the transition temperature at which the superstructure associated with the ACP state starts to grow (160 K) because of the gradual growth of the ACP state.
δ, possibly due to the emergence of ferroelectricity.35 The temperature range of the distorted spectra (130–140 K) is below the transition temperature at which the superstructure associated with the ACP state starts to grow (160 K) because of the gradual growth of the ACP state.
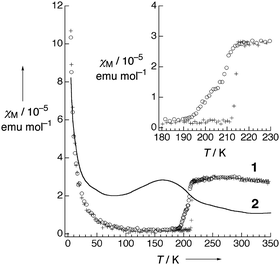 | ||
| Fig. 6 Temperature dependence of magnetic susceptibility (χM) of Pt2(EtCS2)4I (2) and Pt2(n-BuCS2)4I (1; ○: 1st cooling, +: 1st heating, Δ: 2nd cooling). Inset shows the phase transition behavior at around 210 K of 1. Adapted with permission from ref. 33. Copyright 2002 Wiley-VCH. | ||
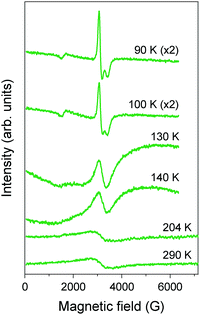 | ||
| Fig. 7 Temperature dependence of ESR spectra of polycrystalline Pt2(EtCS2)4I.35 | ||
Pressure has been applied to not only search the unexplored electronic states, but also control the electronic properties. As shown in Fig. 8, the room-temperature resistivity of Pt2(EtCS2)4I is steadily decreased upon applying hydrostatic pressure of up to 3 GPa principally due to the increase in bandwidth caused by lattice compression.32,36 The conductivity maximum observed at 205 K under ambient pressure rapidly disappears when moderate pressure is applied and clearly revives under higher pressures (ca. 70 K at 2.2 GPa). Of particular importance is that the metallic behavior disappears again above this pressure and the conductivity shows thermally activated behavior. The insulating phase is readily assigned to the CP state based on the crystallographic and Raman studies as a function of pressure. Theoretical calculations predicted that the application of pressure leads to the stabilization of the reentrant CP state.27 The reason must be the same as above-mentioned for low temperatures: the increased V relative to tMM due to the shortened inter-subunit distance under pressure. Similar behavior of the stabilization of the CP state by applying pressure was observed for Pt2(MeCS2)4I (Fig. 9).37 It is interesting to note that the proposed T–P phase diagrams for Pt2(RCS2)4I are quite different from that of (TMTTF)2X (see below), in which the pressure transforms the salts from 1D (Tomonaga–Luttinger liquid) to 3D (Fermi liquid) metals to stabilize the AV state.14,38,39 Although the factors that determine the electronic state under pressure remain unclear, the persistent 1D character of Pt2(RCS2)4I due to the subtle interchain interactions may be a part of the reason.
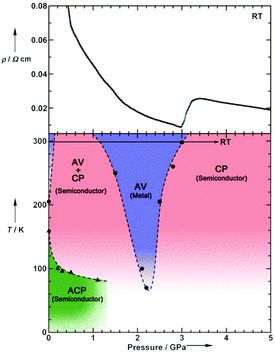 | ||
| Fig. 8 (Upper) Pressure dependence of room-temperature resistivity (ρ) and (lower) electronic T–P phase diagram of Pt2(EtCS2)4I, where a panel presented in the original paper32 was omitted. Adapted with permission from ref. 32. Copyright 2009 Wiley-VCH. | ||
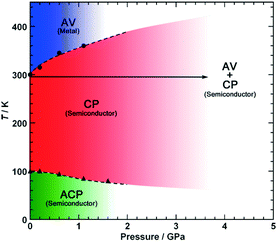 | ||
| Fig. 9 Electronic T–P phase diagram of Pt2(MeCS2)4I. Adapted with permission from ref. 37. Copyright 2016 Wiley-VCH. | ||
A peculiar valence state was found for Pt2(n-PenCS2)4I with longer n-pentyl groups. It has a relatively low room-temperature conductivity (0.84 S cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) but retains metallic behavior down to 255–270 K
40) but retains metallic behavior down to 255–270 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 or 235 K.42 On further cooling, the complex shows an abrupt drop in conductivity at ca. 200 K
41 or 235 K.42 On further cooling, the complex shows an abrupt drop in conductivity at ca. 200 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 or 205 K,42 which is close to a first-order transition temperature (207.4 K) observed for the heat capacity profile.40 At the same temperature, magnetic susceptibility rapidly vanishes with decreasing temperature possibly because of the transition from the paramagnetic (AV) to the nonmagnetic (CDW or ACP) state. To date, the valence state at low temperatures remains highly controversial due to the complicated X-ray diffuse scattering patterns possibly arising from valence fluctuations.41,42 However, it is most likely that the low-temperature phase involves a 3-fold –Pt–Pt–I– unit repetition as –Pt3+–Pt2+–I–Pt2+–Pt3+–I–Pt2.5+–Pt2.5+–I–, comprising alternating ACP and AV states. A similar sign of the 3-fold periodicity along the chain direction was found for Pt2(n-PrCS2)4I43 and Pt2(n-BuCS2)4I.33 Such an alternating chain composed of homovalent and heterovalent dimers has not been found in organic conductors, although there are 2D conducting layers comprising homovalent dimers with different charges (e.g., κ-(BEDT-TTF)4(Et4N)[M(CN)6]·nH2O; BEDT-TTF: bis(ethylenedithio)-TTF, M = Fe3+ and Co3+; n = 244 and 345) and uniform and alternately charged columns (e.g., α-(BEDT-TTF)2I346). The phase diagram of Pt2(RCS2)4I with different alkyl chain lengths is illustrated in Fig. 10.12,18,31–33,40–43,47–51
41 or 205 K,42 which is close to a first-order transition temperature (207.4 K) observed for the heat capacity profile.40 At the same temperature, magnetic susceptibility rapidly vanishes with decreasing temperature possibly because of the transition from the paramagnetic (AV) to the nonmagnetic (CDW or ACP) state. To date, the valence state at low temperatures remains highly controversial due to the complicated X-ray diffuse scattering patterns possibly arising from valence fluctuations.41,42 However, it is most likely that the low-temperature phase involves a 3-fold –Pt–Pt–I– unit repetition as –Pt3+–Pt2+–I–Pt2+–Pt3+–I–Pt2.5+–Pt2.5+–I–, comprising alternating ACP and AV states. A similar sign of the 3-fold periodicity along the chain direction was found for Pt2(n-PrCS2)4I43 and Pt2(n-BuCS2)4I.33 Such an alternating chain composed of homovalent and heterovalent dimers has not been found in organic conductors, although there are 2D conducting layers comprising homovalent dimers with different charges (e.g., κ-(BEDT-TTF)4(Et4N)[M(CN)6]·nH2O; BEDT-TTF: bis(ethylenedithio)-TTF, M = Fe3+ and Co3+; n = 244 and 345) and uniform and alternately charged columns (e.g., α-(BEDT-TTF)2I346). The phase diagram of Pt2(RCS2)4I with different alkyl chain lengths is illustrated in Fig. 10.12,18,31–33,40–43,47–51
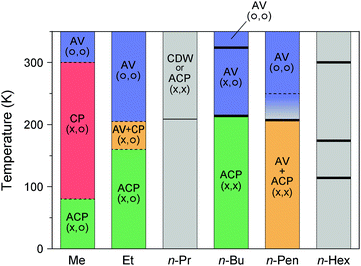 | ||
| Fig. 10 Temperature dependence of the electronic states of Pt2(RCS2)4I with different alkyl chain (R) lengths, where the superlattice structure is not considered.12,18,31–33,40–43,47–51 Gray areas show the temperature range whose electronic state is unknown, and symbols in parentheses indicate the charge (left) and spin (right) degrees of freedom. Thick and thin vertical lines indicate the first- and higher-order transition temperatures, respectively, observed by heat capacity measurements.40,48,49,51 For R = Me, no heat-capacity anomaly was observed at around 300 and 80 K,47 at which phase transitions occur between the AV and CP states and between the CP and ACP states, respectively.18 For R = Et, although numerical data of transition temperatures (ca. 180 and 230 K) observed by the heat capacity measurements are presented in ref. 12 and 50, the source and full extent of the anomalies are not shown. For R = n-Pen, no heat-capacity anomaly was observed at around 250 K,40 at which a conductivity maximum was observed during the resistivity measurements (shown by a dotted line).41,42 | ||
3. (TMTTF)2X family
In the research of organic conductors, most of the interest in the chemistry field is focused on the synthesis of superconductors, which require increased electronic dimensionality to prevent the Peierls transition caused by the electron–phonon interactions in 1D systems.3,14 A good example is the BEDT-TTF cation radical salts mainly developed by Saito group52,53 and Williams and Schlueter group,54,55 which have provided a rich variety of 2D electronic materials with properties ranging from superconductors to quantum spin liquids. However, the collaborative efforts of chemists and physicists over the past decades have opened the possibility of applying (TMTTF)2X to novel 1D physics owing to the various isostructural salts with electronic behavior sensitive to temperature and pressure.In (TMTTF)2X, (TMTTF)2˙+ dimers with an S = 1/2 spin connect to the adjacent dimers within the column mainly through the overlap of π-orbitals as compared to the overlap of M(dz2)–M(dz2) orbitals through X(pz) orbitals in MMX-chain complexes. Herein, it is instructive to show how the columnar assembly in (TMTTF)2X is compressed due to cooling relative to the case of an MMX-chain.56,57 As shown in Fig. 11(a), the heat shrinkage ratio of (TMTTF)2PF6 along the π-stacking column (‖a) is more than five times that of Pt2(MeCS2)4I as a result of weak π–π interactions between the TMTTF molecules. Similarly, the pressure dependence of relative lattice parameter along the chain direction with respect to that under ambient pressure is more significant in (TMTTF)2PF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 than in Pt2(MeCS2)4I (Fig. 11(b)).37 Such a structural feature facilitates the control of electronic behavior via temperature and chemical/physical pressure and therefore offers opportunities for experimental and theoretical works on the investigation of not only the quasi-1D electronic states next to higher-dimensional electronic states, but also the dimensional crossover behavior between them. In this system, 3D ordered electronic states, such as antiferromagnetic ordered and superconducting states, appear at low temperatures under applied pressure.
58 than in Pt2(MeCS2)4I (Fig. 11(b)).37 Such a structural feature facilitates the control of electronic behavior via temperature and chemical/physical pressure and therefore offers opportunities for experimental and theoretical works on the investigation of not only the quasi-1D electronic states next to higher-dimensional electronic states, but also the dimensional crossover behavior between them. In this system, 3D ordered electronic states, such as antiferromagnetic ordered and superconducting states, appear at low temperatures under applied pressure.
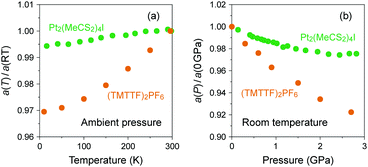 | ||
| Fig. 11 (a) Temperature dependence of relative lattice parameters along the chain direction with respect to those at room temperature (RT) and (b) pressure dependence of relative lattice parameters along the chain direction with respect to those under ambient pressure for Pt2(MeCS2)4I (green circles: data obtained from ref. 37 and 56) and (TMTTF)2PF6 (orange circles: data obtained from ref. 57 and 58). | ||
TMTTF can be synthesized by the homocoupling of 1,3-dithiolium salts,59–61 instead of 1,3-dithiol-2-one, -thione, or -selone commonly used in the coupling reaction to produce TTF skeletons, under basic conditions (Fig. 12). Its purification can be achieved using recrystallization or sublimation methods. TMTTF has electron-donating ability (1st redox potential E1/21 = 0.28 V vs. saturated calomel electrode (SCE)), and therefore, its cation radical salts can be readily prepared by electrooxidation in the presence of appropriate counter anions.3 Organic solvents such as 1,1,2-trichloroethane, acetonitrile, and tetrahydrofuran are commonly used as reaction solvents. Chemical oxidation of TMTTF by acids (HX: X = BF4− and ClO4−) and metathesis of (TMTTF)2BF4 with AX (A: monocation; X = PF6−, SCN−, and Br−) are also employed for synthesizing the (TMTTF)2X salts.62
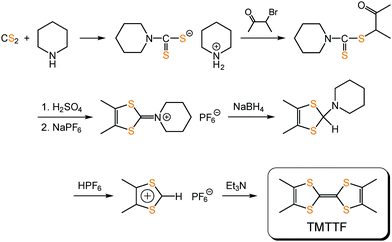 | ||
| Fig. 12 An example of the synthetic scheme of TMTTF.61 | ||
Since the first synthesis of (TMTTF)2X salts in 1977,63 various isostructural salts have been obtained by combining TMTTF with monoanions having octahedral (e.g., PF6−, AsF6−, and SbF6−), tetrahedral (e.g., BF4−, ClO4−, and ReO4−), linear (SCN−), or monoatomic (Br−) geometries. Whereas selenium analogues, i.e. (TMTSF)2X salts, have served as an excellent model for quasi-1D superconductors,13 originated with the first organic superconductor, (TMTSF)2PF6 (Tc = 0.9 K under 1.2 GPa), discovered by Jérome, Bechgaard, and coworkers in 198064 followed by the ClO4 salt (Tc = 1.4 K under ambient pressure),65 the (TMTTF)2X salts with a very rich phase diagram (Fig. 13)39,66 have provided an important clue for exploring the phenomena of 1D physics. A point of interest is that the 1D electronic system cannot be simply described by the Fermi liquid picture with quasiparticle dispersions, which is commonly used to describe conventional metals and semiconductors. As mentioned below, the transport properties can be described in terms of the Tomonaga–Luttinger liquid theory, which shows peculiar spin-charge separations and interactions due to independent spin and charge excitations with different velocities.67
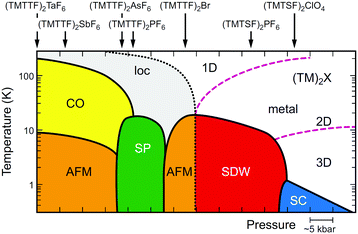 | ||
| Fig. 13 Electronic T–P phase diagram of (TMTTF)2X and (TMTSF)2X,66 in which the ordered states are drawn in colors (loc: Mott insulating state (localization), CO: charge-ordered state, AFM: antiferromagnetic ordered state, SP: spin-Peierls state, SDW: spin-density wave state, SC: superconducting state). Purple dashed lines indicate the dimensional crossover, whereas a black dotted line indicates a metal–insulator transition (see text for details). It is possible that Pt2(RCS2)4I with strong 1D character move toward the lower left direction instead of toward the beneath direction on a left side in this diagram. | ||
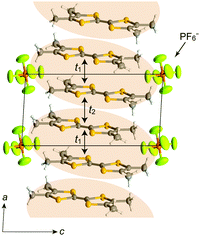
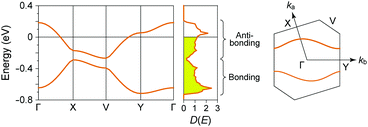
In (TMTTF)2X (space group: P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), the TMTTF molecules with an average charge of +0.5 weakly dimerize in a face-to-face fashion, and the TMTTF dimers with an S = 1/2 spin assemble in a stacking manner via π–π interactions along the a axis (Fig. 14). The zig-zag arrangement is attributed to the steric hindrance of counter anions. For (TMTTF)2PF6, the intradimer (t1) and interdimer (t2) transfer energies at room temperature were estimated to be 230.6 and 170.2 meV, respectively, whereas the inter-column transfer energies are small but substantial (|t| < 25.2 meV). Theoretical calculation using the crystallographic data revealed that the bands are more dispersive along the stacking direction (‖a) than along the side-by-side direction (‖b) and the Femi surface is composed of a wavy 1D hole-like surface along the a axis (Fig. 15). Accordingly, the room-temperature conductivity is the highest along the a axis, and anisotropy is approximately σa
), the TMTTF molecules with an average charge of +0.5 weakly dimerize in a face-to-face fashion, and the TMTTF dimers with an S = 1/2 spin assemble in a stacking manner via π–π interactions along the a axis (Fig. 14). The zig-zag arrangement is attributed to the steric hindrance of counter anions. For (TMTTF)2PF6, the intradimer (t1) and interdimer (t2) transfer energies at room temperature were estimated to be 230.6 and 170.2 meV, respectively, whereas the inter-column transfer energies are small but substantial (|t| < 25.2 meV). Theoretical calculation using the crystallographic data revealed that the bands are more dispersive along the stacking direction (‖a) than along the side-by-side direction (‖b) and the Femi surface is composed of a wavy 1D hole-like surface along the a axis (Fig. 15). Accordingly, the room-temperature conductivity is the highest along the a axis, and anisotropy is approximately σa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σb′
σb′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σc* = 2000
σc* = 2000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.68 The formally three-quarter-filled HOMO band substantially splits into lower (bonding π) and upper (antibonding π*) bands associated with the dimerized structure. Provided that t2 is significantly higher than U within a dimer, i.e., U < 4t2, the upper band is regarded as a half-filled band with W = 0.45 eV. It is noteworthy that this value is significantly smaller than 1.70 eV of an isolated Pt2(MeCS2)4I chain calculated using the first principles method within the density functional theory (DFT) under the assumption of the AV state.69 So far, five kinds of superconductors have been found for (TMTTF)2X (X = PF6−,70,71 AsF6− (Fig. 16),72 SbF6−,73 BF4−,74 and Br− 75) by applying pressure above a few gigapascals (Table 1).
1.68 The formally three-quarter-filled HOMO band substantially splits into lower (bonding π) and upper (antibonding π*) bands associated with the dimerized structure. Provided that t2 is significantly higher than U within a dimer, i.e., U < 4t2, the upper band is regarded as a half-filled band with W = 0.45 eV. It is noteworthy that this value is significantly smaller than 1.70 eV of an isolated Pt2(MeCS2)4I chain calculated using the first principles method within the density functional theory (DFT) under the assumption of the AV state.69 So far, five kinds of superconductors have been found for (TMTTF)2X (X = PF6−,70,71 AsF6− (Fig. 16),72 SbF6−,73 BF4−,74 and Br− 75) by applying pressure above a few gigapascals (Table 1).
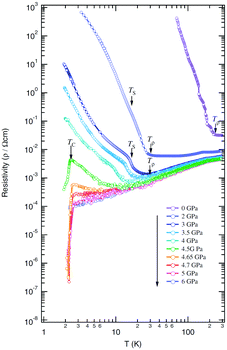 | ||
| Fig. 16 Temperature dependence of resistivity of (TMTTF)2AsF6 under various pressures, where Tρ, TS, and TC are temperatures at minimum resistivity, spin-Peierls transition, and superconducting transition, respectively. Adapted with permission from ref. 72. Copyright 2007 Physical Society of Japan. | ||
| X | V a (Å3) | T σ (K) | T CO (K) | T AO (K) | GS | P c (GPa) | T c (K) | Ref.b |
|---|---|---|---|---|---|---|---|---|
| a V a: anion volume (H. D. B. Jenkins, H. K. Roobottom, J. Passmor and L. Glasser, Inorg. Chem., 1999, 38, 3609); Tσ: temperature at maximum conductivity; TCO: charge-ordering temperature (CP: charge-polarization, ACP: alternate charge-polarization); TAO: anion-ordering temperature; GS: ground state (SP: spin-Peierls, AF: antiferromagnetic ordering, SS: anion-order-induced spin-singlet. The numbers in brackets represent the transition temperature); Pc: critical pressure; Tc: critical temperature. b References for superconductivity. c Not measured. d Not observed. | ||||||||
| PF6− | 109 | 245 | 67 [CP] | SP [15 K] | 5.2 | 1.8 | 70 and 71 | |
| AsF6− | 110 | 105 | 102 [CP] | SP [13 K] | 4.5 | 2.4 | 72 | |
| SbF6− | 121 | 154 | 157 [CP] | AF [8 K] | 5.4 | 2.8 | 73 | |
| TaF6− | 128 | — c | 177 [CP] | AF [9 K] | — d | — d | ||
| BF4− | 73 | 190 | 84 [ACP] | 41 | SS [41 K] | 3.4 | 1.4 | 74 |
| ClO4− | 82 | 230 | — d | 73 | AF [12 K] | — d | — d | |
| ReO4− | 86 | 230 | 230 [ACP] | 157 | SS [157 K] | — d | — d | |
| SCN− | 71 | 240 | 160 [CP] | 160 | AF [7 K] | — d | — d | |
| Br− | 56 | 100 | 20 [CP] | AF [15 K] | 2.6 | 0.8 | 75 | |
Herein, we have mainly described the structural and electronic properties of (TMTTF)2PF6 as an example of (TMTTF)2X formed with centrosymmetric octahedral anions because other relevant salts have qualitatively similar properties to those of (TMTTF)2PF6. (TMTTF)2PF6 shows metallic behavior under ambient conditions as a result of the three-quarter-filled conduction band. The conductivity is ca. 40 S cm−1 at room temperature and exhibits a maximum at around 245 K possibly due to the electron–electron correlations (AV state; Fig. 17(a)).62,76 The fact that the magnetic susceptibility shows no anomaly at around the temperature is indicative of the occurrence of separation between the spin and charge degrees of freedom in 1D electronic systems.77,78
On further cooling, the salt undergoes a phase transition to a 4kF-CDW CO state of Wigner crystal type (= CP; Fig. 17(b)) at 67 K, as observed via13C NMR,79,80 dielectric,81 and optical spectroscopies.66,82 Band structure calculations of (TMTTF)2X (X = PF6−, AsF6−, and SbF6−) demonstrated that the phase transition to the 4kF-CDW CO state occurs below the temperature at which the degree of dimerization, 2(t1 − t2)/(t1 + t2), falls below 0.25.83 The dimer-Mott state is stable at temperatures above which the degree of dimerization is higher than 0.25 due to significant dimerization, whereas weakened dimerization below this temperature bring it into the 4kF-CDW CO state. The same could be speculated for Pt2(RCS2)4I; however, the numerical values of tMM (= t1) and tMXM (= t2) have not been estimated to date.
Based on the IR spectroscopic study, the degree of charge disproportionation, 2δ, which is defined as the difference between the charges of charge-rich and charge-poor TMTTF molecules, increases with the decrease in temperature below 67 K and eventually reaches 0.15 at 10 K (Fig. 18).66,84,85 The 2δ value is apparently smaller than those of (TMTTF)2AsF6 (0.21),66 (TMTTF)2SbF6 (0.29),66 and (TMTTF)2TaF6 (0.28)84 with larger octahedral anions, presumably indicating that the chemical pressure induced by adopting smaller cations has a remarkable effect on the destabilization of the CO state. Additional evidence of the effect of lattice compression on 2δ was provided by the rapid decrease in 2δ upon the application of pressure.86
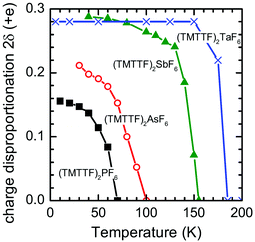 | ||
| Fig. 18 Temperature dependence of the degree of charge disproportionation (2δ) of (TMTTF)2X with X = PF6− (black closed squares), AsF6− (red open circles), SbF6− (green closed triangles), and TaF6− (blue crosses), estimated from the IR spectra.85 | ||
Herein, we have considered that the orientation of the PF6− anions that are dynamically disordered on an inversion center becomes ordered at low temperatures. In this case, the space group changes from P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) to P1 due to the loss of the inversion center; however, the centrosymmetric nature of the anion disturbs the formation of any superstructure. It seems reasonable that the charges of two crystallographically independent TMTTF molecules in a unit cell deviate from the average charge of +0.5, i.e., +(0.5 + δ) and +(0.5 − δ), causing a CP-type CO pattern. However, structural alternation in the stacking columns corresponding to the CO state could not be appreciably detected in crystallographic studies, although symmetry breaking was observed in the NMR spectra.79 Therefore, the CO transition was temporarily considered as a “structureless” transition.87 The first evidence of relevant structural modulation was recently found via synchrotron X-ray diffraction measurements,88 which is not only the same as that previously considered based on experimental (ESR)89 and theoretical90,91 studies, but also implies the formation of a 2D Wigner lattice. In such a 2D layer (within the ab plane), charge-rich TMTTF molecules with ca. +0.6 charge are preferably arranged so as not to be contiguous to each other as a consequence of long-range Coulomb repulsions (sum of the on-site (U) and inter-site (V) Coulomb repulsions).
to P1 due to the loss of the inversion center; however, the centrosymmetric nature of the anion disturbs the formation of any superstructure. It seems reasonable that the charges of two crystallographically independent TMTTF molecules in a unit cell deviate from the average charge of +0.5, i.e., +(0.5 + δ) and +(0.5 − δ), causing a CP-type CO pattern. However, structural alternation in the stacking columns corresponding to the CO state could not be appreciably detected in crystallographic studies, although symmetry breaking was observed in the NMR spectra.79 Therefore, the CO transition was temporarily considered as a “structureless” transition.87 The first evidence of relevant structural modulation was recently found via synchrotron X-ray diffraction measurements,88 which is not only the same as that previously considered based on experimental (ESR)89 and theoretical90,91 studies, but also implies the formation of a 2D Wigner lattice. In such a 2D layer (within the ab plane), charge-rich TMTTF molecules with ca. +0.6 charge are preferably arranged so as not to be contiguous to each other as a consequence of long-range Coulomb repulsions (sum of the on-site (U) and inter-site (V) Coulomb repulsions).
Dielectric permittivity measurements show a peak divergence in the real part of the dielectric constant for (TMTTF)2PF6 (Fig. 19),92 (TMTTF)2AsF6,93 and (TMTTF)2SbF681 at each transition temperature. The unusual dielectric response that has a broad peak as a function of temperature and is strictly frequency-dependent bears the clear signatures of relaxor ferroelectrics, typical of the glass-like freezing of short-range ferroelectric ordering. It is noteworthy that the ground state varies depending on the anions; i.e., spin-Peierls state in (TMTTF)2PF6 and (TMTTF)2AsF6 and antiferromagnetic ordered state in (TMTTF)2SbF6.3,14,39 Theoretical study predicted that the CP-type CO state (including 4kF-CDW) stabilized by the increase in V inhibits the spin-Peierls transition (including 2kF-BOW; Fig. 20(a)), and therefore, (TMTTF)2SbF6, which has a more stable CO state with a higher charge-ordering temperature, undergoes an antiferromagnetic transition (Fig. 20(b)) in place of a spin-Peierls transition at low temperatures.94
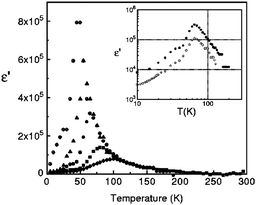 | ||
| Fig. 19 Temperature dependence of the real part of the dielectric permittivity (ε’) of (TMTTF)2PF6 at different frequencies: 1 kHz (⊕), 10 kHz (▲), 100 kHz (●), 1 MHz (■), and 5 MHz (♦). Inset shows the difference between the ε′ of the salt obtained from different batches (100 kHz). Adapted with permission from ref. 92. Copyright 2000 American Physical Society. | ||
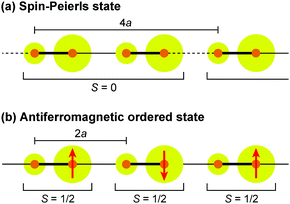 | ||
| Fig. 20 Schematic electronic structures of (a) spin-Peierls state in (TMTTF)2PF6 and (TMTTF)2AsF6 and (b) antiferromagnetic ordered state in (TMTTF)2SbF6.94 Red arrows indicate a magnetically ordered spin, and other specifications are the same as those used in Fig. 17. | ||
Next, the structural and physical properties of (TMTTF)2ReO4 as an example of (TMTTF)2X formed with noncentrosymmetric tetrahedral anions have been described. (TMTTF)2ReO4 has a room-temperature conductivity of ca. 20 S cm−1 and shows metallic behavior down to ca. 230 K,87 at which it undergoes a 2kF-CDW CO (= ACP; Fig. 17(c)) transition observed by various techniques such as X-ray diffraction,83,95 ESR,89 and NMR96 measurements. The noncentrosymmetric ReO4− anions are randomly orientated at room temperature, and the orientational disorder is frozen over two (or more) equivalent orientations upon cooling. An X-ray diffuse scattering study revealed that (TMTTF)2ReO4 undergoes a first-order structural phase transition associated with anion ordering at 157 K, at which a superstructure with a critical wave vector qAO = (1/2,1/2,1/2) to form a 2kF modulation within the π-stacking columns becomes pronounced.97 This transition is accompanied by the displacement of the anions, which results in the sizeable tetramerization of the TMTTF molecules within the column to stabilize the 2kF-CDW CO state (2δ = 0.35 at 200 K and 0.64 at 40 K).98 At present, the precise reason why (TMTTF)2ClO4 does not undergo a CO transition at low temperatures is not fully established; however, it is possible that the occurrence of anion ordering (73 K) prior to charge ordering causes spin-singlet formation due to doubled periodicity along the stacking direction. As shown in ref. 83, the degree of dimerization of (TMTTF)2ClO4 is relatively independent of temperature and remains at a high level, which can affect the suppression of the CO state.29 It must be true that the symmetry of counter anions is responsible for determining the CO pattern, whether CP or ACP, in the TMTTF π-stacking column (Table 1). To date, a successive phase transition from the AV to ACP state passing through the CP state on cooling, as observed for Pt2(RCS2)4I, has not been reported for (TMTTF)2X.
(TMTTF)2X formed with another type of noncentrosymmetric anion, linear SCN−, exhibits some similarities with (TMTTF)2ReO4 in addition to striking differences. With decreasing temperature, (TMTTF)2SCN also undergoes a structural phase transition due to anion ordering at 160 K.99 However, the superstructure is equal to qAO = (0,1/2,1/2), indicating that the CO pattern is of 4kF-CDW-type (= CP), as in the case of (TMTTF)2PF6, because of no phase modulation within the π-stacking column. On further cooling, (TMTTF)2SCN undergoes antiferromagnetic ordering below 7 K, whereas (TMTTF)2PF6 and (TMTTF)2ReO4 show a pronounced phase transition to nonmagnetic ground states arising from the spin-Peierls transition at 15 K and anion-order-induced tetramerization at 157 K, respectively.3,14,39
As described above, the application of pressure modifies the CO behavior and also bring the salts into the 3D ordered electronic states such as antiferromagnetic ordered and superconducting states. Pressure dependence of the CO transition was investigated by 13C NMR spectroscopy.100,101 For example, the CO transition temperature of (TMTTF)2AsF6, which appears to be 102 K under ambient pressure, dramatically decreases with increasing pressure and eventually disappears under a pressure of 0.15 GPa.100 Such a suppression of the CO state, as observed for Pt2(EtCS2)4I below 2.2 GPa (Fig. 8),32 is possibly a reflection of the increased W compared with V.
In the generic phase diagram of (TMTTF)2X and (TMTSF)2X systems shown in Fig. 13, which was originally proposed by Jérome13,102 and subsequently made more sophisticated by Dressel,39,66 “loc” (as Mott insulating state), “1D”, and “2D” regimes are defined on the basis of the anisotropy of transport behavior as “dρa/dT < 0 and dρc/dT < 0”, “dρa/dT > 0 and dρc/dT < 0”, and “dρa/dT > 0 and dρc/dT > 0”, respectively,103 where the a and c axes correspond to the most- and least-conducting directions, respectively. Therefore, the boundary between the “loc” and “1D” regimes is determined as a temperature at which the conductivity along the a axis exhibits a maximum (A charge gap (Δρ) estimated from the slope of the Arrhenius plot is often substituted for the temperature due to thermal inaccessibility). Furthermore, the temperature at which the conductivity along the c axis exhibits a maximum provides a crossover between the “1D” and “2D” regimes and is therefore regarded as the Mott transition temperature (or Mott–Hubbard gap).104 The crossover between the “2D” and “3D” regimes, which is only available for the (TMTSF)2X system, is defined as the upper limit for a low-temperature 3D coherent domain.105 The metal–insulator transition temperature is gradually decreased upon applying pressure possibly because of the decrease in the on-site Coulomb repulsion. This trend is exactly opposite to that found for Pt2(RCS2)4I (R = Me and Et),32,37 although the electronic states just below the metal–insulator transition might be different in kind from each other. Increased electronic dimensionality in addition to the significant lattice compression may modify the electronic state in the favorable direction of a stabilized metallic phase. In fact, the calculated dimensionality parameter, defined as the ratio of inter-column (t⊥) and intra-column (t‖) transfer energies, increases with increasing applied pressure and decreasing temperature (Fig. 21).106 Therefore, it is most likely that on cooling, Pt2(RCS2)4I with a strong 1D character moves towards the lower left direction instead of towards the beneath direction under a certain pressure in the phase diagram shown in Fig. 13. Although the 1D character disturbs the antiferromagnetic ordering due to quantum fluctuations, the metal–insulator transition followed by the emergence of the CO state, as observed for most Pt2(RCS2)4I, seems to be consistent with this possible movement.
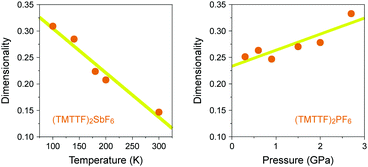 | ||
| Fig. 21 (a) Temperature dependence of dimensionality (see text) of (TMTTF)2SbF6 and (b) pressure dependence of dimensionality of (TMTTF)2PF6 (data obtained from ref. 106). Yellow lines are guides to the eye. | ||
It is fair to say that all (TMTTF)2X salts reside in the Luttinger-liquid regime at high temperatures because of their 1D electronic character. Herein, we focused on the inter-column (‖c) transport behavior in the insulating regime, because the temperature dependence of the resistivity is described by the Luttinger liquid model: ρc ∼ T1−2α, α = 1/4(Kρ + Kρ−1 − 2), where Kρ is the Luttinger parameter (cf., ρa ∼ T16Kρ−3 at T > Δρ for quarter-filled system).67 An electronic system with stronger repulsive energies affords a lower Kρ, and the critical value for Mott transition varies depending on the order of commensurability (Kρ* = 1/n2; n = 1 for half-filled system and n = 2 for quarter-filled system). Clearly, the low Kρ values observed for (TMTTF)2PF6 (0.18)104 and (TMTTF)2AsF6 (0.20)107 are associated with the quarter-filled HOMO band. Since the Kρ values are close to 0.25 above which quarter-filled umklapp scattering is irrelevant, it is apparent that these salts are just on the insulating side of the boundary between the Tomonaga–Luttinger liquid and 1D Mott insulating state. Selenium substitution (TMTTF to TMTSF)103 and application of pressure108 rapidly bring these salts into the metallic regime with higher Kρ values.
4. Outlook and conclusions
The 1D electronic subclass of metal-complex and molecular solids is very broad, and we have only covered the most informative examples in this review. As mentioned above, the half-filled band with antibonding character, which arises from the monocationic dimers as units, leads to the pronounced interdimer interactions owing to the orbital expanding towards the outside of dimers. The increased W as well as the decreased U owing to the dimer formation is considered to be the primary cause for the comparable U and W, which bring the solids into the vicinity of Mott boundary. Although the chemical modification of TMTTF molecules causes a dramatical change in the molecular arrangement in the cation radical salts, the basic structure of MMX-chain complexes remains unchanged because of the covalent bonding between the binuclear metal subunits through the bridging halogens. Considering the fact that the functional groups attached to the dithiocarboxylate ligands in MMX-chain complexes remain rather limited to n-alkyl (from methyl to n-hexyl) groups, attaching other functional groups to impart desired functionalities and longer alkyl groups that serve as van der Waals interaction sites may provide a significant step forward in exploring more versatile electronic materials, apart from the difficulty in synthesizing the ligands. Additionally, the subunits that are separated from each other by a bridging halogen are beneficial not only for the full substitution of Pt with Ni,109,110 but also for the partial substitution of Pt to afford heterobimetallic subunits PtM (M = Ni and Pd).111 Such a replacement while maintaining the basic structure is not simply possible in (TMTTF)2X, in which the columnar assembly of TMTTF molecules is achieved mainly by the weak π–π interactions.The principal advantage of (TMTTF)2X over the MMX-chain complexes might be the tunability of their electronic properties by chemical or physical pressure, which is mainly attributed to the softness of the lattice. The appearance of 3D ordered electronic states such as antiferromagnetic ordered and superconducting states that are not yet found in MMX-chain complexes can best be thought of as a manifestation of the intermolecular π–π and van der Waals interactions as dominant structure-directing forces. Additionally, by studying the relative properties of a variety of (TMTTF)2X, a broad picture of the electronic behavior of this system has depicted not only the 1D regime but also the 1D–2D dimensional crossover regime. We hope that this review, which compares the structural and electronic properties of metal-chain complexes and organic conductors to provide insights into the relevant issues that are currently under debate, will stimulate further experimental and theoretical explorations of new and more advanced electronic materials that might surpass the existing electronic materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Dr Toshikazu Nakamura (Institute for Molecular Science, Japan) and Dr Kenji Yonemitsu (Chuo University, Japan) for their helpful discussion. We also thank Dr Nakamura for providing crystallographic data.Notes and references
- P. Day, Mixed Valence Chemistry and Metal Chain Compounds, in Low-Dimensional Cooperative Phenomena, ed. H. Keller, Plenum, New York, 1975, pp. 191–214 Search PubMed.
- Extended Linear Chain Compounds, ed. E. Conwell and J. S. Miller, Plenum Press, New York, 1982 Search PubMed.
- T. Ishiguro, K. Yamaji and G. Saito, Organic Superconductors, Springer-Verlag, Berlin, 2nd edn, 1998 Search PubMed.
- J. W. Bray, H. R. Hart, Jr., L. V. Interrante, I. S. Jacobs, J. S. Kasper, G. D. Watkins, S. H. Wee and J. C. Bonner, Phys. Rev. Lett., 1975, 35, 744 CrossRef CAS.
- M. Hase, I. Terasaki and K. Uchinokura, Phys. Rev. Lett., 1993, 70, 3651 CrossRef CAS PubMed.
- K. Krogmann and H. D. Hausen, Z. Anorg. Allg. Chem., 1968, 358, 67 CrossRef CAS.
- H. R. Zeller and A. Beck, J. Phys. Chem. Solids, 1974, 35, 77 CrossRef CAS.
- J. P. Ferraris, D. O. Cowan, V. Walatka, Jr. and J. H. Perlstein, J. Am. Chem. Soc., 1973, 95, 948 CrossRef CAS.
- L. B. Coleman, M. J. Cohen, D. J. Sandman, F. G. Yamagishi, A. F. Garito and A. J. Heeger, Solid State Commun., 1973, 12, 1125 CrossRef CAS.
- Semiconductors and Semimetals, ed. E. Conwell, Academic Press, San Diego, 1988, vol. 27 Search PubMed.
- K. Nasu, J. Phys. Soc. Jpn., 1983, 52, 3865 CrossRef CAS.
- Material Designs and New Physical Properties in MX- and MMX-Chain Compounds, ed. M. Yamashita and H. Okamoto, Springer-Verlag, Wien, 2013 Search PubMed.
- D. Jérome, Chem. Rev., 2004, 104, 5565 CrossRef PubMed.
- J.-P. Pouget, P. Alemany and E. Canadell, Mater. Horiz., 2018, 5, 590 RSC.
- H. Wolffram, Dissertation, Königsberg, 1900.
- B. K. Chakraverty, J. Phys. Lett., 1979, 40, L99 CrossRef.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 10, 247 CrossRef CAS.
- H. Kitagawa, N. Onodera, T. Sonoyama, M. Yamamoto, T. Fukuwa, T. Mitani, M. Seto and Y. Maeda, J. Am. Chem. Soc., 1999, 121, 10068 CrossRef CAS.
- C. Bellitto, A. Flamini, L. Gastaldi and L. Scaramuzza, Inorg. Chem., 1983, 22, 444 CrossRef CAS.
- M. Yamashita, S. Takaishi, A. Kobayashi, H. Kitagawa, H. Matsuzaki and H. Okamoto, Coord. Chem. Rev., 2006, 250, 2335 CrossRef CAS.
- H. Iguchi, S. Takaishi and M. Yamashita, Chem. Lett., 2014, 43, 69 CrossRef CAS.
- J. Grote, F. Friedrich, K. Berthold, L. Hericks, B. Neumann, H.-G. Stammler and N. W. Mitzel, Chem. – Eur. J., 2018, 24, 2626 CrossRef CAS PubMed.
- H. Kitagawa, N. Onodera, J.-S. Ahn, T. Mitani, M. Kim, Y. Ozawa, K. Toriumi, K. Yasui, T. Manabe and M. Yamashita, Mol. Cryst. Liq. Cryst., 1996, 285, 311 CrossRef CAS.
- H. Kitagawa, N. Onodera, J.-S. Ahn, T. Mitani, K. Toriumi and M. Yamashita, Synth. Met., 1997, 86, 1931 CrossRef CAS.
- H. Kitagawa and T. Mitani, Coord. Chem. Rev., 1999, 190–192, 1169 CrossRef CAS.
- S. A. Borshch, K. Prassides, V. Robert and A. O. Solonenko, J. Chem. Phys., 1998, 109, 4562 CrossRef CAS.
- S. Yamamoto, J. Phys. Soc. Jpn., 2001, 70, 1198 CrossRef CAS.
- S. Yamamoto, J. Phys. Chem. Solids, 2002, 63, 1489 CrossRef CAS.
- M. Tsuchiizu, H. Yoshioka and Y. Suzumura, J. Phys. Soc. Jpn., 2001, 70, 1460 CrossRef CAS.
- M. Kuwabara and K. Yonemitsu, J. Mater. Chem., 2001, 11, 2163 RSC.
- M. Mitsumi, T. Murase, H. Kishida, T. Yoshinari, Y. Ozawa, K. Toriumi, T. Sonoyama, H. Kitagawa and T. Mitani, J. Am. Chem. Soc., 2001, 123, 11179 CrossRef CAS PubMed.
- K. Otsubo, A. Kobayashi, M. Hedo, Y. Uwatoko and H. Kitagawa, Chem. – Asian J., 2009, 4, 1673 CrossRef CAS PubMed.
- M. Mitsumi, K. Kitamura, A. Morinaga, Y. Ozawa, M. Kobayashi, K. Toriumi, Y. Iso, H. Kitagawa and T. Mitani, Angew. Chem. Int. Ed., 2002, 41, 2767 CrossRef CAS PubMed.
- A. Kobayashi, S. Kitao, M. Seto, R. Ikeda and H. Kitagawa, Inorg. Chem., 2009, 48, 8044 CrossRef CAS PubMed.
- H. Tanaka and S. Kuroda, et al., to be submitted.
- K. Otsubo, A. Kobayashi, H. Kitagawa, M. Hedo, Y. Uwatoko, H. Sagayama, Y. Wakabayashi and H. Sawa, J. Am. Chem. Soc., 2006, 128, 8140 CrossRef CAS PubMed.
- K. Otsubo, T. Suto, A. Kobayashi, R. Ikeda, M. Hedo, Y. Uwatoko and H. Kitagawa, Eur. J. Inorg. Chem., 2016, 4402 CrossRef CAS.
- L. Degiorgi and D. Jérome, J. Phys. Soc. Jpn., 2006, 75, 051004 CrossRef.
- M. Dressel, Naturwissenschaften, 2007, 94, 527 CrossRef CAS PubMed.
- K. Saito, S. Ikeuchi, Y. Nakazawa, A. Sato, M. Mitsumi, T. Yamashita, K. Toriumi and M. Sorai, J. Phys. Chem. B, 2005, 109, 2956 CrossRef CAS PubMed.
- A. Guijarro, O. Castillo, L. Welte, A. Calzolari, P. J. S. Miguel, C. J. Gómez-García, D. Olea, R. di Felice, J. Gómez-Herrero and F. Zamora, Adv. Funct. Mater., 2010, 20, 1451 CrossRef CAS.
- M. Mitsumi, T. Yamashita, Y. Aiga, K. Toriumi, H. Kitagawa, T. Mitani and M. Kurmoo, Inorg. Chem., 2011, 50, 4368 CrossRef CAS PubMed.
- M. Mitsumi, S. Umebayashi, Y. Ozawa, K. Toriumi, H. Kitagawa and T. Mitani, Chem. Lett., 2002, 258 CrossRef CAS.
- A. Ota, L. Ouahab, S. Golhen, Y. Yoshida, M. Maesato and G. Saito, and R. Świetlik, Chem. Mater., 2007, 19, 2455 CrossRef CAS.
- P. Le Maguerès, L. Ouahab, P. Briard, J. Even, M. Bertault, L. Toupet, J. Ramos, C. J. Gomez-García and P. Delhaès, Mol. Cryst. Liq. Cryst., 1997, 305, 479 CrossRef.
- T. Kakiuchi, Y. Wakabayashi, H. Sawa, T. Takahashi and T. Nakamura, J. Phys. Soc. Jpn., 2007, 76, 113702 CrossRef.
- Y. Miyazaki, Q. Wang, A. Sato, K. Saito, M. Yamamoto, H. Kitagawa, T. Mitani and M. Sorai, J. Phys. Chem. B, 2002, 106, 197 CrossRef CAS.
- S. Ikeuchi, K. Saito, Y. Nakazawa, A. Sato, M. Mitsumi, K. Toriumi and M. Sorai, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 115110 CrossRef.
- S. Ikeuchi, K. Saito, Y. Nakazawa, M. Mitsumi, K. Toriumi and M. Sorai, J. Phys. Chem. B, 2004, 108, 387 CrossRef CAS.
- M. Sorai, M. Nakano and Y. Miyazaki, Chem. Rev., 2006, 106, 976 CrossRef CAS.
- S. Ikeuchi, Y. Yamamura, M. Mitsumi, K. Toriumi, H. Saitoh, T. Atake and K. Saito, Chem. Lett., 2009, 38, 1190 CrossRef CAS.
- G. Saito and Y. Yoshida, Bull. Chem. Soc. Jpn., 2007, 80, 1 CrossRef CAS.
- G. Saito and Y. Yoshida, Chem. Rec., 2011, 11, 124 CrossRef CAS PubMed.
- J. M. Williams, A. J. Schultz, U. Geiser, K. D. Carlson, A. M. Kini, H. H. Wang, W.-K. Kwok, M.-H. Whangbo and J. E. Schirber, Science, 1991, 252, 1501 CrossRef CAS PubMed.
- U. Geiser and J. A. Schlueter, Chem. Rev., 2004, 104, 5203 CrossRef CAS PubMed.
- H. Kitagawa, S. Nakagami and T. Mitani, Synth. Met., 2001, 116, 401 CrossRef CAS.
- K. Furukawa, T. Hara and T. Nakamura, J. Phys. Soc. Jpn., 2009, 78, 104713 CrossRef.
- E. Rose, C. Loose, J. Kortus, A. Pashkin, C. A. Kuntscher, S. G. Ebbinghaus, M. Hanfland, F. Lissner, Th. Schleid and M. Dressel, J. Phys.: Condens. Matter, 2013, 25, 014006 CrossRef CAS PubMed.
- J. P. Ferraris, T. O. Poehler, A. N. Bloch and D. O. Cowan, Tetrahedron Lett., 1973, 14, 2553 CrossRef.
- A. Mas, J.-M. Fabre, E. Torreilles, L. Giral and G. Brun, Tetrahedron Lett., 1977, 18, 2579 CrossRef.
- J.-M. Fabre, C. Galaine and L. Giral, J. Phys., Colloq., 1983, 44, C3–1153 CrossRef.
- P. Delhaes, C. Coulon, J. Amiell, S. Flandrois, E. Toreilles, J.-M. Fabre and L. Giral, Mol. Cryst. Liq. Cryst., 1979, 50, 43 CrossRef CAS.
- G. Brun, B. Liautard, S. Peytavin, M. Maurin, E. Toreilles, J.-M. Fabre, L. Giral and J. L. Galigné, J. Phys., Colloq., 1977, 38, C7–266 CrossRef.
- D. Jérome, A. Mazaud, M. Ribault and K. Bechgaard, J. Phys., Lett., 1980, 41, L95 CrossRef.
- K. Bechgaard, K. Carneiro, F. B. Rasmussen and M. Olsen, J. Am. Chem. Soc., 1981, 103, 2440 CrossRef CAS.
- M. Dressel, M. Dumm, T. Knoblauch and M. Masino, Crystals, 2012, 2, 528 CrossRef CAS.
- T. Giamarchi, Chem. Rev., 2004, 104, 5037 CrossRef CAS.
- B. Köhler, E. Rose, M. Dumm, G. Untereiner and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035124 CrossRef.
- A. Calzolari, S. S. Alexandre, F. Zamora and R. di Felice, J. Am. Chem. Soc., 2008, 130, 5552 CrossRef CAS PubMed.
- T. Adachi, E. Ojima, K. Kato, H. Kobayashi, T. Miyazaki, M. Tokumoto and A. Kobayashi, J. Am. Chem. Soc., 2000, 122, 3238 CrossRef CAS.
- D. Jaccard, H. Wilhelm, D. Jérome, J. Moser, C. Carcel and J.-M. Fabre, J. Phys.: Condens. Matter, 2001, 13, L89 CrossRef CAS.
- M. Itoi, M. Kano, N. Kurita, M. Hedo, Y. Uwatoko and T. Nakamura, J. Phys. Soc. Jpn., 2007, 76, 053703 CrossRef.
- M. Itoi, C. Araki, M. Hedo, Y. Uwatoko and T. Nakamura, J. Phys. Soc. Jpn., 2008, 77, 023701 CrossRef.
- P. Auban-Senzier, C. Pasquier, D. Jérome, C. Carcel and J.-M. Fabre, Synth. Met., 2003, 133–134, 11 CrossRef CAS.
- L. Balicas, K. Behnia, W. Kang, P. Auban-Senzier, E. Canadell, D. Jérome, M. Ribault and J.-M. Fabre, Adv. Mater., 1994, 6, 762 CrossRef CAS.
- M. Dressel, S. Kirchner, P. Hesse, G. Untereiner, M. Dumm, J. Hemberger, A. Loidl and L. Montgomery, Synth. Met., 2001, 120, 719 CrossRef CAS.
- C. Coulon, P. Delhaes and S. Flandrois, J. Phys., 1982, 43, 1059 CrossRef CAS.
- M. Dumm, A. Loidl, B. W. Fravel, K. P. Starkey, L. K. Montgomery and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 511 CrossRef CAS.
- D. S. Chow, F. Zamborszky, B. Alavi, D. J. Tantillo, A. Baur, C. A. Merlic and S. E. Brown, Phys. Rev. Lett., 2000, 85, 1698 CrossRef CAS.
- T. Nakamura, K. Furukawa and T. Hara, J. Phys. Soc. Jpn., 2007, 76, 064715 CrossRef.
- P. Monceau, F. Y. Nad and S. Brazovskii, Phys. Rev. Lett., 2001, 86, 4080 CrossRef CAS PubMed.
- M. Dumm, M. Abaker and M. Dressel, J. Phys. IV, 2005, 131, 55 CAS.
- Y. Nogami, T. Ito, K. Yamamoto, N. Irie, S. Horita, T. Kambe, N. Nagao, K. Oshima, N. Ikeda and T. Nakamura, J. Phys. IV, 2005, 131, 39 CAS.
- Y. Oka, N. Matsunaga, K. Nomura, A. Kawamoto, K. Yamamoto and K. Yakushi, J. Phys. Soc. Jpn., 2015, 84, 114709 CrossRef.
- T. Peterseim and M. Dressel, Crystals, 2017, 7, 278 CrossRef.
- I. Voloshenko, M. Herter, R. Beyer, A. Pustogow and M. Dressel, J. Phys.: Condens. Matter, 2017, 29, 115601 CrossRef PubMed.
- C. Coulon, S. S. P. Parkin and R. Laversanne, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3583 CrossRef CAS PubMed.
- S. Kitou, T. Fujii, T. Kawamoto, N. Katayama, S. Maki, E. Nishibori, K. Sugimoto, M. Takata, T. Nakamura and H. Sawa, Phys. Rev. Lett., 2017, 119, 065701 CrossRef PubMed.
- T. Nakamura, J. Phys. Soc. Jpn., 2003, 72, 213 CrossRef CAS.
- H. Seo and H. Fukuyama, J. Phys. Soc. Jpn., 1997, 66, 1249 CrossRef CAS.
- S. Mazumdar, R. T. Clay and D. K. Campbell, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13400 CrossRef CAS.
- F. Nad, P. Monceau, C. Carcel and J.-M. Fabre, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1753 CrossRef CAS.
- F. Nad, P. Monceau, C. Carcel and J.-M. Fabre, J. Phys.: Condens. Matter, 2000, 12, L435 CrossRef CAS.
- K. Yoshimi, H. Seo, S. Ishibashi and S. E. Brown, Phys. Rev. Lett., 2012, 108, 096402 CrossRef PubMed.
- Y. Nogami and T. Nakamura, J. Phys. IV, 2002, 12, Pr9–Pr145 Search PubMed.
- T. Nakamura, K. Furukawa and T. Hara, J. Phys. Soc. Jpn., 2006, 75, 013707 CrossRef.
- S. S. P. Parkin, J. J. Mayerle and E. M. Engler, J. Phys., Colloq., 1983, 44, C3–1105 Search PubMed.
- A. Pustogow, T. Peterseim, S. Kolatschek, L. Engel and M. Dressel, Phys. Rev. B, 2016, 94, 195125 CrossRef.
- C. Coulon, A. Maaroufi, J. Amiell, E. Dupart, S. Flandrois, P. Delhaes, R. Moret, J. P. Pouget and J. P. Morand, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 6322 CrossRef CAS.
- F. Zamborszky, W. Yu, W. Raas, S. E. Brown, B. Alavi, C. A. Merlic and A. Baur, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 081103 CrossRef.
- W. Yu, F. Zhang, F. Zamborszky, B. Alavi, A. Baur, C. A. Merlic and S. E. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 121101 CrossRef.
- D. Jérome, Science, 1991, 252, 1509 CrossRef PubMed.
- J. Moser, M. Gabay, P. Auban-Senzier, D. Jérome, K. Bechgaard and J.-M. Fabre, Eur. Phys. J. B, 1998, 1, 39 CrossRef CAS.
- P. Auban-Senzier, D. Jérome, C. Carcel and J.-M. Fabre, J. Phys. IV, 2004, 114, 41 CAS.
- P. Auban-Senzier, D. Jérome, N. Doiron-Leyraud, S. René de Cotret, A. Sedeki, C. Bourbonnais, L. Taillefer, P. Alemany, E. Canadell and K. Bechgaard, J. Phys.: Condens. Matter, 2011, 23, 345702 CrossRef CAS PubMed.
- A. C. Jacko, H. Feldner, E. Rose, F. Lissner, M. Dressel, R. Valentí and H. O. Jeschke, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155139 CrossRef.
- B. Korin-Hamzić, E. Tafra, M. Basletić, A. Hamzić and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115102 CrossRef.
- A. Pashkin, M. Dressel and C. A. Kuntscher, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165118 CrossRef.
- C. Bellitto, G. Dessy and V. Fares, Inorg. Chem., 1985, 24, 2815 CrossRef CAS.
- M. Mitsumi, Y. Youshida, A. Kohyama, Y. Kitagawa, Y. Ozawa, M. Kobayashi, K. Toriumi, M. Tadokoro, N. Ikeda, M. Okumura and M. Kurmoo, Inorg. Chem., 2009, 48, 6680 CrossRef CAS PubMed.
- G. Givaja, O. Castillo, E. Mateo, A. Gallego, C. J. Gómez-García, A. Calzolari, R. di Felice and F. Zamora, Chem. – Eur. J., 2012, 18, 15476 CrossRef CAS PubMed.
Footnote |
| † This feature article is dedicated to the memory of the late Prof. Peter Day, who passed away on May 19, 2020. |
| This journal is © The Royal Society of Chemistry 2020 |