Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influence of support materials on the structural and electronic properties of gold nanoparticles – a DFT study†‡
Julien
Engel
 *,
Samantha
Francis
and
Alberto
Roldan
*,
Samantha
Francis
and
Alberto
Roldan
 *
*
School of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, Wales, UK. E-mail: RoldanMartinezA@cardiff.ac.uk
First published on 29th August 2019
Abstract
Supported gold nanoparticles are used for a wide range of catalytic processes. In this work, we use dispersion corrected density functional theory (DFT-D) to study the effect of commonly used support materials (MgO, C, CeO2) on small gold particles with up to 19 atoms. Our results show that the preferred cluster shape and morphology is highly dependent on the support material due to different adsorption strength and structural mismatch between the cluster and the surface material. We developed an algorithm to measure the mismatch between the cluster interface and the support surface. Moreover, depending on the support material, the gold clusters exhibit a positive or negative polarisation, which ultimately has strong implications on the catalytic activity of such particles. This behaviour is rationalised by an analysis of the electronic structure of the metal particles and support materials.
Introduction
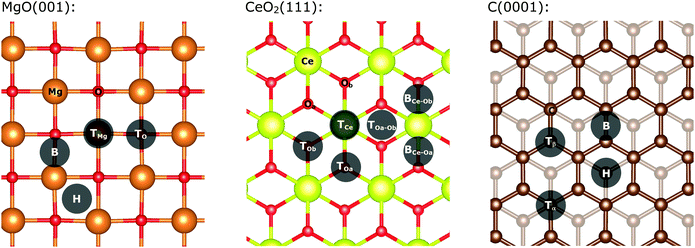
Supported metal catalysts are used in many of the reactions required in the chemical industry.1–3 Their catalytic efficiency is often related to exposed area of the support and structural properties such as supported particles’ size and shape. All these properties are strongly influenced by the interactions between the metal particle and the support material.4,5 Typical support materials for catalytic applications include: carbon-based materials and oxides of main group elements (e.g. MgO, Al2O3, SiO2), transition metals (e.g. TiO2, ZrO2, Fe2O3) and rare-earth metals (CeO2).The choice of the support for a reaction is generally based on screening of common and readily available materials rather than rational design, which requires not only an understanding of the desired properties of the catalyst but also a detailed knowledge regarding the effect that the support material has on the metal properties. To this end, quantum chemical calculations on model systems can offer detailed information on the structural and electronic properties of supported metal particles and their interaction with the support material. In this study, the supports chosen (MgO, C, and CeO2) reflect a small cross section of the typical supports considered for catalyst synthesis. Magnesium oxide (magnesia, MgO) has been used extensively as support material for metal catalysts for a wide range of applications.6–8 Moreover, it is used in other areas such as surface science9 and electronics.10,11 It is an example of a non-reducible metal oxide, that crystallises in a simple rock salt structure,12,13 and its most stable surface, i.e. (001),14 can be prepared relatively defect free.15 Another widely used support material for transition metal catalysts is cerium(IV) oxide (ceria, CeO2); the most prominent rare-earth metal oxide.16 It crystallises in the fluorite structure and the most stable low-index surface is the oxygen-terminated (111) surface.17 In contrast to magnesia, ceria is highly reducible, which allows its application as an oxygen ion conductor. Apart from metal oxides, carbon materials such as graphite or graphene are also commonly used as support materials in catalytic and electronic applications.18–20 Compared to the ionic structures of metal oxides, the pristine surfaces of graphene and graphite are highly homogeneous and lack any polar atoms or groups unless it is highly activated, i.e. defective, oxidised, or doped. α-Graphite crystallises in a layered hexagonal structure. The non-covalent dispersion interaction between the layers is significantly weaker than the covalent interactions within the layers, which results in the (0001) surface to be most stable. This means that the character of the interaction between support and metal cluster is fundamentally different. We have limited the scope of this study to defect-free support materials since it is necessary to develop an understanding of the properties before the additional complexity of defects is introduced.
In terms of the active metal employed in the modelled catalysts, we have used gold clusters, which have been investigated for their catalytic properties since the discovery of their reactivity for reactions such as: the oxidation of alcohols utilising a MgO support,21 hydrochlorination of acetylene with a carbon support,22 and low temperature oxidation of CO on a range of metal-oxide and carbon supports.23,24 Valuable contributions such as these have spurred a wealth of research into the noble metals ability as a catalyst. Many groups have demonstrated decreasing activity for gold at particle sizes above 5 nm25,26 and it has been concluded that activity is highly size-dependent.27 The reasons for this size-dependent activity have been comprehensively credited to differences in the electronic structure and the active site coordination as a result of the properties that nanoparticles exhibit.28–31 These properties include: a high surface-to-bulk ratio,32 the availability of low-coordination atoms,33 and the presence of perimeter sites at the Au–support interface.34 Additionally, catalytic properties of small Au clusters have been attributed to the charge transfer from oxygen vacancies in oxides, highlighting the importance of anchoring sites;35 and the stability of Au clusters against sintering under reaction conditions, both of which can alter reactivity.36 Furthermore, supported metal catalyst properties are influenced by both the substrate-induced strain at the interface37 and the epitaxial strain within the cluster.37 Nevertheless, the quest for understanding the structure activity relationship of supported gold catalysts is still ongoing. The adsorption of gold atoms and clusters on magnesia,38–42 ceria,43–61 and graphene/graphite62–75 has been at the centre of previous computational studies. However, their scope was mostly limited to single adatoms or specific cluster sizes and only one support material. The aim of our investigation is to determine trends for the properties of gold clusters with 1 to 19 atoms and directly compare these between different support materials with special focus on the interface mismatch.
It is intended that the information gathered from computational studies can be used in conjunction with experimental findings to ultimately understand the relationship between the structure of a catalyst and the resulting properties. The recent improvements in the characterisation of catalysts using experimental methods38 in partnership with the advancements in computational ability have meant that characterisation of metal supported catalysts has become increasingly more instructive and have helped to guide the rational design of catalysts with desired properties on demand.76,77
Computational details
Spin-polarised, periodic plane-wave density functional theory calculations were performed with the Vienna Ab Initio Simulation Package (VASP 5).78–80 The density functional of Perdew, Burke, and Ernzerhoff (PBE)81 was used to calculate exchange and correlation contributions. Dispersion interactions were included using Grimme's empirical dispersion correction DFT-D3.82 The importance of long-range interactions for the adsorption of Au on graphene and oxides as well as for the structure of isolated Au clusters was highlighted previously.75,83,84 The projector-augmented wave (PAW) formalism80,85 as implemented in VASP was used to describe the core electrons. A kinetic cut-off was set at 450 eV for MgO and C and 500 eV for CeO2, respectively. A Hubbard approach correction (DFT+U) using the method of Liechtenstein et al. was used on the Ce 4f-orbitals.86–92 The parameters were set to Ueff = 4 eV (U = 5 eV and J = 1 eV), which better reproduce the reduction of CeO2 based on benchmarking calculations (see ESI‡) and previous reports.93,94 Dipole corrections as implemented in the VASP code were applied perpendicular to the surfaces upon adsorption of gold clusters. Bader charges were calculated to assign partial charges to specific atoms.95 Crystal Orbital Hamilton populations (COHP) were calculated with Lobster 2.2.1.96–99 Structures and electron densities were visualised using VESTA.100Slab models
For each studied support material (MgO, CeO2 and C), slab models of their most stable surfaces were created from optimised bulk structures. Two slab models were created for each material, one with a small surface area and a large number of layers and a second one with decreased thickness but larger surface area. This represents a compromise between the computational effort and the strength of the interactions between the periodically repeated clusters. The accuracy of the thinner slab models was verified by appropriate benchmark calculations with respect to the thicker models.The MgO(001) was modelled for clusters with up to four gold atoms by a slab with a (2 × 2 × 2) four-layer supercell of 32 magnesium and 32 oxygen atoms (surface area = 39.6 Å2), the bottom two layers fixed for the calculations representing the bulk. For larger clusters, a two-layer slab system (4 × 4 × 1) consisting of 64 magnesium and 64 oxygen atoms (surface area = 215.5 Å2) was used where the bottom MgO layer was fixed. The slabs were separated by a perpendicular vacuum of 10 Å (up to six Au atoms) and 20 Å (larger gold clusters), respectively.
For CeO2(111), a three-trilayered oxygen-terminated slab (3 × 3 × 3) with 27 cerium and 54 oxygen atoms (surface area = 116.5 Å2) was chosen for clusters with up to six Au atoms. Larger clusters were calculated on a two-trilayered surface (6 × 6 × 2; surface area = 466.0 Å2) with 72 cerium and 144 oxygen atoms. In both cases, the slabs were separated by a vacuum layer of 20 Å and the lowest CeO2 trilayer was fixed in the optimization procedure.
For graphite, first a slab model of the (0001) surface with four layers and 72 carbon atoms was created. The two lowest layers were fixed in the optimisation procedure. Due to the small surface area, a second slab model with one layer of 72 carbon atoms fully relaxed (surface area = 189.6 Å2) was created and the adsorption energies of gold adatoms were benchmarked against the four-layered model. Since the difference in adsorption energies between the models was below 1 meV per atom, a single sheet of graphene with a vacuum gap of 30 Å perpendicular to the surface was used for gold clusters up to 13 atoms. Larger clusters were calculated on a single-layered slab of 162 carbon atoms (surface area = 426.5 Å2) with the same vacuum.
The number of k-points was benchmarked and adjusted for each material and slab size. A 11 × 11 × 1 Monkhorst–Pack grid101 was used for the smaller surfaces of C and MgO and 7 × 7 × 1 for CeO2. For the larger surfaces, we used for C a 7 × 7 × 1 grid and a 3 × 3 × 1 grid for MgO and CeO2.
Cluster models
We employed unbiased genetic algorithms (GA) to build supported clusters smaller than 6 atoms.102 All genetic algorithm (GA) methods generally follow the same procedure whereby an original population is created, a method of reproduction occurs and finally, there is inclusion of mutations into the process. The calculations presented here for Aun (3 ≤ n ≤ 5) were performed using the Birmingham cluster genetic algorithm package as presented by Shayeghi et al.103 We combined it with global optimisation ran at DFT level. Hence, we employed VASP to screen a pool of 20 random structures, which is minimised, and parent structures are chosen by applying a fitness function. The degree of crossover from each parent is weighted (from pool) and random mutation operations are allowed to occur at a rate of 0.1. For a population size of 20 structures and a mutation rate of 0.1, this means 18 offspring are generated from mating and mutants on average since (20 + 18) × 0.1 = 3.8. This rate of mutation balances reduced efficiency from a higher rate, which would impede the mating rate of low energy parents and no mutation reducing structural diversity. Full mutation would essentially make this method a basin hopping approach. A new pool is then created from accepted, lower energy structures. Heiles et al. confirmed the validity of this method for Au, Pd and Au–Pd clusters.104 Due to the vast amount of possible arrangements of large clusters, we used the most stable shapes and positions derived from the GA and followed a built-up procedure for larger structures with several shapes and positions on the surfaces (see ESI‡). Based on the optimised structure of a cluster, Aun, we added an additional gold atom at several reasonable positions to create the structures for the cluster, Aun+1. We also included structures that maximised the exposure of the most stable facets to the vacuum as well as structures based on previous reports on structures of supported38–75 and isolated84,105–126 Aun clusters.We calculated the adsorption energies (Eads) from the total energy of the optimised structure of the gold cluster on the surface (EAun–S), the energy of the optimised naked slab (ES), and the energy of the gold cluster in gas phase retaining the shape from the supported structure (EAun).
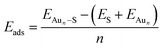 | (1) |
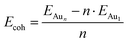 | (2) |
Mismatch calculation
For this work, we developed a mathematical model based on minimal structural information to provide a universal measure of the mismatch between support materials and cluster interfaces.The values shown in this work have been calculated with the python script (mismatch_calculator.py) which is available from the Cardiff University Research Portal at DOI: 10.17035/d.2018.0064964028. See ESI‡ for further details of the mismatch calculations.
Results and discussion
Structure of supported Au clusters
The MgO(001) surface is planar and all magnesium and oxygen positions are equivalent as represented in Fig. 1. There are four main positions for a single gold atom on the support: on top of an oxygen atom (TO), on top a magnesium atom (TMg), on the bridge between oxygen and magnesium (B) and in the void between two magnesium and two oxygen atoms (H). In agreement with previous reports, we found that the most stable position for a single gold atom adsorption on a magnesia support is on top of the oxygen.40,41 Clusters with up to five gold atoms are planar and arranged perpendicularly to the surface. Larger clusters remain planar but are oriented parallel to the surface for all investigated cluster sizes (see ESI‡ for detailed description).There are generally four different positions for a gold adatom on a graphite (0001) surface as shown in Fig. 1.66 The gold atom can be located on top of a carbon atom over another carbon atom in the layer beneath; (top-α-position; Tα) over a carbon atom located over a void in the layer beneath (top-β-position; Tβ), on a hollow position on top of a sub-surface carbon (H), or on a bridge between two carbon atoms (B). In our single-layered model, positions Tα and Tβ are equal (top position; T). Our calculations indicate that the top position is favoured, albeit the energy difference is 0.002 eV. The clusters grow planar and perpendicular to the surface up to four atoms. From five atoms onwards, the clusters are oriented parallel to the surface and remain planar. For Au19/C, a three-dimensional structure was found to be the most stable (see ESI‡ for detailed description of the cluster shapes).
The pristine oxygen-terminated (111) surface of CeO2 has three distinct accessible atoms exposed on the surface (see Fig. 1). These are: an oxygen atom from the highest atomic layer, a cerium atom, and an oxygen atom from the layer below. Our calculations indicate that the most stable position is on the BOa–Ob site (see Fig. 1), although it shows only an energy difference to the TOa position of 0.01 eV. In contrast to the MgO and C-supported particles, the CeO2-supported gold clusters are three-dimensional from four atoms onwards. The only exception is Au7/CeO2, which is nearly planar and parallel to the surface.
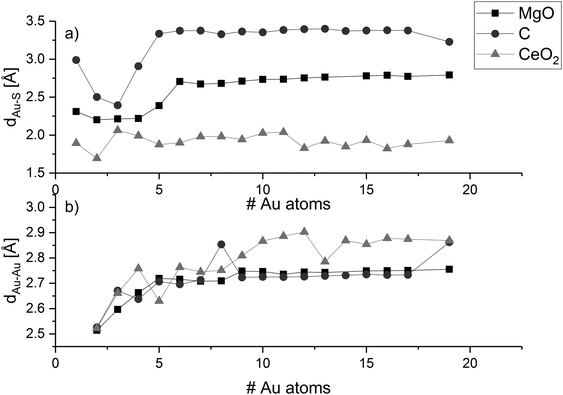
To determine structural trends of the supported gold clusters, we analysed the average height difference between the metal atoms at the cluster interfaces and the top layer of the surfaces (dAu–S—Fig. 2a) as well as the average distances between neighbouring atoms within the cluster (dAu–Au—Fig. 2b).
We can see that dAu–S of a gold adatom on magnesia is 2.31 Å and decreases to 2.20 Å for the gold dimer. With increasing cluster size, the distance increases and converges to a value between 2.71 Å and 2.79 Å when the arrangement of the cluster changes from perpendicular to parallel. This trend can be explained by the distribution of the surface interaction over a larger number of gold atoms, since all gold atoms in these clusters are at the interface to the surface. From five to six gold atoms, the arrangement of the cluster changes from perpendicular to parallel and dAu–S increases from 2.40 to 2.71 Å. While for all larger clusters dAu–S increases up to 2.79 Å. The dAu–S for Au8 and Au9 is significantly larger with 3.06 Å and 3.00 Å, respectively, due to the structural distortion in their shape.
On graphene, the distance of a gold adatom to the support surface is 3.00 Å, substantially larger than on magnesia (2.31 Å). The distance decreases to 2.40 Å for three gold atoms, which is only 0.10 Å larger than on magnesia. In contrast to on MgO, Au3 on graphene has only one gold atom at the interface, which leads to increased interaction of the interface atom with the surface. The Au4 cluster has one gold atom closest to the surface at 2.42 Å, whereas the second atom has a distance of 3.39 Å making it ambiguous whether the second atom should be considered as interface atom. For all gold clusters bigger than Au4, the average distance between the graphene sheet and the interface atoms converges to values in the range between 3.3 and 3.4 Å, which is in the same range as the second interface atom of Au4 (see ESI‡). From Au5 to Au18, the clusters are planar and parallel to the surface so that the surface–interface distance remains ∼3.354 Å. However, at Au19 the shape becomes three-dimensional; the number of interface atoms is reduced, and the surface–interface distance decreases to 3.23 Å. The decrease in dAu–S can be attributed to the decrease in interface gold atoms resulting in a stronger interaction with the surface.
In contrast to the flat surfaces of MgO(001) and C(0001), CeO2(111) has three different atomic layers accessible at the surface. We chose to define the cluster–surface distance solely based on the terminating top oxygen layer, since these atoms are the most likely ones to interact with the cluster. The distance of a single gold atom to the surface is 1.89 Å, which is significantly shorter than for magnesia and graphene, in agreement with its adsorption energies (see below). As on magnesia, a minimum distance is reached for two gold atoms (1.69 Å) as the number of interface gold atoms increases thereafter. At Au3, the average cluster surface distance is 2.06 Å and decreases to 1.88 Å for Au5, which maintain a three gold atoms interface. Au6 features a fourth interface atom, which is reflected in slightly higher distance to the surface, while Au7 switches to a planar shape parallel to the surface with all seven gold atoms at the interface (dAu–S = 1.98 Å). Up to 19 gold atoms, the cluster surface distance remains within the range 1.8 Å to 2.0 Å. The relation between cluster size and number of interfacial atoms seems to determine the dAu–S (and Eads). With larger cluster size, the effect of the number of interface atoms on the surface cluster distance is less pronounced.
As shown in Fig. 2b, the average gold–gold distance increases for all studied support materials with increasing cluster size. For large planar clusters on MgO and C, the average gold–gold distance tends to the value of an isolated gold monolayer (2.74 Å). In contrast, the gold clusters on CeO2 show significantly larger dAu–Au, resulting from the three-dimensional structure of these clusters (and the Au orbital occupation). The value converges to the average interatomic distance of bulk gold (2.88 Å).127
Adsorption and cohesion energies
The adsorption energy of gold clusters on magnesia (Eads) becomes less negative generally with increasing cluster size (Fig. 3a). The adsorption energy declines rapidly from −1.37 eV (for Au1) and converges around −0.57 eV. Previous studies reported adsorption energy for a single gold atom without dispersion correction to be 0.81 eV by Tada et al.128 and 0.87 eV by Jeon et al.129 and 0.78 eV by Coquet et al.,130 which compares very well with our value without dispersion (0.81 eV). A stronger interaction of 0.20 eV can be seen from Au4 to Au5, which corresponds to with an increasing ratio of interface to non-interface atoms. The convergence of the adsorption energy reflects the planar growth of the gold particles on magnesia.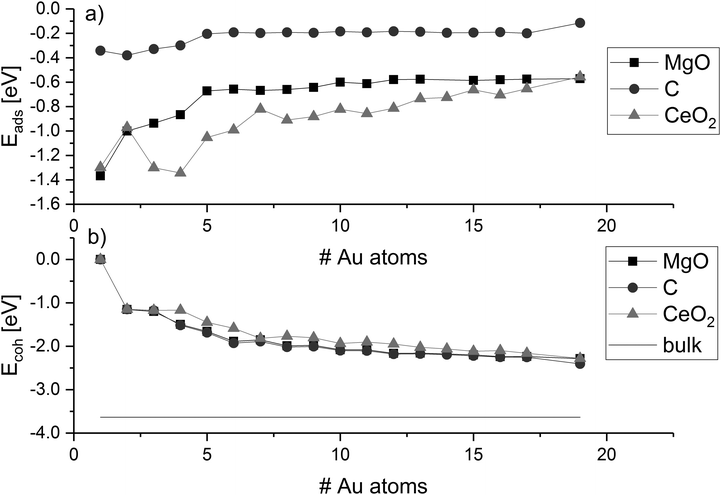 | ||
| Fig. 3 Adsorption energies (Eads) and cohesion energies (Ecoh) of gold clusters on MgO, C, and CeO2; values are connected to guide-the-eye; horizontal line indicates the Au bulk cohesion energy. | ||
The cohesion energy (Ecoh, Fig. 3b) increases with the number of gold atoms on the magnesia, showing an opposite trend than the adsorption energies. The Au2 cluster has a measured cohesion energy of 1.15 eV, this is comparable to the experimental cohesion energy of 1.16 eV quoted by Kittel,131 and the computationally calculated one (1.16 eV) using a correlation-consistent basis set in DFT (rather than planewaves) obtained by Bun et al.132 This can be used to support the idea, that as the cluster grows, the interaction between the gold atoms increases while the average cluster–support interaction decreases. This idea is also corroborated by the trend towards the bulk cohesive energy of gold with cluster size as shown in Fig. 3b. The cohesion energy of bulk gold is calculated to be 3.63 eV, which again is similar to that found experimentally (3.81 eV)131 and computationally (3.73 eV).132 Supported clusters with high cohesion energy have a morphology close to their optimum structure in the gas phase. This means that the structures are either weakly influenced by the support, or the interaction is weakened by the mismatch, i.e. difference in the atomic distances and symmetry between the cluster and the surface adsorption sites. Despite the symmetric mismatch between the square magnesia surface and the hexagonal gold cluster, the addition of gold atoms to the cluster does not affect the average strength of the interaction of the interface with the surface, while the cohesion energy does not indicate any significant distortion of the metal cluster. The transition between planar and three-dimensional Au clusters in the gas phase has been discussed controversially and is strongly dependent on the computational method.133 DFT methods predict higher stability of planar Aun clusters over three-dimensional ones compared to correlated ab initio methods due to the lack of long-range interactions. Therefore, we recalculated the 2D–3D transition using literature-known structures84,105–126 with our dispersion-corrected PBE-D3 method and compared it to plain PBE and the vdW-DF optB88134 (see ESI‡). We found that PBE-D3 and optB88 agree well and predict a higher stability of three-dimensional clusters. Both methods suggest that the transition occurs at eleven Au atoms, earlier than with plain PBE.
In comparison with the results for magnesia, the adsorption energies on graphene are generally lower and in the range of −0.4 eV and −0.1 eV. This agrees with previous reports describing a weak interaction between gold and defect-free graphite/graphene.62,68,69,71,73 As found for MgO, the biggest change in adsorption energy on graphene occurs between Au4 and Au5 due to the change from perpendicular to parallel structures. The gold clusters grow planar on the support surface without any strong distortion of bond distances and angles. For larger parallel planar clusters, the adsorption energy is approximately −0.2 eV and decreases for Au19 to −0.11 eV with the morphology change to a three-dimensional structure. However, the loss in adsorption energy is compensated by an increase in cohesion energy due to the change to the three-dimensional cluster shape. Already at 16 atoms, the cohesion of a different three-dimensional cluster (Au16[10−6]—see ESI‡) is slightly stronger than the one of the planar most stable clusters (Au16[16−0]a), although not strong enough to compete with the decrease in adsorption energy through the loss of interface atoms (see ESI‡ for details on cluster shapes). However, it must be noted here that the strength of the cluster–surface interaction is strongly dependent on the empirical dispersion correction. Therefore, we performed single-point calculations of the PBE-D3-optimised structures of the Au17 and Au19 on C with optB88. In agreement with the PBE-D3 results, the optB88 calculations suggest that the 2D–3D transition of Au clusters on C occurs between 17 and 19 Au atoms. Therefore, it can be concluded that the graphene surface is indeed stabilising planar arrangements of the gold atoms. The Ecoh for magnesia and graphene are nearly the same up to Au19 because of the structural similarities between the clusters on these surfaces.
The adsorption of gold clusters on CeO2(111) is stronger than on MgO(001) and C(0001). The binding of Au clusters to MgO(001) and reduced CeO2(111) interfaces was investigated in experimental studies by electron microscopy and single-crystal adsorption calorimetry.135–137 The trends show that a stronger adhesion of the clusters can be found on reduced CeO2 than on MgO, which agrees well with our results although it has to be noted that we only consider a defect-free CeO2(111) surface. The stronger cluster–surface interaction on CeO2 results in a distortion of the cluster shape from the optimal cluster shape in gas phase. The cohesion energy follows the same trend seen on magnesia and graphene, but it is less negative in line with the cluster charge, see below. While the hexagonal symmetry of the ceria surface matches the hexagonal structure of the gold clusters, a significant mismatch exists in the distance between favourable adsorption sites (dO–O = 3.87 Å) and the optimum Au–Au distance (monolayer: dAu–Au = 2.75 Å). Therefore, the planar growth of the particles would result in the placement of additional metal atoms in unfavourable positions, and hence, ceria promotes the three-dimensional growth at much smaller cluster size representing a distortion of the cluster from the preferred gas-phase structure.
The ratio of the cohesion energy and the adsorption energy (Ecoh/Eads—Fig. 5) seems to indicate which interactions dominate the structure of a cluster. For a high ratio Ecoh/Eads, the structure is dominated by the gold–gold interactions within the cluster whereas a low ratio indicates a preference to interact with (wet) the surface rather than other atoms within the cluster. As described before, gold clusters on magnesia and graphene show similar shapes (as reflected by the similar Ecoh), but the Ecoh/Eads ratio of graphene is significantly higher than the one of magnesia as the metal–metal interactions within the cluster dominate. For ceria, we concluded that the shape of the cluster is dominated by the interactions with the support, i.e. adhesion and mismatch. This is reflected in the Ecoh/Eads ratio, which is the lowest of the three investigated support materials. The cohesion energy is approximately twice as large as the adsorption energy for medium size clusters (∼10 atoms) and this ratio increases to four by Au19.
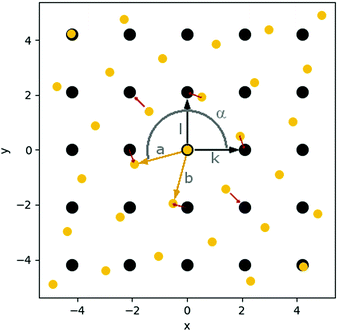 | ||
| Fig. 4 Schematic representation of the grids of surface sites (black; defined by vectors k and l) and cluster atoms (yellow; defined by vectors a and b); angle α defines rotation of cluster grid with respect to surface grid; local mismatch mp at first neighbour atoms is represented with red arrows (see ESI‡ for more details on the mismatch calculation). | ||
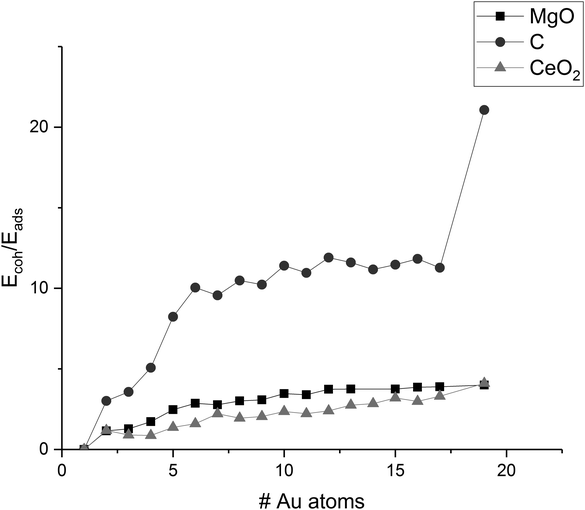 | ||
| Fig. 5 Ratio of Ecoh/Eads of Au clusters on MgO, C, and CeO2; values are connected to guide-the-eye. | ||
Previous studies on small Au clusters show that odd-numbered clusters are less stable than even-numbered ones and a wide range of properties exhibit odd–even oscillations.107,113,121,123,138 Interestingly, we did not find such an odd–even pattern for the adsorption energy of the supported Au clusters. Both MgO and C show almost constant adsorption energies for any cluster larger than four atoms. This indicates that the instability of odd-numbered Au clusters persists after adsorption. Otherwise, the adsorption would be stronger for these structures compared to even-numbered ones. CeO2 shows larger fluctuations of the adsorption energy due to structural effects, which could mask an underlying odd–even oscillation. The cohesion energy shows a small degree of odd–even oscillation for smaller clusters on MgO and C. For larger clusters, the pattern disappears since the value is averaged over the number of Au atoms. No such oscillations can be found for CeO2, which suggests that other factors such as the structural distortion of the cluster by the surface has stronger influence on the energy than the open shell/closed shell configuration. A similar trend can be found for the detachment energies, which describe the energy required for the abstraction of a metal atom from the supported metal cluster (see ESI‡).
Mismatch and wettability
The preferable cluster morphology, i.e. flat versus 3D, is directly related to its wettability, which is influenced by the structural mismatch between the interatomic distances, symmetry of the metals at the interface, and the preferable adsorption sites on the support as well as the relative strength of the metal–metal interactions within the cluster and the metal–surface interactions (Ecoh/Eads ratio).We realised that the comparison of the structural mismatch of two completely different sets (surface/cluster) of materials is more challenging than it appears at the first glance as it not only consists of the deviation of the interatomic distances but also the symmetry of the respective unit cells. The distance part can be easily expressed as the relation of the optimum metal–metal distance (dAu–Au) in the bulk and the distance between the most favoured adsorption sites of a single adatom. Additional to the matching distances, the same symmetry of the adsorption sites on the surface as well as at the cluster interface are required for an optimal binding without distortion of the cluster. The challenge to quantify the mismatch arises from the combination of both contributions into a single value which allows for the comparison of e.g. two materials with the same symmetry but different interatomic distances with two other materials with different unit cell shapes but identical interatomic distances.
Furthermore, it is challenging to derive the mismatch directly from the structures of the supported clusters since the cluster and surface structures are deformed depending on the flexibility of the materials and the strength of the cluster–surface interactions. To isolate the mismatch from other parameters, we developed a simplified mathematical model based on minimal structural information (cf.Fig. 4). This model reduces the complexity of the mismatch to a single scalar value for each interface (see ESI‡ for details). It has to be noted that such simplification inevitably comes with loss of information such as the direction of the mismatch at each respective point. This may be important for anisotropic systems which deformations along particular directions might require less energy than others. Including such information would require parameterisation for each system under study transforming a simple model into a basic force field.
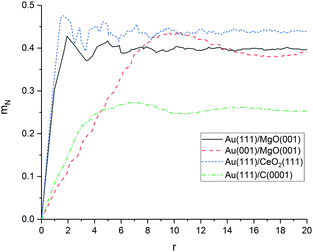
To calculate the mismatch between an undistorted Au(111) layer and the investigated materials (C, MgO, CeO2), we used the structural data from optimised geometries of an isolated Au(111) monolayer and the slab models of the supports. The distance between the Au atoms in the monolayer was found to be 2.74 Å with an angle of 60°. The MgO surface has an angle of 90° and a distance of 2.97 Å between the O atoms, the preferable adsorption site. The carbon atoms in C(0001) are 2.47 Å apart with an angle of 60°. However, a second set of C atoms had to be defined (shifted 2.85 Å and 30°) to account for every C atom in the surface (see Fig. S39) in the ESI‡ for details on the definition of the second set). For the CeO2 surface, we determined a distance of 3.87 Å between the O atoms with an angle of 60°. Hence, these are examples for very different types of mismatch. The length of the Au lattice vectors is only 0.23 Å shorter than the one of the vectors between the oxygen atoms on MgO compared to a difference of 1.12 Å on CeO2. Between the lattice vectors of C and Au is a length difference of 0.28 Å. However, the Au(111) and CeO2(111) surfaces as well as Au(111) and C(0001) share the same lattice angle of 60° while MgO(001) has an angle of 90°.
With the here presented model, we intended to compare these cases to investigate whether the planar cluster growth of an Au(111) layer on C and MgO is a result of better structural match between these materials compared to CeO2, for which we found three-dimensional cluster growth.
The orientation between the cluster and the surface was optimised during the mismatch calculation. For all cases with the same lattice angle of both materials an angle α = 0° and for Au(111)/MgO(001) an angle α = 15° was found as optimum orientation. This agrees well with the calculated structures of the supported clusters. For example, Au19/MgO shows an angle of 14.9° between the surface and the cluster.
As shown in Fig. 6, the average mismatch mN(r) of an adsorbed rigid monolayer with radius r increases linearly for all investigated material combinations before converging to a value depending only on the support material. The initial slope d of the mismatch mN(r) with the radius r is a descriptor for the increasing structural strain on a growing cluster and the magnitude of the structural deformation needed for an ideal fit. The slope is significantly lower for graphene (0.07) than for MgO (0.31) and CeO2 (0.33). The value to which the mismatch converges at infinite size (mN(∞)) is only dependent on the symmetry (lattice angle) of the support material (and the normalisation factor; see ESI‡), since the cluster atoms become equally distributed over all possible positions of the surface unit cell. It represents the average (normalised) distance of equally distributed points to the surface grid.
Our results indicate, that the mismatch on graphene is low and the planar cluster growth on graphene is not only a result of weak interactions between cluster and surface, but also promoted by the good fit between both materials. The results for MgO and CeO2 show that despite their very different structure, both surfaces have a similar mismatch to Au(111). This means that the three-dimensional growth of smaller clusters on CeO2 is most likely caused by stronger interactions between the cluster and the surface rather than a worse structural fit compared to MgO.
In addition to the discussed material combinations, we calculated the mismatch between Au(001) interface and MgO(001). In contrast to Au(111), Au(001) has a lattice angle of 90° and should be a better structural fit to the MgO(001) surface. Indeed, our calculations predict a significantly lower mismatch for Au(001)/MgO(001) (0.05). However, the surface energy of Au(001) is higher (1.359 J m−2) than of Au(111) with (1.137 J m−2).139 The higher surface energy is responsible for the stabilisation of Au(111)/MgO(001) in our calculations. This means, that it can be expected a change from (111) to a (001) facet takes place at the interface to reduce the strain which grows with increasing interface area (r).
Electronic structure
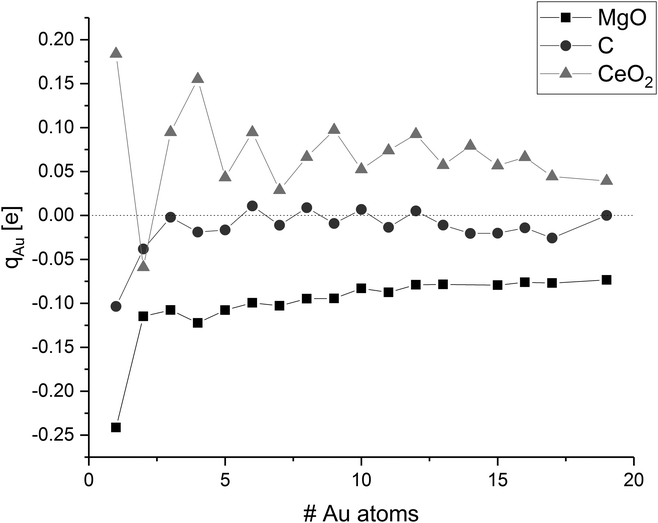
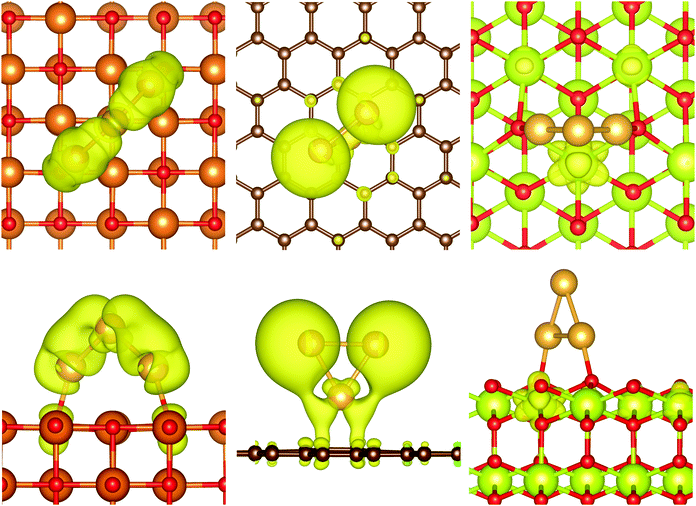
Strong adsorption of clusters on supports is commonly associated with a distortion in their electronic structure, e.g. subtracting or adding electrons into the metal band. These distortions have implications on the cluster morphology and stability, as well as the catalytic activity. Therefore, we investigated changes in the electronic structure and looked at electron transfer between the cluster and the surface using the Bader population analysis (cf.Fig. 8).The Bader charge analysis results show a reduction (gain of electrons) of the gold clusters on the magnesium oxide surface. The average atomic charge transference generally decreases with increasing cluster size and thus, the biggest charge transfer per gold atom was found for a single gold adatom. The gold atom has a negative partial charge of −0.24 e. The additional electron density at the gold atom is mainly taken from the oxygen atom at the interface, which shows a charge difference of +0.19 e compared to the surrounding oxygen atoms. The average charge of the gold atoms in the gold dimer on magnesia is −0.13 e. In this case, the gold atom at the interface is only charged by −0.05 e while the other gold atom on top of the interface atom has a charge of −0.20 e. In contrast to this, the interface atoms in the gold trimer are more negatively charged with −0.18 e and −0.19 e, respectively, than the top gold atom (−0.07 e) adding up to an average charge of −0.15 e. With increasing cluster size, the average charge of the gold atoms decreases to −0.07 e in the case of Au19. This can be explained by the weaker interaction of the gold cluster with the surface as the cluster grows. The gold atoms in the cluster have a stronger interaction to each other (Ecoh) than the one formed by the adsorption of the gold to the surface (Eads) so the charge transfer from the surface to the gold cluster is reduced. The charge of specific gold atoms within a cluster is mainly dependent from the number of neighbouring gold atoms. Low coordinated gold atoms at the corners and edges of the cluster are more negatively polarised than highly coordinated atoms in the centre of the cluster. Interestingly, the height of the atoms over the surface in the planar gold clusters did not have a clear effect on the partial charge of the gold atoms.
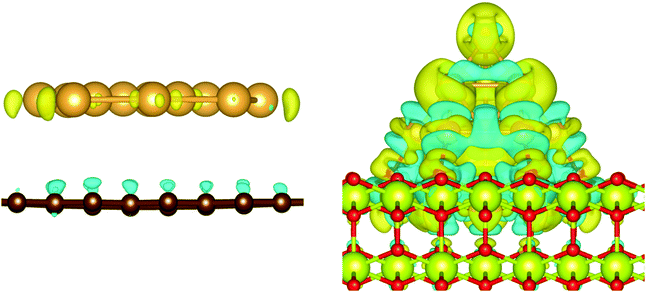
The charge transfer on the C(0001) support is significantly smaller than on magnesia, this is in line with the weaker Eads. While the carbon surface donates a charge of 0.10 e to a single gold adatom, the charge transfer per gold atom for Aun clusters (n > 1) is negligible (0.01 e per atom). The Bader analysis also shows the same charge distribution as seen for the gas phase structures. Fig. 7 depicts the iso-surface of the difference of the electron density of supported Au11 on C(0001) and CeO2(111) and the sum of the electron densities of the separated cluster and surface with the same geometries (electron density flow). The changes in the electron density difference on graphene is very small emphasising the minor changes upon adsorption. In general, the low coordinated atoms at the corners and edges of the cluster show a negative partial charge in both the gas phase and adsorbed structures.
The discussion of the charge transfer between CeO2(111) surfaces and gold adatoms has been controversial in the literature. The standard reduction potentials for Ce4+ to Ce3+ (+1.72 V) and for Au+ to Au0 (+1.69 V) are very similar.140 This allows for a partial oxidation of the gold clusters under reduction of single Ce4+ to Ce3+ ions in the CeO2 surface as indicated by previous computational studies.56 However, combined LDA/GGA calculations by Castellani et al. did not indicate any significant charge transfer.54 Within our calculations, a single gold adatom located on the most stable O–O bridge position has a charge of +0.18 e. Analysis of the difference in α and β spin density shows that the electron density is donated into a Ce 4f orbital. This Ce atom, which is in the same plane as the Au–O bonds, is reduced by 0.16 e and shows a magnetic moment of 0.77 μB indicating an unpaired electron. The location of the reduced Ce atom is consistent with the work by Hernandez et al.56 As described before, adsorption on an O-top position has nearly the same energy. In that case, the charge transfer is increased to 0.24 e. As in the O–O bridge position, electron density is shifted from the gold atom to the 4f orbital of a single Ce atom, which is reduced by 0.18 e and has a magnetic moment of 0.80 μB. We performed further calculations of Au1/CeO2 with different Hubbard parameters to investigate the influence on the charge transfer (see ESI‡ for details). We found that the charge of the gold atom is slightly negative for Ueff ≤ 3 eV, while it becomes significantly positive for higher Hubbard parameters due to an increment in the correlation of the Ce 4f orbitals. This is in agreement with the results of Castellani et al., who used a Ueff value of 3 eV and obtained a charge of −0.02 e of the gold atom.54 For Au2/CeO2, we did not find any reduction of the cerium atoms, since the direction of the charge transfer is from the surface to the gold dimer in this case. All larger clusters considered in this study are oxidised by ceria. The magnitude of the average gold atom charge oscillates, but not depending whether the gold cluster has an odd or even number of electrons as in the case of C. As a general trend, it decreases with increasing cluster size. A clearer picture emerges by looking at the total charge transfer. Odd-numbered clusters with smaller than eight atoms show a charge transfer between 0.18 e and 0.29 e from the cluster to the surface. At these cluster sizes a single Ce4+ ion is reduced to Ce3+. Even-numbered clusters with a size of 2–10 atoms are donating between 0.52 e and 0.62 e into the surface and lead to the reduction of two Ce4+ ions. Three Ce3+ ions could be found for odd-numbered clusters between 9 and 19 atoms which are donating between 0.74 e and 0.87 e into the surface. All investigated even-numbered clusters larger than 10 atoms show a charge transfer of 1.06–1.11 e and four Ce3+ ions. These numbers show that the charge transfer correlates well with the number of reduced Ce ions. On average 0.26 e are donated for each Ce3+ ion from the cluster into the surface. This is significantly less than one electron which is required for the reduction of one Ce4+ ion to Ce3+. However, this constitutes the net charge transfer which also considers the electron density donated back from the surface oxygen atoms into the gold cluster. The amount of Ce3+ ions increases as the cluster grows and covers more of the CeO2 surface. As the number of gold atoms increases faster than the number of Ce3+ ions, the average charge transfer generally decreases with increasing cluster size. The fluctuations between odd and even-numbered clusters are a result of the fact that the reduction of a Ce4+ creates an unpaired electron. Therefore, it is favourable for odd-numbered clusters, which already feature one unpaired electron, to reduce an odd number of Ce4+ ions, while even-numbered clusters reduce an even number of Ce3+ ions.
We used Crystal Orbital Hamilton Population (COHP) to analyse the electronic structure of supported Au3 and Au6 clusters and characterise the bonding between surface and cluster in more detail. Indeed, COHP is a powerful tool to distinguish whether states are contributing to the stabilisation of the structure, or are in fact destabilising it.96
To understand the supported cluster structures, we had first a closer look at the electronic structure of isolated gold clusters. The frontier orbitals in these isolated gold clusters have sd hybrid orbital character. In odd-numbered clusters, e.g. Au3, the HOMO is dominated by contributions from the s orbitals of the gold atoms whereas the occupied orbitals below are dominated by d contributions. Even-numbered clusters, e.g. Au6, have a d-dominated HOMO while the s-dominated state is unoccupied (LUMO). Bearing in mind the electron configuration of gold (s1d10) with completely occupied d orbitals and half occupied s orbitals, a large number of antibonding states are occupied. This suggests that the gold clusters preferably interact with unoccupied surface states to depopulate the antibonding gold-gold states. Alternatively, the interaction of occupied surface states and unoccupied cluster states might stabilise the cluster–surface interactions at cost of destabilisation of the gold–gold interactions within the cluster.
The density of states of the magnesia surface shows a valence band with dominantly O 2p character with low mixing of Mg 2s and 2p states. A band gap of 3.3 eV, clearly underestimated, separates the valence band from a conduction band consisting of Mg 2s and 2p orbitals with low mixing of O 2p states. The pCOHP (Mg–O) indicates bonding character for the entire valence band and antibonding character for the complete conduction band. Very small clusters such as Au3 adsorb perpendicular on the MgO surface and interact with oxygen atoms on the surface. The pDOS of Au3/MgO shows an overlap between the MgO valence band and Au sd states (see ESI,‡ Fig. S4). The valence band is separated by a band gap of 1 eV from a discrete state at the Fermi energy. This highest occupied orbital/band (cf.Fig. 9) is occupied with a single electron and consists of contributions from s and d orbitals at the gold atoms and oxygen pz orbitals. Indeed, mixing between O 2p and Au 5d and 6s orbitals can be found throughout the valence band. While this indicates that the formation of Au–O bonds is favoured, the pCOHP shows that also a large number of antibonding Au–O and Au–Au states are populated. As a result of the bonding, electron density is shifted from the p orbitals of the surface oxygen atoms into the new bands giving a net transfer of charge from the surface to the cluster. As in the case of an isolated Au3 cluster, the singularly occupied highest occupied orbital/band has larger contribution from the Au 6s orbitals than the 5d orbitals of the gold atoms. According to the pCOHP calculation, this orbital is antibonding with respect to the Au–O as well as the Au–Au interactions. This indicates that the magnesia surface can offer only limited stabilisation for odd-numbered gold clusters compared with the isolated clusters and explains that the strong odd–even oscillation of the stability is retained for the adsorbed species. A similar picture can be found for Au6/MgO(001). The DOS shows a valence band 0.6 eV below the Fermi energy. Above the valence band, two discrete states can be found, one directly at the Fermi energy and a second one right above the valence band. These states can be attributed to orbitals consisting of contributions from Au s and d orbitals as well as O p states. Like Au3/MgO, they are strongly antibonding with respect to the Au–Au and Au–O interactions.
 | ||
| Fig. 9 Iso-surfaces of the highest occupied band of Au3/MgO (left), Au3/C (centre), and Au3/CeO2 (right); iso-value of 0.001 e Å−3. | ||
In the case of graphene, the states around the Fermi energy consist of contributions from pz orbitals of all carbon atoms. While all states below the Fermi level are bonding with respect to the C–C interactions, those above are antibonding. Although no net charge transfer between the cluster and the surface could be detected, we found mixing between the Au sd orbitals and the graphene pz orbitals. This is not the case for parallel oriented structures such as Au6/C(0001). For example, the only significant contributions to the two highest occupied bands are from carbon atoms, whereas the next two bands below consist nearly exclusively of gold orbitals. The pCOHP shows bonding and anti-bonding interactions between Au and C pairs, but their magnitude is negligible for parallel oriented clusters such as Au6/C(0001) compared to the Au–Au interactions. This suggests ultimately that no bond between the gold cluster and the surface is created as reflected in the low adsorption energies. In line with this observation, the bands of Au6/C show even less mixing between the cluster and surface orbitals than those of Au3/C. It can be assumed that the dispersive attraction of the parallel oriented cluster exceeds the weak bonding in the case of a perpendicular orientation for clusters with five or more gold atoms. The HOMO of Au3/C resembles the high energy s-dominated HOMO of the isolated cluster with only very small contribution of C 2p orbitals. While the orbital is bonding with respect to the Au–C interaction, the pCOHP shows antibonding character between Au–Au and C–C pairs. This means that the graphene surface does not stabilise the unpaired electron, in full agreement with the weak stability of the odd-numbered clusters. We found that the magnetisation of odd-numbered clusters on graphene disappeared for clusters larger than Au7 due to spin pairing within bands of the gold cluster by equal non-integer occupation of bands with alpha and beta spin. This is an artefact of the smearing employed in the calculation, which broadens the discrete cluster orbitals and allows a non-integer occupation. We excluded any significant effect on the herein reported properties with benchmark calculations with fixed magnetic moment.
The DOS of CeO2 shows a valence band with predominant oxygen 2p character with contributions from Ce 5d states and low contributions of Ce 5p and 4f states. Our calculations showed a band gap of 2.1 eV to a conduction band dominated by localised Ce 4f states. Slight mixing with O 2p states could be identified for the higher states of the conduction band. Analysis of the pCOHP (Ce–O) shows bonding character throughout the valence band, which is decreasing for energies close to the Fermi energy. The conduction band is antibonding with respect to the Ce–O pairs, but it features states with nearly non-bonding character close to the lower edge of the band. These Ce 4f states are available to shift electron density from the antibonding states at the gold clusters reducing Ce4+ ions to Ce3+ without significant destabilisation of the support material. For example, the highest occupied band of Au3/CeO2 (see Fig. 9) is solely located at a Ce atom. Projection of the band on atomic orbitals shows that the highest occupied has nearly exclusively Ce 4f character with only minimal contribution from O 2p states. The pCOHP indicates that this orbital is non-bonding with respect to Au–Au and Au–O pairs and only weakly antibonding between Ce and O. This means that the radical can be shifted from the high energy cluster orbital into a more stable non-bonding surface orbital resulting in the disappearance of the odd–even oscillation in stability. As described before, two Ce4+ ions are reduced for even-numbered clusters. Both Ce 4f orbitals are occupied with a single electron and the open shell singlet and triplet configurations are equivalent in energy. The reduction of the Ce atoms allows for the depopulation of antibonding Au–Au and Au–O states and stabilises the adsorbed structures. Furthermore, it explains why the direction of the charge transfer is reversed compared to MgO.
Since the deposition of the gold clusters breaks the symmetry of the surface, the Ce atoms are non-equivalent. This means, that the total energy of the system is depending on the relative location of the reduced Ce ions to the cluster. To evaluate this influence, we localised the reduced Ce atoms at several positions for selected Au cluster sizes. For this purpose, we increased the Ce–O bond distances at the respective sites to accommodate the larger Ce3+ ions before running a geometry optimisation procedure. This was achieved by replacement of the designated Ce3+ ions with larger La atoms. After a geometry optimisation calculation, the La atoms were replaced back to Ce, now featuring longer Ce–O distances. While the results showed an influence of the localisation of the Ce3+ ions on the total energy, other properties such as the charge transfer were interestingly unaffected. Therefore, as it falls out of the scope of our study, we did not extend the search for the localisation of the reduced Ce atoms for all investigated structures.
Conclusions
We carried out a systematic DFT-D(+U) study on Au clusters supported on MgO(001), C(0001), and CeO2(111). Our results show that the structural and electronic properties of supported gold nanoparticles are highly influenced by the choice of support material. The shape of the metal clusters is generally dependent on three parameters: (i) the preferred isolated structure of the metal cluster, (ii) the mismatch between that preferred structure and the symmetry and distance of the preferred adsorption sites on the surface, and (iii) the relative strength of the metal–metal interactions to the metal–surface interactions. The latter defines whether the shape of the particle is dominated by the metal or the support material and can be assessed based on the ratio of the cohesion and adsorption energy of a particular structure. In general, metal oxide supports such as the herein investigated, i.e. magnesia and ceria, exhibit a significantly stronger interaction with the metal atoms than non-polar supports like defect-free graphene. This leads to a change of the particle shape from its gas phase geometry to fit the surface structure on oxide supports. This change involves the stabilisation of stable conformers of the cluster and the deformation of metal–metal bond distances and angles. The support also modifies the cluster's electronic structure. Based on the charge distribution analysis, we found that the gold clusters on magnesia have negative partial charges, while these are positive on ceria. Due to the weak interaction with graphene, the graphene-supported gold clusters exhibit negligible charge transfer. The direction of the charge transfer was rationalised by analysis of the Crystal Orbital Hamilton Populations (COHP). Electron density from antibonding states in the gold clusters is shifted into unoccupied non-bonding states of CeO2, stabilising the Au–Au interactions within the three-dimensional clusters. Contrarily, we found that magnesia stabilises planar gold clusters.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for funding by the Engineering & Physical Sciences Research Council (EP/P005845/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/P020194). We also acknowledge computing time on the facilities of HPC Wales and the Advanced Research Computing @ Cardiff (ARCCA) at Cardiff University.Notes and references
- Q. Fu, A. Weber and M. Flytzani-Stephanopoulos, Catal. Lett., 2001, 77(1–3), 87 CrossRef CAS.
- X. Zhao, L. Wei, S. Cheng and J. Julson, Catalysts, 2017, 7(3), 83 CrossRef.
- R. Schlögl, Angew. Chem., Int. Ed., 2015, 54(11), 3465 CrossRef PubMed.
- R. Van Den Berg, G. Prieto, G. Korpershoek, L. I. Van Der Wal, A. J. Van Bunningen, S. Lægsgaard-Jørgensen, P. E. De Jongh and K. P. De Jong, Nat. Commun., 2016, 7, 20457 Search PubMed.
- J. C. Frost, Nature, 1988, 334(6183), 577 CrossRef CAS.
- N. M. Julkapli and S. Bagheri, Rev. Inorg. Chem., 2016, 36(1), 1 CAS.
- I. Tomska-Foralewska, M. Zieliński, M. Pietrowski, W. Przystajko and M. Wojciechowska, Catal. Today, 2011, 176(1), 263 CrossRef CAS.
- M. Wu, Y. Fu, W. Zhan, Y. Guo, Y. Guo, Y. Wang and G. Lu, Catalysts, 2017, 7(5), 155 CrossRef.
- M. Bajdich, A. Vojvodic and J. K. Nørskov., Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155401 CrossRef.
- Y. Cho, C. Kim, H.-S. Ahn, E. Cho, T.-E. Kim and S. Han, J. Appl. Phys., 2007, 101(8), 083710 CrossRef.
- P. Wu, G. Cao, F. Tang and M. Huang, Comput. Mater. Sci., 2014, 86, 180 CrossRef CAS.
- K. J. Chang and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30(8), 4774 CrossRef CAS.
- Z. Jian-Zhou, L.-Y. Lu, X.-R. Chen and Y. Lin, Phys. B, 2007, 387(1–2), 245 Search PubMed.
- G. W. Watson, E. T. Kelsey, N. H. De Leeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92(3), 433 RSC.
- C. R. Henry, Surf. Sci. Rep., 1998, 31, 231 CrossRef CAS.
- T. Montini; M. Melchionna; M. Monai and P. Fornasiero, Chemical Reviews, American Chemical Society, 2016, pp. 5987–6041 Search PubMed.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Surf. Sci., 2005, 576(1–3), 217 CrossRef CAS.
- X. Fan, G. Zhang and F. Zhang, Chem. Soc. Rev., 2015, 44(10), 3023 RSC.
- B. F. Machado and P. Serp, Catal. Sci. Technol., 2012, 2(1), 54 RSC.
- P. Serp and J. L. Figueiredo, Carbon materials for catalysis, John Wiley & Sons, 2009 Search PubMed.
- Z. Wang, C. Xu and H. Wang, Catal. Lett., 2014, 144(11), 1919 CrossRef CAS.
- G. J. Hutchings, J. Catal., 1985, 96(1), 292 CrossRef CAS.
- M. Haruta, Gold Bull., 2004, 37(1–2), 27 CrossRef CAS.
- M. D. Hughes, Y. J. Xu, P. Jenkins, P. McMorn, P. Landon, D. I. Enache, A. F. Carley, G. A. Attard, G. J. Hutchings, F. King, E. H. Stitt, P. Johnston, K. Griffin and C. J. Kiely, Nature, 2005, 437(7062), 1132 CrossRef CAS PubMed.
- M. M. Schubert, A. Venugopal, M. J. Kahlich, V. Plzak and R. J. Behm, J. Catal., 2004, 222, 32 CrossRef CAS.
- B. Hvolbæk, T. V. W. Janssens, B. S. Clausen, H. Falsig, C. H. Christensen and J. K. Nørskov, Nano Today, 2007, 14–18 CrossRef.
- X. Zhou, W. Xu, G. Liu, D. Panda and P. Chen, J. Am. Chem. Soc., 2010, 132(1), 138 CrossRef CAS PubMed.
- C. N. R. Rao, G. U. Kulkarni, P. John Thomas and P. P. Edwards, Chem. – Eur. J., 2002, 28–35 CrossRef CAS.
- T. V. W. Janssens, B. S. Clausen, B. Hvolbæk, H. Falsig, C. H. Christensen, T. Bligaard and J. K. Nørskov, Top. Catal., 2007, 44(1–2), 15 CrossRef CAS.
- E. Roduner, Chem. Soc. Rev., 2006, 35(7), 583 RSC.
- L. Liu and A. Corma, Chem. Rev., 2018, 118(10), 4981 CrossRef CAS PubMed.
- A. Roldán, J. M. Ricart and F. Illas, Theor. Chem. Acc., 2011, 128(4–6), 675 Search PubMed.
- N. Lopez, T. V. W. Janssens, B. S. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. K. Nørskov, J. Catal., 2004, 223, 232 CrossRef CAS.
- M. Cargnello, V. V. T. Doan-Nguyen, T. R. Gordon, R. E. Diaz, E. A. Stach, R. J. Gorte, P. Fornasiero and C. B. Murray, Science, 2013, 341(6147), 771 CrossRef CAS PubMed.
- Z. Duan and G. Henkelman, Phys. Chem. Chem. Phys., 2016, 5486(18), 5486 RSC.
- W. Yan, S. M. Mahurin, Z. Pan, S. H. Overbury and S. Dai, J. Am. Chem. Soc., 2005, 127(30), 10480 CrossRef CAS PubMed.
- M. J. Walsh, K. Yoshida, A. Kuwabara, M. L. Pay, P. L. Gai and E. D. Boyes, Nano Lett., 2012, 12(4), 2027 CrossRef CAS PubMed.
- Y. Han, R. Ferrando and Z. Y. Li, J. Phys. Chem. Lett., 2013, 5, 131 CrossRef PubMed.
- J. Goniakowski, A. Jelea, C. Mottet, G. Barcaro, A. Fortunelli, Z. Kuntová, F. Nita, A. C. Levi, G. Rossi and R. Ferrando, J. Chem. Phys., 2009, 130(17), 174702 CrossRef PubMed.
- R. Ferrando and A. Fortunelli, J. Phys.: Condens. Matter, 2009, 21(26), 264001 CrossRef PubMed.
- M. Yulikov, M. Sterrer, T. Risse and H. J. Freund, Surf. Sci., 2009, 603(10–12), 1622 CrossRef CAS.
- L. B. Vilhelmsen and B. Hammer, Phys. Rev. Lett., 2012, 108(12), 126101 CrossRef PubMed.
- Z.-P. Liu, S. J. Jenkins and D. A. King, Phys. Rev. Lett., 2005, 94(19), 196102 CrossRef PubMed.
- Y. Chen, P. Hu, M. H. Lee and H. Wang, Surf. Sci., 2008, 602(10), 1736 CrossRef CAS.
- B.-T. Teng, F.-M. Wu, W.-X. Huang, X.-D. Wen, L.-H. Zhao and M.-F. Luo, ChemPhysChem, 2012, 13(5), 1261 CrossRef CAS PubMed.
- Y. Tang, H. Zhang, L. Cui, C. Ouyang, S. Shi, W. Tang, H. Li and L. Chen, J. Power Sources, 2012, 197, 28 CrossRef CAS.
- H. Y. Kim, H. M. Lee and G. Henkelman, J. Am. Chem. Soc., 2012, 134(3), 1560 CrossRef CAS PubMed.
- M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. C, 2014, 118(37), 21438 CrossRef CAS.
- J. Wang, H. Tan, S. Yu and K. Zhou, ACS Catal., 2015, 5(5), 2873 CrossRef CAS.
- K. J. Zhu, Y. J. Yang, J. J. Lang, B. T. Teng, F. M. Wu, S. Y. Du and X. D. Wen, Appl. Surf. Sci., 2016, 387, 557 CrossRef CAS.
- Y. Luo, Z. Chen, J. Zhang, Y. Tang, Z. Xu and D. Tang, RSC Adv., 2017, 7(22), 13473 RSC.
- S. Tosoni and G. Pacchioni, J. Phys. Chem. C, 2017, 121(51), 28328 CrossRef CAS.
- A. Chutia; D. J. Willock and C. R. A. Catlow, Faraday Discussions, The Royal Society of Chemistry, 2018, pp. 123–145 Search PubMed.
- N. J. Castellani, M. M. Branda, K. M. Neyman and F. Illas, J. Phys. Chem. C, 2009, 113(12), 4948 CrossRef CAS.
- M. F. Camellone and S. Fabris, J. Am. Chem. Soc., 2009, 131(30), 10473 CrossRef PubMed.
- N. C. Hernández, R. Grau-Crespo, N. H. de Leeuw and J. F. Sanz, Phys. Chem. Chem. Phys., 2009, 11(26), 5246 RSC.
- M. Marta Branda, N. C. Hernandez, J. F. Sanz and F. Illas, J. Phys. Chem. C, 2010, 114(4), 1934 CrossRef.
- C. Zhang, A. Michaelides, D. A. King and S. J. Jenkins, J. Am. Chem. Soc., 2010, 132(7), 2175 CrossRef CAS PubMed.
- W. J. Zhu, J. Zhang, X. Q. Gong and G. Lu, Catal. Today, 2011, 165(1), 19 CrossRef CAS.
- C. Zhang, A. Michaelides and S. J. Jenkins, Phys. Chem. Chem. Phys., 2011, 13(1), 22 RSC.
- M. Nolan, J. Chem. Phys., 2012, 136(13), 134703 CrossRef PubMed.
- G. M. Wang, J. J. BelBruno, S. D. Kenny and R. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(19), 195412 CrossRef.
- P. Jensen, X. Blase and P. Ordejón, Surf. Sci., 2004, 564(1–3), 173 CrossRef CAS.
- T. P. Hardcastle, C. R. Seabourne, R. Zan, R. M. D. Brydson, U. Bangert, Q. M. Ramasse, K. S. Novoselov and A. J. Scott, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(19), 195430 CrossRef.
- M. Manadé, F. Viñes and F. Illas, Carbon N. Y., 2015, 95, 525 CrossRef.
- D. Appy, H. Lei, C.-Z. Wang, M. C. Tringides, D.-J. Liu, J. W. Evans and P. A. Thiel, Prog. Surf. Sci., 2014, 89(3–4), 219 CrossRef CAS.
- C. Rajesh and C. Majumder, Appl. Surf. Sci., 2019, 469, 917 CrossRef CAS.
- G. M. Wang, J. J. Belbruno, S. D. Kenny and R. Smith, Surf. Sci., 2005, 576(1–3), 107 CrossRef CAS.
- J. Akola and H. Häkkinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(0001), 1 Search PubMed.
- R. Smith, S. D. Kenny, J. J. Belbruno and R. E. Palmer, Chem. Phys. Solid Surf., 2007, 12, 589 CAS.
- J.-P. Jalkanen, M. Halonen, D. Fernández-Torre, K. Laasonen and L. Halonen, J. Phys. Chem. A, 2007, 111(49), 12317 CrossRef CAS PubMed.
- R. Varns and P. Strange, J. Phys.: Condens. Matter, 2008, 20(22), 225005 CrossRef.
- K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(23), 235430 CrossRef.
- M. Amft, B. Sanyal, O. Eriksson and N. V. Skorodumova, J. Phys.: Condens. Matter, 2011, 23(20), 205301 CrossRef PubMed.
- M. Amft, S. Lebègue, O. Eriksson and N. V. Skorodumova, J. Phys.: Condens. Matter, 2011, 23(39), 395001 CrossRef PubMed.
- A. S. Barnard, N. P. Young, A. I. Kirkland, M. A. Van Huis and H. Xu, ACS Nano, 2009, 3(6), 1431 CrossRef CAS PubMed.
- A. S. Barnard, Rep. Prog. Phys., 2010, 73(8), 86502 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. R. Puigdollers, P. Schlexer and G. Pacchioni, J. Phys. Chem. C, 2015, 119(27), 15381 CrossRef CAS.
- R. M. Olson, S. Varganov, M. S. Gordon, H. Metiu, S. Chretien, P. Piecuch, K. Kowalski, S. A. Kucharski and M. Musial, J. Am. Chem. Soc., 2005, 127(3), 1049 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953 CrossRef PubMed.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276(1365), 238 CrossRef.
- J. Hubbard, Proc. R. Soc. A, 1964, 277(1369), 237 CrossRef.
- J. Hubbard, Proc. R. Soc. A, 1964, 281(1386), 401 CrossRef.
- J. Hubbard, Proc. R. Soc. A, 1965, 285(1403), 542 CrossRef CAS.
- J. Hubbard, Proc. R. Soc. A, 1967, 296(1444), 82 CrossRef CAS.
- J. Hubbard, Proc. R. Soc. A, 1967, 296(1444), 100 CrossRef CAS.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(8), R5467 CrossRef CAS PubMed.
- A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, J. Am. Chem. Soc., 2012, 134(21), 8968 CrossRef CAS PubMed.
- C. Loschen, J. Carrasco, K. M. Neyman and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(3), 035115 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21(8), 084204 CrossRef CAS PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97(33), 8617 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115(21), 5461 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34(29), 2557 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37(11), 1030 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44(6), 1272 CrossRef CAS.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- R. L. Johnston, Dalton Trans., 2003, 4193 RSC.
- A. Shayeghi, D. Götz, J. B. A. Davis, R. Schäfer and R. L. Johnston, Phys. Chem. Chem. Phys., 2015, 17(3), 2104 RSC.
- S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113(18), 2091 CrossRef CAS.
- O. D. Häberlen, S.-C. Chung, M. Stener and N. Rösch, J. Chem. Phys., 1997, 106(12), 5189 CrossRef.
- H. Häkkinen, B. Yoon, U. Landman, X. Li, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2003, 107(32), 6168 CrossRef.
- J. Zhao, J. Yang and J. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(8), 085404 CrossRef.
- F. Remacle and E. S. Kryachko, Advances in Quantum Chemistry, Academic Press, 2004, pp. 423–464 Search PubMed.
- E. M. Fernández, J. M. Soler, I. L. Garzón and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(16), 1 CrossRef.
- E. M. Fernández, J. M. Soler, I. L. Garzón and L. C. Balbás, International Journal of Quantum Chemistry, John Wiley & Sons, Ltd, 2005, vol. 101, pp. 740–745 Search PubMed.
- Y. Shen and J. J. Belbruno, J. Phys. Chem. A, 2005, 109(3), 512 CrossRef CAS PubMed.
- F. Remacle and E. S. Kryachko, J. Chem. Phys., 2005, 122(4), 044304 CrossRef CAS PubMed.
- L. Xiao, B. Tollberg, X. Hu and L. Wang, J. Chem. Phys., 2006, 124(11), 114309 CrossRef PubMed.
- S. Bulusu and X. C. Zeng, J. Chem. Phys., 2006, 125(15), 154303 CrossRef PubMed.
- C. Majumder and S. K. Kulshreshtha, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(15), 155427 CrossRef.
- J. Doye and D. Wales, New J. Chem., 1997, 93(22), 16 Search PubMed.
- Y.-K. Han, J. Chem. Phys., 2006, 124(2), 024316 CrossRef PubMed.
- J. P. Chou, C. R. Hsing, C. M. Wei, C. Cheng and C. M. Chang, J. Phys.: Condens. Matter, 2013, 25(12), 125305 CrossRef CAS PubMed.
- M. Boronat, A. Leyva-Pérez and A. Corma, Acc. Chem. Res., 2014, 47(3), 834 CrossRef CAS PubMed.
- G. Bravo-Pérez, I. L. Garzón and O. Novaro, THEOCHEM, 1999, 493(1), 225 CrossRef.
- H. Häkkinen and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(4), R2287 CrossRef.
- H. Grönbeck and W. Andreoni, Chem. Phys., 2000, 262(1), 1 CrossRef.
- J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(3), 035418 CrossRef.
- H. Häkkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89(3), 33401 CrossRef PubMed.
- S. Gilb, P. Weis, F. Furche, R. Alhrichs and M. M. Kappes, J. Chem. Phys., 2002, 116(10), 4094 CrossRef CAS.
- V. Bonačić-Koutecký, J. Burda, R. Mitrić, M. Ge, G. Zampella and P. Fantucci, J. Chem. Phys., 2002, 117(7), 3120 CrossRef.
- A. Roldán, F. Viñes, F. Illas, J. M. Ricart and K. M. Neyman, Theor. Chem. Acc., 2008, 120(4–6), 565 Search PubMed.
- K. Tada, H. Koga, M. Okumura and S. Tanaka, Chem. Phys. Lett., 2018, 701, 103 CrossRef CAS.
- J. Jeon, B. D. Yu and S. Hyun, J. Korean Phys. Soc., 2016, 69(12), 1776 CrossRef CAS.
- R. Coquet, G. J. Hutchings, S. H. Taylor and D. J. Willock, J. Mater. Chem., 2006, 16(20), 1978 RSC.
- C. Kittel, Introduction to solid state physics, Wiley, 2005 Search PubMed.
- B. Chan and W.-L. Yim, J. Chem. Theory Comput., 2013, 9(4), 1964 CrossRef CAS PubMed.
- S. Tosoni and G. Pacchioni, ChemCatChem, 2019, 11(1), 73 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22(2), 022201 CrossRef PubMed.
- S. Giorgio, M. Cabié and C. R. Henry, Gold Bull., 2008, 41(2), 167 CrossRef CAS.
- S. L. Hemmingson, T. E. James, G. M. Feeley, A. M. Tilson and C. T. Campbell, J. Phys. Chem. C, 2016, 120(22), 12113 CrossRef CAS.
- S. L. Hemmingson and C. T. Campbell, ACS Nano, 2017, 11(2), 1196 CrossRef CAS PubMed.
- L. Xiao and L. Wang, Chem. Phys. Lett., 2004, 392(4–6), 452 CrossRef CAS.
- J. Wang and S.-Q. Wang, Surf. Sci., 2014, 630, 216 CrossRef CAS.
- P. Vanýsek, in CRC Handbook of Chemistry and Physics: a ready-reference book of chemical and physical data, ed. W. M. Haynes, CRC Press, 2011 Search PubMed.
Footnotes |
| † All data created during this research is openly available from the University of Cardiff Research Portal at http://doi.org/10.17035/d.2018.0064964028. |
| ‡ Electronic supplementary information (ESI) available: Structures of the supported Au clusters, evaluation of detachment energies and electrostatic potentials, COHP plots, and results of the DFT+U benchmark calculations can be found. See DOI: 10.1039/c9cp03066b |
| This journal is © the Owner Societies 2019 |