Machine learning provides predictive analysis into silver nanoparticle protein corona formation from physicochemical properties

Abstract

Proteins encountered in biological and environmental systems bind to engineered nanomaterials (ENMs) to form a protein corona (PC) that alters the surface chemistry, reactivity, and fate of the ENMs. Complexities such as the diversity of the PC and variation with ENM properties and reaction conditions make the PC population difficult to predict. Here, we support the development of predictive models for PC populations by relating the biophysicochemical characteristics of proteins, ENMs, and solution conditions to PC formation using random forest classification. The resulting model offers a predictive analysis into the population of PC proteins in Ag ENM systems of various ENM sizes and surface coatings. With an area under the receiver operating characteristic curve of 0.83 and an F1-score of 0.81, a model with strong performance has been constructed based upon experimental data. The weighted contribution of each variable provides recommendations for mechanistic models based upon protein enrichment classification results. Protein biophysical properties such as pI and size are weighted heavily. Yet, ENM size, surface charge, and solution ionic strength also prove essential to an accurate model. The model can be readily modified and applied to other ENM PC populations. The model presented here represents the first step toward robust predictions of PC fingerprints.

---

Environmental significance

The fate and transport of engineered nanomaterials (ENMs) in the biota is mediated by proteins that coat ENMs in a protein corona (PC). An array of in-depth experimental studies have demonstrated the importance of the ENM PC for accuracy in prediction of ENM fate and cell uptake; however, the current approaches to PC characterization require costly and time-consuming methods that must be repeated for each new ENM, protein population, and reaction condition. The random forest classification approach developed herein can model PC populations for an array of ENM properties and reaction conditions, while providing insight into feature importance to define which aspects of protein, ENM, and solvent chemistry are the most important to defining the PC population. The model has the potential for prediction of ENM PC fingerprints across a wide range of ENMs, protein populations, and reaction conditions.

Upon introduction to a biological system, engineered nanomaterials (ENMs) interact with biomolecules, resulting in an alteration of the ENM structure, function, and biophysicochemical properties. The diverse mix of biomolecules sorbed to the ENM includes proteins that form a complex protein corona (PC) containing dozens to hundreds of proteins.^1,2 This diverse and dynamic PC establishes a biological identity for the ENM that is distinct from the synthetic properties of the ENM. The PC influences the cell uptake and toxicity of ENMs, and complicates studies aiming to correlate structure–activity relationships between the synthetic properties of ENMs and their observed biological response.^2–6

Despite the importance of the PC in mediating the biological fate and reactivity of ENMs,^5,7,8 little progress has been made in developing a predictive model for PC formation. Establishing correlations between ENM properties, protein characteristics, and interaction conditions is a complex challenge, because of the infinite number of variations within each factor. An array of proteomic studies have reported qualitative trends in ENM corona populations on an ad hoc basis.^1,4,9,10 In assessment of the role of ENM properties in the PC fingerprint, studies agree that ENM size, surface functionalization, and core composition each mediate PC formation. ENM surface coating dictates the functional groups that the proteins interact with at the surface of the ENM and influences long-range protein–ENM interactions that guide PC formation; thus, the ENM surface chemistry often dramatically alters the relative abundance of individual ENM-adsorbed proteins.^7,11–14 Researchers speculate that the curvature of the ENM mediates protein interaction and possibly facilitates the deflection angle between adjacent proteins in the PC.^7,11,14 Other studies have noted that ENM core composition also influences the PC fingerprint.⁷ This is likely because the core composition alters the physicochemical properties of the associated ligands and some PC coatings may displace the associated ligands upon interaction.

To date, modeling efforts for prediction of ENM–biomolecule interactions have focused primarily upon cellular response and toxicity.^15–18 To improve accuracy, there is a movement toward inclusion of PC information in modeling cellular response,^5,7 but the current models for ENM biological response rely upon expansive PC databases.^7,19–22 Despite this recognition that the ENM PC plays a key role in biological response to ENMs,⁵ no modeling efforts to date have focused upon prediction of the PC fingerprint. Instead, authors rely upon time-consuming and expensive proteomic analysis of the ENM PC.

In support of efforts to model biological response to ENMs, we present a model that provides a predictive analysis for PC fingerprints. This approach represents the first step toward enabling modelers and experimentalists to extend studies beyond the currently available PC databases. The importance of expansion beyond the current dataset is a crucial step, especially for environmentally relevant systems. At this point, the majority of PC studies have focused on PCs formed from human blood serum.^4,7,23,24 Yet, accurate models of ENM ecotoxicity and fate will also require studies of the PCs from an array of environmentally relevant organisms beyond the current dataset.^25,26 The development of a predictive and flexible model for a wide range of PCs and ENMs would increase accuracy and reduce the cost of modeling and experimental efforts in ENM biological response. Herein, we describe the development of a model to relate readily available physicochemical characteristics of proteins, ENM properties, and reaction conditions to the formation of a PC population using ensemble machine learning, i.e. random forest classification (RFC).

Database

A previously published database of yeast protein enrichment on silver ENMs was used for the machine learning model because of the ubiquity of yeast in the environment, widespread use of Ag ENMs in consumer products, and extensive set of proteins within the database. The Ag ENM PC database includes 962 unique yeast proteins characterized for enrichment on Ag ENMs as detailed by Eigenheer et al.¹¹ Protein enrichment was classified by the log of the ratio of protein abundance in solution and on Ag ENMs. Enrichment factors that are positive indicate proteins enriched on Ag ENMs or incorporated into the PC and negative enrichment factors indicate enrichment in solution, or lack of incorporation into the PC (non-PC). The database contains a total of 3012 protein enrichment values recorded as rows with 1805 protein particle pairs classified as PC (60%) and 1207 protein particle pairs classified as non-PC (40%). Each protein is represented by 1960 columns composed of categorical and continuous variables and is assigned to a categorical dependent variable that represents the PC or non-PC class. A link to the database is provided in the ESI† (section S.I.4). For each yeast protein evaluated for enrichment, ten biophysicochemical features were recorded, along with two solution features and two Ag ENM characteristics. The experimental variables included in the fourteen training features are listed in Table 1 with the corresponding range of each feature.

Table 1 Domain of physicochemical features within the training and target dataset used for the machine learning effort

Training feature	Range within dataset (method of determination)	Variable type
Protein characteristics
Isoelectric point	3.77 to 12.55	Continuous
Protein weight	6 to 559 kDa	Continuous
Protein abundance	10^−7.40–10^−4.17	Continuous
% positive amino acids	4.72–39.00	Continuous
% negative amino acids	0–33.33	Continuous
% hydrophilic amino acids	13.80–60.66	Continuous
% aromatic amino acids	0–11.86	Continuous
% cysteine	0–7.14	Continuous
InterPro numbers	Range of 1932	Categorical
Enzyme commission number	Range of 7	Categorical
ENM characteristics
ENM size	10 nm and 100 nm	Categorical
ENM surface charge	Positive (+) and negative (−)	Categorical
Solvent characteristics
Cysteine concentration	0, 0.1 mM	Categorical
NaCl concentration	0, 0.8 mM and 3.0 mM	Categorical
Target features
Protein corona (PC) or not (non-PC)	PC or non-PC	Categorical

---

Across the Ag ENM PC database used for this study, the proteins show a Gaussian distribution of enrichment factors. In other words, few proteins are strongly enriched in either the PC or non-PC population. Yet, the distribution of enrichment factors for ENMs varies significantly with each change in ENM or solution property. For example, the distribution of protein enrichment factors for ENMs with positively and negatively charged surface functionalization is strikingly different, indicating the importance of surface coating in formation of the PC fingerprint. Histograms of the logarithmic enrichment factors for all proteins and for each individual sample set are provided and further analyzed in the ESI† (Fig. S.I.1).

In part because of the large number of proteins evaluated, logarithmic enrichment factors and other protein properties are balanced across the experimental database. By comparison to protein features, ENM and solvent properties are under-weighted in the model training features. When collecting PC characterization data, variations in ENM and solvent properties are more difficult to interrogate than protein properties, since study of new ENMs or reaction conditions requires a new protein–ENM reaction and set of proteomics runs.

Model development

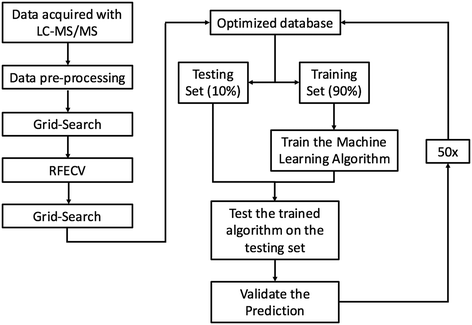
RFC was chosen because it is a robust ensemble learning method that combines multiple decision trees to form a predictive model that is less susceptible to overfitting than a lone decision tree. Although ensemble models have been shown to reduce overfitting,²⁷ RFC can still overfit if each lone decision tree becomes overly complex by growing too deep. To reduce overfitting, each decision tree was grown from a bootstrap sample, and grid search was employed with 5-fold cross-validation to automatically select the model hyper-parameters that minimized the generalization error. Decision trees were not allowed to branch if a node had less than 4 features. Similar approaches have proven successful in analysis of other proteomics datasets²⁸ and other predictions of ENM fate.²⁹ Each decision tree produces a predictive model by splitting data using simple decisional rules.³⁰ RFC then returns the majority vote produced by the group of predictive models. Our implementation of RFC can be summarized into five steps: (1) each protein–particle pair in the database was represented as a vector containing a one hot encoding of each categorical variable, and a normalized representation of each continuous variable as a dimension. (2) 90% of the dataset was randomly partitioned from the database to train the model, leaving a stratified 10% of the data to test the model. (3) 2500 bootstrap samples of size log(n) were drawn from the training partition and a decision tree was grown from each sample. (4) The testing data was fed into the model, and the predictions produced by each tree were aggregated and used to classify proteins as PC or non-PC based on the majority vote between the trees. Majority voting between trees reduces the risk of overfitting as the decision trees containing outliers and noise will be outnumbered by the rest of the decision trees during the voting process. (5) The predictions made by the model were compared to the true PC or non-PC values determined experimentally to validate the model's performance. Steps 1–5 were repeated 50 times, each time with a random dataset partition. Performance metrics are reported as an average over all 50 runs. The machine learning pipeline is summarized in Fig. 1.

Fig. 1 A graphical depiction of the machine learning pipeline. This pipeline describes the operations chained together to produce the predictive model. Data acquired by LC-MS/MS was normalized and non-numerical values were replaced with mean values during the pre-processing step. Grid search was then employed to minimize the generalization error of the model and RFECV was then carried out to optimize the dimensionality of the database. Grid search was then employed again to reduce the generalization error on the optimized database. The model was then run and validated 50 times on randomly selected stratified database partitions to produce performance metrics.

To remove features with no predictive value from the dataset, recursive feature elimination and cross-validation (RFECV) was employed. Although originally included in the model in response to suggestions from Rihn and Joubert,³¹ all 1936 protein InterPro numbers were eliminated from the model by the RFECV analysis. With this elimination, data dimensionality was reduced from 1960 to 24 dimensions. Enzyme commission numbers were also eliminated from the model through RFECV analysis, reducing the database to a final dimensionality of 17 dimensions that include biophysicochemical features of the proteins, ENMs, and solvent (vide infra). A correlation plot (Fig. S.I.2†) was used to investigate linear feature correlation. A threshold of |R| ≤ 0.75 was chosen to discriminate correlated vs. non-correlated variables. As an example of correlated variables, protein length and protein weight were highly correlated, leading to the exclusion of protein length from the RFC analysis (R = 1.0).

Model validation

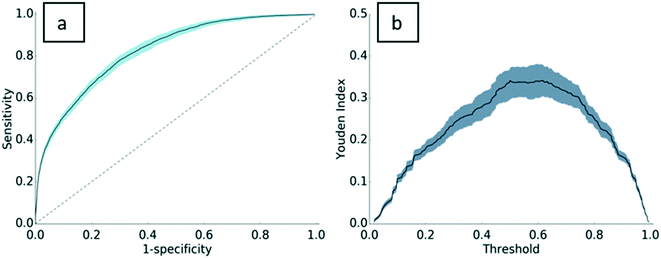
Standard machine learning metrics were used to validate the model, including precision, recall, accuracy, and the F1-score. Precision and recall are widely used performance metrics that offer a well-rounded evaluation of predictive performance. Model precision is 0.76 ± 0.02, indicating that 76% of the PC assignments made by the model were truly PC proteins. Recall is 0.86 ± 0.03. In other words, 86% of the PC proteins in the dataset were predicted as PC. The F1-score, the harmonic mean of precision and recall, is 0.81 ± 0.02 for this model. With an accuracy of 0.75 ± 0.02, the model has good predictive power for both PC proteins and non-PC proteins. A Y-randomization test was carried out to ensure the robustness of the predictive model. After one round of randomization, the accuracy of the model fell to 0.54, implying that the model is robust to perturbations in the dependent variable vector. A link to the results of the Y-randomization test is provided in the ESI† (section S.I.4).

To further validate the model, a receiver operating characteristic (ROC) curve was plotted with 302 decisional thresholds based on the model's outputted probability of binding (Fig. 2a). Generally, the convex shape of the ROC curve indicates a higher true positive rate at the expense of a relatively lower false positive rate. In other words, the likelihood of correctly classifying a protein as PC is high, while incorrect classifications of PC are low. The area under the receiver operating curve (AUROC) for the resulting model is generally considered indicative of the predictive power of the model^32–34 and can be interpreted as the model's ability to correctly classify proteins as PC or non-PC. With an AUROC of 0.83, the model performs significantly higher than the value of 0.5 for a random guess curve. Perhaps more specifically, AUROC scores are evaluated relative to the complexity of the classification task. As the first to test this approach on ENM PC predictions, this work establishes a baseline of AUC performance for future predictive models. To provide a comparative metric for a problem of similar complexity, protein–protein binding predictions, Sain et al.³⁵ reported an AUROC score of 0.7, which is typically considered strong for problems of this complexity. In relation to this, the Youden index defines the threshold in the ROC curve that gives the best performance (Fig. 2b). The threshold where the Youden index is maximum is 0.5. In other words, our ensemble method performs as expected, where most proteins are properly assigned as PC when 50% or more decision trees assign the protein as PC.

Fig. 2 Receiver operating curve (a) and Youden index curve (b) for the final model. The receiver operating curve for the model (a) is shown with a solid line, error bars are in light blue, and the random guess curve is shown with a dashed line. The area under the receiver operating curve (AUROC) is 0.83. The Youden index curve (b) for the model is shown with a solid black line and error bars in grey-blue.

Majority voting results in a probability of PC and non-PC between 0.5–1.0 for each class. When using the model, this probability is a metric of model confidence. Proteins classified by the model with a probability of their assigned class between 0.5–0.6 were properly assigned 55% of the time; in contrast, proteins classified by the model with a probability of their assigned class between 0.9–1.0 were properly assigned 95% of the time. This demonstrates a level of unreliability when predictions fall in the 0.5–0.6 percent range. In our dataset, 22% of predictions fell within this range, when only predictions with a probability above 0.6 were considered. On average, the model improved to an accuracy of 0.81, F1-score of 0.85, recall of 0.91, precision of 0.8, and AUROC of 0.86. Predictions with a probability that falls in the 0.5–0.6 range are not considered reliable, as summarized in Table 2. All model predictions along with their assigned probability are provided in the ESI† (S.I.4).

Table 2 Model accuracy in different likelihood ranges

Likelihood of correct prediction	Accuracy	Percentage of predictions that fall into the likelihood range
0.9–1.0	0.95	0.21
0.8–0.89	0.87	0.19
0.7–0.79	0.74	0.2
0.6–0.69	0.68	0.2
0.5–0.59	0.54	0.2

---

Although RFC is a robust learning method, the algorithm cannot extrapolate beyond the conditions under which it is trained. We have assumed that our experimental database is representative of the true distribution of enrichment factors over the particles and proteins tested, and that the features we selected for training are useful. Due to the size and quality of our database, as well as the predictive power of our model, we believe these assumptions to be valid. In selecting features, we chose robust and readily available features, from either a database (e.g. protein biophysical features) or routine analyses (e.g. particle size). Yet, the model is restricted to the applicability domain of yeast proteins, ENM sizes, ENM surface functionalities, and solvent conditions which are detailed in Table 1.

Features not included in the database may also play a role in the formation of the PC fingerprint. This includes features that are difficult to measure in complex mixtures, such as protein–protein interactions and exchange of the ENM surface coating. It also includes features simply not evaluated in this database, including the ENM shape and core composition, or reaction conditions such as temperature or pH. Perhaps, most notably, ENMs with a hydrophobic coating were not evaluated due to solubility issues making the importance of hydrophobicity difficult to evaluate. In the future, expansion of the database and corresponding features in the training set will strengthen the model and expand its applicability.

Insights into PC fingerprint formation

RFC is useful because it can provide a measure of hierarchical variable importance. Feature importance, as shown in Fig. 3, gives insight into the variables of importance in predicting and controlling ENM–protein interactions.

Fig. 3 Weighted importance of each feature included in the final model. Protein features are shown in green, ENM features in blue, and solvent features in red. Error bars are shown with black lines.

The broad trend indicates that protein biophysical characteristics are more strongly weighted than solvent and ENM characteristics within the model. Although it is tempting to conclude that protein characteristics dominate PC formation, the comparative sample size for ENM and solvent characteristics is simply too small to derive conclusions across protein, ENM, and solvent features. The dataset is simply overwhelmed by proteins and protein biophysical characteristics. The relative importance within each of these three feature sets is, however, useful to compare.

Among protein features, factors contributing to protein charge, including pI and percent of positively and negatively charged amino acids, together make up nearly 50% of the feature importance. This reinforces earlier studies qualitatively reporting the importance of protein charge in PC formation.^11,24 As a long-range interaction, electrostatics must drive initial protein–ENM interactions and, as this data suggests, play a role in the stability of the hard corona. The slightly higher weight of salt concentration over cysteine within solvent features again points to the importance of electrostatics in PC formation.

Across the ENM features examined, ENM size and surface charge are weighted nearly evenly. The importance of size is consistent with other studies.^7,9,36 Although it is somewhat surprising that size plays a key role in PC formation, the increased curvature on small particles impacts the geometry of available binding surfaces, as well as the reactivity of ENM surface ligands. As reported elsewhere, there is some selectivity for protein molecular weight within the PC.^7,11 This data supports correlations between ENM and protein sizes and contributes to the hypothesis that decreased curvature of large ENMs may more easily support larger proteins.

The other protein features that play a role in the model include the percentages of hydrophilic and aromatic amino acids, along with the percentage of cysteine contributing at nearly 25%. Due to the instability of hydrophobic ENMs in solution, our dataset excluded hydrophobic ENMs, possibly resulting in an underrepresentation of the role of hydrophobicity in PC formation.

As publicly available databases with quantitative protein enrichment data expand, the model can be readily tested on PC populations in other systems. Application of the model to a broadened array of ENMs and reaction conditions will refine the model and provide additional insight into PC formation. Indeed, application to new datasets will enhance insights into the contribution of factors such as hydrophobicity, ENM characteristics, and solvent properties in the model.

Conclusions

A machine learning model that predicts the PC population using protein biophysicochemical characteristics, basic ENM properties, and solution conditions was developed. The model was proven robust with a strong AUROC and Youden index evaluation, and has demonstrated high precision and recall. A key feature of the machine learning method is the ability to provide a weighted list of feature importance in the model, and suggest factors mediating protein and ENM charge as the most important, followed by secondary features such as protein and ENM size.

The results demonstrate that an applied machine learning approach can enable the prediction of a PC population with routine experimental data and easily accessed protein biophysical characteristics. Moreover, the model has proven robust without mechanistic insights or experimentally complex variables such as protein–protein interaction maps. Since it relies upon routinely collected PC data, the model can be readily applied to new systems for refinement and to gain new insights into PC formation. As we work towards a strong and flexible model for PC fingerprints, we may eventually be able to save the time and costs of expensive experimental characterization of PCs and enable complete modeling from ENM properties to PC formation and subsequent ENM biological effects.

Methods section

Database development

Protein abundance and enrichment factors were obtained from Eigenheer et al.¹¹ For each protein identified by MS proteomics, biophysical characteristics were obtained from UniProt,³⁷ including molecular weight, pI, enzyme commission numbers,³⁷ and amino acid sequence. Interpro numbers³⁸ were also included when available for a protein. ENM characteristics were assigned based upon experimental characterization. This includes ENM size rounded to 10 or 100 nm and zeta-potential assigned as a binary (either negative or positive).¹¹ Finally, solvent conditions were summarized as two categorical variables. The first variable levels were either 0, 0.8, or 3.0 mM NaCl, while the second variable levels were set at either 0 or 0.1 mM cysteine.

Random forest regression and classification

RFC was chosen as the predictive algorithm due to its relative insensitivity to outliers and noise, and ability to internally produce a list of feature importance.^30,39 Python and the Scikit-learn package were chosen to employ RFC to generate the machine learning model and were derived from the Goldberg et al. model to predict ENM transport behavior.²⁹ Source code is provided at this link <https://github.com/mfindlay23/ENM-Protein-Predictor>.

Dimensionality reduction

To remove noise from the dataset, recursive feature elimination and cross-validation was employed (RFECV). RFECV is a popular dimensionality reduction algorithm that recursively constructs the model, chooses the least important variable (based on mean decrease impurity), removes the variable, and reconstructs the model. At each iteration, 5-fold cross-validation was conducted to determine the predictive power of the model. The iteration with the best power contains the optimum number of features to train the model.

Hyper-parameter tuning

To reduce overfitting, grid search and cross-validation were employed to automatically select the hyper-parameters that reduced the generalization error of the model. Several hyper-parameters limiting the growth of each decision tree were inserted into a grid. Each combination of hyper-parameters was run and validated with 5-fold cross-validation. The hyper-parameters that offered the best generalization error were used to grow the final model.

Validation of the model

To give a clear and unbiased validation of our model, several validation metrics common in the fields of biostatistics and machine learning were employed. These metrics include precision, recall, F1-score, area under the receiver operating characteristic curve (AUROC), and accuracy.^32–34,40 In a binary decision problem, a classifier labels data as either positive or negative. In this case, positive means that a protein will be part of the PC, and negative means that the protein will be non-PC. This gives our classifier four possible outcomes: (1) a protein is properly classified as PC (true positive), (2) a protein is improperly classified as PC (false positive), (3) a protein is properly classified as non-PC (true negative), and (4) a protein is improperly classified as non-PC (false negative). These four possible outcomes can be counted and summarized using our validation metrics. Recall is the number of true positives divided by the total PC-proteins in the dataset. Precision is the number of true positives divided by the sum of true positives and false positives produced by the model. The F1-score is simply the harmonic mean of precision and recall. Accuracy is the number of true positives and true negatives divided by the total number of classifications made by the model. The ROC curve shows how the number of true positives varies with the number of false positives produced by the model at different cutoffs. The AUROC is the area under the ROC curve, and is typically reported as it gives a normalized score between 0 and 1 produced by the ROC curve.

Comparison to other models

Support vector machines (SVMs) and logistic regression (LR) were employed along with the RFC algorithm on the dataset to produce a well-rounded understanding of the predictive power that could be generated from the database. SVM and LR were chosen due to their extensive use in the fields of biostatistics and machine learning. SVM was employed for classification with a radial basis function kernel, and binary LR was fit with a logit model. Both models performed well on the dataset suggesting that future work may benefit from the use of several machine learning algorithms.

Assessing feature importance with random forests

A measure of variable importance was calculated as the mean decrease impurity in the 2500 implemented decision trees.²⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Research reported in this publication was supported by the National Institute of Environmental Health Sciences of the National Institutes of Health awarded to K. E. W. under award number R15ES025929. M. R. F. and D. N. F. were supported by the Roelandts Grant Program in Science and Technology for Social Benefit, Xilinx, and the ALZA Corporation Science Scholar program (D. N. F.).

References

1. I. Lynch, T. Cedervall, M. Lundqvist, C. Cabaleiro-Lago, S. Linse and K. A. Dawson, Adv. Colloid Interface Sci., 2007, 134–135, 167–174.
2. D. Walczyk, F. B. Bombelli, M. P. Monopoli, I. Lynch and K. A. Dawson, J. Am. Chem. Soc., 2010, 132, 5761–5768.
3. A. Albanese, C. D. Walkey, J. B. Olsen, H. Guo, A. Emili and W. C. W. Chan, ACS Nano, 2014, 8, 5515–5526.
4. C. D. Walkey and W. C. W. Chan, Chem. Soc. Rev., 2012, 41, 2780–2799.
5. S. Lin, M. Mortimer, R. Chen, A. Kakinen, J. E. Riviere, T. P. Davis, F. Ding and P. C. Ke, Environ. Sci.: Nano, 2017, 4, 1433–1454.
6. M. Mahmoudi, I. Lynch, M. R. Ejtehadi, M. P. Monopoli, F. B. Bombelli and S. Laurent, Chem. Rev., 2011, 111, 5610–5637.
7. C. D. Walkey, J. B. Olsen, F. Song, R. Liu, H. Guo, D. W. H. Olsen, Y. Cohen, A. Emili and W. C. W. Chan, ACS Nano, 2014, 8, 2439–2455.
8. K. Hamad-Schifferli, Nanomedicine, 2015, 10, 1663–1674.
9. N. Durán, C. P. Silveira, M. Durán and D. S. T. Martinez, J. Nanobiotechnol., 2015, 13, 55.
10. D. Docter, D. Westmeier, M. Markiewicz, S. Stolte, S. K. Knauer and R. H. Stauber, Chem. Soc. Rev., 2015, 44, 6094–6121.
11. R. Eigenheer, E. R. Castellanos, M. Y. Nakamoto, K. T. Gerner, A. M. Lampe and K. E. Wheeler, Environ. Sci.: Nano, 2014, 1, 238–247.
12. C. D. Walkey, J. B. Olsen, H. Guo, A. Emili and W. C. W. Chan, J. Am. Chem. Soc., 2012, 134, 2139–2147.
13. A. Gessner, A. Lieske, B. R. Paulke and R. H. Muller, Eur. J. Pharm. Biopharm., 2002, 54, 165.
14. M. Lundqvist, J. Stigler, G. Elia, I. Lynch, T. Cedervall and K. A. Dawson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14265.
15. X. Bai, F. Liu, Y. Liu, C. Li, S. Wang, H. Zhou, W. Wang, H. Zhu, D. A. Winkler and B. Yan, Toxicol. Appl. Pharmacol., 2017, 323, 66–73.
16. R. Chen and J. E. Riviere, Biological Surface Adsorption Index of Nanomaterials: Modelling Surface Interactions of Nanomaterials with Biomolecules, Springer International Publishing, 2017, pp. 207–253.
17. V. Chandana Epa, F. R. Burden, C. Tassa, R. Weissleder, S. Shaw and D. A. Winkler, Nano Lett., 2012, 12, 5808–5812.
18. N. Basant and S. Gupta, Nanotoxicology, 2017, 11, 20–30.
19. R. Liu, W. Jiang, C. D. Walkey, W. C. W. Chan and Y. Cohen, Nanoscale, 2015, 7, 9664–9675.
20. S. Palchetti, L. Digiacomo, D. Pozzi, G. Peruzzi, E. Micarelli, M. Mahmoudi, G. Caracciolo, W. Gruissem, P. Zimmermann and J. T. Eppig, Nanoscale, 2016, 8, 12755–12763.
21. J. Kuruvilla, A. P. Farinha, N. Bayat, S. Cristobal, A. Musyanovych, J. Kuharev, K. Landfester, H. Schild, O. Jahn, S. Tenzer, V. Mailander, R. D. Smith, J. G. Pounds, T. Liu, F. Reisinger, D. Rios, R. Wang, H. Hermjakob, J. P. Albar, S. Martinez-Bartolome, R. Apweiler, G. S. Omenn, L. Martens, A. R. Jones and H. Hermjakob, Nanoscale Horiz., 2017, 2, 55–64.
22. E. Papa, J. P. Doucet, A. Sangion and A. Doucet-Panaye, SAR QSAR Environ. Res., 2016, 27, 521–538.
23. R. M. Pearson, V. V. Juettner and S. Hong, Front. Chem., 2014, 2, 108.
24. S. Tenzer, D. Docter, J. Kuharev, A. Musyanovych, V. Fetz, R. Hecht, F. Schlenk, D. Fischer, K. Kiouptsi, C. Reinhardt, K. Landfester, H. Schild, M. Maskos, S. K. Knauer and R. H. Stauber, Nat. Nanotechnol., 2013, 8, 772–781.
25. J. Gao, L. Lin, A. Wei and M. S. Sepúlveda, Environ. Sci. Technol. Lett., 2017, 4, 174–179.
26. Y. Hayashi, T. Miclaus, S. Murugadoss, M. Takamiya, C. Scavenius, K. Kjaer-Sorensen, J. J. Enghild, U. Strähle, C. Oxvig, C. Weiss, D. S. Sutherland, M. D. Mason, M. Selzner, M. A. Ostrowski, O. A. Adeyi, A. Zilman, I. D. McGilvray and W. C. W. Chan, Environ. Sci.: Nano, 2017, 4, 895–906.
27. T. Dietterich, in The handbook of brain theory and neural networks, ed. M. A. Arbib, MIT Press, 2nd edn, 2003.
28. A. L. Swan, A. Mobasheri, D. Allaway, S. Liddell and J. Bacardit, OMICS, 2013, 17, 595–610.
29. E. Goldberg, M. Scheringer, T. D. Bucheli, K. Hungerbühler, C.-W. Lam, D. B. Warheit, A. B. Santamaria, M. J. McLaughlin, J. R. Lead, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Environ. Sci.: Nano, 2015, 2, 352–360.
30. L. Breiman, Mach. Learn., 2001, 45, 5–32.
31. B. H. Rihn and O. Joubert, ACS Nano, 2015, 9, 5634–5635.
32. D. M. W. Powers, J. Mach. Learn. Tech., 2011, 2(1), 37–63.
33. J. Davis and M. Goadrich, in Proceedings of the 23rd international conference on Machine learning - ICML ‘06, ACM Press, New York, New York, USA, 2006, pp. 233–240.
34. M. H. Zweig and G. Campbell, Clin. Chem., 1993, 39(4), 561–577.
35. N. Sain, G. Tiwari and D. Mohanty, Sci. Rep., 2016, 6, 31418.
36. Z. Hu, H. Zhang, Y. Zhang, R. Wu and H. Zou, Colloids Surf., B, 2014, 121, 354–361.
37. U. Consortium, Nucleic Acids Res., 2017, 45, D158–D169.
38. R. D. Finn, T. K. Attwood, P. C. Babbitt, A. Bateman, P. Bork, A. J. Bridge, H.-Y. Chang, Z. Dosztányi, S. El-Gebali, M. Fraser, J. Gough, D. Haft, G. L. Holliday, H. Huang, X. Huang, I. Letunic, R. Lopez, S. Lu, A. Marchler-Bauer, H. Mi, J. Mistry, D. A. Natale, M. Necci, G. Nuka, C. A. Orengo, Y. Park, S. Pesseat, D. Piovesan, S. C. Potter, N. D. Rawlings, N. Redaschi, L. Richardson, C. Rivoire, A. Sangrador-Vegas, C. Sigrist, I. Sillitoe, B. Smithers, S. Squizzato, G. Sutton, N. Thanki, P. D. Thomas, S. C. E. Tosatto, C. H. Wu, I. Xenarios, L.-S. Yeh, S.-Y. Young and A. L. Mitchell, Nucleic Acids Res., 2017, 45, D190–D199.
39. L. Breiman, Classification and regression trees, Chapman & Hall, 1993.
40. P. Xu, X. Liu, D. Hadley, S. Huang, J. Krischer and C. J. Beam, J. Proteomics Bioinf., 2014, S9, 006.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7en00466d

---