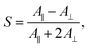Supramolecular control of liquid crystals by doping with halogen-bonding dyes

Abstract

Introducing photochromic or polymeric dopants into nematic liquid crystals is a well-established method to create stimuli-responsive photonic materials with the ability to “control light with light”. Herein, we demonstrate a new material design concept by showing that specific supramolecular interactions between the host liquid crystal and the guest dopants enhance the optical performance of the doped liquid crystals. By varying the type and strength of the dopant–host interaction, the phase-transition temperature, the order parameter of the guest molecules, and the diffraction signal in response to interference irradiation, can be accurately engineered. Our concept points out the potential of supramolecular interactions in liquid-crystal photonics, being valuable for optimizing the design of dye-doped functional liquid-crystalline systems.

---

Introduction

Nematic liquid crystals (LCs) are a promising class of materials for photonic applications.^1–3 Their potential largely stems from their efficient reorientational response to external stimuli. For instance, under light irradiation the LC molecules with strongly anisotropic optical polarizability experience light-induced torque that tends to reorient them in the direction of incident light polarization.⁴ It was shown in the 1990s that by doping nematic LCs with a small amount of light-absorbing dyes, the light-induced torque can be enhanced by orders of magnitude, yielding a new class of photonic materials with extremely high optical nonlinearity.^5,6 Thereafter, several strategies to further increase the nonlinearity, based, e.g., on incorporation of photochromic or polymeric dopants, controlling the surface anchoring, and polymer stabilization, have been proposed.^7–10 The absorption-enhanced optical nonlinearity has been associated with different intermolecular interactions of the host LC with photoexcited versus ground-state dopants,^11,12 yet the detailed role of dopant–host intermolecular interactions on the optical performance of nematic LCs is not clear. For organic materials to redeem their promise in, e.g., photonic computing, it is imperative to design materials whose optical performance can be controlled with compact and inexpensive light sources.

Typical nematic LC molecules, such as 4-cyano-4′-pentylbiphenyl (5CB, Fig. 1a), contain polar substituents that can take part in noncovalent bond formation if the dopant molecules contain complementary functional groups.¹³ Such specific noncovalent interactions have been used to construct supramolecular LC dimers or polymeric complexes from non-liquid-crystalline building blocks.^14,15 In dye-doped LCs, on the other hand, typically less than 1 mol% concentration of the photoactive dopant is sufficient to significantly enhance the optical response,^5,16 and the effect of specific noncovalent interactions between dopants and host LC in such systems has largely been overlooked. The most important studies along these lines have been carried out by Marrucci and co-workers, who have investigated a series of anthraquinone-doped nematic LCs and proposed that hydrogen bonding (HB) and dipole–dipole interactions between photoexcited dye molecules and nematic host play a significant role in the optical torque responsible for the photoinduced reorientation.^17,18 We hypothesize that the photoresponse of dye-doped nematic LCs is also affected by ground-state specific noncovalent interactions, such as halogen bonding, between the dopant molecules and the LC host.

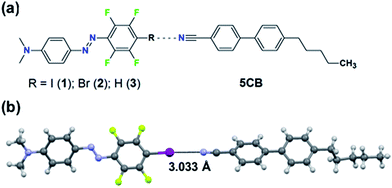Fig. 1 (a) Chemical structures of the studied systems. (b) Crystal structure of the halogen-bonded complex between 1 and 5CB. For clarity, only the most populated conformer of each molecule is shown.

Halogen bonding (XB) is an attractive noncovalent interaction between an electrophilic region associated with a halogen atom in a molecule and a nucleophilic site.¹⁹ It bears some unique characteristics compared to other noncovalent interactions, such as high directionality and adjustable interaction strength via substitution (for instance molecules 1vs.2 in Fig. 1a). Due to its high directionality and tunablility, XB is an effective tool for crystal engineering,^20,21 construction of supramolecular LCs^22–25 and building model systems for understanding what roles weak supramolecular interactions play in functional stimuli-responsive materials. For instance, using molecular libraries of azobenzene compounds, we have pinpointed the favourable role of XB when designing high-performance supramolecular polymers for light-induced surface patterning and optical poling.^26,27 Given (i) the success of XB in the aforementioned applications, and (ii) the fact that the cyano group of 5CB can act as an acceptor for XB and for HB,^28,29 halogen-bonding dyes provide an excellent platform for studying how systematically changing the substitution of one atom in the dopant affects the properties of the doped LC system.

In this article, we demonstrate that specific supramolecular interactions between the dopant molecules and the host LC indeed provide a pathway towards enhanced photoresponse of doped LCs. The study is conducted using three structurally similar dyes with different noncovalent-bond-donating capabilities (molecules 1–3 in Fig. 1a), allowing us to identify that due to its high directionality, halogen-bonded dopants are particularly promising for enhancing the photoresponse of dye-doped liquid crystals.

Results and discussion

The material systems under investigation comprise a small fraction (0.3, 0.5, 1.0 mol%) of the azobenzene molecules 1–3 doped into 5CB (Fig. 1a). The lone pair of electrons of the cyano group of 5CB may act as an acceptor for both XB (with the iodine and bromine atoms of molecules 1 and 2, respectively) and HB (with the para-hydrogen of molecule 3). Density functional theory calculations (see the ESI† for further details), minimizing the energy of the molecules 1–3 in the proximity of 4-cyano-4′-methylbiphenyl (1CB; used as a model compound for 5CB), indicate the existence of XB/HB in the material systems. The interaction energy of the optimized linear supramolecular complexes between the dopants and 1CB evolves in the order 1 (3.09 kcal mol⁻¹) > 3 (2.17 kcal mol⁻¹) > 2 (1.53 kcal mol⁻¹). As pointed out previously, a region of positive electrostatic potential is localized in 1 and 2 along the extension of C–X bond (X = I, Br), whereas that for 3 is essentially hemispherical around the H atom.^26,30,31 Therefore, this set of molecules allows us to control both the interaction strength (1vs.2) and the directionality (2vs.3) while keeping structural, spectral, and physical changes to a minimum.

Experimental evidence of the XB between 5CB and 1 was provided by cocrystallization experiments. The cocrystals were grown from a chloroform solution containing 5CB:1 in a 5 : 1 molar ratio and analyzed with a single-crystal X-ray diffractometer. The crystal structure, shown in Fig. 1b, confirms that the nitrogen atom of the cyano group of 5CB acts as an XB acceptor towards the iodine atom of compound 1. The N⋯I distance in such XB-adduct is 3.033(3) Å, which correlates well with the optimized value of 3.068 Å obtained from DFT calculations, and corresponds to about 86% of the sum of van der Waals radii.³² The C–I⋯N angle is 177.1(5)° or 177.4(7)° for the two disordered populations found in the crystal structure, which is well in line with the calculated value of 179.2° and the high directionality of the halogen bond.³¹ Further details on the crystallographic characterization are given in the ESI.† Complementary support for XB between 5CB and 1 (at 1 mol% doping concentration) was obtained by following the cyano stretching vibration at 2225 cm⁻¹ (see Fig. S2†), which shifted towards higher wavenumbers upon halogen bonding, as expected based on earlier observations.^23,29 The infrared spectroscopic studies also confirmed that 1 is well-dispersed in 5CB at 1 mol% concentration, since the spectrum of 1 in 5CB differs from the spectrum of pure crystalline 1, as shown in Fig. S3.† For molecules 2 and 3, while also well dispersed in 5CB, the intermolecular interactions were too weak to be detected via infrared spectroscopy, and no cocrystals could be grown.

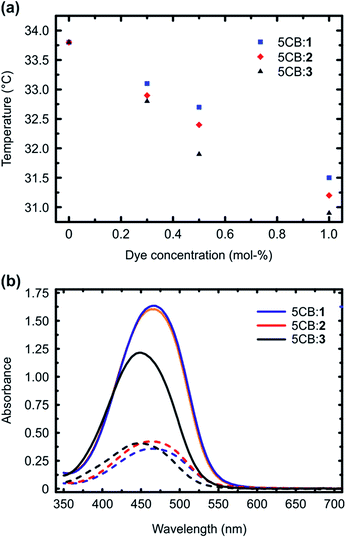
Fig. 2a presents the isotropic-to-nematic phase transition temperatures of the studied mixtures as a function of dye concentration (0.3–1 mol%), obtained with a differential scanning calorimeter (DSC) using a cooling rate of 1 °C min⁻¹. The clearing points, obtained upon 1 °C min⁻¹ heating, are given in the ESI (Fig. S4†), and they follow similar trend. The reported values are obtained by averaging over the second and third cooling/heating scans. Essentially similar transition temperatures were obtained also when determining the phase transitions with a polarized optical microscope, confirming the reliability of the reported values. The phase-transition temperatures systematically decreased as a function of dye concentration for all the systems under investigation. This is expected, since the azobenzenes act as non-mesogenic dopants that destabilize the LC phase. More interestingly, however, systematic difference was observed among the three dopant molecules, and 1, forming the strongest supramolecular bond with 5CB, decreased the phase transition temperatures systematically less than 2 and 3. As shown by previous studies, many different types of interactions between the dopant molecules and the LC host contribute to the final stabilization/destabilization of the LC phases.^33–36 In the present case, however, the molecules are similar in their shape, size, and ground-state dipole moment (computed values are 7.1 D (1), 7.4 D (2), and 6.2 D (3); as a reference the computed dipole moment for 5CB is 6.2 D, being close to that of the dopants). Therefore, we can assume that the effects arising from dipole–dipole interactions, arene–arene interactions, as well as purely steric distortion of the LC state are comparable. In fact, as 1 is capped with the largest atom (iodine), it could be considered sterically the most destabilizing,³³ but despite this, it provides the smallest decrease in the isotropic-to-nematic phase transition temperature in the concentration range studied. This indicates that changing the type and the strength of supramolecular bonding between the dopant and 5CB plays an important role in dictating the properties of the doped LC.

Fig. 2 (a) Isotropic-to-nematic phase transition temperatures as a function of dye doping for the 5CB:x systems, as determined by DSC. (b) Polarized absorption spectra of the 5CB:x systems with 1 mol% dye concentration in planar LC cells with 10 μm thickness, illustrating that the order parameter of the dyes in 5CB develops in the order 1 > 2 > 3. The solid and dashed lines correspond to spectra measured along and perpendicular to the LC director, respectively.

We subsequently studied the doped LCs in planar cells (thickness 10 μm), in order to understand whether the dopant:5CB noncovalent interactions affect the order parameter of the azobenzenes in the homogeneously aligned 5CB matrix. The polarized absorption spectra shown in Fig. 2b (shown for 1 mol% dopant concentration only) provide further proof on the significance of halogen bonding in doped LCs. The order parameter values, determined from polarized absorption spectra using the formula

where A_‖ and A_⊥ are the absorbances in the direction parallel and perpendicular to the LC director, respectively, show a clear trend, evolving in the order 1 (0.54 ± 0.02) > 2 (0.48 ± 0.02) > 3 (0.38 ± 0.02). These values are obtained by averaging over at least 10 independent measurements, conducted from four different LC cells (two with 0.5 mol% and two with 1.0 mol% dopant concentration for each molecule; the doping concentration did not affect the order parameter). The trend in order parameters suggests that by increasing the halogen-bond strength (1vs.2) the dopants accommodate themselves better along the 5CB director, and indicate also that the directionality of noncovalent interaction (2vs.3, XB vs. HB) is important in dictating the alignment order of dopants in the nematic host.

Although the calculated noncovalent interaction is stronger for 3 than for 2, the phase transition temperatures and the order parameter are higher for 2, indicating that 3 destabilizes more the LC phase. The lower order parameter of 3 (Fig. 2b) may be to a minor extent affected by presence of small amount of residual cis-isomers, since the thermal half-life of 3 in 5CB was observed to be at least by a factor of 5 longer than that for 1 and 2 (Fig. S5†). Most of all, however, we attribute the experimental findings to low linearity of the 5CB:3 complex, which has two nonlinear minimum conformations in addition to the linear one similar to that shown in Fig. 1b for 1, associated with the larger extension of the positive electrostatic potential around H as compared to X. Such conformations originate from concomitant formation of C–H⋯N and C–H⋯F hydrogen bonds, the latter involving one of the fluorine atoms adjacent to the para-hydrogen of 3 (see ESI for more detailed discussion†). Their interaction energy is 2.45 kcal mol⁻¹. We believe the competition between the almost isoenergetic conformational minima to be the predominant factor in explaining the differences of 5CB:3 as compared to 5CB:1/2.

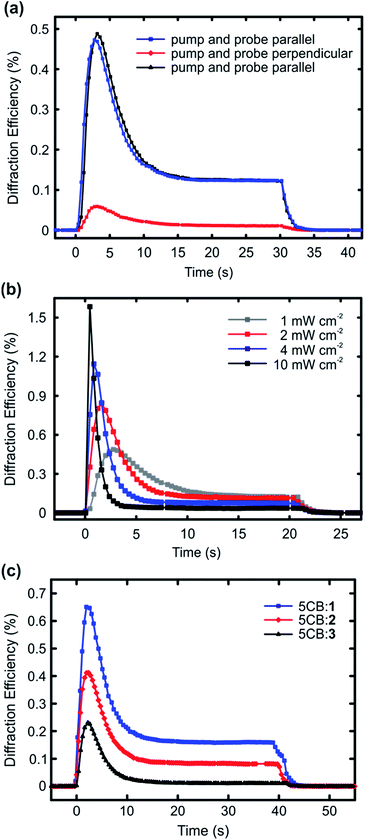
The results presented in Fig. 2 highlight that halogen bonding makes a difference in (i) the extent to which the dopant molecules destabilize the LC phase, and (ii) how efficiently they align themselves along the LC director. Based on these observations, it is reasonable to assume that halogen bonding would also enhance the photoresponse of the doped nematic LCs. To study this, we carried out diffraction experiments from planar LC cells upon interference irradiation. The interfering beams (488 nm, polarization along the LC director; setting the polarization of the interfering beams perpendicular to the LC direction yielded no measurable diffraction signal) were incident on the samples symmetrically, the interference period was set to either 40 μm (Fig. 3a and b) or 30 μm (Fig. 3c), and the intensity of each of the interfering beams was 1 mW cm⁻², unless stated otherwise. The diffraction was measured in the first order with a nonresonant probe beam from a He-Ne laser (633 nm), with polarization coinciding to that of the interfering beams. The used pump–probe polarization combination was chosen because it yielded the largest diffraction efficiency, as illustrated in Fig. 3a using the 1 mol% 5CB:1 sample as an example. This can be explained as follows: at the positions of the interference maxima, light absorption and subsequent photoisomerization create disorder into the molecular alignment, thereby reducing the refractive index n in the direction parallel to LC director in the areas where light intensity is the highest. This leads to a significant refractive-index contrast between the irradiated areas (lower n) and the non-irradiated areas (higher n). If the probe polarization is set perpendicular to the polarization of the interfering beams (and the LC director), the situation is reversed, and the irradiated (disordered) areas exhibit higher n than the non-irradiated (ordered) areas, yet the refractive-index contrast is smaller and the diffraction signal weaker (red curve). Fig. 3a also shows that the gratings, which are dynamic and disappear when the pump beams are turned off, can be re-written several times on the same spot with identical diffraction efficiency (black and blue curves). Fig. 3b presents the intensity dependence of the diffracted signal for the 1 mol% 5CB:1 sample. As can be seen, the maximum diffraction efficiency increases monotonically with light intensity, in a comparable manner as reported earlier by Ouskova et al.³⁶ Detailed analysis of the diffraction kinetics and its intensity dependence are out of the scope of this work, yet to facilitate comparison between 1–3, we decided to work at low-intensity regime (1 mW cm⁻²) where the kinetics is slower.

Fig. 3 (a) The effect of pump–probe polarization combination on the diffraction efficiency of 1 mol% 5CB:1 sample (488 nm; period: 40 μm; intensity: 1 mW cm⁻² for both interfering beams). (b) The intensity dependence of the diffracted signal for 1 mol% 5CB:1 sample (488 nm; period: 40 μm; the intensities given represent the value for each interfering beam). (c) Diffraction efficiency curves for 10 μm planar cells of the 5CB:x mixtures upon exposure to interference pattern of two p-polarized 488 nm laser beams (period: 30 μm; intensity: 1 mW cm⁻²). The irradiation is started at 0 s, and ceased at 30 s (a), 20 s (b), and 40 s (c), after which the diffracted signal quickly vanishes.

The diffraction experiments for 5CB:1, 5CB:2, and 5CB:3, given in Fig. 3c, correlate well with the trend observed for order parameters in Fig. 2. The diffraction efficiency, which can be taken as a figure of merit for the optical response, develops in the order 1 > 2 > 3. The kinetics of the diffracted signal, i.e., diffraction maximum followed by a gradual decay with much slower dynamics, follows the tendencies observed in the literature,^36,37 and is similar to all the studied systems. It suggests that several mechanisms contribute to the overall diffraction efficiency, including for instance molecular diffusion occurring upon irradiation, and non-ideal visibility of the interference pattern, resulting in small amounts of stray light also at the interference minima. We note that there seems to be no direct correlation between the diffraction kinetics and the cis half-lives (Fig. S5†) of the azobenzenes used; for instance the signal vanished instantaneously for all systems when ceasing the irradiation. This is a further indirect indication that molecular diffusion plays a role in the diffraction kinetics. Rather than the dynamics of the diffracted signal, what is significant is the fact that when using structurally similar dopants, halogen bonding between the dopant and the host clearly enhances the optical response of the material system. To the best of our knowledge, this provides a new design principle for LC photonics.

Conclusions

We have shown that supramolecular interactions between azobenzene dopants and a liquid-crystalline host (5CB) affect (i) the phase-transition temperature of the LC system, (ii) the order parameter of the dopant in the LC host, and (iii) the photoresponsive behavior of the material system. Due to its high directionality, halogen bonding is identified as a particularly effective noncovalent interaction in controlling the properties of doped LCs. Halogen bonding also provides the additional benefit of controlling the LC-dopant interaction through single-atom substitution, i.e., with minimum changes to the structural, spectral, and physical properties of the dopant. By taking advantage of the design guidelines presented here and optimizing the molecules in terms of their capability to interact with the liquid-crystalline host (for instance, dopants functionalized with tetrafluorophenol groups are interesting targets for future studies), one can control the miscibility of the dopants into the liquid crystal host, and as a consequence, the optical response of the material system, which is valuable for engineering high-performance liquid-crystal-based photonic devices.

Computational details and experimental

Computational details

The interaction energies for the complexes of 1, 2 and 3 with 1CB and the dipole moments of 1, 2 and 3 were calculated with Gaussian 09 Revision D.01 (ref. 38) at the PBE0/def2-TZVP level of theory. The interaction energies were corrected for the basis set superposition error using the counterpoise method as implemented in Gaussian 09. The QTAIM and IQA analysis were performed with AIMAll (version 16.10.31)³⁹ using the default parameters. Selected geometrical parameters of the optimized complexes are reported in Table S2† together with the associated interaction energies. In Table S3† we report the results of the QTAIM topological analysis.

Synthesis and material preparation

Compounds 1–3 were synthesized as previously reported.⁴⁰ 4′-Pentyl-4-biphenylcarbonitrile (5CB) was purchased from Merck and used as received.

Co-crystallization procedure

Compound 1 was dissolved in chloroform (minimum amount at r.t.), in a clear borosilicate glass vial. 4′-Pentyl-4-biphenylcarbonitrile (5CB) was then added in a 5 : 1 molar ratio and the resulting solution was stirred at r.t. for 30 minutes. Slow evaporation of the solvent led to single crystals, which were cleaned from excess 5CB before data collection.

Single crystal X-ray diffraction analysis

Single crystal X-ray diffraction experiments were carried out on a Bruker Kappa Apex II CCD diffractometer with Mo Kα radiation (λ = 0.71073 Å) and a Bruker Kryoflex low-temperature device. Crystals were mounted on glass fibers. Data collection and reduction were performed by SMART⁴¹ and SAINT⁴² and absorption correction, based on multi-scan procedure, by SADABS.⁴¹ The structures were solved by SHELXS⁴² and refined on all independent reflections by full-matrix least-squares based on F_o² by using SHELX-97.⁴³ Both molecules were disordered; they were refined with restraints both on geometric parameters and ADPs, but with independent and variable population factors.

Infrared spectroscopy

Infrared spectra were measured by drop-casting the starting materials and the complexes on the diamond crystal of a Golden Gate (Specac) attenuated total reflection (ATR) accessory. Spectra were recorded using a Tensor 27 FT-IR spectrometer (Bruker Optics) equipped with a liquid nitrogen-cooled MCT detector. 100 scans were averaged with a 4 cm⁻¹ resolution.

Cell preparation and characterization

For LC cell fabrication, two glass slides were firstly cleaned by successive sonication in acetone, isopropyl alcohol, and deionized water, and subsequently spin-coated with polyimide (JSR, AL1254), cured at 120 °C for 2 h, and rubbed undirectionally. The rubbed glass slides were glued together, maintaining 10 μm separation between the two slides by using spacer beads (Thermo scientific). 5CB and 5CB:x mixtures were infiltrated into the cells, and the filled cells were sealed with epoxy gule. The cells were examined with hot-stage polarized-optical microscope (Olympus BH-2) in order to verify the N–I and I–N phase-transition temperatures, and verify the homogeneous molecular alignment. The cells were also examined with polarized UV-Vis absorption spectroscopy (Jasco V-650) in order to determine the order parameter of molecular alignment, using the absorption bands of the azobenzene dopants as probes.

Diffraction experiments

The optical experiments were conducted using a single-longitudinal-mode, spatially filtered beam from an Ar⁺-laser (Coherent Innova, 488 nm), split into two beams using a beam splitter, that were then combined to yield an interference pattern with a periodicity of either 30 μm or 40 μm. Both beams were p-polarized, impinging on the sample symmetrically, such that the polarization direction coincided with the molecular director. The intensity of each beam was 1 mW cm⁻² (unless otherwise stated). The resulting dynamic diffraction gratings were monitored with a low-power 633 nm probe beam from a He-Ne laser, with polarization parallel to that of the inscription beams (unless otherwise stated). The power of the probing light diffracted into first order was measured as a function of time in order to determine the dynamics of the diffraction efficiency.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work is funded by the Academy of Finland (decision numbers 277091 and 312628) and the Emil Aaltonen foundation, whose support A. P. gratefully acknowledges. J. V. acknowledges the Academy of Finland and Banting Postdoctoral Fellowships Program for generous postdoctoral funding. We are thankful to CSC – IT Center for Science Ltd., administered by the Finnish Ministry of Education, for providing the computing resources for this work.

Notes and references

1. L. Marrucci, Liq. Cryst. Today, 2002, 11, 6–33.
2. V. G. Chigrinov, Liquid Crystal Photonics (Engineering Tools, Techniques and Tables), Nova Science Publishers Inc., New York, USA, 2014.
3. I. C. Khoo, Phys. Rep., 2009, 471, 221–267.
4. N. V. Tabiryan, A. V. Sukhov and B. Y. Zel'dovich, Mol. Cryst. Liq. Cryst., 1986, 136, 1–139.
5. I. Jánossy and T. Kósa, Opt. Lett., 1992, 17, 1183–1185.
6. I. Jánossy, A. D. Lloyd and B. S. Wherrett, Mol. Cryst. Liq. Cryst., 1990, 179, 1–12.
7. I. A. Budagovsky, A. S. Zolot'ko, V. N. Ochkin, M. P. Smayev, A. Y. Bobrovsky, V. P. Shibaev and M. I. Barnik, J. Exp. Theor. Phys., 2011, 106, 172–181.
8. T. Ikeda, J. Mater. Chem., 2003, 13, 2037–2057.
9. L. Lucchetti, M. Di Fabrizio, O. Francescangeli and F. Simoni, Opt. Commun., 2004, 233, 417–424.
10. J. Wang, Y. Aihara, M. Kinoshita, J. Mamiya, A. Priimagi and A. Shishido, Sci. Rep., 2015, 5, 9890.
11. I. Jánossy, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 2957–2963.
12. L. Marrucci and D. Paparo, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 1765–1772.
13. A. Thote and R. B. Gupta, Fluid Phase Equilib., 2004, 220, 47–54.
14. T. Kato, N. Mizoshita and K. Kanie, Macromol. Rapid Commun., 2001, 22, 797–814.
15. C. M. Paleos and D. Tsiourvas, Liq. Cryst., 2001, 28, 1127–1161.
16. R. Muenster, M. Jarasch, X. Zhuang and Y. R. Shen, Phys. Rev. Lett., 1997, 78, 42–45.
17. L. Marrucci, D. Paparo, P. Maddalena, E. Massera, E. Prudnikova and E. Santamato, J. Chem. Phys., 1997, 107, 9783–9793.
18. L. Marrucci, D. Paparo, M. R. Vetrano, M. Colicchio, E. Santamato and G. Viscardi, J. Chem. Phys., 2000, 113, 10361–10366.
19. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
20. G. Berger, J. Soubhye and F. Meyer, Polym. Chem., 2015, 6, 3559–3580.
21. O. S. Bushuyev, A. Tomberg, J. R. Vinden, N. Moitessier, C. J. Barrett and T. Friscic, Chem. Commun., 2016, 52, 2103–2106.
22. D. W. Bruce, P. Metrangolo, F. Meyer, T. Pilati, C. Prasang, G. Resnati, G. Terraneo, S. G. Wainwright and A. C. Whitwood, Chem.–Eur. J., 2010, 16, 9511–9524.
23. L. González, N. Gimeno, R. M. Tejedor, V. Polo, M. B. Ros, S. Uriel and J. L. Serrano, Chem. Mater., 2013, 25, 4503–4510.
24. H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, J. Am. Chem. Soc., 2004, 126, 16–17.
25. F. Fernandez-Palacio, M. Poutanen, M. Saccone, A. Siiskonen, G. Terraneo, G. Resnati, O. Ikkala, P. Metrangolo and A. Priimagi, Chem. Mater., 2016, 28, 8314–8321.
26. M. Saccone, V. Dichiarante, A. Forni, A. Goulet-Hanssens, G. Cavallo, J. Vapaavuori, G. Terraneo, C. J. Barrett, G. Resnati, P. Metrangolo and A. Priimagi, J. Mater. Chem. C, 2015, 3, 759–768.
27. M. Virkki, O. Tuominen, A. Forni, M. Saccone, P. Metrangolo, G. Resnati, M. Kauranen and A. Priimagi, J. Mater. Chem. C, 2015, 3, 3003–3006.
28. P. Metrangolo, T. Pilati, G. Resnati and A. Stevenazzi, Chem. Commun., 2004, 13, 1492–1493.
29. D. Yan, A. Delori, G. O. Lloyd, T. Friscic, G. M. Day, W. Jones, J. Lu, M. Wei, D. G. Evans and X. Duan, Angew. Chem., Int. Ed. Engl., 2011, 50, 12483–12486.
30. A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714.
31. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
32. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
33. I. Vecchi, A. Arcioni, C. Bacchiocchi, G. Tiberio, P. Zanirato and C. Zannoni, J. Phys. Chem. B, 2007, 111, 3355–3362.
34. A. Pizzirusso, M. B. Di Cicco, G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, J. Phys. Chem. B, 2012, 116, 3760–3771.
35. V. E. Williams and R. P. Lemieux, J. Am. Chem. Soc., 1998, 120, 11311–11315.
36. E. Ouskova, A. Pshenychnyi, A. Sanchez-Ferrer, D. Lysenko, J. Vapaavuori and M. Kaivola, J. Opt. Soc. Am. B, 2014, 31, 1456–1464.
37. I. C. Khoo, P. H. Chen, M. Y. Shih, A. Shishido, S. Slussarenko and M. V. Wood, Mol. Cryst. Liq. Cryst., 2001, 358, 1–13.
38. Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, USA, 2016.
39. T. A. Keith, TK Gristmill Software, AIMAll (Version 16.10.31), Overland Park, KS, USA, 2016, http://aim.tkgristmill.com.
40. A. Priimagi, G. Cavallo, A. Forni, M. Gorynsztejn-Leben, M. Kaivola, P. Metrangolo, R. Milani, A. Shishido, T. Pilati, G. Resnati and G. Terraneo, Adv. Funct. Mater., 2012, 22, 2572–2579.
41. SMART, SAINT, and SADABS, Bruker Analytical X-ray Systems, Bruker AXS Inc., Madison, WI, USA, 1999.
42. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
43. C. B. Hubschle, G. M. Sheldrick and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 1281–1284.

---

Footnote

† Electronic supplementary information (ESI) available: CCDC 1535157. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra06397k

---