Single-molecule magnetism in {CoIII2DyIII2}-amine-polyalcohol-acetylacetonate complexes: effects of ligand replacement at the DyIII sites on the dynamics of magnetic relaxation†
Stuart K.
Langley
a,
Nicholas F.
Chilton
 b,
Boujemaa
Moubaraki
a and
Keith S.
Murray
*a
b,
Boujemaa
Moubaraki
a and
Keith S.
Murray
*a
aSchool of Chemistry, Monash University, Building 23, 17 Rainforest Walk, Clayton, Victoria 3800, Australia. E-mail: keith.murray@monash.edu
bSchool of Chemistry, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
First published on 16th July 2015
Abstract
The synthesis of three new tetranuclear heterometallic CoIII–DyIII planar butterfly coordination complexes is reported of molecular formulae [DyIII2CoIII2(OH)2(teaH)2(acac)6]·MeCN (3), [DyIII2CoIII2(OH)2(bdea)2(acac)6]·2H2O (4) and [DyIII2CoIII2(OH)2(edea)2(acac)6]·2H2O·4MeCN (5) (teaH3 = triethanolamine, bdeaH2 = N-n-butyldiethanolamine, edeaH2 = N-ethyldiethanolamine and acacH = acetylacetone) each of which display single-molecule magnet (SMM) behaviour. Importantly these new compounds are related to several {CoIII2DyIII2} SMM compounds allowing for the study of the effect that the subtle changes in structure have on the SMM properties. Ab initio calculations are performed on 3–5, as well as on the related structural derivatives in order to gain insight on the effect the structural changes have on the dynamic magnetic behaviour.
Introduction
Lanthanide ions remain at the forefront for the development of molecular magnetic materials due to their large spin and unquenched orbital magnetic moments.1 Discrete lanthanide species possessing well isolated, magnetically anisotropic bistable ground states can display slow relaxation of the magnetization upon application and removal of a magnetic field.2 This single-molecule magnet (SMM) behaviour continues to be of great interest due to the unique physical properties associated with such systems, namely, magnetic hysteresis and quantum tunnelling of the magnetisation (QTM). Potential applications that can exploit these physical properties are being explored such as extremely high density digital information storage devices, quantum information processing and as ‘spintronic’ devices.3Since the discovery that single-ion lanthanide complexes can exhibit slow relaxation of the magnetisation with an extremely large anisotropic energy barrier (Ueff), research into lanthanide SMMs has grown rapidly.4,5 The size of such a barrier is important and is often regarded as a measure of success of an SMM since it influences the stability of the orientation of the magnetisation upon application and removal of a magnetic field at a particular temperature. Therefore, axiomatically, the larger the energy barrier the longer the relaxation time at a specified temperature, if quantum effects are minimal.
Subsequently, this has resulted in the study of many mono- and poly-nuclear lanthanide and polynuclear heterometallic 3d–4f coordination complexes in search for SMMs with improved properties; the latter being longer relaxation times at higher temperatures, with minimal QTM.5 Recently, for example, Long and co-workers were able to promote strong magnetic exchange in dinuclear LnIII (Ln = Tb and Dy) complexes via the interaction with a dinitrogen, N23−, and/or a bipyrimidine (bpym) radical, which yielded hysteresis loops opening at record temperatures (∼14 K) for a SMM.6 The key aspect was the strong exchange found between the LnIII ions and unpaired electron of the radical ligand, which resulted in a large anisotropy barrier with a slow quantum tunnelling time. Although these results highlight the growing potential in the use of lanthanide ions as SMMs, promoting interactions between lanthanide ions continues to be a difficult challenge, owing to poor orbital overlap between the core-like 4f orbitals. In fact, the observed slow relaxation in polynuclear lanthanide SMMs is generally assigned to single-ion relaxation mechanisms, in which the QTM pathway is extremely fast and efficient, often shortcutting the barrier height and limiting relaxation times. It has been found, however, that the neighbouring ions (in or between clusters) can often act as an exchange bias, where the weak magnetic coupling (dipolar and exchange) can be seen to reduce the zero-field ground state QTM.7 It is important, therefore, to study complexes which display single ion magnetic behaviour, but which are part of a larger motif in order to work towards optimizing properties for future systems, such as lowering the quantum tunnelling rate. Several reviews have elucidated the reasons for the observation of SMM behaviour from a single Ln ion.1a,2,8 The most salient point being that the ligand-field around the LnIII ion controls the ordering and energy separations between the magnetic microstates. The energy difference from the ground to the first excited state often correlates to the barrier height.2,8 It is therefore observed that any change in the geometry and ligand environment around the LnIII ions can drastically affect the electronic structure and thus the dynamic magnetic behaviour.9 A joint experimental and theoretical program aimed at understanding, and ultimately controlling, what is needed of the crystal field, will allow us to design SMMs in the future with vastly improved properties.
With this in mind, we have previously investigated heterometallic {CoIII2DyIII2} SMM complexes for which we have developed a predictable and tuneable synthetic reaction scheme.10 These clusters can be considered, magnetically, as dinuclear DyIII compounds due to the two CoIII ions being diamagnetic. Two distinct families have thus far been synthesised; the first series was isolated using CoII and DyIII salts with amine polyalcohol ligands and benzoate as a co-ligand, and resulted in several complexes of general formula [CoIII2DyIII2(OMe)2(benz)4(L)2(MeOH)x(NO3)y](NO3)z, where L = [teaH]2−, [dea]2−, [mdea]2− or [bdea]2−, these amino-alcohols being the doubly deprotonated versions of triethanolamine, diethanolamine, N-methyldiethanolamine and N-n-butyldiethanolamine, respectively. Each complex displayed the same metallic core and ligand bridging arrangement, where subtle changes in the local coordination environment of the DyIII ions for each complex (variation of the x, y and z parameters given in the above formula) resulted in different dynamic magnetic behaviour for each member of the family.10a,b Further to this, we found we could tune/affect the magnetic behaviour via modification of the benzoate ligand.10e
A second and closely related family of compounds, again displaying an identical butterfly metallic core arrangement, with a slightly modified bridging ligand motif, was isolated upon replacement of benzoate co-ligand by acetylacetonate ([acac]−). The first member displayed the general molecular formula [CoIII2DyIII2(OR)2(L)2(acac)4(NO3)2], with L = [teaH]2− and R = Me (1a), L = [teaH]2− and R = H (1b) and L = [mdea]2− and R = Me (1c).10c Through selective modification of compound 1, we were able to synthesize a second derivative of formula [CoIII2DyIII2(OH)2(bdea)2(acac)2(NO3)4] (2), which displayed a change in the [acac]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NO3]− ratio from 4
[NO3]− ratio from 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in 1 to 2
2 in 1 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, with two chelating nitrate groups coordinated to each of the DyIII ions. This targeted modification resulted in a remarkable six-fold increase in the anisotropy barrier, Ueff, when compared to the series of 1.10d Encouraged by the remarkable change in the magnetic properties due to the chemical modification, we have explored another combination where all of the chelating ligands have been replaced with [acac]−. Here, we report three new heterometallic complexes of formulae [DyIII2CoIII2(OH)2(teaH)2(acac)6]·MeCN (3), [DyIII2CoIII2(OH)2(bdea)2(acac)6]·2H2O (4) and [DyIII2CoIII2(OH)2(edea)2(acac)6]·2H2O·4MeCN (5) (edeaH2 = N-ethyldiethanolamine) along with their interesting magnetic properties as probed by static and dynamic magnetic measurements. A comparison of the experimental magnetic behaviour of 3–5 is made with the previously reported complexes 1 and 2.10c,dAb initio calculations are performed on 3–5, as well as on the related structural derivatives 1 and 2 in order to gain insight on the effect the structural changes have on the dynamic magnetic behaviour.
4, with two chelating nitrate groups coordinated to each of the DyIII ions. This targeted modification resulted in a remarkable six-fold increase in the anisotropy barrier, Ueff, when compared to the series of 1.10d Encouraged by the remarkable change in the magnetic properties due to the chemical modification, we have explored another combination where all of the chelating ligands have been replaced with [acac]−. Here, we report three new heterometallic complexes of formulae [DyIII2CoIII2(OH)2(teaH)2(acac)6]·MeCN (3), [DyIII2CoIII2(OH)2(bdea)2(acac)6]·2H2O (4) and [DyIII2CoIII2(OH)2(edea)2(acac)6]·2H2O·4MeCN (5) (edeaH2 = N-ethyldiethanolamine) along with their interesting magnetic properties as probed by static and dynamic magnetic measurements. A comparison of the experimental magnetic behaviour of 3–5 is made with the previously reported complexes 1 and 2.10c,dAb initio calculations are performed on 3–5, as well as on the related structural derivatives 1 and 2 in order to gain insight on the effect the structural changes have on the dynamic magnetic behaviour.
Experimental
General information
All reactions were carried out under aerobic conditions. All chemicals and solvents were obtained from commercial sources and used without further purification. Elemental analyses (CHN) were carried out by Campbell Microanalytical Laboratory, University of Otago, Dunedin, New Zealand.Synthesis of [DyIII2CoIII2(OH)2(teaH)2(acac)6]·MeCN (3)
Co(acac)2·2H2O (0.15g, 0.5 mmol) and DyCl3·6H2O (0.18 g, 0.5 mmol) were dissolved in MeCN (15 mL), followed by the addition of triethanolamine (0.07 mL, 0.5 mmol), acetylacetone (0.10 mL, 1 mmol) and triethylamine (0.28 mL, 2.0 mmol) to form a dark green solution. This solution was stirred at room temperature for a period of 6 hours. After this time the solution was filtered and the filtrate was allowed to evaporate slowly. Within 2–3 days blue/green crystals of 3 had grown with an approximate yield of 45%. Anal. Calculated (found) for 3: Co2Dy2C44H73O20N3: C, 37.54 (37.90); H, 5.23 (5.62); N, 2.99 (3.12).Synthesis of [DyIII2CoIII2(OH)2(bdea)2(acac)6]·2H2O (4)
Co(acac)2·2H2O (0.15 g, 0.5 mmol) and DyCl3·6H2O (0.18 g, 0.5 mmol) were dissolved in MeCN (15 mL), followed by the addition of N-n-butyldiethanolamine (0.08 mL, 0.5 mmol), acetylacetone (0.1 mL, 1 mmol) and triethylamine (0.28 mL, 2.0 mmol) to give a dark green solution. This solution was stirred at room temperature for a period of 6 hours. After this time the solution was filtered and the filtrate was allowed to evaporate slowly. Within 2–3 days dark green crystals of 4 had grown with an approximate yield of 39%. Anal. Calculated (found) for 4: Co2Dy2C46H82O20N2: C, 38.73 (38.30); H, 5.80 (5.72); N, 1.96 (2.02).Synthesis of [DyIII2CoIII2(OH)2(edea)2(acac)6]·2H2O·4MeCN (5)
Co(acac)2·2H2O (0.15 g, 0.5 mmol) and DyCl3·6H2O (0.18 g, 0.5 mmol) were dissolved in MeCN (15 mL), followed by the addition of N-ethyldiethanolamine (0.07 mL, 0.5 mmol), acetylacetone (0.1 mL, 1 mmol) and triethylamine (0.28 mL, 2.0 mmol) to give a dark green solution. This solution was stirred at room temperature for a period of 6 hours. After this time the solution was filtered and the filtrate was allowed to evaporate slowly. Within 2–3 days dark green crystals of 5 had appeared, in approximate yield of 38%. Anal. Calculated (found) for 5: Co2Dy2C50H86O20N6: C, 39.13 (38.78); H, 5.65 (5.32); N, 5.48 (5.06).X-ray crystallography
X-ray crystallographic measurements for 3 were performed at 100(2) K at the Australian synchrotron MX1 beam-line. The data collection and integration were performed within Blu-Ice11 and XDS12 software programs. Compounds 4 and 5 were measured using a Bruker Smart Apex X8 diffractometer with Mo Kα radiation. The data collection and integration were performed within SMART and SAINT+ software programs, and corrected for absorption using the Bruker SADABS program. Compounds 3–5 were all solved by direct methods (SHELXS-97), and refined (SHELXL-97) by full least matrix least-squares on all F2 data.13 Crystallographic data and refinement parameters for 3–5 are summarized in Table 1. Crystallographic details are available in the ESI† in CIF format. CCDC numbers 1401165 (3), 1401166 (4) and 1401167 (5).| 3 | 4 | 5 | |
|---|---|---|---|
| a Including solvate molecules. b Graphite monochromator. c R 1 = ∑||Fo| − |Fc||/∑|Fo|, wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. | |||
| Formulaa | Co2Dy2C44H73O20N3 | Co2Dy2C46H82O20N2 | Co2Dy2C50H86O20N6 |
| M, g mol−1 | 1406.92 | 1426.00 | 1534.11 |
| Crystal system | Triclinic | Orthorhombic | Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Pccn |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a/Å | 12.394(2) | 17.3414(12) | 11.8706(8) |
| b/Å | 12.855(2) | 23.9462(18) | 11.9902(8) |
| c/Å | 17.927(4) | 13.7765(10) | 12.4045(8) |
| α/° | 78.16(3) | 90 | 68.451(2) |
| β/° | 89.90(3) | 90 | 75.006(2) |
| γ/° | 69.62(3) | 90 | 77.696(2) |
| V/Å3 | 2612.9.7(12) | 5720.8(7) | 1572.47(18) |
| T/K | 100(2) | 123(2) | 123(2) |
| Z | 2 | 4 | 1 |
| ρ calc, [g cm−3] | 1.788 | 1.656 | 1.620 |
| λ /Å | 0.71070 | 0.71073 | 0.71073 |
| Data measured | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199 199 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
| Ind. reflns | 8504 | 8786 | 6808 |
| R int | 0.0550 | 0.0849 | 0.0164 |
| Reflns with I > 2σ(I) | 7496 | 6978 | 6265 |
| Parameters | 663 | 390 | 382 |
| Restraints | 1 | 9 | 0 |
| R 1 (obs), wR2c (all) | 0.0412, 0.1040 | 0.0700, 0.1722 | 0.0221, 0.0522 |
| Goodness of fit | 1.069 | 1.268 | 1.053 |
| Largest residuals/e Å−3 | 1.959, −2.016 | 1.487, −2.182 | 1.705, −0.626 |
Magnetic measurements
The magnetic susceptibility measurements were carried out on a Quantum Design SQUID magnetometer MPMS-XL 7 operating between 1.8 and 300 K for dc-applied fields ranging from 0–5 T. Microcrystalline samples were dispersed in Vaseline in order to avoid torquing of the crystallites. The sample mulls were contained in a calibrated gelatine capsule held at the centre of a drinking straw that was fixed at the end of the sample rod. Ac susceptibilities were carried out under an oscillating ac field of 3.5 Oe and at frequencies ranging from 0.1 to 1500 Hz.Results and discussion
Synthesis
From previous work we have shown that the heterometallic butterfly structural motif (Fig. 1) is a stable and favoured configuration utilizing amine polyalcohol and various co-ligands, such as carboxylates and β-diketonates, even under varying reaction conditions (i.e. ligand modification, metal identity etc.). This being the case, we have found we can manipulate the product of the reaction thus allowing us to decorate the complex with various terminal and bridging ligands, while maintaining the same “magnetic core”. Importantly, it has been shown that modifications can occur at terminal and chelating DyIII sites allowing for subsequent magneto-structural studies.10 The synthetic strategy in the present work targeted the isolation and coordination of two chelating [acac]− ligands at each DyIII centre. In previous examples Dy(NO3)3·6H2O was used as the source of DyIII and it was found that the [NO3]− ion coordinated to the DyIII ions within the tetranuclear complex. By removing the nitrate source, utilizing DyCl3·6H2O, and adding additional acetylacetone we were able to achieve our target of coordinating two [acac]− ligands at each DyIII site. This work suggests that a large range of terminal or chelating ligands can be incorporated into these clusters via simple variations in the reaction conditions and/or starting materials.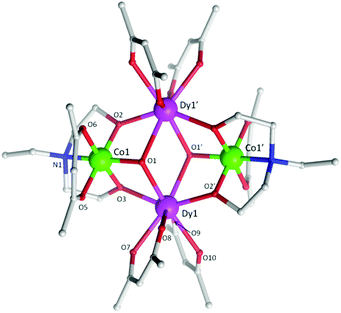 | ||
| Fig. 1 Molecular structure of 5. The H-atoms are omitted for clarity. Colour scheme; CoIII, green; DyIII, purple; O, red; N, blue; C, light grey. | ||
Structural descriptions
Single crystal X-ray diffraction measurements reveal that compounds 3 and 5 crystallize in the triclinic space group, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , while compound 4 crystallizes in the orthorhombic space group Pccn. Compounds 3–5 (Fig. 1 (5) and Fig. S1 (3) and S2 (4)†) were all found to be heterometallic tetranuclear clusters consisting of two CoIII and two DyIII ions. The asymmetric unit for compounds 4 and 5 each contain half of the complex (one CoIII and DyIII ion) each of which lie upon an inversion centre. The asymmetric unit for compound 3, however, consists of two crystallographic unique halves of the cluster, both of which lie upon an inversion centre. The metallic core of all clusters are identical, displaying a planar butterfly motif with the two DyIII ions occupying the ‘body’ positions and the CoIII ions the outer ‘wing-tip’ sites as previously observed for related complexes.10 The metal ions are held together primarily via two μ3 hydroxide ligands, bridging the two DyIII ions to a CoIII ion. Further bridges are provided by the two amine-diol or triol ligands (teaH2− (3), bdea2− (4) and edea2− (5)), which coordinate to the CoIII ions via the N-atom, then bridge to the DyIII sites via two μ2 O-atoms. This core bonding motif is identical to that in compounds 1 and 2.10c,d In the case of 3, the third protonated alcohol arm of the teaH2− ligands are non-coordinating. One [acac]− ligand is then found to chelate to each CoIII ion and two [acac]− ligands chelate the DyIII ions.
, while compound 4 crystallizes in the orthorhombic space group Pccn. Compounds 3–5 (Fig. 1 (5) and Fig. S1 (3) and S2 (4)†) were all found to be heterometallic tetranuclear clusters consisting of two CoIII and two DyIII ions. The asymmetric unit for compounds 4 and 5 each contain half of the complex (one CoIII and DyIII ion) each of which lie upon an inversion centre. The asymmetric unit for compound 3, however, consists of two crystallographic unique halves of the cluster, both of which lie upon an inversion centre. The metallic core of all clusters are identical, displaying a planar butterfly motif with the two DyIII ions occupying the ‘body’ positions and the CoIII ions the outer ‘wing-tip’ sites as previously observed for related complexes.10 The metal ions are held together primarily via two μ3 hydroxide ligands, bridging the two DyIII ions to a CoIII ion. Further bridges are provided by the two amine-diol or triol ligands (teaH2− (3), bdea2− (4) and edea2− (5)), which coordinate to the CoIII ions via the N-atom, then bridge to the DyIII sites via two μ2 O-atoms. This core bonding motif is identical to that in compounds 1 and 2.10c,d In the case of 3, the third protonated alcohol arm of the teaH2− ligands are non-coordinating. One [acac]− ligand is then found to chelate to each CoIII ion and two [acac]− ligands chelate the DyIII ions.
The (acac/acac) configuration found here differs from 1 and 2 where the DyIII ions were in (NO3/acac) and (NO3/NO3) environments, respectively.10c,dFig. 2 shows the different coordination environments for the DyIII ions for compounds 1 (left), 2 (middle) and for the present examples 3–5 (right). The CoIII ions are six-coordinate with octahedral geometries, all displaying an average Co–LN,O bond distance of 1.91 Å. The DyIII ions are all eight-coordinate with distorted square anti-prismatic geometries, with average Dy–O bond lengths of 2.37, 2.38, 2.36 and 2.36 Å Dy1 (3), Dy2 (3), 4 and 5, respectively. Selected bond angles and distances for compounds 3–5 are given in Table 2.
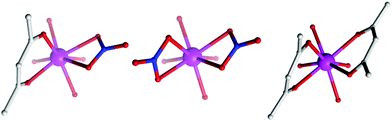 | ||
| Fig. 2 Comparison of the coordination environment of the DyIII ions in 1 (left), 2 (middle) and the present complexes, 3–5 (right). | ||
| 3 | 3a | 4 | 5 | |
|---|---|---|---|---|
| Dy1–O3 | 2.275(4) | 2.286(4) | 2.335(6) | 2.3062(17)IV |
| Dy1–O9 | 2.316(4) | 2.330(4) | 2.346(6) | 2.3395(17) |
| Dy1–O2′ | 2.330(4)I | 2.318(4)II | 2.300(6)III | 2.2901(17) |
| Dy1–O10 | 2.336(5) | 2.371(4) | 2.355(6) | 2.3662(18) |
| Dy1–O8 | 2.364(4) | 2.360(4) | 2.329(6) | 2.3416(17) |
| Dy1–O7 | 2.407(5) | 2.381(4) | 2.323(6) | 2.3332(17) |
| Dy1–O1′ | 2.457(4)I | 2.475(4)II | 2.433(4)III | 2.4607(18)IV |
| Dy1–O1 | 2.458(5) | 2.498(5) | 2.477(5) | 2.4423(17) |
| Co1–O3 | 1.864(4) | 1.859(4) | 1.867(5) | 1.8666(17) |
| Co1–O2 | 1.883(4) | 1.871(4) | 1.862(5) | 1.8681(17) |
| Co1–O6 | 1.903(4) | 1.899(4) | 1.907(6) | 1.9117(17) |
| Co1–O5 | 1.903(5) | 1.900(4) | 1.910(6) | 1.9057(17) |
| Co1–O1 | 1.916(5) | 1.920(5) | 1.927(5) | 1.9201(17) |
| Co1–N1 | 1.989(5) | 1.979(5) | 1.974(8) | 1.977(2) |
| Dy1⋯Dy1′ | 4.050(5) | 4.116(5) | 4.064(6) | 4.041(4) |
| Dy1⋯Co1 | 3.373(5) | 3.376(5) | 3.392(6) | 3.374(4) |
| Dy1′⋯Co1 | 3.352(4) | 3.364(5) | 3.325(6) | 3.364(4) |
| Dy1–O1–Dy1′ | 111.00(4) | 111.17(5) | 111.70(6) | 111.01(4) |
Magnetic measurements
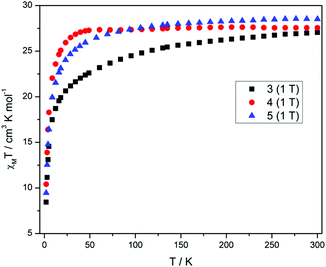
Direct current (dc) magnetic susceptibility measurements (Fig. 3) performed on polycrystalline samples of 3–5 in a magnetic field of 1 T reveal room temperature χMT values of 27.04, 27.55 and 28.51 cm3 K mol−1, in good agreement with the expected value of 28.34 cm3 K mol−1 for two uncoupled DyIII ions, indicating weak exchange, as expected. As the temperature is reduced from 300 K, the χMT values decrease gradually between 300–25 K, before a more rapid decrease below 25 K, reaching values of 8.44, 10.41 and 9.46 cm3 K mol−1 and 2 K for 3–5, respectively. The decrease in χMT in all cases is due to the depopulation of the mJ sub-levels of the ground J state, with the possibility of antiferromagnetic exchange/dipolar interactions also contributing to the behaviour. It must be noted that the decrease of the χMT value for compound 3 is more pronounced than 4 and 5 as the temperature is reduced, which may suggest a difference in the splitting of the single-ion levels for 3 when compared to 4 and 5. The M versus H plots (Fig. S3†), each show sharp increases with increasing H, at low fields and low temperatures, with M then increasing linearly at larger fields, reaching a value of 9.77, 10.86 and 10.06Nβ at 2 K and 5 T, for 3, 4 and 5 respectively. These values are less than expected for two free DyIII ions, again as a result of the loss of degeneracy within the ground J multiplet due to the ligand field.In order to probe the slow relaxation of the magnetization and quantum tunnelling effects within these molecules, variable temperature and frequency alternating current (ac) magnetic measurements were performed, utilizing a 3.5 Oe oscillating field and a zero-applied dc magnetic field. Where necessary, an applied static dc field of varying strength was implemented to check its effect on the relaxation time(s). Measurements on complexes 3–5 reveal the presence of frequency- and temperature-dependent out-of-phase susceptibility (χ′′M) signals, indicative of SMM behaviour. Each compound, however, displays substantially different behaviour, an unexpected result given the near identical nature of the coordination environment for each complex.
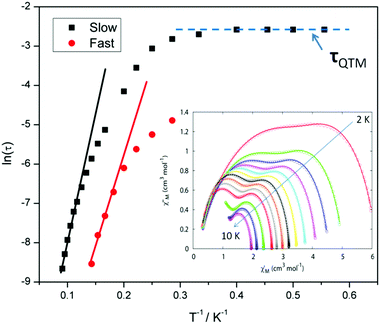
For compound 3 both the χ′′Mversus frequency (Fig. 4, top) and χ′′Mversus temperature (Fig. 4, bottom) plots display two separate maxima indicating two relaxation modes are occurring with differing relaxation timescales. The ac data are repeatable on a separate freshly made sample and on a 4 day aged sample therefrom (ESI Fig. S4†). A similar out-of-phase profile (double maxima) was observed for the related {CoIII2DyIII2} complex reported by Funes et al.14 At a single temperature in the χ′′Mversus frequency plot, the peak maxima observed at lower frequencies denote a slower relaxation time and thus we designate this as the slow process (SP), whereas the higher frequency peak (faster relaxation time) is denoted as the fast process (FP). This is clearly observed for temperatures between 3.5 and 7 K. Isothermal Cole–Cole plots reveal profiles of two fused semi-circles indicating two separate relaxation processes are in operation (Fig. 5, inset). Fits of the data between 2 and 10 K using a generalized Debye model revealed that the slow process has a very narrow distribution of relaxation times with α = 0.10(1), while the fast process has a substantially broader distribution of relaxation times, where 0.43 > α > 0.13. Plots of ln(τ) versus T−1 are linear above 9 and 5.5 K for the slow and fast process, respectively, revealing a thermally activated relaxation mechanism. Fitting to the Arrhenius law [τ = τo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT)] afforded values of Ueff = 71 K (49 cm−1) and τo = 2.7 × 10−7 s (SP) and Ueff = 45 K (31 cm−1) and τo = 3.2 × 10−7 s (FP). Below 9 and 5.5 K, respectively, deviations from Arrhenius behaviour are observed as a curvature in the plot for both pathways, indicating a crossover from a thermally activated to a QTM regime. This behaviour is more clearly observed for the slow process as the relaxation time becomes temperature independent below 3 K, while the χ′′M maxima for the FP are obscured by the SP and thus no low temperature relaxation times could be extracted (Fig. 5). It is found, however, that the SP displays a limiting relaxation time of 76.5 ms due to temperature independent QTM.
exp(Ueff/kBT)] afforded values of Ueff = 71 K (49 cm−1) and τo = 2.7 × 10−7 s (SP) and Ueff = 45 K (31 cm−1) and τo = 3.2 × 10−7 s (FP). Below 9 and 5.5 K, respectively, deviations from Arrhenius behaviour are observed as a curvature in the plot for both pathways, indicating a crossover from a thermally activated to a QTM regime. This behaviour is more clearly observed for the slow process as the relaxation time becomes temperature independent below 3 K, while the χ′′M maxima for the FP are obscured by the SP and thus no low temperature relaxation times could be extracted (Fig. 5). It is found, however, that the SP displays a limiting relaxation time of 76.5 ms due to temperature independent QTM.
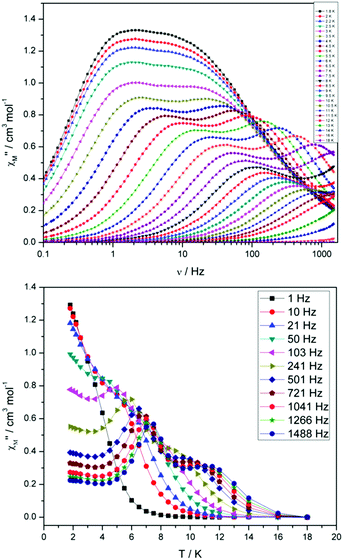 | ||
| Fig. 4 (Top) frequency and (bottom) temperature dependence of the out-of-phase ac susceptibility, χ′′M, of 3 in zero applied dc magnetic field. The solid lines just join the points. | ||
Compounds 4 and 5 display markedly different behaviour to that observed for 3. The χ′′Mversus frequency plot for 4 (Fig. 6, top) reveals a single relaxation mechanism, which becomes independent of temperature below 3 K as expected for a pure quantum regime, with a τQTM time of 1.4 ms. This is also apparent in the χ′′Mversus T plot at low temperatures, with a second increase in χ′′M indicating the onset of QTM (Fig. 6, bottom). Above 4.5 K the relaxation is thermally activated and fitting the data to the Arrhenius law afforded values of Ueff = 27 K (19 cm−1) and τo = 1.0 × 10−6 s (Fig. S5†). As the QTM is fast for 4 between 1.8–3 K, application of a small dc field at 2 K resulted in a significantly different profile, reducing the tunnelling rate (Fig. 7, top). The peak maximum found at 2 K in zero applied field corresponds to a frequency of 167 Hz, which diminishes upon increasing the field, with a lower frequency peak intensifying simultaneously. At 500 Oe, the high-frequency peak has disappeared, with a single peak maximum found at ∼3 Hz. A sweep of the field over a larger range indicated that 500 Oe was also found to be the optimum field, i.e. displaying the longest relaxation time (Fig. S6†). Variable temperature ac measurements were thus performed at 500 Oe (Fig. 7, bottom), the resulting data were fitted to the Arrhenius law, affording values of Ueff = 38 K (26 cm−1) and τo = 2.7 × 10−7 s (Fig. S5†). The larger effective barrier observed nicely illustrates the effect the reduction of tunnelling relaxation time has on the thermally activated relaxation data.
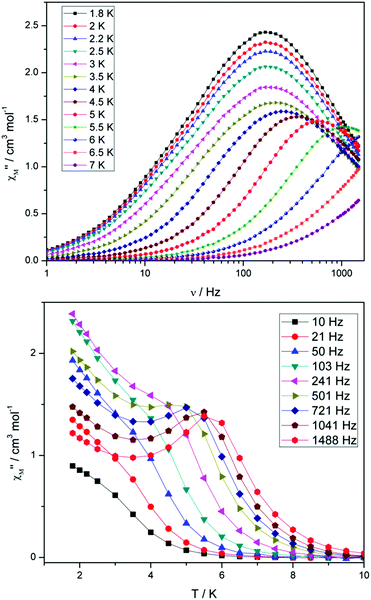 | ||
| Fig. 6 (Top) frequency and (bottom) temperature dependence of the out-of-phase ac susceptibility, χ′′M, of 4 in a zero static dc magnetic field. The solid lines just join the points. | ||
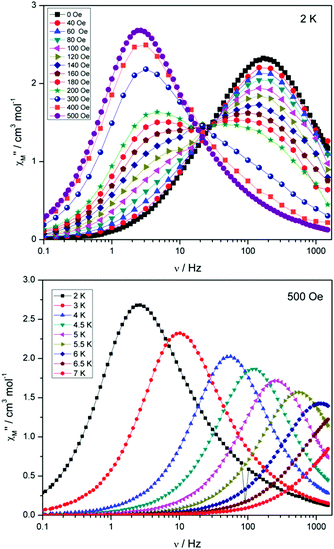 | ||
| Fig. 7 (Top) plot of χ′′Mversus frequency at 2 K for 4 under the application of variable dc fields, ranging from 0 to 500 Oe. (Bottom) plot of χ′′Mversus frequency for 4, with Hdc = 500 Oe. | ||
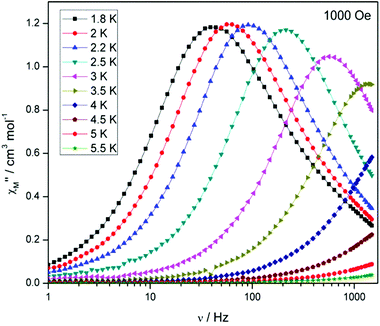
Compound 5, on the other hand, displays an absence of any maxima in χ′′M in both the frequency and temperature dependent plots, under a zero dc magnetic field (Fig. S7†). This is presumably due to fast QTM. Therefore, a variable frequency magnetic field sweep was performed at 2 K to see if the quantum tunnelling relaxation time can be decreased. The results show that the thermally activated relaxation time(s) can now be quantified entering the timescale of the experiment, with an optimum field of 1000 Oe, where the relaxation is slowest (Fig. S8†). Variable frequency (Fig. 8) and variable temperature (Fig. S9†) measurements at this field were thus performed, the resulting data were fitted to the Arrhenius law, affording values of Ueff = 16 K (11 cm−1) and τo = 1.3 × 10−6 s (Fig. S10†).
Interestingly, at much larger fields (>4000 Oe) at 2 K, we observe the appearance of a second peak at low frequency (∼0.3 Hz) at the expense of the higher frequency peak (Fig. S11†). At the optimum field, where the relaxation time is slowest, viz. 6000 Oe, for the low frequency peak, the temperature dependence was investigated (Fig. S12†). The behaviour is somewhat peculiar as the relaxation time displays only a small dependence on the temperature, initially moving to faster relaxation times upon increasing temperature as expected, but above 3 K the relaxation time, unusually, decreases again. This was previously observed in the family of related complexes 1, and efforts to determine the origin of this unusual behaviour are under way.
A comparison of the dynamic magnetic properties of 3, 4 and 5 reveal that the Ueff value is largest for 3 and follows the pattern 3 > 4 > 5. Despite the limited data taken into account in the Orbach analysis, therefore bestowing some uncertainty in the Ueff values, the difference in dynamic behaviour between the SP in 3, that for 4 (requiring a small dc field), and that for 5 (requiring a dc field to see anything at all), is certain. From a structural point of view the only difference is the polyol ligand used ([teaH]2− > [bdea]2− > [edea]2−), indicating a dependence on this “parameter”. This is also observed, with all other structural considerations being equal, for 1a and 1c, with 1c displaying a larger Ueff value ([mdea]2− > [teaH]2−).10c It is then found, again all other things being equal, that the replacement of [OH]− (1b) for [OMe]− (1a), which bridge the two DyIII ions does not affect the relaxation dynamics significantly in these systems.10c A final comparison which can be made, again where all other structural features remain equal, is the effect of the chelating anions bound to the LnIII ions. The comparison of 2 (NO3/NO3) with 4 (acac/acac) and 1b (NO3/acac) with 3 (acac/acac) reveals huge differences in the dynamic behaviours. A simple comparison of Ueff values show up to a six fold increase in the Ueff parameter upon changing the coordination environment of the LnIII ion. These results show that the most important consideration for modulating the dynamic properties is the choice of the coordinated anion. It also revelas that the Ueff value can be tuned by selection of organic R group on the bridging polyol ligand.
While compounds 3–5 reveal SMM behaviour on the fast timescale of the ac experiment, the ultimate test for the utility of a single-molecule magnetic lies in its magnetic hysteresis behaviour, providing relaxation data over a much longer timescale. The most likely candidate to display magnetic hysteresis is compound 3, owing to the largest Ueff barrier in the present series, however no open hysteresis loops were observed (Fig. S13†). This is a consequence of the short QTM time determined from the ac experiment (76.5 ms, zero dc field) compared to the sweep rate of the measurement. At zero magnetic field when the tunnelling probability is high there is a large loss of magnetization. To observe magnetic hysteresis for the present complexes, single crystal measurements at very low temperatures with fast sweep rates would be required.
Ab initio calculations and discussion
In order to understand the behaviour of the present complexes, we have conducted ab initio calculations of the CASSCF/RASSI variety10a,b,e,15 using MOLCAS 7.816 (see ESI† for details) on compounds 1–5. The energy spectra and ground state anisotropy axes are given in Tables S1–S8 and Fig. S14–S21.† All complexes possess strongly anisotropic ground Kramers doublets, with 19.36 < gz < 19.81 and gxy < 0.12, suggesting a large contribution from the mJ = ±15/2 state of the 6H15/2 multiplet of DyIII. The main anisotropy axis of this doublet, for all compounds, is approximately perpendicular to the Dy–Dy vector. This orientation, which is also shared by the first excited state in all complexes, is owed to short Dy–O contacts of around 2.28(3) Å to the bridging oxygen atoms of the polyol ligand, which have an O–Dy–O angle of approximately 145(2)°. These contacts are markedly shorter than those to the bridging [OH]− or [OMe]− oxygen atoms, which average 2.45(4) Å across the series 1–5. The barrier to magnetic relaxation, Ueff, is related to the degree of stabilization of the high angular momentum states of the magnetic ion and for the case of dysprosium(III), is maximized when subject to an axial potential.2,17 The pseudo-axial potential created by the trans O–Dy–O motif, is perturbed by the other coordination bonds to the central bridging [OH]− or [OMe]− groups and the chelating [acac]− or [NO3]− ligands. The core of these tetranuclear clusters is very robust and is more-or-less static upon substitution of the chelating ligand. The observed differences in the magnetic properties can therefore be related to the nature of the chelating ligand. We find that across compounds 1–5, the Dy–O bond lengths for the [acac]− and [NO3]− donors are 2.34(3) Å and 2.46(6) Å, respectively. The shorter bond length of the [acac]− ligand compared to [NO3]− is responsible for a stronger disruption of the pseudo-axial potential at the dysprosium ion, leading to lower Ueff values. For this reason, compound 2 with the (NO3/NO3) configuration has the largest Ueff value of 168 K. However, it seems that the (acac/acac) configuration for 3–5 is not significantly worse than the (acac/NO3) configuration for 1, where Ueff values from 16 to 71 K are found, and therefore we hypothesize that the replacement of even a single [NO3]− ligand for an [acac]− ligand results in a huge decrease in the effective symmetry of the potential. We believe the origin for the different Dy–O bond lengths between the two ligands is simply a steric effect, where the close proximity of the nitrogen atom restricts the approach of the [NO3]− ligand while the more open [acac]− ligand is not as hindered. Furthermore, it seems that the larger negative charge on the [NO3]− donor atoms compared to the [acac]− donor atoms (−2/3 vs. −1/3 in a minimal valence bond model) is either a minor influence compared to the bond length component or that the positively charged nitrogen atom serves to offset the larger negative charge.The two distinct relaxation processes observed for compound 3 likely arise from the two unique molecules in the unit cell, however there is no clear indication of significant differences in the electronic structure between the two species to suggest why this is the case. The decrease in Ueff from 3 > 4 > 5, as evidenced also by the requirement of a DC field to observe slow relaxation for 5, is consistent with a minor loss of axial character of the ground state, where gz decreases as 19.50/19.56, 19.43 and 19.36, respectively. However, the situation is much more complex for these complexes, where it is likely that weak interactions between the DyIII ions are also responsible for providing QTM pathways which allow efficient under-barrier relaxation. This appears to be the case for all compounds 1–5, all of which show Ueff values lower than the first excited Kramers doublet.
Conclusions
Three new DyIII single molecule magnets have been structurally and magnetically characterized. Based on earlier work, we expected these targeted modifications to yield different low temperature dynamic magnetic behaviour which was found to be the case. Compound 3 displays two relaxation processes with anisotropy barriers of 71 and 45 K, each crossing over into a pure quantum tunnelling regime below 3 K. The origin of the two processes is likely to be the presence of two crystallographically unique structural species in the same unit cell. Compound 4 shows a single process, with a barrier of 27 K (in zero dc field) and displays fast QTM below 3 K. Upon application of an optimum dc field of 500 Oe, 4 yielded a barrier of 38 K, with significantly reduced QTM. Compound 5 displayed no observable maxima in χ′′M in zero field but, upon application of a 1000 Oe dc field, a single thermal barrier of 16 K was obtained. The differences in the dynamic properties of the present complexes 3–5 and related complexes 1, compared to those of 2 have been shown to originate from the presence of [acac]− ligands in 1 and 3–5 and their absence in 2. The closer binding of the [acac]− ligand disrupts the pseudo-axial ligand field of the core motif, diminishing the effective barrier to magnetic reversal. Based on these findings, improved dynamic properties may be obtained if more bulky chelating ligands are employed to further increase the equatorial Dy–L distance. Other methods to improve the SMM properties of the core unit may involve the replacement of the bridging [OMe]− ligands with the perfluorinated [OCF3]− analogue, and/or appending electron-donating groups to the polyol, in order to further stabilize the strongly anisotropic ground state.Acknowledgements
The authors acknowledge the facilities and help provided by the Australian Synchrotron MX1 beamline and staff. K.S.M. and S.K.L. thank the Australian Research Council, the Australia-India AISRF program and the School of Chemistry, Monash University, for financial support. N.F.C. thanks The University of Manchester for a President's Doctoral Scholarship and Professor R. E. P. Winpenny for support. The authors acknowledge the continued theoretical advice provided by Professor L. F. Chibotaru, University of Leuven, and experimental assistance provided by Dr W. Phonsri.Notes and references
- (a) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC; (b) J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556 RSC.
- J. D. Rinehardt and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- (a) M. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS PubMed; (b) G. Aromi, D. Aguila, F. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537 RSC; (c) A. Ardavan, O. Rival, J. J. L. Morton, S. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef. l; (d) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed; (e) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357 CrossRef CAS PubMed; (f) H. S. J. Van Der Zant, Nat. Nanotechnol., 2012, 7, 555 CrossRef CAS PubMed; (g) W. Wernsdorfer, Nat. Nanotechnol., 2009, 4, 145 CrossRef CAS PubMed; (h) M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502 CrossRef CAS PubMed.
- See for example (a) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed; (b) S. Takamatsu, T. Ishikawa, S.-Y. Koshihara and N. Ishikawa, Inorg. Chem., 2007, 46, 7250 CrossRef CAS PubMed; (c) C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem. – Eur. J., 2013, 19, 1457 CrossRef CAS PubMed.
- (a) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed; (b) L. R. Piquer and C. Sanudo, Dalton Trans., 2015, 44, 8771 RSC; (c) K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289–290, 74 CrossRef CAS PubMed; (d) J.-L. Liu, J.-Y. Wu, Y.-C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966 CrossRef CAS PubMed.
- (a) J. D. Rhinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef PubMed; (b) J. D. Rhinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef PubMed; (c) S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546 CrossRef CAS PubMed.
- W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406 CrossRef PubMed.
- For example (a) P. Zhang, Y.-N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728 CrossRef CAS PubMed; (b) P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923 RSC; (c) H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1 CrossRef CAS PubMed.
- (a) N. F. Chilton, S. K. Langley, B. Moubaraki, A. Soncini and K. S. Murray, Chem. Sci., 2013, 4, 1719 RSC; (b) D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770 CrossRef CAS PubMed.
- (a) S. K. Langley, N. F. Chilton, L. Ungur, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Inorg. Chem., 2012, 51, 11873 CrossRef CAS PubMed; (b) S. K. Langley, N. F. Chilton, L. Ungur, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Inorg. Chem., 2014, 53, 4303 CrossRef CAS PubMed; (c) S. K. Langley, N. F. Chilton, B. Moubaraki and K. S. Murray, Inorg. Chem., 2013, 52, 7183 CrossRef CAS PubMed; (d) S. K. Langley, N. F. Chilton, B. Moubaraki and K. S. Murray, Chem. Commun., 2013, 49, 6965 RSC; (e) S. K. Langley, C. Le, L. Ungur, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Inorg. Chem., 2015, 54, 3631 CrossRef CAS PubMed.
- T. M. McPhillips, S. E. McPhillips, H. J. Chiu, A. E. Cohen, A. M. Deacon, P. J. Ellis, E. Garman, A. Gonzalez, N. K. Sauter, R. P. Phizackerley, S. M. Soltis and P. Kuhn, Blu-Ice and the Distributed Control System: software for data acquisition and instrument control at macromolecular crystallography beamlines, J. Synchrotron Radiat., 2002, 9, 401 CrossRef CAS PubMed.
- W. J. Kabsch, Appl. Crystallogr., 1993, 26, 795 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- A. V. Funes, L. Carrella, E. Rentschler and P. Alborés, Dalton Trans., 2014, 43, 2361 RSC.
- (a) L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413 CrossRef CAS PubMed; (b) S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. Sci., 2014, 5, 3246 RSC.
- (a) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed; (b) V. Veryazov, P. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626 CrossRef CAS PubMed; (c) G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222 CrossRef.
- (a) N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed; (b) N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101 RSC; (c) N. F. Chilton, Inorg. Chem., 2015, 54, 2097 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, Fig. S1 and S2 structures of 3 and 4; Fig. S3–S13 detailed magnetism plots; Fig. S14–S21 anisotropy directions for 1 to 5; Tables S1–S8 energy spectra calculated for 1 to 5. CCDC 1401165–1401167. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00076a |
| This journal is © the Partner Organisations 2015 |