Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards non-contact pollution monitoring in sewers with hyperspectral imaging†
P.
Lechevallier
 *a,
K.
Villez
*a,
K.
Villez
 b,
C.
Felsheim
c and
J.
Rieckermann
b,
C.
Felsheim
c and
J.
Rieckermann
 a
a
aDepartment of Urban Water Management, Swiss Federal Institute of Aquatic Science & Technology (Eawag), Überlandstrasse 133, 8600 Dübendorf, Switzerland. E-mail: pierre.lechevallier@eawag.ch
bOak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37830, USA
cHeadwall Photonics, 580 Main St, Bolton, MA 01740, USA
First published on 19th February 2024
Abstract
Monitoring water quality in sewers is challenging, particularly because state-of-the-art technologies require contact with the raw wastewater. The presence of fat, oil, grease, and solids makes automated grab sampling difficult and causes sensor fouling. To overcome these limitations, non-contact methods based on light reflectance, such as hyperspectral imaging (HSI), are gaining attention. However, HSI has never been tested for raw wastewater. To assess its accuracy for measuring pollution, we developed a laboratory setup and performed targeted experiments with a combination of raw and diluted wastewater, as well as synthetic turbidity stock solutions. We measured seven pollution variables: chemical oxygen demand, turbidity, dissolved organic compounds, ammonium, total nitrogen, phosphate, and sulphates. We used automated pixel selection and partial least squares regression to retrieve pollution information from the hyperspectral images. Our results, based on 144 samples, suggest that HSI can estimate pollution levels with a precision in the range of state-of-the-art absorbance spectrophotometric methods. Additionally, we found that the combination of pixel and wavelength selection, enabled by the hyperspectral data structure, significantly influences the performance of partial least square modelling. Overall, our findings indicate that HSI is a promising technology for non-contact monitoring of water quality in raw wastewater.
Water impactNon-contact wastewater quality monitoring can revolutionize urban water management. It avoids sensor fouling and corrupted measurements by eliminating physical contact with aggressive wastewater. Hyperspectral monitoring provides near-real-time water quality data with minimal maintenance, enabling cost-effective analyses in sewers and remote areas. Though correlation-based, it empowers researchers, policymakers, and communities to protect water resources, make informed decisions, and foster environmental sustainability. |
1 Introduction
Emissions from urban drainage systems (UDS) cause significant environmental pollution, including the release of particles, microplastics, and nutrients.1 However, there is a lack of knowledge about the occurrence and dynamics of pollutants in UDS, partly because continuous monitoring of raw wastewater is extremely challenging.2 Sensors and sampling equipment that are in contact with wastewater are difficult to manage and maintain due to exposure to grease, fat, solids, etc.3 Non-contact water quality monitoring techniques have the potential to address these challenges, but research on this topic is still limited to seven peer-reviewed publications.4–10In a pioneering study, Russell et al., 2003 measured the light reflection intensity of an 880 nm laser on 200 wastewater samples in the laboratory.5 They obtained promising results for the estimation of oxygen demand (COD) (R2 = 0.79) and suspended solids (R2 = 0.83), but the subsequent field trials were unsatisfactory. We believe that either the use of a laser as a light source was too restricting for pollution measurement, or that external disturbances, such as direct reflection from surface waves or ripples of the moving water, were not adequately filtered out.
More than 10 years later, Agustsson et al., 2014 improved upon the limitations of Russell's single-wavelength setup by using a Xenon light source and a spectrophotometer (200–1100 nm).7 They estimated COD (R2 = 0.85) and turbidity (R2 = 0.96) with slightly better accuracy using a partial least squares (PLS) approach. However, they only used synthetic wastewater, which limits the generalizability of their results. Additionally, the use of a spectrophotometer in real world applications might be challenging due to its limited field of view.11
Fortunately, these limitations can now be overcome with the use of hyperspectral imaging (HSI) technologies. Unlike a spectrophotometer, which measures a single absorbance spectrum representing the total light intensity in the ultraviolet (UV) to near infrared (NIR) range from a surface of interest, a hyperspectral imaging (HSI) system can capture a picture with a spectrum on each pixel. This enables the use of advanced object classification, machine learning, and image analysis techniques on the resulting 3D data-cube structure.12 Recently, HSI has been used to monitor highly polluted industrial wastewater, with promising results.10
To the best of our knowledge, the application of HSI for monitoring the pollution of untreated municipal wastewater has not been explored. In this proof-of-concept study, we aim to assess its potential for high-frequent, precise, and non-contact monitoring of raw urban sewerage. Therefore, we developed a laboratory setup to acquire hyperspectral images of mixtures of real wastewater samples and a synthetic turbidity standard. Our results demonstrate that the use of HSI for pollution monitoring is promising, even if the method is correlation-based. This paper finally discusses the potential for improvements and outstanding questions regarding real-world applications.
2 Material and methods
In this study, hyperspectral images of 144 different mixtures of untreated municipal wastewater with known pollution concentrations were acquired. Data-driven models were trained and validated to retrieve pollution estimations from the hyperspectral data.2.1 Experimental setup for hyperspectral data acquisition
The MV.X hyperspectral imaging system is water-resistant (rated IP66 and IP67), therefore suitable to remotely measure the reflectance of wastewater. It measures 300 spectral bands with a 2 nm spectral resolution in the visible and near infrared (VNIR) range between 400 nm and 1000 nm across a line of 1020 spatial pixels. The temporal resolution ranges from milliseconds to seconds, depending on the lighting conditions and the reflection properties of the object being measured. Additionally, the MV.X is equipped with an embedded processor for fast data processing, allowing for continuous spectral analysis in near-real time.
2.2 Description of the hyperspectral data-cube structure
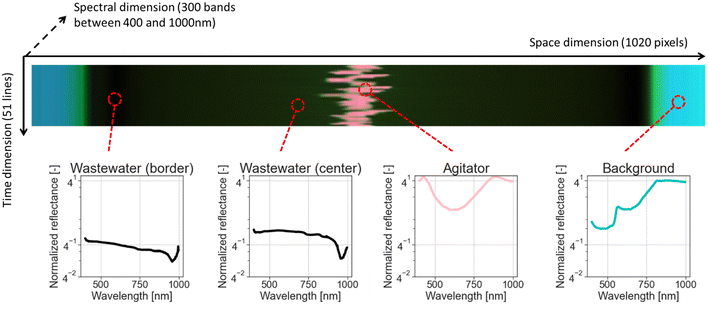
Each hyperspectral data-cube is composed of a series of 10 cm wide lines. Each line is measured as a series of 1020 pixels, and each pixel contains a reflectance spectrum corresponding to 300 wavelength bands. The camera takes a measurement of each line every 200 ms for a duration of 10 s, resulting in 51 lines for a single water sample.A pseudo red-blue-green (RGB) visualization of a data-cube is shown in Fig. 1, with different pixels represented by their spectra. The area of interest, corresponding to the wastewater surface, is represented by the dark pixels. The areas at the border of the cup and in the middle of the cup (due to the magnetic stirrer) have very different spectral signatures and can be easily removed during pre-processing.
2.3 Wastewater sample collection, mixture preparation, and image acquisition
For this first laboratory proof-of-concept experiment, we acquired hyperspectral data-cubes of 144 samples obtained from mixtures of real wastewater from a trunk sewer at Eawag (Dübendorf, Switzerland), synthetic wastewater, and tap water.For the purpose of conducting a first study on the use of HSI for pollution measurement, we consider this dataset sufficient. The mixture generation protocol, despite imposing limitations on the interpretability of the results (discussed in 3.5), made it possible to generate a wide variety of different samples while limiting the amount of laboratory reference measurement.
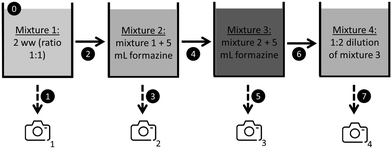
The mixing procedure followed four steps, with hyperspectral data being collected after each one (Fig. 2). The first step consisted of mixing two 100 mL samples from the eight raw wastewaters samples. The second and third step consisted of adding 5 mL of formazine, increasing the turbidity with steps of 96.6NTU and 95.2NTU. Finally, the third mixtures were diluted twice with tap water. Starting with 8 raw wastewater samples, a maximum of 36 combinations were obtained after the first mixing step. Therefore, 144 (36 × 4) different data-cubes could be captured following this procedure.
| Water quality variable | Measurement method | Instrument | Accuracy |
|---|---|---|---|
| COD | Cuvette test | Hach LCK-314 | 3 mg L−1 |
| PO4–P, SO4–S | Ion-chromatography: DIN EN ISO 10304-1, 2009 | Metrohm 930 Compact IC Flex | <0.1 mg L−1 |
| NH4–N | Flow injection analysis: standard method 4500-NH3, EPA 600/4-79-020, 1983 | Lachat QC8500 | 0.2 mg L−1 |
| Turbidity | Turbidimeter: DIN EN ISO 7027-1, 2016 | Hach TL2300 | 2% |
| DOC | TOC analyzer: DIN EN ISO 20236, 2023 | Shimadzu TOC-L CSH | 0.5 mg L−1 |
| TDN | TOC analyzer: DIN EN ISO 20236, 2023 | Shimadzu TOC-L CSH | 0.4 mg L−1 |
Collecting the 144 data-cubes lasted about 9 hours. In our experience, the organic pollution of the wastewater used in this study degrades at a rate of about 10% each day due to biological activity. To account for this, reference pollution measurements were performed before (08:00) and after (17:00) full data acquisition, and the average of both measurements was used as ground truth. Because of the known mixing proportions for the 144 mixtures, we were able to calculate their pollution. An overview of the pollution characteristics of the mixtures is presented in SI B.†
2.4 Chemometric modelling of wastewater pollution
To retrieve wastewater pollution from the hyperspectral data-cubes, a two-step procedure was developed and applied (Fig. 3).Substep 1.1 – conversion to reflectance. The raw images were converted by subtracting the camera noise (dark reference) and dividing by the reflection of the calibration target (white reference).
Substep 1.2 – data-cube re-framing. The data-cubes were cropped (i) to remove border wavelengths showing high noise (400–418 nm and 982–1000 nm), (ii) to remove some sample lines (lines 46 and above) in order to ensure that all the data-cubes have the same dimension, and (iii) to remove pixels that do not represent the water surface (pixels 1 to 110 and 861 to 1020).
Substep 1.3. – pixel selection. A threshold method was used to filter out the outlier pixels not corresponding to the wastewater surface (as highlighted in Fig. 1). Specifically, we created and applied a 2D mask that excludes the lowest and highest 20% of the light reflection intensity values.
Substep 1.4. – extraction of the mean reflectance spectra. The remaining 60% of the pixels were used to calculate the mean and standard deviation of the wastewater reflectance for every wavelength. For all samples and all wavelengths, the obtained standard deviation was below 10% of the mean value, which was a satisfactory criteria to consider this method as reliable. The mean values obtained at every wavelength for a single sample were considered as a spectrum representative of the wastewater surface.
Substep 1.5. – spectra pre-processing. Each spectrum was further processed by applying (i) a Savitzky–Golay filter with a window size of 17 and a polynomial order of 2,17 and (ii) a logarithmic transformation. This pre-processing was found to be leading to optimal PLS model performance in step 2.
Substep 2.1 – classification of the wavelengths. To perform the ISE-PLS, it was first necessary to classify the wavelengths, i.e., the model features, by absolute regression coefficient. For each number of latent variables and each pollution variable, a PLS model was fitted with all the wavelengths to retrieve the wavelength classification. This approach was applicable without input normalization, as the features were already normalized in step 1.1.
Substep 2.2 – optimization of the PLS. The optimization was performed by calculating the performance of each PLS model based on a combination of latent variable number and of discarded wavelength number from the wavelength classification obtained in the previous step. The PLS model performance was measured with the root mean squared error (RMSE) between the reference pollution values and the predictions obtained with leave-one-out cross-validation (LOOCV).
Substep 2.3 – detailed optimal model evaluation. Once the optimal combination was found, we calculated not only the RMSE of the model but additionally the determination coefficient R2 and the relative RMSE to better compare different model performance indicators. The relative RMSE is useful to compare the performance of each model. Table 2 shows previously defined scale rate model performances in the field of wastewater UV-vis spectrophotometry.22
| RMSErelative | Performance rating |
|---|---|
| <5% | Very good |
| 5–10% | Good |
| 10–20% | Satisfactory |
| >20% | Unsatisfactory |
2.5 Numerical experiment to quantify the impact of pixel and wavelength selection on the partial least squares model quality
Due to the multi-dimensionality of the hyperspectral data-cubes, the modelling methods described above rely on (i) a pixel selection for the extraction of a wastewater representative spectrum from the hyperspectral acquisition (Substep 1.3) and (ii) a wavelength selection to select wavelengths that carry relevant information for a given pollution variable (Substeps 2.1 and 2.2). To quantify their respective impacts, we conducted three additional numerical experiments:1. A PLS model was optimized without pixel selection and without wavelength selection.
2. A PLS model was optimized without pixel selection but with wavelength selection.
3. A PLS model was optimized with pixel selection but without wavelength selection.
A comparison between these three models' performances and the result of the previous section was conducted in terms of RMSE for each pollution variable.
3 Results and discussion
3.1 Exploratory analysis of raw reflectance spectra and the effect of turbidity
Fig. 4 (left) shows the 144 raw reflectance spectra extracted from the data-cubes. All spectra have a similar shape, with moderate peaks or bumps at specific wavelengths, such as around 470 nm, 770 nm, and 820 nm. Each of the four mixture types, as defined in Fig. 2, has a distinct spectral signature, which indicates that the use of formazine influences the spectral shape by increasing the light reflection more for shorter wavelengths.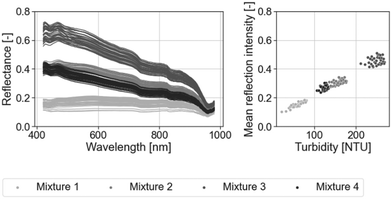 | ||
| Fig. 4 Left: overview of the 144 raw wastewater reflectance spectra extracted from the hyperspectral data-cubes (after step 1.4, see Fig. 3). Right: linear relationship between turbidity and mean reflectance intensity. | ||
Turbidity is linearly (R2 = 0.96, see SI E†) related to the mean reflection intensity of each spectrum, as highlighted in Fig. 4 (right). This linear relationship is only true for turbidity, which is expected because the number of suspended particles determines how much light is reflected. Interestingly, the variance of the reflection intensity also increases with turbidity concentration, indicating that specific methods such as weighted regression models might even provide better estimation than the linear model.23 We will discuss the practical implications of this relationship between turbidity and light reflection in section 3.3.1.
3.2 Overview of the model's performance and parameters for water quality prediction
The water quality predictions of the PLS model are presented in Fig. 5. For all water quality variables except SO4–S, the prediction and laboratory values match each other well (R2 > 0.9).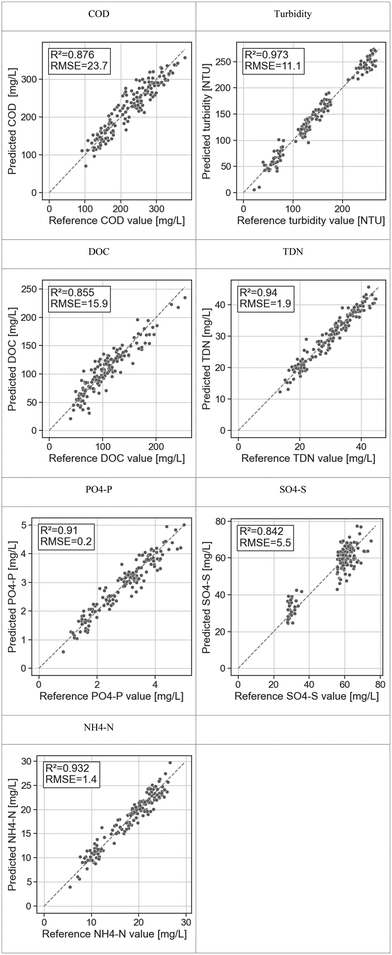 | ||
| Fig. 5 Overview of the PLS regression LOOCV results for each pollution variable. A high R2 value (close to 1) and a low RMSE, arguably, describe a good predictive performance of the PLS model. | ||
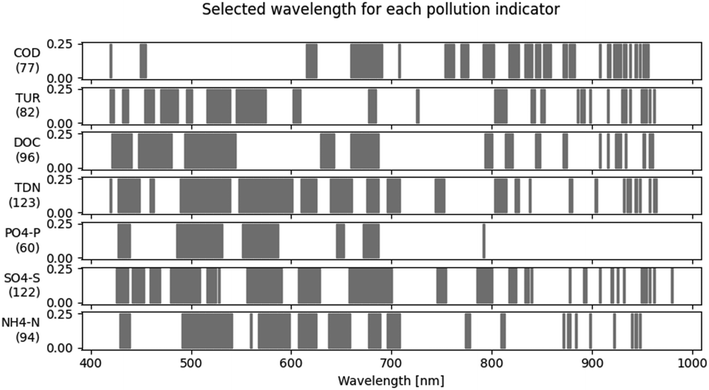
The model's performances and parameters are summarized in Table 3. The optimal number of latent variables is between 12 and 20 (the maximum tested values). This is consistent with the experimental design, as at least 10 latent variables were needed to explain the variability of the mixtures (see 2.3). Sample degradation may also have contributed to increased sample variability. In addition, by using wavelength selection (Steps 2.1 and 2.2), the 280 initial wavelengths could be reduced to 21–44%. Nevertheless, 82% of wavelengths are still used in at least one of the models. An overview of the selected wavelengths for each variable is shown in Fig. 6. The wavelength in the visible range (400–750 nm) plays a predominant role for every variable except COD, where wavelengths above 650 nm are more important.
| Water quality variable | Unit | Min | Max | Optimal number of latent variables | Optimal number of wave-lengths | R 2 | RMSE | RMSE (relative) |
|---|---|---|---|---|---|---|---|---|
| COD | mg L−1 | 91.2 | 379.0 | 19 | 77 | 0.88 | 23.7 | 10.5% |
| Turbidity | NTU | 21.6 | 267.3 | 18 | 82 | 0.97 | 11.1 | 7.6% |
| DOC | mg L−1 | 45.1 | 302.9 | 13 | 96 | 0.85 | 16.0 | 14.9% |
| TDN | mg L−1 | 13.5 | 44.6 | 17 | 123 | 0.94 | 1.9 | 6.6% |
| PO4–P | mg L−1 | 0.8 | 5.0 | 12 | 60 | 0.91 | 0.2 | 9.8% |
| SO4–S | mg L−1 | 27.8 | 74.7 | 18 | 122 | 0.84 | 5.5 | 10.4% |
| NH4–N | mg L−1 | 5.4 | 26.6 | 20 | 94 | 0.93 | 1.4 | 7.9% |
The overall good performance of the modelling approach is reflected in the low RMSE. All the pollution variables are estimated with a relative RMSE of about 10%, which is considered good to satisfactory in wastewater spectrophotometry (Table 2). A similar study with a UV-vis probe in sewers obtained similar results for COD, ammonium, sulphate and phosphate.24 Even if turbidity, DOC, and TDN were not included in this other study, our results suggest that HSI performance in this specific monitoring setup is comparable to that of immersed spectrophotometric probes to measure pollutant concentrations.
3.3 Discussion of the results for each pollution variable
Analysis of the selected wavelengths shows that wavelengths between 400 and 600 nm are the most important. This supports the results of other studies that found that the visible range is significant for turbidity measurement.25,26 Interestingly, accurate turbidity measurements were obtained from laboratory experiments using a standard RGB camera.27,28 Similarly, when we only use the three RGB wavelengths as input into a PLS model, we obtain good predictions for turbidity prediction (RMSE: 12.2 NTU; see SI E†). We plan to investigate this in future work since our results indicate that turbidity might be quantified well using a low-cost camera.
The addition of formazine (C17H13N503) has an impact on the concentration of organically bound nitrogen, and therefore the mixtures with formazine have a different ammonium–TDN ration than typical wastewaters. This did not prevent the PLS model from estimating them accurately, which reinforces the possibility that specific and different features of the reflectance spectra are informative for the estimation of ammonium and TDN. When training a model with the 36 mixtures containing only raw wastewater (analysis presented in SI F†), both ammonium and total dissolved nitrogen are estimated with a precision below 3% (R2 = 0.97), which implies that the use of formazine might even worsen the accuracy of nitrogen compound estimation. Nevertheless, further analysis with more samples is necessary to investigate this.
Despite a low RMSE, Fig. 5 shows that, contrary to the other variables, SO4–S estimations are not reliable. Finally, PO4–P is estimated with a similar precision as NH4–N and TDN. Phosphate and ammonium were initially very well correlated (ρ = 0.95). The selected wavelengths are also similar. However, a big difference is that the optimal PO4–P model uses fewer latent variables12 and wavelengths (60). We could not find any satisfactory explanation for those observations yet.
3.4 Result of the numerical experiment to quantify the benefit of hyperspectral imaging and discussion of further advantages
HSI makes non-contact measurement of a wide range of pollutants possible. The unique HSI data-structure allows for the selection of informative pixels within the field of view, combined with wavelength selection. The results of the numerical experiment to quantify their impact are presented in Table 4.| Pixel selection | Wavelength selection | COD [mg L−1] | Turbidity [NTU] | DOC [mg L−1] | TDN [mg L−1] | PO4–P [mg L−1] | SO4–S [mg L−1] | NH4–N [mg L−1] | |
|---|---|---|---|---|---|---|---|---|---|
| a Compared to the RMSE without optimization. | |||||||||
| No | No | RMSE | 29.8 | 12.8 | 22.5 | 3.6 | 0.4 | 8.3 | 2.7 |
| No | Yes | RMSE | 27.1 | 11.0 | 19.9 | 3.1 | 0.4 | 7.2 | 2.3 |
| % of improvementa | 8.9 | 13.9 | 11.4 | 14.8 | 10.8 | 12.7 | 17.4 | ||
| Yes | No | RMSE | 26.1 | 12.1 | 17.0 | 2.3 | 0.3 | 6.3 | 1.7 |
| % of improvementa | 12.3 | 5.4 | 24.5 | 37.4 | 26.0 | 23.6 | 38.9 | ||
| Yes | Yes | RMSE | 23.8 | 11.1 | 16.0 | 2.0 | 0.3 | 5.6 | 1.4 |
| % of improvementa | 20.2 | 13.1 | 29.0 | 45.6 | 34.9 | 32.9 | 48.0 | ||
The improvements after wavelength selection (8.9–17.4%) are lower than those achieved by pixel selection (5.4–38.9%). As expected, combining both results in the largest improvement (13.1–48.0%, 32% on average). So, this numerical experiment highlights the advantage of HSI for pollution measurement over other measurement techniques with lower spectral and spatial resolution. We believe this to be crucial for UDS application as surface perturbations, including foam, ripples, or floating objects, are ubiquitous in sewer infrastructures and will cause a large number of anomalies.
In addition to the benefits of enabling contactless pollution measurement, HSI has a sampling dimension of several decimetrers, which is on the same spatial scale as the grab samples collected as ground truth. Compared to state-of-the-art submerged spectrophotometers, which operate with an optical window of a few millimeters, we expect that the estimation of pollution is less sensitive to disturbances from wastewater variability and sampling artefacts, such as the position of the sensor in the sewer cross section.
Finally, another advantage of HSI is the potential to extract hydrodynamic information from the hyperspectral data-cubes. Current imaging technology can detect the water level in sewer videos,30,31 measure the water flow32 and detect fat layer accumulation.33 To what extent hyperspectral information could improve this, e.g., by better distinguishing pipe material from water surfaces or by facilitating superior particle-image-velocimetry, should be investigated in future studies.
3.5 Limitations of the experimental design to generalize the results
We identified two major limitations. First, despite collecting HSI data from 144 different mixtures, the pollution variability is low compared to real-world sewage because the mixtures are prepared with a smaller number of initial samples (i.e., 8). This was motivated by the desire to create a simple experimental design to serve as a proof-of-concept for the use of HSI for pollution measurement. Another drawback of this protocol is that the data collection lasted nine hours. During this time, organic compounds in the samples were slightly degraded, which probably changed the wastewater matrix. For future work, continuous cooling of the samples could help stabilize the wastewaters since the organic degradation rate increases with temperature.Second, as highlighted in 3.1 and 3.3.2, the use of formazine has a significant impact on both the spectral reflectance and on the correlation between water quality variables. This limits the generalization of the PLS results and of the wavelength analysis for the real wastewater matrix. To draw conclusions on data without synthetic stock solutions, we tested the modelling approach with 36 of the 144 mixtures without formazine (see SI D†), and obtained similar results as with the 144 mixtures. This is encouraging, but the number of samples is too small to draw reliable conclusions.36
Ultimately, investigating more samples of real wastewater, without synthetic mixtures, will produce more reliable results. We are now planning to collect data over an open channel for several months to critically evaluate the HSI performance in real-world conditions.
3.6 Potential improvement of the chemometric pollution modelling
We deliberately used standard approaches to retrieve pollution from observed spectra because we believe that the regression results are more influenced by the raw data quality than by the methodological approach to data-driven modelling. Nevertheless, for future studies, we identified two potential areas for improvement.First, alternative approaches for wavelength selection can improve the interpretability of the results. Because PLS is based on a reduction of the spectral dimension in the direction of minimal covariance with the targeted pollution variables, PLS weights are not easy to interpret physically.34 In the future, LASSO regression35 seems particularly promising to analyse the more representative wavelengths since this model is designed to discard features of low importance. Other potential methods, such as principal component analysis and the random frog algorithm for variable selection, might also be explored.26
Second, a nested cross-validation procedure suited to the specific data-structure may improve the interpretability of the results. We used LOOCV to minimize the bias from the splitting of the data into a training and a testing set in the model performance estimation.36 However, because each model is trained with all the spectra but one, this procedure can overestimate performance due to data leakage, i.e., the transfer of information about the testing set into the training set. This is particularly relevant when considering that the 144 mixtures are not independent but obtained after mixing a smaller number of raw samples (see 2.3). A nested cross-validation based on the exclusion of all the mixtures containing a specific raw wastewater from the testing set can solve this concern.37
3.7 Knowledge gaps to consider for future sewer application
It was not within the scope of this proof-of-concept study to quantify the influence of light position and light intensity. Stronger lighting could enable positioning the light at a lower angle, which could maximize the amount of diffuse light reflection containing spectral information about the sample composition. This could also reduce the acquisition time for the camera, allowing for a more precise pixel selection by increasing the line acquisition frequency.In UDS, HSI calibration will require more consideration because measurement conditions are not as stable as in controlled laboratory environments. Nonetheless, HSI systems are already widely used for more challenging monitoring tasks, such as the mapping of vegetation in daylight. Therefore, such UDS-specific conditions can be compensated for by selecting specifically stable monitoring sites or by including other sensors, such as a light detector, to control the environment.
On a more general level, it is important to understand the influence of light and camera position relative to the wastewater surface in the HSI measurement because water level and flow vary in sewers. In the future, it may be valuable to develop process-based models that can quantify light reflection in very turbid and variable media, such as wastewater, to account for those UDS variations. Possible approaches could include adapting well-established models such as a sea reflection model,38 the Kubelka–Munk theory,39 or using Monte Carlo simulation.40
Finally, other experimental challenges must be addressed before installing hyperspectral cameras and halogen light sources for routine measurements in UDS. For instance, humidity, aerosols, and a changing sewer atmosphere could cause systematic errors through altered light propagation properties. One possible solution to this problem is on-line calibration with multiple light sources or varying light intensities. Additionally, condensation or splashing water could cause fouling of the camera, so a cleaning system may be necessary.
4 Conclusions
In this study, we investigated a non-contact hyperspectral imager as a novel system to measure wastewater pollution. Based on the satisfactory experimental results and on theoretical as well as practical considerations, we draw the following conclusions:• By combining pixel and wavelength selection with PLS regression, one can accurately estimate pollutant concentrations (relative RMSE below 10%) for four of seven water quality indicators of interest: turbidity, TDN, NH4–N, and PO4–P. Aggregate organic constituents (COD, DOC) were also predicted with a relative RMSE below 15%, which is considered satisfactory.
• The reported accuracies are best for turbidity (7.6%) and TDN (6.6%). We showed that turbidity is directly linked to light reflection intensity, independently of the wavelength. For TDN, we hypothesize that the measurement is made possible by the detection of organically bound nitrogen, but additional research is needed to confirm this.
• Using a hyperspectral imager has several advantages over other imaging techniques with lower spatial or spectral resolution. The water quality predictions were, on average, 32% more precise when using a pixel and a wavelength selection. Furthermore, the benefits of pixel selection might be even greater in real-world applications where many disturbances must be filtered out.
• Our results support historical findings that proposed non-contact imaging technologies based on reflectance spectrophotometry for raw wastewater monitoring in sewers. The hyperspectral imaging system (HSI) deployed in this work brings this promise closer to reality due to being able to circumvent the negative effects of disturbances in the water surface, such as foam, ripples, etc.
List of abbreviations
| COD | Chemical oxygen demand |
| DOC | Dissolved organic carbon |
| HSI | Hyperspectral imaging |
| ISE-PLS | Iterative stepwise elimination – partial least squares |
| LOOCV | Leave-one-out cross validation |
| MAPE | Mean absolute percentage error |
| NH4-N | Ammonium |
| NIR | Near infrared |
| NTU | Nephelometric turbidity unit |
| PLS | Partial least squares |
| PO4–P | Phosphate |
| RMSE | Root mean square error |
| RGB | Red blue green |
| SI | Supplementary information |
| SO4–S | Sulfate |
| TDN | Total dissolved nitrogen |
| UDS | Urban drainage system |
| UV | Ultraviolet |
| VNIR | Visible near infrared |
Code and data availability
Custom Python scripts were developed for this research paper using the Spectral 0.23.1 and the Scikit-learn 1.2.0 Python modules. To make our research reproducible, the codes and the data are openly available here: https://doi.org/10.25678/0007WY.41Author contributions
Conceptualization: PL, JR; experimental setup: PL, CF; data gathering: PL; data analysis and visualization: PL, KV; writing, review and editing: PL, JR, KV, CF; supervision: JR.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Sebastien Blanc for the help in the laboratory setup development, Mathieu Lepot and Andreas Scheidegger for their help in modelling, Christian Förster for the support for Python coding, Sylvia Richter for the laboratory analysis, Adriano Joss and Nicolas Derlon for the insight about Eawag wastewater, Kilian Perrelet for the manuscript review, and the Eawag Urban Water Management department for the financing of the HSI imager. This work is supported by the EU's H2020 research and innovation program grant no. 101008626 (Co-UDLabs Project).References
- EC, Water quality in Europe: effects of the urban wastewater treatment directive: a retrospective and scenario analysis of Dir, 91/271/EEC, LU: Publications Office of the European Union, 2019, [cited 2022 Jun 23], Available from: https://data.europa.eu/doi/10.2760/303163 Search PubMed.
- F. Blumensaat, P. Staufer, S. Heusch, F. Reußner, M. Schütze and S. Seiffert, et al. Water quality-based assessment of urban drainage impacts in Europe – where do we stand today?, Water Sci. Technol., 2012, 304–313 CrossRef CAS PubMed.
- G. Gruber, J. L. Bertrand-Krajewski, J. D. Beneditis, M. Hochedlinger and W. Lettl, Practical aspects, experiences and strategies by using UV/VIS sensors for long-term sewer monitoring, Water Pract. Technol., 2006, 1(1), wpt2006020 CrossRef.
- A. Gitelson, R. Stark and I. Dor, Quantitative near-surface remote sensing of wastewater quality in oxidation ponds and reservoirs: A case study of the Naan system, Water Environ. Res., 1997, 69(7), 1263–1271 CrossRef CAS.
- S. L. Russell, D. R. Marshallsay, B. MacCraith and M. Devisscher, Non-contact measurement of wastewater polluting load – the Loadmon project, Water Sci. Technol., 2003, 47(2), 79–86 CrossRef CAS PubMed.
- U. Natesan, Monitoring the tannery effluent characteristics using remote sensing technique, Asian J. Chem., 2013, 25(7), 3796–3798 CrossRef CAS.
- J. Agustsson, O. Akermann, D. Barry and L. Rossi, Non-contact assessment of COD and turbidity concentrations in water using diffuse reflectance UV-Vis spectroscopy, Environ. Sci.: Processes Impacts, 2014, 16(8), 1897–1902 RSC.
- Z. Xing, J. Chen, X. Zhao, Y. Li, X. Li and Z. Zhang, et al., Quantitative estimation of wastewater quality parameters by hyperspectral band screening using GC, VIP and SPA, PeerJ, 2019, 7, e8255 CrossRef PubMed.
- J. Xie, D. Sun, J. Cai and F. Cai, Waveband selection with equivalent prediction performance for FTIR/ATR spectroscopic analysis of COD in sugar refinery waste water, Comput. Mater. Contin., 2019, 59(2), 687–695 Search PubMed.
- D. Huang, J. Ye, S. Yu, Y. Tian, X. Wen and Y. Wang, et al., Study on a fast non-contact detection method for key parameters of refractory organic wastewater treatment, Biochem. Eng. J., 2022, 177, 108269 CrossRef CAS.
- D. F. Barbin, G. ElMasry, D. W. Sun and P. Allen, Predicting quality and sensory attributes of pork using near-infrared hyperspectral imaging, Anal. Chim. Acta, 2012, 16(719), 30–42 CrossRef PubMed.
- N. Audebert, B. Le Saux and S. Lefevre, Deep learning for classification of hyperspectral data: A comparative review, IEEE Geosci. Remote Sens. Mag., 2019, 7(2), 159–173 Search PubMed.
- G. El Masry and D. W. Sun, in Hyperspectral Imaging for Food Quality Analysis and Control, ed. D. W. Sun, Academic Press, San Diego, 2010, ch. 1, pp. 3–43 Search PubMed.
- M. T. Munir, D. I. Wilson, W. Yu and B. R. Young, An evaluation of hyperspectral imaging for characterising milk powders, J. Food Eng., 2018, 221, 1–10 CrossRef CAS.
- N. Caporaso, M. B. Whitworth and I. D. Fisk, Protein content prediction in single wheat kernels using hyperspectral imaging, Food Chem., 2018, 240, 32–42 CrossRef CAS PubMed.
- G. ElMasry, N. Wang, A. ElSayed and M. Ngadi, Hyperspectral imaging for nondestructive determination of some quality attributes for strawberry, J. Food Eng., 2007, 81(1), 98–107 CrossRef CAS.
- S. Abraham and M. J. E. Golay, Smoothing and Differentiation of Data by Simplified Least Squares Procedures, Anal. Chem., 1964, 36(8), 1627–1639 CrossRef.
- M. Lepot, A. Torres, T. Hofer, N. Caradot, G. Gruber, J. Aubin and J. Bertrand-Krajewski, Calibration of UV/Vis spectrophotometers: A review and comparison of different methods to estimate TSS and total and dissolved COD concentrations in sewers, WWTPs and rivers, Water Res., 2016, 101, 519–534 CrossRef CAS PubMed.
- A. Mašić, A. T. L. Santos, B. Etter, K. M. Udert and K. Villez, Estimation of nitrite in source-separated nitrified urine with UV spectrophotometry, Water Res., 2015, 85, 244–254 CrossRef PubMed.
- T. Mehmood, K. H. Liland, L. Snipen and S. Sæbø, A review of variable selection methods in Partial Least Squares Regression, Chemom. Intell. Lab. Syst., 2012, 118, 62–69 CrossRef CAS.
- Z. Wang, K. Kawamura, Y. Sakuno, X. Fan, Z. Gong and J. Lim, Retrieval of chlorophyll-a and total suspended solids using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) regression based on field hyperspectral measurements in irrigation ponds in Higashihiroshima, Japan, Remote Sens., 2017, 9, 264 CrossRef.
- R. Brito, H. Pinheiro, F. Ferreira, J. Matos and N. Lourenço, In situ UV-Vis spectroscopy to estimate COD and TSS in wastewater drainage systems, Urban Water J., 2014, 11, 261–273 CrossRef CAS.
- R. J. Caroll and D. Ruppert, Transformation and Weighting in Regression, Chapman and Hall/CRC, New York, 2017 Search PubMed.
- M. Pacheco, T. Knutz and M. Barjenbruch, Multi-Parameter calibration of a UV/Vis spectrometer for online monitoring of sewer systems, Water Sci. Technol., 2020, 82(5), 927–939 CrossRef PubMed.
- O. Thomas and C. Burgess, UV-Visible spectrophotometry of water and wastewater, Elsevier Science, Amsterdam, 2017 Search PubMed.
- Y. Guo, C. Liu, R. Ye and Q. Duan, Advances on Water Quality Detection by UV-Vis Spectroscopy, Appl. Sci., 2020, 10(19), 6874 CrossRef CAS.
- D. Mullins, D. Coburn, L. Hannon, E. Jones, E. Clifford and M. Glavin, A novel image processing-based system for turbidity measurement in domestic and industrial wastewater. Water, Water Sci. Technol., 2018, 77(5–6), 1469–1482 CrossRef CAS PubMed.
- Y. Li, X. Wang, Z. Zhao, S. Han and Z. Liu, Lagoon water quality monitoring based on digital image analysis and machine learning estimators, Water Res., 2020, 172, 115471 CrossRef CAS PubMed.
- D. Carreres-Prieto, J. T. García, F. Cerdán-Cartagena and J. Suardiaz-Muro, Wastewater quality estimation through spectrophotometry-based statistical models, Sensors, 2020, 20(19), 5631 CrossRef CAS PubMed.
- H. W. Ji, S. S. Yoo, B. J. Lee, D. D. Koo and J. H. Kang, Measurement of wastewater discharge in sewer pipes using image analysis, Water, 2020, 12(6), 1771 CrossRef.
- L. S. Nguyen, B. Schaeli, D. Sage, S. Kayal, D. Jeanbourquin and D. A. Barry, et al. Vision-based system for the control and measurement of wastewater flow rate in sewer systems, Water Sci. Technol., 2009, 60(9), 2281–2289 CrossRef CAS PubMed.
- J. P. Leitão, S. Peña-Haro, B. Lüthi, A. Scheidegger and M. Moy de Vitry, Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry, J. Hydrol., 2018, 565, 791–804 CrossRef.
- A. M. Moreno-Rodenas, A. Duinmeijer and F. H. L. R. Clemens, Deep-learning based monitoring of FOG layer dynamics in wastewater pumping stations, Water Res., 2021, 202, 117482 CrossRef CAS PubMed.
- T. N. Tran, N. L. Afanador, L. M. C. Buydens and L. Blanchet, Interpretation of variable importance in Partial Least Squares with Significance Multivariate Correlation (sMC), Chemom. Intell. Lab. Syst., 2014, 138, 153–160 CrossRef CAS.
- R. Tibshirani, Regression shrinkage and selection via the Lasso, J. R. Stat. Soc. Series B Stat. Methodol., 1996, 58(1), 267–288 Search PubMed.
- J. L. Myers, A. D. Well, R. F. Lorch and A. Well, Research design and statistical analysis, 3rd edn, Routledge, New York, 2010 Search PubMed.
- D. Krstajic, L. J. Buturovic, D. E. Leahy and S. Thomas, Cross-validation pitfalls when selecting and assessing regression and classification models, J. Cheminf., 2014, 6(1), 10 Search PubMed.
- A. Morel, Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters), J. Geophys. Res.: Oceans, 1988, 93(C9), 10749–10768 CrossRef.
- L. Yang and B. Kruse, Revised Kubelka–Munk theory. I. Theory and application, J. Opt. Soc. Am. A, 2004, 21(10), 1933–1941 CrossRef PubMed.
- L. Ma, F. Wang, C. Wang, C. Wang and J. Tan, Monte Carlo simulation of spectral reflectance and BRDF of the bubble layer in the upper ocean, Opt. Express, 2015, 23(19), 24274 CrossRef CAS PubMed.
- P. Lechevallier and J. Rieckermann, Data and codes for: Towards non-contact pollution monitoring in sewers with hyperspectral imaging, 2022 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ew00541k |
| This journal is © The Royal Society of Chemistry 2024 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: