A comparison of non-covalent interactions in the crystal structures of two σ-alkane complexes of Rh exhibiting contrasting stabilities in the solid state

Abstract

Non-covalent interactions surrounding the cationic Rh σ-alkane complexes within the crystal structures of [(Cy₂PCH₂CH₂PCy₂)Rh(NBA)][BAr^F₄], [1-NBA][BAr^F₄] (NBA = norbornane, C₇H₁₂; Ar^F = 3,5-(CF₃)₂C₆H₃), and [1-propane][BAr^F₄] are analysed using Quantum Theory of Atoms in Molecules (QTAIM) and Independent Gradient Model approaches, the latter under a Hirshfeld partitioning scheme (IGMH). In both structures the cations reside in an octahedral array of [BAr^F₄]⁻ anions within which the [1-NBA]⁺ cation system exhibits a greater number of C–H⋯F contacts to the anions. QTAIM and IGMH analyses indicate these include the strongest individual atom–atom non-covalent interactions between the cation and the anion in these systems. The IGMH approach highlights the directionality of these C–H⋯F contacts that contrasts with the more diffuse C–H⋯π interactions. The accumulative effects of the latter lead to a more significant stabilizing contribution. IGMH %δG^atom plots provide a particularly useful visual tool to identify key interactions and highlight the importance of a –{C₃H₆}– propylene moiety that is present within both the propane and NBA ligands (the latter as a truncated –{C₃H₄}– unit) and the cyclohexyl rings of the phosphine substituents. The potential for this to act as a privileged motif that confers stability on the crystal structures of σ-alkane complexes in the solid-state is discussed. The greater number of C–H⋯F inter-ion interactions in the [1-NBA][BAr^F₄] system, coupled with more significant C–H⋯π interactions are all consistent with greater non-covalent stabilisation around the [1-NBA]⁺ cation. This is also supported by larger computed δG^atom indices as a measure of cation–anion non-covalent interaction energy.

---

1. Introduction

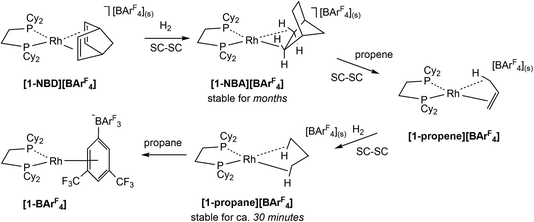
The development of Solid-state Molecular OrganoMetallic (SMOM) chemistry^1–3 has enabled the study of transition metal σ-alkane complexes by single crystal X-ray diffraction. Such complexes are key intermediates in C–H activation processes,^4–6 but are short-lived in solution even at low temperature.⁷ SMOM chemistry exploits gas/solid reactions to effect the single crystal-to-single crystal (SC–SC) transformation of alkene precursor complexes, [(R₂P(CH₂)_nPR₂)M(alkene)][BAr^F₄], to the corresponding σ-alkane complexes, [(R₂P(CH₂)_nPR₂)M(alkane)][BAr^F₄].⁸ Of these [(Cy₂PCH₂CH₂PCy₂)Rh(NBA)][BAr^F₄], [1-NBA][BAr^F₄] (NBA = norbornane, C₇H₁₂; Ar^F = 3,5-(CF₃)₂C₆H₃, Scheme 1), is found to be stable for (at least) months under an inert atmosphere and can be synthesized on a gram scale.^9,10 Variation of the bidentate phosphine,^9,11–13 alkene^11,14–16 and counter-anion^12,17 has produced a range of crystallographically characterised Rh and Co¹⁸ σ-alkane complexes that, in conjunction with computational studies,¹⁹ have been shown to exhibit a range of alkane modes that sit along the η¹_C–H (end-on) to η²_C–H (side-on) continuum.¹¹

Scheme 1 Synthesis of σ-alkane complexes via single crystal-to-single crystal (SC–SC) transformations: (a) [1-NBA][BAr^F₄] by hydrogenation of [1-NBD][BAr^F₄]; (b) [1-propane][BAr^F₄] from [1-NBA][BAr^F₄]via sequential NBA/propene substitution and hydrogenation.

These σ-alkane complexes also exhibit reactivity in the solid state, including fluxional processes,^10,14,15 H/D exchange reactions^10,15,20 and room temperature alkane dehydrogenation,¹⁵ where these last two categories link σ-alkane complexes directly to a C–H bond activation event. Alkane substitution is also possible; for example, exposure of [1-NBA][BAr^F₄], to propene gas (Scheme 1) gives [1-propene][BAr^F₄], in which the Rh–alkene bond is supported by a γ-agostic interaction.¹ Hydrogenation of [1-propene][BAr^F₄] then forms [1-propane][BAr^F₄], featuring the lightest to date alkane to be characterised crystallographically as a σ-complex.¹⁶ The propane ligand in [1-propane][BAr^F₄] exhibits a 1,3-binding mode with two η²_C–H→Rh interactions that are supported by additional contributions from the geminal C–H bonds.

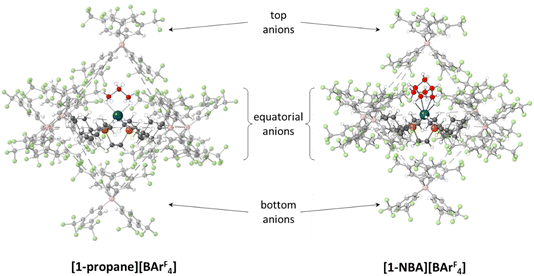
The microenvironments of the Rh cations within the extended crystal structures of [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] are shown in Fig. 1. In both cases the cation resides in a pseudo-octahedral arrangement of [BAr^F₄]⁻ anions with the σ-alkane ligand sitting within a V-shaped pocket defined by two aryl substituents of the adjacent (top) [BAr^F₄]⁻ anion. Despite these similarities, [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] show very different behaviours in the solid state: [1-NBA][BAr^F₄] is stable for months under an inert atmosphere, whereas [1-propane][BAr^F₄] decomposes within 30 minutes via displacement of the alkane by an aryl group of a neighbouring [BAr^F₄]⁻ anion to give zwitterionic [1-BAr^F₄] (Scheme 1). Indeed, crystallographic characterisation of [1-propane][BAr^F₄] required the in situ hydrogenation of [1-propene][BAr^F₄] on a synchrotron beamline (Diamond I19) at 150 K.

Fig. 1 Packing diagrams showing the pseudo-octahedral arrangement of [BAr^F₄]⁻ anions around the Rh cations in [1-NBA][BAr^F₄] and [1-propane][BAr^F₄]. Carbon atoms of the σ-alkane ligands are highlighted in red.

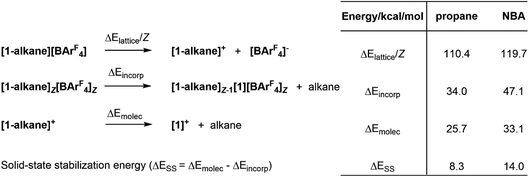
Understanding the stability of these σ-alkane complexes in the solid-state is a central goal for our research in this area, that aims to exploit SMOM chemistry in catalysis.^1,17 In an early study we showed that computed NBA binding energies across a range of [(R₂P(CH₂)_nPR₂)M(alkane)]⁺ molecular cations (i.e. neglecting the effect of the solid-state environment, n = 2; R = Cy, ⁱBu, ⁱPr, OⁱPr; n = 3, R = ⁱPr) showed no correlation with the stability of [(R₂P(CH₂)_nPR₂)M(alkane)][BAr^F₄] salts in the solid state.⁹ Bistoni and co-workers subsequently discussed the role of intramolecular dispersion in the alkane molecular binding energies.²¹ However, our subsequent work has shown the importance of including the solid-state environment via periodic DFT calculations to achieve reasonable structures and energetics for these σ-alkane complexes.¹⁹ In a recent study, normalised lattice energies, alkane incorporation energies and molecular alkane binding energies were computed for a range of [(Cy₂P(CH₂)₂PCy₂)M(alkane)][BAr^F₄] complexes (see Fig. 2 for definitions).¹⁶ All three measures were consistent with the greater stability of [1-NBA][BAr^F₄] over [1-propane][BAr^F₄]; moreover, a significant, additional stabilization provided by the solid-state environment, ΔE_SS, was identified and was larger in [1-NBA][BAr^F₄] (14.0 kcal mol⁻¹cf. 8.3 kcal mol⁻¹).

Fig. 2 Computed normalised lattice energies (ΔE_lattice/Z, where Z is the number of formula units in the unit cell), alkane incorporation energies (ΔE_incorp) and molecular alkane binding energies (ΔE_molec) for [1-NBA][BAr^F₄] and [1-propane][BAr^F₄]. The solid-state stabilization energy (ΔE_SS) is the difference between ΔE_incorp and ΔE_molec. All values are based on relative SCF energies in kcal mol⁻¹ computed with periodic-DFT.

Previously, non-covalent interactions (NCI) plots²² have highlighted broad areas of dispersive stabilisation between the alkane ligand and the neighbouring [BAr^F₄]⁻ anions in these σ-alkane complexes.^{11,13,14,17,18} In addition, more localised disk-like features have suggested the presence of C–H⋯F contacts and we have commented on the potential role of such interactions in conferring stability in the solid state.¹⁷ Here we employ Quantum Theory of Atoms in Molecules (QTAIM) and Independent Gradient Model calculations under the recently proposed Hirshfeld partitioning scheme (IGMH²³) to explore further the role of these non-covalent interactions on the stability of σ-alkane complexes. Our study will focus on the [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] systems as these exhibit each end of the range of stabilities seen to date in crystallographically characterised σ-alkane complexes in the solid state.

2. Results and discussion

2.1. Methodology

Geometries for [1-NBA][BAr^F₄]⁹ and [1-propane][BAr^F₄]¹⁶ were taken from the reported crystal structures and partially optimised with periodic-DFT calculations at the PBE-D3 level using the CP2K program (see ESI† for full details). B, C, P and Rh atoms were fixed at their experimentally determined positions while H and F atoms were fully relaxed in order to provide reliable H atom positions and to resolve any rotational disorder associated with the CF₃ groups. Unit cell parameters were fixed at the experimental values. Intermolecular interactions were analysed between one central Rh cation and the surrounding pseudo-octahedron of [BAr^F₄]⁻ anions. Short contacts within crystal structures were analysed with CrystalExplorer^24,25 with van der Waals radii taken from Alvarez (H: 1.20 Å; C: 1.77 Å; F: 1.46 Å).²⁶ In the following a ‘short contact’ will refer to a distance at or below the sum of the relevant van der Waals radii. Quantum theory of atoms in molecules (QTAIM²⁷) analyses employed the AIMAll program²⁸ and used the extended wavefunction format. Independent gradient model calculations used Multiwfn²⁹ and employed the Hirshfeld partitioning scheme (IGMH method).²³ Surfaces were visualised with VMD.³⁰

2.2. Geometric analysis of the cation microenvironment

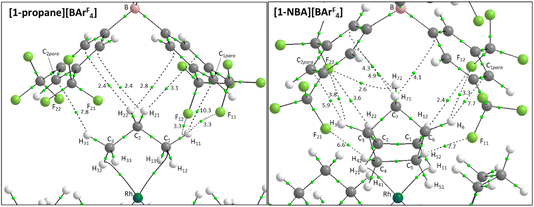
Structures will be analysed in terms of the interaction of the [1-NBA]⁺ and [1-propane]⁺ cations with the octahedral array of the six surrounding [BAr^F₄]⁻ anions. Fig. 3 displays Hirshfeld surfaces for the [1-NBA]⁺ and [1-propane]⁺ cations within this environment and also defines the anion naming system. The axial direction contains the anions sitting above the alkane (the ‘top’ anion) and adjacent to the phosphine backbone (the ‘bottom’ anion) (here obscured by the Hirshfeld surface of the cation as the view is straight down the axial direction). The equatorial anions behave as two distinct pairs, Eq-1 and Eq-3, and Eq-2 and Eq-4, that are distinguished by their alignment with the adjacent phosphine cyclohexyl substituents. Each pair shows a comparable set of non-covalent interactions, as discussed in more detail below. The anion octahedra are slightly compressed with the axial B⋯B distances somewhat shorter than the trans-equatorial B⋯B distances. Within this the Rh centre sits lower along the axial direction in the NBA complex (Rh⋯B_top = 9.83 Å for [1-NBA][BAr^F₄] and 8.02 Å for [1-propane][BAr^F₄]), possibly reflecting the larger size of this alkane ligand.

Fig. 3 Hirshfeld surfaces mapped over d_norm for [1-NBA]⁺ and [1-propane]⁺ within the octahedral arrays of neighbouring [BAr^F₄]⁻ anions with the anion labelling system indicated. Views are taken from above the ‘top’ anion’ looking down the B_top⋯Rh⋯B_bottom axis; the ‘bottom’ anion is obscured by the cation surface.

The Hirshfeld surfaces around the alkanes of the [1-NBA]⁺ and [1-propane]⁺ cations are predominantly white and blue indicating that most inter-ion contacts are at or beyond the sum of the van der Waals radii. The red area under the top anion in the [1-propane][BAr^F₄] system corresponds to a short H⋯C contact between a Me hydrogen on the propane and a para-carbon of the top [BAr^F₄]⁻. An equivalent but weaker feature in [1-NBA]⁺ involves a bridgehead hydrogen on the NBA. Fingerprint plots indicate that H⋯F cation–anion contacts are most prevalent in both structures ([1-NBA][BAr^F₄]: 61.6%; [1-propane][BAr^F₄]: 63.3%) with H⋯H and H⋯C contacts at around 25% and 12% respectively (see Fig. S1–S4† for individual H⋯X fingerprint plots). A number of H⋯F short contacts (i.e. at or below the sum of the van der Waals radii) are seen and these generally involve cyclohexyl hydrogens rather than the alkane ligands. The intense red spot between the cation and Eq-1 in the Hirshfeld surface of [1-propane]⁺ is an example of this and corresponds to a short H⋯F contact of 2.22 Å.

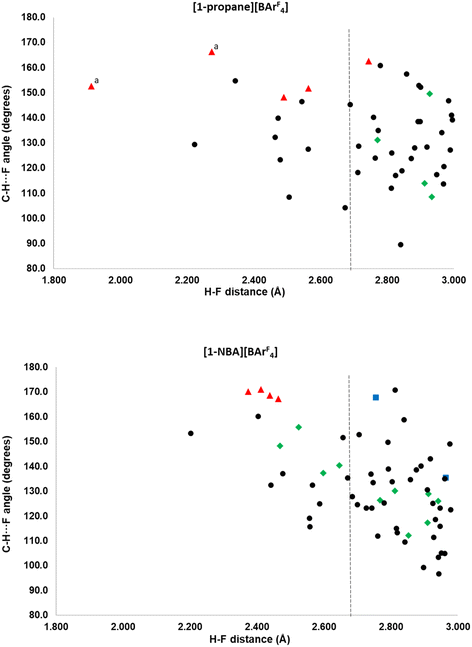
More detail on the distribution of C–H⋯F contacts around the [1-NBA]⁺ and [1-propane]⁺ cations that are below 3.0 Å is provided in the scatterplots in Fig. 4. Three classes of cation–anion contacts are seen: (i) alkane C–H⋯F (in green); (ii) phosphine backbone C–H⋯F (blue) and (iii) phosphine cyclohexyl C–H⋯F contacts (black). In addition a small number of anion–anion C–H⋯F contacts are shown in red. The cyclohexyl C–H⋯F contacts are most common and are more numerous for [1-NBA]⁺ than [1-propane]⁺ (45 compared to 36). There are no cyclohexyl C–H⋯F contacts to the top anion in either structure. No correlation between H⋯F distance and C–H⋯F angle is seen, beyond the absence of short H⋯F contacts with low C–H⋯F angles. [1-NBA]⁺ features two C–H⋯F contacts from the phosphine backbone while no such contacts are seen around [1-propane]⁺. Of the inter-anion C–H⋯F contacts in red (four in [(1-NBA)][BAr^F₄] and seven in [1-propane][BAr^F₄]) all but one is a short contact, and these are also among the closest to linear (150–170°). These features have been taken as evidence for C–H⋯F H-bonding^31–33 and this could be promoted by the relative acidity of the C–H H-bond donors that are located between two CF₃ substituents on the aryl rings. A more detailed discussion of the role of these inter-anion contacts will be the subject of a separate study.

Fig. 4 Scatterplots of H⋯F distance (Å) vs. C–H⋯F angle (degrees) for the [1-NBA]⁺ and [1-propane]⁺ cations within the octahedral arrays of neighbouring [BAr^F₄]⁻ anions. The dashed vertical line indicates the sum of the van der Waals radii for H and F. ^aData points correspond to two equivalent H⋯F contacts.

Comparing the alkane ligands, in [1-propane]⁺ the propane displays four C–H⋯F contacts below 3.0 Å, although none is below the sum of the van der Waals radii. The NBA in [1-NBA]⁺ has 10 C–H⋯F contacts, four of which are short contacts. A general trend towards wider C–H⋯F angles with shorter H⋯F distances can be seen in the alkane C–H⋯F data for [1-NBA][BAr^F₄] and this is similar to the data in Boese, Nangia and Desiraju’s early study on fluorobenzenes, where C–H⋯F H-bonding was proposed especially when more acidic C–H bonds are present.³² This is discussed in the context of the present systems after these C–H⋯F contacts have been considered in more detail via electronic structure analyses.

2.3. Electronic structure analyses

QTAIM molecular graphs were computed for all six cation–anion ion-pairs that can be formed within the [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] ‘octahedra’ – i.e. where the central cation is common to all six ion-pairs and is treated in turn with each adjacent anion. The range of C–H⋯F, C–H⋯C_aryl and C–H⋯H_aryl bond paths characterised are summarised in Table 1. Individual bond critical point (BCP) metrics are listed in the ESI (see Fig. S5–S16†). The C–H⋯F bond paths are most numerous, there being almost twice as many of these as the total of C–H⋯C_aryl and C–H⋯H_aryl bond paths. Overall the [1-NBA]⁺ cation exhibits significantly more bond paths to the surrounding anions (88 cf. 72 around [1-propane]⁺) and this is primarily due to a greater number of C–H⋯F bond paths (61 cf. 46).

Table 1 Summary of bond paths around the cations in [1-NBA][BAr^F₄] and [1-propane][BAr^F₄]

Anion	Bond path	[1-Propane][BAr^F4]		[1-NBA][BAr^F4]
		Number^a	ρ(r)/a.u. × 10^−3	Number	ρ(r)/a.u. × 10^−3
a Values in parentheses indicate the number of C–H⋯F bond paths involving the cyclohexyl substituents within the conical pocket of anion aryl groups (Cyinner), the cyclohexyl outside that pocket (Cyouter) and, where appropriate, the alkane ligand, respectively (see text for details). b One C⋯F bond path is also present; see ESI for details. c Includes C–H⋯F bond paths from the –C2H4– backbone of the diphosphine ligand.
Top	C–H⋯F	2	3.3, 3.3	7	2.6–7.7
	C–H⋯C	6	2.8–10.3	5	4.1–7.7
Eq-1	C–H⋯F	8 (5/2/1)	2.2–14.1	12 (7/4/1)	2.0–8.8
	C–H⋯C	4^b	2.0–4.4	3	2.7–5.4
	C–H⋯H	1	3.5	3	3.9–5.8
Eq-2	C–H⋯F	10 (5/4/1)	1.2–8.2	12 (7/4/1^b)	1.3–6.9
	C–H⋯C	3	1.9–4.4	2	4.0, 4.7
	C–H⋯H	2	4.5, 5.0	2	6.6, 7.9
Eq-3	C–H⋯F	7 (4/3)	1.2–4.5	10 (5/4/1)	2.4–9.1
	C–H⋯C	2	3.6, 5.6	2^b	3.7, 4.4
	C–H⋯H	2	3.2, 5.6	2	5.2, 5.4
Eq-4	C–H⋯F	9 (5/4)	1.5–8.2	9 (3/4/2)	2.6–7.9
	C–H⋯C	2	4.6, 7.0	2	3.1, 3.4
	C–H⋯H	2	4.2, 6.4	2	3.8, 10.2
Bottom	C–H⋯F	10	1.5–10.5	11	1.8–13.0
	C–H⋯C	2	1.3, 1.4	3	2.0–3.5
	C–H⋯H	—		1	2.1
Total	C–H⋯F	46 (29^c/13/4)	1.2–14.1	61 (33^c/16/12)	1.3–13.0
	C–H⋯C	19	1.9–10.3	17	2.0–5.4
	C–H⋯H	7	3.2–6.4	10	2.1–10.2

---

2.3.1. The top ion-pairs. The propane ligand in [1-propane][BAr^F₄] exhibits 10 bond paths in total (four C–H⋯F and six C–H⋯C_aryl) compared to 14 around the NBA in [1-NBA][BAr^F₄] (nine C–H⋯F and five C–H⋯C_aryl). In both cases all but two of these involve the top anion and molecular graphs for these ion-pairs are compared in Fig. 5. For the [1-propane][BAr^F₄] top ion-pair the C₁–H₁₁⋯F₁₁ and C₁–H₁₁⋯F₁₂ bond paths correspond to two of the four C–H⋯F contacts noted above (the remaining two contacts are to equatorial anions, see below). In contrast, the equivalent C₃–H₃₁⋯F_21/22 distances exceed 3.30 Å and no bond path is seen. H₁₁ and H₃₁ also exhibit bond paths and short contacts to the para-carbons on the adjacent Ar^F groups (C_1para and C_2para): these have the largest bond critical point BCP electron densities in this ion-pair (C₁–H₁₁⋯C_1para = 2.52 Å, ρ(r) = 10.3 × 10⁻³ a.u.; C₃–H₃₁⋯C_2para = 2.67 Å, ρ(r) = 7.8 × 10⁻³ a.u.) and correspond to the red feature beneath the top anion noted previously in the Hirshfeld surfaces. The four C–H⋯C_aryl bond paths involving H₂₁ and H₂₂ on the central methylene correspond to long contacts (>3.25 Å; ρ(r) < 3.2 × 10⁻³ a.u.).

Fig. 5 QTAIM molecular graphs for the top ion-pairs in [1-propane][BAr^F₄] and [1-NBA][BAr^F₄], with bond critical bonds (BCPs) in green and selected BCP electron densities, ρ(r), indicated in a.u. × 10⁻³. Bond paths with ρ(r) < 0.001 a.u., intramolecular bond paths and ring critical points (RCP) are omitted for clarity.

Within the [1-NBA][BAr^F₄] ion-pair the –{C₃H₄}– moiety comprising the bridgehead (C₃–H₃ and C₆–H₆) and central bridging methylene (C₇–H₇₁/C₇–H₇₂) bonds behaves as a “propane” fragment and forms two C–H⋯F and five C–H⋯C_aryl bond paths that are equivalent to similar bond paths in [1-propane][BAr^F₄]. Consistent with this, the highest ρ(r) values within this set are for the C₃–H₃⋯C_2para and C₆–H₆⋯C_1para bond paths (ρ(r) = 5.9 × 10⁻³ and 7.7 × 10⁻³ a.u.). The NBA system has additional bond paths from both pairs of exo-C–H bonds. Of these the C₄–H₄₂⋯F₂₁ and C₅–H₅₂⋯F₁₁ bond paths correspond to the two shortest C–H⋯F contacts (2.47 Å and 2.53 Å) and have higher ρ(r) values (7.7 × 10⁻³ a.u. and 6.7 × 10⁻³ a.u.). The C₁–H₁₂⋯F₁₂ and C₂–H₂₂⋯F₂₂ bond paths are weaker, with longer contacts (2.77 Å and 2.94 Å) and lower ρ(r) (3.6 × 10⁻³ a.u. and 2.4 × 10⁻³ a.u.). The final additional feature of the NBA system is a weak C₇–H₇₂⋯F₂₂ bond path (3.02 Å; ρ(r) = 2.6 × 10⁻³ a.u.).

In general, the C–H⋯F BCP metrics computed here are similar to those reported in previous studies of C–H⋯F contacts and show an exponential relationship between the H⋯F distance and ρ(r) (see Fig. S26†).^34–36 Such interactions have been ascribed weak H-bonding character that is enhanced by a more acidic C–H bond.^32,33 An electron deficient cationic Rh(I) centre could enhance such interactions via polarization of both the endo-C–H bonds directly involved in the σ-interaction and, through induction effects, the geminal exo-C–H bonds and beyond.³⁷ To assess this, the molecular graphs in Fig. 5 were recomputed with the {(Cy₂P(CH₂)₂PCy₂)Rh}⁺ fragments removed. Computed QTAIM charges confirmed the alkane hydrogen atoms do indeed become more positively charged when the alkane are bound to Rh, however, the same networks of bond paths with virtually unchanged BCP metrics were seen (see Fig. S25†). This lack of influence of the Rh fragment implies at best weak H-bonding character in these C–H⋯F interactions.

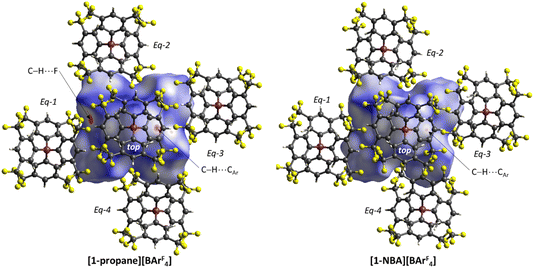
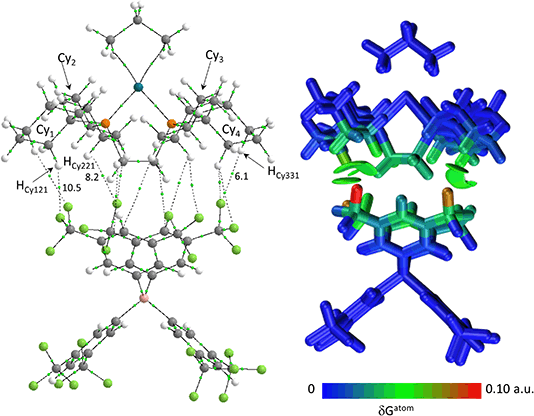
The C–H⋯C_aryl bond paths (six around [1-propane]⁺, five around [1-NBA]⁺) suggest the presence of C–H⋯π type interactions in both ion-pairs.^38–41 Previously, NCI plots have highlighted broad areas of dispersive stabilisation between σ-bound alkanes and the adjacent anions.^{11,13,14,17,18} Here, we have used the Independent Gradient Model (IGM) approach^42,43 to isolate non-covalent interactions between the cation and anion. This method is based on atomic electron densities and uses the descriptor, δG, the difference in the upper limit of the electron density gradient of the non-interacting system vs. the electron density gradient of the interacting system. Here the Hirshfeld partitioning scheme of the molecular electron density proposed by Lu and Chen (and implemented within Multiwfn) is employed to define the atomic electron densities (IGMH approach).²³ The results of these IGMH analyses for the top ion-pairs are displayed in Fig. 6, both as isosurfaces of δG^inter and as colour-coded %δG^atom scores that highlight the atoms that contribute most significantly to these inter-ion interactions. These %δG^atom scores are the sum of all the interactions of a given atom on the cation with all the atoms of the anion; individual atom–atom interactions can also be quantified as δG^atom indices.

Fig. 6 IGMH plots for the [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] top ion-pairs where the cations and anions are defined as separate fragments. Sign(λ₂)ρ-coloured isosurfaces are plotted with δG^inter = 0.003 a.u. and atoms are coloured by %δG^atom to highlight their relative contributions. The insets show all %δG^atom contributions on the cations that are above 1%.

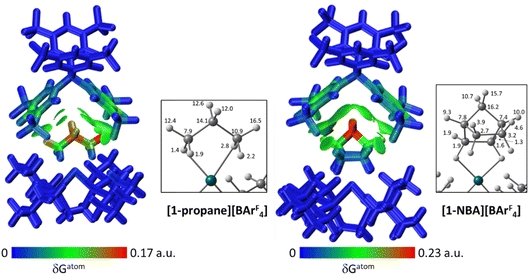
The IGMH isosurfaces amplify the features seen in the QTAIM molecular plots. For [1-NBA][BAr^F₄] distinct disk-like features consistent with exo-C–H⋯F contacts are seen and these are much more pronounced than in [1-propane][BAr^F₄]. The peripheral alkane C–H⋯C_para (anion) contacts are also common to both structures, but these are more extensive in [1-NBA][BAr^F₄]. This is confirmed by the %δG^atom values, where the relative contribution of each atom is represented on a blue–green–red scale (blue: zero; red: the maximum contribution, see also inset for % atomic contributions in the cations). The strongest contributions in [1-NBA][BAr^F₄] are associated with the bridging methylene (C₇, H₇₁ and H₇₂) whereas H₃₁ is most prominent in [1-propane][BAr^F₄]. The atoms involved in the exo-C–H⋯F contacts show little lightening of the blue colour, indicating a minimal contribution. This is confirmed by the %δG^atom values: the bridgehead and bridging methylene atoms that make up the –{C₃H₄}– “propane” fragment within the NBA ligand account for 77.0% of the total interaction, whereas the exo-hydrogen atoms, H₄₂ and H₅₂, that are involved in H⋯F short contacts contribute only 4.6% and 3.9% respectively. The δG^atom indices, that quantify individual atom–atom contributions, show that the H₄₂⋯F₂₁ and H₅₂⋯F₁₁ pairs are ranked 2nd and 4th strongest (1.8% and 1.7%) and are comparable in strength to the H₃⋯C_2para and H₆⋯C_1para pairs (1.9% and 1.8%, see Fig. S11†). These data are also consistent with the similar BCP ρ(r) values computed for the equivalent bond paths. However, H₄₂ and H₅₂ engage in relatively few additional atom–atom contacts whereas all atoms in the –{C₃H₄}– “propane” moiety have numerous atom–atom contributions that accumulate to make them more significant in the inter-fragment interaction. This difference between the directional C–H⋯F contacts and the more diffuse C–H⋯C_aryl contacts is a recurring theme in this study. For [1-propane][BAr^F₄] the equivalent –{C₃H₄}– moiety accounts for 87.0% of the total interaction, but of this only 3.4% is due to H₁₁⋯F₁₁ and H₃₁⋯F₂₂ atom–atom contributions.

Overall, the alkane ligands dominate the cation component to the non-covalent interactions in these ion-pairs: summing %δG^atom values from all atoms of the propane ligand accounts for 94.6% of the interaction while for the NBA ligand the equivalent sum gives 99.5%. These values are summarised in Table 2, where comparison with the other ion-pairs studied below is also made. Also included in Table 2 are the sum of the individual δG^atom indices. These give an indication of the accumulative strength of the non-covalent interactions between the cation and anion and show higher values for [1-NBA][BAr^F₄] over [1-propane][BAr^F₄] (for the top anion 1.39 vs. 0.95).

Table 2 % Contributions for the cations fragments indicated within the six ion-pairs in [1-propane][BAr^F₄] and [1-NBA][BAr^F₄]. δG^atom indices (a.u.) are summed for all atom pairs across each ion-pair

Ion-pair	[1-Propane][BAr^F4]		[1-NBA][BAr^F4]
	% Contribution	ΣδG^atom index	% Contribution	ΣδG^atom index
Top	Propane		NBA
	94.6	0.95	99.5	1.39
Equatorial	Cyinner/Cyouter/propane		Cyinner/Cyouter/NBA
Eq-1	76.0/21.0/2.4	1.14	75.3/20.2/3.8	1.50
Eq-2	83.6/14.9/1.1	0.82	69.3/18.5/11.7	1.24
Eq-3	80.0/16.0/3.3	1.19	82.8/13.2/3.2	1.38
Eq-4	86.4/12.1/1.1	1.05	72.9/15.4/10.5	1.10
Bottom	Cy1–4/C2 backbone		Cy1–4/C2 backbone
	74.9/24.2	0.87	69.0/29.1	1.13

---

2.3.2. ‘Equatorial’ ion-pairs. The data in Table 1 show all four equatorial ion-pairs feature more C–H⋯F bond paths than around the alkanes in the top ion-pairs’, and that these are greater in number around [1-NBA]⁺ than around [1-propane]⁺. Both alkanes show one C–H⋯F bond path to each of the Eq-1 and Eq-3 anions that arise from terminal hydrogen atoms within the “propane” moieties (i.e. H₁₁ and H₃₁ in [1-propane]⁺ and H₃ and H₆ in [1-NBA]⁺), although these have ρ(r) values below 3.2 × 10⁻³ a.u. The H₄₁ and H₅₁exo-hydrogens in [1-NBA]⁺ contribute an additional three bond paths, two of which equate to short contacts (2.60 Å, ρ(r) = 5.8 × 10⁻³ a.u.; 2.65 Å, ρ(r) = 4.9 × 10⁻³ a.u.). All the remaining C–H⋯F bond paths involve cyclohexyl hydrogens. These equatorial ion-pairs also feature several C–H⋯C_aryl bond paths and C–H⋯H_aryl bond paths, the latter always to ortho ring H atoms.

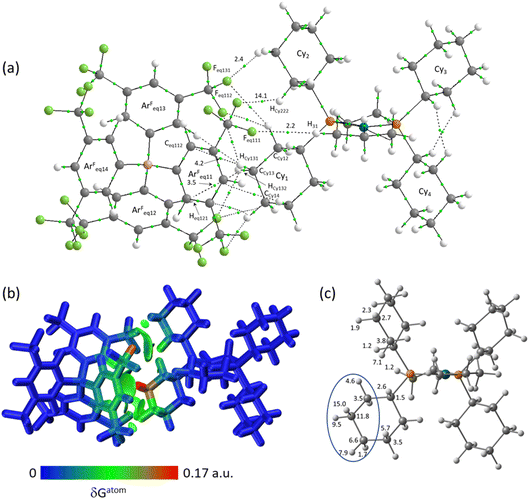
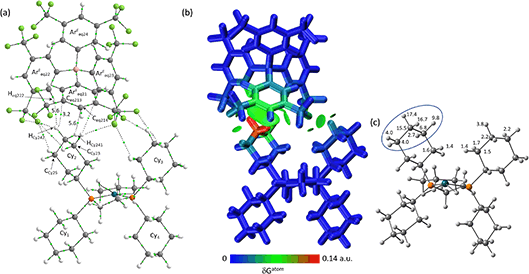
The molecular graph for the ion-pair with Eq-1 in [1-propane][BAr^F₄] is shown in Fig. 7(a). This displays a pattern, common to all these ion-pairs, in which one cyclohexyl substituent (Cy_inner, here Cy₁) sits within a conical pocket defined by three of the anion aryl groups (Ar^F_eq11, Ar^F_eq12 and Ar^F_eq13) while a second cyclohexyl substituent (Cy_outer, here Cy₂) sits outside this pocket. The former displays a range of C–H⋯F, C–H⋯C_aryl and C–H⋯H_aryl bond paths while the latter only exhibits C–H⋯F bond paths. In the Eq-1 ion-pair Cy₁ lies approximately parallel to the aromatic ring of Ar^F_eq11 and shows five C–H⋯F bond paths that are distributed across all three Ar^F groups of the pocket. In contrast the C–H⋯C_aryl bond paths are all directed to carbons on Ar^F_eq11 and the shortest of these involves the C3-axial hydrogen and an ortho ring-carbon (H_Cy131⋯C_eq112 = 3.06 Å; ρ(r) = 4.2 × 10⁻³ a.u.). All these bond paths have low ρ(r) values below 4.2 × 10⁻³ a.u. In contrast, the C3-equatorial hydrogen, H_Cy132, is directed away from Ar^F_eq11 and engages in two C–H⋯F bond paths (ρ(r) = 2.0 × 10⁻³ a.u. and 3.4 × 10⁻³ a.u.) and one C–H⋯H_aryl bond path to H_eq121 (ρ(r) = 3.5 × 10⁻³ a.u.). Cy₂ exhibits two C–H⋯F bond paths, one of which has a very short contact (H_Cy222⋯F_eq112 = 2.22 Å) and the highest ρ(r) value of 14.1 × 10⁻³ a.u. within this ion-pair and indeed across both systems. This corresponds to the intense red C–H⋯F short contact noted on the Hirshfeld surface in Fig. 3 beside Eq-1.

Fig. 7 (a) QTAIM molecular graph for the Eq-1 ion-pair in [1-propane][BAr^F₄] with BCPs in green and showing selected atom labels and BCP electron densities (a.u. × 10⁻³). Bond paths with ρ(r) < 0.001 a.u., intramolecular bond paths and ring critical points (RCP) are omitted for clarity. (b) IGMH plot where the cation and anion are defined as separate fragments. Sign(λ₂)ρ-coloured isosurfaces are plotted with δG^inter = 0.003 a.u. and atoms are coloured by %δG^atom. (c) %δG^atom contributions on the cation that are above 1%, with the propylene motif highlighted (see text for details).

These different interactions are reflected in the IGMH isosurfaces in Fig. 7(b). The C–H⋯F interactions from Cy₂ can be clearly seen with the darker green region equating to the short H_Cy222⋯F_eq112 contact noted above. The orange colour of F_eq112 in the %δG^atom colouring confirms a significant contribution from that atom: the H_Cy222⋯F_eq112 pair also has the single largest atom–atom δG^atom index at 4.1%. More significant, however, is the green isosurface between Cy₁ and Ar^F_eq11. In this case the %δG^atom colouring highlights the C3-axial hydrogen, H_Cy131, in red, indicating the largest single atomic contribution (15.0%). The C3-equatorial hydrogen contributes 9.5% – somewhat lower as it is engaged in more directional C–H⋯F interactions. More generally, the cation interaction is dominated by the –{C₃H₆}– propylene motif centred on the C_Cy12, C_Cy13 and C_Cy14 carbons and ringed in Fig. 7(c). Together these atoms contribute 62.9% of the interaction from the cation.

Within the other equatorial ion-pairs a similar pattern of bond paths is seen, with BCP ρ(r) values generally between 1.0 and 6.0 × 10⁻³ a.u. Any bond paths with higher BCP ρ(r) values all correspond to short contacts below the sum of the relevant van der Waals radii: there are four such C–H⋯F, two C–H⋯C_aryl and one C–H⋯C_aryl bond paths, within which the highest ρ(r) value is 8.2 × 10⁻³ a.u. Of the three remaining equatorial ion-pairs Eq-3 behaves like Eq-1 with one Cy group lying side-on within the conical pocket and the equivalent –{C₃H₆}– propylene motif centred on the C3 methylene group and contributing 62.0% of the cation interaction. With Eq-2 and Eq-4 the inner cyclohexyl groups (Cy₂ and Cy₄, respectively) show a more end-on geometry within the pocket (see Fig. 8 for the ion-pair with Eq-2). As a result, both the equatorial and axial hydrogens of the C4 atom (H_Cy241 and H_Cy242) engage in C–H⋯C_aryl bond paths and this is most clearly seen when visualised as %δG^atom in the IGMH plot. This methylene group alone accounts for 49.6% of the cation interaction with Eq-2 and this increases to 76.9% when expanded to include the neighbouring CH₂ groups (circled in Fig. 8(c)).

Fig. 8 (a) QTAIM molecular graph with Eq-2 in [1-propane][BAr^F₄] with BCPs in green and showing selected atoms and BCP electron densities (a.u. × 10⁻³). Bond paths with ρ(r) < 0.001 a.u., intramolecular bond paths and ring critical points (RCP) are omitted for clarity. (b) IGMH plot where the cation and anion are defined as separate fragments. Sign(λ₂)ρ-coloured isosurfaces are plotted with δG^inter = 0.003 a.u. and atoms are coloured by δG^atom. (c) %δG^atom contributions on the cation that are above 1%, with the propylene motif highlighted (see text for details).

The four equatorial ion-pairs in the [1-NBA][BAr^F₄] system exhibit the same general geometric pattern as in [1-propane][BAr^F₄] with each ion-pair having one inner cyclohexyl group, Cy_inner, within the [BAr^F₄]⁻ conical pocket and one outer Cy group, Cy_outer, outside that pocket. Geometrically the Eq-1/Eq-3 and Eq-2/Eq-4 ion-pairs again form distinct pairs, with the Cy_inner groups being more side-on in the former and interacting primarily through a propylene motif centred on the C3 methylene, while in the latter the Cy_inner groups are more end-on and interact most strongly via the propylene motif centred on the C4 methylene. QTAIM molecular graphs, IGMH isosurfaces and %δG^atom plots for all ion-pairs are provided in the ESI (see Fig. S18–S25†).

Table 2 compares the data for the equatorial ion-pairs in [1-propane][BAr^F₄] and [1-NBA][BAr^F₄]. Here the %δG^atom data have been summed over all atoms of three fragments within the cations: Cy_inner, Cy_outer and the alkane ligand. In each case Cy_inner dominates and a very similar distribution is seen for the Eq-1 and Eq-3 ion-pairs in both systems. The contribution from the alkane ligand is very small (<4%). In contrast, the Eq-2/Eq-4 ion-pairs differ significantly between the two systems: in [1-propane][BAr^F₄] Cy_inner contributes 83.6% and 86.4% respectively, whereas this drops to 69.3% and 72.9% in [1-NBA][BAr^F₄]. The major reason for this is a relatively more significant contribution from the NBA ligand (ca. 11% cf. 1% in [1-propane][BAr^F₄]). In all cases the strength of the non-covalent interactions between the cation and the anions, as gauged by the sum of δG^atom indices, is significantly greater for [1-NBA][BAr^F₄].

2.3.3. Bottom ion-pairs. The QTAIM molecular graph, IGMH isosurface and δG^atom plot for the bottom ion-pair in the [1-propane][BAr^F₄] system are shown in Fig. 9. In this case each of the cyclohexyl substituents, Cy₁–Cy₄, sits above a CF₃ group on the [BAr^F₄]⁻ anion. C–H⋯F bond paths therefore dominate and of the 10 of these, three equate to short H⋯F contacts from axial hydrogen atoms on Cy₁, Cy₂ and Cy₃, for which ρ(r) values are provided in Fig. 9(a). The –C₂H₄– ethylene backbone of the diphosphine ligand also contributes two C–H⋯C_aryl bond paths, albeit with ρ(r) values below 2 × 10⁻³ a.u. In terms of the cation % fragment contributions (Table 2), the cyclohexyl groups total 74.9% and this is distributed approximately evenly over all four substituents. The –C₂H₄– backbone also contributes significantly (24.2%), despite there only being two weak bond paths from this fragment. The equivalent ion-pair in [1-NBA][BAr^F₄] displays eleven C–H⋯F bond paths, two of which correspond to short contacts; one of these has an H⋯F distance of 2.20 Å and a relatively high ρ(r) value of 13.0 × 10⁻³ a.u., and is one of the shortest contacts in either system (see Fig. S16†). The % fragment contributions are now slightly shifted toward the –C₂H₄– backbone. As with the other ion-pairs the ΣδG^atom index value is larger for the [1-NBA][BAr^F₄] system.

Fig. 9 (a) QTAIM molecular graph with the bottom anion in [1-propane][BAr^F₄] with BCPs in green and showing selected atoms and BCP electron densities (a.u. × 10⁻³). Bond paths with ρ(r) < 0.001 a.u., intramolecular bond paths and ring critical points (RCP) are omitted for clarity. (b) IGMH plot where the cation and anion are defined as separate fragments. Sign(λ₂)ρ-coloured isosurfaces are plotted with δG^inter = 0.003 a.u. and atoms are coloured by δG^atom.

2.4. Discussion

A combination of geometric and electronic structure analyses have revealed significant differences in the non-covalent interactions around the Rh cations in the σ-alkane complexes [1-propane][BAr^F₄] and [1-NBA][BAr^F₄]. The NBA system exhibits more C–H⋯F short contacts and bond paths and the NBA ligand contributes more significantly to inter-ion interactions, not only in the top anion where the alkanes dominate, but also in two of the equatorial anions (Eq-2 and Eq-4). ΣδG^atom indices are higher for all the cation–anion ion-pairs in the NBA system. These data are all consistent with previous work that quantified an additional stabilisation in [1-NBA][BAr^F₄] that was due to the solid-state environment (5.7 kcal mol⁻¹, Fig. 2).¹⁶ However, what precisely is the driving force that creates this greater stability and what role does it play, if any, in determining the chemical stability of these crystalline solids?

The presence of several propylene motifs in the cations, either from the propane ligand itself, the cyclohexyl substituents or, for the NBA ligand, a topologically related –{C₃H₄}– moiety, is a recurring pattern in all but the bottom ion-pairs. While this does not discriminate the [1-propane][BAr^F₄] and [1-NBA][BAr^F₄] systems (with their very different chemical stability) it may be that this propylene moiety acts as a privileged motif for the formation of σ-alkane complexes in the solid state, providing a robust environment such that these species are long-lived after the SC–SC transformations necessary for their formation. Other closely related NBA complexes, [(R₂PCH₂CH₂PR₂)Rh(NBA)][BAr^F₄], that lack the rigid propylene motif of the cyclohexyl substituents show very different behaviours: with R = ⁱBu⁸ the system is only stable for a few hours at room temperature whereas with R = ⁱOPr⁹ the corresponding alkane complex cannot be isolated and the formation of the zwitterion [1-BAr^F₄] is observed. The combination of the cyclohexyl substituents and the NBA ligand is clearly particularly favourable.

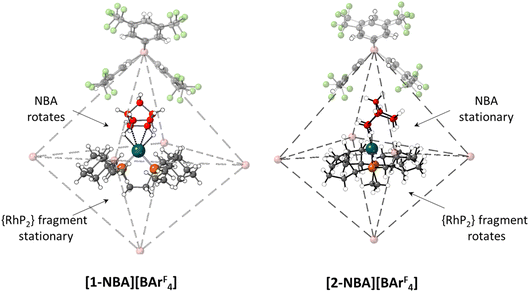
A further indication of the importance of the propylene motif is seen with the cyclopentyl (Cyp) analogue, [(Cyp₂PCH₂CH₂PCyp₂)Rh(NBA)][BAr^F₄], [2-NBA][BAr^F₄].⁴⁴ With [1-NBA][BAr^F₄] hydrogenation of the NBD precursor proceeds with rotation of the NBA ligand such that the plane of the C7 bridging methylene is perpendicular to the {PRhP} coordination plane (see Fig. 10 and Scheme 1). Remarkably, with [2-NBA][BAr^F₄] the NBA ligand is stationary and it is the {Rh(Cyp₂CH₂CH₂PCyp₂)}⁺ fragment that rotates. Thus the excision of a single methylene group from each of the phosphine substituents significantly perturbs the behaviour of the system in the SC–SC transformation.

Fig. 10 Packing diagrams contrasting the relative orientations of the NBA and {RhP₂} fragments in [1-NBA][BAr^F₄] and [2-NBA][BAr^F₄]. The top anion is shown in full along with the B atoms of the other anions within the octahedral array. Carbon atoms of the σ-alkane ligands are highlighted in red.

Returning to the [1-NBA][BAr^F₄] system, in the top anion the NBA ligand shows enhanced C–H⋯F interactions compared to the propane structure. In addition, the more diffuse C–H⋯π interactions appear energetically more significant and the presence of the C7 methylene bridge in the NBA confers additional interactions that are not possible for propane. The NBA appears to be a particularly good fit to this pocket and its presence has knock-on effects around the anionic octahedral array. The enhanced contribution of C–H⋯F contacts has already been noted for Eq-2 and Eq-4, however, even for Eq-1 and Eq-3, where the % contributions of the Cy_inner and Cy_outer cyclohexyl substituents are very similar (and the alkane ligands play a negligible role, Table 2) the overall strength of interaction as gauged via the δG^atom indices is greater for the NBA system. A range of geometrical parameters were assessed to account for this difference, however no coherent trend could be found. The overall dimensions of the anion octahedron may give some clue: as mentioned in the introduction the Rh cation sits lower down the axial direction in [1-NBA][BAr^F₄] while the octahedron of anions itself is slightly compressed along the equatorial axes (B-1⋯B-3 = 19.26 Å cf. 19.94 Å in [1-propane][BAr^F₄]; B-2⋯B-4 = 19.04 Å cf. 19.41 Å in [1-propane][BAr^F₄]). One possibility is that the octahedral array of anions is more perturbed in [1-propane][BAr^F₄] and evidence for this is seen in the wider range of C–H⋯F anion–anion contacts in this system (1.91–2.75 Å, Fig. 4) whereas these cluster around 2.40 Å in [1-NBA][BAr^F₄]. Relating these differences to specific contributions is challenging, however, and most likely the differences in behaviour reflect an accumulation of small effects arising from the subtly different orientations of the cations within each octahedral array of anions, as well as the detailed shape of the octahedra themselves.

Computed BCP ρ(r) values and δG^atom indices indicate that the C–H⋯F interactions provide the strongest non-covalent interactions in these systems and these two metrics also show a strong correlation (see Fig. S27†). By these measures the C–H⋯C_aryl contacts are less significant; however in these systems such bond paths flag up more diffuse C–H⋯π interactions that incorporate several atom–atom contributions, the accumulative effect of which is much more significant. While this issue is well-known, and has been addressed in model systems such as the benzene dimer through comparison of QTAIM and NCI plots,⁴⁵ the use of the IGMH isosurfaces and quantification via %δG^atom contributions provide a particularly graphic illustration of these points. The contributions of the more directional C–H⋯F short contacts are less significant, although the presence of many more of these contacts in [1-NBA][BAr^F₄] compared to [1-propane][BAr^F₄] may still play a role in the greater stability of the former.

On this note, the recent synthesis of [1-NBA][S-BAr^F₄] where S-BAr^F₄ is the Mecking anion in which –SF₅ groups replace the –CF₃ substituents in [BAr^F₄]⁻ is particularly interesting.¹⁷ This species provides a robust σ-alkane complex that is geometrically analogous to [1-NBA][BAr^F₄] in the solid state. Moreover, (unlike its [BAr^F₄] congener) it is completely insoluble in alkane solvents, making it an interesting candidate for a heterogeneous SMOM catalyst. The greater number of C–H⋯F short contacts in [1-NBA][S-BAr^F₄] make it an attractive system for comparison with the current study. This will be the topic of future work, along with the application of high-level quantum mechanical calculations to quantify non-covalent interactions in these systems and benchmark the IGMH approach.

3. Conclusions

Non-covalent interactions around the cationic Rh σ-alkane complexes within the solid state structures of [1-NBA][BAr^F₄] and [1-propane][BAr^F₄] have been compared. Geometric and QTAIM analyses highlight a greater number of C–H⋯F contacts around the [1-NBA]⁺ cation and the shortest of these correspond to the strongest individual atom–atom non-covalent interactions between the cation and anions in these systems. IGMH plots show the high directionality of these C–H⋯F interactions, and that these contrast with the more diffuse nature of C–H⋯π interactions. The accumulative nature of these C–H⋯π interactions that are distributed over many adjacent atom pairs results in these being more significant in the overall array of cation–anion non-covalent interactions. IGMH δG^atom plots provide a particularly useful graphic guide to identifying key non-covalent interactions between the cation and anions. An important contribution from –{C₃H₆}– propylene motifs on both the alkane ligands and the phosphine cyclohexyl substituents is highlighted and these are more significant for [1-NBA][BAr^F₄] than [1-propane][BAr^F₄]. All measures point to greater non-covalent stabilisation between the cation and anions in [1-NBA][BAr^F₄] and this follows the greater stability of this species in the solid state.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the EPSRC for funding via awards EP/W015498/1 and EP/W015552/1.

References

1. F. M. Chadwick, A. I. McKay, A. J. Martinez-Martinez, N. H. Rees, T. Krämer, S. A. Macgregor and A. S. Weller, Chem. Sci., 2017, 8, 6014–6029.
2. S. D. Pike and A. S. Weller, Philos. Trans. R. Soc., A, 2015, 373, 20140187.
3. K. A. Reid and D. C. Powers, Chem. Commun., 2021, 57, 4993–5003.
4. R. H. Crabtree, Chem. Rev., 1985, 85, 245–269.
5. C. Hall and R. N. Perutz, Chem. Rev., 1996, 96, 3125–3146.
6. A. S. Weller, F. M. Chadwick and A. I. McKay, in Advances in Organometallic Chemistry, ed. P. J. Pérez, Academic Press, 2016, vol. 66, pp. 223–276.
7. For a recent example of the characterisation of σ-alkane complexes in solution see: J. D. Watson, L. D. Field and G. E. Ball, J. Am. Chem. Soc., 2022, 144, 17622–17629.
8. S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648–1651.
9. S. D. Pike, F. M. Chadwick, N. H. Rees, M. P. Scott, A. S. Weller, T. Krämer and S. A. Macgregor, J. Am. Chem. Soc., 2015, 137, 820–833.
10. F. M. Chadwick, T. Krämer, T. Gutmann, N. H. Rees, A. L. Thompson, A. J. Edwards, G. Buntkowsky, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2016, 138, 13369–13378.
11. A. J. Martínez-Martínez, B. E. Tegner, A. I. McKay, A. J. Bukvic, N. H. Rees, G. J. Tizzard, S. J. Coles, M. R. Warren, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2018, 140, 14958–14970.
12. A. I. McKay, A. J. Martínez-Martínez, H. J. Griffiths, N. H. Rees, J. B. Waters, A. S. Weller, T. Krämer and S. A. Macgregor, Organometallics, 2018, 37, 3524–3532.
13. S. K. Furfari, B. E. Tegner, A. L. Burnage, L. R. Doyle, A. J. Bukvic, S. A. Macgregor and A. S. Weller, Chem.–Eur. J., 2021, 27, 3177–3183.
14. F. M. Chadwick, N. H. Rees, A. S. Weller, T. Krämer, M. Iannuzzi and S. A. Macgregor, Angew. Chem., Int. Ed., 2016, 55, 3677–3681.
15. A. I. McKay, A. J. Bukvic, B. E. Tegner, A. L. Burnage, A. J. Martinez-Martinez, N. H. Rees, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2019, 141, 11700–11712.
16. A. J. Bukvic, A. L. Burnage, G. J. Tizzard, A. J. Martínez-Martínez, A. I. McKay, N. H. Rees, B. E. Tegner, T. Krämer, H. Fish, M. R. Warren, S. J. Coles, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2021, 143, 5106–5120.
17. L. R. Doyle, E. A. Thompson, A. L. Burnage, A. C. Whitwood, H. T. Jenkins, S. A. Macgregor and A. S. Weller, Dalton Trans., 2022, 51, 3661–3665.
18. T. M. Boyd, B.E. Tegner, G. J. Tizzard, A. J. Martínez-Martínez, S. E. Neale, M. A. Hayward, S. J. Coles, S. A. Macgregor and A. S. Weller, Angew. Chem., Int. Ed., 2020, 59, 6177–6181.
19. A. G. Algarra, A. L. Burnage, M. Iannuzzi, T. Krämer, S. A. Macgregor, R. E. M. Pirie, B. Tegner and A. S. Weller, in 21st Century Challenges in Chemical Crystallography II: Structural Correlations and Data Interpretation, ed. D. M. P. Mingos and P. R. Raithby, Springer International Publishing, Cham, 2020, pp. 183–228.
20. S. A. Macgregor, T. Krämer, F. M. Chadwick and A. S. Weller, Helv. Chim. Acta, 2022, 2023(106), e202200154.
21. Q. Lu, F. Neese and G. Bistoni, Phys. Chem. Chem. Phys., 2019, 21, 11569–11577.
22. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
23. T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555.
24. M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer17, University of Western Australia, 2017, https://hirshfeldsurface.net/.
25. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
26. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
27. R. F. W. Bader, Atoms in Molecules, Oxford University Press, 1990.
28. T. A. Keith, AIMAll, 2009–2017, http://aim.tkgristmill.com.
29. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
30. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
31. E. D’Oria and J. J. Novoa, CrystEngComm, 2008, 10, 423–436.
32. V. R. Thalladi, H. C. Weiss, D. Blaser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710.
33. P. A. Deck, M. J. Lane, J. L. Montgomery, C. Slebodnick and F. R. Fronczek, Organometallics, 2000, 19, 1013–1024.
34. R. Shukla and D. Chopra, CrystEngComm, 2015, 17, 3596–3609.
35. P. Panini, R. G. Gonnade and D. Chopra, New J. Chem., 2016, 40, 4981–5001.
36. H. Omorodion, B. Twamley, J. A. Platts and R. J. Baker, Cryst. Growth Des., 2015, 15, 2835–2841.
37. L. J. L. Häller, M. J. Page, S. A. Macgregor, M. F. Mahon and M. K. Whittlesey, J. Am. Chem. Soc., 2009, 131, 4604–4605.
38. J. Ran and M. W. Wong, J. Phys. Chem. A, 2006, 110, 9702–9709.
39. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900.
40. R. Gopi, N. Ramanathan and K. Sundararajan, Spectrochim. Acta, Part A, 2017, 181, 137–147.
41. R. M. Kumar, M. Elango, R. Parthasarathi, D. Vijay and V. Subramanian, J. Chem. Sci., 2012, 124, 193–202.
42. C. Lefebvre, G. Rubez, H. Khartabil, J.-C. Boisson, J. Contreras-García and E. Hénon, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936.
43. C. Lefebvre, H. Khartabil, J.-C. Boisson, J. Contreras-García, J.-P. Piquemal and E. Hénon, ChemPhysChem, 2018, 19, 724–735.
44. A. I. McKay, T. Krämer, N. H. Rees, A. L. Thompson, K. E. Christensen, S. A. Macgregor and A. S. Weller, Organometallics, 2017, 36, 22–25.
45. C. Narth, Z. Maroun, R. A. Boto, R. Chaudret, M.-L. Bonnet, J.-P. Piquemal and J. Contreras-García, in Applications of Topological Methods in Molecular Chemistry, ed. E. Alikhani, R. Chauvin, C. Lepetit and B. Silvi, Springer, 2016, vol. 22, pp. 491–527.

---

Footnote

† Electronic supplementary information (ESI) available: Full computational details and references, computed Cartesian coordinates, tables and images for QTAIM and IGMH calculations. See DOI: https://doi.org/10.1039/d3fd00009e

---