Mapping the effects of physical and chemical reduction parameters on local atomic distributions within bimetallic nanoparticles†
Hannah M.
Johnson
 a,
Acacia M.
Dasher
a,
Madison
Monahan
b,
Soenke
Seifert
c and
Liane M.
Moreau
a,
Acacia M.
Dasher
a,
Madison
Monahan
b,
Soenke
Seifert
c and
Liane M.
Moreau
 *a
*a
aDepartment of Chemistry, Washington State University, Pullman, WA 99164, USA. E-mail: liane.moreau@wsu.edu
bDepartment of Chemistry, University of Washington, Seattle, WA 98195, USA
cX-ray Sciences Division, Argonne National Laboratory, Argonne, IL 60439, USA
First published on 9th March 2022
Abstract
Bimetallic nanoparticles prove advantageous over their monometallic counterparts due to the tunable, hybrid properties that result from combining different atomic species in a controlled way. The favorable optical and catalytic properties resulting from AgAu nanoparticle formation have been widely attributed to the existence of Ag–Au bonds, the maximization of which assumes the formation of a homogeneous alloy. Despite the importance of atomic scale structure in these systems, synthetic studies are typically not paired with structural characterization at the atomic scale. Herein, a comprehensive synthetic exploration of physical and chemical reduction parameters of resulting nanoparticle products is complemented with thorough X-ray characterization to probe how these parameters affect atomic scale alloy distributions within AgAu nanoparticles. Presented evidence shows Ag is substantially underincorporated into nanoparticle constructs compared with solution Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratios regardless of precursor
Au ratios regardless of precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio or volume of reductant added. Both Ag and Au exhibit significant local clustering, with Ag distributed preferentially towards the nanoparticle surface. Most significantly, the results of this investigation suggest that reduction parameters alone can affect the local alloy distributions and homogeneity within bimetallic nanoparticles, even when the ratio of metallic precursors remains constant. Overall, this investigation presents the ability to control alloy distributions using kinetics and provides new considerations for optimizing synthetic methods to produce functional bimetallic nanoparticles.
reductant ratio or volume of reductant added. Both Ag and Au exhibit significant local clustering, with Ag distributed preferentially towards the nanoparticle surface. Most significantly, the results of this investigation suggest that reduction parameters alone can affect the local alloy distributions and homogeneity within bimetallic nanoparticles, even when the ratio of metallic precursors remains constant. Overall, this investigation presents the ability to control alloy distributions using kinetics and provides new considerations for optimizing synthetic methods to produce functional bimetallic nanoparticles.
Introduction
Bi- and multi-metallic nanoparticles (NPs) have promising applications in the electronic, energy, and medical industries due to the synergistic optical and electronic characteristics resulting from combining favorable aspects of their monometallic constituents.1 NPs made of noble metals are of particular interest towards these applications: the ability to finely tune their local surface plasmon resonance (LSPR),2–5 their efficacy as catalysts,6–11 their low biotoxicity, and their facile synthesis in aqueous media under air-stable conditions make them an attractive and accessible technology. Additionally, the common FCC crystal structure as well as similar lattice parameters and bonding characteristics inherent to noble metals make them ideal candidates for the successful synthesis of NP alloys that exhibit mixed metal bonding. The capability to create structures that maximize mixed metal bonds is critical to their functionality, given that tunable optical properties and catalytic mechanisms are widely attributed to the NP atomic scale characteristics.12,13 CO oxidation, for example, is proposed to occur most effectively via AgAu NPs which maximize Ag–Au local coordination.14Despite the arguments made connecting atomic scale structure to property attributes within multi-metallic NPs, studies that report the synthesis of such nanocrystals do not universally experimentally investigate the distributions of the respective metallic species at the atomic level. Such in-depth atomic level characterization is necessary, however, given that studies have previously found that the resulting alloy distributions are not homogeneous,13,15–18 as has often been the assumption within NP syntheses utilizing two species that are miscible. Atomic-scale clustering within multi-metallic NPs, however, is justified and even expected from a thermodynamic standpoint. Firstly, bond energies are not uniform between mono-metallic and multi-metallic species. For example, in the case of AgAu, the bond dissociation energies follow the trend Au–Au > Au–Ag > Ag–Ag,19 which intuitively suggests favorability towards Au clustering. This concept is further enhanced by the well-known differences observed in nanoscale vs. bulk structures. Prior computational studies have found that the tendency of bimetallic noble metal NPs to display janus or core–shell versus alloyed arrangements depends not only on temperature and the ratio of secondary metal introduced, but also on particle size, with smaller particles tending to favor atomic scale segregation.20
The aforementioned considerations make it necessary to both (a) thoroughly characterize local atomic coordination within multi-metallic NPs in order to accurately map compositional distributions at the atomic scale, and (b) correlate synthetic parameters to atomic scale distributions, in order to promote favorable optical and catalytic performance via synthetic control. These aforementioned requirements are explored in this presented study, which pairs a systematic investigation of synthetic reduction parameters with comprehensive X-ray characterization on the atomic- and nanometer-length scales. Specifically, AgAu NPs were synthesized based on a previously reported protocol used to make pure Ag or Au NPs using ascorbic acid (AA) as both a reducing agent and surface capping agent.21 This approach enables reduction of both Ag and Au at room temperature, allowing for separation of the effects of temperature (which has been previously determined to promote homogeneity)22,23 on the reaction kinetics from the synthetic factors probed. Additionally, NPs synthesized using AA as a synthetic reagent without an added surfactant species do not exhibit evidence of having strong-binding surface ligands or a tendency towards anisotropic growth, thereby reducing the possibility of characterization complications from surface facet-specific or strong binding effects.
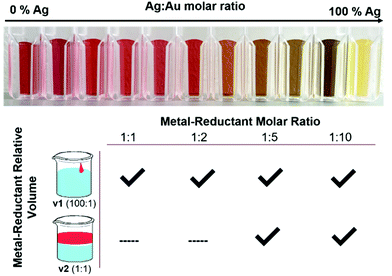
Parameters that have the potential to affect reduction kinetics were specifically investigated, both because NPs are metastable, kinetic products, as well as because alloy homogeneity is not thermodynamically favorable. The prevailing hypothesis of this work is that kinetics can be used to influence atomic scale distributions within multi-metallic NPs, which is not a concept at the forefront of prior synthetically-driven investigations. Towards this end, three key components that affect reduction kinetics within AgAu NP formation (see Fig. 1) were explored: (1) the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratio initially introduced into solution, (2) the metal
Au ratio initially introduced into solution, (2) the metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant molar ratio used to form the NP constructs, and (3) the volume of reductant added (small, concentrated volume versus larger, more dilute volume). The Ag
reductant molar ratio used to form the NP constructs, and (3) the volume of reductant added (small, concentrated volume versus larger, more dilute volume). The Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratio was probed to determine the amount of Ag incorporated into the NP construct as a function of the relative amount introduced into solution. This is an important consideration given that Ag+ has a greater barrier for reduction (0.8 V vs. SHE for the Ag+/Ag redox pair) than does Au3+ (1.5 V vs. SHE for the Au3+/Au pair). The metal
Au ratio was probed to determine the amount of Ag incorporated into the NP construct as a function of the relative amount introduced into solution. This is an important consideration given that Ag+ has a greater barrier for reduction (0.8 V vs. SHE for the Ag+/Ag redox pair) than does Au3+ (1.5 V vs. SHE for the Au3+/Au pair). The metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio was varied from 1
reductant ratio was varied from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 10-fold excess reductant, in order to observe its effects given that it would be expected to achieve faster reduction kinetics where there is a greater concentration of reductant in solution. The reductant volume used was either 1 part reductant to 100 parts precursor solution or 1 part reductant to 1 part precursor solution, with the final AA concentration in solution being the same in both cases. Surprisingly, despite the possibility for the diffusion of the reductant through solution to affect precursor reduction and subsequent NP growth, this a synthetic parameter that is often overlooked. Together, systematically varying these parameters, combined with comprehensive structural and compositional characterization, will provide insight into their impacts on atomic scale incorporation and distribution within AgAu NPs.
1 to 10-fold excess reductant, in order to observe its effects given that it would be expected to achieve faster reduction kinetics where there is a greater concentration of reductant in solution. The reductant volume used was either 1 part reductant to 100 parts precursor solution or 1 part reductant to 1 part precursor solution, with the final AA concentration in solution being the same in both cases. Surprisingly, despite the possibility for the diffusion of the reductant through solution to affect precursor reduction and subsequent NP growth, this a synthetic parameter that is often overlooked. Together, systematically varying these parameters, combined with comprehensive structural and compositional characterization, will provide insight into their impacts on atomic scale incorporation and distribution within AgAu NPs.
In order to accurately correlate the aforementioned synthetic parameters with atomic and structural mapping of the resulting NPs over multiple length scales, a comprehensive X-ray focused approach was used. Notably, X-ray methods prove advantageous in this context due to their capability to present statistically relevant information on NP structure in a global manner; collected data is representative of millions to billions of NPs and is therefore accurately representative of sample averages. X-ray fluorescence was used to trace the actual incorporation percentages of Ag vs. Au compared with solution-introduced ratios, and UV-vis spectroscopy considered differences in the optical signatures that result upon varying synthetic conditions. The nanoscale morphology and size distributions were probed using electron microscopy (TEM) and, more prominently, small angle X-ray scattering (SAXS). Atomic scale coordination was determined using X-ray absorption fine structure spectroscopy (XAFS) and used in conjunction with morphological and compositional information to infer broader structural trends. Overall, results from this investigation support the hypothesis that the kinetic factors affecting reduction within multi-metallic NP synthesis, in particular the mode of reductant introduction into the precursor solution, do indeed impact the resulting atomic scale distributions. This finding has broad implications for optimizing multi-metallic NPs for their preferential use as optical sensors and heterogeneous catalysts and provides insight into how alloy homogeneity can be synthetically targeted.
Methods
Synthesis of AgAu NPs
Gold(III) chloride trihydrate (Aldrich, >99.9%), silver(I) nitrate (Aldrich, 99.99%), L-ascorbic acid (Aldrich, >99%), and sodium hydroxide (Macron, ACS-grade), were all used as received without additional purification. All H2O used to make solutions was UltraPure Type 1 Deionized Water (ChemWorld). All glassware was washed with aqua regia prior to use and all solutions were used fresh.Two protocols were followed that differed in the relative volumes of the metal and reducing solutions: method “v1” utilized 20 mL metal + 0.2 mL reductant (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v), and method “v2” utilized 10 mL metal + 10 mL reductant (1
1 v/v), and method “v2” utilized 10 mL metal + 10 mL reductant (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v). The concentrations of these solutions were adjusted accordingly to yield the desired molar ratio between the metal and the reductant; the final volume of all reactions was 20 mL but could be scaled up to at least 500 mL without differences in the product obtained.
1 v/v). The concentrations of these solutions were adjusted accordingly to yield the desired molar ratio between the metal and the reductant; the final volume of all reactions was 20 mL but could be scaled up to at least 500 mL without differences in the product obtained.
In a typical synthesis, stock solutions of HAuCl4 and AgNO3 (v1 = 0.5 mM, v2 = 1.0 mM) were prepared and set aside. An aqueous solution of AA was prepared fresh, its concentration dependent on the desired metal-reductant molar ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 1
5, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) and the volume method used. In quick succession, the AA solution was made alkaline with the addition of 10 M NaOH in a 2
10) and the volume method used. In quick succession, the AA solution was made alkaline with the addition of 10 M NaOH in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NaOH
1 NaOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AA ratio. While this solution stirred for ∼1 minute, the desired starting ratio of the HAuCl4 and AgNO3 solutions was added to a clean 20 mL vial and stirred vigorously, followed by rapid addition of the appropriate volume of the AA solution. The reaction occurred instantaneously, indicated by the color change of the solutions from slightly yellow/cloudy (from the ready precipitation of AgCl) to varying shades of red, yellow, or brown. The solutions were allowed to stir for an additional 30 minutes and then were removed to rest overnight prior to further cleaning or analysis. Prior to X-ray measurements, samples were cleaned 3× via centrifugation at 8000 rpm and resuspended in 18.2 MΩ deionized water.
AA ratio. While this solution stirred for ∼1 minute, the desired starting ratio of the HAuCl4 and AgNO3 solutions was added to a clean 20 mL vial and stirred vigorously, followed by rapid addition of the appropriate volume of the AA solution. The reaction occurred instantaneously, indicated by the color change of the solutions from slightly yellow/cloudy (from the ready precipitation of AgCl) to varying shades of red, yellow, or brown. The solutions were allowed to stir for an additional 30 minutes and then were removed to rest overnight prior to further cleaning or analysis. Prior to X-ray measurements, samples were cleaned 3× via centrifugation at 8000 rpm and resuspended in 18.2 MΩ deionized water.
X-ray fluorescence spectroscopy
X-ray fluorescence spectra were collected on a Bruker S4 T-Star X-ray fluorometer using a tungsten excitation source. Samples were prepared by dropcasting 5 μL onto a clean quartz disc. Survey spectra were collected from 0–35 keV for 25 minutes each and the relative composition of Ag and Au was quantified using the Kα and Lα lines, respectively, by the Bruker ESPRIT software. Samples were prepared to less than one monolayer of particles to minimize effects of varying self-absorption through the sample at the different fluorescence line energies. Based on manual calculations using a 20 nm particle size, it is estimated that the effects of self-absorption account for less than 4% deviation in the reported atomic percentages and were therefore neglected.Transmission electron microscopy
TEM images were taken using an FEI Tecnai G2 20 Twin TEM equipped with a 200 kV LaB6 electron source. Images were collected in bright field mode using a 4 K Eagle camera. To prepare samples for TEM, NP solutions were dropcast onto a carbon-coated copper TEM grid and allowed to dry in a desiccator. In cases where the NPs proved particularly unstable through the drying process, the instability was mitigated by first depositing and drying a layer of 0.5 mM ascorbic acid before deposition of the NP solution. See the text and Fig. S12† for details.UV-vis spectroscopy
UV-vis spectra were collected using either an Agilent Cary 5000 UV-vis spectrophotometer from 200–800 nm or using a Thermo Scientific Evolution 300 UV-Vis spectrophotometer from 190–800 nm. In both cases, a 1 cm quartz cuvette was used, with samples dispersed in 1 mL 18.2 MΩ deionized water.Energy-dispersive X-ray mapping
EDX images were taken using a FEI Tecnai G2 F20 SuperTwin TEM operated at 200 keV in S/TEM mode with an EDAX Elite T detector. The samples were prepared as previously mentioned and dried in a desiccator for 2 h prior to imaging. EDX maps were collected using a spot size of 7, amp time of 7.58 μs, dwell time of 50 μs, image resolution of 512 × 400, and 8–16 frames per map to limit sample drift and damage while maximizing signal.Powder X-ray diffraction
PXRD patterns were collected on a Rigaku MiniFlex diffractometer using a Cu Kα source (1.5402 Å), an accelerating voltage of 40 kV, and a beam current of 15 mA. Samples were prepared as films by repeatedly dropcasting several layers of cleaned, concentrated NPs onto a substrate and allowing each layer to dry in a desiccator between depositions.Small angle X-ray scattering
SAXS patterns were collected at sector 12-ID-C of the Advanced Photon Source (APS) at Argonne National Laboratory (ANL) with an incident energy of 12.00 keV. Samples were measured using a flow cell, which was cleaned between measurements using Alconox solution and deionized water. The sample was oscillated in and out of the beam using the flow cell throughout the duration of the measurement. A beam size of 0.1 mm × 0.5 mm was used and attenuators and exposure times chosen to ensure that irradiation damage to the sample minimal based on repeatability from scan to scan. 2D patterns were converted to 1D using NIKA24 and 1D patterns were background subtracted and fit to a spherical form factor averaged over a Schulz-Zimm distribution using IRENA.25 Details of the SAXS modeling and analysis are included in the ESI.†X-ray absorption fine structure spectroscopy
XAFS spectra were collected at room temperature at beamline 4-1 at the Stanford Synchrotron Radiation Lightsource (SSRL). Data was collected both at the Ag K and Au L3 absorption edges (25.514 keV and 11.919 keV, respectively), using a slit size of 1 mm vertical × 3–4 mm horizontal and a Si (220) phi = 0 monochromator. Data was collected to a k value of 14 Å−1 in both transmission and fluorescence mode using a 30-element solid state Canberra Ge detector. Energies were calibrated to an Ag or Au foil. The foil was placed between the second and a third ion chamber during all sample measurements for simultaneous probing of the standard to correct for any energy drift observed over time. Ag, Au and AgAu NP samples were washed three times via centrifugation to remove excess free ions from solution and resuspended in water. In this process, the samples were concentrated to nanomolar concentrations of NP to improve counting statistics. The samples were then placed into 4 mm inner diameter polypropylene tubes and mounted on a slotted aluminum holder for measurement.Subsequent to measurement, transmission data and deadtime corrected fluorescence data were processed and analyzed using the IFEFFIT software package.26 Individual scans were merged (or summed in the case of fluorescence) for their respective samples and the background removed using the AUTOBK algorithm.27 Data were Fourier transformed from 2.5–13 Å−1 in k and fit in R-space to multiple k-weights (1–3) to relevant theoretical pathways generated using FEFF6.28 The number of variables varied in the fit were limited to be less than two thirds the number of independent points and the fit was allowed to vary to achieve minimization of χ2. In particular, coordination numbers, bond lengths, and mean-squared disorder values were extracted at minimum for the first Ag or Au coordination shell. Details of the fitting procedures can be found in the ESI.† It should be noted that a smaller subset of samples (as indicated in the ESI†) were measured using XAFS due to the length of measurement and limitation of synchrotron beamtime.
Results
NP composition compared with Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Au solution ratio
Au solution ratio
As shown in Fig. 1, not all reduction conditions produced stable colloids; in particular, the dilute mixing volume v2 at low molar ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) caused the solutions to either remain clear or crash into bulk aggregates entirely. This can be explained by considering the kinetics of the initial (first-order) nucleation step, which occurs essentially instantaneously when the alkaline reductant is added to the metal solution. Although the final metal-reductant molar ratio is the same in the case of both v1 and v2, the reaction kinetics are influenced directly by the absolute concentrations of the solutions as they come in contact, which is quite different in the strong, localized reduction of v1 versus the weak, diffuse reduction of v2. Nanoparticles are metastable, kinetic products, and thus the kinetics of their initial nucleation have a large effect on the product that is obtained. Specifically, there appears to be a reductant concentration threshold below which the initial burst nucleation is not sufficiently rapid to lead to complete colloid formation, even when the overall stoichiometry allows it.
2) caused the solutions to either remain clear or crash into bulk aggregates entirely. This can be explained by considering the kinetics of the initial (first-order) nucleation step, which occurs essentially instantaneously when the alkaline reductant is added to the metal solution. Although the final metal-reductant molar ratio is the same in the case of both v1 and v2, the reaction kinetics are influenced directly by the absolute concentrations of the solutions as they come in contact, which is quite different in the strong, localized reduction of v1 versus the weak, diffuse reduction of v2. Nanoparticles are metastable, kinetic products, and thus the kinetics of their initial nucleation have a large effect on the product that is obtained. Specifically, there appears to be a reductant concentration threshold below which the initial burst nucleation is not sufficiently rapid to lead to complete colloid formation, even when the overall stoichiometry allows it.
Using the six other conditions that did produce stable colloids, XRF was used to quantify the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au compositional ratio incorporated into the NPs compared with the amounts introduced into solution. XRF proves advantageous over more conventional ICP-based methods for the case of Ag
Au compositional ratio incorporated into the NPs compared with the amounts introduced into solution. XRF proves advantageous over more conventional ICP-based methods for the case of Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au due to the tendency of Ag to precipitate as a salt when dissolved in halogenated acids; XRF, in contrast, does not require dissolution of the NPs.
Au due to the tendency of Ag to precipitate as a salt when dissolved in halogenated acids; XRF, in contrast, does not require dissolution of the NPs.
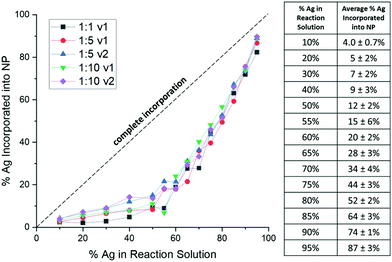
Consistently, XRF results show that Ag is underincorporated into the NPs in comparison to what solution trends would expect, which has previously been observed in AgAu NP formation,29 but not correlated to a mathematical trend. Instead of a linear trend with increasing Ag in solution, the curves for each reduction condition follow the same exponential trend (Fig. 2), suggesting that there is an initial barrier before Ag incorporation becomes more facile. While it is not entirely surprising that Ag is underincorporated, it is notable that the degree of the underincorporation is entirely insensitive to the mode or kinetics of reduction and nucleation.
Importantly, this demonstrates that solution atomic percentages of miscible metals cannot be assumed to reflect the actual NP composition, but rather that the picture is more complicated. Overall, results reveal that Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au solution ratio alone controls the NP composition but does not itself accurately reflect the composition of the products due to predictable nonlinearity in the incorporation of the different metal species.
Au solution ratio alone controls the NP composition but does not itself accurately reflect the composition of the products due to predictable nonlinearity in the incorporation of the different metal species.
Trends in NP morphology
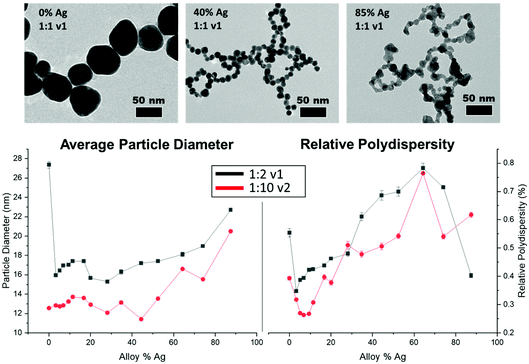
TEM results (Fig. 3, top) show that all NP samples exhibit quasi-spherical morphology, with a single NP population rather than a bi-modal or multi-modal mixture of populations. Supplementary EDX maps of elemental distribution (Fig. S13†) also support the presence of a single population of mixed-metal NPs. Within the large number of samples probed, key trends emerge; overall, all bimetallic NPs were constrained to sizes between 10 and 20 nm, whereas the endpoints (0 or 100% Ag NPs) tended to be significantly larger, especially at lower reductant ratios (Fig. S9 and Tables S2, S3†). As the atomic % Ag within the bimetallic NPs is increased, they become less stable, as evidenced by significant fusing observed on the TEM grid upon drying, which was not observed in particles with lower Ag incorporation. This problem was partially circumvented by depositing a layer of AA onto the grid prior to NP dropcasting (Fig. S11†), which provided a more native and stabilizing environment for the NPs but nevertheless provides support that the surface chemistry of the NPs may be changing as a function of Ag incorporation (as has been independently observed30), and that other means of morphological analysis are required.The instability of Ag-rich samples upon drying on TEM grids, as well as a desire to statistically evaluate trends in NP size with a robust sample size, prompted characterization using SAXS to extract the form factor to precisely determine morphological parameters and trends in NP polydispersity. Additionally, the high throughput nature of SAXS enabled measurements to be performed on 96 different samples that sufficiently surveyed the reduction parameter space of interest. As suggested from TEM, SAXS data could be fit using a single NP population in all cases with a spherical form factor, suggesting that NP anisotropy (or the linear aggregated chains suggested by TEM) was not observed in solution in any case. Trends shown in Fig. 3, bottom and Tables S2–S7† reveal differences in NP size and dispersity trends with varying reduction parameters. As NPs become more Ag-rich, polydispersity increases, meaning that the NPs become less uniform, and average size increases relatively consistently as well. Increasing the stoichiometry of the reductant had significant effects on NP size and uniformity, with particles tending towards smaller overall sizes and lower polydispersity throughout. The reductant volume introduced had little systematic effect on NP size and polydispersity compared with the concentration of the reductant.
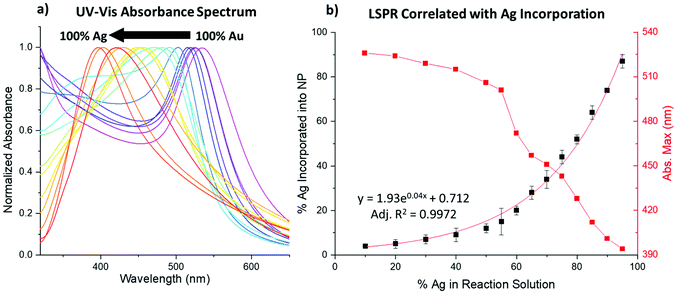
UV-vis spectroscopy signatures
UV-vis spectroscopy results show the LSPR blue-shifts as a function of increasing Ag% within the NPs. At the observed sizes, typically, pure Au NPs absorb at λmax ∼520 nm and pure Ag NPs absorb at λmax ∼400 nm,31 and the bimetallic NPs systematically absorb in these ranges, approaching the Ag value for samples with increased Ag incorporation (Fig. 4a and Fig. S1–S6†). Notably, doublet peaks are only subtly observed at higher reductant ratios, which would be more pronounced if core/shell NPs had been formed.4,32 Rather, single peaks systematically vary, most connectedly with the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratio incorporated into the sample as traced using XRF. Fig. 4b shows that the decrease in the LSPR peak position directly mimics the exponential curve that reflects Ag incorporation into the NPs. When accounting for particle composition, the shift aligns closely with the previously noted linear dependence of the LSPR on the alloy Ag/Au ratio.31
Au ratio incorporated into the sample as traced using XRF. Fig. 4b shows that the decrease in the LSPR peak position directly mimics the exponential curve that reflects Ag incorporation into the NPs. When accounting for particle composition, the shift aligns closely with the previously noted linear dependence of the LSPR on the alloy Ag/Au ratio.31
The reductant ratios and volumes, in contrast, appear to affect the spectra to a lesser extent than composition alone. Still, small changes can be observed between samples that display similar atomic % Ag (Fig. S7†). Given that the NP size and composition of the samples are similar, these changes can only be attributed to differences in atomic scale structure between the samples, which are further discussed in the following sections. The effects of differing atomic scale coordination on the NP UV-vis absorbance spectra are anticipated to be subtle, which is in line with these observations.
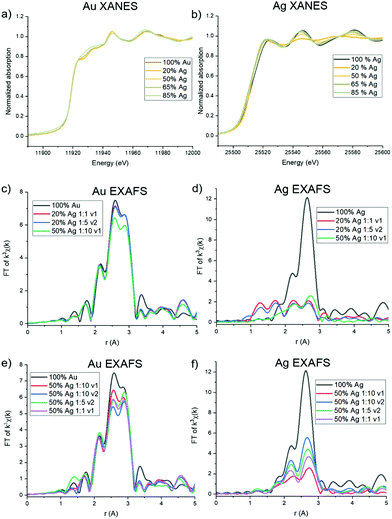
Ag and Au atomic scale coordination
Trends in the atomic coordination environment surrounding Ag and Au atoms were probed using XAFS. The X-ray absorption near edge structure (XANES) region provides information regarding the Ag and Au oxidation states and differences in the potential surrounding the core atom. From the Au L3 edge (Fig. 5a) it can be observed that the Au samples with low Ag incorporation well-match the features typically observed for a bulk Au0 foil. Upon additional Ag incorporation, however, as shown with 65 and 85% solution Ag introduced, the white line (which is the first main peak after the sharp increase of the edge, ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 eV in Au and ∼22
920 eV in Au and ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 eV in Ag) begins to increase and rounds out, but not in such a way that is suggestive of ionization, where the white line would become sharper due to decreased d-state occupancy.33 Rather, it is likely that this change results from increased coordination to Ag atoms, keeping the Au in the zero valent state, as has previously been observed in systems that exhibit Ag–Au coordination.34 The Ag K edge (Fig. 5b) exhibits expected Ag0 signatures reminiscent of a bulk Ag0 foil for all spectra, with the exception of a slight sharpening of the white line for samples with lower Ag incorporation, and to a trend observed in the 20 atomic % solution Ag samples and the 50 atomic % solution Ag sample with the highest reductant ratio (1
520 eV in Ag) begins to increase and rounds out, but not in such a way that is suggestive of ionization, where the white line would become sharper due to decreased d-state occupancy.33 Rather, it is likely that this change results from increased coordination to Ag atoms, keeping the Au in the zero valent state, as has previously been observed in systems that exhibit Ag–Au coordination.34 The Ag K edge (Fig. 5b) exhibits expected Ag0 signatures reminiscent of a bulk Ag0 foil for all spectra, with the exception of a slight sharpening of the white line for samples with lower Ag incorporation, and to a trend observed in the 20 atomic % solution Ag samples and the 50 atomic % solution Ag sample with the highest reductant ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) and smaller reductant volume (v1). For these samples, a dampening of the near edge region and sharpening of the white line is observed. Such signatures are similar to what has been previously observed for AgCl,35 suggesting that these samples contain some fractionation of ionized Ag+, and potentially as AgCl or an Ag/Cl-containing complex (see below). This is also substantiated by PXRD pattern of the 20 atomic % solution Ag NPs (Fig. S14†), which shows two sharp diffraction peaks that do not correspond to the FCC packing of Ag and Au and instead align well with the presence of AgCl and/or Ag2O; these impurities were not observed in the PXRD patterns of NPs with higher Ag incorporation.
10) and smaller reductant volume (v1). For these samples, a dampening of the near edge region and sharpening of the white line is observed. Such signatures are similar to what has been previously observed for AgCl,35 suggesting that these samples contain some fractionation of ionized Ag+, and potentially as AgCl or an Ag/Cl-containing complex (see below). This is also substantiated by PXRD pattern of the 20 atomic % solution Ag NPs (Fig. S14†), which shows two sharp diffraction peaks that do not correspond to the FCC packing of Ag and Au and instead align well with the presence of AgCl and/or Ag2O; these impurities were not observed in the PXRD patterns of NPs with higher Ag incorporation.
The extended EXAFS region of the spectra is sensitive to atomic scale attributes surrounding the Au or Ag atoms depending on cL3 edge (Fig. 5c). The lower Ag-incorporation samples appear to greatly mimic pure Au NPs, which is in line with Au-rich coordination, and then tend towards the increased presence of Au–Ag bonds. Interestingly, no evidence of Au–Ag coordination is observed in the spectra for the 20% solution Ag samples, and inclusion of Au–Ag pathways did not improve the goodness of fit of the modeled structure. Such a result either means that there are so few Au–Ag bonds that they cannot be detected within the limit of the measurement or that Ag is in fact not incorporated into the particles at the lowest solution percentages. A lack of Ag incorporation for these samples was further supported by Ag K edge data (Fig. 5d), which shows significant dampening of the expected FCC Ag or Au signatures and emergence of lower-R pathways. Indeed, fitting models for these samples could account for no more than 3 Ag–Au or Ag–Ag coordinated atoms, which leads to the conclusion that a majority of the Ag is in fact not incorporated into the NPs. Rather, it is likely that a Cl-containing cluster has formed, which is likely to occur based on excess Cl− in solution from the Au precursor, and is suggested by the similarity of the XANES spectrum to AgCl. Unfortunately, the complexity of the structure precluded its precise identification; however, it is not simply a mixture of NP-incorporated Ag and AgCl (or Ag2O) since it could not be modelled using these pathways alone.
Notably, both Au L3 and Ag K EXAFS data showed distinct spectral differences for samples with the same atomic % Ag. This was demonstrated by comparing spectra collected for 50 atomic % solution Ag samples with varying reductant ratios and reductant volumes (Fig. 5e and f). Differences in the first shell peak shapes (around 2.6 Å) compared with 100% Au and 100% Ag show that Au–Ag bonding is indeed present in the structures to varying degrees (see Fig. S16† for detailed fitting models). The 50 atomic % solution Ag sample synthesized using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 reductant ratio with a small, concentrated volume of reductant introduced, showed the starkest differences. Interestingly, the EXAFS spectra at the Ag K edge for this sample could not be fit using Ag–Ag and Ag–Au pathways alone. Rather, the data suggests that Cl is also coordinated (Fig. S16.18†). This finding suggests that Ag is either forming a chlorinated complex on the NP surface (since coordination to Ag and Au suggest it is still incorporated into the NP surface layers) or a combination of incorporated and unincorporated Ag is present. When a larger reductant volume is used under otherwise identical conditions, full incorporation of Ag into the NPs is instead observed. Likewise, full incorporation is also observed when lower reductant ratios are used. This finding suggests that (1) excess reductant may lead to fast, preferential reduction of Au, forming an Au-rich NP core before Ag has the opportunity to sufficiently incorporate and (2) reductant ratio and volume both have the capacity to affect the incorporation and atomic distribution of Ag within Au, independent of overall NP composition.
10 reductant ratio with a small, concentrated volume of reductant introduced, showed the starkest differences. Interestingly, the EXAFS spectra at the Ag K edge for this sample could not be fit using Ag–Ag and Ag–Au pathways alone. Rather, the data suggests that Cl is also coordinated (Fig. S16.18†). This finding suggests that Ag is either forming a chlorinated complex on the NP surface (since coordination to Ag and Au suggest it is still incorporated into the NP surface layers) or a combination of incorporated and unincorporated Ag is present. When a larger reductant volume is used under otherwise identical conditions, full incorporation of Ag into the NPs is instead observed. Likewise, full incorporation is also observed when lower reductant ratios are used. This finding suggests that (1) excess reductant may lead to fast, preferential reduction of Au, forming an Au-rich NP core before Ag has the opportunity to sufficiently incorporate and (2) reductant ratio and volume both have the capacity to affect the incorporation and atomic distribution of Ag within Au, independent of overall NP composition.
Discussion
Local dispersion vs. clustering in AgAu NPs
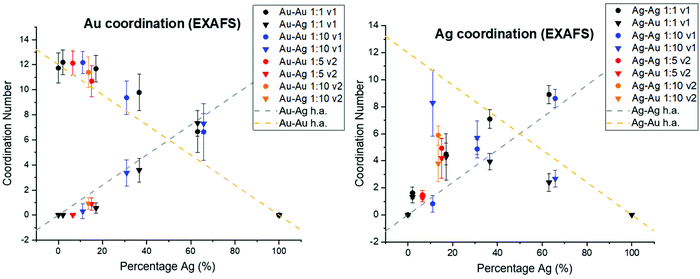
In order to consider whether or not the NPs formed in this study resulted in homogeneous alloys or exhibited local clustering, coordination numbers extracted from XAFS analysis were compared with expected trends for homogeneous alloys (Fig. 6). For both the case of Ag and Au, deviation from homogeneity is observed. Specifically, Au–Au coordination is consistently favored compared with Au–Ag, which would result from local Au-rich clustering regions. Local clustering is further shown through calculating Cowley's parameter36 for the investigated samples, which are tabulated in Table 1. According to Cowley's parameter (calculation details in the ESI†), a positive value corresponds to a tendency towards clustering whereas a negative value corresponds to a tendency towards dispersion. With the exception of the 50 atomic % solution Ag sample that exhibited chloride formation due to under- or surface-incorporation, this parameter was positive in all cases, providing additional evidence for local clustering within all synthesized NPs. Such a result shows the assumption that homogeneous alloys of Ag and Au are created based on miscibility alone is likely unreasonable and should not be considered without thorough atomic scale support.| Sample | α for Au | α for Ag |
|---|---|---|
20% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v1 1 v1 |
1 | 0.54 |
20% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 v2 5 v2 |
1 | 0.51 |
50% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v1 1 v1 |
0.74 | 0.41 |
50% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v1 10 v1 |
0.77 | −0.02 |
50% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v2 10 v2 |
0.50 | 0.54 |
50% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 v2 5 v2 |
0.44 | 0.47 |
65% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v1 10 v1 |
0.28 | 0.15 |
65% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v1 1 v1 |
0.13 | 0.48 |
85% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v1 10 v1 |
0.17 | 0.36 |
85% Ag 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v1 1 v1 |
0.20 | 0.38 |
The extent of Au vs. Ag domains was further investigated using the method developed by Calvin et al.37 for determining domain size based on NP coordination numbers, since the presence of undercoordinated atoms indicates that they are on the domain surface. In this case, Au–Au and Ag–Ag coordination were used to determine the cluster sizes of Au and Ag regions within the NPs (Table S8†). Results showed that the sizes of Au domains were generally significantly larger than Ag domains. The sizes of the domains, however, were also affected by the reductant volume used. Specifically, lower Cowley's parameter values and smaller Au domain sizes were observed for the cases where the volume of reductant solution introduced was greater. This trend was significant; for example, the Au domain sizes were decreased by 50–75% when v2 was used instead of v1, under otherwise identical conditions. As may be expected, Au domain sizes within the NPs decreased and Ag domain sizes increased with increasing Ag content.
Variation in NP surface vs. interior composition
Surface segregation of Ag or Au was considered through comparing total coordination numbers of Ag and Au (Fig. 7). Ag is consistently undercoordinated compared with Au, particularly for lower incorporation ratios. Ag and Au are both FCC metals, so an atom in the NP interior will have a coordination number of 12. For samples where the coordination number is less than 12 outside of error, it therefore follows that a percentage of the atoms must reside in surface sites, which would exhibit lower coordination. Assuming an FCC {111} surface (since this is the lowest energy facet), the percentage of Ag atoms on the NP surface vs. interior were calculated and compared with the overall fraction of surface atoms within the NP (Table S9†). In all AgAu NP samples, the fraction of surface vs. interior Ag atoms greatly exceeds the fraction of total atoms that are on the NP surface. In fact, results suggest that almost all of the Ag is surface-bound until the solution Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratios become Ag-rich. This result reveals that Ag is segregated towards the NP surface, whereas Au (which remains fully coordinated throughout) clusters in the NP interior. This experimental result is in agreement with computational predictions,38–41 and may be in part due to the lower surface energy of Ag compared with Au42 but can also result from slower kinetic incorporation of Ag. Overall, this creates a NP that is not core/shell (since significant mixed-metal coordination exists) but rather has an Au core and diffuse Ag that is more highly concentrated at the NP surface.
Au ratios become Ag-rich. This result reveals that Ag is segregated towards the NP surface, whereas Au (which remains fully coordinated throughout) clusters in the NP interior. This experimental result is in agreement with computational predictions,38–41 and may be in part due to the lower surface energy of Ag compared with Au42 but can also result from slower kinetic incorporation of Ag. Overall, this creates a NP that is not core/shell (since significant mixed-metal coordination exists) but rather has an Au core and diffuse Ag that is more highly concentrated at the NP surface.
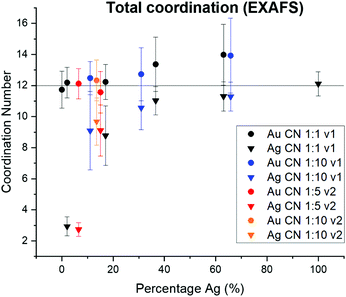 | ||
| Fig. 7 From total EXAFS coordination numbers, Ag is consistently undercoordinated within AgAu NPs, whereas Au retains the bulk value of 12. This suggests that Ag dominates NP surface sites. | ||
The effect of Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Au solution ratio
Au solution ratio
Greater Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au precursor ratios in solution did result in the formation of NPs with increasing amounts of Ag. It is important, however, to recall that these trends were not linear. Rather, there was a barrier to Ag incorporation (as evidenced further in that samples even with 20% solution Ag showed only unincorporated Ag). It was not until larger solution ratios were applied that Ag actually incorporated into the NP lattice itself. Even with higher Ag
Au precursor ratios in solution did result in the formation of NPs with increasing amounts of Ag. It is important, however, to recall that these trends were not linear. Rather, there was a barrier to Ag incorporation (as evidenced further in that samples even with 20% solution Ag showed only unincorporated Ag). It was not until larger solution ratios were applied that Ag actually incorporated into the NP lattice itself. Even with higher Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au solution ratios, Ag consistently underincorporates compared with Au, and its incorporation follows an exponential curve. Observed Ag underincorporation may be due to (1) the formation of AgCl as a byproduct due to the high Cl− concentration from the Au precursor, particularly at lower solution Ag content, (2) the relative difference in reduction potential favoring Au reduction and resulting in Au-rich particles, or (3) galvanic replacement of initially incorporated Ag with Au atoms. The most likely scenario is a combination of the first and second explanations. EXAFS and XRD results both suggest that AgCl is formed in samples with high amounts of HAuCl4 precursor and lower amounts of AgNO3, and Au reduction is inherently more favorable. The possibility for a small degree of galvanic replacement of Ag with Au cannot be ruled out, as it has previously been reported in systems where both Ag+ and Au3+ are co-reduced.43 Experimental evidence, however, is not in line with previously reported trends for spherical NPs where galvanic replacement is the predominant mechanism15 due to (1) a lack of inherent porosity or hollowing that results from the 3
Au solution ratios, Ag consistently underincorporates compared with Au, and its incorporation follows an exponential curve. Observed Ag underincorporation may be due to (1) the formation of AgCl as a byproduct due to the high Cl− concentration from the Au precursor, particularly at lower solution Ag content, (2) the relative difference in reduction potential favoring Au reduction and resulting in Au-rich particles, or (3) galvanic replacement of initially incorporated Ag with Au atoms. The most likely scenario is a combination of the first and second explanations. EXAFS and XRD results both suggest that AgCl is formed in samples with high amounts of HAuCl4 precursor and lower amounts of AgNO3, and Au reduction is inherently more favorable. The possibility for a small degree of galvanic replacement of Ag with Au cannot be ruled out, as it has previously been reported in systems where both Ag+ and Au3+ are co-reduced.43 Experimental evidence, however, is not in line with previously reported trends for spherical NPs where galvanic replacement is the predominant mechanism15 due to (1) a lack of inherent porosity or hollowing that results from the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ag
1 Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au exchange ratio and (2) excess solution Au3+ in cases of higher Ag incorporation, which needed to be removed via rigorous centrifugation. Therefore, it is unlikely that galvanic replacement is the predominant reason for underincorporation of Ag.
Au exchange ratio and (2) excess solution Au3+ in cases of higher Ag incorporation, which needed to be removed via rigorous centrifugation. Therefore, it is unlikely that galvanic replacement is the predominant reason for underincorporation of Ag.
Fig. 8, top shows trends in NP atomic and nanometer-scale structural evolution as a function of increasing Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au solution precursor ratios. Increasing Ag content results in higher polydispersity but also maximizes Ag–Au coordination as Ag becomes increasingly incorporated into the NP interior, evidenced through XAFS coordination numbers. It is also interesting to note that the Ag
Au solution precursor ratios. Increasing Ag content results in higher polydispersity but also maximizes Ag–Au coordination as Ag becomes increasingly incorporated into the NP interior, evidenced through XAFS coordination numbers. It is also interesting to note that the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au precursor ratio did in fact induce significant morphological changes compared to the pure Au or Ag endpoints. Specifically, any mixed ratio at all seemed to direct the resulting NPs towards a smaller size regime, even at stoichiometric reductant ratios that tend to favor larger sizes and facile aggregation in mono-metallic systems. This may be related to the capability of Ag to act as a growth-directing agent in anisotropic Au NP syntheses;44–46 as the Au-rich core first formed accumulates more Ag on its surface, it is possible its growth may be hampered by the less reactive “shell” and subsequently limited to sizes below pure Au NPs.
Au precursor ratio did in fact induce significant morphological changes compared to the pure Au or Ag endpoints. Specifically, any mixed ratio at all seemed to direct the resulting NPs towards a smaller size regime, even at stoichiometric reductant ratios that tend to favor larger sizes and facile aggregation in mono-metallic systems. This may be related to the capability of Ag to act as a growth-directing agent in anisotropic Au NP syntheses;44–46 as the Au-rich core first formed accumulates more Ag on its surface, it is possible its growth may be hampered by the less reactive “shell” and subsequently limited to sizes below pure Au NPs.
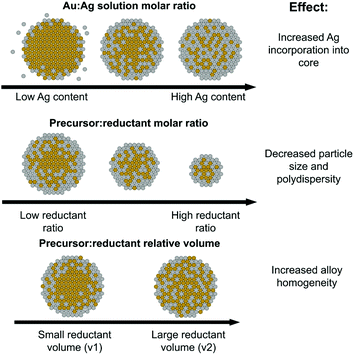 | ||
Fig. 8 Schematic of the roles of Ag solution atomic % (top), precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio (middle) and precursor reductant ratio (middle) and precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant relative volume (bottom) on the resulting local atomic and nanoscale structure. reductant relative volume (bottom) on the resulting local atomic and nanoscale structure. | ||
The role of precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) reductant ratio
reductant ratio
As pictorially represented in the Fig. 8 (middle) schematic, the higher the precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio used, the smaller and more uniform the resulting NPs. Smaller particle formation is not a particularly surprising finding given that prior work suggests that increased reductant can promote the formation of a larger number of initial nuclei.47 Unfortunately, it is possible that the uniformity is in part a result of poor Ag incorporation, as evidenced in particular by the 50 atomic % solution Ag sample with a 1
reductant ratio used, the smaller and more uniform the resulting NPs. Smaller particle formation is not a particularly surprising finding given that prior work suggests that increased reductant can promote the formation of a larger number of initial nuclei.47 Unfortunately, it is possible that the uniformity is in part a result of poor Ag incorporation, as evidenced in particular by the 50 atomic % solution Ag sample with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 precursor
10 precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio, which evidenced a lack of Ag incorporation into the NPs when compared with its counterparts at other reductant ratios. Given that Ag incorporation overall led to greater polydispersity, it is possible that the increased reduction potential in solution encouraged faster Au reduction, which potentially formed an Au-rich particle before Ag incorporation could take place. This result suggests that a strategy to improve incorporation of a secondary species in a multi-metallic NP synthesis does not benefit from increasing the amount of reductant. While this may improve the overall reduction capability of the solution, the relative ease of reduction between varying species complicates uniform incorporation.
reductant ratio, which evidenced a lack of Ag incorporation into the NPs when compared with its counterparts at other reductant ratios. Given that Ag incorporation overall led to greater polydispersity, it is possible that the increased reduction potential in solution encouraged faster Au reduction, which potentially formed an Au-rich particle before Ag incorporation could take place. This result suggests that a strategy to improve incorporation of a secondary species in a multi-metallic NP synthesis does not benefit from increasing the amount of reductant. While this may improve the overall reduction capability of the solution, the relative ease of reduction between varying species complicates uniform incorporation.
The role of reductant volume introduced
Reductant volume, despite being a parameter often ignored in synthetic reactions in favor of considering an overall solution concentration of reductant alone, provided evidence for having the greatest effect on NP local structure homogeneity. For the case where samples all had similar Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au incorporation ratios, those with a larger reductant volume resulted in increased Au–Ag bonding and smaller Au domain sizes (see Fig. 8, bottom schematic). These trends provide support that larger, more dilute volumes of reductant can actually increase the homogeneity of the resulting bimetallic NP constructs. While further investigation is required to determine the mechanistic modality through which this is possible, one potential reason is the more uniform diffusion of the reductant through the solution, which would promote more widespread reduction rather than a faster, local reduction event at the site of introduction of a concentrated droplet. It is possible that a faster local reduction event could promote the effects observed for the higher reductant concentration case, where sufficient time is not allotted for diffusion to take place before dominating reduced Au forms into condensed nuclei. Regardless of the exact mechanism, these results suggest that the volume of reductant introduced is a parameter that should be more extensively considered when developing synthetic reactions and could serve as a potential starting place for maximizing multi-metallic bonds over local clustering within multi-metallic NPs with miscible constituents.
Au incorporation ratios, those with a larger reductant volume resulted in increased Au–Ag bonding and smaller Au domain sizes (see Fig. 8, bottom schematic). These trends provide support that larger, more dilute volumes of reductant can actually increase the homogeneity of the resulting bimetallic NP constructs. While further investigation is required to determine the mechanistic modality through which this is possible, one potential reason is the more uniform diffusion of the reductant through the solution, which would promote more widespread reduction rather than a faster, local reduction event at the site of introduction of a concentrated droplet. It is possible that a faster local reduction event could promote the effects observed for the higher reductant concentration case, where sufficient time is not allotted for diffusion to take place before dominating reduced Au forms into condensed nuclei. Regardless of the exact mechanism, these results suggest that the volume of reductant introduced is a parameter that should be more extensively considered when developing synthetic reactions and could serve as a potential starting place for maximizing multi-metallic bonds over local clustering within multi-metallic NPs with miscible constituents.
Conclusions
Through combining a systematic synthetic investigation of the parameters that affect reduction within bimetallic AgAu NPs with comprehensive characterization at the atomic and nanometer length scales, this work thoroughly explored the influence of the synthetic parameter space on the resulting atomic scale distributions and alloy homogeneity. The results present emerging evidence that reduction kinetics can be used to control atomic arrangement and maximize multi-metallic bonding. XRF analysis reveals that atomic percentages within bimetallic NPs are not well-represented by the precursor ratios introduced. Rather, Ag incorporation faces an initial barrier, then follows an exponential rather than linear trend for incorporation. Local Au and Ag clustering is consistently observed within the NPs based on XAFS-derived parameters combined with morphological information obtained from TEM and SAXS, with Ag segregated towards the NP surface. Use of higher reductant ratios has the capability to stunt Ag incorporation due to the fast formation of Au nuclei. Using a larger, more dilute volume of reductant results in increased alloy homogeneity and Ag dispersion, likely due to greater uniformity in diffusion which may translate to diffusive trends towards initial particle formation.Despite the natural propensity of Au and Ag to cluster and segregate within these nanostructures, the generation of highly alloyed materials through the maximization of mixed Au–Ag bonds continues to be the ultimate goal of investigations such as this. Our findings show that alloy homogeneity can in fact be manipulated by the kinetic environment of the initial nucleation and growth stages, particularly regarding the mode of introduction and diffusion of the reductant. It is also necessary to consider the exponential trend that quantifies Ag incorporation as a function of Ag solution ratio; for example, assuming that Au–Ag bonds are maximized in a fully alloyed construct composed of 50% Ag and 50% Au, it is critical to anticipate that upwards of 80% solution Ag is required to generate a construct with the desired composition. Other parameters outside the scope of this study can further encourage alloying, including thermal annealing processes and post-synthetic etching of Ag-rich areas from an otherwise alloyed structure. The collective utilization of many of these concepts will be necessary to ultimately exercise rational control over the atomic-scale structure of designed materials.
As an aggregate, the findings reported in this study demonstrate that the formation of homogeneous alloys for the case of room temperature multi-metallic NP synthesis is likely not a valid assumption. Rather, atomic-scale characterization of such systems is required to determine the extent of species segregation. It is possible, however, to tune reduction kinetics to promote alloy homogeneity, which has important implications for catalytic reactions such as CO-oxidation, whose favored mechanisms rely on the existence of multi-metallic bonds. Optical properties appear to be much less affected by atomic scale coordination environment than by Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratios within the NPs. Accurate determination of processing/structure/property relationships requires synthetic investigations be paired with thorough structural characterization, particularly at the atomic scale, when relevant performance is suspected to rely on detailed structural attributes.
Au ratios within the NPs. Accurate determination of processing/structure/property relationships requires synthetic investigations be paired with thorough structural characterization, particularly at the atomic scale, when relevant performance is suspected to rely on detailed structural attributes.
Author contributions
H. Johnson and L. Moreau designed the experiments and wrote the manuscript. H. Johnson and A. Dasher performed the nanoparticle synthesis and purification and collected UV-vis spectroscopy and TEM data. M. Monahan prepared samples and collected and analyzed EDX maps. S. Seifert collected the SAXS data, which was analyzed by H. Johnson and L. Moreau. XAFS experiments were designed and analyzed by L. Moreau. All authors reviewed and contributed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. Johnson was supported by the Research Assistantship for Diverse Scholars (RADS) Fellowship at Washington State University. The authors acknowledge Ryan Davis for his assistance with collecting XAFS data at SSRL beamline 4-1. TEM and XRF measurements were performed at the Franceschi Microscopy & Imaging Center (FMIC) at Washington State University. SSRL is supported by the U.S. Department of Energy, Office of Basic Energy Sciences under contract no. DEAC02-76SF00515. SAXS measurements at APS beamline 12ID-C used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.References
- A. Zaleska-Medynska, M. Marchelek, M. Diak and E. Grabowska, Adv. Colloid Interface Sci., 2016, 229, 80–107 CrossRef CAS PubMed
.
- J. K. Majhi and P. K. Kuiri, J. Nanopart. Res., 2020, 22, 86 CrossRef CAS
.
- P. Srinoi, Y.-T. Chen, V. Vittur, M. D. Marquez and T. R. Lee, Appl. Sci., 2018, 8, 1106 CrossRef
.
- A. K. Samal, L. Polavarapu, S. Rodal-Cedeira, L. M. Liz-Marzán, J. Pérez-Juste and I. Pastoriza-Santos, Langmuir, 2013, 29, 15076–15082 CrossRef CAS PubMed
.
- T. Zhang, X. Li, C. Li, W. Cai and Y. Li, Chem. Mater., 2021, 33, 2593–2603 CrossRef CAS
.
- A. K. Singh and Q. Xu, ChemCatChem, 2013, 5, 652–676 CrossRef CAS
.
- G. Sharma, A. Kumar, S. Sharma, M. Naushad, R. P. Dwivedi, Z. A. Alothman and G. T. Mola, J. King Saud Univ., Sci., 2019, 31, 257–269 CrossRef
.
- N. Toshima and T. Yonezawa, New J. Chem., 1998, 22, 1179–1201 RSC
.
- B. Lim, M. Jiang, P. H. C. Camargo, E. C. Cho, J. Tao, X. Lu, Y. Zhu and Y. Xia, Science, 2009, 324, 1302–1305 CrossRef CAS PubMed
.
- D. Wang and Y. Li, Adv. Mater., 2011, 23, 1044–1060 CrossRef CAS PubMed
.
- X. Zhu, J. Xu, H. Zhang, X. Cui, Y. Guo, S. Cheng, C. Kan and J. Wang, Chem. Sci., 2020, 11, 3198–3207 RSC
.
- C. J. DeSantis, R. G. Weiner, A. Radmilovic, M. M. Bower and S. E. Skrabalak, J. Phys. Chem. Lett., 2013, 4, 3072–3082 CrossRef CAS
.
- C. J. Wrasman, A. Boubnov, A. R. Riscoe, A. S. Hoffman, S. R. Bare and M. Cargnello, J. Am. Chem. Soc., 2018, 140, 12930–12939 CrossRef CAS PubMed
.
- A.-Q. Wang, J.-H. Liu, S. D. Lin, T.-S. Lin and C.-Y. Mou, J. Catal., 2005, 233, 186–197 CrossRef CAS
.
- L. M. Moreau, C. A. Schurman, S. Kewalramani, M. M. Shahjamali, C. A. Mirkin and M. J. Bedzyk, J. Am. Chem. Soc., 2017, 139, 12291–12298 CrossRef CAS PubMed
.
- J. Erlebacher, M. J. Aziz, A. Karma, N. Dimitrov and K. Sieradzki, Nature, 2001, 410, 450–453 CrossRef CAS PubMed
.
- B. Goris, L. Polavarapu, S. Bals, G. Van Tendeloo and L. M. Liz-Marzán, Nano Lett., 2014, 14, 3220–3226 CrossRef CAS PubMed
.
- A. Frenkel, Z. Kristallogr. – Cryst. Mater., 2007, 222, 605–611 CrossRef CAS
.
-
J. Rumble, CRC Handbook of Chemistry and Physics, CRC Press, 102 edn, 2021 Search PubMed
.
- H. Peng, W. Qi, S. Li and W. Ji, J. Phys. Chem. C, 2015, 119, 2186–2195 CrossRef CAS
.
- L. Malassis, R. Dreyfus, R. J. Murphy, L. A. Hough, B. Donnio and C. B. Murray, RSC Adv., 2016, 6, 33092–33100 RSC
.
- C. Gao, Y. Hu, M. Wang, M. Chi and Y. Yin, J. Am. Chem. Soc., 2014, 136, 7474–7479 CrossRef CAS PubMed
.
- T. Zhang, Y. Sun, L. Hang, H. Li, G. Liu, X. Zhang, X. Lyu, W. Cai and Y. Li, ACS Appl. Mater. Interfaces, 2018, 10, 9792–9801 CrossRef CAS PubMed
.
- J. Ilavsky, J. Appl. Crystallogr., 2012, 45, 324–328 CrossRef CAS
.
- J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353 CrossRef CAS
.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed
.
- M. Newville, P. Līviņš, Y. Yacoby, J. J. Rehr and E. A. Stern, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 14126–14131 CrossRef CAS PubMed
.
- A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576 CrossRef CAS
.
- C. Wang, H. Yin, R. Chan, S. Peng, S. Dai and S. Sun, Chem. Mater., 2009, 21, 433–435 CrossRef CAS
.
- Y. Ni, C. Kan, L. He, X. Zhu, M. Jiang and D. Shi, Photonics Res., 2019, 7, 558–565 CrossRef CAS
.
- S. Link, Z. L. Wang and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 3529–3533 CrossRef CAS
.
- L. Lu, G. Burkey, I. Halaciuga and D. V. Goia, J. Colloid Interface Sci., 2013, 392, 90–95 CrossRef CAS PubMed
.
-
G. Bunker, Introduction to XAFS: A Practical Guide to X-ray Absorption Fine Structure Spectroscopy, Cambridge University Press, Cambridge, 2010 Search PubMed
.
- I. J. Godfrey, A. J. Dent, I. P. Parkin, S. Maenosono and G. Sankar, J. Phys. Chem. C, 2017, 121, 1957–1963 CrossRef CAS
.
- Y. Yang, W. Liu, X. Gao and M. Chen, Hydrometallurgy, 2019, 186, 252–259 CrossRef CAS
.
- J. M. Cowley, Phys. Rev., 1965, 138, A1384–A1389 CrossRef
.
- S. Calvin, M. M. Miller, R. Goswami, S. F. Cheng, S. P. Mulvaney, L. J. Whitman and V. G. Harris, J. Appl. Phys., 2003, 94, 778–783 CrossRef CAS
.
- L. Deng, W. Hu, H. Deng, S. Xiao and J. Tang, J. Phys. Chem. C, 2011, 115, 11355–11363 CrossRef CAS
.
- L. Wei, W. Qi, B. Huang and M. Wang, Comput. Mater. Sci., 2013, 69, 374–380 CrossRef CAS
.
- S. V. Doronin, Mendeleev Commun., 2020, 30, 288–290 CrossRef CAS
.
- A. L. Gould, A. J. Logsdail and C. R. A. Catlow, J. Phys. Chem. C, 2015, 119, 23685–23697 CrossRef CAS
.
- W. R. Tyson and W. A. Miller, Surf. Sci., 1977, 62, 267–276 CrossRef CAS
.
- J. Xu, Q. Yun, H. Zhang, Y. Guo, S. Ke, J. Wang, X. Zhu and C. Kan, Chem. Commun., 2021, 57, 8332–8335 RSC
.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS
.
- M. L. Personick, M. R. Langille, J. Zhang and C. A. Mirkin, Nano Lett., 2011, 11, 3394–3398 CrossRef CAS PubMed
.
- J. Zhang, M. R. Langille, M. L. Personick, K. Zhang, S. Li and C. A. Mirkin, J. Am. Chem. Soc., 2010, 132, 14012–14014 CrossRef CAS PubMed
.
- E. E. Finney and R. G. Finke, J. Colloid Interface Sci., 2008, 317, 351–374 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting materials include extended methods, TEM images, UV-vis spectra, XRF data, SAXS patterns and fitting details, XAFS data and associated models and derived parameters, and sample calculations of parameters based on local structure determination (PDF). See DOI: 10.1039/d1nr06231j |
| This journal is © The Royal Society of Chemistry 2022 |