Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparative analysis of lanthanide excited state quenching by electronic energy and electron transfer processes†
David
Parker
 *ab,
Jack D.
Fradgley
*ab,
Jack D.
Fradgley
 a,
Martina
Delbianco
a,
Martina
Delbianco
 a,
Matthieu
Starck
a,
Matthieu
Starck
 a,
James W.
Walton
a,
James W.
Walton
 a and
Jurriaan M.
Zwier
a and
Jurriaan M.
Zwier
 c
c
aDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: david.parker@dur.ac.uk
bDepartment of Chemistry, Hong Kong Baptist University, Kowloon Tong, Hong Kong
cCisbio Bioassays, 30200 Codolet, BP 84175, France
First published on 5th November 2021
Abstract
The relative sensitivities of structurally related Eu(III) complexes to quenching by electron and energy transfer processes have been compared. In two sets of 9-coordinate complexes based on 1,4,7-triazacyclononane, the Eu emission lifetime decreased as the number of conjugated sensitising groups and the number of unbound ligand N atoms increased, consistent with photoinduced electron transfer to the excited Eu(III) ion that is suppressed by N-protonation. Quenching of the Eu 5D0 excited state may also occur by electronic energy transfer, and the quenching of a variety of 9-coordinate complexes by a cyanine dye with optimal spectral overlap occurs by an efficient FRET process, defined by a Förster radius (R0) value of 68 Å and characterised by second rate constants in the order of 109 M−1 s−1; these values were insensitive to changes in the ligand structure and to the overall complex hydrophilicity. Quenching of the Eu and Tb excited states by energy transfer to Mn(II) and Cu(II) aqua ions occurred over much shorter distances, with rate constants of around 106 M−1 s−1, owing to the much lower spectral overlap integral. The calculated R0 values were estimated to be between 2.5 to 4 Å in the former case, suggesting the presence of a Dexter energy transfer mechanism that requires much closer contact, consistent with the enhanced sensitivity of the rate of quenching to the degree of steric shielding of the lanthanide ion provided by the ligand.
Introduction
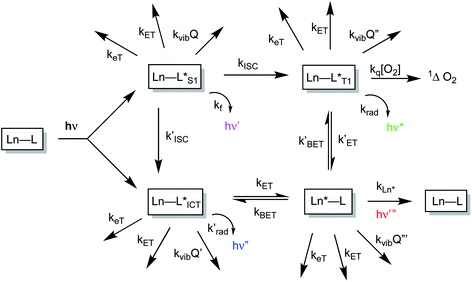
The sensitised emission of lanthanide luminescence has been studied in detail because of the wide range of applications that have arisen in developing luminescence bioassays, in devising targeted optical imaging agents and in the creation of selective analytical probes and sensors for a wide range of analytes.1–4 The salient properties of the sensitising chromophore have been considered in depth, and key design criteria have emerged.5–7 In particular, careful consideration has been given to the photophysical properties of the sensitiser, notably its molar absorptivity (high ε) at the excitation wavelength, the energies of its internal charge transfer (ICT), singlet and triplet states and the size of the energy gap that determines the facility of inter-system crossing. A small S1–T1 energy gap favours a fast rate of intersystem crossing, kISC, which typically needs to be >109 s−1 to compete with kf, which is of the order of 3 × 108 s−1. These features determine the choice of the excitation wavelength (λexc), the efficiency of triplet excited state formation and the energetic feasibility of the overall process that allows intramolecular energy transfer to proceed, thereby populating the lanthanide excited state.A mechanistic scheme (Scheme 1) can be put forward that characterises the competing pathways in sensitised lanthanide emission.7 The salient excited states have a transient existence and are subject to different radiative or non-radiative decay processes, each defined by a rate constant. A downhill energy cascade requires that the sensitising excited state donor lies close in energy, but more than about 10 kBT (2050 cm−1 at ambient temperature) higher than the accepting lanthanide excited state. In this way, any back energy transfer process is not prone to thermal activation. The excited states possess notably different lifetimes: the relaxed S1 and ICT states live for a few nanoseconds, the triplet state may often exist for a few microseconds, but the lanthanide excited state is the longest lived, with lifetimes ranging from the microsecond (e.g. Dy, Yb, Nd, Er) to the millisecond (Eu, Tb) domain. The long lifetime and large pseudo-Stokes’ shifts that epitomise sensitised lanthanide luminescence have allowed the use of time-gated methods of data acquisition for spectroscopy or microscopy, averting problems associated with Rayleigh light scattering, self-absorption or auto-fluorescence.
The non-radiative deactivation of the lanthanide excited state may occur by three main pathways involving the transfer of charge, electronic energy or vibrational energy. The key aspects of each of these quenching processes have been reported and considered in detail previously.7–10 In this article, examples of charge and electronic energy transfer are compared and considered in the context of enhancing our understanding of the mechanism of the underlying photophysical processes, thereby informing the design of bright lanthanide complexes that are inherently resistant to excited state deactivation. The examples described here relating to charge transfer are of particular interest to the creation of pH-responsive probes that may permit the tracking of receptor internalisation into cells.11 And, with regard to energy transfer, the efficiency of Förster resonance energy transfer (FRET)12 from an excited lanthanide ion to a strongly absorbing cyanine dye forms the basis of many commercial time-resolved luminescence bioassays13 and is contrasted here with the inefficiency of energy transfer to weakly absorbing transition metal aqua ions.
Results and discussion
Charge transfer quenching of the Eu excited state
Intramolecular electron transfer processes from the HOMO of a proximate electron rich aryl group or a nitrogen lone pair orbital to the Eu 5D0 excited state provide examples where the Eu emission lifetime can be reduced. Consider the following series of complexes, [EuL1–6] (Fig. 1).14–16 The first three Eu complexes, [EuL1–3], contain increasing numbers of electron rich chromophores with a simple methyl group in the upper aryl ring and are compared with the behaviour of [EuL4–6], where a diethylamino substituent is present in the upper phenyl ring that is not in direct conjugation with the alkyne bond.16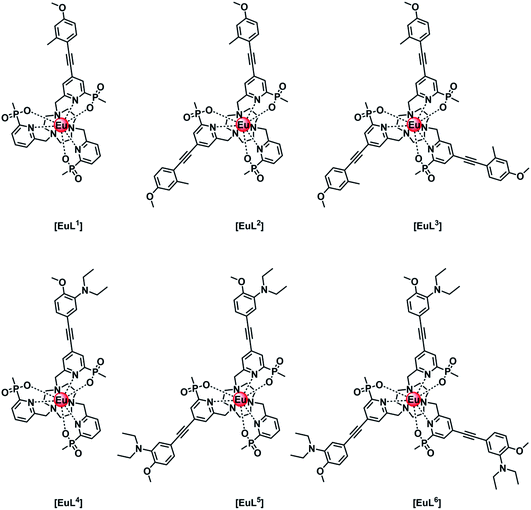 | ||
| Fig. 1 Europium(III) complexes with different numbers of aryl–alkynyl sensitising groups that are pH independent [EuL1–3] and pH sensitive [EuL4–6] in their emission behaviour.14–16 | ||
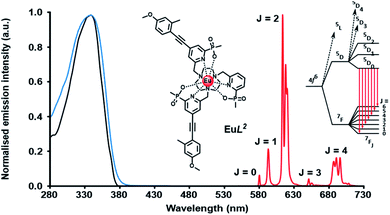
A typical Eu emission spectrum (Fig. 2) highlights the large pseudo-Stokes’ shift and the characteristic spectral fingerprint of europium(III) luminescence for this series of complexes. The emission from the europium(III) 5D0 excited state decays mono-exponentially. The lifetime for each complex was measured in water and values are compared in Table 1. With [EuL1–3], there is a small decrease in the lifetime of the emission as the number of chromophores increases, suggesting that charge transfer from the electron rich sensitising moiety quenches the Eu excited state to some degree.8,17 Of course, the overall quenching process will also involve vibrational energy transfer to some degree, e.g. to higher overtones of the alkyne stretch, aryl ring vibrations or C–H stretches. In the former case, the triple bonds are located about 7 Å from the metal centre, and given the r−6 dependence of vibrational energy transfer, such a process is likely to be very inefficient. In the former case, this has been established through many examples involving deuterated ligands.17 For each europium(III) complex, the metal-based emission lifetime was found to be independent of complex concentration over the range 1 to 50 μM, and did not change on degassing the solution to remove oxygen, in both acidic and basic media.
| Complex | τ Eu /ms | Comment |
|---|---|---|
| a 295 K, 0.1 M NaCl, H2O. b pH 8, 0.1 M NaCl, H2O. c pH 4, 0.1 M NaCl, H2O; pKa values are 6.75, 6.30 and 6.21, respectively for [EuHnL4–6]+. | ||
| [EuL1] | 1.39 | Small lifetime reduction with increasing number of electron rich chromophores |
| [EuL2] | 1.27 | |
| [EuL3] | 1.21 | |
| [EuL4] | 0.53b | Electron transfer quenching increases with the number of N-substituted chromophores |
| [EuL5] | 0.34b | |
| [EuL6] | 0.25b | |
| [EuHL4]+ | 1.16c | N-protonation suppresses electron transfer quenching |
| [EuH2L5]2+ | 1.00c | |
| [EuH3L6]3+ | 0.84c | |
The Weller equation18 (eqn (1)) considers the free energy of activation for an electron transfer process and can be applied to assess the feasibility of the quenching of the europium excited state by intramolecular electron transfer from the highest filled orbital, e.g., the lone pair orbital on N present in the conjugate base form of [EuL4–6]. The likelihood of the electron transfer event is predicted for photo-induced electron transfer processes.
| ΔGeT = nF([Eox − Ered] − ES − e2/εr) J mol−1 | (1) |
In the original description, Eox is the oxidation potential of a donor (e.g. a nitrogen lone pair or the HOMO of an electron rich aromatic group), Ered is the reduction potential of the acceptor (e.g. an aryl group or a Ln3+ ion), ES is the singlet excited state energy in eV and e2/εr is an attractive energy term related to the formation of a radical ion pair; this term is often less than +0.2 eV. This equation estimates the free energy of activation for the electron transfer step involving a particular excited state highlighting the facility of photo-induced electron transfer to those lanthanide ions with smaller Ered potential terms, where the Ln3+ oxidation state is relatively stabilised, e.g. Eu3+, Yb3+ and to a lesser extent, Sm3+.
The irreversible one electron oxidation potential of a typical N,N-dialkylaniline, such as N,N-dimethylaniline, is +0.76 V in acetonitrile (vs. standard calomel electrode),19 which rises to about 1.0 V for a trialkylamine such as N,N-dimethylbenzylamine, where the nitrogen lone pair is not in conjugation with the aromatic ring.20 The reduction potential of the Eu3+ ion when coordinated by an anionic polydentate ligand that stabilises the +3 oxidation state lies in the range −0.8 to −1.1 V, based on literature values8,21 in MeCN, and can be estimated to be −1.0 V here. The energy of the Eu3+ 5D1 and 5D0 excited states lie at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and 17
100 and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 cm−1; the latter energy value is equivalent to +2.13 eV or 206 kJ mol−1.
220 cm−1; the latter energy value is equivalent to +2.13 eV or 206 kJ mol−1.
| ΔGeT = F[(0.76 + 1.0) − 2.13–0.2] = −0.57, F = −55 kJ mol−1 | (2) |
Given these values, the free energy for the electron transfer process from the π-conjugated N lone pair orbital to the Eu3+ ion is energetically favourable by 55 kJ mol−1 (eqn (2)). Such an analysis assumes that the excited state reduction potential of the europium ion is the same as it is in the ground state.
The Weller analysis shows that the Eu excited state is prone to quenching by an intramolecular electron transfer process associated with the nitrogen lone pair of the conjugated diethylamino group. Next, the behaviour of the Eu(III) complexes of ligands L4–L6 is considered; each of these complexes exhibits a pronounced pH dependence of emission intensity and lifetime, following excitation of the ligand chromophore and intramolecular energy transfer to the Eu ion; their behaviour has been described in detail previously.16 The large lifetime and emission intensity variations in these complexes has led to the creation of targeted luminescent pH probes for cells being developed to monitor receptor internalisation and endosomal acidification in real time.11
The rate of proton transfer to and from nitrogen in aqueous solution (typically 1010 s−1) occurs much more quickly than both the rate of decay of the excited europium ion (Table 1, 103 s−1) and the intermediate ligand ICT or triplet excited states. Furthermore, the rate of electron transfer from the lone pair orbital to the excited Eu ion is faster than the rate of energy transfer populating the Eu* 5D0 state, and much faster than the rate of decay of the Eu excited state itself. Thus, during the long lifetime of the Eu* 5D0 excited state in solution, over the pH range of 4 to 8, deprotonation of the amine group occurs readily, allowing fast electron transfer to occur from the unprotonated chromophore to the Eu ion, quenching the Eu excited state and shortening the ‘time-averaged’ observed lifetime. Such an effect is more likely to occur with increasing numbers of chromophores bearing the amine group, consistent with the observation that the tris-amine complex, [EuL6], has the shortest measured emission lifetime at pH 8 (0.25 ms, Table 1), and the complex with only one amine-containing chromophore, [EuL4] has the longest, both when protonated at pH 4 (1.16 ms) and as its conjugate base at pH 8 (0.53 ms).
In a key control experiment, comparing behaviour with sensitised emission after excitation of the chromophore at the isosbestic wavelength of 332 nm, the same pH dependence of the Eu emission lifetime was observed for [EuL4–6], following direct excitation of the Eu ion at 397 nm. Thus, it is the Eu 5D0 excited state that is being quenched by charge transfer in each of these cases, and not an intermediate ligand excited state.
Efficient energy transfer involving a cyanine dye acceptor
The rate of Förster resonance energy transfer (FRET), kT, from a donor (D) to an acceptor (A) is commonly described by eqn (3),12,22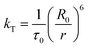 | (3) |
| R0 = (Jk2Φ0η−4)1/6 × (9.79 × 102) | (4) |
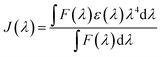 | (5) |
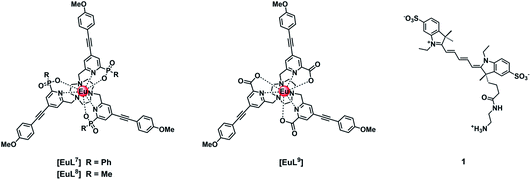
Three neutral highly luminescent Eu(III) complexes, [EuL7–9] (Fig. 3) were chosen as donors, as they form well defined charge neutral complexes and their photophysical properties have been investigated in detail; they are amongst the brightest Eu(III) coordination complexes reported that absorb strongly beyond 340 nm in protic media.2,14,15,24 The acceptor chosen for the energy transfer studies was the commercially available cyanine dye, 1 (Fig. 3), which also possesses no overall charge at neutral pH. It was selected because it and its analogues have been used in many commercial Eu-based FRET assays, and it has a large extinction coefficient at 647 nm (270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1). The emission spectral form of the three Eu(III) complexes presents a near-optimal profile for efficient energy transfer to this cyanine dye. Indeed, the intense hypersensitive emission band associated with the ΔJ = 2 transition (5D0 to 7F2 at 610–620 nm) provides a very good spectral overlap with the dye acceptor absorption band (Fig. 4). Furthermore, the low intensity of Eu emission at 670 nm permits separate monitoring of the two emissive species without significant spectral overlap.
000 M−1 cm−1). The emission spectral form of the three Eu(III) complexes presents a near-optimal profile for efficient energy transfer to this cyanine dye. Indeed, the intense hypersensitive emission band associated with the ΔJ = 2 transition (5D0 to 7F2 at 610–620 nm) provides a very good spectral overlap with the dye acceptor absorption band (Fig. 4). Furthermore, the low intensity of Eu emission at 670 nm permits separate monitoring of the two emissive species without significant spectral overlap.
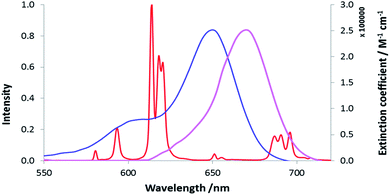 | ||
| Fig. 4 Absorbance (blue) and emission (purple) spectra of the cyanine dye, 1, compared to the [EuL7] emission spectrum (red), (MeOH, 295 K). | ||
Studies of energy transfer in methanol
In the rapid diffusion limit, energy transfer from a donor to an acceptor is assumed to obey pseudo-first order kinetics (eqn (6)–(9)).25,26 Hence, a plot of τ0/τ vs. [Q] gives a straight line with a slope equal to k2/k0, allowing the second order rate constant for energy transfer, k2, and the Stern–Volmer quenching constant, typically expressed as KSV−1, to be estimated.| 1/τ0 = k0 | (6) |
| 1/τ = kobs | (7) |
| kobs = k0 + k2[Q] | (8) |
| τ0/τ = kobs/k0 = 1 + k2/k0[Q] = 1 + KSV[Q] | (9) |
The quenching of the three Eu(III) complexes by the cyanine dye, 1, was examined by observing changes in the Eu(III) 5D0 excited state lifetime as a function of the added acceptor concentration, over the range of 0.3 to 5 μM using 5 μM solutions of the Eu(III) complex. The values of k2 were found to be 0.64, 0.57 and 1.40 × 109 M−1 s−1 for [EuL7–9] respectively (Fig. S1, Tables S1† and 2). The order of the rate constants revealed a slightly enhanced rate of energy transfer with the carboxylate derivative, compared to those of the two phosphinate complexes, which gave very similar results within experimental error. The spectral overlap integrals (J) and, hence, the Förster radii (R0) for each Eu(III) complex with this acceptor were also estimated in MeOH using eqn (4) and (5), respectively. The shorter lifetime of the less sterically shielded tris-carboxylate complex, [EuL9], was accompanied by a slightly larger second order rate constant, k2. The similar emission quantum yields and spectral overlap integrals, J, meant that the Förster radius, R0, for each complex was the same, within experimental error, i.e. 68 (±1) Å.
| [EuL7] | [EuL8] | [EuL9] | |
|---|---|---|---|
| a The spectral overlap integral was calculated for the region 550 < λ < 720 nm. The refractive index for MeOH is 1.328, compared to 1.333 for H2O. Errors on τ0, and ϕem are ±10%. b The values of the Stern–Volmer quenching constants under these conditions, KSV−1 are: 1.24 μM, 1.49 μM and 0.75 μM for [EuL7–9], respectively. | |||
| J/M−1 cm3 | 1.016 × 10−12 | 1.184 × 10−12 | 1.109 × 10−12 |
| ϕ | 0.52 | 0.43 | 0.48 |
| τ 0/ms | 1.26 | 1.18 | 0.95 |
| R 0/nm | 6.81 | 6.77 | 6.86 |
| k 2/M−1 s−1 × 109 | 0.64 | 0.57 | 1.40 |
Study of energy transfer in water
Due to the extremely low water solubility of [EuL7] and the carboxylate analogue [EuL9] it was only possible to carry out the quenching studies in water (50 mM HEPES, 50 mM NaCl, pH = 7.4) for the P–Me derivative, [EuL8]. It was decided to examine different MeOH/water compositions to check if there was any significant solvent effect.The results (Fig. S2† and Table 3) revealed a 2.8 fold increase in the value of k2 in water compared to that in MeOH, tentatively related to the higher dielectric constant of water. No differences in k2 were observed between 100% MeOH and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 MeOH/H2O. The absence of variation in the mixed solvent can be ascribed to the specific solvation of the complex by methanol. Soper has shown that in binary mixtures of water and alcohols, local clusters of alcohol molecules occur (or vice versa), so that the more hydrophobic Eu complex is likely to undergo specific solvation by a methanol cluster.27
50 MeOH/H2O. The absence of variation in the mixed solvent can be ascribed to the specific solvation of the complex by methanol. Soper has shown that in binary mixtures of water and alcohols, local clusters of alcohol molecules occur (or vice versa), so that the more hydrophobic Eu complex is likely to undergo specific solvation by a methanol cluster.27
| Solvent | Gradient | τ 0/ms | k 2/M−1 s−1 × 109 (±0.05) |
|---|---|---|---|
| MeOH | 0.62 | 1.18 | 0.57 |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (50 H2O (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) 50) |
0.67 | 1.11 | 0.56 |
| H2O | 1.64 | 1.03 | 1.59 |
A variety of structurally similar hydrophilic Eu(III) complexes was studied (ESI, Fig. S3†) in water, examining energy transfer to the cyanine dye. No significant dependence of the rate of energy transfer on the nature and number of the coordinating anionic donor groups was evident. Neither was any correlation found between complex hydrophilicity (comparing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values) and the second order rate constant, k2, characterising the rate of energy transfer quenching.
P values) and the second order rate constant, k2, characterising the rate of energy transfer quenching.
Inefficient energy transfer involving Mn2+ and Cu2+ aqua ions
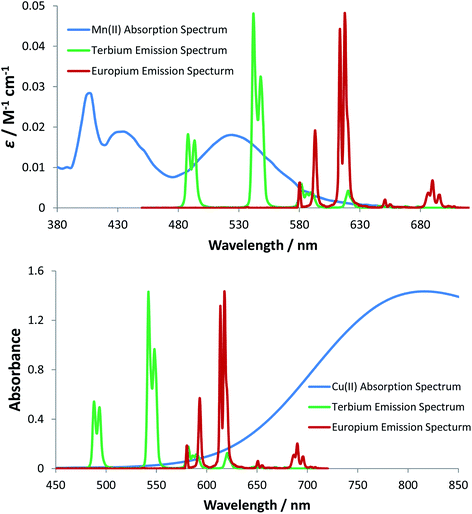
The quenching of lanthanide emission by metal ions is an important aspect in bioassays because ions like Mn2+ are used in millimolar concentrations as cofactors in certain kinases, and therefore understanding their quenching behaviour can help in the development of optimal probes.28 Sporadic reports have described the quenching of the emission of various Eu and Tb complexes in water by transition metal ion salts.29–34 In these studies, the lanthanide complexes that were examined were often of ill-defined speciation and the influence of competitive lanthanide ion dissociation complicated some of the systems studied, such that both static and dynamic quenching processes were sometimes observed. Typically, quenching by copper(II) ions was found to be faster than that by Cr3+, Mn2+, Co2+ and Ni2+ aqua ions, with dynamic quenching postulated to occur by an energy transfer process, with second order rate constants of about 106 to 107 M−1 s−1 for copper(II) quenching. Much less work has been reported on quenching by Mn2+ salts, apart from comments about the enhanced sensitivity to the nature of the ligand in lanthanide coordination complexes.34
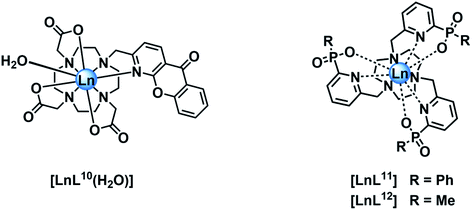
In empirical screening assays, the emission intensity and lifetime of Eu and Tb complexes has often been measured in the presence of a million fold excess of MnCl2, serving as a simple means of assessing the ability of the complex to resist intermolecular quenching of the lanthanide excited state. Such preliminary screens had shown that the charge neutral lanthanide complexes of L10, possessing an azaxanthone sensitiser, were quenched rather efficiently by Mn2+,34 whereas the charge neutral complexes of L11 and L12 with phosphinate groups were much more resistant to quenching. The latter two complexes are 9-coordinate and adopt a tricapped trigonal prismatic geometry35 in which the lanthanide ion is much more shielded (Ph > Me) from the environment compared to [LnL10], where a more open square anti-prismatic coordination geometry occurs, with a water molecule capping the open axial position.36
A solution of MnCl2 was added to a solution of [Eu·L10] (H2O, 100 μM complex, 0.1 M HEPES, 0.1 M NaCl, pH 7.4, 295 K) to give final Mn2+ concentrations of 0.1 and 10 mM. Upon the addition of Mn2+, both the emission and excited state lifetime of [EuL10] decreased, and there was no change in the Eu emission spectral form. The ratios I0/I and τ0/τ, where I and τ refer to the intensity and lifetime of Eu emission, respectively, were very similar, consistent with predominant dynamic quenching of the Eu excited state. To understand better which excited state is quenched, the emission spectrum of [EuL10] was recorded at each Mn2+ concentration, following excitation of the sensitising group (λex = 328 nm) or after direct excitation of the Eu3+ ion (λex = 397 nm). Despite the low signal to noise ratio following direct excitation, it was apparent that the spectral form was not changing and the extent of quenching was the same within experimental error, i.e. independent of the mode of excitation. Such behaviour is consistent with dynamic quenching of the lanthanide excited state, rather than any sensitiser excited state.
Luminescence titrations were also carried out with [EuL10] and [TbL10], measuring their emission spectra and lifetimes in the presence of increasing concentrations of Mn2+. The intensity of emission decreases with increasing [Mn2+]. To quantify the rate of quenching, Stern–Volmer plots were examined (Fig. 4). The variation of either I0/I or τ0/τ with [Mn2+] gave very similar slopes, consistent with predominant dynamic quenching. From the gradients of the slopes, Stern–Volmer quenching constants, KSV−1, of 1.22 and 0.16 mM were calculated for [EuL10] and [TbL10], respectively. The plots showed no deviation from linearity, consistent with a single bimolecular quenching process (Fig. 5).
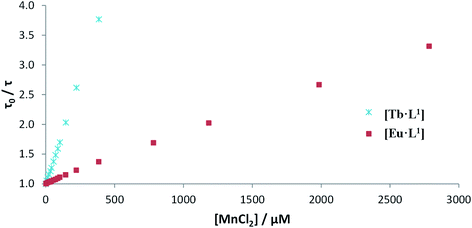 | ||
| Fig. 5 Stern–Volmer plots for the quenching of [EuL10] and [TbL10] by MnCl2 (H2O, 20 μM complex, 0.1 M HEPES, 0.1 M NaCl, pH 7.4, 295 K). | ||
Stern–Volmer quenching constants were calculated for the three pairs of Tb and Eu(III) complexes to allow a comparative analysis (Table 4). The tri(phenylphosphinate) C3 symmetric complexes, [EuL11] and [TbL11],36 and their methylphosphinate analogues, [LnL12], form the core structures in the EuroTracker™ series of emissive lanthanide probes.2,14,15,23,24 In each case, the Tb3+ species was found to be more susceptible to quenching by Mn2+. Such behaviour is not consistent with a quenching mechanism involving electron transfer to the Ln* state, as the reduction of Tb3+ is highly energetically unfavourable. According to the Weller equation, even the photo-induced electron transfer from Mn2+ to Eu3+ is energetically unfavourable, with a ΔGET = +22 kJ mol−1 (assuming that Eox(Mn2+) = +1.51 V, Ered(Eu3+) = −1.0 V, ELn* = +2.13 eV and e2/εr = 0.15). The only plausible alternative mechanism involves energy transfer, which is highly dependent upon the distance between the donor lanthanide complex and the d block aqua complex acceptor.
| Complex | K SV −1/mM | |
|---|---|---|
| Mn2+ (aq.) | Cu2+ (aq.) | |
| [EuL10] | 1.22 | 0.08 |
| [TbL10] | 0.16 | 0.18 |
| [EuL11] | 12.3 | 3.78 |
| [TbL11] | 4.00 | 8.50 |
| [EuL12] | 7.69 | 2.30 |
| [TbL12] | 1.81 | 3.75 |
| Complex | k 2/M−1 s−1 × 106 | |
|---|---|---|
| Mn2+ (aq.) | Cu2+ (aq.) | |
| [EuL10] | 1.44 | 21.9 |
| [TbL10] | 3.43 | 3.05 |
| [EuL11] | 0.06 | 0.19 |
| [TbL11] | 0.08 | 0.04 |
| [EuL12] | 0.08 | 0.28 |
| [TbL12] | 0.21 | 0.10 |
Parallel quenching studies were carried out with aqueous CuCl2 solutions to investigate any differences in the ability of the two first row transition metals to deactivate the Ln* excited state. An electron transfer quenching process was also not thermodynamically feasible in this case. Under the same conditions as for the Mn2+ quenching experiments, Cu2+ was found to reduce both the emission intensity and the excited state lifetime of each complex to similar extents. The Stern–Volmer quenching constants and second order rate constants were determined and compared with the values measured for Mn2+ quenching (Table 4). In the presence of Cu2+, the Eu complexes were quenched more efficiently than by Mn2+. There was around a threefold increase in the rate constant for [EuL11] and a 15 fold increase for the more sterically accessible complex, [EuL10]. The observed behaviour contrasts with quenching by Mn2+, where slightly higher rate second order constants were found for the Tb3+ analogues. The smallest rate constant values were found for the Eu/Tb complexes of the most shielded ligand, L11. The highest rate constant (2.2 × 107 M−1 s−1) was found in the quenching of [EuL10] by the aqua Cu2+ ion; this value is of the same magnitude as the highest rate constants reported earlier, e.g. with the rather kinetically labile anionic tris-chelate Eu(III) complex of oxy-diacetate.33
For energy transfer to occur between Ln* and Mn2+, some spectral overlap is required between the donor emission and acceptor absorption spectra. The absorption spectrum of MnCl2 has an absorption maximum at 520 nm that arises from the spin-forbidden d–d transition of the high-spin d5 Mn2+ aqua ion, resulting in a very low molar extinction coefficient (ε = 0.018 M−1 cm−1). The emission spectra of [EuL11] and [TbL11] are also shown (Fig. 6), and reveal that spectral overlap exists between both Ln3+ emission spectra and the Mn2+ absorption spectrum. It is also apparent that the spectral overlap is greater for the Tb3+ complex, explaining the observed higher values of k2 and lower values of KSV−1 for Tb3+ complexes of a common ligand. The very low molar extinction coefficient of Mn2+ and the very small spectral overlap integral seem to disfavour the hypothesis that Förster energy transfer quenching is operative. However, the excited state lifetimes of these Ln3+ complexes are relatively long (in the millisecond range), and over this period many diffusive encounters can take place between Mn2+ ions and the lanthanide excited state, increasing the probability of the energy transfer process.37
The absorption spectrum of CuCl2 was also measured in water and revealed the characteristic broad d–d transition of the aqua ion, centred at 810 nm. In contrast to the absorption of the Mn2+ aqua ion, the corresponding Cu2+ transition is spin allowed, resulting in a higher molar extinction coefficient (11 M−1 cm−1), compared to that of the Mn2+ aqua ion.38 The Cu2+ absorption band tails into the spectral region of Eu3+ emission and to a lesser extent Tb3+ emission (Fig. 6), consistent with the higher rate of quenching of the Eu complexes by copper aqua ions and supporting the hypothesis of an energy transfer quenching mechanism. In summary, and compared to Mn2+, the greater molar extinction coefficient of the Cu2+ aqua ion and the better spectral overlap with Eu3+ emission explain the higher rate of quenching by Cu2+ for each Eu(III) complex studied here.
The spectral overlap integrals (J) and, hence, the Förster radii (R0) for each donor lanthanide complex with Mn2+ and Cu2+ acceptors were estimated in water, using eqn (4) and (5), respectively (Table 5). The estimated values of R0 are much smaller for the Mn2+ aqua ion acceptor, consistent with the feeble spectral overlap integral associated with its low molar extinction coefficient, which is 600 times smaller than that for Cu2+ and 15 million times smaller than that for the near IR dye, 1, discussed above, for which the R0 values were around 68 Å. Indeed, the short distances found in this case (R0 between 2.8 to 4.4 Å for Mn2+ quenching) fall within the range where the mechanism of energy transfer is collisional, operates over a short encounter distance and may involve the Dexter energy exchange mechanism39 and not only Förster resonance energy transfer into the copper 2T2g orbital, which is more likely to operate with the aqua copper(II) ion.40
| Complex | R 0/Å (calc.) | |
|---|---|---|
| Mn2+ (aq.) | Cu2+ (aq.) | |
| [EuL10] | 2.4 | 9.9 |
| [TbL10] | 4.0 | 7.6 |
| [EuL11] | 3.5 | 11.6 |
| [TbL11] | 4.0 | 8.3 |
| [EuL12] | 3.4 | 12.1 |
| [TbL12] | 4.4 | 9.2 |
Summary and conclusions
The lanthanide excited state may be subject to quenching by electron (charge) transfer and by vibrational and electronic energy transfer processes, leading to a reduction in its lifetime. For Eu(III) complexes, a ligand to metal charge transfer state may lie close in energy to the Eu 5D0 excited state, leading to potential energy surface crossing. Such a situation is more prevalent in cationic complexes with ligands that are charge neutral and do not stabilise the Eu(III) oxidation state as efficiently as those containing hard anionic ligands, such as O or N donors.8 More commonly, fast electron transfer occurs from a ligand HOMO, such as a π or lone pair orbital, exemplified here with a set of six Eu(III) complexes where the lifetime was shortest for the complexes with the most high lying π orbitals or the most N atoms. In the latter case, N-protonation suppressed photoinduced electron transfer and the pH dependence of the Eu emission lifetime was identical when populating the 5D0 state by direct excitation or via the more efficient sensitised emission pathway that involves ligand excited states. Such observations confirm that it is the Eu excited state that is being quenched directly in these cases. Consideration was given to the utility of semi-empirical calculations of the energy of the key ligand, charge transfer and europium excited states involved in such a quenching process. However, the limited accuracy of such calculations, as exemplified in recent examples using DFT and modified Judd–Ofelt theory,41,42 meant that such work was not undertaken for these complexes.Electronic energy transfer was examined from a Eu donor to a cyanine dye acceptor with which very good spectral overlap occurs. The calculated Förster radii (R0) values did not change significantly with the structure of the Eu(III) complexes, each of which gave rise to very similar Eu emission spectral fingerprint. Thus, with R0 values averaging around 68 Å, the nature of the ligand anionic groups and the aryl sensitiser substituents did not affect this long range FRET process. Nor was any correlation found between complex hydrophilicity and the value of the second order rate constant, k2, that characterises the rate of energy transfer quenching. In contrast, energy transfer to the Cu(II) and especially the Mn(II) aqua ion was much more inefficient, with rate constants 1000 times smaller, owing to the much smaller spectral overlap integral. In these and earlier reported cases, the steric shielding created by the ligand plays a key role in defining the sensitivity to quenching, especially with Mn(II) aqua ions for which more open coordination complex structures show the greatest sensitivity to Mn(II) quenching.34 Such behaviour is consistent with a predominant short range collisional quenching mechanism, and suggests that a Dexter energy transfer mechanism operates, at least in part. It requires wave-function overlap, which occurs most efficiently when the distance between the excited Eu ion and the quenching acceptor species is minimised.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank EPSRC for grant (EP/L01212X/1) and studentship support.References
- S. E. Bodman and S. J. Butler, Chem. Sci., 2021, 12, 2716–2734 RSC
.
- E. Mathieu, A. Sipos, E. Demeyere, D. Phipps, D. Sakaveli and K. E. Borbas, Chem. Commun., 2018, 54, 10021–10035 RSC
.
- A. B. Aletti, D. M. Gillen and T. Gunnlaugsson, Coord. Chem. Rev., 2018, 354, 98–120 CrossRef CAS
.
- M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed
.
- S. J. Butler, M. Delbianco, L. Lamarque, B. K. McMahon, E. R. Neil, R. Pal, D. Parker, J. W. Walton and J. M. Zwier, Dalton Trans., 2015, 44, 4791–4803 RSC
.
- E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552 CrossRef CAS PubMed
.
- D. Parker, J. D. Fradgley and K.-L. Wong, Chem. Soc. Rev., 2021, 50, 8193–8213 RSC
.
- D. Kovacs, E. Mathieu, S. R. Kiraev, E. Demeyere, A. Sipos and K. E. Borbas, J. Am. Chem. Soc., 2020, 142, 13190–13200 CrossRef CAS PubMed
.
- A. Beeby, I. M. Clarkson, R. S. Dickins, S. Faulkner, D. Parker, L. Royle, A. S. de Sousa, J. A. G. Williams and M. Woods, J. Chem. Soc., Perkin Trans. 2, 1999, 493–503 RSC
.
- M. W. Mara, D. S. Tatum, A.-M. March, G. Doumy, E. G. Moore and K. N. Raymond, J. Am. Chem. Soc., 2019, 141, 11071–11081 CrossRef CAS PubMed
.
- J. D. Fradgley, M. Starck, M. Laget, E. Bourrier, E. Dupuis, L. Lamarque, E. Trinquet, J. M. Zwier and D. Parker, Chem. Commun., 2021, 57, 5814–5817 RSC
.
- R. Algar, N. Hildebrandt, S. S. Vogel and I. L. Medintz, Nat. Methods, 2019, 16, 815–829 CrossRef PubMed
.
- J. M. Zwier, H. Bazin, L. Lamarque and G. Mathis, Inorg. Chem., 2014, 53, 1854–1866 CrossRef CAS PubMed
.
- M. Soulié, F. Latzko, E. Bourrier, V. Placide, S. J. Butler, R. Pal, J. W. Walton, P. L. Baldeck, B. LeGuennic, C. Andraud, J. M. Zwier, L. Lamarque, D. Parker and O. Maury, Chem.–Eur. J., 2014, 20, 8636–8646 CrossRef PubMed
.
- S. J. Butler, L. Lamarque, R. Pal and D. Parker, Chem. Sci., 2014, 5, 1750–1756 RSC
.
- M. Starck, J. D. Fradgley, R. Pal, J. M. Zwier, L. Lamarque and D. Parker, Chem.–Eur. J., 2021, 27, 766–777 CrossRef CAS PubMed
.
- M. T. Berry, P. S. May and H. Xu, J. Phys. Chem., 1996, 100, 9216–9222 CrossRef CAS
.
- A. Weller, Pure Appl. Chem., 1968, 16, 115–124 CAS
.
- H. Yang, D. O. Wipf and A. J. Bard, J. Electroanal. Chem., 1992, 331, 913–924 CrossRef CAS
.
- M. Sheykan, S. Khani, M. Abbasnia, S. Shaabanzadeh and M. Joafshan, Green Chem., 2017, 19, 5940–5948 RSC
.
- D. Parker, Coord. Chem. Rev., 2000, 205, 109–130 CrossRef CAS
.
- H. Sahoo, J. Photochem. Photobiol., C, 2011, 12, 20–30 CrossRef CAS
.
- J. W. Walton, A. Bourdolle, S. J. Butler, M. Soulie, M. Delbianco, B. K. McMahon, R. Pal, H. Puschmann, J. M. Zwier, L. Lamarque, O. Maury, C. Andraud and D. Parker, Chem. Commun., 2013, 49, 1600–1602 RSC
.
- M. Starck, R. Pal and D. Parker, Chem.–Eur. J., 2016, 22, 570–580 CrossRef CAS PubMed
.
- C. F. Meares and T. G. Wensel, Acc. Chem. Res., 1984, 17, 202–209 CrossRef CAS
.
- D. D. Thomas, W. F. Carlsen and L. Stryer, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 5746–5750 CrossRef CAS PubMed
.
- S. Dixit, J. Crain, W. C. K. Poon, J. L. Finney and A. K. Soper, Nature, 2002, 416, 829–832 CrossRef CAS PubMed
.
- M. J. Knape, M. Ballez, N. C. Burghardt, B. Zimmermann, D. Bertinetti, A. P. Kornev and F. W. Herberg, Metallomics, 2017, 9, 1576–1584 CrossRef CAS PubMed
.
- W. DeW Horrocks Jr, B. Holmquist and B. L. Vallee, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 4764–4768 CrossRef PubMed
.
- D. T. Cronce and W. DeW Horrocks, Biochemistry, 1992, 31, 7963–7969 CrossRef CAS PubMed
.
- D. H. Metcalf, J. P. Bolender, M. S. Driver and F. S. Richardson, J. Phys. Chem., 1993, 97, 553–564 CrossRef CAS
.
- M. A. Kessler, Anal. Chim. Acta, 1998, 364, 125–129 CrossRef CAS
.
- B. C. Barja, A. Remorino, M. J. Roberti and P. F. Aramendia, J. Argent. Chem. Soc., 2005, 93, 81–96 CAS
.
- D. Parker, J. W. Walton, L. Lamarque and J. M. Zwier, Eur. J. Inorg. Chem., 2010, 3961–3966 CrossRef CAS
.
- J. W. Walton, R. Carr, N. H. Evans, A. M. Funk, A. M. Kenwright, D. Parker, D. S. Yufit, M. Botta, S. De Pinto and K.-L. Wong, Inorg. Chem., 2012, 51, 8042–8051 CrossRef CAS PubMed
.
- P. A. Atkinson, K. S. Findlay, F. Kielar, R. Pal, R. A. Poole, H. Puschmann, S. L. Richardson, P. A. Stenson, A. L. Thompson, J. Yu and D. Parker, Org. Biomol. Chem., 2006, 4, 1707–1722 RSC
.
- L. Stryer, D. D. Thomas and C. F. Meares, Annu. Rev. Biophys. Bioeng., 1982, 11, 203–222 CrossRef CAS PubMed
.
- S. R. Qiu, B. C. Wood, B. R. Ehrmann, S. G. Demos, P. E. Miller, K. I. Schaffers, T. I. Suratwala and R. K. Brow, Phys. Chem. Chem. Phys., 2015, 17, 18913–18923 RSC
.
- P. A. Brayshaw, J.-C. G. Bünzli, P. Froidenaux, J. M. Harrowfield, Y. Kim and A. N. Sobolev, Inorg. Chem., 1995, 34, 2068–2076 CrossRef CAS
.
- K. Szyszka, S. Targonska, A. Lewinska, A. Watras and R. J. Wiglusz, Nanomaterials, 2021, 11, 464–482 CrossRef CAS PubMed
.
- A. G. Cosby, J. J. Woods, P. Nawrocki, T.
J. Sorensen, J. J. Wilson and E. Boros, Chem. Sci., 2021, 12, 9442–9451 RSC
.
- G. Hovhannesyn, V. Boudon and M. Lepers, J. Lumin., 2022, 241, 118456 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Photophysical data and selected spectra. See DOI: 10.1039/d1fd00059d |
| This journal is © The Royal Society of Chemistry 2022 |