Structure of N₂H₄^•+ formed in X-irradiated Li(N₂H₅)SO₄ single crystals

Abstract

X-irradiated Li(N₂H₅)SO₄ single crystals were investigated using ESR and ENDOR spectroscopy at several temperatures. The hydrazine radical cation N₂H₄^•+ was selectively produced by irradiation at room temperature. From the analysis of the orientation dependent ENDOR spectra, the ¹H-hfc tensors of the cation radical were precisely obtained and the radical structure was supported by theoretical calculations. It is suggested that the cation radical has a planar π* structure D_2h (²B_2g) in the crystal down to 230 K. By using the evaluated ¹H-hf tensor the powder ESR line shape was successfully simulated. Concomitant with the radical formation, the N–N bond of N₂H₄^•+ is suggested to reorient so as to optimize hydrogen bond interactions. ¹H-ENDOR line splitting for the N₂H₄^•+ radical was observed at temperatures below 230 K. Apparently this splitting is due to a reversible structural change where one of the NH₂ moieties in N₂H₄^•+ becomes slightly bent out of the molecular plane, whereas the other one remains planar. This deformation evidently arises from interactions between the cation radical, adjacent H₂N–NH₃⁺ molecules and the SO₄–LiO₄ framework. Interacting N₂H₅⁺···N₂H₄^•+···N₂H₅⁺ molecules along the c-axis are proposed to explain the deformation mechanism.

---

Introduction

Crystalline (orthorhombic) lithium hydrazinium sulfate, Li(N₂H₅)SO₄ (abbreviated as LiHzS hereafter) is known to be a good proton conductor.¹ The conductivity is highly anisotropic; along the c-axis it is 10³ times higher than in the a–b plane at room temperature.¹ The dielectric properties,^2,3 crystal structures,^4–9 dynamics and phase transition^10–13 have been intensively studied by many groups. It has been proposed that the N–H···N chain between two –NH₂ groups along the c-axis plays an important role for the proton conductivity. As shown in Fig. 1, one of the protons of the –NH₂ group in H₂N–NH₃⁺ is linked in a chain of N–H···N bonds, whereas the protons of the –NH₃ group are hydrogen-bonded to the SO₄ and LiO₄ framework.

Fig. 1 Illustration of the arrangement of LiHzS molecules in the crystal highlighting the N–H···N chain of hydrogen bonds believed to be important for the proton conductivity of these crystals.

Significant reduction of the conductivity was reported by Hilczer et al.¹⁴ in a crystal with damage induced by ionizing irradiation. Morawski et al.¹⁵ carried out ESR and ESE studies on irradiated LiHzS single crystals to deduce the nature of the radiation defects and their dynamic behavior. These authors suggested that the decrease in conductivity was a result of γ-irradiation producing N˙H–NH₃⁺ radicals and consequently that the hydrogen-bond between adjacent N₂H₅⁺ molecules was broken.¹⁵ These studies further confirmed that tunneling of protons along the N–H···N chain activated by the –NH₂ group rotation is the preferred mechanism for the conductivity in these solids.^15–17

Generally, ESR (electron spin resonance) studies of single crystals containing paramagnetic centers give very useful information about anisotropic parameters such as g and hfc (hyperfine coupling) tensors, and the free radical structure and orientation in the crystalline lattice is amenable to be determined from those parameters. A paramagnetic center interacts with surrounding molecules or nuclei, and due to these interactions, the radical species in a crystal may have a structure slightly different from that of the energetically most stable one. This difference, however, is usually indistinguishable by ESR because of line broadening. The ENDOR (electron nuclear double resonance) technique, however, is a quite powerful technique to resolve hf couplings hidden within the ESR line width, and a more accurate evaluation of hfc tensors is possible. Sagstuen et al.¹⁸ observed ¹H-ENDOR spectra of irradiated N₂H₅HC₂O₄ (abbreviated as HzHO hereafter) and successfully obtained ¹H-hfc tensors of the N₂H₄^•+ radical species. These authors also detected a small degree of asymmetry of the species.

So far no ENDOR investigation on the structure of the radical produced in LiHzS has been carried out. It is desirable to obtain accurate hfc tensors and information about orientation and small structural changes of the radical in LiHzS for the purpose of understanding the mechanisms governing proton transfer processes in this system.

Experiment and calculation

Single crystals of Li(N₂H₅)SO₄ were prepared from aqueous solutions by slow evaporation at room temperature. The LiHzS crystal is orthorhombic with space group Pna2₁,² being elongated along the c-axis.

The crystals were irradiated at room temperature for 1 h using X-ray tube with a W anode operated at 70 kV and 20 mA (approximate dose rate 250 Gy min⁻¹). The irradiated crystals were mounted to the goniometer head of a Weissenberg X-ray diffraction camera, and the crystallographic axes were aligned to rotation axis of the camera within 1.0° using oscillation diagrams. The crystals were transferred to quartz rod for ESR and ENDOR measurements. As described below, some misalignment took place during the transfer process. This was corrected for during data analysis.

X-band ESR and ENDOR spectra were recorded using a Bruker ELEXSYS E580 spectrometer in CW-mode equipped with an EN 801 ENDOR cavity. The ENDOR spectra were obtained with a Bruker E250 ENDOR accessory and a ENI RF 500 amplifier. The radiofrequency (rf) modulation depth for ENDOR measurements was 190 kHz. The sample temperature was regulated by a Bruker VT4111 temperature controller using a cold nitrogen gas flow.

The ENDOR data were analyzed to obtain experimental hfc tensors by using the program ‘‘Magres ’’ written by W. H. Nelson.²²

The theoretical calculations were performed using the Gaussian 94 program.²³

Results

Assignment and geometry of the radical species

The ESR spectra recorded along each crystallographic axis at room temperature coincided with those previously reported.¹⁵ The spectral features were almost identical also at 240 K, although small changes within the line widths occurred (Fig. 2). Fig. 3 shows the corresponding ENDOR spectra recorded with the magnetic field locked at the central position of the ESR spectra (about 340 mT). The temperature for the ENDOR measurements was 240 K, since strongly bonded protons (A and B lines in Fig. 3) were not easily detectable at room temperature but clearly observed at around this temperature. The ENDOR spectra at each axis show a number of intense lines at around the proton Larmor frequency (ca. 14.55 MHz), these signals arise from weakly bonded protons surrounding the paramagnetic center. At least four, two and three kinds of weak couplings were observed at a//B, b//B and c//B, respectively. These couplings are attributable to protons in adjacent H₂N–NH₃⁺ molecule. In the high frequency region (20–50 MHz), two lines were observed which are due to strongly bonded protons. Pairing low-frequency lines were not observable. It should be noted that the lines marked by * are instrumental artifacts due to non-linearities of the rf power amplifier, and are observed at half the frequency of a real signal. In the low frequency range (<10 MHz), signals due to ⁷Li⁺ were detected at 5.8 MHz which is the Larmor frequency of ⁷Li. Only when a//B, a pair of ¹⁴N resonance lines was observed at around 9.0 MHz accompanied with further splitting due to nitrogen quadrupole interaction (totally four lines); the center frequency corresponds to half the ¹⁴N hfc at this orientation in this case.

Fig. 2 X-band ESR spectra of an X-irradiated Li(N₂H₅)SO₄ single crystal, recorded at 240 K. The magnetic field is parallel to a, b and c axes of the crystal, respectively. Dashed curves are calculated spectra based on the proton hfc parameter presented in Table 1 together with the reported ¹⁴N hfc.¹⁹

Fig. 3 ENDOR spectra corresponding to the ESR in Fig. 2 recorded at 240 K. The external magnetic field was locked to the central field of the ESR (ca. 340 mT). The lines marked by * is the 2nd harmonic of a real line due to the non-linearity of the rf power amplifier.

All sets of angular dependent ENDOR spectra were recorded at 240 K by rotating the irradiated LiHzS crystal about the three crystallographic axes. Fig. 4 shows a plot of the ENDOR frequencies of the A and B lines observed at the dif ferent orientations. The angular variations for both A and B lines were accompanied with site splitting. There are four symmetry-related molecular sites in an orthorhombic structure and by rotation about a crystallographic axis, sets of two are always magnetically equivalent and cannot be distinguished by EPR. For rotation about the a and b axes, there were, however, slight misalignments of the crystal on the sample holder, and for this reason further line splitting (all four molecular sites resolved) occurred, and thus coinciding data points at 〈a〉 and 〈b〉 in the figure were not obtained. The ENDOR data were successfully analyzed by taking these misalignments into account and experimental hfc tensors for the A and B resonance lines were evaluated and are reported in Table 1.

Fig. 4 The angular variation of the high frequency ENDOR resonance lines from the strongly bonded protons in the N₂H₄^•+ cation radical. Solid curves are theoretical fit calculated using the ¹H-hfc tensor parameters in Table 1.

Table 1 Hyperfine tensors for strongly coupled protons in the N₂H₄^•+ in the irradiated Li(N₂H₅)SO₄ and N₂H₅HC₂O₄¹⁸ crystals; as for I and II, one of two tensors are given, respectively: those tensors are obtained by angular variation of the A resonance lines

Eigenvectors
Principal value/MHz	a	b	c
A	−59.64	0.406	0.647	−0.645	This work
−37.34	0.234	−0.756	−0.611	240 K
+2.28	0.883	−0.097	0.459
B	−0.963	−0.255	−0.087
0.258	−0.779	−0.572
−0.078	0.573	−0.816
I	−64.20	0.389	0.642	−0.661	This work
−42.13	0.241	−0.763	−0.600	200 K
−2.38	0.889	−0.074	0.452
II	−54.51	0.391	0.666	−0.636
−33.63	0.191	−0.733	−0.652
4.28	0.901	−0.133	0.413
I	−61.11	0.315	−0.497	0.809	Ref. 18
−39.26	0.935	0.013	−0.355	295 K
2.01	0.166	0.868	0.468
II	−59.33	0.306	−0.515	0.800
−37.52	0.938	0.029	−0.345
3.09	0.160	0.857	0.490

---

The evaluated principal values are identical for the A and B. Moreover, they are in good agreement with the proton hfc tensors of N₂H₄^•+ reported for the HzHO single crystal,^18,19 and the isotropic ¹H-hf (31.57 MHz) is very close to that of N₂H₄^•+ detected in aqueous sulfonic acid solution (30.8 MHz).²⁴ Thus it is proposed that the radical formed in LiHzS is the N₂H₄^•+ species.

The principal values are −59.64, −37.34 and +2.28 MHz, and are expected to be along the perpendicular to the N–H bond, vertical to the NHH plane and along the N–H bond direction, respectively. Sagstuen et al.¹⁸ reported two different hfc tensors for N₂H₄^•+ in the HzHO single crystal due to two physically inequivalent sets of protons at 295 K. Since only one set of ¹H-hfc tensor was evaluated in the present work, this means that all four protons are physically equivalent even at 240 K; it is striking that the principal values obtained for LiHzS crystal are intermediate between two different values in the HzHO which suggests that N₂H₄^•+ is more flexible to average the hfc in the former crystalline lattice than in the latter. The eigenvectors relative to the crystallographic axes of each principal value are also given in Table 1. Both hfc tensors have one common axis (z[cmb.circ]₁, z[cmb.circ]₂) and two other axes (x[cmb.circ]₁, x[cmb.circ]₂ and ŷ₁, ŷ₂) make an angle of 120.0° corresponding to the HNH sp² bonding angle. This means that N₂H₄^•+ species exhibits a planar structure in the present crystal, whereas a slightly bent structure was suggested in the HzHO crystal. Thus, ENDOR signals A and B are each attributable to two of the four protons in N₂H₄^•+, respectively, which are chemically equivalent but magnetically inequivalent; if the N₂H₄^•+ molecule exhibits a planar D_2h structure, the hfc tensors of the two protons in trans sites are identical.

Theoretical calculations for N₂H₄^•+ have been performed by Almlöf et al.²⁵ by using unrestricted Hartree–Fock level of theory (UHF) and showed good agreement with our experimental values. In the present work, the ¹H-hf tensor of N₂H₄^•+ cation radical was theoretically evaluated using DFT (density functional theory) methods and is shown in Fig. 5. The single point calculation was performed employing the B3LYP density function with the 6-31++G(d,p) basis set based on an optimized structure evaluated using the MP2 method with the 6-31++G(d,p) basis set, i.e. B3LYP/6-31++G(d,p)//MP2/6-31++G(d,p). The N₂H₄^•+ molecule was optimized to be a D_2h planar structure in which the unpaired electron is delocalized in nitrogen 2p_π* orbital (²B_2g). The theoretical principal values of hfc tensor based on the optimized structure are also in good agreement with the experimental ones. The principal axes of the tensor were evaluated to be perpendicular to the N–H bond, vertical to the NHH plane and along the bond direction; the theoretical hfc tensor results are included in Fig. 5 together with experimental values. The nitrogen hfc tensor was also calculated and showed good agreement with that previously reported.¹⁹

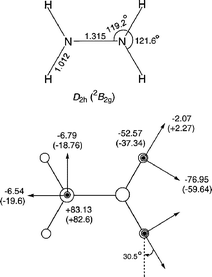Fig. 5 Optimized geometry and calculated hfc tensor for the N₂H₄^•+ cation radical (B3LYP/6-31++G(d,p)//MP2/6-31++G(d,p)). Experimental values of ¹H and ¹⁴N²¹ couplings are given in parentheses.¹⁹

Powder ESR spectra of irradiated sulfate compounds are shown in Fig. 6. The ESR line shapes of LiHzS and HzHO are very similar, and both are in good agreement with the simulated spectrum of N₂H₄^•+ using the proton hfc parameter presented in Table 1 together with the reported ¹⁴N hfc.¹⁹ The ESR pattern of irradiated N₂H₆SO₄ single crystal has been also assigned to N₂H₄^•+,²¹ although the powder pattern shown in Fig. 6 has a slightly different line shape due to differences in anisotropic parameters. The ESR spectra of the single crystal in Fig. 2 were also simulated by using the same hfc tensors as the powder case: small degree of inconsistencies are due to the nitrogen couplings.

Fig. 6 ESR spectra of irradiated powder of (a) Li(N₂H₅)SO₄, (b) N₂H₅HC₂O₄ and (c) N₂H₆SO₄. Dashed curve is the ESR simulation for the N₂H₄^•+ radical obtained using the ¹H-hfc tensors obtained in this work (Table 1) and the ¹⁴N-hfc tensor reported in ref. 19.

As commented in the Introduction, the radical produced in LiHzS by γ-ray irradiation was previously suggested to exhibit the structure H N˙–NH₃⁺,¹⁵ although the powder ESR line shape is similar to that in Fig. 6(a). In the present study, the ENDOR investigation using single crystal and powder ESR line simulations clearly shows that it is the N₂H₄^•+ species which is predominantly produced.

Temperature dependent ¹H-ENDOR

By lowering the temperature the N₂H₄^•+ radical may demonstrate structural changes due to interactions with neighboring molecules, because molecular motions are expected to be suppressed at lower temperatures. If some kind of phase transition takes place, the ENDOR lines of weakly bonded proton can even change dramatically. For these reasons, the temperature dependence of the ENDOR spectra was investigated. The spectra were recorded for c//B in the temperature range 10 K to 285 K. The ENDOR frequencies of the A and B resonance lines did not change down to 235 K. At 230 K, however, the lines started to broaden, and eventually split into two lines below this temperature (Fig. 7). The line splitting is well resolved at 218 K; Δν between the split lines at c//B is 3.78 MHz for A and 2.28 MHz for the B resonance line. Upon further lowering of the temperature, the line splitting gradually became larger and the line shape became sharper, and at 10 K Δν is 5.91 MHz for A and 3.71 MHz for the B resonance line (Fig. 8). The changes in the ENDOR spectrum were reversible in the temperature region 10 to 285 K.

Fig. 7 Changes in the ENDOR line shape with decreasing temperature, recorded with the magnetic field parrallel with the c-axis.

Fig. 8 A plot of the temperature dependent ENDOR frequencies of the strongly bonded protons in the N₂H₄^•+ cation radical. (Upper plot is for the A resonance line, and the lower plot for the B resonance line.)

The ENDOR lines of the weakly bonded protons did not change to any large extent. The complexity of those signals at 110 K is mainly due to the appearance of intense nitrogen resonance lines accompanied by quadrupole splitting. To further investigate the splitting of the A and B lines, the angular dependent ENDOR spectra were measured at 200 K, where the split lines are well resolved. Thus, two different hfc tensors were obtained for each line (Table 1). The isotropic hfc constants at 200 K are −36.24 and −27.95 MHz and Δa_iso, referred to the values at 240 K, are thus −4.67 for I and+3.62 MHz for II (Table 1). Clearly at 200 K two kinds of pairs of physically equivalent protons exist in the radical which most probably is due to asymmetric deformation by lowering the temperature. Comparing the evaluated eigenvectors of the ¹H-hfc tensors at 200 K with the corresponding eigenvectors at 240 K, the angles of deviation are 1.51, 1.08 and 1.55° for I (the numerically larger hf), and 0.93, 4.28 and 3.58° for II (the numerically smaller hf). It is obvious that the deformation is larger for the smaller hf II and the observations suggest that the –NH₂ moiety has become bent out of the molecular plane. The angles of deviation 1.51° for I and 0.93° for II are in a direction perpendicular to the N–H bond. Apparently, this direction is less affected by the deformation process than the other two principal directions. This deformation will be further discussed in conjunction with theoretical calculations in the next section.

Discussions

Reorientation of the N₂H₄^•+

Edlund et al.¹⁹ reported that the N₂H₄^•+ radical is reoriented concomitant with its formation in HzHO in a way that the N–N bond is rotated through 60° in the a–c plane from its original direction. It is reasonable that reorientation occurs because the radical cation has a planar structure; by the abstraction of hydrogen from the –NH₃ group, nitrogen hybridization changes from sp³ to sp² and a pure 2p_z orbital. By this structural change, hydrogen bonds shown in Fig. 1 (dotted lines) are broken and the N₂H₄^•+ molecule finds a new equilibrium position so as to optimize the intermolecular interaction with respect to hydrogen bond and dynamics.

The N–N bond of the N₂H₅⁺ fragment in the undamaged LiHzS crystal is directed along (0.581, 0.813, 0.042), whereas the bond of the radical is along (0.804, 0.476, −0.357). Those vectors make angle of 33.0°: the N–N bond direction of the N₂H₄^•+ has changed also in the LiHzS crystal. This reorientation results in the 2p_z orbital of N₂H₄^•+ (perpendicular to the molecular plane) becoming oriented to lone-pair orbital (LPO) direction: the angles between the direction of the 2p_z orbital of the N₂H₄^•+ radical and that of the N–H_α and N–H_β bonds of the neighboring N₂H₅⁺ molecule (NH_αH_β–NH₃⁺) are 108.3 and 111.7, respectively. These angles are very close to the sp³ bonding angle ∠HNH. Thus, it is possible that nitrogen 2p_z orbital of the N₂H₄^•+ molecule is oriented so as to become parallel with the LPO of the N₂H₅⁺ molecule. Furthermore, the N–N direction of the N₂H₄^•+ molecule makes almost same angle with the N–H_α and N–H_β bond directions of the N₂H₅⁺ molecule (54.3 and 59.6°): this means the N₂H₄^•+ molecule is symmetrically located with respect to the –NH₂ group of N₂H₅⁺ molecule through the LPO. Assuming that the nitrogen atom of N₂H₄^•+ is located 3.0 Å away from N(1) of N₂H₅⁺ molecule based on X-ray diffraction data,^4,5 the orientation in the N₂H₅⁺···N₂H₄^•+···N₂H₅⁺ part is proposed as shown in Fig. 9. Considering that the LPO of the N₂H₅⁺ molecule originally is partially oriented towards one of the two protons to form an effective N–H···N chain (Fig. 1), the generation of N₂H₄^•+ consequently might contribute to the proton conductivity loss in irradiated LiHzS.¹⁴

Fig. 9 Schematic representations of the interacting N₂H₅⁺···N₂H₄^•+···N₂H₅⁺ models. Detailed explanations are given in the text.

Structural deformation of the N₂H₄^•+

It is suggested that planar N₂H₄^•+ radical fragment becomes structurally distorted at the temperatures where ENDOR line splitting is observed. Similar line splitting was also reported for HzHO at room temperature,¹⁸ and was rationalized as one of the –NH₂ moieties in N₂H₄^•+ being slightly bent. In LiHzS, the N₂H₄^•+ remains planar even at 240 K. Since the planar structure is most stable for the N₂H₄^•+ as confirmed by the theoretical calculations above, the deformation at lower temperatures must be brought about by weak interactions with the framework and/or neighboring H₂N–NH₃⁺ molecule. The angle between the eigenvectors for the −42.13 MHz principal value (planar part (I)) and for the −33.63 MHz principal value (bending part (II)) is 4.5°. Supposing that both vectors are along 2p_z orbitals of each nitrogen (hybrid-like 2p_z orbital for bending part), the value of 4.5° corresponds to a bending angle θ of 2.5° (Fig. 9). The structural deformation of N₂H₄^•+ might be due to a hindered motion of the radical when the thermal energy is not sufficiently large to overcome the intermolecular interactions.

Theoretical calculations were carried out to attain further understanding of the deformation mechanism. As noted in the previous section, the ¹H-hfc of the bending part (II) decreased in absolute value compared to the planar structure, on the other hand the absolute value of the ¹H-hfc value of the other part increased. This hfc change can be interpreted as follows. The nitrogen spin orbital of the bending –NH₂ part in the N₂H₄^•+ contributes a weak hydrogen bond to the neighboring N₂H₅⁺ molecule, and consequently the nitrogen acquires some sp³-like orbital nature. The absolute value of the ¹H-hfc consequently decreases by a positive spin contribution from the sp³-like spin orbital. By the interaction between 2p_z of the N(2) and the LPO of N(3), spin density on the N(2) is partially shifted to the N(1) and then ¹H-hfc of the planar –NH₂ part numerically increases (Fig. 9). We propose a simple model shown in Fig. 9 in which the N₂H₄^•+ cation radical is put in between two N₂H₅⁺ molecules in the c-axis direction (N₂H₅⁺···N₂H₄^•+···N₂H₅⁺) and the geometry of the two N₂H₅⁺ molecules is fixed based on the molecular orientation in the unirradiated crystal (Fig. 1). The site geometry of the N₂H₄^•+ is obtained as follows. The interacting nitrogen N(2) of the N₂H₄^•+ molecule was located 3.0 Å from N(3) as discussed above. The rotation of the N(1)–N(2) bond about any axes was frozen (assuming those motions are restricted by the hydrogen bonds (Fig. 9). Furthermore, the non-interacting –N(1)H₂ group was kept planar. Next, the bending angle θ was evaluated by optimizing the remaining variable geometrical parameters and the corresponding ¹H-hfc tensors were calculated using the B3LYP/6-31++G(d,p)//B3LYP/6-31G(d,p) density functional method. The optimized geometry exhibited a bent angle θ of +22.1° (positive direction of the c-axis). The lower N₂H₅⁺ molecule (H₂N(3)–NH₃) has a large contribution to the structural deformation compared to the upper molecule through the weak bonding between 2p_z orbital of the N(2) and the LPO. Consequently, the N₂H₄^•+ and the lower N₂H₅⁺ form a dimer like structure combined through the LPO and 2p_z orbital of the N(2) and this is reflected in the positive bent angle. Thus, the hydrogen bonding between the N₂H₄^•+ cation radical and the two N₂H₅⁺ molecules leads the cation radical into a bent structure. Probably the theoretically evaluated bending angle is too large, because the calculation of isotropic ¹H-hfc for the bending –N(2)H₂ group resulted in 1.25 and 4.17 MHz and these are very different from the experimental value of −27.95 MHz. The bending is likely to be somewhat restricted by hydrogen bonding with oxygen atoms in the molecular framework: the hydrogen bonding could also be a reason why the –N(1)H₂ part remains planar. To obtain reasonable ¹H-hfc's we fixed the bending angle to the experimental value of +2.5° and optimized the remaining variable parameters. As a result, the geometry obtained exhibits reasonable theoretical isotropic hfcs −40.70 and −40.85 MHz (−40.78 MHz in average) for the bending –N(2)H₂ group and −45.60 and −45.58 MHz (−45.59 MHz in average) for the planar –N(1)H₂ group. The difference from experimental ¹H-isotropic hfc (Δa_iso) between planar (240 K) and bending N₂H₄^•+ (200 K) was −4.67 (planar part) and +3.62 (bending part). Whereas the Δa_iso between the optimized structure of the isolated N₂H₄^•+ (−43.86 MHz) (Fig. 5) and the bending N₂H₄^•+ in the N₂H₅⁺–N₂H₄^•+–N₂H₅⁺ model (Fig. 9) are −1.73 (planar part) and +3.09 MHz (bending part), and these are close to the experimental values. We conclude that the bent structure of the N₂H₄^•+ cation radical is brought about by the weak bonding with the LPO of one of neighboring N₂H₅⁺ molecules, and that the degree of bending is restricted by the surrounding oxygen atoms. At temperatures above 230 K, molecular vibration of the N₂H₄^•+ radical and/or the N₂H₅⁺ molecules to some extent can break these interactions, and for this reason the N₂H₄^•+ radical exhibits a planar structure is above 230 K.

Conclusions

The N₂H₄^•+ cation radical is produced in X-irradiated Li(N₂H₅)SO₄ single crystals and has been identified by using ENDOR spectroscopy. ¹H-hfc tensors were precisely determined from angular variation ENDOR spectra. The cation radical is suggested to be a planar π* radical above 230 K, and this structure was also supported by density functional theoretical calculations. It is suggested that the N₂H₄^•+ radical reoriented subsequent to its formation. By lowering the temperature below 230 K, each of the ¹H-ENDOR lines attributed to the N₂H₄^•+ radical split into two lines, the splitting increased upon further temperature reduction. From the angular variation analysis for each of the split lines, it was suggested that the planar cation radical deformed into an asymmetrical structure in which one –NH₂ moiety is slightly bent, whereas the other moiety remains planar. This deformation is caused by weak bonding interactions between the 2p_z orbital of the N₂H₄^•+ and the lone-pair orbital of one of neighboring N₂H₅⁺ molecules and theoretical calculation employing a simple model N₂H₅⁺···N₂H₄^•+···N₂H₅⁺ along the c-axis supported this deformation mechanism.

Acknowledgements

The present study has been financially supported by NFR (Swedish National Science Research Council), STINT (The Swedish Foundation for International Cooperation in Research and Higher Education) and NorFa (Nordic Academy for Advanced Studies).

References

1. J. Vanderkooy, J. D. Cuthbert and H. E. Petch, Can. J. Phys., 1964, 42, 1871.
2. R. Pepinsky, K. Vedam, Y. Okaya and S. Hoshino, Phys. Rev., 1958, 111(6), 1467.
3. V. H. Schmidt, J. E. Drumheller and F. L. Howell, Phys. Rev. B, 1971, 4, 4582.
4. M. R. Anderson and I. D. Brown, Acta Crystallogr. Sect. B, 1974, 30, 831.
5. T. Fukami and R.-H. Chen, Jpn. J. Appl. Phys., 1998, 37, 925.
6. N. Niizeki and H. Koizumi, J. Phys. Soc. Jpn., 1964, 19, 132.
7. J. H. Van den Hende and H. Boutin, Acta Crystallogr., 1964, 17, 660.
8. I. D. Brown, Acta Crystallogr., 1964, 17, 654.
9. V. M. Padmanabhan and R. Balasubramanian, Acta Crystallogr., 1967, 22, 532.
10. J. D. Cuthbert and H. E. Petch, Can. J. Phys., 1963, 41, 1629.
11. F. L. Howell and V. H. Schmidt, J. Chem. Phys., 1969, 51(5), 1983.
12. R. R. Knispel and H. E. Petch, Can. J. Phys., 1971, 49, 870.
13. L. Godfrey, J. Philip and M. T. Sebastian, J. Appl. Phys., 1994, 75, 2393.
14. B. Hilczer, M. Pukacka and A. Sabat, Fiz. Dielektr, Radiospektr., 1979, XI, 69.
15. P. Morawski, S. K. Hoffmann, W. Hilczer and J. Goslar, Acta Phys. Pol. A, 1997, 91, (6), 1121.
16. A. Kawada, A. R. McGhie and M. M. Labes, J. Chem. Phys., 1970, 52 (6), 3121.
17. K. D. Kreuer, W. Weppner and A. Rabenau, Solid State Ionics, 1981, 3/4, 353.
18. E. Sagstuen, O. Awadelkarim, A. Lund and J. Masiakowski, J. Chem. Phys., 1986, 85(6), 3223.
19. O. Edlund, A. Lund and Å. Nilsson, J. Chem. Phys., 1968, 49(2), 749.
20. D. S. Babu, G. S. Sastry, M. D. Sastry and R. M. Kadam, Phase Transitions, 1989, 15, 29.
21. S. Gade, B. Johnson, K. Hendrich, R. Knispel and J. W. Harrell and Jr, J. Chem. Phys., 1981, 75(9), 4742.
22. W. H. Nelson and C. R. Nave, J. Chem. Phys., 1981, 74(5), 2710.
23. Gaussian 94, Revision E.3, M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon, C. Gonzalez, and J. A. Pople, Gaussian, Pittsburgh, PA, 1995..
24. J. Q. Adams and J. R. Thomas, J. Chem. Phys., 1963, 39, 1904.
25. J. Almlöf, A. Lund, K.-Å and Thuomas, Chem. Phys., 1975, 7, 465.

---