Decoding the AlPO₄ and LATP surface with a combined NMR-DFT approach

Abstract

A milestone in the development of next generation high-performance lithium ion batteries is the understanding and targeted engineering of hybrid electrolytes, consisting of a polymer and a ceramic component, and in particular their interfaces. Nuclear magnetic resonance (NMR) spectroscopy is a powerful non-destructive technique for unraveling the intricate interface structures and ion dynamics in these materials, yet data interpretation often relies on empirical rules that have been devised using data from the bulk of materials. By exploiting the synergies between advanced NMR experiments and density functional theory (DFT) simulations, AlPO₄ is studied as a model for the surface of the well-known solid ion conductor Li_1+xAl_xTi_2−x(PO₄)₃ with 0.3 ≤ x ≤ 0.5 (LATP), which is a promising candidate for the ceramic component of a hybrid electrolyte. By combining the multi-nuclear NMR techniques cross-polarization (CP) and transfer of populations in double resonance (TRAPDOR) on AlPO₄ powder with DFT calculations of NMR observables for a variety of surface models, the surface structure of commercial AlPO₄ is elucidated. It is shown that even after extended drying, the surface of AlPO₄ is hydroxylated, exhibiting a TRAPDOR-estimated ¹H–²⁷Al quadrupolar coupling constant, C_Q, of 5.8 ± 0.9 MHz. The joint theoretical-experimental approach also enables first insights into the bonding motifs of organic entities on functionalized AlPO₄ surfaces as a model for LATP surfaces. Surface interactions and the presence of functional groups upon silanization of hydroxylated surfaces are confirmed both on AlPO₄ and LATP. We demonstrate that observables, which are experimentally as well as theoretically accessible, provide information on interfacial bonding motifs, interatomic distances, and interactions, surpassing the capabilities of either NMR or DFT techniques alone.

---

1 Introduction

Even though lithium ion batteries (LIBs) have already been established industrially since the 1990s,¹ they are still lacking in certain areas such as energy and power density, long cycle life, and safety.^2,3 Hybrid electrolytes consisting of a composite of ion-conducting polymers and superionic ceramics have the potential to combine the mechanical flexibility and improved fabrication of the polymer with the superior ionic conductivity and improved chemical stability and aging behavior of the superionic ceramic.^4–6 At room temperature, the ceramic usually exhibits the higher ionic conductivity, but with higher temperatures the ionic conductivity of the polymer increases.⁷ However, the interfacial resistance between the polymer and ceramic phases has turned out to be a major obstacle for the successful application of composite electrolytes.⁴ The complex interface behavior of polymers and ceramics has already been studied in relation to features such as the degree of polymer crystallization.⁸

Experimental as well as theoretical studies have elucidated various atomistic processes and structure–property relationships for different superionic electrolytes, yet atomistic structure, ionic transport,^9,10 and degradation processes¹¹ even in pure solid electrolytes remain poorly understood. In comparison, hybrid materials such as ceramic–polymer composites and their interfaces are much more challenging and represent an active and controversial field of research.^12–14 A systematic quantification of the different mobility contributions within and across the different phases and interfaces to the overall ionic conductivity is still lacking. Although, several hypotheses address the impact and mechanisms of ionic motion along or across the ceramic–polymer interface,^4,12 it is generally unknown how the polymer and the ceramic are connected at the molecular level, and whether they are separated by a passivated or hydrated ceramic surface that either strongly enhances or blocks ionic conductivity.¹² Nevertheless, a thorough understanding of ceramic–polymer interfaces is essential for targeted and efficient functionalization of ceramic nanoparticles and engineering of the interface in order to improve the interfacial resistance and make hybrid electrolytes industrially relevant. So far, this was mainly investigated for the electrolyte–electrode interface,^15–20 but offers also potential for the ceramic–polymer interface. Surfaces were already successfully modified, as for example Kuhnert et al. demonstrated for lithium lanthanum zirconium oxide (LLZO)²¹ or Li et al.²² for LATP that was coated with ZnO via atomic layer deposition. Another approach was chosen by Scharf et al., who described the grafted electrolyte Al₂O₃_PCL with polycaprolactone.²³

The ceramic material of interest in this work is Li_1+xAl_xTi_2−x(PO₄)₃ with x = 0.5 (LATP) from the structural family of Na super ionic conductors (NASICON), which shows a high ionic conductivity (10⁻⁴–10⁻³ S cm⁻¹) and an advantageous resistance to dendrite formation and growth over long cycling times.²⁴ The properties of LATP can be significantly influenced by the synthesis route, such as by the sintering and annealing parameters^25–27 as well as interfacial Mg²⁺ doping.²⁸ Due to the structural complexity of LATP, AlPO₄ can be used as a model system since it is structurally similar to LATP, but easier to compute by means of density functional theory (DFT). Even though LATP possesses more chemical species than AlPO₄, structural similarities such as PO₄ tetrahedral motifs exist.²⁹ Moreover, AlPO₄ is a well-studied material both experimentally^30–32 and theoretically³³ in all of its phases. Several phases of AlPO₄ including berlinite, cristobalite, and tridymite, are structural analogs of the corresponding polymorphs of SiO₂, while its hydrated form variscite (AlPO₄·2H₂O) represents a distinct phase.^34–36 Amongst the anhydrous AlPO₄ phases, the berlinite, which is isostructural with α-quartz, is known to be the most stable at room temperature.³⁷ AlPO₄ has been relevant in catalysis for several decades already.^38,39 Both for catalysis and as a model system for interfaces in hybrid electrolytes, its surface properties are of interest.^40,41

Modifications and functionalizations of ceramic surfaces such as zeolites in order to tune catalytic surface properties is an established procedure.⁴² One method of catalytic surface modification is the silanization of surface hydroxy groups, which leads to the assumption that silanization of solid electrolytes exhibiting hydroxy groups at the surface can also affect the interfacial properties, such as the interfacial resistance at the ceramic–polymer interface.

To obtain structural information of the bulk of a solid material, magic angle spinning (MAS) nuclear magnetic resonance (NMR) is a standard technique, as anisotropic interactions can be (partially) averaged out, resulting in narrower signals in the NMR spectra. This technique already provided various insights for solid electrolytes, such as the impact of the LATP stoichiometry on the presence of the side phase AlPO₄,⁴³ the Li mobility and cation location in other NASICON materials,⁴⁴ or the dopant site occupancy of Al and Ga in the LLZO lattice.⁴⁵

The transfer of populations in double resonance (TRAPDOR) NMR technique enables the surface-sensitive detection of “invisible” Al species experiencing large quadrupolar coupling by exploiting dipolar recoupling of these nuclei through radio frequency (RF) irradiation during the dipolar evolution phase. This effect is induced by rotationally induced level crossings, and is measured using the spin-echo difference method.^46,47 Using the TRAPDOR techniques in combination with multi-quantum (MQ) NMR techniques, materials such as amorphous lithium phosphorus oxynitrides (LiPON),⁴⁸ zeolites,⁴⁹ or aluminophosphate frameworks⁵⁰ have already been investigated. TRAPDOR experiments can be correlated to theoretical atomistic models by comparing the experimental and calculated quadrupolar coupling constant. The first principles simulation of quadrupolar coupling constants with plane wave DFT is well established and has been shown to provide reliable, quantitative predictions in particular for ²⁷Al.^51–54

In this work, a combination of DFT simulations and NMR techniques is applied to investigate AlPO₄, which is studied as a model system for LATP. First, the bulk properties are investigated by comparing experimental and simulated chemical shift differences as well as cross-polarization magic angle spinning (CPMAS) experiments. Then the surface is analyzed with respect to the molecular structure, involving experimental TRAPDOR NMR experiments. The quadrupolar coupling constant obtained from the TRAPDOR experiments is compared to the computed quadrupolar coupling constants of hydrated and hydroxylated surface models. Finally, the surface is modified using silanization to set the stage for more complex ceramic–polymer interfaces as they exist in hybrid electrolytes.

2 Materials and methods

Additional details on Materials and methods^55–61 can be found in the ESI,† Section S1.

2.1 Sample preparation

AlPO₄ powder was procured from Sigma-Aldrich (99.99% trace metal basis), in the following referred to as commercial sample. The commercial sample was dried under vacuum at 120 °C for 63 h using a pressure of 100 mbar, in the following referred to as dried sample. Commercial (non-dried, stored under ambient atmosphere) and dried AlPO₄ were packed into MAS NMR rotors (3.2 mm in diameter). The CPMAS and TRAPDOR experiments were conducted on the dried AlPO₄ sample.

For surface silanization, both AlPO₄ (99.99% trace metal basis, Sigma-Aldrich, dried for 17 h at 120 °C) and LATP⁶² (stored under argon atmosphere) were dispersed in toluene. Trimethoxy-(2-phenylethyl)silane (TMPES, Sigma-Aldrich) was added. The product was centrifuged and washed with toluene, cyclohexane, and ethanol. It was dried at 60 °C and 100 mbar overnight. The samples were packed into MAS rotors (3.2 mm in diameter) under argon atmosphere.

2.2 NMR

¹H, ³¹P, and ²⁷Al measurements were conducted on a Bruker Avance III HD spectrometer with a 9.4 T magnet. A 3.2 mm triple resonance H/X/Y CPMAS probe was used for all samples. All measurements took place with a probe temperature of 20 °C. The working frequencies were 400.2 MHz for ¹H, 162.0 MHz for ³¹P, and 104.3 MHz for ²⁷Al. No decoupling was used in the pulse sequence. The samples were measured at a spinning frequency of 20 kHz if not stated differently. Pseudo-Voigt fits of the ¹H and ²⁷Al MAS NMR spectra were conducted using OriginPro 2021b (OriginLab Corporation, Northampton, MA, USA).

³¹P{¹H} as well as ²⁷Al{¹H} CPMAS NMR experiments were conducted using different contact times.

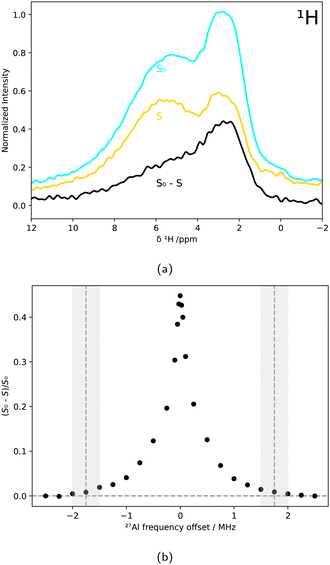
For the TRAPDOR experiments, first a rotor-synchronized ¹H spin-echo sequence (90°–nτ_r–180°–nτ_r) as depicted in Fig. 1a was applied, with τ_r being one rotor period and n representing an integer number. Then the procedure was repeated with irradiating the ²⁷Al nuclei in between the two ¹H pulses, as shown in Fig. 1b. Due to the ²⁷Al irradiation, refocusing of the ¹H spins is prevented if they are coupled to ²⁷Al nuclei. Rotationally induced level crossings between quadrupolar satellite transitions and the RF frequency perturb the spin states synchronously with the spinning frequency, enabling dipolar recoupling.^{47,63 27}Al{¹H} TRAPDOR experiments were conducted by measuring ¹H MAS NMR spectra (MAS spinning rate of 5 kHz) both with and without ²⁷Al irradiation for different ²⁷Al frequency offsets. The signal ratio between S₀ (no ²⁷Al irradiation) and S (irradiation of ²⁷Al) was calculated based on the spinning side bands within the integration interval ranging from −93 ppm to 105 ppm. The cut-off frequency 2ν_Q, for which the TRAPDOR effect is no longer observable, determines the quadrupolar coupling constant by^47,64

where I is the spin quantum number (I(²⁷Al) = 5/2).

Fig. 1 Scheme of the TRAPDOR pulse sequences without ²⁷Al irradiation (a) and with ²⁷Al irradiation (b).

2.3 SEM-EDX

The specimen holders were prepared with silanized AlPO₄ (TMPES) and silanized LATP (TMPES). The measurements were conducted on a Quanta FEG 650 scanning electron microscope (FEI), equipped with additional energy-dispersive X-ray spectroscopy equipment (SEM-EDX). An Everhard Thornley detector was used to detect the secondary electrons.

2.4 Computational methods

2.4.1 DFT simulations. DFT calculations were conducted using the plane wave, pseudopotential electronic structure code CASTEP⁶⁵ v.23. In this work, the C19 family of pseudopotentials was used that, in the case of Al and P, treats the 3s and 3p electrons explicitly. The Perdew–Burke–Ernzerhof (PBE) exchange correlation functional⁶⁶ was employed for all the calculations.

NMR observables were calculated with the GIPAW method⁶⁷ as implemented in CASTEP⁶⁵ v.23 with on-the-fly generated GIPAW pseudopotentials. The CASTEP calculations yield the isotropic shielding σ^iso, which is converted into chemical shift δ, i.e. shielding difference, by

δ = σ^iso_ref − σ^iso_sample (2)

where the reference σ^iso_ref is aligned with a suitable experimental chemical shift.

2.4.2 Bulk simulations. The crystal structures of the three 4-fold coordinated AlPO₄ phases berlinite, and the cristobalite and tridymite phases were obtained from the Materials Project database.⁶⁸ This also applies to the hydrated structure variscite (AlPO₄·2H₂O), where Al is 6-fold coordinated to O in an octahedral geometry. Additionally, the structure of the zeolite-derivative UiO-7 (Al₃₂P₃₂O₁₂₈·62H₂O), a rehydrated aluminium phosphate species, was used to study 5-fold coordinated Al atoms in addition to its 4-fold and 6-fold coordinated Al atoms, which is shown in ESI,† Fig. S1.⁶⁹

2.4.3 Surface simulations. In this study, three different berlinite surfaces were generated by cleaving a 2 × 2 × 2 berlinite supercell across the 001, 100 and 110 planes and adding a 20 Å vacuum region on top of the generated surface. Due to its similarities with α-quartz, previous studies have assumed that the most stable berlinite surface is isostructural with the α-quartz reconstructed surface.⁴⁰ However, Swang et al. compared the geometry and stability of different surface models based on the reconstructed α-quartz surface (quartz-berlinite) and a symmetry-broken surface presenting a buckled motif with a protruding, 3-fold coordinated P atom and 5-fold coordinated Al (buckled-berlinite), which they determined to be the structure with the lowest energy (cf. ESI,† Fig. S2).⁴¹ Additional geometry relaxation of the first two layers of these surfaces, while the atomic positions of the other layers are fixed, leads to the desired models. Convergence tests show that a slab of six layers is sufficient and that the self-consistent dipole correction⁷⁰ is required.

The interactions between the buckled-berlinite surface and water molecules is divided between hydroxylation and hydration. The first describes the removal of an oxygen atom from the surface and the addition of two –OH groups to two P atoms ((P-OH)₂-berlinite, cf. Fig. 2), two Al atoms ((Al-OH)₂-berlinite), or one on both atoms ((Al-OH)(P-OH)-berlinite). The latter is stabilized by hydrogen bonds between water and different Al atoms (cf. ESI,† Fig. S3), either the Al in the protruding part of the buckle motif (Al_high(H₂O)-berlinite), in the sunken part of the surface (Al_low(H₂O)-berlinite) or at the surface level (Al_middle(H₂O)-berlinite).

Fig. 2 Structural model of (P-OH)₂-berlinite with the Al–P dative bond depicted by a dashed line. Al, P, O, and H atoms are represented in blue, green, red, and white, respectively.

2.4.4 Modified surface simulations. The physisorption between TMPES and the (P-OH)₂-berlinite surface was studied by placing the hydroxylated TMPES molecule perpendicular to the surface of the structure without chemical bonds. For comparison, the chemisorbed structure was obtained by replacing an OH group on one of the P–OH surface groups with a P–O–Si bond between the silane and the surface P atom.

3 Results and discussion

3.1 AlPO₄

The bulk structure of the AlPO₄ powder samples is scrutinized by combining conventional 1D MAS solid state NMR spectroscopy of ¹H, ²⁷Al, and ³¹P nuclei with DFT simulations. The viability of the computational NMR techniques employed in this study is evaluated by a benchmarking analysis, comparing experimental^36,37 and calculated NMR observables of berlinite and variscite as reliable models for 4- and 6-fold coordinated AlPO₄ as well as other AlPO₄ phases. The benchmarking yields quantitative results for quadrupolar coupling constants C_Q and qualitatively correct assignment of the ²⁷Al chemical shielding based on the coordination environments as shown in literature before (details in the ESI†).^51–54

3.1.1 Commercial AlPO₄ sample. The measured ²⁷Al MAS NMR spectrum depicted in Fig. 3 of the commercial AlPO₄ sample reveals the existence of 4-fold (38 ppm)^71,72 and 6-fold (−13 ppm)^71,72 O-coordinated Al nuclei, as well as a small contribution of 5-fold coordinated Al nuclei (10 ppm).^54,73

Fig. 3 The ²⁷Al MAS NMR spectra of the commercial (black) and the 63 h dried (red) AlPO₄ samples were normalized to their respective integral and scaled to the maximum intensity of the spectrum from the dried sample. The vertical bars represent the DFT calculated σ^iso of the Al nuclei in berlinite (green), variscite (orange), and UiO-7 (blue, where the dotted, solid and dashed lines indicate 4, 5 and 6-fold coordinated Al atoms, respectively). The calculated berlinite σ^iso was aligned with the δ(²⁷Al) signal maximum of dried AlPO₄ at 36 ppm.

The 4-fold coordinated Al environment is in agreement with the crystal structure of berlinite. In contrast to that, the 5- and 6-fold coordinated Al cannot be correlated with any structural motifs in pure crystalline AlPO₄, neither berlinite, nor the less stable phases tridymite or cristobalite, which contain exclusively tetrahedrally coordinated Al nuclei. Hence, the signals from 20 to −40 ppm can only be attributed to either amorphous structures,⁷⁴ zeolite-like motifs,⁷⁵ or partially hydrated AlPO₄ phases.

DFT simulated isotropic ²⁷Al shieldings of berlinite (4-fold coordinated Al), variscite (6-fold coordinated Al), and UiO-7⁶⁹ (4-, 5- and 6-fold coordinated Al) confirm the assignment of the local Al environments and reproduce the δ(²⁷Al) within ±5 ppm when aligning the calculated berlinite σ^iso with the δ(²⁷Al) signal maximum of dried AlPO₄ at 36 ppm (cf. next section). Thus, the DFT results can reproduce the experimental ²⁷Al NMR spectrum of commercial AlPO₄ with hydrous AlPO₄ phases. In order to further investigate the mixture of AlPO₄ hydrates and anhydrous AlPO₄ in commercial AlPO₄ powder, the presence of AlPO₄ hydrates in the sample was studied in more detail using ¹H MAS NMR spectroscopy.

Fig. 4 reveals a broad ¹H signal centered at 5.4 ppm for commercial AlPO₄. Moreover, there is an additional upfield shoulder at 3–5 ppm that indicates the existence of a second, different type of ¹H local environment.

Fig. 4 The ¹H MAS NMR spectra of the commercial (black) and the dried (red) AlPO₄ samples were normalized to the respective rotor content mass and scaled to the maximum signal intensity of the spectrum from commercial AlPO₄. The asterisks denote signals attributed to impurities. The vertical bars represent the DFT calculated σ^iso of the ¹H atoms in variscite (orange) and the ¹H atoms from the OH group in (P-OH)₂-berlinite (yellow). The σ^iso of the H₂O protons in UiO-7 are differentiated into H₂O attached to a 5-fold (solid blue line) and 6-fold (dashed blue line) coordinated Al atom and the average of σ^iso(¹H) of the H atoms in the same structural motif is depicted. The theoretical chemical shieldings σ^iso were referenced by aligning 6-fold coordinated UiO-7 with the δ(¹H) signal maximum of commercial AlPO₄ at 5.4 ppm.

To assign the overlapping signals, the DFT simulated ¹H shieldings in variscite (orange) and UiO-7 (blue) were analyzed, as depicted in Fig. 4. The ¹H chemical shift of the 6-fold coordinated Al species in UiO-7 involving H₂O is referenced to the broad experimental signal centered at 5.4 ppm, which is in the δ range for water molecules. The distribution of DFT simulated δ appears to be shifted with respect to the experimental signal, since the structural degrees of freedom of the rather mobile protons are not sampled sufficiently by DFT and the alignment with experiment is not unambiguous. But the simulated chemical shift range of about 9 ppm matches the experimental signal range and suggests that the sample also contains hydrated species with a mixture of 5- and 6-fold coordinated Al. There is no clear distinction of ¹H shifts of H₂O attached to a 6-fold coordinated Al versus a 5-fold coordinated Al, since the simulated ¹H shifts of variscite and UiO-7 overlap. The distribution of signals is likely dominated by hydrogen bonds of different strengths between the coordinated H₂O and its environment.

The combination of ²⁷Al and ¹H MAS NMR spectra indicates clearly that the commercial AlPO₄ sample contains a mixture of anhydrous and hydrous AlPO₄, presumably in different phases. In order to remove water and dehydrate the hydrous AlPO₄ phases, the sample was dried as described in Section 2.

3.1.2 Dried AlPO₄ sample. The ²⁷Al MAS NMR spectrum of the dried sample shows that most of the 6-fold coordinated bulk Al species are transformed to 4-fold coordinated Al upon drying. Pseudo-Voigt fits of the three signals at different drying times (cf. ESI,† Fig. S5a–c) also revealed that the signal of 5-fold coordinated Al at 10 ppm remains constant within the limits of experimental accuracy. The maximum of the 4-fold coordinated ²⁷Al signal shifted from 38 ppm to 36 ppm upon drying.

Analogously to the ²⁷Al MAS NMR spectra, also the ¹H MAS NMR spectra were measured at different stages of drying of the AlPO₄ sample. The broad signal at 5.4 ppm decayed upon drying, which emphasized the signal at 3.0 ppm causing the shoulder in the spectrum of the non-dried sample (Fig. 4).

Using a pseudo-Voigt fit for the signal at 3.0 ppm, it was revealed that its intensity did not change systematically during the drying process (cf. ESI,† Fig. S6). In contrast, after drying the sample for 63 h, the broad signal attributed to water decreased by 81% compared to the commercial sample. The DFT calculated distribution of σ^iso showed that the removed signal corresponds best to H₂O in the 6-fold coordinated Al environment in UiO-7, characterized by the absence of hydrogen bonds, yet also H₂O in a 5-fold coordinated Al environments as well as some of the downfield ¹H resonances of H₂O in variscite are in the vicinity. Hence, the decaying signal is attributed to the removal of crystal water upon drying as expected and previously reported for variscite,³⁴ which is in agreement with the development of the signals in the ²⁷Al MAS NMR spectra. However, the constant signal at δ(¹H) = 3.0 ppm indicates that some type of more strongly bound H₂O or OH entities are remaining.

In Fig. 5, the ³¹P NMR spectrum of the commercial AlPO₄ sample shows only one broad signal centered at −25.2 ppm, corresponding to 4-fold coordinated P in an amorphous environment.⁷³ Upon drying, the signal in the ³¹P NMR spectrum becomes narrower, which is presumably due to the more ordered, less heterogeneous crystal structure as well as reduced relaxation owing to the removal of the mobile proton species. Moreover, its center is shifted from −25.2 ppm to about −26.3 ppm, indicating a reduction in the variety of P coordination environments and a larger average Al–O–P bond angle.^76,77

Fig. 5 ³¹P MAS NMR spectra of the commercial (black) and the dried (red) AlPO₄ sample. The vertical bars represent the DFT calculated σ^iso of the P nuclei in berlinite (green), UiO-7 (blue), and variscite (orange). The calculated berlinite σ^iso was referenced to the δ(³¹P) signal maximum of dried AlPO₄ at −26.3 ppm. The decreased signal-to-noise ratio after drying might be caused by the prolonged relaxation times due to the removal of water molecules, which presumably drive relaxation, while the delay times were identical for the two experiments.

The DFT simulated ³¹P shielding is referenced by aligning σ^iso of berlinite with the signal maximum of dried AlPO₄ at a chemical shift of −26.3 ppm, as shown in Fig. 5. The calculation of the ³¹P shieldings in berlinite and variscite predicted a chemical shift difference between both systems of about 1.3 ppm that agrees well with the shift observed in the spectrum during the drying process. For UiO-7, considerably lower chemical shifts for ³¹P were predicted by DFT, probably due to the differently coordinated neighbouring Al nuclei. The average ³¹P chemical shift of −36.9 ppm is still within the experimental spectrum.

Further investigations were done by conducting CPMAS experiments, exploring the spatial proximity of H and P nuclei. Fig. 6 shows that ³¹P{¹H} CPMAS measurements of the dried sample probing the interatomic distance of H and P result in an upfield shift of the signal towards lower chemical shift values for longer contact times t_contact.

Fig. 6 ³¹P{¹H} CPMAS NMR spectra of dried AlPO₄ for a contact time of 1 ms (orange) and of 7 ms (blue) with a MAS spinning rate of 10 kHz. The spectra were normalized to the respective maximum intensity.

The location of the maximum intensity decreased from −22.4 ppm (t_contact = 1 ms) to −24.9 ppm (t_contact = 7 ms), indicating that ³¹P nuclei closer to ¹H nuclei have higher chemical shift values, since short contact times are sufficient to obtain polarization transfer from ¹H to ³¹P. In contrast, P nuclei that are located farther away from H atoms need longer contact times for polarization enhancement. Thus, it is assumed that hydrated phases such as variscite at higher chemical shift values already contribute to the CPMAS signal at short contact times due to the short P–H distances. For longer contact times, also berlinite-like P nuclei coupling to either surface hydrogen or neighbouring hydrated phases can contribute to the CPMAS signal. This is in agreement with the ³¹P MAS NMR spectra shown in Fig. 5.

In contrast to ³¹P{¹H} CPMAS, the ²⁷Al{¹H} CPMAS of dried AlPO₄ did not provide any signal, contradicting a spatial proximity of ¹H and ²⁷Al nuclei. However, the large quadrupolar coupling of ²⁷Al species can give rise to a signal too broad to be observed in this type of experiment due to second-order quadrupolar coupling that is not completely averaged out using MAS.^78,79 Detection sensitivity is further reduced due to fast quadrupol relaxation accelerated by the loss of local symmetry.⁸⁰

To sum up, both experimental ¹H, ²⁷Al, and ³¹P MAS NMR as well as DFT simulations of different hydrous and anhydrous AlPO₄ models confirmed that the commercial AlPO₄ sample consists of a mixture of anhydrous AlPO₄ with 4-fold coordinated Al as in berlinite, and different hydrous phases with 5- and 6-fold coordinated Al in amorphous environments. Upon drying, the 6-fold coordinated hydrous Al species (δ(²⁷Al) = −13 ppm) and its corresponding H₂O contribution (δ(¹H) = 5.4 ppm) were largely removed from the sample. However, a small contribution of about 11–12% of presumably 5-fold coordinated Al as well as a H₂O or OH signal at δ(¹H) = 3 ppm remained and was not notably affected by the drying procedure. ³¹P{¹H} and ²⁷Al{¹H} CPMAS experiments confirmed the spatial proximity of ¹H and ³¹P but not of ¹H and ²⁷Al. Nevertheless, the NMR study of the bulk AlPO₄ indicates that berlinite is a reliable model for the predominant local atomistic motifs in the non-crystalline bulk of the dried AlPO₄ sample. The CPMAS results are not conclusive with regard to the hydrogen configuration in dried AlPO₄, but ¹H and ²⁷Al MAS NMR indicates that the drying procedure predominantly removes weakly coordinated crystal water while some more strongly bound ¹H species remain. Hence, additional structure models of undercoordinated Al and P on AlPO₄ surfaces, capable of forming strong interactions with either H₂O or OH, were developed (Section 3.1.1). They are going to be correlated to TRAPDOR experiments in the following, probing the interaction between ²⁷Al and ¹H (Section 3.2).

3.1.3 AlPO₄ surface models. In order to achieve reliable models for the interaction between the berlinite surface and water or organic molecules, the structure and properties of the pristine surface need to be determined first. Of the generated and studied 001, 100, and 110 surfaces, only the last one shows a significant structural reordering upon relaxation, with an energy decrease of 0.2 eV per atom, while the 001 surface is the energetically most stable one (6 eV per atom more stable than 100 and 110).

The quartz-berlinite and buckled-berlinite surfaces were also studied, and their energies were determined to be 0.05 and 0.1 eV per atom lower than 001, respectively, which is in agreement with previous studies⁴¹ (cf. ESI†). Hence, the buckled-berlinite surface was set as the initial model for studying the interactions between AlPO₄ and water or organic groups.

3.2 Water on AlPO₄ surface

Conventional MAS NMR spectroscopy is a bulk method, and distinguishing minor contributions such as particular minority phases or surfaces is challenging. Thus, selective techniques such as TRAPDOR are required to tackle the structure elucidation of the AlPO₄ surface.

The ²⁷Al{¹H} TRAPDOR experiments shown in Fig. 7a, which exploit the reduction of ¹H signal intensity due to dipolar coupling with nearby ²⁷Al nuclei, directly confirmed the spatial proximity between H and Al nuclei. The broad signal centered around δ(¹H) = 3 ppm was particularly affected by ²⁷Al irradiation, as seen in the difference spectrum (black).

Fig. 7 ²⁷Al{¹H} TRAPDOR measurements of AlPO₄ powder that was dried for 63 h. (a) Measured ¹H NMR spectrum S₀ without irradiating ²⁷Al (light blue), measured spectrum S upon also irradiating ²⁷Al nuclei (yellow), and a TRAPDOR difference spectrum (black) for an exemplary ²⁷Al frequency offset of O2 = 0.1 MHz. (b) TRAPDOR profile depicting (S₀ − S)/S₀ as a function of the ²⁷Al frequency offset O2. The cutoff frequency of 1.75 ± 0.25 MHz is depicted by vertical dashed lines and grey bars.

By analyzing (S₀ − S)/S₀ for different ²⁷Al frequency offsets O2, the quadrupolar coupling constant was calculated from the cutoff frequency at 1.75 ± 0.25 MHz, marked in Fig. 7b. Using eqn 1, a C_Q of 5.8 ± 0.9 MHz was obtained.

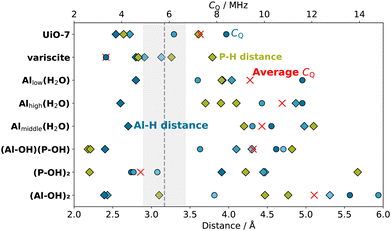
To determine the molecular structure that caused the TRAPDOR effect with C_Q = 5.8 ± 0.9 MHz, computational models of hydrated and hydroxylated AlPO₄ surfaces were evaluated for comparison. According to the computational study from Swang et al., the most energetically favourable interaction between the berlinite surface and water is the one represented in the (P-OH)₂-berlinite model, where two P atoms are coordinated with –OH groups, allowing the formation of an Al–P dative bond that stabilizes the system (Fig. 2). In this structure, both H atoms are closer to P (2.2 Å) than to Al (3.9 Å), which is consistent with the CPMAS results. Our DFT calculations predict a C_Q of 4.4, 4.7, and 5.5 MHz for the three closest Al atoms to the OH groups. Since the OH group can rotate, the effective C_Q is expected to be an average of the closest Al nuclei and is in good agreement with the C_Q deduced from the TRAPDOR experiments. Furthermore, the ¹H chemical shift of the surface OH groups corresponds well with the signal at δ(¹H) = 3 ppm, which remains at a constant intensity despite drying in Fig. 4 (yellow line).

The other hydrated and hydroxylated surface models, besides being energetically less stable, fail to provide the geometrical properties and NMR parameters observed experimentally as depicted in Fig. 8. In particular, the surface hydration on Al as described by the Al_i(H₂O)-berlinite (i = high, middle, low) models, whose stability rely solely on the formation of hydrogen bonds, result in a notable increase of the ²⁷Al C_Q to beyond 10 MHz for the closest Al and at least 7 MHz for the other Al in close proximity due to the breaking of the tetrahedral geometry of the electric field gradient tensor on the Al atom. Moreover, the distance between the H atoms and the closest P atoms on the surface rises to more than 4 Å, which is expected to render the distance-sensitive cross polarization ineffective for anything but the longest contact times. Since a CP signal was also obtained for a rather short contact time of 1 ms, it is concluded that the hydrated surface Al structures are not a main component of the sample.

Fig. 8 Al–H distances (blue diamonds), P–H distances (green diamonds), and ²⁷Al C_Q (blue circles) of the Al and the P atoms closest to H in the studied computational models of UiO-7, variscite, and the different models of hydrated/hydroxylated berlinite surfaces. The Al–H distances and their respective ²⁷Al C_Q are sorted according to shortest (dark blue), second (middle blue), and third shortest (light blue). Red crosses indicate the average of the plotted C_Q values. The experimental TRAPDOR ²⁷Al C_Q value of 5.8 ± 0.9 MHz is indicated by a vertical dashed line with a grey bar depicting the experimental uncertainty.

Fig. 9 Structural models of the isolated TMPES molecule (grey box), the two chemisorbed TMPES (purple boxes) and the two physisorbed TMPES (red boxes). Al, P, O, and H atoms are represented in blue, green, red, and white, respectively. C, H, and Si atoms are depicted in black, white, and orange, respectively.

The 5-fold coordinated Al (δ(²⁷Al) = 10 ppm, Fig. 3) as well as the H species (δ(¹H) = 3 ppm, Fig. 4) that remain unaffected by the drying of AlPO₄ can be interpreted as either water on a 5-fold coordinated Al in bulk modelled by UiO-7 or as hydroxylated surface P simulated by (P-OH)₂-berlinite, where the quantitative agreement of NMR observables as well as interatomic distances is even better for the latter than the former.

3.3 Organic functionalization of AlPO₄ and LATP surface

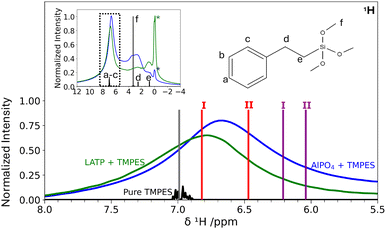
The surface models of AlPO₄ do not only facilitate the elucidation of structural motifs for remnant H contributions, but also serve as starting point for understanding functionalized surfaces of hybrid electrolytes. Using the silanization procedure as described in Section 2, AlPO₄ powder, as well as LATP powder were silanized with TMPES. SEM-EDX revealed the presence of Si at the powder surfaces, with an EDX-determined Si mass fraction of only <1% (cf. ESI,† Fig. S9 and S10). In addition, for each sample several one-point measurements were conducted. All points from within the sample exhibit a small silicon signal at around 1.75 keV, which is in agreement with other silanization processes from literature.⁸¹ Thus, it is expected that the distribution of silicon at the inorganic surface is rather homogeneous.

By comparing the ¹H MAS NMR spectra in Fig. 10, the presence of TMPES in the ceramic powders is verified by the aromatic phenyl signal a–c, also present for the silanized ceramics. In comparison to the aromatic signal a–c, signal f at 3.3 ppm resulting from the methoxy groups exhibits a lower intensity in the silanized ceramic samples, indicating that the methoxy groups are partially removed during the silanization process on the ceramic surface. Nevertheless, the spectra of the silanized ceramics still feature a significant broad signal in the range of 1.5 ppm to 4.2 ppm, which is more pronounced for the silanized AlPO₄ than for LATP. Even though disentangling the individual contributions of the signals of the methylene group (d, 2.5 ppm) and potentially residual TMPES methoxy groups (f, 3.3 ppm) overlapping with the ¹H signal of dried AlPO₄ (cf. Fig. 4) at 3.0 ppm is not possible, the broad signal supports the SEM-EDX findings that the surface silanization is incomplete and that free OH groups remain.

Fig. 10 ¹H MAS NMR spectra of pure TMPES (black) (MAS spinning rate = 2.6 kHz), AlPO₄ silanized with TMPES (blue), and LATP silanized with TMPES (green) (MAS spinning rate = 20 kHz), showing the frequency range of the phenyl protons a–c. The full spectrum is shown as an inset in the upper left corner. Vertical lines indicate the computed σ^iso average from protons a–c of the isolated TMPES molecule (grey), the chemisorbed TMPES models (purple) and the physisorbed ones (red). The average of the calculated σ^iso of the H atoms in the aromatic ring of the isolated TMPES molecule was aligned with the average experimental ¹H signal at 7 ppm. The asterisks denote signals attributed to impurities.

Fig. 10 shows that the chemical shift of the phenyl protons shifts from about 7.0 ppm to 6.7 ppm for the AlPO₄ sample upon silanization and to 6.8 ppm for the LATP sample. The changes in aromatic chemical shifts upon interaction with the ceramic can be compared to the calculated chemical shifts of exemplary physisorbed and chemisorbed structures of TMPES on the (P-OH)₂-berlinite surface as described in Section 2 (Fig. 9). The comparison between the calculated NMR spectrum of the models with TMPES on the AlPO₄ surface and the isolated TMPES molecule reveals an upfield shift of the average aromatic signals by 0.79 ppm and 0.96 ppm for the chemisorbed (purple I and II) and by 0.18 ppm and 0.53 ppm for the two physisorbed (red I and II) TMPES models.

The comparison, which should only be considered a reasonable approximation, suggests that TMPES is rather physisorbed than chemisorbed on both the LATP and the AlPO₄ surfaces. The smaller change in the aromatic signal upon silanization of LATP in comparison to AlPO₄ suggests a weaker physisorption interaction.

Anything beyond this qualitative, basic evaluation requires a thorough sampling of the configuration space of TMPES on AlPO₄ with molecular dynamics, which is beyond the scope of this work.

Despite the proof of qualitative silanization, the silanization was incomplete for all investigated samples. One reason for the small yield is the fact that TMPES is apolar and thus it is unfavorable for it to come into contact with the hydroxy groups at the surface of LATP or AlPO₄. Moreover, trimethoxy silanes have the tendency to form films on surfaces instead of binding as single molecules.⁸² To further investigate the silanized ceramic surface using NMR experiments, such as TRAPDOR, and DFT simulations, a more quantitative silanization of the ceramic surface is required.

4 Conclusion

By simulating ¹H, ²⁷Al, and ³¹P NMR spectra of berlinite (AlPO₄), variscite (AlPO₄·2H₂O), and a zeolite-based UiO-7 structure of hydrous AlPO₄ (Al₃₂P₃₂O₁₂₈·62H₂O) using DFT and comparing them with experimental MAS NMR spectra, commercially available AlPO₄ powder is identified as a mixture of anhydrous and hydrous phases with 4-, 5-, and 6-fold coordinated Al atoms. The NMR experiments reveal that upon drying of the AlPO₄ powder the 6-fold coordinated Al environment largely transforms to a 4-fold coordination environment due to a removal of crystal water, while about 12% of the Al remain in a 5-fold coordinated environment. Based on DFT simulations, the remnant 5-fold coordinated Al as well as the constant proton signal at δ(¹H) = 3 ppm in dried AlPO₄ are mapped to 5-fold coordinated Al motifs from UiO-7 as well as hydroxylated P on the AlPO₄ surface. TRAPDOR NMR experiments yielding a ²⁷Al C_Q of 5.8 ± 0.9 MHz substantiate the model of hydroxylated P on the surface, agreeing well with the simulated C_Q of 4.4 to 5.5 MHz.

Aiming for functionalizing the surface hydroxy groups, AlPO₄ and LATP were silanized with TMPES, which was verified with ¹H MAS NMR measurements and corresponding simulated spectra, as well as with SEM/EDX measurements. The TMPES–AlPO₄ bonding interaction is discussed qualitatively by comparison to different DFT models comparing chemisorbed and physisorbed bonding motifs. The TMPES–AlPO₄ bonding interaction is studied by different DFT models comparing chemisorbed and physisorbed bonding motifs. The qualitative comparison of experimental and simulated NMR confirms the SEM-EDX result of incomplete, low-percentage silanization of the AlPO₄ and suggests a physisorbed interaction between TMPES and AlPO₄ rather than a chemical bond.

The results highlight the importance of combining theoretical and experimental efforts, as this allows structural elucidation not only of bulk material but also of complex interfaces, including their modification. Transferring the knowledge from the model system AlPO₄ towards the solid electrolyte material LATP and hybrid solid-state electrolytes holds future potential to understand and finally improve the relevant interfaces by reducing interfacial resistance, which is crucial for efficient, long-range lithium ion transport.

Future investigations regarding the ionic conductivity of the silanized samples compared to non-silanized samples can be conducted, for example, using exchange spectroscopy (EXSY) or diffusion NMR measurements. Prior to these measurements and corresponding simulations, a more quantitative surface silanization needs to be achieved.

Author contributions

Javier Valenzuela Reina: investigation, data curation, methodology, visualization, writing – original draft. Vera M. Barysch: investigation, data curation, formal analysis, visualization, writing – original draft. Conrad Szczuka: conceptualization, investigation, writing – review editing. Simone S. Köcher: project administration, supervision, writing – original draft, writing – review & editing. Josef Granwehr: conceptualization, funding acquisition, project administration, supervision, writing – review & editing. Christoph Scheurer: conceptualization, funding acquisition, project administration, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

Data for this article, including NMR measurements, structure models, and DFT results will be made available on JülichDATA at https://doi.org/10.26165/JUELICH-DATA/MZPCAS following the publication of the paper.

Acknowledgements

All the authors would like to thank Prof. Dr Rüdiger-A. Eichel for his support, Dr Martin Ihrig for providing the LATP samples, Dr Elisabeth Robens for conducting the SEM-EDX measurements, Viviana Piccinni for contributing to the DFT calculations, and Dr Emmanouil Veroutis, Dr Anna Windmüller, and Johannes Spiegel for facilitating the study. JVR, VB, CSz, JG, and ChS acknowledge funding by the Bundesministerium für Bildung und Forschung (BMBF) within the Verbundprojekt AdamBatt (FKZ: 13XP0305A and 03XP0305D) and AdamBatt-2 (FKZ: 13XP0558A and 03XP0558D). ChS acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the cluster of excellence EXC 2089: e-conversion, project number 390776260. All computational resources were provided by the Max Planck Computing and Data Facility (MPCDF).

References

1. M. V. Reddy, A. Mauger, C. M. Julien, A. Paolella and K. Zaghib, Materials, 2020, 13, 1884.
2. T. Rahman and T. Alharbi, Batteries, 2024, 10, 220.
3. F. Ghani, K. An and D. Lee, Batteries, 2024, 10, 340.
4. M. Keller, A. Varzi and S. Passerini, J. Power Sources, 2018, 392, 206–225.
5. A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16.
6. J. G. Kim, B. Son, S. Mukherjee, N. Schuppert, A. Bates, O. Kwon, M. J. Choi, H. Y. Chung and S. Park, J. Power Sources, 2015, 282, 299–322.
7. J. Zhang, X. Zang, H. Wen, T. Dong, J. Chai, Y. Li, B. Chen, J. Zhao, S. Dong, J. Ma, L. Yue, Z. Liu, X. Guo, G. Cui and L. Chen, J. Mater. Chem. A, 2017, 5, 4940–4948.
8. E. Trevisanello, T. Ates, S. Passerini, F. H. Richter and J. Janek, J. Electrochem. Soc., 2022, 169, 110547.
9. H. S. Dhattarwal, R. Somni and R. C. Remsing, Nat. Commun., 2024, 15, 121.
10. M. Monchak, T. Hupfer, A. Senyshyn, H. Boysen, D. Chernyshov, T. Hansen, K. G. Schell, E. C. Bucharsky, M. J. Hoffmann and H. Ehrenberg, Inorg. Chem., 2016, 55, 2941–2945.
11. S. Hao, S. R. Daemi, T. M. Heenan, W. Du, C. Tan, M. Storm, C. Rau, D. J. Brett and P. R. Shearing, Nano Energy, 2021, 82, 105744.
12. S. C. Sand, J. L. Rupp and B. Yildiz, Chem. Soc. Rev., 2025, 54, 178–200.
13. Y. Horowitz, M. Lifshitz, A. Greenbaum, Y. Feldman, S. Greenbaum, A. P. Sokolov and D. Golodnitsky, J. Electrochem. Soc., 2020, 167, 160514.
14. J. Peng, Y. Xiao, D. A. Clarkson, S. G. Greenbaum, T. A. Zawodzinski and X. C. Chen, ACS Appl. Polym. Mater., 2020, 2, 1180–1189.
15. N. Tolganbek, A. Serikkazyyeva, S. Kalybekkyzy, M. Sarsembina, K. Kanamura, Z. Bakenov and A. Mentbayeva, Mater. Adv., 2022, 3, 3055–3069.
16. H.-K. Tian, R. Jalem, B. Gao, Y. Yamamoto, S. Muto, M. Sakakura, Y. Iriyama and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 54752–54762.
17. Y. Liu, Q. Sun, Y. Zhao, B. Wang, P. Kaghazchi, K. R. Adair, R. Li, C. Zhang, J. Liu, L.-Y. Kuo, Y. Hu, T.-K. Sham, L. Zhang, R. Yang, S. Lu, X. Song and X. Sun, ACS Appl. Mater. Interfaces, 2018, 10, 31240–31248.
18. F. Ichihara, K. Niitsu, Y. Tanaka, Y. Niwa, K. Mitsuishi, S. Miyoshi, T. Ohno and T. Masuda, J. Phys. Chem. C, 2023, 127, 15043–15050.
19. S. Stegmaier, R. Schierholz, I. Povstugar, J. Barthel, S. P. Rittmeyer, S. Yu, S. Wengert, S. Rostami, H. Kungl, K. Reuter, R.-A. Eichel and C. Scheurer, Adv. Energy Mater., 2021, 11, 2100707.
20. L. Wang, Z. Xie, X. Wu, Y. Xiao, H. Hu and Y. Liang, Small, 2025, 2411658.
21. E. Kuhnert, C. Slugovc, G. Trimmel, M. Wilkening and D. Rettenwander, ECS Meet. Abstr., 2020, MA2020-02, 962.
22. C.-F. Li, R. Muruganantham, W.-C. Hsu, M. Ihrig, C.-T. Hsieh, C.-C. Wang and W.-R. Liu, J. Taiwan Inst. Chem. Eng., 2023, 144, 104681.
23. F. Scharf, A. Krude, P. Lennartz, M. Clausnitzer, G. Shukla, A. Buchheit, F. Kempe, D. Diddens, P. Glomb, M. M. Mitchell, T. Danner, A. Heuer, A. Latz, M. Winter and G. Brunklaus, Small, 2024, 20, 2404537.
24. R. DeWees and H. Wang, ChemSusChem, 2019, 12, 3713–3725.
25. E. Winter, P. Seipel, T. Zinkevich, S. Indris, B. Davaasuren, F. Tietz and M. Vogel, Z. Phys. Chem., 2022, 236, 817–837.
26. V. Siller, A. Morata, M. N. Eroles, R. Arenal, J. C. Gonzalez-Rosillo, J. M. L. del Amo and A. Tarancón, J. Mater. Chem. A, 2021, 9, 17760–17769.
27. C. V. Chandran, S. Pristat, E. Witt, F. Tietz and P. Heitjans, J. Phys. Chem. C, 2016, 120, 8436–8442.
28. S. Stegmaier, K. Reuter and C. Scheurer, Nanomaterials, 2022, 12, 2912.
29. G. Redhammer, D. Rettenwander, S. Pristat, E. Dashjav, C. Kumar, D. Topa and F. Tietz, Solid State Sci., 2016, 60, 99–107.
30. S. Al-Omari, F. Afaneh, R. Elsad, Y. Rammah and Z. Khattari, Radiat. Phys. Chem., 2024, 215, 111377.
31. P. J. Byrne, J. E. Warren, R. E. Morris and S. E. Ashbrook, Solid State Sci., 2009, 11, 1001–1006.
32. D. H. Brouwer, J.-M. Chézeau and C. A. Fyfe, Microporous Mesoporous Mater., 2006, 88, 163–169.
33. N. Li, H. Hu, F. Guo and H. Tao, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2021, 36, 248–254.
34. M. Ardit, B. L. Phillips and D. L. Bish, Am. Mineral., 2022, 107, 1385–1395.
35. P. Goj, B. Handke and P. Stoch, Sci. Rep., 2022, 12, 17495.
36. D. Müller, E. Jahn, G. Ladwig and U. Haubenreisser, Chem. Phys. Lett., 1984, 109, 332–336.
37. K. Druppel, A. Hosch and G. Franz, Am. Mineral., 2007, 92, 1695–1703.
38. M. A. Harmer and A. J. Vega, Solid State Nucl. Magn. Reson., 1995, 5, 35–49.
39. J. M. Thomas, Angew. Chem., Int. Ed. Engl., 1994, 33, 913–937.
40. A. Jhunjhunwala, J. F. Vetelino and J. C. Field, J. Appl. Phys., 1977, 48, 887–892.
41. E. Sagvolden, M. F. Sunding and O. Swang, J. Phys. Chem. C, 2020, 124, 6683–6688.
42. E. Pérez-Botella, S. Valencia and F. Rey, Chem. Rev., 2022, 122, 17647–17695.
43. A. Best, M. Forsyth and D. R. Macfarlane, Solid State Ion., 2000, 136, 339–344.
44. K. Arbi, W. Bucheli, R. Jiménez and J. Sanz, J. Eur. Ceram. Soc., 2015, 35, 1477–1484.
45. S. Vema, A. H. Berge, S. Nagendran and C. P. Grey, Chem. Mater., 2023, 35, 9632–9646.
46. Z. Gan, J. Magn. Reson., 2019, 306, 86–90.
47. C. P. Grey and A. J. Vega, J. Am. Chem. Soc., 1995, 117, 8232–8242.
48. R. Bayzou, J. Trébosc, A.-K. Landry, R. B. Nuernberg, B. Pecquenard-Le Cras, F. Le Cras, F. Pourpoint and O. Lafon, J. Magn. Reson., 2023, 354, 107530.
49. A. Abraham, R. Prins, J. A. van Bokhoven, E. R. van Eck and A. P. Kentgens, Solid State Nucl. Magn. Reson., 2009, 35, 61–66.
50. D. H. Brouwer, J.-M. Chézeau and C. A. Fyfe, Microporous Mesoporous Mater., 2006, 88, 163–169.
51. R. Lizárraga, E. Holmström, S. C. Parker and C. Arrouvel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094201.
52. P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101.
53. J. V. Reina, F. Civaia, A. F. Harper, C. Scheurer and S. S. Köcher, Faraday Discuss., 2024, 255, 266–287.
54. A. F. Harper, S. P. Emge, P. C. Magusin, C. P. Grey and A. J. Morris, Chem. Sci., 2023, 14, 1155–1167.
55. S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1989, 62, 2429–2430.
56. A. Grünert, W. Schmidt and F. Schüth, Catal. Lett., 2020, 150, 2951–2958.
57. S. Dong, W. Shi, J. Zhang and S. Bi, ACS Earth Space Chem., 2019, 3, 1353–1361.
58. S. Sturniolo, T. F. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson., 2016, 78, 64–70.
59. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
60. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
61. L. L. C. Schrödinger, The PyMOL Molecular Graphics System, 2025, https://www.pymol.org/.
62. B. Davaasuren and F. Tietz, Solid State Ion., 2019, 338, 144–152.
63. J. G. Longstaffe, B. Chen and Y. Huang, Microporous Mesoporous Mater., 2007, 98, 21–28.
64. S. Prasad, H.-T. Kwak, T. Clark and P. J. Grandinetti, J. Am. Chem. Soc., 2002, 124, 4964–4965.
65. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
67. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
68. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
69. H. Fjellvåg, D. E. Akporiaye, E. Halvorsen, A. Karlsson, K. Kongshaug and K. Lillerud, Solid State Sci., 2001, 3, 603–611.
70. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
71. M. Stöcker, Stud. Surf. Sci. Catal., 1994, 85, 429–507.
72. R. Lookman, P. Grobet, R. Merckx and K. Vlassak, Eur. J. Soil Sci., 1994, 45, 37–44.
73. J. Klinowski, Molecular Sieves: Crystalline Systems, John Wiley & Sons, Ltd, 2007.
74. V. Sarou-Kanian, A. N. Gleizes, P. Florian, D. Samélor, D. Massiot and C. Vahlas, J. Phys. Chem. C, 2013, 117, 21965–21971.
75. F. Ji, C. Zhang and Y. Mi, Chem. Pap., 2023, 78, 1217–1226.
76. R. H. Meinhold and N. J. Tapp, J. Chem. Soc., Chem. Commun., 1990, 219–220.
77. D. Müller, E. Jahn, G. Ladwig and U. Haubenreisser, Chem. Phys. Lett., 1984, 109, 332–336.
78. D. Freude and J. Haase, in Quadrupole Effects in Solid-State Nuclear Magnetic Resonance, ed. H. Pfeifer and P. Barker, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993, pp. 1–90.
79. F. Deng, Y. Yue and C. Ye, Solid State Nucl. Magn. Reson., 1998, 10, 151–160.
80. S. Berger, J. Nolde, T. Yüksel, W. Tremel and M. Mondeshki, Molecules, 2018, 23, 808.
81. O. G. Cisneros-Pineda, W. H. Kao, M. I. Loría-Bastarrachea, Y. Veranes-Pantoja, J. V. Cauich-Rodríguez and J. M. Cervantes-Uc, Mater. Sci. Eng., C, 2014, 40, 157–163.
82. G. T. Hermanson, Silane Coupling Agents, Academic Press, Boston, 3rd edn, 2013, ch. 13, pp. 535–548.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ya00079c

‡ These authors contributed equally to this work.

---