Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Free energy modelling of a spherical nanoparticle at an oil/water interface
Zhiwei
Huang
 *a and
Joseph L.
Keddie
*a and
Joseph L.
Keddie
 b
b
aDepartment of Chemistry, Syracuse University, Syracuse, New York 13244, USA. E-mail: zhuan126@syr.edu
bSchool of Mathematics & Physics, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford GU2 7XH, UK
First published on 9th June 2025
Abstract
Interest in Pickering emulsions, which are stabilized by nanoparticles, has been driven by their superior stability and a desire to avoid the use of conventional surfactants. However, understanding of the chemical and physical phenomena governing particle stabilization at liquid/liquid interfaces remains limited because of the complexity of these systems. In particular, discrepancies can emerge between the inherent thermodynamic and the observed three-phase contact angles in such systems (particle/oil/water). We address this issue by modifying the classic equation for the free energy of a spherical nanoparticle at an oil/water interface. Our model defines the range of three-phase contact angles that enable successful Pickering stabilization. The model shows that the highest destabilization energy occurs when θ equals the position angle α, rather than 90°, as found in the conventional model. Our findings have significant implications for the identification of candidate Pickering stabilizers and the design of the emulsification process.
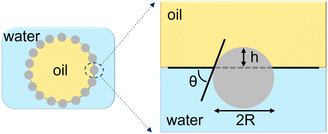
The classic theory for Pickering emulsions suggests that the free energy of an isolated particle at an oil/water interface is determined by the particle wettability and the interfacial tension.1 Consider the free energy argument derived by Binks and Lumsdon2, for a single spherical particle of radius R adsorbing at an oil/water interface having a three-phase contact angle θ measured in the water phase, as is depicted in Fig. 1. The geometry determines that the depth of immersion h of the particle into the oil phase is equal to R(1 − cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). The area of contact between the particle and the oil is 2πRh = 2πR2(1 − cos
θ). The area of contact between the particle and the oil is 2πRh = 2πR2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). The planar area of the oil/water interface eliminated by the presence of the particle is:
θ). The planar area of the oil/water interface eliminated by the presence of the particle is:A = πR2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = πR2(1 − cos θ = πR2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (1) |
The total free energy of the system changes as a particle adsorbs at the interface because of the expansion or loss of the oil/water and particle/liquid interfacial areas. Assuming the particle is sufficiently small (less than 2 μm) so that the effect of gravity is negligible,3 and the oil/water interface remains planar up to the contact line with the particle, the free energy, E, required to remove the particle from the interface into the water phase is given by:
E = 2πR2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)(Γsw − Γso) + πR2(1 − cos θ)(Γsw − Γso) + πR2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)Γow θ)Γow | (2) |
Γso − Γsw = Γow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (3) |
Therefore eqn (2) simplifies to this commonly-used equation:
E = πR2Γow(1 ± cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 θ)2 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is negative for particle removal to the water phase and positive for particle removal to the oil phase. From this equation, it can be concluded that the free energy of adsorption of a particle at an interface is always greater than the particles thermal energy, even in the case of very small solid particles. For example, the amount of energy required to remove a radius R = 100 nm solid spherical particle from an oil/water interface (Γow = 50 mN m−1, θ = 90°) is ΔE = 1.6 × 10−15 J, which is orders of magnitude greater than kT (4.1 × 10−21 J) at a temperature of T = 295 K, where k is the Boltzmann constant. Therefore, in this case, when the solid particles are positioned at the oil/water interface, they can be thought of as being irreversibly adsorbed.
θ is negative for particle removal to the water phase and positive for particle removal to the oil phase. From this equation, it can be concluded that the free energy of adsorption of a particle at an interface is always greater than the particles thermal energy, even in the case of very small solid particles. For example, the amount of energy required to remove a radius R = 100 nm solid spherical particle from an oil/water interface (Γow = 50 mN m−1, θ = 90°) is ΔE = 1.6 × 10−15 J, which is orders of magnitude greater than kT (4.1 × 10−21 J) at a temperature of T = 295 K, where k is the Boltzmann constant. Therefore, in this case, when the solid particles are positioned at the oil/water interface, they can be thought of as being irreversibly adsorbed.
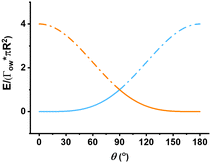
Generally, it is accepted that only particles with appropriate wettability as given by θ can stabilize Pickering emulsions. From the well-known eqn (4) for the energy to remove a particle from an interface, we plot the graph shown in Fig. 2. Observing the trends in Fig. 2, it is apparent that the energy required to displace the particle from the interface to the water phase peaks when the three-phase contact angle, θ is 90°, implying that the emulsion is most stable when this condition holds. When the θ value exceeds 90°, it costs less energy for the particle to detach and move into the oil phase.
Despite this accepted concept, an experimental report has been published that is inconsistent with the expectations of this model. Facal Marina and co-workers5 showed that hydrophilic particles (with a low value of θ) can act as Pickering emulsion stabilizers without any modification of their wettability. They achieved emulsification by applying an unconventional method to force the dispersion of hydrophilic particles in the oil phase prior to emulsification. The general concept is to disperse the nanoparticle in a liquid phase of opposite polarity prior to emulsification in the wetting phase. For example, as illustrated in Fig. 3, we schematically represent the concept proposed by Facal Marina et al., where hydrophilic particles initially dispersed in the oil phase migrate to the oil/water interface and are thought to become trapped at a position corresponding to a contact angle of 90°, owing to the high detachment energy that would prevent further movement. Therefore, the authors proposed that stable Pickering emulsions may be produced using hydrophilic particles initially present in an oil phase.
 | ||
| Fig. 3 Schematic diagrams illustrating the interpretation presented in ref. 5 (Fig. 4a). The energy to remove a particle from the oil/water interface, E (given by eqn (4) is graphed against the three-phase contact angle.) The black arrows indicate the relative energy states corresponding to different particle positions (shown in the inset diagram) as was interpreted in ref. 5. Note that these graphs intentionally mirror the interpretation from ref. 5, in which detachment energies at various contact angles (θ) were considered. Strictly speaking, at equilibrium, the three-phase contact angle (θ) is fixed, whereas the position angle (α) can vary dynamically. The purpose of this illustration is to highlight the discrepancy between interpretations based solely on the detachment energy and the rigorous interfacial free energy analysis provided by our generalized model (eqn (5) and Fig. 4 and 5). | ||
This analysis suggests that, potentially, all rigid particles can be effective stabilizers at an oil/water interface, irrespective of their wettability. If this analysis holds true, it will have significant implications for research and applications related to Pickering emulsions, as it would greatly broaden the pool of viable stabilizers. However, there is a conflict with the free energy eqn (4) which states that the stabilization energy is at a minimum when the wettability of a particle θ is close to either 0° or 180°.
In the experiments of Facal Marina et al.,5 other factors might have contributed to the stability of the Pickering emulsions, such as the presence of impurities in the oil phase (hexadecane with a purity of 99%) that might have adsorbed onto the silica surface or localized at the oil/water interface. Even so, there are still several questions that remain unresolved. For instance, once the hydrophilic particle in Fig. 3 reaches a θ value of 90° (as depicted in the middle diagram), how can we be certain that the particle will not continue moving into the water phase?
Answering this question requires a deeper reflection on the meaning of eqn (4). This equation was derived by combining the energy equation of a particle at the oil/water interface (2) with Young's eqn (3).6 When merging the two equations, the same contact angle θ is used. We know that in a complex system, the position of the particle at the interface can be influenced by a variety of factors, such as electrostatic7 and van der Waals8 interactions between particles and liquid molecules. Additionally, when the particle size is small (on the scale of nanometers), the relative contribution of line tension to the total energy at the interface becomes significant at the interface.9
For a given system, the interfacial energies between the particle, oil, and water phases are predetermined. Therefore, the inherent (theoretical) three-phase contact angle of the particle is not related to the physical positioning of a nanoparticle at an interface. Because in eqn (4), Γso, Γsw and Γow are inherent properties between the phases, the three-phase contact angle (hitherto called θ according to convention) should be a constant value. Now, let us define α as a position angle, which will change value according to a particle's instantaneous position as it passes across an interface. Then eqn (2) and (3) can be consolidated as a dimensionless energy expression:
 | (5) |
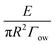 for convenience. The sign before the first “1” is negative when moving the particle from the interface into the water phase, and positive when moving the particle from the interface into the oil phase. Here, θ is solely related to the interfacial free energies of the particle via Young's equation, and α is given by the particle's current position at the interface. The value of α can be altered by external forces emanating from the surroundings, such as mechanical agitation (e.g., stirring or sonication), or by applied fields (such as gradient magnetic10 or electric11), or even the intrinsic electric fields at the oil/water interface.12 These forces can displace the particle from its equilibrium position at the interface, resulting in a scenario where the position angle α differs from the intrinsic contact angle θ. Fig. 4a provides a schematic clearly explaining the difference between the three-phase contact angle and the position angle.
for convenience. The sign before the first “1” is negative when moving the particle from the interface into the water phase, and positive when moving the particle from the interface into the oil phase. Here, θ is solely related to the interfacial free energies of the particle via Young's equation, and α is given by the particle's current position at the interface. The value of α can be altered by external forces emanating from the surroundings, such as mechanical agitation (e.g., stirring or sonication), or by applied fields (such as gradient magnetic10 or electric11), or even the intrinsic electric fields at the oil/water interface.12 These forces can displace the particle from its equilibrium position at the interface, resulting in a scenario where the position angle α differs from the intrinsic contact angle θ. Fig. 4a provides a schematic clearly explaining the difference between the three-phase contact angle and the position angle.
Eqn (5) allows us to consider a variety of particles with a diverse range of wettabilities and various positions at the oil/water interface. Using the equation, we constructed the contour diagrams of Fig. 4 showing the energy required to displace particles from the oil/water interface into either the water or oil phase.
In this convention, a positive value of E* defines the energy required to move the particle from the interface into a pure liquid phase, allowing the possible stabilization of the particle with the given θ and α at the interface. Provided that E* is sufficiently large, and in the absence of external energy input, the particle will be stable at the interface. However, a negative value of E* defines an unstable state for the particle. The particle has the possibility to move towards one of the liquid phases until it reaches a stable state (a positive energy value). In Fig. 4b, a positive energy value is observed in the blue-shaded areas above the 0.0 contour line.
For a more detailed investigation, we have selected five different types of particles, each with different inherent three-phase contact angles θ equal to 0°, 60°, 90°, 120° and 180°, to illustrate the energy cost required to displace the particles from the interfaces into either the water or oil phase, as shown in Fig. 5. The wettability of these five particles can be categorized as: 0° corresponds to superhydrophilic, 60° to hydrophilic, 90° to amphiphilic, 120° to oleophilic, and 180° to superoleophilic.
It is recognized that when E exceeds the thermal energy kT, the particle can be stabilized at the interface. Using the parameters Γow = 50 mN m−1 and R = 100 nm, we can calculate that:
 | (6) |
In Fig. 5a and b, less energy is required to move the particle into the water phase than into the oil phase across all α ranges, indicating the favorability to migrate into the water phase. Similarly, in Fig. 5c and d, the particle is more likely to move into the oil phase. Therefore, the dashed line energy curve can be ignored in future considerations.
In Fig. 5a and c, it can be observed that when the particle is either superhydrophilic or superoleophilic (θ equals 0° or 180°), the particle may not be able to stay at the interface. For example, when the particle is superhydrophilic (θ close to 0°), the energy consumption when moving it to the water phase is zero or negative across all ranges of position angle α, indicating that this process can occur spontaneously. When the particle is hydrophilic (θ equals 60°), the energy value is positive when α ranges from 0° to 90°, suggesting that the particle can only stabilize at the interface within this range. The energy reaches a peak when both θ and α equal 60°. When α varies from 60° (for example, exceeds 90°), the particle will move towards the water phase spontaneously until α reaches 60° to reach equilibrium, assuming that no external force is applied. A similar analysis can be applied to a particle with a three-phase contact angle, θ of 120°, as is shown Fig. 5d.
If a particle is stabilized with an α value that results in a negative E*, then a higher external energy (such as mechanical agitation, an applied gradient magnetic or electric field) is required to overcome the negative energy value.
The curves for the two liquid phases coincide when θ equals 90°. The highest energy value occurs when α also equals 90°. This value is the highest among all scenarios (Fig. 5a–d) as the E* is equal to 1. This implies that, for particles of the same size and at the same interface, the particle with θ equal to 90° will make the most stable Pickering emulsion, which agrees with the existing theory, as shown in Fig. 2.
Compared with the predictions of eqn (4), our model provides a more comprehensive understanding of the energy required to move a particle (with θ ranging from 0° to 180°) from an oil/water interface (with α ranging from 0° to 180°) into either the water or oil phase. In a real system, particles at a liquid/liquid interface typically experience various interactions (both particle/particle and particle/environments), leading to a discrepancy between the inherent three-phase contact angle and the observed three-phase contact angle (position angle). The three-phase contact angle can be determined by Young's eqn (3), and a range of methods have been developed to measure the three-phase position angles experimentally, including the gel trapping technique13,14 and the classic captive drop method15,16, which make it possible to calculate a more accurate free energy of a spherical nanoparticle at the interface.
While it may not be feasible to stabilize an oil/water interface using a superhydrophilic or superoleophilic particle (α equals 0° or 180°), it may be possible to use a slightly less hydrophilic or oleophilic particle. To find the smallest and highest α value, it is necessary to consider thermal energy. We can set E to be greater than or equal to the thermal energy as follows:
E = πR2Γow(2(±1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)cos α)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 1 − cos2 θ + 1 − cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) ≥ 10kT + 2πRτ α) ≥ 10kT + 2πRτ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (7) |
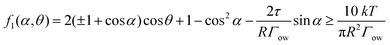 | (8) |
In this equation,  represents the contribution of line tension effects, while
represents the contribution of line tension effects, while  accounts for thermal fluctuations. The term 2(±1 + cos
accounts for thermal fluctuations. The term 2(±1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)cos
α)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 1 − cos2
θ + 1 − cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α primarily describes the destabilization energy. Both particle size (R) and interfacial tension (Γow) play crucial roles: larger values of R or Γow reduce the influence of line tension and thermal energy. Conversely, when R or Γow decreases, the destabilization energy must increase for the particle to maintain stability.
α primarily describes the destabilization energy. Both particle size (R) and interfacial tension (Γow) play crucial roles: larger values of R or Γow reduce the influence of line tension and thermal energy. Conversely, when R or Γow decreases, the destabilization energy must increase for the particle to maintain stability.
For assumed values of R and Γow, eqn (8) is plotted in Fig. 6, which reveals those α and θ pairs that satisfy the conditions in the equation, indicating stable particles at the interface. When θ equals 90°, the calculated value of α can range from 0.4° to 179.6°. The most hydrophilic particle of the lowest θ is only 14.2°. If the initial position angle is higher than 14.2° and no external forces are applied, the particle may move toward the water phase initially, but will eventually stabilize at 14.2°. A similar analysis can be conducted to find the most oleophilic particle in Fig. 6, which is 165.8°. For a θ of 60° and 120°, the position angle α falls within the range of 0.7° and 89.8° and of 179.3° and 90.2°, respectively. These results closely align with the findings in Fig. 4, highlighting the significant difference in the magnitude of the thermal energy and the destabilization energy.
 | ||
| Fig. 6 Graph plotted from eqn (8). This graph is used to find the α − θ pairs that make the energy consumption of removing a particle from the interface equal to the thermal energy at T = 295 K (the blue and orange curves), or larger than the thermal energy (shaded area). Here it is assumed that Γow = 50 mN m−1 and R = 100 nm. | ||
Experimental evidence supporting this concept can be found in many well-studied switchable emulsions, where external environmental stimuli alter the surface chemistry, and thus the wettability of stabilizing particles, thus triggering emulsion destabilization. For example, in the work of Richards and Evans on light-responsive Pickering emulsions,18 exposure to blue light induced a rapid trans-to-cis isomerization in azobenzene-functionalized particles, rendering them more hydrophobic. It can be inferred from our model in Fig. 6 that upon light exposure, the contact angle θ rapidly increases (above 120°), while α initially remains unchanged due to the ultrafast nature of the chemical change (on the order of 1–10 ps).19 This sudden shift places the Pickering particles in an unstable region of the diagram (white), which explains the observed emulsion destabilization as the particles desorb from the interface.
Additional evidence highlights the possibility of superhydrophilic and superoleophilic particles as effective stabilizers for Pickering emulsions. As reviewed by Aveyard et al.,20 superhydrophilic barium sulfate particles, with a three-phase position angle as low as 0°, and superoleophilic hydrophobic silica particles, with a position angle exceeding 175°, have both been demonstrated to stabilize emulsions effectively. Considering that our calculations assumed specific values for R and Γow, which are somewhat different from the R and Γow used in Aveyard et al.’s review, their findings are broadly consistent with the predictions of our model.
Hence, going back to Fig. 3, it becomes apparent that the explanation put forth by Facal Marina et al. may require further refinement. Specifically, for the hydrophilic silica particles used in their study, the destabilization energy curve should be different to the curve for particles with a three-phase contact angle θ of 90°. This suggests that the particle will not remain locked at the 90° position angle, but rather continue to move until the position angle aligns with the inherent three-phase contact angle of the silica particles. The stabilization of the system is attributed to the still very high destabilization energy even in the case of hydrophilic particles, and the interaction forces between particles and between particles and liquids may also contribute to or even dominate the stability of the system, as is also highlighted by the authors.
In most previous studies that evaluated free energy in the context of Pickering emulsions, the measured three-phase contact angle has typically been used for free energy calculations.20 Our work proposes that the ideal position of a particle at the interface may differ from the inherent three-phase contact angle because of various effects from the environments. As a result, the calculation of the destabilization energy needs to be approached differently. In conclusion, the findings from our model indicate the following:
1. For a given particle with an intrinsic three-phase contact angle θ, the highest destabilization energy occurs when the position angle α, equals θ, rather than 90°, as is found in the standard model, illustrated in Fig. 2.
2. When a particle is positioned at the interface with a specific position angle, α, resulting in a negative stabilization energy E in eqn (5), it necessitates a higher external energy contribution (such as mechanical agitation (e.g., stirring or sonication), an applied gradient magnetic or electric field, or even intrinsic electric fields at the oil/water interface) to counterbalance the unfavorable energy state and maintain the particle in that non-equilibrium position.
3. If a particle is at the oil/water interface but the initial position angle α is different from the particle's inherent three-phase contact angle θ, the particle may spontaneously move toward the position where θ equals α and then stabilize the system when the external forces causing the deviation are removed or diminished.
4. A lower particle size (R) or oil/water interfacial tension (Γow) will generally require a higher destabilization energy for the particle to maintain stability. For a given R and Γow, the range of contact angles that can be successful Pickering stabilizers can be calculated using our model. Thus, this research will help in the search for new Pickering stabilizers and aid the development of emulification methods.
5. This analysis is useful for real Pickering emulsion systems, as the influence of external forces or fields may influence the particle's position at the interface, leading to a different position angle α, compared to the inherent three-phase contact angle θ. We hope that the model inspires future research to test it.
Author contributions
Zhiwei Huang: conceptualization, formal analysis, investigation, methodology, writing – original draft. Joseph L. Keddie: supervision, funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the China Scholarship Council.References
- S. Levine, B. D. Bowen and S. J. Partridge, Colloids Surf., 1989, 38, 325–343 CrossRef CAS.
- B. P. Binks and S. Lumsdon, Langmuir, 2000, 16, 8622–8631 CrossRef CAS.
- B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41 CrossRef CAS.
- T. Young, Philos. Trans. R. Soc. London, 1805, 65–87 CrossRef.
- P. Facal Marina, J. Xu, X. Wu and H. Xu, Chem. Sci., 2018, 9, 4821–4829 RSC.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, Burlington, MA, 3rd edn, 2011 Search PubMed.
- R. Hogg, T. W. Healy and D. W. Fuerstenau, Trans. Faraday Soc., 1966, 62, 1638–1651 Search PubMed.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- J. Faraudo and F. Bresme, J. Chem. Phys., 2003, 118, 6518–6528 CrossRef CAS.
- H. Yang, S. Wang, W. Zhang, J. Wu, S. Yang, D. Yu, X. Wu, Y. Sun and J. Wang, Sci. Rep., 2020, 10, 16565 CrossRef CAS PubMed.
- K. Hwang, P. Singh and N. Aubry, Electrophoresis, 2010, 31, 850–859 CrossRef CAS PubMed.
- L. Shi, R. A. LaCour, N. Qian, J. P. Heindel, X. Lang, R. Zhao, T. Head-Gordon and W. Min, Nature, 2025, 640, 87–93 Search PubMed.
- V. N. Paunov and O. J. Cayre, Adv. Mater., 2004, 16, 788–791 CrossRef CAS.
- O. J. Cayre and V. N. Paunov, Langmuir, 2004, 20, 9594–9599 CrossRef CAS PubMed.
- J. W. De Folter, M. W. Van Ruijven and K. P. Velikov, Soft Matter, 2012, 8, 6807–6815 RSC.
- T. Kostakis, R. Ettelaie and B. S. Murray, Langmuir, 2006, 22, 1273–1280 CrossRef CAS PubMed.
- M. Robins and D. Hibberd, Emulsion flocculation and creaming, in Modern Aspects of Emulsion Science, ed. B. P. Binks, The Royal Society of Chemistry, 1998, ch. 4, pp. 115–144 Search PubMed.
- K. D. Richards and R. C. Evans, Soft Matter, 2022, 18, 5770–5781 RSC.
- A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234–3243 CrossRef CAS PubMed.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100, 503–546 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |