Ligand-modulated metallophilicity: influence of π-acceptor and σ-donor strength

Abstract

Metal–metal (M–M) closed-shell interaction, also known as metallophilicity, is frequently observed in d¹⁰ and d⁸ metal complexes featuring a close M–M distance. It has shown a significant impact on diverse chemical systems, influencing structural, catalytic, and photophysical properties. The strength of both M–M interactions and the resulting M–M distances is highly dependent on various types of coordinating ligands. Recent studies have revealed that metallophilicity is repulsive in nature due to strong M–M Pauli repulsion (Q. Wan, J. Yang, W.-P. To and C.-M. Che, Strong metal–metal Pauli repulsion leads to repulsive metallophilicity in closed-shell d8 and d10 organometallic complexes, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019265118). However, little is known about the role of ligands in M–M repulsions. Here, we elucidate how metal–ligand (M–L) coordination modulates M–M repulsion through two key mechanisms: π-backbonding and σ-donor interactions. By systematically evaluating ligands spanning a spectrum of π-accepting and σ-donating strengths, we uncover opposing ligand effects. Strong π-backbonding weakens M–M Pauli repulsion, enabling shorter intermetallic distances, whereas the σ-donating interaction increases the repulsion, lengthening M–M contacts. These computational insights establish a ligand-design framework for tuning metallophilicity in closed-shell metal complexes and advance the fundamental understanding of M–M interactions from the perspective of M–L coordination.

---

Introduction

Metallophilicity has been extensively studied in a wide range of d⁸ and d¹⁰ metal complexes, including Au(I), Au(III), Ag(I), Cu(I), Pt(0), Pd(0), Pt(II), Pd(II), Ir(I) and Rh(I).^1–12 These closed-shell metal complexes have important applications across various research fields, ranging from supramolecular self-assembly to advanced (opto)electronic materials and photocatalytic systems.^{2,7,8,13–16} In supramolecular chemistry, M–M interactions are recognized as a key driving force guiding the self-assembly process.^7,17,18 In optoelectronics, incorporating M–M interactions into excited states would facilitate radiative decay and is particularly important in the design of phosphorescent materials.^19–21 In photocatalysis, M–M interactions facilitate hydrogen atom abstraction through an inner-sphere electron transfer mechanism.^22–24 A comprehensive understanding of M–M interactions is crucial, as it can provide valuable guidance for the molecular design. Despite its broad utility, the fundamental nature of metallophilicity has long been debated.^{3,5,6,25–35} Recent breakthroughs show that metallophilicity is inherently repulsive, dominated by M–M Pauli repulsion between metal centers rather than stabilizing interactions, as supported by computational and spectroscopic studies across Au(I), Ag(I), Cu(I), Rh(I), Pt(II), and Pd(II) systems.^36–39

While the repulsive nature of metallophilicity has been revealed, the role of ligands in modulating this repulsion remains a critical unresolved question. Ligands are well known to exert dramatic control over M–M distances: for instance, Au(I) complexes exhibit Au–Au separations spanning from non-interacting (>3.8 Å) to significantly shorter than the sum of van der Waals radii (∼2.5 Å), depending on the ligand identity, as summarized in several comprehensive reviews.^3,5 Such variability highlights the dual capacity of ligands to either amplify or mitigate repulsive M–M interactions, yet the mechanistic origins of this modulation remain poorly defined. In this work, we address this gap by systematically dissecting how σ-donor and π-acceptor ligands tune M–M Pauli repulsion (Scheme 1).

Scheme 1 Top: previous work, repulsive M–M interaction in closed-shell d⁸ and d¹⁰ transition metal complexes. Bottom: this work, the role of π-acceptor and σ-donor ligands in M–M interactions.

Transition metal atoms can coordinate with a wide range of ligands, which are broadly categorized as π-acceptors, π-donors or σ-donors (Scheme 1).⁴⁰ π-Acceptor ligands, such as CO and nitriles (R–C≡N), feature low-energy π* orbitals that accept electron density from filled metal d-orbitals, enabling π-backbonding interactions. In contrast, strong σ-donor ligands like cyanide (CN⁻) and alkynides (R–C≡C⁻) coordinate through lone pairs, donating electron density to vacant metal orbitals (d/s/p). These contrasting bonding mechanisms exert striking effects on metallophilicity: structural studies reveal that π-acceptors promote shortened M–M distances, while σ-donors favour elongation, as shown in Fig. 1 and 7.^3,5

Fig. 1 Chemical structures (a), X-ray crystal structures (b) and optimized structures (c) of d⁸ Rh(I) metal complexes with or without π-acceptor ligands studied in this work. Calculations were performed at the PBE0-GD3BJ/SDD(Rh)/6-31G* (other elements) level of theory using the PCM solvent model for acetonitrile (ACN) in Gaussian 16.

Here, we bridge this gap through computational investigation of ligand-mediated M–M interactions. By utilizing energy decomposition analysis (EDA) and natural orbital for chemical valence (NOCV) methods, we demonstrate that π-backbonding interactions delocalize electron density from metal centers to ligand π* orbitals, attenuating M–M Pauli repulsion and enabling closer M–M contacts. Conversely, strong σ-donor ligands enhance metal (n + 1)s-nd hybridization, intensifying Pauli repulsion and elongating M–M distances. These insights explain well the experimental structural trends shown in Fig. 1 and 7. Our findings not only resolve longstanding ambiguities in ligand–metallophilicity relationships but also establish ligand-design principles to tailor M–M interactions in functional materials for supramolecular assembly, catalysis, and optoelectronic applications.

Results and discussion

Role of π-acceptor ligands

To investigate the role of π-acceptor ligands, we analysed a series of Rh(I) complexes with or without π-acceptor ligands (Fig. 1). Specifically, we compared the M–M distances in the following pairs using their corresponding X-ray crystal structures:

• Rh(terpy)Cl (Rh-1)⁴¹ vs. [Rh(terpy)N≡CCH₃]⁺ (Rh-2)⁴²

• Rh(CO)₂ClNH₂CH₃ (Rh-3)⁴³ vs. [Rh(CO)₂(N≡CCH₃)₂]⁺ (Rh-4).⁴⁴

Here, Rh-2 and Rh-4 incorporate π-acceptor ligands (acetonitrile), while Rh-1 and Rh-3 lack such ligands. Notably, aside from Cl⁻ and N≡CCH₃, both Rh-1 and Rh-2 coordinate to the same terpyridine (terpy) ligand; aside from Cl⁻/NH₂CH₃ and N≡CCH₃, both Rh-3 and Rh-4 coordinate to the same CO ligand. These comparisons exclude the potential influence of other ligand effects such as London dispersion and so on. As shown in Fig. 1, key structural trends emerged in the structural comparison: replacing the Cl⁻ ligand in Rh-1 with the π-acceptor ligand CH₃C≡N (Rh-2) shortened the Rh–Rh distance from 4.90 Å (Rh-1) to 3.07 Å (Rh-2). Substituting the Cl⁻ and NH₂CH₃ ligands in Rh-3 with CH₃C≡N ligands in Rh-4 reduced the Rh–Rh distance from 3.39–3.41 Å (Rh-3) to 3.15–3.18 Å (Rh-4). These results demonstrate that coordination of π-acceptor ligand is closely related to the short M–M distances observed in the crystal structures of d⁸ Rh(I) complexes.

The M–M distance trend observed in X-ray crystal structures was further validated through computational optimization of dimeric structures, thereby excluding contributions from the crystal packing effect. As shown in Fig. 1c, the optimized structures retain the key experimental trends (Fig. 1a and b): Rh complexes with π-acceptor ligands exhibit shorter Rh–Rh distances than analogues without such ligands (Rh-1 vs. Rh-2; Rh-3 vs. Rh-4). Notably, both optimized configurations of the [Rh-1]₂ dimer shown in Fig. 1c maintain longer Rh–Rh distances than those of [Rh-2]₂. This consistency between solution-phase calculations and solid-state structural data indicates that the observed distance variations are primarily driven by ligand electronic properties rather than crystal packing or solvent effects.

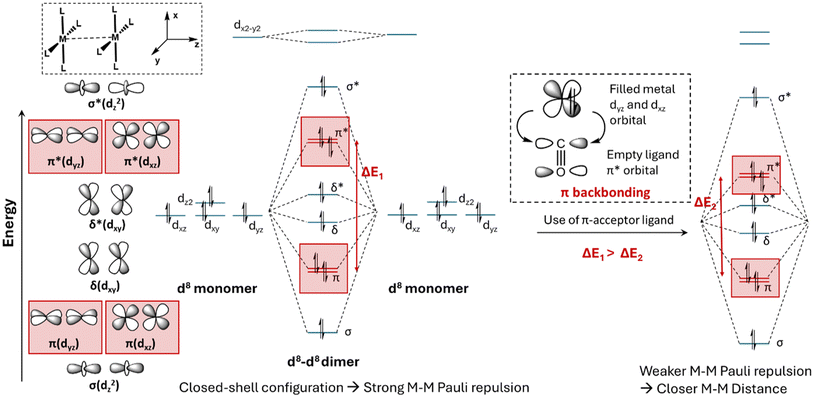
For d⁸–d⁸ closed-shell systems, the role of π-acceptor ligands in reducing M–M Pauli repulsion can be rationalized through an illustrative molecular orbital (MO) diagram shown in Scheme 2. First, we need to consider the ligand field splitting diagram of a metal with a d⁸ electronic configuration.⁴⁰ As shown in Scheme 2, for a d⁸ metal complex (e.g., Rh(I), Ir(I), Pt(II), or Pd(II)) with square planar coordination geometry, d_x²−y² is a strongly antibonding orbital with respect to M–L interactions and remains unoccupied, while d_z² is a weakly antibonding orbital and remains occupied.⁴⁰ The remaining three orbitals (d_xz, d_xy and d_yz) are degenerate, non-bonding and occupied M–L orbitals.⁴⁰

Scheme 2 Schematic illustration of the role of the π-acceptor ligand in weakening the M–M Pauli repulsion for d⁸–d⁸ closed-shell metal complexes. Schematic illustration of the MO for d¹⁰–d¹⁰ closed-shell metal complexes has been provided in the ESI.†

Next, we need to derive the formation of M–M bonding and antibonding orbitals from the occupied d orbitals of two d⁸ metal atoms.⁴⁰ Defining the M–M bond axis as the z-axis, then the two d_z² orbitals can overlap in a σ-type manner to form a bonding σ orbital and an antibonding σ* orbital (Scheme 2). Similarly, the d_xz and d_yz orbitals can overlap with another set of d_xz and d_yz orbitals in a π-fashion, forming two degenerate bonding π orbitals and two degenerate antibonding π* orbitals. Since the π orbital overlap is smaller than the σ overlap, the energy splitting between the bonding and antibonding π orbitals is smaller than that between the bonding and antibonding σ orbitals. Furthermore, the d_xy orbital can overlap with another d_xy orbital in a δ-type manner, resulting in bonding δ orbitals and antibonding δ* orbitals. The δ orbital overlap is even smaller than the π overlap, leading to an energy splitting between the bonding δ and the antibonding δ* orbitals that is smaller than those for the π and π* orbitals, as illustrated in Scheme 2.

In Scheme 2, the M–M bonding orbitals—comprising one σ, two π, and one δ orbital—along with the corresponding antibonding orbitals (one σ*, two π*, and one δ*), are fully occupied. As demonstrated in our previous work on Rh(I), Pt(II) and Pd(II) systems, the closed-shell electronic configuration of two d⁸ metals with planar coordination geometry results in strong M–M Pauli repulsion, the magnitude of which is reflected in the energy splitting between the occupied M–M bonding and antibonding orbitals.^36,37

The M–L coordination bond plays a critical role in determining both the energy levels and electron density distribution of the metal d orbitals.⁴⁰ This, in turn, modulates the extent of M–M orbital overlap, thereby influencing the magnitude of M–M Pauli repulsion and the resulting M–M distances observed in the crystal structures of these complexes. Among various types of M–L coordination bonds, π-backbonding is a particularly important interaction in transition metal complexes. This interaction typically occurs when a ligand, such as carbon monoxide, accepts electron density from the metal through the overlap of a metal d orbital and a ligand π* orbital. This process, termed “back-bonding,” stabilizes the metal's d orbitals as the ligand acts as a π-acceptor. Consequently, M–M π and π* orbitals are stabilized, as illustrated in Scheme 2. Since M–M Pauli repulsion is positively correlated with the degree of overlap between two occupied d orbitals,^45,46 it is expected that the presence of π-acceptor ligands weakens M–M Pauli repulsion arising from π-type interactions, leading to shorter M–M distances.

To computationally prove the speculation illustrated in Scheme 2, we performed Energy Decomposition Analysis (EDA),^47–49 Natural Orbitals for Chemical Valence (NOCV) analysis, molecular orbital (MO) diagram calculations, and high-level Domain-based Local Pair Natural Orbital Coupled Cluster with Singles, Doubles, and perturbative Triples (DLPNO-CCSD(T)) computations on Rh complexes, using the AMS (Amsterdam Modeling Suite) 2024.1^50,51 and ORCA 6.0 package.^52,53

We first examined the formation of π-backbonding interactions between the metal and the ligand in complexes Rh-1 and Rh-2. EDA-NOCV⁵⁴ analysis decomposes electron density changes into chemically understandable components using fragment molecular orbitals. Herein, the energetic quantification of M–L π interactions was calculated for the Rh–Cl bonds in the optimized Rh-1 monomer and the Rh–N bonds in the optimized Rh-2 monomer. The NOCV deformation density channels are depicted in Fig. 2 with the red and blue regions symbolizing the depletion and accumulation of electron density, respectively. One NOCV deformation density channel corresponding to Rh–Cl π-bonds shows electron transfer from the Rh atom to the Cl atom, with an orbital energy of −2.34 kcal mol⁻¹ of Rh-1. Similarly, one NOCV deformation density channel, representing Rh–N π-bonds, exhibits electron transfer from the Rh atom to the N atom, with a stronger orbital energy of −8.99 kcal mol⁻¹ of Rh-2.

Fig. 2 Calculated EDA-NOCV deformation density contributions to (a) the Rh → Cl π-type interaction in Rh-1 and (b) the Rh → N π-type interaction in Rh-2, together with the calculated orbital interaction energies corresponding to each π interaction. Isovalue = 0.001. Charge transfer occurred from red to blue.

The difference in the energy of NOCV calculations between Rh-1 and Rh-2 indicates different π-accepting abilities between –Cl⁻ and the –N≡CCH₃ ligand. For the N≡CCH₃ ligand, the N atom forms a triple bond with the C atom, consisting of one σ bond and two π bonds. The two empty π* orbitals in the N≡CCH₃ ligand lie at relatively low energy, enabling efficient acceptance of d electron density from the Rh atom. The NOCV analysis suggests that stronger π-backbonding interaction occurs in Rh-2, leading to a reduction in the d orbital's electron density in Rh-2 compared to Rh-1. This is expected to reduce the dπ–dπ* orbital splitting energy and weaken the M–M Pauli repulsion in the Rh-2 dimer compared to the Rh-1 dimer. Next, we conducted MO calculations on the Rh-1 and Rh-2 dimers to validate this hypothesis.

Based on this consideration, we examined and compared the dπ–dπ* orbital splitting energy in the optimized Rh-1 and Rh-2 dimers using MO calculations. As shown in Fig. 3, the orbital splitting energy between the M–M π(d_xz–d_xz) bonding orbital and the π*(d_xz–d_xz) antibonding orbital was calculated to be 0.408 eV in Rh-1 and 0.393 eV in Rh-2. The orbital splitting energy for M–M π-type interactions between the two Rh atoms is consistently smaller in Rh-2 than that in Rh-1. In comparison to the Rh-1 dimer, we expect that the smaller dπ–dπ* orbital energy splitting in the Rh-2 dimer would lead to decreased M–M Pauli repulsion.^36,37 Finally, we calculated the M–M Pauli repulsion in the Rh-1 and Rh-2 dimers to prove this relationship.

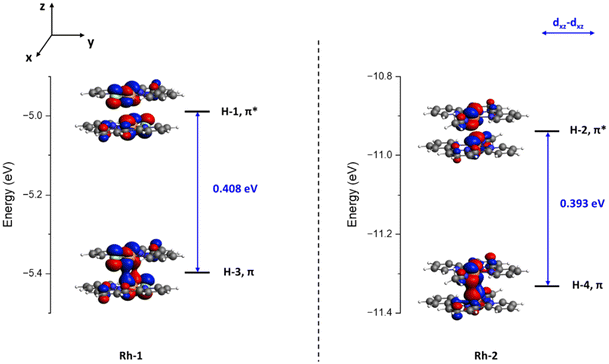Fig. 3 Calculated MO diagram for the Rh-1 dimer (left) and the Rh-2 dimer (right), highlighting the dπ bonding and dπ* antibonding orbitals. Isovalue = 0.03.

M–M Pauli repulsion for the Rh-1 and Rh-2 dimers has been calculated using the EDA method, and the results are plotted in Fig. 4. In the calculations, the M–M distance in the Rh(I) dimers 1 and 2 was set from 3.3 Å to 2.9 Å, to compare the M–M Pauli repulsion at equal M–M distances. As shown in Fig. 4a, Rh–Rh Pauli repulsion increased with the decrease of the Rh–Rh distance in both the Rh-1 and Rh-2 dimers, and the M–M Pauli repulsion in the Rh-1 dimer is always stronger than that in the Rh-2 dimer. For instance, at an Rh–Rh distance of 3.0 Å, the M–M Pauli repulsion was 32.60 kcal mol⁻¹ in the Rh-1 dimer, compared to 29.82 kcal mol⁻¹ in the Rh-2 dimer, representing a 2.78 kcal mol⁻¹ reduction. This calculated trend in M–M Pauli repulsion for Rh-1 and Rh-2 aligns with the trend observed in the M–M distances from their respective X-ray crystal structures (Fig. 1). The trend in Rh–Rh Pauli repulsion has been further validated through DLPNO-CCSD(T) calculations, which confirm that the Rh-2 complex—featuring the π-accepting CH₃CN ligand—exhibits weaker metal–metal Pauli repulsion than Rh-1 (Fig. S1†).

Fig. 4 Calculated M–M Pauli repulsion of (a) Rh-1 and Rh-2 dimers and (b) Rh-3 and Rh-4 dimers, by changing the M–M distance. For EDA calculations at non-equilibrium M–M distances, fragment geometries were frozen while varying metal–metal separation.

The results of EDA, NOCV and MO calculations demonstrate a mechanistic pathway: the ligand's π-accepting ability directly influences the M–M dπ–dπ* orbital splitting energy, which in turn determines the magnitude of M–M Pauli repulsion. To summarize, coordination to π-acceptor ligands decreases the dπ–dπ*(M–M) orbital splitting and weakens M–M Pauli repulsion, facilitating the formation of close M–M contact in the Rh-2 complex compared to Rh-1.

Similarly, NOCV calculations were performed on the Rh-3 and Rh-4 monomers, revealing total Rh → L π-bonding interactions of −17.42 and −18.99 kcal mol⁻¹, respectively (Fig. S2†). At every M–M distance in Fig. 4b, stronger M–M Pauli repulsion is observed in the Rh-3 dimer (with Cl⁻/NH2CH₃ ligands) than in the Rh-4 dimer (with π-acceptor N≡CCH₃ ligands). The NOCV and EDA results suggest that the stronger π-backbonding interaction in Rh-4 contributes to weaker M–M Pauli repulsion, and consequently, a shorter M–M distance in Rh-4 (3.15–3.18 Å) than in Rh-3 (3.39–3.41 Å) shown in Fig. 1.

In addition to the Rh(I) d⁸ systems, the relationship between the d¹⁰–d¹⁰ Pauli repulsion and the π acceptor ligand is demonstrated in the MO diagram of Scheme S1.† Different from the d⁸ closed-shell metal atom with four fully occupied metal d orbitals, the d¹⁰ metal atom has five fully occupied d orbitals.⁴⁰ These d orbitals, when interacting between two metal atoms, contribute to one σ-type bonding and antibonding orbital, two π-type bonding and antibonding orbitals, and two δ-type bonding and antibonding orbitals. Similarly, the formation of π-backbonding interactions between the d¹⁰ metal atom and the ligand stabilizes the M–M π-type bonding and antibonding orbitals, leading to weakened M–M Pauli repulsion in d¹⁰–d¹⁰ metal complex systems (Scheme S1†).

To further validate the relationship between ligand π-accepting ability and M–M Pauli repulsion, we systematically evaluated diverse ligands (L = NH₃, PH₃, CO, NCCH₃, CNCH₃, CCCH₃, CN, Cl, Br, I) in [Rh(terpy)L]₂ dimers (model system). Following structural optimization, we correlated M–M distances with three parameters: molecular volume (reflecting steric effects), ligand–ligand (L–L) dispersion interactions, and M–M Pauli repulsion energy. In Fig. 5, M–M distances show no clear correlation with the molecular volume or L–L dispersion but exhibit a positive correlation with both M–M Pauli repulsion energy and ligand π-accepting strength (Fig. 5, 6 and Table S1†). As shown in Fig. 5, increasing M–M distances in [Rh(terpy)L]₂ dimers (L = CO → Cl⁻) correlate with progressively stronger M–M Pauli repulsion. Correspondingly, enhanced Pauli repulsion occurs concomitantly with weakened Rh → L π-interactions, as evidenced by the EDA-NOCV analysis in Fig. 6. This absence of steric/L–L dispersion correlations, coupled with electronic dependence, provides evidence that ligand π-accepting capability primarily governs M–M distances through Pauli repulsion modulation.

Fig. 5 Model system [Rh(terpy)L]₂ and correlation analysis. Chemical structures of the [Rh(terpy)L]₂ dimer (top) with the corresponding plots of the molecular volume, L–L dispersion interaction, and M–M Pauli repulsion versus the M–M distance in the fully optimized geometries (bottom). All data points are tabulated in Table S1.†

Fig. 6 Calculated EDA-NOCV deformation orbital energies correspond to the Rh → L π interaction in the model system of Rh(terpy)L. All data points are tabulated in Table S1.†

Notably, for relatively large ligands, steric or dispersion effects could potentially dominate.³³ For instance, the dispersion interactions and softness of ligand fragments have previously been reported to govern intermolecular interactions in the Rh(I) and Au(I) closed-shell systems, while the metals play a relatively minor role.^{32–34,55,56} The magnitude of ligand–ligand (L–L) dispersion interactions strongly depends on the ligand size.^33,34 Furthermore, recent studies demonstrate that ligand–metal interplay critically influences non-covalent interactions.^55,57 However, within the scope of this work—focused on investigating the electronic tuning effects via ligands—our analyses confirm that the observed M–M distance trends are linked to the π-accepting ligand modulation ability of M–M Pauli repulsion in smaller ligand systems.

Role of σ-donor ligands

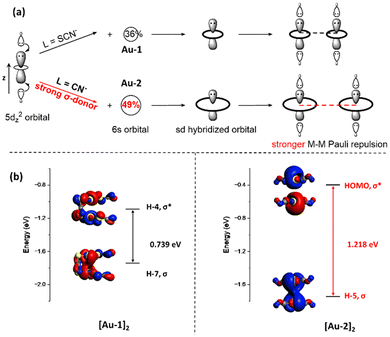
To explore the effect of the σ-donating ability of ligands on M–M interactions, several examples of Pt(II) and Au(I) complexes have been studied (Fig. 7). We compared the M–M distances in [Au(SCN)₂]⁻ (Au-1) and [Au(CN)₂]⁻ (Au-2), where CN⁻ is a stronger σ-donor. As shown in Fig. 7a, replacing the SCN⁻ ligand in Au-1 with the CN⁻ ligand in Au-2 resulted in a longer Au–Au distance of 3.64 Å, compared to 3.0064–3.070 Å in Au-1 (K⁺ as the countercation).^5,58–60 We also compared the M–M distances in [Pt(terpy)C≡CC₆H₅]⁺ (Pt-1), Pt(C^N^N)C≡CC₆H₅ (Pt-2), [Pt(C^N^N)N≡CCH₃]⁺ (Pt-3), and Pt(N^C^N)C≡CC₆H₅ (Pt-4), where Pt-1 and Pt-3 complexes have only one strong σ-donor ligand of C⁻, while Pt-2 and Pt-4 complexes have two C⁻ ligands.^61–64 As shown in Fig. 7b, a close Pt–Pt distance of 3.37 Å was observed in the crystal structure of Pt-1. By changing the terpyridine ligand (N^N^N) into the (C^N^N)⁻ ligand and (N^C^N)⁻ ligand, the distances became longer in Pt-2 (6.43 Å) and Pt-4 (4.89 Å). Substituting the⁻C≡CC₆H₅ ligand in Pt-2 with the N≡CCH₃ ligand in Pt-3 resulted in a reduction of the Pt–Pt distance from 6.43 to 3.28 Å. Additionally, the Pt–Pt contact in Pt-1 and Pt-3 is nearly perpendicular to the planar Pt complex, revealing a face-to-face close packing form. In contrast, this angle deviates significantly from 90° in Pt-2 and Pt-4. These structural findings suggest that in Pt-2 and Pt-4, which feature two strong σ-donor C⁻ ligands, close Pt–Pt contacts are unfavourable. In contrast, Pt-1 and Pt-3 complexes, which contain only one C⁻ ligand, exhibit close Pt–Pt contacts.

Fig. 7 Chemical structures of (a) Au(I) and (c) Pt(II) metal complexes, together with the experimentally resolved M–M distance in their crystal structures. Note: for Au-1 and Au-2, the Au–Au distance is different when changing the countercation.⁵ We compared Au-1 and Au-2 with the same countercation here: ⁿBu₄N[Au-1]: d(Au–Au) = 3.0700 Å, K[Au-1]: d(Au–Au) = 3.0064/3.0430 Å. K[Au-2]: d(Au–Au) = 3.64 Å, ⁿBu₄N[Au-2]: no close Au–Au contact. Optimized structures of (b) Au(I) and (d) Pt(II) metal complexes. Calculations were performed at the PBE0-GD3BJ/SDD(Au, Pt)/6-31G* (other elements) level of theory using the PCM solvent model for ACN in Gaussian 16.

The M–M distance trend observed in X-ray crystal structures was validated through computational optimization of the dimeric species. As shown in Fig. 7b and d, optimized structures replicate key experimental trends from Fig. 7a and c: [Au-1]₂ exhibits shorter Au–Au distances than [Au-2]₂, and [Pt-1]₂ shows reduced Pt–Pt distances compared to [Pt-2]₂. This consistency between computational and crystallographic data confirms that the observed variations originate from intrinsic electronic properties rather than crystal packing effects.

For the σ-bonding interaction between a metal and a ligand, the ligand donates electron density to the metal's empty d or s orbital through σ-type M–L interaction, which influences the composition, energy, and electron density distribution of metal orbitals. The role of strong σ-donor ligands in strengthening the M–M Pauli repulsion for d⁸–d⁸ and d¹⁰–d¹⁰ closed-shell systems is shown in Scheme S2† and Fig. 8a, respectively.

Fig. 8 (a) Illustration scheme showing the role of the σ-donor ligand in strengthening the M–M Pauli repulsion for d¹⁰–d¹⁰ closed-shell metal complexes. Complexes Au-1 and Au-2 were used as the example. (b) Calculated MO diagram for the Au-1 dimer (left) and the Au-2 dimer (right) to highlight the dσ(M–M) bonding and dσ*(M–M) antibonding orbitals. Isovalue = 0.03.

For the d¹⁰ metal complexes such as Au(I), Ag(I), or Cu(I), (n + 1)s-nd orbital hybridization plays a critical role in the formation of M–L σ-type coordination bonds (n = 3 for Cu(I), 4 for Ag(I) and 5 for Au(I)).^36,37 As shown in Fig. 8a, part of the empty (n + 1)s orbitals are used to accept electron density from σ-donor ligands. Defining the M–L bond direction as the z-axis, the (n + 1)s-nd orbital hybridization reduces the metal orbital's lobe size along the z-axis while increasing its size in the xy-plane.⁴⁰ When two metal atoms approach each other in the xy-plane, their sd-hybridized orbitals overlap, resulting in the formation of a bonding σ(M–M) orbital and an antibonding σ(M–M)* orbital.^36,37 Coordination with a stronger σ-donor ligand enhances the extent of (n + 1)s orbital hybridization. This, in turn, increases the metal's electron density in the xy plane, resulting in greater orbital splitting and stronger M–M Pauli repulsion.

To validate the schematic diagram plotted in Fig. 8a, we conducted MO calculations on Au-1 and Au-2 dimers (Fig. 8b). Because of the stronger σ-donor ligand C≡N⁻ in Au-2, a greater contribution from the Au-6s orbital was observed in its 6s–5d hybridized orbital (49% in Au-2 vs. 36% in Au-1). The increased Au-6s orbital contribution enlarges the metal orbital's lobe size in the xy plane, thereby increasing the orbital splitting energy in the Au-2 dimer compared to the Au-1 dimer. As shown in Fig. 8b, the orbital splitting energy between the M–M σ(6s–5d) bonding orbital and the M–M σ*(6s–5d) antibonding orbital is calculated to be 0.739 eV in [Au-1]₂ and 1.218 eV in [Au-2]₂. This larger orbital splitting energy in [Au-2]₂ indicates stronger Au–Au Pauli repulsion in [Au-2]₂ compared to that in [Au-1]₂.

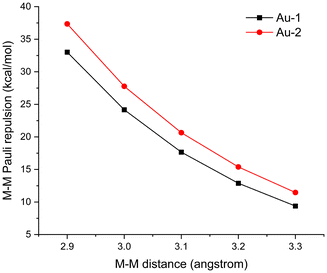
We next performed EDA calculations on the Au-1 and Au-2 dimers (Fig. 9). In the calculations, M–M distances in these Au(I) dimers were set from 3.3 Å to 2.9 Å to compare the M–M Pauli repulsion at equal M–M distances. Au–Au Pauli repulsion increased with the decrease of the Au–Au distance for both Au-1 and Au-2 dimers, and the M–M Pauli repulsion in the Au-1 dimer is always stronger than that in the Au-2 dimer. For example, at an Au–Au distance of 3.0 Å, the M–M Pauli repulsion is 27.7 kcal mol⁻¹ in the Au-1 dimer, while it is 24.2 kcal mol⁻¹ in the Au-2 dimer. Relaxation density (defined as the electron density difference between the metal atom after ligand coordination and its pre-coordination state) of Mulliken population on the metal's s-orbitals (Δs) was examined to further characterize the ligand's σ-donating ability for complexes Au-1 and Au-2. The calculated trend of M–M Pauli repulsion in Au-1 and Au-2 is consistent with the calculated relaxation density. Specifically, Au-2 exhibits a larger 6s-orbital relaxation density (Δs = 0.9073) with the CN⁻ ligand than Au-1 exhibits with the SCN⁻ ligand (Δs = 0.8455), indicating that the CN⁻ ligand donates more electron density to the Au-6s orbital. To summarize, coordination to strong σ-donor ligands increases the dσ(M–M)-dσ*(M–M) orbital splitting and strengthens the M–M Pauli repulsion, preventing the formation of close M–M contact in the Au-2 complex compared to Au-1.

Fig. 9 Calculated M–M Pauli repulsion of Au-1 and Au-2 dimers by changing the M–M distance. For EDA calculations at non-equilibrium M–M distances, fragment geometries were frozen while varying metal–metal separation.

Let us now consider the role of σ-bonding interaction in d⁸–d⁸ systems. As previously noted, in square-planar d⁸ metal complexes, the nd_x²−y² orbital is unoccupied and strongly antibonding regarding the M–L coordination.³⁷ This orbital does not contribute to M–M Pauli repulsion. In contrast, the nd_z² weakly antibonding orbital is fully occupied and significantly contributes to M–M Pauli repulsion through the M–M σ-type interaction (Scheme 2 and S2†).³³ Importantly, the nd_z² orbital can accept the ligand's electron density by the hybridization with higher empty metal-(n + 1)s orbitals to weaken the M–L antibonding interaction (n = 4 for Rh(I) and Pd(II), n = 5 for Ir(I) and Pt(II)). The relative component of the hybridized (n + 1)s orbitals is closely related to the σ-donating ability of ligands, similar to d¹⁰–d¹⁰ systems. We compared the Pt-6s orbital's population in Pt-1 and Pt-2, where the Pt-1 complex has one strong σ-donor C⁻ ligand and the Pt-2 complex has two strong σ-donor C⁻ ligands.

As shown in Scheme S2,† more Pt-6s orbital's components show up in the Pt-5d_z² orbital for Pt-2 (23%) than in Pt-1 (20%). In the calculated Mulliken population, Pt-2 also has more Pt-6s orbital's relaxation density than Pt-1 after ligand coordination (Δs = 0.1151 in Pt-2 vs. 0.0001 in Pt-1). The increased electron density in the Pt-6s orbital of the Pt-2 complex compared to Pt-1 is expected to amplify the Pt–Pt Pauli repulsion, which consequently elongates the Pt–Pt bond distance.

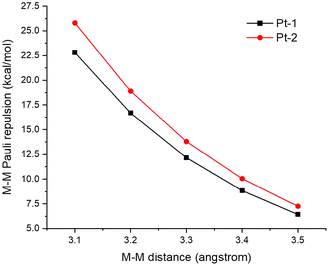
Next, we calculated and compared the M–M Pauli repulsion in Pt-1 and Pt-2 dimers (Fig. 10). M–M distances in the Pt(II) dimers were set from 3.5 Å to 3.1 Å for the comparison of M–M Pauli repulsion at equal M–M distances. As revealed in Fig. 10, the M–M Pauli repulsion in the Pt-2 dimer is always stronger than that in the Pt-1 dimer, which is consistent with the electronic configuration calculations.

Fig. 10 Calculated M–M Pauli repulsion of Pt-1 and Pt-2 dimers by changing the M–M distance. For EDA calculations at non-equilibrium M–M distances, fragment geometries were frozen while varying metal–metal separation.

Conclusions

In summary, we studied the relationship between ligands (broadly categorized as π-acceptors and/or σ-donors) and M–M Pauli repulsion in a series of d⁸ and d¹⁰ closed-shell metal complexes. With π-acceptor ligands such as nitriles and isocyanides, M–M Pauli repulsion is weakened by the transfer of electron density from the closed-shell metal atom to the π-acceptor ligand's empty orbital. This results in shorter M–M distances in their respective X-ray crystal structures. Conversely, σ-donor ligands, such as cyanide (CN⁻) and alkynides (R–C≡C⁻), strengthen M–M Pauli repulsion by transferring electron density from the ligand's lone pair of orbitals to the metal's empty (n + 1)s orbital, leading to longer M–M distances. This work provides valuable insights into the design of d⁸ and d¹⁰ metal complexes with controlled M–M distances by leveraging M–L coordination interactions. These findings also deepen the understanding of metallophilicity and offer a framework for tailoring M–M interactions in functional materials, with potential applications in catalysis, supramolecular assembly, and optoelectronics.

Author contributions

Q. W. designed and supervised the project. Y. Z. carried out the calculations. Both authors contributed to the editing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been uploaded as part of the ESI.†

Acknowledgements

Q. W. thanks the startup fund (Project No. 4933633 and 5501780) and the Direct Grant supported by the Chinese University of Hong Kong, Hong Kong (Project No. 4053703) and the support from the Research Grants Council of Hong Kong under the Early Career Scheme (Project No. 24305125). The authors thank the open fund (Project No. 6907430) of the State Key Laboratory of Synthetic Chemistry. The authors thank the computing resources provided by the Nansha Branch of the National Supercomputer Center in Guangzhou. Y. Z. thanks Dr. Shuo Xu from the University of Hong Kong for helpful discussions.

References

1. H. Schmidbaur, Ludwig Mond lecture. High-carat Gold Compounds, Chem. Soc. Rev., 1995, 24, 391–400.
2. V. W.-W. Yam and K. K.-W. Lo, Luminescent polynuclear d¹⁰ metal complexes, Chem. Soc. Rev., 1999, 28, 323–334.
3. H. Schmidbaur and A. Schier, A briefing on aurophilicity, Chem. Soc. Rev., 2008, 37, 1931–1951.
4. V. W.-W. Yam and E. C.-C. Cheng, Highlights on the recent advances in gold chemistry—a photophysical perspective, Chem. Soc. Rev., 2008, 37, 1806–1813.
5. H. Schmidbaur and A. Schier, Aurophilic interactions as a subject of current research: an up-date, Chem. Soc. Rev., 2012, 41, 370–412.
6. H. Schmidbaur and A. Schier, Argentophilic Interactions, Angew. Chem., Int. Ed., 2015, 54, 746–784.
7. V. W.-W. Yam, V. K.-M. Au and S. Y.-L. Leung, Light-Emitting Self-Assembled Materials Based on d⁸ and d¹⁰ Transition Metal Complexes, Chem. Rev., 2015, 115, 7589–7728.
8. G. Ghosh, T. Ghosh and G. Fernández, Controlled Supramolecular Polymerization of d⁸ Metal Complexes through Pathway Complexity and Seeded Growth, ChemPlusChem, 2020, 85, 1022–1033.
9. J. Zheng, Z. Lu, K. Wu, G.-H. Ning and D. Li, Coinage-Metal-Based Cyclic Trinuclear Complexes with Metal–Metal Interactions: Theories to Experiments and Structures to Functions, Chem. Rev., 2020, 120, 9675–9742.
10. F. Mendizabal and P. Pyykkö, Aurophilic attraction in binuclear complexes with Au(I) and Au(III). A theoretical study, Phys. Chem. Chem. Phys., 2004, 6, 900–905.
11. D. Blasco, F. Reboiro, D. Sundholm, M. E. Olmos, M. Monge and J. M. López-de-Luzuriaga, A “gold standard” computational proof for the existence of gold(III) aurophilicity, Dalton Trans., 2023, 52, 2219–2222.
12. T. E. Karpiuk, S. Mahato, T. Storr and D. B. Leznoff, Unusually short unsupported Au(III)⋯Au(III) aurophilic contacts in emissive lanthanide tetracyanoaurate(III) complexes, Chem. Commun., 2024, 60, 3914–3917.
13. M. Mauro, A. Aliprandi, D. Septiadi, N. S. Kehr and L. De Cola, When self-assembly meets biology: luminescent platinum complexes for imaging applications, Chem. Soc. Rev., 2014, 43, 4144–4166.
14. K. M. C. Wong, M. M. Y. Chan and V. W. W. Yam, Supramolecular Assembly of Metal–Ligand Chromophores for Sensing and Phosphorescent OLED Applications, Adv. Mater., 2014, 26, 5558–5568.
15. A. Aliprandi, D. Genovese, M. Mauro and L. De Cola, Recent Advances in Phosphorescent Pt(II) Complexes Featuring Metallophilic Interactions: Properties and Applications, Chem. Lett., 2015, 44, 1152–1169.
16. N. Bäumer, J. Matern and G. Fernández, Recent progress and future challenges in the supramolecular polymerization of metal-containing monomers, Chem. Sci., 2021, 12, 12248–12265.
17. M. J. Mayoral, C. Rest, V. Stepanenko, J. Schellheimer, R. Q. Albuquerque and G. Fernández, Cooperative Supramolecular Polymerization Driven by Metallophilic Pd⋯Pd Interactions, J. Am. Chem. Soc., 2013, 135, 2148–2151.
18. A. Aliprandi, M. Mauro and L. De Cola, Controlling and imaging biomimetic self-assembly, Nat. Chem., 2016, 8, 10.
19. Q. Wan, W. P. To, C. Yang and C. M. Che, The Metal–Metal-to-Ligand Charge Transfer Excited State and Supramolecular Polymerization of Luminescent Pincer PdII–Isocyanide Complexes, Angew. Chem., Int. Ed., 2018, 57, 3089–3093.
20. K. Tuong Ly, R.-W. Chen-Cheng, H.-W. Lin, Y.-J. Shiau, S.-H. Liu, P.-T. Chou, C.-S. Tsao, Y.-C. Huang and Y. Chi, Near-infrared organic light-emitting diodes with very high external quantum efficiency and radiance, Nat. Photonics, 2017, 11, 63–68.
21. Y. Zhang, J. Miao, J. Xiong, K. Li and C. Yang, Rigid Bridge-Confined Double-Decker Platinum(II) Complexes Towards High-Performance Red and Near-Infrared Electroluminescence, Angew. Chem., Int. Ed., 2022, 61, e202113718.
22. N. S. Lewis, K. R. Mann, J. Gordon and H. B. Gray, Oligomerization and Two-Center Oxidative Addition Reactions of a Dimeric Rhodium(I) Complex, J. Am. Chem. Soc., 1976, 98, 7461–7463.
23. D. M. Roundhill, H. B. Gray and C. M. Che, Pyrophosphito-Bridged Diplatinum Chemistry, Acc. Chem. Res., 1989, 22, 55–61.
24. S. Witzel, A. S. K. Hashmi and J. Xie, Light in Gold Catalysis, Chem. Rev., 2021, 121, 8868–8925.
25. V. Andrianov, Y. T. Struchkov and E. Rossinskaja, A new type of organogold compound. The molecular structure of [(π-C₅H₅)Fe(π-C₅H₄)Au₂(PPh₃)₂]-⁺[BF₄]⁻, J. Chem. Soc., Chem. Commun., 1973, 338–339.
26. K. M. Anderson, A. E. Goeta and J. W. Steed, Au⋯Au Interactions: Z‘ > 1 Behavior and Structural Analysis, Inorg. Chem., 2007, 46, 6444–6451.
27. M. J. Katz, K. Sakai and D. B. Leznoff, The use of aurophilic and other metal–metal interactions as crystal engineering design elements to increase structural dimensionality, Chem. Soc. Rev., 2008, 37, 1884–1895.
28. N. S. Harisomayajula, S. Makovetskyi and Y. C. Tsai, Cuprophilic interactions in and between molecular entities, Chem. – Eur. J., 2019, 25, 8936–8954.
29. P. K. Mehrotra and R. Hoffmann, Cu(I)-Cu(I) Interactions. Bonding Relationships in d¹⁰-d¹⁰ Systems, Inorg. Chem., 1978, 17, 2187–2189.
30. P. Pyykkö and Y. Zhao, Ab initio Calculations on the (ClAuPH₃)₂ Dimer with Relativistic Pseudopotential: Is the “Aurophilic Attraction” a Correlation Effect?, Angew. Chem., Int. Ed. Engl., 1991, 30, 604–605.
31. P. Pyykkö, Strong Closed-Shell Interactions in Inorganic Chemistry, Chem. Rev., 1997, 97, 597–636.
32. P. Pyykkö, N. Runeberg and F. Mendizabal, Theory of the d¹⁰−d¹⁰ Closed-Shell Attraction: 1. Dimers Near Equilibrium, Chem. – Eur. J., 1997, 3, 1451–1457.
33. S. Grimme and J.-P. Djukic, Cation−Cation “Attraction”: When London Dispersion Attraction Wins over Coulomb Repulsion, Inorg. Chem., 2011, 50, 2619–2628.
34. M. Andrejić and R. A. Mata, M. Andrejić and R. A. Mata, Study of ligand effects in aurophilic interactions using local correlation methods, Phys. Chem. Chem. Phys., 2013, 15, 18115–18122.
35. X. Yu, T. Jin, K. Wang, D. Li and L. Cheng, Benchmark studies on the large errors of calculated binding energies in metallophilic interactions, J. Chem. Phys., 2022, 156, 104103.
36. Q. Wan, J. Yang, W.-P. To and C.-M. Che, Strong metal–metal Pauli repulsion leads to repulsive metallophilicity in closed-shell d⁸ and d¹⁰ organometallic complexes, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019265118.
37. S. Xu, Q. Wan, J. Yang and C.-M. Che, Anisotropic Metal–Metal Pauli Repulsion in Polynuclear d¹⁰ Metal Clusters, J. Phys. Chem. Lett., 2024, 15, 2193–2201.
38. M. B. Brands, J. r. Nitsch and C. l. F. Guerra, Relevance of Orbital Interactions and Pauli Repulsion in the Metal–Metal Bond of Coinage Metals, Inorg. Chem., 2018, 57, 2603–2608.
39. Z. R. Wong, T. K. Schramm, M. Loipersberger, M. Head-Gordon and F. D. Toste, Revisiting the Bonding Model for Gold(I) Species: The Importance of Pauli Repulsion Revealed in a Gold(I)-Cyclobutadiene Complex, Angew. Chem., Int. Ed., 2022, 61, e202202019.
40. Y. Jean, Molecular orbitals of transition metal complexes, Oxford University Press, 2005. Page 37–94: M–L σ-interactions. Page 98–138: M–L π-type interactions. Page 51–53: electronic configuration of square-planar ML₄ complexes. Page 74–76: electronic configuration of linear ML₂ complexes. Page 170–175: metal–metal σ-, π- and δ-type interactions.
41. B. C. de Pater, H.-W. Frühauf, K. Vrieze, R. de Gelder, E. J. Baerends, D. McCormack, M. Lutz, A. L. Spek and F. Hartl, Strongly Nucleophilic RhI Centre in Square-Planar Complexes with Terdentate (κ³) 2,2′:6′,2′′-Terpyridine Ligands: Crystallographic, Electrochemical and Density Functional Theoretical Studies, Eur. J. Inorg. Chem., 2004, 2004, 1675–1686.
42. D. Inoki, T. Matsumoto, H. Nakai and S. Ogo, Experimental Study of Reductive Elimination of H₂ from Rhodium Hydride Species, Organometallics, 2012, 31, 2996–3001.
43. K. Jang, I. G. Jung, H. J. Nam, D.-Y. Jung and S. U. Son, One-Dimensional Organometallic Molecular Wires via Assembly of Rh(CO)₂Cl(amine): Chemical Control of Interchain Distances and Optical Properties, J. Am. Chem. Soc., 2009, 131, 12046–12047.
44. M. E. Prater, L. E. Pence, R. Clérac, G. M. Finniss, C. Campana, P. Auban-Senzier, D. Jérome, E. Canadell and K. R. Dunbar, A Remarkable Family of Rhodium Acetonitrile Compounds Spanning Three Oxidation States and with Nuclearities Ranging from Mononuclear and Dinuclear to One-Dimensional Chains, J. Am. Chem. Soc., 1999, 121, 8005–8016.
45. J. H. Jansen and M. S. Gordon, An approximate formula for the intermolecular Pauli repulsion between closed shell molecules, Mol. Phys., 1996, 89, 1313–1325.
46. J. A. Rackers and J. W. Ponder, Classical Pauli repulsion: An anisotropic, atomic multipole model, J. Chem. Phys., 2019, 150, 084104.
47. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method: I. The transition state method, Theor. Chim. Acta, 1977, 46, 1–10.
48. T. Ziegler and A. Rauk, CO CS, N2, PF3, and CNCH3 as σ Donors and π Acceptors. A Theoretical Study by the Hartree-Fock-Slater Transition-State Method, Inorg. Chem., 1979, 18, 1755–1759.
49. T. Ziegler and A. Rauk, A theoretical study of the ethylene-metal bond in complexes between Cu⁺, Ag⁺, Au⁺, Pt⁰, or Pt²⁺ and ethylene, based on the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1558–1565.
50. C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Towards an order-N DFT method, Theor. Chem. Acc., 1998, 99, 391–403.
51. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
52. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
53. F. Neese and F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
54. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
55. Y. Cornaton and J.-P. Djukic, Noncovalent interactions in organometallic chemistry: from cohesion to reactivity, a new chapter, Acc. Chem. Res., 2021, 54, 3828–3840.
56. P. Pyykkö, J. Li and N. Runeberg, Predicted ligand dependence of the Au(I)⋯Au(I) attraction in (XAuPH₃)₂, Chem. Phys. Lett., 1994, 218, 133–138.
57. N. A. Bokach and V. Y. Kukushkin, From covalent to noncovalent: The role of metals in activating ligand sites toward noncovalent interactions (NCIs), Coord. Chem. Rev., 2025, 529, 216440.
58. N. L. Coker, J. A. Krause Bauer and R. C. Elder, Emission Energy Correlates with Inverse of Gold−Gold Distance for Various [Au(SCN)₂]⁻ Salts, J. Am. Chem. Soc., 2004, 126, 12–13.
59. A. Rosenzweig and D. T. Cromer, The Crystal Structure of KAu(CN)₂, Acta Crystallogr., 1959, 12, 709–712.
60. R. J. Schubert and K.-J. Range, Tetra-n-butylammoniumdicyanoaurat(I), (n-C₄H₉)₄NAu(CN)₂/Tetra-n-butylammonium Dicyanoaurate(I), (n-C₄H₉)₄NAu(CN)₂, Z. Naturforsch., B: J. Chem. Sci., 1990, 45, 1118–1122.
61. V. W.-W. Yam, R. P.-L. Tang, K. M.-C. Wong and K.-K. Cheung, Synthesis, Luminescence, Electrochemistry, and Ion-Binding Studies of Platinum(II) Terpyridyl Acetylide Complexes, Organometallics, 2001, 20, 4476–4482.
62. W. Lu, B.-X. Mi, M. C. Chan, Z. Hui, C.-M. Che, N. Zhu and S.-T. Lee, Light-Emitting Tridentate Cyclometalated Platinum(II) Complexes Containing σ-Alkynyl Auxiliaries: Tuning of Photo- and Electrophosphorescence, J. Am. Chem. Soc., 2004, 126, 4958–4971.
63. E. C. Constable, R. P. Henney, T. A. Leese and D. A. Tocher, Cyclopalladated and cycloplatinated complexes of 6-phenyl-2,2′-bipyridine: platinum-platinum interactions in the solid state, J. Chem. Soc., Chem. Commun., 1990, 513–515.
64. Y. Chen, K. Li, W. Lu, S. S.-Y. Chui, C.-W. Ma and C.-M. Che, Photoresponsive Supramolecular Organometallic Nanosheets Induced by Pt^II⋯Pt^II and C—H⋯π Interactions, Angew. Chem., Int. Ed., 2009, 48, 9909–9913.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5qi01270h

---