Open Access Article
Open Access ArticleThe timeless relevance of size-match selectivity in macrocyclic Fe(III) complexes†
Sara
Camorali
a,
Alessandro
Nucera
ab,
Marco
Saccone
 a,
Fabio
Carniato
a,
Fabio
Carniato
 a,
Mauro
Botta
a,
Mauro
Botta
 a,
Francesco
Blasi
b,
Zsolt
Baranyai
a,
Francesco
Blasi
b,
Zsolt
Baranyai
 *c and
Lorenzo
Tei
*c and
Lorenzo
Tei
 *a
*a
aDipartimento di Scienze ed Innovazione Tecnologica, Università del Piemonte Orientale, Viale T. Michel 11, 15121 Alessandria, Italy. E-mail: lorenzo.tei@uniupo.it
bBracco Research Centre, Bracco Imaging S.p.A., Via Ribes 5, 10010 Colleretto Giacosa, Italy
cCRB Trieste, Bracco Imaging SpA, AREA Science Park, 34149 Basovizza, TS, Italy. E-mail: zsolt.baranyai@bracco.com
First published on 9th April 2025
Abstract
Given the recent emergence of Fe(III) complexes as promising MRI contrast agents, there has been significant interest in understanding their coordination chemistry, particularly the delicate balance among their thermodynamic and redox stability, kinetic inertness, and efficient relaxation enhancement. Herein, we report a comprehensive investigation into the thermodynamic and redox stability, dissociation kinetics, and 1H relaxivity of four Fe(III) complexes featuring hexadentate triaza-macrocycle triacetate ligands, with ring sizes ranging from 9 to 12. An increase in the cavity size of the macrocycles resulted in an increase in their thermodynamic and redox stability, with a maximum of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL = 33.6 for the 11-membered [Fe(UNTA)], followed by a slight decrease in the value for the 12-membered [Fe(DOTRA)]. From the dissociation kinetics of the complexes in a basic environment, it was observed that the order of inertness followed the size of the macrocycles with [Fe(DOTRA)] being the most inert complex with a t1/2 of 1 × 106 days at pH 7.4. Subsequently, the experimental results were validated through computational analysis. Employing the quantum theory of atoms in molecules and the interaction region indicator, we evaluated the shapes, volumes, and intramolecular interactions within the four Fe(III) complexes and confirmed the best size-match for the Fe(III) complex with the 11-membered macrocyclic triacetate ligand. Conversely, relaxivity exhibited the opposite trend of decreasing values with increasing ring size. This trend is attributed to the variations in electronic parameters. Notably, none of the complexes exhibited a coordinated water molecule, resulting in inherently low relaxivity.
KFeL = 33.6 for the 11-membered [Fe(UNTA)], followed by a slight decrease in the value for the 12-membered [Fe(DOTRA)]. From the dissociation kinetics of the complexes in a basic environment, it was observed that the order of inertness followed the size of the macrocycles with [Fe(DOTRA)] being the most inert complex with a t1/2 of 1 × 106 days at pH 7.4. Subsequently, the experimental results were validated through computational analysis. Employing the quantum theory of atoms in molecules and the interaction region indicator, we evaluated the shapes, volumes, and intramolecular interactions within the four Fe(III) complexes and confirmed the best size-match for the Fe(III) complex with the 11-membered macrocyclic triacetate ligand. Conversely, relaxivity exhibited the opposite trend of decreasing values with increasing ring size. This trend is attributed to the variations in electronic parameters. Notably, none of the complexes exhibited a coordinated water molecule, resulting in inherently low relaxivity.
Introduction
Functionalized macrocycles and their metal complexes have played significant and impactful roles in the biomedical field over the past 30 years. Their primary applications span diagnostic imaging techniques, such as positron emission tomography (PET) and magnetic resonance imaging (MRI), and therapeutic approaches, such as radionuclide therapy and targeted alpha therapy (TAT). Additionally, they are central to combined theranostic strategies, including TAT/single photon emission computed tomography (SPECT) and imaging-guided drug delivery. Despite their diverse applications, these metal complexes share a common objective: ensuring patient safety during and after administration. To meet the clinical standards, three key criteria must be satisfied, including high thermodynamic stability, kinetic inertness, and optimal performance.MRI is one of the most widely used diagnostic techniques owing to its non-invasive nature, absence of ionizing radiation, unlimited tissue penetration, exceptional intrinsic contrast, and outstanding temporal and spatial resolution (on the millimeter scale). Thus, it can be applied to virtually any part of the body. To enhance its analytical sensitivity and reduce the acquisition times, contrast agents (CAs) are frequently employed. A typical CA comprises a paramagnetic metal ion (e.g., Gd3+, Mn2+, or Fe3+) complexed with an organic polydentate ligand. Since 1989, research has predominantly focused on macrocyclic gadolinium(III) complexes, which are considered the most reliable for ensuring both patient safety and diagnostic accuracy.1 However, with advancements in technology, such as higher magnetic field strength scanners, there is growing interest in developing a new generation of more efficient CAs to meet the evolving demands of modern imaging. The primary parameter used to evaluate the efficiency of a CA is relaxivity, which measures the increase in the water proton relaxation rate (R1,2 = 1/T1,2) caused by a 1 mM solution of the CA. Although Gd(III) complexes generally exhibit higher relaxivity owing to their greater number of unpaired electrons, Mn(II) and Fe(III) complexes have garnered significant attention owing to their improved safety profiles and comparable efficacy to Gd-based CAs.2–4 In high-spin Fe(III) complexes, the combination of a short electron spin relaxation time and a reduced distance between the metal center and the coordinated water protons or other exchangeable protons (rGdH, rMnH, and rFeH are estimated to be ca. 3.1 Å, 2.83 Å, and 2.69 Å, respectively)4 contributes to their promising relaxivity values. Notably, at magnetic field strengths of ≤1.5 T, Gd(III) exhibits higher relaxivity than Mn(II) and Fe(III). However, at higher fields (>1.5 T), Fe(III) has the potential to match or even surpass the relaxivity of Gd(III).5 An important advantage of Fe(III) over Mn(II) is the charge-to-radius ratio of its paramagnetic ion. Iron's higher charge (3+ compared to 2+) and smaller ionic radius (0.64 Å vs. 0.80 Å) confer greater hardness and acidity, facilitating the formation of complexes with enhanced thermodynamic stability and kinetic inertness. The macrocyclic scaffolds commonly used for Gd(III) or Mn(II) complexation are typically based on the 12-membered cyclen ring (1,4,7,10-tetraazacyclododecane)6 and the pyridine-containing pyclen ring (3,6,9,15-tetraazabicyclo[9.3.1]pentadeca-1(15),11,13-triene).7,8 The macrocyclic chelators commonly used for Fe(III) complexation are typically based on the 9-membered ring of 1,4,7-triazacyclononane (TACN). Morrow and collaborators recently investigated various TACN derivatives featuring pendant arms with donor groups such as alcohol, carboxylic, phosphonic, phenolic, and carboxamide functional groups, as well as their combination (Fig. 1).9–12 These Fe(III) complexes have been extensively tested both in vitro and in vivo as MRI contrast agents, demonstrating promising results in terms of stability, relaxivity, and contrast enhancement in MRI applications. The increasing interest towards high-spin Fe(III) MRI contrast agents can also be recognized from the flourishing literature on Fe(III)-based nanosystems for T1 MRI imaging and MRI-guided theranostics.13
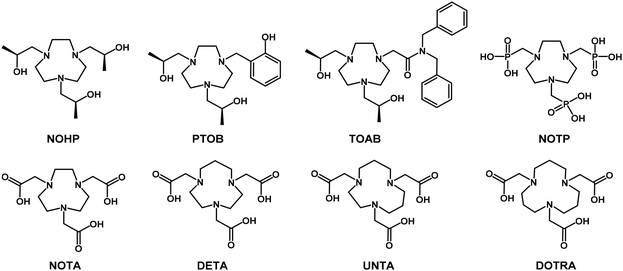 | ||
| Fig. 1 Functionalized triazamacrocyclic ligands for Fe(III) complexation discussed in the present work. | ||
It is well established that a key principle in designing selective ligands involves considering the influence of chelate ring size on metal ion size-based selectivity.14–16 According to the chelate ring size rule, replacing a 5-membered chelate ring with a 6-membered ring in a ligand increases the thermodynamic selectivity for smaller metal ions relative to larger ones. Given that the high-spin Fe3+ is a small trivalent metal ion with a hexacoordinated ionic radius of 0.645 Å, we hypothesized that substituting ethylene with propylene bridges in the triazamacrocycle framework would enhance the thermodynamic stability of the resulting Fe(III) complexes. To test this hypothesis, we investigated a series of Fe(III) complexes featuring four different triazamacrocycles functionalized with acetic acid pendant arms (Fig. 1). This study aimed to systematically evaluate the effects of increasing the macrocyclic ring size on the thermodynamic and redox stability, kinetic inertness, and relaxometric performance of the complexes.
The synthesis, acid–base properties and protonation sequence for these hexadentate ligands, i.e. 1,4,7-triazacyclononane-N,N′,N′′-triacetic acid (NOTA), 1,4,7-triazacyclodecane-N,N′,N′′-triacetic acid (DETA), 1,4,8-triazacycloundecane-N,N′,N′′-triacetic acid (UNTA) and 1,5,9-triazacyclododecane-N,N′,N′′-triacetic acid (DOTRA), were reported previously by Geraldes et al.17,18 However, to the best of our knowledge, no systematic study on the complexation properties of these ligands with transition metal ions has been reported to date. Thus, in this work, we conducted a detailed analysis of the solution thermodynamic, kinetic, and relaxometric properties of Fe(III) complexes with these four ligands. Additionally, a DFT study was performed to confirm the structures of the complexes, as well as to examine their interatomic surfaces and molecular volumes.
Results and discussion
Synthesis
The synthesis of the four ligands was achieved using the previously reported procedures with slight modifications.17,18 In particular, during the alkylation of the macrocycles with tert-butyl bromoacetate, the formation of a quaternary ammonium byproduct was observed, especially as the macrocycle size increased. As a result, the reaction time was adjusted accordingly. Additionally, it was found crucial to promptly remove any remaining tert-butyl bromoacetate from the reaction mixture to prevent further alkylation. After purification, the ligands were fully characterized by 1H and 13C NMR and ESI-MS, with the recorded spectra consistent with that reported in the literature.Protonation constants of ligands
The protonation constants of DETA, UNTA, and DOTRA were previously determined by Geraldes et al. using pH-potentiometry and 1H-NMR spectroscopy in a 0.1 M NaCl ionic background.17 To determine the stability constants of the Fe(III) complexes, the choice of ionic background (e.g., salts such as KCl, NaCl, KNO3, NaNO3) is critical. The cation (e.g., Na+) can interact with the ligand during the protonation constant measurements, while the anion (e.g., Cl−) may form weak complexes with the Fe3+ ion during the stability constant determinations. Therefore, careful selection of the ionic background is essential to ensure accurate and reliable results (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeCl = 0.81, log
KFeCl = 0.81, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeCl2 = 0.25, 2.6 M NaClO4, 25 °C).19 Thus, to ensure reliable results, the equilibrium studies were repeated in a 0.15 M NaNO3 solution. The protonation constants, defined by eqn (S1),† were determined using both pH-potentiometry and 1H-NMR spectroscopy, with the latter tracking the chemical shift variations in non-labile protons as a function of pH.
KFeCl2 = 0.25, 2.6 M NaClO4, 25 °C).19 Thus, to ensure reliable results, the equilibrium studies were repeated in a 0.15 M NaNO3 solution. The protonation constants, defined by eqn (S1),† were determined using both pH-potentiometry and 1H-NMR spectroscopy, with the latter tracking the chemical shift variations in non-labile protons as a function of pH.
The 1H-NMR titration curves (Fig. S1–S3†) exhibit distinct shifts at specific pH values, corresponding to the protonation and deprotonation events of the ligand. The observed chemical shifts (δobs) were fitted to eqn (S2),† and the obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values are listed in Table 1. The comparison of the log
KHi values are listed in Table 1. The comparison of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values of UNTA, DETA and DOTRA obtained by the pH-potentiometric and 1H NMR data in 0.15 M NaNO3 solution are in a good agreement with that measured in 0.1 M NaCl solutions.
KHi values of UNTA, DETA and DOTRA obtained by the pH-potentiometric and 1H NMR data in 0.15 M NaNO3 solution are in a good agreement with that measured in 0.1 M NaCl solutions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi) and total basicity (∑log
KHi) and total basicity (∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi) of NOTA, DETA, UNTA and DOTRA ligands (25 °C). The 3σ values are shown in parenthesis. Values with blue and red colours refer to the protonation of the amino N- and carboxylate O-donor atoms, respectively
KHi) of NOTA, DETA, UNTA and DOTRA ligands (25 °C). The 3σ values are shown in parenthesis. Values with blue and red colours refer to the protonation of the amino N- and carboxylate O-donor atoms, respectively
The basicity of the ring nitrogen atoms increased as the ring size expanded from nine to twelve members. This is attributed to the preference for forming six-membered chelate rings and the reduced electrostatic repulsion during protonation. The significantly higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1 values observed for UNTA and DETA can be explained by the potential formation of the different tautomers in their mono- and di-protonated forms, as well as the encapsulation of the H3O+ ion within the larger rings. Furthermore, previous studies have shown that the presence of Na+ ions significantly decreases the log
KH1 values observed for UNTA and DETA can be explained by the potential formation of the different tautomers in their mono- and di-protonated forms, as well as the encapsulation of the H3O+ ion within the larger rings. Furthermore, previous studies have shown that the presence of Na+ ions significantly decreases the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1 values of NOTA, DETA, UNTA, and DOTRA due to the formation of Na+ complexes.17,20,21 The ∑log
KH1 values of NOTA, DETA, UNTA, and DOTRA due to the formation of Na+ complexes.17,20,21 The ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values (Table 1) indicate that the total basicity of the NOTA, UNTA, DETA, and DOTRA ligands increased with ring size from nine to eleven members but remained nearly constant for the twelve-membered DOTRA ligand. Based on the ∑log
KHi values (Table 1) indicate that the total basicity of the NOTA, UNTA, DETA, and DOTRA ligands increased with ring size from nine to eleven members but remained nearly constant for the twelve-membered DOTRA ligand. Based on the ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values, the stability constants of the Fe(III) complexes would be expected to increase as the ring size increases from nine to eleven and twelve members. However, the stability constants are also influenced by the size match between the relatively small Fe3+ ion (65 pm) and the coordination cage formed by the triazamacrocyclic triacetate ligands, which may play a significant role in determining the overall stability of these complexes.
KHi values, the stability constants of the Fe(III) complexes would be expected to increase as the ring size increases from nine to eleven and twelve members. However, the stability constants are also influenced by the size match between the relatively small Fe3+ ion (65 pm) and the coordination cage formed by the triazamacrocyclic triacetate ligands, which may play a significant role in determining the overall stability of these complexes.
Equilibrium properties of the Fe(III) complexes
The stability and protonation constants of the Fe(III) complexes with NOTA, DETA, UNTA, and DOTRA, as defined by eqn (1) and (2), were determined using pH-potentiometry and spectrophotometry at 25 °C in 0.15 M NaNO3 solution, and the results are summarized in Table 2. | (1) |
 | (2) |
| [Fe(NOTA)] | [Fe(DETA)] | [Fe(UNTA)] | [Fe(DOTRA)] | ||
|---|---|---|---|---|---|
| I | 0.15 M NaNO3 | 0.1 M KCl | 0.15 M NaNO3 | ||
a H+–L competition reaction for Fe(III)–ion monitored using spectrophotometry ([H+] = 0.01–3.2 M, 25 °C, I = [Na+] + [H+] = 0.15 M, [H+] ≤ 0.15 M).
b ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ref. 23.
c pFe = −log[Fe3+]free, [L] = 10 μM, [Fe3+] = 1 μM, pH = 7.4.
d pH = 7.0, 0.15 M KNO3, 25 °C, Fig. S12.†
e Ref. 23.
c pFe = −log[Fe3+]free, [L] = 10 μM, [Fe3+] = 1 μM, pH = 7.4.
d pH = 7.0, 0.15 M KNO3, 25 °C, Fig. S12.†
e ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ref. 24 (0.05 M LiClO4, 20 °C). Ref. 24 (0.05 M LiClO4, 20 °C).
|
|||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL KFeL |
27.50 (6)a | 28.3b | 32.00 (6) | 33.6 (4) | 33.24 (8) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeHL KFeHL |
— | — | — | 1.87 (7) | 1.96 (5) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeLH−1 KFeLH−1 |
9.12 (4) | — | 7.64 (4) | 9.30 (4) | 10.59 (5) |
| pFec | 23.70 | — | 26.90 | 28.04 | 28.03 |
| E 1/2 vs. NHEd (V) | 0.21/0.20e | 0.28 | 0.36 | 0.41 | |
The equilibrium reaction (eqn (3)) was analyzed across a [H+] range of 0.01–3.6 M, maintaining a constant ionic strength (I = [Na+] + [H+] = 0.15 for samples where [H+] ≤ 0.15 M). The formation of Fe3+, FeHL, FeL, and HxL species (x = 4 and 5; y = 3, 4, and 5) was considered. The representative absorption spectra for the Fe3+–NOTA system are displayed in Fig. 2. In the wavelength range of 360–440 nm, the molar absorptivity of Fe3+ is significantly lower than that of the Fe(III) complexes. Therefore, the observed increase in absorbance values for the Fe3+–NOTA system at [H+] > 0.01 M can be attributed to the predominant formation of FeL species under these conditions.
| Fe3+ + HxL ⇌ [Fe(Hx−yL)] + yH+ | (3) |
The protonation constants of the Fe(III) complexes were determined using pH-potentiometric titrations conducted in the pH range of 1.7–12.0 ([FeL] = 10 mM). At pH > 6.0, the titration curves reveal a base consumption process, which can be attributed to the hydrolysis of the Fe(III) ion through coordination with an OH− ion (eqn (4) and Fig. S4–S7†). Additionally, this behavior may result from the dimerization of FeL and FeLH−1 species, forming μ-oxo dimers (eqn (S4) and (S5)†), respectively, a phenomenon previously observed in Fe(III) complexes with EDTA and its derivatives.5
| FeLH−1 + H+ ⇌ FeL | (4) |
According to the method proposed by Gustafson and Martell,22 the protonation and dimerization constants of the FeL and FeLH−1 species were determined through pH-potentiometric titrations of the Fe(III)-triaza macrocyclic complexes conducted in the pH range of 4.0–12 ([FeL] = 0.01 M, 0.15 M NaNO3, 25 °C). Analysis of the pH-potentiometric data ([FeL]tot, [NaOH]tot, pH, pA and pKw, Fig. S8–S11†) indicates that under our experimental conditions, dimerization of the FeL and FeLH−1 species does not occur.
The stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL) of the Fe(III) complexes (Table 2) increased with an increase in the ring size from nine to eleven but slightly decreased for the twelve-membered DOTRA ligand. The equilibrium constants associated with the formation of FeLH−1 species decreased from [Fe(NOTA)] to [Fe(DETA)], and then increased from [Fe(DETA)] to [Fe(DOTRA)]. As expected from the ∑log
KFeL) of the Fe(III) complexes (Table 2) increased with an increase in the ring size from nine to eleven but slightly decreased for the twelve-membered DOTRA ligand. The equilibrium constants associated with the formation of FeLH−1 species decreased from [Fe(NOTA)] to [Fe(DETA)], and then increased from [Fe(DETA)] to [Fe(DOTRA)]. As expected from the ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values of the ligands, the conditional stability (pFe) of the Fe(III) complexes increased from [Fe(NOTA)] to [Fe(UNTA)] and [Fe(DOTRA)]. To assess the impact of size matching between the small Fe3+ ion and the coordination cages of NOTA, DETA, UNTA, and DOTRA on the stability constants of the Fe(III) complexes, the log
KHi values of the ligands, the conditional stability (pFe) of the Fe(III) complexes increased from [Fe(NOTA)] to [Fe(UNTA)] and [Fe(DOTRA)]. To assess the impact of size matching between the small Fe3+ ion and the coordination cages of NOTA, DETA, UNTA, and DOTRA on the stability constants of the Fe(III) complexes, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL values were plotted as a function of ∑log
KFeL values were plotted as a function of ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi value (Fig. 3). The log
KHi value (Fig. 3). The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL values increased monotonically (slope: 1.64) with an increase in the ∑log
KFeL values increased monotonically (slope: 1.64) with an increase in the ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values. However, the stability constant of [Fe(UNTA)] is approximately one log
KHi values. However, the stability constant of [Fe(UNTA)] is approximately one log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K unit higher than expected. This deviation can be attributed to the superior size match between the Fe3+ ion and the coordination cage of UNTA. These observations suggest that the coordination cages of NOTA and DETA are too small, while the inner cavity of DOTRA is too large for the optimal accommodation of the Fe3+ ion.
K unit higher than expected. This deviation can be attributed to the superior size match between the Fe3+ ion and the coordination cage of UNTA. These observations suggest that the coordination cages of NOTA and DETA are too small, while the inner cavity of DOTRA is too large for the optimal accommodation of the Fe3+ ion.
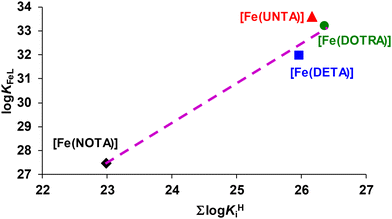 | ||
Fig. 3 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL values of the Fe-triazamacrocyclic complexes as a function of the ∑log KFeL values of the Fe-triazamacrocyclic complexes as a function of the ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi values of NOTA, DETA, UNTA and DOTRA. KHi values of NOTA, DETA, UNTA and DOTRA. | ||
Alternatively, the unusual variations in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeLH−1 values (Table 2) cannot be explained solely by the stability constants of the Fe(III) complexes; structural features must also be considered. Based on the X-ray structures of the [Cr(NOTA)] and [Fe(NOTA)] complexes, the central Cr(III) and Fe(III) ions are six-coordinated by three nitrogen and three oxygen atoms from the hexadentate NOTA ligand. These coordination geometries exhibit a distorted octahedral environment for Cr(III) and a distorted prismatic environment for Fe(III), which may influence their respective stability and behavior.24 The degree of distortion from a regular octahedral arrangement of the N3O3 donor atoms can be quantified by the twist angle between the planes formed by the nitrogen and oxygen donor atoms. A twist angle of 0° corresponds to a prismatic geometry, while 30° represents an octahedral geometry. The twist angles for the [Cr(NOTA)] and [Fe(NOTA)] complexes are 24.5° and 12.6°, respectively, indicating a stronger tendency toward an octahedral environment for Cr(III) and a prismatic environment for Fe(III).24 In the Fe(III) complexes formed with NOTA, DETA, UNTA, and DOTRA ligands, the formation of FeLH−1 species occurs through the substitution of a carboxylate group with an OH− ion as it was found for Fe(III) and Ga(III) complexes with triazacyclononane-triphosphinate (TRAP) chelators.25 Given the significant differences in the inner cavity sizes of the triaza-macrocyclic triacetate ligands, it can be inferred that the coordination environment of the Fe(III) ion transitions from a distorted prismatic geometry in [Fe(NOTA)] to a distorted octahedral geometry in [Fe(DOTRA)]. In the [Fe(DETA)] complex, one of the carboxylate groups is weakly coordinated and can be substituted by an OH− ion, facilitated by the octahedral coordination environment of the Fe(III) ion. In [Fe(UNTA)], the improved size match between the Fe3+ ion and the coordination cage of UNTA reduces the likelihood of forming the FeLH−1 species. Conversely, in [Fe(DOTRA)], the significantly larger ring size of the DOTRA ligand creates notable electrostatic repulsion between the negatively charged carboxylate groups and the incoming OH− ion, which can hinder its coordination to the Fe(III) ion. Additionally, the electrostatic repulsion between the negatively charged carboxylate groups and the OH− ion in the FeLH−1 species may further prevent the dimerization of FeL and FeLH−1 species via the formation of a μ-oxo bridge.
KFeLH−1 values (Table 2) cannot be explained solely by the stability constants of the Fe(III) complexes; structural features must also be considered. Based on the X-ray structures of the [Cr(NOTA)] and [Fe(NOTA)] complexes, the central Cr(III) and Fe(III) ions are six-coordinated by three nitrogen and three oxygen atoms from the hexadentate NOTA ligand. These coordination geometries exhibit a distorted octahedral environment for Cr(III) and a distorted prismatic environment for Fe(III), which may influence their respective stability and behavior.24 The degree of distortion from a regular octahedral arrangement of the N3O3 donor atoms can be quantified by the twist angle between the planes formed by the nitrogen and oxygen donor atoms. A twist angle of 0° corresponds to a prismatic geometry, while 30° represents an octahedral geometry. The twist angles for the [Cr(NOTA)] and [Fe(NOTA)] complexes are 24.5° and 12.6°, respectively, indicating a stronger tendency toward an octahedral environment for Cr(III) and a prismatic environment for Fe(III).24 In the Fe(III) complexes formed with NOTA, DETA, UNTA, and DOTRA ligands, the formation of FeLH−1 species occurs through the substitution of a carboxylate group with an OH− ion as it was found for Fe(III) and Ga(III) complexes with triazacyclononane-triphosphinate (TRAP) chelators.25 Given the significant differences in the inner cavity sizes of the triaza-macrocyclic triacetate ligands, it can be inferred that the coordination environment of the Fe(III) ion transitions from a distorted prismatic geometry in [Fe(NOTA)] to a distorted octahedral geometry in [Fe(DOTRA)]. In the [Fe(DETA)] complex, one of the carboxylate groups is weakly coordinated and can be substituted by an OH− ion, facilitated by the octahedral coordination environment of the Fe(III) ion. In [Fe(UNTA)], the improved size match between the Fe3+ ion and the coordination cage of UNTA reduces the likelihood of forming the FeLH−1 species. Conversely, in [Fe(DOTRA)], the significantly larger ring size of the DOTRA ligand creates notable electrostatic repulsion between the negatively charged carboxylate groups and the incoming OH− ion, which can hinder its coordination to the Fe(III) ion. Additionally, the electrostatic repulsion between the negatively charged carboxylate groups and the OH− ion in the FeLH−1 species may further prevent the dimerization of FeL and FeLH−1 species via the formation of a μ-oxo bridge.
Kinetic inertness of the Fe(III)-complexes
The kinetic inertness of the [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)], and [Fe(DOTRA)] complexes was assessed by monitoring their transchelation reactions with the HBED ligand (eqn (5)). These reactions were followed spectrophotometrically by tracking the absorption band of the resulting [Fe(HBED)]− species in the pH range of 7.5–12.5 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFe(HBED) = 39.68, 0.1 M KNO3, 25 °C).26 The HBED ligand was used in 10- and 20-fold excess to ensure pseudo-first-order kinetic conditions ([FeL] = 0.2 mM, 0.15 M NaNO3, 25 °C).
KFe(HBED) = 39.68, 0.1 M KNO3, 25 °C).26 The HBED ligand was used in 10- and 20-fold excess to ensure pseudo-first-order kinetic conditions ([FeL] = 0.2 mM, 0.15 M NaNO3, 25 °C).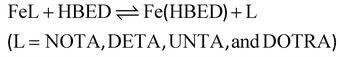 | (5) |
The kinetic data presented in Fig. S13† demonstrate that the kd values are independent of [HBED] and increase with [OH−] (and pH), indicating that the rate-determining step of the transchelation reactions is the dissociation of the Fe(III) complexes. This is followed by a rapid reaction between the free Fe3+ ion and the HBED ligand. Considering the species distribution in the Fe3+–NOTA, Fe3+–DETA, Fe3+–UNTA, and Fe3+–DOTRA systems, the dependence of the kd values on [OH−] can be attributed to the spontaneous dissociation (k0, eqn (S8)†) and OH−-ion assisted dissociation (kOH, eqn (S9) and kOH2, eqn (S10)†) of the FeLH−1 species, which dominate in the investigated pH range. The proposed mechanism for the transchelation of the [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)] and [Fe(DOTRA)] complexes is illustrated in Scheme 1. The rate and the protonation constants characterizing the transchelation reactions of these Fe(III) complexes are summarized in Table 3. Additionally, the calculated half-lives (t1/2) for the dissociation of the Fe(III) complexes at physiological pH (pH = 7.4) are provided.
 | ||
| Scheme 1 Proposed reaction pathways for the transmetalation reactions of [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)] and [Fe(DOTRA)] complexes with HBED (L = NOTA, DETA, UNTA and DOTRA). | ||
| Fe(NOTA) | Fe(DETA) | Fe(UNTA) | Fe(DOTRA) | |
|---|---|---|---|---|
| a t 1/2 values of [Fe(EDTA)]− and [Fe(CDTA)]− are 66 and 8.9 × 104 hours at pH = 7.4 and 25 °C.5 b Parameter fixed during the fitting. | ||||
| k 0 (s−1) | 0b | (5 ± 1) × 10−8 | (2.3 ± 0.5) × 10−8 | — |
| k OH (s−1 M−1) | (4.7 ± 0.5) × 10−3 | (2.5 ± 0.7) × 10−4 | (3.2 ± 0.3) × 10−4 | (2 ± 2) × 10−5 |
| k OH 2 (s−1 M−2) | 0.5 ± 0.2 | (8 ± 2) × 10−4 | (1.7 ± 0.7) × 10−4 | (4.0 ± 0.8) × 10−5 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH KH |
12.20 (3) | — | — | — |
| t 1/2 (hours) at pH = 7.4 | 4.8 × 104 | 1.9 × 106 | 1.4 × 106 | 2.4 × 107 |
The comparison of the rate constants in Table 3 reveals that the rates of both the spontaneous and OH−-assisted dissociation of Fe(III) complexes decrease with an increase in the macrocycle ring size. The significantly slower OH−-assisted dissociation of [Fe(DOTRA)] can likely be attributed to the electrostatic repulsion between the attacking OH− ion and the densely packed carboxylate groups surrounding the Fe(III) ion. Interestingly, the dissociation rate constant (kd) of [Fe(NOTA)] under near-physiological conditions (pH = 7.4, 25 °C) is approximately two times smaller than that of the Fe(III) complex formed with the open-chain CDTA ligand ([Fe(CDTA)]−), suggesting that the latter complex exhibits greater kinetic inertness. The comparison of the half-lives (t1/2 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/kd) presented in Table 3 indicates that the kinetic inertness of [Fe(DETA)] and [Fe(UNTA)] is about 40 times higher than that of [Fe(NOTA)], but approximately 12 times lower than that of [Fe(DOTRA)].
2/kd) presented in Table 3 indicates that the kinetic inertness of [Fe(DETA)] and [Fe(UNTA)] is about 40 times higher than that of [Fe(NOTA)], but approximately 12 times lower than that of [Fe(DOTRA)].
Redox stability of the Fe(III)-complexes
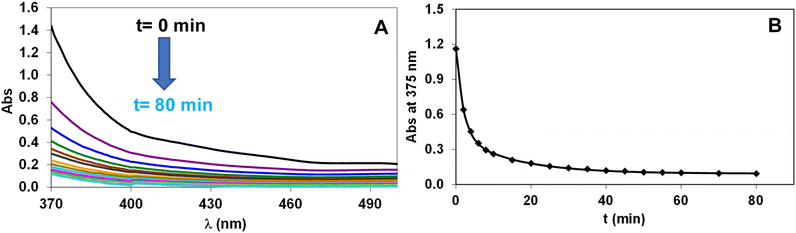
The redox stability of the Fe(III) complexes was investigated by spectrophotometry following the ascorbic acid-mediated reduction to Fe(II) (eqn (6)). Some characteristic absorption spectra of the [Fe(NOTA)]–ascorbic acid reacting system are shown in Fig. 4.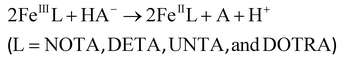 | (6) |
In the presence of excess ascorbic acid, the reduction of the Fe(III)-complexes can be treated as a pseudo-first-order process and the pseudo-first-order rate constant (kobs) characterizing the reduction of the Fe(III)-complexes can be calculated using eqn (11) (see Experimental section), where kd = kobs. The kobs for the ascorbic acid-mediated reduction of [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)] and [Fe(DOTRA)] were found to be (4.4 ± 0.4) × 10−3, (5.8 ± 0.7) × 10−3, (1.0 ± 0.1) × 10−3 and (1.5 ± 0.2) × 10−3 s−1, respectively.
Based on the protonation constants of ascorbic acid (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1 = 11.34, log
KH1 = 11.34, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH2 = 4.04, 0.1 M KNO3 25 °C),27 the dominant species under our experimental conditions is monohydrogen ascorbate HA− (pH = 7.4, 25 °C, 0.15 M NaNO3). The electron-transfer between the ascorbate anion (HA−) and the FeIIIL complexes may proceed via two potential mechanisms, i.e., an inner-sphere pathway, involving the formation of a ternary FeIIIL–HA intermediate through substitution of the inner-sphere water molecule, or an outer-sphere mechanism, driven by weak interactions between the ascorbate anion and the FeIIIL complexes.5,27,28 FeIIIL may also be rapidly reduced by the radical formed in the first oxidation step of ascorbic acid. In fact, the presence of free radicals in the oxidation of ascorbic acid was confirmed by EPR measurements.29–31
KH2 = 4.04, 0.1 M KNO3 25 °C),27 the dominant species under our experimental conditions is monohydrogen ascorbate HA− (pH = 7.4, 25 °C, 0.15 M NaNO3). The electron-transfer between the ascorbate anion (HA−) and the FeIIIL complexes may proceed via two potential mechanisms, i.e., an inner-sphere pathway, involving the formation of a ternary FeIIIL–HA intermediate through substitution of the inner-sphere water molecule, or an outer-sphere mechanism, driven by weak interactions between the ascorbate anion and the FeIIIL complexes.5,27,28 FeIIIL may also be rapidly reduced by the radical formed in the first oxidation step of ascorbic acid. In fact, the presence of free radicals in the oxidation of ascorbic acid was confirmed by EPR measurements.29–31
Our previous studies demonstrated that the reduction of [Fe(EDTA)]− and [Fe(CDTA)]− by monohydrogen ascorbate (HA−) occurs through a rapid inner-sphere mechanism involving the formation of an FeIIIL–HA intermediate ([Fe(EDTA)]−: kobs = 0.058 s−1, [Fe(CDTA)]−: kobs = 0.029 s−1, [ascorbic acid] = 0.02 M, pH = 7.40, [HEPES] = 0.01 M, 0.15 M NaNO3, 25 °C).5 However, the reduction rate (kobs) of [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)] and [Fe(DOTRA)] is about 10–58 times lower than that of [Fe(EDTA)]− and [Fe(CDTA)]−, which can be explained by the predominance of the outer-sphere electron transfer process.28 This process is significantly slower because of the lack of an exchangeable inner-sphere water molecule.
In contrast, the reduction rates of [Fe(NOTA)] and [Fe(DETA)] are approximately 4–5 times higher than that of [Fe(UNTA)] and [Fe(DOTRA)]. Equilibrium studies of the Fe(III) complexes suggest that one of the carboxylate groups in [Fe(NOTA)] and [Fe(DETA)] is weakly coordinated and can be replaced by an OH− ion. The slightly faster reduction of [Fe(NOTA)] and [Fe(DETA)] can be attributed to the partial contribution of an inner-sphere mechanism, facilitated by the substitution of a carboxylate group with the monohydrogen ascorbate (HA−) anion, leading to the transient formation of the FeIIIL–HA intermediate.
Among the Fe(III) complexes formed with triaza macrocyclic ligands, [Fe(UNTA)] exhibited the slowest reduction mediated by ascorbic acid.27,32 Based on this relationship, it can be inferred that the difference in stability constants between the Fe(III) and Fe(II) complexes with UNTA is greater than that observed with DOTRA. Specifically, the 11-membered UNTA macrocycle demonstrated higher selectivity for Fe(III) over Fe(II) ions compared to the 12-membered DOTRA, which is likely due to the better size match between the Fe(III) ion and the coordination cage of UNTA.
Alternatively, the cyclic voltammetry measurements reveal an increase in the E1/2 values of [Fe(NOTA)], [Fe(DETA)], [Fe(UNTA)] and [Fe(DOTRA)] from 0.21 to 0.41 V (Fig. S12† and Table 2).
Theoretical analysis
To obtain a deeper understanding of the chemical structure of the iron(III) complexes, we evaluated their shape, volume and the intramolecular interactions they experience through quantum theory of atoms in molecules (QTAIM)33 and interaction region indicator (IRI).34 Full details about the methodology are given in the ESI† and the DFT-optimized structures of the complexes are given below (Fig. 5). Regarding the solid-state structures, only that of [Fe(NOTA)] is known,24 and our DFT-computed structure closely resembles the X-ray crystal structure determined. Examining the coordination environment around the iron atom, we observed distinct differences in the orientation of the donor atom planes. In the highly symmetric [Fe(NOTA)] and [Fe(DOTRA)] complexes, the planes formed by the three oxygen donor atoms and the three nitrogen donor atoms are nearly parallel, with dihedral angles of 1.50° and 0.05°, respectively. In contrast, these planes are not parallel in [Fe(DETA)] and [Fe(UNTA)], with larger dihedral angles of 4.12° and 9.01°, respectively. Furthermore, the distance between the planes, defined as the separation between the centroids of the two iron-coordinated rings of oxygen and nitrogen atoms, decreased from [Fe(NOTA)] (2.303 Å) to [Fe(DOTRA)] (2.091 Å). This reduction clearly indicates a shrinkage in the cavity surrounding the iron atom (see below).The geometric descriptors discussed above were further elucidated through QTAIM analysis, which provides access to quantitative data, particularly via the calculation of interatomic surfaces (IAS). The key QTAIM properties summarized in Table 4 offer a detailed view of the molecular volumes of the four triazamacrocyclic triacetate ligands. These volumes follow the order of NOTA < DETA < UNTA < DOTRA, exhibiting a linear increase as the number of CH2 groups in the ligands increases (Fig. S14†). The IAS of the iron atom also shows the same behavior, with a QTAIM-derived atomic volume that is minimum for [Fe(NOTA)] and maximum for [Fe(DOTRA)] (Fig. S15†). However, the volume of the cavity including the iron atom follows the trend of [Fe(DOTRA)] < [Fe(UNTA)] < [Fe(DETA)] < [Fe(NOTA)], which is justified by the geometrical considerations given above.
| Fe(NOTA) | Fe(DETA) | Fe(UNTA) | Fe(DOTRA) | |
|---|---|---|---|---|
| V tot (Å)3 | 2323.991 | 2455.407 | 2588.795 | 2730.448 |
| V Fe (Å)3 | 54.984 | 56.901 | 57.011 | 58.330 |
| V [Fe+3O+3N] (Å)3 | 530.977 | 524.632 | 522.742 | 519.872 |
| Charge(Fe) | 1.413 | 1.413 | 1.419 | 1.420 |
| ρ (O–Fe BCPs) | 0.1 | 0.09–0.1 | 0.09–0.1 | 0.1 |
| ∇2ρ (O–Fe BCPs) | 0.47 | 0.48–0.55 | 0.54–0.57 | 0.57 |
| ρ (N–Fe BCPs) | 0.09 | 0.07–0.09 | 0.07–0.08 | 0.07 |
| ∇2ρ (N–Fe BCPs) | 0.35 | 0.34–0.36 | 0.32–0.34 | 0.29 |
The iron–carboxylate and iron–nitrogen bonding was also studied by QTAIM. The values of ρ at the O–Fe and N–Fe BCPs (in the range of 0.09–0.1 and 0.07–0.09, respectively) and the values of ∇2ρ (in the range 0.47–0.57 and 0.29–0.35) imply closed-shell interactions with partial ionicity.35 Interestingly, in the [Fe(DETA)] complex, one of the O–Fe bonds features a particularly low value of ρ at the BCP (0.088), which indicates a weaker coordination. This confirms the lower log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeLH−1 and the decoordination of one carboxylate donor substituted by a hydroxide anion at pH > 8.
KFeLH−1 and the decoordination of one carboxylate donor substituted by a hydroxide anion at pH > 8.
To fully characterize the covalent and non-covalent interactions in the complexes, we performed the interaction region indicator (IRI) analysis on our complexes. IRI is defined as follows:
 | (7) |
The IRI analysis, which reveals both covalent bonds and non-covalent interactions, can be used to better understand the coordination environment of the metal center. According to our analysis, two important consideration can be envisaged, as follows: (1) the interior of the larger triaza macrocycle in [Fe(DOTRA)] is sterically less crowded, with weak attractive forces present within the internal cavity. In contrast, the smallest triaza macrocycle in [Fe(NOTA)] exhibits some steric repulsions, as indicated by the tan regions. (2) The larger red isosurfaces near the iron–carboxylate bonds in the [Fe(DOTRA)] complex highlight stronger destabilizing forces, indicating that the Fe(III)-containing cage is more sterically crowded in [Fe(DOTRA)] compared to [Fe(NOTA)], despite the larger size of the macrocycle. A detailed analysis of the IRI isosurfaces of our complexes reveals that regions dominated by repulsive interactions are most pronounced in the [Fe(NOTA)] complex, followed by the [Fe(DETA)] complex (Fig. 6 and Fig. S16†). In contrast, the other complexes exhibit fewer and relatively similar repulsive regions. This observation aligns well with the thermodynamic measurements, supporting the superior stability of the [Fe(UNTA)] and [Fe(DOTRA)] complexes compared to the others.
Relaxometric analysis
The effectiveness of a T1-weighted MRI probe is determined by its proton longitudinal relaxivity (r1). This value, typically measured across various magnetic field strengths, is often compared to that of clinically approved contrast agents based on Gd(III) chelates. The parameter r1 is primarily influenced by two contributions, i.e., the inner sphere (IS) and outer sphere (OS) interactions (r1 = rIS1 + rOS1). When the inner sphere contribution is active, it predominantly affects the overall relaxivity value. However, for the Fe(III) chelates studied in this work, the low relaxivity values observed at high magnetic fields suggest the absence of inner sphere water (q = 0), indicating that the relaxivity is primarily driven by the outer sphere contribution (Table 5). As shown in Table 5, the r1 values at 1.5 and 3.0 T for [Fe(NOTA)] are comparable to that of the non-hydrated [Fe(DTPA)]2−. Furthermore, a gradual decrease in r1 was observed when transitioning from [Fe(NOTA)] to [Fe(DOTRA)], which is likely due to the changes in electronic parameters arising from the structural differences between the two complexes.| [Fe(NOTA)] pH = 7.5 | [Fe(DETA)] pH = 4.3 | [Fe(UNTA)] pH = 7.0 | [Fe(DOTRA)] pH = 7.0 | [Fe(DTPA)]2− pH = 7.0 | |
|---|---|---|---|---|---|
| r 1 1.5 T | 0.79 | 0.67 | 0.56 | 0.42 | 0.71 |
| r 1 3.0 T | 0.81 | 0.71 | 0.59 | 0.44 | 0.72 |
Changes in the relaxometric characteristics of these chelates were also evident when monitoring the pH dependence of r1. This analysis can be useful for evaluating the speciation in solution and the potential occurrence of hydrolysis processes or structural changes in the complexes. In Fig. 7, the variation in r1 as a function of pH for the Fe(III) complexes is presented alongside the species distribution diagram, allowing us to assess whether the r1 variation correlates with changes in the species. In the case of [Fe(NOTA)], the r1 value measured at 298 K and 1.5 T remained relatively constant across the pH range investigated, thereby excluding demetallation processes. The relaxivity value of [Fe(UNTA)] is constant over a wide pH range from 2 to 9. An increase in r1 value was observed at pH > 9, which is likely due to the structural change resulting from the substitution of one carboxylate donor with a hydroxide ion. In the case of [Fe(DOTRA)], below pH 4, there is a gradual increase in relaxivity, which is probably due to the protonation of a carboxylate donor, enhancing acid-catalysed proton exchange. Distinct behaviour was noted for [Fe(DETA)], where the relaxivity remained constant in the pH range of 3.0–5.5, after which a progressive decrease in r1 occurred around neutral and basic pH. This decrease continued until the values approached zero at pH > 9.5. This behaviour may be attributed to the structural change linked to the decoordination of a carboxylate group and its replacement by a hydroxide anion, which alters the electronic parameters of the complex, thus limiting the r1 value at both low and high magnetic fields (Fig. S17†).
 | ||
| Fig. 7 Species distribution curves and pH dependence of r1 of [Fe(NOTA)] (A), [Fe(DETA)] (B), [Fe(UNTA)] (C) and [Fe(DOTRA)] (D) at 1.5 T and 298 K. | ||
To investigate the factors influencing the relaxometric properties of the various chelates in detail, the 1H relaxivity values were measured across a range of applied magnetic fields from 0.01 to 500 MHz (nuclear magnetic relaxation dispersion, NMRD, profiles), at different temperatures. The 1H NMRD curves shown in Fig. 8 (and in Fig. S18–S21†) were analysed by considering the outer sphere contribution to relaxivity (rOS1), which is defined by the water molecules diffusing in close proximity to the Fe(III) chelate.36 As outlined in the Freed model, which is commonly used for the mathematical analysis of 1H NMRD profiles of non-hydrated paramagnetic chelates, rOS1 depends on the distance between the outer sphere water molecules and the metal complex (a), the relative diffusion coefficient of solute and water (D), and the electronic relaxation time (Tie) (eqn (8)).
 | (8) |
 | ||
Fig. 8
1H NMRD profiles at 298 K of [Fe(NOTA)] ( ) (pH = 7.5), [Fe(DETA)] ( ) (pH = 7.5), [Fe(DETA)] ( ) (pH = 4.3), [Fe(UNTA)] ( ) (pH = 4.3), [Fe(UNTA)] ( ) (pH = 7.0) and [Fe(DOTRA)] (◊) (pH = 7.0). ) (pH = 7.0) and [Fe(DOTRA)] (◊) (pH = 7.0). | ||
The electron relaxation times are governed by the parameters of mean square transient ZFS energy (Δ2) and its correlation time τV (eqn (9) and (10)).
 | (9) |
 | (10) |
The analysis of the 1H NMRD profiles at different temperatures (Fig. S18–S21†) was performed by allowing the Δ2 parameter to exhibit temperature dependence. This dependence was modelled using an Arrhenius relationship, with the corresponding activation energy denoted as EΔ. For all the complexes, the observed decrease in relaxivity with an increase in temperature at all the applied magnetic fields can be attributed to the decrease in the diffusion coefficient (D).
The data analysis was performed by setting certain parameters to standard values. Specifically, the diffusion coefficient (D), the closest approach distance (a) of the proton nuclei of outer-sphere water molecules to the Fe(III) ion, and the energy associated with the τV parameter were fixed at 2.3 × 10−5 cm2 s−1, 3.6 Å, and 1.0 kJ mol−1, respectively. Excellent agreement between the experimental r1 profiles and the theoretical model was achieved using the parameters listed in Table 6. The mean square transient zero-field splitting energy (Δ2) exhibited an exponential increase from [Fe(NOTA)] to [Fe(DOTRA)], which is likely attributed to the variations in the ligand cavity size and geometry. Concomitantly, the τV parameter decreased from 3.5 ps to 0.4 ps, reflecting a reduction in the effective volume experienced by the metal ion within the different chelates.
Based on these results and in agreement with the literature,5,37 the relaxivity values of the Fe(III) chelates, in particular at high magnetic fields, are influenced by the electronic relaxation parameters (Δ2 and τV). The data presented here suggest that lower r1 values correspond to higher Δ2 values.
Experimental
Materials and methods
Reagents and solvents were purchased from Sigma-Aldrich-Merck and used without further purification. For thin-layer chromatography and column chromatography, Merck Silica gel 60 F254 silica (0.063–0.200 mm; 70–230 mesh ASTM) was used. UV light (254 nm) or alkaline potassium permanganate were used for stain visualization in TLC. For HPLC purification and mass spectra, a coupled HPLC-MS system equipped with a Waters 1525 binary HPLC pump system using XBridge Phenyl 3.5 μm (4.6 × 150 mm) analytical columns and for purification a Waters XBridge Prep Phenyl OBD 5 μm (19 × 100 mm) column were used. A Waters 3100 Mass Detector with ESI+ source and quadrupole was used as the mass analyser. The 1H and 13C NMR spectra were recorded using a Bruker Avance III 500 MHz spectrometer equipped with a 5 mm PABBO probe and BVT-3000 temperature control unit, using tetramethylsilane (TMS) as a reference for chemical shifts (δ [ppm]). Multiplicities were reported as singlet (s), broad singlet (bs), doublet (d), double doublet (dd), triplet (t), quartet (q) or multiplet (m). The samples were prepared in 5 mm NMR tubes by dissolving the compounds in appropriate deuterated solvents.Fe(NO3)3 was prepared by dissolving Fe2O3 (99.9%, Fluka) in 6 M HNO3 and evaporating the excess acid. The solid Fe(NO3)3 was dissolved in 0.1 M HNO3 solution. The concentration of the Fe(NO3)3 solution was determined by using the standardized Na2H2EDTA in excess. The excess Na2H2EDTA was measured with standardized ZnCl2 solution and xylenol orange as the indicator. The H+ concentration of the Fe(NO3)3 solution was determined by pH potentiometric titration in the presence of excess Na2H2EDTA. The concentration of the H3NOTA, H3DETA, H3UNTA, H3DOTRA and H2HBED solutions was determined by pH-potentiometric titrations in the presence and absence of a 40-fold excess of Ca2+. The pH-potentiometric titrations were made with standardized 0.2 M NaOH.
The synthesis of 1,4,7-triazacyclodecane (TACD) and 1,4,8-triazacycloundecane (TACUD) macrocycles was performed following a modified Richman-Atkins procedure.38 1,5,9-Triazacyclododecane and NOTA were purchased from CheMatech (France). The synthesis of DETA, UNTA and DOTRA was accomplished by modification of the published procedures.17,18
DETA: (Waters Atlantis Prep 5 μm (19 × 100 mm)) ((A): H2O + 0.1% TFA, (B): MeOH, flow = 17 mL min−1, from 0 to 2 min: 50% B, from 2 to 15 min from 50% B to 93%, from 15 to 16 min from 93% to 100% B, from 16 to 19 min 100% B, from 19 to 20 min from 100% to 50% B).
UNTA: (Waters Atlantis Prep 5 μm (19 × 100 mm)) ((A): H2O + 0.1% TFA, (B): MeOH, flow = 17 mL min−1, from 0 to 2 min: 50% B, from 2 to 10 min from 50% B to 72%, from 10 to 10.5 min from 72% to 100% B, from 10.5 to 12.5 min 100% B, from 12.5 to 13 min from 100% to 50% B).
DOTRA: (Waters Atlantis Prep 5 μm (19 × 100 mm)) ((A): H2O + 0.1% TFA, (B): MeOH, flow = 17 mL min−1, from 0 to 2 min: 50% B, from 2 to 13 min from 50% B to 67%, from 13 to 15 min from 67% to 100% B, from 15 to 18 min 100% B, from 18 to 19 min from 100% to 50% B).
Synthesis of the Fe(III) chelates
An equimolar amount of the ligands (NOTA, DETA, UNTA and DOTRA) was added to a 47.3 mM Fe(NO3)3 stock solution in HNO3. The pH of the aqueous solution was corrected to 3.5 with diluted NaOH (0.1 M) and the complexation reaction was carried out under stirring at 70 °C overnight. At the end of the reaction, the solution was neutralized with diluted NaOH and small amounts of precipitate were removed by filtration.Relaxometric analysis
The magnetic-field dependence of the longitudinal relaxation rate of solvent protons (1H NMRD profiles) was measured in aqueous solution by using a variable field relaxometer equipped with an HTS-110 3T Metrology Cryogen-free Superconducting Magnet (Mede, Italy), operating in the overall range of proton Larmor frequencies of 20–120 MHz (0.47–3.00 T). The measurements were performed using the standard inversion recovery sequence (20 experiments, 2 scans) with a typical 90° pulse width of 3.5 μs and the reproducibility of the data was within ±0.5%. The temperature was controlled with a Stelar VTC-91 heater airflow. Additional points in the 0.01–10 MHz frequency range were collected on a Fast-Field Cycling (FFC) Stelar SmarTracer Relaxometer. T1 values at 500 MHz were collected with a Bruker NMR spectrometer operating at 11.7 T. All experiments were repeated three times with the reproducibility of the data within ±0.5%. The concentration of Fe3+ in the different solutions was determined by using bulk magnetic susceptibility (BMS) shift measurements performed at 11.7 T,39 and confirmed by ICP-MS analysis after mineralization of the samples with HNO3 65% at 408 K.Equilibrium measurements
The stability and protonation constants of the FeIII complexes formed using the NOTA, DETA, UNTA and DOTRA ligands were determined by pH-potentiometric and spectrophotometric studies. The protonation constants of the Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA) complexes were determined using pH-potentiometry by titrating the pre-prepared complexes from pH = 1.7 to pH = 12 with 0.2 M NaOH ([FeL] = 0.005 M). In the case of the pH measurements and titrations, a Metrohm 888 Titrando titration workstation Metrohm-6.0234.110 combined electrode was used. Equilibrium measurements were carried out at a constant ionic strength (0.15 M NaNO3) in 6 mL sample at 25 °C. The solutions were stirred, and N2 was bubbled through them. The titrations were performed in the pH range of 1.7–12.0. KH-phthalate (pH = 4.005) and borax (pH = 9.177) buffers were used to calibrate the pH meter. For the calculation of [H+] from the measured pH values, the method proposed by Irving et al. was used as follows.40 A 0.01 M HNO3 solution was titrated with standardized NaOH solution at 0.15 M NaNO3 ionic strength. The differences (A) between the measured (pHread) and calculated pH (−log[H+]) values were used to obtain the equilibrium H+ concentration from the pH values measured in the titration experiments (A = 0.02). For the equilibrium calculations, the stoichiometric water ionic product (pKw) was also needed to calculate the [OH−] values under basic conditions. The VNaOH–pHread data pairs of the HNO3–NaOH titration obtained in the pH range 10.5–12.0 were used to calculate the pKw value (pKw = 13.78).The stability constants of the Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA) complex were determined by spectrophotometry studies of the Fe3+–NOTA, Fe3+–DETA, Fe3+–UNTA and Fe3+–DOTRA systems at the absorption band of FeIII complexes at [H+] = 0.01–3.6 M in the wavelength range of 350–800 nm. The concentration of Fe3+, NOTA, DETA, UNTA and DOTRA was 0.002 M. The H+ concentration in the samples was adjusted with the addition of calculated amounts of 6 M HNO3 (I = [Na+] + [H+] = 0.15, [H+] ≤ 0.15 M). The samples were kept at 25 °C for a week. The absorbance values of the samples were determined at 7 wavelengths (378, 381, 390, 400, 410, 420 and 430 nm). For the calculation of the stability and protonation constants of Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA), the molar absorptivities of Fe3+, Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA) were determined by recording the spectra of 1.0 × 10−3, 1.5 × 10−3, 2.0 × 10−3 and 2.5 × 10−3 M solutions of Fe3+, Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA) solutions, respectively. The absorption spectra of the Fe(NOTA), Fe(DETA), Fe(UNTA) and Fe(DOTRA) solutions were recorded in the pH range of 1.7–7.5. All spectrophotometric measurements were performed at 25 °C in 0.15 M NaNO3 solution. The pH was adjusted by the stepwise addition of concentrated NaOH or HNO3 solution. The spectrophotometric measurements were performed using a PerkinElmer Lambda 365 UV-Vis spectrophotometer, using 1.0 cm cells. The protonation and stability constants were calculated using the PSEQUAD program.41
1H NMR measurements
1H NMR measurements were performed with a Bruker Avance III (9.4 T) spectrometer, equipped with a Bruker Variable Temperature Unit (BVT), Bruker Cooling Unit (BCU) and BB inverse z gradient probe (5 mm) at 298 K. The 1H NMR chemical shifts of the DETA, UNTA and DOTRA ligands were also determined as a function of pH to evaluate some of the protonation constants of the ligands. For these experiments, a 0.01 M solution of DETA, UNTA and DOTRA ligands in 0.15 M NaNO3 aqueous solution was prepared (a capillary with D2O was used for lock). The pH was adjusted by the stepwise addition of concentrated NaOH and HNO3 solutions (both prepared in H2O). At −log[H+] > 12, the OH− concentration in the samples was adjusted with the addition of calculated amounts of 19.3 M NaOH solution (I = [NaNO3] + [NaOH] = 0.15, [NaOH] ≤ 0.15 M). The chemical shifts are reported in ppm, relative to t-BuOH for 1H as the external standard. The protonation constants were determined by fitting the chemical shift versus pH data using Micromath Scientist, version 2.0 (Salt Lake City, UT).Kinetic studies
The kinetic inertness of the Fe(III) complexes with NOTA, DETA, UNTA and DOTRA was characterized by the rates of the transchelation reactions taking place with HBED ligand. The exchange reactions with HBED were studied by spectrophotometry, following the formation of the Fe(HBED) complexes at 480 nm with a PerkinElmer Lambda 365 UV-Vis spectrophotometer. The concentration of the FeL complex was 0.2 mM, while the concentration of HBED was 10 and 20 times higher, to guarantee pseudo-first-order conditions. The temperature was maintained at 25 °C and the ionic strength of the solutions was kept constant, 0.15 M for NaNO3. The exchange rates were studied in the pH range of about 7.4–12.5. For keeping the pH values constant, HEPES (pH range 7.4–8.5), piperazine (pH range 8.5–10.5) and Na2HPO4 (pH range 11.0–12.5) buffers (0.01 M) were used. The pseudo-first-order rate constants (kd) were calculated by fitting the absorbance data to.| At = (A0 − Ap)e−kdt + Ap | (11) |
Conclusions
In conclusion, this work presented a systematic study of Fe(III) complexes with hexadentate chelators based on trisubstituted triazamacrocycles with acetic arms, varying in cavity size from a 9-membered ring (NOTA) to 10-membered (DETA), 11-membered (UNTA) and 12-membered rings (DOTRA). The thermodynamic, kinetic and redox analyses of the four complexes revealed that increasing the cavity size enhanced the thermodynamic stability, with the maximum for [Fe(UNTA)], followed by a slight decrease for [Fe(DOTRA)]. This trend is also reflected in the redox stability of the complexes when exposed to endogenous reductants such as ascorbic acid. The kinetic inertness, assessed through transchelation reactions with the HBED ligand, showed that the more compact [Fe(DOTRA)] complex exhibited the slowest rate of spontaneous and OH−-assisted dissociation, being one order of magnitude more inert than [Fe(UNTA)] and [Fe(DETA)]. These findings were corroborated by both computational and 1H relaxometric studies. DFT analyses revealed that an increase in cavity size results in the enhanced encapsulation of the metal ion within the macrocyclic cavity, leading to a more compact complex structure. Although all the complexes exhibit q = 0, and therefore unsuitable for development as MRI contrast agents, the relaxometric studies demonstrated a variation in electronic parameters from [Fe(NOTA)] to [Fe(DOTRA)], resulting in a decrease in relaxivity. Also, although the 11-membered macrocycle offers superior stability, it is crucial to consider the impact of electronic parameters on relaxivity when selecting an optimal Fe(III)-based contrast agent.Author contributions
Conceptualization: LT, ZB, FB and MB. Supervision LT, ZB, MB. Funding acquisition: LT and MB. SC carried out the synthesis and characterization of the ligands. FC carried out the relaxometric study. AN and ZB carried out the thermodynamic, kinetic and redox experiments. FC and MB analysed the relaxometric data. MS performed the computational study. LT, ZB, MS, FC and MB wrote the manuscript. All the authors reviewed the manuscript.Data availability
The datasets supporting this article have been uploaded as part of the ESI.† Additional data can be provided upon reasonable request to the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Professor Mauro Ravera (UPO) for the cyclic voltammetry measurements. M. B. and A. N. acknowledge the project NODES, which has provided funding from the Ministero dell'Università e della Ricerca (MUR-M4C2 1.5 of PNRR with grant agreement no. ECS00000036). F. C. acknowledges financial support from PRIN 2022 PNRR (PNRR M4C2, ID P20224R8YZ). LT acknowledges the EU under the Next Generation EU program for support of the PRIN 2022 project (ID 20224B4285).References
- J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- M. Botta, F. Carniato, D. Esteban-Gómez, C. Platas-Iglesias and L. Tei, Mn(II) Compounds as an Alternative to Gd-Based MRI Probes, Future Med. Chem., 2019, 11, 1461–1483 CrossRef CAS PubMed.
- E. A. Kras, E. M. Snyder, G. E. Sokolow and J. R. Morrow, Distinct Coordination Chemistry of Fe(III)-Based MRI Probes, Acc. Chem. Res., 2022, 55, 1435–1444 CrossRef CAS PubMed.
- N. Kuźnik and M. Wyskocka, Iron(III) Contrast Agent Candidates for MRI: a Survey of the Structure-Effect Relationship in the Last 15 Years of Studing, Eur. J. Inorg. Chem., 2016, 445–458 CrossRef.
- Z. Baranyai, F. Carniato, A. Nucera, D. Horváth, L. Tei, C. Platas-Iglesias and M. Botta, Defining the conditions for the development of the emerging class of FeIII-Based MRI Contrast Agents, Chem. Sci., 2021, 12, 11138–11145 RSC.
- G. J. Stasiuk and N. J. Long, The Ubiquitous DOTA and its derivatives: The impact of 1,4,7,10-Tetraazacyclododecane-1,4,7,10-Tetraacetic acid on biomedical imaging, Chem. Commun., 2013, 49, 2732 RSC.
- C. Robic, M. Port, O. Rousseaux, S. Louguet, N. Fretellier, S. Catoen, C. Factor, S. Le Greneur, C. Medina, P. Bourrinet, I. Raynal, J.-M. Idée and C. Corot, Physicochemical and Pharmacokinetic Profiles of Gadopiclenol: A New Macrocyclic Gadolinium Chelate With High T1 Relaxivity, Invest. Radiol., 2019, 54, 475–484 CrossRef CAS PubMed.
- G. Nizou, E. Molnár, N. Hamon, F. K. Kálmán, O. Fougère, O. Rousseaux, D. Esteban-Gòmez, C. Platas-Iglesias, M. Beyler, G. Tircsó and R. Tripier, Pyclen-Based Ligands Bearing Pendant Picolinate Arms for Gadolinium Complexation, Inorg. Chem., 2021, 60, 2390–2405 CrossRef CAS PubMed.
- E. M. Snyder, D. Asik, S. M. Abozeid, A. Burgio, G. Bateman, S. G. Turowski, J. A. Spernyak and J. R. Morrow, A class of Fe III macrocyclic complexes with alcohol donor groups as effective T1 MRI Contrast Agents, Angew. Chem., 2020, 132, 2435–2440 CrossRef.
- E. A. Kras, S. M. Abozeid, W. Eduardo, J. A. Spernyak and J. R. Morrow, Comparison of phosphonate, hydroxypropyl and carboxylate pendants in Fe(III) macrocyclic complexes as MRI Contrast Agents, J. Inorg. Biochem., 2021, 225, 111594 CrossRef CAS PubMed.
- D. Asik, S. M. Abozeid, S. G. Turowski, J. A. Spernyak and J. R. Morrow, Dinuclear Fe(III) hydroxypropyl-appended macrocyclic complexes as MRI probes, Inorg. Chem., 2021, 60(12), 8651–8664 CrossRef CAS PubMed.
- E. A. Kras, R. Cineus, M. R. Crawley and J. R. Morrow, Macrocyclic complexes of Fe(iii) with mixed hydroxypropyl and phenolate or amide pendants as T 1 MRI probes, Dalton Trans., 2024, 53, 4154–4164 RSC.
- M. Botta, C. F. G. C. Geraldes and L. Tei, High spin Fe(III)-doped nanostructures as T1 MR imaging probes, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2023, 15, e1858 CAS.
- R. D. Hancock and A. E. Martell, Ligand design for selective complexation of metal ions in aqueous solution, Chem. Rev., 1989, 89, 1875–1914 CrossRef CAS.
- R. D. Hancock, Chelate ring size and metal ion selection. The basis of selectivity for metal ions in open-chain ligands and macrocycles, J. Chem. Educ., 1992, 69, 615 CrossRef CAS.
- R. D. Hancock and L. J. Bartolotti, A DFT analysis of the effect of chelate ring size on metal ion selectivity in complexes of polyamine ligands, Polyhedron, 2013, 52, 284–293 CrossRef CAS.
- C. F. G. C. Geraldes, A. D. Sherry, M. P. M. Marques, M. C. Alpoim and S. Cortes, Protonation Scheme for Some Triaza Macrocycles Studied by Potentiometry and NMR Spectroscopy, J. Chem. Soc., Perkin Trans. 2, 1991, 137 RSC.
- S. Cortes, E. Brucher, C. F. G. C. Geraldes and A. D. Sherry, Potentiometry and NMR Studies of 1,5,9-Triazacyclododecane-N,N′,N′′-Triacetic Acid and Its Metal Ion Complexes, Inorg. Chem., 1990, 29, 5–9 CrossRef CAS.
- P. Amico, R. P. Bonomo, R. Cali, V. Cucinotta, P. G. Daniele, G. Ostacoli and E. Rizzarelli, Ligand-ligand interactions in metal complexes. Thermodynamic and spectroscopic investigation of simple and mixed copper(II) and zinc(II) substituted-malonate complexes with 2,2′-bipyridyl in aqueous solution, Inorg. Chem., 1989, 28(18), 3555–3561 CrossRef CAS.
- R. Yang and L. J. Zompa, Metal Complexes of Cyclic Triamines. 1. Complexes of 1,4,7-Triazacyclononane ([9]aneN3) with Nickel(II), Copper(II), and Zinc(II), Inorg. Chem., 1976, 15, 1499–1502 CrossRef CAS.
- L. J. Zompa, Metal complexes of cyclic triamines. 2. Stability and electronic spectra of nickel(II), copper(II), and zinc(II) complexes containing nine- through twelve-membered cyclic triamine ligands, Inorg. Chem., 1978, 17, 2531–2536 CrossRef CAS.
- R. L. Gustafson and A. E. Martell, Hydrolytic Tendencies of Ferric Chelates 1, J. Phys. Chem., 1963, 67, 576–582 CrossRef CAS.
- E. T. Clarke and A. E. Martell, Stabilities of the Fe(III), Ga(III) and In(III) chelates of N,N′,N′′-triazacyclononane triacetic acid, Inorg. Chim. Acta, 1991, 181, 273–328 CrossRef CAS.
- K. Wieghardt, U. Bossek, P. Chaudhuri, W. Herrmann, B. C. Menke and J. Weiss, 1,4,7-Triazacyclononane-N,N′,N′′-triacetate (TCTA), a new hexadentate ligand for divalent and trivalent metal ions. Crystal structures of [CrIII(TCTA)], [FeIII(TCTA)], and Na[CuII(TCTA)].bul.2NaBr.bul.8H2O, Inorg. Chem., 1982, 21, 4308–4314 CrossRef CAS.
- A. Vágner, A. Forgács, E. Brücher, I. Tóth, A. Maiocchi, A. Wurzer, H.-J. Wester, J. Notni and Z. Baranyai, Equilibrium Thermodynamics, Formation, and Dissociation Kinetics of Trivalent Iron and Gallium Complexes of Triazacyclononane-Triphosphinate (TRAP) Chelators: Unraveling the Foundations of Highly Selective Ga-68 Labeling, Front. Chem., 2018, 6, 170 CrossRef PubMed.
- R. Ma, R. Motekaitis and A. Martell, Stability of metal ion complexes of N,N′-bis(2-hydroxybenzyl) ethylenediamine-N,N′-diacetic acid, Inorg. Chim. Acta, 1994, 224, 151 CrossRef CAS.
- M. Taqui-Khan and A. E. Martell, The kinetics of the reaction of iron(III) chelates of aminopolycarboxylic acids with ascorbic acid, J. Am. Chem. Soc., 1968, 90, 3386–3389 CrossRef PubMed.
- E. Pelizzetti, E. Mentasti and E. Pramauro, Outer-sphere oxidation of ascorbic acid, Inorg. Chem., 1978, 17, 1181–1186 CrossRef CAS.
- C. Lagercrantz, Free Radicals in the Auto-Oxidation of Ascorbic Acid, Acta Chem. Scand., 1964, 18, 562–562 CrossRef CAS.
- H. Dahn, L. Loewe and C. A. Bunton, Über die Oxydation von Ascorbinsäure durch salpetrige Säure Teil VI: Übersicht und Diskussion der Ergebnisse. 18. Mitteilung über Reduktone und 1,2,3-Tricarbonylverbindungen, Helv. Chim. Acta, 1960, 43, 320–333 CrossRef CAS.
- Y. Kirino, P. L. Southwick and R. H. Schuler, Electron Spin Resonance Spectra of Radicals Related to the Intermediates in the Oxidation of Ascorbic Acid. Substituted 2,3,4-Trioxopyrrolidine Radical Anions, J. Am. Chem. Soc., 1974, 96, 673–677 CrossRef CAS.
- A. E. Martel, R. J. Motekaitis, D. Chen, R. D. Hancock and D. McManus, Selection of new Fe(lll)/Fe(ll) chelating agents as catalysts for the oxidation of hydrogen sulfide to sulfur by air, Can. J. Chem., 1996, 74, 1872–1879 CrossRef.
- R. F. W. Bader, A Quantum Theory of Molecular Structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and Q. Chen, Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions, Chem. Methods, 2021, 1, 231–239 CrossRef CAS.
- P. Popelier, Atoms in Molecules: An Introduction, Pearson Education, Harlow, 2000 Search PubMed.
- J. W. Walton, R. Carr, N. H. Evans, A. M. Funk, A. M. Kenwright, D. Parker, D. S. Yufit, M. Botta, S. De Pinto and K.-L. Wong, Isostructural series of nine-coordinate chiral lanthanide complexes based on triazacyclononane, Inorg. Chem., 2012, 51, 8042–8056 CrossRef CAS PubMed.
- A. Nucera, F. Carniato, Z. Baranyai, C. Platas Iglesias and M. Botta, Characterization of the Fe(III)-Tiron System in Solution through an Integrated Approach Combining NMR Relaxometric, Thermodynamic, Kinetic, and Computational Data, Inorg. Chem., 2023, 62, 4272–4283 CrossRef CAS PubMed.
- M. Briellmann, S. Kaderli, C. J. Meyer and A. D. Zuberbühler, Synthesis and Copper(I) Complexes of a Series of 9- to 13-Membered N3 Macrocycles, Helv. Chim. Acta, 1987, 70, 680–689 CrossRef CAS.
- D. F. Evans, The determination of the paramagnetic susceptibility of substances in solution by nuclear magnetic resonance, J. Chem. Soc., 1959, 2003 RSC.
- H. M. Irving, M. G. Miles and L. Pettit, A study of some problems in determining the stoichiometric proton dissociation constants of complexes by potentiometric titrations using a glass electrode, Anal. Chim. Acta, 1967, 38, 475–488 CrossRef CAS.
- L. Zékány and I. Nagypál, in Computational Method for Determination of Formation Constants, ed. D. J. Legett, Plenum, New York, 1985 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details: thermodynamic, kinetic and redox studies. DFT optimized structures and NMRD profiles. See DOI: https://doi.org/10.1039/d5qi00431d |
| This journal is © the Partner Organisations 2025 |