Advanced association theory for monoethylene glycol: thermodynamic perturbation theory, Monte Carlo simulation, and equation of state parametrization
Received
7th December 2024
, Accepted 8th March 2025
First published on 10th March 2025
Abstract
Thermodynamic perturbation theory (TPT) is a breakthrough in developing an equation of state for systems containing hydrogen bonding. In this work, we derive the association contribution to Helmholtz's free energy for spherical particles composed of four patchy sites and verified it by performing Monte Carlo (MC) simulations. The theory suggests that the site placement significantly impacts the system's phase behavior at constant temperature and density. We apply our theory to correlate and predict the experimental phase behavior data of pure monoethylene glycol (MEG) and its binary mixtures with non-associating molecules (including methane, ethane, propane, and hydrogen) and compare the theory's performance with the case where the association contribution to the system's pressure is based on first-order TPT (TPT1). Our theory outperforms TPT1 in terms of error and predictive capabilities for the physical properties of pure MEG. In the binary mixture application, TPT1 presents a better predictive ability for the mole fraction of the non-associating molecule in the glycol-rich liquid than our theory.
1. Introduction
Monoethylene glycol (MEG) has various applications in hydrate inhibition,1–4 gas separation,5 and toluene catalytic oxidation.6 The phase behavior of MEG is crucial in designing experiments and operation conditions in these applications. MEG was studied by Grenner et al.7 in the PC SAFT framework, where the 4C association scheme (two negative and two positive sites) was considered for MEG. In addition, Kruger et al.8 considered various association schemes for MEG in the cubic plus association (CPA) EoS framework. They presented multiple idealizations for the association sites of MEG. Among these, the 4F association scheme, which includes two negative and two bipolar sites, provided the most accurate phase behavior predictions.
A thermodynamic study of fluid behavior is feasible by incorporating the necessary idealizations. In molecular studies, one of these idealizations is related to the geometrical structure of the objective molecule. Patchy particles are used to idealize the structures of hydrogen-bonding molecules in statistical thermodynamics, spanning applications from molecular simulation to the derivation of equations of state (EoS). This molecular model facilitates analytical evaluations of graphs of partition functions in various ensembles. In molecular biology,9 the globular proteins are represented by patchy spherical particles, enabling researchers to study their self-assembly. In the thermodynamic study of polymer–enzyme conjugate formation,10 the polymer chain is represented by a connected chain of patchy spherical particles, where each patch is equivalent to a specific functional group. All these mentioned idealizations facilitated the thermodynamic modeling of self-assembly.
Wertheim's thermodynamic perturbation theory (TPT)11–14 is used to study the phase behavior of patchy particles. Wertheim developed the original theory for molecules containing monovalent associating sites. There are several studies where the researchers developed TPT-based models for particles containing multivalent patchy associating sites.15–18 First-order TPT (TPT1) considers the first-order graphs in Wertheim's theory. The TPT1 formulation demonstrates limited predictive capabilities when an association in one patch interferes with an association in another. In this case, TPT1 overcounts the number of particles self-assembled into chain formations. Wertheim developed the resumed TPT1 for hard spheres with glue spot bonding and applied it to equilibrium polymerization.19 Depending on the placement of sites, particles self-assemble into ring formation. TPT considers all types of associating ring structures. In this context, Sear and Jackson20 developed an analytical formulation for the integrals corresponding to ring graphs in TPT. The original formulation of TPT does not consider the doubly-bonded dimer graphs. Sear and Jackson21 evaluated the doubly-bonded dimer graph and investigated its contribution to Helmholtz's free energy of the system studied by Wertheim in equilibrium polymerization. Furthermore, the geometrical integrals associated with resumed TPT1, rings, and doubly-bonded dimers require careful mathematical investigation for patchy sites. Marshall and Chapman22 developed TPT for a two-patch system to address this by simultaneously considering resumed TPT1, rings, and doubly-bonded dimers. They evaluated the geometrical integrals as a function of bond angle and patch size. As a result, their theory's results agreed with the Monte Carlo (MC) simulation.
TPT quantifies the contribution of highly directional attractive forces to Helmholtz's free energy. By integrating this theory and physical contributions such as ideal gas, hard-chain, hard-sphere, and dispersion, the EoS that describes the system is obtained. Moreover, the statistical associating fluid theory (SAFT) developed by Chapman23 combines physical terms with TPT1. Consequently, the derived EoS is a general formulation that is applied to all systems. However, moving from TPT1 to higher-order graphs in TPT makes the SAFT formulation case-specific. In this context, Haghmoradi et al.24 developed a new TPT formulation that can be applied to water by assuming that water is a spherical particle composed of one divalent (oxygen) and two monovalent (hydrogen) patchy sites. Similarly, Haghmoradi and Chapman25 developed TPT for hydrogen fluoride by idealizing its molecular structure as a spherical patchy particle with two monovalent patches. Their final EoS successfully predicted the phase change data. Additionally, Marshall26 considered the contribution of the doubly-bonded dimer graphs in EoS formulation for various carboxylic acids. The theory was applied to acid–alkane and acid–alcohol mixtures, and their Txy and Pxy phase diagrams were successfully predicted. In another work, Marshall27 investigated the effect of steric hindrance in associating chain formation in EoS derivation for methanol and ethanol. The new EoS outperformed TPT1 in predicting liquid density and heat of vaporization.
In this work, we develop the TPT for a patchy particle characterized by four patchy sites, taking into account the effect of ring, double-bond, and steric hindrance in chain formation. This work advances the previous research conducted by Marshall and Chapman22 on a two-patch system. To validate our theory, we perform Monte Carlo (MC) simulations in both the NVT and NPT ensembles. Additionally, we integrate our theory with the physical terms in PC SAFT and apply the EoS to predict the phase behavior of MEG.
2. Theory and simulation
2.1. Theory
Statistical thermodynamics is a powerful tool in developing equations of state. In this area, all fundamental equations are based on the probability of finding particles at specific conditions (location, orientation, and momentum). This probabilistic evaluation of states is done in various ensembles, including canonical, Gibbs, and grand canonical ensembles. The normalizer of the probability function is called the partition function. In the grand canonical ensemble, the grand partition function represents the sum of all possible microstates in a system with fixed volume, temperature, chemical potential, and external potential. This sum is represented by graphical cluster expansion, where the points carry a fugacity factor in each graph and are connected via bonds. This cluster expansion is called fugacity expansion. The grand partition function is expressed with density expansion using an appropriate topological reduction, where each point carries a density factor. Wertheim used this density expansion to develop the thermodynamic perturbation theory (TPT) for fluids with highly directional attractive forces. In this theory, the residual Helmholtz's free energy due to attractive forces is expressed as follows:| |  | (1) |
| | 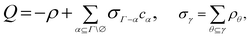 | (2) |
| |  | (3) |
where A, AR, ρ, ρ0, V, kB, and T, are the Helmholtz free energy, Helmholtz free energy at reference conditions, number density, monomer density, volume, Boltzmann constant, and temperature, respectively. The term Δc(0)/V is the associating graph contribution to the fundamental graph sum that encodes all the highly directional attractive interactions. In eqn (2), ρθ is the density of molecules bonded at the site set θ. The central part of developing the theory is the evaluation of Δc(0)/V. The molecular model studied in this work is a spherical four-patch particle (Fig. 1). Patch size is represented by βc, and the angle between the centers of two adjacent patches, A and B, is shown by αAB. In this molecular model, the patches are distributed around the equator. The square-well potential is used to define the interaction between two patches on particles 1 and 2 (φSP(12)), as described by Bol:28| |  | (4) |
which has proven highly effective in describing interactions between patchy particles. Wertheim first used the notation (1) in eqn (4), which represents the location and orientation of a particle. r12 denotes the distance between the centers of particles (1) and (2). β(1)S defines the angle between the center of the patch S and the line connecting the centers of particles (1) and (2). The constraints rc and βc are set such that it ensures the patches are monovalent. According to Kalyuzhnyi et al.,16βc = 27° and rc = 1.1d (d is the particle diameter) secure a monovalent patch. In deriving the theory, the non-identical patches interact via a similar potential, i.e., εSP = ε for S ≠ P, and association is not allowed for identical patches (εSS = 0).
 |
| | Fig. 1 Schematics of patchy particles. (a) Patch size. (b) The angle between adjacent sites. | |
The next step is to evaluate the integrals in the term Δc(0)/V. This work considers the first-order (TPT1), chain, double-bond (DB), and ring graphs:
| |  | (5) |
All possible dimers for the proposed patchy particle are considered to evaluate the term Δ
cTPT1/
V. According to the Wertheim's theory
| |  | (6) |
where
fSP(12) is the Mayer
f-function for the square-well potential (= exp(
φSP(12)/
kBT) − 1) and
gHS(12) signifies the two-body correlation function for the hard sphere reference fluid. To evaluate this integral, a precise approximation for
gHS(12) is needed. The following relation proposed by Chapman
23 is assumed to be true in the bonding range:
| |  | (7) |
where
| | | p = 17.87η2 + 2.47η, η = πρd3/6. | (8) |
Substituting
eqn (4), (7) and (8) into the
eqn (6) and evaluating the integral yield:
| | 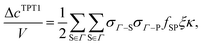 | (9) |
| |  | (10) |
| |  | (11) |
We evaluate the chain contribution in five steps. The angles
αBC and
αAD are kept above 90°; therefore, there is no steric hindrance blocking the chain of particles connected at site sets BC and AD. The five chain classes include chains of AB, CD, AB–CD, AB–CD–AB, and CD–AB–CD (the corresponding graphs are presented in
Fig. 2):
| | | Δcchain = ΔcchainAB + ΔcchainCD + ΔcchainAB–CD + ΔcchainAB–CD–AB + ΔcchainCD–AB–CD. | (12) |
 |
| | Fig. 2 Graphs of various chains contributing to Δcchain. (a) ΔcchainAB, (b) ΔcchainCD, (c) ΔcchainAB–CD, (d) ΔcchainAB–CD–AB, and (e) ΔcchainCD–AB–CD. | |
The corresponding integral of the first term in TPT is given by
| |  | (13) |
| | | XSPn = σΓ−S(1)σΓ−AB(2)⋯σΓ−AB(n + 1)σΓ−P(n + 2), | (14) |
| | | YSPn = fSA(12)fAB(23)⋯fAB(n, n + 1)fBP(n + 2). | (15) |
In
eqn (12), the term
GHS(1⋯
n) represents the
n-body correlation function. An analytical form of this term facilitates the evaluation of the integral in
eqn (13). Kalyuzhnyi
et al.16 proposed the following relation for the
n-body correlation function:
| |  | (16) |
where
fHS(
rij) is the Mayer
f-function for the hard-sphere potential function. Taking into account the resummation properties of the graph in
eqn (12) yields
| | 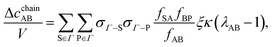 | (17) |
where
| |  | (18) |
and
ΨAB is the ratio of the number of states where three colloids are associated with no core overlap between the non-bonded particles and the number of states if there was no steric hindrance and patches A and B were independent. Marshall and Chapman
22 evaluated this probability function, and we use their results in
eqn (18). If the probability equates to one,
i.e.,
αAB is more than 90°, Δ
cchainAB/
V vanishes.
The same approach is applied in evaluating ΔcchainCD:
| |  | (19) |
where
| |  | (20) |
The following contribution is Δ
cchainAB–CD. The graphical form of its repeating pattern is presented in
Fig. 2c. By taking advantage of the assumption
fAC =
fAD =
fBC =
fBD, and performing the calculation similar to
eqn (13)–(16), the following equations are obtained:
| |  | (21) |
| |  | (22) |
| |  | (23) |
| |  | (24) |
By taking advantage of the resummation properties of the summation of
eqn (21), it is expressed in the following form:
| |  | (25) |
The remaining chain contributions (Δ
cchainAB–CD–AB and Δ
cchainCD–AB–CD) are evaluated similarly:
| |  | (26) |
| |  | (27) |
| |  | (28) |
| | 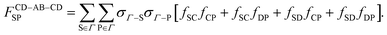 | (29) |
For the particular case of A = C (
i.e.,
fAC = 0) and B = D (
i.e.,
fBD = 0), the combined chain equations presented in
eqn (25)–(29) are converted into the following form:
| | 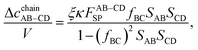 | (30) |
| | 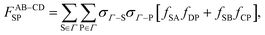 | (31) |
| | 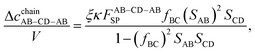 | (32) |
| |  | (33) |
| | 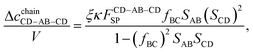 | (34) |
| |  | (35) |
A cycle or ring is the self-assembly structure contributing to the association graph. Marshal and Chapman's method
22 is deployed to evaluate the ring integral. The ring integral value (
Θ(n)) depends on the patch size, the angle between patches, and the number of particles in the ring formation. In this formulation, the number of particles varies between 3 and 10. The details of ring formation are available in the literature.
22 We consider rings of the same patch pairs. Therefore, four types of rings are considered:
| | 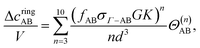 | (36) |
| |  | (37) |
| | 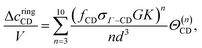 | (38) |
| |  | (39) |
where
K is the bond volume (= 4π
d2(
rc −
d)
κ), and
G = 2
pgHS(
d)/(
rc/
d + 1)
p.
The last contribution to the association graph considered is due to the double bond between two particles. According to eqn (4), when two patches overlap, two particles associate via two bonds. We consider the overlap between patch sets {A, B} and {C, D}. Three types of double bonds possibly exist (Fig. 3). The corresponding integral in the association graph is expressed as
| | | Δcdouble-bond = Δcdouble-bondAB + Δcdouble-bondCD + Δcdouble-bondAB–CD, | (40) |
| |  | (41) |
| |  | (42) |
| |  | (43) |
 |
| | Fig. 3 Different types of doubly-bonded dimers. (a) Dimers double-bonded at {A, B}, (b) dimers double-bonded at {C, D}, and (c) double-bonded at {A, B} and {C, D}. | |
We use Marshall and Chapman's method22 to evaluate the integral (eqn (40)–(43)). A double bond occurs if the two particles are oriented such that the line connecting the center of the two particles crosses the overlapped areas. The integrals are evaluated in terms of these probability functions:
| | 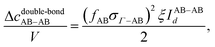 | (44) |
| |  | (45) |
| |  | (46) |
where the term
Id represents the probability of double bond formation. Marshall and Chapman
22 evaluated this probability as a function of the ratio between the overlap's area and a sphere's area. Since two particles are involved in this interaction, each probability is defined as the product of these ratios:
| |  | (47) |
| |  | (48) |
| |  | (49) |
where
Φ represents the surface area of patch overlap. The details of its mathematical formulation are presented in the literature.
22
In Wertheim's theory, the term σΓ−α represents the density of particles not bonded at the site set α. According to this definition, the fraction of particles not bonded at a site set α (Xα) is defined as
| |  | (50) |
In the multi-density formalism of TPT, densities are defined in
eqn (45), which
P(
α) = {
γ} is the partitioning of site set
α into non-zero sets.
| |  | (51) |
By setting
α =
Γ and combining
eqn (50) and (51), the monomer fraction (
X0) is calculated using the following relation:
| |  | (52) |
The coefficients behind each term consider the symmetry (
e.g.,
cαcβ =
cβcα). The fraction of particles bonded
n-times (
Xn) is obtained using
eqn (50)–(52):
| |  | (53) |
| |  | (54) |
| |  | (55) |
| | 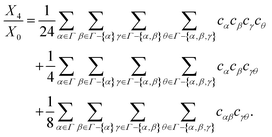 | (56) |
The contribution of association interaction to the internal energy of the system (
Eassoc/
NkBT) is calculated using the classical thermodynamic relations:
| |  | (57) |
The next step is to derive the pressure of the system. From classical thermodynamics, we know that the pressure of the system is related to the chemical potential (
μ) and Helmholtz's free energies of the system:
| |  | (58) |
The following relation gives the association's contribution to the chemical potential of a pure system:
| |  | (59) |
2.2. Simulation
In this work, the results of the proposed theory are compared with the Monte Carlo (MC) simulation in the NVT and NPT ensembles. The sampling is based on the Metropolis method.29 Each simulation contains 256 particles. The acceptance ratio in MC simulations is 0.4. The NVT simulation performs 3 × 106 cycles. A cycle includes 256 random trial moves, where relocation and reorientation of a random particle are performed in each move. For each NVT simulation, the system is equilibrated for 106 cycles, and then the interested properties are averaged over 2 × 106 cycles. The NPT simulation runs for 12 × 106 cycles. The volume change is tried after each cycle. In this simulation, the system is equilibrated for 10 × 106 cycles, and the averaging is performed for the rest of the cycles.
3. Results and discussion
3.1. Theory and simulation
This part presents the comparison between theory and simulation for two general cases. In the first case (Case 1), all non-identical patches interact with each other at a constant potential (εSP = ε for S ≠ P), and there is no interaction between identical patches (εSS = 0). In the second case (Case 2), εAB = εAD = εBC = εCD = ε ≠ 0, and the other interactions equal zero. In all cases, αBC = αAD. The schematic of Case 1 and Case 2 is presented in Fig. 4. The identical patches in Case 2 are represented by the same color.
 |
| | Fig. 4 Schematics of Case 1 and Case 2 in the theory and simulation study. In both cases, identical patches do not associate (εSS = 0). In Case 1, all patches are non-identical, and in Case 2, A is identical to C, and B is identical to D. | |
Table 1 lists the summary of the subcases where the theory is compared with NVT simulation. The motivation of this comparison is to investigate the effect of temperature on fractions of particles bonded n-times and internal energy of the system at constant patch placement and packing fraction. In the comparison of the theory with NPT Monte Carlo simulation, the motivation is to study the variation of pressure with packing fraction at constant temperature and patch placement (Table 2).
Table 1 List of Case 1 and Case 2 subcases in theory and NVT simulations comparison study. In all subcases, αBC = αAD
| Patchy particle model |
α
AB
|
α
CD
|
η
|
| Case 1 |
45° |
35° |
0.1, 0.3 |
| 45° |
40° |
0.1, 0.3 |
| 45° |
45° |
0.1, 0.3 |
| 30° |
30° |
0.1 |
|
|
| Case 2 |
30° |
30° |
0.1 |
| 35° |
35° |
0.2 |
| 40° |
40° |
0.1, 0.2 |
| 45° |
45° |
0.2 |
| 50° |
50° |
0.1, 0.2 |
Table 2 List of Case 1 and Case 2 subcases in theory and NPT simulations comparison study. In all subcases, αBC = αAD
| Patchy particle model |
α
AB
|
α
CD
|
ε/kBT |
| Case 1 |
45° |
45° |
3.0, 3.5, 4.0 |
| 60° |
35° |
3.0, 3.5, 4.0 |
|
|
| Case 2 |
50° |
50° |
3.0, 4.5 |
Case 1: in the first subcase, αAB = 45° and η = 0.1. The ring integral in eqn (30) is non-zero, most of which is contributed by the term n = 3. Rings of BC (eqn (31)) and AD (eqn (33)) rarely form because the angles αBC and αAD are higher than 120°, making Θ(n)BC and Θ(n)AD negligible. Fig. 5 shows the results of NVT simulation and theory for Xn values as a function of αCD and ε/kBT. The Ring contribution associated with eqn (32) (ΔcringCD/V) is similar to eqn (30) at αCD = 45°, and it becomes less significant at αCD = 40° and αCD = 35°. All double-bond contributions presented in eqn (38)–(40) are non-zero and significantly affect the variation of bonded fractions with temperature. By increasing ε/kBT, monomer (Fig. 5a) and fully self-assembled (Fig. 5e) fractions monotonically decrease and increase, respectively. The other bonded fractions (X1, X2, and X3 in Fig. 5b–d) present a maximum to ε/kBT. The variation of the fractions with the bond angle αCD is pronounced on each subplot. When the bond angle αCD decreases from 45° to 35°, the chain integrals in eqn (19), (25), (26) and (28), which prevent self-assembly, become more significant, but the double-bond integrals in eqn (39) and (40) increase by decreasing αCD, promoting the self-assembly. The theory and simulation results show that lowering the bond angle αCD promotes the fraction of fully bonded particles (Fig. 5e). This analysis is repeated at η = 0.3, and the same trend is observed (Fig. 6). The variation of X3 as a function of αCD (Fig. 5d and 6d) differs in the studied temperature range. In Fig. 5d, from high temperature to ε/kBT = 5.8 (theory's prediction), X3 increases by lowering αCD, and the trend is reversed at lower temperatures. In Fig. 6d, the theory predicts this reversed behavior at ε/kBT = 5.6. The Monte Carlo simulation verifies theory in terms of this trend for X3. The theory and Monte Carlo simulation predict similar behavior for X2 (Fig. 5c and 6c).
 |
| | Fig. 5 Subcase of Case 1. αAB = 45° and η = 0.1. (a) Monomer fraction, (b) fraction of particles bonded once, (c) fraction of particles bonded twice, (d) fraction of particles bonded three times, and (e) fraction of particles bonded four times. Lines and points represent the results of theory and simulation, respectively. | |
 |
| | Fig. 6 Subcase of Case 1. αAB = 45° and η = 0.3. (a) Monomer fraction, (b) fraction of particles bonded once, (c) fraction of particles bonded twice, (d) fraction of particles bonded three times, and (e) fraction of particles bonded four times. Lines and points represent the results of theory and simulation, respectively. | |
The theory and simulation results for the internal energy of the two studied subcases are presented in Fig. 7. The trend is captured by Monte Carlo simulation. The results are compared with TPT1. At lower temperatures, TPT1 significantly deviates from the current theory.
 |
| | Fig. 7 Theory and simulation results for the internal energy (E* = Eassoc/NkBT) of the subcases presented in Fig. 4 and 5. (a) η = 0.1 and (b) η = 0.3. | |
To highlight the deviation level of TPT1, our theory and TPT1 prediction of the fraction of particles in monomer, chain (Xchain), double bond (Xdb), and chain–double bond (Xchain–db) states are compared with Monte Carlo simulation for η = 0.1 and αAB = αCD = 30°. The selected bond angles are such that all ring integrals are negligible. Therefore, a bonded particle is either in chain (Xchain), double bond (Xdb), or a combination of chain and double bond (Xchain–db) state. The analytical equations for these fractions are presented in Appendix A. The results are presented in Fig. 8. In TPT1, a particle is either in monomer or chain (dashed green line) state. In this subcase, the chain developments of this work (eqn (17)–(35)) significantly modify various chain formations. TPT1 ignores steric hindrance and double bond formation. As a result, the TPT1-predicted chain fraction deviates from the chain fraction obtained by Monte Carlo simulation (green squares).
 |
| | Fig. 8 Subcase of Case 1. αAB = αCD = 30° and η = 0.1. Theory and Monte Carlo simulation results for fraction of particles in monomer (X0), chain (Xchain), and double bond and chain (![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) db = Xdb + Xchain–db) states. db = Xdb + Xchain–db) states. | |
The NPT Monte Carlo simulation is performed for two subcases in Case 1. Fig. 9 represents the theory and simulation results of the dimensionless pressure (P* = Pd3/kBT) at various temperature and packing fraction ranges. In the first subcase (Fig. 9a), αAB = αCD = 45°. All double-bond contributions studied in this work are active, while in Fig. 9b (αAB = 60° and αCD = 35°), only one double-bond contribution (eqn (39)) is non-zero. The theory underpredicts the NPT Monte Carlo simulation data at higher packing fractions.
 |
| | Fig. 9 Theory and simulation results for the pressure of subcases in Case 1. (a) αAB = 45°, αCD = 45°, and (b) αAB = 60°, αCD = 45°. | |
Case 2: in this case, there is no association between the patches in the subsets {A, C} and {B, D}, i.e., fAC = fBD = 0. The theory and NVT simulation results for the Xn values are investigated for two constant packing fractions. In the first subcase, η is set to 0.1. The results are presented in Fig. 10. In this subcase, αAB = αCD = α, and αBC = αAD = 180° − α. The results are presented for three different α values (30°, 40°, and 50°). The results of the theory (solid lines) and simulation (points) are compared with TPT1 (dashed lines). The theory and simulation are compared at an elevated packing fraction of η = 0.2 in the next subcase (Fig. 11). The definition of α is similar to the previous subcase. This subcase presents results for four different α values (35°, 40°, 45°, and 50°).
 |
| | Fig. 10 Subcase of Case 2. αAB = αCD = α η = 0.1. (a) Monomer fraction, (b) fraction of particles bonded once, (c) fraction of particles bonded twice, (d) fraction of particles bonded three times, and (e) fraction of particles bonded four times. Lines and points represent the results of theory and simulation, respectively. | |
 |
| | Fig. 11 Subcase of Case 2. αAB = αCD = α η = 0.2. (a) Monomer fraction, (b) fraction of particles bonded once, (c) fraction of particles bonded twice, (d) fraction of particles bonded three times, and (e) fraction of particles bonded four times. Lines and points represent the results of theory and simulation, respectively. | |
The internal energy of the two subcases (theory and simulation) are presented in Fig. 12 and compared with TPT1. By decreasing α, the doubly-bonded association structures are promoted, and the system's internal energy decreases. Current theory and NVT simulation verify this trend. Two sets of NPT simulations are performed for this case. The results are presented in Fig. 13.
 |
| | Fig. 12 Theory and simulation results for the internal energy of the subcases presented in Fig. 12 and 13. (a) η = 0.1, and (b) η = 0.2. | |
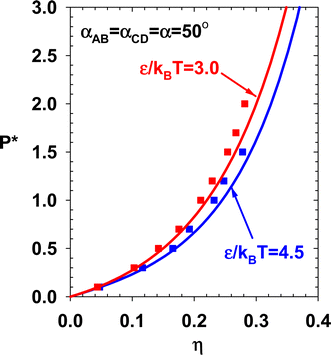 |
| | Fig. 13 Theory and simulation results for the pressure of subcases in Case 2. | |
3.2. Monoethylene glycol's phase behavior calculation
3.2.1 Pure monoethylene glycol.
In the previous section, our proposed theory was evaluated against Monte Carlo simulation results. Building on this, we now aim to apply the theory to correlate and predict the phase behavior of MEG. MEG is assumed as a sphere with four patchy sites {A, B, C, D}, where A = C and B = D. The patch subsets {A, C} and {B, D} are equivalent to hydrogen and oxygen sites, respectively. This idealization of the molecular structure of MEG is illustrated in Fig. 14.
 |
| | Fig. 14 Idealization of the molecular structure of monoethylene glycol (MEG) as a patchy particle with four patchy associating sites. | |
Various contributions to Helmholtz's free energy (A/NkBT) of the system are considered in obtaining the equation of state. These contributions include ideal gas (AIG/NkBT), hard-sphere (AHS/NkBT), hard-chain (AChain/NkBT), dispersion (ADisp/NkBT), and association (AAssoc/NkBT), as described by
| |  | (60) |
The hard-sphere, hard-chain, and dispersion terms are selected from the PC-SAFT model developed by Gross and Sadowski.
30 Our proposed association theory and TPT1 is used in the last term. The contribution due to hard-chain formation is automatically zero because we consider one spherical segment in our molecular structure idealization.
The EoS parametrization is performed for our theory and the case where the TPT1 is used in development of AAssoc/NkBT. In the parametrization of our theory, the fitting parameters are the diameter of the molecule (d), dispersion energy (εDisp/k), association energy (εAssoc/k), and the bond angle α. The parameter m represents the number of spherical segments. In parametrizing the model where TPT1 is used in AAssoc/NkBT, d, εDisp/k, and εAssoc/k are adjusted because the TPT1 formulation is not a function of α. The experimental saturation pressure and saturated liquid density data are used in the EoS parametrization. The adjusting parameters and absolute average relative deviation (AARD) for our theory and TPT1 are listed in Table 3. The experimental data31 used in the EoS parameterization are at the reduced temperature (Tr = T/TC) of 0.40 ≤ Tr ≤ 0.92. Fig. 15a shows the saturation pressure, and Fig. 15b represents the saturated liquid density results for our theory (blue solid lines), TPT1 (black dashed lines), and experimental data (red points). Our theory performs more efficiently in predicting the phase change data regarding AARD and trends.
Table 3 List of the adjusting parameters and AARDs for our theory and PC SAFT
| Parameter |
Our theory |
PC SAFT |
|
M
|
1 |
1 |
|
d (Å) |
4.4405 |
4.5285 |
|
ε/kB (K) |
499.6781 |
414.9272 |
|
ε
Assoc/kB (K) |
2195.0390 |
2535.4177 |
|
α (°) |
37.7861 |
— |
| AARD (saturation pressure) |
0.0356 |
0.0513 |
| AARD (saturated liquid density) |
0.0111 |
0.0170 |
 |
| | Fig. 15 (a) Saturation pressure and (b) saturated liquid density of MEG. Line and point represent our theory and experimental data.31 | |
The fractions of molecules self-assembled in six different configurations in the saturated liquid are presented in Fig. 16 as a function of temperature for our theory. The first three fractions include molecules in chains (Xchain), double-bonds (Xdb), and ring (Xring) structures (Fig. 16a). Fig. 16b represents the fraction of molecules in the chain and double bond (Xchain–db), chain and ring (Xchain–db). In PC SAFT, the chain is the only self-assembly formation (dashed black line in Fig. 16a). The final formula for these fractions is presented in Appendix A. Another analysis is the fraction of molecules bonded n-times (eqn (52)–(56)). This analysis is presented in Fig. 17 for our theory and PC SAFT. The analysis in Fig. 16 and 17 can be compared with future spectroscopy data of MEG.
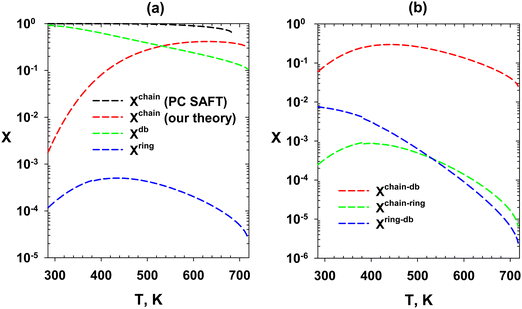 |
| | Fig. 16 Fractions of different self-assembly configurations in the saturated liquid of MEG. (a) Fractions of the molecules self-assembled into the chain, double bond, and ring formations. (b) Fractions of molecules self-assembled into chain-double bond, chain-ring, and ring-double bond formations. | |
 |
| | Fig. 17 Fractions of molecules bonded n-times in the saturated liquid of MEG. (a) Monomer fraction, (b) fraction of particles bonded once, (c) fraction of particles bonded twice, (d) fraction of particles bonded three times, and (e) fraction of particles bonded four times. Blue and red lines represent our theory and PC SAFT. | |
The predictive performance of our theory and PC SAFT is evaluated on two data sets. The enthalpy of vaporization is presented in Fig. 18a. The computational thermodynamics scheme used in calculating the enthalpy (H) of each phase is as follows:
| |  | (61) |
 |
| | Fig. 18 (a) Molar vaporization enthalpy of MEG and (b) compressed liquid density of MEG at various reduced pressure and temperature ranges. Solid lines, dashed lines, and points represent our theory, PC SAFT, and experimental data.31,32 | |
Fig. 18b shows our theory and PC SAFT's compressed liquid density data32 prediction in wide pressure and temperature ranges. In Fig. 18b, our theory (solid lines) outperforms PC SAFT (dashed lines) at pressures of 0.098, 49.030, 98.060, and 147.100 MPa, especially at lower temperatures. However, at the other pressures (196.130 and 245.60 MPa), our model shows some deviations, leading to an overprediction relative to the experimental data.
In this work, three different types of extension of TPT1 are studied in a single model. The sole effect of each extension is investigated in EoS parametrization. Table 4 lists the adjusting parameters where TPT1 + chain, TPT1 + double bond, and TPT1 + ring consider the association contribution of EoS. The prediction of these three models' vapor pressure and saturated liquid density is presented in Fig. 19 and compared with our theory and PC SAFT.
Table 4 List of the adjusting parameters and AARDs for TPT1 + chain, TPT1 + double bond, and TPT1 + ring
| Parameter |
TPT1 + chain |
TPT1 + double bond |
TPT1 + ring |
|
M
|
1 |
1 |
1 |
|
d (Å) |
4.5029 |
4.4374 |
4.5282 |
|
ε/kB (K) |
442.5478 |
407.0383 |
415.1417 |
|
ε
Assoc/kB (K) |
2482.0340 |
2444.5518 |
2534.8661 |
|
α (°) |
77.3542 |
36.8342 |
78.7862 |
| AARD (saturation pressure) |
0.0399 |
0.0491 |
0.0510 |
| AARD (saturated liquid density) |
0.0154 |
0.0238 |
0.0172 |
 |
| | Fig. 19 (a) Saturation pressure and (b) saturated liquid density of MEG. Blue, red, green, gray, and dashed black lines represent association theories based on our theory, TPT1 + double bond, TPT1 + ring, TPT1 + chain, and PC SAFT. Point represents experimental data.31 | |
3.2.2 Binary mixtures of MEG and light gases.
This part applies the theory to MEG and non-associating gas mixtures. The light gases include methane (CH4), ethane (C2H6), propane (C3H8), and hydrogen (H2). Due to the availability of experimental vapor–liquid (VL) and liquid–liquid (LL) equilibria data for methane, ethane, and propane, the data points are divided into two sets. The first data set is used to adjust the model's unknown parameters. Then, the model's capability to predict the second data set is investigated. The adjusting parameter is the binary interaction parameter (BIP) between MEG and gas, denoted by kij. This parameter modifies the physical cross-interaction between MEG and gas in the dispersion term in eqn (60). The association contribution to Helmholtz's free energy is zero for pure light gases. As a result, the theory is converted to PC SAFT for pure light gases. Table 5 lists the PC SAFT parameters for the gases.
Table 5 PC SAFT parameters of the studied light gases
| Component |
m
|
d (Å) |
ε/kB (K) |
Ref. |
| CH4 |
1.0000 |
3.7039 |
150.0300 |
Gross and Sadowski30 |
| C2H6 |
1.6069 |
3.5206 |
191.4200 |
Gross and Sadowski30 |
| C3H8 |
2.0020 |
3.6184 |
208.1100 |
Gross and Sadowski30 |
| H2 |
0.6800 |
3.5400 |
31.5700 |
Alanazi et al.33 |
The model's parametrization considers a linear temperature-dependent BIP, i.e., kij = C1 + C2T. The AARD of mole fraction of gas in the glycol-rich phase in the VLE data is the objective function in adjusting C1 and C2. The final adjusted forms of BIP and AARD are presented in Table 6 for the association model based on PC SAFT and our theory. In all cases, the BIP decreases with temperature.
Table 6 The AARD and adjusted BIP relations between MEG and different light gases
| Gas |
k
ij
|
AARD (%) |
| PC SAFT |
Our theory |
PC SAFT |
Our theory |
| CH4 |
0.1877–2.7350 × 10−4T |
0.4115–9.4758 × 10−4T |
1.85 |
2.33 |
| C2H6 |
0.0931–2.2373 × 10−4T |
0.2397–5.9309 × 10−4T |
2.18 |
2.77 |
| C3H8 |
0.0509–2.1393 × 10−4T |
0.1637–4.5614 × 10−4T |
2.18 |
3.31 |
| H2 |
0.9793–1.6383 × 10−3T |
1.6036–4.0885 × 10−3T |
1.03 |
1.38 |
The EoS parametrization and predictive capability results are presented in Fig. 20–23. Points, dashed, and solid lines represent the experimental data, PC SAFT, and our theory. In Fig. 20a, the adjusted models for the MEG/methane system are plotted at various temperatures and pressures. Then, the predictive capability of the two models is investigated (Fig. 20b) at three temperatures and elevated pressures. At 323.15 K, our theory and PC SAFT similarly predict the experimental data. At 373.15 K, our theory outperforms PC SAFT in predicting the methane solubility in MEG. Finally, at 398.15 K, PC SAFT presents better prediction performance at elevated pressures. The next studied system is the MEG/ethane mixture. The results are presented in Fig. 21. The experimental ethane mole fractions in the glycol-rich phase in VLE of MEG/ethane experiments are used to adjust the two models (Fig. 21a). The predictive performance of the adjusted models is investigated at 298.15 and 323.15 K and elevated pressures (Fig. 21b). The experimental data points include VLE and LLE. The two models underpredict and overpredict the data at 298.15 and 323.15 K, respectively. The PC SAFT-based model presents a better predictive capability than the model based on our theory. The phase behavior study of the MEG/propane system is performed in the temperature range of 298.15 to 398.15 K. The results are presented in Fig. 22. The models are parametrized versus the experimental VLE data (mole fraction of propane in glycol-rich phase). The results are presented in Fig. 22a. The predictive capability of the two models is studied at the same temperatures and elevated pressures where pure propane is in the liquid state (Fig. 22b); therefore, the system is in LLE. Both models similarly predict the LLE data. In the experimental data of MEG/ethane and MEG/propane systems, provided the temperature is less than the gas's critical temperature, the VLE is converted to LLE by pressurizing the system at a constant temperature. During this transition, the dependency of the mole fraction of ethane and propane in glycol-rich liquid on pressure significantly decreases. This physics is captured by the two models in the predictive capability analysis. The last studied binary mixture is the MEG/hydrogen system (Fig. 23). The available data include the solubilities presented in Fig. 23. These data are used in theory parametrization. PC SAFT and our theory present similar phase behavior for this system.
 |
| | Fig. 20 Methane mole fraction in the glycol-rich phase in VLE of the MEG/methane system. (a) Adjusted models and experimental data,34 and (b) predictive capability of models and experimental data.35 The solid and dashed lines represent our theory and PC SAFT, respectively. | |
 |
| | Fig. 21 Ethane mole fraction in the glycol-rich phase in VLE and LLE of the MEG/ethane system. (a) Adjusted models and experimental data,36 and (b) predictive capability of models and experimental data.36 The solid and dashed lines represent our theory and PC SAFT, respectively. | |
 |
| | Fig. 22 Propane mole fraction in the glycol-rich phase in VLE and LLE of MEG/propane system. (a) Adjusted models and experimental VLE data,37 and (b) Predictive capability of models and experimental LLE data.37 The solid and dashed lines represent our theory and PC SAFT, respectively. | |
 |
| | Fig. 23 Hydrogen mole fraction in the glycol-rich phase in VLE of MEG/hydrogen system (adjusted models and experimental data38). The solid and dashed lines represent our theory and PC SAFT, respectively. | |
4. Summary and conclusion
In this work, we developed an association theory for particles with four patchy sites based on Wertheim's thermodynamic perturbation theory (TPT). The theory advances Wertheim's first-order TPT (TPT1) by considering all steric hindrances preventing chain formations, ring, and doubly-bonded association structures in Helmholtz's free energy calculation. The results are compared with the Monte Carlo (MC) simulation in the NVT and NPT ensembles. The contribution of our theory to Helmholtz free energy is integrated with the hard-sphere and dispersion terms of the perturbed-chain statistical associating fluid theory (PC-SAFT) to predict the phase behavior of MEG. One of the fitting parameters (bond angle between two adjacent oxygen and hydrogen sites) of our theory quantifies the placement of patchy sites in the idealized molecular structure of MEG. The adjusted bond angle shows that associating rings of three molecules and doubly-bonded structures are present, and all types of steric hindrance terms correcting associating chain formations are active. The predictive performance of the derived theory and PC SAFT-based theory is investigated to predict the MEG's vaporization enthalpy and compressed liquid density. The two theories show close predictive capability for vaporization enthalpy. Our theory outperformed PC SAFT in predicting the compressed liquid density. The derived theory and PC SAFT are applied to the mixture of binary MEG and non-associating molecules. The two theories similarly predict the phase behavior data (mole fraction of non-associating molecules in the glycol-rich phase). If the density of the glycol-rich liquid in equilibrium is of interest, our theory is a better choice.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Conflicts of interest
There are no conflicts to declare.
Appendices
Appendix A
Fractions of MEG molecules in different association configurations: in this part, the derivations are based on eqn (52)–(56) by considering the active terms. The decomposition of cAB and cCD is as follows:| |  | (A1) |
| |  | (A2) |
Xchain is given by| | | Xchain = Xchain1 + Xchain2 + Xchain3 + Xchain4 | (A3) |
| | | Xchain2 = X0(cAcB + cAcC + cAcD + cBcC + cBcD + cCcD + cchainAB + cchainCD) | (A5) |
| | | Xchain3 = X0[cAcBcC + cAcBcD + cAcCcD + cBcCcD + cchainAB(cC + cD) + cchainCD(cA + cB)] | (A6) |
| | | Xchain4 = X0(cAcBcCcD + cCcDcchainAB + cAcBcchainCD + cchainABcchainCD) | (A7) |
The next fraction is the fraction of molecules that are in double-bond configuration. When a molecule is in this state, it is either bonded twice or four times:| | | Xdb2 = X0(cdbAB + cdbCD) | (A9) |
Similarly, when a molecule is in a ring configuration, it is bonded either two or four times. The fraction of molecules in a ring configuration is given by| | | Xring = Xring2 + Xring4 | (A11) |
| | | Xring2 = X0(cringAB + cringCD) | (A12) |
| | | Xring4 = X0cringABcringCD | (A13) |
The next set of fractions are the fractions of molecules in combined configurations. The fraction of molecules in chain and double-bond structure is given by| | | Xchain–db = Xchain–db3 + Xchain–db4 | (A14) |
| | | Xchain–db3 = X0[cdbAB(cC + cD) + cdbCD(cA + cB)] | (A15) |
| | | Xchain–db4 = X0[cdbCD(cAcB + cchainAB) + cdbAB(cCcD + cchainCD)] | (A16) |
The fraction of molecules bonded in chain and ring structure is calculated as| | | Xchain–ring = Xchain–ring3 + Xchain–ring4 | (A17) |
| | | Xchain–ring3 = X0[cringAB(cC + cD) + cringCD(cA + cB)] | (A18) |
| | | Xchain–ring4 = X0[cringCD(cAcB + cchainAB) + cringAB(cCcD + cchainCD)] | (A19) |
Finally, the fraction of molecules in double-bond and ring structure is calculated using the following equations:| | | Xdb–ring = X0(cringABcdbCD + cdbABcringCD) | (A20) |
Acknowledgements
The authors acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada (NSERC) and all member companies of the SHARP Research Consortium: Canadian Natural Resources Limited (CNRL), Cenovus Energy, Imperial Oil Limited, Kuwait Oil Company, Strathcona Resources, and Suncor Energy. In addition, the support of the Department of Chemical and Petroleum Engineering and the Schulich School of Engineering at the University of Calgary is highly appreciated.
References
- A. P. Semenov, Y. Gong, V. I. Medvedev, A. S. Stoporev, V. A. Istomin, V. A. Vinokurov and T. Li, New insights into methane hydrate inhibition with blends of vinyl lactam polymer and methanol, monoethylene glycol, or diethylene glycol as hybrid inhibitors, Chem. Eng. Sci., 2012, 315, 64–76 Search PubMed.
- Y. H. Sohn and Y. Seo, Effect of monoethylene glycol and kinetic hydrate inhibitor on hydrate blockage formation during cold restart operation, Chem. Eng. Sci., 2017, 168, 444–455 CrossRef CAS.
- M. Z. Z. Abidin, Z. M. Aman, E. F. May, M. L. Johns and X. Lou, Hydrate dispersion stability in synergistic hydrate inhibition of monoethylene glycol and anti-agglomerants, Chem. Eng. Sci., 2023, 269, 118462 CrossRef CAS.
- R. Masoudi, B. Tohidi, A. Danesh, A. C. Todd, R. Anderson, R. W. Burgass and J. Yang, Measurement and prediction of gas hydrate and hydrated salt equilibria in aqueous ethylene glycol and electrolyte solutions, Chem. Eng. Sci., 2005, 60, 4213–4224 CrossRef CAS.
- N. Gao, R. Zhang, X. Peng, T. Zhang, B. Liu, C. Sun, G. Chen and C. Deng, Rigorous modeling and optimization of hybrid absorption-adsorption separation process of H2/CH4 using ZIF-8/glycol/water slurry, Chem. Eng. Sci., 2024, 299, 120474 CrossRef CAS.
- J. Gong, S. Rong, J. Wang and Y. Zhou, Oxygen vacancy-engineered in ethylene glycol solvated α-MnO2 for low temperature catalytic oxidation of toluene, Chem. Eng. Sci., 2023, 280, 119053 CrossRef CAS.
- A. Grenner, G. M. Kontogeorgis, N. von Solms and M. L. Michelsen, Application of PC-SAFT to glycol containing systems – PC-SAFT towards a predictive approach, Fluid Phase Equilib., 2007, 261, 248–257 CrossRef CAS.
- F. Kruger, G. M. Kontogeorgis and N. von Solms, New association schemes for mono-ethylene glycol: Cubic-Plus-Association parameterization and uncertainty analysis, Fluid Phase Equilib., 2018, 458, 211–233 CrossRef CAS.
- V. Vlachy, Y. V. Kalyuzhnyi, B. Hribar-Lee and K. A. Dill, Protein Association in Solution: Statistical Mechanical Modeling, Biomolecules, 2023, 13, 1703 CrossRef CAS PubMed.
- H. Butovych, Y. V. Kalyuzhnyi, T. Patsahan and J. Ilnytskyi, Modeling of polymer–enzyme conjugates formation: thermodynamic perturbation theory and computer simulations, J. Mol. Liq., 2023, 385, 122321 CrossRef CAS.
- M. S. Wertheim, Fluids with Highly Directional Attractive Forces. I. Statistical Thermodynamics, J. Stat. Phys., 1984, 35, 19–34 CrossRef.
- M. S. Wertheim, Fluids with Highly Directional Attractive Forces. II. Thermodynamic Perturbation Theory and Integral Equations, J. Stat. Phys., 1984, 35, 35–47 CrossRef.
- M. S. Wertheim, Fluids with Highly Directional Attractive Forces. III. Multiple Attraction Sites, J. Stat. Phys., 1986, 42, 459–476 CrossRef.
- M. S. Wertheim, Fluids with Highly Directional Attractive Forces. IV. Equilibrium Polymerization, J. Stat. Phys., 1986, 42, 477–492 CrossRef.
- Y. V. Kalyuzhnyi, H. Docherty and P. T. Cummings, Resummed thermodynamic perturbation theory for central force associating potential. Multi-patch models, J. Chem. Phys., 2011, 135, 014501 CrossRef CAS PubMed.
- Y. V. Kalyuzhnyi, H. Docherty and P. T. Cummings, Resummed thermodynamic perturbation theory for central force associating potential: one-patch model, J. Chem. Phys., 2010, 133, 044502 CrossRef CAS PubMed.
- Y. V. Kalyuzhnyi, B. D. Marshall, W. G. Chapman and P. T. Cummings, Second-order resummed thermodynamic perturbation theory for central-force associating potential: multi-patch colloidal models, J. Chem. Phys., 2013, 139, 044909 CrossRef CAS PubMed.
- B. D. Marshall and W. G. Chapman, Thermodynamic perturbation theory for self-assembling mixtures of divalent single patch colloids, Soft Matter, 2014, 10, 5168–5176 RSC.
- M. S. Wertheim, Thermodynamic perturbation theory of polymerization, J. Chem. Phys., 1987, 87, 7323–7331 CrossRef CAS.
- R. P. Sear and G. Jackson, The ring integral in a thermodynamic perturbation theory for association, Mol. Phys., 1996, 87, 517–521 CAS.
- R. P. Sear and G. Jackson, Thermodynamic perturbation theory for association into doubly bonded dimers, Mol. Phys., 1994, 82, 1033–1048 CAS.
- B. D. Marshall and W. G. Chapman, Thermodynamic perturbation theory for associating fluids with small bond angles: effects of steric hindrance, ring formation, and double bonding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052307 Search PubMed.
-
W. G. Chapman, PhD Dissertation, Cornel University, 1988.
- A. Haghmoradi, D. Ballal, W. A. Fouad, L. Wang and W. G. Chapman, Combination of monovalent and divalent sites on an associating species: application to water, AIChE J., 2021, 67, e17146 CAS.
- A. Haghmoradi and W. G. Chapman, Bond cooperativity and ring formation in hydrogen fluoride thermodynamic properties: a two-density formalism framework, J. Chem. Phys., 2019, 150, 174503 Search PubMed.
- B. D. Marshall, A general mixture equation of state for double bonding carboxylic acids with ≥2 association sites, J. Chem. Phys., 2018, 148, 174103 CrossRef PubMed.
- B. D. Marshall, A molecular equation of state for alcohols which includes steric hindrance in hydrogen bonding, J. Chem. Phys., 2018, 149, 044505 CrossRef PubMed.
- W. Bol, Monte Carlo simulations of fluid systems of waterlike molecules, Mol. Phys., 1982, 45, 605–616 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- J. Gross and G. Sadowski, Perturbed-chain SAFT: an equation of state based on a perturbation theory for chain molecules, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS.
-
T. E. Daubert and R. P. Danner, Physical and Thermodynamic Properties of Pure Chemicals: Data Compilation, Hemisphere, New York, 2003 Search PubMed.
- D. I. Sagdeev, M. G. Fomina, G. K. Mukhamedzyanov and I. M. Abdulagatov, Experimental study of the density and viscosity of polyethylene glycols and their mixtures at temperatures from 293 K to 465 K and at high pressures up to 245 MPa, Fluid Phase Equilib., 2012, 315, 64–76 CrossRef CAS.
- A. Alanazi, S. Bawazeer, M. Ali, A. Keshavarz and H. Hoteit, Thermodynamic modeling of hydrogen–water systems with gas impurity at various conditions using cubic and PC-SAFT equations of state, Energy Convers. Manage.: X, 2022, 15, 100257 CAS.
- F.-Y. Jou, F. D. Otto and A. E. Mather, Solubility of methane in glycols at elevated pressures, Can J. Chem. Eng., 1994, 72, 130–133 CrossRef CAS.
- D.-Q. Zheng, W.-D. Ma, R. Wei and T.-M. Guo, Solubility study of methane, carbon dioxide and nitrogen in ethylene glycol at elevated temperatures and pressures, Fluid Phase Equilib., 1999, 155, 277–286 CrossRef CAS.
- F. Y. Jou, K. A. G. Schmidt and A. E. Mather, Vapor–liquid equilibrium in the system ethane + ethylene glycol, Fluid Phase Equilib., 2006, 240, 220–223 CrossRef CAS.
- F. Y. Jou, F. D. Otto and A. E. Mather, The solubility of propane in 1,2-ethanediol at elevated pressures, J. Chem. Thermodyn., 1993, 27, 37–40 CrossRef.
- E. Brunner, Solubility of hydrogen in diols and their ethers, J. Chem. Thermodyn., 1980, 12, 993–1002 CrossRef CAS.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*

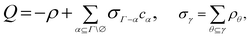





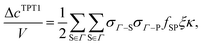





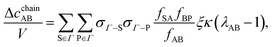











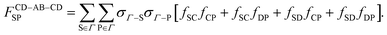
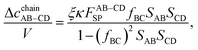
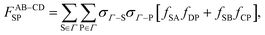
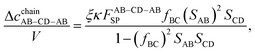

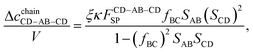

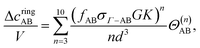

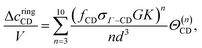





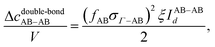











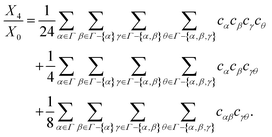
























![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif)




