Open Access Article
Open Access ArticleComputational investigation of the effects of polymer grafting on the effective interaction between silica nanoparticles in water†
Yuvraj
Singh
 a,
Chandan K.
Choudhury
a,
Chandan K.
Choudhury
 b,
Rikhia
Ghosh
b,
Rikhia
Ghosh
 c and
Rakesh S.
Singh
c and
Rakesh S.
Singh
 *d
*d
aDepartment of Physics, Indian Institute of Science Education and Research (IISER) Tirupati, Tirupati, Andhra Pradesh 517619, India
bPrescience Insilico Private Limited, Bengaluru, Karnataka 560066, India
cDepartment of Pharmacological Sciences, Icahn School of Medicine, Mount Sinai, New York 10029, USA
dDepartment of Chemistry, Indian Institute of Science Education and Research (IISER) Tirupati, Tirupati, Andhra Pradesh 517619, India. E-mail: rssingh@iisertirupati.ac.in
First published on 22nd August 2024
Abstract
Understanding and control of the effective interaction between nanoscale building blocks (colloids or nanoparticles) dispersed in a solvent is an important prerequisite for the development of bottom-up design strategies for soft functional materials. Here, we have employed all-atom molecular dynamics simulations to investigate the impact of polymer grafting on the solvent-mediated effective interaction between the silica nanoparticles (Si-NPs) in water, and in turn, on its bulk structural and thermodynamic properties. We found that the nature of the short grafting polymers [characterized by their interaction with water (hydrophobicity or hydrophilicity) and molecular weight] has a profound effect on the range and strength of the effective interaction between the Si-NPs. The hydrophobic polymer [such as polyethylene (PE)]-grafting of Si-NP gives rise to a more attractive interaction between the Si-NPs compared to the hydrophilic polymer [such as polyethylene glycol (PEG)] and non-grafted cases. This study further provides fundamental insights into the molecular origin of the observed behavior of the effective pair interactions between the grafted Si-NPs. For PE-grafted Si-NPs, the confined water (water inside the cavity formed by a pair of Si-NPs) undergoes a partial dewetting transition on approaching below a critical inter-particle separation leading to a stronger attractive interaction. Furthermore, we report that the effective attraction between the PE-grafted Si-NPs can be reliably controlled by changing the grafting PE density. We have also investigated the bulk structural and thermodynamic behavior of the coarse-grained Si-NP system where the particles interact via effective interaction in the absence of water. We believe that the insights gained from this work are important prerequisites for formulating rational bottom-up design strategies for functional materials where nano- (or, colloidal) particles are the building blocks.
1 Introduction
Nanoparticles and colloids offer exciting potential for creating soft materials.1,2 These materials are well-known for their unique phase behavior, and their versatility finds applications in various scientific and technological fields, including plasmonics,3,4 photovoltaics,5 and chemical/biological sensing.6 Therefore, there is now a growing need for systematic bottom-up design strategies for these materials to cater to the diverse applications ranging from materials to biological sciences.7–20 Self-assembly processes play a pivotal role in designing soft functional materials across various scales in nature. In the self-assembly route of synthesizing materials, the inter-particle interactions guide the building blocks to spontaneously self-assemble into the target structure. In the case of nanoparticles or colloids, the self-assembly relies on solvent-mediated effective interactions among these particles, orchestrating the formation of desired self-assembled structures.The solvent-mediated (effective) interaction between the nanoscale particles can be easily tuned by manipulating the characteristics of the particles,21–24 the properties of the solvent,25,26 and the thermodynamic conditions.27 For example, nanoparticles functionalized with ligands such as short DNA strands are widely used to alter the effective interaction between the nanoparticles to get the desired self-assembled structures.28–30 Hence, functionalizing nanoparticles with ligands or changing the characteristics of the solvent provides a means to adjust and control the inter-particle interactions—offering a versatile approach to influence the self-assembly process and ultimately tailor the properties of the resulting materials. There is now a growing interest in designing nanoscale building blocks with anisotropic shape (e.g., see ref. 21 and 31–35) or with specific directional interactions (e.g., Janus and patchy nanoparticles/colloids36–40) to control the morphology and size of the self-assembled aggregates. This control of morphology and size of aggregates at length scales of interest is vital for tuning material properties. For example, nanoscale patterns are crucial for charge separation and recombination in photovoltaics, self-assembled aggregate structures significantly affect bulk conductivity, etc.41
Much attention has been devoted to understand the profound influence of the nature of the underlying free energy landscape on the pathways of self-assembly of molecular and colloidal systems.42–45 However, lesser attention has been devoted in understanding the interplay between local interactions and global free energy landscape (containing multiple crystalline and fluid phases) of the system, especially when the constituents are nanoscale particles. Understanding the intricate interplay between the local interactions and the global free energy landscape holds the key to predictably design the target materials. Recently, computer simulations have proven essential in depicting complex structures achievable by altering the interaction potential among these building blocks.46,47 In a recent study, Jiang et al.48 reported that interactions between DNA strands of distinct sequences result in the aggregation of DNA-conjugated gold nanoparticles.49 Another noteworthy study, particularly in the realm of DNA-mediated isotropic interactions,50 has shown the feasibility of tuning such interactions to facilitate particle self-assembly. This method holds promise for constructing custom-designed functional materials. Many recent studies, such as of Mittal et al.,49 have successfully achieved different crystal structures by manipulating the attractive and repulsive ranges of pair potentials between DNA-functionalized nanoparticles. Despite significant breakthroughs in the characterization and control of local inter-particle interactions at nanoscales,50–52 there is still a distinct lack of (a) systematic and predictive approaches to alter two-body effective interactions, and (b) robust mapping of the local pair interactions to the bulk structural and thermodynamic properties. These are the important prerequisites for the synthesis of target materials through a bottom-up self-assembly route.
In this work, we aim to explore the impact of polymer (or, ligand) grafting on the (solvent-mediated) effective interaction between the nanoparticles, and in turn, on bulk structural and thermodynamic properties. We have used silica nanoparticle (Si-NP) as our model system, and to modulate interactions between Si-NPs, we employed polymers (ranging from hydrophilic to hydrophobic)—polyethylene glycol (PEG), polyethylene (PE), and polymethyl methacrylate (PMMA)—grafted onto the surface of the Si-NP. The selection of these specific polymers is grounded in experimental studies, where successful grafting of these polymers onto the surface of Si-NPs has been demonstrated.53–55 Additionally, our choice of polymers aligns with the availability of well-optimized force field parameters ensuring accurate in silico all-atom representation in our computational model. Here, the effective interaction between the Si-NPs is characterized by computing the potential of mean force (PMF) between two (bare or grafted) Si-NPs at two different temperatures. The PMF of the bare Si-NP serves as a reference point for our study, enabling an exploration of how grafting with PEG, PMMA, and PE influences inter-particle interactions (measured in terms of the position, depth and shape of the PMF). We have also probed the molecular origin (rooted in solvent) of the dependence of the PMF on the nature of the grafting polymer, and the structural and thermodynamic behavior of bulk coarse-grained systems consisting of many Si-NPs interacting via effective pair interactions.
The organization of the rest of the paper is as follows. In Section 2 the computational modelling of the grafted Si-NPs and molecular dynamics (MD) simulation details are presented. In Sections 3.1 and 3.2, we discuss the solvent-mediated effective interactions between two grafted Si-NPs and the solvent arrangement around them. The microscopic structural origin of the changes of the solvent-mediated interactions through polymer grafting is discussed in Sections 3.3–3.5. The effects of grafting polymer density on the PMF of PE-grafted Si-NPs are discussed in Section 3.6 and the structural and thermodynamic properties of the coarse-grained bulk Si-NP system are presented in Section 3.7. The major conclusions from this work are summarized in Section 4.
2 Simulation and modeling details
2.1 Grafted Si-NP modelling
The bare (or, non-functionalized) Si-NP of diameter 2 nm was modelled using CHARMM-GUI.56 All the oxygen atoms on the Si-NP surface were saturated with hydrogen atoms to ensure valency satisfaction. The CHARMM36 force field was employed, and the force-field parameters for Si-NP were adopted from the work of Lopes et al.56 To generate the grafted Si-NPs, the bare Si-NP was grafted with three different polymers—PEG, PE, and PMMA—each composed of five monomer units (referred as 5-mer; see Fig. 1). The surface hydrogen atoms serve as anchoring points for polymer grafting. The grafting surface density is 1.75 chains nm−2 (22 grafted chains; 25% of the available attachment sites on the Si-NP surface are occupied by polymers) unless stated otherwise. The force field parameters for PEG, PMMA and PE were adopted from the works of Vorobyov et al.,57 and Eslami et al.,58 and Choi et al.,59 respectively. The procedures outlined in ref. 54 were followed for the PEG grafting. Similarly, PMMA and PE were grafted using the procedures outlined in ref. 53 and 55, respectively. We would like to make a note here that in this work, the grafted groups (5-mers) are referred to as polymer chains. However, in reality, they are short oligomers and not polymer chains.2.2 MD simulation protocol
We have used a combination of GROMACS (version 2021.5)60 and PLUMED (version 2.8.1)61 to perform all-atom MD simulations and compute the PMF between the polymer-grafted Si-NPs. We performed MD simulations in an isothermal–isobaric (NPT) ensemble on a system consisting of two Si-NPs in a solvent containing N ∼ 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TIP3P water62 molecules in a cubic box at 1 bar pressure. The average box length is ∼12 nm at the thermodynamic conditions studied here. The short-range van der Waals interaction potential was truncated at 1.2 nm, and long-range corrections were applied to the short-range interaction for energy and pressure. The coulombic interaction was truncated at 1.2 nm, and the particle mesh Ewald (PME)63 was used to compute the long-range contributions to the electrostatic interaction. The Nóse–Hoover thermostat64,65 was used to maintain a constant temperature with 0.4 ps relaxation time. Constant pressure was maintained using Parrinello–Rahman barostat66 with 2 ps relaxation time. We have used 2 fs time step to propagate the trajectories. The rigid body constraints were implemented using the linear constraint solver (LINCS)67 algorithm and periodic boundary conditions were applied in all three directions. For the analysis of water arrangement around a single Si-NP, we performed MD simulations on a system consisting of a single nanoparticle of diameter 2 nm in a cubic box (average box length is ∼8 nm) at temperature 300 K and pressure 1 bar. We ran the simulations for 300 ns to ensure the proper thermal equilibration of the system.
000 TIP3P water62 molecules in a cubic box at 1 bar pressure. The average box length is ∼12 nm at the thermodynamic conditions studied here. The short-range van der Waals interaction potential was truncated at 1.2 nm, and long-range corrections were applied to the short-range interaction for energy and pressure. The coulombic interaction was truncated at 1.2 nm, and the particle mesh Ewald (PME)63 was used to compute the long-range contributions to the electrostatic interaction. The Nóse–Hoover thermostat64,65 was used to maintain a constant temperature with 0.4 ps relaxation time. Constant pressure was maintained using Parrinello–Rahman barostat66 with 2 ps relaxation time. We have used 2 fs time step to propagate the trajectories. The rigid body constraints were implemented using the linear constraint solver (LINCS)67 algorithm and periodic boundary conditions were applied in all three directions. For the analysis of water arrangement around a single Si-NP, we performed MD simulations on a system consisting of a single nanoparticle of diameter 2 nm in a cubic box (average box length is ∼8 nm) at temperature 300 K and pressure 1 bar. We ran the simulations for 300 ns to ensure the proper thermal equilibration of the system.
2.3 PMF computation
We performed umbrella sampling to compute the PMF with the distance between the center-of-mass of the Si-NPs (denoted as, rcom) as a reaction coordinate. For the umbrella sampling, depending on the system (bare or grafted), we employed two force constants for the umbrella potential: 2000 kJ mol−1 nm−2, and 750 kJ mol−1 nm−2. The system underwent equilibration for at least 100 ns in each window to ensure equilibration and proper sampling of the available configuration space. After this initial equilibration, we ran the simulations for >200 ns in each window to get the converged probability distribution of the reaction coordinate. Subsequently, we employed the weighted histogram analysis method (WHAM) to compute the PMF from the probability distributions.683 Results and discussion
3.1 Solvent-mediated effective pair interactions between grafted Si-NPs
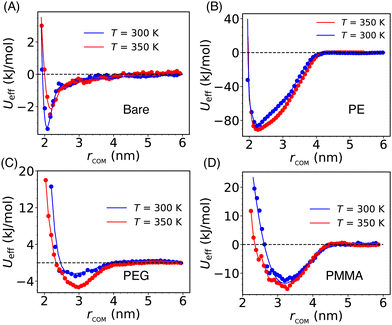
The solvent-mediated effective inter-particle interactions are characterized by computing the PMF which provides a comprehensive view of the free energy landscape along a chosen reaction coordinate. The PMF for both the bare and grafted Si-NPs is calculated using the distance between their respective center-of-mass, rcom, as reaction coordinate (see Fig. 2). To explore the effects of temperature on the PMF, we computed it at two different temperatures: 300 K and 350 K. We note a drastic effect of polymer grafting on the PMF. Also, the position of the PMF minimum—which is a measure of the effective Si-NP diameter (σeff)—is delicately sensitive to the type of the grafting strand.The effective interaction (or, PMF) for the bare Si-NP is short-range compared to the grafted Si-NPs and shows a very weak attraction (3.5 kJ mol−1 or ∼1.5kBT at 300 K; kB is Boltzmann's constant) near the contact distance (Fig. 2A). Contrary to this, the PMF of the PE-grafted Si-NP exhibits a highly attractive nature (85 kJ mol−1 or ∼35kBT at 300 K), surpassing that of the bare Si-NP by more than 20 times near ambient temperature. Additionally, the interaction range (measured by the width of the PMF basin) has increased to ∼4 nm, exceeding that of the bare Si-NP by more than 1.5 times. However, the σeff remains close to 2 nm (bare Si-NP diameter). These observations are intriguing and indicate that the attachment of a common (hydrophobic) polymer, PE, significantly modulates the PMF. Like the bare Si-NP, the PMF for the PEG-grafted Si-NPs shows a marginally stable basin compared to the PE-grafted case. The strength of the effective interaction (measured by the depth of the PMF basin) between two PMMA-grafted Si-NPs in water is 12 kJ mol−1 (or, ∼5kBT at 300 K). We further note that the PMF for the PEG and PMMA-grafted Si-NPs shows a softer repulsive core compared to the bare and PE-grafted Si-NPs. The effective diameter σeff is also significantly higher (>3 nm) for these two cases. These differences in the effective diameter and softness can be understood in terms of the grafting polymer's mass (or, occupied volume) and conformational arrangement around the Si-NP in water. We also note that the computed effective interactions do not change noticeably on increasing the temperature from 300 K to 350 K.
The above reported PMF behavior can be qualitatively rationalized in the following way (a more detailed quantitative explanation is provided in the next section). The PEG (H-(OCH2CH2)n-OH) is hydrophilic, and water serves as a good solvent since the terminal OH group of PEG can form H-bond with water. However, PE is hydrophobic in nature. In the presence of a good solvent (for example, PEG in water), the grafting polymer chains tend to adopt extended conformations, leading to an increase in the effective diameter of the Si-NP. Under these conditions, the PMF exhibits a soft repulsive core starting at a larger (>2 nm) inter-particle separation (e.g., see Fig. 2C). However, for the bad solvent case (for example, PE in water), we observe a relatively hard repulsive core with a smaller effective diameter (see Fig. 2B). Furthermore, the PMMA-grafted Si-NP shows a higher effective diameter (∼3.1 nm) due to its larger molecular weight (the weight of the polymer of length 5 for PMMA, PEG, and PE is 501.6, 238.3, and 142.3 amu, respectively).
Thus, the nature of the grafting polymers profoundly affects the range and strength of the effective interaction between the nanoparticles. A predictive control over the effective interaction between the nanoscale particles dispersed in solvent via polymer grafting can provide a reliable way of altering the self-assembly pathways and kinetics, including the self-assembled structure and in turn its function. It has already been reported that the range and strength of the effective interaction between the colloids has a drastic effect on the phase diagram and nucleation kinetics.42,69 To understand the molecular origin of the alteration of the effective interaction via polymer grafting, in the subsequent sections (Sections 3.2 and 3.3) we have characterized the density and structure of water molecules around the grafted Si-NP (including bare) and also confined in-between the Si-NPs.
3.2 Water density and structure around grafted Si-NPs
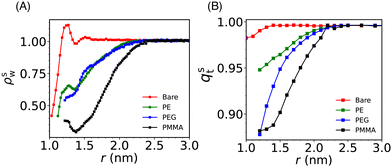
Solvent plays a crucial role in deciding the range and strength of the effective interaction between the dispersed nano/mesoscale particles. Therefore, it is crucial to first characterize the arrangement of solvent/water molecules around grafted Si-NPs and its dependence on the nature of the polymer, such as hydrophilic or hydrophobic. To characterize the water arrangement around grafted Si-NPs, we have computed the water density and tetrahedral order profiles around a single Si-NP submerged in water. In Fig. 3A we show the scaled radial density (ρsw) and tetrahedral order parameter (qst) profiles in the radially outward direction from the center-of-mass of the Si-NP. The ρsw is defined as, ρsw(r) = ρw(r)/ρbw, where ρw(r) is the density of water molecules inside a spherical shell of radius r (from the center-of-mass of the Si-NP) and width Δr, and ρbw is the bulk water density at the same thermodynamic condition. The scaled tetrahedral order parameter profile qst is defined similarly as qt(r)/qt–bw, where qt–bw is the tetrahedral order (qt) of the bulk water. The qt of the ith water molecule is defined as,70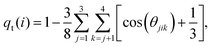 | (1) |
The ρsw profile shows a maximum at around 1 nm for the bare Si-NP suggesting that many water molecules are sticking (more than the bulk) to the Si-NP surface (see Fig. 3A). The silica surfaces exhibit hydrophilic characteristics primarily due to the presence of silanol groups (Si–O–H) on the surface. These groups, featuring oxygen atoms with partial negative charge readily get H-bonded with the water molecules. A well-defined maximum in ρsw(r) in the vicinity of the Si-NP surface also suggests that the interfacial water molecules are highly structured. A similar enhanced water density near the surface is also reported for the gold(Au)-NP when hydroxyl tails are introduced on the surface.71 The incorporation of a hydroxyl tail on the Au-NP's surface enhances the formation of hydrogen bonds between the water and the hydroxyl tail. In the vicinity of the grafted (PE, PEG, and PMMA) Si-NPs, the water density around the Si-NP surface is significantly lower compared to the bulk. This observed lower water density in the vicinity of the grafted Si-NPs is due to the interfacial region being occupied by the grafting polymer atoms (see Fig. S1 in the ESI†). Also, the decrease of water density for the case of PMMA is more compared to the PE and PEG. This can be attributed to the more number of particles present in the 5-mer PMMA polymer compared to the other grafting polymers of the same length.
The computed qst profiles (see Fig. 3B) show that, for the bare Si-NP, even though the water density is approximately 40–60% of the bulk density near the (Si-NP–water) interface, interfacial water molecules are highly tetrahedral (97% of qt–bw). This arises because water tends to form H-bonds with the –(OH) groups on the Si-NP surface. We observe a significant decrease in water's tetrahedral order around the Si-NP for all the grafted Si-NPs with the PE-grafted Si-NP showing the higher tetrahedrality compared to the PEG and PMMA-grafted Si-NPs. The enhanced tetrahedrality for the PE case can be understood in terms of its hydrophobic nature. The hydrophobic PE polymers are mostly wrapped around the Si-NP surface and does not perturb considerably the water network compared to the hydrophilic PEG polymers. Interestingly, we also note that, both the water density and tetrahedral order reach their respective bulk value at ∼2.4 nm from the centre of the Si-NP for all the grafted Si-NPs (Fig. 3A and B).
A detailed analysis of the behavior of qst profile around the Si-NP necessitates a comprehensive study of the nature of the interaction between different polymers and water molecules. This could also involve investigating the specific bonding patterns, and steric hindrances the polymer chains exert. Nevertheless, the behavior of water's density and order around a single Si-NP provides us a reference point to study Si-NP surface polarity-induced structural perturbation in the solvent where two or many Si-NPs are present and its consequences on the (solvent-mediated) effective interaction between them. We also note that the solvent distribution around the Si-NP in the presence of more than one Si-NP could be very different. However, for a dilute Si-NP system, we expect to have a similar solvent distribution in the vicinity of each Si-NP.
3.3 Density and structural behavior of water confined between Si-NPs
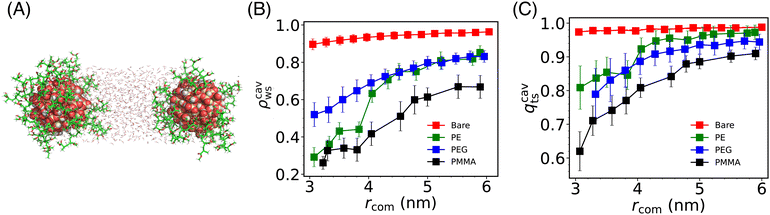
To understand the molecular origin (induced by solvent) of the change of the effective interaction on changing the grafting polymers, we probed the density and structural behavior of water molecules confined between the two Si-NPs (see Fig. 4A) as a function of inter-particle separation, and its dependence on the type of grafting polymer. We calculated the scaled density (ρcavws) and tetrahedral order (qcavts) of these (confined) water molecules (see Fig. 4A and B). The ρcavws is defined as, ρcavws = ρcavw/ρbw, where ρcavw is the density of water inside the cylindrical cavity of length rcom and radius 1 nm. Similarly, qcavts is defined as, qcavts = qcavt/qt–bw, where qcavt is the tetrahedral order of the confined water and qt–bw is the bulk water tetrahedral order. We note a monotonic decrease of both ρcavws and qcavts on reducing the inter Si-NP separation distance rcom. For the bare Si-NP, the decrease ρcavws as well as qcavts is relatively insignificant compared to the grafted Si-NPs. This insensitivity of the confined water density and structural order is correlated with the shallow depth in the PMF (∼3 kJ mol−1) of the bare Si-NP, which implies a weak attractive interaction at shorter distances.Like the bare Si-NP, the PEG-grafted Si-NP also shows a very similar shallow PMF depth but with a larger effective diameter (σeff ∼ 3 nm). Although both the bare and PEG-grafted Si-NPs have similar potential depths, ρcavs and qcavts for PEG at smaller rcom is ∼22% less than that of the bare Si-NP case at lower distances (see Fig. 4B and C). This notable solvent density difference can be understood in terms of the volume occupied by PEG polymers in an extended conformation (as PEG is hydrophilic, it tends to extend its conformation in water). Consequently, the PEG-grafted system experiences additional pressure due to the grafting polymer chain atoms, which compensates for the reduced water contribution (see also Fig. S2A in the ESI†).
Again, contrary to the bare Si-NP, in the case of PE-grafted Si-NP, the ρcavws and qcavts shows a drastic change on lowering rcom near rcom = 4 nm. This sudden decrease of ρcavws shows a close resemblance with the cavitation (or, dewetting) transition of the water molecules confined between two hydrophobic plates72–75 (see also Fig. S2B in the ESI†). Here, however, we are not observing a complete cavitation but rather ∼20% decrease in the density of water. This partial cavitation (or, dewetting) can be understood in terms of the competition between the hydrophilic Si-NP surface's favorable interaction with water and the grafted PE–polymer's hydrophobic character. This partial dewetting creates a substantial pressure difference between the outside and in-between the Si-NPs, compelling the Si-NPs to remain in closer proximity. This is also evident from the PMF where the attractive force starts dominating around the same distance (4 nm) and continues to dominate until the hard repulsive core is encountered. This type of dewetting-induced attraction is known to play an important role in many of the biophysical phenomena, such as, protein folding, protein–ligand binding etc.76
The water density and structural order for the PMMA-grafted Si-NP is lowest among the other cases which is a consequence of the large volume occupied by the PMMA 5-mer due to its high molecular weight. Similar to the PE-grafted Si-NP, the water density confined inside the PMMA Si-NPs also shows a rapid change (compared to the bare and PEG-grafted cases) around 4.5 nm which again is correlated with the enhanced attraction compared to the bare and PEG-grafted Si-NPs. However, unlike the PE-grafted case, the total number of heavy atoms (atoms excluding hydrogen) monotonically increases on decreasing the inter-particle separation rcom (see Fig. S2C in the ESI†). Therefore, the enhanced interaction between the PMMA-grafted Si-NPs in water compared to the bare and PEG-grafted cases (see Fig. 2) can not be unambiguisely attributed to (partial) dewetting-induced attraction.
To gain deeper insights into water rearrangement inside the cavity, in Fig. 5, we have reported the scaled water density profile in between the two Si-NPs for rcom = 5.5 nm and 4.0 nm. At a larger separation of the Si-NPs, confined water density reaches the bulk density around the center of the cavity. However, for smaller inter-particle separation, there is a drastic decrease in the density inside the cavity for all the grafted Si-NP cases. The bare Si-NP shows bulk-like density even for this smaller inter-particle separation of 4.0 nm. The decrease in water density inside the cavity for the PE-grafted Si-NPs is significantly greater compared to the bare and PEG-grafted Si-NPs. This observation further establishes that the enhanced attraction between the PE-grafted Si-NPs in water is dewetting-induced. In contrast, for PMMA-grafted Si-NPs, the decrease in water density inside the cavity is primarily due to the large volume occupied by the heavy PMMA 5-mers (see Fig. S2C in the ESI†).
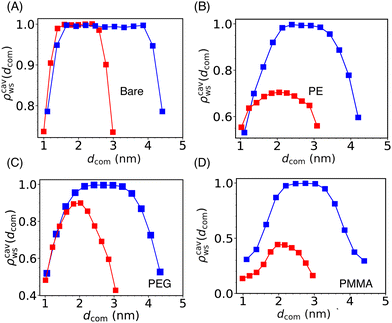 | ||
| Fig. 5 The scaled water density (ρcavws) profile inside the cylindrical cavity formed by two Si-NPs (see Fig. 4A) fixed at a center-to-center separation of 5.5 nm (blue) and 4.0 nm (red) for the bare (A), PE-grafted (B), PEG-grafted (C), and PMMA-grafted (D) Si-NP. Here, dcom represents the distance from the center of the Si-NP along the direction connecting the centres of the two Si-NPs. We note that, at lower inter-particle separation (4.0 nm), the cavity water density for the case of PE and PMMA-grafted Si-NPs is significantly lower than the bare and PEG-grafted Si-NPs. | ||
3.4 Structural behavior of the grafting polymers of Si-NPs
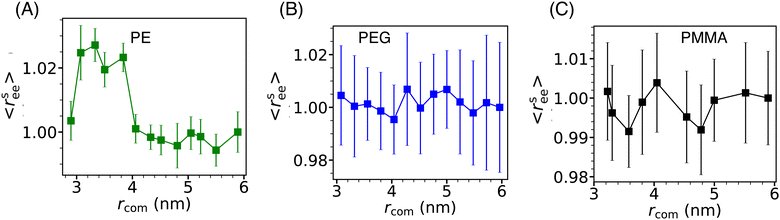
The conformation properties of polymers are highly sensitive to solvent properties and confinement.77,78 Therefore, the conformations of grafting polymer chains are also expected to depend on the inter-Si-NP separation (rcom) and the cavity water density (ρcavw). To investigate this, we computed the scaled mean end-to-end distance (〈rsee〉) of the grafting polymer chains as a function of the inter-Si-NP separation (see Fig. 6). Here, 〈rsee〉 = 〈ree〉/〈r0ee〉, where 〈ree〉 is the average end-to-end distance and 〈r0ee〉 is the average end-to-end distance when two Si-NPs are maximally separated (i.e., rcom ∼ 6 nm) in a cubic box of average box length of 12 nm. We find that the grafting polymer conformation is highly sensitive to the inter-Si-NP separation in the case of PE. At the onset of the partial dewetting transition (rcom ∼ 4 nm), the short PE chains acquire relatively elongated conformational states. The 〈ree〉 decreases with further reduction in rcom (around 3 nm) as the PE chains of different Si-NPs start directly interacting with each other. This manifestation of the partial dewetting transition on the conformation of the grafting polymer is an interesting aspect of this study. In contrast, we did not observe any systematic change in the conformations of PEG and PMMA with varying rcom.3.5 Water's dynamical behavior in solvent-separated grafted Si-NPs
The dynamical behavior of water molecules confined in the cavity formed by a pair of Si-NPs (see Fig. 4A) can be characterized by computing their translational mobility. The translational mobility (μ) of a tagged water molecule i is defined as, μ(i) = |ri(t + Δt) −ri(t)|, where ri represents the position of the oxygen atom of the ith water molecule, t denotes the time, and Δt is a pre-defined time interval. Here, Δt is judiciously chosen as 10τs; τs is the structural relaxation time (defined as the time at which the self-intermediate scattering function decays to zero) of bulk TIP3P water at T = 300 K and P = 1 bar, which is 2 ps. To determine the mobility of water molecules within the cavity, we tagged the water molecules inside the cavity at the initial time and as time progressed, some of the tagged water molecules exited the cavity. We excluded all the tagged water molecules that left the cavity on the chosen Δt from the calculation of the mobility. Fig. 7 depicts the water's mobility distribution within the cavity of varying sizes rcom. We observe that, in the case of the bare Si-NP, the mobility distribution remains relatively insensitive to the cavity size rcom. This observation is in agreement with the relatively weak dependence of the density and structural (tetrahedral) order of the confined water for the bare Si-NP (Fig. 4B and C).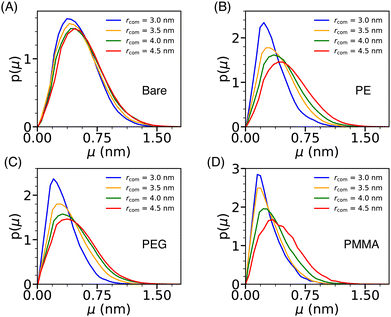 | ||
| Fig. 7 The normalized distribution of the translational mobility (μ) of the water molecules (p(μ)) inside the cylindrical cavity formed by two Si-NPs (see Fig. 4A) for the bare (A), PE-grafted (B), PEG-grafted (C), and PMMA-grafted (D) Si-NP. | ||
However, the scenario is different for the grafted Si-NPs. At lower rcom, mobility distribution peaks at a lower value than the bulk. The peak gradually shifts towards higher mobility as the rcom increases and eventually will merge with the bulk distribution. This trend seems a bit counter-intuitive as decreasing inter-particle separation leads to the decrease of both the density and structural order of the confined water, which should give rise to higher mobility. To understand this behavior, we computed the polymer atom number density profile inside the cylindrical cavity formed by two grafted Si-NPs for a given inter-particle separation (see Fig. S3 in the ESI†). We found that, even though the water density decreases on decreasing the inter-particle separation, the available volume is occupied by the grafting polymer units, giving rise to a sluggish translation mobility. Thus, polymer grafting influences water mobility within the cavity by hindering the translation dynamics due to the excluded volume (volume occupied by the grafting polymers) effect. The binding (H-bonding) of the confined water molecules with the grafting polymer strands could also give rise to a sluggish water mobility. However, this aspect is not explored here.
3.6 Effects of grafting polymer density on the effective pair interaction between PE-grafted Si-NPs
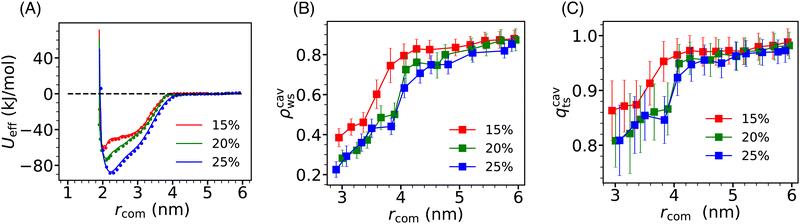
Due to the significant alteration of the effective interaction between Si-NPs in water by hydrophobic PE grafting compared to PEG and PMMA grafting, we expanded our study by systematically exploring the influence of surface ligand density on the PMF profile of PE-grafted Si-NPs. In Fig. 8A, we present the PMF profiles for three different surface PE coverages (quantified by the number of attachment sites on the Si-NP surface occupied by PE 5-mers)—15%, 20%, and 25%. As depicted in the figure, the depth of the PMF gradually increases with higher PE grafting densities. Moreover, the position of the PMF minimum (representing the effective diameter of the Si-NP) marginally shifts to higher values with increased PE-grafting density. The width of the PMF basin (indicating the effective interaction range), however, remains largely unchanged with varying grafting density. Thus, the strength of the effective interaction between Si-NPs can be reliably controlled by modulating the surface polarity of the Si-NP's hydrophilic surface through hydrophobic polymer grafting.To further investigate the underlying solvent-driven mechanisms of the above observation, we examined the inter-particle separation dependence of the scaled average density ρcavws and tetrahedral order qcavts (defined in Section 3.3) of water molecules confined between two Si-NPs for all three grafting polymer densities (see Fig. 8B and C). We observe a sharp decrease in ρcavws and qcavts when rcom falls below 4 nm for all three surface coverage cases. Notably, this decrease is more gradual for the 15% surface coverage compared to the 20% and 25% surface coverage cases. The density and tetrahedral order of water inside the cavity (confined water) are relatively higher for the 15% surface coverage which may be responsible for the shallower PMF minimum observed in this case. However, for the 20% and 25% surface coverage cases, the density and tetrahedral order of confined water are very similar (within reported statistical error). Therefore, further microscopic analysis is needed to elucidate the increase in effective inter-particle attraction observed with increasing PE surface coverage from 20% to 25%.
So far we have discussed the alteration of the local two-body effective interaction between the Si-NPs via polymer grafting and the molecular origin of the same. However, now the natural question arises—how does this alternation of the inter-particle effective interaction affect the bulk structural and thermodynamic properties of the system containing many Si-NPs dispersed in water (or, solvent, in general)? We have tried to address this in the next section by adopting a coarse-grained approach.
3.7 Structural and thermodynamic behavior of the bulk coarse-grained Si-NP system
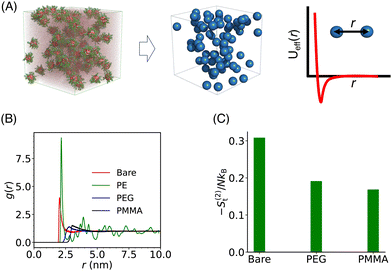
In our coarse-grained representation of the system containing many Si-NPs dispersed in water, the Si-NPs interact via the isotropic two-body effective interaction (see Fig. 9A) in the absence of water. That is, the Si-NPs are approximated as spherical particles and the solvent effects on the inter-particle interaction are accounted implicitly by (solvent-mediated) effective pair interactions (see Section I in the ESI,† for the details). We have neglected here the effects of many-body correlations on the two-body (effective) interaction between the Si-NPs dispersed in water. To probe the structural features of the bulk Si-NP systems (both bare and polymer-grafted Si-NP systems with 25% surface ligand coverage), in Fig. 9B, we show the radial distribution function (RDF, denoted as g(r)) of the system. The RDFs provide information about the local structural features of the system and also many thermodynamic properties can be derived from them. The bare, PEG, and PMMA-grafted Si-NP systems show a weaker spatial correlation compared to the PE-grafted case. We further investigated the stronger spatial correlation observed for the PE-grafted case by conducting all-atom molecular dynamics simulations on a system containing 10 Si-NPs dispersed in TIP3P water at T = 300 K and P = 1 bar. Our findings reveal that the PE-grafted Si-NPs exhibit a significantly higher propensity to aggregate compared to bare Si-NPs and those grafted with PEG and PMMA (see Fig. S4 in the ESI†), consistent with the predictions from coarse-grained simulations (Fig. 9B).We also computed the two-body approximation of the translational contribution to the excess (relative to that of the ideal gas at the same thermodynamic condition) entropy (S(2)t), defined in terms of the RDF as,79,80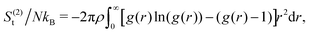 where ρ is the number density, N is the number of Si-NPs. The S(2)t measures the reduction of the entropy (or, the number of accessible states) with respect to the ideal gas limit due to two-body inter-particle correlations. In Fig. 9C, we show the S(2)t for both the bare and polymer-grafted Si-NP systems. We observe that the S(2)t is significantly lower for the PEG and PMMA-grafted Si-NP systems compared to the bare Si-NP. We have not calculated the S(2)t for the PE-grafted Si-NP system as the system spontaneously crystallizes near ambient conditions (see the RDF of the PE-grafted Si-NP system reported in Fig. 9B).
where ρ is the number density, N is the number of Si-NPs. The S(2)t measures the reduction of the entropy (or, the number of accessible states) with respect to the ideal gas limit due to two-body inter-particle correlations. In Fig. 9C, we show the S(2)t for both the bare and polymer-grafted Si-NP systems. We observe that the S(2)t is significantly lower for the PEG and PMMA-grafted Si-NP systems compared to the bare Si-NP. We have not calculated the S(2)t for the PE-grafted Si-NP system as the system spontaneously crystallizes near ambient conditions (see the RDF of the PE-grafted Si-NP system reported in Fig. 9B).
From the effective interaction potential, it is possible to evaluate the second virial coefficient B2(T), defined as 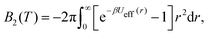 where β = 1/kBT. The calculated B2(T) values are approximately −34.0, −1.6 × 102, −6.7 × 103, and −2.2 × 1015 (in units of nm3) for the bare, PEG, PMMA and PE grafted Si-NPs, respectively. At the level of B2(T), the equation of state is given as, βP ≈ ρ + B2(T)ρ2, where ρ is the number density of the dispersed Si-NPs. For colloidal or protein solutions, it is reported that for those solvent conditions that are known to promote crystallization, B2 is restricted to a narrow range of small negative values.69,81 Therefore, controlling B2 through polymer grafting could have strong implications on the kinetics and pathways of self-assembly of Si-NPs.
where β = 1/kBT. The calculated B2(T) values are approximately −34.0, −1.6 × 102, −6.7 × 103, and −2.2 × 1015 (in units of nm3) for the bare, PEG, PMMA and PE grafted Si-NPs, respectively. At the level of B2(T), the equation of state is given as, βP ≈ ρ + B2(T)ρ2, where ρ is the number density of the dispersed Si-NPs. For colloidal or protein solutions, it is reported that for those solvent conditions that are known to promote crystallization, B2 is restricted to a narrow range of small negative values.69,81 Therefore, controlling B2 through polymer grafting could have strong implications on the kinetics and pathways of self-assembly of Si-NPs.
4 Conclusions
The primary objective of this study is to investigate the solvent-mediated effective interaction between Si-NPs and modulate it through Si-NP's surface modification (such as polymer grafting). By modifying the surface properties of Si-NPs, we have demonstrated our ability to tailor their interaction with the surrounding environment, and between them. We found that the nature of the grafting strands [characterized by their interaction with water (hydrophobic or hydrophilic) and molecular weight] has a profound effect on the range and strength of the effective interaction between the Si-NPs. The hydrophobic polymer (PE)-grafting gives rise to a more attractive interaction between the Si-NPs compared to the hydrophilic polymer or non-grafted cases. This study further provides fundamental insights into the molecular origin of the alteration of the effective interactions between the Si-NPs. For PE-grafted Si-NPs, the confined water (water inside the cavity formed by a pair of Si-NPs) undergoes a partial dewetting transition (characterized by a sudden drop in density and tetrahedral order) on approaching below a critical inter-particle separation leading to a stronger attractive interaction. We also observed that the hydrophilic and/or higher molecular weight polymer grafting gives rise to a softer repulsive core compared to the bare case. We further probed the effects of grafting polymer density on the PMF of PE-grafted Si-NPs. We find that the effective attraction between the Si-NPs gradually increases on increasing the PE grafting density. Finally, we also investigated the bulk structural behavior of the coarse-grained Si-NP system where the particles interact via the (solvent-mediated) effective interaction in the absence of water. The bare, PEG, and PMMA-grafted Si-NP systems show a weaker spatial correlation compared to the PE-grafted Si-NP system.It is worth noting here that, due to the computationally intensive nature of the all-atom modelling of grafted Si-NP systems, in this work, we have not computed the PMF between the Si-NPs of diameter >2 nm. It would be interesting to explore how the effective interaction depends on the size of the Si-NP, in addition to the length of the grafting polymer chains and solvent properties. We also acknowledge that in our CG simulations, the grafted Si-NPs are modelled as spheres, which neglects the entropic contributions of the grafting groups. This approximation could potentially influence the overall system's bulk behavior. Therefore, employing a more refined modelling approach that accounts for this entropic factor would be desirable to more accurately capture the full complexity of the system.
On a general note, this study provides deeper insights into the surface polarity control through nanoparticle surface–ligand grafting and its effect on solvent-mediated interaction between the dispersed nanoparticles in solvent. This study also sheds new light on the non-trivial relationship between the effective interaction between the nanoscale building blocks and the bulk structural and thermodynamic properties. These insights are important prerequisites for finding rational inverse (bottom-up) design strategies for soft functional materials. An interesting avenue for future research would be to map the local (effective) interactions onto the nature of the free energy landscape containing fluid and crystalline phase(s) of the system. This control of the global free energy landscape through local interactions can potentially enable us to control the self-assembly pathways and kinetics by avoiding the undesired structures (or, minima in the free energy landscape).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the anonymous reviewers for their insightful comments and suggestions. R. S. S. acknowledges financial support from DST-SERB (Grant No. SRG/2020/001415 and CRG/2023/002975). Y. S. acknowledges financial support from IISER Tirupati. The computations were performed at the IISER Tirupati computing facility and at PARAM Brahma at IISER Pune.Notes and references
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed.
- C. N. Likos, Soft Matter, 2006, 2, 478–498 RSC.
- J. A. Fan, C. Wu, K. Bao, J. Bao, R. Bardhan, N. J. Halas, V. N. Manoharan, P. Nordlander, G. Shvets and F. Capasso, Science, 2010, 328, 1135–1138 CrossRef CAS PubMed.
- K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297 CrossRef CAS PubMed.
- M. Karg, T. A. König, M. Retsch, C. Stelling, P. M. Reichstein, T. Honold, M. Thelakkat and A. Fery, Mater. Today, 2015, 18, 185–205 CrossRef CAS.
- K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Chem. Rev., 2012, 112, 2739–2779 CrossRef CAS PubMed.
- M. Dijkstra and E. Luijten, Nat. Mater., 2021, 20, 762 CrossRef CAS PubMed.
- Z. M. Sherman, M. P. Howard, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, J. Chem. Phys., 2020, 152, 140902 CrossRef CAS PubMed.
- S. Torquato, Soft Matter, 2009, 5, 1157–1173 RSC.
- V. Pryamtisyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, J. Chem. Phys., 2009, 131, 221102 CrossRef PubMed.
- B. Srinivasan, T. Vo, Y. Zhang, O. Gang, S. Kumar and V. Venkatasubramanian, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18431–18435 CrossRef CAS PubMed.
- L. Cademartiri and K. J. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef CAS PubMed.
- T. Vo, V. Venkatasubramanian, S. Kumar, B. Srinivasan, S. Pal, Y. Zhang and O. Gang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4982–4987 CrossRef CAS PubMed.
- A. L. Ferguson, J. Phys.: Condens. Matter, 2017, 30, 043002 CrossRef PubMed.
- A. W. Long and A. L. Ferguson, Mol. Syst. Des. Eng., 2018, 3, 49–65 RSC.
- S. Whitelam and I. Tamblyn, Phys. Rev. Lett., 2021, 127, 018003 CrossRef CAS PubMed.
- H. Dehne, A. Reitenbach and A. Bausch, Nat. Commun., 2021, 12, 6811 CrossRef CAS PubMed.
- J. Russo, F. Romano, L. Kroc, F. Sciortino, L. Rovigatti and P. Šulc, J. Phys.: Condens. Matter, 2022, 34, 354002 CrossRef CAS PubMed.
- G. M. Coli, E. Boattini, L. Filion and M. Dijkstra, Sci. Adv., 2022, 8, eabj6731 CrossRef PubMed.
- A. Bupathy, D. Frenkel and S. Sastry, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2119315119 CrossRef CAS PubMed.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- Q. Chen, J. Yan, J. Zhang, S. C. Bae and S. Granick, Langmuir, 2012, 28, 13555–13561 CrossRef CAS PubMed.
- E. R. Liepold, A. Smith, B. Lin, J. de Pablo and S. A. Rice, J. Chem. Phys., 2019, 150, 044904 CrossRef PubMed.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos and V. Pryamitsyn, et al. , Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- G. Hummer, S. Garde, A. E. Garcia, M. E. Paulaitis and L. R. Pratt, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1552–1555 CrossRef CAS PubMed.
- J. Engstler and N. Giovambattista, J. Phys. Chem. B, 2018, 122, 8908–8920 CrossRef CAS PubMed.
- R. Zangi, M. Hagen and B. J. Berne, J. Am. Chem. Soc., 2007, 129, 4678–4686 CrossRef CAS PubMed.
- E. W. Gehrels, W. B. Rogers and V. N. Manoharan, Soft Matter, 2018, 14, 969–984 RSC.
- A. Hensley, W. M. Jacobs and W. B. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2114050118 CrossRef CAS PubMed.
- E. W. Gehrels, W. B. Rogers, Z. Zeravcic and V. N. Manoharan, ACS Nano, 2022, 16, 9195–9202 CrossRef CAS PubMed.
- A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Nature, 2009, 462, 773–777 CrossRef CAS PubMed.
- S. Sacanna and D. J. Pine, Adv. Colloid Interface Sci., 2011, 16, 96–105 CAS.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- M. Dijkstra, Adv. Chem. Phys., 2014, 156, 35–71 CrossRef.
- Y.-L. Lin, C.-S. Chiou, S. K. Kumar, J.-J. Lin, Y.-J. Sheng and H.-K. Tsao, J. Phys. Chem. C, 2011, 115, 5566–5577 CrossRef CAS.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801 CrossRef PubMed.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581–600 CrossRef CAS PubMed.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS.
- F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558 Search PubMed.
- A. Neophytou, D. Chakrabarti and F. Sciortino, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109776118 CrossRef CAS PubMed.
- M. Karg, T. A. König, M. Retsch, C. Stelling, P. M. Reichstein, T. Honold, M. Thelakkat and A. Fery, Mater. Today, 2015, 18, 185–205 CrossRef CAS.
- P. R. ten Wolde and D. Frenkel, Science, 1997, 277, 1975–1978 CrossRef CAS PubMed.
- M. Santra, R. S. Singh and B. Bagchi, J. Phys. Chem. B, 2013, 117, 13154–13163 CrossRef CAS PubMed.
- R. S. Singh and B. Bagchi, J. Chem. Phys., 2014, 140, 164503 CrossRef PubMed.
- M. Santra, R. S. Singh and B. Bagchi, Phys. Rev. E, 2018, 98, 032606 CrossRef CAS.
- W. D. Piñeros, M. Baldea and T. M. Truskett, J. Chem. Phys., 2016, 145, 1–7 CrossRef PubMed.
- W. D. Piñeros, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, J. Chem. Phys., 2018, 148, 1–8 CrossRef PubMed.
- B. Peng, Z. Liu and Y. Jiang, J. Phys. Chem. B, 2022, 126, 847–857 CrossRef CAS PubMed.
- R. Mao, B. Minevich, D. McKeen, Q. Chen, F. Lu, O. Gang and J. Mittal, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302037120 CrossRef CAS PubMed.
- B. W. Rogers and J. C. Crocker, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15687 CrossRef PubMed.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Phys. Chem. Chem. Phys., 2016, 18, 6373–6393 RSC.
- F. Sciortino, Y. Zhang, O. Gang and S. K. Kumar, ACS Nano, 2020, 14, 5628–5635 CrossRef CAS PubMed.
- R. Francis, N. Joy, E. Aparna and R. Vijayan, Polym. Rev., 2014, 54, 268–347 CrossRef CAS.
- A. Akbari, R. Yegani and B. Pourabbas, Colloids Surf., A, 2015, 484, 206–215 CrossRef CAS.
- J. Pribyl, B. Benicewicz, M. Bell, K. Wagener, X. Ning, L. Schadler, A. Jimenez and S. Kumar, ACS Macro Lett., 2019, 8, 228–232 CrossRef CAS PubMed.
- P. E. M. Lopes, V. Murashov, M. Tazi, E. Demchuk and A. D. MacKerell, J. Phys. Chem. B, 2006, 110, 2782–2792 CrossRef CAS PubMed.
- I. Vorobyov, V. M. Anisimov, S. Greene, R. M. Venable, A. Moser, R. W. Pastor and A. D. MacKerell, J. Chem. Theory Comput., 2007, 3, 1120–1133 CrossRef CAS PubMed.
- H. Eslami, M. Rahimi and F. Müller-Plathe, Macromolecules, 2013, 46, 8680–8692 CrossRef CAS.
- Y. K. Choi, S.-J. Park, S. Park, S. Kim, N. R. Kern, J. Lee and W. Im, J. Chem. Theory Comput., 2021, 17, 2431–2443 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701 CrossRef CAS PubMed.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci and R. A. Broglia, et al. , Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and G. L. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- S. Nösè, Mol. Phys., 1984, 52, 255 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- D. Bauer, WHAM – An efficient weighted histogram analysis implementation written in Rust, Zenodo, 2021 Search PubMed.
- D. Rosenbaum, P. C. Zamora and C. F. Zukoski, Phys. Rev. Lett., 1996, 76, 150–153 CrossRef CAS PubMed.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318–321 CrossRef CAS PubMed.
- A.-C. Yang and C.-I. Weng, J. Phys. Chem. C, 2010, 114, 8697–8709 CrossRef CAS.
- M. Kanduc, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767 CrossRef CAS PubMed.
- S. Sharma and P. G. Debenedetti, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4365 CrossRef CAS PubMed.
- R. C. Remsing, E. Xi, S. Vembanur, S. Sharma, P. G. Debenedetti, S. Garde and A. J. Patel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8181 CrossRef CAS PubMed.
- S. Banerjee, R. S. Singh and B. Bagchi, J. Chem. Phys., 2015, 142, 134505 CrossRef PubMed.
- B. J. Berne, J. D. Weeks and R. Zhou, Annu. Rev. Phys. Chem., 2009, 60, 85 CrossRef CAS PubMed.
- C. Williams, F. Brochard and H. L. Frisch, Annu. Rev. Phys. Chem., 1981, 32, 433 CrossRef CAS.
- J. Kraus, P. Müller-Buschbaum, T. Kuhlmann, D. W. Schubert and M. Stamm, Europhys. Lett., 2000, 49, 210 CrossRef CAS.
- F. Saija and P. V. Giaquinta, J. Phys.: Condens. Matter, 1996, 8, 8137 CrossRef CAS.
- T. T. R. Chopra and J. Errington, J. Phys. Chem. B, 2010, 114, 10558 CrossRef PubMed.
- A. George and W. W. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, D50, 361 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00512k |
| This journal is © The Royal Society of Chemistry 2024 |