Open Access Article
Open Access ArticleConcentration and temperature dependent interactions and state diagram of dispersions of copolymer microgels†
José
Ruiz-Franco
 abc,
Rodrigo
Rivas-Barbosa
abc,
Rodrigo
Rivas-Barbosa
 bd,
Mayra A.
Lara-Peña
de,
José R.
Villanueva-Valencia
bd,
Mayra A.
Lara-Peña
de,
José R.
Villanueva-Valencia
 d,
Angel
Licea-Claverie
d,
Angel
Licea-Claverie
 f,
Emanuela
Zaccarelli
f,
Emanuela
Zaccarelli
 *ab and
Marco
Laurati
*ab and
Marco
Laurati
 *e
*e
aCNR Institute of Complex Systems, Uos Sapienza, Piazzale Aldo Moro 2, 00185, Roma, Italy. E-mail: emanuela.zaccarelli@cnr.it
bDepartment of Physics, Sapienza University of Rome, Piazzale Aldo Moro 2, 00185 Roma, Italy
cPhysical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, 6708WE Wageningen, The Netherlands
dDivisión de Ciencias e Ingenierías, Universidad de Guanajuato, Lomas del Bosque 103, 37150 León, Mexico
eDipartimento di Chimica and CSGI, Università di Firenze, 50019 Sesto Fiorentino, Italy. E-mail: marco.laurati@unifi.it
fCentro de Graduados e Investigación en Química del Tecnológico Nacional de México/Instituto Tecnológico de Tijuana, 22500 Tijuana, Mexico
First published on 2nd May 2023
Abstract
We investigate by means of small angle neutron scattering experiments and numerical simulations the interactions and inter-particle arrangements of concentrated dispersions of copolymer poly(N-isopropylacrylamide)–poly(ethylene glycol methyl ether methacrylate) (PNIPAM–PEGMA) microgels across the volume phase transition (VPT). The scattering data of moderately concentrated dispersions are accurately modeled at all temperatures by using a star polymer form factor and static structure factors calculated from the effective potential obtained from simulations. Interestingly, for temperatures below the VPT temperature (VPTT), the radius of gyration and blob size of the particles significantly decrease with increasing the effective packing fraction in the non-overlapping regime. This is attributed to the presence of charges in the system associated with the use of an ionic initiator in the synthesis. Simulations using the experimentally corroborated interaction potential are used to explore the state diagram in a wide range of effective packing fractions. Below and slightly above the VPTT, the system undergoes an arrest transition mainly driven by the soft repulsion between the particles. Only well above the VPTT the system is found to phase separate before arresting. Our results highlight the versatility and potential of copolymer PNIPAM–PEGMA microgels to explore different kinds of arrested states balancing attraction and repulsion by changing temperature and packing fraction.
1 Introduction
Microgel particles are cross-linked polymer networks of colloidal size. Their internal polymer structure can be sensitive to external stimuli, such as temperature,1 pH,2 or external fields,3 by accurately tailoring its physicochemical properties. This results in colloids with variable physical and chemical properties, which offer the possibility to explore fundamental physics problems, and can be exploited in multiple applications. One of the most studied types of microgels is made of thermoresponsive poly(N-isopropylacrylamide) (PNIPAM), which exhibits a volume phase transition (VPT) at temperature Tc ≈ 32 °C.4,5 Thus, the size and stiffness of the particle can be tuned by changing the temperature.6 In particular, for T < Tc, microgels are soft and display a spherical core-corona architecture, whereas for T > Tc, the stiffness increases and the particles undergo a collapse,7,8 which is an echo of the underlying coil-to-globule transition of PNIPAM chains. This is driven by a change in the polymer affinity to the solvent,9 which also results in the modification of microgel–microgel interactions at the colloidal length scale. In particular, experiments show the onset of an effective attraction in the collapsed state, signaled by aggregation and phase separation in highly concentrated suspensions.10,11 The adaptability of PNIPAM microgels has contributed to their wide diffusion in applications such as drug delivery,12,13 regenerative scaffolds,14 biosensing15 and inks for bio-interfaces design,16 to name a few.Furthermore, PNIPAM microgels can be programmed to have specific stimuli-response and/or additional properties through the inclusion of a second type of polymer. This inclusion can be realized in different ways: one possibility is that the second component is incorporated in the form of a separated shell or core, giving rise to so-called core–shell microgels. The second polymer can be non-thermoresponsive like poly(ethylene glycol) (PEG) or its methacrylated variant PEGMA, providing a more biocompatible shell for biomedical applications.17,18 Alternatively, it can also be thermosensitive, leading to core–shell microgels exhibiting a complex swelling behavior that cannot be approximated as the sum of the transitions from each polymer.19–21 Also classified as core–shell microgels are systems where PNIPAM acts as a shell surrounding hard particles, i.e., non-thermoresponsive ones such as gold or polystyrene silica.22,23 The resulting microgel acquires new functionalities thanks to the stimuli-responsive shell.24 The second component can be also incorporated within the PNIPAM network, leading in this case to so-called copolymer microgels. It is possible to produce interpenetrating network (IPN) microgels, where the networks of PNIPAM and the additional polymer are chemically non-crosslinked with one another.25,26 In this case, a micro-phase separation is induced by playing with the stimuli-response of each polymer type, generating a non-uniform collapse.27,28 A different scenario occurs when polymer chains, rather than a full network, are attached within the PNIPAM network.18,29–32 In the case of a thermoresponsive copolymer, such as poly(N-isopropyl-methacrylamide) (PNIPMAM) or poly-N,N-diethylacrylamide (PDEAAM), microgels present anomalous deswelling and variation of the VPT temperature.29,30 Instead, addition of a non-thermoresponsive, hydrophilic comonomer like PEGMA leads to a shift of the VPT temperature to larger values and to a progressive reduction of the magnitude of deswelling,17,33 that was attributed to a changed balance in hydrophobicity and hydrophilicity. In these microgels PEGMA is expected to be mainly concentrated on the exterior of the particle, due to precipitation of PNIPAM under the synthesis conditions.17,18,31 However NMR studies in ref. 31 indicate that at least a fraction of PEGMA becomes immobilized during collapse across the VPT. Recently, through a combination of SANS measurements and monomer-resolved simulations, we confirmed that PNIPAM-co-PEGMA copolymer microgels exhibit a heterogeneous collapse, with the formation of two denser regions, responsible for the shift of the VPT transition to higher temperatures.32 In the same work we also showed that the experimental particle form factor can be best described assuming that part of the PEGMA, mostly distributed on the periphery of the particle, is contained within the PNIPAM network, coherent with indications of ref. 31. Furthermore, simulations evidenced the presence in this case of an enhanced attraction above the VPT temperature, different from ionic copolymerized microgels34 in which the effective attraction emerging from the solvophobicity of the cores can be partially shielded, preventing or retarding phase separation in highly concentrated suspensions. While previous studies allowed a thorough characterization of the single particle shape and responsiveness, essentially unexplored remains the effect of copolymerization on the inter-particle interactions at moderate and high particle concentrations and as a function of temperature. This is crucial for applications of copolymer microgels in developing electronic and photonic devices,35,36 drug delivery25 and cultivation of adherently growing cells.37 In addition, the presence of PEGMA paves the way toward biomedical applications,38–40 due to its non-cytotoxicity41 and, thus, increased biocompatibility.
The aim of the present work is that of elucidating the interactions of copolymer microgels of PNIPAM–PEGMA. In particular, we explore a range of temperatures crossing the VPT as a function of microgel concentration. This procedure combines small-angle neutron scattering (SANS) experiments and numerical simulations. SANS measurements at different concentrations are described by using the static structure factors obtained from the effective interactions calculated through monomer-resolved simulations. We find that below and close to the VPTT, the interactions are soft and repulsive, so that a star polymer or Hertzian description well captures the structure of the resulting copolymer microgels. We also find a general reduction of the microgel size that happens before particle overlap with increasing concentration. On the other hand, above the VPTT, the size reduction is less pronounced owing to the more compact conformation. We further use the calculated effective interactions to study the static and dynamic properties of concentrated dispersions as a function of packing fraction at these different temperatures, finding the onset of dynamical arrest at relatively large packing fractions below the VPTT. Such onset is shifted to lower concentrations as T increases. At the highest studied T phase separation also occurs, thus retarding the dominant role of attraction with respect to standard PNIPAM microgels. Our results link the microgel morphology controlled by tuning the internal polymer network and its effects on the behavior of PNIPAM–PEGMA copolymer microgel dispersions.
2 Materials and methods
2.1 Experimental system
We report in the ESI† also a SEM image of a representative PNIPAM–PEGMA collapsed particle confirming that there is no evidence of a PNIPAM(core)–PEGMA(shell) internal structure of the particles.
2.2 Numerical simulations
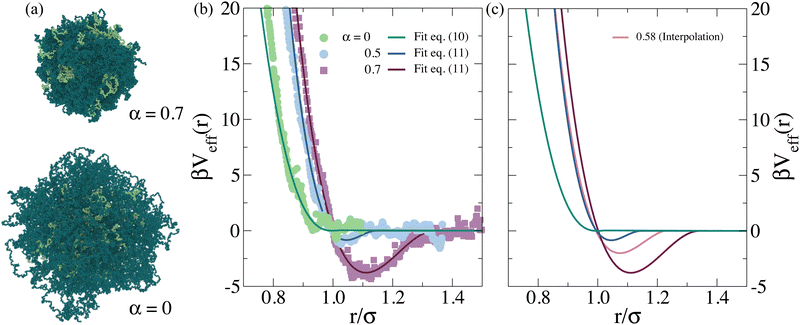
We consider copolymer PNIPAM–PEGMA microgels that were previously assembled following two steps,32 and whose final structure was fixed using the Kremer–Grest bead-spring model.47 Thus, all particles interact via a Weeks–Chandler–Andersen (WCA) potential, defined as: | (1) |
 | (2) |
 | (3) |
According to our previous study in ref. 32, here we focus on the case where PEGMA chains are attached within the polymer network since this conformation was found to reproduce the experimental particle morphology. For this type of copolymer microgels, the effective interaction between two microgels was evaluated by using the umbrella sampling technique at different values of α, where a series of independent configurations along a reaction coordinate are sampled by using a bias potential.53,54 In our case, we have considered the centers of mass distance between two copolymer microgels as the reaction coordinate, with the bias potential being harmonic. Then, we evaluate the bias probability distribution Pb(r,Δi) of finding the macromolecules' centers of mass at distance r given the equilibrium length of the spring μi from our simulations. Later, the contribution from the bias potential is removed, Pu(r,Δi) and subsequently unbiased probability distributions are merged into P(r) via a least-squares method. In this way, the potential of mean force is expressed as
| Veff(r) = −kBT[P(r)] + C, | (4) |
For α = 0.0, the effective interaction numerically calculated is well-fitted by a Hertzian model, that is usually employed for microgels,6,55 which is expressed as
| βVH(r) = U(1 − r/σH)5/2θ(1 − r/σH), | (5) |
Instead, evidence of an effective attraction is already found for α ∼ 0.5, well below the PNIPAM VPTT, while the evaluation of the potential was possible until α = 0.7. We could just use the calculated potential as a numerical table, but it is more practical to adopt a phenomenological analytical form. To this aim, we fit the numerical potential with the expression,
 | (6) |
Using the Hertzian potential in eqn (5) for α = 0.0 and the attractive potentials Veff(r) in eqn (6) for different values of α, we then perform Langevin dynamics (LD) simulations, where the total force on the i-th particle is expressed as
| Fi = FCi + FDi + FRi. | (7) |
Here, FCi = −∇Veff(r) represents the conservative force. The second term represents the drag force, defined as FDi = −ξmivi with friction coefficient fixed to be ξ = 10mi/t, mi specifies the mass and vi is the particle velocity. Finally, FRi is the random force characterized by 〈FRi〉 = 0 and 〈FRi(t)FRi(t′)〉 = 6ξkbTδ(t − t′).
In all cases, we consider N = 2000 polydisperse particles whose diameters are described by a Schultz distribution56 with unitary mean and standard deviation equal to PD = 25%, matching the experimental polydispersity. The packing fraction is thus defined as  where V represents the volume of the simulation box. Since the temperature effects are encrypted in the effective potential interaction, we always maintain the temperature T = ε/kb in our simulations. All beads have unit mass, and the integration time step is
where V represents the volume of the simulation box. Since the temperature effects are encrypted in the effective potential interaction, we always maintain the temperature T = ε/kb in our simulations. All beads have unit mass, and the integration time step is  . The Langevin equation was integrated using the self-adaptive OVRVO scheme, which is suitable for both equilibrium and nonequilibrium dynamics.57,58
. The Langevin equation was integrated using the self-adaptive OVRVO scheme, which is suitable for both equilibrium and nonequilibrium dynamics.57,58
2.3 Small-angle neutron scattering (SANS)
| I(Q) = ϕV(Δρ)2P(Q)S(Q) | (8) |
 | (9) |
For T = 40 °C an additional blob term was included in the expression of the form factor to take into account the possible presence of structural heterogeneity of the corona induced by the presence of PEGMA inside the network that hinders the deswelling transition of PNIPAM. The expression of the form factor reads in this case:
 | (10) |
 | (11) |
For the potential calculated for α = 0.7, the copolymer microgel collapses (see Fig. 1(a)), and we find the occurrence of phase separation also at very low packing fractions. This is also confirmed by the calculation of the second virial coefficient normalized to the hard sphere value,  also reported in Table S3 (ESI†). To compare to experimental data, which do not show phase separation in the SANS investigated range, we adopt an interpolation of the effective potential in the range α ∈ [0.5, 0.7]. In order to choose the right value of α we use the following additional information from experiments: (i) at 40 °C the system presents phase separation at a packing fraction ϕeff ∼ 1.6, amounting to ϕ ≳ 0.18, as indicated by the strong increase of turbidity and by additional velocimetry measurements, which show the occurrence of total slip in the sample, a typical response of attractive samples;64 (ii) at 30 °C full phase separation is never observed, although at large packing fractions the system displays characteristic features of gelation. Taking into account these facts, we consider effective potentials at a value of α for which these features are approximately reproduced and, at the same time, that are able to fit the experimental SANS data. The interaction potentials that fulfill these requirements correspond to roughly α = 0.5 for 30 °C and α = 0.58 for 40 °C and are shown in Fig. 1(b).
also reported in Table S3 (ESI†). To compare to experimental data, which do not show phase separation in the SANS investigated range, we adopt an interpolation of the effective potential in the range α ∈ [0.5, 0.7]. In order to choose the right value of α we use the following additional information from experiments: (i) at 40 °C the system presents phase separation at a packing fraction ϕeff ∼ 1.6, amounting to ϕ ≳ 0.18, as indicated by the strong increase of turbidity and by additional velocimetry measurements, which show the occurrence of total slip in the sample, a typical response of attractive samples;64 (ii) at 30 °C full phase separation is never observed, although at large packing fractions the system displays characteristic features of gelation. Taking into account these facts, we consider effective potentials at a value of α for which these features are approximately reproduced and, at the same time, that are able to fit the experimental SANS data. The interaction potentials that fulfill these requirements correspond to roughly α = 0.5 for 30 °C and α = 0.58 for 40 °C and are shown in Fig. 1(b).
3 Results
3.1 Effects of concentration below the VPTT
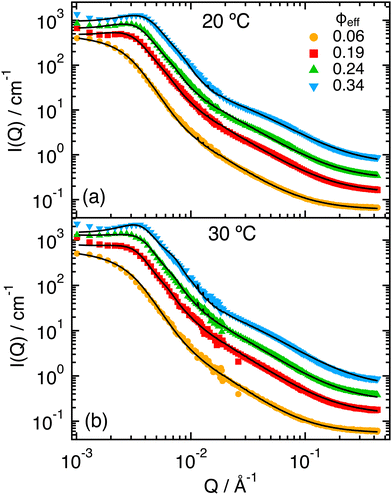
The experimental SANS scattering intensities measured at T = 20 °C for increasing ϕeff (Fig. 2) show the progressive appearance of a peak in the region for Q < 10−2 Å−1, that indicates the increasing contribution of interactions through the structure factor S(Q). The peak moves to larger Q values with increasing ϕeff as a consequence of the reduced inter-particle average distance. However, we notice that the whole intensity curve progressively shifts towards larger Q values, which indicates that the particle size also reduces with increasing ϕeff. One can also note the growth of a shoulder at around Q ≈ 7 × 10−2 Å−1 with increasing packing fraction. This is reminiscent of what was observed for the form factor when increasing T across the VPT,32 where it was associated to the progressive shrinking and compaction of the particles and the formation of a non-uniform density profile due to the presence of the PEGMA within the PNIPAM network. For samples with ϕeff ≥ 0.19 some extra scattering in the region of low Q-values before the structure factor peak might be the result of inhomogeneities and partial aggregation. This extra scattering was not considered in the modeling presented in what follows. Similar behavior was observed for the measurements at T = 30 °C, that are reported in Fig. 2b. | ||
| Fig. 3 Parameters obtained by fitting the SANS scattering intensities I(Q) using eqn (8), with the form factor P(Q) corresponding to the Dozier model of eqn (9) and the structure factor S(Q) calculated by modeling the interactions through the potential obtained from simulations (with α = 0.0 for 20 °C and α = 0.5 for 30 °C) or from the star polymer potential (with f = 500), as a function of ϕeff: (a) radius of gyration Rg and blob size ξ1, (b) Same parameters normalized by their values at the smallest value of ϕeff, R0g and ξ01. (c) Exponent μ1 and (d) packing fraction used for the calculation of S(Q), ϕ. | ||
Concerning the blob size, one observes (Fig. 3a) that it remains almost constant up to ϕeff = 0.19 (ξ1 ≈ 200 Å) and then reduces down to about one fourth for ϕeff = 0.34 (ξ1 ≈ 50 Å). Moreover, the relative shrinkage of the blob, ξ1/ξ01, at high ϕeff values becomes larger than that of the core, Rg/R0g (Fig. 3b), where R0g and ξ01 are the values of Rg and ξ obtained at the smallest measured ϕeff. According to the Daoud and Cotton model of a star polymer,73 the blob size and radius of gyration should be linked through the expression 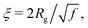 being f the number of arms of the star. The different dependence on ϕeff observed for Rg and ξ thus suggests that the effective value of f for the microgels changes with changing packing fraction, which reflects a change in the conformation of the polymer chains for the different values of ϕeff. In particular, the stronger reduction of ξ at large ϕeff would correspond to an increase in f, that is consistent with a compaction of the microgel due to collapse. Note also that the relative variation of ξ and Rg appears similar to that of the corona and core observed for T-induced deswelling of PNIPAM microgels with the same kind of ionic initiator.74
being f the number of arms of the star. The different dependence on ϕeff observed for Rg and ξ thus suggests that the effective value of f for the microgels changes with changing packing fraction, which reflects a change in the conformation of the polymer chains for the different values of ϕeff. In particular, the stronger reduction of ξ at large ϕeff would correspond to an increase in f, that is consistent with a compaction of the microgel due to collapse. Note also that the relative variation of ξ and Rg appears similar to that of the corona and core observed for T-induced deswelling of PNIPAM microgels with the same kind of ionic initiator.74
The coefficient μ1 remains approximately constant as a function of ϕeff for both temperatures. At T = 20 °C we found μ ≈ 0.66, which corresponds to good solvent conditions (ν = 3/5). It increases slightly for T = 30 °C, as expected from the closer vicinity of this temperature to the LCST. Finally, the packing fraction used to calculate the structure factors used to model the data, ϕ, shows a different trend for the two interaction potentials (Fig. 3d). For the star polymer potential it is approximately equal to ϕeff, except for the most concentrated sample, where it is slightly smaller. Instead, for the calculated effective potential in Fig. 1, ϕ is initially slightly smaller but comparable to ϕeff, while it remains almost constant around ϕ = 0.16 for ϕeff ≳ 0.2. This trend might be reflecting the progressive reduction in particle size that we associated with charge effects, that competes with the increase in particle number density.
3.2 Effects of concentration above the VPTT
The SANS intensities measured at T = 40 °C (Fig. 4) for increasing ϕeff show, as for the lower temperatures, changes in the region Q < 10−2 Å−1 associated with the effects of the structure factor S(Q). However, in this case the variation is much more moderate and does not result in a clear peak in I(Q). This can be attributed to the particle deswelling that occurs above the VPTT, and the consequent reduction of the effective volume fraction of the system. In addition, one observes that the Guinier regime of the curves shifts to larger Q values with increasing ϕeff, indicating a further reduction of the particle size with increasing packing fraction. Finally, one can notice the presence of a pronounced shoulder around Q ≈ 10−2 Å−1, which has been associated in previous work to the non-homogeneous density profile of the particles at high T, that is induced by the presence of the unresponsive PEGMA in the interior of the PNIPAM network.32 Note that the shoulder becomes increasingly pronounced with increasing ϕeff, and that an additional small inflection seems to develop around Q ≈ 10−1 Å−1 for the samples with larger ϕeff. | ||
| Fig. 5 Parameters obtained by fitting the SANS scattering intensities I(Q) using eqn (8), with the form factor P(Q) corresponding to the Dozier model of eqn (9) and the structure factor S(Q) calculated by modeling the interactions through the potential obtained from simulations for α = 0.58, as a function of ϕeff (a) radius of gyration Rg and blob sizes ξ1 and ξ2, (b) Same parameters normalized by their values at the smallest value of ϕeff, R0g, ξ01 and ξ02, (c) Exponents μ1 and μ2, (d) Packing fraction used for the calculation of S(Q), ϕ. | ||
The values obtained for the exponents μ1 and μ2 (Fig. 5c) shed some light on the different nature of the two blob terms. Indeed μ1, which was already associated to the blob scattering of PNIPAM below the VPTT, attains now a value of about 2, which is consistent with the poor nature of the water solvent at T = 40 °C (ν = 1/3). It is also approximately constant for all samples. Instead μ2, which is also constant for all values of ϕeff, presents a value of 0.66, which indicates good solvent conditions (ν = 3/5). This suggests that the second blob term can be associated with the PEGMA chains. Results in Fig. 5b thus indicate that the size of PEGMA blobs tends to slightly increase with packing faction, possibly as an effect of a larger available volume when the PNIPAM chains collapse.
Finally, the values of the fitting packing fraction ϕ are quite small and slightly increase with increasing ϕeff. This is consistent with the deswelling transition, that leads to a consistent reduction of the packing fraction associated with the reduction of the particle size. The fact that the value increases monotonically is different from what observed at smaller temperatures. This is however in agreement with the fact that the size reduction induced by the increase of ϕeff is now much less pronounced, and therefore does not dominate over the increase in particle number density as for the lower temperatures. Finally, we note that the highest measured ϕ is still below the value at which we find indications of phase separation (≈0.18), consisting in a strong increase of turbidity and the onset of total wall slip in velocimetry measurements, as already mentioned in section “Data analysis” (data not shown).
3.3 Arrested states in copolymer microgels
The satisfactory comparison between measured and calculated scattering intensities has validated the effective interactions that we have estimated from simulations over the investigated range of packing fractions. Now, we use simulations to extend such range and to study theoretically the behavior of the dispersions at higher packing fractions until an arrested state is formed or the onset of phase separation is detected. To this aim, we perform LD simulations of polydisperse particles with PD = 25%. We consider the three different effective interactions, corresponding to the three temperatures studied in experiments (α = 0.0, 0.50, 0.58). At T = 20 °C, the interactions are fully compatible with a repulsive Hertzian model, described in eqn (5). For the other two temperatures, an additional attraction arises in the effective potential, and we use the phenomenological expression given in eqn (6), with the parameters provided in Table S3 (ESI†). In the simulations, we monitor both static and dynamic properties with varying ϕ until the system is not able to equilibrate any longer due to an intervening arrest or phase separation.First, we calculate the static structure factors S(Q) of the polydisperse system, defined as
 | (12) |
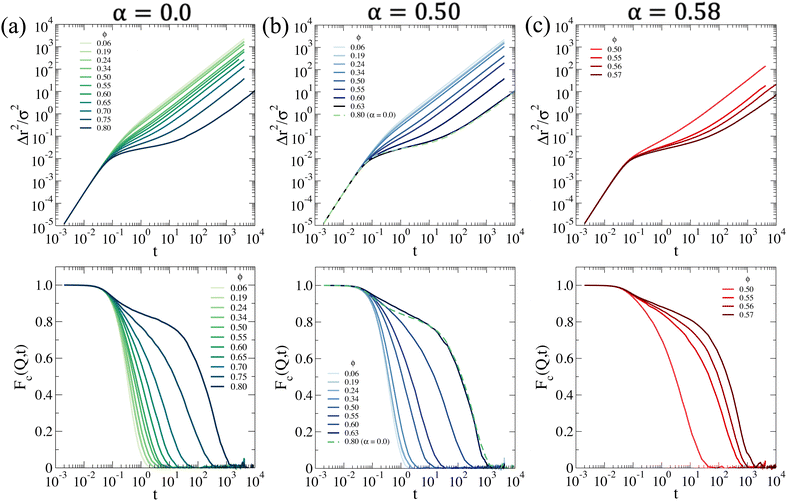
 being averaged over all particles and 〈⋯〉 the average over different configurations. From Fig. 6a, we see that at low temperatures a non-monotonic behavior of the main peak of S(Q) occurs for ϕ ≳ 0.50. This loss of local order is typical of Hertzian systems, where a reentrant behavior of static correlations has been previously reported.76,77 However, interestingly, the addition of a large polydispersity in the present system introduces a novel feature in the behavior of S(Q) with respect to monodisperse Hertzian, namely that with the further increase of ϕ the first peak eventually goes below 1. We thus wonder whether we are seeing an unphysical behavior due to the pure Hertzian modeling. Indeed, it is well-known that microgels have a complex inner structure, with a more compact core, that has been for example modeled as a multi-Hertzian to take this into account.78 We thus repeat simulations for representative state points, where we consider the addition of a steeper repulsion, modeling the inner core, at shorter distances, as discussed in more detail in the ESI.† The size of the inner core is taken from the experimental Rg. We find that the effects of the core are not observed in the investigated range of ϕ and its presence becomes evident only at much larger packing fractions, where dynamical arrest has already taken place (as shown below). Thus, the anomalous feature of S(Q) having the main peak below 1 is the result of the combination of the Hertzian model and the large polydispersity of the system, as also discussed in the ESI.† It is important to note that similar behaviors of S(Q) at high concentrations have been previously reported for polydisperse eye-lens proteins79 and also, for anisotropic antibodies.80 It remains to be investigated in the present systems whether such features hold at high ϕ, where steeper excluded volume effects may enter into play and prevent the softening related to the Hertzian modeling. This should be addressed in future works by performing measurements of the system at higher ϕ or by trying to perform simulations of monomer-resolved microgels, rather than of a coarse-grained model.
being averaged over all particles and 〈⋯〉 the average over different configurations. From Fig. 6a, we see that at low temperatures a non-monotonic behavior of the main peak of S(Q) occurs for ϕ ≳ 0.50. This loss of local order is typical of Hertzian systems, where a reentrant behavior of static correlations has been previously reported.76,77 However, interestingly, the addition of a large polydispersity in the present system introduces a novel feature in the behavior of S(Q) with respect to monodisperse Hertzian, namely that with the further increase of ϕ the first peak eventually goes below 1. We thus wonder whether we are seeing an unphysical behavior due to the pure Hertzian modeling. Indeed, it is well-known that microgels have a complex inner structure, with a more compact core, that has been for example modeled as a multi-Hertzian to take this into account.78 We thus repeat simulations for representative state points, where we consider the addition of a steeper repulsion, modeling the inner core, at shorter distances, as discussed in more detail in the ESI.† The size of the inner core is taken from the experimental Rg. We find that the effects of the core are not observed in the investigated range of ϕ and its presence becomes evident only at much larger packing fractions, where dynamical arrest has already taken place (as shown below). Thus, the anomalous feature of S(Q) having the main peak below 1 is the result of the combination of the Hertzian model and the large polydispersity of the system, as also discussed in the ESI.† It is important to note that similar behaviors of S(Q) at high concentrations have been previously reported for polydisperse eye-lens proteins79 and also, for anisotropic antibodies.80 It remains to be investigated in the present systems whether such features hold at high ϕ, where steeper excluded volume effects may enter into play and prevent the softening related to the Hertzian modeling. This should be addressed in future works by performing measurements of the system at higher ϕ or by trying to perform simulations of monomer-resolved microgels, rather than of a coarse-grained model.
We now focus at intermediate temperatures (α = 0.5), where the addition of a moderate attraction has significant effects on the structure, as shown in Fig. 6b. In particular, we can equilibrate the system up to ϕ ∼ 0.62, above which the dynamics becomes too slow (as discussed in the following) and, contrary to the α = 0.0 case, we do not observe a reentrance in the first peak of S(Q). Rather, the peak monotonically increases as in standard fluids. This indicates that the attraction is compensating the Hertzian tendency to shrink and thus induce a reentrant behavior. In addition, at high Q, we observe a structure factor that is overall staying above 1, again contrary to the case of α = 0.0 where it is largely below this. However, we can exclude any sign of heterogeneity in the samples, as there is no upturn of S(Q) visible at low Q, as also evident from the snapshots, shown in Fig. 6b. This is also confirmed by the fact that the large-Q behavior of S(Q) tends to 1 in all cases. Completely different is the situation at α = 0.58, shown in Fig. 6c, where we clearly detect phase separation, that is evident in the ϕ = 0.15 snapshot and also from the increase in S(Q → 0). We did not follow the phase separation in detail and do not aim to trace a rigorous boundary for it from simulations, but just to qualitatively establish the behavior of the system for this value of α in comparison to experiments, where also phase separation at effective packing fractions above those studied by SANS was detected. Interestingly, we again find homogeneous systems for ϕ ≳ 0.50, as shown from the behavior of S(Q) at low wavevectors. In this case, we can equilibrate the system up to ϕ ∼ 0.57.
On the basis of these results, we then monitor the dynamics and approach dynamical arrest of the microgels outside the phase separation region. First, we calculate the mean squared displacement (MSD) 〈Δr2(t)〉, expressed as
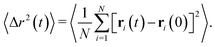 | (13) |
MSD results are shown in Fig. 7a. At T = 20 °C, the system begins to display signs of arrest at ϕ ∼ 0.65, where a plateau in the MSD develops, signaling the onset of caging. This plateau becomes longer and longer until ϕ = 0.80, that is the highest value of ϕ that we are able to equilibrate within our simulation time. On the other hand, the arrested state at T = 30 °C occurs at much smaller packing fractions. However, it is interesting to note that if we superimpose the MSD at ϕ = 0.63 for T = 30 °C and ϕ = 0.80 for T = 20 °C, which share a similar value of the self-diffusion coefficient, the two behaviors are quite similar to each other. Hence, despite the clear differences observed in the behavior of S(Q), the approach to dynamical arrest seems to be similar for these two cases. Hence, the presence of attraction at the higher temperature favours the formation of bonds between the microgels and, thus, induces an anticipated arrest at a lower ϕ, but once this is obtained, the exploration of the cage, the average localization and the time to diffusion are very similar between the two states (with the exception of minor changes in the exploration of the plateau, not visible due to the log–log scale). This is because attraction is of very low-strength (with the minimum depth of the potential ∼−1kBT, see Fig. 1) and, therefore, both arrested states are eventually dominated by the short-distance Hertzian repulsion. We also calculate MSDs for the non-phase-separating states at α = 0.58, which suggest that at the end of phase separation the system is still ergodic, becoming arrested for ϕ ≳ 0.55.
Next, we compute the collective intermediate scattering function Fc(Q,t), defined as
 | (14) |
Finally, we try to sketch a phase diagram using the information inferred from the static properties at a single microgel and dynamics features explored by numerical simulations of samples with copolymer microgel. To determine the glass region, we first extract the long-time self-diffusion coefficient defined as
 | (15) |
To have an operational definition of the glass transition, since we cannot rely on the power-law fits, we consider the system to be “arrested” within the simulation timescale when D ≲ 10−4 (in simulation units). Similarly, we attribute that the onset of the nonergodicity corresponds with a relaxation time τα ≳ 103. With these definitions, we can draw a tentative line of dynamic arrest of our copolymer microgels as a function of ϕ in a summarizing state diagram, reported in Fig. 8(c), which confirms the fact that by increasing T, the system arrests at a lower packing fraction. In the figure, we also show the values of the VPTT for pure PNIPAM microgels and for the present ones as a reference and notice that the macroscopic phase separation region seems to occur only above the VPT temperature. Simulations also suggest that the arrest line meets the tentative binodal on its right-hand side, leaving a liquid pocket at high ϕ and T in between the region of phase separated states and dynamically arrested states.
4 Conclusions
In this work we reported an investigation, combining SANS experiments and numerical simulations, of the temperature and concentration dependent interactions and state diagram of copolymer microgels made of PNIPAM and PEGMA. SANS data measured for moderately concentrated dispersions below and above the VPTT were accurately modeled at different packing fractions by calculating static structure factors using the effective interaction potentials obtained from simulations. At T = 20 °C the system is well described by a Hertzian model with the interaction being repulsive and rather soft, as indicated also by the fact that use of the star polymer potential also provides a good description of the experimental structure factors. Increasing temperature, the interaction as expected becomes more and more attractive. Already at T = 30 °C, well below the VPTT occurring for PNIPAM–PEGMA microgels around VPTT ∼ 37 °C, we find evidence of a weak attraction ∼1kBT at its minimum. This indicates that the fraction of PEGMA chains that resides in the interior of the microgel hinders a complete collapse of the network and enhance the exterior hydrophobic interactions rather than screening them. Further increase of T above the VPTT induces the occurrence of phase separation already at quite low packing fractions (∼0.15–0.20). It will be interesting in the future to compare these results with detailed studies of PNIPAM homopolymer microgels.The SANS experiments also allow us to get useful insights on the modification of the interior structure of the particle as a function of microgel concentration. In particular, we find the interesting result that below the VPTT a significant reduction of the particle core radius and polymer blob scattering is observed well before particle overlap with increasing concentration. On the basis of previous studies,65 we interpret this finding as associated with a concentration dependent osmotic unbalance arising from the presence of residual charges on the surface of the particles due to the use of an ionic initiator in the synthesis. In comparison with previous investigations, the reduction of the particle size appears to be more pronounced, which could be attributed to the larger softness of the poorly cross-linked particles used in this study, that is associated with the star-like particle architecture. In agreement with this interpretation, the reduction becomes almost negligible in the deswollen, compact state above the VPTT.
Using the effective interaction potential validated by comparison with SANS experiments, we additionally performed simulations to explore the state diagram of the system in the region of large packing fractions at the three studied temperatures. We find that, well below the VPTT (T = 20 °C), an arrested state, dominated by the Hertzian repulsion, is formed at large packing fractions ϕlg ≳ 0.8, with the large value of ϕlg compared to hard-sphere like particles arising from the pronounced particle softness and polydispersity. This state is characterized by a structure factor that becomes non-monotonic in its first peak and goes below 1 at high concetrations. Instead, at intermediate temperatures (T = 30 °C) an arrested state is already formed at considerably smaller packing fractions, ϕhg ≳ 0.63, due to the presence of the weak attraction induced by the increasing hydrophobic character of the PNIPAM monomers and the increased compactness of the particles. Finally, above the VPTT for PNIPAM–PEGMA copolymer microgels (T = 40 °C), we find evidence of phase separation at low packing fraction, ϕhg ∼ 0.15, whereas an arrested state emerges at ϕhg ≳ 0.56. An important difference in the numerical model with respect to homopolymer PNIPAM microgels is found in the α-values that are found to reproduce the experimental behavior. While for PNIPAM microgels the VPTT, occurring at ∼32 °C, corresponds to roughly α ∼ 0.65,8,50,51 here we find that a smaller value of α ∼ 0.58 describes the data above the VPTT. We recall that α quantifies the strength of solvophobic attraction between NIPAM monomers only and, thus, it is possible that for copolymer microgels where also additional interactions between PNIPAM and PEGMA are at play, the scale of such effective temperature changes. It will be important to further test this hypothesis for different kinds of copolymer microgels in the future. Finally, it will also be interesting to investigate the high concentration regime and the approach to the arrest in future experiments in order to validate the numerical findings. In particular, it would be intriguing to verify whether there exists a pocket of liquid states at high ϕ and T, as well as the anomalous behavior of S(Q) and to gain more complete information about the tunable interactions of copolymer microgels below and above the VPTT.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Fabrizio Camerin for valuable discussions and Gavino Bassu for assistance with the SEM measurements. R. R.-B., M. L.-P. and M. L. acknowledge support from the project “A1-S-9098” funded by Conacyt within the call “Convocatoria de Investigación Básica 2017–2018” and from “Consorzio per lo Sviluppo dei Sistemi a Grande Interfase” (CSGI). R. R.-B. and E. Z. acknowledge funding from H2020 Marie Curie Actions of the European Commission (ITN SUPERCOL, Grant Agreement 860914). We acknowledge the support of the National Institute of Standards and Technology, U.S. Department of Commerce, in providing the neutron research facilities used in this work and Y. Liu for assistance in using beamline NG7.Notes and references
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- V. Nigro, R. Angelini, M. Bertoldo, V. Castelvetro, G. Ruocco and B. Ruzicka, J. Non-Cryst. Solids, 2015, 407, 361–366 CrossRef CAS.
- T. Colla, P. S. Mohanty, S. Nöjd, E. Bialik, A. Riede, P. Schurtenberger and C. N. Likos, ACS Nano, 2018, 12, 4321–4337 CrossRef CAS PubMed.
- B. Sierra-Martin, J. J. Lietor-Santos, A. Fernandez-Barbero, T. T. Nguyen and A. Fernandez-Nieves, Microgel Suspensions: Fundamentals and Applications, 2011, pp. 71–116 Search PubMed.
- F. Scheffold, Nat. Commun., 2020, 11, 1–13 CrossRef PubMed.
- L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906 CrossRef CAS.
- K. Kubota, S. Fujishige and I. Ando, J. Phys. Chem., 1990, 94, 5154–5158 CrossRef CAS.
- A. Ninarello, J. J. Crassous, D. Paloli, F. Camerin, N. Gnan, L. Rovigatti, P. Schurtenberger and E. Zaccarelli, Macromolecules, 2019, 52, 7584–7592 CrossRef CAS PubMed.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, Phys. Chem. Chem. Phys., 2018, 20, 9997–10010 RSC.
- J. Wu, G. Huang and Z. Hu, Macromolecules, 2003, 36, 440–448 CrossRef CAS.
- I. Bischofberger and V. Trappe, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- Y. Bae, W.-D. Jang, N. Nishiyama, S. Fukushima and K. Kataoka, Mol. BioSys., 2005, 1, 242–250 RSC.
- Y. Guan and Y. Zhang, Soft Matter, 2011, 7, 6375–6384 RSC.
- D. R. Griffin, W. M. Weaver, P. O. Scumpia, D. Di Carlo and T. Segura, Nat. Mater., 2015, 14, 737–744 CrossRef CAS PubMed.
- M. M. Ali, S. Su, C. D. Filipe, R. Pelton and Y. Li, Chem. Commun., 2007, 4459–4461 RSC.
- S. Schmidt, M. Zeiser, T. Hellweg, C. Duschl, A. Fery and H. Möhwald, Adv. Funct. Mater., 2010, 20, 3235–3243 CrossRef CAS.
- D. Gan and L. A. Lyon, Macromolecules, 2002, 35, 9634–9639 CrossRef CAS.
- W. Leobandung, H. Ichikawa, Y. Fukumori and N. A. Peppas, J. Appl. Polym. Sci., 2003, 87, 1678–1684 CrossRef CAS.
- I. Berndt, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2005, 127, 9372–9373 CrossRef CAS PubMed.
- G. R. Hendrickson, M. H. Smith, A. B. South and L. A. Lyon, Adv. Funct. Mater., 2010, 20, 1697–1712 CrossRef CAS.
- M. Cors, O. Wrede, A.-C. Genix, D. Anselmetti, J. Oberdisse and T. Hellweg, Langmuir, 2017, 33, 6804–6811 CrossRef CAS PubMed.
- L. Zha, Y. Zhang, W. Yang and S. Fu, Adv. Mater., 2002, 14, 1090–1092 CrossRef CAS.
- G. Zhou, A. Elaissari, T. Delair and C. Pichot, Colloid Polym. Sci., 1998, 276, 1131–1139 CrossRef CAS.
- N. Welsch, Y. Lu, J. Dzubiella and M. Ballauff, Polymer, 2013, 54, 2835–2849 CrossRef CAS.
- X. Xia and Z. Hu, Langmuir, 2004, 20, 2094–2098 CrossRef CAS PubMed.
- V. Nigro, R. Angelini, M. Bertoldo, E. Buratti, S. Franco and B. Ruzicka, Polymers, 2021, 13, 1353 CrossRef CAS PubMed.
- V. Y. Rudyak, E. Y. Kozhunova and A. V. Chertovich, Soft Matter, 2020, 16, 4858–4865 RSC.
- E. Y. Kozhunova, V. Y. Rudyak, X. Li, M. Shibayama, G. S. Peters, O. V. Vyshivannaya, I. R. Nasimova and A. V. Chertovich, J. Colloid Interface Sci., 2021, 597, 297–305 CrossRef CAS PubMed.
- M. Keerl, V. Smirnovas, R. Winter and W. Richtering, Macromolecules, 2008, 41, 6830–6836 CrossRef CAS.
- M. Keerl, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2009, 131, 3093–3097 CrossRef CAS PubMed.
- J. Es Sayed, C. Lorthioir, P. Perrin and N. Sanson, Soft Matter, 2019, 15, 963–972 RSC.
- R. Rivas-Barbosa, J. Ruiz-Franco, M. A. Lara-Peña, J. Cardellini, A. Licea-Claverie, F. Camerin, E. Zaccarelli and M. Laurati, Macromolecules, 2022, 55, 1834–1843 CrossRef CAS PubMed.
- A. Serrano-Medina, J. Cornejo-Bravo and A. Licea-Claveríe, J. Colloid Interface Sci., 2012, 369, 82–90 CrossRef CAS PubMed.
- G. Del Monte, F. Camerin, A. Ninarello, N. Gnan, L. Rovigatti and E. Zaccarelli, J. Phys.: Condens. Matter, 2020, 33, 084001 CrossRef PubMed.
- C. Graf and A. van Blaaderen, Langmuir, 2002, 18, 524–534 CrossRef CAS.
- C. M. Soukoulis and M. Wegener, Nat. Photonics, 2011, 5, 523–530 CrossRef CAS.
- K. Uhlig, T. Wegener, J. He, M. Zeiser, J. Bookhold, I. Dewald, N. Godino, M. Jaeger, T. Hellweg and A. Fery, et al. , Biomacromolecules, 2016, 17, 1110–1116 CrossRef CAS PubMed.
- M. Zhang, X. Li, Y. Gong, N. Zhao and X. Zhang, Biomaterials, 2002, 23, 2641–2648 CrossRef CAS PubMed.
- K. Bjugstad, K. Lampe, D. Kern and M. Mahoney, J. Biomed. Mater. Res., Part A, 2010, 95, 79–91 CrossRef CAS PubMed.
- L. Luo Zheng, V. Vanchinathan, R. Dalal, J. Noolandi, D. J. Waters, L. Hartmann, J. R. Cochran, C. W. Frank, C. Q. Yu and C. N. Ta, J. Biomed. Mater. Res., Part A, 2015, 103, 3157–3165 CrossRef PubMed.
- L. Hartmann, K. Watanabe, L. L. Zheng, C.-Y. Kim, S. E. Beck, P. Huie, J. Noolandi, J. R. Cochran, C. N. Ta and C. W. Frank, J. Biomed. Mater. Res., Part B, 2011, 98, 8–17 CrossRef PubMed.
- M. Lara-Peña, A. Licea-Claverie, I. Zapata-González and M. Laurati, J. Colloid Interface Sci., 2021, 587, 437–445 CrossRef PubMed.
- J. S. Hyatt, C. Do, X. Hu, H. S. Choi, J. W. Kim, L. A. Lyon and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 030302 CrossRef PubMed.
- X. Di, X. Peng and G. B. McKenna, J. Chem. Phys., 2014, 140, 054903 CrossRef PubMed.
- C. Agbugba, B. Hendriksen, B. Chowdhry and M. Snowden, Colloids Surf., A, 1998, 137, 155–164 CrossRef CAS.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- T. Soddemann, B. Dünweg and K. Kremer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 409–419 CrossRef CAS.
- F. Lo Verso, J. A. Pomposo, J. Colmenero and A. J. Moreno, Soft Matter, 2015, 11, 1369–1375 RSC.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS PubMed.
- A. J. Moreno and F. L. Verso, Soft Matter, 2018, 14, 7083–7096 RSC.
- R. Chudoba, J. Heyda and J. Dzubiella, J. Chem. Theory Comput., 2017, 13, 6317–6327 CrossRef CAS PubMed.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- R. Blaak, B. Capone, C. N. Likos and L. Rovigatti, Forschungszentrum Jülich, 2015, 209–258 Search PubMed.
- D. Paloli, P. S. Mohanty, J. J. Crassous, E. Zaccarelli and P. Schurtenberger, Soft Matter, 2013, 9, 3000–3004 RSC.
- A. G. Mailer, P. S. Clegg and P. N. Pusey, J. Phys.: Condens. Matter, 2015, 27, 145102 CrossRef PubMed.
- D. A. Sivak, J. D. Chodera and G. E. Crooks, J. Phys. Chem. B, 2014, 118, 6466–6474 CrossRef CAS PubMed.
- J. Ruiz-Franco, L. Rovigatti and E. Zaccarelli, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 1–13 CrossRef CAS PubMed.
- J. S. Higgins and H. C. Benoit, Polymers and Neutron Scattering, Clarendon Press, 1st edn, 1997 Search PubMed.
- W. D. Dozier, J. S. Huang and L. J. Fetters, Macromolecules, 1991, 24, 2810–2814 CrossRef CAS.
- J. Clara-Rahola, A. Fernandez-Nieves, B. Sierra-Martin, A. B. South, L. A. Lyon, J. Kohlbrecher and A. Fernandez Barbero, J. Chem. Phys., 2012, 136, 214903 CrossRef CAS PubMed.
- C. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450 CrossRef CAS.
- M. Doucet, J. H. Cho, G. Alina, J. Bakker, W. Bouwman, P. Butler, K. Campbell, M. Gonzales, R. Heenan, A. Jackson, P. Juhas, S. King, P. Kienzle, J. Krzywon, A. Markvardsen, T. Nielsen, L. O'Driscoll, W. Potrzebowski, R. F. Leal, T. Richter, P. Rozycko, T. Snow and A. Washington, SasView version 4.1.2, 2017 Search PubMed.
- S. G. Hatzikiriakos, Soft Matter, 2015, 11, 7851–7856 RSC.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS PubMed.
- U. Gasser, A. Scotti and A. Fernandez-Nieves, Phys. Rev. E, 2019, 99, 042602 CrossRef CAS PubMed.
- K. Kratz, A. Lapp, W. Eimer and T. Hellweg, Colloids Surf., A, 2002, 197, 55–67 CrossRef CAS.
- M. Wolfe and C. Scopazzi, J. Colloid Interface Sci., 1989, 133, 265–277 CrossRef CAS.
- A. Jusufi, C. N. Likos and H. Löwen, Phys. Rev. Lett., 2001, 88, 018301 CrossRef PubMed.
- I. Romero-Sanchez, I. Pihlajamaa, N. Adžic, L. E. Castellano, E. Stiakakis, C. N. Likos and M. Laurati, ACS Nano, 2022, 16, 2133–2146 CrossRef CAS PubMed.
- I. C. Romero-Sanchez, L. E. Castellano and M. Laurati, Macromolecules, 2022, 55, 4459–4468 CrossRef CAS.
- J. E. Houston, L. Fruhner, A. de la Cotte, J. R. González, A. V. Petrunin, U. Gasser, R. Schweins, J. Allgaier, W. Richtering, A. Fernandez-Nieves and A. Scotti, Sci. Adv., 2022, 8, eabn6129 CrossRef CAS PubMed.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- G. Del Monte, D. Truzzolillo, F. Camerin, A. Ninarello, E. Chauveau, L. Tavagnacco, N. Gnan, L. Rovigatti, S. Sennato and E. Zaccarelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109560118 CrossRef PubMed.
- P. Pusey, Liquids, freezing and the glass transition, North-Holland, Amsterdam, 1991 Search PubMed.
- L. Berthier, A. J. Moreno and G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 060501 CrossRef PubMed.
- F. Camerin, N. Gnan, J. Ruiz-Franco, A. Ninarello, L. Rovigatti and E. Zaccarelli, Phys. Rev. X, 2020, 10, 031012 CAS.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- F. Roosen-Runge, A. Gulotta, S. Bucciarelli, L. Casal-Dujat, T. Garting, N. Skar-Gislinge, M. Obiols-Rabasa, B. Farago, E. Zaccarelli and P. Schurtenberger, et al. , Biophys. J., 2020, 119, 2483–2496 CrossRef CAS PubMed.
- N. Skar-Gislinge, F. Camerin, A. Stradner, E. Zaccarelli and P. Schurtenberger, Mol. Pharmaceutics, 2023, 20, 2738–2753 CrossRef CAS PubMed.
- A. M. Puertas, C. De Michele, F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Chem. Phys., 2007, 127, 144906 CrossRef PubMed.
- S. Gupta, J. Stellbrink, E. Zaccarelli, C. N. Likos, M. Camargo, P. Holmqvist, J. Allgaier, L. Willner and D. Richter, Phys. Rev. Lett., 2015, 115, 128302 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00120b |
| This journal is © The Royal Society of Chemistry 2023 |