Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Puncturing of soft tissues: experimental and fracture mechanics-based study†
Matteo
Montanari
 a,
Roberto
Brighenti
a,
Roberto
Brighenti
 a,
Michele
Terzano
a,
Michele
Terzano
 b and
Andrea
Spagnoli
b and
Andrea
Spagnoli
 *a
*a
aDepartment of Engineering and Architecture, University of Parma, Parco Area delle Scienze 181/A, 43124 Parma, Italy. E-mail: spagnoli@unipr.it; Tel: +39 0521 905927
bInstitute of Biomechanics, Graz University of Technology, Stremayrgasse 16/2, 8010 Graz, Austria
First published on 10th May 2023
Abstract
The integrity of soft materials against puncturing is of great relevance for their performance because of the high sensitivity to local rupture caused by rigid sharp objects. In this work, the mechanics of puncturing is studied with respect to a sharp-tipped rigid needle with a circular cross section, penetrating a soft target solid. The failure mode associated with puncturing is identified as a mode-I crack propagation, which is analytically described by a two-dimensional model of the target solid, taking place in a plane normal to the penetration axis. It is shown that the force required for the onset of needle penetration is dependent on two energy contributions, that are, the strain energy stored in the target solid and the energy consumed in crack propagation. More specifically, the force is found to be dependent on the fracture toughness of the material, its stiffness and the sharpness of the penetrating tool. The reference case within the framework of small strain elasticity is first investigated, leading to closed-form toughness parameters related to classical linear elastic fracture mechanics. Then, nonlinear finite element analyses for an Ogden hyperelastic material are presented. Supporting the proposed theoretical framework, a series of puncturing experiments on two commercial silicones is presented. The combined experimental–theoretical findings suggest a simple, yet reliable tool to easily handle and assess safety against puncturing of soft materials.
1. Introduction
Puncturing of soft solids is characterised by complex mechanisms of progressive failure and penetration of a cutting tool into a target material.1 The analysis and experimental measurement of puncturing and cutting forces are of great interest for a diversified range of engineering applications, including optimisation of high-precision cutting machines in the food industry,2–4 mechanical characterisation of soft polymers5–8 and biological tissues,9–13 optimisation of surgical tools14–18 and design of advanced drug delivery systems.19,20 Research concerning the mechanics of puncturing is particularly active in the realm of soft biological tissues.21 Scientists are taking inspiration by puncturing systems found in nature to develop new bio-inspired solutions.22,23 In addition, biological tissue-mimicking phantoms obtained by additive manufacturing techniques are employed in medical training,24–26 thanks to their capability to replicate the mechanical conditions encountered in surgical procedures involving cutting and puncturing.27A central part in the mechanics of puncturing is played by fracture mechanics.28,29 Studying the deep penetration of a rigid needle into the skin, Shergold and Fleck,1,30 recorded the load-displacement curves for different indenters and observed that the crack geometry is highly dependent on the indenter tip and on the material properties of the soft solid. Detailed finite element (FE) analyses enabled a better understanding of the complex interaction between the tool and the target material,31,32 including the complex scenarios enabled by highly deformable and asymmetric indenters.33 More recently, needle insertion in soft solids has been reconsidered in the works by Fakhouri et al.7 and Fregonese and Bacca.34 Friction plays a major role in puncturing of soft tissues.35 For instance, it was observed that the fracture is altered by friction and result in higher cutting forces.10,36 Furthermore, rate-dependent effects have been analysed in terms of the insertion velocity17,37,38 and correlated to tissue damage in biological tissues.39
Overall, puncturing soft solids involves crack propagation at large strains, interaction with the geometry and mechanical properties of the penetrating tool, effects of the insertion technique and of friction exerted against the target material.40 In addition, we should consider that when puncturing is studied in relation to biological tissues, such as the human skin, an anisotropic and heterogeneous nature is involved.41 The complexities of fracture in soft materials are well-known and it is reasonable to assume that some peculiar aspects, including large deformation prior to crack propagation and rate-dependent effects, persist during puncturing. For recent accounts on this topic, the reader is referred to the reviews by Long and Hui42 and Spagnoli et al.43 In particular, Spagnoli et al.43 have shown how the blunting of a crack tip due to large deformations interacts with a characteristic size of the indenter in determining the condition for penetration. Depending on the mechanical properties of the tissue, the size of the indenter can act as a limiting constraint on the free blunting of the crack, as previously suggested by Hui et al.44 This latter aspect is crucial in discriminating between puncturing and tearing as distinct failure modes.45 As brilliantly observed by Gent,46 the limited blunting during cutting of soft solids might explain why cutting a material is much easier than tearing it.
The investigation of the fracture behaviour of a soft material during puncturing is of particular importance, as this can determine its sensitivity to local rupture caused by rigid hitting objects and affect the structural integrity of the material. Guided by the above-mentioned challenge, in the present paper we aim at studying experimentally the puncture-driven failure in soft materials and the related mechanical modelling. An experimental campaign is carried out, involving different puncturing experiments on two commercial silicones and a sharp-tipped rigid circular needle. Thanks to its good mechanical, thermal, and electrical properties and stability, as well as high deformability, low-toxicity and bio-compatibility, silicone is one of the most widely used polymeric materials. An analytical planar model of cutting, recently proposed by the authors,47,48 is then introduced to describe the mechanism of crack propagation observed during puncturing. Closed-form solutions are obtained for the dimensionless penetration force as a function of the relative fracture toughness of the material.49 Finite element analyses on an Ogden's hyperelastic material are presented to validate the simplified model proposed. A further validation of the theoretical findings is provided by the experimental results, which complement analogous data available in the literature.
2. Mechanics of puncturing
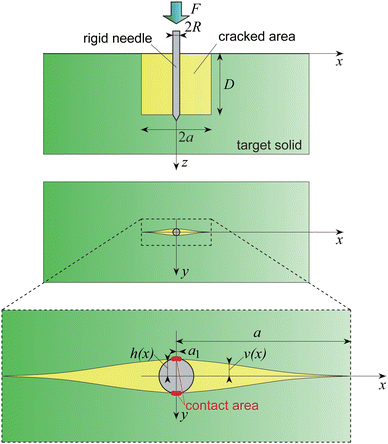
The mechanics of an object piercing a target solid is characterised by two stages: an initial stage of indentation and a subsequent stage of penetration. In the former, the tip of the indenter is in contact with the target solid, which accumulates strain energy while the indentation progresses. The indentation stage terminates when an energetically favourable mechanism of laceration takes place in the target solid.34 This mechanism features the development of a crack linearly increasing its depth with the penetration length of the indenter. According to Shergold and Fleck,30 for soft materials either mode-II crack ring or mode-I planar cracks develop for flat-bottomed punch and sharp-tipped punch, respectively.In the present paper, a rigid sharp-tipped punch (needle) of radius 2R is assumed to penetrate a large soft solid along the z direction, leading to a mode-I cracking in the solid (Fig. 1). The puncturing process which takes place in the material can be described using an energy-based formulation. Neglecting additional inelastic phenomena in the bulk of the material, the increment of external work generated by the puncturing force is consumed by the elastic strain energy, the work of fracture and the frictional dissipation. The general incremental form of the energy balance is
| dUext = dUs + dUG + dUf, | (1) |
Following the initial stage of indentation, penetration is characterised, unless otherwise stated, by a steady-state condition, where a mode-I planar crack of size 2a × D propagates (the crack area is defined by the region |x| ≤ a and 0 ≤ z ≤ D in Fig. 1). Unless othervise stated, the crack (semi-) length refers to the nominal size in the undeformed configuration of the target solid. The strain energy G available per unit increase in area of one fracture surface, dA = 2adD, is given by
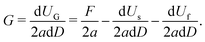 | (2) |
The critical condition of crack propagation is expressed as dUG/dD = 2aGc, where Gc is the fracture energy of the material. In this way, eqn (2) can be employed to derive the force corresponding to the onset of steady-state penetration, hereafter denoted as penetration force Fp.
3. Experiments on silicone samples
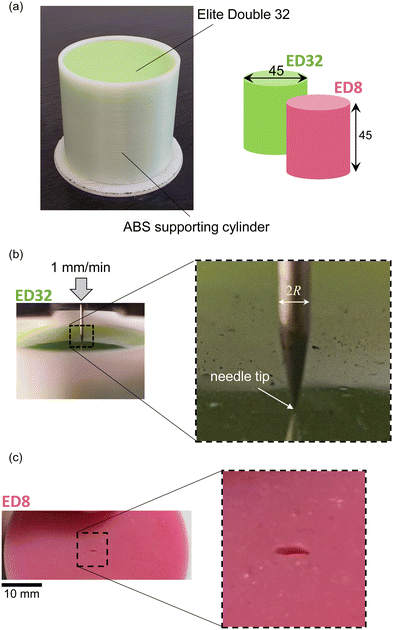
Silicone samples have been prepared with two silicone rubbers, with the commercial denomination Elite Double 32 (ED32) and Elite Double 8 (ED8) (Zhermack Dental). The samples are made of Polyvinyl Siloxane (PVS) silicone elastomers, widely employed for model duplication in the dentistry field. The number in the commercial denomination of the silicone elastomers under consideration refers to the Shore A hardness (equal to 32 and 8, respectively). A representative silicone sample is illustrated in Fig. 2a. A 3D printed ABS supporting cylinder is manufactured, in which the silicone samples are cast. Such a supporting element is deemed not to affect the overall mechanical response during needle penetration, as demonstrated by the vertical deflection on the surface of the silicone specimens, localized near the spot of needle penetration, and by preliminary finite element calculations.Puncturing experiments have been performed on cylindrical samples with diameter and height equal to 45 mm. A sharp-tipped steel punch (tip opening angle α in the range 35 to 45 deg) with circular cross-section having different diameters (2R = 1.28, 1.50, 2.15, 2.72 mm) is inserted under displacement-control into the target material at a constant speed of 1 mm min−1 (Fig. 2b). A view of the mode I cracking developing on the surface of a representative ED8 silicone sample is depicted in Fig. 2c.
A preliminary set of experiments has been performed in order to characterise the mechanical behaviour of the materials. Firstly, four 15 × 55 × 3 mm3 specimens for each silicone were manufactured and then tested in uniaxial tension at an average strain rate of 0.001 s−1 (5 mm min−1) until failure (Fig. 3a). The experimental uniaxial tensile curves have been fitted with an incompressible Ogden strain-energy function
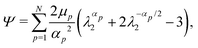 | (3) |
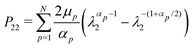 .
.
In the fitting of experimental curves, single-term Ogden strain-energy functions (N = 1) are employed. For the ED8 silicone, the best fitting turns out to be that of an Ogden function with μ = 0.061 MPa and α = 2.54, while for ED32 silicone, the best fitting is obtained with a Neo-Hookean material (α = 2) with μ = 0.405 MPa.
Further tests are conducted on 50 × 10 × 3 mm3 specimens, containing a 12.5 mm edge crack created with a sharp cutter, in order to estimate the fracture energy Gc (see Fig. 3b). This configuration, known in the literature as pure-shear, is widely used to characterise the fracture behaviour of elastomers and hydrogels.42 The same strain rate of 0.001 s−1 as that adopted in the tensile tests was used for the ED32 silicone, while a strain rate of 1 s−1 was employed for the ED8 silicone in order to avoid the so-called sideways crack propagation50 (Fig. 3c). Note that the values of Gc are calculated by considering the strain energy in the uncracked sample related to the strain at peak stress in the cracked samples. This criterion is adopted as the strain corresponding to the crack initiation cannot be clearly identified from experiments. It is worth mentioning that the resulting values of fracture energy might underestimate the actual values, particularly in the case of ED8 silicone where the post-peak softening is rather mild (see Fig. 3b). For instance, by considering the limit case of strain at complete specimen failure, the resulting average value of Gc for ED8 would be equal to 1.348 N mm−1 instead of 0.754 N mm−1. All the mechanical tests were performed using a universal testing machine Galdabini Quasar 2.5 with a sampling frequency set to 10 Hz, at a room temperature of 20, 24 hours after the preparation of the specimens. The results of the mechanical characterisation are summarised in Fig. 3, where the mechanical parameters of interest are shown.
Results of the puncturing experiments are illustrated in Fig. 4. Here, the force–displacement curves obtained during the puncturing tests are shown separately for each needle diameter, along with a comparison in terms of the penetration force between the two silicones (Fig. 4c). The penetration force Fp is identified in the experimental force–displacement curves as the onset of steady-state penetration, following the material rupture and subsequent relaxation.
4. Plane strain linear elastic model of puncturing
4.1. Analytical formulation
In this section, a theoretical model for the steady-state penetration of puncturing, based on linear elastic fracture mechanics (LEFM), is presented. Specifically, we describe here the insertion of a rigid circular needle into a semi-infinite linearly elastic solid, having Young modulus E and Poisson's ratio ν. The assumptions of small-scale yielding at the crack tip, frictionless contact at the needle-material interface and infinitesimal strains are introduced. This model was presented for a more general case of a rigid elliptical wedge in Terzano et al.47 and Spagnoli et al.,48 to which the reader is referred for an in-depth presentation.Let us consider a section of the solid normal to the needle axis, corresponding to a plane of equation z = ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) with 0 <
with 0 < ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) < D (refer to the enlarged view in Fig. 1). The resulting two-dimensional problem is characterised by plane strain conditions, at least for not too small values of z. A crack extends along the region |x| ≤ a, y = 0 (note that, within the framework of linear elasticity, the undeformed and deformed configurations of the target solid are assumed to coincide, so that there is no distinction between the initial crack length and the current one under loading). Let v(x) describe the opening displacement of the crack and
< D (refer to the enlarged view in Fig. 1). The resulting two-dimensional problem is characterised by plane strain conditions, at least for not too small values of z. A crack extends along the region |x| ≤ a, y = 0 (note that, within the framework of linear elasticity, the undeformed and deformed configurations of the target solid are assumed to coincide, so that there is no distinction between the initial crack length and the current one under loading). Let v(x) describe the opening displacement of the crack and  the circular cross-section profile of the needle. It was shown in Terzano et al.47 that the crack surfaces detach from the needle profile at a coordinate |x| = a1, so that the crack is traction-free for a1 ≤ |x| < a (see Fig. 1). A boundary value problem (BVP) can be defined, from which the position of the point of separation a1 and the stress intensity factor (SIF) at the crack tip K are obtained. Because of the double symmetry, only one quarter of the geometry can be considered. The following set of equations defines the BVP47
the circular cross-section profile of the needle. It was shown in Terzano et al.47 that the crack surfaces detach from the needle profile at a coordinate |x| = a1, so that the crack is traction-free for a1 ≤ |x| < a (see Fig. 1). A boundary value problem (BVP) can be defined, from which the position of the point of separation a1 and the stress intensity factor (SIF) at the crack tip K are obtained. Because of the double symmetry, only one quarter of the geometry can be considered. The following set of equations defines the BVP47
| v(x) = h(x), σy(x) ≤ 0 for |x| ≤ a1; | (4) |
| v(x) > h(x), σy(x) = 0 for a1 < |x| < R; | (5) |
| v(x) > 0, σy(x) = 0 for R ≤ |x| < a; | (6) |
| v(x) = 0 for |x| ≥ a; | (7) |
| τxy(x) = 0 for y = 0. | (8) |
The BVP described by (4)–(7) is decomposed into two different cases, which are solved separately (Fig. 5). Fig. 5a shows the well-known solution of a crack of length 2R in an infinite plate subjected to a uniform pressure σ0 applied to its surfaces.51 The resulting opening displacement is
 | (9) |
| σy(x) = σ0 for |x| ≤ R, | (10) |
 | (11) |
 | ||
| Fig. 5 Decomposition of the solution of the boundary value problem illustrated in the bottom sketch of Fig. 1 (due to symmetry only a quarter of the original problem is treated here). (a) Equivalence between the rigid circular wedge and a crack of length 2R with an applied pressure σ0. (b) A crack of length 2s is considered, with prescribed stresses on its surface, in order to equilibrate the stress field from (a). Notice the discontinuity in the displacement derivative at x = a. | ||
Comparing this solution with the equations defining the BVP, we notice that the condition of zero normal stresses in (5) and (6) is not satisfied on the open part of the crack, i.e. a1 ≤ x < a. Therefore, a corrective solution is superposed on the previous, obtained by considering a crack of length 2s = (a − a1) (Fig. 5b). The following stresses need to be applied to its surfaces
| σy(x) = σ0 for a1 ≤ |x| < R, | (12) |
 | (13) |
Details of the solution to this problem are provided in Terzano et al.47. The unilateral contact conditions defined in (4) exclude singularities at x = a1. Instead, we expect a stress singularity at x = a, where we can define a mode-I SIF K. Using a recursive procedure, we obtain the results illustrated in Fig. 6a. Here, the position of the point of separation a1 and the SIF at the crack tip K are illustrated against the normalised needle radius R/a. The SIF is normalised with respect to KR, namely the stress intensity factor related to the needle filling the entire crack (R/a = 1). This is defined as
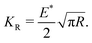 | (14) |
 | ||
| Fig. 6 Plane strain linear elastic model of puncturing. (a) Normalised SIF and contact length against relative radius of the needle. (b) Normalised strain energy against relative radius of the needle, for an incompressible material. Results in (a and b) are compared with geometrically nonlinear finite element analyses on a linear elastic material. (c) Normalised penetration force against normalised fracture energy, for an incompressible material and Hertz contact pressure distribution, from eqn (21). | ||
Fig. 6a can be employed to determine the critical condition of crack propagation, for a given radius of the needle and fracture toughness Kc. According to the LEFM model, a planar crack of semi-length a forms so that K = Kc at the crack tips. The critical value of the relative radius R/ac, along with the critical value of the contact relative semi-length a1/ac, are therefore obtained from Fig. 6a by posing K = Kc. Note that, according to the present model, the needle penetration produces a mode-I crack propagation provided that R ≥ Rc, where Rc is a material-based sharpness parameter, defined as47
 | (15) |
It is worth noticing that the relevant sharpness of the needle is that related to its cross-sectional roundness, i.e. to the radius R, consistently with the two-dimensional treatment of the physical problem (a unit thickness slice of the target material taken normal to the penetration axis is considered). The tapering of the sharp tip of the needle is not relevant in this respect; the only effect of a sharp-tipped needle, e.g. as compared to that of a flat-bottomed needle, is to promote the mode-I fracture mechanism during penetration.
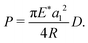 | (16) |
Making use of (14) to express KR, it turns out that
 | (17) |
On the other hand, by assuming a uniform contact pressure equal to σ0 = E*/2 – which, according to (9), produces a maximum crack flank displacement equal to R – we get
 | (18) |
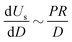 . Specifically, for the Hertz distribution in (16) we derive
. Specifically, for the Hertz distribution in (16) we derive | (19) |
Results of the normalised strain energy per unit thickness, considering the two theoretical distributions of contact pressure described above, are illustrated in Fig. 6b as a function of the relative needle radius R/a.
| Fp = πμa12+ 2aGc, | (20) |
 | (21) |
The values of a1/ac and R/ac are inferred from the theoretical results shown in Fig. 6a, for a given value of fracture toughness. Notice that fracture energy and fracture toughness are related by Irwin's equation Gc = Kc2/E* = Kc2/4μ. According to the LEFM model proposed, a mode-I penetration mechanism can occur only if Gc/(μR) ≤ π, derived from the condition (15). However, if a fracture criterion different from that of LEFM is used, higher values of the normalised fracture energy might be allowed (see Section 5).
4.2. Finite element verification
In order to verify the theoretical results obtained above, a unit-thickness slice of the target solid centred at z =![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≤ D is analysed using a finite element (FE) model in the commercial software Abaqus.53 Due to symmetry conditions, only a quarter of this slice is described by the FE models. To enforce the condition of semi-infinite solid assumed in the theoretical formulation, a large plate with dimensions 20a × 20a, being a the crack semi-length, has been modelled. Plane strain 8-node isoparametric elements are used. A suitable mesh is adopted, with minimum size of the elements near the crack equal to a/100. Nonlinear springs (with a penalty compressive stiffness and nearly zero stiffness in tension) are introduced to simulate the unilateral frictionless contact between needle and target material. Incremental static geometrically nonlinear analyses are carried out, by keeping a constant and varying R (R/a = 0.1,0.2,…,1). The needle is pushed against the target material by an incremental displacement from 0 to R.
≤ D is analysed using a finite element (FE) model in the commercial software Abaqus.53 Due to symmetry conditions, only a quarter of this slice is described by the FE models. To enforce the condition of semi-infinite solid assumed in the theoretical formulation, a large plate with dimensions 20a × 20a, being a the crack semi-length, has been modelled. Plane strain 8-node isoparametric elements are used. A suitable mesh is adopted, with minimum size of the elements near the crack equal to a/100. Nonlinear springs (with a penalty compressive stiffness and nearly zero stiffness in tension) are introduced to simulate the unilateral frictionless contact between needle and target material. Incremental static geometrically nonlinear analyses are carried out, by keeping a constant and varying R (R/a = 0.1,0.2,…,1). The needle is pushed against the target material by an incremental displacement from 0 to R.
Comparisons between FE results and theory in terms of contact length a1/a, SIF K/KR and strain energy Us are presented in Fig. 6a and b. An almost perfect agreement between theoretical and numerical results is observed for a1/a and K/KR, while the best approximation of the strain energy is obtained by considering the Hertz contact pressure distribution.
5 Large strain numerical analyses of puncturing
Penetration of soft solids inevitably involves large deformation well beyond the range of validity of linear elasticity. Consequently, a refined analysis of the penetration mechanism needs to be carried out numerically by means of finite strain elasticity models. In the following, FE analyses under geometrical and material nonlinearity are carried out. The hyperelastic Ogden model is adopted, whose strain-energy function is expressed by | (22) |
The ratio R/a is made to vary and the needle is modelled as a circular rigid body in frictionless hard contact with the material, where the displacement along the y axis of the needle centroid is prescribed. A detailed view of the adopted mesh, along with a plot of the deformed configuration related to full penetration in the case of R/a = 0.5 is illustrated in Fig. 7, being a the initial crack length while the current one in the deformed solid is part of the solution.
The FE results for the hyperelastic constitutive model are shown in Fig. 8a and b in terms of normalised contact length and strain energy. A comparison with the FE results presented in Section 4.2 and related to linear elasticity is also provided. Note that the results related to contact length (Fig. 8a) are not directly employed in the subsequent calculation of the penetration force, but they might offer an insight on the contact behaviour between rigid needle and target material as its constitutive model is made to vary.
Similarly to Section 4.1.2, we need to determine the critical condition for crack propagation in order to derive the penetration force Fp. We have computed the J-integral from the FE analyses, which in elastic materials is path-independent and provides the crack driving energy G.54 Then, the critical condition of crack propagation is attained when Jint = G = Gc. Fig. 8c reports the normalised crack driving energy G as a function of the relative needle radius, for the hyperelastic and the linear elastic models. Recall that the curves shown in Fig. 8 were obtained from FE analyses for specific values of the ratio R/a. For this reason, we have fitted them with an appropriate function in order to have the full range. In addition, we have also extrapolated the results in Fig. 8b and c with the same fitting functions for some simulations that did not attain convergence.
6 Discussion and conclusions
This paper presents some experimental results related to the puncturing of soft silicone elastomers, and discusses the validity of a recently proposed model, based on linear elastic fracture mechanics (LEFM), to describe the penetration mechanism of a rigid circular needle into a soft target material. The needle has a sharp tip, so that penetration is governed by the development of a planar mode-I crack due to the contact pressure at the needle-material interface. A simple closed-form expression is obtained for the dimensionless penetration force as a function of the relative fracture toughness of the material. The theoretical model is verified by running geometrically nonlinear finite element (FE) analyses, where the unilateral frictionless contact between the needle and the target material is described.Thanks to its simplified assumptions, the present LEFM model offers a first insight on the mechanics of puncturing in soft materials. A more accurate description is provided by means of FE analyses using Ogden's hyperelastic model to describe the finite strain deformation of soft materials. Assuming an energy-based fracture condition for the target material, the curves reported in Fig. 8b and c provide a critical condition for puncturing in terms of penetration force Fp. As explained in Section 4.1.2, the dimensionless form of the penetration force is expressed as
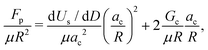 | (23) |
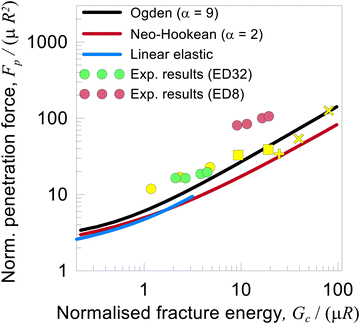 | ||
| Fig. 9 Theoretical and experimental results of normalised penetration force against the normalised fracture energy. Symbols in yellow refer to literature data.30 Silicone rubber Sil8800, symbol °: μ = 2.7 MPa, α = 2.5, Gc = 3.1 N mm−1, R = 0.25, 0.5, 1 mm; silicone rubber B452, symbol: μ = 0.4 MPa, α = 3, Gc = 3.8 N mm−1, R = 0.5, 1 mm; sheep skin, symbol +: μ = 0.11 MPa, α = 9, Gc = 2.5 N mm−1, R = 0.5 mm; human skin, symbol ×: μ = 0.11 MPa, α = 9, Gc = 2.5 N mm−1, R = 0.15, 0.3 mm. | ||
The combined experimental–theoretical framework can be employed as a simple tool to assess the critical condition of puncturing, given a specific combination of material parameters and indenter geometry. Firstly, the critical ratio R/ac is determined from the curves of Fig. 8c, for a material fracture energy Gc. The numerator in the first term of the right-hand side of (23) is then computed from Fig. 8c, once the ratio R/ac is known. At this point, the normalised penetration force Fp is known.
Fig. 9 shows a comparison between the theoretical-numerical results and the puncturing experiments of Section 1 performed on commercial silicones Elite Double 8 (ED8) and Elite Double 32 (ED32). In addition, literature results taken30 are added. The comparison between theoretical-numerical results and experimental data seems fairly satisfactory, in line with the trend of results reported in the literature, e.g. see ref. 30 and 34. In particular, for the silicone rubber ED32, the experimental results seem to match fairly well with both the model and the corresponding literature data.30 On the other hand, we speculate that the discrepancy between the predicted and experimentally obtained values of penetration force occurring for silicone ED8 might partly depend on the calculated value of the fracture energy (see discussion in Section 3 in relation to Fig. 3b), as a higher value of Gc would lead to a shift of experimental data points of ED8 in Fig. 9 towards the theoretical curves (note that complementary experimental tests – see ESI,† demonstrated negligible strain rate-dependence in material's rigidity and penetration force in the velocity ranges under consideration). Finally, Fig. 9 shows that using different constitutive models (the two values of α equal to 2 and 9 in the single-term Ogden function are selected to encompass a broad range of material response in relation to strain hardening) no significant differences in the penetration force are observed, at least not as large as to prevail on the scatter of experimental data.
In conclusion, our study seems to support the theoretical and experimental findings on puncturing available in the literature. An original aspect of the present work is related to the derivation of a closed form solution of the penetration force, fully based on LEFM arguments. This provides a simplified, first approximation quantity to assess safety against puncturing of soft materials.
Author contributions
Matteo Montanari: data curation; methodology; visualization; writing – original draft. Roberto Brighenti: funding acquisition; writing – review & editing. Michele Terzano: conceptualization; writing – review & editing. Andrea Spagnoli: conceptualization; supervision; writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the support from European Unions Horizon 2020 Research and Innovation Programme (H2020-WIDESPREAD-2018, SIRAMM) under Grant Agreement No. 857124.References
- O. A. Shergold and N. A. Fleck, Experimental Investigation Into the Deep Penetration of Soft Solids by Sharp and Blunt Punches, With Application to the Piercing of Skin, J. Biomech. Eng., 2005, 127, 838–848, DOI:10.1115/1.1992528.
- R. W. McGorry, P. C. Dowd and P. G. Dempsey, Cutting moments and grip forces in meat cutting operations and the effect of knife sharpness, Appl. Ergon., 2003, 34, 375–382, DOI:10.1016/S0003-6870(03)00041-3.
- S. M. Goh, M. N. Charalambides and J. G. Williams, On the mechanics of wire cutting of cheese, Eng. Fract. Mech., 2005, 72, 931–946, DOI:10.1016/j.engfracmech.2004.07.015.
- S. Schuldt, Y. Schneider and H. Rohm, High-speed cutting of foods: Cutting behavior and initial cutting forces, J. Food Eng., 2018, 230, 55–62, DOI:10.1016/j.jfoodeng.2018.02.024.
- F. Baldi, F. Bignotti, I. Peroni, S. Agnelli and T. Riccò, On the measurement of the fracture resistance of polyacrylamide hydrogels by wire cutting tests, Polym. Test., 2012, 31, 455–465, DOI:10.1016/j.polymertesting.2012.01.009.
- A. E. Forte, F. D'Amico, M. N. Charalambides, D. Dini and J. G. Williams, Modelling and experimental characterisation of the rate dependent fracture properties of gelatine gels, Food Hydrocolloids, 2015, 46, 180–190, DOI:10.1016/j.foodhyd.2014.12.028.
- S. Fakhouri, S. B. Hutchens and A. J. Crosby, Puncture mechanics of soft solids, Soft Matter, 2015, 11, 4723–4730, 10.1039/C5SM00230C.
- T. T. Duncan, J. M. Sarapas, A. P. Defante, K. L. Beers and E. P. Chan, Cutting to measure the elasticity and fracture of soft gels, Soft Matter, 2020, 16, 8826–8831, 10.1039/D0SM01174F.
- T. Azar and V. Hayward, Estimation of the Fracture Toughness of Soft Tissue from Needle Insertion, in Biomedical Simulation, ed. F. Bello and P. J. E. Edwards, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 166–175, ISBN 3540705201 Search PubMed.
- C. T. Nguyen, T. Vu-Khanh, P. I. Dolez and J. Lara, Puncture of elastomer membranes by medical needles. Part I: Mechanisms, Int. J. Fract., 2009, 155, 75–81, DOI:10.1007/s10704-009-9326-7.
- C. Gokgol, C. Basdogan and D. Canadinc, Estimation of fracture toughness of liver tissue: Experiments and validation, Med. Eng. Phys., 2012, 34, 882–891, DOI:10.1016/j.medengphy.2011.09.030.
- A. C. Barnett, Y.-S. Lee and J. Z. Moore, Fracture Mechanics Model of Needle Cutting Tissue, J. Manuf. Sci. Eng., 2015, 138, 0110005, DOI:10.1115/1.4030374.
- M. Terzano, A. Spagnoli, D. Dini and A. E. Forte, Fluid-solid interaction in the rate-dependent failure of brain tissue and biomimicking gels, J. Mech. Behav. Biomed. Mater., 2021, 119, 104530, DOI:10.1016/j.jmbbm.2021.104530.
- T. Frick, D. Marucci, J. Cartmill, C. Martin and W. Walsh, Resistance forces acting on suture needles, J. Biomech., 2001, 34, 1335–1340, DOI:10.1016/S0021-9290(01)00099-9.
- S. DiMaio and S. Salcudean, Needle insertion modeling and simulation, IEEE Trans. Robot. Autom., 2003, 19, 864–875, DOI:10.1109/TRA.2003.817044.
- S. Misra, K. B. Reed, B. Schafer, K. T. Ramesh and A. M. Okamura, Mechanics of Flexible Needles Robotically Steered through Soft Tissue, Int. J. Robot. Res., 2010, 29, 1640–1660, DOI:10.1177/0278364910369714.
- M. Mahvash and P. Dupont, Mechanics of dynamic needle insertion into a biological material, IEEE Trans. Biomed. Eng., 2010, 57, 934–943, DOI:10.1109/TBME.2009.2036856.
- S. Y. Ko and F. R. Y. Baena, Toward a Miniaturized Needle Steering System With Path Planning for Obstacle Avoidance, IEEE Trans. Biomed. Eng., 2013, 60, 910–917, DOI:10.1109/TBME.2012.2227741.
- W. Shu, H. Heimark, N. Bertollo, D. J. Tobin, E. D. O'Cearbhaill and A. N. Annaidh, Insights into the mechanics of solid conical microneedle array insertion into skin using the finite element method, Acta Biomater., 2021, 135, 403–413, DOI:10.1016/j.actbio.2021.08.045.
- V. D. Sree, A. Ardekani, P. Vlachos and A. B. Tepole, The biomechanics of autoinjector-skin interactions during dynamic needle insertion, J. Biomech., 2022, 134, 110995, DOI:10.1016/j.jbiomech.2022.110995.
- P. S. L. Anderson, Making a point: shared mechanics underlying the diversity of biological puncture, J. Exp. Biol., 2018, 221, jeb187294, DOI:10.1242/jeb.187294.
- P. S. L. Anderson, J. LaCosse and M. R. Pankow, Point of impact: the effect of size and speed on puncture mechanics, Interface Focus, 2016, 6, 20150111, DOI:10.1098/rsfs.2015.0111.
- L. Kundanati, R. Guarino, M. Menegon and N. M. Pugno, Mechanics of snake biting: Experiments and modelling, J. Mech. Behav. Biomed. Mater., 2020, 112, 104020, DOI:10.1016/j.jmbbm.2020.104020.
- Z. Tan, C. Parisi, L. D. Silvio, D. Dini and A. E. Forte, Cryogenic 3D Printing of Super Soft Hydrogels, Sci. Rep., 2017, 7, 16293, DOI:10.1038/s41598-017-16668-9.
- L. B. Bezek, M. P. Cauchi, R. D. Vita, J. R. Foerst and C. B. Williams, 3D printing tissue-mimicking materials for realistic transseptal puncture models, J. Mech. Behav. Biomed. Mater., 2020, 110, 103971, DOI:10.1016/j.jmbbm.2020.103971.
- L. B. Bezek, C. A. Chatham, D. A. Dillard and C. B. Williams, Mechanical properties of tissue-mimicking composites formed by material jetting additive manufacturing, J. Mech. Behav. Biomed. Mater., 2022, 125, 104938, DOI:10.1016/j.jmbbm.2021.104938.
- A. Leibinger, A. E. Forte, Z. Tan, M. J. Oldfield, F. Beyrau, D. Dini and F. R. Y. Baena, Soft Tissue Phantoms for Realistic Needle Insertion: A Comparative Study, Ann. Biomed. Eng., 2016, 44, 2442–2452, DOI:10.1007/s10439-015-1523-0.
- A. G. Atkins, Fracture toughness and cutting, Int. J. Prod. Res., 1974, 12, 263–274, DOI:10.1080/00207547408919554.
- A. Stevenson and K. A. Malek, On the Puncture Mechanics of Rubber, Rubber Chem. Technol., 1994, 67, 743–760, DOI:10.5254/1.3538707.
- O. A. Shergold and N. A. Fleck, Mechanisms of deep penetration of soft solids, with application to the injection and wounding of skin, Proc. R. Soc. A, 2004, 460, 3037–3058, DOI:10.1098/rspa.2004.1315.
- M. J. Oldfield, D. Dini, G. Giordano and F. R. Y. Baena, Detailed finite element modelling of deep needle insertions into a soft tissue phantom using a cohesive approach, Comput. Methods Biomech. Biomed. Eng., 2013, 16, 530–543, DOI:10.1080/10255842.2011.628448.
- B. Takabi and B. L. Tai, A review of cutting mechanics and modeling techniques for biological materials, Med. Eng. Phys., 2017, 45, 1–14, DOI:10.1016/j.medengphy.2017.04.004.
- M. Terzano, D. Dini, F. R. Y. Baena, A. Spagnoli and M. Oldfield, An adaptive finite element model for steerable needles, Biomech. Model. Mechanobiol., 2020, 19, 1809–1825, DOI:10.1007/s10237-020-01310-x.
- S. Fregonese and M. Bacca, Piercing soft solids: A mechanical theory for needle insertion, J. Mech. Phys. Solids, 2021, 154, 104497, DOI:10.1016/j.jmps.2021.104497.
- S. Fregonese and M. Bacca, How friction and adhesion affect the mechanics of deep penetration in soft solids, Soft Matter, 2022, 18, 6882–6887, 10.1039/D2SM00638C.
- A. Spagnoli, R. Brighenti, M. Terzano and F. Artoni, Cutting resistance of soft materials: Effects of blade inclination and friction, Theor. Appl. Fract. Mech., 2019, 101, 200–206, DOI:10.1016/j.tafmec.2019.02.017.
- S. Jiang, P. Li, Y. Yu, J. Liu and Z. Yang, Experimental study of needle-tissue interaction forces: Effect of needle geometries, insertion methods and tissue characteristics, J. Biomech., 2014, 47, 3344–3353, DOI:10.1016/J.JBIOMECH.2014.08.007.
- M. Khadem, C. Rossa, R. S. Sloboda, N. Usmani and M. Tavakoli, Mechanics of Tissue Cutting During Needle Insertion in Biological Tissue, IEEE Rob. Autom. Lett., 2016, 1, 800–807, DOI:10.1109/LRA.2016.2528301.
- F. Casanova, P. R. Carney and M. Sarntinoranont, In vivo evaluation of needle force and friction stress during insertion at varying insertion speed into the brain, J. Neurosci. Methods, 2014, 237, 79–89, DOI:10.1016/j.jneumeth.2014.08.012.
- D. J. van Gerwen, J. Dankelman and J. J. van den Dobbelsteen, Needle-tissue interaction forces – A survey of experimental data, Med. Eng. Phys., 2012, 34, 665–680, DOI:10.1016/j.medengphy.2012.04.007.
- J. D. T. Tubon, O. Moreno-Flores, V. D. Sree and A. B. Tepole, Anisotropic damage model for collagenous tissues and its application to model fracture and needle insertion mechanics, Biomech. Model. Mechanobiol., 2022, 1–16, DOI:10.1007/s10237-022-01624-y.
- R. Long and C.-Y. Hui, Fracture toughness of hydrogels: measurement and interpretation, Soft Matter, 2016, 12, 8069–8086, 10.1039/C6SM01694D.
- A. Spagnoli, R. Brighenti, M. Cosma and M. Terzano, Fracture in soft elastic materials: Continuum description, molecular aspects and applications, Advances in Applied Mechanics, Elsevier Inc., 2022, pp. 255–307 DOI:10.1016/bs.aams.2021.07.001.
- C.-Y. Hui, A. Jagota, S. J. Bennison and J. D. Londono, Crack blunting and the strength of soft elastic solids, Proc. R. Soc. A, 2003, 459(2034), 1489–1516, DOI:10.1098/rspa.2002.1057.
- B. Zhang and S. B. Hutchens, On the relationship between cutting and tearing in soft elastic solids, Soft Matter, 2021, 17, 6728–6741, 10.1039/D1SM00527H.
- A. N. Gent, Adhesion and Strength of Viscoelastic Solids. Is There a Relationship between Adhesion and Bulk Properties?, Langmuir, 1996, 12, 4492–4496, DOI:10.1021/la950887q.
- M. Terzano, A. Spagnoli and P. StÅhle, A fracture mechanics model to study indentation cutting, Fatigue Fract. Eng. Mater. Struct., 2018, 41, 821–830, DOI:10.1111/ffe.12750.
- A. Spagnoli, M. Terzano, R. Brighenti, F. Artoni and P. StÅhle, The fracture mechanics in cutting: A comparative study on hard and soft polymeric materials, Int. J. Mech. Sci., 2018, 148, 554–564, DOI:10.1016/j.ijmecsci.2018.09.013.
- A. Spagnoli, R. Brighenti, R. Alberini, M. Montanari and M. Terzano, On Mode I crack mechanism in the puncturing of soft tissues, Proc. Struct. Integr., 2022, 41, 656–663, DOI:10.1016/j.prostr.2022.05.074.
- S. Lee and M. Pharr, Sideways and stable crack propagation in a silicone elastomer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9251–9256, DOI:10.1073/pnas.1820424116.
- K. B. Broberg, Cracks and Fracture, Elsevier Science, 1999, ISBN 9780080503271 Search PubMed.
- K. L. Johnson, Contact Mechanics, Cambridge University Press, 1987 Search PubMed.
- Dassault Systèmes SIMULIA, Abaqus 2018, Documentation, 2018.
- J. R. Rice, A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks, J. Appl. Mech., 1968, 35, 379–386, DOI:10.1115/1.3601206.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00011g |
| This journal is © The Royal Society of Chemistry 2023 |