Effective calcium doping at the B-site of BaFeO_3−δ perovskite: towards low-cost and high-performance oxygen permeation membranes

Abstract

A cost-effective doping strategy was developed to enhance the oxygen permeability and structural stability of BaFeO_3−δ. We demonstrated that the alkaline earth metal element Ca, which is usually considered an A-site dopant for perovskite oxides, can be successfully introduced into the B-site of BaFeO_3−δ. The cubic perovskite structure of BaFe_1−xCa_xO_3−δ was stabilized down to room temperature for the Ca-doping concentration range from 5 to 15 at%. First principles calculations not only proved the preference of Ca at the B-site with lower defect formation energies than the A-site, but also demonstrated that the migration of the oxygens located greater distances from the Ca position is characterized by lower barrier energies than those in the Ca vicinity and even lower than that for the undoped BaFeO_3−δ. We found that these favourable, low energy barrier paths away from the Ca sites exert more pronounced effects on the oxygen migration at diluted dopant concentrations, and hence, the material with x = 0.05 level of substitution shows a higher oxygen permeability with a lower activation energy compared to the undoped or highly-doped BaFeO_3−δ. The BaFe_0.95Ca_0.05O_3−δ membrane is characterized by a high oxygen permeability of 1.30 mL cm⁻² min⁻¹ at 950 °C and good long-term stability at 800/900 °C, as obtained over 200 h. Therefore, the feasibility and applicability of Ca-doping at the B-site of the perovskite can be highlighted, which allows for the enhancement of the oxygen migration ability, originating from the appropriate tuning of the lattice structure.

---

1 Introduction

Oxygen plays a critical role in the industrial sector, and the oxygen market has experienced ever-increasing demand because clean energy technologies and chemical process operations, such as oxy-fuel combustion, partial oxidation of methane (POM), smelt manufacturing, and medical treatment, require tonnage quantities of oxygen as a feed. This makes oxygen separation an important large-scale technology.^1–4 Currently, the most commonly used commercial method for oxygen production, cryogenic distillation, requires a very low temperature (approximately −185 °C) and a high pressure, making it relatively inefficient and expensive.¹ To address these issues, ceramic membrane separation technology, which is based on mixed ionic–electronic conductors (MIEC), has attracted extensive attention. The method offers a viable alternative for the reduction of the energy penalty and construction costs, at least by 35%, compared to traditional, cryogenic distillation-type air separation.⁵ MIEC membranes can also be used for POM processes, oxygen-fuel combustion, as well as ammonia synthesis, and can be integrated into one reactor, having high selectivity and conversion efficiency and also enabling a simplified production procedure.^6,7 Therefore, it is indeed a promising technology, as documented since 1980s in a large number of reported scientific works and patents. It also proved to be feasible in a large-scale application by several institutions, including Fraunhofer Institute for Ceramic Technologies and Systems, in which a highly-reliable oxygen production device based on MIEC was shown to steadily operate for at least 2500 h.⁸

A dense ceramic oxygen-permeable membrane was firstly reported by Teraoka et al. on a MIEC-type perovskite oxide with La_1−xSr_xCo_1−yFe_yO_3−δ composition in the 1980s.⁹ With an increasing oxygen vacancy concentration and a decreasing average bond strength upon introduction of Sr and Co at A- and B-sites, respectively, the oxygen permeability was found to increase and reach the highest flux value of 3.1 mL cm⁻² min⁻¹ for SrCo_0.8Fe_0.2O_3−δ material at 850 °C. These results have attracted considerable attention to cobalt-based perovskite-type oxygen ionic transport membranes during the past decades. Recent investigations on mixed-conducting oxide materials and membranes with various A/B-site compositions have shown that Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ and BaCo_0.7Fe_0.2Nb_0.1O_3−δ oxides are the most promising candidates, on an account of their high oxygen permeability, which takes advantage of the fact that the A-site is occupied by large Ba²⁺ cations.^10,11 However, these cobalt-based materials always suffer from a structural instability and a corresponding oxygen permeability degradation during long term operation, which have been ascribed as originating from the reduction of cobalt ions under the low oxygen partial pressure atmospheres at elevated temperatures.^12–14 Furthermore, the high price of cobalt is another factor that may limit the widespread application of such cobalt-based membranes. Therefore, development of cobalt-free materials for MIEC membrane applications seems very important.

Already a large number of cobalt-free membranes have been developed to improve the reduction resistance, such as BaFe_1−xCe_xO_3−δ, Ba_0.5Sr_0.5Fe_0.8Zn_0.2O_3−δ, La_1−xSr_xCr_1−yFe_yO_3−δ.^15–17 Considering the oxygen permeability in conjunction with the stability in the reducing atmosphere, BaFeO_3−δ is believed to be one of the most promising cobalt-free MIECs. The merits of BaFeO_3−δ are strongly associated with the presence of Fe at the B-site, which has a higher B–O bond strength, as well as a full occupation of the A-site by Ba cations, allowing it to sufficiently expand the lattice structure, which is beneficial for oxygen migration.^18–22 However, since the Shannon radii-based tolerance factor (t) is higher than 1, which is a result of a large mismatch between the size of the A- and B-site cations, BaFeO_3−δ has been found to maintain the oxygen vacancy-disordered, cubic perovskite structure only at temperatures higher than 825 °C. At lower temperatures, a phase transformation from cubic to a low symmetry structure occurs and is accompanied by a large volume change, as well as a seriously declined oxygen permeability.^18,22

In order to stabilize the cubic structure of BaFeO_3−δ down to lower temperatures, various dopants have been introduced to either the A-site or B-site, such as at the A-site: La, Ca, Sm and at the B-site: Ce, La, Y, Cu, Ni, Zr, Ta, In, Gd, Nb.^18–29 For tuning the lattice structure to cubic, A-site dopants are always chosen to be smaller than Ba cations, while B-site dopants are selected to be larger than Fe cations, according to the required decrease of the tolerance factor (t).³⁰ For the two doping strategies, the B-site doping with larger cations is more preferred because the expanded lattice is beneficial for oxygen ion diffusion, which is in contrast to the A-site doping with smaller cations than Ba.^20,22,28 Most of the promising candidates for the B-site dopants are rare earth elements because of their common moderate valence (+3), relatively large ionic radius, and strong reduction resistance in comparison to the transition metal elements, which lead to a high oxygen vacancy concentration, stable perovskite cubic structure and good structural stability, respectively.^22,28 Despite the advantages of the rare earth dopants, the higher bond strength between such metals and oxygen anions, compared to that of the Fe–O bond, is unfavourable for oxygen migration in the lattice. It also should be mentioned that the high price and scarce resources of rare earth metals may seriously restrict applications of such MIECs in industrial, large-scale applications.

Herein, we report for the first time a novel BaFeO_3−δ-based perovskite, doped with the cheap and abundant alkaline earth metal Ca²⁺ at the B-site. Usually, Ca²⁺ is regarded as an A-site dopant because of its similar properties with respect to Ba, being in the same main group of the periodic table. However, considering the much smaller ionic radius of Ca²⁺, similar in the BO₆ octahedron to the rare earth elements, it appears to be a very promising potential B-site dopant for tuning the lattice structure of BaFeO_3−δ. The advantages of Ca²⁺ include its low valence state (+2) and a relatively weak Ca–O bond strength compared with the rare earth element–oxygen bonds, and it would endow the host BaFeO_3−δ material with a high oxygen vacancy concentration and a low oxygen migration energy. As a result, a high oxygen permeation flux through such designed membranes can be expected. In this article, the effects of Ca-doping on the lattice structure, oxygen nonstoichiometry, electrical conductivity, oxygen surface exchange and bulk diffusion, oxygen permeability and long term stability were systematically investigated. First principles calculations were also conducted to explore the location preference of Ca atoms and to understand the oxygen migration behaviour in the materials. The experimental results confirm the anticipated superior oxygen permeability of doped BaFe_1−xCa_xO_3−δ for a low-level doping degree, which stems from a complex influence of Ca on the crystal structure, oxygen nonstoichiometry and transport properties. Abundant resources and the low price of all the elements as well as the recorded excellent performance of BaFe_1−xCa_xO_3−δ make the elaborated membrane materials very competitive for practical industry applications.

2 Experimental

2.1 Materials preparation

BaFe_1−xCa_xO_3−δ (0 ≤ x ≤ 0.15) oxides were prepared via an ethylenediamine tetraacetic acid (EDTA)–citric acid combustion method as described previously.²⁸ The stoichiometric raw materials of Ba(NO₃)₂ (AR, Sinopharm), Fe(NO₃)₃ 9H₂O (AR, Sinopharm), and Ca(NO₃)₂·4H₂O (AR, Sinopharm) were dissolved in distilled water with the addition of several drops of nitric acid (65–68%, AR, Sinopharm) to obtain a clear metal nitrate solution. Thereafter, the EDTA and citric acid were added into the solution at a molar ratio of 1 : 1.5 : 1 with respect to the total amount of metal ions. The pH value was adjusted to 8 with ammonia (28.0–30.0%, AR, Sinopharm). After being heated to evaporate the water in a bath at 80 °C, the solution turned to a transparent gel, which was then pre-fired at 250 °C and calcined at 850 °C in air for 6 h to get the oxide powder precursors. The obtained powders were thoroughly ground in a mortar with the addition of several drops of 1 wt% PVA and then pressed into disks (Φ ∼ 19 mm, thickness of 1–2 mm) and bars (2 × 7.5 × 42 mm³) under a uniaxial pressure of 300 MPa followed by sintering in air at 1200 °C for 4 h. The sintered, dense disks were polished to a proper thickness for oxygen permeation studies.

2.2 Materials characterization

The phase composition and crystal structure of the synthesized samples were examined by powder X-ray diffraction (XRD) using a D/teX Ultra diffractometer (Ultima IV, Rigaku Co., Japan). Measurements were conducted with Cu Kα radiation (λ = 1.5406 Å) in the 10–100° range. High-temperature XRD studies were performed in air up to 900 °C on a Panalytical Empyrean diffractometer equipped with an Anton Paar 1200N oven-chamber and PIXcel3D detector. The temperature program was set to 10 °C min⁻¹ heating and cooling rates, and XRD data were collected in the 10–110° range at each temperature with an interval of 100 °C. After an equilibration at the desired temperature for 5 min, the scan lasted around 50 minutes. The Rietveld method was applied to refine the recorded XRD patterns using the General Structure Analysis System (GSAS) with some complementary tests done using EXPO software.^31–33

The microstructure and element distribution on the surface of the sintered membranes (x = 0.05 and 0.15) were analysed by scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDXS) using a LEO-1450 scanning electron microscope equipped with a spectrometer (Noran System 7, Thermo Scientific, USA) at excitation voltages of 20 kV for SEM and EDXS analyses. The electron probe microanalysis (EPMA, JEOL, JXA-8100) was also conducted to analyse the chemical composition of the sintered membranes (x = 0.05 and 0.15). X-ray photoelectron spectroscopy (XPS) data were obtained using a Thermo ESCALAB 250X (USA) electron spectrometer with a 150 W Al Kα X-ray source.

The temperature-dependent weight of the BaFe_1−xCa_xO_3−δ (x = 0.025, 0.05 and 0.15) samples was characterized by thermogravimetric analysis (TG) on a TA Instruments Q5000 IR (USA) apparatus in air or argon with a flow rate of 100 mL min⁻¹ from 25 to 900 °C. According to the TG results and the initial oxygen nonstoichiometry, δ₀, which was evaluated with iodometric titration method,³⁴ the oxygen nonstoichiometry δ_t at high temperatures was calculated using eqn (1),

where m₀ is the initial weight, m_t is the weight at a particular temperature point, and M is the molar mass of the respective BaFe_1−xCa_xO₃ with stoichiometric oxygen content.

The electrical conductivity of the considered materials was measured by a four-terminal DC method in air from 200 °C to 900 °C. The chemical bulk diffusion coefficient (D_chem) and surface exchange coefficient (k_chem) were determined with the electrical conductivity relaxation (ECR) method. Before measurements, a dense sinter with bar shape was placed in a furnace and tested at temperatures between 650 °C and 850 °C with an interval of 50 °C. The material was supplied with a 10 vol% O₂/N₂ gas mixture at a constant flow of 200 mL min⁻¹ for about 1 h to reach the steady-state. By abruptly switching the atmosphere from 10 vol% to 20 vol% O₂/N₂ gas mixture, the electrical conductivity changed due to the variation of the oxygen partial pressure, and the dependence on time was recorded by a four-terminal DC method using a high-precision digital multimeter (Keithley 2100). Then, the oxygen ion diffusion and surface exchange coefficients were obtained by fitting the recorded electrical conductivity relaxation curves based on Fick's second law.^35–37

2.3 Oxygen permeation measurement

The oxygen permeation properties of the prepared BaFe_1−xCa_xO_3−δ membranes were measured utilizing gas chromatography and a vertical, high-temperature oxygen permeation apparatus described in previous work.²⁸ After being polished, the as-prepared BaFe_1−xCa_xO_3−δ membranes were sealed on a quartz tube by a silver ring with an effective inner circular area of 1.28 cm². Compressed air was applied to sweep one side of the membrane as the feed gas with a flow rate of 120 mL min⁻¹ [STP]. On the other side of the membrane, high purity helium (>99.999%) was introduced into the quartz tube as a carrier gas with a flow rate of 60 mL min⁻¹ [STP]. Gas flow rates were monitored by a mass-flow meter (Sevenstar, DC-07, China). The outlet gas, a mixture of helium and permeated oxygen, was then injected into the gas chromatograph with a TCD detector (GC, SP2100, China). In the present work, no nitrogen leaks were detected, confirming that the membranes were well-sealed and gas-tight. The oxygen permeation flux was calculated using eqn (2),where C_O2 stands for the measured oxygen concentration in the outlet gas on the sweep side, F is the flow rate of the helium, and S is the effective circular area of the membranes.

2.4 First principles calculation

In order to understand the Ca-doping effect on oxygen ion transport properties, the oxygen migration barrier energies were calculated utilizing CASTEP (Cambridge Serial Total Energy Package) code,^38,39 which is based on the density-functional theory (DFT) and plane-wave pseudopotential (PWP) method. For the exchange–correlation potential in the generalized gradient approximation (GGA), the PBE scheme was employed.^40,41 The cut-off energy of the plane waves was 400 eV, and the atomic coordinates of the simulated structures were optimized by an iterative process using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to minimize the energy with respect to the atomic positions.⁴² The tolerance for self-consistence was set at 5 × 10⁻⁶ eV per atom for total energy, 0.01 eV Å⁻¹ for force, 0.02 GPa for maximum stress, and 5 × 10⁻⁴ Å for the maximum displacement. The Brillouin zone integrations were approximated using a special 3 × 3 × 3 k-point sampling scheme of Monkhorst–Pack for the unit cell.⁴³ The valence electronic configurations were taken as O-2s²2p⁴, Fe-3d⁶4s², Ca-3s²3p⁶4s² and Ba-5s²5p⁶6s² for the ground-state electronic structure calculations. A spin polarization calculation was adopted, and the formal spin was used as the initial one. After the successful geometry optimization on defective supercells of the starting and ending configurations, the linear synchronous transit/quadratic synchronous transit (LST/QST) were used to calculate the oxygen transition barrier energies.⁴⁴

3 Results and discussion

The phase composition and crystal structure of the as-sintered BaFe_1−xCa_xO_3−δ samples (x = 0.025–0.15) were characterized through room temperature XRD examinations as presented in Fig. 1, and the data was analysed by applying the Rietveld method (Fig. S1†). The structural parameters derived from the refinements are listed in Table S1.† It was found that the phase composition of a sample with x = 0.025 can be approximated as a mixed dual phase with triclinic distorted perovskite and cubic perovskite and presents obvious superstructure-related peaks (Fig. S1a†).^45,46 Data for samples with higher doping content, x = 0.05–0.15, can be refined well with the cubic structure, and no other impurity phase was observed up to the resolution and sensitivity of the XRD method (Fig. S1b–d†). The fitted lattice parameters, as listed in Table S1,† were found to increase with the Ca content. This coincided with the shift of the 110 reflex position, as shown in the enlarged XRD patterns of Fig. 1b, and confirms the successful substitution of the larger Ca cations (r(Ca²⁺) = 1 Å at 6-fold coordination) for Fe ions (r(Fe³⁺) = 0.645/0.55 (HS/LS) Å, r(Fe⁴⁺) = 0.585 Å at 6-fold coordination) with the expanded unit cell volume.⁴⁷ While the presence of Ca cations at the B-site in various perovskite oxides was already shown,^48,49 this is to our knowledge, the first report on such doping in BaFeO_3−δ. In order to provide strong evidence supporting this effect, additional independent techniques were utilized, including first principles calculations, as discussed below.

Fig. 1 XRD patterns of BaFe_1−xCa_xO_3−δ samples (x = 0.025–0.15) after sintering in air at 1200 °C for 4 h.

For further exploration of the location preference of Ca in the cubic perovskite BaFeO_3−δ oxide, first principles calculations were employed to identify the energy cost of substitutional defect formation for doping of Ca at A- or B-sites. The defect formation energies (E_form) were calculated using the following eqn (3),

E_form = E_defect − E_host + μ_host − μ_dope (3)

where E_defect and E_host are the energies of the defective and perfect crystal structure, respectively, and μ_host and μ_dope are the chemical potentials of the host atoms and the dopant atoms, respectively.^50,51 The 2 × 2 × 2 cubic perovskite supercell of Ba₈Fe₈O₂₃ with one oxygen vacancy was regarded as the host, and one Ca atom was introduced into the supercell to replace one A-site Ba atom or one B-site Fe atom. Such replacement was considered at different relative locations with respect to the oxygen vacancy. Thus, the investigated defective supercells were denoted as A-site: Ba₇CaFe₈O₂₃-1, Ba₇CaFe₈O₂₃-2, and B-site: Ba₈Fe₇CaO₂₃-1, Ba₈Fe₇CaO₂₃-2, Ba₈Fe₇CaO₂₃-3, according to the increasing distance between the Ca defect and the oxygen vacancy, as illustrated in Fig. S2.† As can be seen in Table 1, Ca defects substituting for B-site (Fe) in all three assumptions exhibit lower formation energies than in the two cases of substitution for the A-site (Ba) atoms. It can be therefore stated that from an energetic point of view, the Ca-doping at the B-site is more favourable.

Table 1 Calculated E(Ca_Ba) and E(Ca_Fe) for Ba₈Fe₈O₂₃ supercell. Ba₈Fe₈O₂₃-1, Ba₈Fe₈O₂₃-2 and Ba₈Fe₈O₂₃-3 denote different possibilities of Ca and the oxygen vacancy location in the corresponding host supercells and are listed according to the increasing distance between the defects

	Ba8Fe8O23-1	Ba8Fe8O23-2	Ba8Fe8O23-3
E(CaBa)/eV	1.19	1.00	—
E(CaFe)/eV	0.81	0.10	0.41

---

Besides, to further confirm the distribution of Ca in the samples, distribution of the elements was studied by EPMA and EDXS methods for compounds with x = 0.05 and 0.15. Both results (Tables S2 and S3†) indicate that the combined molar fraction of Fe and Ca is similar to that of Ba. With an increase of the Ca-doping content to 0.15, the molar fraction of Ca increases to three times that of the x = 0.05 sample, which follows the designed cation ratios in the materials. Moreover, the symmetric nature of the Ca 2p XPS spectrum, as shown in Fig. S3d,† demonstrates only one kind of chemical environment of Ca, which is most likely in the perovskite phase. In addition, the membranes show dense microstructures (Fig. 2a and e), and the EDXS mapping analysis (Fig. 2) reveals a homogeneous distribution of Ba, Ca and Fe elements, with no phase segregation detected up to the resolution of the method. Considering that some secondary phase should emerge if the Ca dopant would occupy the A-site rather than the B-site, the above results with a combination of structural chemical analysis and first principles calculations, as well as additional studies (e.g. attempt to synthesize Ba_0.85Ca_0.15FeO_3−δ, Fig. S4†), provide strong support to Ca-doping at the B-site of the BaFe_1−xCa_xO_3−δ lattice.

Fig. 2 Microstructure of BaFe_1−xCa_xO_3−δ membranes with x = 0.05 (a–d) and 0.15 (e–h) sintered at 1200 °C for 4 h: (a and e) SEM micrographs, (b–d, f–h) EDXS elemental distribution of Ba, Ca and Fe in panel (a and e).

In order to assess the phase stability of BaFe_1−xCa_xO_3−δ materials at high temperatures, in situ XRD measurements were conducted on powder samples with x = 0.025, 0.05 and 0.15 under an air atmosphere in a cooling process within the temperature range from 900 °C to room temperature. The representative results are presented with the corresponding PDF standard cards of the related structures in Fig. 3. A phase transition for BaFe_0.975Ca_0.025O_3−δ material from high-temperature cubic to triclinic perovskite symmetry was found to occur below 600 °C, as shown in Fig. 3a. A single phase cubic perovskite phase for samples with x = 0.05 and 0.15 (Fig. 3b and S5†) is maintained throughout the whole temperature range, and no phase transition could be evidenced. The XRD patterns of both materials were refined using the Rietveld method by assuming the presence of Ca at the A-site or B-site, respectively. Better results (smallest residues) were obtained if Ca was placed at the Fe site (Table S4†). These results also support previous findings that the Ca dopant is substituting the Fe, rather than the barium site.

Fig. 3 In situ XRD patterns of BaFe_1−xCa_xO_3−δ samples with x = 0.025 (a) and x = 0.05 (b) collected from high to room temperature.

The lattice parameters of the two cubic samples (x = 0.05 and 0.15) were calculated based on the Rietveld refinement of the in situ XRD results (Fig. 3b and S5†), and the results are plotted in Fig. S6.† The values increase with temperature, and the dependence appears to be accelerated when the temperature is higher than 400 °C. This is associated with the so called chemical expansion known to appear for such MIEC-type materials. The effect adds to the basic thermal expansion and originates from the release of the lattice oxygen, causing repulsion of two of the B-site cations in the immediate vicinity of a generated oxygen vacancy, as well as an associated increase in the Fe radius with reduced valence.⁵² By applying the linear fitting to the temperature-dependent lattice parameter data in low (25–300 °C) and high (600–900 °C) temperature ranges, the linear expansion coefficients (TEC) could be obtained as 17.8 × 10⁻⁶ and 29.0 × 10⁻⁶ K⁻¹ for x = 0.05 sample, and as 14.9 × 10⁻⁶ and 38.8 × 10⁻⁶ K⁻¹ for x = 0.15 material (shown in inset of Fig. S6†), respectively. Such results are comparable with other reported BaFeO_3−δ-based materials.^19,53 Apparently, Ca-doping decreases the TECs in the low temperature range, while it exerts an opposite effect at the high temperature range. The decreased TEC at low temperatures is most likely due to a decrease in the oxygen deficiency with Ca-doping, as is presented in Fig. 4. Such influence is expected to decrease the anharmonicity of atomic vibrations.⁵⁴ On the other hand, the increased TECs in the high temperature range mostly result from larger changes of the oxygen deficiency with Ca-doping between 600 and 900 °C, as evidenced in the TG results (Fig. 4). The impact of Ca-doping on the thermal reducibility of BaFe_1−xCa_xO_3−δ was further analysed by TG (Fig. 4a). It should be mentioned that since there are some adsorbates being adsorbed on the material's surface, all samples exhibited a weight loss below 300 °C at the first heating process (Fig. S7†).²⁷ During the following cycles, this kind of extrinsic weight change was eliminated, and thus, data from the second thermal cycle could be taken into consideration for oxygen nonstoichiometry calculations (Fig. 4b). The weight of the samples with x = 0.05 and 0.15 starts to decrease from ∼300 °C, which is ascribed to the thermal reduction of Fe ions and the corresponding release of lattice oxygen. This is in agreement with the previously mentioned variation of the temperature-dependent lattice parameter plots (Fig. S6†). It is worth to mention that there is an unusual weight loss and recovery in the middle temperature range for the sample with x = 0.025, which might be related to the structural transition (Fig. 3a) or possibly to some other transformation related to the electric or magnetic properties of the material. While this phenomenon was also observed in repeated studies, further tests are needed to elucidate its nature.

Fig. 4 TG results (a) and temperature dependent oxygen nonstoichiometry (b) of BaFe_1−xCa_xO_3−δ powder samples with x = 0.025, 0.05 and 0.015 in synthetic air; flow of air: 100 mL min⁻¹, heating/cooling rate: 10 °C min⁻¹.

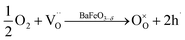
Combining the TG results with the room temperature oxygen nonstoichiometry obtained by an iodometric titration technique, the oxygen vacancy concentrations at higher temperatures were calculated and plotted in Fig. 4b. The values were found to decrease with the increasing Ca-doping content (Table S5†), while the calculated average valence of Fe increases, suggesting a charge compensation mechanism by varying the B-site element valence, rather than generating more oxygen vacancies. The defects produced by the acceptor-type Ca-doping in BaFeO_3−δ can be expressed by eqn (4)–(6):

Such acceptor doping induces the generation of electronic holes for charge compensation (eqn (4)), while the stronger Ca–O bond, compared to the Fe–O bond, causes the decrease of the concentration of the oxygen vacancies, but a concomitant increase in the amount of the electronic holes (eqn (5)). Those electronic holes can be expressed as the increase of the valence of Fe cations (eqn (6)). Such a charge compensation mechanism might be associated with the reduced lattice distortion by substitution of larger Ca and doping for Fe cations, which makes Fe ions not necessarily increase their radius by reduction of the valence, and therefore, for mitigating lattice distortion.

The Ca-doping also has impacts on the electronic transport performance of BaFe_1−xCa_xO_3−δ. The temperature dependence of the electrical conductivity of BaFe_1−xCa_xO_3−δ in the Arrhenius plot is shown in Fig. 5. For most of the MIECs, the electrical conductivity mostly comes from the electronic component, since its magnitude is usually at least one or two orders larger than that of ionic conductivity.²³ In the corresponding Arrhenius coordinates, the electronic conductivity increases linearly with the increase of the temperature in a lower temperature range, indicating a Zener double-exchange mechanism via B–O–B bonds. At higher temperatures, the electronic conductivity deviates from the former linear trend, showing a fast decrease. This is associated with the lattice oxygen release at those temperatures, which would cause a partial annihilation of the electrical holes, and thus, decrease the concentration of the p-type charge carriers, as described by eqn (7).

Fig. 5 Temperature dependence of electrical conductivity of BaFe_1−xCa_xO_3−δ (x = 0.025, 0.05, 0.10 and 0.015) samples in air, represented as an Arrhenius-type plot.

In addition, increasing the oxygen vacancy concentration breaks the B–O–B charge transfer, as the oxygen is needed for the double exchange mechanism to occur.⁵² Furthermore, Fig. 5 also reveals that the substitution of redox-inactive Ca cations for Fe at the B-site decreases the electronic conductivity, even though the Ca substitution leads to a higher average valence of Fe (Table S5†). This can be understood considering that Ca-doping also severs the B–O–B conduction path, with the inability of Ca 3d orbitals to connect with the O 2p states, which leads to breaking the conduction network.

The oxygen bulk diffusion coefficients (D_chem) and surface exchange coefficients (k_chem) of the BaFe_1−xCa_xO_3−δ materials with x = 0.025–0.15 were measured by ECR method in the temperature range of 650–850 °C. Fig. 6a shows the typical ECR curves for the BaFe_1−xCa_xO_3−δ dense samples being collected after a sudden change of the oxygen partial pressure from 0.1 to 0.2 atm at 800 °C. Based on ECR theory,^35–37 the oxygen bulk diffusion coefficients (D_chem) and surface exchange coefficients (k_chem) of the tested materials were calculated by fitting the ECR data. Both of the coefficients were found to decrease with the Ca-doping content, as shown in Fig. 6b and c. The calculated activation energies, extracted from the corresponding Arrhenius plots of the temperature dependence of D_chem and k_chem, exhibit the lowest value for the x = 0.025 sample, and increase with the Ca-doping content, implying that the oxygen bulk migration and surface oxygen exchange process are hindered by introducing more Ca cations into the B-sites. The lower activation energy of k_chem than D_chem is probable due to the high activity of the oxygen reduction reaction of BaFeO_3−δ based materials,⁵⁵ which is also found in some other similar perovskite-type MIEC materials.⁵⁶ Nevertheless, it is worth mentioning that the x = 0.025 sample exhibits a very fast oxygen bulk diffusion and surface exchange kinetics, with the coefficients of 1.21 × 10⁻⁴ cm² s⁻¹ and 3.97 × 10⁻³ cm s⁻¹ at 700 °C, respectively, which is among the highest level of many advanced perovskite MIECs.^36,53

Fig. 6 ECR plots of BaFe_1−xCa_xO_3−δ (x = 0.025–0.15) at 800 °C after a sudden change of oxygen partial pressure from 0.1 to 0.2 atm (a); temperature dependence of D_chem (b) and k_chem (c). Note: only high-temperature data of (c) were used to calculate E_a.

In order to advance the understanding of the Ca-doping effect on oxygen migration behaviour, first principles calculations were applied to elucidate the oxygen vacancy transport energy through different routes in the crystal lattice, in which a Ca atom was incorporated into a 2 × 2 × 2 BaFeO₃ supercell by substituting one Fe atom. The BaFeO₃ pristine cell was also constructed for comparison (Fig. 7a). It shows only one equivalent oxygen vacancy migration path in the lattice, of which the corresponding oxygen migration energy is 0.91 eV.²⁸ In the Ca-doped lattice, the coordination environment of the oxygen vacancy is obviously diversified. There are three possible sites for oxygen vacancies: nearest, second nearest and third nearest neighbours to the Ca dopant. They are donated as V_O1, V_O2 and V_O3, respectively, and depicted in Fig. 7b, which are equivalent to the Ca_Fe models of Ba₈Fe₇CaO₂₃-1, Ba₈Fe₇CaO₂₃-2, Ba₈Fe₇CaO₂₃-3 in Fig. S2.† Those models, at first, were separately optimized in terms of geometry, which was successfully done with the energy reaching the respective minimums. It was found that the state with the oxygen vacancy at the V_O1 position possesses the highest potential energy compared to the other two states, as shown in Fig. 7c, implying an unstable state for the location in the vicinity of the Ca²⁺ cations. The other two sites are more favourable for the presence of the oxygen vacancies. This finding could also be rationalized by a measured decrease of the oxygen vacancy concentration with the increasing Ca-doping content, as previously outlined in Fig. 4b.

Fig. 7 First principles calculations models of (a) Ba₈Fe₈O₂₄ and (b) Ba₈Fe₇CaO₂₄. (c) Potential energy diagram for oxygen vacancy migration through different routes in Ba₈Fe₇CaO₂₄. The V_O1, V_O2 and V_O3 are denoted as different possible sites for oxygen vacancy occupation.

From a geometry point of view, there are five primitive oxygen migration paths between the three kinds of oxygen vacancies and neighbouring oxygen atoms, as shown in Fig. 7c. The individual oxygen migration energy for different paths is calculated and listed in Table 2. Among the five paths, the largest value of the migration barrier energy (1.82 eV) occurs when the oxygen anions migrate along the path closest to the Ca cations, which might be correlated with a high basicity of calcium and may limit the removal of oxygen anions with high acidity. The increase in the activation energy of D_chem, as mentioned in Fig. 6b, can be attributed to the increased proportion of high barrier energy paths with a higher Ca-doping content. Nevertheless, the barrier energies along other migration paths exhibit much lower values than that in pristine BaFeO_3−δ (0.91 eV). Since the lattice structure is expanded by doping the larger Ca cations, the barrier energies of the other migration paths, away from Ca, could probably be decreased by crossing the bottleneck of Ba–Fe–Ba in the cubic perovskite lattice. Thus, considering the coexistence of both promoted and impeded oxygen migration paths, there should be an optimal Ca-doping content, at which the cubic structure can be maintained under a minimized restriction on the oxygen ion migration.

Table 2 Oxygen ion migration barrier energies for different transport paths in the Ba₈Fe₇CaO₂₄ supercell

	Migration barrier energy [eV]
	VO1	VO2	VO3
VO1	1.82	0.89
VO2	0.19	0.49	0.36
VO3		0.66	0.50

---

The oxygen permeation fluxes of the BaFe_1−xCa_xO_3−δ membranes (x = 0–0.15) with a 1.0 mm thickness were measured at temperatures between 800 and 950 °C using pure He as the sweep gas (Fig. 8a). For all doped membranes, a linearly increasing trend of the oxygen permeability with temperature was observed, indicating a thermal activation process of the oxygen permeation. At the same time, the oxygen permeation flux of the pristine BaFeO_3−δ membrane exhibits a very low value at low temperatures and an abrupt increase around ∼825 °C. This is ascribed to the phase transition of BaFeO_3−δ from the oxygen vacancy ordered hexagonal structure to the disordered cubic perovskite structure.³⁴ Because as evidenced in Fig. 3a, the phase transition temperature of the x = 0.025 sample is decreased by B-site substitution to ∼600 °C, and in the range of 800–950 °C, the membrane shows a gradual increase in the oxygen permeation flux. However, this membrane with x = 0.025 doping content delivers the highest oxygen permeability of 1.39 mL cm⁻² min⁻¹ at 950 °C, which is considerably high for the cobalt-free membrane. Due to the increased activation energy of the oxygen bulk diffusion (Fig. 6b) and the reduced oxygen vacancy concentration (Table S5†), a further increase in the Ca-doping level leads to a gradual decrease in the oxygen permeability.

Fig. 8 (a) Temperature dependent oxygen permeation fluxes of BaFe_1−xCa_xO_3−δ with 1.0 mm thickness (F_air = 120 mL min⁻¹, F_He = 60 mL min⁻¹); (b) variation of the calculated activation energies and oxygen permeation fluxes at 900 °C upon doping content.

The activation energies of the oxygen permeability of the x = 0–0.15 samples were also calculated from the corresponding Arrhenius-type temperature dependent oxygen permeation plots according to the Wagner equation.^22,25 The obtained dependence of the activation energies and the oxygen permeability at 900 °C on Ca-doping content is depicted in Fig. 8b. In contrast to the changes of the oxygen permeability, the opposite behaviour can be seen for the activation energy of the oxygen permeation, which markedly decreases first and then increases gradually with the Ca-doping content. Compared with pure BaFeO_3−δ, the lower activation energy of the slightly doped samples x = 0.025 and 0.05 can be ascribed to the expanded lattice structure, caused by the large-size Ca substitution and the resulting favourable transport paths away from the Ca position, as discussed in the section for the first principles calculations (Fig. 7). However, with a further increase in the doping content, the growing proportion of the high-barrier paths around the Ca positions outweighs the positive effect of other low energy barrier paths and leads to the increase of the activation energy. Thus, slight doping (x = 0.025, 0.05) is beneficial to maximize the advantages of the low barrier paths, and in consideration for the effective stabilization of the cubic perovskite structure in the whole temperature range of 25 to 950 °C, the x = 0.05 dopant level is preferred as the most suitable one. It should be mentioned that the apparent activation energy of the oxygen permeation for the x = 0.05 membrane (0.34 eV) is lower than that of the D_chem (0.92 eV). The inconsistency is likely coming from the different testing methods with non-identical conditions.^57,58 This effect was also shown in other works.^53,59,60

The long-term stability of the x = 0.05 membrane with 0.6 mm thickness was then examined at 800/900 °C under a He/Air gradient. The oxygen permeability is stable for 200 h with no obvious deterioration, as shown in Fig. 9, indicating the excellent structural stability of the BaFe_0.95Ca_0.05O_3−δ material. The tested x = 0.05 membrane was also subjected to XRD examination to evaluate its surface structure change after long-term operation, and there were no impurity phases observed, apart from the original cubic perovskite phase, as shown in Fig. S8.† In contrast to the easy reduction and decomposition of cobalt-based perovskite membranes in a low partial pressure atmosphere,^12–14 the Ca-doped cobalt-free BaFe_0.95Ca_0.05O_3−δ membrane displays a high structural stability with good long term operational reliability. These results strongly suggest that Ca-doped BaFeO_3−δ is a promising oxygen permeation membrane material, taking into account its excellent performance and cheap and abundant material resources.

Fig. 9 Long term stability of BaFe_0.95Ca_0.05O_3−δ membrane with 0.6 mm thickness for 100 h at either 900 or 800 °C.

The resistance of oxygen permeable membranes against low oxygen partial pressure reduction and CO₂ erosion is of great importance in practical industrial applications. The chemical and structural stability of the BaFe_1−xCa_xO_3−δ membranes with x = 0.05 and 0.15 was evaluated by treating the fresh membranes in 5 vol% H₂/Ar and in 2 vol% CO₂/N₂ at 800 °C for 8 h, respectively. The surface phase structure and morphology of the treated membranes were studied by XRD and SEM examinations. For samples treated in 5 vol% H₂/Ar, even though the surfaces of both the membranes changed and some segregates are exsolved, as shown in Fig. S9a and b,† the surface impurities are undetectable, and the main phase structure is maintained (Fig. S10†), demonstrating that the surface damage is not so severe. It can be stated that the BaFe_1−xCa_xO_3−δ materials have a good chemical and structural stability in reducing atmospheres. Furthermore, the SEM images indicate that Ca-doping mitigates the phase segregation and enhances the structural stability of materials. When treated in a CO₂-containing atmosphere (2 vol% CO₂/N₂), some remarkable changes on the surface structure were observed. XRD analysis reveals precipitation of BaCO₃ and BaFe₂O₄ impurity phases (Fig. S10†), while SEM observation shows an emergence of large segregates on the membrane surface (Fig. S9c and d†), indicating the weaker resistance towards CO₂ erosion compared to H₂ reduction. Nevertheless, the respective XRD peak intensities of the secondary phases decreased remarkably with the increasing Ca-doping level, suggesting that the B-site Ca-doping enhances the tolerance of BaFe_1−xCa_xO_3−δ towards CO₂.

4 Conclusions

Cheap and abundant calcium was successfully introduced into the B-site of BaFe_1−xCa_xO_3−δ materials to stabilize the cubic perovskite structure to room temperature and provide disordered oxygen vacancies and three-dimensional isotropic oxygen transport paths. The Ca preferred to locate at the B-site of cubic perovskite BaFeO_3−δ with lower Ca defect formation energies, as documented by first principles calculations and other conducted studies. With increasing the Ca-doping content, the phase transition temperature of the sample with x = 0.025 decreased from ∼825 °C to ∼600 °C, and a fully stable cubic perovskite phase can be achieved for samples with a higher dopant content of x = 0.05–0.15. The charge compensation of Ca substituting for Fe is achieved by generation of the electronic holes, but not oxygen vacancies. The Ca substitution for Fe decreases the electrical conductivity of BaFe_1−xCa_xO_3−δ, due to the presence of redox-inactive Ca cations in the B–O–B conduction paths, impeding the Zener double-exchange process. The ECR measurements reveal that although Ca-doping causes the increase in activation energy for both oxygen ion migration and surface oxygen exchange kinetics, the sample with x = 0.025 exhibits values of the oxygen ion bulk diffusion coefficient and surface exchange coefficient the highest among the reported works. First principles calculations also demonstrate that the Ca dopant limits the mobility of its nearest oxygens, but it promotes the second- and third-nearest oxygens to move. Therefore, two opposite effects induced by such doping are expected, and there is an optimum composition, at which the negative effect is minimized. In this work, the sample x = 0.025 shows the lowest oxygen migration energy and the highest oxygen permeability (1.39 mL cm⁻² min⁻¹ at 950 °C), while, the x = 0.05 sample, with a totally stabilized cubic perovskite structure still shows a much lower oxygen migration energy and higher oxygen permeability (1.30 mL cm⁻² min⁻¹ at 950 °C) compared to the pristine BaFeO_3−δ in its cubic state at high temperatures. Meanwhile, the 5 at% Ca-doped BaFeO_3−δ exhibits much more stable oxygen permeability at 800/900 °C for 200 h with no degradation, suggesting BaFe_0.95Ca_0.05O_3−δ perovskite oxide is a promising oxygen separation membrane material. The Ca-doped membranes exhibit good reduction resistance at high temperatures, and Ca-doping improves the resistance towards CO₂ erosion. These finding offers a much deeper understanding of the individual oxygen ion migration behaviour in the doped lattice and provide valuable guidelines for the chemistry design of high performance MIECs.

Acknowledgements

This work was financially supported by National Basic Research Program of China (2013CB934003, 2012CB215405), Guangdong Industry-Academy-Research Alliance (2012B091100129), National Nature Science Foundation of China (51302275) and Program of Introducing Talents of Discipline to Universities (B14003).

References

1. S. Gupta, M. K. Mahapatra and P. Singh, Mater. Sci. Eng., R, 2015, 90, 1.
2. P. M. Geffroy, J. Fouletier, N. Richet and T. Chartier, Chem. Eng. Sci., 2013, 87, 408.
3. A. Thursfield, A. Murugan, R. Franca and I. S. Metcalfe, Energy Environ. Sci., 2012, 5, 7421.
4. J. Sunarso, S. Baumann, J. M. Serra, W. A. Meulenberg, S. Liu, Y. S. Lin and J. C. Diniz da Costa, J. Membr. Sci., 2008, 320, 13.
5. K. Zhang, J. Sunarso, Z. Shao, W. Zhou, C. Sun, S. Wang and S. Liu, RSC Adv., 2011, 1, 1661.
6. M. Puig-Arnavat, M. Søgaard, K. Hjuler, J. Ahrenfeldt, U. B. Henriksen and P. V. Hendriksen, Energy, 2015, 91, 852.
7. J. Zhu, G. Liu, Z. Liu, Z. Chu, W. Jin and N. Xu, Adv. Mater., 2016, 28, 3511.
8. Fraunhofer Institute for Ceramic Technologies and Systems IKTS, http://www.ikts.fraunhofer.de/en/departments/environmental_process_engineering/high_temperature_separation/high-temperature_membranes_storage_materials/long-term_operation_oxygen_generator.html, accessed August 2016.
9. Y. Teraoka, H. Zhang, S. Furukawa and N. Yamazoe, Chem. Lett., 1985, 14, 1743.
10. Z. Shao, G. Xiong, H. Dong, W. Yang and L. Lin, Sep. Purif. Technol., 2002, 25, 97.
11. Y. Cheng, H. Zhao, D. Teng, F. Li, X. Lu and W. Ding, J. Membr. Sci., 2008, 322, 484.
12. F. Liang, H. Jiang, H. Luo, J. Caro and A. Feldhoff, Chem. Mater., 2011, 23, 4765.
13. J. Yi, M. Schroeder, T. Weirich and J. Mayer, Chem. Mater., 2010, 22, 6246.
14. K. Efimov, Q. Xu and A. Feldhoff, Chem. Mater., 2010, 22, 5866.
15. W. Li, X. Zhu, S. Chen and W. Yang, Angew. Chem., 2016, 128, 8708.
16. H. Wang, C. Tablet, A. Feldhoff and J. Caro, Adv. Mater., 2005, 17, 1785.
17. S. Gupta, J. J. Adams, J. R. Wilson, E. G. Eddings, M. K. Mahapatra and P. Singh, Appl. Energy, 2016, 165, 72.
18. T. Kida, D. Takauchi, K. Watanabe, M. Yuasa, K. Shimanoe, Y. Teraoka and N. Yamazoe, J. Electrochem. Soc., 2009, 156, E187.
19. J. Wang, K. Y. Lam, M. Saccoccio, Y. Gao, D. Chen and F. Ciucci, J. Power Sources, 2016, 324, 224.
20. J. Wang, M. Saccoccio, D. Chen, Y. Gao, C. Chen and F. Ciucci, J. Power Sources, 2015, 297, 511.
21. X. Zhu, H. Wang and W. Yang, Chem. Commun., 2004, 9, 1130.
22. F. Liang, K. Partovi, H. Jiang, H. Luo and J. Caro, J. Mater. Chem. A, 2013, 1, 746.
23. X. Liu, H. Zhao, J. Yang, Y. Li, T. Chen, X. Lu, W. Ding and F. Li, J. Membr. Sci., 2011, 383, 235.
24. T. Kida, A. Yamasaki, K. Watanabe, N. Yamazoe and K. Shimanoe, J. Solid State Chem., 2010, 183, 2426.
25. K. Watanabe, D. Takauchi, M. Yuasa, T. Kida, K. Shimanoe, Y. Teraoka and N. Yamazoe, J. Electrochem. Soc., 2009, 156, E81.
26. Q. Liao, Y. Wang, Y. Chen and H. Wang, Chin. J. Chem. Eng., 2016, 24, 339.
27. Y. Lu, H. Zhao, X. Cheng, Y. Jia, X. Du, M. Fang, Z. Du, K. Zheng and K. Swierczek, J. Mater. Chem. A, 2015, 3, 6202.
28. Y. Lu, H. Zhao, X. Chang, X. Du, K. Li, Y. Ma, S. Yi, Z. Du, K. Zheng and K. Świerczek, J. Mater. Chem. A, 2016, 27, 10454.
29. D. Xu, F. Dong, Y. Chen, B. Zhao, S. Liu, M. O. Tade and Z. Shao, J. Membr. Sci., 2014, 455, 75.
30. R. L. Cook and A. F. Sammells, Solid State Ionics, 1991, 45, 311.
31. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR 86-748, 2004.
32. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
33. A. Altomare, C. Cuocci, C. Giacovazzo, A. Moliterni, R. Rizzi, N. Corriero and A. Falcicchio, J. Appl. Crystallogr., 2013, 46, 1231.
34. X. Zhu, H. Wang and W. Yang, Solid State Ionics, 2006, 177, 2917.
35. F. Ciucci, Solid State Ionics, 2013, 239, 28.
36. D. Chen and Z. Shao, Int. J. Hydrogen Energy, 2011, 36, 6948.
37. B. Hu, Y. Wang, Z. Zhu, C. Xia and H. J. M. Bouwmeester, J. Mater. Chem. A, 2015, 3, 10296.
38. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567.
39. M. D. Segall, J. D. L. Philip, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
40. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
42. B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233.
43. X. Zhang, C. Fan, Y. Wang, Y. Wang, Z. Liang and P. Han, Comput. Mater. Sci., 2013, 71, 135.
44. T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225.
45. S. Mori, J. Am. Ceram. Soc., 1965, 48, 165.
46. S. Mori, J. Am. Ceram. Soc., 1966, 49, 600.
47. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751.
48. W. H. Kan, M. Chen, J. Bae, B. Kim and V. Thangadurai, J. Mater. Chem. A, 2014, 2, 8736.
49. L. Zhang, O. P. Thakur and A. Feteira, Appl. Phys. Lett., 2007, 90, 142914.
50. Z. M. Baiyee, C. Chen and F. Ciucci, Phys. Chem. Chem. Phys., 2015, 17, 23511.
51. F. Blanc, D. S. Middlemiss, Z. Gan and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 17662.
52. K. Partovi, B. Geppert, F. Liang, C. H. Rüscher and J. Caro, Chem. Mater., 2015, 27, 2911.
53. F. Dong, D. Chen, Y. Chen, Q. Zhao and Z. Shao, J. Mater. Chem., 2012, 22, 15071.
54. E. V. Tsipis, M. V. Patrakeev, V. V. Kharton, A. A. Yaremchenko, G. C. Mather, A. L. Shaula, I. A. Leonidov, V. L. Kozhevnikov and J. R. Frade, Solid State Sci., 2005, 7, 355.
55. F. Dong, Y. Chen, D. Chen and Z. Shao, ACS Appl. Mater. Interfaces, 2014, 6, 11180.
56. E. Bucher, A. Egger, P. Ried, W. Sitte and P. Holteppels, Solid State Ionics, 2008, 179, 1032.
57. J. Maier, Solid State Ionics, 1998, 112, 197.
58. J. Maier, Solid State Ionics, 2000, 135, 575.
59. K. Watenabe, M. Yuasa, T. Kida, Y. Teraoka, N. Yamazoe and K. Shimanoe, Adv. Mater., 2010, 22, 2367.
60. E. Girdauskaite, H. Ullmann, V. V. Vashook, U. Guth, G. B. Caraman, E. Bucher and W. Sitte, Solid State Ionics, 2008, 179, 385.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta00907k

---