CNC–Al2O3–Ti: a new unit for micro scale strain sensing†
Chengwei Li,
Lujun Pan*,
Chenghao Deng and
Peng Wang
School of Physics and Optoelectronic Technology, Dalian University of Technology, No. 2 Linggong Road, Ganjingzi District, Dalian 116024, PR China. E-mail: lpan@dlut.edu.cn
First published on 26th October 2016
Abstract
A highly elastic strain sensing unit, consisting of a single modified carbon nanocoil (CNC) as the substrate, a layer of titanium film as the sensing layer and an Al2O3 film as the insulation layer between them, has been fabricated and studied. This unit has the ability of transforming a large macro longitudinal stretching to a small local torsional strain. According to the changes of resistance with the strain, it is found that the resistance variation of the unique three-dimensional helical composite structure is as high as 30% in the deformation of micrometer scale, and the ratio of resistance change to overall strain of the composite and the average strain of Ti particles reach 5 and 100, respectively. It provides a theoretical and experimental foundation for the applications of the strain sensing to the micro-electromechanical systems or microsensing systems.
1. Introduction
Resistive strain sensors can be applied to measure the strains produced by the deformations of objects. The advantage of this kind of sensors is that the strain variation of the mechanical components can be transformed into resistance variation. Nanomaterials have the characteristics of small size and high integration, therefore they are widely used in e-skins, wearable instruments and other micro sensing devices.1,2 Much research about strain sensors has been reported currently, and lots of nanomaterials can be used in strain sensors. Gong et al. made a kind of pressure sensor, with a micro electrode on polydimethylsiloxane (PDMS) substrate, covered by gold nanowire networks. The sensor shows an excellent stability, with the gauge factor of less than 10.2 Zhao et al. reported a strain sensor, in which the nano graphene film was fixed in the micro metal electrode on mica substrate. It owns high gauge factor, which can achieve 300, but its strain range is less than 0.5%.3 By controlling the nucleation density of graphene nanoparticles, Zhao et al. increased the gauge factor of the strain sensor to 500, but its strain range is still less than 2%.4 Yamada et al. moved the aligned single-wall carbon nanotube (CNT) array, which were partly disposed by isopropyl alcohol, to a dog-bone shaped PDMS, the CNT alignment direction and the tensile direction were vertical. Through this method, SWCNT array formed a regular structure, which has the tight and loose parts. This strain sensor has a large strain range, which can reach to 280%, and a high stability under large strain. However, the gauge factor is low. Especially when the strain are less than 40% and more than 60%, the gauge factor are only 0.82 and 0.06, respectively.5 Kim et al. fixed two layers of aligned long silver nanowires in a pre-tensiled PDMS, and the direction of the two layers are vertical. This kind of strain sensor has excellent properties that shows sensing in different directions. Its strain range is about 30%, and the gauge factor is about 20.6 Gold nanoparticles were aligned into gold wires by Farcau et al. using self-assembly transitive system, and then the gold wires were fixed in the micro electrodes on polyethylene glycol terephthalate (PET). Its strain range is about 3%, and the gauge factor is about 40.7 Micro electrodes were printed on the polyimide substrate by Li et al. through the method of aerosol jet printed technology, and then an aligned carbon nanotube network was covered on the micro electrodes. The strain of the sensor is less than 1%, and gauge factor is about −40.8An as-grown carbon nanocoil (CNC) is generally a mixture of amorphous and polycrystalline structures, whose graphitized degree is between graphite and amorphous carbon, which is shown in the TEM image,9–12 electron diffraction patterns,10,12 Raman spectra,10,13 and XRD spectra.14 Owning to the unique three-dimensional helical structure, CNCs have superior mechanical properties and good electrical conductivity, with the elastic coefficient of 0.12 N m−1, and the resistivity of 1 × 10−4 Ωm at room temperature.9–11,15–18 At the same time, CNCs also have excellent thermal and optical properties.10,11,19 The strain sensing unit based on a single CNC has unique advantages. It can get a larger strain because of the spring-like structure of the CNC. On the other hand, the scale of the strain sensing unit can be controlled in micro-order, and it does not need a complicated technique to fabricate the unit. In addition, titanium, as a common metal material, has a resistivity of 5.5 × 10−7 Ωm, and tensile strength of 180 kg mm−2. It has the advantages of good corrosion resistance and low price as well. Higher performance and lower cost of the sensing unit with prospective applications in the micro/nano electromechanical systems are expected.
2. Experimental
2.1. Preparation of CNC-based sensing unit
The CNCs used in this experiment were synthesized as follows. Fe2(SO4)3/SnCl2 solution was used as the catalyst precursor to be dropped on the quartz substrates, and dried at 60 °C for 10 min. Then the samples were calcined at 710 °C for 30 min in order to oxidize the catalysts. Carbon nanocoils were synthesized on these substrates by a thermal chemical vapor deposition system at 710 °C for 30 min by introducing acetylene gas of 15 sccm in an Ar gas with a flow rate of 325 sccm.13,20,21 The preparation process for fabricating a single CNC sensing unit is shown in Fig. 1. A tungsten tip was used to contact the tip of a CNC protrudent from the bush of the as-grown CNCs as shown in Fig. 1a. Then the contact between the single CNC and the tungsten tip was enhanced by silver paste, and the single CNC was extracted, which is showed by Fig. 1b. To solidify the silver paste and enhance the contact between the CNC and tungsten tip, the single CNC was dried for 2 hours at 60 °C. And then a Al2O3 film was firstly sputtered onto the surface of the single CNC by a vacuum magnetron sputtering system (JCP-200, BTSC563). The sputtering process was conducted under the working pressure of 1 Pa and the power of 100 W in an Ar atmosphere at the room temperature for 20 min. Then, a Ti film was sputtered onto the Al2O3 film under the sputtering conditions as in Ar atmosphere, at room temperature, under the working pressure of 1 Pa, and the power of 50 W.As shown in Fig. 1c, the free end of the single composite CNC was fixed on one side of the Au electrode, and the contact between the free end and the Au electrode was enhanced by silver paste. After the silver paste was dried, the single composite CNC was peeled off the tungsten tip by another clean and sharp tungsten tip. Then the free side of the composite CNC was fixed on the other Au electrode through silver paste, ensuring that the single composite CNC between the Au electrodes was tight, as shown in Fig. 1d. The inset shows the scanning electron microscopy (SEM; JEOL JCM-5000) image of the single composite CNC hung between the two gold electrodes.
2.2. Preparation of CNC–Ti composite and its resistance measurements
Ti films were sputtered for 8 min, 16 min, 24 min, 32 min and 64 min on glass substrates. Then, the thickness of the films were measured by atomic force microscope (AFM; Agilent PicoPlus II, Agilent, Santa Clara, CA).A single CNC was fixed on the electrode with the method mentioned above without the deposition of Al2O3 and Ti films, and its initial resistance was measured by a high-precision source meter (Agilent B2902A). Then, a series of Ti films were deposited by successive sputtering on the surface of the single CNC in a time series from 0 to 25 minutes. The resistance was measured every time before the next time sputtering.
2.3. Evaluation of the strain sensing properties of the single composite CNC
The single composite CNC was pushed by a tungsten tip to induce a small amount of deformation, which can be regarded as the tensile effect of the CNC. At the same time, the real-time detection of resistance change was performed by the high-precision source meter. Fig. 2 shows the position changes of the single composite CNC during a stretching and releasing process under an optical microscope. | ||
| Fig. 2 The position changes of the single composite CNC during stretching and releasing process under an optical microscope. | ||
2.4. Finite element analysis for the strain of CNC
The stretching process was modeled by Comsol Multiphysics, and a small piece of CNC was chosen for the finite element analysis. The modeling conditions were set as followings: the fiber diameter, coil diameter and pitch of the CNC were 200, 400 and 800 nm, respectively. The number of turns was 2. One side of the CNC was fixed, and the other side of the CNC was stretched along the axial direction for 6.6%. The strain on the CNC was analyzed. Two representative Ti particles were attached onto the CNC. The distance change between the two particles was simulated.3. Results and discussion
3.1. The influence of Ti film thickness on the resistance of CNC–Ti composite
Fig. 3a shows a linear relationship between the thickness of the film and sputtering time. In Fig. 3b, the resistance changes of CNC–Ti composites under different sputtering time is plotted. With the increase of the sputtering time, the thickness of Ti film on the surface of CNC is increased gradually, which improve the conductivity of the CNC–Ti composite. It is found that the distinct drop of the resistance from 912 to 575 kΩ occurs between the sputtering time of 12 to 14 min, corresponding to the Ti film thickness of approximately 20 nm. This distinct drop of resistance originates from the transition of Ti film structure from discontinuous particles to quasi-continuous film.22,23 More details will be discussed later.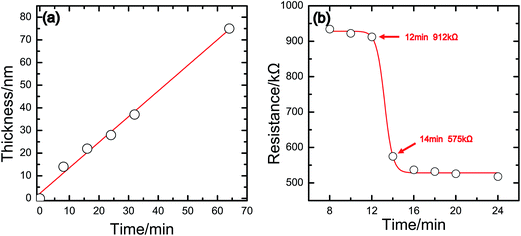 | ||
| Fig. 3 (a) Relationship between the thickness of Ti film and sputtering time. (b) Relationship between the resistance of the CNC composite and sputtering time. | ||
3.2. The distribution of Ti particles on the surface of CNC
The growth of metal on non-metal materials is generally Volmer–Weber growth. With the increase of film thickness, the size of the discrete metal particle stops growing at a critical state, accompanying with the space between the metal particles being gradually filled. The dramatic change in resistance between the sputtering time of 12 to 14 min corresponds to the conversion from discontinuous particles to the quasi-continuous film. When the sputtering time is 12 min (sample 1), the Ti particles on the CNC surface form a single layer, and the spacing between adjacent particles is large, as shown in Fig. 4a and c. When the sputtering time is 14 min (sample 2), the Ti particles on CNC surface partially form double layers. The spacing between adjacent particles is smaller than 12 min, and some adjacent particles are connected to each other, as shown in Fig. 4b and d. It can be concluded that 20 nm is the critical thickness to turn discontinuous particles into quasi-continuous film on the surface of CNC. Therefore, the composite with Ti film thickness of 20 nm was chosen for the further strain tests. The Raman spectra of Ti film demonstrates its good stability in air, as shown in Fig. S1.† | ||
| Fig. 4 The distribution of Ti particles on the surface of the CNC. FE-SEM images of (a) sample 1 and (b) sample 2. TEM images of (c) sample 1 and (d) sample 2. | ||
3.3. The resistance change of the CNC–Al2O3–Ti composite structure in the process of stretching
Fig. 5a shows the resistance change of the CNC–Al2O3–Ti composite in the process of cyclic stretch. It is found that the resistance of the composite is increased during stretching process. When the overall strain is increased from 0 to 6.6%, the resistance increases from 600 to 800 kΩ, the ratio of resistance to strain is 5. We have performed 4 cycles of stretching, and the resistance change in each cycle is stable.The strain under different level of stretching was modeled by Comsol Multiphysics. Fig. 5c shows the strain distribution when the overall strain was 6.6%. It is observed from the graph that the internal center of the CNC has the largest strain and the external center has the smallest strain. According to the result of simulation, from internal to external part, the strain gradually decreases from 1.5% to 0.3%. For the Ti particles on the surface of the composite, the spacing between adjacent particles and the surface strain is closely correlated. As shown in Fig. 5c, we choose the location of the internal center as a reference point, and the distance change between adjacent Ti particles at the location has been calculated by finite element method. When the overall strain is 6.6%, the distance change between adjacent particles at this location is 1%. Through the simulation analysis under different strain, it is found that the strain has a linear relation with the change of particle spacing. When the composite in the initial position, the distance between adjacent particles was fixed, which is 3.7 nm according to the statistical average in Fig. 4d. When the composite is stretched, the distance between adjacent Ti particles is increased, as shown in Fig. 5b. When the overall strain is 3.7%, the distance increased by 0.58% and when the overall strain is 6.6%, the distance increased by 1.03%.
According to the results of finite element simulation, the relationship between resistance and distance change rate of adjacent Ti particles' distance is obtained, as shown in Fig. 5d. The resistive effect in the composite structure can be described as the distance change between adjacent Ti particles. The resistance of a film generally increases exponentially when the average distance between adjacent particles is extended by an external applied strain. The relationship between the resistance R and the average particle distance s can be given by3,4
In this equation, N is the number of conducting paths and L is the number of particles within a conducting path; e, m, and h are the electron charge, mass, and the Plank constant, respectively; A2 is the effective area; and φ is the barrier height between adjacent particles. The resistance in an original state is 600 kΩ, and the average distance s between adjacent Ti particles in an original state can be counted from Fig. 4d which is about 3.7 nm, and the average particle size d is about 7.4 nm, so  , where LCNC is the total length of CNC;
, where LCNC is the total length of CNC;  nm2;
nm2; 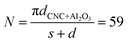 . The only unknown parameter r can be calculated to be 23.87. So the relationship between the resistance R and average particle distance s (nm) can be expressed as,
. The only unknown parameter r can be calculated to be 23.87. So the relationship between the resistance R and average particle distance s (nm) can be expressed as,
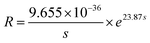 | (1) |
Assuming that all of the distance between adjacent Ti particles is constant in the process of stretching, the resistance in this case is resistance lower limit, which is 600 kΩ, and the minimum resistance is derived from the distance between adjacent Ti particles on the surface of the composite. Fig. 5c shows that the internal part of the composite has the largest strain, but the strain in the whole composite is not fixed. From internal to external part, the strain gradually decreases from 1.5% to 0.3%, so the overall strain is smaller than the internal strain. Assuming that all of the distance between adjacent Ti particles has the same change as the internal part in the process of stretching, the resistance in this case is resistance upper limit, which is the resistance curve under the condition of maximum strain. According to the eqn (1) and the resistance change measured from the experiment, we calculate the change of average distance under two different stretching levels of 3.7% and 6.6% are 0.27% and 0.34%. They are in the range of the simulation result of 0–1%, as shown in Fig. 5c and d.
It is found from the calculation that when the overall strain of the composite reached 6.6%, the average surface strain between adjacent particles is only 0.34%. The unique helical structure can transform the large overall strain to small surface strain. At the same time, under the strain of 0.34%, the change rate of resistance reaches 33%, and the gauge factor reaches 100. The performance comparison of CNC–Al2O3–Ti composite with other strain sensing units is shown in Table 1. The great flexibility originated from the helical morphology and the high sensitivity make the strain sensing unit a promising candidate in micro/nano strain sensor or NMES.
4. Conclusions
We have built up a kind of strain sensing unit using three-dimensional spring-like CNC as a template. The CNC substrate was successively sputtered by Al2O3 layer and Ti layer to form CNC–Al2O3–Ti composite structure. It is found that the Ti film with a thickness of 20 nm is the critical state from discontinuous particles to quasi-continuous film, and therefore the most sensitive state to external strain. When the overall strain is increased from 0 to 6.6%, the resistance can be changed from 600 to 800 kΩ, and the change rate reaches 33%, the ratio of resistance to strain is 5. When the overall strain is 6.6%, the average distance between adjacent Ti particles reaches 0.34%, and the ratio of resistance change to the particles' average strain of particles reaches 100. The microscaled strain sensing unit owns unique structural characteristics and can be fabricated by simple techniques with low cost, and the high sensitivity make the strain sensing unit a promising candidate in micro/nano strain sensor or NMES.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11274055, 61137005).References
- G. Walker, J. Soc. Inf. Disp., 2012, 20, 413–440 CrossRef
.
- S. Gong, W. Schwalb, Y. W. Wang, Y. Chen, Y. Tang, J. Si, B. Shirinzadeh and W. L. Cheng, Nat. Commun., 2014, 5, 163–180 Search PubMed
.
- J. Zhao, C. L. He, R. Yang, Z. W. Shi, M. Cheng, W. Yang, G. B. Xie, D. M. Wang, D. X. Shi and G. Y. Zhang, Appl. Phys. Lett., 2012, 101, 3307–3314 Search PubMed
.
- J. Zhao, G. L. Wang, R. Yang, X. B. Lu, M. Cheng, C. L. He, G. B. Xie, J. L. Meng, D. X. Shi and G. Y. Zhang, ACS Nano, 2015, 9, 1622–1629 CrossRef CAS PubMed
.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi, D. N. Futaba and K. Hata, Nat. Nanotechnol., 2011, 6, 296–301 CrossRef CAS PubMed
.
- K. K. Kim, S. Hong, H. M. Cho, J. Lee, Y. D. Suh, J. Ham and S. H. Ko, Nano Lett., 2015, 15, 5240–5247 CrossRef CAS PubMed
.
- C. Farcau, N. M. Sangeetha, H. Moreira, B. Viallet, J. Grisolia, D. Ciuculescu-Pradines and L. Ressier, ACS Nano, 2011, 5, 7137–7143 CrossRef CAS PubMed
.
- S. Li, J. G. Park, S. Wang, R. Liang, C. Zhang and B. Wang, Carbon, 2014, 73, 303–309 CrossRef CAS
.
- H. Ma, K. Nakata, L. J. Pan, K. Hirahara and Y. Nakayama, Carbon, 2014, 73, 71–77 CrossRef CAS
.
- Y. M. Sun, C. W. Wang, L. J. Pan, X. Fu, P. H. Yin and H. L. Zou, Carbon, 2016, 98, 285–290 CrossRef CAS
.
- H. Ma, L. J. Pan, Q. Zhao, Z. B. Zhao and J. S. Qiu, Carbon, 2012, 50, 778–783 CrossRef CAS
.
- Q. Zhao, L. J. Pan, H. Ma and T. Wang, Diamond Relat. Mater., 2012, 22, 33–36 CrossRef CAS
.
- R. X. Cui, L. J. Pan and C. H. Deng, Carbon, 2015, 89, 47–52 CrossRef CAS
.
- K. Nishimura, N. Okazaki, L. J. Pan and Y. Nakayama, Jpn. J. Appl. Phys., Part 2, 2004, 43, L471–L474 CrossRef CAS
.
- M. Zhang, Y. Nakayama and L. J. Pan, Jpn. J. Appl. Phys., Part 2, 2000, 39, L1242–L1244 CAS
.
- X. Q. Chen, S. L. Zhang, D. A. Dikin, W. Q. Ding, R. S. Ruoff, L. J. Pan and Y. Nakayama, Nano Lett., 2003, 3, 1299–1304 CrossRef CAS
.
- T. Hayashida, L. Pan and Y. Nakayama, Phys. B, 2002, 323, 352–353 CrossRef CAS
.
- T. Yonemura, Y. Suda, H. Shima, Y. Nakamura, H. Tanoue, H. Takikawa, H. Ue, K. Shimizu and Y. Umeda, Carbon, 2015, 83, 183–187 CrossRef CAS
.
- H. Ma, L. J. Pan, Q. Zhao and W. Peng, Nanoscale, 2013, 5, 1153–1158 RSC
.
- R. X. Cui, L. J. Pan, D. W. Li, H. Ma and W. Peng, Carbon, 2014, 76, 455–458 CrossRef CAS
.
- X. Fu, L. J. Pan, Q. Wang, C. Y. Liu, Y. M. Sun, M. Asif, J. Qin and Y. Y. Huang, Carbon, 2016, 99, 43–48 CrossRef CAS
.
- R. M. Hill, Proc. R. Soc. London, Ser. A, 1969, 309, 377–395 CrossRef CAS
.
- R. L. Parker and A. Krinsky, J. Appl. Phys., 1963, 34, 2700–2708 CrossRef CAS
.
- M. Y. Huang, T. A. Pascal, H. Kim, W. A. Goddard and J. R. Greer, Nano Lett., 2011, 11, 1241–1246 CrossRef CAS PubMed
.
- Y. Y. Shang, X. D. He, Y. B. Li, L. H. Zhang, Z. Li, C. Y. Ji, E. Z. Shi, P. X. Li, K. Zhu, Q. Y. Peng, C. Wang, X. J. Zhang, R. G. Wang, J. Q. Wei, K. L. Wang, H. W. Zhu, D. H. Wu and A. Y. Cao, Adv. Mater., 2012, 24, 2896–2900 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra22361c |
| This journal is © The Royal Society of Chemistry 2016 |




