Simulation study and experiment verification of the creep mechanism of a nickel-based single crystal superalloy obtained from microstructural evolution

Abstract

Molecular dynamics (MD) simulations and experiments were used to understand the creep properties and microstructural evolution of a nickel-based single crystal superalloy. By observing the microstructural evolution using MD simulations, we have found a P-type rafting in the [001] crystal orientation owing to dislocations cutting into the γ′ phase. The deflected γ phases lead to an L-type rafting, indicating it is an inferior creep property in the [011] crystal orientation. Unlike the [001] and [011] crystal orientations, dislocations climb over to the γ′ phase without rafting in the [111] crystal orientation, which manifests a superior creep property. In addition, by comparing the effect between temperature and stress on the creep properties, the results suggest that the creep of the [111] crystal orientation was strongly influenced by stress, whereas the creep properties of the [001] and [011] crystal orientations were significantly affected by temperature. Furthermore, the experimental results are consistent with the MD simulations. This study provides fundamental guidance for the rational design and testing of nickel base single crystal superalloy for structural applications.

---

1. Introduction

Nickel-based single crystal superalloys are remarkable for their excellent reliability and mechanical properties at temperatures up to 1000 °C and beyond.¹ They are widely used for blades and vanes in gas turbines. Much of the recent research has focused on the effect of adding elements, external loads, orientations and temperature on the high-temperature creep behavior. The effect of adding Ru to the superalloys was investigated in terms of their interfacial dislocation networks, high-temperature creep resistance, γ/γ′ phase compositions, and lattice misfit.^2–4 In addition, a single crystal nickel-based superalloy containing 4.2% Re was studied in terms of its deformation mechanism and microstructural evolution.⁵ Moreover, Co–Al–W alloys were tested with the additions of Ni, Ta, Cr and Mo, and indicated that the alloys that exhibited superior creep properties have a high volume fraction of γ′.⁶ Considering the influence of an applied stress on the γ′ directional coarsening, a preferential orientation of the γ′ rafting in the dendrite core was dependent on the sign of the sum of the applied stress and a critical equivalent stress, rather than the applied stress.⁷ The deformation mechanism of SRR99 single crystals were studied using the 〈001〉, 〈011〉 and 〈111〉 orientations.⁸ The creep resistance of the 〈001〉 orientation specimen was higher than that found for the 〈011〉 orientation. In addition, lamellar γ′ rafting was easy to incline at 45° to the stress axis in the 〈011〉 orientated specimens.⁹ Thermal cycles strongly affect the creep behavior at 1150 °C when compared to 950 °C. Repetitive precipitation and dissolution of small γ′ rafting were the reasons for this behaviour at higher temperature.¹⁰ The stacking faults (SFs) presented in the γ matrix are the main cause of failure in the tensile behavior and deformation mechanism of a nickel-based single crystal superalloy at different temperatures. Interfacial dislocation networks cause a high-flow stress at higher temperature, which leads to a weak resistance to the slip dislocations.¹¹

With a growing interest in using nickel-based single crystal superalloys for blades and vanes in gas turbines, it is necessary to facilitate the existing understanding of their creep pathways and mechanical stabilities, in particular, the creep mechanics considering dislocations glide or climb. Although many experimental studies have provided an abundant amount of information that has been essential for the better understanding of creep behavior, the experimental methods used have limitations in determining the dynamic behavior of creep, measuring their microstructural evolution. However, little attention has been given to the creep mechanism using the dynamic display technique. Most experimental studies have analyzed and inferred the microstructure after creep. Thus, the previous results are inconclusive. Furthermore, few experimental or theoretical investigations have been reported on the creep properties and microstructural evolution on an atomic level. Therefore, we have used atomic simulations to study the creep behavior of nickel-based single crystal superalloys.

In this study, we have explored the creep properties and microstructural evolutions of Ni/Ni₃Al systems under different orientations, temperatures and stresses using MD simulations. By analyzing the effect of slip dislocations ([001] and [011] crystal orientations) and climb ([111] crystal orientation) on the dynamic mechanism of creep. We found that the creep properties of the [001] and [011] crystal orientations are sensitive to temperature, and the creep property of the [111] crystal orientation is sensitive to stress. Moreover, the simulation results were verified by experiments and showed that the [001] crystal orientation has P-type rafting, whereas the [011] crystal orientation develops to an L-type rafting, and the rafting of the [111] crystal orientation was not prominent. The results perfectly proved the correctness and rationality of the results obtained from the MD simulations.

2. Computational and experimental methods

An extended interlayer model was used for MD simulations.¹² The model sizes were different because the various crystal orientations have different lattice constants in the nickel-based single crystal superalloys. The lattice constants of the γ phase and γ′ phase were defined as 3.52 Å and 3.2 Å, respectively. Three different phase interfaces, (001), (110) and (111), were studied using MD simulations to investigate the creep mechanism and microstructural evolution. For the X and Z directions, the lengths of the γ′ phase and γ phase are 20a_γ′ and 22a_γ, respectively, whereas the sizes of the γ phase and γ′ phase were 2a_γ and 2a_γ′ along the Y direction. We used the size of the [001] crystal orientation system as a reference dimension. To investigate the creep properties in the same size under two other crystal orientations, areas that were greater than the standard size were removed to obtain the models of the [011] and [111] crystal orientations.

The local lattice disorder around an atom was identified using the centrosymmetry parameter (CSP),^13,14 and it is defined as follows:

where the N nearest neighbors or each atom are identified and R⃑_i and R⃑_i+N/2 are vectors from the central atom to a particular pair of nearest neighbors.

A full relaxation was performed before tensile loading. The systems were relaxed for 100 ps with a constant time step of 3 fs under an NPT ensemble to lower the stress levels. A Nose–Hoover thermostat was applied to maintain the system temperature at a constant value.¹⁵ Atoms in the bottom and top three-layers were fixed as loading regions. The visualization tool atomeye was used in the MD simulations¹⁶ to draw the microstructures. Periodic boundary conditions were applied in the X, Y and Z directions. All simulations were performed using an MD code LAMMPS with an embedded-atom method (EAM) potential.^17,18 To estimate the creep properties and microstructural evolution, similar to the established experimental method, the creep behavior of the nickel-based single crystal superalloys was studied at 0.3 GPa, 0.4 GPa, 0.5 GPa and 1100 K, 1200 K and 1300 K, respectively. These parameters are based on the creep experiment as below.

For the creep experiment, crystal orientations were controlled strictly in the production of the creep samples. The maximum deviation of the rod axis from [001], [011] and [111] directions were laid within 7°. We adopted a standard tensile creep specimen (Φ 5 mm × 25 mm) to investigate the creep mechanism of the nickel-based single crystal superalloy from the microstructural evolution and dislocations. The single crystal superalloy DD6 was entirely heat treated (1290 °C, 1 h + 1300 °C, 2 h + 1315 °C, 4 h, AC), and then ageing heat treated for two stages: 1120 °C, 4 h, AC + 870 °C, 32 h, AC.^19,20 The creep experiments were carried out at 1000 °C, 300 MPa and 900 °C, 500 MPa using a GTW504 high temperature creep testing apparatus.²¹ Before and after the creep of the single crystal superalloy DD6, the morphology of the microstructures was observed using SEM (FEI Quanta 300)^22,23 and TEM (JEM-2100), respectively.

Essentially, the third stage of creep was not permitted in the application of the nickel-based single crystal superalloys. Moreover, it was difficult to achieve a creep rupture using the MD simulations. Considering the abovementioned reasons, the creep properties of the nickel-based single crystal superalloys were mainly studied in their first and second stages. According to the relationship between the theory of crystal slip and creep property, the shear strain of creep (γ_c^α) and slip system were set up as follows:²⁴

γ_c^α = ατⁿt^p (2)

where α, n and p are the creep parameters, τ is the resolved shear stress of the slip system, and t is the creep time. The creep parameters are the same for the same slip systems.

The relationship between the creep strain of the slip system (γ_c^α) and the macro creep strain (ε_ij) was set up as follows:²⁵

where n is the total of the slip system, m_i^α and n_i^α represent the direction of the slip system and the ith component of the unit normal vector of the slip plane, respectively. If several slip systems are opened at the same time, the macro creep strain is the sum of creep strain in all the slip systems.

3. Results and discussion

3.1 MD simulations

3.1.1 The effects of crystal orientation on the creep property and microstructural evolution. First, the system was relaxed at 1100 K and then a constant tensile load (0.4 GPa) was applied on the top plane. At the instant of stretching, the creep strains evolve considerably as shown in Fig. 1, which indicate that the instantaneous strain was tremendous. Three types of crystal orientations are manifested as elastic deformation about 15 ps in the first stage of creep. A great variability in the change of creep strain was observed in the second stage; in the [011], [001] and [111] crystal orientations, the creep strains were 0.12, 0.08 and 0.075, respectively. The crystal anisotropies of the creep properties are shown in their creep resistance. Upon comparing the magnitude of the steady creep strain, the [111] crystal orientation had the greatest creep resistance, followed by the [001] crystal orientation and finally, the [011] crystal orientation.

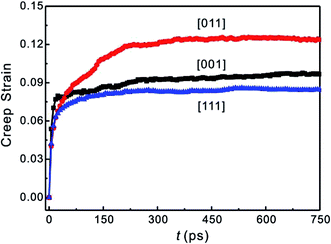Fig. 1 Uniaxial tensile creeps strain versus time for the [001], [011] and [111] crystal orientations.

Previously reported experimental creep studies have considered the relationship between the crystal orientation and γ′ phase rafting, in which the cubic γ′ phase would be transformed into a laminar or columnar structure during stable creep. The degree of γ′ phase rafting (R) can be measured by the ratio of length (L) and thickness (T) in the laminar structure, that is R = L/T. The larger the R value is, the higher is the degree of γ′ rafting. The transformation of two directions (length L and thickness T) were approximately the same value in the second stage of stable creep, indicating that the above formula can be converted to R = L/D. Therefore, it was easy to identify the rafting type from the creep structure. In the columnar structure, the rafting direction was parallel to the tensile direction. In order to keep consistent with the rafting behavior in the experiments, the laminar and the columnar rafting were defined as N-type and P-type rafting in the MD simulations, respectively.

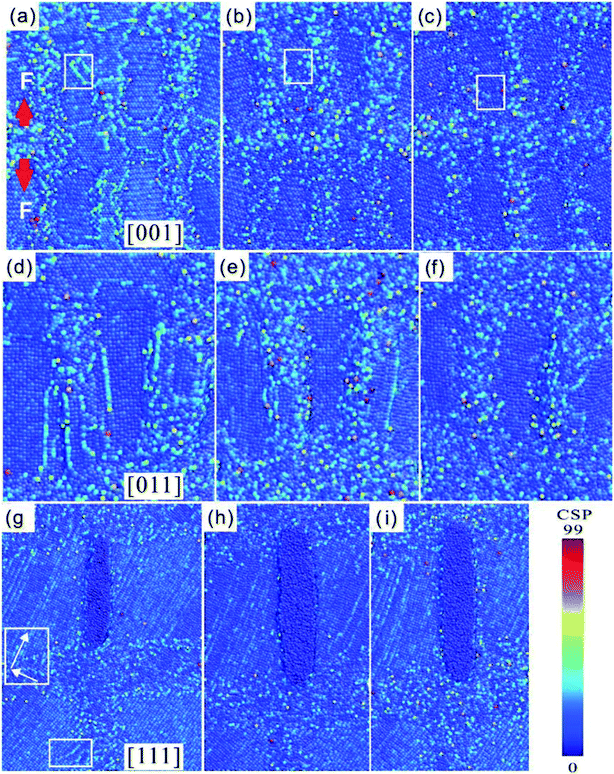
Dislocations first appear near the interface because of the lattice mismatch that exists between the γ phase and γ′ phase, as shown in Fig. 2(a). The γ phase continuously squeezes the γ′ phase under tensile loading. Then, the γ′ phase was elongated along the loading direction and finally transformed into a columnar structure, as shown in Fig. 2(b). There were two types of deformations at the intersection of the γ′ phase. The first was perpendicular to the tensile direction with a diverging trend near area A. Dislocations of γ′ phases were unevenly distributed because the dislocation densities of γ phases in the vertical direction are smaller than those found in the horizontal direction. The second was the aggregation of the γ phase near the B area. As the creep time increased to 312 ps, lots of dislocations in the γ phase moved to the γ/γ′ interface, which led to stress concentration. Moreover, the degree of mismatch changed constantly along the vertical direction in the γ phase and dislocations were stimulated along the vertical direction in the γ phase. When the stress concentration reached a certain degree, the dislocations in the vertical direction gradually cut into the γ′ phase near the C area, as shown in Fig. 2(c). The resistance of deformation of the γ′ phase decreased with an increase in the number of dislocations in the γ′ phase. The rafting direction of the γ′ phase was parallel to the tensile loading axis with a P-type rafting.

Fig. 2 Microstructural evolution at 1100 K and 0.4 GPa. The [001] crystal orientation: (a) 1 ps, (b) 132 ps and (c) 312 ps. The [011] crystal orientation: (d) 1 ps, (e) 90 ps and (f) 300 ps. The [111] crystal orientation: (g) 1 ps, (h) 132 ps and (i) 318 ps. Plots (a)–(i) are simulation snapshots that are colored based on the CSP.

In the [011] crystal orientation, the intersection of the γ phase sustained a compressive stress, which was perpendicular to the direction of the stress axes. The dislocation firstly emerged in the γ phase and then cut into the γ′ phase from the vertical γ phase, as shown in Fig. 2(e). This behavior greatly reduced the creep resistance of the γ′ phase. Furthermore, the incline of area A in the vertical γ phase will cause the γ′ phase to deflect gradually. Finally, an L-type rafting was formed, as shown in Fig. 2(f). This was consistent with the creep behavior of the [011] crystal orientation observed in the experiments. The dislocation slipped along the [01̄1] direction because the stress in the horizontal γ phase was lower than that found in the vertical γ phase. For the [011] crystal orientation, we noted that the γ phase gradually was deflected under the effect of stress, indicating that the effect of stress was the main reason for the lowest creep properties observed for the [011] crystal orientation.

Dislocations appear in the γ phase with almost no change in the shape of the γ phase and γ′ phase as shown in Fig. 2(g). The intersection area A was continuously accumulated in the γ phase, but dislocations of the γ phase do not cut into the γ′ phase. The shapes of the γ phase remain steady in the second stage. Area B of the vertical γ′ phase was squeezed by pressure from the γ phase, as shown in Fig. 2(h). As a result, a small percentage of dislocations climbed over the γ phase to arrive at the γ′ phase, as shown in Fig. 2(i). When compared with [001] and [011] crystal orientations, the rafting rate of the γ′ phase was found to be the slowest in the [111] crystal orientation. Essentially, the γ′ phases retained their cubic shape without rafting.

The dislocation of the γ phase a/2[11̄0] cut into the γ′ phase near the coherent interface between the vertical γ and γ′ phase, as shown in Fig. 3(a). Furthermore, the dislocation a/2[11̄0] decomposed into partial dislocation a/3[12̄1], partial dislocation a/6[112̄] and Shockley stacking fault (SSF) in the γ′ phase. This can be written as follows:

a/2[11̄0] → a/3[12̄1] + a/6[112̄] + SSF (4)

Fig. 3 Dislocation slipping in the [001] crystal orientation. (a) 1100 K/0.4 GPa, 456 ps and (b) 1000 K/720 MPa, 75 h.

The above stacking fault was found after 75 h of creep at 1000 K and 720 MPa, as shown in Fig. 3(b).²⁶ This not only proved the correctness of the MD simulations, but also revealed that the stress concentration of the vertical γ phase was much higher than that observed on the horizontal γ phase theoretically.

The rafting degree of the γ′ phase can be represented using the formula R = L/D in the [001] and [111] crystal orientations.²⁷ Fig. 4(a) shows the relationship between time and the rafting degree R in the [001] crystal orientation. There was no rafting in the γ′ phase before tensile loading, and the value of R was 1. There were no changes to the value of R before 15 ps without rafting in the γ′ phase. After 15 ps, the value of R increased rapidly. The microstructural evolution of the γ′ phase showed that the dislocations in the γ phase gradually propagated during creep. The γ′ phase was elongated along the tensile direction. Then, the γ phase squeezed the γ′ phase. Finally, the γ′ phases were rafted. Dislocation slips mainly appeared in the γ phase near 312 ps. The creep resistance of the γ′ phase was still strong, indicating that the rafting rate of the γ′ phase was quite slow. Dislocations of the vertical γ phase gradually cut into the γ′ phase after 312 ps, resulting in a decreasing creep resistance in the γ′ phase and entering a rapid rafting stage. The microstructural evolution of the γ′ phase showed that it had been completely rafted in 340 ps, and the value of R was approximately 3.6. Fig. 4(b) shows the relationship between creep time and the rafting degree of the γ′ phase in the [111] crystal orientation. When compared to the [001] and [011] crystal orientations, it displayed an extremely slow growth rafting rate for the γ′ phase. We observed that the γ′ phases retained their cubic shape without rafting.

Fig. 4 The relationship between creep time and the degree of γ′ phase rafting. (a) The [001] crystal orientation. (b) The [111] crystal orientation.

3.1.2 The effects of temperature on the creep property and microstructural evolution. With the creep temperature increasing from 1100 K to 1300 K, the creep strain of the [001] crystal orientation increased from 0.085 to 0.145 in the steady creep stage, having increased by 70.6%. The creep time of the [011] crystal orientation at 1100 K was longer than that observed at 1200 K, and the speed of creep rupture was faster at 1300 K than that observed at 1200 K. The creep strains of the [111] crystal orientation increased from 0.08 to 0.13 when the temperature changed from 1100 K to 1300 K. The creep strain was increased by 62.5% as shown in Fig. 5. This shows that the creep properties were sensitive to temperature. When comparing the second stage of creep strain, the creep strain of the [011] crystal orientation was found to be the highest, followed by the [001] crystal orientation and the creep strain of the [111] crystal orientation was the lowest.

Fig. 5 The creep strains of the three crystal orientations ([001], [011] and [111]) as a function of time at different creep temperatures (1100 K, 1200 K and 1300 K) at 0.4 GPa.

Dislocations cut into the γ′ phase from the vertical γ phase at 1100 K in the [001] crystal orientation, and the rafting process of the γ′ phase was accelerated at 1200 K, as shown in Fig. 6(a)–(c). Dislocations of γ phase were activated, and then slipped to the γ phase at 1300 K because of the small critical resolved shear stress, and the dislocations easily slipped to the γ′ phase. Moreover, the degree of rafting reached its maximum value. As the temperature increased, the critical resolved shear stress reduced, and the dislocations more easily slipped to the γ′ phase, which resulted in the rafting of the γ′ phase.

Fig. 6 The microstructural evolution at different temperatures. The [001] crystal orientation: (a) 1100 K, 312 ps, (b) 1200 K, 102 ps and (c) 1300 K, 75 ps. The [011] crystal orientation: (d) 1100 K, 174 ps, (e) 1200 K, 72 ps and (f) 1300 K, 48 ps. The [111] crystal orientation: (g) 1100 K, 180 ps, (h) 1200 K, 102 ps and (i) 1300 K, 60 ps. Plots (a)–(i) are colored based on the CSP.

The rafting direction of the γ′ phase had a certain degree with the stress axis for the L-type rafting in the [011] crystal orientation. The rafting process was also accelerated by increasing the temperature. Dislocations of the γ phase have a higher critical shear stress at 1100 K, as shown in Fig. 6(d)–(f). When the temperatures were 1200 K and 1300 K, the dislocations in the γ phase slipped from the coherent interface to the γ′ phase without separating due to a decrease in the γ′ phase creep resistance at high temperature, indicating that the dislocation slip was the rafting mechanism of the [011] crystal orientation. On the contrary, dislocations in the γ phase cutting into the γ′ phase and dislocations dissociating at low temperature were the rafting mechanism of the γ′ phase.

Dislocations climbed over from the γ phase to the γ′ phase at 1100 K, as shown in the white marking of Fig. 6(g). Lots of atoms near the vertical γ phase moved along the Y direction from 1200 K to 1300 K with an increase in the number of dislocations, as shown in Fig. 6(h)–(i). The shapes of the γ′ phase and γ phase did not change, and the atoms of the vertical γ phase moved along the Y direction. The stress concentration in the γ phase increased due to thermal activation, and dislocations slipped to the γ′ phase. The steady creep stage of the [111] crystal orientation was caused by dislocations climbing at low temperature. Moreover, dislocations slipped to the γ′ phase due to thermal activation at high temperature, indicating that the steady creep was caused by the dislocation slip at high temperatures.

3.1.3 The effects of stress on the creep property and microstructural evolution. Creep curves are shown under different stresses in Fig. 7. The figure shows that the increase in creep strain of the [011] crystal orientation was the highest, followed by the [001] crystal orientation and the creep strain of the [111] crystal orientation was the lowest. During the second creep stage, the stress increased from 0.3 GPa to 0.5 GPa, and the creep strain of the [001] crystal orientation increased by 66.7%. The strain of the [011] crystal orientation was greater than the [001] crystal orientation in the second creep stage, which illustrates that the creep resistance of the [011] crystal orientation was lower than the [001] crystal orientation. When the stress was 0.5 GPa, the [011] crystal orientation started to creep and ruptured after 200 ps. The effect of temperature on the [011] crystal orientation was more significant than on the stress. The creep strain increments were 0.053, 0.075 and 0.12 in the [111] crystal orientation during the second creep stage, as shown in Fig. 7. The creep strain of the [111] crystal orientation increased by 126.4%, which was much higher than that observed in the [001] crystal orientation. Thus, the creep of the [111] crystal orientation was less than that of the [001] crystal orientation when the stresses were 0.3 GPa and 0.4 GPa, respectively. However, the above results were in contrast with the result found at 0.5 GPa, indicating the role of stress was greater than the effect of temperature in the [111] crystal orientation.

Fig. 7 The creep strain of the three crystal orientations ([001], [011] and [111]) as a function of time under different stresses (0.3 GPa, 0.4 GPa and 0.5 GPa) at 1100 K.

By observing the microscopic creep evolution of the [001] crystal orientation in the steady creep stage shown in Fig. 8, we found that the dislocations of the γ phase cut into the γ′ phase and then developed into P-type rafting. The dislocations had different pathways to cut into the γ′ phase under different stress. The rafting mechanism was that the dislocations cut into the γ′ phase when the stresses were 0.3 GPa and 0.5 GPa. Moreover, the dislocations not only cut into the γ′ phase, but also decomposed into partial dislocations and stack faults at 0.4 GPa. When compared with the effect between temperature and stress on the creep of the [001] crystal orientation, stress played only a small role in the rafting progress.

Fig. 8 Microstructural evolution at different stresses. The [001] crystal orientation: (a) 0.3 GPa, 348 ps, (b) 0.4 GPa, 276 ps and (c) 0.5 GPa, 246 ps. The [011] crystal orientation: (d) 0.3 GPa, 114 ps, (e) 0.4 GPa, 90 ps and (f) 0.5 GPa, 72 ps. The [111] crystal orientation: (g) 0.3 GPa, 420 ps, (h) 0.4 GPa, 252 ps and (i) 0.5 GPa, 216 ps. Plots (a)–(i) are colored based on the CSP.

The progress of the creep microstructures of the [011] crystal orientation under different stresses are shown in Fig. 8(d)–(f). When the stress was 0.3 GPa, dislocations firstly emerged in the γ phase and then separated among the vertical γ phases, and finally, dislocations of γ phase cut into the γ′ phase resulting in a decrease in the γ′ phase creep resistance. The γ′ phase was pushed downwards and inclined to the same side of the inclined vertical γ phase with L-type rafting. Dislocations cut into the γ′ phase and break down into a stacking fault at 0.4 GPa. Dislocations were much easier to slip from the γ phase to the γ′ phase at 0.5 GPa. When compared with the effect of temperature on the creep properties of the [011] crystal orientation, stress also played a small role in the rafting progress.

The progress of the creep microstructure of the [111] crystal orientation under different stresses is shown in Fig. 8(g)–(i). Dislocations firstly emerged in the γ phase at 0.3 GPa. When the stress concentrations of the horizontal γ phases reached a certain degree, they provided an abundance of energy for dislocations climbing over to the γ′ phase. Dislocations climbed along the white arrow and then turned to the direction perpendicular to the horizontal γ phase, as shown in Fig. 8(g). The dislocations of the γ phase quickly climbed to the γ′ phase at 0.4 GPa with the same climbing direction, as shown in Fig. 8(h). Moreover, when the stress was 0.5 GPa, the number of dislocation-climbing was greater than that found at the lower stress (0.3 GPa and 0.4 GPa). Based on the above analysis, we knew that the rafting mechanism of the [111] crystal orientation was dislocation-climbing. When compared with the effect of stress on the creep behavior of the [111] crystal orientation, temperature had less of an affect on the rafting progress.

3.2 Creep experiments of the nickel-based single crystal superalloy DD6

The morphology of the creep microstructure was observed using SEM. The γ′ phase of the [001] crystal orientation was stretched along the tensile direction. Adjacent γ′ phases gradually merged to form a rafting structure. The rafting direction of the [001] crystal orientation was parallel to the stress axis. The γ′ phase almost completely rafted near the fracture area at 1000 °C, 300 MPa, as shown in Fig. 9(a). The rafting degree of the γ′ phase was much lower at 900 °C, 500 MPa than that found at 1000 °C, 300 MPa as shown in Fig. 9(d), indicating that the γ′ phase rafting level of the [001] crystal orientation was larger at a relatively high temperature. As the width of the longitudinal matrix channel increased, the transverse matrix channel gradually faded, and finally led to P-type rafting. This was consistent with the results obtained by the MD simulations.

Fig. 9 The creep morphology of the different crystal orientations observed by SEM. The creep morphology of the [001] crystal orientation: (a) 1000 °C, 300 MPa and (d) 900 °C, 500 MPa. The creep morphology of the [011] crystal orientation: (b) 1000 °C, 300 MPa and (e) 900 °C, 500 MPa. The creep morphology of the [111] crystal orientation: (c) 1000 °C, 300 MPa and (f) 900 °C, 500 MPa.

The rafting phenomenon of the nickel-based single crystal was evident at 1000 °C, 300 MPa, and the rafting direction²⁸ had a degree of ±45° with the stress axis in Fig. 9(b). Based on the analysis of the MD simulations, the stress direction had a degree of 45° with the transverse and longitudinal matrix channel. The stress decomposed into two types of shear stresses, which were parallel to the transverse and longitudinal matrix channel, respectively. The γ′ phase rafted and then connected at a degree of 45° with the stress axis under shear stress in Fig. 9(e). When compared with the results of rafting at 1000 °C, 300 MPa, the rafting degree was small at 900 °C, 500 MPa, and the microstructure of the γ′ phase changed from rectangle to diamond. The rafting also had a degree of 45° with the stress axis with L-type rafting. The experiment fully proved the correctness of the MD simulation results.

The rafting degree was lower at 1000 °C, 300 MPa than that observed at 900 °C, 500 MPa in the [111] crystal orientation, shown in Fig. 9(c) and (f), indicating that the influence of stress was more significant than temperature. The creep properties of the [111] crystal orientation were affected by the dislocation net near the interface. The matrix channel sustained a uniform shear stress, which resulted in a decrease in the stress concentration and stagnation of the γ′ phase rafting showing that the creep resistance was improved.

A small amount of γ phase dislocations cut into the γ′ phase and tangle with each other. The shape of the γ′ phase changed from cubic to an irregular bar with P-type rafting at 1000 °C, 300 MPa in Fig. 10(a). Dislocations not only propagated in the γ phase at 900 °C, 500 MPa shown in Fig. 10(d), but also an amount of dislocations cut into the γ′ phase. Because of the interactions among the dislocation nets, the external stress was completely released and the γ′ phase rafting was postponed,²⁹ which could extend the creep life. It was found that the [001] crystal orientation was greatly influenced by temperature. The creep feature was consistent with the results obtained using the MD simulations.

Fig. 10 The dislocation morphology of the different crystal orientations observed by TEM after creep. The dislocation morphology of the [001] crystal orientation: (a) 1000 °C, 300 MPa and (d) 900 °C, 500 MPa. The dislocation morphology of the [011] crystal orientation: (b) 1000 °C, 300 MPa and (e) 900 °C, 500 MPa. The dislocation morphology of the [111] crystal orientation: (c) 1000 °C, 300 MPa and (f) 900 °C, 500 MPa.

For the [011] crystal orientation, there were a small amount of dislocations in the γ′ phase and γ phase owing to the small stress at 1000 °C, 300 MPa as shown in Fig. 10(b). However, the rafting of the γ′ phase was severe. The dislocation density of the γ phase in the [011] crystal orientation was quite large and lots of dislocations accumulated near the γ/γ′ interface under 900 °C, 500 MPa, as shown in Fig. 10(e). Moreover, a large amount of dislocations cut into the γ′ phase. There were some dislocation lines with different directions in the γ phase, indicating that the cross-slip of dislocation appeared in the matrix. Although the dislocation nets impeded dislocation slipping and prompted stress relaxation, some dislocations cut into the γ′ phase. The density of dislocations in the γ phase was larger at high stress. Lots of γ phase dislocations cut into the γ′ phase at high temperature, which increased the rafting rate of the γ′ phase. The experimental results showed that the creep of the [011] crystal orientation was greatly influenced by temperature. This was consistent with the results obtained using the MD simulations.

The γ′ phases connect with each other at 900 °C and 500 MPa, as shown in Fig. 10(f). By comparing the degree of rafting near the fracture area between 900 °C, 500 MPa and 1000 °C, 300 MPa, we found that the rafting was more prominent at 900 °C and 500 MPa. This shows that the creep of the [111] crystal orientation was more sensitive to stress, which was also consistent with the results obtained using the MD simulations.

4. Conclusions

In this study, the creep mechanism and microstructural evolution of nickel-based single crystal superalloys were first investigated under different crystal orientations, temperatures and stresses using MD simulations. The creep resistance of the nickel-based single crystal superalloy took on an evident crystal anisotropy. On comparing the magnitude of steady creep strain among the three crystal orientations, the [111] crystal orientation was found to have the greatest creep resistance, followed by the [001] crystal orientation and then the [011] crystal orientation. Dislocations in the vertical direction gradually cut into the γ′ phase and led to a P-type rafting in the [001] crystal orientation. Moreover, the γ phase deflected and resulted in the poor creep property of the [011] crystal orientation with L-type rafting. However, dislocations initially emerged in the γ phase in the [011] crystal orientation. When the stress concentration of the horizontal γ phase reached a certain degree, some dislocations climbed over to the γ′ phase, but no rafting appeared. Furthermore, we found that the creep of the [111] crystal orientation was strongly influenced by stress, whereas the creep properties of the [001] and [011] crystal orientations were significantly affected by temperature. For comparison, we also employed creep experiments to study the creep properties and microstructural evolution of a nickel-based single crystal superalloy. The experimental results were consistent with those obtained using the MD simulations. Our theoretical predictions and understanding of creep properties and microstructural evolution of nickel-based single crystal superalloys will enable the rational design and testing of nickel-based single crystal superalloys for structural applications.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (No. 51210008). The authors would like to thank Professor Xinhong Xiong and Master candidate Rong Huang from the Wuhan University of Technology for helpful discussions.

References

1. R. Reed, T. Tao and N. Warnken, Acta Mater., 2009, 57, 5898–5913.
2. L. Carroll, Q. Feng and T. Pollock, Metall. Mater. Trans. A, 2008, 39, 1290–1307.
3. A. Yeh and S. Tin, Metall. Mater. Trans. A, 2006, 37, 2621–2631.
4. R. Hobbs, L. Zhang, C. Rae and S. Tin, Mater. Sci. Eng., A, 2008, 489, 65–76.
5. S. Tian, Y. Su, B. Qian, X. Yu, F. Liang and A. Li, Mater. Des., 2012, 37, 236–242.
6. M. S. Titus, A. Suzuki and T. M. Pollock, Scr. Mater., 2012, 66, 574–577.
7. K. Cheng, C. Jo, T. Jin and Z. Hu, Mater. Des., 2010, 31, 968–971.
8. L. Wang, Y. Liu, J. Yu, Y. Xu, X. Sun, H. Guan and Z. Hu, Mater. Sci. Eng., A, 2009, 505, 144–150.
9. D. Chatterjee, N. Hazari, N. Das and R. Mitra, Mater. Sci. Eng., A, 2010, 528, 604–613.
10. B. Viguier, F. Touratier and E. Andrieu, Philos. Mag., 2011, 91, 4427–4446.
11. X. Wang, J. Liu, T. Jin and X. Sun, Mater. Sci. Eng., A, 2014, 598, 154–161.
12. Z. Zhu, H. Basoalto, N. Warnken and R. Reed, Acta Mater., 2012, 60, 4888–4900.
13. Y. Gao, H. Wang, J. Zhao, C. Sun and F. Wang, Comput. Mater. Sci., 2011, 50, 3032–3037.
14. Y. Gao, Y. Fu, W. Sun, Y. Sun, H. Wang, F. Wang and J. Zhao, Comput. Mater. Sci., 2012, 55, 322–328.
15. D. Huang, Q. Zhang and P. Qiao, Comput. Mater. Sci., 2011, 50, 903–910.
16. J. Li, Modell. Simul. Mater. Sci. Eng., 2003, 11, 173.
17. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
18. S. Plimpton, Comput. Mater. Sci., 1995, 4, 361–364.
19. L. Yang and J. R. Li, Adv. Mater. Res., 2013, 816, 90.
20. K. Stiller, P. Warren, V. Hansen, J. Angenete and J. Gjønnes, Mater. Sci. Eng., A, 1999, 270, 55–63.
21. Y. Xingfu, T. Sugui, D. Hongqiang, Y. Huichen, W. Minggang, S. Lijuan and C. Shusen, Mater. Sci. Eng., A, 2009, 506, 80–86.
22. A. Kaniyoor and S. Ramaprabhu, AIP Adv., 2012, 2, 032183.
23. T. Yu, Q. Deng, G. Dong and J. Yang, Appl. Surf. Sci., 2011, 257, 5098–5103.
24. G. Leverant, B. Kear and J. Oblak, Metall. Trans., 1973, 4, 355–362.
25. J. Hutchinson, Proc. R. Soc. London, Ser. A, 1976, 348, 101–127.
26. S. Li and Z.-q. Hu, J. Univ. Sci. Technol. Beijing, 2010, 32, 1459–1463.
27. N. Matan, D. Cox, C. Rae and R. Reed, Acta Mater., 1999, 47, 2031–2045.
28. G. Han, J. Yu, Z. Hu and X. Sun, Mater. Charact., 2013, 86, 177–184.
29. T. Ichitsubo, D. Koumoto, M. Hirao, K. Tanaka, M. Osawa, T. Yokokawa and H. Harada, Acta Mater., 2003, 51, 4033–4044.

---