Cation ordering induced semiconductor to half metal transition in La₂NiCrO₆

Abstract

La₂NiCrO₆, previously proposed to be a candidate of half metallic antiferromagnetism, is revisited using the first-principles calculation. Electron correlation is considered and cation ordering effects are studied by arranging Ni and Cr atoms along [111] and [001]. For the [111] case, which corresponds to an ordered double perovskite, a monoclinic structure is predicted to be the most stable. In contrast to the previous study, it is insulating from the calculation of electron structure. Attractively, the magnetic coupling of Ni and Cr is sensitive to electron correlation, i.e., it is antiferromagnetic in the GGA calculation, whereas the ferromagnetic state is favoured when electron correlation (U) is turned on. For the [001] case, it is ferromagnetic whether U is included or not. Interestingly, a semiconductor to half metal transition is expected according to the GGA + U method, and the half metallic character could be preserved under both compressive and tensile strain.

---

Introduction

Double perovskites (A₂BB′O₆, e.g., La₂NiMnO₆ and La₂CoMnO₆), a class of ferromagnetic (FM) insulator that is rarely found in the nature, have gained considerable attention in the last few years.^1–14 They are attractive because of multifunctional properties such as magnetocapacitance,¹ magnetodielectronic effect,¹ and magnetoresistance up to relatively high temperature,² which provide intriguing prospects in industrial applications. On the other hand, understanding the underlying mechanism behind the FM insulator is also impressive for fundamental physics. In double perovskite, the coordination number of each transition metal is six, i.e., the transition metal and the neighboring oxygens form an octahedron (Fig. 1). The five degenerate orbitals then split into two groups, i.e., the lower t_2g (threefold) and higher e_g (twofold) states. In the Ni/Mn ordered case, the insulating nature is easy to understand, in which the 3d orbitals of Ni²⁺ (3d⁸, t_2g⁶e_g²↑) and Mn⁴⁺ (3d³, t_2g³↑)^3,4 are half filled (e_g² for Ni, t_2g³ for Mn). However, it is not so obvious for La₂CoMnO₆, in which the 3d orbitals of Co²⁺ (3d⁷, t_2g³↑t_2g²↓e_g²↑) are partially filled. Indeed, previous density functional calculations give a half metallic (HM) solution even when electron correlation (U) is included for both Co and Mn.⁵ Until recently, an alternative explanation gives the origin as the Coulomb-assisted spin–orbit coupling (SOC).⁶ To date, many aspects are still under debate, and cation ordering is proposed as the main contributor. For instance, the Curie temperature (T_c) is about 240 K for the ordered La₂CoMnO₆ and it is reduced to ∼150 K for randomly ordered case.⁷ The saturation magnetization is 5.7 μ_B per f.u. for the ordered state,⁸ close to 6.0 μ_B per f.u. for high spin (HS) states of Co²⁺ (3d⁷, t_2g³↑t_2g²↓e_g²↑) and Mn⁴⁺ (3d³, t_2g³↑), and it falls to 3.5 μ_B per f.u. in the disordered sample.^9,10 Disorder also leads to a structure transition from monoclinic to orthorhombic symmetry. Similarly, in La₂NiMnO₆, both the total magnetic moment (from 4.8 μ_B per f.u. to 3.7 μ_B per f.u.) and T_c (from ∼270 K to ∼138 K) are found to be decreased by disordering.^11–13 These are generally due to the different ionic configurations in the disordered case, i.e., Co³⁺/Mn³⁺ and Ni³⁺/Mn³⁺. Recently, by designing a Ni/Mn(Co/Mn) ordering along the [001] and [110] direction, HM electronic structure is obtained in La₂NiMnO₆ and La₂CoMnO₆, which is useful for modern functional materials.¹⁴ In contrast to the disordered case, the valence states are expected to be between 3+ and 4+ for Mn and between 3+ and 2+ for Ni and Co.

Fig. 1 Schematic structure of La₂NiCrO₆ with Ni/Cr along the [111] and [001] directions. The green and purple octahedra are NiO₆ and CrO₆, respectively, with Ni and Cr in the center. Small red spheres are oxygen and big grey spheres are La atoms.

La₂NiCrO₆, the counterpart of La₂NiMnO₆ and La₂CoMnO₆, was initially studied by Pickett with the aim to search for half metallic antiferromagnetism (HM-AFM).¹⁵ Both Ni and Cr were supposed to be 3+. In the ideal cubic structure, the crystal field splitting is small; thus, the d⁷ ion (Ni) will be in HS state (3d⁷, t_2g³↑t_2g²↓e_g²↑) and it will balance the d³ moment of Cr (3d³, t_2g³↓). However, the FM coupled Ni and Cr is found to be lower by 0.15 eV. This is similar to the magnetic configuration of La₂NiMnO₆ and La₂CoMnO₆. It is noticed that although structural relaxation is expected to change the magnetic state, no further studies are available. Thus, it is worthwhile to investigate whether the HM-AFM character could survive under structure relaxation. Inspired by these considerations, La₂NiCrO₆ is revisited in this study by the first principles calculation based on the density functional theory (DFT). Electron correlation, which is important for 3d electrons but not considered in the previous study,¹⁵ is included. Importantly, the cation disordering effect is simulated by changing the arrangement of Ni/Cr arranged along [111] (corresponding to ordered double perovskite) to [001] directions. In reality, this can be implemented by layer-by-layer growth techniques in the form of a thin film.

Computational method

The initial structures were predicted by the SPUDS program.¹⁶ This program has been widely employed to predict the structures of un-synthesized compounds. According to the Glazer tiling notation,^17,18 seven symmetries are predicted for double perovskites, namely, Fm3̄m (no. 225, a⁰a⁰a⁰), Pn3̄ (no. 201, a⁺a⁺a⁺), R3̄ (no. 148, a⁻a⁻a⁻), P4/mnc (no. 128, a⁰a⁰c⁺), I4/m (no. 87, a⁰a⁰c⁻), P2₁/n (no. 14, a⁻b⁺a⁻) and I2/m (no. 12, a⁰b⁻b⁻). All these structures are then optimized by the Vienna Ab Initio Simulation Package (VASP),^19–22 based on the projector augmented-wave (PAW) method.^23,24 The calculations were also performed using the WIEN2K program,^25,26 which is based on the full-potential linearized augmented plane wave (FPLAPW) method with the dual basis set. The reliability of the calculations in the two basis sets has been cross-checked.

For the self-consistent calculation with the projector augmented-wave, the plane wave cut-off energy was chosen to be 500 eV. The meshes of k-points (including the magnitude of the cell and number of atoms) adopted are listed in Table 1. For the self-consistent field iterations, the convergence tolerances were selected as the difference in total energy and the maximum force being within 1.0 × 10⁻⁵ eV and 1.0 × 10⁻² eV Å⁻¹, respectively. The plane wave expansion cut-offs were 7.0 for expanding the wave function (RKMAX) in the FPLAPW method. In the complete Brillouin zone, 1000 k-points were used. The values of the atomic sphere radii (R_MT) were chosen as 2.3, 1.9, 1.9 and 1.5 a.u. for La, Ni, Cr and O, respectively.

Table 1 The magnitude of cell, number of atoms and the k-points used in calculation

	Magnitude of cell	Number of atoms	Meshes of k-points
			Optimization	Energy calculation
Fm3̄m	4	40	5 × 5 × 5	7 × 7 × 7
Pn3̄	4	40	5 × 5 × 5	7 × 7 × 7
R3̄	1	10	5 × 5 × 5	7 × 7 × 7
P4/mnc	2	20	5 × 5 × 3	7 × 7 × 5
I4/m	2	20	5 × 5 × 3	7 × 7 × 5
P21/n	2	20	5 × 5 × 3	7 × 7 × 5
I2/m	2	20	5 × 5 × 3	7 × 7 × 5

---

For both the methods, the exchange–correlation energy was treated by the generalized gradient approximation (GGA-PBE).²⁷ Electron–electron Coulomb repulsion interactions or electron correlation (U) for the transition elements in combination with the double-counting correction were considered in the rotationally invariant form (GGA + U) with a single effective Hubbard parameter, U_eff = U − J.²⁸ A series of U values were selected for transition metals, i.e., 0.5–6.0 eV for Cr and 0.5–8.0 eV for Ni, (with U_Ni > U_Cr as Ni follows Cr in the periodic table). Our calculations indicate that for the selected U values, the main conclusions are consistent. Therefore, unless specified, we choose the results from U_Ni = 6.0 eV and U_Cr = 4.0 eV for discussion.

Results and discussion

Ni/Cr arranged along [111] direction

When Ni/Cr is arranged along the [111] direction, it corresponds to an ordered double perovskite, i.e., there are six Ni–O–Cr linkages for each Ni(Cr). To determine the ground state (including both the crystal symmetry and magnetic configurations), structure relaxations were carried out for all the seven crystal structures predicted from the SPUDS program with both magnetic coupling (i.e., Ni/Cr FM and AFM coupled) and electron correlations considered. The energy difference is listed in Table 2.

Table 2 The relative energy (meV per two formula units) for Ni/Cr along [111] arrangements from GGA and GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) method. The energy of P2₁/n symmetry with FM state is set to be zero

	FM		AFM
	GGA	GGA + U	GGA	GGA + U
Fm3̄m	1109.7	2032.4	1345.9	2447.5
Pn3̄	566.9	1185.8	655.7	899.2
R3̄	93.1	205.2	115.9	296.8
P4/mnc	520.4	566.5	60.9	1433.2
I4/m	328.2	955.7	312.7	955.7
P21/n	0	0	−54.2	109.8
I2/m	100.4	106.2	172.8	245.8

---

In the GGA calculation, the AFM coupled Ni and Cr in monoclinic symmetry is favoured, which is in agreement with the expectation that structure relaxation will change magnetic state. However, when electron correlation is included (even with a very small value, i.e., U_Ni = U_Cr = 0.5 eV), the FM state is the most stable. This means that the ground state is sensitive to electron correlation. A similar phenomenon is observed in other double perovskite transition metal oxides. Taking La₂CrFeO₆ as an example,²⁹ it is ferrimagnetic in the GGA calculation, which is in contradiction with the experimentally reported ferromagnetic state, whereas the inclusion of electron correlation will make the ferromagnetic coupling more stable.

Regardless of the magnetic state, monoclinic P2₁/n is the most stable, indicating the presence of structure distortions. Moreover, both the correlation and magnetic coupling have little effect on the structural parameters (less than 0.3%). Thus, only the structural parameters from GGA (FM) are given in Table 3. It is found that, due to the crystal distortion, the six Ni–O(Cr–O) bonds are divided into three groups. This will make the degenerated d states split. However, all the bond lengths are close to each other. Therefore, the sub-orbits are expected to be close in energy. Given that the radii of Ni³⁺ (0.70 Å for low spin (LS) and 0.74 Å for HS) are smaller than that of Cr³⁺ (0.76 Å), the larger Ni–O bond lengths suggests a Ni²⁺ (0.83 Å)/Cr⁴⁺ (0.69 Å) configuration, in contrast to the previous study.¹⁵ The Ni–O–Cr bond angles (Table 3) substantially deviate from the ideal 180° angle, which weakens the electron hopping interactions in this bridge.

Table 3 Optimized structure parameters for [111] and [001] arrangements from GGA method

			[111]	[001]
Space group			P21/n	P21/b
a			5.517 Å	5.493 Å
b			5.577 Å	5.499 Å
c			7.802 Å	7.839 Å
α/β			89.99°	90.01°
O1		x	0.7216	0.7168
		y	0.2961	0.2836
		z	0.0408	0.0400
O2		x	0.7981	0.7168
		y	0.7798	0.2833
		z	0.0425	0.4644
O3		x	0.0781	0.0722
		y	0.4807	0.4883
		z	0.2418	0.2422
Ni–O1			2.078 Å × 2
Ni–O2			2.079 Å × 2	1.980 Å × 2, 1.979 Å × 2
Ni–O3			2.063 Å × 2	2.060 Å × 2
Cr–O1			1.937 Å × 2	1.987 Å × 2, 1.984 Å × 2
Cr–O2			1.946 Å × 2
Cr–O3			1.937 Å × 2	1.941 Å × 2
Bond angles	In-plane		155.1°(Ni–O1–Cr)	157.9°(Ni–O2–Ni)
			154.1°(Ni–O2–Cr)	156.3°(Cr–O1–Cr)
	Out-of-plane		154.3°(Ni–O3–Cr)	156.8°(Ni–O3–Cr)

---

It is interesting to note that for either the Ni³⁺(S = 3/2)/Cr³⁺(S = 3/2) or Ni²⁺(S = 1)/Cr⁴⁺(S = 1) configuration, once the spin is antiparallel, the magnetization is zero. The calculated spin magnetic moment is 1.66 μ_B for Cr and −1.48 μ_B for Ni (Table 4), close to the theoretical value of the Ni²⁺(S = 1)/Cr⁴⁺(S = 1) configuration. Including this in the interstitial sites, the net magnetic moment is zero, consistent with the abovementioned analysis. Because it is AFM coupling in the GGA method, the next concern is whether it is half metallic to obtain HM-AFM. In the density of states (DOS) (Fig. 2, left, GGA), it is observed that there is a gap as large as 1.2 eV in the spin-down channel, which is formed between the filled Ni 3d states and unoccupied Cr 3d states. In the spin-up channel, it is the hybrid Ni 3d-O 2p-Cr 3d electrons in the neighborhood of the Fermi level. From the band structure (inset of Fig. 2), it is clear that a small gap of ∼0.1 eV is formed in the spin-up channel, making the [111] case a semiconductor. This is similar for La₂NiMnO₆ in which GGA gives an insulating nature. However, it is different from La₂CoMnO₆, in which the insulating nature is driven by the Coulomb-enhanced SOC.

Table 4 Magnetic moment (μ_B) for individual transition metals and total magnetic moment from GGA and GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) methods

		Ni	Cr	Total
[111]	GGA	−1.48	1.66	0.00
	GGA + U	1.76	1.95	4.00
[001]	GGA	1.17	2.19	4.00
	GGA + U	1.55	2.31	4.00

---

Fig. 2 Density of states for Ni/Cr along [111] arrangement from the GGA method. The inset is the band structure of the spin-up channel near the Fermi level.

Turning to the FM state from the GGA + U calculations, it is also insulating (Fig. 3). The band gap in the vicinity of the Fermi level becomes larger with increasing U values (not shown). Fig. 3 shows the DOS and band structure from U_Ni = 6.0 eV and U_Cr = 4.0 eV, which are the typical values for these two elements.^30–32 The small gap in the spin-up channel is 0.90 eV and the larger one in the spin-down channel is 2.8 eV. In the spin-up channel, the Ni 3d states are all occupied, and from the partial DOS (Fig. 4, left), it is seen that three orbitals, namely, d_yz, d_xz and d_x²y², are occupied (the three orbitals correspond to conventional t_2g states if the crystallographic xy plane is rotated by 45° from the basal plane). This indicates that Ni is in the 2+ state (3d⁸, t_2g⁶e_g²↑, S = 1), similar to that in La₂NiMnO₆ (ref. 4). The calculated orbital occupancy for each orbital (Table 4) is also consistent with this configuration. For Cr 3d states (Fig. 4, right), which mainly occupy the spin-up channel, they are split and this is the reason for the insulating behavior. Concerning the orbital occupancy, it might not be so obvious because of the hybridization, for instance, it is only 0.76 for the fully populated d_yz (Table 5).

Fig. 3 Density of states and band structure for Ni/Cr along [111] arrangement from the GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) method.

Fig. 4 Partial density of states of Ni/Cr along the [111] arrangement of Ni/Cr from GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) method.

Table 5 Orbital occupancy for transition metals from GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) method

			dz^2	dx^2y^2	dxy	dxz	dyz
[111]	Ni	up	0.94	0.93	0.95	0.92	0.91
		dn	0.10	0.85	0.16	0.89	0.90
	Cr	up	0.36	0.57	0.37	0.45	0.76
		dn	0.18	0.08	0.18	0.08	0.06
[001]	Ni	up	0.94	0.92	0.84	0.91	0.92
		dn	0.18	0.90	0.18	0.83	0.88
	Cr	up	0.27	0.83	0.26	0.53	0.83
		dn	0.15	0.05	0.13	0.06	0.05

---

Compared with the GGA calculation, the spin magnetic moment is increased to 1.74 μ_B for Ni and 1.95 μ_B for Cr (Table 4) in GGA + U calculations. This is understandable because the application of U localizes the electrons.

Ni/Cr arranged along [001] direction

Perovskite oxide films and superlattices are recent hot topics owing to the development of film-grown technologies such as pulsed laser deposition (PLD) and molecular beam epitaxy (MBE). It is feasible to grow cations with different stacking arrangements, which provides an opportunity to better understand the influence of disordering. In the following study, Ni/Cr was arranged along the [001] direction. Different from the [111] case, for each Ni(Cr) there are four Ni–O–Ni(Cr–O–Cr) linkages (in-plane) and two Ni–O–Cr linkages (out-of-plane). This internal environment variation leads to the change in the crystal structure into P2₁/b, which is still monoclinic. According to the structure parameters mentioned in Table 3, it is seen that the in-plane parameters (a and b) are smaller but c is slightly larger compared with the [111] case. It is also seen that the in-plane Ni–O bond distances are considerably smaller than the out-of-plane ones, making the NiO₆ octahedra elongated. In contrast, the CrO₆ octahedra are compressed. The bond angles are also far from the ideal 180° due to distortion.

In contrast to the [111] case, the FM state is favored with and without U for the [001] case. In the GGA calculation, the energy difference is small, i.e., 4.5 meV, and it increases with increasing U. Fig. 5 plots the DOS for the [001] case. It is on the end-point of half-metal to metal transition in the GGA method because the Ni spin-down conduction band is on the edge of the Fermi level. Obviously, a small U value will push the unoccupied state to higher energy region, forming a gap in the spin-down channel. In the DOS from the GGA + U calculation with U_Ni = 6.0 eV and U_Cr = 4.0 eV (Fig. 5), a large gap (∼3.6 eV) in the spin-down channel is formed. Moreover, in the spin-up channel, most Ni 3d states are pushed down to lower energy region and Cr 3d states are almost split. However, a small amount of electrons are preserved in the neighborhood of the Fermi level (inset of Fig. 5) making this case half metallic.

Fig. 5 Density of states for Ni/Cr along [001] arrangement from the GGA and GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) methods. The inset is the band structure near the Fermi level of the spin-up channel.

For 3d metals, electron correlation is important. For instance, besides the electronic structure change, valence states of transition metals would also be different when U is considered in the un-synthesized NiCrO₃ (ref. 32). For the present cases, small U values will introduce an interesting feature, i.e., a semiconductor to half-metal transition. A similar transition is reported for La₂NiMnO₆ and La₂CoMnO₆ (ref. 14). For these two cases, the origin is explained by the extension of e_g states as a result of additional Mn–O–Mn, Ni–O–Ni or Co–O–Co linkages. This holds true for the Ni–O–Ni bridges of the title compound. As seen in the PDOS (Fig. 6), the Ni d_xy electrons run over the Fermi level, which is fully filled in the [111] case. Thus, the number of electrons reduces by 0.11 (from 0.95 to 0.84) (Table 5). To balance this, the Cr 3d electrons in the conduction band move downwards to provide additional electrons; moreover, they play the role of conduction electrons. Obviously, the reduction of Ni 3d states makes the valence state of Ni enhanced, whereas the situation for Cr is the opposite. Therefore, similar to La₂NiMnO₆ and La₂CoMnO₆ (ref. 14), mixed valence states of Ni²⁺/Cr⁴⁺ and Ni³⁺/Cr³⁺ are assumed.

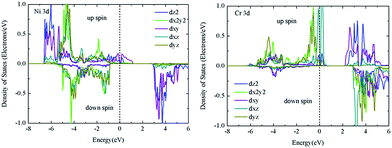Fig. 6 Partial density of states of Ni/Cr along [001] arrangement from GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) method.

From Table 4, it is seen that the magnetic moment of Ni is reduced. Hence, Ni³⁺ should be in the LS state (3d⁷, t_2g⁶e_g¹↑, S = 1/2), disagreement with previous speculation.¹⁵ In contrast, because of the larger moment of Cr³⁺(S = 3/2), the magnetic moment of Cr is increased (Table 4). In addition, the longer Cr–O bond length gives less hybridization with oxygen, which will also contribute to the enhancement of the Cr magnetic moment. However, the net magnetic moment of 4.00 μ_B per f.u. remains, which is a requirement for half metallic compounds.

Finally, strain often exists in films, which appears due to the mismatch between substrate and sample, and this will make the physical properties different from bulk. To simulate this effect, the electronic structure during compression as well as expansion of its equilibrium lattice constant is studied. In the calculation, parameter c is set to be compressed (elongated) by 2% and kept fixed, meanwhile atomic positions and parameters a and b are optimized. The magnetic coupling of Ni and Cr is not influenced by the strain effect, which remains ferromagnetic in both compressive and tensile cases. From the total DOS (Fig. 7), it is seen that half metallic character could be preserved in both compressive and tensile strain from the GGA + U method. However, in the GGA calculation, it is normal metal for the compressive case because the conduction band moves downward in the spin-down channel. This is understandable considering that the electronic wave function becomes more overlapped as the atomic distance gets closer. The situation is opposite for the case of tensile strain. Thus, a gap is formed in the spin-down channel with the conduction band moving upward. Therefore, a half metallic nature could be obtained in both GGA and GGA + U methods under tensile strain.

Fig. 7 Total density of states of Ni/Cr along [001] arrangement under compressive and tensile strain from the GGA and GGA + U (U_Ni = 6.0 eV and U_Cr = 4.0 eV) methods.

Conclusions

La₂NiCrO₆ with cation ordering in both [111] and [001] direction is investigated by density functional theory. The effects of electron correlation are important to decide both magnetic and electronic states. Within reasonable U values, a semiconductor to half-metal transition is expected with the Ni/Cr arrangement changing from [111] to [001]. Under both compressive and tensile strains, the half metallic character could be preserved. The lattice constant of SrTiO₃ (3.905 Å) is close to the in-plane parameter of the [001] case (3.905√2 ≈ 5.515, close to a and b), which is usually chosen to be the substrate. It is interesting that the LaNiO₃–LaCrO₃ superlattice grown on SrTiO₃ substrate could be of potential use in spintronics. Further experimental investigations are suggested from this theoretical study.

Acknowledgements

The authors thank the National Natural Science Foundation of China (Grant nos 21403185, 21221061, 21201148, and 21303156), the Natural Science Foundation of Hebei (Grant no. B2015203268, B2011203121) and China Postdoctoral Science Foundation (Grant no. 2014M551048) for financial support.

Notes and references

1. N. S. Rogado, J. Li, A. W. Sleight and M. A. Subramanian, Adv. Mater., 2005, 17, 2225.
2. R. N. Mahato, K. Sethupathi and V. Sankaranarayanan, J. Appl. Phys., 2010, 107, 09D714.
3. M. Hashisaka, D. Kan, A. Masuno, M. Takano, Y. Shimakawa, T. Terashima and K. Mibu, Appl. Phys. Lett., 2006, 89, 032504.
4. H. Das, U. V. Waghmare, T. Saha-Dasgupta and D. D. Sarma, Phys. Rev. Lett., 2008, 100, 186402.
5. S. H. Lv, H. P. Li, Z. C. Wang, L. Han, Y. Liu, X. J. Liu and J. Meng, Appl. Phys. Lett., 2011, 99, 202110.
6. S. Baidya and T. Saha-Dasgupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035131.
7. A. J. Barón-González, C. Frontera, J. L. García-Muñoz, J. Roqueta and J. Santiso, J. Phys.: Conf. Ser., 2010, 200, 092002.
8. H. Z. Guo, A. Gupta, T. G. Calvarese and M. A. Subramanian, Appl. Phys. Lett., 2006, 89, 262503.
9. R. I. Dass and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 014401.
10. P. A. Joy, Y. B. Khollam and S. K. Date, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8608.
11. R. I. Dass, J.-Q. Yan and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064415.
12. M. P. Singh, C. Grygiel, W. C. Sheets, P. Boullay, M. Hervieu, W. Prellier, B. Mercey, C. Simon and B. Raveau, Appl. Phys. Lett., 2007, 91, 012503.
13. M. P. Singh, K. D. Truong, S. Jandl and P. Fournier, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224421.
14. M. Zhu, Y. Lin, E. W. C. Lo, Q. Wang, Z. J. Zhao and W. H. Xie, Appl. Phys. Lett., 2012, 100, 062406.
15. W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10613.
16. M. W. Lufaso and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725.
17. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Sci., 1972, 28, 3384.
18. A. M. Glazer, Acta Crystallogr., Sect. A: Found. Crystallogr., 1975, 31, 756.
19. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
20. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
21. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
23. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
24. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
25. K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28, 259.
26. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augmented Plane Wave and Local Orbitals Program for Calculating Crystal Properties, Technical University Wien, Vienna, 2001.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
28. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467.
29. K. Miura and K. Terakura, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 104402.
30. H. H. Chen, A. J. Millis and C. A. Marianetti, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 111, 116403.
31. M. J. Han and M. van Veenendaal, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195102.
32. K.-W. Lee and W. E. Pickeet, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 180406(R).

---