Exploring highly energetic aliphatic azido nitramines for plasticizers

Abstract

A set of energetic aliphatic azido nitramines was designed and studied with the B3LYP/6-31G* method of density functional theory to find new promising azido nitramines applicable to propellants as plasticizers and to investigate the effect of the methylene nitramino group (–CH₂NNO₂–) on performance. The reliability of the theoretical method was tested by comparing the theoretical densities with the experimental data. The thermodynamic properties (heat capacity, enthalpy, entropy, and heat of formation), density (ρ), detonation pressure (P), detonation velocity (D), specific impulse (I_s) and stability were predicted. With the increase in the number of –CH₂NNO₂– groups (n), the thermodynamic properties, ρ, P, and D increase, while the stability decreases slightly. There are linear relationships between thermodynamic properties and n. A –CH₂NNO₂– group improves the heat of formation by 67.59 kJ mol⁻¹ on average. I_s reaches the maximum when n = 4 and changes little when n ≥ 5. It is worth noting that I_ss of all title compounds are higher than that of HMX (1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane, a famous explosive).

---

1 Introduction

The common way to improve the output energy of propellants is to add certain amounts of highly energetic explosives, such as RDX (hexahydro-1,3,5-trinitro-1,3,5-trizine) and HMX (1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane). However, this may also bring some problems, such as, high flame temperature and serious ablation of gun barrel. Therefore, it is necessary to mix energetic plasticizers or other additives into the propellants. Nitrate ester plasticizers have good plasticizing effects and high energy, but they also have undesired high volatility and impact sensitivity. Compared with nitrate ester plasticizers, azido plasticizers, especially azido nitramine plasticizers which have two kinds of energetic groups (i.e., nitramino (–NNO₂) and azido (–N₃)) in molecules have better stability and compatibility with other components of propellants (e.g. binders)¹ and have been attracting more and more attentions.^2–10 Researches found that azido nitramine plasticizers can adjust the average molecular weight of combustion products, increase the nitrogen content and hence reduce the characteristic signal, and improve the energy and specific impulse of propellants. Although this type of compounds has attracted great interests, effects of structures on their performance are still unclear. Therefore, in this paper, eight aliphatic azido nitramines (Fig. 1) were studied using the density functional theory (DFT). Thereinto, compounds 1–4 have been synthesized and reported,^2–4 particularly for compound 3 (1,7-diazido-2,4,6-trinitrazaheptane), extensive studies have been carried out both experimentally and theoretically.^8–11

Fig. 1 Structures of title compounds with the numbering of some N–NO₂ bonds.

Since the output energy (detonation pressure, detonation velocity, specific impulse) and stability are the important parameters for characterizing and evaluating the performance of energetic materials, they, together with the related thermodynamic properties and density of these compounds were investigated. In terms of the energetic property and stability, we try to (I) search for new azido nitramine plasticizers with better properties and (II) investigate the role of –CH₂NNO₂– groups in the molecular design of the azido nitramines. Since specific impulse (I_s) is the most vital parameter to weigh the performance of propellants, in this work, two kinds of idealized stoichiometric decomposition reactions were designed to predict reliable I_ss. Based on the well-predicted I_ss to screen promising energetic plasticizers makes this study more meaningful.

2 Theoretical methods

Molecular geometries of the title compounds were fully optimized using the DFT-B3LYP method^12,13 in combination with the 6-31G* basis set.¹⁴ Many studies^15,16 have shown that accurate molecular structures and other properties can be produced at this level. The density (ρ) was evaluated with ρ = M/V_m, where M is the molecular weight. V_m is the average molar volume obtained with the Monte Carlo integration scheme by setting the number of points to 20 000 per Bohr,³ which is basically equivalent to the average of 1000 default runs.¹⁷ Previous studies^17,18 have indicated that the theoretical ρ calculated using this method is very close to the experimental crystal density for azido compounds.

To discuss the effect of the number (n) of –CH₂NNO₂– groups on the thermodynamic properties, heat capacity (C⁰_p,m), enthalpy (S⁰_m), and entropy (H⁰_m) at different temperatures (200 to 800 K) were calculated using a self-compiled program and the heat of formation (HOF) was calculated from the isodesmic reaction (1). This procedure has been proved to be very successful¹⁹ and widely used in previous studies.^20–22

N₃(CH₂)_n+1(NNO₂)_nN₃ + (n + 1)CH₄ + 2nNH₃ → 2CH₃N₃ + nNH₂NO₂ + 2nCH₃NH₂ (n = 1–8) (1)

The reaction enthalpy (ΔH_r) of the isodesmic reaction at 298 K was calculated using the following equation:

ΔH_r = ∑ΔH_f,P − ∑ΔH_f,R = ΔE₀ + ΔE_ZPV + ΔH_T + ΔnRT (2)

where ΔH_f,P and ΔH_f,R are HOFs of products and reactants at 298 K, respectively. ΔE₀ and ΔE_ZPV are the differences between the total energies at 0 K and between the zero-point vibrational energies of products and reactants, respectively, and ΔH_T is the thermal enthalpy correction from 0 to 298 K. The ΔH_fs of the reference compounds except CH₃N₃ and NH₂NO₂ are taken from the experimental values. For CH₃N₃ and NH₂NO₂ which lack of experimental data, additional calculations were performed at the G2 level to get accurate ΔH_f from the atomization reaction. Previous researches have verified the reliability of the procedure.²³

Detonation velocity (D) and detonation pressure (P) were predicted using the empirical Kamlet–Jacobs equations.²⁴

D = 1.01(NM̄^0.5Q^0.5)^0.5(1 + 1.30ρ) (3)

P = 1.558ρ²NM̄^0.5Q^0.5 (4)

where ρ is the density (g cm⁻³), N is the moles of gas produced by per gram of reactant, M̄ is the average molar weight of detonation products, and Q is the chemical energy of detonation (cal g⁻¹). N, M̄ and Q were determined according to the largest exothermicity principle.²⁵

Specific impulse (I_s) is the most vital parameter for characterizing and evaluating the performance of propellants. It was calculated using the following equations. First, the proportional specific impulse I_s,p was estimated using eqn (5),²⁶ which has been employed by many studies.^15,27

I_s,p ∼ T_C^1/2N^1/2 (5)

To use eqn (5), it is necessary to determine the combustion temperature (T_C) and the molar number of products (N) produced by per unit weight of propellant. T_C was calculated using eqn (6).

ΔH_C = C_p(T_C − T₀) (6)

where ΔH_C is the enthalpy of combustion and can be calculated from the HOFs of the reactant (ΔH_f,R) and product (ΔH_f,P).

ΔH_C = ∑ΔH_f,R − ∑ΔH_f,P (7)

The HOFs of products are known and that of reactant was computed from the above mentioned isodesmic reaction.

Since eqn (5) is a proportion relationship, the obtained I_s,p isn't an absolute value. So the relative specific impulse (I_s,r) to HMX (1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane) was predicted with eqn (8). Then the absolute specific impulse (I_s) of the title compounds was estimated by multiplying the experimental I_s of HMX (265.10 s (ref. 28)) with eqn (9).

I_s,r = I_s,p/I_s,p(HMX) (8)

I_s = 265.10I_s,r (9)

The thermal stability was investigated by evaluating the bond dissociation energy (E_BD). To obtain more accurate results, in this study, E_BDs of possible initiation bonds were calculated using eqn (10).

E_BD(A–B) = E_A˙ + E_B˙ − E_A–B − E_BSSE (10)

where A–B stands for the neutral molecule and A˙ and B˙ for the radical products of the dissociation of the A–B bond; E_A–B, E_A˙ and E_B˙ are their corresponding total energies corrected by the zero-point vibrational energies. E_BSSE is the basis set superposition error (BSSE) calculated with the method proposed by Boys–Bernardi counterpoise,²⁹ which was usually neglected in previous works.^18,21,22

All calculations except for D, P, and I_s were performed with the Gaussian program package.³⁰

3 Results and discussion

3.1 Thermodynamic properties

Thermodynamic properties of the title compounds were evaluated and tabulated in Table 1. It can be seen that C⁰_p,m, S⁰_m, and H⁰_m increase evidently with the increasing temperature (T) from 200 to 800 K. This is because at the higher temperature, the vibrations of molecules are intensified and make more contributions to the thermodynamic properties, but at the lower temperature, the main contributions are from the translation and rotation. Therefore, the increasing temperature leads to the increase of thermodynamic functions.

Table 1 Thermodynamic properties of the title compounds at different temperatures

Property	T/K	1	2	3	4	5	6	7	8
C^0p,m/J mol^−1 K^−1	200.00	132.32	185.11	241.09	298.40	351.11	404.18	458.81	513.45
	300.00	170.96	243.64	317.27	392.18	464.92	537.40	610.25	683.63
	400.00	205.44	295.64	385.94	477.07	567.57	657.45	747.18	837.77
	500.00	234.00	338.55	442.93	547.83	652.75	757.00	860.94	965.81
	600.00	256.98	372.88	488.59	604.62	720.88	836.55	951.89	1068.06
	700.00	275.47	400.33	525.04	649.99	775.15	899.85	1024.25	1149.36
	800.00	290.49	422.50	554.42	686.56	818.80	950.72	1082.37	1214.61
S^0m/J mol^−1 K^−1	200.00	425.42	475.75	575.20	637.13	729.99	811.30	880.34	968.69
	300.00	486.45	562.01	687.48	776.01	894.06	1000.60	1095.25	1209.31
	400.00	540.48	639.42	788.41	900.75	1042.24	1172.08	1290.05	1427.64
	500.00	589.50	710.17	880.88	1015.08	1178.37	1329.87	1469.45	1628.84
	600.00	634.27	775.04	965.82	1120.18	1303.64	1475.20	1634.77	1814.32
	700.00	675.32	834.66	1043.98	1216.92	1418.99	1609.08	1787.14	1985.31
	800.00	713.12	889.61	1116.07	1306.18	1525.45	1732.68	1927.84	2143.19
H^0m/kJ mol^−1	200.00	18.54	23.97	31.19	37.60	44.29	50.60	56.95	63.83
	300.00	33.72	45.44	59.14	72.17	85.14	97.73	110.47	123.75
	400.00	52.59	72.48	94.39	115.74	136.9	157.63	178.51	200.02
	500.00	74.61	104.26	135.93	167.11	198.07	228.53	259.12	290.42
	600.00	99.20	139.9	182.60	224.84	266.88	308.36	349.94	392.32
	700.00	125.86	178.61	233.35	287.65	341.78	395.30	448.88	503.34
	800.00	154.18	219.79	287.37	354.55	421.56	487.92	554.31	621.65

---

Taking compound 4 as an example, the relationships between the thermodynamic functions and the temperature are expressed in Fig. 2(a) and shown as follows (R² is the correlation coefficient and SD is the standard deviation). Obviously, the increments for C⁰_p,m and S⁰_m decrease, while that for H⁰_m increases with the increasing temperature. The corresponding correlation coefficients are all close to 1. These equations will be helpful for further studies on the other physical, chemical, and explosive properties of the title compounds at various temperatures.

C⁰_p,m = 71.68 + 1.23T − 6.09 × 10⁻⁴T²; R² = 0.99994, SD = 1.31035

S⁰_m = 339.32 + 1.59T − 4.84 × 10⁻⁴T²; R² = 0.99996, SD = 1.82154

H⁰_m = −18.64 + 0.21T + 3.22 × 10⁻⁴T²; R² = 0.99988, SD = 1.55821

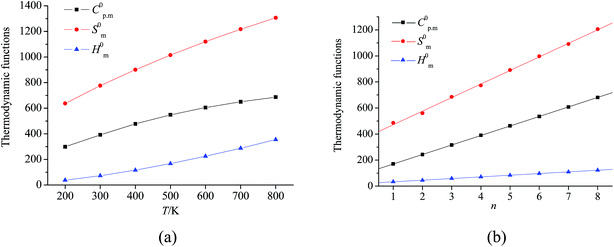Fig. 2 Relationships between C⁰_p,m (J mol⁻¹ K⁻¹), S⁰_m (J mol⁻¹ K⁻¹), H⁰_m (kJ mol⁻¹) and T (K) for compound 4 (a), and n at 298 K (b).

In addition, the thermodynamic properties increase with the increasing number of –CH₂NNO₂– group under the same temperature, and there are good linear relationships between C⁰_p,m, S⁰_m, H⁰_m and n. As an example, relationships between n and thermodynamic properties at 298 K are depicted in Fig. 2(b) and shown as follows:

C⁰_p,m = 97.45 + 71.94n; R = 0.99999, SD = 0.73798

S⁰_m = 367.34 + 104.11n; R = 0.99930, SD = 10.34251

H⁰_m = 20.19 + 12.77n; R = 0.99993, SD = 0.39382

Obviously, incorporation of the –CH₂NNO₂– group exhibits a positive effect on thermodynamic properties.

3.2 Energetic properties

Table 2 lists the molecular weight, oxygen balance (OB = [16 × (c − 2a − b/2)] × 100/M, where a, b and c are respectively the number of C, H, and O atoms of the compound C_aH_bO_cN_d), calculated density, HOF, detonation pressure, and detonation velocity. For comparison, the calculated and experimental detonation properties of HMX are also summarized in Table 2. Evidently, the calculated detonation properties basically agree with the available experimental values. For example, the predicted ρ, D, and P of HMX are 1.90 g cm⁻³, 9.08 km s⁻¹, 37.66 GPa, respectively and the corresponding experimental results are 1.91 g cm⁻³, 9.10 km s⁻¹ and 39.00 GPa;³¹ the predicted ρ of 1, 2, and 3 are 1.45, 1.70, and 1.71 g cm⁻³, respectively and the corresponding experimental results are 1.43, 1.70, and 1.71 g cm⁻³.³² The calculated and experimental densities of 4 have a relative big deviation, for which we can not provide a definite reason. One possible reason is that the experiment has provided the density of one of the polymorphs for 4. Comparing the D and P of 3 and 4 obtained in this work with those of Zhou, et al.³³ a slight deviation exists, which can be attributed to the different formulas for calculating D and P. Our results are much closer to those reported in ref. 3 or ⁹.

Table 2 Detonation properties of the title compounds

Compound	M/g mol^−1	OB/%	ρ/g cm^−3	ΔHf/kJ mol^−1	D/km s^−1	P/GPa
1	172.11	−37.19	1.45 (1.43 (ref. 32))	651.04	7.65	22.59
2	246.15	−32.50	1.70 (1.70 (ref. 32))	713.95	8.55	31.36
3	320.18	−29.98	1.71 (1.71 (ref. 32), 1.65 (ref. 33))	778.56	8.59 (8.30 (ref. 9), 8.105 (ref. 33))	31.76
4	394.22	−28.41	1.74 (1.67 (ref. 3), 1.56 (ref. 33))	864.83	8.73 (8.30 (ref. 3), 7.839 (ref. 33))	33.11 (29.5 (ref. 3))
5	468.26	−27.34	1.77	933.76	8.83	34.22
6	542.30	−26.55	1.78	996.61	8.90	35.00
7	616.34	−25.96	1.79	1047.81	8.92	35.24
8	690.38	−23.18	1.80	1120.38	8.97	35.74
HMX	296.16	−21.61	1.90 (1.91 (ref. 31))	73.31	9.08 (9.10 (ref. 31))	37.66 (39 (ref. 31))

---

Fig. 3 presents the relationships between ρ, ΔH_f, P, D, OB and n. Obviously, all the parameters increase with n, suggesting that incorporating the –CH₂NNO₂– group has a positive effect on the energy performance of aliphatic azido nitramines. There exists a good linear relationship between HOF and n, one –CH₂NNO₂ group increases the HOF by 67.59 kJ mol⁻¹ on average. Compared with the energetic plasticizers widely used in solid propellants, such as ethylene glycol dinitrate (EGDN, ρ = 1.48 g cm⁻³, D = 8.00 km s⁻¹, P = 25.07 GPa) and nitroglycerine (NG, ρ = 1.54 g cm⁻³, D = 8.03 km s⁻¹, P = 5.92 GPa),²⁷ all title compounds have better detonation performance and may be potential energetic plasticizers. When n = 8, OB, D, and P (−23.18%, 8.97 km s⁻¹, and 35.74 GPa, respectively) are very close to the values of HMX. Since using compound 3 as a high-energy oxidant to replace RDX in the modified double-base propellants partly can markedly enhance the burning rate, reduce the pressure exponent, and improve the performance level,¹⁰ the higher OBs of 4–8 make them more attractive.

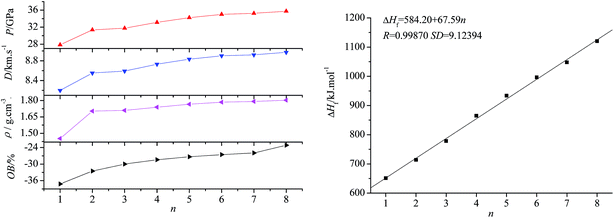Fig. 3 Relationships between OB, ρ, D, P, ΔH_f and n.

For evaluating the I_s using eqn (5), it is necessary to establish the identities and amounts of gaseous products. In this paper, two kinds of idealized stoichiometric decomposition reactions (I and II in Table 3) were designed. Reaction (I) is obtained according to the largest exothermicity principle,²⁵ i.e., all the N atoms turn into N₂, the O atoms react with the H atoms to give H₂O at first, and then form CO₂ with the C atoms. If the number of O atoms is more than that needed to oxidize H and C atoms, the redundant O atoms will convert into O₂. If the content of O is not enough to fully oxidize H and C atoms, the remaining H atoms will convert into H₂, and C atoms will exist as solid-state C. Reaction (II) is obtained according to the principle proposed by Politzer, et al.²⁶ i.e., O atoms form H₂O with the H atoms first and then CO with the C atoms, rather than CO₂ to achieve the maximum of gas products. For the limitation of the quantity of O, the C atoms do not completely convert into CO₂, nor CO, that means the true I_s may be between the values obtained from the reactions (I) and (II). Table 3 gives ΔH_C, C_p, T_C, N, I_s,p, I_s and corresponding reactions. Fig. 4 shows the variation of I_s with n. Obviously, the designed reactions have a significant effect on I_ss. I_ss obtained from (II) are higher than those obtained from (I). However, the variation trends are consistent, that is, I_s varies up and down with the changes of n from 1 to 8 and it reaches the maximum value at n = 4, and when n exceeds 5, I_s essentially keeps the constant. It is worth noting that all title compounds possess higher I_s than HMX, which makes these compounds more attractive.

Table 3 Two kinds of idealized decomposition reactions and some I_s related parameters for the title compounds^a

Compound	Idealized reaction	ΔHC/kJ mol^−1	Cp/J mol^−1 K^−1	TC/K	N	Is,p	Is/s
a Cp of H2O, CO2, CO, N2, and C are 33.33, 37.65, 29.1, 28.86, 8.53 J mol^−1 K^−1 and HOF are −241.83, −393.51, −110.50, 0, 0 kJ mol^−1, respectively.
1	C2H4N8O2 = 4N2 + 2H2O + 2C	−1134.64	232.20	5184.63	0.0349	13.44	268.83
2	(I) C3H6N10O4 = 5N2 + 3H2O + 1/2CO2 + 5/2C	−1636.10	286.10	6016.78	0.0345	14.41	276.79
	(II) C3H6N10O4 = 5N2 + 3H2O + CO + 2C	−1549.85	292.40	5598.59	0.0366	14.31	286.10
3	(I) C4H8N12O6 = 6N2 + 4H2O + CO2 + 3C	−2139.26	371.60	6055.04	0.0344	14.42	276.95
	(II) C4H8N12O6 = 6N2 + 4H2O + 2CO + 2C	−1966.76	384.20	5417.25	0.0375	14.25	284.92
4	(I) C5H10N14O8 = 7N2 + 5H2O + 3/2CO2 + 7/2C	−2694.08	457.10	6192.00	0.0342	14.56	279.61
	(II) C5H10N14O8 = 7N2 + 5H2O + 3CO + 2C	−2435.33	476.00	5414.39	0.0380	14.35	287.01
5	(I) C6H12N16O10 = 8N2 + 6H2O + 2CO2 + 4C	−3171.56	542.60	6143.27	0.0342	14.49	278.20
	(II) C6H12N16O10 = 8N2 + 6H2O + 4CO + 2C	−2826.56	567.80	5276.24	0.0384	14.24	284.77
6	(I) C7H14N18O12 = 9N2 + 7H2O + 5/2CO2 + 9/2C	−3672.96	628.10	6145.88	0.0341	14.48	278.04
	(II) C7H14N18O12 = 9N2 + 7H2O + 5CO + 2C	−3241.71	659.60	5212.81	0.0387	14.21	284.10
7	(I) C8H16N20O14 = 10N2 + 8H2O + 3CO2 + 5C	−4162.71	713.60	6131.54	0.0341	14.45	277.54
	(II) C8H16N20O14 = 10N2 + 8H2O + 6CO + 2C	−3645.21	751.40	5149.37	0.0389	14.16	283.15
8	(I) C9H18N22O16 = 11N2 + 9H2O + 7/2CO2 + 11/2C	−4673.83	799.10	6147.02	0.0340	14.47	277.76
	(II) C9H18N22O16 = 11N2 + 9H2O + 7CO + 2C	−4070.08	843.20	5125.09	0.0391	14.16	283.10
HMX	(I) C4H8N8O8 = 4N2 + 4H2O + 2CO2 + 2C	−1827.51	342.00	5641.75	0.0338	13.81	265.10 (ref. 28)
	(II) C4H8N8O8 = 4N2 + 4H2O + 4CO	−1482.51	367.20	4335.49	0.0405	13.26

---

Fig. 4 Correlations between n and I_s obtained from two kinds of reactions.

Fig. 5 depicts the variation of C_p, ΔH_C, T_C, N with n for reaction (I). Clearly, there are good linear correlations between C_p, ΔH_C and n (Fig. 5(a)). The correlation equations are ΔH_C = −634.61 − 505.79n (R = −0.99991, SD = 17.78174) and C_p = 130.90 + 82.87n (R = 0.99899, SD = 9.85303). T_C increases rapidly with n from 1 to 2 and changes little when n exceeds 4, while N decreases continuously with n from 1 to 8 (Fig. 5(b)).

Fig. 5 Correlations between C_p, ΔH_C, N, T_C and n for the reaction (I).

3.3 Stability

3.3.1 Energy gap between frontier orbitals. Based on the frontier orbital theory,³⁴ the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) determines the molecular reactivity, such as the ability to absorb light and to react with other species. The molecule with a smaller energy gap is expected to have a higher reactivity and a lower stability in the chemical or photochemical processes with electron transfer or leap.³⁵ Table 4 summarizes the energies of HOMO and LUMO (E_HOMO and E_LUMO), and their energy gaps (E_g). According to the calculated results, the E_gs of the title compounds slightly decrease sequentially from 5.55 eV to 5.02 eV with n from 1 to 8, which shows that incorporation of the –CH₂NNO₂– group will slightly decrease the chemical or photochemical stability.

Table 4 Energies of the frontier orbits and their gaps

	1	2	3	4	5	6	7	8
EHOMO/a.u.	−0.27675	−0.27860	−0.28111	−0.27502	−0.28227	−0.27649	−0.27547	−0.27452
ELUMO/a.u.	−0.07293	−0.08014	−0.08332	−0.08728	−0.09506	−0.09000	−0.08996	−0.08993
Eg/eV	5.55	5.40	5.38	5.11	5.09	5.07	5.05	5.02

---

3.3.2 Stabilization interaction energy. The stabilization interaction energy (E₂) between the donor (i) and acceptor (j) was estimated based on the NBO analysis using the following equation.³⁶

E₂ = q_iF(i,j)²/(E_j − E_i) (11)

where q_i is the donor orbital occupancy; E_i and E_j are diagonal elements (orbital energies) and F(i,j) is the off-diagonal NBO Fock matrix element. To elucidate the effect of the number of –CH₂NNO₂– groups on the stability of the N–N bond in –NNO₂ groups, the delocalization from the lone pair of oxygen (n_O) into σ* antibonding orbital of N–NO₂ (σ^*_N–N) was studied. The corresponding E₂ of n_O → σ^*_N–N are summarized in Table 5. The lowest E₂s of n_O → σ^*_N–N in each compound are 48.75, 48.60, 47.74, 47.58, 45.76, 45.02, 44.68, and 43.88 kcal mol⁻¹, respectively. Since E₂ reflects the delocalization trend of electrons from i to j, and the lower the E₂, the weaker the interaction,³⁷ we can find that the delocalization trend of electrons from n_O to σ^*_N–N decreases with n from 1 to 8. In addition, the lower E₂ corresponds to the longer r_N–N. For example, compound 8 has the lowest E₂ of n_O → σ^*_N–N(4) (see Fig. 1 for the numbering of N–N bonds) and the longest r_N–N(4) (1.401 Å), while compound 1 possesses the highest E₂ of n_O → σ^*_N–N(1) and the shortest r_N–N(1) (1.376 Å). Generally, the larger the bond length is, the lower stability the bond has. This suggests that the stability of the title compounds may slightly decrease with the increasing number of –CH₂NNO₂– groups.

Table 5 Stabilization interaction energy (E₂/kcal mol⁻¹) of n_O → σ^*_N–N

	1	2	3	4	5	6	7	8
nO → π^*N–N(1)	48.75	48.60	47.74	50.84	50.62	46.64	44.88	46.72
nO → π^*N–N(2)		48.64	48.62	47.58	54.3	49.38	46.94	48.54
nO → π^*N–N(3)					45.76	45.02	52.06	47.62
nO → π^*N–N(4)							44.68	43.88

---

3.3.3 Bond dissociation energy. The bond dissociation energy (E_BD) is often used to investigate the thermal stability and pyrolysis mechanism for energetic compounds. Generally, the bond that requires the minimum energy to break is the weakest bond and is most likely to be the trigger bond. Our previous research¹¹ on the pyrolysis mechanism of compound 3 showed that the rupture of N–NO₂ and N–N₂ (via the hydrogen transfer) may happen simultaneously as the initial step of pyrolysis. Since the basis set superposition error has not been considered for the calculation of E_BD, E_BD(N–NO₂) is overestimated. E_BD(N–NO₂) with and without correction of BSSE are 135.62 and 154.83 kJ mol⁻¹,¹¹ respectively. According to the BSSE-corrected E_BD, the pyrolysis may proceed much easier. The BSSE-corrected E_BDs of N–NO₂ for all title compounds were listed in Table 6. Clearly, when n ≤ 3, the pyrolysis is initiated from the rupture of the outside N–N bond, i.e., N–N(1), while when n > 3, it starts from the breaking of the inner N–N bond. The lowest E_BD(N–NO₂) decreases from compound 1 to compound 8, suggesting that incorporating more –CH₂NNO₂– groups into the molecule decrease the stability of the compound. It is noteworthy that all E_BD(N–NO₂) of the title compounds satisfy the stability requirement of energetic compounds (E_BD ≈ 80–120 kJ mol⁻¹ (ref. 38)). To show the variation of the chemical and thermal stability more intuitively, Fig. 6 was plotted. Obviously, the variation trends of E_g, E_BD, and E₂ are the same, i.e., they all decrease with the increase of n.

Table 6 Bond dissociation energy (E_BD/kJ mol⁻¹) of N–NO₂

	1	2	3	4	5	6	7	8
N–N(1)	152.36	140.35	135.62	138.73	135.63	134.84	135.25	144.55
N–N(2)		148.27	145.05	132.08	130.56	128.32	139.26	134.95
N–N(3)					126.34	122.43	126.68	125.70
N–N(4)							119.87	118.83

---

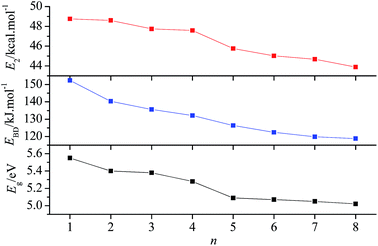Fig. 6 Variation of E_g, E₂, and E_BD with n.

Compared with the synthesized 1–4, compounds 5, 6, 7, and 8 all have good energetic properties, which suggests that they are attractive candidates as the components of propellants. In fact, to be a good energetic additive, it needs to have not only good energetic properties but also good compatibility with other components in the propellants. Since the main purpose of this work is to screen new azido nitramines from the viewpoint of energetic properties and stabilities and to investigate the role of –CH₂NNO₂– groups in the design of the azido nitramines, the compatibility of the screened compounds with binders (such as GAP) will be investigated in the coming works. We will also investigate whether they are helpful for improving the mechanical properties of propellants.

4 Conclusions

Eight aliphatic azido nitramines were studied using the B3LYP/6-31G* method of density functional theory. Their thermodynamic properties, density, detonation pressure, and detonation velocity increase while stability decreases with the increasing number of –CH₂NNO₂– groups. Specific impulse (I_s) varies up and down, and it reaches the maximum value when n = 4 and maintains essentially a constant value when n > 5. All title compounds satisfy the stability requirement of energetic compounds. Compared with the synthesized compounds 1–4, compounds 5–8 are all potential promising plasticizers for propellants. This paper demonstrates how the –CH₂NNO₂– group affects the performance of azido nitramines and provides guidance for the molecular design for this kind of compounds.

Acknowledgements

We gratefully thank the National Natural Science Foundation of China (no. 21403110), the Research Fund for Natural Science Foundation of Jiangsu Province (no. BK20130755), and the “Excellent Plan and Zijin Star” Research Foundation of NUST for their support to this work. J. Yang would like to thank the Innovation Project for Postgraduates in Universities of Jiangsu Province (grant no. KYLX_0346) for partial financial support.

References

1. J. E. Flanagan, M. B. Frankel and E. F. Witucki, US Pat., 4141910, 1979.
2. J. E. Flanagan and M. B. Frankel, US Pat., 4085123, 1978.
3. R. A. Henry and W. P. Norris, US Pat., 4362583, 1982.
4. A. Helmy, Investigation of New Energetic Ingredients for Minimum Signature Propellants, AIAA/SAE/ASME 20th Joint Propulsion Conference, Cincinnati, Ohio, 1984.
5. T. M. Klapoetke, B. Krumm and F. X. Steemann, Propellants, Explos., Pyrotech., 2009, 34, 13–23.
6. J. L. Wang, Y. P. Ji, F. L. Gao, W. Guo and S. T. Ren, Chin. J. Energ. Mater., 2011, 19, 693–696.
7. Y. P. Ji, Y. Lan, P. R. Li, W. Wang, F. Ding and Y. J. Liu, Chin. J. Explos. Propellants, 2008, 31, 44–46.
8. Y. Oyumi, A. Rheingold and T. Brill, J. Phys. Chem., 1987, 91, 920–925.
9. Z. Z. Zhang, B. Z. Wang, Z. C. Shi, Y. P. Ji, Q. Liu and C. H. Zhu, Chin. J. Explos. Propellants, 2003, 26, 3–5.
10. Z. M. Dang, F. Q. Zhao, L. S. Wen, C. M. Yin and D. M. Tu, Journal of Xi'an Jiaotong University, 2000, 34, 88–92.
11. J. Q. Yang, F. Wang, J. Y. Zhang, G. X. Wang and X. D. Gong, J. Mol. Model., 2013, 19, 5367–5376.
12. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
13. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
14. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
15. G. X. Wang, X. D. Gong, Y. Liu, H. C. Du, X. J. Xu and H. M. Xiao, J. Comput. Chem., 2011, 32, 943–952.
16. G. X. Wang, X. D. Gong, Y. Liu, H. C. Du, X. J. Xu and H. M. Xiao, J. Hazard. Mater., 2010, 177, 703–710.
17. J. Q. Yang, G. X. Wang, F. Wang and X. D. Gong, Mol. Simul., 2014, 40, 491–497.
18. J. Q. Yang, H. Yan, X. L. Zhang, G. X. Wang and X. D. Gong, Struct. Chem., 2014, 25, 931–940.
19. W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC press: Taylor and Francis Group LLC, 2012.
20. Y. Liu, X. D. Gong, L. J. Wang, G. X. Wang and H. M. Xiao, J. Phys. Chem. A, 2011, 115, 1754–1762.
21. F. Wang, H. Du, J. Zhang and X. Gong, J. Phys. Chem. A, 2011, 115, 11788–11795.
22. J. Y. Zhang, H. C. Du, F. Wang, X. D. Gong and Y. S. Huang, J. Phys. Chem. A, 2011, 115, 6617–6621.
23. F. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115, 11852–11860.
24. M. J. Kamlet and S. Jacobs, J. Chem. Phys., 1968, 48, 23–35.
25. P. Politzer and J. S. Murray, Cent. Eur. J. Energ. Mater., 2011, 8, 209–220.
26. P. Politzer, J. Murray, M. Grice, P. Sjoberg, G. Olah and D. Squire, Chemistry of Energetic Materials, New York, 1991.
27. G. X. Wang, X. D. Gong, H. C. Du, Y. Liu and H. M. Xiao, J. Phys. Chem. A, 2011, 115, 795–804.
28. Y. F. Liu, H. M. An and R. J. Yang, Chin. J. Explos. Propellants, 2001, 24, 48–49.
29. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 553–556.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman Jr, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.05, Gaussian, Wallingford CT, 2004.
31. M. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. Sikder, B. Gandhe and A. S. Rao, J. Hazard. Mater., 2009, 161, 589–607.
32. D. Badgujar, M. Talawar, S. Asthana and P. Mahulikar, J. Hazard. Mater., 2008, 151, 289–305.
33. X. Zhou and Y. Yu, Sci. Technol. Energ. Mater., 1991, 52, 251–259.
34. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986.
35. H. Dong and F. Zhou, Performance of High Energetic Explosive and Related Compounds, Science Press, Beijing, 1989.
36. F. Weinhold, in Natural Bond Orbital Analysis Programs: NBO 5.0/5.G Program Manual, Madison, Wisconsin, 1996, pp. 1–23.
37. W. Zheng, N.-B. Wong, W.-K. Li and A. Tian, J. Phys. Chem. A, 2004, 108, 11721–11727.
38. H. M. Xiao, X. J. Xu and L. Qiu, Theoretical Design of High Energy Density Materials, Science Press, Beijing, 2008.

---