Harnessing flow and microfluidics to direct inorganic crystal growth and architecture
Michael
Emmanuel
 a,
Dezső
Horváth
a,
Dezső
Horváth
 b,
Ágota
Tóth
b,
Ágota
Tóth
 *c and
Ali
Abou-Hassan
*c and
Ali
Abou-Hassan
 *de
*de
aDepartment of Chemical Sciences, Gombe State University, PMB 127, Tudun Wada Gombe, Gombe State, Nigeria
bDepartment of Applied and Environmental Chemistry, University of Szeged, Szeged, Hungary
cDepartment of Physical Chemistry and Materials Science, University of Szeged, Szeged, Hungary. E-mail: atoth@chem.u-szeged.hu
dSorbonne Université, CNRS UMR 8234, Laboratoire de PHysico-chimie des Électrolytes et Nansoystèmes mes InterfaciauX, PHENIX, F-75252 Paris, France. E-mail: ali.abou_hassan@sorbonne-universite.fr
eInstitut Universitaire de France (IUF), 75231 Paris, France
First published on 21st November 2025
Abstract
This review explores how flows and microfluidics manipulate inorganic crystal nucleation, growth, and self-organization under far-from-equilibrium conditions. Different microfluidic platforms—including continuous-flow, droplet-based, and emerging paper-based devices—are presented for their ability to control mixing, supersaturation, and polymorph selection. Analytical tools, both in situ (optical, spectroscopic, XRD, TEM) and ex situ (SEM, UV-vis, Raman), to provide multi-scale insights into crystallization dynamics are presented. The review highlights how microfluidics enables precise tuning of morphology and kinetics, reproduces biomimetic conditions, and allows crystal self-organization into complex architectures. Finally, current challenges such as clogging are discussed alongside perspectives for integrating advanced characterization techniques and extending microfluidic crystallization strategies to new material systems.
1 Introduction
Supersaturation, S = C − C* (or relative supersaturation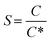 ), where C is the bulk concentration and C* is the solubility, is the universal driving force that governs crystal formation in any system—ionic, molecular, metallic, or covalent.1 At thermodynamic equilibrium, crystals grow when supersaturation slowly relaxes to solubility equilibrium. In poorly mixed systems, local fluctuations in ΔC can lead to unwanted secondary nucleation, producing a mixture of impure crystals rather than well-defined ones.2 However, through manipulation of mass transport (flow and diffusion), S can be tuned to allow the control over the crystal's growth conditions, limiting excessive nucleation and uncontrolled growth. This can lead to crystals with selective dimensions, morphology, and crystallinity. In addition, while diffusion alone is insufficient to sustain growth, the transfer of species and their attachment to the surface of the crystal can be enhanced under flow conditions.3 Indeed, flow enhances mass transport, ensuring a steady solute supply to the crystal surface and facilitating diffusion-limited growth.
), where C is the bulk concentration and C* is the solubility, is the universal driving force that governs crystal formation in any system—ionic, molecular, metallic, or covalent.1 At thermodynamic equilibrium, crystals grow when supersaturation slowly relaxes to solubility equilibrium. In poorly mixed systems, local fluctuations in ΔC can lead to unwanted secondary nucleation, producing a mixture of impure crystals rather than well-defined ones.2 However, through manipulation of mass transport (flow and diffusion), S can be tuned to allow the control over the crystal's growth conditions, limiting excessive nucleation and uncontrolled growth. This can lead to crystals with selective dimensions, morphology, and crystallinity. In addition, while diffusion alone is insufficient to sustain growth, the transfer of species and their attachment to the surface of the crystal can be enhanced under flow conditions.3 Indeed, flow enhances mass transport, ensuring a steady solute supply to the crystal surface and facilitating diffusion-limited growth.
In addition, flow-driven systems can help to control the nucleation and growth of different crystal's polymorphs by pushing the system into states not accessible in static conditions. This is achieved by introducing different mixing conditions, resulting in a different spatial concentration gradient, putting the system away from thermodynamic equilibrium. Consequently, under continuous flow, any system can maintain a permanent supersaturation that can sustain nucleation and growth. Unlike conventional bulk mixing crystallization, where homogeneous stirring often leads to the formation of a mixture of thermodynamically preferred structures, flow-driven conditions can stabilize metastable kinetic phases by adjusting local supersaturation and species transport. For example, in calcium carbonate precipitation, flow-driven processes have been shown to favor the selective formation of calcite over vaterite by influencing the local environment at the nucleation site.4 Similarly, in lithium phosphate crystallization, the flow conditions in a microfluidic setup allowed the control of polycrystalline growth patterns by adjusting flow rates and reagent concentrations. These findings explain how flow can be used as a tool for polymorph selection, offering a pathway to tailor material properties for specific applications.5
As flow-driven systems, small dimension channels, such as microfluidic setups, offer the possibility of recreating geometric boundaries, physicochemical, and hydrodynamic conditions as those encountered in nature.6 This controlled environment is beneficial for some bioinspired or mimetic studies. For example, it was used in the context of kidney stone formation to study the precipitation of calcium oxalate. By carefully adjusting flow rates and reactant concentrations, it was possible to investigate the formation of calcium oxalate monohydrate (COM) versus the dihydrate (COD), showing the direct impact of flow on crystallization outcomes. Such studies not only advance our understanding of pathological mineralization but also provide pathways on how to optimize synthetic crystallization processes.6,7
Flows can be used much more than only for controlling crystal nucleation and growth via local S. It can also play an active role in their self-organization into complex multi-hierarchical superstructures by coupling of mass transport, kinetics, and interactions.8–11 Ordered arrays of crystals, patterns, sculptures, bands of crystallization, and much more complex structures can be created by taking advantage of it. Motivated by the large number of advantages offered by flow driven systems particularly microfluidics in the field of inorganic crystal formation and their self-organization,5,12–14 here we review various recent reports related to this topic, focusing particularly on inorganic ionic crystals, being the widest form of crystals investigated in literature.15,16 While numerous reviews have been written on the role of flow chemistry and microfluidics in controlling the nucleation and growth of inorganic nanomaterials,17–19 to date and to the best of our knowledge, there are no reviews dealing with the manipulation of ionic crystals' growth and their organization using flows and microfluidics. This review explores how flow-driven systems such as microfluidics can be used to tune and manipulate inorganic crystal formation and self-organization under far-from-equilibrium conditions. We first outline fundamental nucleation and growth theories, emphasizing how flow alters mass transport, diffusion, and shear effects. This is followed by a detailed analysis of different microfluidic platforms reported in the literature for controlling mixing, supersaturation, and polymorph selection of inorganic crystal structures. The analytical tools, both in situ and ex situ, available are also presented. We also highlight how microfluidics enables precise tuning of morphology and kinetics, reproducing biomimetic conditions, and reveals pathways of crystal self-organization into complex architectures. Finally, current challenges such as clogging and evaporation control are discussed alongside perspectives for integrating advanced characterization techniques and extending microfluidic crystallization strategies to new material systems.
2 Fundamentals of flow-driven crystal growth
2.1 Nucleation and growth in bulk
Nucleation is a critical step in crystal development and growth. It entails the appearance of a new phase in the solution through the aggregation of atoms, molecules, or particles. Thermodynamic parameters such as supersaturation (S) and interfacial energies dictate the driving forces for nucleation. However, under far-from-equilibrium conditions, these parameters are constantly replenished, leading to the stabilization of metastable phases and complex morphologies. Kinetic factors define the rates of nucleation and growth. In microfluidic systems, confined environments and controlled flow conditions can significantly influence transport and kinetic factors such as diffusion and reaction times.5 Several theories have been developed to describe nucleation, each with its own assumptions and mathematical formulations.1,2,20 Crystal nucleation and growth of inorganic ionic materials from aqueous solution has been reviewed thoroughly in details recently by Gebauer et al.21In classical nucleation theory (CNT), the main assumption is that nucleation occurs through the emergence of small clusters (the so-called nuclei) of the new phase, which consequently grow or shrink depending on the thermodynamic driving forces.1,2,20,22,23 This theory is often viewed as being universal. In CNT, nuclei are always assumed to be spherical and different from the parent phase. Furthermore, the Gibb's free energy change (ΔG) for nucleation has two contributions, bulk and surface terms, given for the formation of a nucleus with radius r as
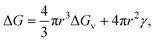 | (1) |
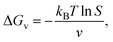 | (2) |
By setting 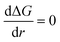 in eqn (1), the size of the critical radius r*, when the nucleus is stable, is determined as
in eqn (1), the size of the critical radius r*, when the nucleus is stable, is determined as
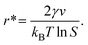 | (3) |
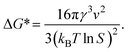 | (4) |
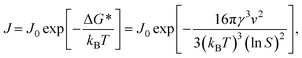 | (5) |
While CNT is mathematically very-well formulated and is consistent with thermodynamic laws, there are some quantitative observations which cannot be interpreted using CNT. For systems where nuclei are not spherical or where intermediate phases exist, the classical nucleation theory does not hold; hence, a non-classical approach must be taken. Among these approaches, the two-step nucleation theory. It describes crystallization as a process that occurs through an intermediate metastable phase rather than a direct transition from the solute to the crystal,27,28 as suggested by CNT. This theory proposes that nucleation occurs in two steps: the formation of a dense liquid-like droplet followed by crystallization within the droplet. The free energy change for the two steps can be written as
| ΔG = ΔGliquid + ΔGcrystal, | (6) |
Another approach is the atomistic nucleation theory. It considers the discrete nature of atoms and molecules (unlike the CNT, where the nucleus is considered as a continuum) and seeks to provide a better understanding of nucleation. This theory is useful in biomineralization, and heterogeneous nucleation, by accounting for molecular interactions, structural fluctuations, and the role of metastable intermediates in crystal formation. Clusters of n molecules are assumed to grow or shrink slowly by the addition or loss of a single molecule, following a series of bimolecular reactions.23,29 The free energy barrier for nucleation in an atomistic framework can be expressed as:
 | (7) |
Crystal growth describing how atoms, ions, or molecules assemble into a crystalline structure can be discussed within several theoretical frameworks.2,30 The Burton–Cabrera–Frank theory, also known as spiral growth theory, developed in 1951,31 describes growth through screw dislocations, where atomic layers continuously grow around a dislocation core, avoiding the need for repeated nucleation. The growth rate v follows
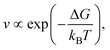 | (8) |
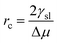 | (9) |
2.2 Far-from-equilibrium crystal growth
A dynamic state maintained by a continuous force such as a flow of mass and energy prevents the system from reaching a thermodynamic equilibrium, therefore, being considered far-from equilibrium. Microfluidic platforms can allow to create a far from-equilibrium conditions. Indeed by precise manipulation of the flow of reactants steep dynamic concentration gradients can be generated. This can lead to dynamic localized supersaturation levels that keep the system away from equilibrium, promoting sometimes nucleation, and influencing crystal growth dynamics that are not easily obtained in batch systems.13,33–35 In addition to flow manipulations, external gradients, such as electric potential and temperature gradients, maintain a far-from-equilibrium state by inducing localized supersaturation spikes and perturbing the local solute distribution.36 The next section will discuss the effects of flow on crystal's growth.2.3 Flow-induced effects
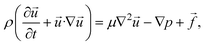 | (10) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is the velocity vector, p is the pressure, is the dynamic viscosity, and f represents body forces (e.g., gravity or electric fields).37–40 The continuity equation41,42 for mass transfer in an incompressible fluid guarantees that the mass flow rate remains constant along the channel. This implies that the volume flow rate is conserved throughout the flow. Since the fluid density doesn't change, a constant volume flow rate also means a constant mass flow rate as in
is the velocity vector, p is the pressure, is the dynamic viscosity, and f represents body forces (e.g., gravity or electric fields).37–40 The continuity equation41,42 for mass transfer in an incompressible fluid guarantees that the mass flow rate remains constant along the channel. This implies that the volume flow rate is conserved throughout the flow. Since the fluid density doesn't change, a constant volume flow rate also means a constant mass flow rate as in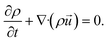 | (11) |
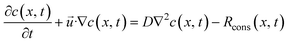 | (12) |
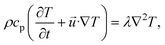 | (13) |
The Péclet number (Pe), defined as the ratio of convective to diffusive transport rates, is a critical dimensionless parameter
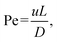 | (14) |
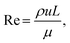 | (15) |
In a Y-shaped microfluidic chip where two reactant solutions are injected, the diffusion of reactants across the dynamical interface of the two incoming streams plays an important role in determining where nucleation occurs. For example, in the work reported by Zhao et al.49 and Ádám et al.,50 the transverse mixing of Ca2+ and CO32− ions in microfluidic cells created localized precipitation zones, wherediffusion controls the spatial distribution of CaCO3 precipitates. Zhao et al.49 reported that lower flow rates and increased pore heterogeneity enhance precipitation by providing more nucleation sites and prolonging reactant interactions. In contrast, higher flow rates lead to narrow precipitation bands as a result of advection-dominated transport, limiting transverse mixing and reaction efficiency. The growth of the calcite and vaterite polymorphs were characterized by Ádám et al.50 The growth of calcite edges illustrated in Fig. 1 shows a square root dependence on time if observed from nucleation.
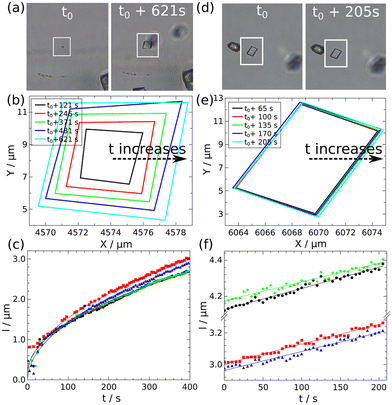 | ||
| Fig. 1 Microscopic images of two calcite crystals at two-time instances (a) and (d), temporal changes in the contour lines of the crystals (b) and (e), and the growth of their sides as a function of time (c) and (f) with t0 denoting the starting time of monitoring.50 Reproduced from ref. 50 with permission from the Royal Society of Chemistry. | ||
Microfluidics can be used to design nonlinear concentration gradients in a controlled manner as introduced by Selimović et al.51 It allows for the generation and monitoring of concentration gradients on a small and reliable scale. To measure the concentration gradient in the channels, a dye solution and pure water are injected through different inlets. The concentration levels are obtained from measurements of the light absorbance through the solution mixture at different positions on the channel based on Beer's law.
A flow-generated concentration gradient can influence the crystal morphology transition. He et al.52 investigated the effects of ion compositions on crystal morphology transitions in a microfluidic chip with a well-defined concentration gradient. They used a serpentine Christmas tree-shaped microfluidic chip configuration as shown in Fig. 2 to study the transition of crystal morphology at different [Ca2+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CO32−] ratios.
[CO32−] ratios.
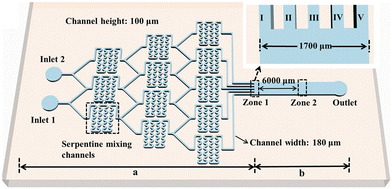 | ||
| Fig. 2 Schematic illustration of the Christmas-tree microfluidic chip with the trunk (b) and the branches (a). The branches with three levels are designed to have a serpentine structure to enhance mixing. Zone 1 is the outlets of the branches, and zone 2 is the detection area for crystal characterization. The inset is the enlarged image of zone 1.52 Reprinted in part with permission from ref. 52. Copyright 2020 American Chemical Society. | ||
In Fig. 3 in zone 1, crystals formed only around outlets II–IV and none at outlets I and V, since the supersaturation gradient generated by the flow is higher around the center of the channel.
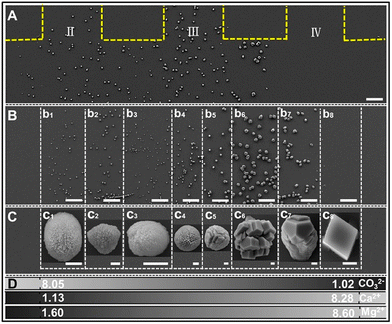 | ||
| Fig. 3 SEM images of crystals in zone 1 (A) and zone 2 (B and C) under the condition ([CaCl2] = [MgCl2] = [Na2CO3] = 10 mM). (D) Concentration distributions of ions in units of mM. The yellow dashed lines indicate the PDMS channel walls. c1–c8 correspond to the typical crystals in b1–b8, respectively. The scale bars represent 50 μm in (A) and (B) and 1 μm in (C). II–IV denotes the outlet channels in zone 1 as defined in Fig. 2.52 Reprinted with permission from ref. 52. Copyright 2020 American Chemical Society. | ||
Supersaturation is a critical driver for nucleation; it critically influences the spatial and temporal variation in the concentration of solutes, especially in microchannels. The concentration gradient can significantly affect crystal nucleation and growth by influencing supersaturation levels. In microchannels, the confined geometry of the channels and the laminar flow conditions create concentration gradients, which can lead to localized regions of high supersaturation, especially at the contact point of two or more solutions.5 These regions support nucleation events because increased supersaturation increases the likelihood of molecular collisions and cluster formation.5,53
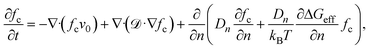 | (16) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is the spatial diffusion coefficient, n is the total number of clusters with Dn cluster size, and ΔGeff is the effective nucleation barrier in the diffusion regime.
is the spatial diffusion coefficient, n is the total number of clusters with Dn cluster size, and ΔGeff is the effective nucleation barrier in the diffusion regime.
The effect of shear flow on nucleation includes altering the transport of clusters and the evolution of their distribution. Shear flow also changes ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , the spatial diffusion coefficients of the molecular cluster57–59 with the shear rate (
, the spatial diffusion coefficients of the molecular cluster57–59 with the shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) given by
) given by
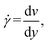 | (17) |
In an experiment where the shear rate can be tuned and maintained for a long period, a microscope can be adapted to the microchannel for on-chip monitoring of the crystals, particles, and aggregates that are formed. The data presented in Fig. 4 demonstrate that shear with a rate between 1 and 10 s−1 decreases solubility and promotes nucleation.60–63 When a shear rate of 10 s−1 was applied for 10 minutes, the number of crystals per image ranged from 13 to 73, while applying a shear rate of 1 s−1 for the same duration resulted in only 0 to 11 crystals per image. The nucleation rate increases monotonically with shear rate, with about 20 times the increase from the lowest shear rate of 1.0 s−1 to the highest shear rate investigated.
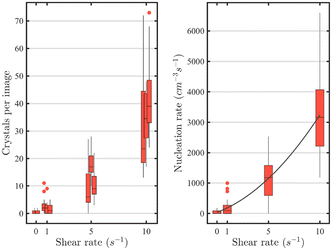 | ||
| Fig. 4 Left: influence of the shear rate on the number of crystals formed per picture. Right: calculations of the nucleation rates for the crystallization in shear flow in function of shear rate. Experiments performed with 25 mg mL−1 lysozyme, 30 mg mL−1 of NaCl at 40 °C.60 Reprinted with permission from ref. 60. Copyright 2020 American Chemical Society. | ||
3 Microfluidic platforms and their roles in controlled flow-driven crystallization
Microfluidic platforms have revolutionized the study of crystallization and synthesis by enabling precise control over mixing, reaction times, and supersaturation levels, thereby facilitating a detailed examination of nucleation and growth mechanisms. In addition it allows easy scaling-up by comparison to batch processes. Typically, three different type of platforms have been employed for microfluidic studies: continuous-flow, droplet-based, and paper-based microfluidics.3.1 Continuous-flow microfluidics
In continuous flow microfluidics, reagents mix by interdiffusion at the dynamical interface. These platforms offer distinct advantages over traditional batch methods, including reduced scale-up risks, enhanced reproducibility, and the ability to maintain constant supersaturation through continuous replenishment of the reacting ions. Continuous-flow microfluidic devices, in particular, have gained attention for their ability to generate a steady-state environment that mimics natural and industrial crystallization processes. This approach for instance, allows researchers to explore the impact of flow dynamics on crystallization kinetics, polymorphism, and morphology.6,49,64–67 Maintaining a constant flow creates the possibility for reproducible control over crystal nucleation and growth.Zhao, et al.49 investigated calcium carbonate precipitation in microfluidic environments where transverse mixing played an important role in regulating crystal formation. Their study demonstrated how flow conditions influence the spatial distribution of precipitates, revealing distinct zones of nucleation and growth. By manipulation of the flow rates and reactant concentrations, they observed variations in crystal size and morphology, which provided insights into the mechanisms of biomineralization.
To investigate the formation of calcium oxalate, a component of kidney stones, a reversible microfluidic system operating by laminar mixing was employed to mimic the biological process while allowing investigation of the interface using several characterization techniques as shown in Fig. 5a.6,68
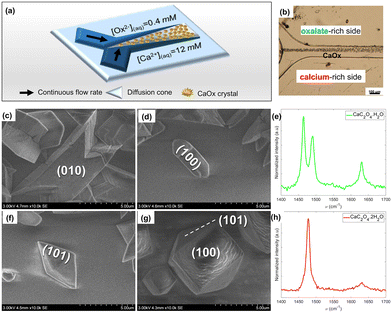 | ||
| Fig. 5 CaOx crystal precipitation under co-laminar mixing of aqueous solutions of oxalate ions (0.4 mM) and calcium ions (12.0 mM). (a) Simplified summary scheme. (b) Light micrograph of the collecting duct-like microchannel. (c–h) SEM micrographs and their associated Raman spectra (λexc = 532 nm): (c) “twinned” monohydrated CaOx (CaC2O4·H2O, COM), (d) “boat-like” COM, (e) COM crystal Raman spectrum, (f) “flatted-bipyramid” dihydrated CaOx (CaC2O4·2H2O, COD), (g) COD, (h) standard COD crystal Raman spectrum.68 Reprinted with permission from ref. 68. Copyright 2020 American Chemical Society. | ||
In the microchannel along the interdiffusion zone, a mixture of the two calcium oxalate polymorphs was formed. Toward the oxalate-rich side (Fig. 5b), the monohydrate calcium oxalate (COM, “twinned” and “boat-like” prismatic crystals, Fig. 5c–e) form dominates, while on the calcium-rich side (Fig. 5b), more dihydrates (COD, flattened tetragonal bipyramids, Fig. 5f–h), form as shown in Fig. 6.
 | ||
| Fig. 6 SEM image of precipitated crystals obtained in the microfluidic device from oxalate and calcium solutions at the dynamic interface. The white inset shows a zoom of the upper part of the precipitate containing twinned crystals. The red inset shows a zoom of the lower part of the precipitate containing mixed twinned and tapered bipyramid crystals.6 Reproduced from ref. 6 with permission from the Royal Society of Chemistry. | ||
Rakotozandriny et al.,68 varied injection rates to control polymorph selection. Injection rates up to 2.0 μL min−1 promote COM nucleation and growth. However, at an injection rate of as low as 0.02 μL min−1, the amount of COM crystals decreased from 96% to 60%, showing that regardless of the injection rates, COM always dominates. These findings were confirmed69 by mapping the spatiotemporal crystal habit distributions in the channel and supported by numerical simulation. The growth rate also depends on the ratio of [Ca2+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Ox2−] injected into the microchannels.7 As [Ca2+]
[Ox2−] injected into the microchannels.7 As [Ca2+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Ox2−] decreases with increasing concentration of Ox2−, an increase in COD growth rate was observed at a constant injection rate. The growth rate of the COM was found to be significantly lower than that of the COD under different supersaturation levels.
[Ox2−] decreases with increasing concentration of Ox2−, an increase in COD growth rate was observed at a constant injection rate. The growth rate of the COM was found to be significantly lower than that of the COD under different supersaturation levels.
Overall, continuous-flow microfluidic systems offer a versatile platform for studying flow-driven crystallization processes. By enabling real-time observation and control of reaction parameters, these platforms help to understand the fundamental mechanisms governing crystal nucleation, growth, and polymorphism.
3.2 Droplet-based microfluidics
Droplet microfluidics is a transformative platform for inorganic crystallization, offering good control over nucleation and growth processes within confined microenvironments, reproducibility and high throughput generation and screening of chemical reactions.70 By generating monodisperse droplets, it is possible to systematically study crystallization dynamics, where reproducibility and efficiency in crystal formation are critical. This technique is particularly advantageous for screening inorganic compounds since controlling parameters such as supersaturation, temperature, and pH are crucial for tailoring crystal properties. In addition, unlike continuous flow, where the walls of the channel may interfere in nucleation and growth of crystals, here the reagents are isolated from the microchannel wall by an inert lubricant film. For example, the use of a droplet-based microfluidic platform71 to investigate the nucleation kinetics of calcium oxalate monohydrate allowed for precise monitoring of pseudopolymorphic transitions and the effects of various inhibitors on crystallization processes.Droplet-based microfluidics are efficient and robust platforms for controlling calcium carbonate crystallization as well, allowing the regulation of crystal polymorphs (calcite, vaterite) and size distributions. The confinement significantly stabilizes the amorphous calcium carbonate (ACC) and alters its crystallization pathway, favoring vaterite as an intermediate phase before calcite formation.72 These findings show the critical role of confined geometry and reduced aggregation in stabilizing metastable phases. Droplets act as isolated microreactors, enabling precise control over supersaturation, phase transitions, and aggregation dynamics. Using droplet microfluidics, researchers could exploit these confinement effects to prolong ACC stability, direct polymorph selection, and study transient intermediates in high-throughput setups. This approach has potential for applications in biomineralization, materials synthesis, and pharmaceutical crystallization, where controlling metastable phases and pathways is important.
The encapsulation of reactants in picoliter droplets within a segmented flow system gives homogeneous nucleation environments free from impurities and wall interactions,73 which are common limitations in bulk or continuous flow methods. The adjustment of reagent concentrations between 4 and 12 mM allowed selective polymorph formation: pure calcite at 4 mM, pure vaterite at 8 mM, and mixed phases were produced at higher concentrations. In contrast, bulk and continuous-flow systems produced inconsistent polymorph mixtures with broader size distributions due to heterogeneous nucleation and residence time variability. A novel platform combining droplet microfluidics with synchrotron-based powder XRD to investigate crystallization dynamics, particularly the identification of effective nucleating agents for calcium carbonate has been presented by Levenstein, et al.74 By encapsulating reactions in segmented water-in-oil droplets within a serpentine microfluidic device, the system offers highly controlled environments that minimize convection, inhomogeneity, and beam damage, while allowing time-resolved tracking of nucleation and polymorph evaluation. They have demonstrated that this platform enables rapid screening of nucleants with high sensitivity, revealing that bioactive glasses significantly reduce induction times due to their surface chemistry and topography.
A droplet microfluidic system integrating three-dimensional (3D) inverse colloidal crystals (ICCs) – a spongious matrix with regularly and densely formed 3D interconnected micropores – was presented by Mashiyama and co-workers. It can achieve high-throughput droplet generation (>100 kHz) with precise size control.75 By engineering PDMS microchannels with sacrificial PMMA microparticles, the system enables tunable droplet formation through adjustable flow rates, fluid viscosities, and pore dimensions, demonstrated via alginate (Fig. 7) and collagen microparticle synthesis. The sacrificial PMMA microparticles are incorporated into the PDMS during microchannel fabrication to create controlled porous structures once the PMMA is removed. These pores act as constrictions that facilitate droplet breakup.
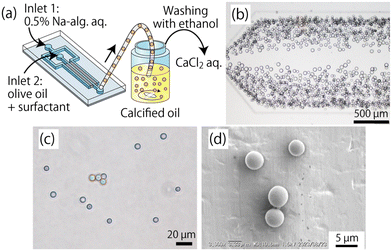 | ||
| Fig. 7 Production of Ca-alginate (Ca-alg) microparticles. (a) Schematic image showing the production process of the Ca-alg particles. (b) Microscopic image showing the droplets of Na-alg. Solution in the observation area. (c) Micrograph showing the obtained Ca-alg particles suspended in a CaCl2 solution. (d) SEM image of the dried Ca-alg microparticles.75 Adapted from ref. 75 with permission from the Royal Society of Chemistry. | ||
This platform holds significant potential for crystallization applications, where monodisperse droplets serve as isolated microreactors for controlled nucleation and growth. The scalability, uniformity, and throughput of the ICC-based design could advance the high-throughput screening of crystallization conditions, biomineralization studies, or protein crystallization by providing consistent environments at unprecedented speeds while minimizing operational instability and channel clogging inherent to conventional systems.
The versatility of droplet microfluidics extends to its compatibility with various analytical techniques, allowing for real-time monitoring and characterization of crystallization processes.
Recent reviews on microfluidic platforms showed that the choice of materials (like PDMS, thermoplastics, or paper) and fabrication methods (such as soft lithography or 3D printing) greatly influence the cost of the device and its performance. These early decisions are crucial, as they shape how well the microfluidic device will function for its intended application.76–79 Reviews focussed on geometry and flow explain how features like channel layout, mixing designs, and reactor structures are chosen to control flow behavior, shear forces, and contact interfaces. These are vital for ensuring reproducible and consistent chemical reactions in continuous microreactor systems.80,81 Application-oriented reviews, such as those in cell-free biology, diagnostics, and organ-on-chip systems, explain the importance of integrating on-chip pumps, valves, and sensor interfaces. They emphasize that achieving modular connectivity is important in moving a prototype toward reliable, automated workflows.76,81–83
4 Analytical tools
Analytical methods employed in microfluidic systems are critical for monitoring, measuring, and interpreting fluid flow behavior, reaction dynamics, and material properties on the microscale. Depending on what is being investigated, these tools can be classified as optical, electrical, spectroscopic, or imaging. In the common scenario of crystallization from solution in microfluidics, ex situ characterization encounters various sampling challenges, as the isolation and drying of the product may lead to phase changes and aggregation.4.1 In situ analytical techniques
In situ techniques enable real-time monitoring of crystallization dynamics within microfluidic systems without disturbing the flow or chemical environment.Integrated XRD and Raman spectroscopy have been employed in flow crystallization environments to enable time-resolved analysis of crystal morphology and growth kinetics. The microfocus XRD setup can detect structures in suspensions as dilute as 0.1 wt% in 10 seconds, while Raman spectroscopy, using dual-laser probes (532 and 785 nm), has identified molecular species in both solid and solution phases, even at low concentrations. These tools can facilitate the study of solute depletion and phase transitions, such as the real-time nucleation of mirabilite (Na2SO4·10H2O).84
In situ optical microscopy5,6,50,69 and time-resolved synchrotron XRD have been employed to characterize crystallization within microfluidic flow systems. This demonstrates the advantages of flow in preventing fouling and enabling reproducible monitoring of crystallization stages, such as the transition from amorphous calcium carbonate to calcite.85
In situ liquid cell transmission electron microscopy (TEM) has been employed to directly visualize the nucleation pathways of calcium carbonate (CaCO3) with unprecedented spatiotemporal resolution. This technique enables real-time observation of particle formation and phase transitions within a flow-driven system, revealing the coexistence of both classical and non-classical nucleation mechanisms. Specifically, it has been identified that CaCO3 could nucleate directly from solution as crystalline phases, or indirectly through amorphous calcium carbonate (ACC) intermediates, which subsequently transform into vaterite or aragonite while maintaining physical contact with the precursor phase. The direct transformation of ACC to calcite was not observed, supporting previous assertions that this pathway is unlikely.86 The study, with the aid of in situ technique has provided an explanation for the crystallization pathways and mechanisms of calcium carbonate precipitation.
The determination of crystal induction time was monitored in a flow reactor using a polarized light microscopic technique with two polarizing filters by Ibis et al.71 This technique enabled the enhancement of contrast between the crystal and the surrounding. This ensures that the background becomes darker, while the formed crystals shine brighter and can be easily imaged. Using this technique, pseudo-polymorphic forms of the calcium oxalate monohydrate.
4.2 Ex situ analytical techniques
Ex situ techniques involve collecting samples from microfluidic systems for subsequent offline analysis, often providing structural, compositional, or morphological data.Scanning electron microscopy (SEM) was performed on microchannel walls post-experimentally to examine surface-bound crystals and confirm the effects of fouling in continuous versus segmented flow. SEM images in Fig. 8) showed dense deposition near T-junctions in continuous flow and more discrete, controllable growth in segmented systems.85 A combination of optical microscopy, SEM coupled with a field emission gun (or SEM-FEG), and SEM coupled with energy-dispersive X-ray (or SEM-EDX) analysis has been used to examine the crystal morphology of calcium oxalate and the composition of the carbonated hydroxyapatite coating obtained from a flow-driven setup. Raman microscopy was used to distinguish the phases of COM and COD, while AAS quantified calcium ion depletion in the effluent to deduce crystallization kinetics.87
 | ||
| Fig. 8 Time-resolved images of the T-junction during continuous flow experiments at (a) ambient and (b) elevated temperatures and segmented flow experiments (c) without a buffer flow and (d) with a buffer flow and a nucleating agent. The last panels display SEM micrographs of the final state of the T-junction obtained ex situ after the respective experiment. Scale bars are 200 μm in optical images and are 50 μm in SEM images.85 Reproduced from ref. 85 with permission from the Royal Society of Chemistry. | ||
The optical properties of CdSe crystals synthesized in a continuous-flow capillary reactor have been analyzed ex situ using UV-visible absorption and photoluminescence (PL) spectroscopy. These techniques are sensitive to the effects of confinement, allowing for indirect estimation of the particle size and distribution. The UV-visible spectra revealed that by varying the temperature at a fixed flow rate, the absorbance and the crystal size increase with increasing temperature. These peak positions were quantitatively correlated with established size–energy relationships, allowing estimation of average particle diameters. Meanwhile, PL spectroscopy confirmed the size-dependent emission behavior, where smaller nanocrystals exhibited emission peaks at shorter wavelengths. The narrowness of both absorption and PL peaks across samples indicated a relatively monodisperse size distribution. Based on established empirical correlations, the spectral features have been used to infer size distributions.88
Combining in situ and ex situ analytical techniques with microfluidic crystallization platforms gives excellent insight into the complex dynamics of nucleation, growth, and phase transformation. Raman microscopy, SAXS, CLSM, and XRD are all in situ methods that give non-invasive real-time information on reaction kinetics, local supersaturation, and structural evolution. This allows for fast feedback and process optimization. Furthermore, ex situ techniques such as SEM, TEM, UV-vis, PL spectroscopy, and AAS enable high resolution morphological, structural, and compositional analysis of the final products. These tools work together to bridge the observation and mechanism, resulting in a comprehensive multiscale understanding of crystallization events in microfluidic environments and laying the foundation for scalable material synthesis.
5 Morphological and kinetic outcomes
Beyond traditional batch reactors, microfluidic platforms enable unprecedented manipulation of chemical reaction's hydrodynamic and physico-chemical conditions. These include mixing dynamics, confinement, and gradient generation such as SS and interfacial phenomena, leading to distinct and tunable morphological and kinetic outcomes. Understanding these relationships is crucial for the design of functional materials.By tuning the mixing conditions of precursor streams within microchannels, an almost instantaneous and homogeneous generation of supersaturation can be achieved. This directly impacts nucleation kinetics. Studies show that higher supersaturation, achieved by faster mixing or higher concentrations, significantly increases nucleation rates. For example, Laval et al.89 demonstrated controlled precipitation of CaCO3 with nucleation rates tuned to orders of magnitude simply by adjusting the flow velocity and the geometry of the mixer. Similarly, Chen et al. quantified the dramatic acceleration of nucleation kinetics for various salts under rapid microfluidic mixing compared to stagnant conditions. This fine control over nucleation onset and density is largely unattainable in batch systems.
A flow-driven microfluidic device described as a “crystal hotel” (shown in Fig. 9(a–d)) was developed by Gong et al.90 to control calcium carbonate crystallization in mimetic natural biomineralization conditions. The confinement within the microchambers patterned with pillars, directed crystal shapes, while flow rates, calcium concentration, and additives (such as Mg2+ and polyacrylic acid, PAA) modulated the frequency of nucleation, growth rates, and crystal structures. Additives significantly influenced crystal morphology and structure—Mg2+ promoted smoother, more isotropic forms and slowed growth, while PAA induced irregular, oligocrystalline growth through front pinning. Surface functionalization with carboxylated self-assembled monolayers further enabled crystal orientation control, showing the capacity of the microfluidic system for tunable and biomimetic crystal engineering.
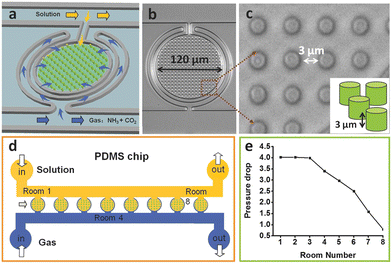 | ||
| Fig. 9 Schematic diagram of the crystal hotel and a magnification of a section with an inset showing the height of the room. a–c) The PDMS device is composed of circular rooms, numbered R1–R8, which are internally patterned with pillars. Each room is surrounded by a circular channel (blue arrow) from which it is separated by a PDMS membrane, which is used to provide gas flow to the room, and a direct feeding channel that supplies solution (yellow arrow). d) The device is positioned on an inverted microscope and crystallization is achieved by supplying CaCl2 solution and vapor released from (NH4)2CO3 powder via two syringe pumps. e) A sevenfold pressure drop in the gas feed occurs across the eight rooms.90 Reproduced under terms of the CC-BY license.90 Copyright 2015, Wiley. | ||
The impact of the influence of the ionic composition on the morphological and kinetic outcomes of calcium carbonate crystallization was studied in a flow-driven microfluidic chip. The device enabled a real-time, high-throughput screening of crystallization behavior under controlled flow conditions, revealing that different combinations of cations and anions significantly impacted both the shape and growth dynamics of the resulting crystals. For instance, Na+ and Cl− supported the formation of typical rhombohedral calcite, while ions like K+, SO42−, and particularly Mg2+ induced irregular, aggregated, or rounded morphologies, with Mg2+ also markedly slowing down nucleation and growth rates due to its inhibitory role. The spatial confinement of the microfluidic setup and well-defined mixing zones allowed reproducible crystallization results to be achieved, mimicking biological mineralization environments. Furthermore, the time-resolved imaging capabilities of the system captured dynamic morphological transitions and growth rates in response to subtle changes in ionic conditions, leading to the construction of a morphology transition map as shown in Fig. 3.52
Microfluidics is also used to reproduce crystallization conditions observed in some organs. In this context, calcium phosphate, another composition of kidney stones that is not commonly investigated was studied by Wei et al.91 They showed that when calcium chloride and sodium phosphate solutions are introduced through separate inlets and rapidly mixed within the channel, calcium phosphate crystals nucleated and deposited within approximately 10 minutes, forming dense black clusters that grew to several micrometers in size and adhere directly to the epithelial cell walls. Confocal Raman microscopy revealed the emergence of a characteristic phosphate peak near 960 cm−1,92 confirming the formation of hydroxyapatite.
The incorporation of calcium oxalate growth within a microfluidic channel coated with carbonated apatite produces distinct morphological variations that explain the role of Randall's plaque in the formation of kidney stones. In an uncoated channel and under flow, most of the calcium oxalate crystals formed are the monohydrate forms exhibiting “boat-like” and “twinned” crystal structures alongside a few dihydrate forms (Fig. 10(a–c)). When the channel was coated with carbonated apatite, a component of Randall's plaque, the number of crystals formed reduced, eliminating the “boat-like” crystals and forming larger dihydrate bipyramidal calcium oxalate crystals and some fewer monohydrate twinned crystals (Fig. 10(d–f)). Extending the reaction time to about 24 h promoted the exclusive formation of the monohydrate form (Fig. 10(g and h)) due to the presence of calcite (known to promote the formation of calcium oxide monohydrate) generated by the dissolution of carbonated apatite.87
 | ||
| Fig. 10 Crystallization of CaOx in the microchannel after infusion of calcium and oxalate solutions. a–c) Scenario A (SA): uncoated channel – a) SEM-FEG image of the glass coverslip at 300 m from the microchannel junction with an optical micrograph of the microchannel in the insert. b and c) SEM images of crystals collected at the end of the channel. d–f) Scenario B (SB): carbonated apatite coated channel – d) SEM-FEG image of the glass coverslip at 300 μm from the microchannel junction with an optical micrograph of the microchannel in the insert and enlarged images of crystals formed in the channel. g) Scenario C (SC): SEM-FEG image of the carbonated apatite coated coverslip at 300 μm from the microchannel junction. The white arrow in all figures indicates the direction of the flow. h) Magnification of the zone delimited by a white circle in image g). The red arrows indicate similar protuberance structures on the surface of carbonated apatite and CaOx crystals. The inset in a and b shows a full view of the microchannel used.87 Reproduced from ref. 87 with permission from the Royal Society of Chemistry. | ||
Flow exerts a decisive influence on crystal polymorphism in microfluidic systems by altering both the chemical composition and morphology of deposits through changes in shear stress and mass transport regimes. It was demonstrated that tuning the flow ratein a glass microchannel downstream of a continuous-flow reactor shifts the product from dendritic, needle-like potassium tert-pentoxide crystals at low Reynolds and Peclet numbers (Re ≈ 1.5, Pe ≈ 17) to densely packed, irregular potassium bromide clusters at higher values (Re ≈ 15, Pe ≈ 160) as shown in the SEM images in Fig. 11.33 The combination of convection, diffusion, particle–surface chemistry, and shear-induced microstructural rearrangement enables flow-mediated control over polymorph selection with applications in designing processes to encourage specific crystal forms.
 | ||
| Fig. 11 Detailed morphology of the clusters. SEM images at increasing magnifications of the dendritic-needle like crystals deposited onto the glass microchannel at Re 1.5 (a–e); SEM images at increasing magnifications of the irregular clusters deposited onto the glass micro-channel walls for Re 15 (d–f).33 Reprinted from ref. 33, with permission from Elsevier. | ||
In addition to the hydrodynamic conditions, additional species that can modulate crystal's formation and their final morphology can be introduced. The effect of green tea on the morphology of calcium oxalate crystals in a flow-driven microfluidic device was investigated. Catechins (polyphenolic compounds) are found in green tea especially epigallocatechin gallate (EGCG) which has an inhibitory effect on CaOx stone formation. When the solutions of calcium and oxalate ions were co-flown into a microchannel in the absence of green tea (Fig. 12(a and b)), a mixture of rare flatted bipyramidal COD crystals and dominant COM crystals of maximum size ≈8 μm and ≈24 μm, respectively, was formed. When green tea was added to either the calcium or oxalate ions, the ensuing product contained predominantly COD with a sparse amount of COM (Fig. 12(c–h)). An overall effect of the presence of the green tea on the morphology and crystal habit was confirmed to be due to the conditions at the interface where green tea is present. It was also shown that the crystallization kinetics were also altered due to the presence of the green tea, through the increase in the induction time.
 | ||
| Fig. 12 SEM micrographs depicting the effect of green tea on CaOx crystallization in the collecting duct-like microchannel device according to experimental conditions: (a and b) CaOx1 (Ox2−(aq) + Ca2+(aq)); (c and d) CaOx2 (Ox2−(GT) + Ca2+(aq)); (e and f) CaOx3 (Ox2−(aq) + Ca2+(GT)); (g and h) CaOx4 (Ox2−(GT) + Ca2+(GT)). In all conditions, solutions are continuously injected in the microfluidic device at Qtot = 2.00 μL min−1 for 2 h.68 Reprinted with permission from ref. 68. Copyright 2020 American Chemical Society. | ||
6 Flow-induced self-organization of inorganic crystals
The formation of intricately sculptured microcrystals that mimic the biomineralization pattern observed in nature is possible with the aid of a flow-driven microfluidics system. Microfluidic systems support the self-organization of complex crystal structures. For example, when CO2 was introduced into a microfluidic channel containing solutions of barium chloride and sodium silicate, microstructures of BaCO3–SiO2 such as corals, vases, petals, and helices were formed. The flow condition created periodic spatiotemporal bands of nucleation, while diffusion-limited growth and local pH gradients directed the morphogenesis of thin-walled architectures. This confined geometry offered by the microfluidic systems allowed crystal fronts to split, curl, and stabilize into patterned structures, with morphology that is fine-tuned by pH-regulated silica passivation at the growth interface.8Chemical gardens are products of self-organization that emerge from a spontaneous precipitation process. When solutions of metal salts (like nickel chloride) and sodium hydroxide are co-flown in a temperature-controlled microfluidic device, thin metal hydroxide membranes Ni(OH)2 form at the liquid–liquid interface (Fig. 13). These membranes grow unidirectionally into the metal salt solution by a diffusion-controlled process. Their internal morphologies evolve into layered bands and dendritic microstructures that appear randomly and self-organize along the reactive boundary. It was reported that despite the expectation of accelerated diffusion at higher temperatures, the effective diffusion coefficient remained nearly independent of temperature between 10–40 °C, suggesting that competing factors such as increased solubility or morphological changes balance out.9,10,13
 | ||
| Fig. 13 (a and b) Micrographs of the precipitate membrane after 4 h growth at 20 °C. Scale bars correspond to 100 μm (a) and 50 μm (b).10 Reprinted in part with permission from ref. 10. Copyright 2021 American Chemical Society. | ||
The erratic growth of chemical gardens, typically observed in batch media, can be eliminated in a flow geometry because of the restriction placed on lateral expansion. This restriction promotes periodic rupture of membrane-bound droplets of cobalt solution, which precipitate to form regularly spaced layers. When cobalt chloride and sodium silicate solutions are injected into a channel, self-organization10,93 of the crystals occurs to form oscillatory budding dynamics that are significantly arranged by the confinement in the channel. The precipitation tubes appeared as ordered membranes,34 separated by valleys rich in cobalt, yielding a hierarchical microstructure. The injection rate of cobalt ions determines the wavelength of these self-organized membranes. At low flow rates, the wavelengths remain nearly constant, but as the injection rate increases, the wavelength decreases. On the other hand, the flow rate of the silicate only enhances confinement and regularity without strongly affecting the wavelength.11
7 Conclusions and outlook
Flow-driven systems such as microfluidics are powerful tools compared to conventional methods for manipulating the formation and organization of inorganic crystals. By creating conditions far from equilibrium, supersaturation, transport, and local environments are controlled. These parameters determine the polymorphism, morphology, and kinetics of crystal formation. Through the combination of in situ and ex situ analytical tools, it is possible to gain a detailed understanding of the phenomena band identify mechanistic aspects. In addition to reproducibility and easy screening of experimental conditions, microfluidic geometries can mimic the confinement, hydrodynamic, and physicochemical boundary conditions observed in natural biomineralization situations, making them a valuable platform for fundamental studies and the design of materials. However, despite significant progress in the use of flow and microfluidics in the field of inorganic crystallization, several challenges remain. Integration of advanced real-time probes, such as light scattering or diffraction techniques,94 optical imaging techniques, and operando spectroscopy, will be necessary77,95,96 for a better characterization of the dynamical chemical environment and for tracking of the crystal's formation. Furthermore, as shown, to date, the majority of inorganic systems studied are ionic crystals. Future work should extend beyond these crystals, including molecular crystals, etc., but also more complex hybrid, multicomponent, and multifunctional systems, where flow-induced conditions could generate new phases and architectures. So far, the main focus has been on controlling the crystalline phase, morphology, and organization of crystals using conventional or bio-inspired approaches; however, how flow can create defects in the crystal and introduce new functionalities has been rarely explored. Furthermore, bio-inspired and paper-based microfluidics offer interesting opportunities for sustainable and inexpensive platforms, with potential applications in the fields of health, energy, and environmental technologies.97,98 Extending microfluidic crystallization to industrial flow rates requires overcoming the issues of clogging, evaporation, and material compatibility.Author contributions
M. E. conceptualisation, data curation, manuscript editing, and initial draft preparation; D. H.: conceptualization, manuscript editing, and initial draft preparation; A. T.: design, conceptualisation, data curation; initial draft preparation, and manuscript editing; A. A.-H. design, data curation, conceptualisation, initial draft preparation, and manuscript editing.Conflicts of interest
There are no conflicts to declare.Data availability
No new data were generated or analysed as part of this highlight.Acknowledgements
A. A.-H. acknowledges funding from Institut Universitaire de France. A. T. and D. H. are grateful for the financial support from the National Research, Development, and Innovation Office (K138844 and TKP2021-NVA-19).References
- Crystallization Technology Handbook, ed. A. Mersmann, CRC Press, 2001 Search PubMed.
- J. W. Mullin, Crystallization, Elsevier, 2001 Search PubMed.
- F. Mura and A. Zaccone, Effects of shear flow on phase nucleation and crystallization, Phys. Rev. E, 2016, 93, 042803 CrossRef PubMed.
- B. Bohner, G. Schuszter, D. Horváth and Á. Tóth, Morphology control by flow-driven self-organizing precipitation, Chem. Phys. Lett., 2015, 631, 114–117 CrossRef.
- M. Emmanuel, D. Horváth and Á. Tóth, Flow-driven crystal growth of lithium phosphate in microchannels, CrystEngComm, 2020, 22, 4887–4893 RSC.
- G. Laffite, C. Leroy, C. Bonhomme, L. Bonhomme-Coury, E. Letavernier, M. Daudon, V. Frochot, J.-P. Haymann, S. Rouzière and I. T. Lucas, et al., Calcium oxalate precipitation by diffusion using laminar microfluidics: toward a biomimetic model of pathological microcalcifications, Lab Chip, 2016, 16, 1157–1160 RSC.
- F. İbiş-Özdemir, R. Smeets, J. Wang, P. Dhand, M. Mohamedhoesein, F. M. Penha, J. Grievink, A. E. van der Heijden, H. J. Kramer and H. B. Eral, Crystal growth of calcium oxalate mono-and dihydrate under laminar flow in microfluidic devices, CrystEngComm, 2025, 27, 337–346 RSC.
- C. N. Kaplan, W. L. Noorduin, L. Li, R. Sadza, L. Folkertsma, J. Aizenberg and L. Mahadevan, Controlled growth and form of precipitating microsculptures, Science, 2017, 355, 1395–1399 CrossRef CAS.
- J. A. Nogueira, B. C. Batista, M. A. Cooper and O. Steinbock, Shape evolution of precipitate membranes in flow systems, J. Phys. Chem. B, 2023, 127, 1471–1478 CrossRef CAS.
- Q. Wang and O. Steinbock, Chemical garden membranes in temperature-controlled microfluidic devices, Langmuir, 2021, 37, 2485–2493 CrossRef CAS PubMed.
- D. Spanoudaki, F. Brau and A. De Wit, Oscillatory budding dynamics of a chemical garden within a co-flow of reactants, Phys. Chem. Chem. Phys., 2021, 23, 1684–1693 RSC.
- D. Kim, C. Olympiou, C. P. McCoy, N. J. Irwin and J. D. Rimer, Time-Resolved Dynamics of Struvite Crystallization: Insights from the Macroscopic to Molecular Scale, Chem. – Eur. J., 2020, 26, 3555–3563 CrossRef CAS PubMed.
- Q. Wang, M. R. Bentley and O. Steinbock, Self-organization of layered inorganic membranes in microfluidic devices, J. Phys. Chem. C, 2017, 121, 14120–14127 CrossRef CAS.
- F. Brau, F. Haudin, S. Thouvenel-Romans, A. De Wit, O. Steinbock, S. S. S. Cardoso and J. H. E. Cartwright, Filament dynamics in confined chemical gardens and in filiform corrosion, Phys. Chem. Chem. Phys., 2018, 20, 784–793 RSC.
- L. Brammer, Developments in inorganic crystal engineering, Chem. Soc. Rev., 2004, 33, 476–489 RSC.
- W. H. Baur, One hundred years of inorganic crystal chemistry–a personal view, Crystallogr. Rev., 2014, 20, 64–116 CrossRef CAS.
- A. Abou-Hassan, O. Sandre and V. Cabuil, Microfluidics in inorganic chemistry, Angew. Chem., Int. Ed., 2010, 49, 6268–6286 CrossRef CAS.
- R. Chauhan, N. Minocha, P. Coliaie, P. G. Singh, A. Korde, M. S. Kelkar, M. Langston, C. Liu, N. Nazemifard, D. Patience, D. Skliar, N. K. Nere and M. R. Singh, Emerging microfluidic platforms for crystallization process development, Chem. Eng. Res. Des., 2023, 197, 908–930 CrossRef CAS.
- J. Jang, W.-S. Kim, T. S. Seo and B. J. Park, Over a decade of progress: Crystallization in microfluidic systems, Chem. Eng. J., 2024, 495, 153657 CrossRef CAS.
- M. Emmanuel, P. Papp, G. Schuszter, Á. Deák, L. Janovák, Á. Tóth and D. Horváth, Nucleation kinetics of lithium phosphate precipitation, CrystEngComm, 2022, 24, 4447–4453 RSC.
- D. Gebauer, J. D. Gale and H. Cölfen, Crystal Nucleation and Growth of Inorganic Ionic Materials from Aqueous Solution: Selected Recent Developments, and Implications, Small, 2022, 18, 2107735 CrossRef CAS PubMed.
- D. Kashchiev, Classical nucleation theory approach to two-step nucleation of crystals, J. Cryst. Growth, 2020, 530, 125300 CrossRef CAS.
- K. F. Kelton and A. L. Greer, Nucleation in Condensed Matter: Applications in Materials and Biology, Elsevier, 2010, vol. 15 Search PubMed.
- C. Devos, T. Van Gerven and S. Kuhn, A review of experimental methods for nucleation rate determination in large-volume batch and microfluidic crystallization, Cryst. Growth Des., 2021, 21, 2541–2565 CrossRef CAS.
- C. Brandel and J. H. ter Horst, Measuring induction times and crystal nucleation rates, Faraday Discuss., 2015, 179, 199–214 RSC.
- N. P. Das, B. Müller, Á. Tóth, D. Horváth and G. Schuszter, Macroscale precipitation kinetics: Towards complex precipitate structure design, Phys. Chem. Chem. Phys., 2018, 20, 19768–19775 RSC.
- P. G. Vekilov, Nucleation, Cryst. Growth Des., 2010, 10, 5007–5019 CrossRef CAS.
- P. R. ten Wolde and D. Frenkel, Enhancement of protein crystal nucleation by critical density fluctuations, Science, 1997, 277, 1975–1978 CrossRef CAS.
- G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Crystal nucleation in liquids: Open questions and future challenges in molecular dynamics simulations, Chem. Rev., 2016, 116, 7078–7116 CrossRef CAS PubMed.
- D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth-Heinemann, 2000 Search PubMed.
- W. K. Burton, N. Cabrera and F. C. Frank, The growth of crystals and the equilibrium structure of their surfaces, Philos. Trans. R. Soc., A, 1951, 243, 299–358 CrossRef.
- J. J. De Yoreo and P. G. Vekilov, Principles of crystal nucleation and growth, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef CAS.
- A. Perazzo, L. Sicignano, G. Tomaiuolo, R. Marotta, R. Andreozzi and S. Guido, Tuning crystal structure in a micro-scale reactive flow, Chem. Eng. Sci., 2019, 207, 581–587 CrossRef CAS.
- B. C. Batista and O. Steinbock, Growing inorganic membranes in microfluidic devices: Chemical gardens reduced to linear walls, J. Phys. Chem. C, 2015, 119, 27045–27052 CrossRef CAS.
- J. A. Nogueira, B. C. Batista, M. A. Cooper and O. Steinbock, Nonclassical Crystallization Causes Dendritic and Band-Like Microscale Patterns in Inorganic Precipitates, Angew. Chem., Int. Ed., 2023, 62, e202306885 CrossRef CAS.
- L. F. Alexander and N. Radacsi, Application of electric fields for controlling crystallization, CrystEngComm, 2019, 21, 5014–5031 RSC.
- J. M. Martel and M. Toner, Inertial focusing in microfluidics, Annu. Rev. Biomed. Eng., 2014, 16, 371–396 CrossRef CAS.
- R. M. Cotta, K. M. Lisboa, M. F. Curi, S. Balabani, J. N. Quaresma, J. S. Perez-Guerrero, E. N. Macêdo and N. S. Amorim, A review of hybrid integral transform solutions in fluid flow problems with heat or mass transfer and under Navier–Stokes equations formulation, Numer. Heat Transfer, Part B, 2019, 76, 60–87 CrossRef.
- J. N. Shadid, R. S. Tuminaro and H. F. Walker, An inexact Newton method for fully coupled solution of the Navier–Stokes equations with heat and mass transport, J. Comput. Phys., 1997, 137, 155–185 CrossRef.
- J.-Y. Jung and H.-Y. Kwak, Fluid flow and heat transfer in microchannels with rectangular cross section, Heat Mass Transfer, 2008, 44, 1041–1049 CrossRef CAS.
- H. Arastoopour, D. Gidaspow and E. Abbasi, Computational transport phenomena of fluid-particle systems, Springer, 2017 Search PubMed.
- P. D. Genick Bar-Meir, Basics of Fluid Mechanics, Potto Project Publishing, 2013, vol. Version (0.3. 0.3 December 5, 2010) Search PubMed.
- S. Vafaei, J. A. Yeager, P. Daluga and B. Scherer, Forced convection nanofluid heat transfer as a function of distance in microchannels, Materials, 2021, 14, 3021 CrossRef CAS PubMed.
- Y. Ding, H. Alias, D. Wen and R. A. Williams, Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids), Int. J. Heat Mass Transfer, 2006, 49, 240–250 CrossRef CAS.
- H. Chen, W. Yang, Y. He, Y. Ding, L. Zhang, C. Tan, A. A. Lapkin and D. V. Bavykin, Heat transfer and flow behaviour of aqueous suspensions of titanate nanotubes (nanofluids), Powder Technol., 2008, 183, 63–72 CrossRef CAS.
- Y. Yu, Y. Liu, X. Wang, D. Oberthür, K. Dierks and C. Betzel, Effects of forced solution flow on lysozyme crystal growth, Cryst. Res. Technol., 2010, 45, 380–386 CrossRef CAS.
- T. Dinh and T. Cubaud, Role of interfacial tension on viscous multiphase flows in coaxial microfluidic channels, Langmuir, 2021, 37, 7420–7429 CrossRef CAS PubMed.
- H. Ender and J. Kierfeld, From diffusive mass transfer in Stokes flow to low Reynolds number Marangoni boats, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 1–25 CrossRef.
- C. Zhao, Y. Xiao, J. Chu, R. Hu, H. Liu, X. He, Y. Liu and X. Jiang, Microfluidic experiments of biological CaCO3 precipitation in transverse mixing reactive environments, Acta Geotech., 2023, 18, 5299–5318 CrossRef.
- R. M. Ádám, P. Papp, D. Horváth and Á. Tóth, Diffusion-driven growth of calcium carbonate polymorphs in microchannels, RSC Adv., 2024, 14, 39618–39624 RSC.
- S. Selimović, W. Y. Sim, S. B. Kim, Y. H. Jang, W. G. Lee, M. Khabiry, H. Bae, S. Jambovane, J. W. Hong and A. Khademhosseini, Generating nonlinear concentration gradients in microfluidic devices for cell studies, Anal. Chem., 2011, 83, 2020–2028 CrossRef.
- H. He, L. Chen, Z. Wang, L. Zhang, T. Ge, X. Xiang, S. Wang, Y. Huang and S. Li, Screening the Ion compositions on crystal morphology transitions by a microfluidic chip with a well-defined concentration gradient, Cryst. Growth Des., 2020, 20, 6877–6887 CrossRef CAS.
- L. Li, J. R. Sanchez, F. Kohler, A. Røyne and D. K. Dysthe, Microfluidic control of nucleation and growth of CaCO3, Cryst. Growth Des., 2018, 18, 4528–4535 CrossRef CAS.
- C. Yang, J. Zhang, D. L. Koch and X. Yin, Mass/heat transfer from a neutrally buoyant sphere in simple shear flow at finite Reynolds and Peclet numbers, AIChE J., 2011, 57, 1419–1433 CrossRef CAS.
- M. H. Duits, S. Ghosh and F. Mugele, Measuring advection and diffusion of colloids in shear flow, Langmuir, 2015, 31, 5689–5700 CrossRef CAS.
- D. Reguera and J. Rubı, Homogeneous nucleation in inhomogeneous media. I. Nucleation in a temperature gradient, J. Chem. Phys., 2003, 119, 9877–9887 CrossRef CAS.
- D. Reguera and J. Rubı, Homogeneous nucleation in inhomogeneous media. II. Nucleation in a shear flow, J. Chem. Phys., 2003, 119, 9888–9893 CrossRef CAS.
- I. Śliwa and A. V. Zakharov, Shear-driven mechanism of temperature gradient formation in microfluidic nematic devices: theory and numerical studies, Symmetry, 2021, 13, 1533 CrossRef.
- I. Śliwa, P. V. Maslennikov and A. V. Zakharov, Two shear driven flow regimes in microfluidic nematic devices: Tumbling and laminar, J. Mol. Liq., 2021, 340, 117205 CrossRef.
- S. Stroobants, M. Callewaert, M. Krzek, S. Chinnu, P. Gelin, I. Ziemecka, J. F. Lutsko, W. De Malsche and D. Maes, Influence of shear on protein crystallization under constant shear conditions, Cryst. Growth Des., 2020, 20, 1876–1883 CrossRef CAS.
- A. Penkova, W. Pan, F. Hodjaoglu and P. G. Vekilov, Nucleation of protein crystals under the influence of solution shear flow, Ann. N. Y. Acad. Sci., 2006, 1077, 214–231 CrossRef CAS PubMed.
- S. Jiang and J. H. ter Horst, Crystal nucleation rates from probability distributions of induction times, Cryst. Growth Des., 2011, 11, 256–261 CrossRef CAS.
- R. Murai, H. Y. Yoshikawa, H. Kawahara, S. Maki, S. Sugiyama, T. Kitatani, H. Adachi, K. Takano, H. Matsumura and S. Murakami, et al., Effect of solution flow produced by rotary shaker on protein crystallization, J. Cryst. Growth, 2008, 310, 2168–2172 CrossRef CAS.
- D. Che, X. Zhu, P. Liu, Y. Duan, H. Wang, Q. Zhang and Y. Li, A facile aqueous strategy for the synthesis of high-brightness LaPO4: Eu nanocrystals via controlling the nucleation and growth process, J. Lumin., 2014, 153, 369–374 CrossRef CAS.
- P. Coliaie, M. S. Kelkar, N. K. Nere and M. R. Singh, Continuous-flow, well-mixed, microfluidic crystallization device for screening of polymorphs, morphology, and crystallization kinetics at controlled supersaturation, Lab Chip, 2019, 19, 2373–2382 RSC.
- Y. Zeng, J. Cao, Z. Wang, J. Guo, Q. Zhou and J. Lu, Insights into the confined crystallization in microfluidics of amorphous calcium carbonate, Cryst. Growth Des., 2018, 18, 6538–6546 CrossRef CAS.
- M. Jiang, Z. Zhu, E. Jimenez, C. D. Papageorgiou, J. Waetzig, A. Hardy, M. Langston and R. D. Braatz, Continuous-flow tubular crystallization in slugs spontaneously induced by hydrodynamics, Cryst. Growth Des., 2014, 14, 851–860 CrossRef CAS.
- K. Rakotozandriny, S. Bourg, P. Papp, Á. Tóth, D. Horváth, I. T. Lucas, F. Babonneau, C. Bonhomme and A. Abou-Hassan, Investigating CaoX crystal formation in the absence and presence of polyphenols under microfluidic conditions in relation with nephrolithiasis, Cryst. Growth Des., 2020, 20, 7683–7693 CrossRef CAS.
- P. Papp, S. Bourg, M. Emmanuel, Á. Tóth, A. Abou-Hassan and D. Horváth, Spatiotemporal distribution of calcium oxalate crystals in a microchannel, Cryst. Growth Des., 2023, 23, 8116–8123 CrossRef CAS.
- B. Zheng, J. D. Tice, L. S. Roach and R. F. Ismagilov, A droplet-based, composite PDMS/glass capillary microfluidic system for evaluating protein crystallization conditions by microbatch and vapor-diffusion methods with on-chip X-ray diffraction, Angew. Chem., Int. Ed., 2004, 43, 2508–2511 CrossRef CAS.
- F. Ibis, T. W. Yu, F. M. Penha, D. Ganguly, M. A. Nuhu, A. E. Van Der Heijden, H. J. Kramer and H. B. Eral, Nucleation kinetics of calcium oxalate monohydrate as a function of pH, magnesium, and osteopontin concentration quantified with droplet microfluidics, Biomicrofluidics, 2021, 15, 064103 CrossRef CAS PubMed.
- Y. Wang, M. Zeng, F. C. Meldrum and H. K. Christenson, Using confinement to study the crystallization pathway of calcium carbonate, Cryst. Growth Des., 2017, 17, 6787–6792 CrossRef CAS.
- A. Yashina, F. Meldrum and A. Demello, Calcium carbonate polymorph control using droplet-based microfluidics, Biomicrofluidics, 2012, 6, 022001 CrossRef.
- M. A. Levenstein, C. Anduix-Canto, Y.-Y. Kim, M. A. Holden, C. González Niño, D. C. Green, S. E. Foster, A. N. Kulak, L. Govada and N. E. Chayen, et al., Droplet microfluidics xrd identifies effective nucleating agents for calcium carbonate, Adv. Funct. Mater., 2019, 29, 1808172 CrossRef.
- S. Mashiyama, R. Hemmi, T. Sato, A. Kato, T. Taniguchi and M. Yamada, Pushing the limits of microfluidic droplet production efficiency: engineering microchannels with seamlessly implemented 3D inverse colloidal crystals, Lab Chip, 2024, 24, 171–181 RSC.
- A.-G. Niculescu, C. Chircov, A. C. Bîrcă and A. M. Grumezescu, Fabrication and applications of microfluidic devices: A review, Int. J. Mol. Sci., 2021, 22, 2011 CrossRef CAS PubMed.
- A. Abou-Hassan, O. Sandre and V. Cabuil, in Microfluidic Devices in Nanotechnology: Applications, John Wiley & Sons, 2010, pp. 323–360 Search PubMed.
- J. Zhang, C. Gong, X. Zeng and J. Xie, Continuous flow chemistry: New strategies for preparative inorganic chemistry, Coord. Chem. Rev., 2016, 324, 39–53 CrossRef CAS.
- M. Ildefonso, N. Candoni and S. Veesler, A cheap, easy microfluidic crystallization device ensuring universal solvent compatibility, Org. Process Res. Dev., 2012, 16, 556–560 CrossRef CAS.
- A.-G. Niculescu, D. E. Mihaiescu and A. M. Grumezescu, A review of microfluidic experimental designs for nanoparticle synthesis, Int. J. Mol. Sci., 2022, 23, 8293 CrossRef CAS PubMed.
- N. Candoni, R. Grossier, M. Lagaize and S. Veesler, Advances in the use of microfluidics to study crystallization fundamentals, Annu. Rev. Chem. Biomol. Eng., 2019, 10, 59–83 CrossRef.
- A. K. Baranwal and S. J. Maerkl, A comprehensive review of Microfluidic approaches in cell-free synthetic biology, Front. Synth. Biol, 2024, 2, 1397533 CrossRef.
- M. Ildefonso, E. Revalor, P. Punniam, J.-B. Salmon, N. Candoni and S. Veesler, Nucleation and polymorphism explored via an easy-to-use microfluidic tool, J. Cryst. Growth, 2012, 342, 9–12 CrossRef CAS.
- T. Turner, C. O'Shaughnessy, X. He, M. Levenstein, L. Hunter, J. Wojciechowski, H. Bristowe, R. Stone, C. Wilson and A. Florence, et al., Flow-Xl: a new facility for the analysis of crystallization in flow systems, J. Appl. Crystallogr., 2024, 57, 1299–1310 CrossRef CAS.
- M. A. Levenstein, Y.-Y. Kim, L. Hunter, C. Anduix-Canto, C. G. Niño, S. J. Day, S. Li, W. J. Marchant, P. A. Lee and C. C. Tang, et al., Evaluation of microflow configurations for scale inhibition and serial X-ray diffraction analysis of crystallization processes, Lab Chip, 2020, 20, 2954–2964 RSC.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways, Science, 2014, 345, 1158–1162 CrossRef CAS.
- S. Bourg, K. Rakotozandriny, I. T. Lucas, E. Letavernier, C. Bonhomme, F. Babonneau and A. Abou-Hassan, Confining calcium oxalate crystal growth in a carbonated apatite-coated microfluidic channel to better understand the role of Randall's plaque in kidney stone formation, Lab Chip, 2024, 24, 2017–2024 RSC.
- B. K. Yen, N. E. Stott, K. F. Jensen and M. G. Bawendi, A continuous-flow microcapillary reactor for the preparation of a size series of CdSe nanocrystals, Adv. Mater., 2003, 15, 1858–1862 CrossRef CAS.
- P. Laval, J.-B. Salmon and M. Joanicot, A microfluidic device for investigating crystal nucleation kinetics, J. Cryst. Growth, 2007, 303, 622–628 CrossRef CAS.
- X. Gong, Y.-W. Wang, J. Ihli, Y.-Y. Kim, S. Li, R. Walshaw, L. Chen and F. C. Meldrum, The crystal hotel: a microfluidic approach to biomimetic crystallization, Adv. Mater., 2015, 27, 7395 CrossRef CAS PubMed.
- Z. Wei, P. K. Amponsah, M. Al-Shatti, Z. Nie and B. C. Bandyopadhyay, Engineering of polarized tubular structures in a microfluidic device to study calcium phosphate stone formation, Lab Chip, 2012, 12, 4037–4040 RSC.
- P. Timchenko, E. Timchenko, E. Pisareva, M. Y. Vlasov, L. Volova, O. Frolov and A. Kalimullina, Experimental studies of hydroxyapatite by Raman spectroscopy, J. Opt. Technol., 2018, 85, 130–135 CrossRef CAS.
- Q. Wang, M. R. Bentley and O. Steinbock, Self-Organization of Layered Inorganic Membranes in Microfluidic Devices, J. Phys. Chem. C, 2017, 121, 14120–14127 CrossRef CAS.
- M. A. Levenstein, C. Chevallard, F. Malloggi, F. Testard and O. Taché, Micro- and milli-fluidic sample environments for in situ X-ray analysis in the chemical and materials sciences, Lab Chip, 2025, 25, 1169–1227 RSC.
- J. Polte, R. Erler, A. F. Thünemann, F. Emmerling and R. Kraehnert, SAXS in combination with a free liquid jet for improved time-resolved in situ studies of the nucleation and growth of nanoparticles, Chem. Commun., 2010, 46, 9209–9211 RSC.
- A. Abou-Hassan, O. Sandre, S. Neveu and V. Cabuil, Synthesis of goethite by separation of the nucleation and growth processes of ferrihydrite nanoparticles using microfluidics, Angew. Chem., 2009, 121, 2378–2381 CrossRef.
- M. Tarara, P. D. Tzanavaras and G. Z. Tsogas, Development of a paper-based analytical method for the colorimetric determination of calcium in saliva samples, Sensors, 2022, 23, 198 CrossRef PubMed.
- L.-L. Shen, G.-R. Zhang and B. J. Etzold, Paper-based microfluidics for electrochemical applications, ChemElectroChem, 2020, 7, 10–30 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |
