Diffusion-assisted synthesis of crystalline materials in rigid gels
Norbert
Német
ab,
Gábor
Holló
c,
Sung Ho
Yang
 d,
Bilge
Baytekin
d,
Bilge
Baytekin
 ef,
Gábor
Schuszter
ef,
Gábor
Schuszter
 g,
István
Szalai
g,
István
Szalai
 h,
Federico
Rossi
h,
Federico
Rossi
 i and
István
Lagzi
i and
István
Lagzi
 *aj
*aj
aDepartment of Physics, Institute of Physics, Budapest University of Technology and Economics, H-1111 Budapest, Hungary. E-mail: lagzi.istvan.laszlo@ttk.bme.hu
bDepartment of Organic Chemistry and Technology, Budapest University of Technology and Economics, H-1111 Budapest, Hungary
cDepartment of Fundamental Microbiology, University of Lausanne, 1015 Lausanne, Switzerland
dDepartment of Chemistry Education, Korea National University of Education (KNUE), Cheongju 28173, Republic of Korea
eDepartment of Chemistry, Bilkent University, 06800, Ankara, Turkey
fUNAM, Bilkent University, 06800, Ankara, Turkey
gDepartment of Physical Chemistry and Materials Science, University of Szeged, H-6720 Szeged, Hungary
hLaboratory of Adaptive and Autonomic Materials, Institute of Chemistry, Eötvös Loránd University, H-1117 Budapest, Hungary
iDepartment of Physical Sciences, Earth and Environment, University of Siena, 53100 Siena, Italy
jHUN-REN–BME, Condensed Matter Physics Research Group, Budapest University of Technology and Economics, H-1111 Budapest, Hungary
First published on 18th November 2025
Abstract
This study explores diffusion-assisted synthesis in rigid gel matrices, utilizing reaction–diffusion processes to fabricate crystalline materials with controlled size and morphology. The presented techniques focus on synthesizing various classes of materials, such as inorganic precipitates, metal–organic frameworks, and gold nanoparticles, using gel column and flow-through gel reactors, as well as reactive wet stamping. In these setups, the reagents are initially spatially separated, and one of the reagents diffuses into gels containing the other reagent, producing crystals with sizes that increase linearly from the gel interface. The gel matrix prevents sedimentation and aggregation, allowing the undisturbed growth of larger crystals. Additionally, the experimental setup provides a spatiotemporal control over the mass flux of the reagents, thus controlling the rates of nucleation and crystal growth. Theoretical models can explain the linear dependence of the crystal size and attribute larger crystal sizes to regions of lower supersaturation, which favor growth over nucleation. We also discuss advanced methods, including orthogonal diffusion and electric field-assisted synthesis, that can enhance spatial control and crystal morphology. Compared to traditional bulk wet synthesis, diffusion-assisted methods offer exceptional control over crystal size, shape, and dispersity. Prospects include scaling up macroscopic crystal synthesis, refining reactor designs for 2D and 3D configurations, and exploring applications in catalysis, biomedicine, and environmental remediation.
1 Introduction
Reaction–diffusion (RD) processes describe the fundamental mechanisms by which chemical species interact through reactions and the molecular diffusion of these species, leading to the spontaneous emergence of complex patterns over time and space.1 These processes drive diverse phenomena in chemistry, biology, and physics, which are crucial in symmetry breaking from initially homogeneous conditions (Fig. 1).2–4 While pattern formation is the most striking manifestation of RD dynamics, these also drive essential processes such as signal transduction in biological systems,5–7 cellular self-regulation,8,9 the organization of spatial networks,10–14 and the structuring of minerals.15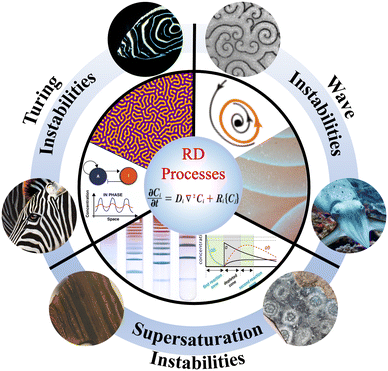 | ||
| Fig. 1 Examples of pattern formation generated by RD processes. These include laboratory experiments and the corresponding pattern found in natural systems. Wave instabilities might generate traveling waves, such as those found in the Belousov–Zhabotinsky reaction, reproduced from ref. 28 with permission from Elsevier, copyright 2009, and described by a limit cycle in a multidimensional phase space, reproduced from ref. 29, licensed under the Creative Commons Attribution License. RD waves can be commonly found in slime molds, and cuttlefish signaling, reproduced from ref. 30, licensed under the Creative Commons Attribution License. Turing instabilities stem from an activation–inhibition mechanism between two species with different diffusivities, reproduced from ref. 31 with permission from Elsevier, copyright 2012, and may generate labyrinthine patterns, reminiscent of those found in the skin of many mammals and fish. Supersaturation instabilities are typical of Liesegang phenomena, reproduced from ref. 32, licensed under the Creative Commons Attribution License. They are relevant for understanding mineral patterns such as banded iron formation (Precambrian, South Africa, courtesy of the Earth Sciences Museum, – SIMUS – University of Siena, Italy) and diorites (picture: Emmanuel Douzery, Wikipedia). | ||
Mathematically, RD systems are governed by a set of coupled second-order partial differential equations that describe the spatiotemporal evolution of the concentration of the chemical species. The general form of the RD equations is the following:
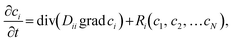 | (1) |
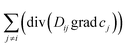 , describing the transport of species ith induced by the concentration gradients of species jth, when Dij are large enough, even reversible linear systems may evolve in spatial pattering.16 Cross-diffusion and differential diffusion may also produce more complex behaviors when generating advective motions.17–19
, describing the transport of species ith induced by the concentration gradients of species jth, when Dij are large enough, even reversible linear systems may evolve in spatial pattering.16 Cross-diffusion and differential diffusion may also produce more complex behaviors when generating advective motions.17–19
Depending on the form of Ri and the ratio between the diffusivities Dii, RD systems may undergo different dynamic instabilities, and small perturbations of the initial homogeneous state develop into either stationary or spatiotemporal patterns. Stationary patterns are generated by supercritical Turing or Turing-like instabilities, where differences in diffusion rates between interacting species, typically an activator and an inhibitor, result in stripes, hexagons, or labyrinthine structures.20,21 First predicted by Turing in his seminal paper “The Chemical Basis of Morphogenesis”,22 these stationary patterns were experimentally found in the chlorite–iodide–malonic acid (CIMA) reaction in the early 1990s23,24 and subsequently discovered in other nonlinear chemical systems,25,26 leading to the development of a systematic approach for their rational design.27
Moving patterns, such as waves and spirals, emerge in RD systems when they undergo subcritical instabilities and exhibit excitability (e.g., Belousov–Zhabotinsky reaction).20,21,33 In excitable systems, small perturbations to the initial steady state typically decay without significant impact. However, when a disturbance exceeds a critical threshold, it triggers a pronounced, transient response, in which the system undergoes a large excursion away from equilibrium. This dynamic evolution continues until the system relaxes to its original stable state.
Another class of RD structures is the periodic precipitation (PP) or Liesegang phenomenon, which arises from a precipitation or supersaturation instability.34–36 In a typical Liesegang system, one reactant diffuses into a gelled medium containing another reactant, and when local supersaturation exceeds a threshold, periodic precipitation bands form. These patterns form through nucleation and growth driven by supersaturation during the diffusion of reacting chemical compounds.
RD processes have found an increasing interest in technological applications, such as in micro- and nanotechnology, offering pathways for controlled self-assembly and pattern formation.37–39 In microfabrication, RD principles are employed to create spatially ordered structures useful for developing sensors, microfluidic devices, and photonic crystals. By manipulating diffusion gradients and reaction kinetics, it is possible to engineer highly organized structures at the microscopic scale. Similarly, integrating RD dynamics with self-assembling matrices such as micelles and lipid bilayers in biomimetic systems allows for synthesizing dynamic structures that emulate biological complexity.21,40–42 RD processes extend into ecological systems, explaining spatial organization in ecosystems, such as vegetation patterns in arid landscapes and spatial predator–prey distributions.2,43
This highlight article presents recent advances in the material design and synthesis of crystalline materials utilizing RD processes in rigid gel matrices.
2 Results
2.1. Synthesis of inorganic precipitates, MOFs, and gold nanoparticles
Since the discovery of periodic precipitation in 1896,44 studies have been devoted to exploring and investigating new precipitation systems, ranging from inorganic reactions to the interaction of oppositely charged nanoparticles.45 The most common way is to perform these experiments in a test tube (quasi-1D collinear setup), where initially one of the reagents is homogeneously distributed in a gel (called the inner electrolyte), and after the gelation process, the solution of the other reagents (called the outer electrolyte) is placed on top of the gel column.36 Another widely used setup is the wet stamping (WETS) technique, in which a thin gelatin film containing the inner electrolyte is first prepared on a substrate from a hot liquid gel solution using a spin coater.46–50 After gelation, the outer electrolyte is delivered to the film from an agarose stamp with various features. In all these experiments, the concentration of the outer electrolyte is one to two orders of magnitude greater than that of the inner electrolyte. This condition ensures that nucleation and crystal growth are governed by the diffusive flux of the outer (invading) electrolyte. Periodic precipitation is the backbone of self-organization and pattern formation in RD systems. However, it was only in the last decade that studies employed diffusion-assisted nucleation and growth in material design and synthesis.The first study dealing with material synthesis was the formation of silver dichromate nano- and microparticles utilizing the WETS technique (Fig. 2a).51 Silver ions were delivered from an agarose stamp into the gelatin gel, in which dichromate ions were homogeneously distributed. The process yielded well-separated precipitation rings containing silver dichromate particles (Fig. 2b).
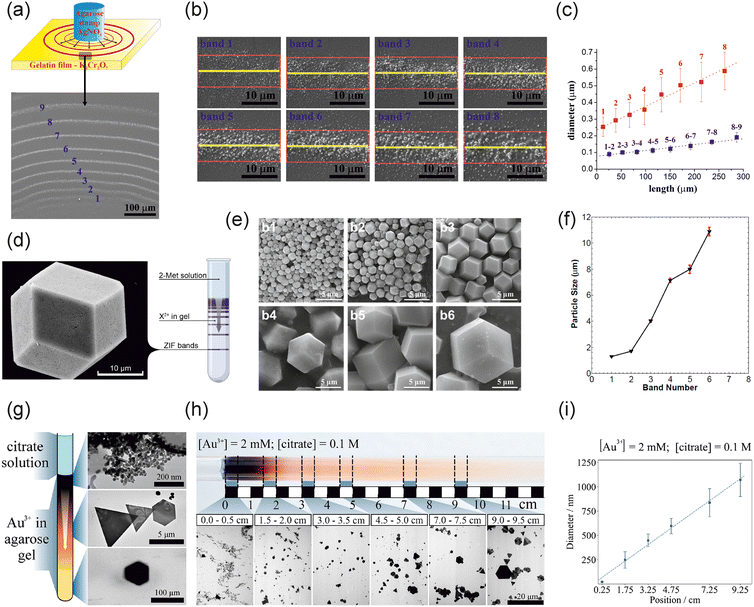 | ||
| Fig. 2 Synthesis of crystalline materials in gels. (a) Experimental setup and formation of precipitation rings. (b) Scanning electron micrographs of the precipitation rings. (c) Dependence of the average size of formed particles in precipitation rings (red symbols) and interband regions (blue symbols) on the distance measured from the gel stamp containing silver ions, reprinted from ref. 51 with permission from American Chemical Society, copyright 2015. (d) Experimental setup for the synthesis of MOFs in a gel, reproduced from ref. 52, licensed under the Creative Commons Attribution License. (e) Scanning electron micrographs of the crystals extracted from various gel segments, and (f) their size variation along the gel column, reprinted from ref. 53 with permission from American Chemical Society, copyright 2018. (g) Experimental setup for the synthesis of AuNPs in a gel. (h) Transmission electron micrographs of the generated AuNPs extracted from various gel segments. (i) Dependence of the average size of formed AuNPs on the distance measured from the liquid–gel interface, reproduced from ref. 77, licensed under the Creative Commons Attribution License. | ||
The striking observation was that the average particle size increased linearly with the distance measured from the junction point of electrolytes (Fig. 2c). The dispersity of particles in each ring increased as well.
This linear dependence of the particle size was further proved in a new chemical system: the metal–organic frameworks (MOFs).52–55 MOFs are porous polymers comprising metal cations coordinating to organic linker molecules.56 Due to their unique crystalline structures, MOFs have been utilized in various applications, including catalysis, chromatography, gas storage, purification, and electronics.57–65 In the synthesis, cations (Zn2+ and Co2+) were distributed in a rigid agarose gel prepared using water and N,N-dimethylformamide (DMF, Fig. 2d).53 The role of DMF was to facilitate the deprotonation of linker molecules (2-methylimidazole, MeIm). Once the precipitation was completed, the gel column was divided into equidistant zones, and the crystals were extracted from them using DMF. The analysis revealed the formation of zeolitic imidazolate frameworks-8 and 67 (ZIF-8 and ZIF-67), with a linearly increasing size from the liquid–gel interface (Fig. 2e and f). Using diffusion-assisted synthesis, the average crystal size ranged from 100 nm to 55 μm.
The third chemical system in which the RD setup was used is the synthesis of gold nanoparticles (AuNPs). AuNPs have been applied in various fields, including catalysis, biomedicine, electronics, optics, sensing, environmental applications, and cosmetics.66–76 In a typical experiment, the rigid agarose gel column was prepared in test tubes containing a prescribed concentration of gold salt. After the gelation, a citrate solution was poured on top of the hydrogel column (Fig. 2g).77 The citrate concentration was greater than that of the gold salt because an excess of citrate is needed to synthesize AuNPs. Also, it ensured the continuous diffusion flux of citrate into the gel. Afterwards, the generated AuNPs were extracted from the gel. Fig. 2h shows AuNPs at various distances from the liquid–gel interface. Near the interface, only spherical particles of the size of ∼20–30 nm formed. Further from the interface, the size of AuNPs became greater, and nanoplates (triangles, truncated triangles, and hexagons) appeared in the samples with a maximum size of ∼80 μm. With an increasing distance from the liquid–gel interface, the probability of the formation of nanoplates with various shapes increased. Similarly to the previous systems, the size of particles scaled linearly with the distance measured from the interface (Fig. 2i).
Although the previously presented systems are chemically different, they share the same common characteristics. Namely, in all cases, crystallization is driven by nucleation and growth. The RD process is conducted at room temperature and generates larger crystals than conventional methods because small hydrated ions can diffuse in the gel matrix. However, this matrix supports bigger particles, avoiding their sedimentation and aggregation due to the attractive van der Waals forces.78 Diffusion allows slow, controlled changes in concentration, leading to steady crystal growth and producing crystals with fewer internal stresses, cracks, or inclusions.
2.2. Theoretical consideration
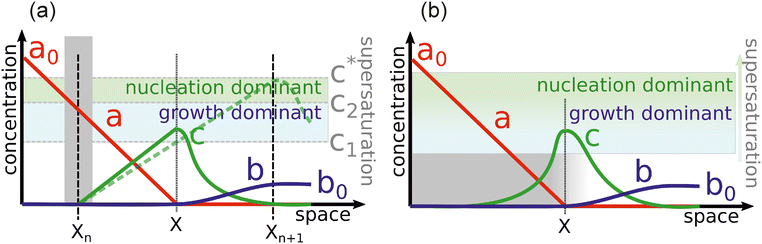
In this section, we discuss particle size and dispersity variation in a gel when the outer electrolyte (A) diffuses into the gel and reacts with the inner electrolyte (B) via the reaction A + B → C. The outer electrolyte is present in large concentration and volume, thus its concentration can be considered constant at the liquid–gel interface. It is assumed that the reaction product C is a mobile chemical species (“seed”), which can later transform into an immobile precipitate within the precipitation zone as C → P. In general, the characteristic particle size depends on multiple parameters, including reaction rate, stoichiometry, crystalline phase, temperature, and competing reactions, such as complexation. One of the most critical parameters is the level of supersaturation.79 For example, in the case of a sparingly soluble salt, supersaturation with respect to the solubility product somewhat expresses the tendency of the system to undergo phase change, and most of the time, it also accompanies an increase in reaction rate. According to thermodynamics, even a slight supersaturation leads to crystallization (cyan and green shaded areas in Fig. 3a), although it may take an infinite amount of time. However, in practically relevant systems, supersaturation must reach some reasonable limits to observe crystallization within the time scale of the experiment. This kinetic precipitation threshold is now c* (Fig. 3a). High concentrations of C lead to rapid nucleation (the concentration (c) stays for long between concentrations c2 and c* after the onset of first nucleation, green area in Fig. 3a). Since a large number of small nuclei are formed, they are crowded and thus the neighbouring supply is limited for their growth. As a consequence, relatively small particles form with a narrow size distribution. However, as a drawback, crystallinity may be poor in some chemical systems due to the sudden stop after an intense initial growth. On the other hand, in regions of lower supersaturation (c stays for a long time between concentration c1 and c2 after the onset of first nucleation, cyan area in Fig. 3a), nucleation is a somewhat rare event. Thus, the average distance between particles is larger. Consequently, plenty of supply is available for the nuclei to grow further, resulting in larger particles. However, especially in systems dependent on various transport processes such as diffusion or flow, the environment of nuclei can be dramatically different, and crystals will cover a wide size distribution. The situation becomes even more complex because nucleation is stochastic in both time and space when supersaturation is low. Therefore, two nuclei might also be close to each other and suppress each other's growth, while another nucleus is located in an open area and can grow freely. Since the crystal growth rate is typically dependent on the particle surface (the larger the surface, the faster the growth), the size distribution tends to become wider with increasing crystallization time. Furthermore, since the number of nuclei is relatively low and they can be far apart, while already nucleated particles have been grown to a given size, it is possible that nucleation in another region may occur. All these can result in continuous widening of the size distribution over time, which is regrettable. In contrast to what has been said above, an appropriately set out-of-equilibrium system, where the influx of reactants can be controlled in space and time, provides an opportunity to overcome some of those difficulties and end up with spatially distinct and relatively narrow size distributions.80 In the following, simple models are examined to investigate these effects. First, we illustrate the increase in particle size and dispersity in Liesegang patterns using a simplified explanation based on the discrete precipitation zones that are observed.51 Then, we extend the discussion to continuous precipitation zones. In our simplified model of the Liesegang phenomenon, a linear concentration profile of the outer electrolyte is assumed, extending from the gel surface to the reaction front at position x. Similarly, a linear profile of the intermediate (C) is assumed, with its concentration dropping to zero at the previous precipitation zone xn (Fig. 3a). When constant concentrations are maintained at the boundaries of a region (e.g., ϕ(0) = 0 and ϕ(L) = ϕL), the steady-state solution of diffusion equation ∂tϕ = D∇2ϕ = 0 is linear: ϕ(x) = ϕLx/L. In our system, this linear approximation holds on the left side of the reaction front under quasi-stationary conditions, provided the process is diffusion-controlled and precipitation reactions (C → P) occur exclusively at the designated precipitation zones at xn. However, a similar linear profile is not observed on the right side of the reaction front because only the nth precipitation zone has formed at this stage. The formation of the next precipitation zone at xn+1 is triggered when the concentration of reaction product reaches a critical threshold c* at that location. This asymmetry in the concentration profile arises due to the incomplete development of precipitation zones on the right side, reflecting the dynamic and spatially heterogeneous nature of the Liesegang process. As the reaction front moves from xn to the next precipitation zone xn+1, there is a region where seed growth becomes significantly more dominant than nucleation. We refer to this as the growth-dominant region (Fig. 3), which occurs when the concentration (c) lies between c1 and c2. Based on findings discussed in ref. 51, it is assumed that particle size is proportional to the distance l along x the front spends in this growth-dominant concentration range between c1 and c2. In a quasi-stationary state, the influx of A (ja) equals the outflow of C (jc) between precipitation zones, where no additional reaction occurs for C (i.e., no precipitate forms):∂tc = −∇![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) = 0, ja = jc. = 0, ja = jc. | (2) |
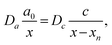 | (3) |
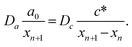 | (4) |
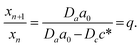 | (5) |
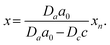 | (6) |
 | (7) |
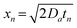 , implying that the particle size increases with the square root of time:
, implying that the particle size increases with the square root of time: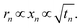 | (8) |
This behaviour was also observed in a macroscopic pattern formation. The Cahn–Hilliard equation was employed to describe the formation and dissolution (complex formation) of aluminium hydroxide precipitate in excess hydroxide ions.81 Both experimental data and numerical simulations in that study revealed a linear relationship between the distance from the liquid–gel interface and characteristic wavelength of the pattern, consistent with the findings of our simplified RD model. This agreement across different systems and modelling approaches further supports the validity of the results presented here. Furthermore, the same argument holds for all concentration ranges: not only does the growth-dominant region lengthen with distance from the gel surface, but so does the nucleation-dominant region (between c2 and c*). This explains the presence of smaller particles alongside larger ones, resulting in increased dispersity with distance. As mentioned earlier, these system characteristics can be exploited for practical applications. Since the banded pattern provides a visually obvious discrimination of precipitation regions, products of various sizes can be easily separated. Although the Liesegang setup has the drawback that particle size and dispersity increase at larger distances from the liquid–gel interface, the diffusion-mediated synthesis can be further improved. If large liquid tanks feed a gel sheet (i.e., the diffusive mixing region of reactants) from two sides, the influx of reactants can be modulated in time. Initially, if high supersaturation is confirmed in the gel, nucleation will be favored, and multiple crystals will grow simultaneously. The diffusive flux will decrease by lowering the reactant concentrations in the tanks. Therefore, the concentration in the gel decreases, and as a result, nucleation becomes less dominant compared to the growth of already existing but small particles. Overall, the particle size and dispersity can be controlled without the need for multistep synthesis protocols, where tiny particles must be first separated and then placed into a growth medium for more controlled crystallization. Fig. 3b presents similar, simplified concentration profiles, which, in contrast to what was shown before, lead to continuous precipitation regions. In this case, the balance equation in eqn (2) is extended with a reaction term accounting for the conversion of C into the precipitate P (C → P), which occurs throughout the gel rather than in discrete precipitation zones, as in Liesegang patterns. Assuming first-order kinetics, the balance equation in a quasi-stationary state for a small region with volume V and surface Ω can be expressed as:
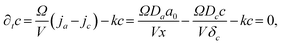 | (9) |
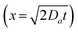 , Ostwald ripening becomes more pronounced: smaller particles dissolve while larger ones grow due to differences in solubility (smaller particles have higher surface energy). This further increases particle size with distance from the gel surface.
, Ostwald ripening becomes more pronounced: smaller particles dissolve while larger ones grow due to differences in solubility (smaller particles have higher surface energy). This further increases particle size with distance from the gel surface.
2.3. Biomineralization in RD systems
Unlike crystallization in free aqueous media, crystallization in biological systems occurs through slow diffusion across membranes, vesicle-mediated transport, and regulated mass transfer, leading to controlled biomineralization. Periodic precipitation in rocks has inspired studies on biomineralization, focusing on commonalities in slow diffusion. Hydrogels have been widely used as a medium for generating Liesegang patterns in laboratory settings, which is also essential in biomedical research for the development of artificial tissues and drug delivery.82–86 Recently, hydrogels have been employed as a diffusion-controlling matrix to regulate patterns of biominerals.87–89Calcium phosphate, the primary inorganic component of bones and teeth, exhibits various crystalline phases and has been intensively investigated for fundamental studies on bone formation and biomedical applications.90,91 When calcium ions diffuse into a gelatin hydrogel containing phosphate, periodic Liesegang bands appear.92 Interestingly, these bands exhibit internal heterogeneity. A whiter layer at the ends of all bands was visibly identifiable to the naked eye (Fig. 4a). While extensive research has been conducted on Liesegang pattern formation, studies on the microstructure of individual bands are rare. Scanning electron microscopy (SEM) analysis confirmed the presence of higher-density crystallization at the band edges. The slow diffusion within the hydrogel facilitates real-time tracking of band formation, revealing that each band consists of two sub-bands separated by a void region (Fig. 4b). A simulation assuming highly stable intermediates successfully explained this phenomenon (Fig. 4c). Amorphous calcium phosphate (ACP), a well-known precursor in calcium phosphate crystallization, is significantly more stable than previously studied Liesegang pattern-forming materials, allowing for prolonged stability of intermediate. In addition, previous studies on prenucleation clusters suggest a complex, multistep nucleation process, which reinforces the proposed mechanism.
 | ||
| Fig. 4 (a) Optical micrograph of a calcium phosphate periodic pattern. (b) Single-band formation analysed optically (top) and spatiotemporally (bottom). The scale bar is 1 mm. (c) Simulated pattern and cross-sectional profile. Control (left) and result (right) when a threshold is applied. (d) Optical micrograph of the periodic pattern in the presence of polyacrylic acid. (e) Scheme of band formation with no PAA (top) and PAA (bottom), reproduced from ref. 95, licensed under the Creative Commons Attribution License. | ||
In biomineralization, anionic macromolecules and insoluble matrices cooperate to regulate crystallization.90 Anionic macromolecules bind chemically or physically to cations, intermediates, and growing crystal surfaces, often inhibiting nucleation and controlling phase selection.93,94 Inspired by these biological macromolecules, polyacrylic acid (PAA) was introduced into a hydrogel containing phosphate ions, and calcium diffusion resulted in the formation of ultrathin Liesegang bands (Fig. 4d).95 Unlike conventional Liesegang pattern studies that manipulate pattern formation by additives such as cations, anions, or organic acids96–98 this biomimetic approach demonstrated precise control over band structure. The band thinning effect induced by PAA was successfully simulated using a threshold concentration model, where stabilized intermediates slow down crystallization (Fig. 4c). This simulation aligns with previous studies suggesting that anionic macromolecules stabilize intermediates, leading to lower supersaturation during crystallization (Fig. 4e).
While periodic pattern formation in diffusion-controlled environments is an intriguing topic and often applicable to interesting platforms for cell culture, its applicability to biomaterials is limited due to nonuniform mineral distribution.87,88 Bone, teeth, and cartilage replacements require large-scale, uniform organic–inorganic composites. Inspired by the ability of PAA to thin Liesegang bands, cationic polyethylenimine (PEI) was introduced into the hydrogel to achieve homogeneous crystallization.99 At low PEI concentrations, a high-density pattern of ultrathin bands formed, while higher concentrations resulted in uniform calcium phosphate crystallization over lengths exceeding several centimetres, yielding macroscale hydrogel–calcium phosphate composites. This effect was successfully simulated by assuming reduced intermediate diffusion rates, suggesting that PEI either increased intermediate size or enhanced interactions with the gelatin network. However, SEM and X-ray diffraction (XRD) analysis revealed no evidence of increased intermediate size, suggesting that PEI primarily enhanced electrostatic or chemical interactions between the intermediates and the hydrogel matrix. These findings demonstrate that incorporating cationic macromolecules can effectively regulate diffusion-controlled crystallization, offering a new strategy for synthesizing large-scale, uniform biomaterials.
2.4. Pattern control using inner and outer parameters, complex pattern design, and development of environmental sensors
RD systems are sensitive to the inner and outer ‘environment’. Therefore, RD patterns can be controlled by manipulating environmental parameters once their effects on a particular system are determined. This is easier said than done since many parameters affect the RD pattern formation. The concentrations of reagents100–102 and gels,35,103,104 the degree of cross-linking in gels,105,106 impurities in the gels,35 pH and the polarity of media,50,102,107 electric fields,108–111 mechanical fields,112 temperature113–117 and presence of radiation118,119 are some of these parameters. Their effect on an RD system also depends on its other physical and chemical parameters. Mutual interaction among these effects causes crosstalk and introduces additional complexity. Yet, investigations into parameter alterations led to the establishment of mathematical models to elucidate and simulate the RD processes.The above-mentioned physical/chemical parameters that affect the pattern development can also be combined with microscopic120 and macroscopic features of the medium, which can lead to additional complexity – a desired feature for complex pattern and material design. In a study,121 simple geometrical boundaries were created around the developing pattern, and the pattern was set to continue its formation in a different gel concentration medium across the boundary. The ‘refraction’ of the pattern waves changed the band spacings, and the refraction angle depended on the boundary's macroscopic shape. In addition, crystal morphologies also altered when the waves traveled into the new gel concentration region.
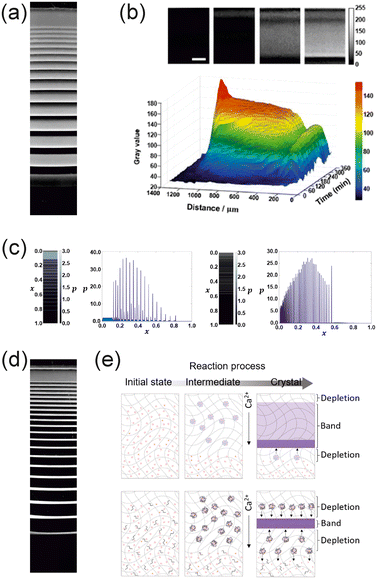
In addition to providing insight into the mechanism of RD formation, the results obtained in the parameter-based experimental studies opened up a way to use RD systems as probes and recorders of their environment. RD systems ‘live’ and develop under the influence of above-mentioned mechanical, physical, and chemical parameters. If the systems are unleashed to progress in a changing environment, the developing RD pattern bears the marks of change. In one example,122 clear changes in the band spacing of CuCrO4 RD patterns resulting from development in different environmental temperatures (Fig. 5a) were used to record various temperature changes during a couple of hours of pattern development. The ramp steepness, magnitude, and duration of the change could be tracked back by ‘reading’ the band spacing and widths of the pattern (Fig. 5b). In another study,112 mechanical deformation in the gel environment was probed using the same principle. CuCrO4 patterns formed in a stretchable polyacrylamide hydrogel medium were used to record the mechanical deformation of up to 50% in the polyacrylamide gel within the medium during the pattern formation process. The time and duration of change – a stretching ‘pulse’ could be visually detected by recorded alterations in the band spacing (Fig. 6a). The thermal and mechanical input not only changes the macroscopic band properties but also affects the size of the precipitate particles formed in the precipitate-forming RD systems. This sensitivity can be used to obtain various products with different particle size distributions, which are located and spatially separated in the medium – an ideal platform for probing function versus size, e.g., the catalytic activities of differently sized particles.123 On the other hand, the environmental changes in the form of a sharp ramp or a pulse can alter/reverse the particle size trends observed in patterns developed in environments with no change.
 | ||
| Fig. 5 Temperature tracking and recording. (a) CuCrO4 bands formed in hydrogels at designated temperatures. With the increase in temperature, wider “depletion zones” between precipitation bands, and precipitation beginning farther away, are observed, along with more extensive patterns. (b) Spacing coefficients of the patterns shown in (a). (c) A refrigerator that did not work overnight between the 5th and 9th hours can be identified by the changes in the Liesegang pattern developing in the fridge, reproduced from ref. 122, licensed under the Creative Commons Attribution License. | ||
 | ||
| Fig. 6 Mechanical deformation recording. (a) and (b) the CuCrO4 bands formed in hydrogels under different stretching cycles of the hydrogel show distinctly different patterns in parallel with the time and duration of the stretching pulse, reprinted from ref. 112 with permission from Wiley, copyright 2020. (c) RD patterns can be used in the development of artificial skin patterns, reprinted from ref. 124 with permission from Wiley, copyright 2023. | ||
These studies demonstrate that the RD pattern formation systems can be viewed as ‘living’ systems that can track and record environmental changes. The systems' fragility to inner and outer conditions and stimuli can be used as a synthetic advantage to regulate the preparation of complex material architectures87,105,112,122–124 (Fig. 6b) and reach hard-to-obtain patterns of (also secondarily forming) matter112 and radiation.125
2.5. Synthesis of MOFs and AuNPs in an antagonistic diffusion setup
The flow-through gel reactor design proposed by Dúzs and Szalai offers an innovative and efficient method for maintaining controlled nonequilibrium reaction environments.126 This open reactor configuration continuously supplies fresh reactants into a gel matrix through separate flow channels (Fig. 7a). By adjusting the position of channels and concentrations in the input feed solutions, the chemical gradients inside the gel can be controlled, influencing the formation of reaction zones. The ability to scale the reactor geometry to match the actual chemistry is a key advantage of these reactors. The design offers the possibility of miniaturization for microfluidic applications or scaling up for industrial processes. In the latter case, not the increase in diameter but the increase in the length of the reactor could be beneficial as the crystals form in the gel zone between the flow channels. Still, the fact that the product must be extracted by destruction of the gel is a limitation. A possible solution would be to include an additional middle channel from which the products can be extracted. The three-channel configuration enables more complex reaction environments and facilitates chemical communication between reaction zones through diffusive coupling. The advantages of flow-through gel reactors, including improved reaction control, scalability, efficiency, and sustainability, have been demonstrated through various chemical systems, such as precipitation, oscillatory reactions, and nanoparticle synthesis. | ||
| Fig. 7 Nanoparticle synthesis in flow-through gel reactor. Scheme of gel reactor used in the synthesis (a). Top view of the inter-channel zone ((b) and (f)). ZIF-8 particle size at different spatial positions along the direction of cross-gradients represented in SEM micrographs ((c)–(e)). Representative TEM micrographs of particles isolated from the purple (g) and red (h) regions, reproduced from ref. 80, licensed under the Creative Commons Attribution License. | ||
Flow-through gel reactors have been applied for the controlled synthesis of crystalline materials, particularly MOFs and AuNPs.80 The traditional synthesis methods of nanoparticles rely on bulk or flow chemistry techniques, where reagent concentrations gradually decrease, affecting crystal growth and size control. The constant mass fluxes of reactants in a flow-through hydrogel-based reactor offer the possibility of controlling crystal size and dispersity by regulating reagent gradients in time and space.
ZIF-8 crystals were synthesized in a gel reactor containing two parallel flow-through channels.80 These channels provided a continuous reactant supply, ensuring constant concentration gradients inside the gel (Fig. 7a). The diffusion-driven RD process enabled crystal formation in the inter-channel zone without bulk mixing, minimizing uncontrolled nucleation. For ZIF-8 synthesis, zinc nitrate (Zn2+) and 2-MeIm were the precursors. Solutions of these precursors, each made in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of DMF and H2O, were pumped through the separated channels made in the agarose gel matrix. The concentration ratio of Zn2+ to 2-MeIm was optimized at 1
1 mixture of DMF and H2O, were pumped through the separated channels made in the agarose gel matrix. The concentration ratio of Zn2+ to 2-MeIm was optimized at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 for effective crystal growth. Crystals formed in the middle region of the gel reactor, where the two reactants met (Fig. 7b–e). The phase purity and structural identity of crystals were determined using X-ray diffraction.
10 for effective crystal growth. Crystals formed in the middle region of the gel reactor, where the two reactants met (Fig. 7b–e). The phase purity and structural identity of crystals were determined using X-ray diffraction.
The synthesis time was between 24 to 168 hours. The average size of the MOF crystals and the dispersity increased in time during the first 72 hours. At longer synthesis times (e.g., 168 hours), due to particle degradation, the average size was smaller, and the dispersity was more pronounced than after 72 hours. Increasing the zinc ion concentration led to larger but more disperse crystals, while lower concentrations produced smaller and more uniform particles. The properties of products vary along the cross-section of the gel, as the distance from the sources (i.e., channels) affects the characteristics of the crystals. The largest particles formed in the middle zone, while smaller particles formed closer to the channels, with almost the same dispersity. One of the most significant findings of this study was that the synthesis in flow-through gel reactors yielded ZIF particles that were significantly larger, one to two orders of magnitude larger, than those obtained from a well-mixed batch process with the same initial reactant concentrations. Another surprising observation was the formation of ZIF-8 crystals near the channel, which contained Zn2+ ions with characteristics similar to those of the crystals formed at the 2-MeIm side. This contradicts previous observations that only a high excess of 2-MeIm favors the formation of ZIF-8, especially in the aqueous phase.127,128
AuNPs were also synthesized in the flow-through gel reactor.80 A standard redox reaction-based synthetic route was used, where sodium citrate reduced gold chloride in a polyacrylamide (PAA) gel.129 The hydrogel matrix helped stabilizing nanoparticle formation while preventing aggregation. A four- or ten-fold excess of citrate was used, and the synthesis time was 6–24 hours at room temperature. In the two channels, continuous flows of an aqueous solution of HAuCl4·3H2O and an aqueous solution of sodium citrate were used to maintain fixed gradients in the gel, ensuring nonequilibrium conditions. The size distribution of AuNPs was determined using TEM (Fig. 7f–h).
The RD process formed distinct nanoparticle zones across the gel. A purple region contained larger (10–50 nm) nanoparticles and aggregates, and a red region contained smaller (∼6 nm) uniform AuNPs, due to a higher local citrate concentration stabilizing smaller particles. Compared to the conventional Turkevich synthesis,129 this method achieves sub-10 nm AuNPs at room temperature, which is typically challenging without the use of reducing agents.
This study presents a novel nonequilibrium synthesis method, demonstrating that although the local concentrations of reagents predominantly govern the nucleation, the mass fluxes of reagents can effectively control the crystal growth. This finding enables precise control over crystal size and dispersity, and, unlike bulk methods, allows for spatial and kinetic tuning of materials. Flow-through gel reactors could be extended to synthesizing other nanomaterials, offering the potential for scalable and environmentally friendly material synthesis. Future work could explore adapting the technique to other MOFs and composite materials, while refining reactor designs for industrial-scale implementation.
2.6. Synthesis of MOFs in an electric field (enhancing the effect of diffusion)
Besides diffusion-controlled methods, ZIF-8 crystallization can also be influenced by a direct electric field, which generates an enhanced mass transport flux of Zn2+ ions. The electric field can effectively control pattern structures in RD systems by causing ion migration.130–137 This idea was implemented and utilized it in an electric field-assisted synthesis of ZIF-8 crystals in a gel matrix.2-MeIm was homogeneously distributed in a rigid agarose gel (hosted in a U-shaped tube) using a mixture of distilled water and DMF with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For better conductivity, potassium nitrate was used as an inert salt (Fig. 8). Zinc acetate and 2-MeIm (dissolved in the mixture of water and DMF containing KNO3) were placed on the top of gel surfaces. Platinum wires were used as electrodes and placed into solutions. The galvanostatic condition was applied in experiments, which were conducted at room temperature for three days. A control experiment was also carried out in the absence of an electric field (diffusion-assisted synthesis) using the same setup.
1. For better conductivity, potassium nitrate was used as an inert salt (Fig. 8). Zinc acetate and 2-MeIm (dissolved in the mixture of water and DMF containing KNO3) were placed on the top of gel surfaces. Platinum wires were used as electrodes and placed into solutions. The galvanostatic condition was applied in experiments, which were conducted at room temperature for three days. A control experiment was also carried out in the absence of an electric field (diffusion-assisted synthesis) using the same setup.
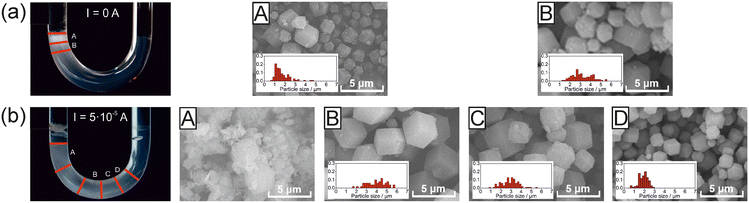 | ||
| Fig. 8 Effect of an electric field on the distribution of the ZIF crystals in a U-shaped glass tube (optical photograph), morphology of the ZIF-8 particle, and size distribution (insets, using SEM micrographs) extracted from different segments of the agarose gel using (a) I = 0 and (b) I = 5 × 10−5 A electric currents. A–D denote the segments of the agarose gel from which the particles were extracted after 3 days, reproduced from ref. 138, licensed under the Creative Commons Attribution License. | ||
According to XRD and SEM measurements of the MOFs, electric current influenced the crystallinity and average size of ZIF-8 crystals in the gelled matrix by facilitating the migration of charged chemical species. By increasing the electric current, the length of the precipitation domain increased, expanding towards the cathode, and the length of the zone containing fewer particles at the anodic side also increased (Fig. 8b, panels B–D). In the case of low electric currents, both the average size of ZIF-8 particles and their dispersity increased along the gel tube from the liquid–gel interface of the anodic side. This finding is similar to the results obtained in the synthesis using solely diffusion as the mass transport mechanism. By increasing the electric current, the trend reversed, namely, both the size and dispersity decreased. However, at the highest electric current used (I = 2 × 10−4 A), particles lost their crystalline shape and became amorphous close to the gel surface at the cathode side. This method provides a facile and scalable way to adjust particle morphology in spatially inhomogeneous conditions. It enables us to control the application-related physical and chemical properties of MOFs using a RD framework combined with an electric field.138
In a pure RD scenario, higher supersaturation near the liquid–gel interface resulted in smaller particles with higher particle concentrations. However, farther from the interface, lower supersaturation creates larger particles with lower particle concentrations (Fig. 8a). In an electric field, enhanced mass transport of zinc ions and charged intermediates created a higher supersaturation in segments farther from the liquid–gel interface, generating smaller particles. Under a moderate electric current, an optimal value (I = 5 × 10−5 A) was found, resulting in ZIF-8 with an average particle size of ∼4 μm (Fig. 8b), which is twice as large as those made by the diffusion-mediated method alone.
2.7. Crystal synthesis in orthogonal diffusion
In terms of ion concentration and level of supersaturation, hydrogel-based crystallization studies can provide conditions more similar to those found in biological systems, where ions are supplied slowly through blood vessels, cell membranes, and intracellular fluids over a prolonged period, leading to the formation of biominerals. Previous hydrogel-based crystallization studies have utilized single-direction or opposite-direction diffusion fluxes to control crystal formation along a one-dimensional (collinear) flux. To introduce greater complexity and mimic more diverse microenvironments, a two-dimensional control system was developed using orthogonal ion diffusion (Fig. 9a).139 By diffusing calcium and carbonate ions perpendicularly into a hydrogel, distinct calcium carbonate (CaCO3) structures were spatially regulated.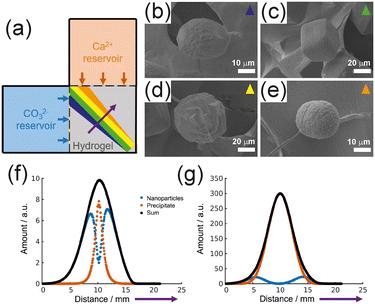 | ||
| Fig. 9 (a) Experimental scheme and SEM micrographs of CaCO3 crystals: (b) otoconia (blue), (c) rhombohedra (green), (d) rosettes (yellow), and (e) spheres (orange). Simulation of crystallization at an early (f) and a late (g) stage. Amount of nanoparticles, precipitate, and the sum of them as a function of the direction marked as a purple arrow in (a), reproduced from ref. 139, licensed under the Creative Commons Attribution License. | ||
Crystallization progressed diagonally along the intersection of two ion fluxes, forming four distinct CaCO3 morphologies: otoconia, rhombohedral, rosette, and sphere (Fig. 9b–e). These shapes formed spatially dependently, with otoconia forming closest to the carbonate reservoir and spheres forming near the calcium reservoir. Crystallization occurred rapidly in the initial stages and slowed over time due to decreasing ion fluxes. The highest crystal density was found near the reservoirs and decreased with increasing distance from the reservoirs. pH measurements confirmed that different morphologies formed under distinct pH conditions, with higher pH favouring otoconia and lower pH favouring spheres. SEM and energy-dispersive X-ray spectroscopy (EDS) analysis revealed that the crystal surface texture influenced the incorporation of the hydrogel, thereby affecting the morphology. Crystals near the calcium reservoir exhibited rough surfaces due to nanoparticle aggregation in an acidic environment, where amorphous calcium carbonate (ACC) persisted before forming spherical structures. In contrast, crystals near the carbonate reservoir developed smooth surfaces via an ion-by-ion growth mechanism in a high-pH environment, resulting in the formation of calcite. Mathematical modelling aligned with experimental findings, demonstrating that ion flux and pH gradients dictated crystallization patterns. Nonstoichiometric calcium-rich regions facilitated rapid ACC formation due to supersaturation, leading to submicron spherical aggregates (Fig. 9f). Meanwhile, carbonate-rich regions promoted slow crystallization, where Ostwald ripening contributed to the growth of distorted calcite, such as otoconia (Fig. 9g). In near-stoichiometric regions, larger crystals, including rosettes and rhombohedra, formed due to balanced ion flux. These findings provide new insights into biomineralization, underscoring the role of diffusion control in determining phase selection and crystal growth. The ability to spatially regulate crystallization within a hydrogel presents promising applications in biomaterials, tissue engineering, and controlled mineralization studies.
3 Summary
This article highlighted the advantage of diffusion-assisted synthesis of crystalline materials. The traditional and most widely used methods for generating crystals are wet synthesis routes. In these approaches, all reagents are homogeneously distributed in the reactor and mixed continuously throughout the process. Usually, those are one-step methods, which are simple and highly reproducible. However, they have several drawbacks, namely, the generated particles are sub-micron particles, and one experimental condition produces only particles with a given average size and shape. Additional growing steps (seed-mediated growth) and/or using additives (e.g., surfactants, macromolecules) are necessary to overcome this limitation. In contrast, diffusion-assisted synthesis creates a library of crystals with various sizes and shapes, spatially distributed throughout the gel matrix during a single synthesis, which is a main advantage of all methods presented. The gel matrix controls diffusive fluxes, thus determining the local concentrations and their temporal variation. The key element in the synthesis is that the rigid gel is entirely permeable to small hydrated ions (reagents) and nuclei. The gel matrix does not hinder the mass transport of small chemical species since the gel pore size ranges from ∼300 nm to ∼800 nm, depending on the chemical composition of the gel and the gel monomer concentration.140 The formed crystals may become entrapped within the matrix, avoiding sedimentation and aggregation, thus they can grow undisturbed. On the other hand, the diffusion-assisted approach has several drawbacks, including long synthesis time and post-synthetic purification of crystals. In the purification and separation process, several organic solvents (e.g., DMF) can be used to disrupt the hydrogel structure and separate the crystals. Most methods (synthesis in gel column and thin gel layer) can generate only a moderate amount of crystals. However, the antagonistic diffusion setup (possibly extended with the effect of an electric field) can be upscaled to laboratory scale by increasing the size of the gel reactor and the diameters of the channels inside the reactor.In this highlight article, we briefly reviewed diffusion-assisted synthesis of crystalline materials in rigid gel matrices, focusing on how RD processes enable controlled nucleation, growth, and spatial patterning of crystals. We presented recent successes in the synthesis of inorganic precipitates, MOFs, and AuNPs using gel columns, reactive wet stamping, flow-through gel reactors, and electric field-assisted methods. A key finding was the linear relationship between crystal size and distance from the liquid–gel interface, which can be explained by the dynamics of supersaturation. Specifically, low supersaturation favors growth over nucleation, resulting in larger crystals. We also explored biomineralization, demonstrating how additives such as PAA and PEI can fine-tune patterning and produce uniform or spatially controlled biomaterials. Advanced methods developed, such as orthogonal diffusion, flow-through reactors, and electric field-assisted synthesis, offer greater control over crystal morphology, size distribution, and spatial organization than traditional bulk methods.
4 Future perspectives
The diffusion-assisted synthesis may present future challenges, including testing the linear correlation between particle size and the distance measured from the liquid–gel interface. Theory provides no limitation to synthesize macroscopic crystals (with a size of several cm) of MOFs and AuNPs. Secondly, most methods have been considered quasi-1D setups, i.e., fluxes of chemical species are collinear. To go beyond this, we proposed a method involving orthogonal diffusion fluxes of reagents. In the future, research should focus on reactor design of various shapes in 2D (triangular, square, etc.) and 3D (tetragonal, cubic, etc.), where reagents and additives can diffuse from edges and planes of the rigid gel reactor. In this setup, each spatial point has different distances from the reservoirs. Therefore, each point exhibits a unique rate of change in the concentrations of chemical species driven by diffusion, which determines the local concentrations and generates various local environments for nucleation and growth. Lastly, a promising new direction could be the application of RD processes in environmental remediation, where precipitation reaction and diffusion of compounds can separate various heavy metal cations in a hydrogel column.141,142Author contributions
Conceptualization: all authors; writing – original draft: all authors; writing – review and editing: all authors.Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.Acknowledgements
This research was supported by the HUN-REN Hungarian Research Network, the National Research, Development and Innovation Office of Hungary (K146071, K134687, and K138844), the Ministry of Culture and Innovation, and the National Research, Development and Innovation Office under Grant No. TKP2021-EGA-02. G. S. thanks the Bolyai János Research Fellowship (BO/00586/23/7).References
- I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press, New York, 1998 Search PubMed.
- J. D. Murray, Mathematical Biology, Springer-Verlag, Berlin, 2002 Search PubMed.
- P. Ball, Archit. Des., 2012, 82, 22–27 Search PubMed.
- P. Ball, Philos. Trans. R. Soc., B, 2015, 370, 20140218 CrossRef.
- M. J. Berridge, Nature, 1997, 386, 759–760 CrossRef CAS PubMed.
- J. A. Papin, T. Hunter, B. O. Palsson and S. Subramaniam, Nat. Rev. Mol. Cell Biol., 2005, 6, 99–111 CrossRef CAS PubMed.
- T. Nakano, A. W. Eckford and T. Haraguchi, Molecular Communication, Cambridge University Press, 2013 Search PubMed.
- M. Falcke, Adv. Phys., 2004, 53, 255–440 CrossRef CAS.
- J. Schütze, T. Mair, M. J. Hauser, M. Falcke and J. Wolf, Biophys. J., 2011, 100, 809–813 CrossRef.
- M. Toiya, H. O. González-Ochoa, V. K. Vanag, S. Fraden and I. R. Epstein, J. Phys. Chem. Lett., 2010, 1, 1241–1246 CrossRef CAS.
- K. Torbensen, F. Rossi, S. Ristori and A. Abou-Hassan, Lab Chip, 2017, 17, 1179–1189 RSC.
- T. Litschel, M. M. Norton, V. Tserunyan and S. Fraden, Lab Chip, 2018, 18, 714–722 RSC.
- F. Rossi, S. Ristori and A. Abou-Hassan, Acc. Chem. Res., 2024, 57(18), 2607–2619 CrossRef CAS PubMed.
- A. Paikar, X. Li, L. Avram, B. S. Smith, I. Sütő, D. Horváth, E. Rennert, Y. Qiu, Á. Tóth, S. Vaikuntanathan and S. N. Semenov, Chem. Sci., 2025, 16, 659–669 RSC.
- J. H. Kruhl, Fractals and Dynamic Systems in Geoscience, Springer, Berlin Heidelberg, Softcover reprint of the original 1st edn 1994 edition, 2014 Search PubMed.
- V. K. Vanag and I. R. Epstein, Phys. Chem. Chem. Phys., 2009, 11, 897–912 RSC.
- M. A. Budroni and A. De Wit, Chaos, 2017, 27, 104617 CrossRef CAS PubMed.
- M. A. Budroni, F. Rossi and L. Rongy, ChemSystemsChem, 2021, 4, e2100023 Search PubMed.
- M. A. Budroni and F. Rossi, Phys. Chem. Chem. Phys., 2024, 26, 29185–29226 RSC.
- M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys., 1993, 65, 851–1112 CrossRef CAS.
- V. K. Vanag and I. R. Epstein, Int. J. Dev. Biol., 2009, 53, 673–681 CrossRef.
- A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37–72 Search PubMed.
- V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Phys. Rev. Lett., 1990, 64, 2953–2956 CrossRef CAS.
- P. De Kepper, V. Castets, E. Dulos and J. Boissonade, Phys. D, 1991, 49, 161–169 CrossRef CAS.
- K. J. Lee, W. D. McCormick, Q. Ouyang and H. L. Swinney, Science, 1993, 261, 192–194 CrossRef CAS.
- V. K. Vanag and I. R. Epstein, Phys. Rev. Lett., 2001, 87, 228301 CrossRef CAS.
- J. Horvath, I. Szalai and P. De Kepper, Science, 2009, 324, 772–775 CrossRef CAS.
- F. Rossi and M. L. T. Liveri, Ecol. Modell., 2009, 220, 1857–1864 CrossRef CAS.
- C. Beta, L. Edelstein-Keshet, N. Gov and A. Yochelis, eLife, 2023, 12, e87181 CrossRef CAS PubMed.
- S. Sawai, X.-J. Guan, A. Kuspa and E. C. Cox, Genome Biol., 2007, 8, R144 CrossRef.
- L. Marcon and J. Sharpe, Curr. Opin. Genet. Dev., 2012, 22, 578–584 CrossRef CAS.
- S. Farkas, F. Gazdag, M. Detrich, M. Mészáros, G. Holló, G. Schuszter and I. Lagzi, J. Phys. Chem. Lett., 2023, 14, 10382–10387 CrossRef CAS PubMed.
- A. F. Taylor, Prog. React. Kinet. Mech., 2002, 27, 247–325 CrossRef CAS.
- H. K. Henisch, Crystals in Gels and Liesegang Rings, Cambridge University Press, 1988 Search PubMed.
- I. Lagzi, Langmuir, 2012, 28, 3350–3354 CrossRef CAS PubMed.
- H. Nabika, M. Itatani and I. Lagzi, Langmuir, 2020, 36, 481–497 CrossRef CAS.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- B. A. Grzybowski, K. J. M. Bishop, C. J. Campbell, M. Fialkowski and S. K. Smoukov, Soft Matter, 2005, 1, 114–128 RSC.
- B. A. Grzybowski, Chemistry in Motion: Reaction-Diffusion Systems for Micro- and Nanotechnology, Wiley, Chichester, U.K., 1st edn, 2009 Search PubMed.
- S. C. Muller and M. J. B. Hauser, in Handbook of Biomimetics, NTS books, Tokyo, 2000, pp. 87–100 Search PubMed.
- F. Rossi, S. Ristori, M. Rustici, N. Marchettini and E. Tiezzi, J. Theor. Biol., 2008, 255, 404–412 CrossRef CAS.
- K. Showalter and I. R. Epstein, Chaos, 2015, 25, 097613 CrossRef PubMed.
- R. S. Cantrell and C. Cosner, Spatial Ecology via Reaction-Diffusion Equations, John Wiley & Sons, 2004 Search PubMed.
- R. E. Liesegang, Naturwiss. Wochenschr., 1896, 11, 353–362 Search PubMed.
- I. Lagzi, B. Kowalczyk and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 58–60 CrossRef CAS.
- B. A. Grzybowski and C. J. Campbell, Mater. Today, 2007, 10, 38–46 CrossRef CAS.
- C. J. Campbell, E. Baker, M. Fialkowski and B. A. Grzybowski, Appl. Phys. Lett., 2004, 85, 1871–1873 CrossRef CAS.
- C. J. Campbell, E. Baker, M. Fialkowski, A. Bitner, S. K. Smoukov and B. A. Grzybowski, J. Appl. Phys., 2005, 97, 126102 CrossRef.
- R. Klajn, M. Fialkowski, I. T. Bensemann, A. Bitner, C. J. Campbell, K. Bishop, S. Smoukov and B. A. Grzybowski, Nat. Mater., 2004, 3, 729–735 CrossRef CAS PubMed.
- S. K. Smoukov, A. Bitner, C. J. Campbell, K. Kandere-Grzybowska and B. A. Grzybowski, J. Am. Chem. Soc., 2005, 127, 17803–17807 CrossRef CAS PubMed.
- R. M. Walliser, F. Boudoire, E. Orosz, R. Tóth, A. Braun, E. C. Constable, Z. Rácz and I. Lagzi, Langmuir, 2015, 31, 1828–1834 CrossRef CAS.
- S. Farkas, M. S. Fonyi, G. Holló, N. Német, N. Valletti, Á. Kukovecz, G. Schuszter, F. Rossi and I. Lagzi, J. Phys. Chem. C, 2022, 126, 9580–9586 CrossRef CAS.
- D. Saliba, M. Ammar, M. Rammal, M. Al-Ghoul and M. Hmadeh, J. Am. Chem. Soc., 2018, 140, 1812–1823 CrossRef CAS.
- R. Zakhia Douaihy, M. Al-Ghoul and M. Hmadeh, Small, 2019, 15, 1901605 CrossRef.
- P. Damacet, E. O. Shehayeb and K. A. Mirica, J. Am. Chem. Soc., 2025, 147, 1584–1594 CrossRef CAS.
- H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS.
- M. M. Salehi, F. Esmailzadeh and F. Hassanzadeh-Afruzi, Physicochemical Aspects of Metal-Organic Frameworks, ed. A. Maleki and R. Taheri-Ledari, Springer International Publishing, Cham, 2023, pp. 197–305 Search PubMed.
- A. Dhakshinamoorthy, Z. Li and H. Garcia, Chem. Soc. Rev., 2018, 47, 8134–8172 RSC.
- D. Yang and B. C. Gates, ACS Catal., 2019, 9, 1779–1798 CrossRef CAS.
- K. Yusuf, A. Aqel and Z. Alothman, J. Chromatogr. A, 2014, 1348, 1–16 CrossRef CAS.
- Z.-Y. Gu, C.-X. Yang, N. Chang and X.-P. Yan, Acc. Chem. Res., 2012, 45, 734–745 CrossRef CAS.
- V. Stavila, A. A. Talin and M. D. Allendorf, Chem. Soc. Rev., 2014, 43, 5994–6010 RSC.
- H. Li, L. Li, R.-B. Lin, W. Zhou, Z. Zhang, S. Xiang and B. Chen, EnergyChem, 2019, 1, 100006 CrossRef.
- Y. Lu, P. Samorì and X. Feng, Acc. Chem. Res., 2024, 57, 1985–1996 CrossRef CAS.
- V. F. Yusuf, N. I. Malek and S. K. Kailasa, ACS Omega, 2022, 7, 44507–44531 CrossRef CAS.
- D. T. Thompson, Nano Today, 2007, 2, 40–43 CrossRef.
- A. Corma and H. Garcia, Chem. Soc. Rev., 2008, 37, 2096 RSC.
- G. Han, P. Ghosh and V. M. Rotello, Nanomedicine, 2007, 2, 113–123 CrossRef CAS PubMed.
- Y.-C. Yeh, B. Creran and V. M. Rotello, Nanoscale, 2012, 4, 1871–1880 RSC.
- K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Chem. Rev., 2012, 112, 2739–2779 CrossRef CAS PubMed.
- N. Elahi, M. Kamali and M. H. Baghersad, Talanta, 2018, 184, 537–556 CrossRef CAS PubMed.
- J. Fan, Y. Cheng and M. Sun, Chem. Rec., 2020, 20, 1474–1504 CrossRef CAS PubMed.
- G. Schmid and B. Corain, Eur. J. Inorg. Chem., 2003, 2003, 3081–3098 CrossRef.
- V. Amendola, R. Pilot, M. Frasconi, O. M. Maragò and M. A. Iatì, J. Phys.: Condens. Matter, 2017, 29, 203002 CrossRef.
- H. Nakanishi, K. J. M. Bishop, B. Kowalczyk, A. Nitzan, E. A. Weiss, K. V. Tretiakov, M. M. Apodaca, R. Klajn, J. F. Stoddart and B. A. Grzybowski, Nature, 2009, 460, 371–375 CrossRef CAS PubMed.
- P. Slepička, N. Slepičková Kasálková, J. Siegel, Z. Kolská and V. Švorčík, Materials, 2019, 13, 1 CrossRef.
- S. Farkas, G. Holló, G. Schuszter, Á. Deák, L. Janovák, V. Hornok, M. Itatani, H. Nabika, D. Horváth, Á. Tóth and I. Lagzi, J. Phys. Chem. C, 2021, 125, 26116–26124 CrossRef CAS.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS.
- Handbook of Industrial Crystallization, ed. A. S. Myerson, D. Erdemir and A. Y. Lee, Cambridge University Press, 3rd edn, 2019 Search PubMed.
- B. Dúzs, G. Holló, G. Schuszter, D. Horváth, Á. Tóth, I. Szalai and I. Lagzi, Sci. Rep., 2022, 12, 222 CrossRef PubMed.
- A. Volford, I. Lagzi, F. Molnár and Z. Rácz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 055102 CrossRef CAS PubMed.
- L. Zhouyue, W. Quankang, S. Shengtong, Z. Wencheng and W. Peiyi, Adv. Mater., 2017, 29, 1700321 CrossRef.
- X. Xue, Y. Hu, S. Wang, X. Chen, Y. Jiang and J. Su, Bioact. Mater., 2022, 12, 327–339 CAS.
- J. Song, E. Saiz and C. R. Bertozzi, J. Am. Chem. Soc., 2003, 125, 1236–1243 CrossRef CAS.
- S. Sun, L. Mao, Z. Lei, S. Yu and H. Cölfen, Angew. Chem., Int. Ed., 2016, 55, 11765–11769 CrossRef CAS.
- X. Zhang, B. Wu, S. Sun and P. Wu, Adv. Funct. Mater., 2020, 30, 1910425 CrossRef CAS.
- W. Choi, M. Lee, H. Yong, D. Heo, T. Jun, H. Ryu, J.-Y. Kim, D. Cui, D. Y. Ryu, S.-Y. Lee, S.-H. Choi, B.-S. Kim, J. Kim, S. Y. Jung, S. Lee and J. Hong, Sci. Adv., 2024, 10, eadl3075 CrossRef CAS PubMed.
- M. M. Eltantawy, M. A. Belokon, E. V. Belogub, O. I. Ledovich, E. V. Skorb and S. A. Ulasevich, Adv. NanoBiomed Res., 2021, 1, 2000048 CrossRef CAS.
- Y. Wang, C. Fang, L.-B. Mao, Y.-H.-Z. Feng, Y.-F. Meng, H.-C. Wang, S.-H. Yu and Z.-L. Wang, Mater. Today Bio, 2025, 32, 101775 CrossRef CAS.
- H.-P. Yu and Y.-J. Zhu, Chem. Soc. Rev., 2024, 53, 4490–4606 RSC.
- D. Qin, N. Wang, X.-G. You, A.-D. Zhang, X.-G. Chen and Y. Liu, Biomater. Sci., 2022, 10, 318–353 RSC.
- M. Jo, Y. S. Cho, G. Holló, J.-M. Choi, I. Lagzi and S. H. Yang, Cryst. Growth Des., 2021, 21, 6119–6128 CrossRef CAS.
- Y. Qi, Z. Ye, A. Fok, B. N. Holmes, M. Espanol, M.-P. Ginebra and C. Aparicio, ACS Biomater. Sci. Eng., 2018, 4, 2758–2766 CrossRef CAS PubMed.
- R. Fujisawa, Front. Biosci., 2012, 17, 1891 CrossRef CAS.
- Y. S. Cho, M. Moon, G. Holló, I. Lagzi and S. H. Yang, Langmuir, 2022, 38, 2515–2524 CrossRef CAS PubMed.
- Y. S. Shen, E. J. Zdanuk and R. H. Krock, Metall. Trans., 1971, 2, 2839–2844 CrossRef CAS.
- V. D. Salve, K. D. Takale, P. S. Kulkarni and S. D. Kulkarni, Colloids Surf., A, 2023, 679, 132598 CrossRef CAS.
- L. M. Barge, K. H. Nealson and J. Petruska, Chem. Phys. Lett., 2010, 493, 340–345 CrossRef CAS.
- H. Kim, G. Holló, C. M. Heo, I. Lagzi, H. Lee and S. H. Yang, Cryst. Growth Des., 2024, 24, 8794–8802 CrossRef CAS.
- R. Matalon and A. Packter, J. Colloid Sci., 1955, 10, 46–62 CrossRef CAS.
- Z. Rácz, Phys. A, 1999, 274, 50–59 CrossRef.
- L. Badr and R. Sultan, J. Phys. Chem. A, 2009, 113, 6581–6586 CrossRef CAS PubMed.
- Z. Shreif, L. Mandalian, A. Abi-Haydar and R. Sultan, Phys. Chem. Chem. Phys., 2004, 6, 3461 RSC.
- A. Toramaru, T. Harada and T. Okamura, Phys. D, 2003, 183, 133–140 CrossRef CAS.
- M. Itatani, Q. Fang, K. Unoura and H. Nabika, J. Phys. Chem. B, 2020, 124, 8402–8409 CrossRef CAS.
- É. Kárpáti-Smidróczki, A. Büki and M. Zrínyi, Colloid Polym. Sci., 1995, 273, 857–865 CrossRef.
- G. Holló, D. Zámbó, A. Deák, F. Rossi, R. Cucciniello, P. Lo Nostro, H. Nabika, B. Baytekin, I. Lagzi and M. Itatani, J. Phys. Chem. B, 2022, 126, 8322–8330 CrossRef PubMed.
- R. Makki, M. Al-Ghoul and R. Sultan, J. Phys. Chem. A, 2009, 113, 6049–6057 CrossRef CAS.
- I. Lagzi, Phys. Chem. Chem. Phys., 2002, 4, 1268–1270 RSC.
- M. Al-Ghoul and R. Sultan, J. Phys. Chem. A, 2003, 107, 1095–1101 CrossRef CAS.
- I. Bena, M. Droz and Z. Rácz, J. Chem. Phys., 2005, 122, 204502 CrossRef CAS PubMed.
- M. Morsali, M. T. A. Khan, R. Ashirov, G. Holló, H. T. Baytekin, I. Lagzi and B. Baytekin, Adv. Mater., 2020, 32, 1905779 CrossRef CAS PubMed.
- M. Parsa, S. Harmand, K. Sefiane, M. Bigerelle and R. Deltombe, Langmuir, 2015, 31, 3354–3367 CrossRef CAS PubMed.
- S. Thomas, I. Lagzi, F. Molnár and Z. Rácz, Phys. Rev. Lett., 2013, 110, 078303 CrossRef PubMed.
- M.-A. Han, S.-H. Jeon and Y.-J. Kang, J. Korean Chem. Soc., 2008, 52, 356–361 CrossRef CAS.
- T. Antal, M. Droz, J. Magnin, A. Pekalski and Z. Rácz, J. Chem. Phys., 2001, 114, 3770–3775 CrossRef CAS.
- D. Ezzeddine, H. El-Rassy and R. Sultan, Chem. Phys. Lett., 2019, 734, 136735 CrossRef CAS.
- I. Das, S. S. Das, A. Pushkarna and S. Chand, J. Colloid Interface Sci., 1989, 130, 176–183 CrossRef CAS.
- Y. Kanazawa and Y. Asakuma, J. Cryst. Process Technol., 2014, 04, 65–70 Search PubMed.
- T. Ban, M. Kaji, Y. Nagatsu and H. Tokuyama, ACS Omega, 2017, 2, 8027–8032 CrossRef CAS PubMed.
- E. S. Akbulut, G. Holló, I. Lagzi and B. Baytekin, Cryst. Growth Des., 2023, 23, 8718–8725 CrossRef CAS.
- M. T. A. Khan, J. Kwiczak-Yiğitbaşı, P. Tootoonchian, M. Morsali, I. Lagzi and B. Baytekin, ACS Appl. Mater. Interfaces, 2022, 14, 7252–7260 CrossRef CAS.
- P. Tootoonchian, J. Kwiczak-Yiğitbaşı, M. Turab Ali Khan, R. Chalil Oglou, G. Holló, F. Karadas, I. Lagzi and B. Baytekin, Chem. – Eur. J., 2023, 29, e202301261 CrossRef CAS PubMed.
- H. Qiao, S. Sun and P. Wu, Adv. Mater., 2023, 35, 2300593 CrossRef CAS.
- H. Arı, R. Uzunlar, E. S. Akbulut, I. Lagzi and B. Baytekin, Soft Matter, 2025, 21, 3005–3011 RSC.
- B. Dúzs and I. Szalai, Commun. Chem., 2020, 3, 168 CrossRef PubMed.
- M. He, J. Yao, Q. Liu, K. Wang, F. Chen and H. Wang, Microporous Mesoporous Mater., 2014, 184, 55–60 CrossRef CAS.
- O. Kolmykov, J.-M. Commenge, H. Alem, E. Girot, K. Mozet, G. Medjahdi and R. Schneider, Mater. Des., 2017, 122, 31–41 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55 RSC.
- M. Watzl and A. F. Münster, J. Phys. Chem. A, 1998, 102, 2540–2546 CrossRef CAS.
- B. K. Agarwalla, S. Galhotra and J. K. Bhattacharjee, J. Math. Chem., 2014, 52, 188–197 CrossRef CAS.
- R. Feeney, S. L. Schmidt and P. Ortoleva, Phys. D, 1981, 2, 536–544 CrossRef.
- S. V. Amrutha, A. Sebastian, P. Sibeesh, S. Punacha and T. K. Shajahan, J. Phys. Chem. C, 2022, 126, 19618–19626 CrossRef CAS.
- R. Sultan and R. Halabieh, Chem. Phys. Lett., 2000, 332, 331–338 CrossRef CAS.
- V. Kireev, B. Shalabayeva, N. Jaichibekov, A. Nizamova and Z. Kozhabay, J. Phys.: Conf. Ser., 2019, 1391, 012120 CrossRef.
- Á. Tóth, D. Horváth and W. Van Saarloos, J. Chem. Phys., 1999, 111, 10964–10968 CrossRef.
- Z. Virányi, A. Szommer, Á. Tóth and D. Horváth, Phys. Chem. Chem. Phys., 2004, 6, 3396–3401 RSC.
- N. Német, G. Holló, N. Valletti, S. Farkas, B. Dúzs, Á. Kukovecz, G. Schuszter, I. Szalai, F. Rossi and I. Lagzi, Mater. Adv., 2024, 5, 1199–1204 RSC.
- Y. S. Shin, G. Holló, I. Lagzi and S. H. Yang, Cryst. Growth Des., 2024, 24, 9994–10002 CrossRef CAS.
- J. Rahbani, A. R. Behzad, N. M. Khashab and M. Al-Ghoul, Electrophoresis, 2013, 34, 405–408 CrossRef CAS PubMed.
- Q. Wang and E. Nakouzi, Environ. Sci. Technol. Lett., 2023, 10, 1188–1194 CrossRef CAS.
- Q. Wang, Y. Fu, E. A. Miller, D. Song, P. J. Brahana, A. Ritchhart, Z. Xu, G. E. Johnson, B. Bharti, M. L. Sushko and E. Nakouzi, ChemSusChem, 2025, e202402372 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |