Open Access Article
Open Access ArticleSustainable hydrogen production via CO2-assisted BH3 + BH3 reaction: a computational analysis†
Trinh Le Huyen *,
Tran Thi Thanh Huyen
*,
Tran Thi Thanh Huyen ,
Cao Chi Nam
,
Cao Chi Nam and
Pham Cam Nam
and
Pham Cam Nam *
*
Faculty of Chemical Engineering, University of Science and Technology, Danang University, Danang 550000, Vietnam. E-mail: pcnam@dut.udn.vn; tlhuyen@dut.udn.vn
First published on 10th July 2025
Abstract
The activation and utilization of carbon dioxide (CO2) for hydrogen production represents a central challenge in the development of sustainable and carbon-neutral energy systems. Borane (BH3), a potent Lewis acid with high reactivity toward small molecules, has emerged as a promising candidate for CO2 activation and hydrogen release. However, the mechanistic effects of incorporating multiple CO2 molecules into BH3-based systems remain poorly understood. In this study, density functional theory (DFT) calculations were conducted to explore the reaction mechanisms of a dimeric BH3 system in the presence of zero to three CO2 molecules. Potential energy surfaces were constructed at the M06-2X/6-311++G(3df,2p) level to identify key intermediates, transition states, reaction energies, and activation barriers. The computational results reveal a stepwise mechanism involving BH3–CO2 adduct formation and distinct transition states, with CO2 playing a significant role in modulating both thermodynamic stability and kinetic accessibility. Notably, the inclusion of CO2 stabilizes multi-component complexes and lowers activation barriers, thereby facilitating hydrogen release. These findings underscore the dual function of CO2 as both a structural stabilizer and an energetic facilitator, offering valuable insights into CO2 valorization and hydrogen generation in the context of sustainable energy applications.
1 Introduction
One of the key areas of interest in organoboron chemistry1 is the reactivity of boron hydrides, especially the interaction of borane (BH3) and its derivatives with small molecules.2–4 Borane, a strong Lewis acid,5 readily participates in a variety of chemical transformations, including hydroboration,6 coordination with Lewis bases, and activation of small molecules.7 Among these, the reaction between borane and carbon dioxide (CO2)8,9 has attracted considerable attention due to its potential implications in CO2 fixation, catalysis, and hydrogen storage applications.10–16 Borane-based reagents offer a promising strategy for CO2 utilization through chemical–physical transformation. Borane, a strong electrophile, can react with CO2 directly or in the presence of additional reactants, leading to various reduction and activation pathways.17 However, a comprehensive mechanistic understanding of this reaction remains incomplete in some experimental and computational studies in some experimental and computational studies.9,10 Theoretical methods, particularly density functional theory (DFT), are valuable tools for elucidating reaction mechanisms, providing insight into electronic structures, energy landscapes, and dynamics of intermediate and transition states. The borane–CO2 interaction involves initial adduct formation and subsequent structural rearrangements that determine the reaction pathway. Intermediate stability is influenced by electronic effects, solvation, and CO2 stoichiometry. Experimental and computational studies show borane can reduce CO2 under suitable conditions, yielding formate, carbonate, or methane derivatives, depending on the reaction environment and mechanism.10,17A fundamental question regarding this reaction is why two borane molecules are required instead of a single BH3 reacting with multiple CO2 molecules. This requirement arises could be from several key factors: Although BH3 is a strong Lewis acid, a single molecule has limited capacity to coordinate with multiple CO2 molecules, whereas the presence of two BH3 molecules enables more efficient cooperative activation of CO2. Additionally, the formation of multinuclear boron species plays a crucial role in stabilizing transition states and lowering reaction barriers, thereby facilitating CO2 conversion. The interaction between two BH3 molecules also increases the likelihood of forming cyclic of B–H atoms,18–20 which are more stable. Furthermore, theoretical studies indicate that intermediates involving two BH3 molecules exhibit higher stability due to boron–boron interactions,21,22 leading to more favorable reaction pathways.
To effectively address these challenges, a comprehensive investigation into the electronic and structural changes occurring throughout the reaction is essential. In particular, the competition between a concerted single-step CO2 insertion and stepwise, radical-mediated pathways highlights the need for in-depth theoretical analysis. Recent advancements in DFT methodologies offer a powerful framework for accurately predicting transition states, activation barriers, and the thermodynamic viability of proposed mechanisms. In this study, we utilize state-of-the-art computational techniques to systematically explore the borane–CO2 reaction, with a focus on identifying key intermediates and transition states, as well as elucidating structure–reactivity relationships that underpin CO2 activation. Furthermore, recent DFT-based investigations on boron hydride species such as BH4− reacting with radical HO˙23 provide valuable complementary insights into hydrogen evolution mechanisms and radical reactivity within boron chemistry.
To gain deeper insights into the electronic nature of the reaction, we incorporated quantum chemical analyses, such as the electron localization function (ELF) to examine the bonding characteristics of critical species, offering valuable insights into the electronic rearrangements governing the reaction. Additionally, potential energy surface (PES) calculations were performed to delineate viable reaction pathways and characterize transition states, providing a comprehensive picture of borane–CO2 interactions at the molecular level.
Infrared (IR) spectral simulations were also conducted to compare theoretical vibrational frequencies with experimental data, aiding in the identification of reaction intermediates and key transition states.
Kinetic modeling complemented our mechanistic investigation by estimating reaction rate constants and activation parameters along the preferred reaction pathways. By integrating PES mapping with kinetic analysis, we constructed a detailed reaction model that accounts for both thermodynamic and kinetic considerations, ultimately providing a predictive framework for borane-mediated CO2 activation. The findings of this study contributed to a more profound understanding of boron-based CO2 transformation processes, paving the way for the rational design of boron-containing catalysts and reagents. A deeper comprehension of these fundamental reaction mechanisms facilitated the development of efficient CO2 conversion strategies, thereby supporting broader efforts in sustainable carbon utilization. Furthermore, the insights gained from this research extended to other borane-mediated small molecule activations, expanding the scope of organoboron chemistry beyond traditional hydroboration and synthetic applications. The computational methodology employed in this work served as a valuable reference for future experimental validation and further advancements in borane–CO2 chemistry.
2 Computational methods
All electronic structure calculations were carried out using the Gaussian 09 (ref. 24) suite of programs. The geometries of reactants, products, intermediates, and transition states involved in the reactions of BH3 + BH3 + nCO2 (n = 0–3) were optimized by employing the Minnesota functional (M06-2X) in combination with the 6-311++G(3df,2p) basis set.25 This methodological framework enabled the precise optimization of BH3 structure in the presence of CO2, providing valuable insights into molecular interactions and structural characteristics.Subsequent to geometry optimization, a detailed vibrational frequency analysis was conducted to characterize each stationary point. These computed vibrational frequencies were instrumental in confirming the nature of stationary points and applying zero-point energy (ZPE) corrections. Such calculations were essential for evaluating the stability and energetic properties of molecular species, thereby deepening our comprehension of their fundamental behavior. For open-shell species, the restricted formalism (M06-2X) was adopted to ensure accuracy.
Transition states were located using the Synchronous Transit-Guided Quasi-Newton (STQN) methodology, specifically employing the Quadratic Synchronous Transit (QST2 & QST3) approach when necessary. To validate the connectivity between transition states and their respective reactants and products, intrinsic reaction coordinate (IRC) analyses were performed.
The influence of CO2 was systematically explored by progressively varying the number of CO2 molecules (n = 0–3) within the system. For each configuration, geometry optimization, vibrational analysis, and electronic energy calculations were performed to evaluate the influence of CO2 on reaction mechanisms, energy barriers, and product distribution. The Electron Localization Function (ELF)26 approach was employed to determine the localization of excess electrons by partitioning the total electron density into distinct basins. Complementary to ELF analysis, the Atoms-in-Molecule (AIM) framework27 utilized to investigate electron density distribution, with both analyses were conducted using the Multiwfn program.28
A crucial aspect of this study was the determination of the rate constant (k), which serves as a key parameter in quantifying reaction kinetics. Using transition state theory (TST) under standard conditions (1 M concentration at 298.15 K), rate constants were computed via eqn (1).29–36 All kinetic parameters were estimated in the gas phase using conventional TST, incorporating the partition functions of the reactants (BH3, BH3, CO2) and transition states. The ChemRate software37 was employed for all kinetic calculations.
 | (1) |
3 Results and disscusions
3.1 Gas-phase hydrogen release: the BH3 + BH3 → BH2BH2 + H2 reaction
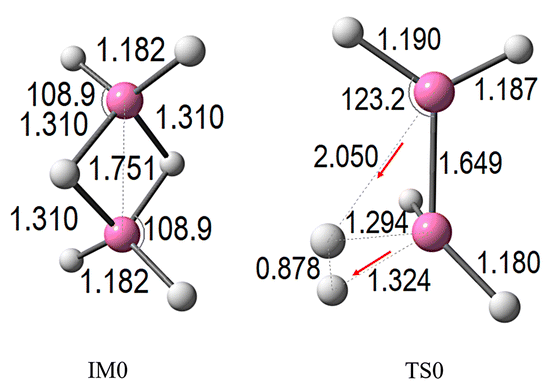
The BH3 + BH3 dehydrogenation mechanism was re-examined using M06-2X/6-311++G(3df,2p), with a focus on benchmarking against existing literature.In the initial stage, BH3 interacts with BH3, leading to the formation of an intermediate complex, designated as IM0. This species subsequently progresses to a transition state, TS0, which corresponds to the highest energy point along the reaction coordinate, where hydrogen dissociation is actively occurring. The optimized structures of IM0 and TS0, along with key geometric parameters, are illustrated in Fig. 1. The corresponding relative energies, referenced to the isolated reactants, are depicted in the potential energy surface shown in Fig. 2 (green curve, where n = 0 denotes the absence of CO2 molecules).
The interaction between two BH3 molecules leads to the formation of diborane(6) (B2H6). Structural parameters shown in Fig. 1 indicate that the two BH3 units are bridged via B–H bonds with calculated bond lengths of 1.310 Å, and a B–B distance of 1.751 Å, obtained at the M06-2X/6-311++G(3df,2p) level. These values are in close agreement with the data reported by D. Sethio et al.,20 who employed the CCSD(T)/cc-pVTZ method, reporting 1.315 Å and 1.763 Å, respectively. Moreover, the computed bond lengths also show strong consistency with the experimental values of 1.314 Å and 1.747 Å obtained by J. L. Duncan,41 further demonstrating the reliability and accuracy of the selected computational model. As shown in Fig. 2, the binding energy for dimer formation leading to B2H6 (IM0) is calculated to be −36.96 kcal mol−1, representing a pre-transition state complex. This process proceeds via the transition state TS0, which features an activation barrier of 2.63 kcal mol−1 relative to the isolated reactants. Analysis of the vibrational modes at TS0 reveals a key imaginary frequency of −340.19 cm−1, corresponding to a concerted H2 elimination mechanism. In this step, each BH3 unit contributes a single hydrogen atom to form the H2 molecule, while the two BH3 units move closer together, shortening the B–B distance to 1.649 Å. In the TS0, the hydrogen atom from the upper BH3 (in Fig. 2) separates, with a B⋯H distance of 2.050 Å, while the lower BH3 provides a hydrogen atom with a B⋯H distance of 1.324 Å. These two hydrogen atoms combine to form molecular H2, which dissociates from the remaining B2H4 fragment. The final relative energy of this product is 0.47 kcal mol−1. This mechanism highlights that the H2 release from B2H6 proceeds via a much lower activation energy pathway compared to direct cleavage of two hydrogen atoms from a single BH3 unit, which requires a significantly higher energy input of 89.14 kcal mol−1, as reported by Q. Ge et al.42 This finding underscores the cooperative role of the BH3 dimer in facilitating efficient H2 evolution, offering valuable insight into borane-based hydrogen storage and release processes.
3.2 Influence of single CO2 molecule on the BH3 + BH3 dehydrogenation mechanism
As above discussed, the H2 release process from B2H6 is thermodynamically unfavorable, owing to its endothermic nature (ΔH > 0). This highlights the importance of identifying suitable co-reactants that could drive the reaction toward thermodynamic feasibility. Although species such as SiH4, NH3, H2O, and CO have been investigated,43–46 the potential influence of CO2 has not been thoroughly explored. This motivates the present investigation into the B2H6 + nCO2 reaction, aimed at understanding how CO2 interacts with electron-deficient boranes. Such interactions are directly relevant to CO2 activation and conversion, both of which are crucial challenges in carbon management. Furthermore, exploring the chemical behavior of B2H6 under CO2 atmosphere provides valuable insight into how small molecules, particularly CO2, influence hydrogen release from boron hydrides, ultimately linking to clean hydrogen production and carbon recycling technologies.To assess the effect of CO2 on the dehydrogenation pathway of BH3 + BH3, we conducted a computational investigation of the BH3 + BH3 + CO2 reaction at the same theoretical level (Fig. 3).
 | ||
| Fig. 3 Calculated molecular structures of species along the gas-phase BH3 + BH3 + 3CO2 reaction pathway, optimized at M06-2X/6-311++G(3df,2p), displaying key bond lengths (Å) and bond angles (°). | ||
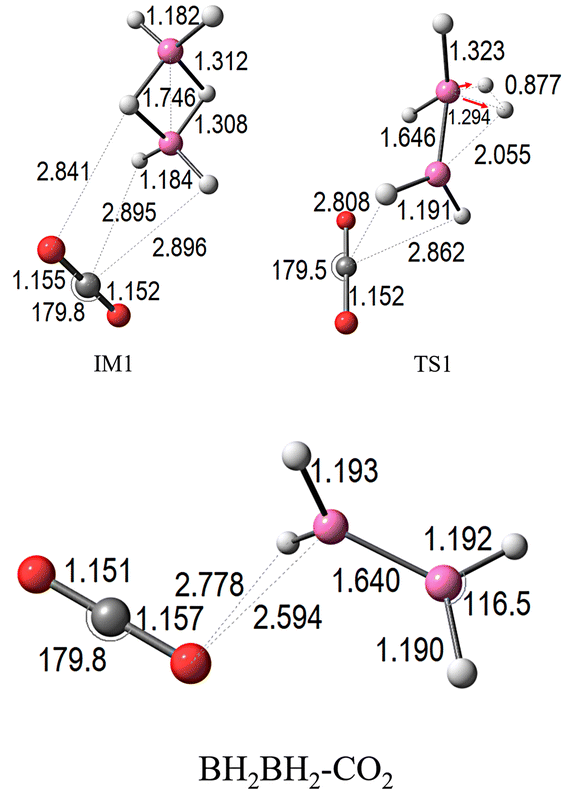
As presented in Fig. 2 (blue line, n = 1), the initial interaction between BH3–BH3 and CO2 forms a stable complex, serving as the reference point with a relative electronic energy (ΔE + ZPE) set at 0.0 kcal mol−1. Progressing along the reaction coordinate, this interaction leads to the formation of intermediate IM1, which exhibits considerable stabilization at −37.78 kcal mol−1, highlighting the strong association between the reactants, particularly through the participation of CO2. The conversion from IM1 to the corresponding transition state (TS1) requires surpassing an activation barrier of only 1.2 kcal mol−1, markedly lower than the 2.63 kcal mol−1 required in the absence of CO2 (TS0). This clear reduction in barrier height underscores the catalytic-like influence of CO2 in promoting the process.
At TS1 (see Fig. 3), notable structural rearrangements are observed: two B–H bonds within BH3 extend to 1.323 Å and 2.055 Å, indicating partial bond cleavage during H2 evolution. Simultaneously, the B–B bond contracts slightly to 1.646 Å. The CO2 fragment interacts strongly within the complex, maintaining C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths near 1.15 Å and a nearly linear O
O bond lengths near 1.15 Å and a nearly linear O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle of 179.5°. These structural changes correspond to an imaginary frequency of −332.32 cm−1, associated with a vibrational mode representing the concerted H2 release and atomic rearrangement. Beyond this transition state, the pathway leads to the exergonic formation of BH2BH2–CO2 and H2, with a final relative energy of −0.83 kcal mol−1. The presence of CO2 not only lowers the activation barrier but also enhances both CO2 capture and H2 generation, offering a dual benefit relevant to clean energy production and carbon management.
O angle of 179.5°. These structural changes correspond to an imaginary frequency of −332.32 cm−1, associated with a vibrational mode representing the concerted H2 release and atomic rearrangement. Beyond this transition state, the pathway leads to the exergonic formation of BH2BH2–CO2 and H2, with a final relative energy of −0.83 kcal mol−1. The presence of CO2 not only lowers the activation barrier but also enhances both CO2 capture and H2 generation, offering a dual benefit relevant to clean energy production and carbon management.
3.3 Influence of double CO2 molecules on the BH3 + BH3 dehydrogenation mechanism
In this section, the influence of two CO2 molecules on the dehydrogenation pathway of the BH3BH3 complex is investigated. Calculations were conducted using the M06-2X/6-311++G(3df,2p) level of theory. The initial interaction among BH3 + BH3 + 2CO2 establishes a reference electronic energy (including ZPE) of 0.0 kcal mol−1. As the reaction proceeds, this interaction leads to the formation of an intermediate complex (IM2, Fig. 4) with a significantly lower energy of −38.85 kcal mol−1 (see Fig. 2), indicating strong stabilization due to cooperative binding by the two CO2 molecules. The subsequent transformation from IM2 to the product state requires overcoming a remarkably low activation barrier of −0.91 kcal mol−1, which is considerably reduced compared to the barriers for TS0 (2.63 kcal mol−1) and TS1 (1.20 kcal mol−1). This substantial reduction highlights the pronounced catalytic effect arising from the second CO2, further accelerating the dehydrogenation process. At the TS2 structure, significant geometric rearrangement is observed: the B–H bond contracts to 1.309 Å, while the opposite B–H bond within the lower BH3 unit elongates to 2.013 Å, marking the onset of H2 release. Simultaneously, the B–B bond contracts slightly to 1.646 Å. Both CO2 molecules exhibit strong interactions with the evolving product complex, with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths of approximately 1.155 Å and nearly linear O
O bond lengths of approximately 1.155 Å and nearly linear O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angles of 179.6°. The imaginary frequency associated with TS2 is calculated as −445.71 cm−1, corresponding to a vibrational mode coordinating the concerted release of H2 and the structural adjustment of the CO2 framework.
O angles of 179.6°. The imaginary frequency associated with TS2 is calculated as −445.71 cm−1, corresponding to a vibrational mode coordinating the concerted release of H2 and the structural adjustment of the CO2 framework.
As the reaction progresses, the final products BH2BH2–2CO2 and H2 form with an overall exergonicity of −2.74 kcal mol−1, demonstrating that the incorporation of a second CO2 not only further reduces the activation energy but also enhances the efficiency of both dehydrogenation and CO2 capture, underscoring its potential significance in combined hydrogen production and carbon utilization strategies.
3.4 Influence of triple CO2 molecules on the BH3 + BH3 dehydrogenation mechanism
To gain deeper insight into the CO2-assisted dehydrogenation process, we examined the pathway involving BH3 + BH3 in the presence of three CO2 molecules. The optimized structures of the intermediate and transition state are illustrated in Fig. 5 | ||
| Fig. 5 M06-2X/6-311++G(3df,2p) optimized geometries of species along the BH3 + BH3 + 3CO2 gas-phase reaction pathway, with key bond lengths (Å) and bond angles (°). | ||
The corresponding potential energy profile, including ZPE corrections, indicates that the initial BH3 + BH3 + 3CO2 complex starts at 0.0 kcal mol−1 (Fig. 2). The reaction proceeds through the formation of an intermediate species, IM3, which is significantly stabilized at −39.85 kcal mol−1 (Fig. 5). Notably, the introduction of three CO2 molecules further reduces the activation energy required for dehydrogenation. The computed activation barrier at the transition state TS3 is only −2.35 kcal mol−1, a substantial decrease compared to the previous cases: TS0 (2.63 kcal mol−1), TS1 (1.20 kcal mol−1), and TS2 (−0.91 kcal mol−1). This progressive reduction highlights the catalytic role of CO2 in facilitating the H2 release from the BH3 + BH3 complex. At TS3, the vibrational analysis reveals an imaginary frequency of −561.83 cm−1, associated with the concerted release of H2 and structural reorganization involving CO2. Structural changes at this point include the contraction of the B–H bond to 1.299 Å, while the opposite BH3 unit elongates its B–H bond to 1.990 Å, indicating active bond cleavage leading to H2 formation. Simultaneously, the B–B distance contracts to 1.645 Å. The three CO2 molecules maintain strong interactions with the complex, characterized by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths ranging from 1.152 Å to 1.156 Å and nearly linear O
O bond lengths ranging from 1.152 Å to 1.156 Å and nearly linear O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angles close to 179.7°. The reaction ultimately yields BH2BH2–3CO2 and H2, with an overall energy release of −5.55 kcal mol−1. This systematic investigation, increasing the number of CO2 molecules from 1 to 3, underscores the remarkable adaptability of the BH3 + BH3 system as both a hydrogen carrier and a CO2 sorbent. With a single CO2 molecule, catalytic enhancement is already observed; adding two and eventually three CO2 molecules progressively lowers the activation barriers from TS0 (2.63 kcal mol−1) to TS2 (−0.91 kcal mol−1) and TS3 (−2.35 kcal mol−1).
O angles close to 179.7°. The reaction ultimately yields BH2BH2–3CO2 and H2, with an overall energy release of −5.55 kcal mol−1. This systematic investigation, increasing the number of CO2 molecules from 1 to 3, underscores the remarkable adaptability of the BH3 + BH3 system as both a hydrogen carrier and a CO2 sorbent. With a single CO2 molecule, catalytic enhancement is already observed; adding two and eventually three CO2 molecules progressively lowers the activation barriers from TS0 (2.63 kcal mol−1) to TS2 (−0.91 kcal mol−1) and TS3 (−2.35 kcal mol−1).
This dual reactivity hydrogen release coupled with CO2 capture positions BH3 + BH3 as a promising candidate for advanced energy materials. It offers both a sustainable route for hydrogen generation, essential for clean energy technologies, and an effective platform for CO2 sequestration, contributing to carbon management strategies. This unique synergy between hydrogen storage and carbon capture highlights the potential of borane-based systems in future catalytic and energy storage applications, aligning with global efforts toward sustainable energy and environmental remediation.
3.5 IR spectra and vibrational features of BH3BH3–n(CO2) complexes (n = 0 to 3)
Fig. 6 presents the infrared (IR) spectra of four species: BH3BH3 (a), BH3BH3–CO2 (b), BH3BH3–2CO2 (c), and BH3BH3–3CO2 (d) which generated based on vibrational frequency results obtained from quantum chemical calculations performed at the M06-2X/6-311++G(3df,2p) level of theory (Table S2†). These spectra reveal distinct shifts in the low-frequency region (0–500 cm−1) upon sequential incorporation of CO2 molecules into the BH3BH3 framework. For pristine BH3BH3 (spectrum a), no prominent absorption bands are observed within this range, indicating the absence of external molecular interactions. However, after coordination with a single CO2 molecule (spectrum b), new vibrational peaks emerge, attributable to modes induced by CO2 binding. With the addition of a second CO2 molecule (spectrum c), these features become more prominent, reflecting enhanced interaction strength. In the case of BH3BH3–3CO2 (spectrum d), the intensities of these peaks further increase, signaling more complex vibrational coupling arising from multiple CO2 incorporations. Collectively, these spectral changes provide clear evidence of progressive CO2 integration, which profoundly modifies the vibrational signature of the parent BH3BH3 species. | ||
| Fig. 6 Calculated IR spectra of: (a) BH3–BH3, (b) BH3–BH3–CO2, (c) BH3–BH3–2CO2, and (d) BH3–BH3–3CO2, obtained at the M06-2X/6-311++G(3df,2p) level of theory. | ||
3.6 Analysis of electrostatic interactions in the BH3BH3–nCO2 system
Analysis of the electron localization function (ELF)26 maps for the BH3BH3–nCO2 complexes (shown in Fig. 7a–c) provides clear evidence of direct contact between the hydrogen atoms from the boron hydride framework and oxygen atoms from the CO2 molecules. These interactions primarily take place at the interface between the boron-containing fragment and the adsorbed CO2 units, where increased electron density suggests partial covalent character. Supporting this interpretation, topological analysis using atoms-in-molecules (AIM)27 theory (Fig. 7d–f) reveals the presence of distinct bond critical points (BCPs) that correspond to these interaction sites. Such findings indicate that the bonding mechanism is consistent with a Lewis acid–base interaction, where the boron centers function as electron acceptors, while the oxygen atoms of CO2 act as electron donors. Together, the ELF and AIM data provide strong confirmation that stable and cooperative bonding occurs when CO2 interacts with the BH3BH3 system. To further clarify the stabilizing role of CO2, we calculated the interaction energies (Ebd) for the formation of the BH3BH3·nCO2 adducts using the expression:| Ebd = E[BH3BH3·nCO2] − E[BH3BH3] − nE[CO2] (kcal mol−1) |
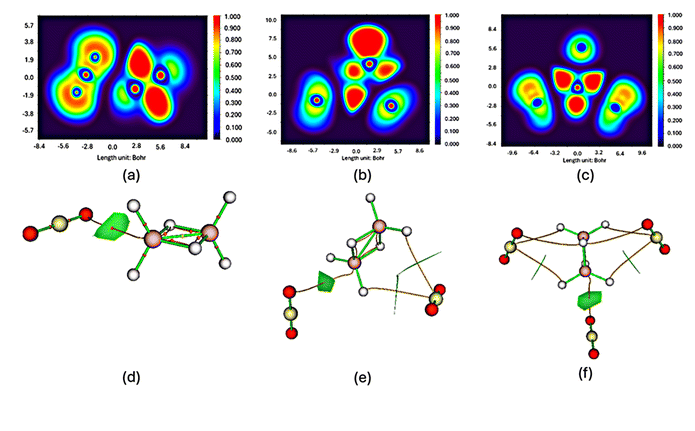 | ||
| Fig. 7 ELF and AIM maps of the BH3BH3–CO2 (a and d); BH3BH3–2CO2 (b and e), and BH3BH3–3CO2 (c and f), calculated at M06-2X/6-311++G(3df,2p) level. | ||
The resulting interaction energies are −0.81 kcal mol−1 (n = 1), −1.89 kcal mol−1 (n = 2), and −2.89 kcal mol−1 (n = 3), confirming a progressively stronger stabilization effect as more CO2 molecules are introduced. This trend indicates not only additive but also cooperative binding interactions between the BH3 dimer and CO2 molecules. Additionally, structural analysis reveals that the B–B bond length decreases from 1.751 Å (in IM0) to 1.645 Å (in TS3), while the B–H bonds involved in H2 formation show slight elongation. These trends, consistent across the reaction coordinate, indicate that CO2 not only stabilizes the complex electronically but also induces favorable geometric changes that facilitate hydrogen release. This quantitative structural and energetic evidence reinforces the dual role of CO2 as both a structural stabilizer and a reactivity modulator in the BH3 dimer system.
3.7 CO2 adsorption capacity of the BH3 + BH3 complex and comparison with conventional adsorbents
To evaluate the CO2 capture potential of the BH3 + BH3 complex, we computed its CO2 adsorption capacity under conditions where one, two, and three CO2 molecules are incorporated into the structure. The adsorption capacity, expressed in mmol CO2 per gram of BH3, was determined based on the molecular weight of the system and the stoichiometry of CO2 binding. The calculated adsorption capacities were subsequently compared with values reported for conventional hybrid sorbents, including graphene oxide (GO)-based composites, metal–organic frameworks (MOFs), and hydrogen boride (HB) sheets. These materials, summarized in Table 1.Notably, the CO2 adsorption capacity of the BH3 + BH3 complex far exceeds those of conventional sorbents, such as Fe3O4-rGO (2.50 mmol g−1), GO-UiO-66 (3.37 mmol g−1), GO-ZnO (1.94 mmol g−1), and N-doped rGO-Zn (3.31 mmol g−1). This striking enhancement can be attributed to the strong chemisorptive interactions between CO2 and the electron-deficient boron centers within the BH3–BH3 system, further stabilized through cooperative binding effects arising from the flexible, adaptive nature of the dimeric boron hydride framework. In contrast, most conventional hybrid sorbents primarily rely on physisorption mechanisms, which are inherently weaker and less selective under ambient conditions. The extraordinarily high adsorption capacity observed for the BH3–BH3 complex can, at least in part, be attributed to the fact that this system is evaluated at the molecular level, where individual interactions between BH3 units and CO2 molecules are fully resolved. At this scale, the inherent chemical reactivity of the boron centers and the flexibility of the B–H framework allow for highly efficient CO2 trapping. This result serves as a molecular-level signal indicating the strong intrinsic affinity of boron hydrides for CO2, which could potentially be translated into larger-scale materials with engineered porosity and connectivity. This molecular insight is further supported by previous investigations into the CO2 adsorption properties of hydrogen boride (HB) sheets, a class of metal-free two-dimensional materials composed of boron and hydrogen in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio. Recent studies51 have demonstrated that pristine HB sheets exhibit negligible CO2 adsorption under ambient conditions. However, hydrogen-deficient HB sheets in which some surface hydrogen atoms are removed demonstrate reproducible physisorption of CO2 at 297 K, with a saturation coverage of only 2.4 × 10−1 mmol g−1. The exceptional CO2 uptake of the BH3–BH3 complex further reinforces its potential as a dual-functional platform, capable of simultaneously acting as a high-performance CO2 capture material and an efficient hydrogen storage medium. This combined functionality not only advances the development of integrated carbon capture and utilization (CCU) systems, but also provides a promising molecular design strategy for next-generation carbon management and clean hydrogen technologies. By leveraging its unique molecular structure and intrinsic reactivity, the BH3–BH3 complex exemplifies how fundamental molecular chemistry can inspire the design of innovative materials for sustainable energy and environmental applications.
1 stoichiometric ratio. Recent studies51 have demonstrated that pristine HB sheets exhibit negligible CO2 adsorption under ambient conditions. However, hydrogen-deficient HB sheets in which some surface hydrogen atoms are removed demonstrate reproducible physisorption of CO2 at 297 K, with a saturation coverage of only 2.4 × 10−1 mmol g−1. The exceptional CO2 uptake of the BH3–BH3 complex further reinforces its potential as a dual-functional platform, capable of simultaneously acting as a high-performance CO2 capture material and an efficient hydrogen storage medium. This combined functionality not only advances the development of integrated carbon capture and utilization (CCU) systems, but also provides a promising molecular design strategy for next-generation carbon management and clean hydrogen technologies. By leveraging its unique molecular structure and intrinsic reactivity, the BH3–BH3 complex exemplifies how fundamental molecular chemistry can inspire the design of innovative materials for sustainable energy and environmental applications.
3.8 Kinetic study
This section investigates the hydrogen release kinetics from the BH3 dimer in the presence of increasing numbers of CO2 molecules. Key parameters, including equilibrium constants (Keq) and unimolecular rate constants (ku), were determined to assess how CO2 influences both thermodynamic and kinetic aspects of the process.3.9 Equilibrium constants
The equilibrium constants for the association between BH3 + BH3 and BH3 + BH3 + nCO2 (with n = 0, 1, 2, 3) are summarized in Table 2. The data reveal a systematic decline in equilibrium constants as more CO2 molecules are incorporated into the system. Without CO2, the equilibrium constant reaches 1.10 × 1020, indicative of an extremely favorable formation of the BH3 dimer. When a single CO2 is introduced, the equilibrium constant drops to 5.96 × 1015, followed by 3.17 × 1010 for the two CO2 system, and finally 4.14 × 105 when three CO2 molecules are present. This decreasing trend reflects the competitive stabilization provided by CO2 coordination, which shifts the equilibrium away from simple dimer formation toward the formation of CO2-stabilized adducts. Despite this gradual reduction in Keq, the values remain sufficiently large to indicate a strong thermodynamic driving force toward product formation in all cases. This implies that, while CO2 reduces the preference for direct BH3 dimerization, it promotes formation of more complex BH3–BH3–CO2 adducts, ensuring that CO2 incorporation does not hinder the overall hydrogen release process. Instead, CO2 contributes to restructuring the pathway to favor products where both hydrogen evolution and CO2 capture occur simultaneously.| Reaction | Keq |
|---|---|
| BH3 + BH3 ⇌ BH3–BH3 | 1.10 × 1020 |
| BH3 + BH3 + CO2 ⇌ BH3–BH3–CO2 | 5.96 × 1015 |
| BH3 + BH3 + 2CO2 ⇌ BH3–BH3–2CO2 | 3.17 × 1010 |
| BH3 + BH3 + 3CO2 ⇌ BH3–BH3–3CO2 | 4.14 × 105 |
3.10 Rate constants for hydrogen release
The unimolecular rate constants (ku) associated with hydrogen release from each intermediate complex (IMn) to its corresponding transition state (TSn) are presented in Table 3. The results indicate a clear increasing trend in rate constants as the number of CO2 molecules rises. For the reaction involving only BH3 + BH3, the rate constant is 3.3 × 10−16 s−1. When one CO2 molecule is introduced, the rate decreases slightly to 2.4 × 10−16 s−1, while the system with two CO2 molecules accelerates to 1.7 × 10−15 s−1. The fastest hydrogen release occurs when three CO2 molecules are present, reaching 1.2 × 10−14 s−1. This enhancement in ku highlights the catalytic role of CO2, where increasing CO2 coordination stabilizes the intermediates through favorable electrostatic and Lewis acid–base interactions. This stabilization reduces activation barriers, enabling a more efficient transition to the hydrogen release step. This trend reflects that CO2 coordination alters the reaction pathway, creating a smoother and more thermodynamically favored transition from reactants to products. Interestingly, the simultaneous decrease in equilibrium constants (Keq) and increase in rate constants (ku) with growing CO2 content reflects a mechanistic shift in the reaction. In the absence of CO2, dimer formation is exceptionally favored thermodynamically, but hydrogen release is relatively slow. As more CO2 is incorporated, the system shifts from direct dimerization to forming multi-component adducts, which, while slightly less stable, allow for faster hydrogen evolution. This transition highlights a CO2-induced catalytic enhancement, where CO2 plays a dual role: facilitating hydrogen release while simultaneously being captured into the product complex. This dual functionality makes the BH3–BH3–CO2 system particularly attractive for applications in clean energy and carbon management. It not only enables controlled hydrogen release, but also contributes to efficient CO2 capture, offering a promising integrated solution for hydrogen storage and carbon mitigation technologies.| Reaction | ku (s−1) |
|---|---|
| BH3 + BH3 → BH2BH2 + H2 | 3.3 × 10−16 |
| BH3 + BH3 + CO2 → BH2BH2–CO2 + H2 | 2.4 × 10−16 |
| BH3 + BH3 + 2CO2 → BH2BH2–2CO2 + H2 | 1.7 × 10−15 |
| BH3 + BH3 + 3CO2 → BH2BH2–3CO2 + H2 | 1.2 × 10−14 |
4 Conclusions
This study employed Density Functional Theory (DFT) calculations and kinetic modeling to illuminate the reaction between BH3, BH3, and CO2, with a specific focus on hydrogen release and CO2 capture mechanisms. Our findings reveal a significant influence of CO2 on the BH3–BH3 system:(a) CO2 significantly alters the hydrogen evolution pathway: as the number of CO2 molecules increases, the reaction mechanism shifts, leading to reduced energy barriers and enhanced stabilization of intermediates.
(b) Strong CO2–BH3–BH3 interactions enhance CO2 adsorption and shift thermodynamic equilibrium: computed equilibrium constants and binding energies demonstrate a high affinity, favoring stable multi-molecular adduct formation, crucial for combined hydrogen storage and carbon capture.
(c) The BH3–BH3 + (CO2)n system functions as a dual-functional platform for clean energy: it simultaneously releases hydrogen and captures CO2, offering a promising strategy to address both clean hydrogen generation and CO2 reduction. The system's tunability with varying CO2 amounts allows for optimization of both processes, showcasing its potential for energy storage and carbon management.
In essence, this work establishes the BH3–BH3 + nCO2 system as a highly promising candidate for integrated hydrogen storage and carbon capture. Future research should prioritize experimental validation and system optimization to fully realize its potential for sustainable energy solutions.
4.1 Influence of CO2 on hydrogen evolution
The introduction of CO2 significantly reshapes the reaction pathway and modifies the energy profile of the BH3–BH3 system. As the number of CO2 molecules increases from one to three, the reaction mechanism progressively shifts, reducing the energy barriers and enhancing the stabilization of intermediate species.4.2 Equilibrium and interaction energies
The computed equilibrium constants (Keq) and binding energies reveal strong interactions between CO2 and the BH3–BH3 complex. This strong affinity not only enhances CO2 adsorption but also impacts the thermodynamic equilibrium, with increasing CO2 concentration favoring the formation of stable multi-molecular adducts. Such robust binding further supports the feasibility of utilizing this system for combined hydrogen storage and carbon capture.4.3 Dual-functional platform for clean energy
The ability to simultaneously release hydrogen and capture CO2 highlights the multifunctionality of the BH3–BH3 complex. This dual capability offers a promising strategy to simultaneously address two pressing challenges: clean hydrogen generation and CO2 reduction. By adjusting the amount of available CO2, the system can be tuned to optimize both processes, presenting valuable potential for energy storage and carbon management technologies.In summary, this study identifies the BH3–BH3 + nCO2 system as a compelling candidate for integrated hydrogen storage and carbon capture applications. Future efforts should focus on experimental validation and further fine-tuning of system conditions to fully unlock its potential for sustainable energy solutions.
Data availability
Data will be made available on request.Author contributions
Trinh Le Huyen: conceptualization, methodology, validation, data curation, formal analysis, visualization, writing – original draft, writing – review & editing. Tran Thi Thanh Huyen and Chi Nam Cao: data curation and visualization. Pham Cam Nam: supervision, software, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Trinh Le Huyen was funded by the Postdoctoral Scholarship Programme of Vingroup Innovation Foundation (VINIF), code VINIF.2023.STS.23. This work was supported by The University of Danang – University of Science and Technology, code number of Project: T2024-02-34. During the preparation of this paper, generative AI and AI-assisted technologies were employed for grammar and spelling checks and sentence rewriting as needed. Following the use of these tools, the content was reviewed and edited to ensure accuracy, and we take full responsibility for the publication's content.References
- L. Kong and C. Cui, Synlett, 2021, 32, 1316–1322 CrossRef CAS.
- T. Fehlner, Inorg. Chem., 1973, 12, 98–102 CrossRef CAS.
- J. M. Galbraith, G. Vacek and H. F. Schaefer III, J. Mol. Struct., 1993, 300, 281–288 CrossRef.
- G. Parshall, J. Am. Chem. Soc., 1964, 86, 361–364 CrossRef CAS.
- V. Jonas, G. Frenking and M. T. Reetz, J. Am. Chem. Soc., 1994, 116, 8741–8753 CrossRef CAS.
- N. Miyaura, Catalytic Heterofunctionalization, 2001, pp. 1–45 Search PubMed.
- F. G. A. Stone, in Advances in Inorganic Chemistry and Radiochemistry, Elsevier, 1960, vol. 2, pp. 279–313 Search PubMed.
- D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082 CrossRef PubMed.
- A. B. Burg and H. Schlesinger, J. Am. Chem. Soc., 1937, 59, 780–787 CrossRef CAS.
- M. Mohammadi, S. A. Siadati, S. Ahmadi, S. Habibzadeh, M. R. Poor Heravi, Z. Hossaini and E. Vessally, Front. Chem., 2022, 10, 1003086 CrossRef CAS PubMed.
- T.-X. Zhao, G.-W. Zhai, J. Liang, P. Li, X.-B. Hu and Y.-T. Wu, Chem. Commun., 2017, 53, 8046–8049 RSC.
- J. J. Vajo, Boron-Based Hydrogen Storage: Ternary Borides and Beyond, HRL Laboratories, LLC, Malibu, CA (United States), 2016 Search PubMed.
- A. Züttel, M. Hirscher, B. Panella, K. Yvon, S. i. Orimo, B. Bogdanović, M. Felderhoff, F. Schüth, A. Borgschulte and S. Goetze, Hydrogen as a Future Energy Carrier, 2008, pp. 165–263 Search PubMed.
- M. M. Lin, J. T. Zheng and W.-Y. Yu, J. Taiwan Inst. Chem. Eng., 2024, 158, 105069 CrossRef CAS.
- B. Soleimani, M. N. Shahrak and K. S. Walton, J. Taiwan Inst. Chem. Eng., 2024, 163, 105638 CrossRef CAS.
- M. Ejaz, M. G. Mohamed and S.-W. Kuo, J. Taiwan Inst. Chem. Eng., 2025, 106098 CrossRef.
- K. Fujiwara, S. Yasuda and T. Mizuta, Organometallics, 2014, 33, 6692–6695 CrossRef CAS.
- L. A. Curtiss and J. A. Pople, J. Chem. Phys., 1988, 89, 4875–4879 CrossRef CAS.
- J.-D. Dill, P. v. R. Schleyer and J. Pople, J. Am. Chem. Soc., 1975, 97, 3402–3409 CrossRef CAS.
- D. Sethio, L. M. L. Daku and H. Hagemann, Int. J. Hydrogen Energy, 2016, 41, 6814–6824 CrossRef CAS.
- C. F. Lane, Chem. Rev., 1976, 76, 773–799 CrossRef CAS.
- E. Muetterties, Boron Hydride Chemistry, Elsevier, 2012 Search PubMed.
- T. Le Huyen and P. C. Nam, J. Taiwan Inst. Chem. Eng., 2025, 170, 105993 CrossRef.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussia revision A.02, Gaussian Inc., Wallingford, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119(2), e25686 CrossRef.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87(15), 2664–2682 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3(2), 107–115 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43(4), 1823–1835 CrossRef CAS.
- E. Velez, J. Quijano, R. Notario, E. Pabon, J. Murillo, J. Leal and G. Alarcon, J. Phys. Org. Chem., 2009, 22(10), 971–977 CrossRef CAS.
- H. Boulebd, A. Mechler, N. T. Hoa and Q. V. Vo, New J. Chem., 2020, 44(23), 9863–9869 RSC.
- E. Dzib, J. L Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy: A Program for computing Rate Constants in the Gas Phase and in Solution, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- V. Mokrushin, V. Bedanov, W. Tsang, M. Zachariah, V. Knyazev and W. McGivern, Chemrate, NIST, Gaithersburg, MD, 2002 Search PubMed.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- E. L. I. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100(10), 2984–2991 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35(11), 1303 CrossRef CAS.
- J. Duncan and J. Harper, Mol. Phys., 1984, 51, 371–380 CrossRef CAS.
- J. Liu, J. Aeschleman, L. Rajan, C. Che and Q. Ge, in Materials Issues in A Hydrogen Economy, World Scientific, 2009, pp. 234–243 Search PubMed.
- S.-W. Hu, Y. Wang, X.-Y. Wang, T.-W. Chu and X.-Q. Liu, J. Phys. Chem. A, 2003, 107, 9974–9983 CrossRef CAS.
- S. Sakai, J. Phys. Chem., 1995, 99, 9080–9086 CrossRef CAS.
- M. L. McKee, J. Phys. Chem., 1992, 96, 5380–5385 CrossRef CAS.
- S.-W. Hu, Y. Wang and X.-Y. Wang, J. Phys. Chem. A, 2003, 107, 1635–1640 CrossRef CAS.
- W. Li, X. Jiang, H. Yang and Q. Liu, Appl. Surf. Sci., 2015, 356, 812–816 CrossRef CAS.
- Y. Cao, Y. Zhao, Z. Lv, F. Song and Q. Zhong, J. Ind. Eng. Chem., 2015, 27, 102–107 CrossRef CAS.
- D. Zhou, Q. Liu, Q. Cheng, Y. Zhao, Y. Cui, T. Wang and B. Han, Chin. Sci. Bull., 2012, 57, 3059–3064 CrossRef CAS.
- W. Li, H. Yang, X. Jiang and Q. Liu, Appl. Surf. Sci., 2016, 360, 143–147 CrossRef CAS.
- T. Goto, S.-i. Ito, S. L. Shinde, R. Ishibiki, Y. Hikita, I. Matsuda, I. Hamada, H. Hosono and T. Kondo, Commun. Chem., 2022, 5, 118 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra03449c |
| This journal is © The Royal Society of Chemistry 2025 |