 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Entanglements in polymer nanocomposites containing spherical nanoparticles†
Argyrios
Karatrantos
*a,
Nigel
Clarke
*a,
Russell J.
Composto
b and
Karen I.
Winey
b
aDepartment of Physics and Astronomy, University of Sheffield, Sheffield S3 7RH, UK. E-mail: argyrioskaratrantos@gmail.com; n.clarke@sheffield.ac.uk
bDepartment of Materials Science and Engineering, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA
First published on 2nd February 2016
Abstract
We investigate the polymer packing around nanoparticles and polymer/nanoparticle topological constraints (entanglements) in nanocomposites containing spherical nanoparticles in comparison to pure polymer melts using molecular dynamics (MD) simulations. The polymer–nanoparticle attraction leads to good dispersion of nanoparticles. We observe an increase in the number of topological constraints (decrease of total entanglement length Ne with nanoparticle loading in the polymer matrix) in nanocomposites due to nanoparticles, as evidenced by larger contour lengths of the primitive paths. An increase of the nanoparticle radius reduces the polymer–particle entanglements. These studies demonstrate that the interaction between polymers and nanoparticles does not affect the total entanglement length because in nanocomposites with small nanoparticles, the polymer–nanoparticles topological constraints dominate.
1 Introduction
The dynamics of long polymers is controlled by entanglements, which are topological constraints imposed by the other chains. These can dramatically change the polymer viscosity, dynamics, mechanical and tribological properties. In this paper we explore how spherical nanoparticles affect rheology by studying the entanglements in polymer–nanoparticle composites in the cases when the polymer radius of gyration (Rg) is larger than1–4 or of the order of the nanoparticle diameter (D).5–9The quality of nanoparticle dispersion10,11 can play an important role on the polymer structure thus on polymer entanglements. In a well dispersed polystyrene (PS) chains/(PS) nanoparticles nanocomposite,12 neutron scattering showed polymer chain expansion for polymer chains with radius of gyration larger than the nanoparticle radius (R), similar to the study of poly(dimethylsiloxane)/polysilicate nanocomposites.13 This has also been observed recently by simulations14,15 and a thermodynamic model16 but it is contrary to other recent studies of PS/silica10,11,17 nanocomposites where polymers are unperturbed, and in poly(ethylene-propylene)(PEP)/silica nanocomposites5 where the polymer chains are contracted at very high nanoparticle loading; however, in some of the previous studies10,17 good nanoparticle dispersion has not been achieved and in some others5,13 transmission electron microscopy (TEM) data were not reported, so the extent of dispersion is unknown.
Spherical nanoparticles can affect the primitive path and entanglement network of long polymers.18 An increase of the entanglement polymer density is the origin of mechanical reinforcement in nanocomposites.19–23 In particular it was shown using a slip-link model,24 that in nanocomposites with “bare” fillers, a relatively small level of reinforcement was evidenced,23 which is not verified in PS/silica and poly(methyl-methacrylate)/silica nanocomposites.25 In addition, in ref. 23 was shown that the viscosity of the nanocomposite, η, seems to be independent of the state of dispersion and can be predicted by the classical Einstein law: η = η0(1 + 2.5)ϕ (where η0 is the viscosity of the pure polymer melt, and ϕ is the nanoparticle volume fraction). However, the reinforcement is considerably higher when nanocomposites contain nanoparticles with grafted chains.23 Such an observation was also reported recently by molecular dynamics simulations.26 In addition, other parameters may also play a role on mechanical reinforcement such as size and shape of fillers, polymer matrix, interaction between fillers and matrix, and computer simulations20,21,27–31 have been used extensively to answer that fundamental problem.
The geometry of the nanoparticle (such as buckyball, graphene, nanodiamond32,33 or nanorod34–36) can also affect the polymer/nanoparticle entanglement network. However in most of the entanglement network studies, a dilute nanoparticle regime32–34,36–38 has been investigated, in which the polymer entanglement network, excluding the nanoparticles, remains unaffected. Only the MD study of nanoparticles R = 5 (where Rg ≈ D)39 and Monte Carlo (MC) study by Termonia,40,41 have been performed at nanoparticle loadings above percolation. It is worthy to note that the MC study40,41 is based on a body-centered-cubic (bcc) lattice in which the nanoparticles are fixed, and the polymer free volume remains constant irrespective of the nanoparticle size, which is not the real case in an experiment.5,42,43
In this article, we investigate the polymer packing (free volume) in nanocomposites which contain spherical nanoparticles as fillers. We calculate the number of monomers between entanglements, entanglements per chain44 and primitive path (the shortest path connecting the two ends of the polymer chain subject to the topological constraints)45 in both polymer melts and nanocomposites of oligomers and weakly entangled polymers by using topological algorithms44,46–48 and applying different entanglements estimators.47 The rest of this paper is organized as follows. In Section 2, the theoretical background is given for the entanglement analysis that is implemented in polymer melts and polymer nanocomposites. In Section 3, we discuss first the primitive path and entanglements of the polymer model used in this study. In polymer nanocomposites, we investigate the free volume and entanglements as a function of polymer molecular weight, volume fraction of fillers, interaction of polymers with fillers and nanoparticle radius in comparison to theoretical relations. Finally, in Section 4, conclusions are presented.
2 Estimators for entanglement length Ne
In polymer melts of sufficiently long flexible chain molecules, neighboring chains strongly interpenetrate and entangle with each other.49 Thus, the motion of polymers whose degree of polymerization is greater than the “entanglement length” Ne is confined to a tube-like region.The Ne is determined by the estimator of Everaers et al.45 (which we denote as classical S-coil), evaluated using the geometrical Z1 algorithm.44,46–48 This Ne estimator is determined by statistical properties of the primitive path as a whole coil and evaluated for a given number of monomers N in the polymer chain as follows:
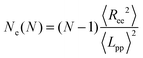 | (1) |
Another estimator for the entanglement length can be used by measuring the number of interior “kinks”44,46 which is considered to be proportional to the number of entanglements. The estimator on the number of “kinks”, 〈Z〉, is denoted here as classical S-kink is given by:44
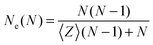 | (2) |
In addition, there are modified estimators that provide an upper bound for Ne, such as the modified S-coil,47 but they tend to overestimate Ne for weakly entangled chains:
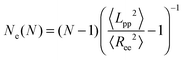 | (3) |
In order to eliminate the systematic errors that appear in the previous estimators47 and to obtain an accurate N-independent value, we use an ideal Ne estimator (M-coil),47 which requires simulation of multiple systems of different chain lengths, using coil properties:
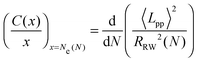 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ for N = 200, where τRouse(Ne) = 5000τ is obtained for semiflexible polymers from Fig. 9 in ref. 52).
000τ for N = 200, where τRouse(Ne) = 5000τ is obtained for semiflexible polymers from Fig. 9 in ref. 52).
3 Results and discussion
3.1 Polymer melt
The chain and primitive path dimensions as calculated from the Z1 algorithm44,46–48 for the polymer melts, of the semiflexible model used in this study, are presented in Table 1.| N p | N | L | R ee 2 | L pp | 〈Z〉 |
|---|---|---|---|---|---|
| 6000 | 10 | 41.328 | 15.2 | 3.75 | 0.02 |
| 3000 | 20 | 41.328 | 34.24 | 5.93 | 0.25 |
| 1250 | 40 | 38.891 | 69.29 | 9.82 | 0.94 |
| 1200 | 50 | 41.328 | 93.25 | 11.65 | 1.27 |
| 600 | 80 | 38.365 | 152.9 | 17.7 | 2.23 |
| 6000 | 100 | 41.328 | 190.98 | 20.58 | 2.78 |
| 300 | 160 | 38.365 | 313.4 | 32.05 | 3.51 |
| 118 | 200 | 30.454 | 389 | 37.59 | 5.4 ± 0.3 |
We depict the behavior of the M-coil estimator (eqn (4)) for the semiflexible Kremer–Grest (KG) polymer model studied, in Fig. 1, in comparison with results47 of the fully flexible KG model.53 From Fig. 1, it can be extracted that for the polymer model used in this study, Ne ≈ 59.7, while the value obtained from the S-coil estimator (eqn (1)) is 54.9. Other methodologies than the primitive path analysis, such as mean square displacement measurements (MSD),51,54 can predict a much different Ne value.51,54 The MSD methodology assumes validity of the reptation model and assumptions made to come up with the numerical prefactors. By adding an intrinsic bending potential52 the Kuhn length,49lk, increases (for the polymer model used: lk = 〈Ree2〉/Lc = 2.02, where Lc is the contour length of the polymer chain) and the packing length p45 (the characteristic length at which polymers start to interpenetrate) decreases, thus the Ne value unavoidly decreases for a semiflexible model55 in comparison to the fully flexible Kremer–Grest model.53 The glass transition of a polymer model which contains a bending potential (but not a torsional potential) is Tg = 0.4.52
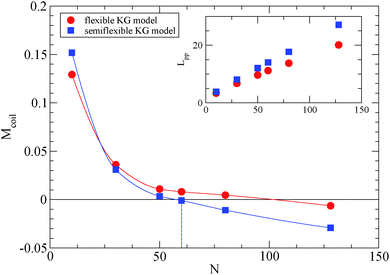 | ||
| Fig. 1 Simulations yield Ne for the semiflexible polymer model used in this study estimated from the M-coil estimator (eqn (4)). Solid lines interpolating between data points have been added to guide the eye. For comparison, MD simulations of fully flexible Kremer–Grest model (circles)53 are included. Inset: Dependence of Lpp for different polymers in the frozen particle limit. | ||
3.2 Nanocomposites
For nanocomposites, we consider systems of spherical nanoparticles in a dense polymer melt. In the nanocomposite systems studied, a total number of Nt = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 monomers were used in a cubic cell with nanoparticles of radius R = 1 or 2 (in nanocomposites with nanoparticles R = 4 and polymer matrices N ≤ 160, Nt = 9440 monomers were used, whereas for R = 4 and polymer matrices N = 200 the total number of monomers was Nt = 23
600 monomers were used in a cubic cell with nanoparticles of radius R = 1 or 2 (in nanocomposites with nanoparticles R = 4 and polymer matrices N ≤ 160, Nt = 9440 monomers were used, whereas for R = 4 and polymer matrices N = 200 the total number of monomers was Nt = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600). We define the nanoparticle (filler) volume fraction ϕ in our simulations as
600). We define the nanoparticle (filler) volume fraction ϕ in our simulations as 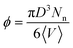 , where D is the nanoparticle diameter and 〈V〉 is the total average volume of the nanocomposite simulation box during the NPT simulation. The mass of nanoparticle is m = 0.85πD3/6. Details of the nanocomposite systems studied (equilibration, length of the simulations) are given in ref. 14 and in Table 2.
, where D is the nanoparticle diameter and 〈V〉 is the total average volume of the nanocomposite simulation box during the NPT simulation. The mass of nanoparticle is m = 0.85πD3/6. Details of the nanocomposite systems studied (equilibration, length of the simulations) are given in ref. 14 and in Table 2.
| ϕ (%) | L(σm) | N n | ||
|---|---|---|---|---|
| R = 1 | R = 2 | R = 4 | ||
| 5.5 | 31.157 | 400 | — | — |
| 10.3 | 31.863 | 800 | 100 | 5 |
| 14.5 | 32.569 | 1200 | — | — |
| 18.2 | 33.282 | 1600 | 200 | 10 |
| 24.2 | 34.653 | 2400 | 300 | 15 |
| 36 | 38.53 | 4906 | — | — |
In the next sections we investigate the effect of nanoparticle volume fraction, polymer–nanoparticle interaction and nanoparticle radius on the entanglement length Ne and primitive path. In the nanocomposite systems studied we consider the case of the primitive path analysis for both the frozen particle limit, where nanoparticles are held fixed in space during the primitive path analysis, and the phantom particle limit. In the phantom particle limit nanoparticles are unable to restrict polymer motion on the time scales relevant to reptation dynamics. We approximate this limit, by removing the nanoparticles from the simulated system prior to the primitive path analysis. In the frozen particle limit, the Ne contains two types of entanglements: polymer–polymer and polymer–nanoparticle entanglements, whereas in the phantom limit, it contains only polymer–polymer entanglements.
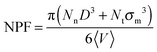 | (5) |
As can be seen in Fig. 2, the net packing fraction can increase (free volume decreases) as nanoparticle loading increases. This effect becomes stronger by dispersing large nanoparticles as also reported in ref. 57. While in ref. 57 only the dilute nanoparticle loading has been explored, we show the net packing fraction for a wider nanoparticle concentration range. The polymer nanoparticle interaction alters the free volume dramatically in the case of small nanoparticles R = 1. Since the smaller nanoparticles have a high interfacial area which increases with the nanoparticle loading, it is shown that the interfacial area is a factor that controls the packing fraction of such nanocomposite. However in nanocomposites containing larger attractive nanoparticles such as of size R = 4, the interfacial area diminishes and does not contribute to the net packing fraction. The polymer matrix has a slight effect on NPF calculations (shown in Fig. 2), an unentangled polymer matrix can reduce slightly the net packing fraction of the nanocomposites for all nanoparticle loadings. By dispersing attractive nanoparticles in the polymer matrix the polymer density around the nanoparticles increases.14 By tuning the polymer–nanoparticle interaction εmp, not only the interface but also the dispersion and aggregation behavior (which have been explored by molecular dynamics simulations14,21,58,59) of the nanoparticles in nanocomposites is altered. It was shown that attractive nanoparticles of radii R = 1–4 can be dispersed in an unentangled or entangled polymer matrix (Rg/R ≈ 0.4–8)14 in agreement to previous simulation studies.21 However, for repulsive polymer nanoparticle interaction, poor dispersion is observed for Rg/R ≈ 0.4–4 (in our case radii R = 2 to R = 4),14 which has also been observed experimentally for systems with weak interactions such as polystyrene–silica nanocomposite10,17 and possibly for a repulsive nanoparticle nanocomposite such as PEP–silica.5
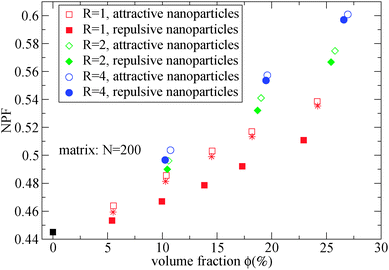 | ||
| Fig. 2 Net packing fraction for polymers of N = 200, calculated using eqn (5), for different nanoparticle loading and radius for repulsive (filled symbols) and attractive (open symbols) nanoparticles. (i) Polymer melt (black square), (ii) R = 1 (red squares), (iii) R = 2 (green diamonds), (iv) R = 4 (blue circles). The star symbols denote the NPF for nanocomposites containing R = 1 attractive nanoparticles in unentangled (N = 10) polymer matrix. | ||
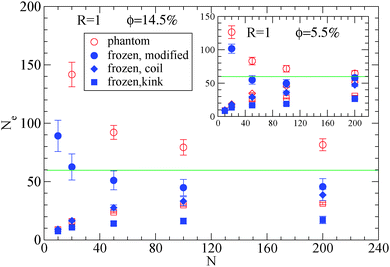 | ||
| Fig. 3 Dependence of Ne using eqn (1), (2) and (3), in the frozen (filled symbols) and phantom (open symbols) particle limits of nanocomposites with attractive small nanoparticles of R = 1, for nanoparticle loading ϕ = 14.5%: (i) modified S-coil estimator: eqn (3) (circles), (ii) classical S-coil estimator: eqn (1) (diamonds), (iii) classical S-kink estimator: eqn (2) (squares). Inset: Estimators for nanoparticle loading ϕ = 5.5%. The green line denotes the Ne for pure polymer melts as extracted by eqn (4). | ||
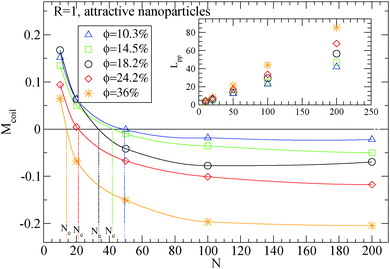 | ||
| Fig. 4 Dependence of Ne using eqn (4) in the frozen particle limit in nanocomposites with attractive small nanoparticles of R = 1 for different nanoparticle loading: (i) 10.3% (triangles), (ii) 14.5% (squares), (iii) 18.2% (circles), (iv) 24.2% (diamonds), (ii) 36% (star symbols). Inset: Dependence of Lpp for different polymers in the frozen particle limit. The vertical lines show the Ne extracted values at each nanoparticle loading. | ||
Moreover, we depict in Table 3, the Ne values (and number of “kinks” 〈Z〉) in the frozen particle limit as calculated by the S-coil, S-kink and S-modified estimators for long polymers N = 200, in nanocomposites at different nanoparticle loading, for both repulsive (Re) and attractive (A) nanoparticles. It can be seen that outside the error margin there is no difference in these Ne (and 〈Z〉) values. The Ne values estimated from M-coil agree with those estimated from S-coil for long polymers (N = 200), within the error margin. Similarly, for nanocomposites consisted of a matrix of polymers N = 100, the type of nanoparticles do not alter the Ne in the frozen particle limit (results not shown). Thus in the case where small nanoparticles are dispersed in a polymer matrix, the polymer–nanoparticle interaction does not play any role on the primitive path. The topological constraints created by nanoparticles seem to dominate the entanglement network even if the polymer dimensions can be altered14 by the polymer nanoparticle interaction. We also report in Table 3 the number of kinks 〈Z〉 in the phantom limit. We can see that in the phantom limit, 〈Z〉 decreases with nanoparticle loading (whereas it increases in the frozen limit due to polymer nanoparticle entanglements). This shows that nanoparticle loading reduces the polymer–polymer entanglements for nanocomposites containing nanoparticles of radius R = 1.
| ϕ (%) | Type | N e(S-coil) | N e(S-kink) | N e(m.S-coil) | 〈Z〉 | 〈Z〉(ph.) |
|---|---|---|---|---|---|---|
| 22.9 | Re | 18.2 ± 2.1 | 8.1 ± 0.8 | 19.4 ± 2.4 | 23.8 ± 1.9 | 3.7 ± 0.1 |
| 24.2 | A | 23.2 ± 1.9 | 7.6 ± 0.7 | 25.6 ± 2.5 | 25.6 ± 1.7 | 4.3 ± 0.1 |
| 17.3 | Re | 32.8 ± 6.5 | 15.3 ± 3.9 | 37.2 ± 8.5 | 12.9 ± 3.5 | 4.7 ± 0.2 |
| 18.2 | A | 31.8 ± 5.4 | 11.1 ± 2.5 | 36.5 ± 7.3 | 17.7 ± 3.5 | 4.7 ± 0.2 |
| 13.8 | Re | 44.8 ± 4.9 | 21.2 ± 3.4 | 54.6 ± 7.4 | 8.7 ± 1.8 | 4.5 ± 0.2 |
| 14.5 | A | 38.6 ± 4.9 | 17.1 ± 3.1 | 45.6 ± 7 | 11.1 ± 2.3 | 4.8 ± 0.2 |
| 10 | Re | 47.2 ± 2.2 | 24.9 ± 1.8 | 57.8 ± 3.4 | 7.1 ± 0.7 | 4.9 ± 0.2 |
| 10.3 | A | 47.4 ± 2.3 | 22.7 ± 1.7 | 58.3 ± 3.5 | 7.9 ± 0.7 | 5.1 ± 0.1 |
| 5.4 | Re | 53.9 ± 3.5 | 28.8 ± 1.1 | 68.8 ± 6 | 5.9 ± 0.3 | 5 ± 0.2 |
| 5.5 | A | 47.2 ± 2.3 | 26.6 ± 0.9 | 58.1 ± 3.7 | 6.5 ± 0.3 | 5.5 ± 0.2 |
The concept of entanglement length is useful because it relates changes in structure to rheological properties.45,55,60 In polymer melts and semidilute solutions, a temperature and concentration dependent material constant, the plateau shear modulus G0N, which is of the order of 106 Pa, or five orders of magnitude smaller than the shear modulus of ordinary solids, is related to rheological entanglement length, Nrheole, by eqn (6):45,61
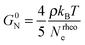 | (6) |
| f(ϕ) = 1 + [η]βϕ + a2(βϕ)2 + a3(βϕ)3 + ⋯ | (7) |
The addition of small nanoparticles in the polymer matrix decreases the Ne value, as shown in Fig. 4, thus the plateau shear modulus G0N increases, according to eqn (6), since it is approximately inverse proportional to Ne. In Fig. 5 we depict a comparison between the plateau modulus experimental measurements,56 theoretical predictions56,69 and simulation data for the Ne(ϕ = 0)/Ne(ϕ) ratio, at different nanoparticle loadings. The ratio of Ne(ϕ)/Ne(ϕ = 0), as calculated by our simulations, decreases with the nanoparticle volume fraction. At a volume fraction, ϕ = 24.2%, there is approximately 60% decrease in Ne mainly due to the polymer–nanoparticle entanglements. Instead in a polymer nanorod composite such a decrease in Ne appears at a much smaller nanorod volume fraction, ϕnanorod ≈ 11%.34 It seems from Fig. 5 that the Ne decrease in nanocomposites with small nanoparticles follows quantitatively the theoretical trends of Guth–Gold relation (eqn (7)), however eqn (7) is not necessarily proportional to the ratio of Ne values. The Einstein relation66 is invalid for a such small nanoparticle composite, in contrast to nanocomposites with bare spherical nanoparticles studied through the slip-link model.23 Small nanoparticles, such as R = 1, can reinforce polymers effectively. All three estimators in Fig. 5 show that the mechanical reinforcement effect in nanocomposites can be induced by the change of primitive path network due to the additional topological constraints created by small nanoparticles.
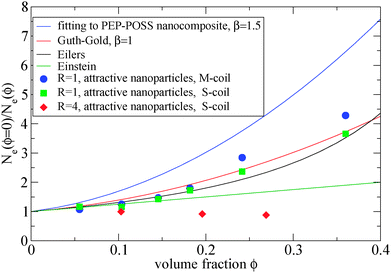 | ||
| Fig. 5 Dependence of Ne(ϕ = 0)/Ne(ϕ) ratio in the frozen particle limit at different nanoparticle loading: (i) fitting of eqn (7) on PEP-POSS nanocomposite56 (blue line), (ii) Guth–Gold relation (red line), (iii) Eilers relation (black line), (iv) Einstein relation (green line), (v) attractive nanoparticles: R = 1, M-coil estimator: eqn (4) (circles) (vi) attractive nanoparticles: R = 1 S-coil estimator: eqn (1) (squares) (vii) attractive nanoparticles: R = 4 S-coil estimator: eqn (1) (diamonds). The simulation data are shown for a matrix: N = 200. | ||
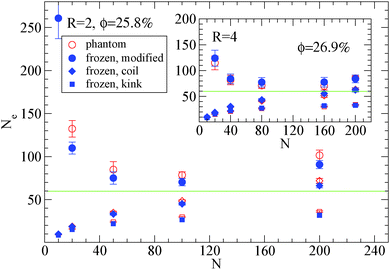 | ||
| Fig. 6 Dependence of Ne using eqn (1), (2) and (3), in the frozen (filled blue symbols) and phantom (open symbols) particle limits of nanocomposites with attractive nanoparticles of R = 2 for nanoparticle loading ϕ = 25.8%: (i) modified S-coil estimator: eqn (3) (circles), (ii) classical S-coil estimator: eqn (1) (diamonds), (iii) classical S-kink estimator: eqn (2) (squares). Inset: Estimators of nanocomposites at ϕ = 26.9% with nanoparticles of R = 4. The green line denotes the Ne for pure polymer melts as extracted by eqn (4). | ||
Also we can observe that in nanocomposites with nanoparticles of R = 2 in a polymer matrix N = 200 (see Fig. 6) the Ne in the phantom limit is enhanced with respect to its polymer melt value. In order to investigate further the polymer path network, we calculated the polymer tube diameter37,72 and depict it in Fig. 7:
| 〈αpp〉 = 〈Ree2〉/Lpp(ph) | (8) |
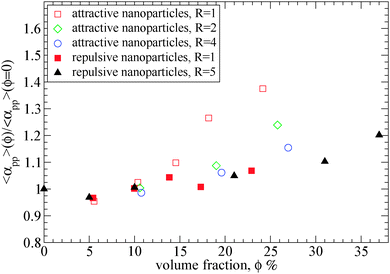 | ||
| Fig. 7 Tube diameter αpp of polymers (N = 200) at different nanoparticle loading normalized with its value in bulk, obtained from primitive path analysis at the phantom limit for different nanoparticle volume fractions: (i) attractive nanoparticles (R = 1) (open squares), (ii) attractive nanoparticles (R = 2) (diamonds), (iii) attractive nanoparticles (R = 4) (circles) (iv) repulsive nanoparticles (R = 1) (filled squares), (v) repulsive nanoparticles (R = 5) (filled triangles).39 The tube diameter of polymers (N = 200) in bulk is: αpp = 10.35. | ||
As can be seen in Fig. 7, for attractive small nanoparticles, the tube diameter increases with the nanoparticle loading, whereas for repulsive nanoparticles it remains constant in agreement to the data by Li et al.39 This increase means that such small nanoparticles (R = 1) do alter the polymer network, and the polymers disentangle with nanoparticle loading. This implies that in the case of attractive nanoparticles, the Ne in the phantom limit is increased, as observed in Fig. 3. While the total Ne (in the frozen limit) of the nanocomposite decreases with the nanoparticle loading (see Fig. 4), the polymer–polymer entanglements convert to polymer–nanoparticle entanglements approximately for nanoparticle loading ϕ ≥ 15%. This disentanglement effect does also appear in thin polymer films,73 under cylindrical confinement,74,75 on a bare flat surface76 and on the vicinity of large repulsive spherical nanoparticles at a high nanoparticle loading.39 Furthermore, the polymer chain dynamics can also be affected by the nanoparticle volume fraction. Since by increasing the nanoparticles loading the tube diameter increases, that can enhance the polymer chain's diffusivity. However, direct studies of diffusion remain quite difficult to study the slow reptational dynamics of nanocomposites using molecular dynamics simulations.
4 Conclusions
The polymer density, polymer/polymer and polymer/nanoparticle topological constraints (entanglements) of polymers in melts and nanocomposites containing spherical nanoparticles were investigated by means of molecular dynamics simulations. We applied different Ne(N) estimators for the calculation of the number of entanglements in our systems, and extracted the N-independent entanglement length Ne. We observe that the total Ne decreases even with low volume fraction of small nanoparticles, and significantly for ϕ ≥ 25%. This decrease of Ne, in the nanocomposite, originates from the polymer/nanoparticle entanglements, because the contour length of the primitive path, Lpp, increases with the addition of nanoparticles. In order for polymer nanoparticles entanglements to be formed, the polymers need to be substantially larger than the nanoparticles in order to wrap around them, and in that case the nanoparticles act as topological constraints. Interaction between polymers and nanoparticles does not affect the total entanglement length when there is good nanoparticle dispersion. For the case of attractive small nanoparticles (such as R = 1) the polymer–polymer entanglements decrease (increase of tube diameter) due to the expansion of the polymer chains for ϕ ≥ 15%. This effect on the polymer network is enhanced by the nanoparticle loading. Instead for the case of repulsive nanoparticles the tube diameter remains the same up to ≈ 24% nanoparticle loading in agreement with previous studies.39Acknowledgements
We thank Prof. M. Kröger for providing us the Z1 algorithm modified for nanocomposites and useful discussions. This research was funded by the EPSRC/NSF Materials Network program EP/5065373/1 (EPSRC: NC, AK) and DMR-1210379 (NSF: KIW, RJC).References
- M. Mu, N. Clarke, R. J. Composto and K. I. Winey, Macromolecules, 2009, 42, 7091 CrossRef CAS.
- A. Karatrantos and N. Clarke, Soft Matter, 2011, 7, 7334 RSC.
- W. S. Tung, V. Bird, R. J. Composto, N. Clarke and K. I. Winey, Macromolecules, 2013, 46, 5345 CrossRef CAS.
- A. Karatrantos, R. J. Composto, K. I. Winey and N. Clarke, Macromolecules, 2011, 44, 9830 CrossRef CAS.
- K. Nusser, S. Neueder, G. J. Schneider, M. Meyer, W. Pyckhout-Hintzen, L. Willner, A. Radulescu and D. Richter, Macromolecules, 2010, 43, 9837 CrossRef CAS.
- G. J. Schneider, K. Nusser, L. Willner, P. Falus and D. Richter, Macromolecules, 2011, 44, 5857 CrossRef CAS.
- S. Gam, J. S. Meth, S. G. Zane, C. Chi, B. A. Wood, M. E. Seitz, K. I. Winey, N. Clarke and R. J. Composto, Macromolecules, 2011, 44, 3494 CrossRef CAS.
- S. Gam, J. S. Meth, S. G. Zane, C. Chi, B. A. Wood, K. I. Winey, N. Clarke and R. J. Composto, Soft Matter, 2012, 8, 6512 RSC.
- C. C. Lin, S. Gam, J. S. Meth, N. Clarke and K. I. Winey, Macromolecules, 2013, 46, 4502 CrossRef CAS.
- S. Sen, Y. Xie, S. K. Kumar, H. Yang, A. Bansal, D. L. Ho, L. Hall, J. B. Hooper and K. S. Schweizer, Phys. Rev. Lett., 2007, 98, 128302 CrossRef PubMed.
- M. K. Crawford, R. J. Smalley, G. Cohen, B. Hogan, B. Wood, S. K. Kumar, Y. B. Melnichenko, L. He, W. Guise and B. Hammouda, Phys. Rev. Lett., 2013, 110, 196001 CrossRef CAS PubMed.
- A. Tuteja, P. M. Duxbury and M. E. Mackay, Phys. Rev. Lett., 2008, 100, 077801 CrossRef PubMed.
- A. I. Nakatani, W. Chen, R. G. Schmidt, G. V. Gordon and C. C. Han, Polymer, 2001, 42, 3713 CrossRef CAS.
- A. Karatrantos, N. Clarke, R. J. Composto and K. I. Winey, Soft Matter, 2015, 11, 382 RSC.
- A. L. Frischknecht, E. S. McGarrity and M. E. Mackay, J. Chem. Phys., 2010, 132, 204901 CrossRef PubMed.
- P. S. Stephanou, J. Chem. Phys., 2015, 142, 064901 CrossRef PubMed.
- N. Jouault, F. Dalmas, S. Said, E. Di Cola, R. Schweins, J. Jestin and F. Boue, Macromolecules, 2010, 43, 9881 CrossRef CAS.
- R. A. Riggleman, G. Toepperwein, G. J. Papakonstantopoulos, J.-L. Barrat and J. J. de Pablo, J. Chem. Phys., 2009, 130, 244903 CrossRef PubMed.
- Q. W. Yuan, A. Kloczkowski, J. E. Mark and M. A. Sharaf, J. Polym. Sci., Polym. Phys. Ed., 1996, 34, 1647 CrossRef CAS.
- D. Gersappe, Phys. Rev. Lett., 2002, 89, 058301 CrossRef PubMed.
- J. Liu, Y. Wu, J. Shen, Y. Gao, L. Zhang and D. Cao, Phys. Chem. Chem. Phys., 2011, 13, 13058 RSC.
- A. Kutvonen, G. Rossi and T. Ala-Nissila, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041803 CrossRef PubMed.
- E. Masnada, S. Merabia, M. Couty and J. L. Barrat, Soft Matter, 2013, 9, 10532 RSC.
- A. E. Likhtman, Macromolecules, 2005, 38, 6128 CrossRef CAS.
- N. Jouault, F. Dalmas, F. Boue and J. Jestin, Polymer, 2012, 53, 761 CrossRef CAS.
- G. D. Hattemer and G. Arya, Macromolecules, 2015, 48, 1240 CrossRef CAS.
- A. Karatrantos, N. Clarke and M. Kröger, Polym. Rev., 2015 DOI:10.1080/15583724.2015.1090450.
- A. Kutvonen, G. Rossi, S. R. Puisto, N. K. J. Rostedt and T. Ala-Nissila, J. Chem. Phys., 2012, 137, 214901 CrossRef PubMed.
- E. Jaber, H. Luo, W. Li and D. Gersappe, Soft Matter, 2011, 7, 3852 RSC.
- V. Padmanabhan, J. Chem. Phys., 2013, 139, 144904 CrossRef PubMed.
- A. A. Gavrilov, A. V. Chertovich, P. G. Khalatur and A. Khokhlov, Macromolecules, 2014, 47, 5400 CrossRef CAS.
- Y. Li, Polymer, 2011, 52, 2310 CrossRef CAS.
- Y. Li, M. Kröger and W. K. Liu, Macromolecules, 2012, 45, 2099 CrossRef CAS.
- A. Karatrantos, N. Clarke, R. J. Composto and K. I. Winey, Soft Matter, 2013, 9, 3877 RSC.
- A. Karatrantos, R. J. Composto, K. I. Winey and N. Clarke, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 40, 012027 CrossRef.
- G. N. Toepperwein, N. C. Karayiannis, R. A. Riggleman, M. Kröger and J. J. de Pablo, Macromolecules, 2011, 44, 1034 CrossRef CAS.
- L. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853 CrossRef CAS PubMed.
- A. Karatrantos, R. J. Composto, K. I. Winey, M. Kröger and N. Clarke, Macromolecules, 2012, 45, 7274 CrossRef CAS.
- Y. Li, M. Kröger and W. K. Liu, Phys. Rev. Lett., 2012, 109, 118001 CrossRef PubMed.
- Y. Termonia, Polymer, 2010, 51, 4448 CrossRef CAS.
- Y. Termonia, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 687 CrossRef CAS.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho and H.-C. Horn, Nat. Mater., 2003, 2, 762 CrossRef CAS PubMed.
- C. Ohrt, T. Koschine, K. Rätzke, F. Faupel, L. Willner and G. J. Schneider, Macromolecules, 2014, 55, 143 CAS.
- M. Kröger, Comput. Phys. Commun., 2005, 168, 209 CrossRef.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823 CrossRef CAS PubMed.
- S. Shanbhag and M. Kröger, Macromolecules, 2007, 40, 2897 CrossRef CAS.
- R. S. Hoy, K. Foteinopoulou and M. Kröger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031803 CrossRef PubMed.
- N. C. Karayiannis and M. Kröger, Int. J. Mol. Sci., 2009, 10, 5054 CrossRef CAS PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986 Search PubMed.
- P. J. Flory, Statistical Mechanics of Chain Molecules, Hanser, Munchen, 1989 Search PubMed.
- A. E. Likhtman, S. K. Sukumaran and J. Ramirez, Macromolecules, 2007, 40, 6748 CrossRef CAS.
- M. Bulacu and E. van der Giessen, J. Chem. Phys., 2005, 123, 114901 CrossRef PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057 CrossRef CAS.
- M. Putz, K. Kremer and G. S. Grest, Europhys. Lett., 2000, 49, 735 CrossRef CAS.
- N. Uchida, G. s. Grest and R. Everaers, J. Chem. Phys., 2008, 128, 044902 CrossRef PubMed.
- K. Nusser, G. I. Schneider, W. Pyckhout-Hintzen and D. Richter, Macromolecules, 2011, 44, 7820 CrossRef CAS.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2012, 109, 198301 CrossRef PubMed.
- D. Meng, S. K. Kumar, S. Cheng and G. S. Grest, Soft Matter, 2013, 9, 5417 RSC.
- T. K. Patra and J. K. Singh, J. Chem. Phys., 2013, 138, 144901 CrossRef PubMed.
- S. K. Sukumaran, G. S. Grest, K. Kremer and R. Everaers, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 917 CrossRef CAS.
- R. Everaers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 022801 CrossRef PubMed.
- K. Nusser, G. J. Schneider and D. Richter, Macromolecules, 2013, 46, 6263 CrossRef CAS.
- H. Eggers and P. Schuemmer, Rubber Chem. Technol., 1996, 69, 253 CrossRef CAS.
- G. Heinrich, M. Kluppel and T. A. Vilgis, Curr. Opin. Solid State Mater. Sci., 2002, 6, 195 CrossRef CAS.
- E. T. Kopesky, T. S. Haddad, G. H. McKinley and R. E. Cohen, Polymer, 2005, 46, 4743 CrossRef CAS.
- A. Einstein, Ann. Phys., 1906, 19, 289 CrossRef CAS.
- H. J. Smallwood, J. Appl. Phys., 1944, 15, 758 CrossRef CAS.
- E. Guth and O. Gold, Phys. Rev., 1938, 53, 322 CAS.
- V. H. Eilers, Kolloid-Z., 1941, 3, 313 CrossRef.
- A. Tuteja and M. E. Mackay, Nano Lett., 2007, 7, 1276 CrossRef CAS PubMed.
- R. Mangal, S. Srivastava and L. A. Archer, Nat. Commun., 2015, 6, 7198 CrossRef PubMed.
- F. Lahmar, C. Tzoumanekas, D. N. Theodorou and B. Rousseau, Macromolecules, 2009, 42, 7485 CrossRef CAS.
- H. Meyer, T. Kreer, A. Cavallo, J. P. Wittmer and J. Baschnagel, Eur. Phys. J.: Spec. Top., 2007, 141, 167 CrossRef.
- D. Sussman, W. S. Tung, K. Winey, K. S. Schweizer and R. A. Riggleman, Macromolecules, 2014, 47, 6462 CrossRef CAS.
- W. S. Tung, R. J. Composto, R. A. Riggleman and K. Winey, Macromolecules, 2015, 48, 2324 CrossRef CAS.
- M. Vladkov and J. L. Barrat, Macromolecules, 2007, 40, 3797 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02010g |
| This journal is © The Royal Society of Chemistry 2016 |
