A generalized Read–Shockley model and large scale simulations for the energy and structure of graphene grain boundaries†
Abstract
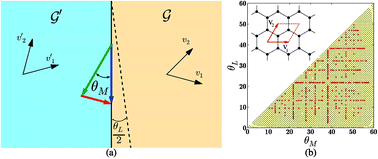
The grain boundary (GB) energy is a quantity of fundamental importance for understanding several key properties of graphene. Here we present a comprehensive theoretical and numerical study of the entire space of symmetric and asymmetric graphene GBs. We have simulated over 79 000 graphene GBs to explore the configuration space of GBs in graphene. We use a generalized Read–Shockley theory and the Frank–Bilby relation to develop analytical expressions for the GB energy as a function of the misorientation angle and the line angle, and elucidate the salient structural features of the low energy GB configurations.

 Please wait while we load your content...
Please wait while we load your content...